Experimental and Numerical Research on p-y Curve of Offshore Photovoltaic Pile Foundations on Sandy Soil Foundation
Abstract
1. Introduction
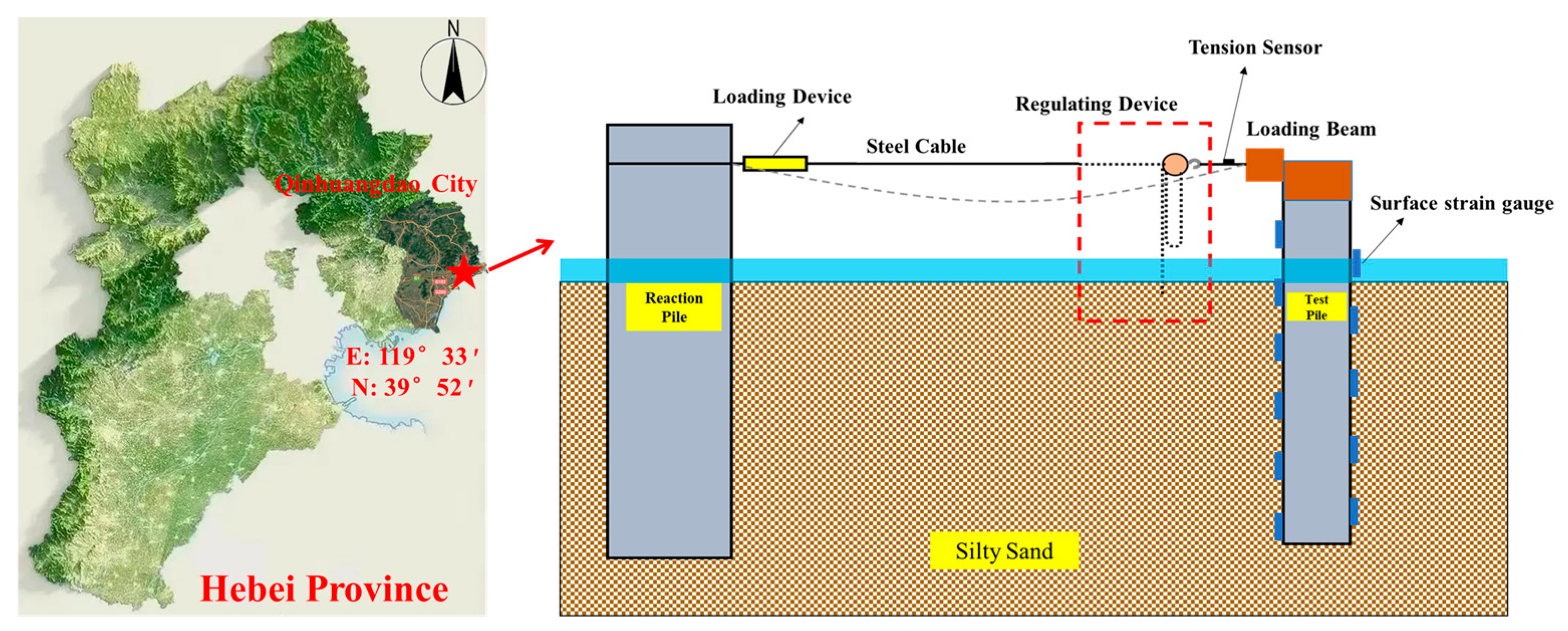
2. Field Test Methods
2.1. Experimental Setup
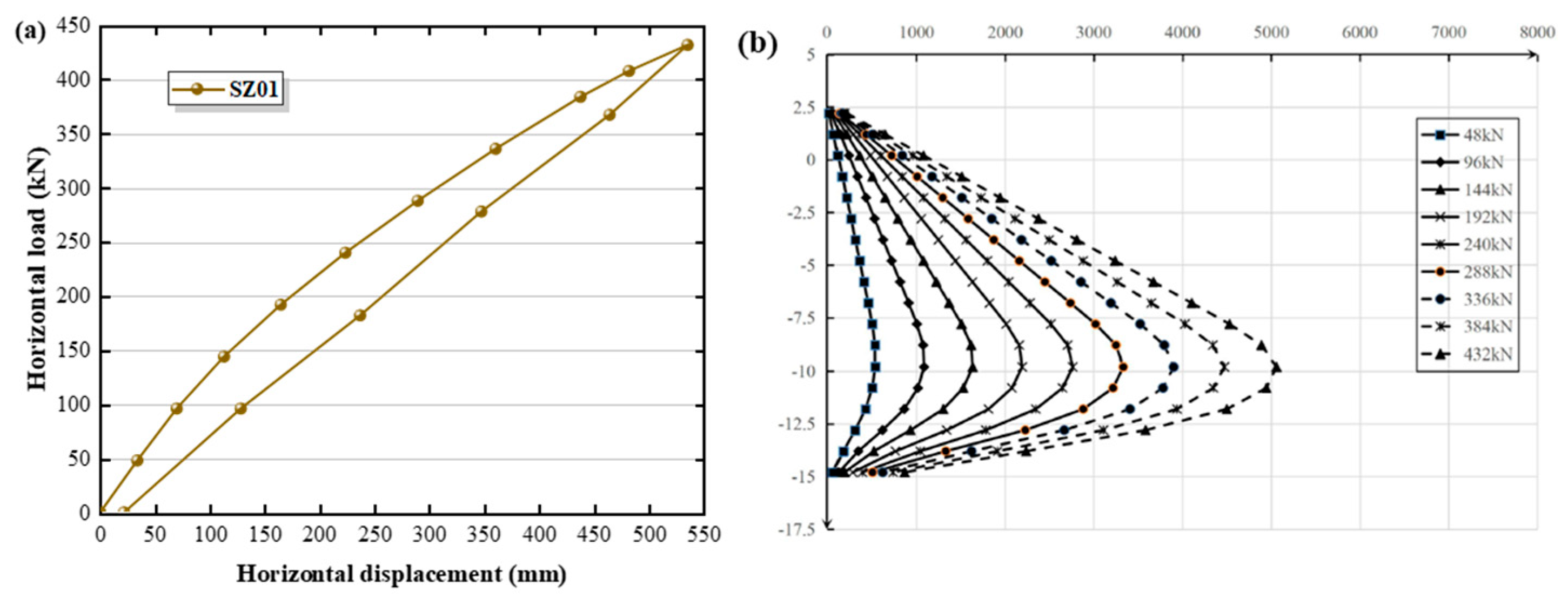
2.2. Analysis of the Field Test
3. Numerical Calculation
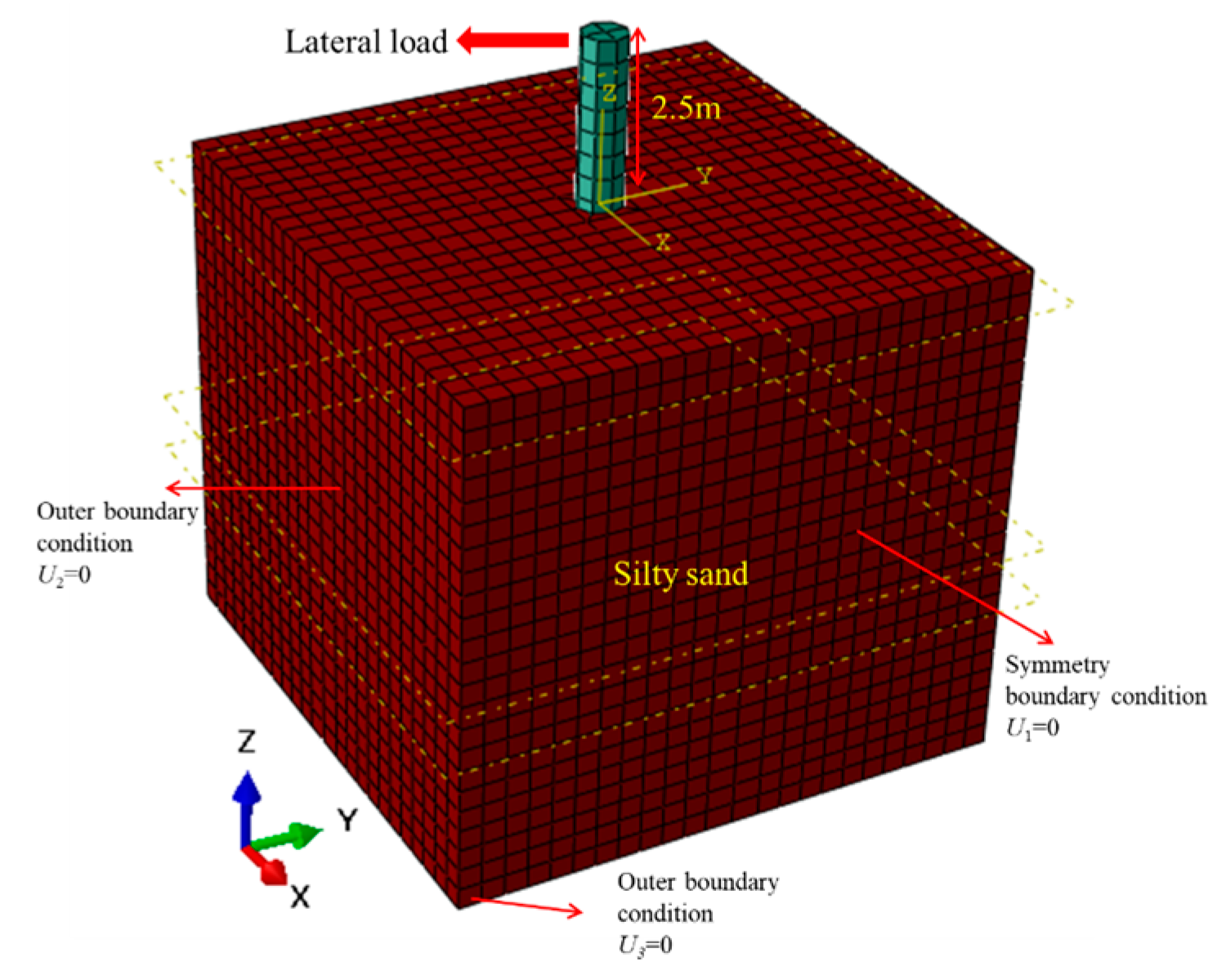
3.1. Finite Element Model Establishment
3.2. Verification of the Finite Element Model
4. Result and Discussion
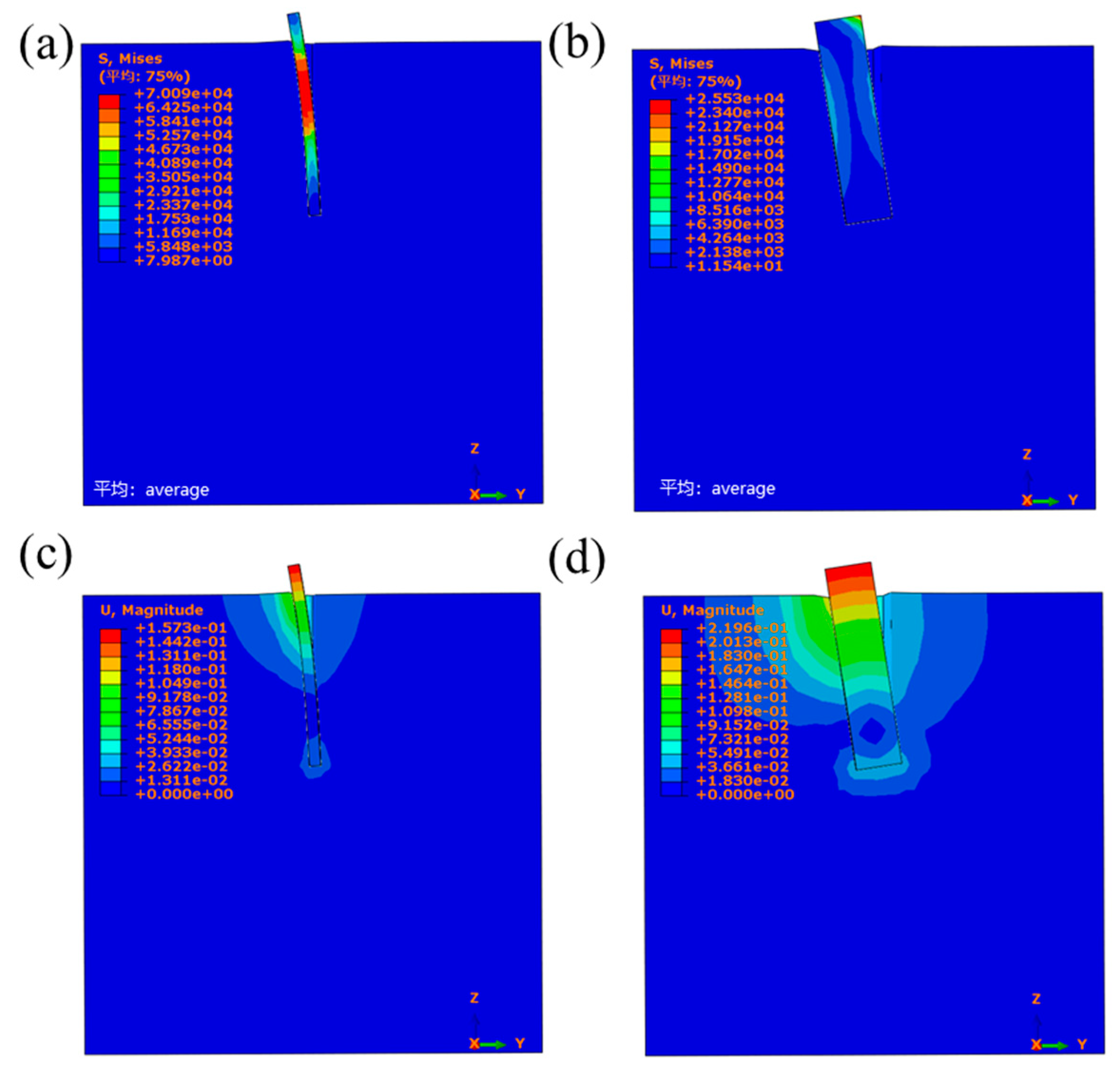
4.1. Analysis of Destruction Patterns
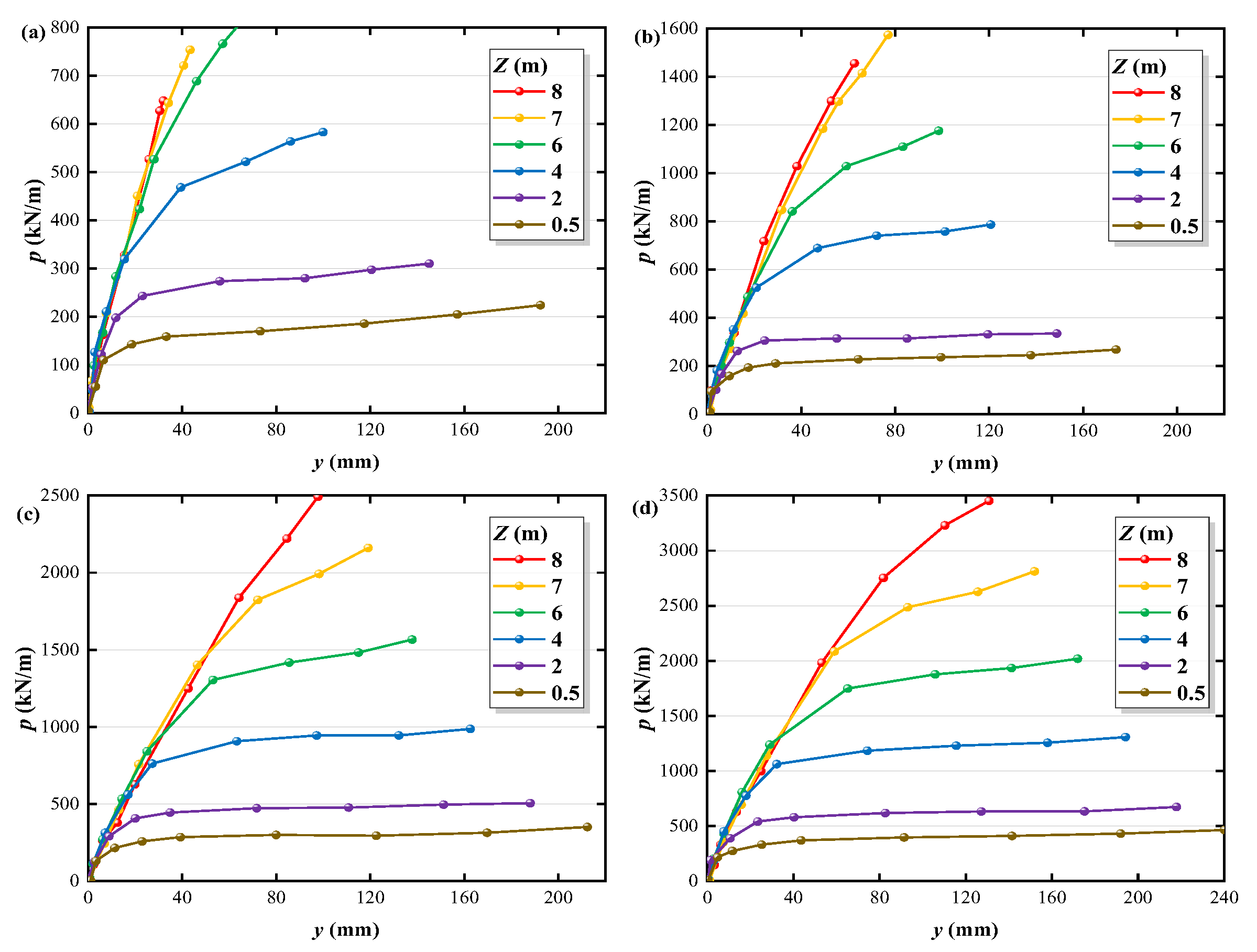
4.2. Analysis of p-y Curve Characteristics
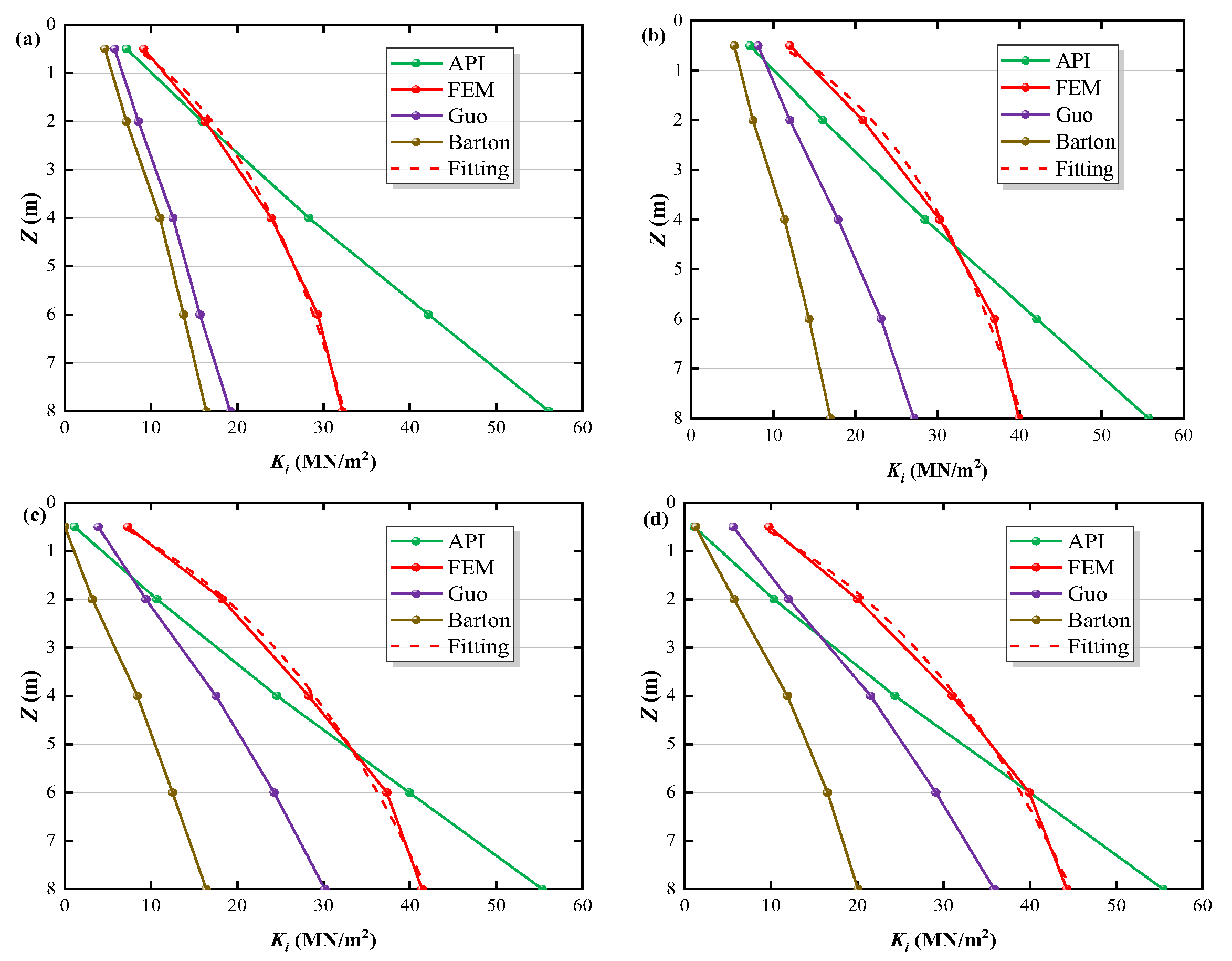
4.3. Initial Stiffness Analysis
4.4. Analysis of Soil’s Ultimate Resistance
4.5. Comparative Analysis of Norms
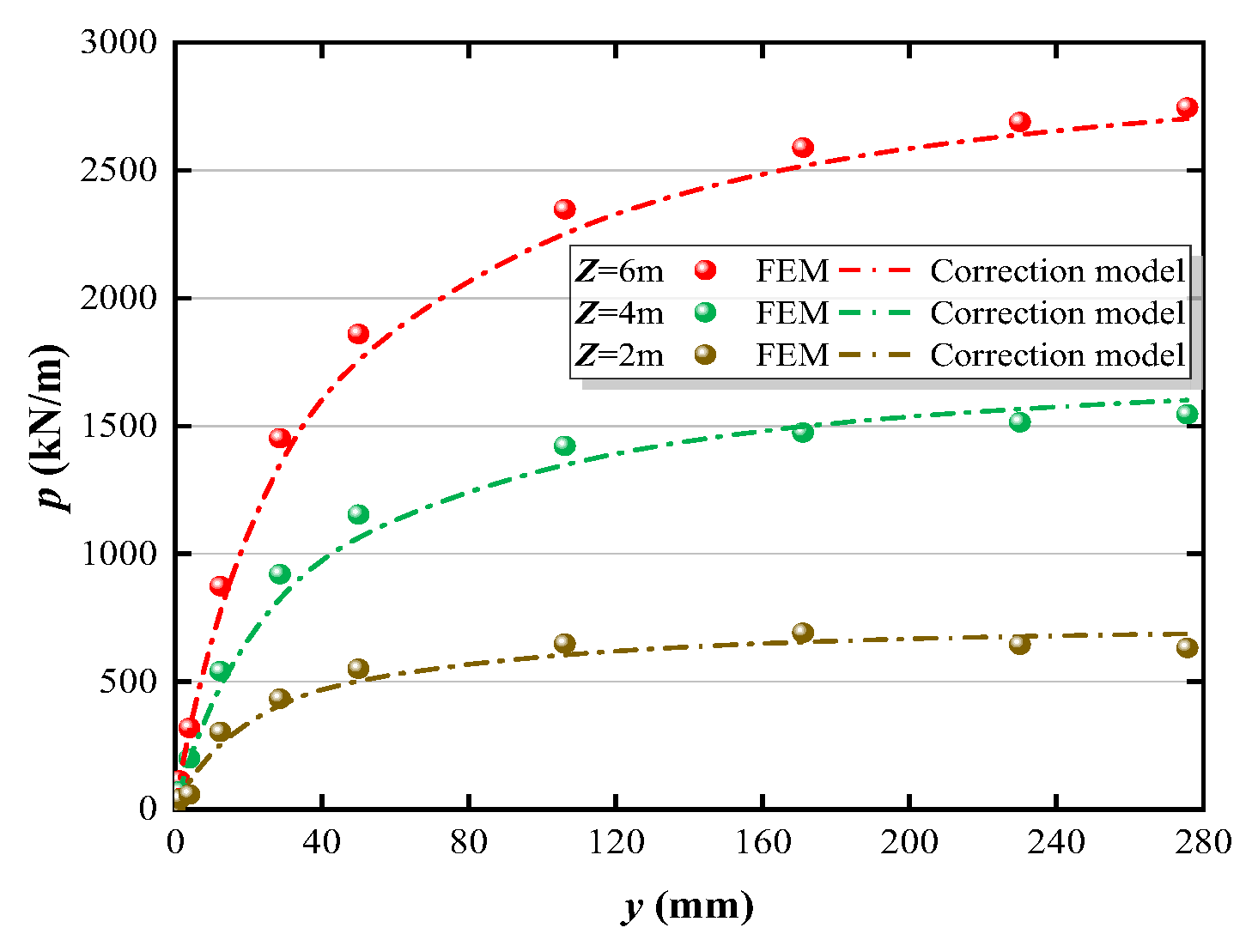
4.6. Correction of p-y Curve
4.7. Design and Construction
5. Conclusions
- (1)
- Under the action of horizontal ultimate load, the failure mode of the fixed offshore photovoltaic single-pile foundation in sandy soil foundation is mainly the wedge-shaped failure of the shallow soil around the pile. With the increase in pile diameter, the failure depth of the shallow soil increases, but the severe failure area is within 8 m below the mud surface.
- (2)
- In sandy soil foundation, the initial stiffness Ki and ultimate resistance pu of the offshore photovoltaic fixed single-pile foundation are in a power function model with pile diameter and distance from the mud surface. The fitting determination coefficient R2 is greater than 0.96, and the fitting relationship is good.
- (3)
- For sandy soil foundation, the p-y curve obtained by API specification and hyperbolic model has a large error, and both underestimate the bearing capacity of the soil. However, the corrected hyperbolic model proposed in this paper is in good agreement with the numerical model, and this method has certain guiding significance for the optimization design of offshore photovoltaic fixed single-pile foundation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ahmad, M.; Jiang, P.; Majeed, A.; Umar, M.; Khan, Z.; Muhammad, S. The dynamic impact of natural resources, technological innovations and economic growth on ecological footprint: An advanced panel data estimation. Resour. Policy 2020, 69, 101817. [Google Scholar] [CrossRef]
- Hu, J.K.; Teng, K.; Li, C.J.; Li, X.P.; Wang, J.; Lund, P.D. Review of recent water photovoltaics development. Oxf. Open Energy 2023, 2, oiad005. [Google Scholar] [CrossRef]
- Pérez, J.A.; Ponce-Torres, A.; Ríos, J.D.; Sánchez-González, E. Fatigue Behavior of H-Section Piles under Lateral Loads in Cohesive Soil. Buildings 2024, 14, 3228. [Google Scholar] [CrossRef]
- Wang, L.; Li, J.X.; Bai, W.Y.; Xie, X.Y.; Mao, X.; Ren, Z.F.; Liu, J.K. Study on the bearing capacity optimization and performance of photovoltaic support in desert sand and gravel area based on bionics. Sci. Rep. 2025, 15, 9638. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Li, R.Q.; Yang, S.C.; Liu, J.W.; Guo, Z.; Feng, L.Y.; Shang, W.C.; Zhu, L.; Du, B.K. Field load testing and numerical analysis of offshore photovoltaic steel pipe piles. Soil Dyn. Earthq. Eng. 2025, 188, 109034. [Google Scholar] [CrossRef]
- Liu, G.L.; Fu, S.J.; Zhao, X.F.; Jiang, W.; Li, D.; Fu, S.B. Frost jacking characteristics of steel pipe screw piles for photovoltaic support foundations in high-latitude and low-altitude regions. Soils Found. 2023, 63, 101277. [Google Scholar]
- Su, X.J.; Li, Z.H.; Wang, Q.; Li, J.X.; Xie, X.Y.; Mao, X.; Ren, Z.F.; Liu, J.K. Comparison and Optimization of Bearing Capacity of Three Kinds of Photovoltaic Support Piles in Desert Sand and Gravel Areas. Buildings 2024, 14, 2559. [Google Scholar] [CrossRef]
- Al-Atroush, M.E.; Aboelela, A.E.; Hemdan, E.E. Beyond p-y method: A review of artificial fi cial intelligence approaches for predicting lateral capacity of drilled shafts in clayey soils. J. Rock Mech. Geotech. Eng. 2024, 16, 3812–3840. [Google Scholar]
- Park, J.J.; Yang, K.H.; Hu, J.C.h. Analysis of p-y Curve of Drilled Shafts Socketed into Basalt at Jeju Island. Int. J. Offshore Polar Eng. 2017, 27, 374–382. [Google Scholar] [CrossRef]
- Kim, Y.; Jeong, S.; Won, J. Effect of Lateral Rigidity of Offshore Piles Using Proposed p-y Curves in Marine Clay. Mar. Georesources Geotechnol. 2009, 27, 53–77. [Google Scholar] [CrossRef]
- Wang, X.F.; Li, S.X.; Li, J.L. Experimental and numerical study on lateral response of pile-group for offshore wind turbines in sand. Mar. Georesources Geotechnol. 2023, 41, 524–543. [Google Scholar] [CrossRef]
- Yoo, M.T.; Choi, J.I.; Han, J.T.; Kim, M.M. Dynamic P-Y Curves for Dry Sand from Centrifuge Tests. J. Earthq. Eng. 2013, 17, 1082–1102. [Google Scholar] [CrossRef]
- Bouzid, D.A. Numerical Investigation of Large-Diameter Monopiles in Sands: Critical Review and Evaluation of Both API and Newly Proposed p-y Curves. Int. J. Geomech. 2018, 18, 04018141. [Google Scholar] [CrossRef]
- Hotak, A.H.; Zhao, Q.H.; Rasheedy, B.A. Review of soil liquefaction effect on the bridge response and comparative study of P-Y methods for soil liquefaction. Multiscale Multidiscip. Model. Exp. Des. 2025, 8, 95. [Google Scholar] [CrossRef]
- Khan, Z.; Ali, S.; Umar, M.; Kirikkaleli, D.; Jiao, Z.L. Consumption-based carbon emissions and International trade in G7 countries: The role of Environmental innovation and Renewable energy. Sci. Total Environ. 2020, 730, 138945. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.J.; Pu, L.J.; Zhai, C.M. A Review of Static and Dynamic p-y Curve Models for Pile Foundations. Buildings 2024, 14, 1507. [Google Scholar] [CrossRef]
- Dash, S.R.; Bhattacharya, S. Experimental p-y curves for liquefied soils from centrifuge tests. Earthq. Eng. Eng. Vib. 2021, 20, 863–876. [Google Scholar] [CrossRef]
- Wang, H.; Wang, L.Z.; Hong, Y.; He, B.; Zhu, R.H. Quantifying the influence of pile diameter on the load transfer curves of laterally loaded monopile in sand. Appl. Ocean. Res. 2020, 101, 102196. [Google Scholar] [CrossRef]
- Liu, P.; Jiang, C. A new p-y curve criterion for piles in proximity to undrained clay slopes. Comput. Geotech. 2023, 164, 105801. [Google Scholar] [CrossRef]
- Lim, H.; Jeong, S. Simplified p-y curves under dynamic loading in dry sand. Soil Dyn. Earthq. Eng. 2018, 113, 101–111. [Google Scholar] [CrossRef]
- Wang, M.Y.; Wang, M.; Cheng, X.L.; Lu, Q.; Lu, J.Q. A New p-y Curve for Laterally Loaded Large-Diameter Monopiles in Soft Clays. Sustainability 2022, 14, 15102. [Google Scholar] [CrossRef]
- JGJ 106-2014; Technical Code for Testing of Building Foundation Piles. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2014.
- Zhang, X.; Zhou, R.; Xu, C. Study on Corrected p-y Curve Model of Pile Foundation of Offshore Wind Turbines. Acta Energiae Solaris Sin. 2023, 44, 290–297. [Google Scholar]
- Zhang, X.-l.; Zhou, R.; Zhang, G.-L.; Han, Y. A corrected p-y curve model for large-diameter pile foundation of offshore wind turbine. Ocean. Eng. 2023, 273, 114012. [Google Scholar] [CrossRef]
- He, R.; Zhu, T.; Ma, B.; Guo, Z. Lateral static stiffness of offshore monopile socketed in soft rock. Mar. Struct. 2022, 86, 103302. [Google Scholar] [CrossRef]
- Institute, A.P. Recommended Practice for Planning, Designing and Constructing Fixed Offshore Platforms-Working Stress Design; American Petroleum Institute Publishing Services: Washington, DC, USA, 2000. [Google Scholar]
- Klinkvort, R.T.; Hededal, O. Effect of load eccentricity and stress level on monopile support for offshore wind turbines. Can. Geotech. J. 2014, 51, 966–974. [Google Scholar] [CrossRef]
- Bitang, G.W.Z. Laterally loaded fixedheaded piles in sand. In Proceedings of the 9th Australia New Zealand Conference on Geomechanics, Auckland, New Zealand, 8–11 February 2004; pp. 88–94. [Google Scholar]
- Barton, Y.O. Laterally Loaded Model Piles in Sand: Centrifuge Tests and Finite Element Analyses. Doctoral Dissertation, University of Cambridge, Cambridge, UK, 1982. [Google Scholar]
- Sørensen, S.P.H.; Ibsen, L.B.; Augustesen, A.H. Effects of diameter on initial stiffness of p-y curves for large-diameter piles in sand. In Numerical Methods in Geotechnical Engineering; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Kallehave, D.; Thilsted, C.L.; Liingaard, M.A. Modification of the API p-y Formulation of Initial Stiffness of Sand. In Proceedings of the 7th International Conference: Offshore Site Investigation and Geotechnics: Integrated Technologies-Present and Future, London, UK, 12–14 September 2012. [Google Scholar]
- Kim, D.; Choo, Y.W.; Kwak, K. Comparison of Lateral Behavior of Rock-Socketed Large-Diameter Offshore Monopiles in Sands with Different Relative Densities. Int. J. Offshore Polar Eng. 2015, 25, 156–160. [Google Scholar]
- Zhu, B.; Zhu, R.; Luo, J.; Chen, R.; Kong, L. Model tests on characteristics of ocean and offshore elevated piles with large lateral deflection. Chin. J. Geotech. Eng. 2010, 32, 521–530. [Google Scholar]





| Research Aspect | What Has Been Done (Established Knowledge and Transferable Insights) | What Remains Scarce (The Specific Research Gap for Offshore PV) |
|---|---|---|
| General Industry Context | Acknowledged as an emerging industry with vast potential, but overall technology is in its early stages and faces challenges in reliability and integration. Industry experts emphasize the need for bold innovation and customized solutions for different sea areas | Comprehensive technical standards and mature, widely applicable design methods are lacking. |
| Specific Technical Challenges | Key technical difficulties have been identified, including structural durability in high salt-spray environments, stability under typhoons and strong waves, and ensuring the economic feasibility of foundations | In-depth studies on the mechanical deformation mechanisms under these complex loads (e.g., wave-ice-wind coupling) are not thoroughly addressed. |
| Foundation Testing and Analysis Methods | 1. For Offshore Wind (Monopiles): Advanced methods beyond traditional p-y curves have been developed to analyze lateral deformation of large-diameter monopiles under long-term cyclic loads, using cyclic triaxial tests and numerical modeling. 2. For Laboratory Use: A specialized pile-soil interaction test system has been developed for jacket platforms, capable of applying static, cyclic, and impact loads. A lab-scale bearing performance detection device for offshore PV piles has also been proposed. | 1. The application and validation of these advanced analysis methods (from offshore wind) specifically for offshore PV pile foundations are scarce. 2. Research on full-scale or large-scale field testing methods for the mechanical deformation of installed offshore PV piles is particularly lacking. |
| Pile Number | Pile Length (m) | Section Size (mm) | Pile Tip Elevation (m) | The Soil Layer at the Pile Tip | Burial Depth (m) | Endurance Resistance (kN) |
|---|---|---|---|---|---|---|
| SZ01 | 17.5 | 1500 | −12.34 | Silt | 15.21 | 1341 |
| Soil Layer | Layer Thickness (m) | Effective Unit Weight of Soil (kN/m3) | Coefficient of Internal Friction (°) | Relative Density | Soil–Pile Friction Angle (°) |
|---|---|---|---|---|---|
| Silt | 30 | 9.2 | 29 | 0.25 | 26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, S.; Chen, H.; Lv, G.-e.; Jia, X.; Li, X. Experimental and Numerical Research on p-y Curve of Offshore Photovoltaic Pile Foundations on Sandy Soil Foundation. J. Mar. Sci. Eng. 2025, 13, 1959. https://doi.org/10.3390/jmse13101959
Fu S, Chen H, Lv G-e, Jia X, Li X. Experimental and Numerical Research on p-y Curve of Offshore Photovoltaic Pile Foundations on Sandy Soil Foundation. Journal of Marine Science and Engineering. 2025; 13(10):1959. https://doi.org/10.3390/jmse13101959
Chicago/Turabian StyleFu, Sai, Hongxin Chen, Guo-er Lv, Xianlin Jia, and Xibin Li. 2025. "Experimental and Numerical Research on p-y Curve of Offshore Photovoltaic Pile Foundations on Sandy Soil Foundation" Journal of Marine Science and Engineering 13, no. 10: 1959. https://doi.org/10.3390/jmse13101959
APA StyleFu, S., Chen, H., Lv, G.-e., Jia, X., & Li, X. (2025). Experimental and Numerical Research on p-y Curve of Offshore Photovoltaic Pile Foundations on Sandy Soil Foundation. Journal of Marine Science and Engineering, 13(10), 1959. https://doi.org/10.3390/jmse13101959






