Adaptive Antidisturbance Stabilization of Active Helideck Systems with Prescribed Performance via Saturation-Triggered Boundaries
Abstract
1. Introduction
- (1)
- We incorporate novel saturation-triggered boundaries into the PPC framework. This mechanism allows the prescribed performance boundaries to be dynamically adjusted upon the detection of input saturation, which effectively prevents the control error from transgressing into the singular region and thus resolves the control singularity problem inherent in conventional PPC.
- (2)
- An auxiliary dynamic system (ADS) is designed to further mitigate the adverse effects of input saturation. By incorporating a novel piecewise continuous function vector and robustifying terms, the proposed ADS is engineered to remain functional even under recurrent saturation conditions and ensures asymptotic stability of the stabilization errors, thereby overcoming the limitations of discontinuity and ineffectiveness in existing ADS approaches.
- (3)
- Leveraging the internal model principle, we model the complex ship-motion-induced disturbances as outputs of a linear exosystem with known dynamics but unknown parameters. These parameters are then accurately estimated online via adaptive techniques, enabling asymptotic disturbance estimation and rejection.
2. Materials and Methods
3. Main Results
3.1. Saturation-Triggered Boundaries
- Under positive saturation (), relax while fixing ;
- Under negative saturation (), relax while fixing ;
3.2. Adaptive Antidisturbance Prescribed Performance Control
3.3. Stability Analysis
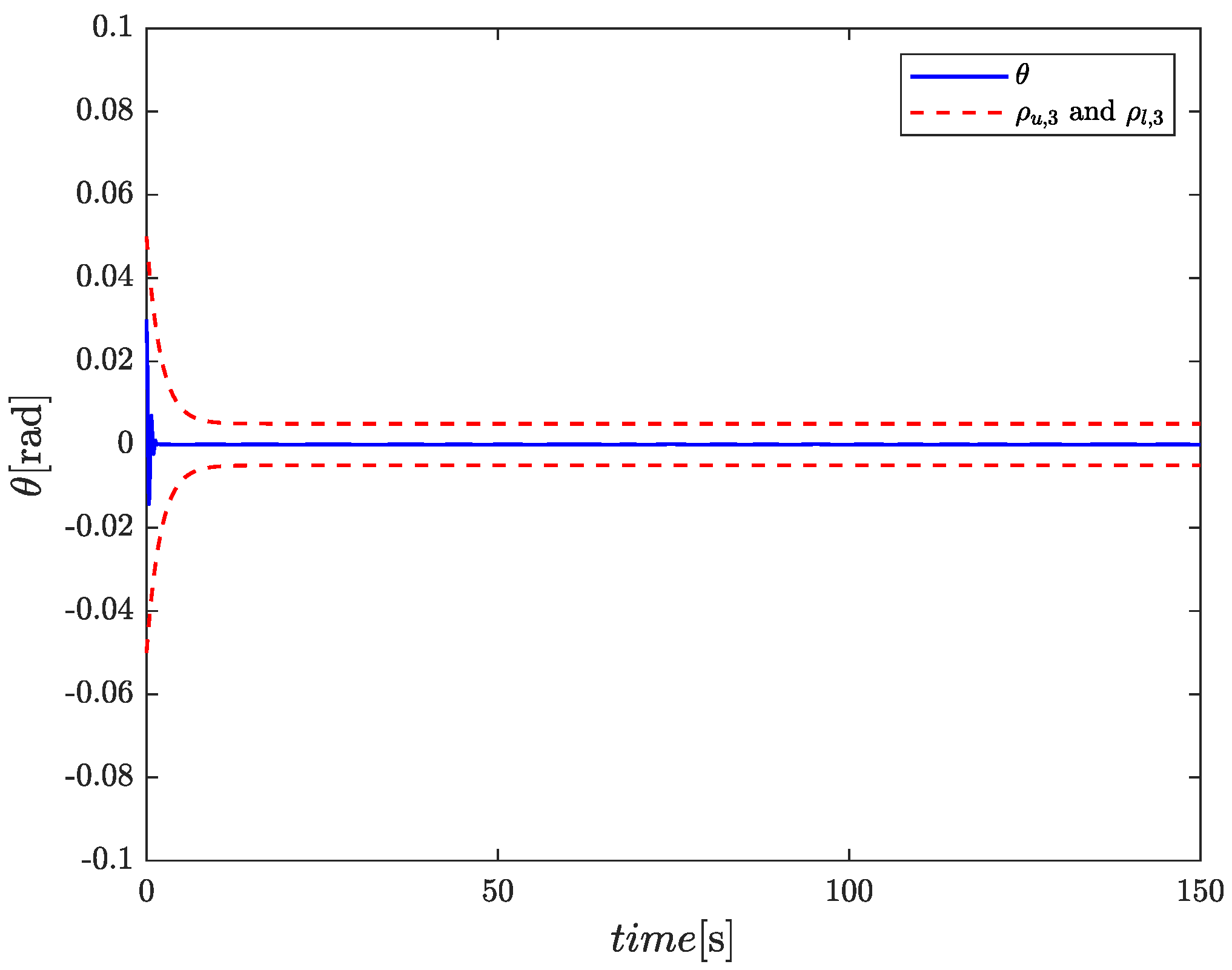
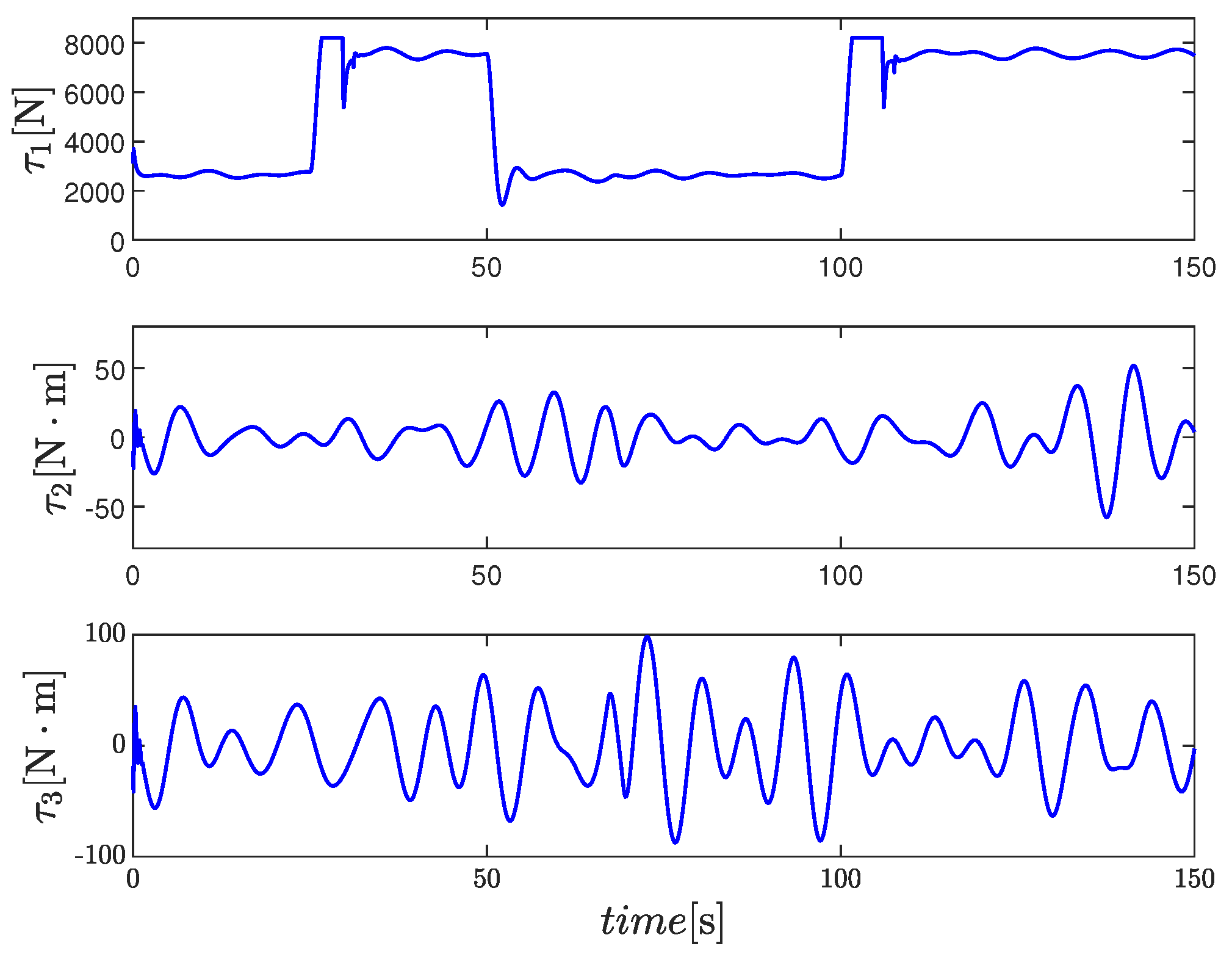
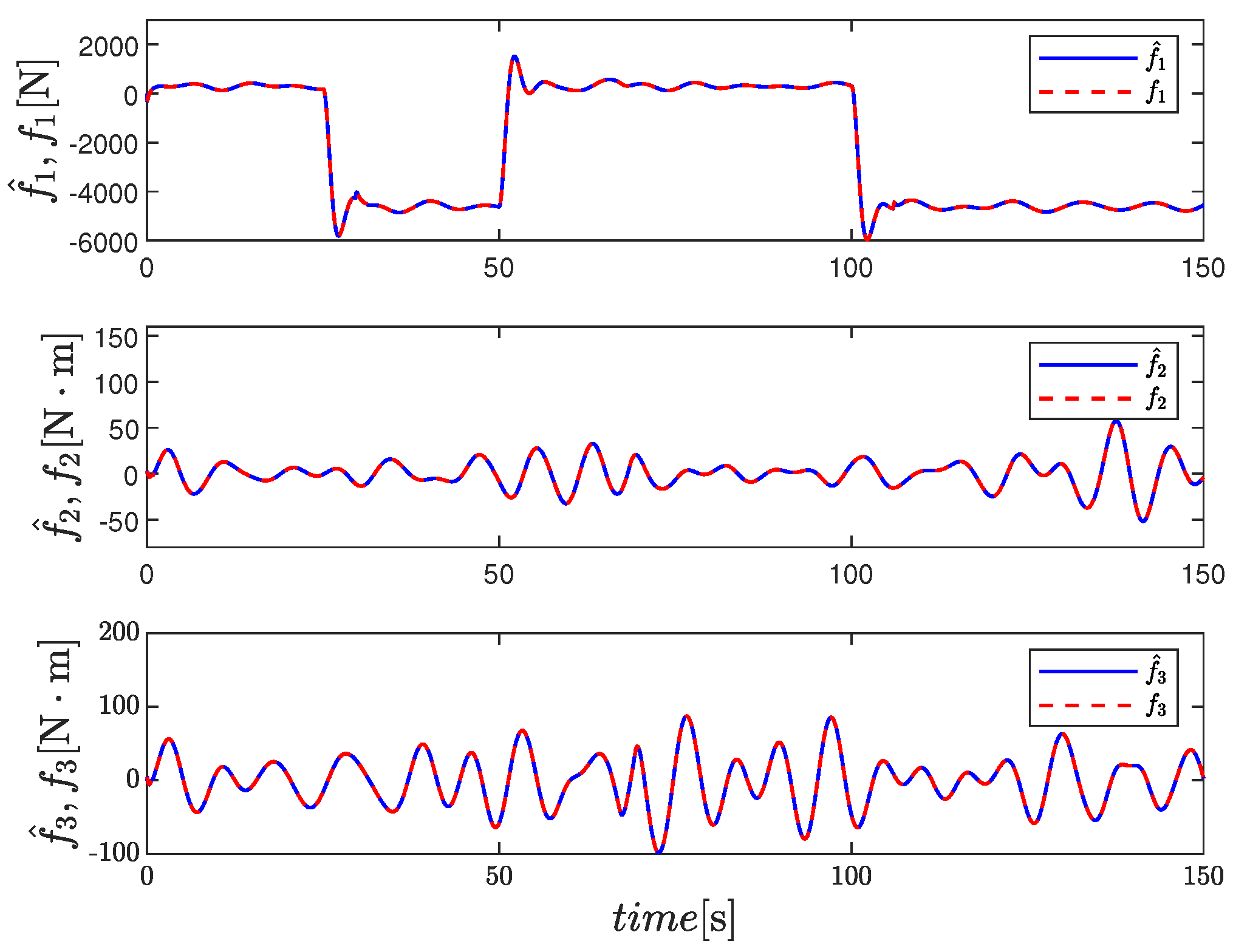
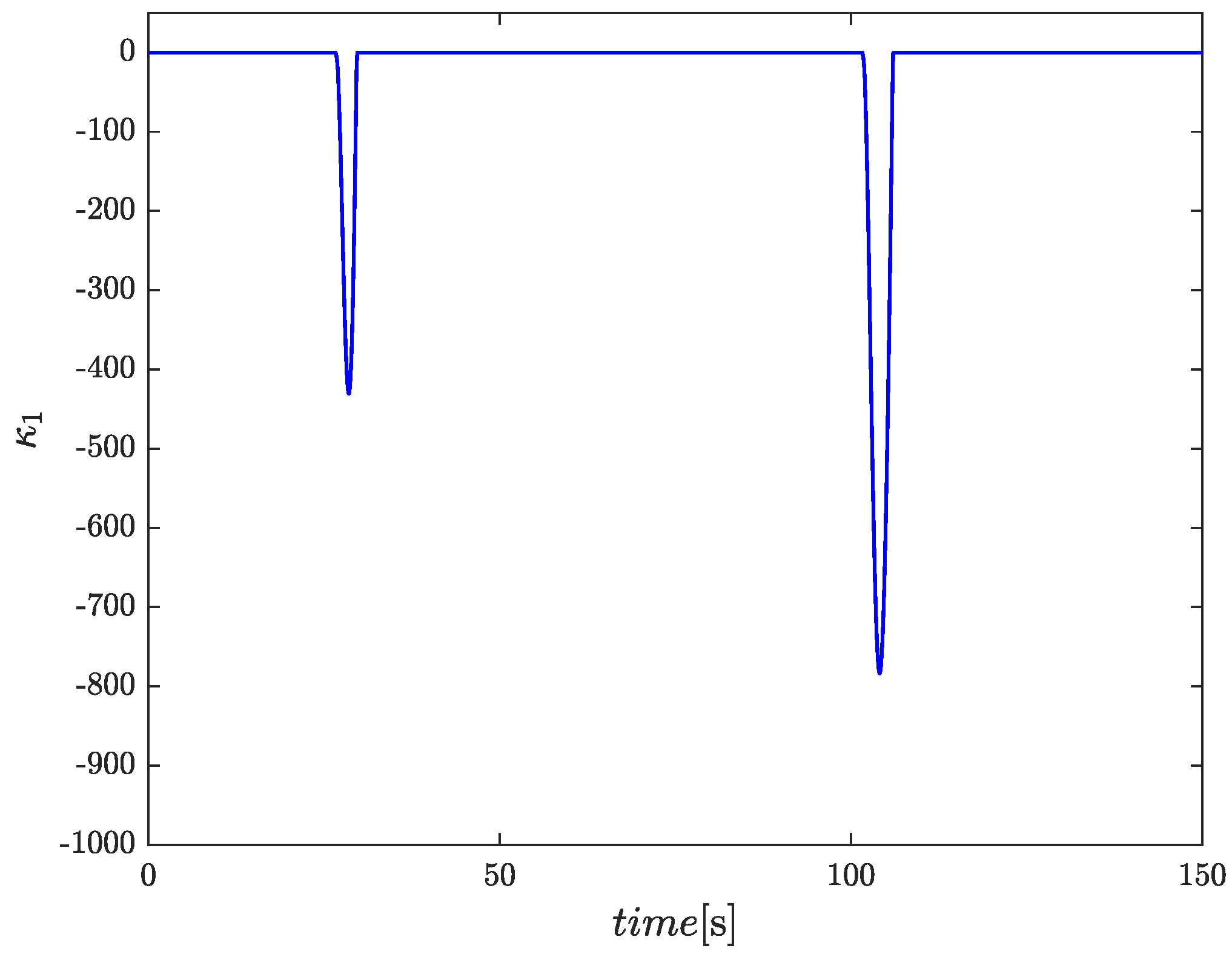
4. Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. The Mathematical Model Matrices of the AHS
References
- Shi, Y.J.; Su, D.C.; Xu, G.H. Numerical investigation of the influence of passive/active flow control on ship/helicopter dynamic interface. Aerosp. Sci. Technol. 2020, 106, 106205. [Google Scholar] [CrossRef]
- Su, D.C.; Xu, G.H.; Huang, S.L.; Shi, Y.J. Numerical investigation of rotor loads of a shipborne coaxial-rotor helicopter during a vertical landing based on moving overset mesh method. Eng. Appl. Comput. Fluid Mech. 2019, 13, 309–326. [Google Scholar] [CrossRef]
- Newman, S. The safety of shipborne helicopter operation. Aircr. Eng. Aerosp. Technol. 2004, 76, 487–501. [Google Scholar] [CrossRef]
- Shukla, S.; Singh, S.N.; Sinha, S.S.; Vijayakumar, R. Comparative assessment of URANS, SAS and DES turbulence modeling in the predictions of massively separated ship airwake characteristics. Ocean Eng. 2021, 229, 108954. [Google Scholar] [CrossRef]
- Brewczynski, D.; Tora, G. Dynamic positioning system of helicopter pad on the ship. J. KONES Powertrain Transp. 2014, 21, 21–27. [Google Scholar] [CrossRef]
- Brewczynski, D.; Tora, G. Dynamics model of stabilization mechanism for helicopter pad. J. KONES Powertrain Transp. 2016, 23, 61–68. [Google Scholar] [CrossRef]
- Campos, A.; Quintero, J.; Saltaren, R.; Ferre, M.; Aracil, R. An active helideck testbed for floating structures based on a stewart-gough platform. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008. [Google Scholar]
- Chen, Y.M.; Ye, J.W.; Zhang, X.L.; Liang, F.L. Experimental study on a stabilized platform system for shipborne helicopter. In Proceedings of the 21st International Offshore and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011. [Google Scholar]
- Erenoglu, L.; Eksin, L.; Yesil, E.; Guzelka, M.J. An intelligent hybrid fuzzy PID controller. In Proceedings of the 20th European Conference on Modelling and Simulation, Bonn, Germany, 28–31 May 2006. [Google Scholar]
- Chen, W.; Wang, S.; Li, J.; Lin, C.; Yang, Y.; Ren, A.; Li, W.; Zhao, X.; Zhang, W.; Guo, W.; et al. An ADRC-based triple-loop control strategy of ship-mounted Stewart platform for six-DOF wave compensation. Mech. Mach. Theory 2023, 184, 105289. [Google Scholar] [CrossRef]
- Du, Z.; Chen, X.; Zhang, Q.; Yang, Y. An extended state observer-based sliding mode control method for hydraulic servo system of marine stabilized platforms. Ocean Eng. 2023, 279, 114386. [Google Scholar] [CrossRef]
- Qiang, H.; Wang, Y.; Wang, R.; Liu, K.; Kang, S.; Yang, J. Model predictive control considering load disturbance of ship-borne hydraulic parallel platform. IEEE Access 2024, 12, 197201–197216. [Google Scholar] [CrossRef]
- Tang, G.; Lei, J.; Du, H.; Yao, B.; Zhu, W.; Hu, X. Proportional-integral-derivative controller optimization by particle swarm optimization and back propagation neural network for a parallel stabilized platform in marine operations. J. Ocean Eng. Sci. 2025, 10, 1–10. [Google Scholar] [CrossRef]
- Cai, Y.; Zheng, S.; Liu, W.; Qu, Z.; Zhu, J.; Han, J. Adaptive robust dual-loop control scheme of ship-mounted Stewart platforms for wave compensation. Mech. Mach. Theory 2021, 164, 104406. [Google Scholar] [CrossRef]
- Wen, Y.; Li, W.; Zhou, S.; Gao, F.; Chen, W. Robust sliding mode control with adaptive gravity estimation of ship-borne Stewart platform for wave compensation. Appl. Ocean Res. 2024, 148, 104004. [Google Scholar] [CrossRef]
- Wang, W.; Ning, Y.; Zhang, Y.; Xu, P.; Li, B. Linear active disturbance rejection control with linear quadratic regulator for Stewart platform in active wave compensation system. Appl. Ocean Res. 2025, 156, 104469. [Google Scholar] [CrossRef]
- Ahmadi, S.S.; Rahmanii, A. Nonlinear model predictive control of a stewart platform based on improved dynamic model. Int. J. Theor. Appl. Mech. 2020, 18–26. [Google Scholar]
- Mochida, R.; Ishimura, K.; Akita, T.; Kon, T. High-precision pointing control using stewart platform with adaptive model predictive control. J. Spacecr. Rockets 2025, 1–18. [Google Scholar] [CrossRef]
- Ding, Z.; Zhao, F.; Lang, Y.; Jiang, Z.; Zhu, J. Anti-disturbance neural-sliding mode control for inertially stabilized platform with actuator saturation. IEEE Access 2019, 7, 92220–92231. [Google Scholar] [CrossRef]
- Zhang, M.; Guan, Y.; Li, Q.; Sun, Z.; Duan, Z. Adaptive nonlinear control for the stabilized platform with disturbance and input saturation. IEEE Access 2020, 8, 200774–200788. [Google Scholar] [CrossRef]
- Hu, A.; Qiao, H.; Yang, W.; Liu, M.; Guo, Y. Stewart platform control input anti-saturation sliding mode controller design. In Proceedings of the 2024 Chinese Intelligent Systems Conference, Guilin, China, 26–27 October 2024; pp. 192–201. [Google Scholar]
- Bechlioulis, C.P.; Rovithakis, G.A. Robust adaptive control of feedback linearizable mimo nonlinear systems with prescribed performance. IEEE Trans. Autom. Control 2008, 53, 2090–2099. [Google Scholar] [CrossRef]
- Bu, X.; Luo, R. Attitude Control with discrete-time prescribed performance for seeker stabilized platform via event-triggered neural approximation. IEEE Trans. Ind. Inform. 2025, 21, 1853–1861. [Google Scholar] [CrossRef]
- Du, J.; Hu, X.; Krstić, M.; Sun, Y. Robust dynamic positioning of ships with disturbances under input saturation. Automatica 2016, 73, 207–214. [Google Scholar] [CrossRef]
- Liu, W.; Du, J.; Li, J.; Li, Z. Stabilization control of 3-DOF parallel vessel-borne platform with dynamic uncertainties and unknown disturbances. Appl. Ocean Res. 2022, 126, 103271. [Google Scholar] [CrossRef]
- Wang, T.; Yang, H.; Zhang, Q.; Fang, J.; Lai, Z.; Feng, R.; Wei, J.; Wang, Z. Non-inertial dynamic analysis of 3-sps/u parallel platform by screw theory and kane’s method. Actuators 2024, 13, 430. [Google Scholar] [CrossRef]
- Yong, K.; Chen, M.; Shi, Y.; Wu, Q. Flexible performance-based robust control for a class of nonlinear systems with input saturation. Automatica 2020, 122, 109268. [Google Scholar] [CrossRef]
- Shi, Y.; Xie, W.; Zhang, G.; Dong, H.; Zhang, W. Event-triggered saturation-tolerant control for autonomous underwater vehicles with quantitative transient behaviors. IEEE Trans. Veh. Technol. 2023, 72, 9857–9867. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.; Zhu, J.; Liu, Y.; Zhang, M.; Su, Z. Flexible prescribed performance-based approaching control for uav aerial recovery under multiwind disturbances. Chin. J. Aeronaut. 2025, 38, 103282. [Google Scholar] [CrossRef]
- Krstic, M.; Kanellakopoulos, I.; Kokotovic, P. Nonlinear and Adaptive Control Design; John Wiley & Sons Inc.: New York, NY, USA, 1995. [Google Scholar]
- Nikiforov, V. Nonlinear servo compensation of unknown external disturbances. Automatica 2001, 37, 1647–1653. [Google Scholar] [CrossRef]
- Levant, A. Higher-Order Sliding Modes, differentiation and output feedback control. Int. J. Control 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Ge, S.; Wang, J. Robust adaptive tracking for time varying uncertain nonlinear systems with unknown control coefficients. IEEE Trans. Autom. Control 2003, 48, 1463–1469. [Google Scholar]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley & Sons: Chichester, UK, 2011. [Google Scholar]
- China’s New Military Weapons. 2020. Available online: https://www.china-arms.com/2020/12/ar500b-unmanned-helicopter-first-flight/ (accessed on 9 September 2022).
- Stanisławski, J. A simulation model for computing the loads generated at landing site during helicopter take-off or landing operation. Trans. Aerosp. Res. 2019, 255, 65–81. [Google Scholar] [CrossRef]

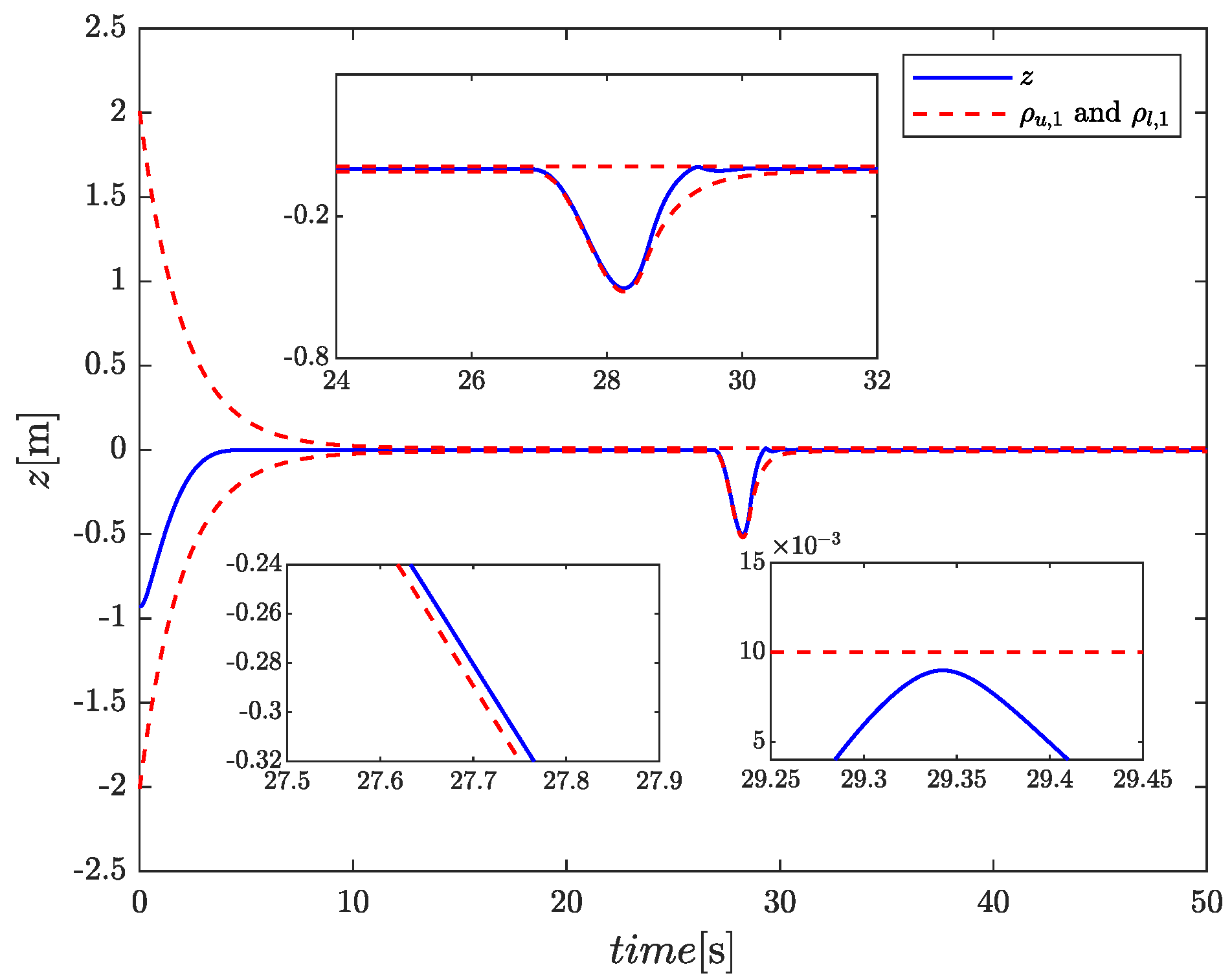
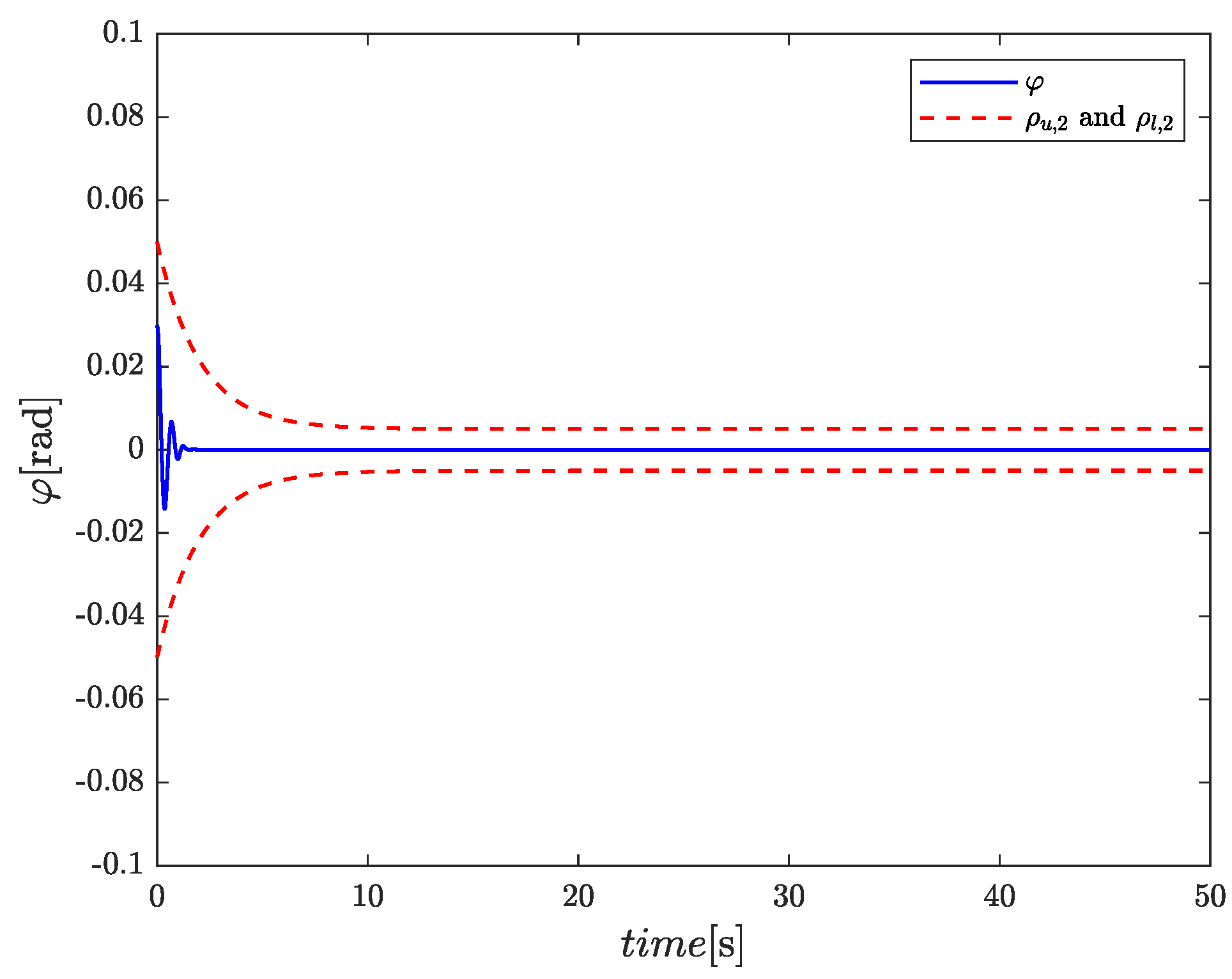
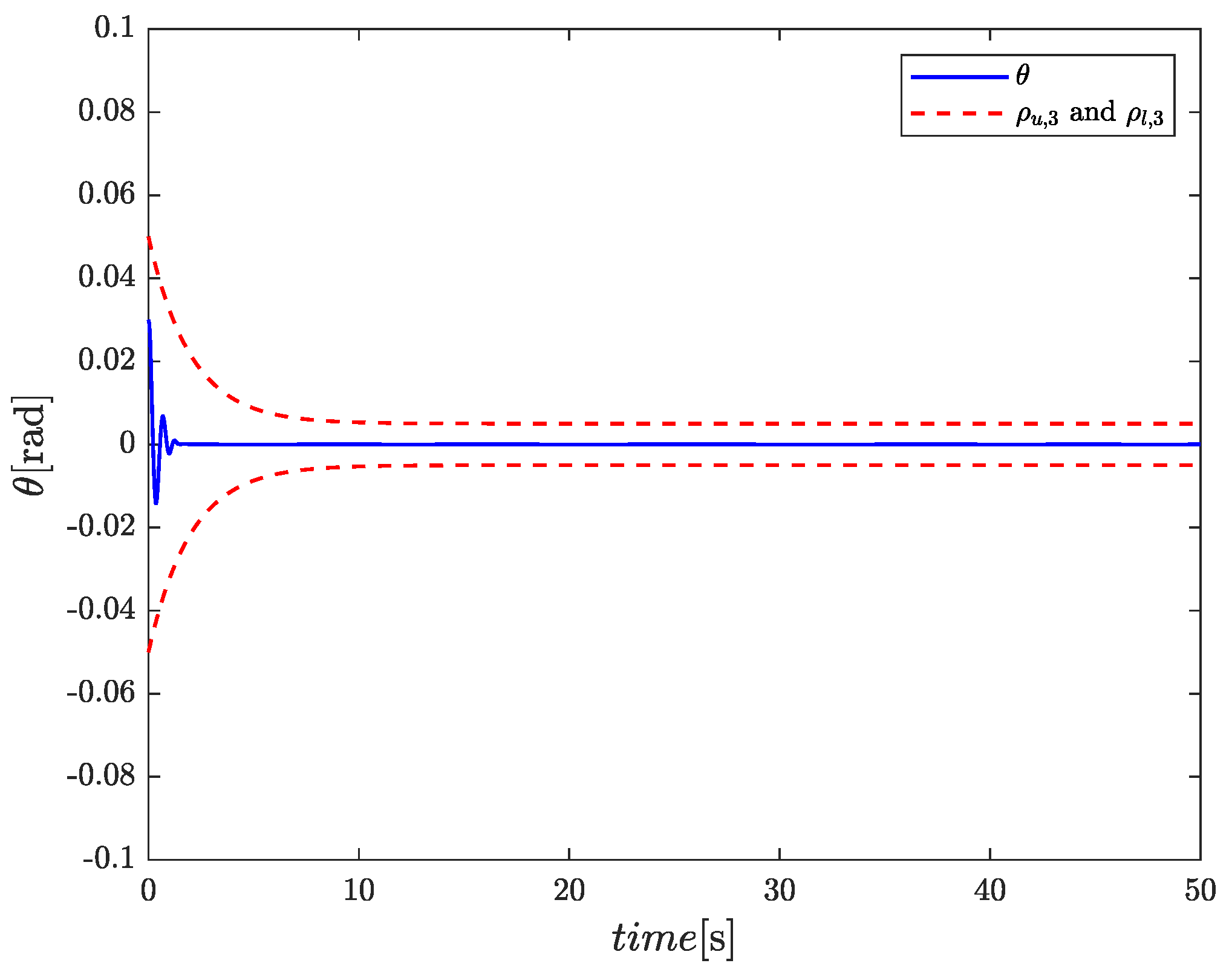


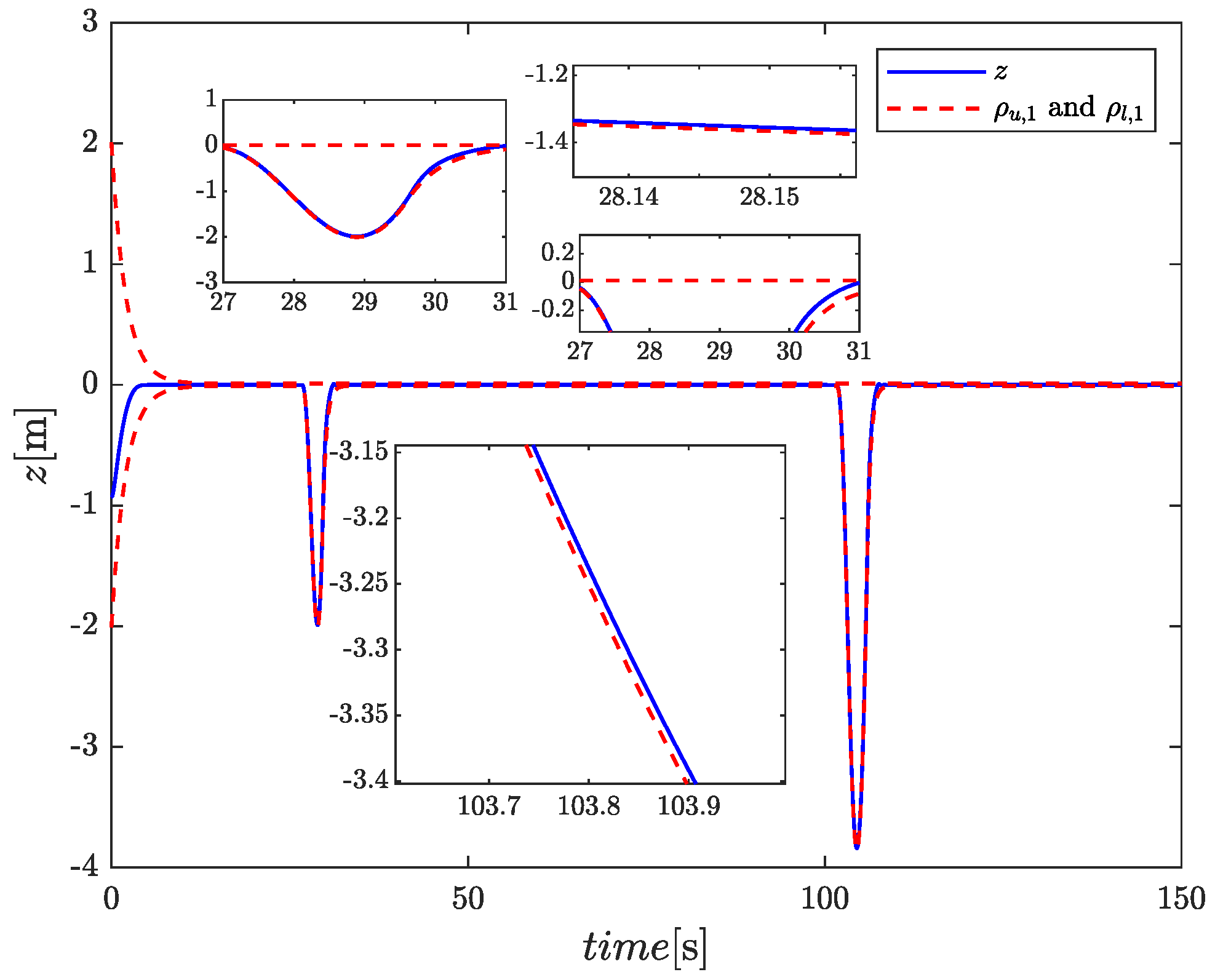

| Parameters | Values |
|---|---|
| 300 kg | |
| 10.59 kg· | |
| 10.59 kg· | |
| 19.85 kg· | |
| g | 9.8 m/ |
| Parameter | Value |
|---|---|
| Length between perpendiculars | 82.8 m |
| Breadth | 19.2 m |
| Draft | 6 m |
| Mass | kg |
| Displacement |
| Parameter | Sea State 2 | Sea State 4 |
|---|---|---|
| Spectrum type | ITTC | |
| Significant wave height | 0.5 m | 2.5 m |
| Peak frequency | 0.8 rad/s | 0.6 rad/s |
| Mean wave direction | ||
| Wave spreading factor | 2 | 3 |
| Parameter | Value |
|---|---|
| Maximum take-off weight | 500 kg |
| Mission load weight | 70 kg |
| Maximum endurance time | 4 h |
| Operating radius | 100 km |
| Maximum endurance speed | 140 km/h |
| Cruising speed | 120 km/h |
| Category | Parameter | Value |
|---|---|---|
| Parameters in the saturation-triggered boundaries | , | 0.5 |
| , | 2.01 | |
| , , , | 0.05 | |
| , | 0.01 | |
| , , , | 0.005 | |
| 1 | ||
| 1.1 | ||
| Parameters in the intermediate control vector | ||
| Parameters in the ADS | ||
| 10 | ||
| 2 | ||
| 0.01 | ||
| 0.1 | ||
| Parameters in the ADE | ||
| Parameters in the control law | ||
| 10 | ||
| 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Hu, X.; Du, J. Adaptive Antidisturbance Stabilization of Active Helideck Systems with Prescribed Performance via Saturation-Triggered Boundaries. J. Mar. Sci. Eng. 2025, 13, 1949. https://doi.org/10.3390/jmse13101949
Li J, Hu X, Du J. Adaptive Antidisturbance Stabilization of Active Helideck Systems with Prescribed Performance via Saturation-Triggered Boundaries. Journal of Marine Science and Engineering. 2025; 13(10):1949. https://doi.org/10.3390/jmse13101949
Chicago/Turabian StyleLi, Jian, Xin Hu, and Jialu Du. 2025. "Adaptive Antidisturbance Stabilization of Active Helideck Systems with Prescribed Performance via Saturation-Triggered Boundaries" Journal of Marine Science and Engineering 13, no. 10: 1949. https://doi.org/10.3390/jmse13101949
APA StyleLi, J., Hu, X., & Du, J. (2025). Adaptive Antidisturbance Stabilization of Active Helideck Systems with Prescribed Performance via Saturation-Triggered Boundaries. Journal of Marine Science and Engineering, 13(10), 1949. https://doi.org/10.3390/jmse13101949






