Numerical Study of the Flow Around Twin Straight-Bladed Darrieus Hydrokinetic Turbines
Abstract
1. Introduction
2. Materials and Methods
2.1. Operational Non-Dimensional Parameters of Hydrokinetic Turbines
2.2. Computational Model and Numerical Setup
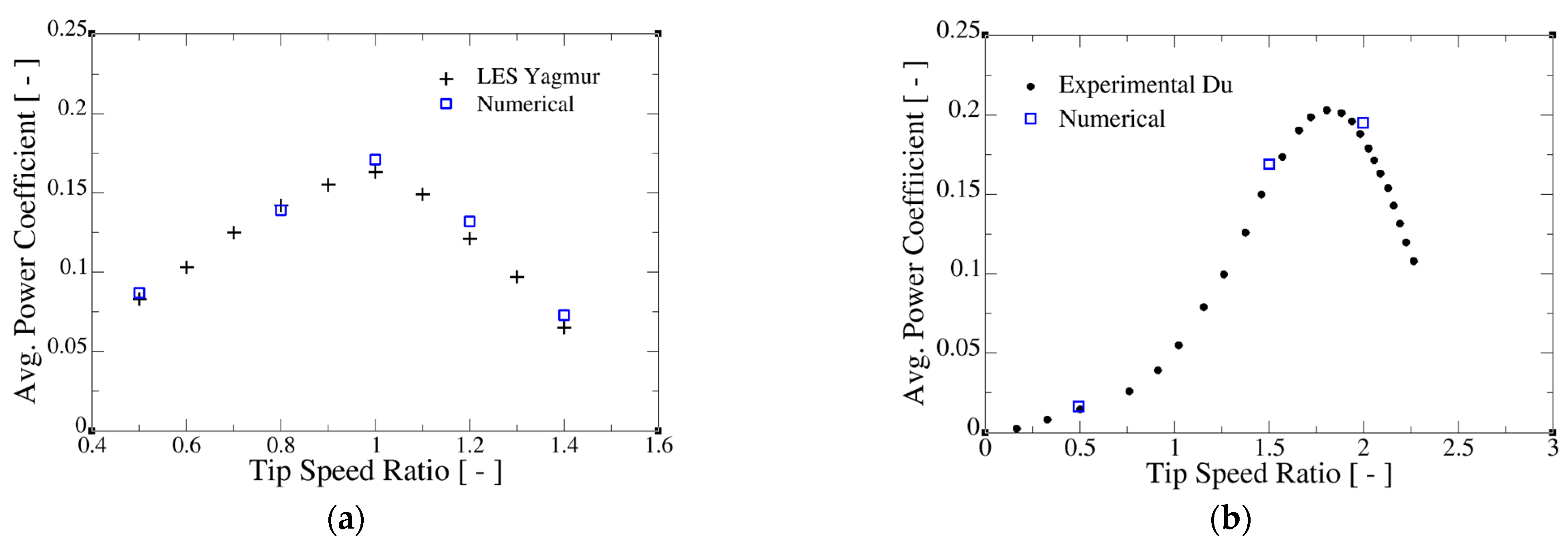
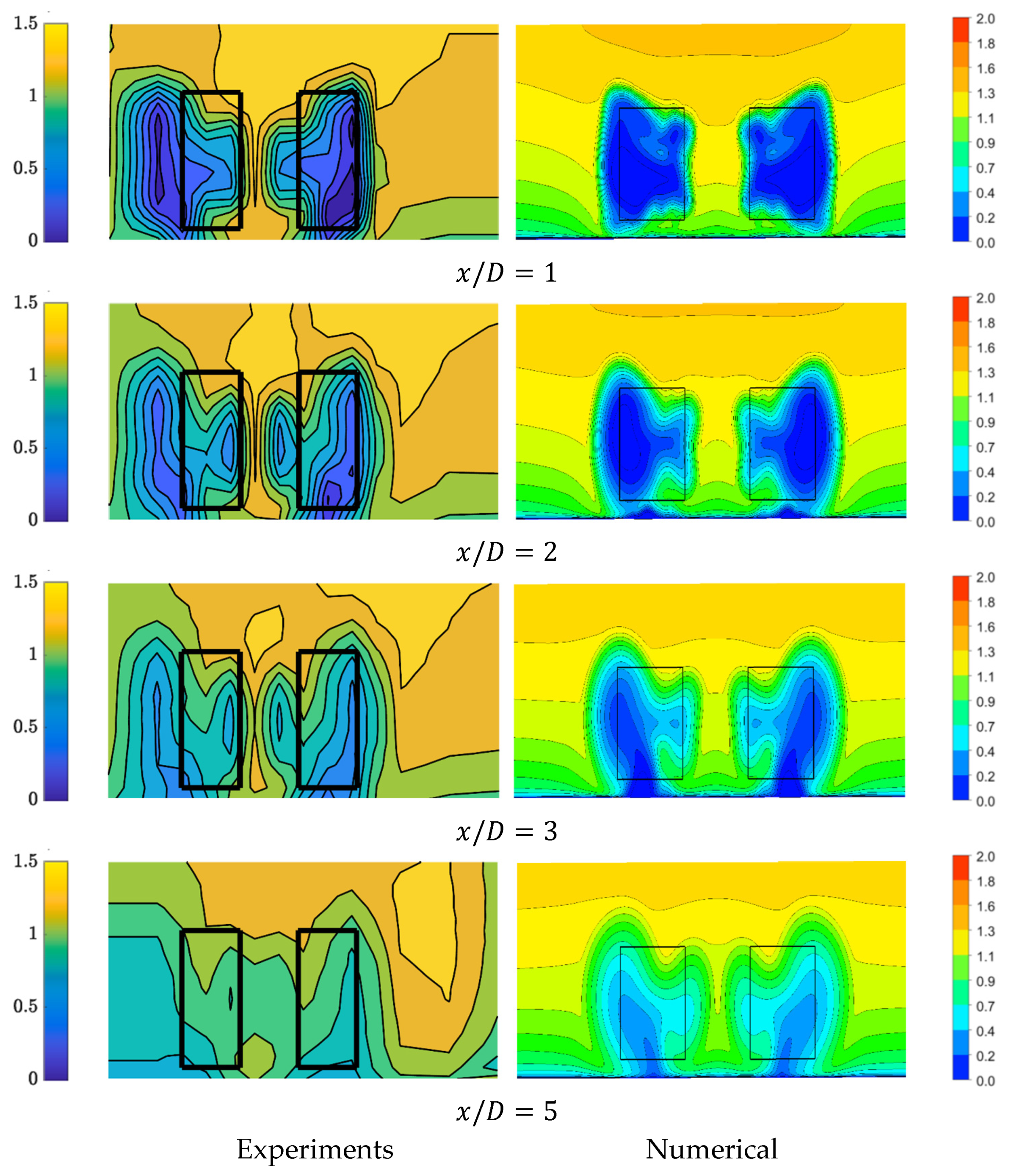
2.3. Validation of the Computations
3. Integral Parameters Results
3.1. Performance of the Isolated Turbine
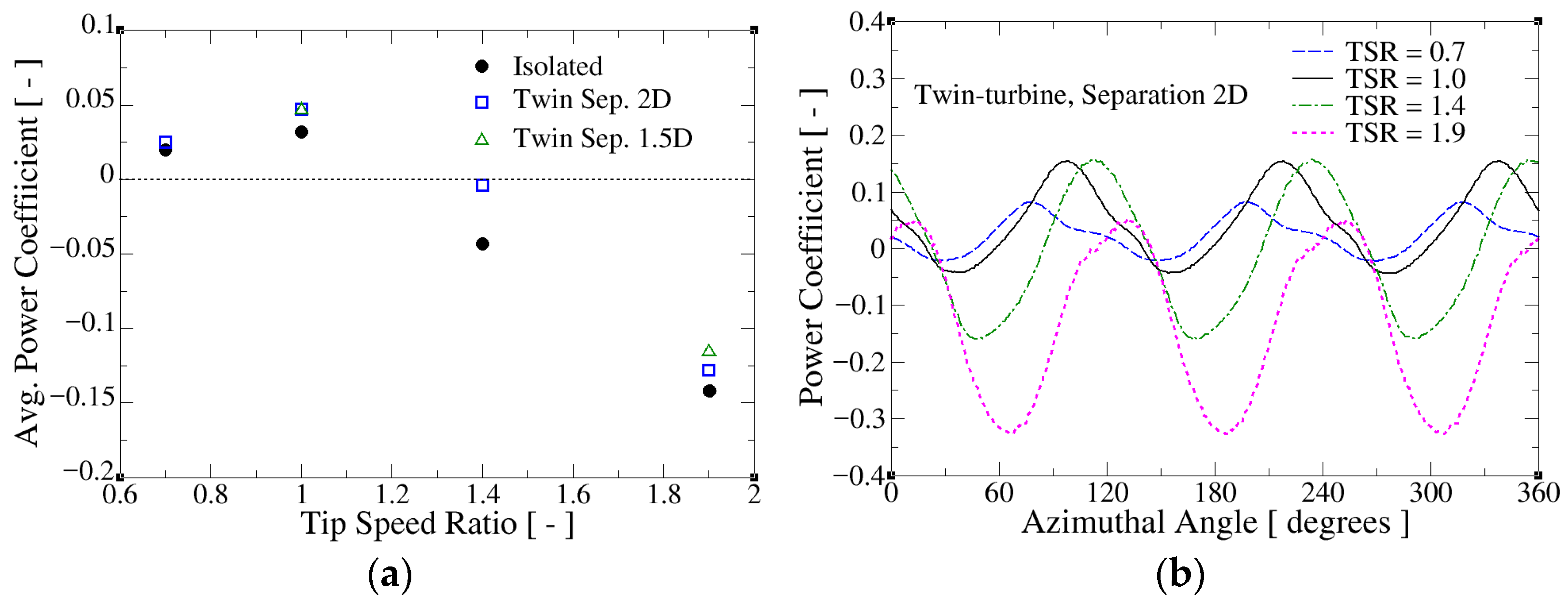
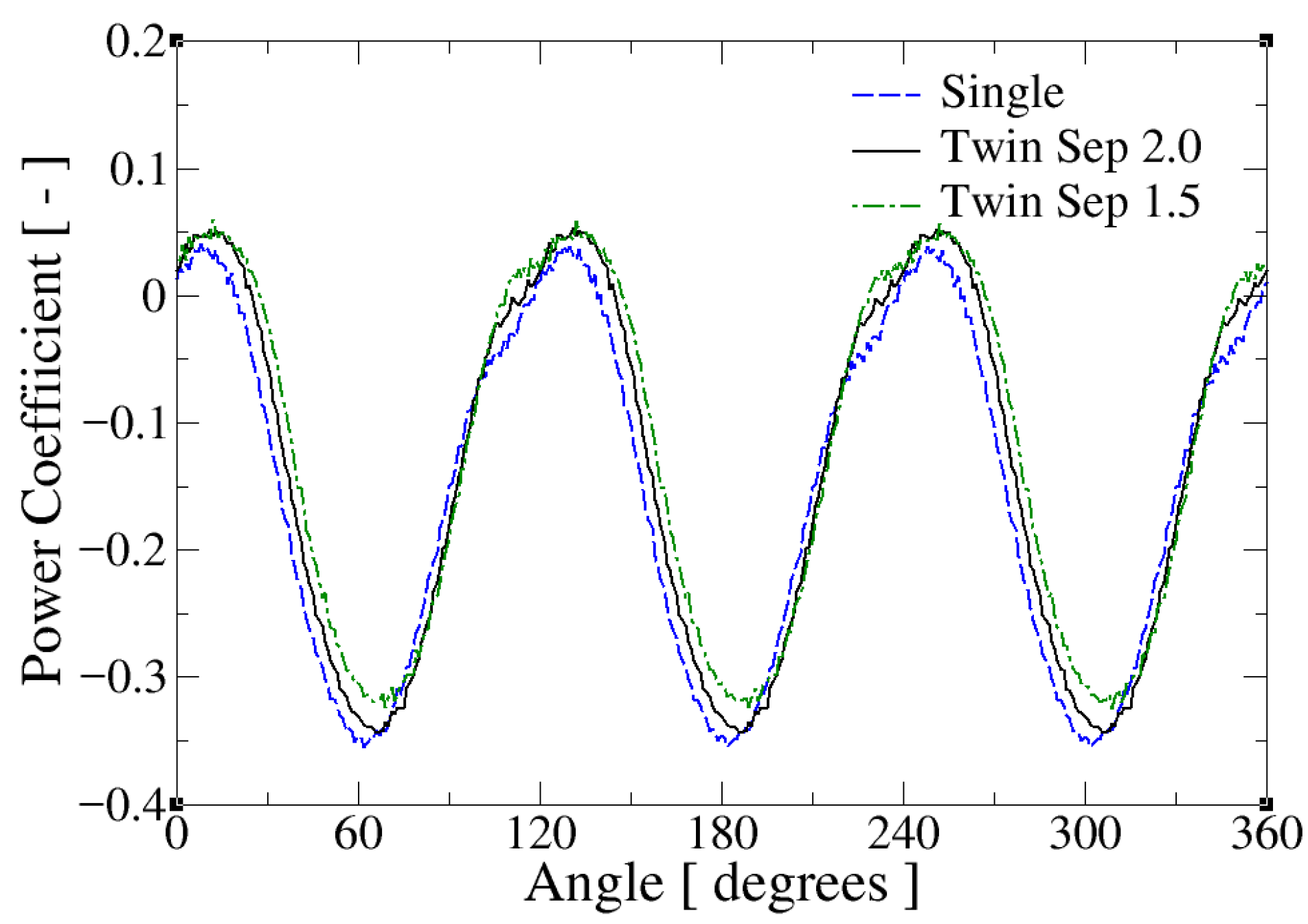
3.2. Performance of Twin-Turbine Configuration
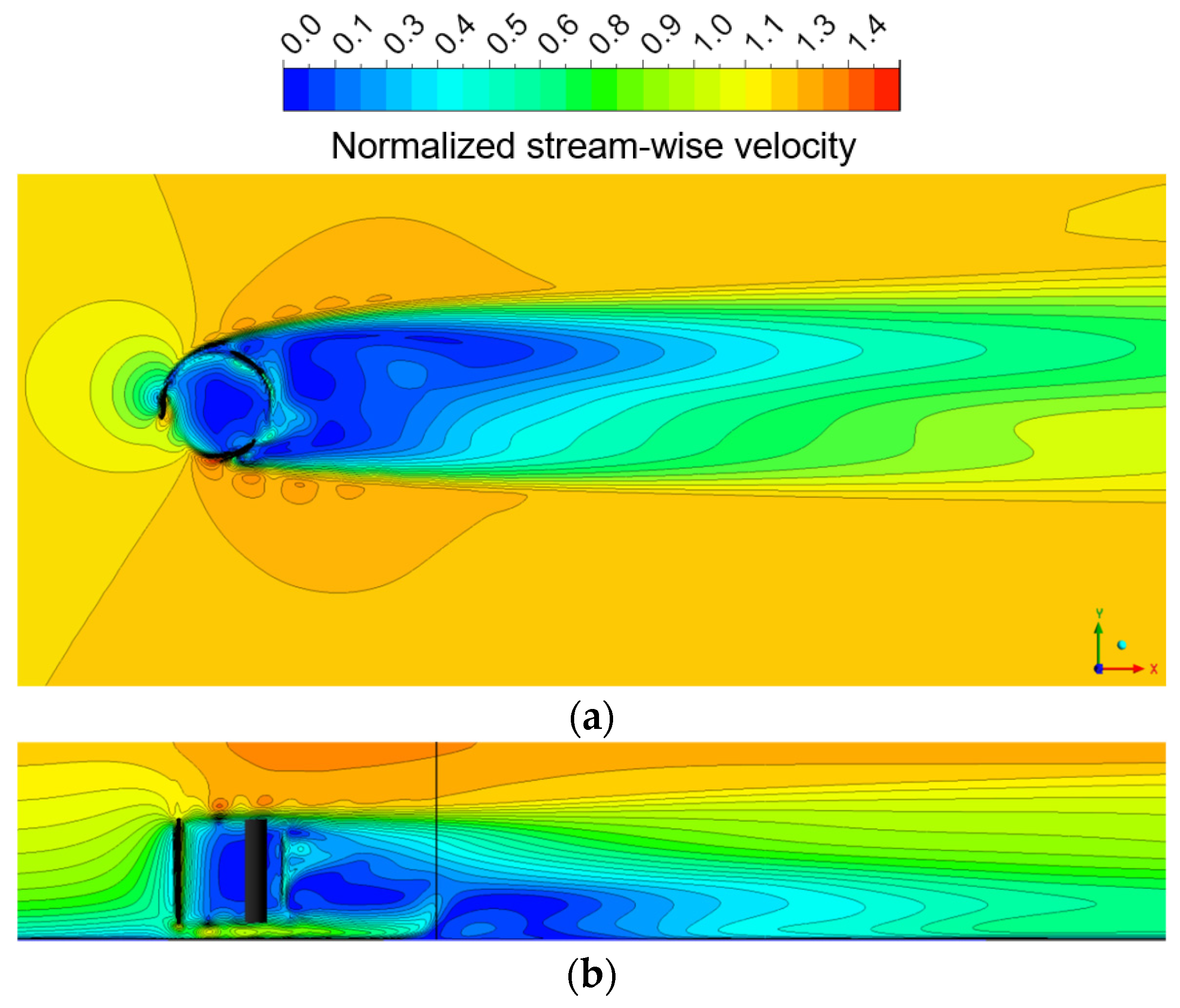
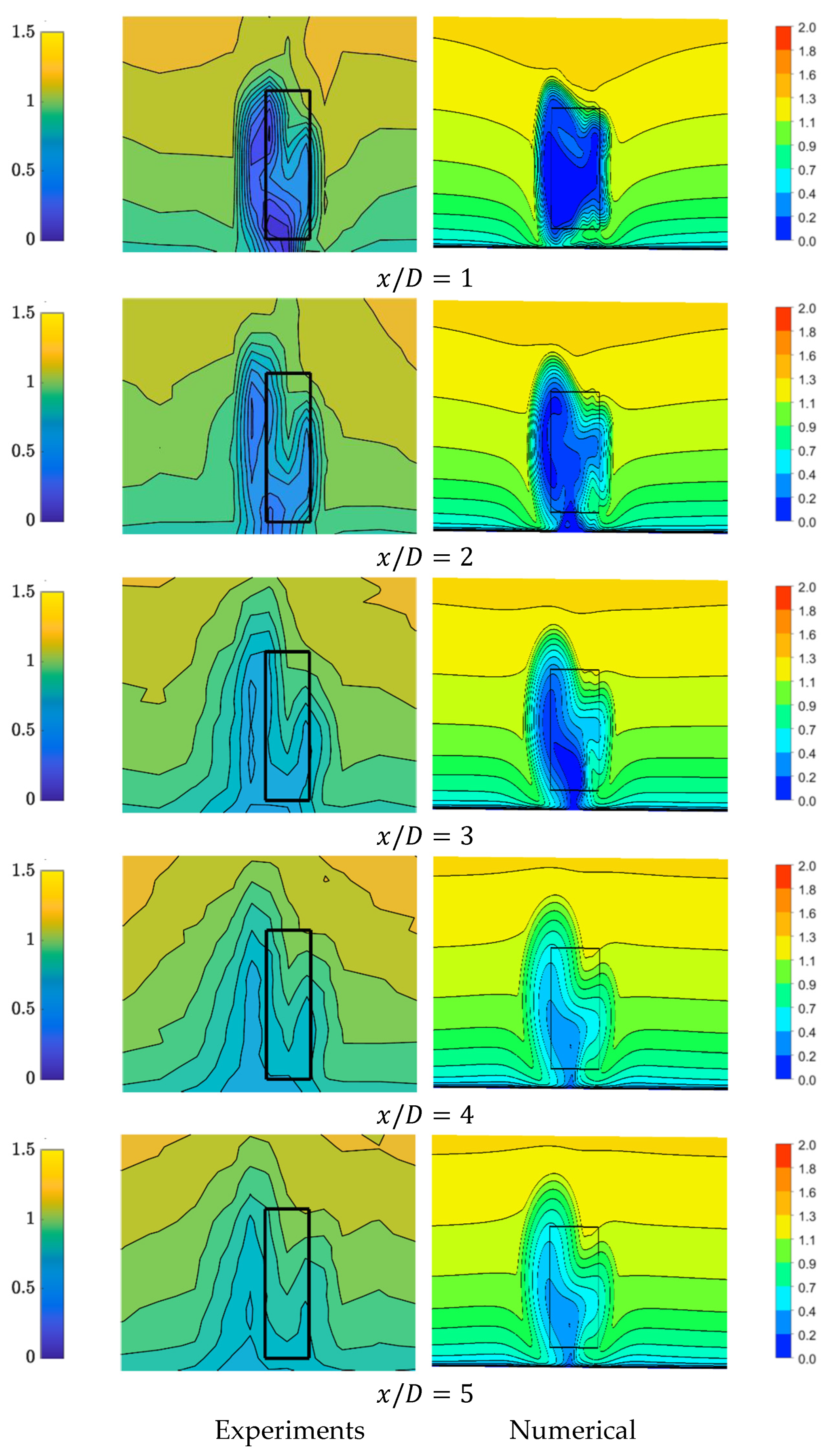
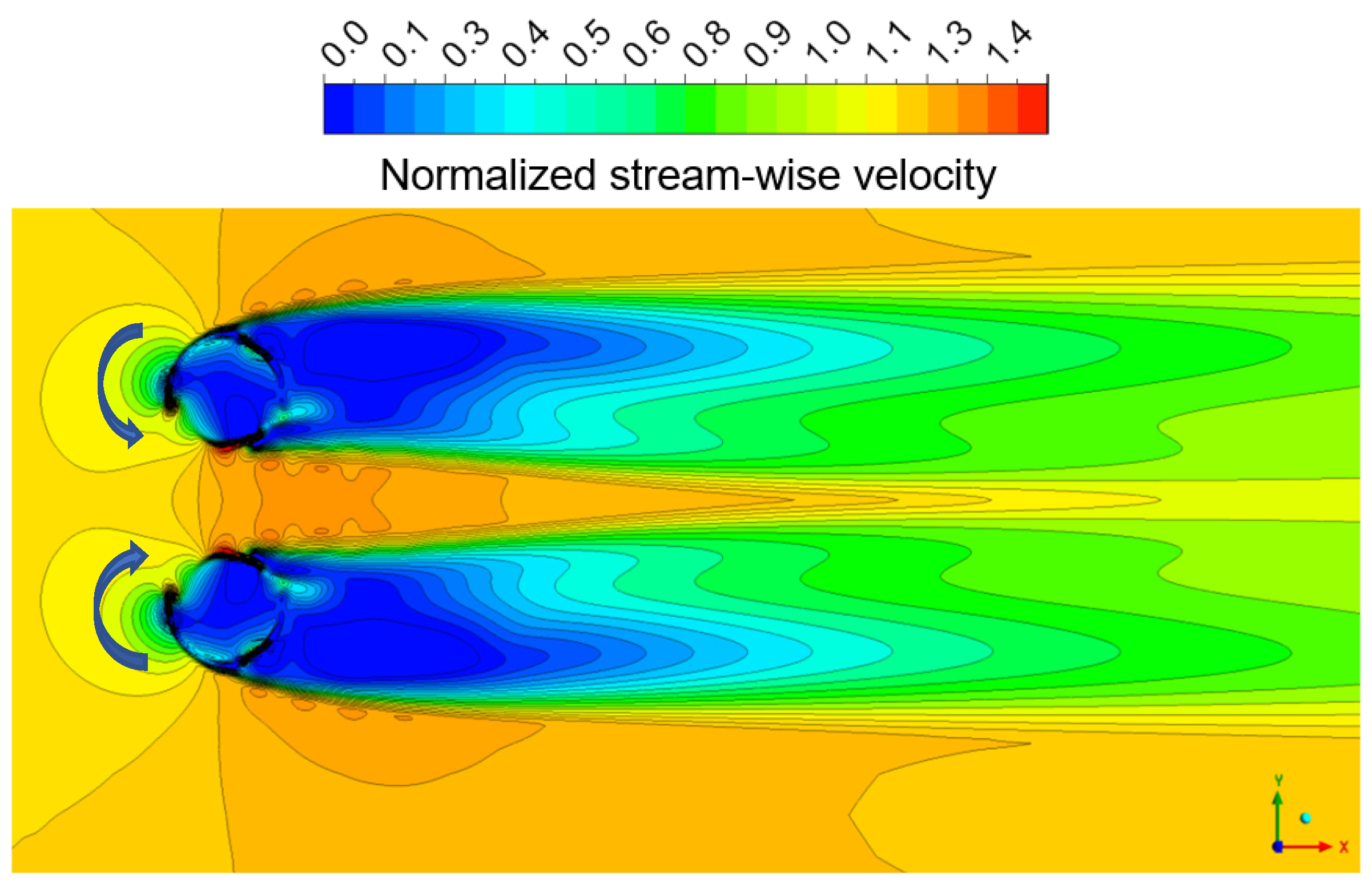
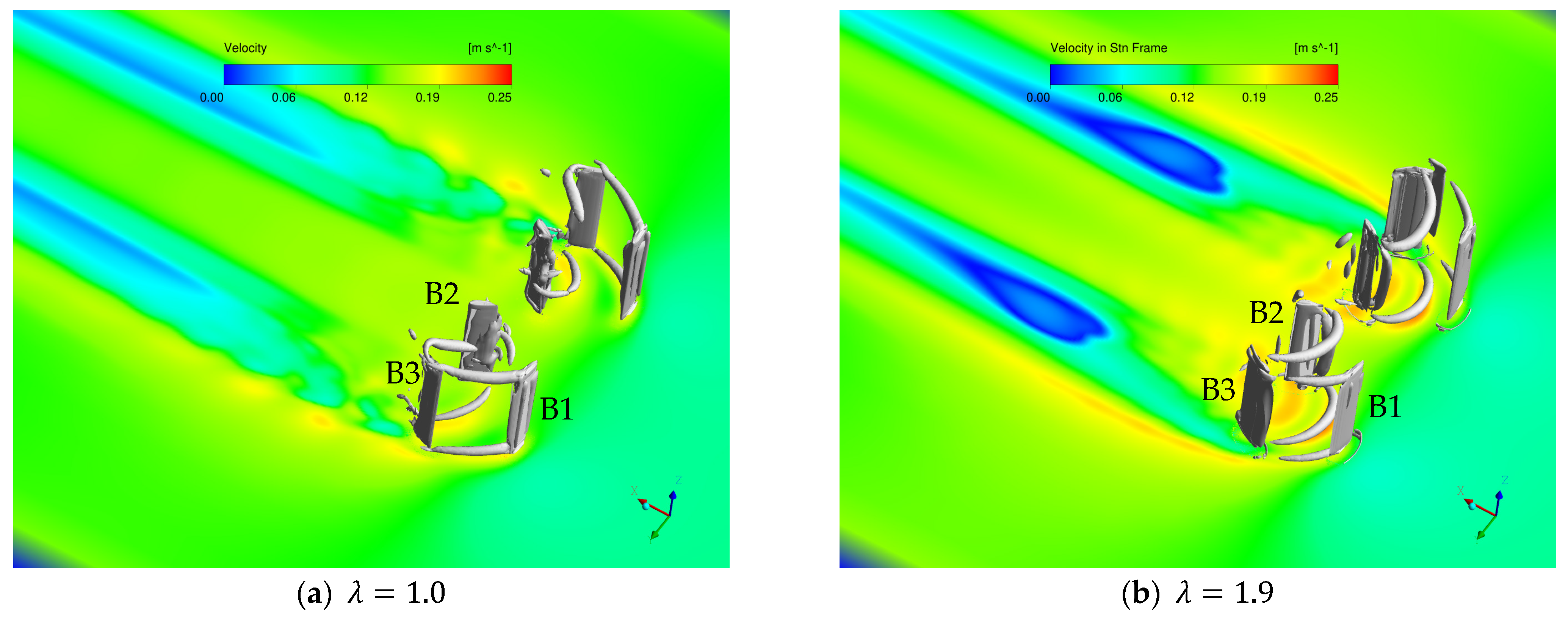
3.3. Wake Flow Visualization in the Twin-Turbine Arrangement
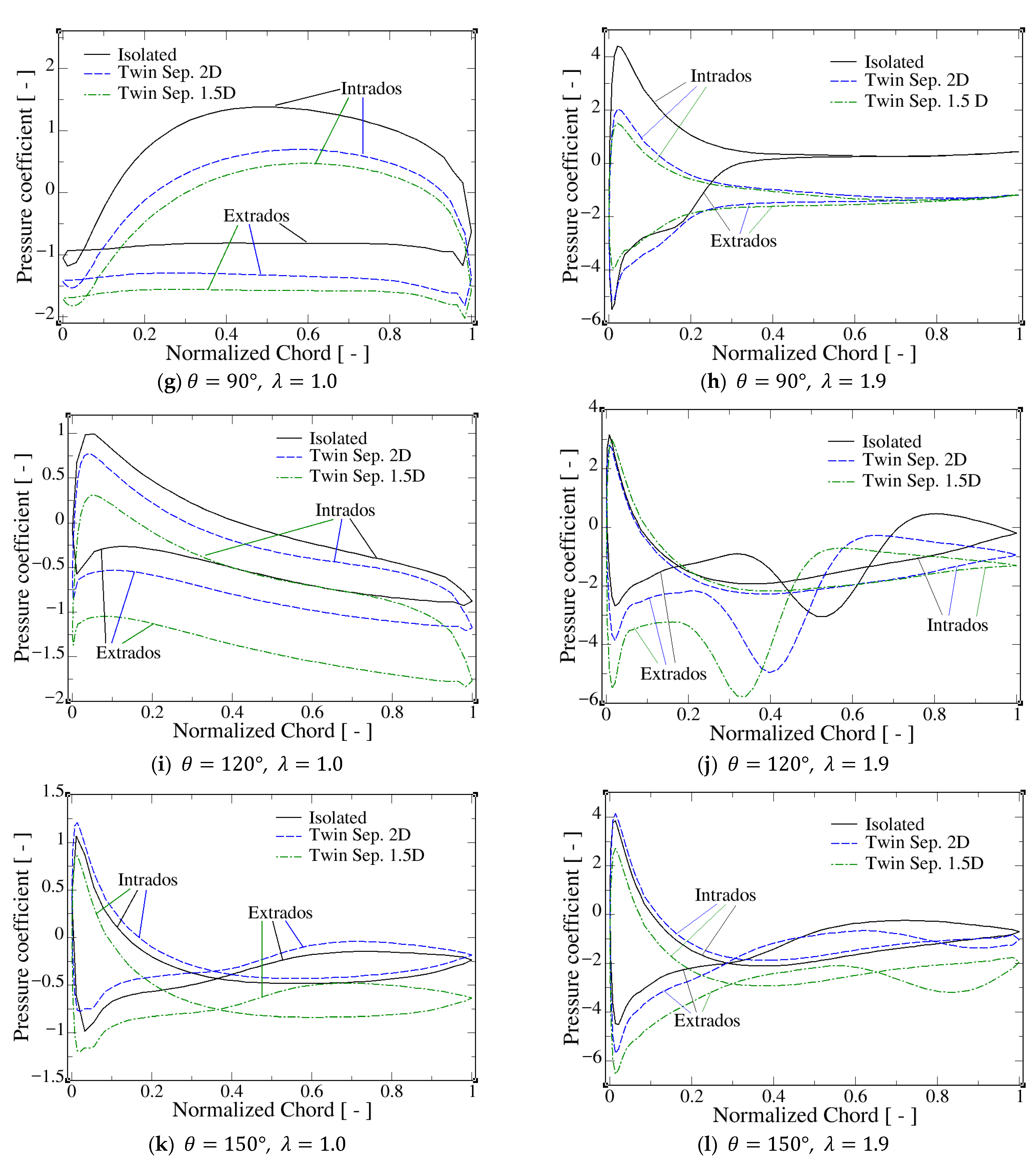
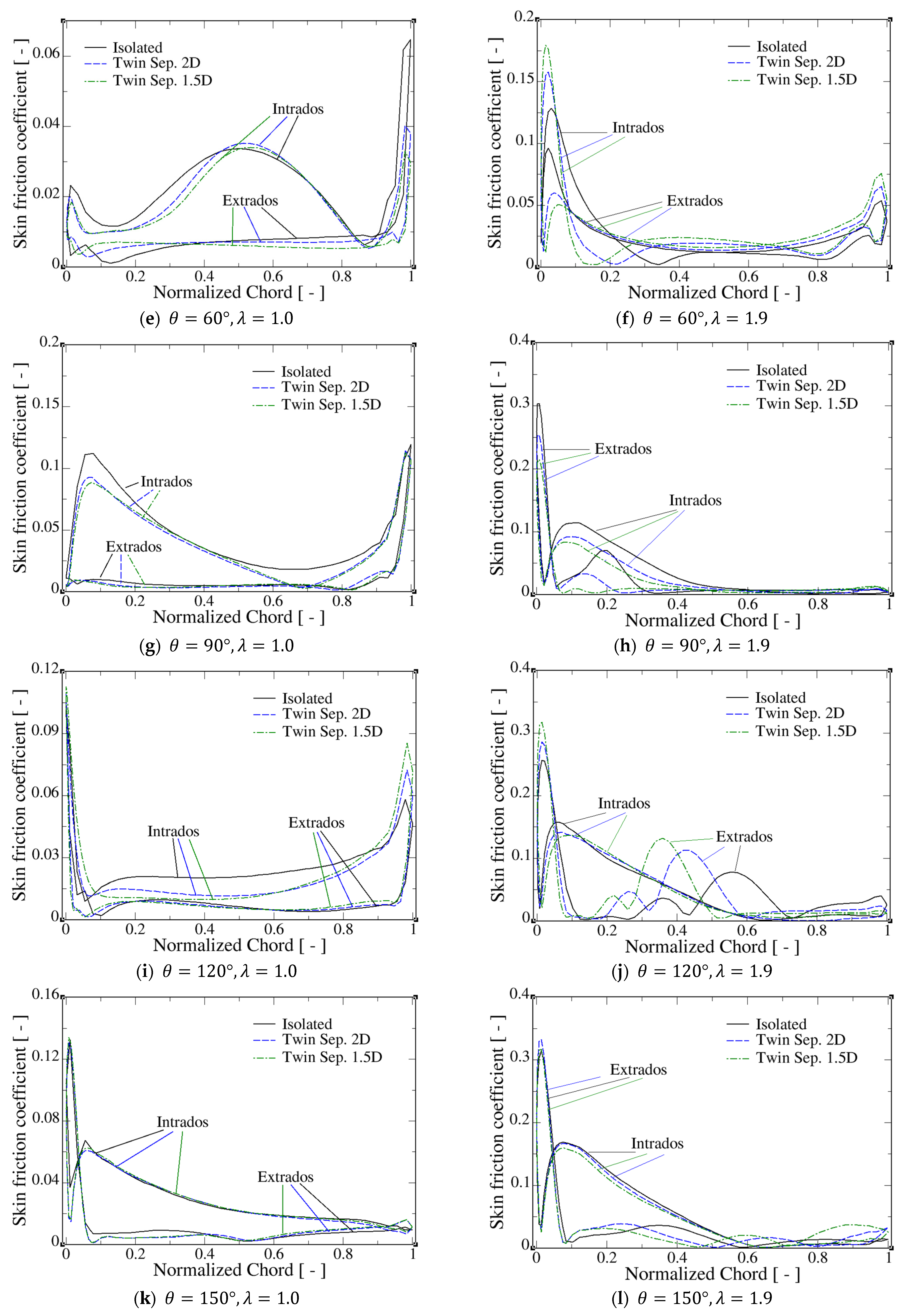
4. Influence of Turbine Separation on the Aerodynamic Behavior of the Blades
Behavior of the Pressure and Skin Friction Coefficients in Single- and Twin-Turbine Setups
5. Conclusions
- The simulations revealed predominantly symmetrical wake patterns behind the turbines in computational models, contrasting with experimental results which displayed certain asymmetries. However, despite this discrepancy, qualitative agreement was observed in wake evolution and velocity deficits, especially for the flow regions in proximity to the turbines. The experimental wakes showed earlier wake mixing and faster recovery than simulations predicted, likely due to measurement restrictions and flow perturbations not captured in the numerical models.
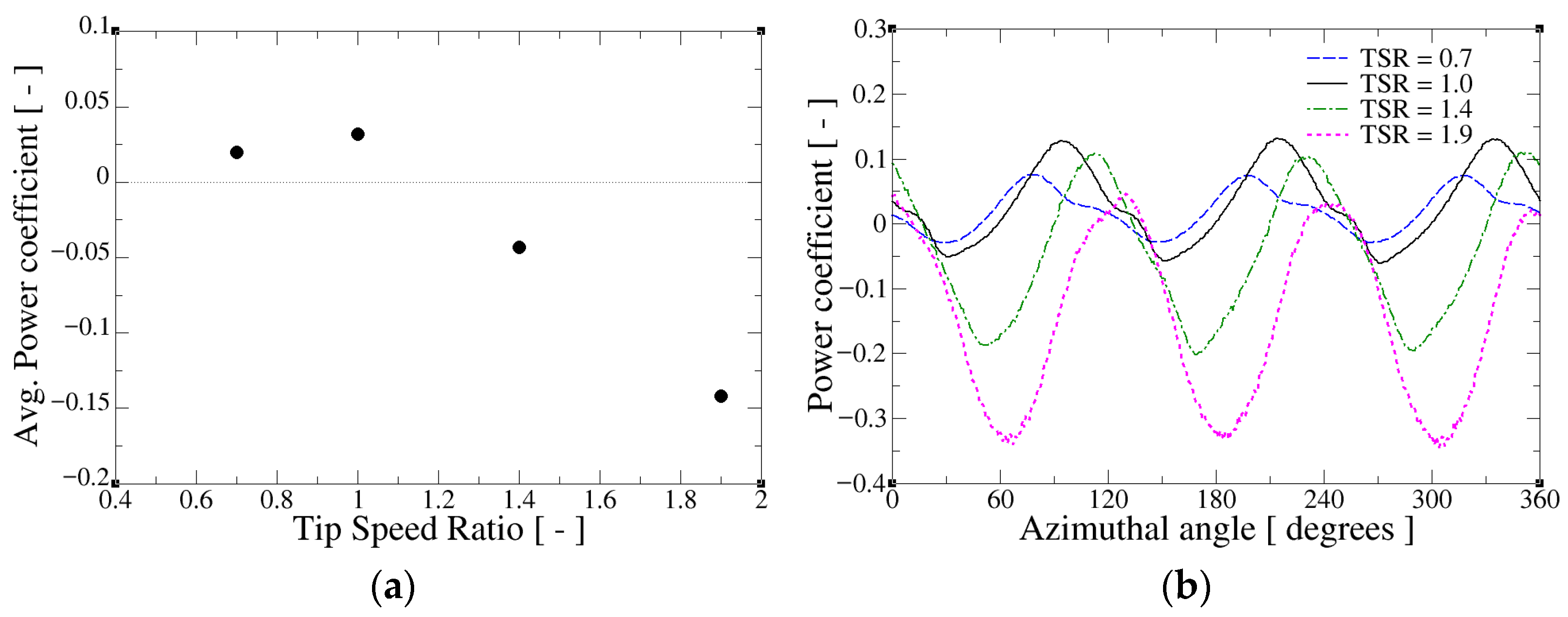
- The twin-turbine configuration yielded improved energy extraction compared to single turbines. Specifically, the combined power output was slightly higher than the sum of individual performances, primarily owing to the interactions between turbines that affected flow acceleration and wake interactions. In particular, the TT2D configuration showed an increase of approximately 40% in the mean power coefficient compared with the single-turbine case. Further reducing the spacing between turbines in the TT1.5D configuration resulted only in a marginal variation of , which became negligible at the optimal tip speed ratio of . Although wake recovery was slower in the twin system, the overall efficiency gains underscored the potential benefits of turbine clustering for deploying in real-world riverine and tidal flows.
- Visualization of flow structures and analysis of skin friction and pressure coefficient distributions across the blade surfaces quantified the impact of turbine interactions on blade hydrodynamics. Specifically, in the twin-turbine configuration, the bound vortex detachment process is slowed compared to the single-turbine case, altering the distribution of friction lines on the intrados and extrados and thereby modifying the hydrodynamic forces acting on the blades. This delayed vortex shedding, induced by the interaction between the turbine blades at the angular positions where they are closest to each other, produces a temporary increase in lift, which accounts for the torque enhancement observed in the twin-turbine arrangement.
- The limitations of the present work are mainly associated with the symmetrical boundary conditions imposed at the flume free surface and with the turbulence model employed. To address cases with lower turbine immersion depths, proper modeling of free surface deformation is required (e.g., through VOF techniques). Likewise, high-fidelity simulations within the Large Eddy Simulation framework would provide a more detailed resolution of wake development. However, implementing both approaches would substantially increase the computational cost, and this challenge will be addressed in our future work.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bakken, T.H.; Sundt, H.; Ruud, A.; Harby, A. Development of Small Versus Large Hydropower in Norway—Comparison of Environmental Impacts. Energy Procedia 2012, 20, 185–199. [Google Scholar] [CrossRef]
- Lain, S.; Lopez Mejia, O.D. Special Issue on “CFD Modelling and Simulation of Water Turbines”. Processes 2022, 10, 2410. [Google Scholar] [CrossRef]
- Reddy, K.B.; Bhosale, A.C.; Saini, R.P. Performance parameters of lift-based vertical axis hydrokinetic turbines—A review. Ocean Eng. 2022, 266, 113089. [Google Scholar] [CrossRef]
- Kinzel, M.; Araya, D.B.; Dabiri, J.O. Turbulence in vertical axis wind turbine canopies. Phys. Fluids 2015, 27, 115102. [Google Scholar] [CrossRef]
- Gorlov, A. Development of the Helical Reaction Hydraulic Turbine; Final Technical Report; Northeastern University: Boston, MA, USA, 1998. [Google Scholar] [CrossRef]
- Mejia, O.D.L.; Quiñones, J.J.; Laín, S. RANS and Hybrid RANS-LES Simulations of an H-Type Darrieus Vertical Axis Water Turbine. Energies 2018, 11, 2348. [Google Scholar] [CrossRef]
- López, O.D.; Mejia, O.E.; Escorcia, K.M.; Suarez, F.; Lain, S. Comparison of Sliding and Overset Mesh Techniques in the Simulation of a Vertical Axis Turbine for Hydrokinetic Applications. Processes 2021, 9, 1933. [Google Scholar] [CrossRef]
- Lain, S.; Taborda, M.A.; López, O.D. Numerical Study of the Effect of Winglets on the Performance of a Straight Blade Darrieus Water Turbine. Energies 2018, 11, 297. [Google Scholar] [CrossRef]
- Kunasekaran, M.; Hyung Rhee, S.; Venkatesan, N.; Samad, A. Design optimization of a marine current turbine having winglet on blade. Ocean Eng. 2021, 239, 109877. [Google Scholar] [CrossRef]
- Barbarić, M.; Batistić, I.; Guzović, Z. Numerical study of the flow field around hydrokinetic turbines with winglets on the blades. Renew. Energy 2022, 192, 692–704. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, B.; Jing, F.; Mei, Y. Hydrodynamic performance and flow field characteristics of tidal current energy turbine with and without winglets. J. Mar. Sci. Eng. 2023, 11, 2344. [Google Scholar] [CrossRef]
- El-Sawy, M.; Shehata, A.S.; Elbatran, A.H.A.; Tawfiq, A. Numerical simulation of flow in hydrokinetic turbine channel to improve its efficiency by using first and second-law efficiency analysis. Ocean Eng. 2022, 244, 110400. [Google Scholar] [CrossRef]
- Doan, M.N.; Obi, S. Numerical study of the dynamic stall effect on a pair of cross-flow hydrokinetic turbines and associated torque enhancement due to flow blockage. J. Mar. Sci. Eng. 2021, 9, 829. [Google Scholar] [CrossRef]
- Guillaud, N.; Balarac, G.; Goncalvès, E.; Zanette, J. Large Eddy Simulations on Vertical Axis Hydrokinetic Turbines—Power coefficient analysis for various solidities. Renew. Energy 2020, 147, 473–486. [Google Scholar] [CrossRef]
- Ouro, P.; Runge, S.; Luo, Q.; Stoesser, T. Three-dimensionality of the wake recovery behind a vertical axis turbine. Renew. Energy 2019, 133, 1066–1077. [Google Scholar] [CrossRef]
- Müller, S.; Muhawenimana, V.; Sonnino-Sorisio, G.; Wilson, C.A.M.E.; Cable, J.; Ouro, P. Fish response to the presence of hydrokinetic turbines as a sustainable energy solution. Sci. Rep. 2023, 13, 7459. [Google Scholar] [CrossRef]
- Lust, E.E.; Bailin, B.H.; Flack, K.A. Performance characteristics of a cross-flow hydrokinetic turbine in current only and current and wave conditions. Ocean Eng. 2021, 219, 108362. [Google Scholar] [CrossRef]
- Gauvin-Tremblay, O.; Dumas, G. Two-way interaction between river and deployed cross-flow hydrokinetic turbines. J. Renew. Sustain. Energy 2020, 12, 034501. [Google Scholar] [CrossRef]
- Gauvin-Tremblay, O.; Dumas, G. Hydrokinetic turbine array analysis and optimization integrating blockage effects and turbine-wake interactions. Renew. Energy 2022, 181, 851–869. [Google Scholar] [CrossRef]
- Morales-Ramirez, C.M.; Benavides-Morán, A.; López-Mejía, O.D. Integrated overset mesh and volume of fluid method for modeling free-surface dynamics in vertical axis hydrokinetic turbines at low Reynolds numbers. Phys. Fluids 2025, 37, 037106. [Google Scholar] [CrossRef]
- Alkan, E.; Yuce, M.I.; Öztürkmen, G. Evaluation of Wake Structure Induced by Helical Hydrokinetic Turbine. Water 2025, 17, 2203. [Google Scholar] [CrossRef]
- Runge, S.; Stoesser, T.; Morris, E.; White, M. Technology Readiness of a Vertical-Axis Hydro-Kinetic Turbine. J. Power Energy Eng. 2018, 6, 63–85. [Google Scholar] [CrossRef]
- El Fajri, O.; Bhushan, S.; Thompson, D.; O’Doherty, T. Numerical investigation of shallow-water effects on hydrokinetic turbine wake recovery. Int. Mar. Energy J. 2020, 3, 25–35. [Google Scholar] [CrossRef]
- Dong, G.; Zhao, Z.; Xu, C.; Qin, J. Wake dynamics of side-by-side hydrokinetic turbines in open channel flows. Phys. Fluids 2024, 36, 115166. [Google Scholar] [CrossRef]
- Müller, S.; Muhawenimana, V.; Wilson, C.A.M.E.; Ouro, P. Experimental investigation of the wake characteristics behind twin vertical axis turbines. Energy Convers. Manag. 2021, 247, 114768. [Google Scholar] [CrossRef]
- Zhang, A.; Liu, S.; Ma, Y.; Hu, C.; Li, Z. Field tests on model efficiency of twin vertical axis helical hydrokinetic turbines. Energy 2022, 247, 123376. [Google Scholar] [CrossRef]
- Moreau, M.; Germain, G.; Maurice, G. Experimental performance and wake study of a ducted twin vertical axis turbine in ebb and flood tide currents at a 1/20th scale. Renew. Energy 2023, 214, 318–333. [Google Scholar] [CrossRef]
- Ma, Y.; Zhu, Y.; Zhang, A.; Hu, C.; Liu, S.; Li, Z. Hydrodynamic performance of vertical axis hydrokinetic turbine based on Taguchi method. Renew. Energy 2022, 186, 573–584. [Google Scholar] [CrossRef]
- Chen, D.; Ma, Y.; Hu, C.; Zhao, T. Efficiency optimization of twin vertical-axis helical hydrokinetic turbines (VAHHTs) based on Taguchi method. Appl. Ocean Res. 2023, 138, 103618. [Google Scholar] [CrossRef]
- Ma, Y.; Hu, C.; Li, Y.; Li, L.; Deng, R.; Jiang, D. Hydrodynamic Performance Analysis of the Vertical Axis Twin-Rotor Tidal Current Turbine. Water 2018, 10, 1694. [Google Scholar] [CrossRef]
- Widyawan, H.B.; Satrio, D.; Mukhtasor. Numerical Investigation of Vertical-Axis Hydrokinetic Turbine on Side-by-Side Configuration. J. Phys. Conf. Ser. 2024, 2828, 012027. [Google Scholar] [CrossRef]
- Mohamed, O.S.; Melani, P.F.; Soraperra, G.; Brighenti, A.; Ferrara, G.; Betti, V.; Schippa, L.; Guerrero, M.; Balduzzi, F.; Bianchini, A. Three-dimensional CFD-ALM-VOF modeling of hydrokinetic turbines in realistic open-channel conditions. Ocean Eng. 2024, 313, 119411. [Google Scholar] [CrossRef]
- Sørensen, J.N.; Shen, W.Z. Numerical Modeling of Wind Turbine Wakes. J. Fluids Eng. 2002, 124, 393–399. [Google Scholar] [CrossRef]
- Posa, A. Wake characterization of coupled configurations of vertical axis wind turbines using Large Eddy Simulation. Int. J. Heat Fluid Flow 2019, 75, 27–43. [Google Scholar] [CrossRef]
- Posa, A. Dependence of the wake recovery downstream of a Vertical Axis Wind Turbine on its dynamic solidity. J. Wind. Eng. Ind. Aerodyn. 2020, 202, 104212. [Google Scholar] [CrossRef]
- Mohamed, O.S.; Melani, P.F.; Soraperra, G.; Brighenti, A.; Ferrara, G.; Betti, V.; Balduzzi, F.; Bianchini, A. Development of a computationally efficient CFD model for vertical-axis hydrokinetic turbines. Ocean Eng. 2025, 324, 120692. [Google Scholar] [CrossRef]
- Cacciali, L.; Battisti, L.; Dell’Anna, S. Multi-Array Design for Hydrokinetic Turbines in Hydropower Canals. Energies 2023, 16, 2279. [Google Scholar] [CrossRef]
- Velásquez, L.; Rengifo, J.; Saldarriaga, A.; Rubio-Clemente, A.; Chica, E. Optimization of Vertical-Axis Hydrokinetic Turbines: Study of Various Geometric Configurations Using the Response Surface Methodology and Multi-Criteria Decision Matrices. Processes 2025, 13, 1950. [Google Scholar] [CrossRef]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application, 2nd ed.; Wiley: Chichester, UK, 2009. [Google Scholar]
- Roy, S.; Branger, H.; Luneau, C.; Bourras, D.; Paillard, B. Design of an offshore three-bladed vertical axis wind turbine for wind tunnel experiments. OMAE2017-61512. In Proceedings of the ASME 2017 36th International Conference on Ocean, Offshore and Arctic Engineering OMAE2017, Trondheim, Norway, 25–30 June 2017. [Google Scholar] [CrossRef]
- López, O.D.; Botero, N.; Nunez, E.E.; Lain, S. Performance Improvement of a Straight-Bladed Darrieus Hydrokinetic Turbine through Enhanced Winglet Designs. J. Mar. Sci. Technol. 2024, 12, 977. [Google Scholar] [CrossRef]
- Handa, B. Three-Dimensional Computational Fluid Dynamic Analysis of a Large-Scale Vertical Axis Wind Turbine. J. Aerosp. Eng. Mech. 2021, 5, 417–440. [Google Scholar] [CrossRef]
- Raciti-Castelli, M.; Englaro, A.; Benini, E. The Darrieus wind turbine: Proposal for a new performance prediction model based on CFD. Energy 2011, 36, 4919–4934. [Google Scholar] [CrossRef]
- Fertahi, S.D.; Samaouali, A.; Kadiri, I. CFD comparison of 2D and 3D aerodynamics in H-Darrieus prototype wake. E-Prime Adv. Electr. Eng. Electron. Energy 2023, 4, 100178. [Google Scholar] [CrossRef]
- Contreras, L.T.; Lopez, O.D.; Lain, S. Computational Fluid Dynamics Modelling and Simulation of an Inclined Horizontal Axis Hydrokinetic Turbine. Energies 2018, 11, 3151. [Google Scholar] [CrossRef]
- Gebreslassie, M.G.; Sanchez, S.O.; Tabor, G.R.; Belmont, M.R.; Bruce, T.; Payne, G.S.; Moon, I. Experimental and CFD analysis of the wake characteristics of tidal turbines. Int. J. Mar. Energy 2016, 16, 209–219. [Google Scholar] [CrossRef]
- McNaughton, J.; Afgan, I.; Apsley, D.D.; Rolfo, S.; Stallard, T.; Stansby, P.K. A simple sliding-mesh interface procedure and its application to the CFD simulation of a tidal-stream turbine. Int. J. Numer. Methods Fluids 2014, 74, 250–269. [Google Scholar] [CrossRef]
- Steger, J.L.; Dougherty, F.; Benet, J.A. A Chimera Grid Scheme; American Society of Mechanical Engineers, Fluids Engineering Division (Publication) FED: New York, NY, USA, 1983; Volume 5. [Google Scholar]
- Menter, F.J. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 269–289. [Google Scholar] [CrossRef]
- Langtry, R.B.; Menter, F.R. Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes. AIAA J. 2009, 47, 2894–2906. [Google Scholar] [CrossRef]
- Karakaya, D.; Elçi, S. Numerical Assessment of Vertical Axis Hydrokinetic Turbine Efficiencies With Different Grate Protections. IET Renew. Power Gener. 2025, 19, e70060. [Google Scholar] [CrossRef]
- Yagmur, S.; Kose, F.; Dogan, S. A study on performance and flow characteristics of single and double H-type Darrieus turbine for a hydro farm application. Energy Convers. Manag. 2021, 245, 114599. [Google Scholar] [CrossRef]
- Du, L. Numerical and Experimental Investigations of Darrieus Wind Turbine Start-Up and Operation. Ph.D. Thesis, Durham University, Durham, UK, 2016. Available online: http://etheses.dur.ac.uk/11384/1/Longhuan_Du_Thesis.pdf?DDD10+ (accessed on 20 November 2024).
- Spentzos, A.; Barakos, G.; Badcock, K.; Richards, B.; Wernert, P.; Schreck, S.; Raffel, M. Investigation of Three-Dimensional Dynamic Stall Using Computational Fluid Dynamics. AIAA J. 2005, 43, 1023–1033. [Google Scholar] [CrossRef]
- Tobak, M.; Peak, D.J. Topology of three-dimensional separated flows. Annu. Rev. Fluid. Mech. 1982, 14, 61–85. [Google Scholar] [CrossRef]
- Laín, S.; Cortés, P.; López, O.D. Numerical Simulation of the Flow around a Straight Blade Darrieus Water Turbine. Energies 2020, 13, 1137. [Google Scholar] [CrossRef]
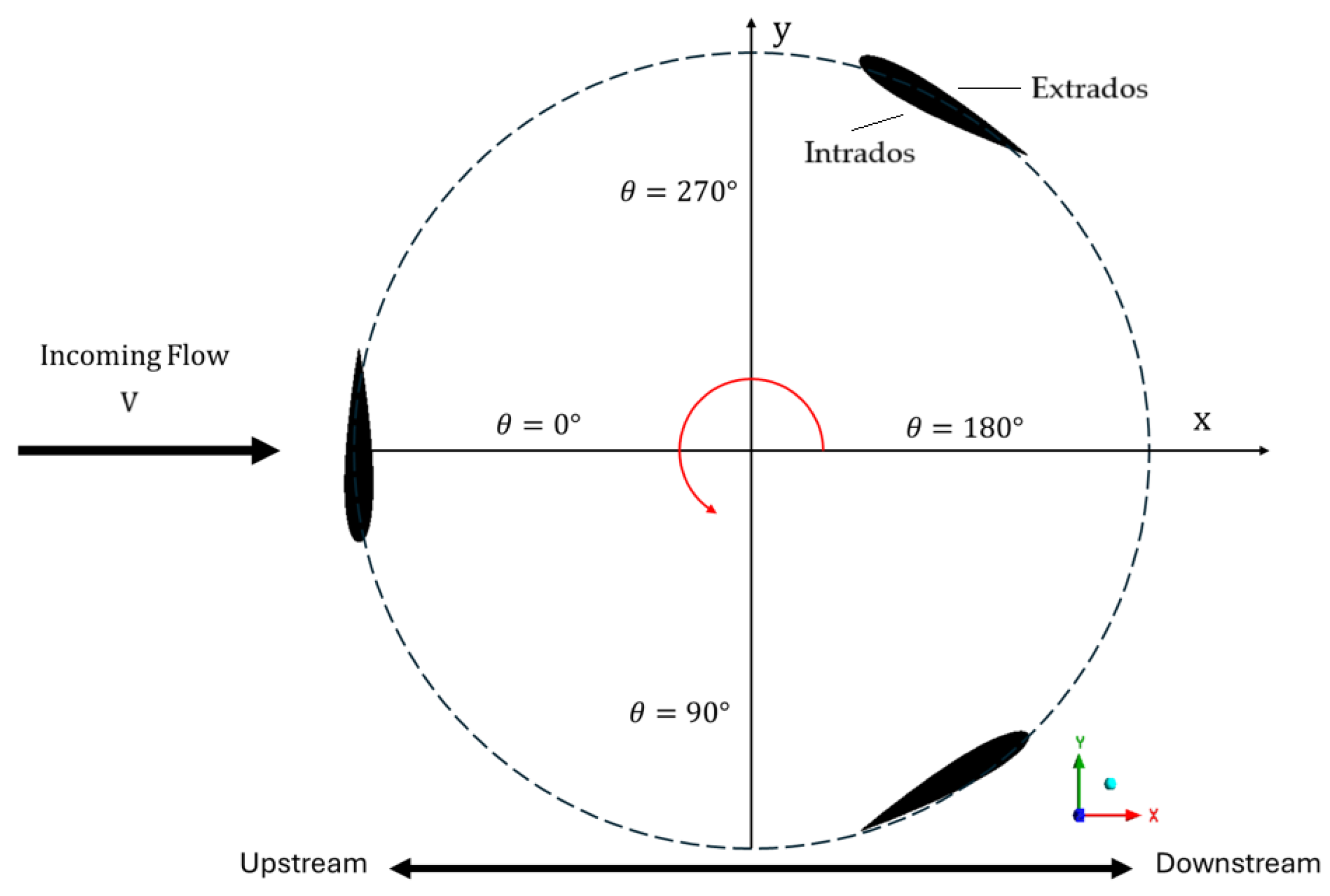
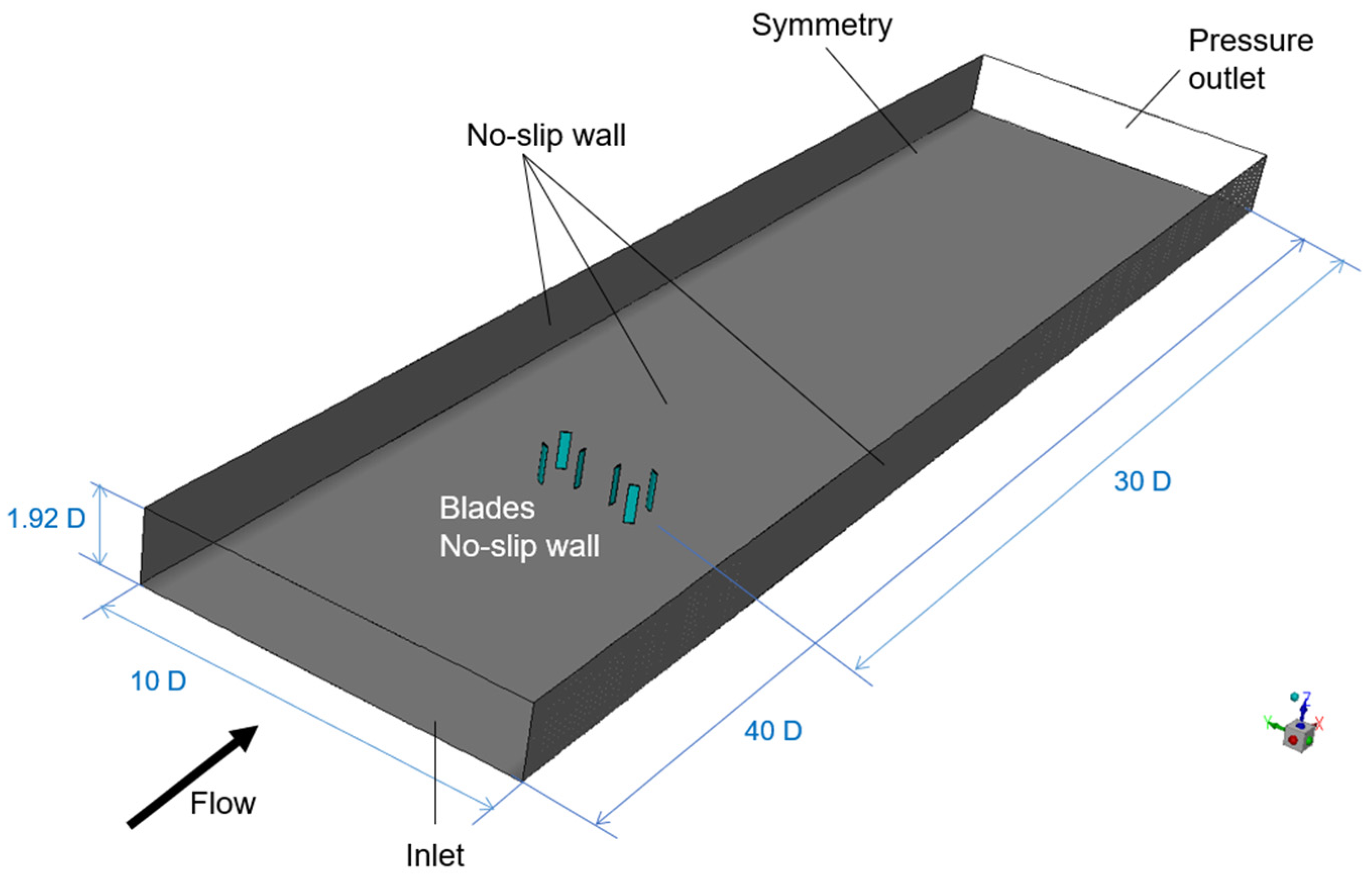
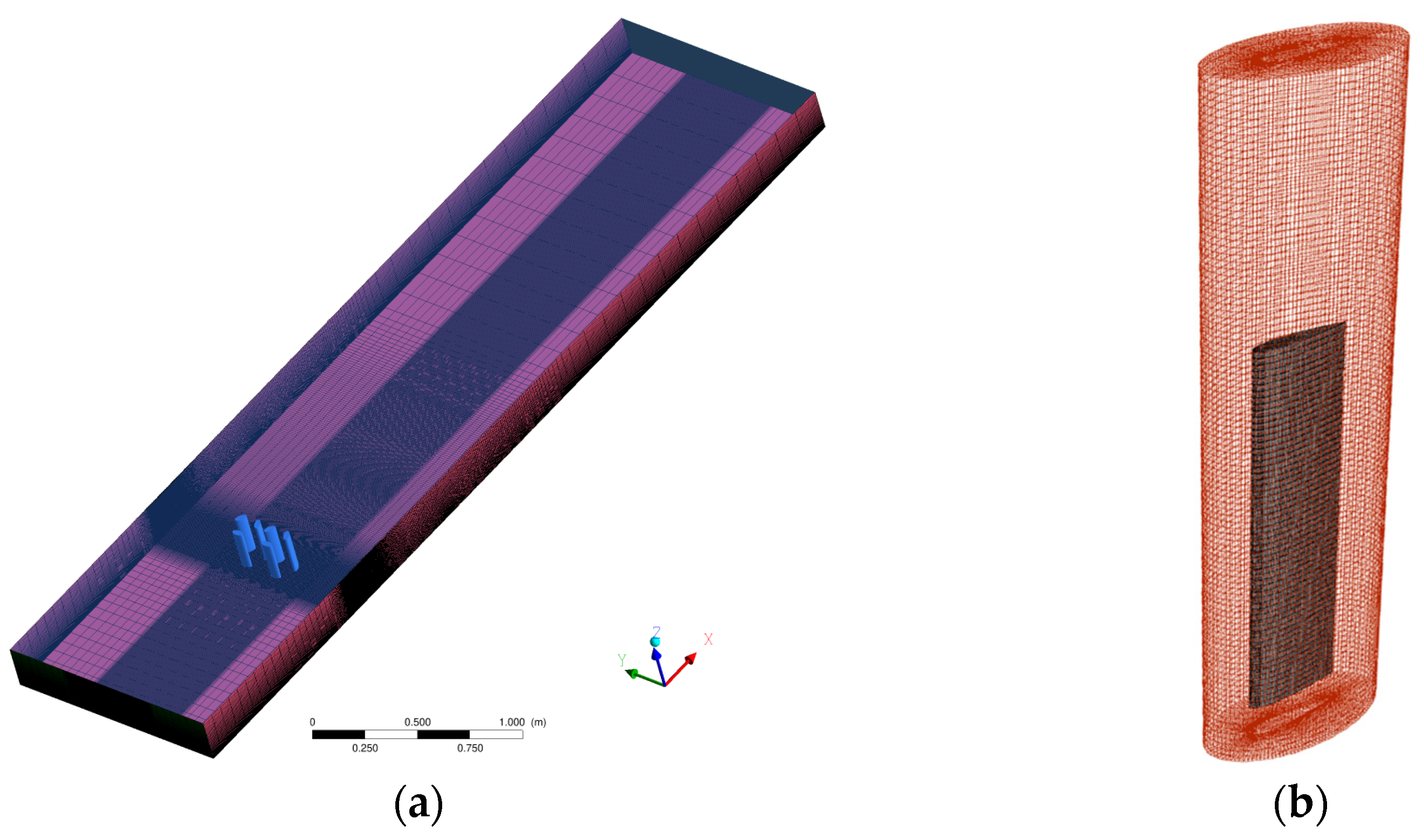



| Parameter | Value |
|---|---|
| Profile of the blades | NACA0015 |
| Turbine diameter () | 0.12 m |
| Blade span () | 0.12 m |
| Chord length () | 0.03 m |
| Number of blades () | 3 |
| Solidity | 0.24 |
| Parameter | Value |
|---|---|
| Volumetric flow | m3/s |
| Flow depth | m |
| Average upstream velocity | m/s |
| Bulk Reynolds number | |
| Froude number |
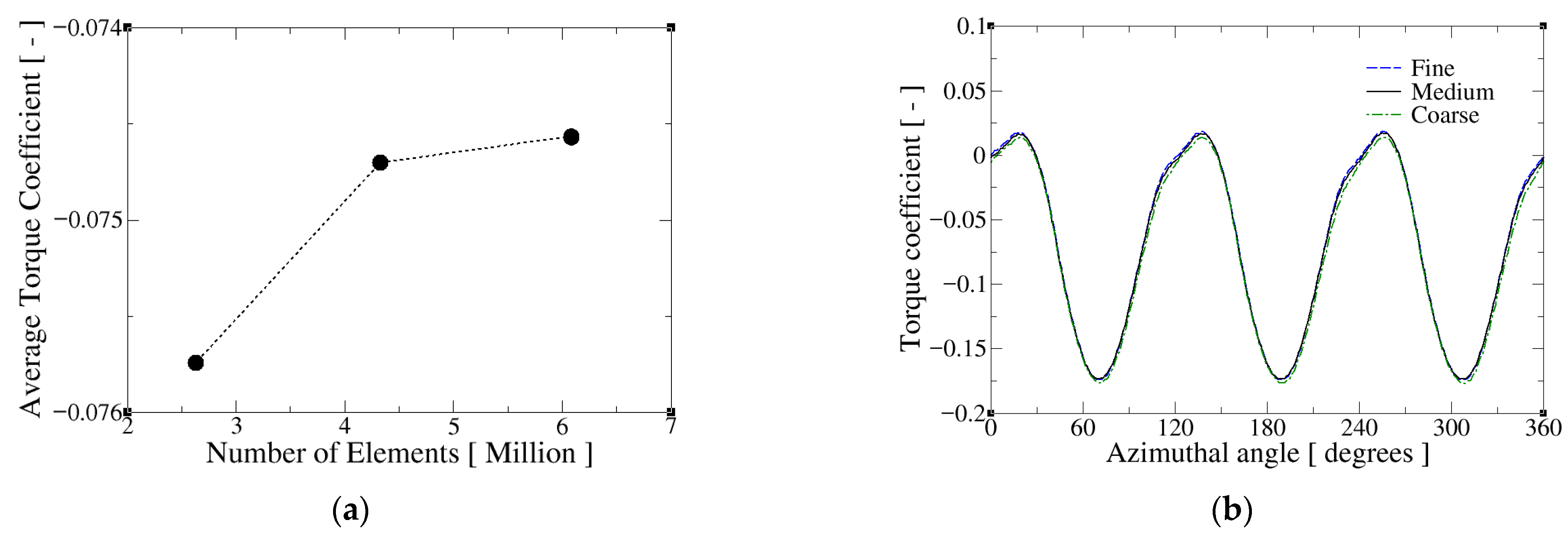
| Cell Number in Domain (in Million) | |||
|---|---|---|---|
| Grid | Background | ) | Total |
| Coarse | 1.32 | 0.43 | 2.6 |
| Medium | 1.85 | 0.78 | 4.2 |
| Fine | 2.58 | 1.17 | 6.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laín, S.; Viveros, M.; Benavides-Morán, A.; Ouro, P. Numerical Study of the Flow Around Twin Straight-Bladed Darrieus Hydrokinetic Turbines. J. Mar. Sci. Eng. 2025, 13, 1947. https://doi.org/10.3390/jmse13101947
Laín S, Viveros M, Benavides-Morán A, Ouro P. Numerical Study of the Flow Around Twin Straight-Bladed Darrieus Hydrokinetic Turbines. Journal of Marine Science and Engineering. 2025; 13(10):1947. https://doi.org/10.3390/jmse13101947
Chicago/Turabian StyleLaín, Santiago, Miguel Viveros, Aldo Benavides-Morán, and Pablo Ouro. 2025. "Numerical Study of the Flow Around Twin Straight-Bladed Darrieus Hydrokinetic Turbines" Journal of Marine Science and Engineering 13, no. 10: 1947. https://doi.org/10.3390/jmse13101947
APA StyleLaín, S., Viveros, M., Benavides-Morán, A., & Ouro, P. (2025). Numerical Study of the Flow Around Twin Straight-Bladed Darrieus Hydrokinetic Turbines. Journal of Marine Science and Engineering, 13(10), 1947. https://doi.org/10.3390/jmse13101947








