Mechanism and Optimization of Acoustic Absorption of an Underwater Lattice-Reinforced Meta-Absorber
Abstract
1. Introduction
2. Analytical Model and Method
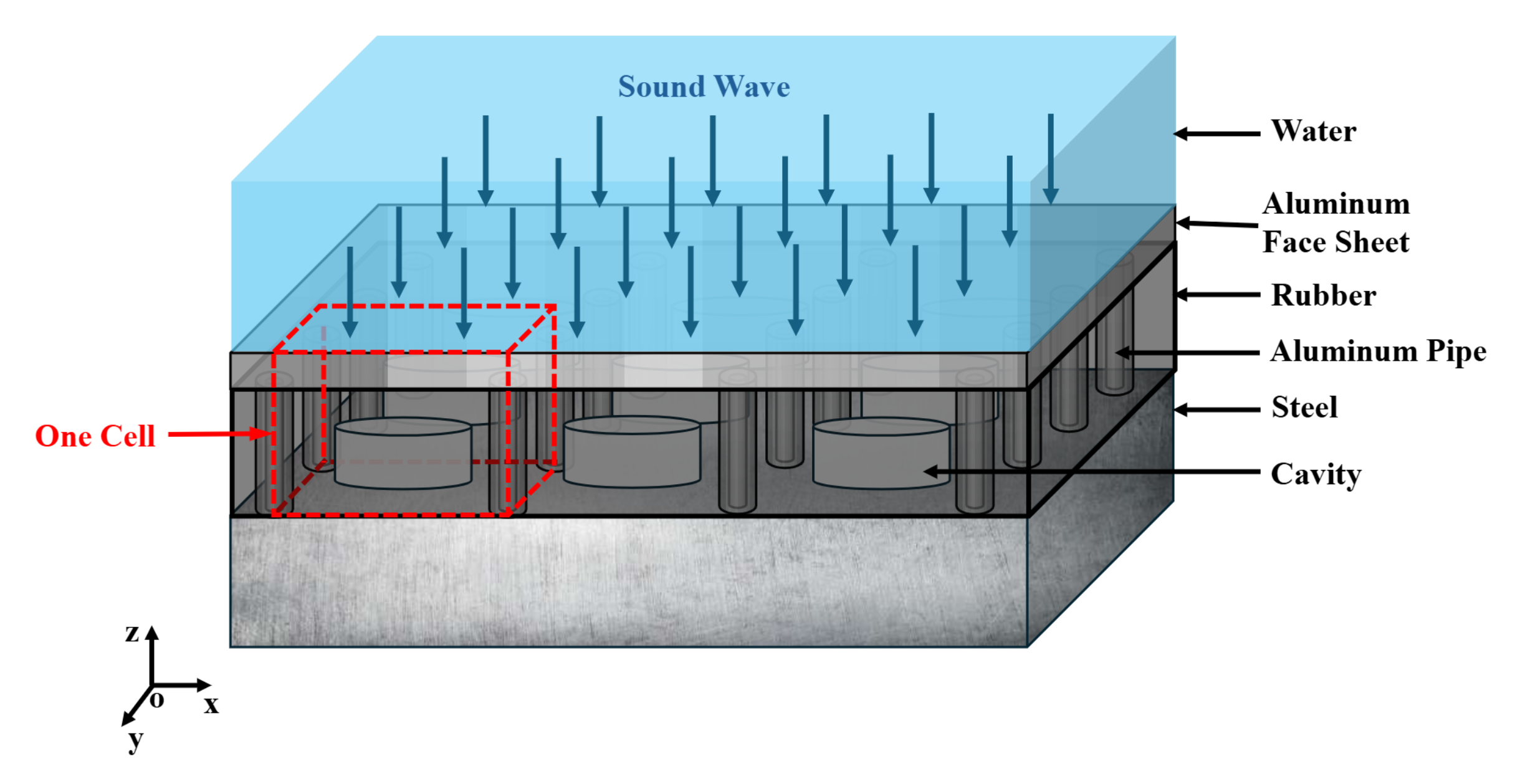
2.1. Theoretical Model
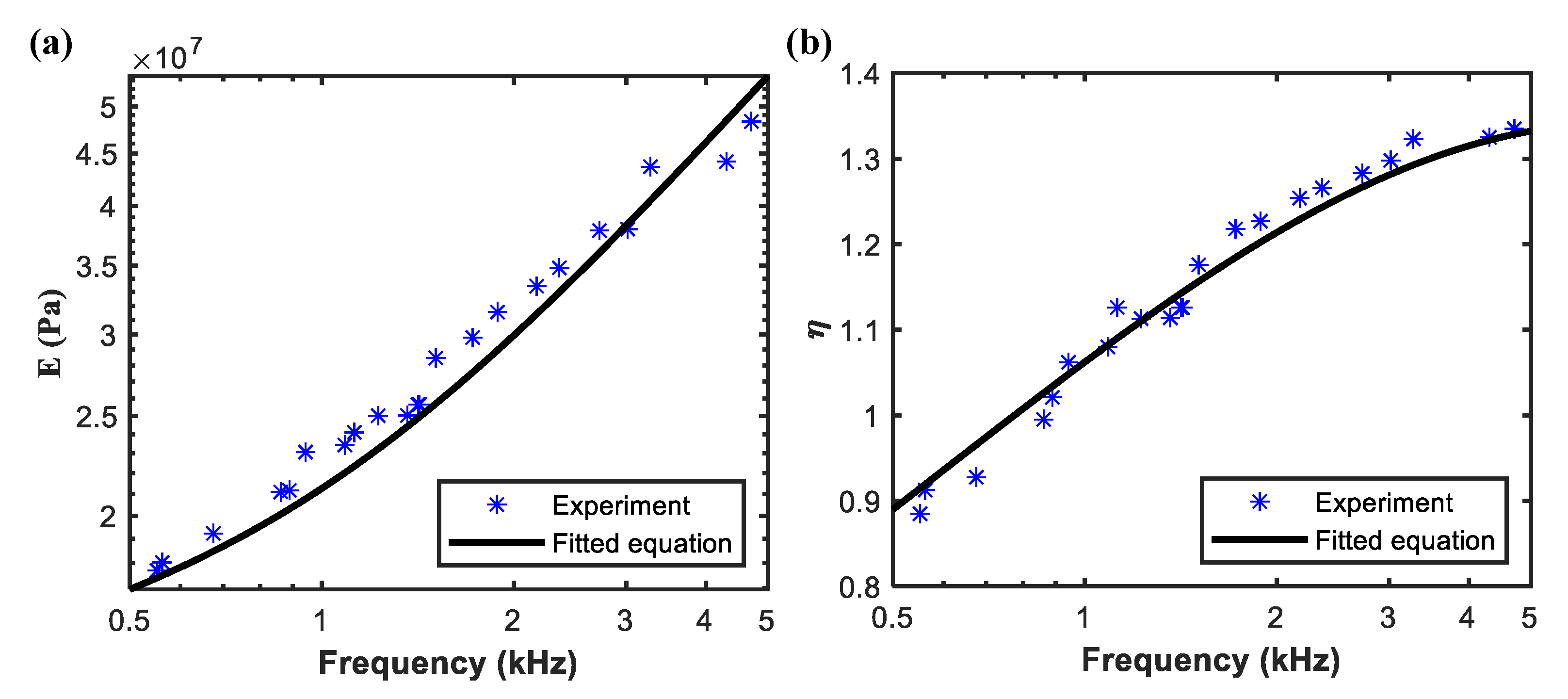
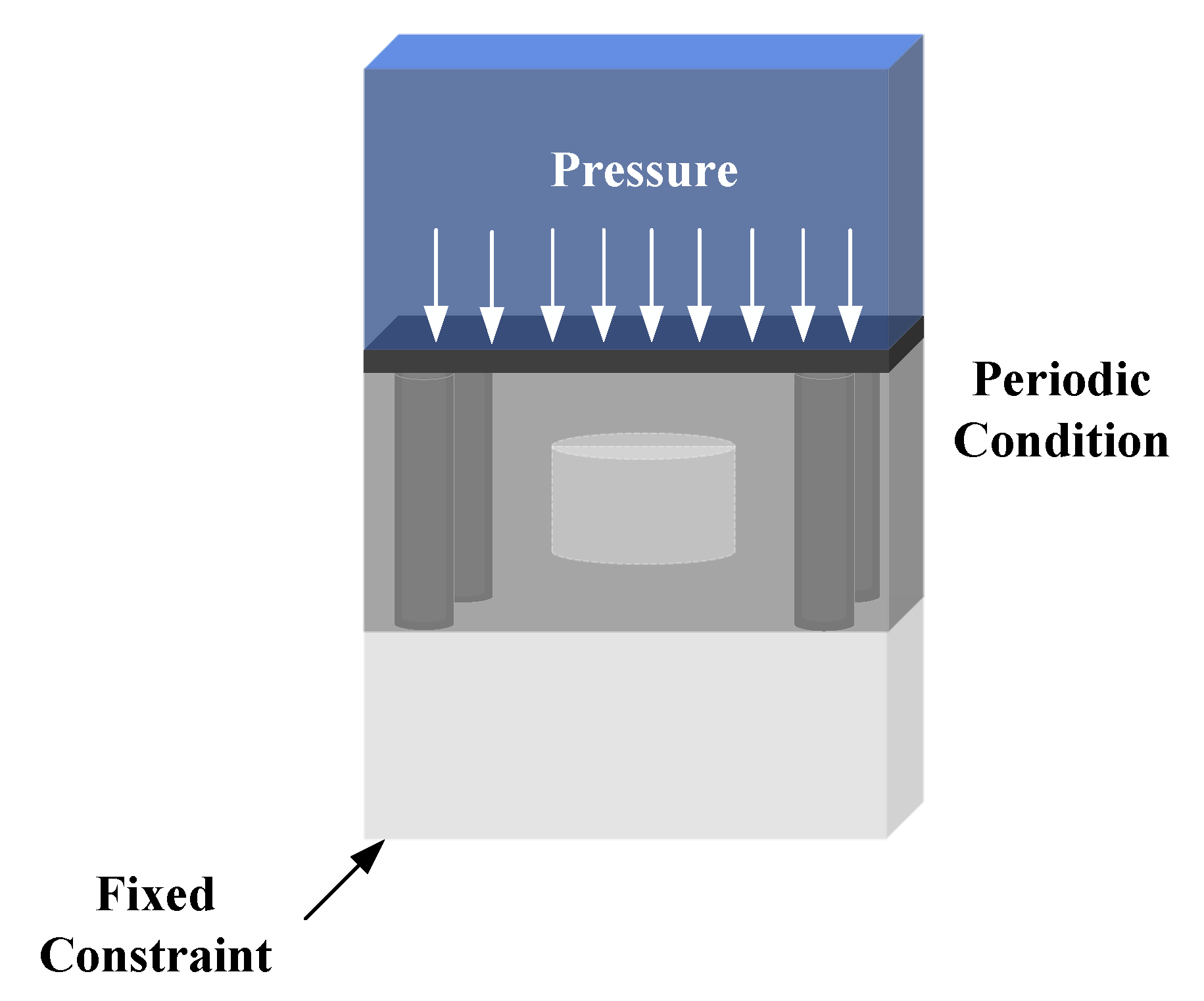
2.2. Finite Element Method
3. Sound Absorption Characteristics and Mechanism
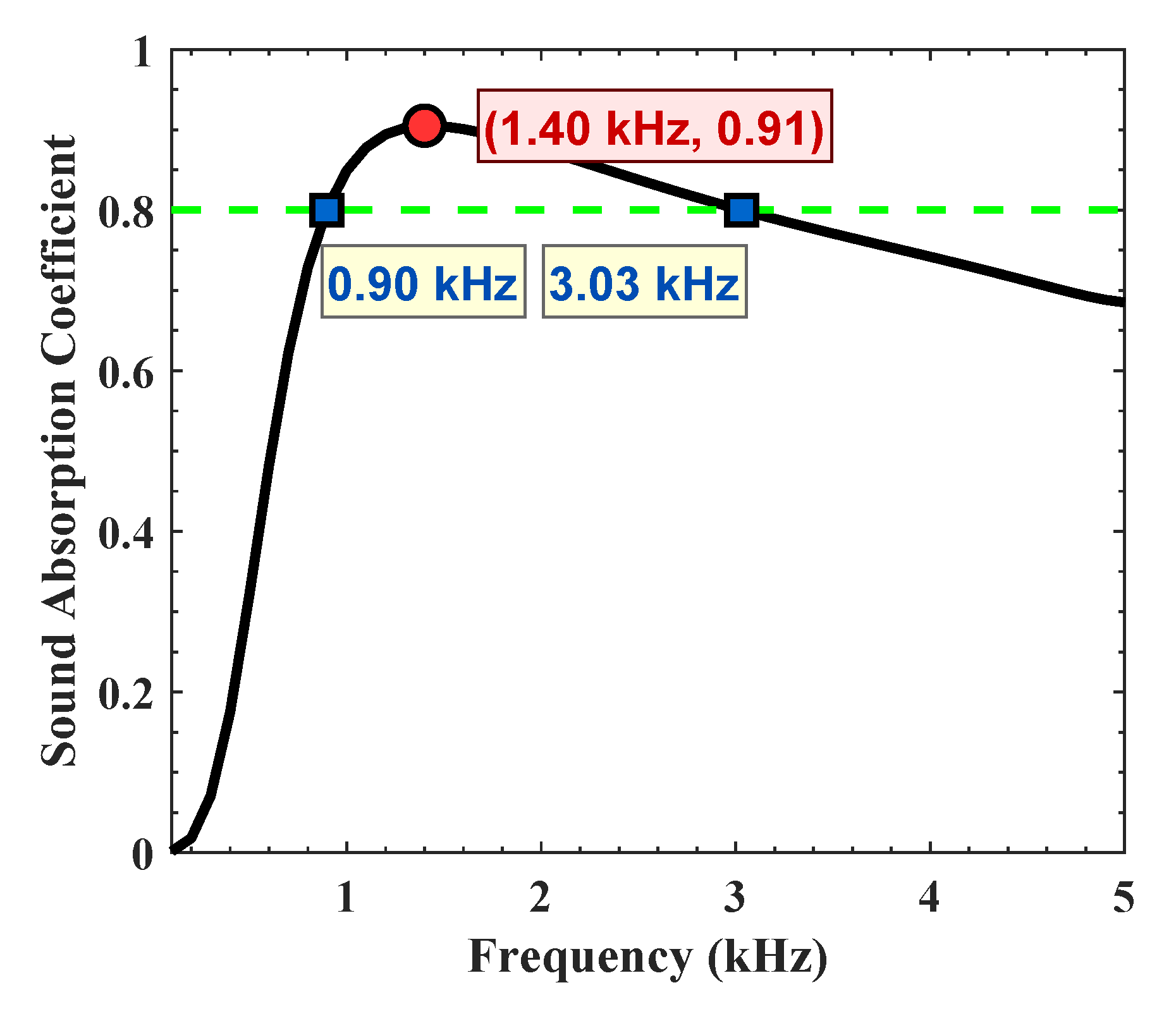
3.1. Sound Absorption Characteristic
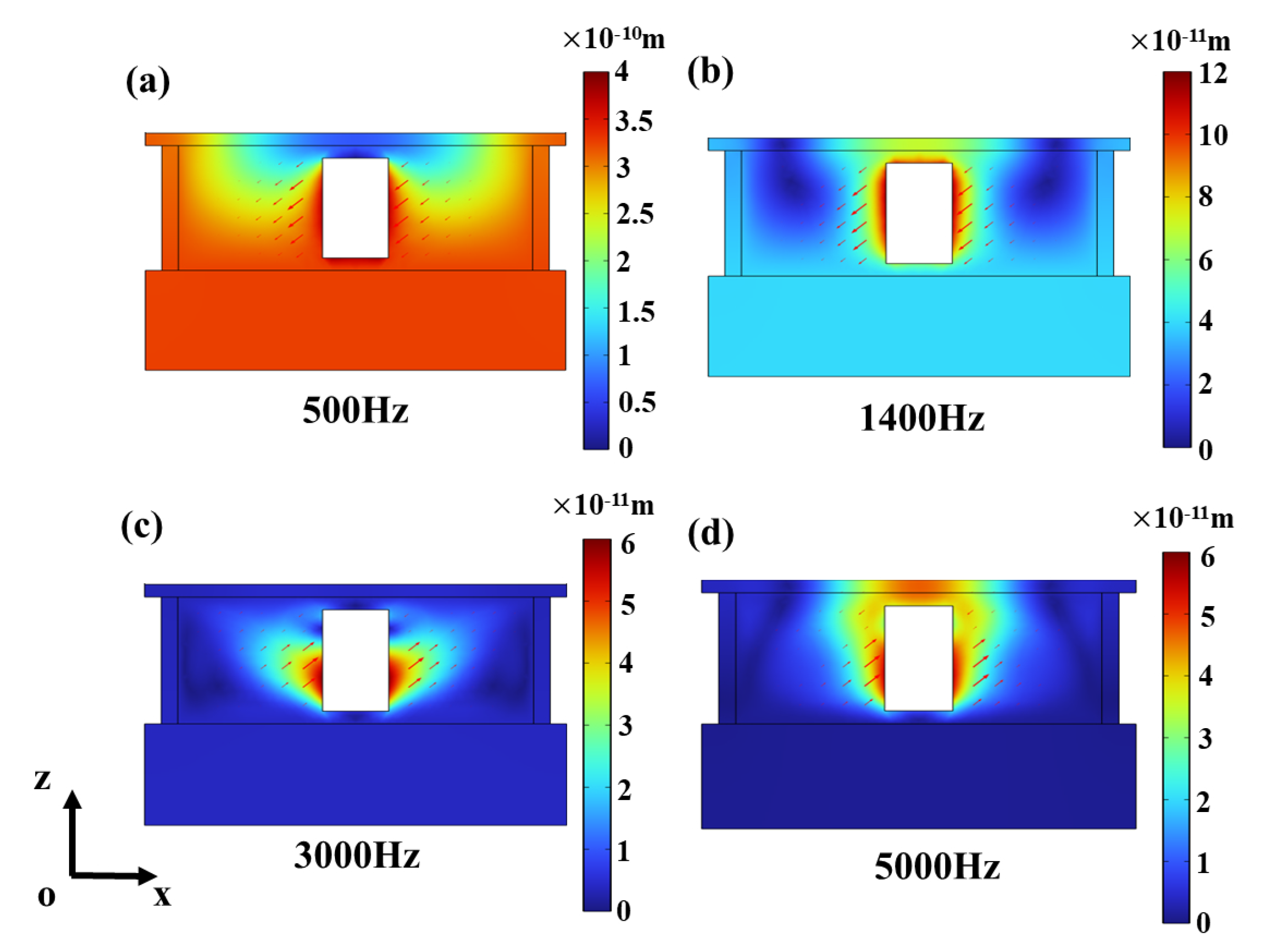
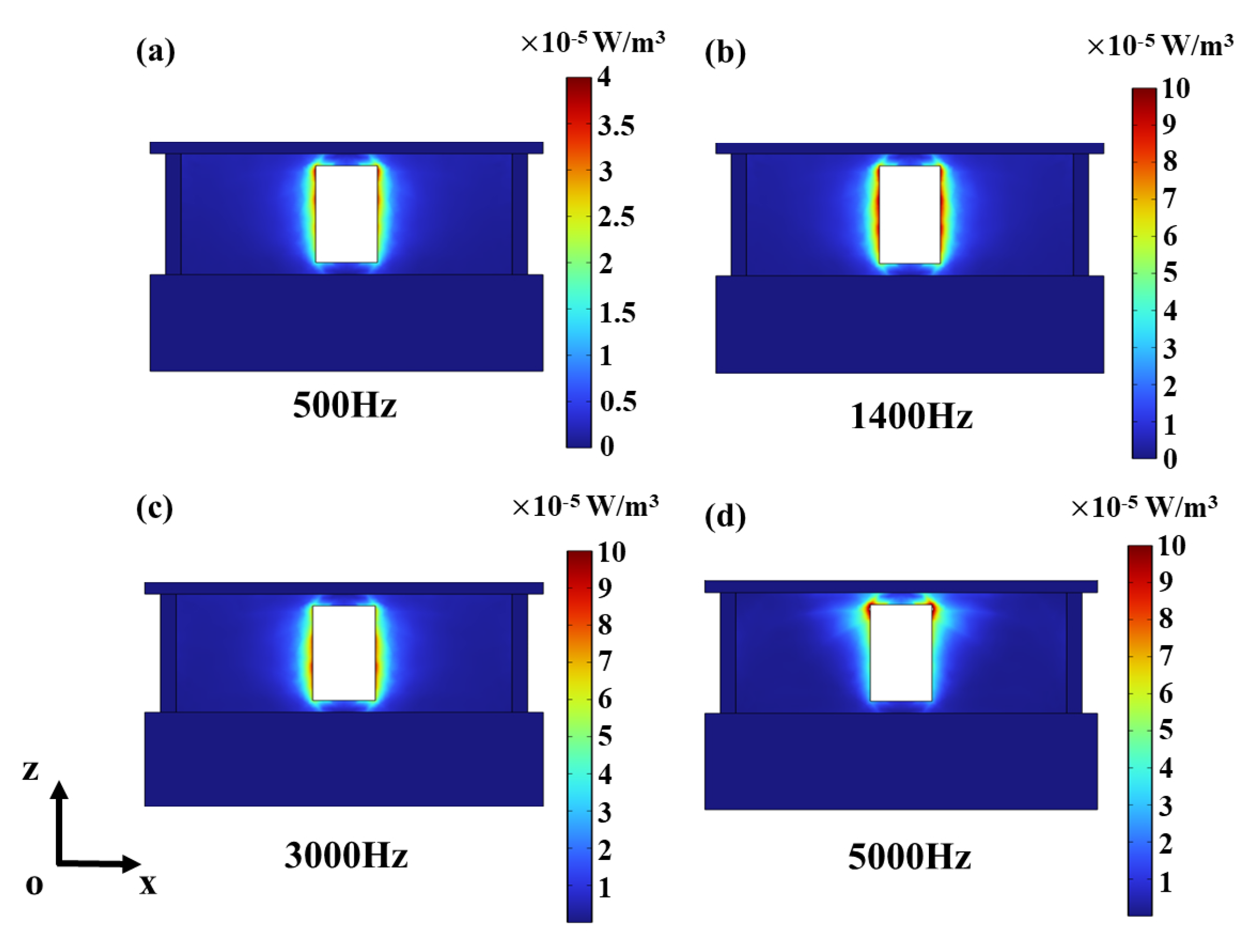
3.2. Sound Absorption Mechanism
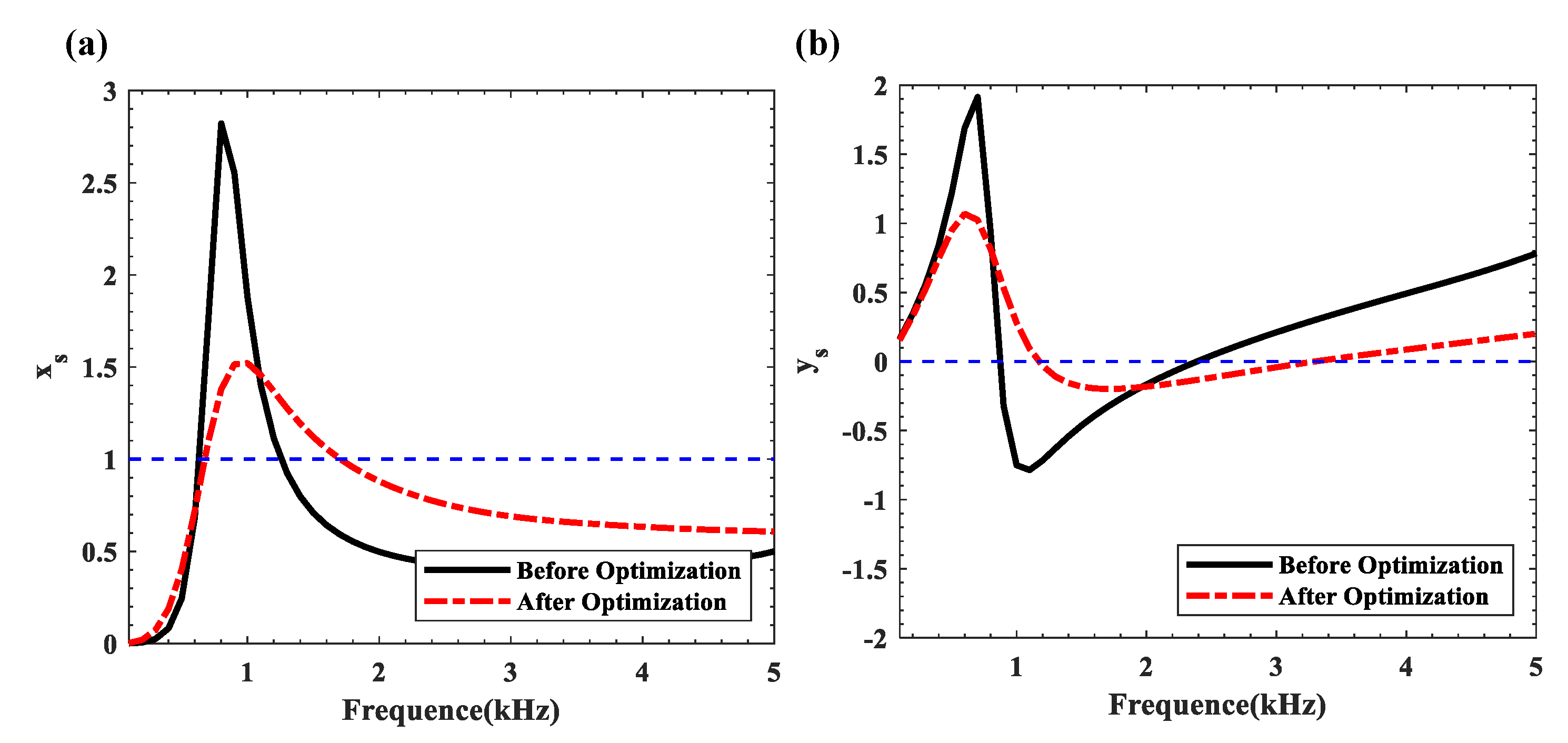
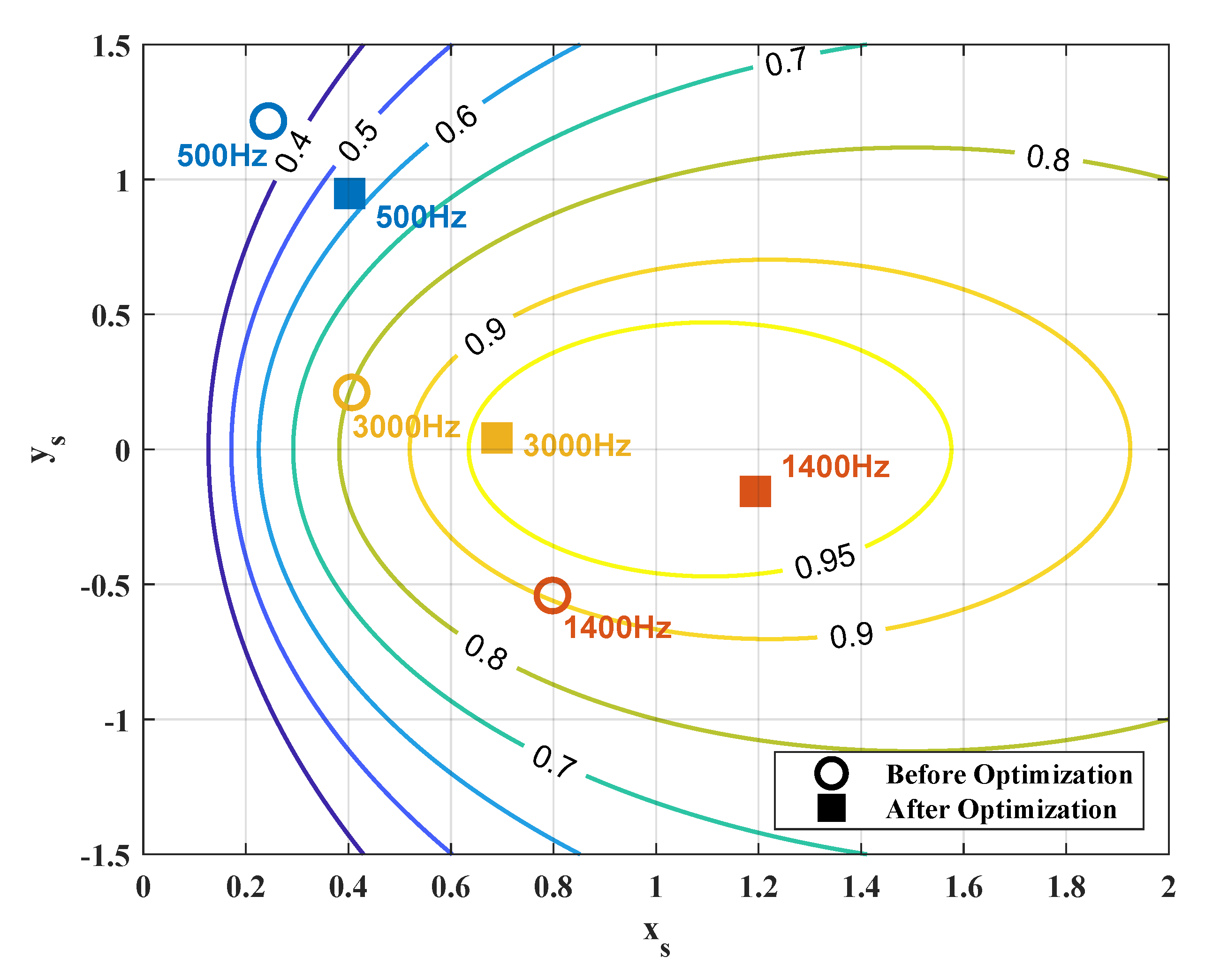
4. Optimization Design
5. Result Discussions
5.1. Parameter Influence on the Sound Absorption
5.1.1. Influence of Cavity Radius
5.1.2. Influence of Aluminum Pipe Wall Thickness
5.1.3. Influence of Lattice Period
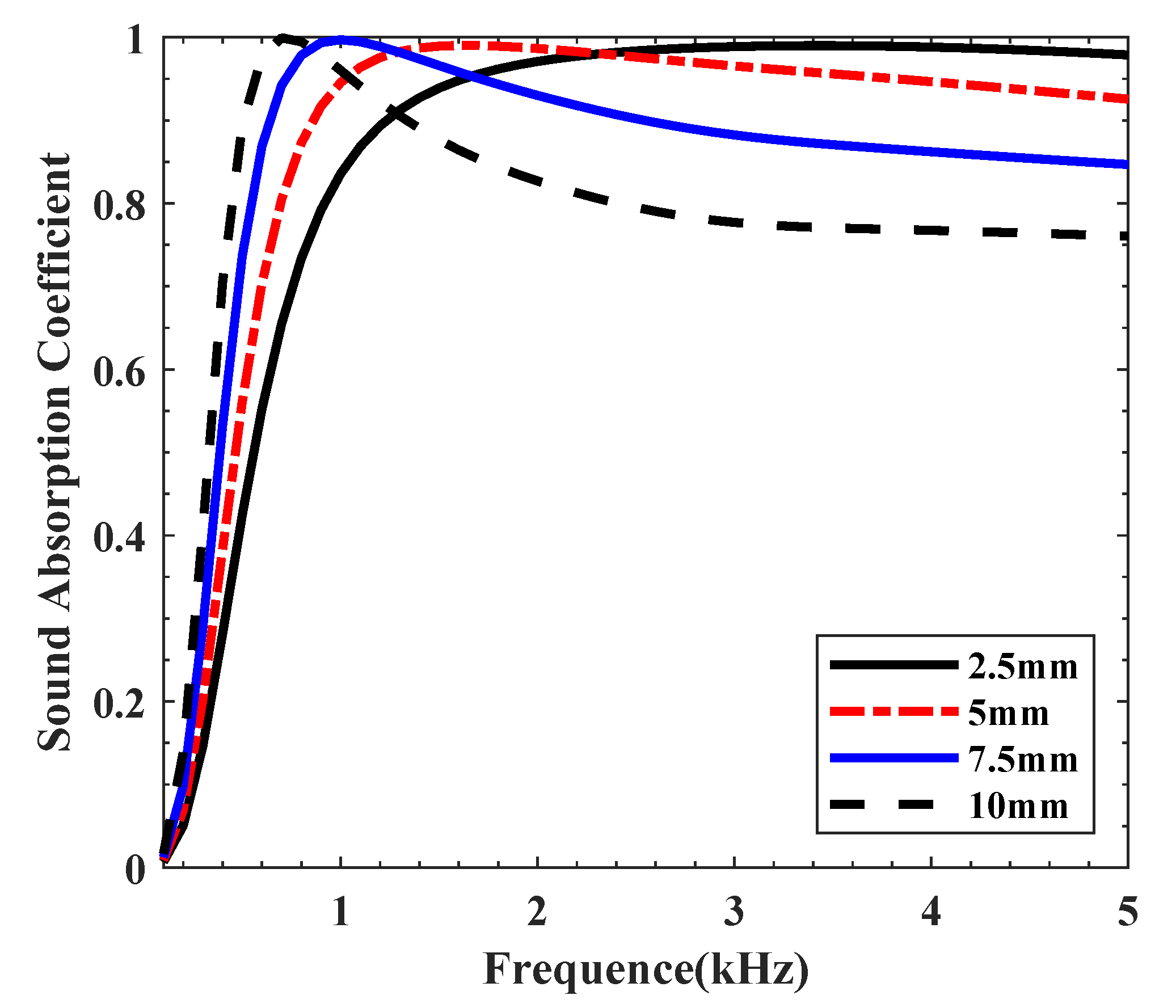
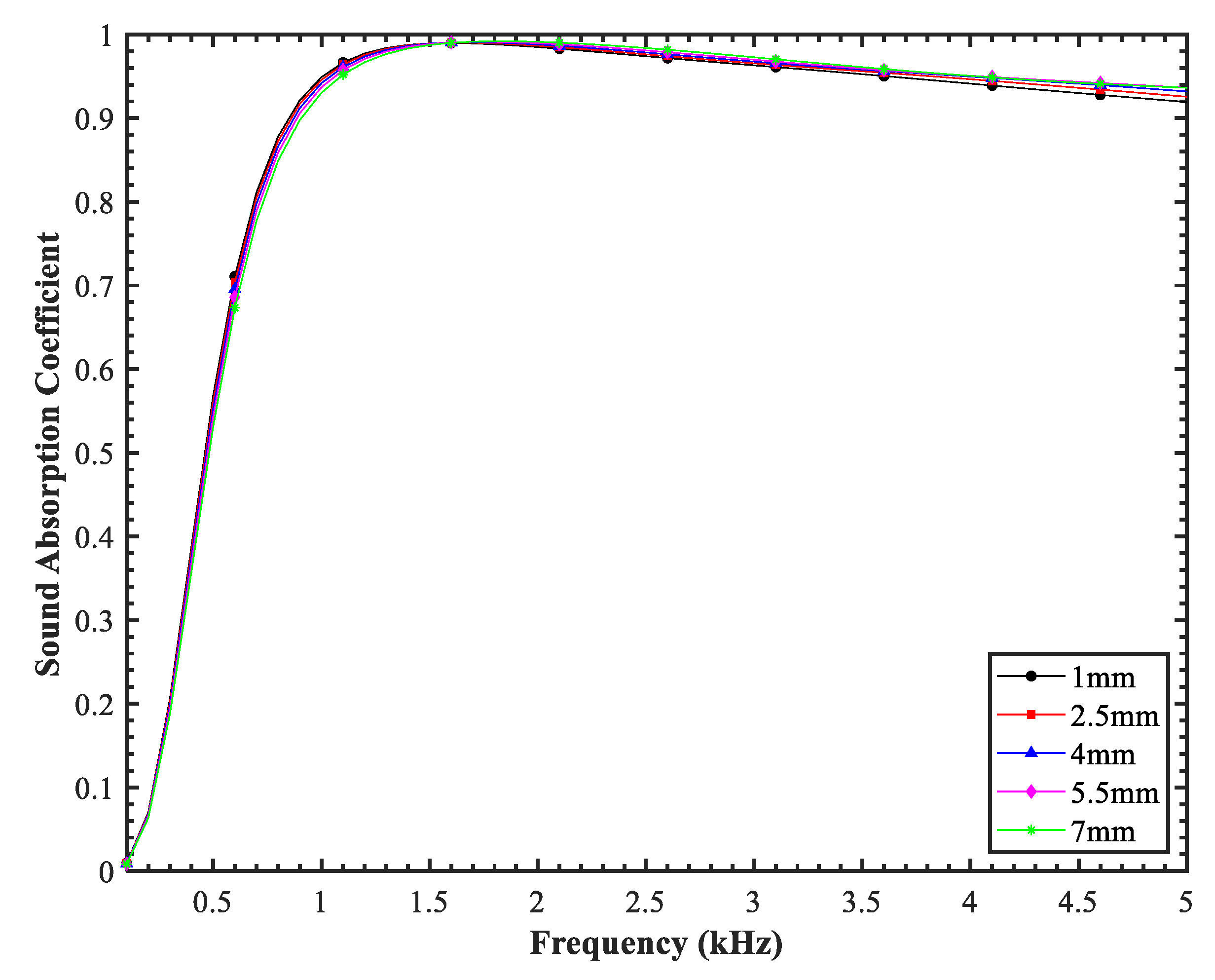
5.1.4. Influence of Face Sheet Thickness
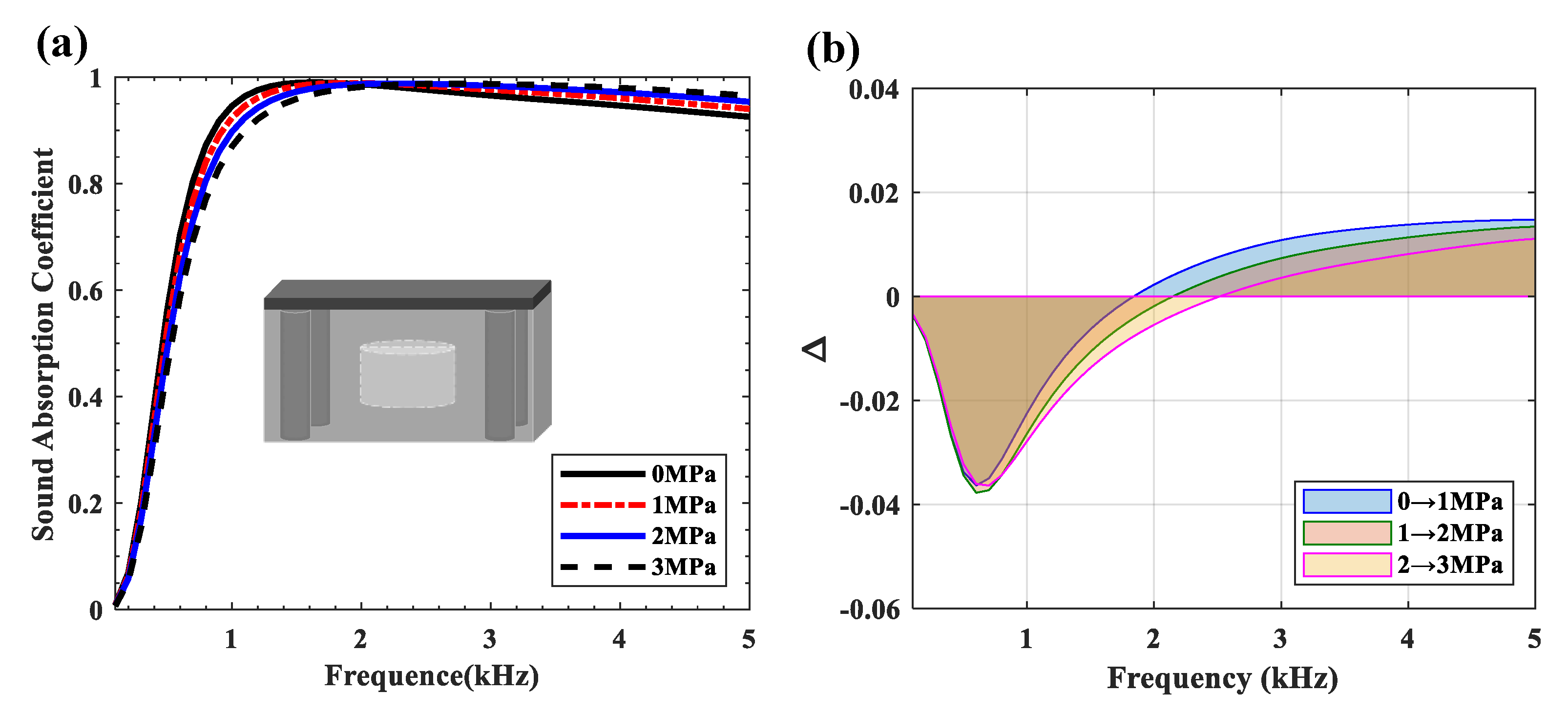
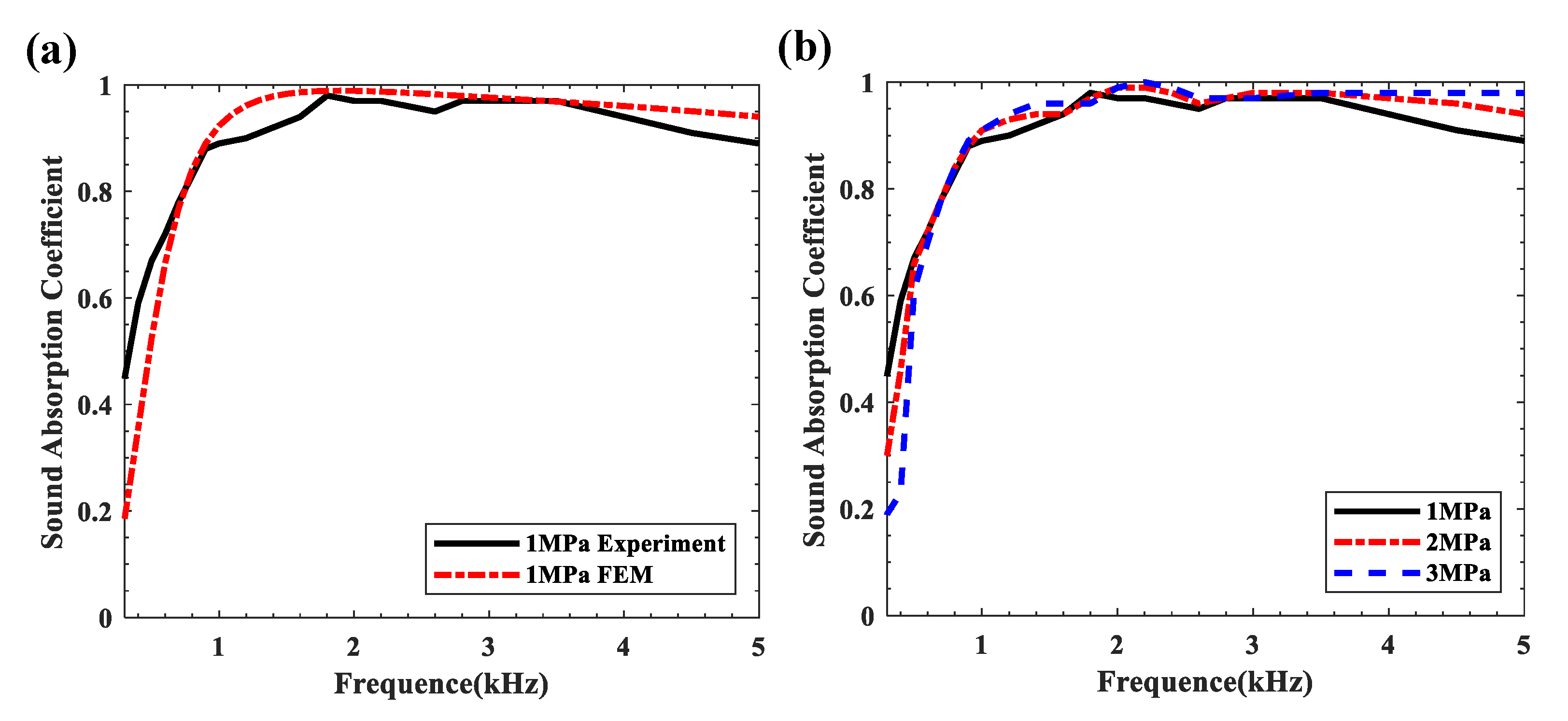
5.2. Influence of Hydrostatic Pressure
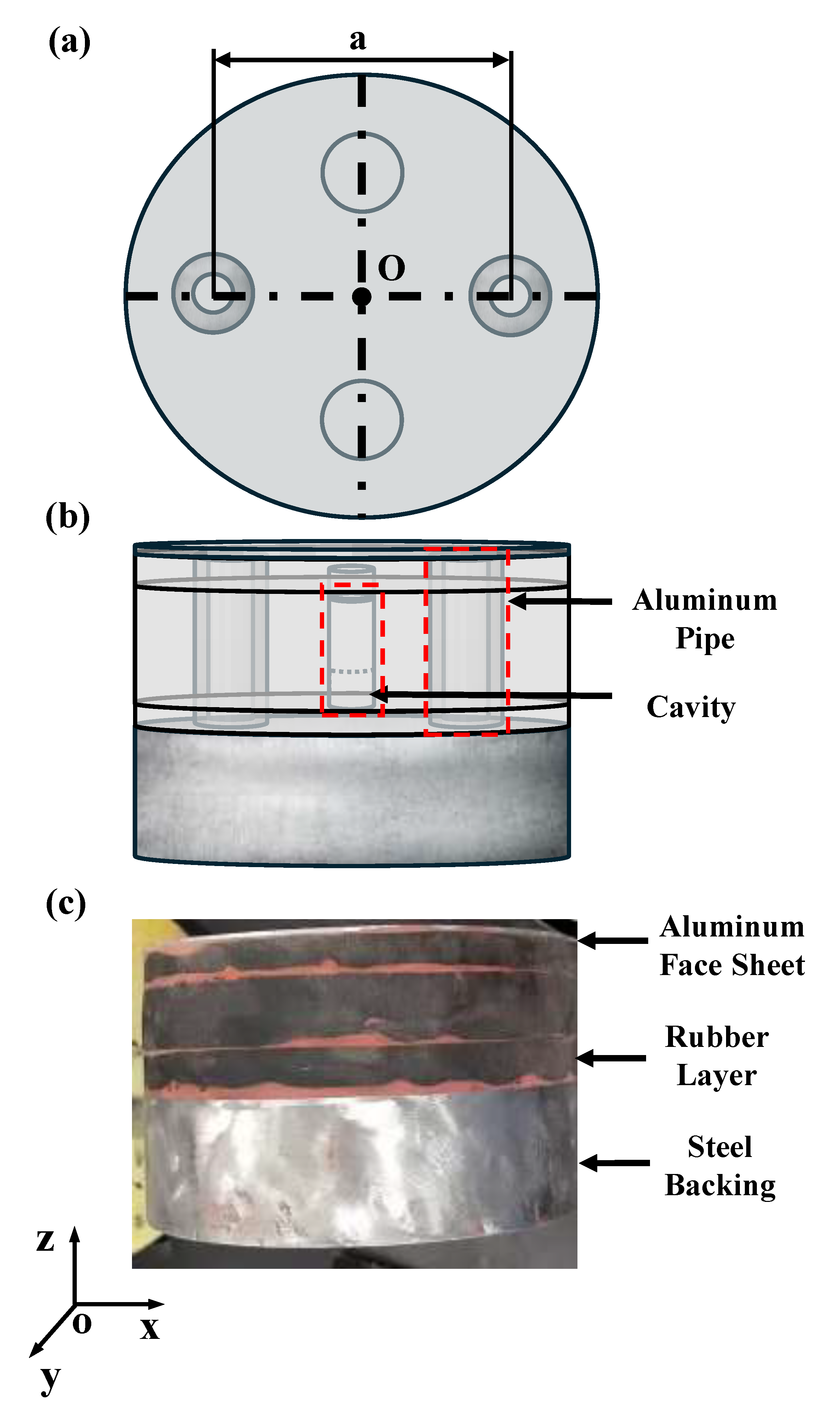
6. Experiment
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, X.; Meng, L.; Liu, Z.; Yang, F.; Jiang, X.; Yang, J. Multifunctional Integrated Underwater Sound Absorption Materials: A Review. Appl. Sci. 2023, 13, 5368. [Google Scholar] [CrossRef]
- Zhang, W.; Xin, F. Broadband low-frequency sound absorption via Helmholtz resonators with porous material lining. J. Sound Vib. 2024, 578, 118330. [Google Scholar] [CrossRef]
- Gao, N.; Wang, M.; Liang, X.; Pan, G. On-demand prediction of low-frequency average sound absorption coefficient of underwater coating using machine learning. Results Eng. 2025, 25, 104163. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, Y.; Gao, N. Recent study progress of underwater sound absorption coating. Eng. Rep. 2023, 5, e12627. [Google Scholar] [CrossRef]
- Liu, J.; Yang, H.; Zhao, H.; Wang, Y.; Yu, D.; Wen, J. A lightweight waterborne acoustic meta-absorber with low characteristic impedance rods. Int. J. Mech. Sci. 2023, 255, 108469. [Google Scholar] [CrossRef]
- Zeng, Q.; Zhang, J.; Xiao, Y.; Li, B.; Hou, H.; Cheng, B. Low-frequency broadband underwater metasurface with embedded curved rough neck. Mod. Phys. Lett. B 2025, 39, 2550132. [Google Scholar] [CrossRef]
- Lane, R. Absorption mechanisms for waterborne sound in Alberich anechoic layers. Ultrasonics 1981, 19, 28–30. [Google Scholar] [CrossRef]
- Meng, H.; Wen, J.; Zhao, H.; Wen, X. Optimization of locally resonant acoustic metamaterials on underwater sound absorption characteristics. J. Sound Vib. 2012, 331, 4406–4416. [Google Scholar] [CrossRef]
- Meng, T. Simplified model for predicting acoustic performance of an underwater sound absorption coating. J. Vib. Control 2014, 20, 339–354. [Google Scholar] [CrossRef]
- Gao, N.; Huang, Q.; Pan, G. Ultra-broadband sound absorption characteristics in underwater ultra-thin metamaterial with three layer bubbles. Eng. Rep. 2024, 6, e12939. [Google Scholar] [CrossRef]
- Jia, X.; Jin, G.; Shi, K.; Bu, C.; Ye, T. A hybrid acoustic structure for low-frequency and broadband underwater sound absorption. J. Low Freq. Noise Vib. Act. Control 2022, 41, 1160–1177. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, Y.; Yu, D.; Wang, G.; Wen, J.; Wen, X. Absorptive properties of three-dimensional phononic crystal. J. Sound Vib. 2007, 303, 185–194. [Google Scholar] [CrossRef]
- Shi, K.; Jin, G.; Liu, R.; Ye, T.; Xue, Y. Underwater sound absorption performance of acoustic metamaterials with multilayered locally resonant scatterers. Results Phys. 1999, 12, 132–142. [Google Scholar] [CrossRef]
- Zou, H.; Su, L.; Zhang, Y.; Zhang, M.; Yu, W.; Wang, X.; Xia, X.; Chen, H.; Zhang, X.; Zhao, A. A novel broadband underwater sound absorption metastructure with multi-oscillators. Int. J. Mech. Sci. 2024, 271, 109137. [Google Scholar] [CrossRef]
- Wang, H.; Cui, Z.; He, X.; Ren, Z.; Xiang, P.; Dong, H. Underwater acoustic absorbing metamaterials by material-structure-functionality collaborative optimization. Int. J. Mech. Sci. 2024, 281, 109573. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, B.; Yan, K.; Liu, J.; Chen, M.; Jiang, H.; Wang, Y. Rayleigh beam underwater metamaterial for low-frequency and broadband sound absorption. Mater. Today Commun. 2024, 38, 108332. [Google Scholar] [CrossRef]
- Feng, F.; He, C.; Cui, Z.; Ying, T.; Cai, J.; Tao, M. Topology optimization of multi-material underwater broadband sound absorption metamaterial based on genetic algorithm. J. Acoust. Soc. Am. 2025, 157, 3482–3496. [Google Scholar] [CrossRef] [PubMed]
- Veselago, V.G. The electrodynamics of substances with simultaneously negative values of ε and μ. Sov. Phys. Uspekhi 1968, 10, 509. [Google Scholar] [CrossRef]
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling Electromagnetic Fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef] [PubMed]
- Cummer, S.; Christensen, J.; Alù, A. Controlling sound with acoustic metamaterials. Nat. Rev. Mater. 2016, 1, 16001. [Google Scholar] [CrossRef]
- Iannace, G.; Ciaburro, G.; Trematerra, A. Metamaterials acoustic barrier. Appl. Acoust. 2021, 181, 108172. [Google Scholar] [CrossRef]
- Davies, B.; Szyniszewski, S.; Dias, M.A.; de Waal, L.; Kisil, A.; Smyshlyaev, V.P.; Cooper, S.; Kamotski, I.V.; Touboul, M.; Craster, R.V.; et al. Roadmap on metamaterial theory, modelling and design. J. Phys. D Appl. Phys. 2025, 58, 203002. [Google Scholar] [CrossRef]
- Feng, Y.; Qiao, J.; Li, L. Acoustic behavior of composites with gradient impedance. Mater. Des. 2020, 193, 108870. [Google Scholar] [CrossRef]
- Zhang, Y.; Cheng, L. Ultra-thin and broadband low-frequency underwater acoustic meta-absorber. J. Mech. Sci. 2021, 210, 106732. [Google Scholar] [CrossRef]
- Fang, X.; Yin, X.; Wu, J.; Li, Y.; Li, H.; Wang, W.; Li, Y.; Wu, W. Underwater metagratings for sub-kilohertz low frequency and broadband sound absorption. Int. J. Mech. Sci. 2023, 260, 108630. [Google Scholar] [CrossRef]
- Shi, K.; Li, D.; Hu, D.; Shen, Q.; Jin, G. A New Multi-Mechanism Synergistic Acoustic Structure for Underwater Low-Frequency and Broadband Sound Absorption. J. Mar. Sci. Eng. 2023, 11, 2373. [Google Scholar] [CrossRef]
- Gao, N.; Lu, K. An underwater metamaterial for broadband acoustic absorption at low frequency. Appl. Acoust. 2020, 169, 107500. [Google Scholar] [CrossRef]
- Zhang, H.; Hao, P.; Gao, Y.; Cheng, Y.; Li, G.; Hu, N.; Qi, Z. Underwater Low-Frequency Sound Absorbing Metamaterials Based on Wave-Mode Transformation and Local Resonance Mechanism. Acta Phys. Pol. A 2021, 140, 455–462. [Google Scholar] [CrossRef]
- Zhang, R.; Song, Y.; Hou, H.; Gao, N. Underwater metastructure with broadband sound absorption capability in low-frequency range above 20 Hz. Mod. Phys. Lett. B 2020, 35, 2150039. [Google Scholar] [CrossRef]
- Shi, K.; Li, D.; Hu, D.; Yu, X.; Ding, C.; Jin, G. Underwater sound absorption characteristics of the acoustic metamaterials with multiple coupling substructure. J. Low Freq. Noise Vib. Act. Control 2025, 44, 1001–1019. [Google Scholar] [CrossRef]
- Wei, Y.; Zhao, H.; Wang, Y.; Zhong, J.; Sun, Y.; Zheng, Z.; Yang, H.; Wen, J. A review of hydroacoustic absorbing materials under hydrostatic pressure. Chin. Sci. Bull. 2024, 69, 2368–2379. (In Chinese) [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, H.; Yan, H.; Zhang, H.; Li, T.; Wang, C.; Liu, J.; Zhong, J.; Yu, D.; Wen, J. Acoustically soft and mechanically robust hierarchical metamaterials in water. Phys. Rev. Appl. 2023, 20, 054015. [Google Scholar] [CrossRef]
- Zhang, Y.; Tong, M.; Rui, X.; Wang, G.; Yang, F. Deep-subwavelength and hydrostatic-pressure-resistant meta-absorber for broadband low-frequency underwater sound. Appl. Phys. Express 2024, 17, 077001. [Google Scholar] [CrossRef]
- Shi, K.; Hu, D.; Li, D.; Jin, G. Sound absorption behaviors of composite functionally graded acoustic structure under hydrostatic pressure. Appl. Acoust. 2023, 211, 109474. [Google Scholar] [CrossRef]
- Zhang, Y.; Tong, M.; Rui, X.; Wang, G.; Yang, F.; Zhou, Q.; Cheng, L.; He, B. Ultrathin and pressure-resistant meta-coating with embedded tree-shaped acoustic black hole for broadband low-frequency underwater sound absorption. Appl. Acoust. 2024, 225, 110171. [Google Scholar] [CrossRef]
- Gao, N.; Yu, H.; Liu, J.; Deng, J.; Huang, Q.; Chen, D.; Pan, G. Experimental investigation of composite metamaterial for underwater sound absorption. Appl. Acoust. 2023, 211, 109466. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, Y. Phononic glass: A robust acoustic-absorption material. J. Acoust. Soc. Am. 2012, 132, 694–699. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Zhao, X.; Wang, K.; Song, H.; Cui, Z. Influence of Deformation on Sound-Absorbing Performance Under Hydrostatic Pressure. Int. J. Acoust. Vib. 2022, 27, 344–353. [Google Scholar] [CrossRef]
- Zheng, Z.; Yang, H.; Wang, M.; Wang, Y.; Zhong, J.; Ma, W.; Liang, C.; Wen, J.; Chen, X. Realization of lightweight and pressure-resistant sandwich metasurfaces for underwater sound absorption through topology optimization. Mech. Syst. Signal Process. 2025, 224, 112205. [Google Scholar] [CrossRef]
- Wang, L.; Hu, Y.; Zhang, X.; Li, S.; Li, S.; Zhang, H. Design and compressive behavior of a wood-based pyramidal lattice core sandwich structure. Eur. J. Wood Wood Prod. 2020, 78, 123–134. [Google Scholar] [CrossRef]
- Karagözlü, C.; Ayli, E.; Tanabi, H.; Sabuncuoglu, B. Artificial neural networks for predicted bending properties of additively manufactured pyramidal lattice truss core sandwich structures. Mater. Today Commun. 2025, 47, 112926. [Google Scholar] [CrossRef]
- Guo, H.; Yuan, H.; Zhang, J.; Ruan, D. Review of sandwich structures under impact loadings: Experimental, numerical and theoretical analysis. Thin-Walled Struct. 2024, 196, 111541. [Google Scholar] [CrossRef]
- Zhou, Z.; Chen, M. Predicting effective moduli of a Z-reinforced core with cavities using a novel theoretical approach and a micromechanics finite element method. Int. J. Mech. Sci. 2019, 161, 105085. [Google Scholar] [CrossRef]
- Shi, C.; Wang, J.; Zhu, J.; Ni, A.; Li, X. Flatwise compression properties of trapezoidal lattice-web reinforced foam core sandwich composites. Acta Mater. Compos. Sin. 2022, 39, 590–600. [Google Scholar]
- Rasouli Rizi, S.; Nosraty, H.; Mirdehghan, S.A. Effects of stitching parameters on the flexural properties of stitched foam core sandwich composites. J. Compos. Mater. 2024, 58, 2343–2361. [Google Scholar] [CrossRef]
- Selver, E.; Kaya, G.; Dalfi, H. Experimental and theoretical study of sandwich composites with Z-pins under quasi-static compression loading. Adv. Struct. Eng. 2021, 24, 2720–2734. [Google Scholar] [CrossRef]
- Li, K.; Zhou, Z.; Huang, Z.; Lin, Y.; Chen, M.; Yang, P.; Li, Y. Underwater sound absorption characteristic of the rubber core sandwich structure with funnel-shaped cavities reinforced by carbon fiber columns. Appl. Acoust. 2023, 208, 109375. [Google Scholar] [CrossRef]
- Luo, Y.; Lou, J.; Zhang, Y. Sound absorption performance of composite grid sandwich structure with local resonance element. J. Vib. Shock 2022, 41, 291–296. (In Chinese) [Google Scholar]
- Li, K.; Mao, L.; Chen, Z.; Huang, Z.; Zhou, Z.; Li, Y. Sound absorption mechanism and characteristic of a pressure-resistant sandwich structure supported by carbon fiber truss and embedded cavities in rubber core. Appl. Acoust. 2025, 229, 110386. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, Y.; Zhang, X.; Li, L.; Chen, M.; Fang, D. Broadband underwater sound absorbing structure with gradient cavity shaped polyurethane composite array supported by carbon fiber honeycomb. J. Sound Vib. 2020, 479, 115375. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution? A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Chung, J.Y.; Blaser, A. Transfer function method of measuring in-duct acoustic properties. I. Theory. J. Acoust. Soc. Am. 1980, 68, 914–921. [Google Scholar] [CrossRef]





| Notation | a | t | ||||||
|---|---|---|---|---|---|---|---|---|
| Value (mm) | 90 | 5 | 5 | 40 | 10 | 5 | 50 | 5 |
| Notation | a | t | ||||||
|---|---|---|---|---|---|---|---|---|
| Value (mm) | 70 | 4.5 | 2.5 | 30 | 5 | 7 | 40 | 1 |
| Frequency Band | Before Optimization | After Optimization |
|---|---|---|
| 500–5000 Hz | 0.78 | 0.94 |
| 500–2000 Hz | 0.79 | 0.91 |
| 2000–5000 Hz | 0.77 | 0.96 |
| Pressure (MPa) | Frequency Band (Hz) | ||
|---|---|---|---|
| 500–5000 | 500–2000 | 2000–5000 | |
| 1 | 0.90 | 0.86 | 0.95 |
| 2 | 0.91 | 0.87 | 0.97 |
| 3 | 0.92 | 0.87 | 0.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Z.; Zhao, H.; Zhang, W.; Sun, Y.; Liu, Z.; Yang, J.; Wen, J. Mechanism and Optimization of Acoustic Absorption of an Underwater Lattice-Reinforced Meta-Absorber. J. Mar. Sci. Eng. 2025, 13, 1944. https://doi.org/10.3390/jmse13101944
Yin Z, Zhao H, Zhang W, Sun Y, Liu Z, Yang J, Wen J. Mechanism and Optimization of Acoustic Absorption of an Underwater Lattice-Reinforced Meta-Absorber. Journal of Marine Science and Engineering. 2025; 13(10):1944. https://doi.org/10.3390/jmse13101944
Chicago/Turabian StyleYin, Zhenkai, Honggang Zhao, Wenzheng Zhang, Yao Sun, Zihao Liu, Jingfan Yang, and Jihong Wen. 2025. "Mechanism and Optimization of Acoustic Absorption of an Underwater Lattice-Reinforced Meta-Absorber" Journal of Marine Science and Engineering 13, no. 10: 1944. https://doi.org/10.3390/jmse13101944
APA StyleYin, Z., Zhao, H., Zhang, W., Sun, Y., Liu, Z., Yang, J., & Wen, J. (2025). Mechanism and Optimization of Acoustic Absorption of an Underwater Lattice-Reinforced Meta-Absorber. Journal of Marine Science and Engineering, 13(10), 1944. https://doi.org/10.3390/jmse13101944





