Uncertainty Evaluation Method of Marine Soil Wave Velocity Prediction Model Based on Point Estimation Method and Bayesian Principle

Abstract

The spatial variability of soil shear wave velocity (V_s) significantly influences the results of site seismic response analysis. Based on the collected measured V_s values of silty clay in a certain sea area in China, this study divides the V_s data into one set of on-site sample data and six sets of historical data. A power function is used to establish the regression equation between V_s and depth h, and the joint prior distribution of the mean and variance for parameters a and b in the power function is derived using historical data. The joint posterior distribution of parameters a and b is obtained by applying the Bayesian formula to the on-site sample data. Using the maximum a posteriori mean values of a and b combined with the point estimation method, the mean and standard deviation of the predicted V_s values as functions of depth h are derived. The accuracy of the point estimation results is verified using Monte Carlo simulation. Compared to the V_s values predicted using only the mean values of a and b derived from on-site sample data, the V_s values predicted based on the maximum a posteriori mean values of a and b are closer to the measured V_s values. Accordingly, the results of the site seismic response analysis also align more closely with those calculated using the true V_s values.

1. Introduction

The shear wave velocity of soil is a critical parameter reflecting the dynamic properties of soil, and it is essential for site classification, liquefaction potential evaluation of sandy soils, and seismic response analysis of engineering sites. Influenced by depositional environments and human engineering activities, the physical and mechanical parameters of soil exhibit spatial variability [1,2,3,4,5]. The variability of soil shear wave velocity significantly impacts the results of liquefaction potential evaluation and site seismic response analysis [6,7,8,9,10,11]. In existing research, methods for studying the spatial variability of soil shear wave velocity can be broadly categorized into two types. The first category involves statistically analyzing measured values of soil shear wave velocity to quantify the variability of V_s values; this approach requires sufficient measured borehole data. The second category establishes predictive models between V_s values and soil burial depth (h), and then compares the model-predicted values with the measured V_s values to derive the uncertainty characteristics of the V_s values predicted by the model [12,13,14,15,16]. These two categories of methods are currently primarily used to evaluate the uncertainty of shear wave velocity in onshore soils.

Seabed sites are typically soft soil sites, and China’s maritime areas are historically prone to strong earthquakes. Under strong seismic loading, the results of seismic response analysis for soft soil sites are highly sensitive to the variability of V_s. Even relatively small variability in V_s can trigger significant differences in the seismic response analysis results for soft soil sites [17]. Therefore, research on the spatial variability of marine soil V_s values will contribute to further revealing the impact of marine soil V_s uncertainty on the variability of seabed site seismic response analysis results. This is of great significance for ensuring the seismic safety of marine engineering.

Offshore operations face significant challenges and high costs, making it difficult to evaluate the spatial variability of marine soil V_s through extensive in situ measurements. The V_s value of soil exhibits a strong correlation with burial depth (h) [14]. When sample data are scarce, a regression equation between marine soil V_s and h can be established to predict V_s values at various depths [13,18].

The mean and standard deviation of geotechnical parameters are crucial metrics for quantifying their uncertainty. With abundant measured data, statistical analysis of soil V_s values at different depths can be performed to determine the mean and standard deviation of V_s at each depth. However, when measured data are limited, the evaluation of V_s prediction model accuracy typically relies on the goodness-of-fit of the regression equation (V_s vs. h) and the residuals between predicted V_s values (from the regression) and measured V_s values. This approach fails to provide the standard deviation of V_s values predicted by the regression equation at different depths [12,13,19,20]. Extensive field data indicate that for soil parameters significantly influenced by overburden pressure, both the mean and standard deviation vary with depth (h) [6,7,8,9,10,11,21,22]. Consequently, existing methods that use regression goodness-of-fit and residual magnitude as uncertainty evaluation metrics cannot accurately characterize model uncertainty.

Bayesian statistics is a theoretical framework for statistical analysis under limited sample sizes. It utilizes accumulated experimental data of a specific geotechnical parameter as prior information to make an initial estimation of the parameter’s distribution. Subsequently, based on the limited sample data from a specific project, it derives posterior information to reassess the uncertainty of the geotechnical parameter [23,24,25,26,27,28]. This approach effectively mitigates estimation errors arising from insufficient field test data and has gained widespread application [23,24,25,26,27].

The point estimation method is a simple and accurate approach for studying error propagation [29,30,31,32]. This study utilizes collected measured soil shear wave velocity data from boreholes in a certain sea area in China. The shear wave velocity data are divided into one set of on-site sample data and six sets of historical data serving as prior information samples. A power function is employed to fit the relationship between measured V_s values and depth (h). The mean and variance of the fitting parameters in the power function model are statistically derived from the six sets of historical data, thereby obtaining the prior distributions of the mean and variance of the fitting parameters. The posterior distribution of the parameters is then derived by combining the prior distribution with the on-site data. Finally, using the posterior estimates of the model parameters, the point estimation method is applied to analyze the variation in uncertainty in V_s predictions that are obtained from the power function model with depth. This aims to provide guidance for evaluating the uncertainty of marine soil V_s predictions when on-site sample sizes are limited.

2. Uncertainty Analysis Based on the Point Estimation Method

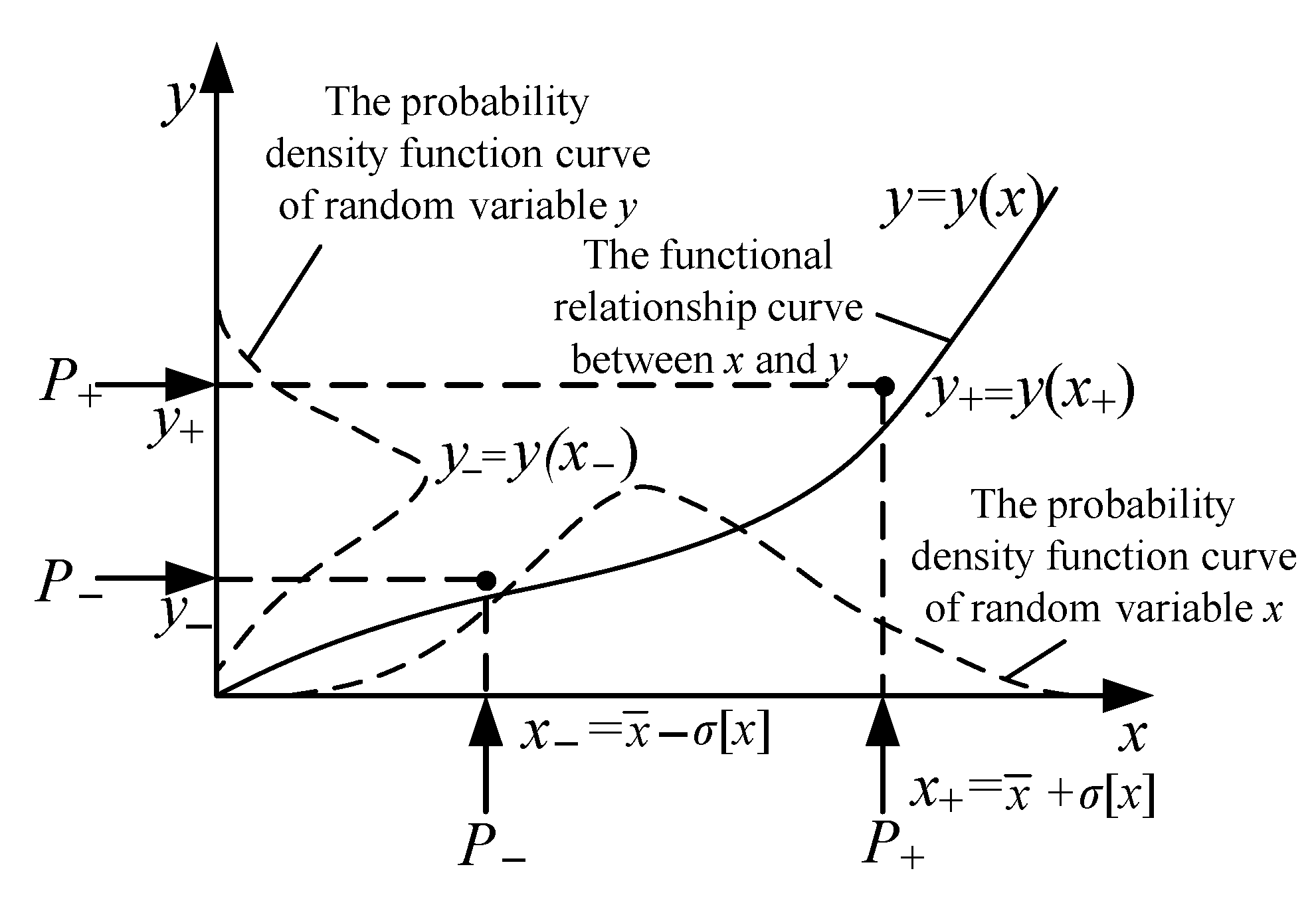
2.1. Fundamental Principles of the Point Estimation Method

As shown in Figure 1, the principle of the point estimation method is to approximate the range of the independent variable x in the function y = f(x) between x₊ and x₋, where x₊ = $x̅$ + σ[x]; x₋ = $x̅$ − σ[x]. Here, $x̅$ and σ[x] represent the average value and variability measure of the random variable x, respectively. By using these two estimates of x (x₋ and x₊) with the corresponding algorithm, two estimates of the random variable y (y₋ and y₊) can be generated.

Figure 1 illustrates the information transfer schematic for a univariate function. In practical problems, the number of independent variables is often more than one. Taking the bivariate function y = f(x₁, x₂) as an example, the variability of each random variable x_i(i = 1, 2)can be characterized using the following approach [29,30]:

$$\left.\begin{array}{c}{x}_{i+}=\overline{x_i}+\sigma \left[x_i\right]\\ x_{i-}=\overline{x_i}-\sigma \left[x_i\right]\end{array}\right\},$$

(1)

In the equation: $\overline{x_i}$ represents the mean of the i-th random variable x_i; $\sigma \left[x_i\right]$ represents the standard deviation of the random variable x_i;

x_i+ and x_i− denote the upper and lower bounds of the range of the random variable x_i, respectively. When considering the variability of both x₁ and x₂, the values of the bivariate function y (denoted as y_±±) are given by:

$$y_{\pm \pm }=f({x̅}_1\pm \sigma [x_1],{x̅}_2\pm \sigma [x_2\left]\right),$$

(2)

The first moment of the function y, i.e., its mean value E[y], is given by:

$$E\left[y\right]=p_{++}{y}_{++}+p_{+-}{y}_{+-}+p_{-+}{y}_{-+}+p_{--}{y}_{--},$$

(3)

The second moment of the function y is E[y²]:

$$E\left[y^2\right]=p_{++}{y}_{++}^2+p_{+-}{y}_{+-}^2+p_{-+}{y}_{-+}^2+p_{--}{y}_{--}^2,$$

(4)

where p₊₊, p₋₋, p₊₋ and p₋₊ are weight coefficients:

$$\left.\begin{array}{c}{p}_{++}=p_{--}={\displaystyle \frac{1+{\rho }_{x1,x2}}{4}}\\ p_{+-}=p_{-+}={\displaystyle \frac{1-{\rho }_{x1,x2}}{4}}\end{array}\right\},$$

(5)

In the equation, ${\rho }_{x1, x2}$ represents the correlation coefficient between x₁ and x₂.

$${\rho }_{x_1,x_2}=\frac{Cov (x_1,x_2)}{\sqrt{V[x_1] V[x_2]}},$$

(6)

In the equation, COV(x₁, x₂) denotes the covariance between x₁ and x₂; V[x₁] and V[x₂] represent the variances of x₁ and x₂, respectively. The standard deviation of the function y, denoted as σ[y], is:

$$\sigma [y]=\sqrt{E\left[y^2\right]-E[y{]}^2},$$

(7)

2.2. Uncertainty Propagation in the Power Function Prediction Model

Evaluating the variability of soil V_s values using extensive measured data are a straightforward and effective method. As shown in Figure 2, however, this approach has several limitations when assessing the variability of soil V_s values. While measured data can directly provide the variation in the standard deviation of V_s with depth, this method relies on extensive in situ measurements, which are difficult to achieve for marine engineering projects. Secondly, measured V_s values often lack continuity along the depth direction (h). When V_s test values are missing within a specific depth range, the variability of V_s values within that range cannot be determined. Additionally, when evaluating V_s variability using measured data, only the variability of V_s values above the maximum measured depth can be assessed; it cannot characterize the variability of V_s values below the maximum measured depth.

When measured data are insufficient, it is common practice to establish a regression equation between soil V_s values and depth (h) using a limited set of measured data based on the least squares method. This equation is then used to predict soil V_s values at various depths (h). By further comparing the residuals between predicted V_s values and measured V_s values, the accuracy of the regression equation can be evaluated [19,20].

The standard deviation is a critical indicator for assessing the variability of soil parameters. However, the least squares method cannot directly provide the distribution of the standard deviation of predicted V_s values. As shown in Figure 3, extensive field data demonstrate that the standard deviation of soil V_s values exhibits nonlinear variation with depth (h) [6,7,8,9,10,11,21]. The residual comparison approach fails to reflect this characteristic.

The shear wave velocity (V_s) of the specimen was measured using a pair of piezoelectric ceramic bender elements installed in the top and bottom platens of the HX-100 cyclic triaxial apparatus. Undisturbed marine soil samples were prepared into solid cylinders with a diameter of 3.91 cm and a height of 8.0 cm using the rotary cutting method. The prepared specimen was enveloped with a rubber membrane and mounted in the triaxial cell. After completion of the consolidation process, the V_s value of the soil specimen was tested. Multi-frequency sinusoidal wave signals within the range of 1 to 40 kHz (rather than single-frequency signals) were employed as the excitation source. The shear wave travel time was determined more accurately by comprehensively analyzing the received signals corresponding to each excitation frequency. This study adopted the first arrival method in the time domain to determine the propagation velocity of shear waves through the specimen.

When the soil depth is zero, the shear wave velocity must necessarily be zero. Using a power function to describe the relationship between V_s and h ensures that the shear wave velocity is zero at zero depth, whereas other forms such as linear or quadratic functions fail to guarantee this condition. The relationship between soil V_s values and depth (h) is typically nonlinear [14]. Therefore, a nonlinear function is required to describe their relationship. Taking the power function as an example, the relationship between soil shear wave velocity V_s(h) and depth (h) at any given depth is expressed as:

$$V_s\left(h\right)=a{h}^b,$$

(8)

In the equation, a and b are fitting parameters.

For the same soil type, Equation (8) is used to fit the relationship between V_s and h for each borehole, yielding the mean values ($\overline{a},\overline{ b}$) and standard deviations (σ[a], σ[b]) of parameters a and b for that soil type. According to Equation (3), the mean value of soil V_s at any depth h, denoted as E[V_s(h)], is:

$$E\left[V_s\right(h\left)\right]=p_{++} {V_s}_{++}+p_{+-} {V_s}_{+-}+p_{-+} {V_s}_{-+}+p_{--} {V_s}_{--},$$

(9)

In the equation, the weight functions are defined as: p₊₊ = p₋₋ = (1 + ${\rho }_{a,b})$/4, p₊₋ = p₋₊ = (1 − ${\rho }_{a,b})$/4; ${\rho }_{a,b}$ denotes the correlation coefficient between parameters a and b:

$${\rho }_{a,b}={\displaystyle \frac{COV(a,b)}{\sqrt{V\left[a\right]V\left[b\right]}}},$$

(10)

In the equation, COV(a,b) denotes the covariance between a and b; V[a] and V[b] represent the variances of a and b, respectively; V_s±± is expressed as:

$$V_{\mathrm{s} \pm \pm }=(\overline{a}\pm \sigma [a])h^{(\overline{b}\pm \sigma [b])},$$

(11)

The standard deviation of soil V_s at different depths, denoted as σ[V_s(h)], is given by:

$$\sigma [V_s(h)]=\sqrt{E\left[V_s^2\right]-E\left[V_s\right(h){]}^2},$$

(12)

In the equation, $E\left[V_s^2\right]$ represents the second moment of V_s:

$$E[V_{\mathrm{s}}^2]=p_{++}{V}_{\mathrm{s}++}^2+p_{+-}{V}_{\mathrm{s}+-}^2+p_{-+}{V}_{\mathrm{s}-+}^2+p_{--}{V}_{\mathrm{s}--}^2,$$

(13)

Through Equations (8)–(13), the mean and standard deviation of soil V_s at any depth h can be obtained.

3. Bayesian Inference for Power Function Fitting Parameters a and b

The method in Section 2.2 transforms the direct estimation of the standard deviation of V_s into the estimation of fitting parameters a and b. Therefore, accurately characterizing the variability of parameters a and b is fundamental to ensuring a reasonable evaluation of V_s uncertainty. When the number of on-site boreholes is insufficient, the estimation of the variability of parameters a and b may be inaccurate. Bayesian statistics integrate prior information, historical data, and on-site sample data to predict parameter variability [33]. This approach mitigates inaccuracies in estimating parameter variability caused by insufficient on-site sample data.

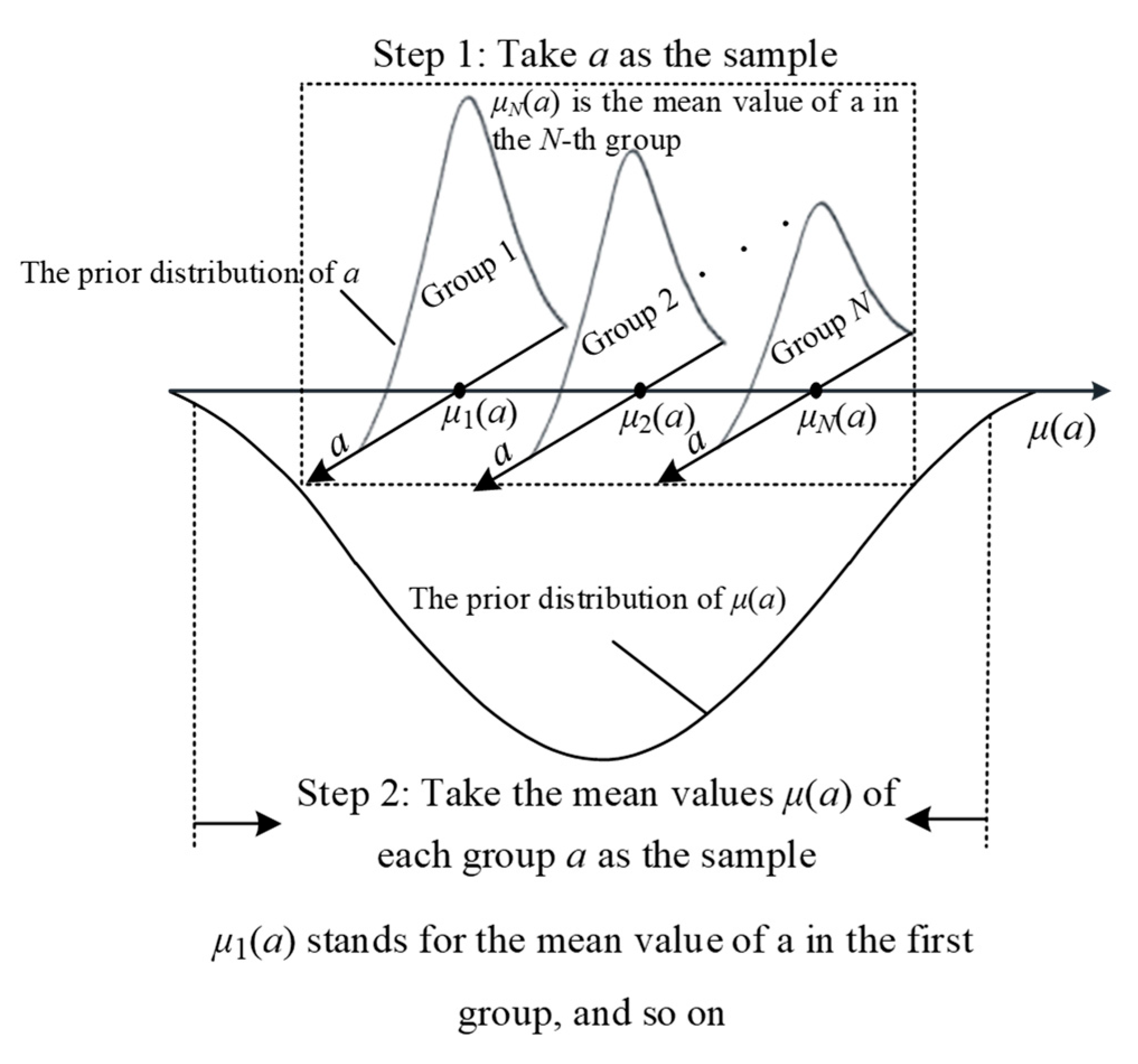
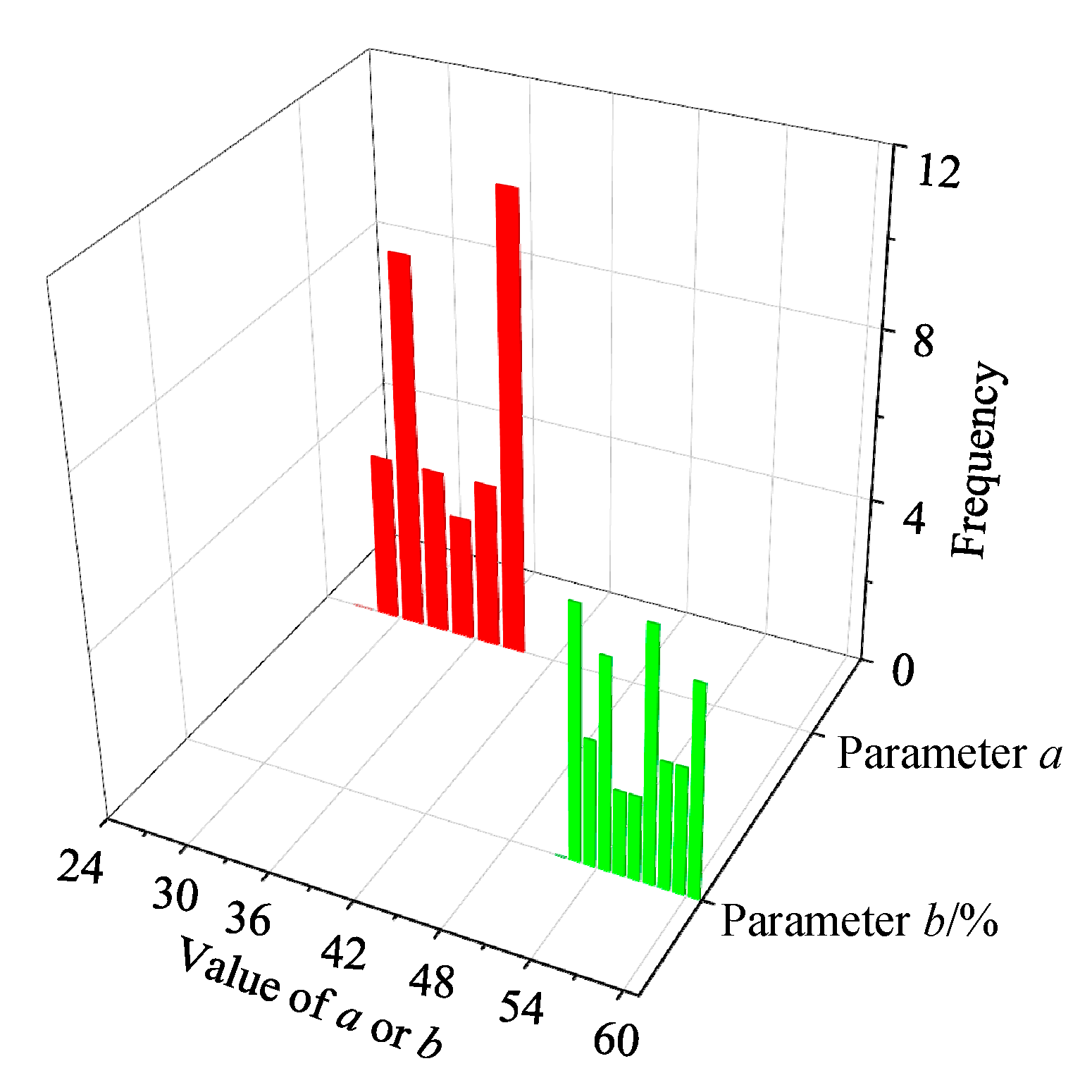
3.1. Prior Information

When applying Bayesian theory to infer parameter variability, it is first necessary to specify the type of prior distribution for the parameters. The Normal–Inverse Gamma distribution is a commonly used prior distribution that jointly models the mean and variance of a parameter [34,35,36]. Taking the fitting parameter a of the power function model as an example, assume the joint prior distribution of the mean and variance of a follows a Normal–Inverse Gamma distribution π(μ, σ²):

$$\pi \left(\mu ,{\sigma }^2\right)=\pi \left(\mu |{\sigma }^2\right)\pi \left({\sigma }^2\right),$$

(14)

In the equation, π(σ²) denotes the prior probability density distribution function for the variance σ² of parameter a; π(μ|σ²) represents the prior probability density distribution function for the mean μ of parameter a given its variance σ².

The prior distribution of μ can be assumed to follow a normal distribution:

$$\pi \left(\mu \right|{\sigma }^2)=N\left({\mu }_0,{\sigma }^2/{\kappa }_0\right),$$

(15)

In the equation, N(μ₀,σ²/κ₀) denotes that the mean μ of parameter a follows a normal distribution with mean μ₀ and variance σ²/κ₀. The prior distribution for the variance σ² of parameter a can be expressed as:

$$\pi \left({\sigma }^2\right)=IGa({\upsilon }_0/2,{\upsilon }_0{\sigma }_0^2/2),$$

(16)

In the equation, $IGa({\upsilon }_0/2,{\upsilon }_0{\sigma }_0^2/2)$ represents that the variance σ² of parameter a follows an Inverse Gamma distribution with mean ${\upsilon }_0/2$ and variance ${\upsilon }_0{\sigma }_0^2/2$. The hyperparameters μ₀, κ₀, v₀ and σ₀ in Equations (15) and (16) need to be determined. If the prior samples are divided into m groups, the estimates for parameters μ₀, σ² and κ₀ in Equation (15) can be determined from the prior sample information. The estimate for μ₀, denoted as ${\mu }_0^{\prime }$, is given by [34,35,36]:

$${{\mu }_0}^{\prime }={\displaystyle \frac{{\sum }_{i=1}^m\overline{x_i}}{m}},$$

(17)

In the equation, $\overline{x_i}$ represents the mean of the i-th group of prior samples. The estimate for σ², denoted as ${\sigma }^{2\prime }$, is:

$${\sigma }^{2\prime }={\displaystyle \frac{1}{m}}{\sum }_{i=1}^m{s^2}_i,$$

(18)

In the equation, $s_i^2$ represents the variance of the i-th group of prior samples. The estimate for κ₀, denoted as ${{\kappa }_0}^{\prime }$, is:

$${{\kappa }_0}^{\prime }={\displaystyle \frac{{\sigma }^{2\prime }}{[{\sigma }^2/{\kappa }_0{]}^{\prime }}}={\displaystyle \frac{{\sum }_{i=1}^m{s}_i^2}{{\sum }_{i=1}^m{\left[\overline{x_i}-\left({\sum }_{i=1}^m\overline{x_i}\right)/m\right]}^2}},$$

(19)

The parameters ${\upsilon }_0/2$ and ${\upsilon }_0{\sigma }_0^2/2$ in the inverse gamma distribution shown in Equation (16) can be estimated as follows [34,35,36]:

The mean of the variances of the prior sample data, denoted as ${\mu }_{{\sigma }^2}$, is calculated using the method of moments:

$${\mu }_{{\sigma }^2}={\sigma }^{2\prime }={\displaystyle \frac{1}{m}}{\sum }_{i=1}^m{s^2}_i,$$

(20)

The variance of the prior sample data, denoted as ${\upsilon }_{{\sigma }^2}$, is calculated using the method of moments:

$${\upsilon }_{{\sigma }^2}={\displaystyle \frac{1}{m-1}}{\sum }_{i=1}^m{\left({s^2}_i-{\mu }_{{\sigma }^2}\right)}^2,$$

(21)

Subsequently, the estimates for ${\upsilon }_0/2$ and ${\upsilon }_0{\sigma }_0^2/2$ are obtained as follows:

$$\left.\begin{array}{c}{\displaystyle \frac{{\upsilon }_0}{2}}={\displaystyle \frac{{{\mu }^2}_{{\sigma }^2}}{{\upsilon }_{{\sigma }^2}}}+2\\ {\displaystyle \frac{{\upsilon }_0{\sigma }_0^2}{2}}={{\mu }^2}_{{\sigma }^2}\left({\displaystyle \frac{{{\mu }^2}_{{\sigma }^2}}{{\upsilon }_{{\sigma }^2}}}+1\right)\end{array}\right\},$$

(22)

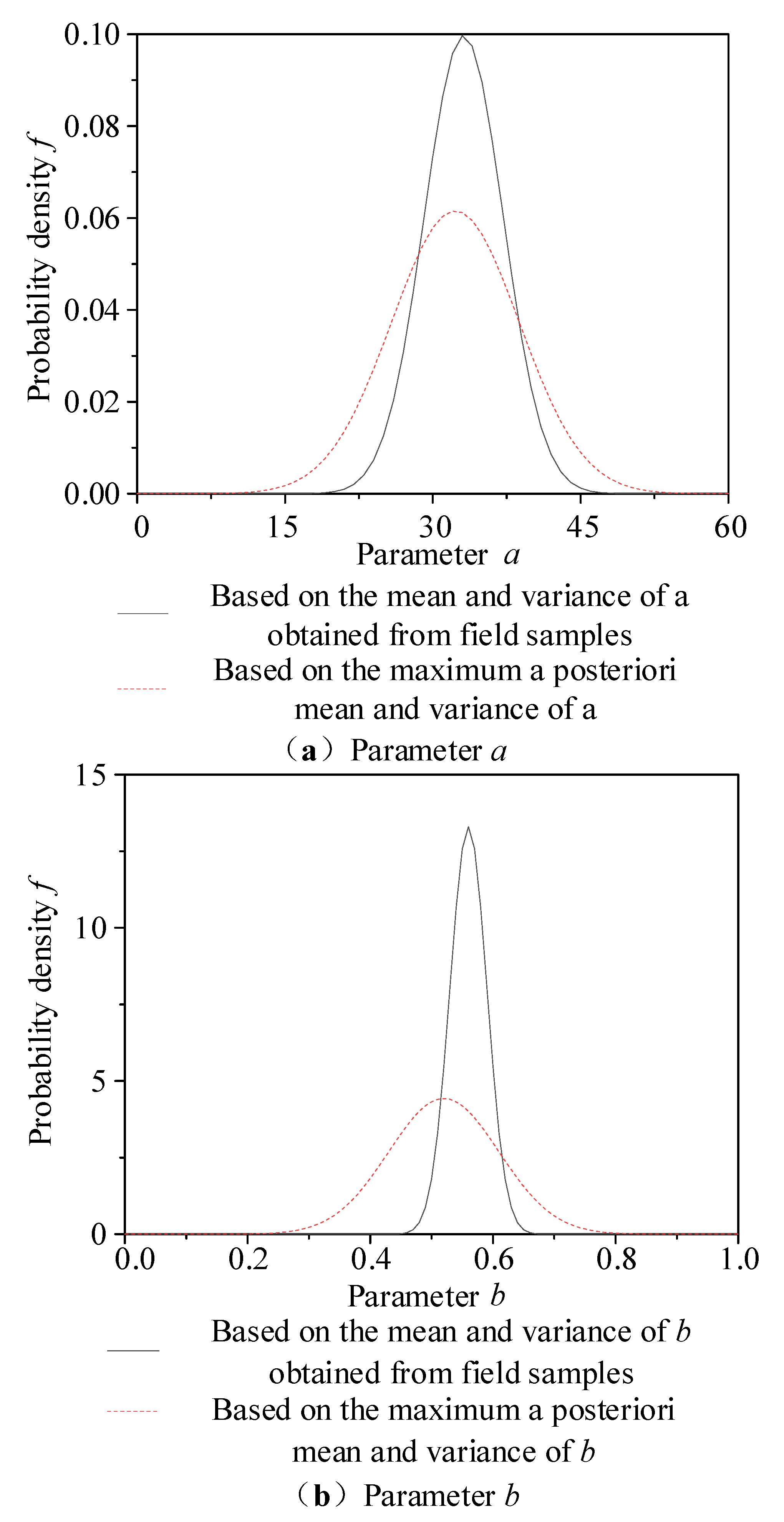
3.2. Posterior Information

After determining the parameters in the prior distribution of the geotechnical parameter, the posterior distribution of the geotechnical parameter is obtained by combining on-site sample information:

$$\pi \left(\mu ,{\sigma }^2|x\right)={\displaystyle \frac{p\left(x|\mu ,\sigma \right)\pi \left(\mu |{\sigma }^2\right)\pi \left({\sigma }^2\right)}{m\left(x\right)}},$$

(23)

In the equation, p(x| μ, σ) is the probability density function of the random variable x with parameters μ and σ. p(x| μ, σ) can also be regarded as the likelihood function for μ and σ given the on-site sample x. m(x) denotes the marginal distribution of the random variable x:

$$m(x)=\iint p\left(x|\mu ,{\sigma }^2\right)\pi \left(\mu |{\sigma }^2\right)\pi \left({\sigma }^2\right)d(\mu )d({\sigma }^2),$$

(24)

In Equation (23), m(x) is a proportionality factor independent of μ and σ² and can be omitted. Therefore, Equation (23) can be simplified as:

$$\pi \left(\mu ,{\sigma }^2|x\right)\propto {\left({\sigma }^2\right)}^{-({\upsilon }_n/2+1.5)}\mathit{exp}\left[{\displaystyle \frac{-1}{2{\sigma }^2}}\left({\upsilon }_n{\sigma }_n^2+{\kappa }_n{\left(\mu -{\mu }_n\right)}^2\right)\right],$$

(25)

In the equation, μ_n, ν_n, κ_n and σ_n are parameters of the posterior distribution, which can be obtained by combining the parameters of the prior distribution with on-site sample information:

$$\left.\begin{array}{c}{\mu }_n={\displaystyle \frac{{\kappa }_0}{{\kappa }_0+n}}{\mu }_0+{\displaystyle \frac{n}{{\kappa }_0+n}}\overline{x}\\ {\kappa }_n={\kappa }_0+n\\ {\upsilon }_n={\upsilon }_0+n\\ {\upsilon }_n{\sigma }_n^2={\upsilon }_0{\sigma }_0^2+(n-1)s^2+{\displaystyle \frac{{\kappa }_{0}n}{{\kappa }_0+n}}{\left({\mu }_0-\overline{x}\right)}^2\end{array}\right\},$$

(26)

In the equation, n represents the number of on-site samples; $x̅$ denotes the mean of the on-site samples; s² denotes the variance of the on-site samples. According to Bayesian principles, the mean and variance of the posterior distribution remain random variables. Among these, the most probable mean and variance are termed the maximum a posteriori (MAP) mean μ_MD and MAP variance ${\sigma }_{\mathrm{MD}}^2$:

$$\left.\begin{array}{c}{\mu }_{\mathrm{MD}}={\displaystyle \frac{{\kappa }_0}{{\kappa }_0+n}}{\mu }_0+{\displaystyle \frac{n}{{\kappa }_0+n}}\overline{x}\\ {\sigma }_{\mathrm{MD}}^2=2{\displaystyle \frac{{\upsilon }_0{\sigma }_0^2+(n-1)s^2+({\kappa }_{0}n/{\kappa }_0+n)({\mu }_0-\overline{x}{)}^2}{{\upsilon }_0+n+3}}\end{array}\right\},$$

(27)

Figure 4 illustrates the workflow of Bayesian inference for the power function fitting parameters a and b in this study.

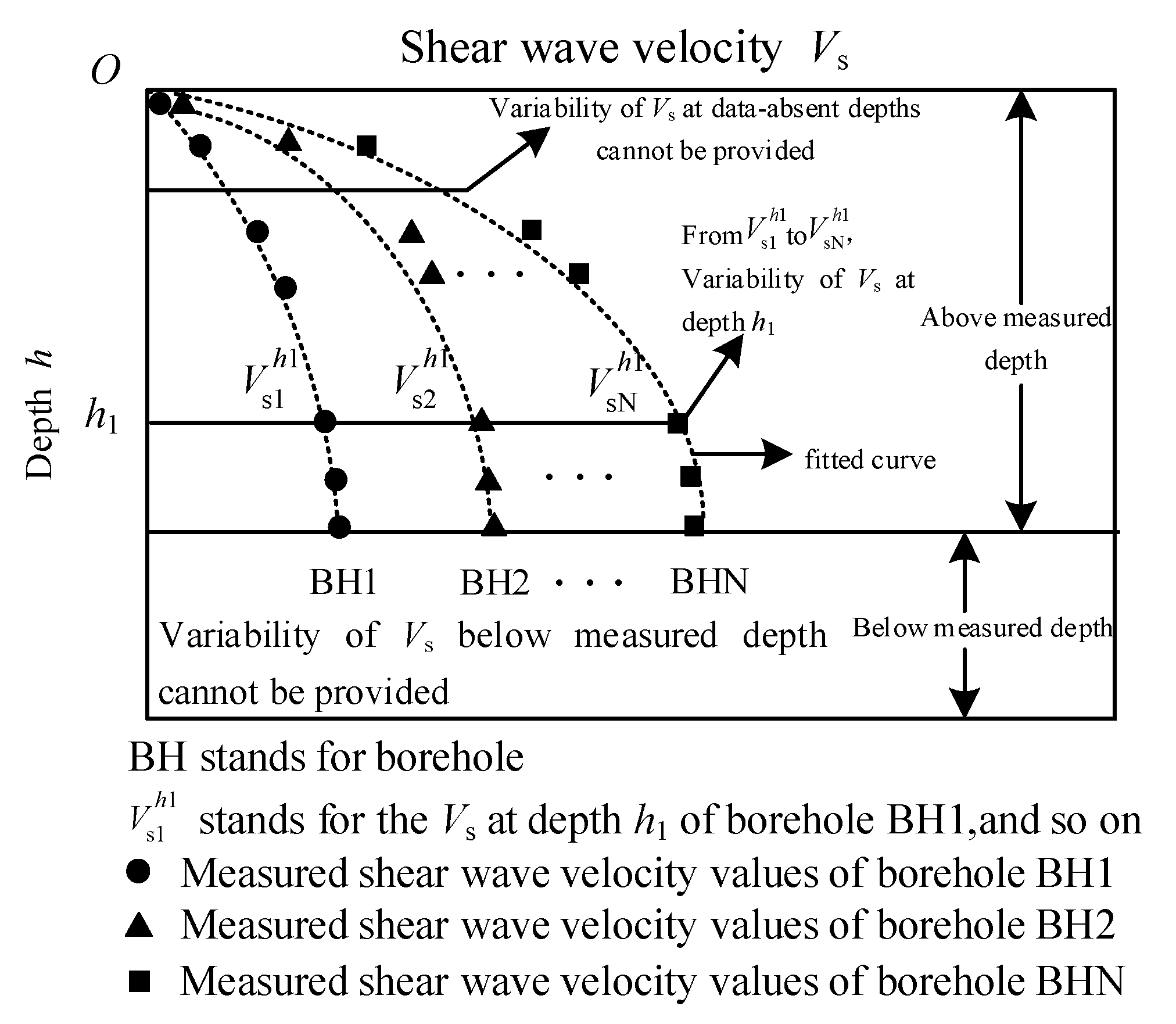
4. Uncertainty Analysis of Predicted V_s Values for Soils in a Certain Bay in China

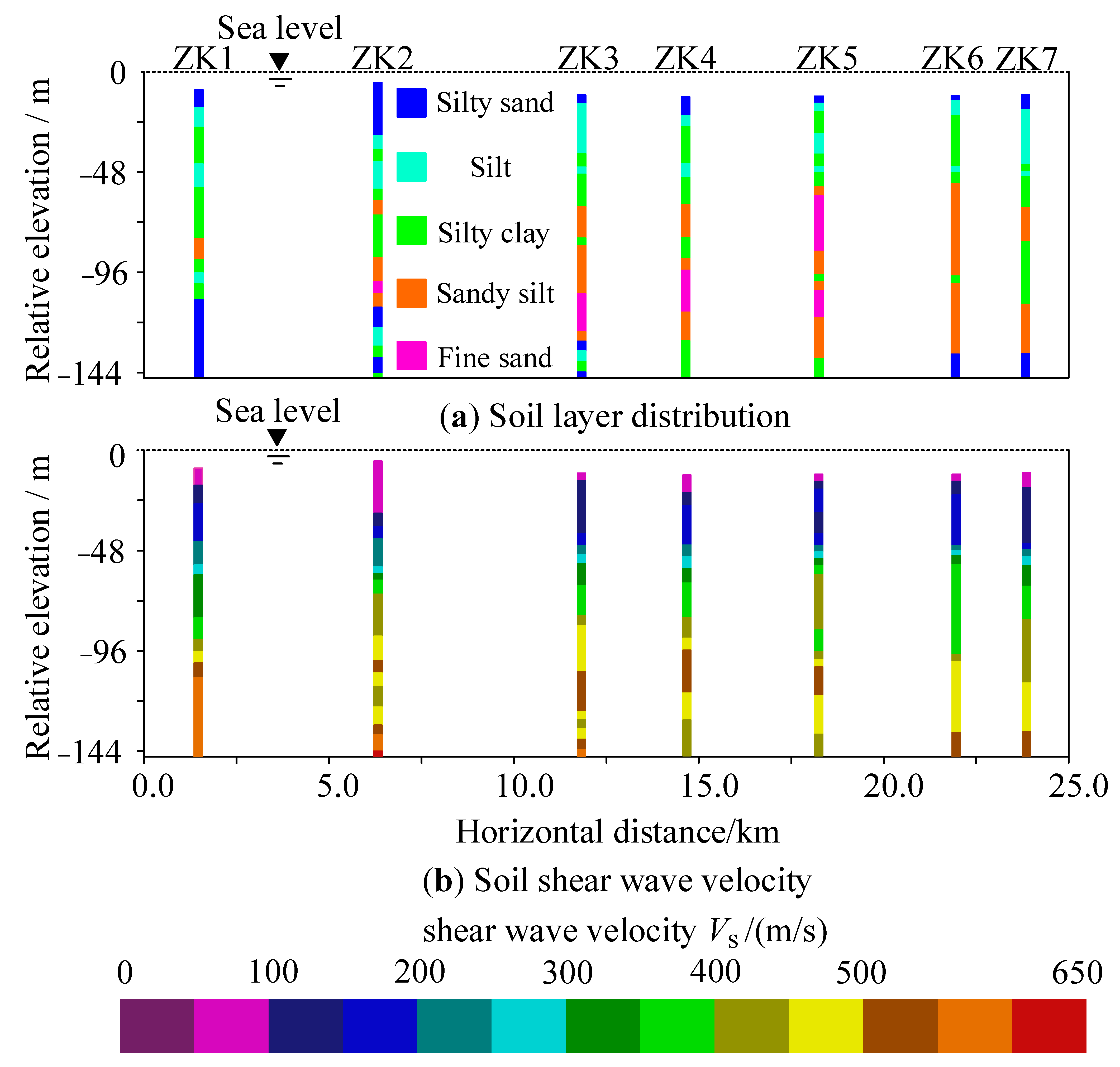
4.1. Site Overview

The certain sea area in China is located in northeastern China. Over recent decades, extensive marine engineering projects have been constructed in sea areas, accumulating a certain volume of test data for the physical and mechanical parameters of marine soils. However, due to the high costs and technical challenges of seabed drilling operations, the number of accumulated boreholes remains significantly limited compared to those in terrestrial sites. The characteristics of marine soil physical and mechanical parameters in the certain sea area are still fraught with uncertainty, urgently necessitating a scientifically robust method for evaluating this uncertainty. This study takes a site in a Chinese bay as an example and employs Bayesian theory combined with the point estimation method to evaluate the uncertainty of shear wave velocity (V_s) for marine soils in this region. Within a 25 km radius of this site, only seven boreholes exist. The soil types and measured V_s values for each borehole are shown in Figure 5. The relationship between V_s and depth h for each soil type within the boreholes was fitted using the power function shown in Equation (8), yielding the distributions of parameters a and b, as summarized in

Table 1. Statistical characteristics of S- wave velocity fitting parameters of soils.

Category	Soil Type	Parameter a		Parameter b
		Mean	Standard Deviation	Mean	Standard Deviation
On-site	Silty Sand	25.13	3.48	0.65	0.06
On-site	Silt	23.02	4.24	0.58	0.05
On-site	Silty Clay	33.14	4.00	0.56	0.03
On-site	Sandy Silt	73.35	7.78	0.40	0.04
On-site	Fine Sand	111.59	12.47	0.33	0.02
Maximum Posterior	Silty Sand	24.53	6.38	0.58	0.11
Maximum Posterior	Silt	22.09	7.53	0.50	0.13
Maximum Posterior	Silty Clay	32.29	6.48	0.52	0.09
Maximum Posterior	Sandy Silt	72.88	11.87	0.36	0.08
Maximum Posterior	Fine Sand	110.06	19.12	0.30	0.06

.

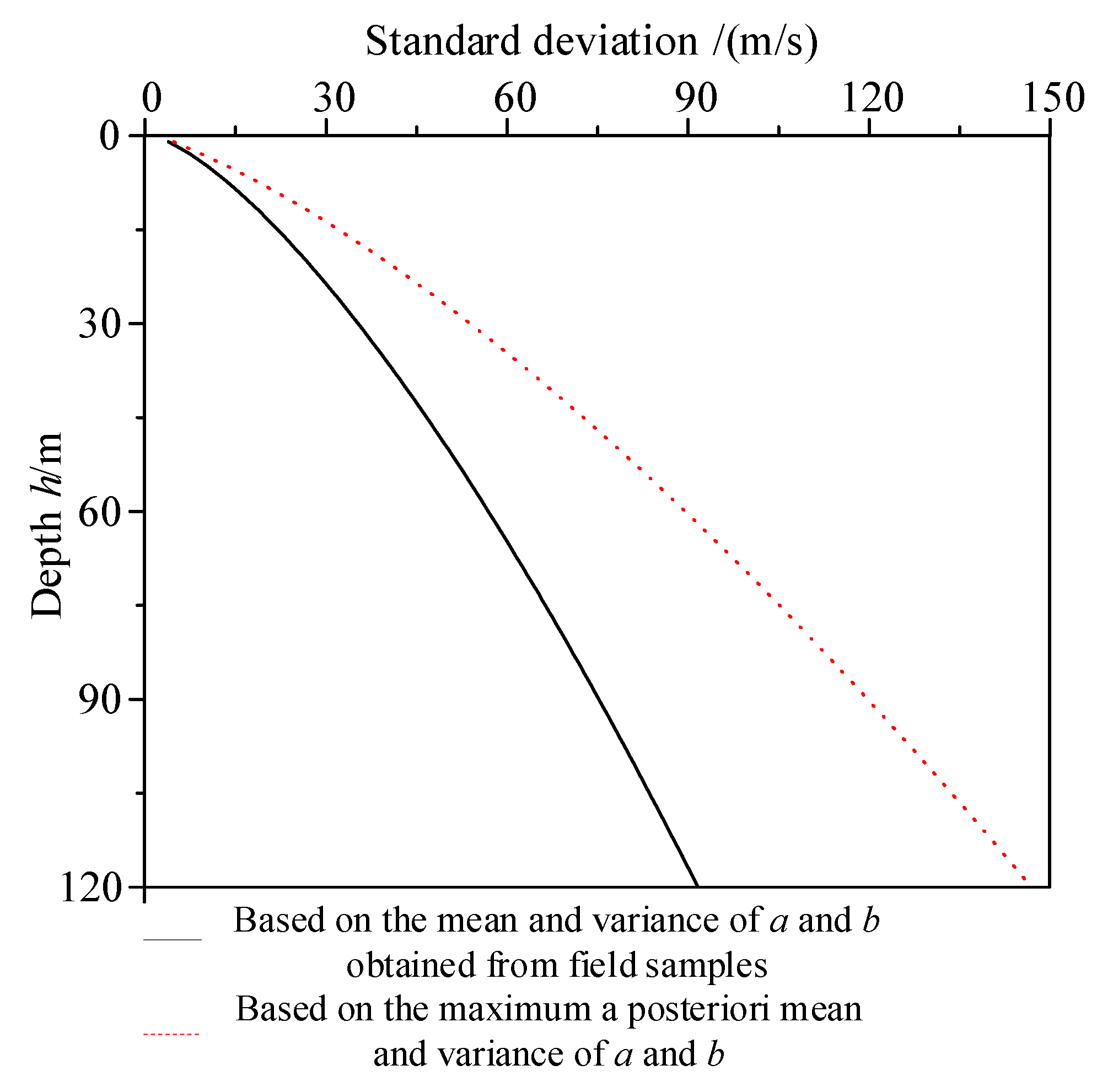
4.2. Uncertainty Analysis of Predicted V_s Values for Soils in the Study Area Based on Bayesian Theory and Point Estimation Method

Subsequently, the method described in Section 2 was employed to estimate parameters a and b. This estimation integrates prior information with on-site sample data, as shown in Figure 5. Previous engineering projects across this sea area have provided 36 boreholes. The data from these boreholes, which reveal the soil layer distribution and V_s values in the relevant regions, serve as prior samples for soil stratification and V_s distribution. Meanwhile, the borehole data from the specific site illustrated in Figure 5 constitutes the on-site sample distribution for this study.

As illustrated in Figure 6, taking parameter a of the power function for silty clay as an example, the 36 boreholes are divided into six groups, each containing six boreholes. The boreholes in this study were grouped based on the distances between their respective locations, with those in close proximity to each other being assigned to the same group.

Using the power function in Equation (8), the relationship between V_s and depth (h) for silty clay in each borehole is fitted, yielding six values of a per group along with their mean and variance. Subsequently, these means and variances of a are treated as samples to estimate the prior distributions for the mean and variance of a. The same procedure is applied to estimate the prior distributions for the mean and variance of parameter b.

Figure 7 presents the distributions of parameters a and b derived from prior samples of silty clay. Figure 8 shows the prior distributions of the mean and variance for fitting parameters a and b of silty clay calculated using the method in Section 2 based on the data in Figure 7. Through the Kolmogorov–Smirnov test at a significance level of 0.05, the means of fitting parameters a and b for silty clay both conform to a normal distribution, while the variances of a and b both conform to an inverse gamma distribution. Using the method in Section 2 and combining the on-site sample information of a and b provided in Table 1, the posterior probability distributions of a and b are obtained. The maximum posterior distribution of a and b is derived using Equation (27).

Table 1 presents the mean and variance of fitting parameters a and b for five types of marine soils obtained solely from the on-site sample information shown in Figure 5, along with the maximum posterior mean and maximum posterior variance of parameters a and b derived using the method in Section 2. Figure 9 shows the probability density distribution curves of fitting parameter a and b for silty clay obtained from the maximum posterior mean and maximum posterior variance of a and b, compared with those derived solely from the on-site sample information. Relative to the probability density curves of a and b estimated using only on-site sample information, the curves obtained from the maximum posterior mean and maximum posterior variance become lower and wider. This indicates that using only scarce on-site borehole information will underestimate the variability of fitting parameters a and b for silty clay.

By substituting the maximum posterior mean and maximum posterior variance of silty clay fitting parameters a and b into the point estimation method procedure outlined in Equations (9)–(13), the standard deviation of V_s values for silty clay within the 0–120 m depth range is obtained, as shown in Figure 10. For comparison, Figure 10 also includes the standard deviation of silty clay calculated over the same 0–120 m depth range using the point estimation method based solely on the mean and variance of a and b derived from on-site sample information (Table 1). The former is significantly larger than the latter, demonstrating that relying exclusively on on-site sample information while neglecting prior information will underestimate the variability of silty clay V_s values along the depth direction.

The red dots in Figure 11 represent the differences between the predicted V_s values for each soil type (calculated using Equation (8) with the mean values of parameters a and b derived solely from on-site samples in Table 1) and the measured V_s values for each soil type (shown in Figure 5). The black dots represent the differences between the predicted V_s values (calculated using Equation (8) with the maximum posterior mean values of parameters a and b for each soil type from Table 1) and the measured V_s values. The predicted V_s values for each soil type obtained from the maximum posterior mean of a and b are closer to the measured V_s values, indicating that combining prior information with sample information enables more accurate prediction of soil V_s values in the study area.

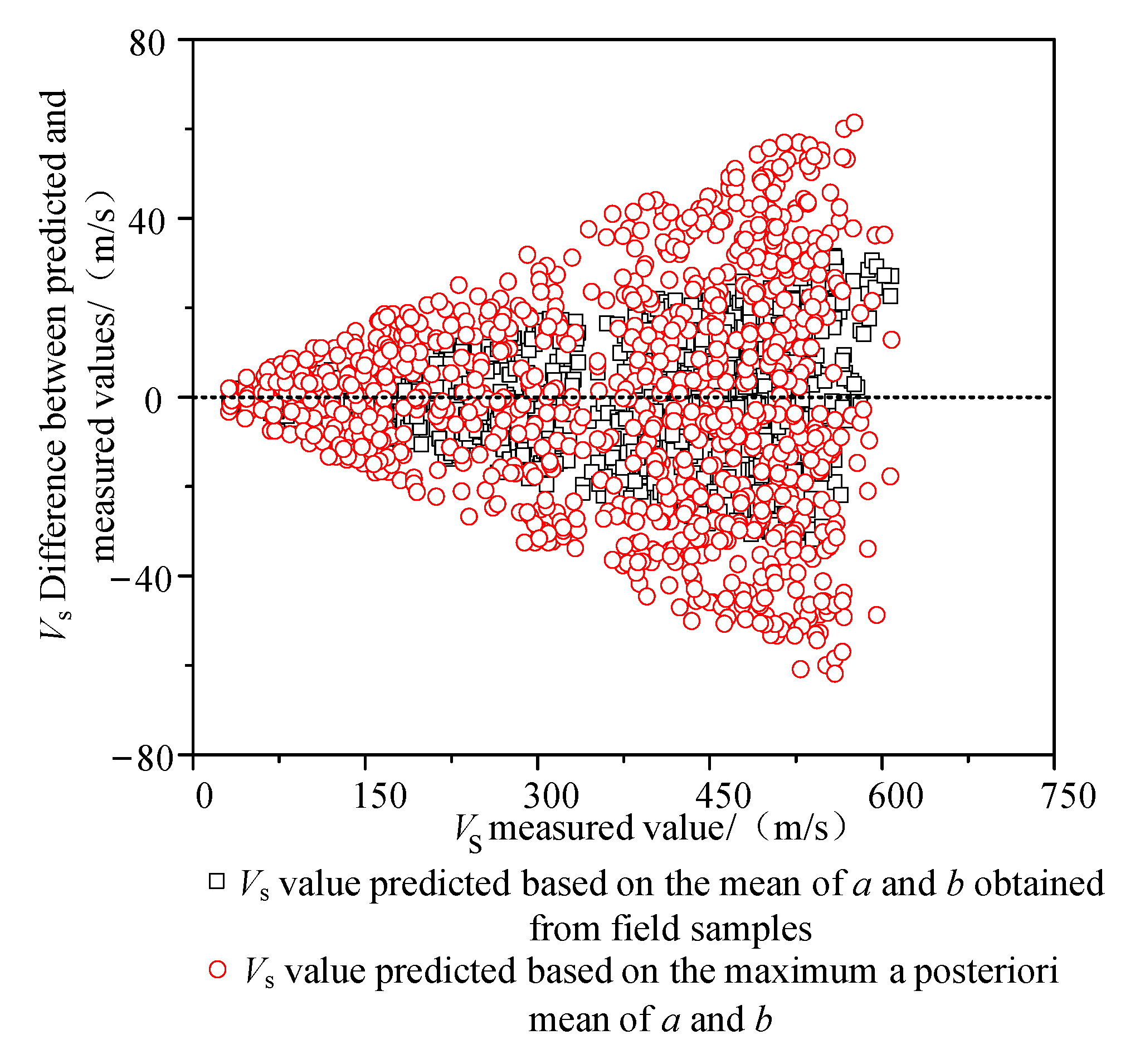
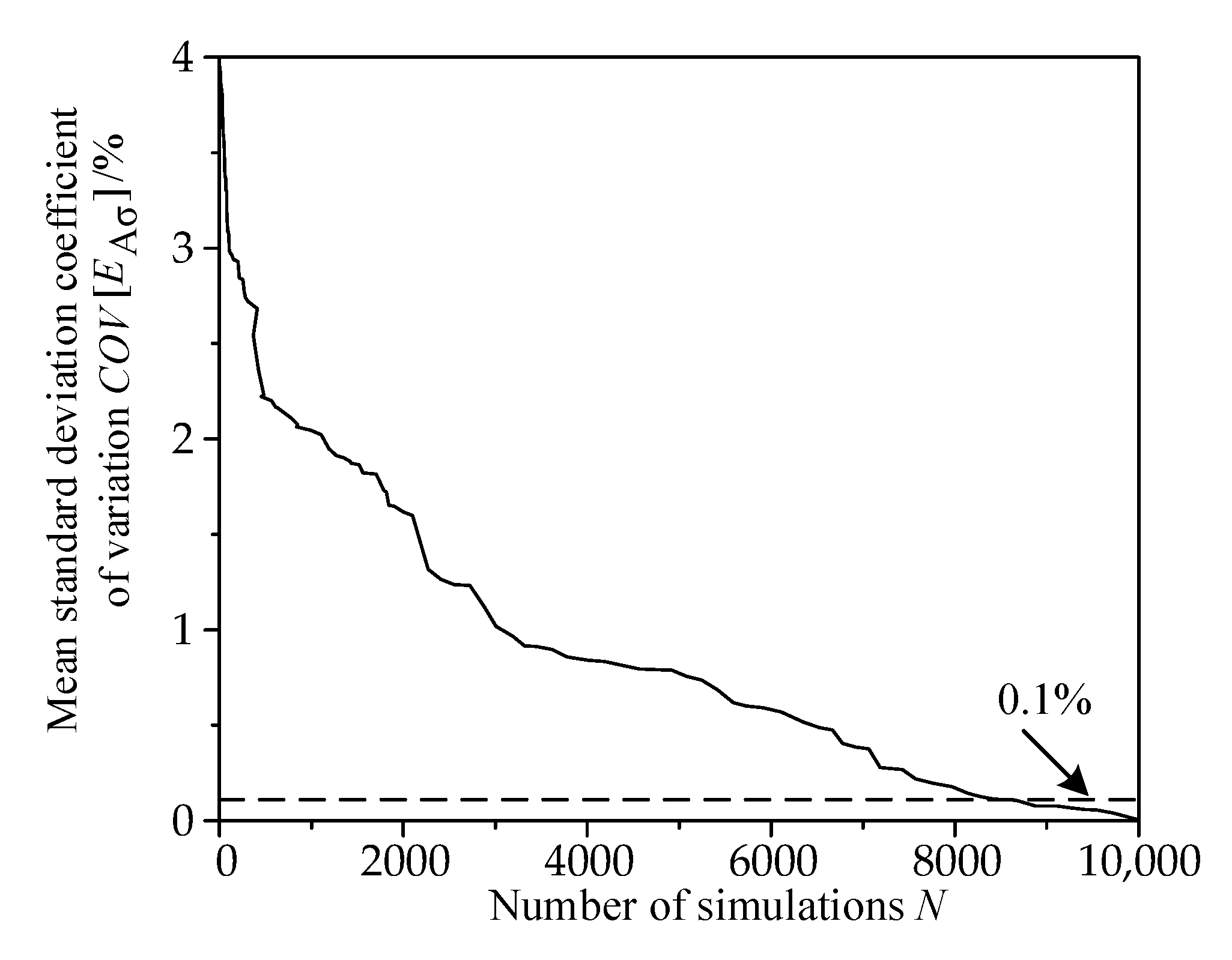
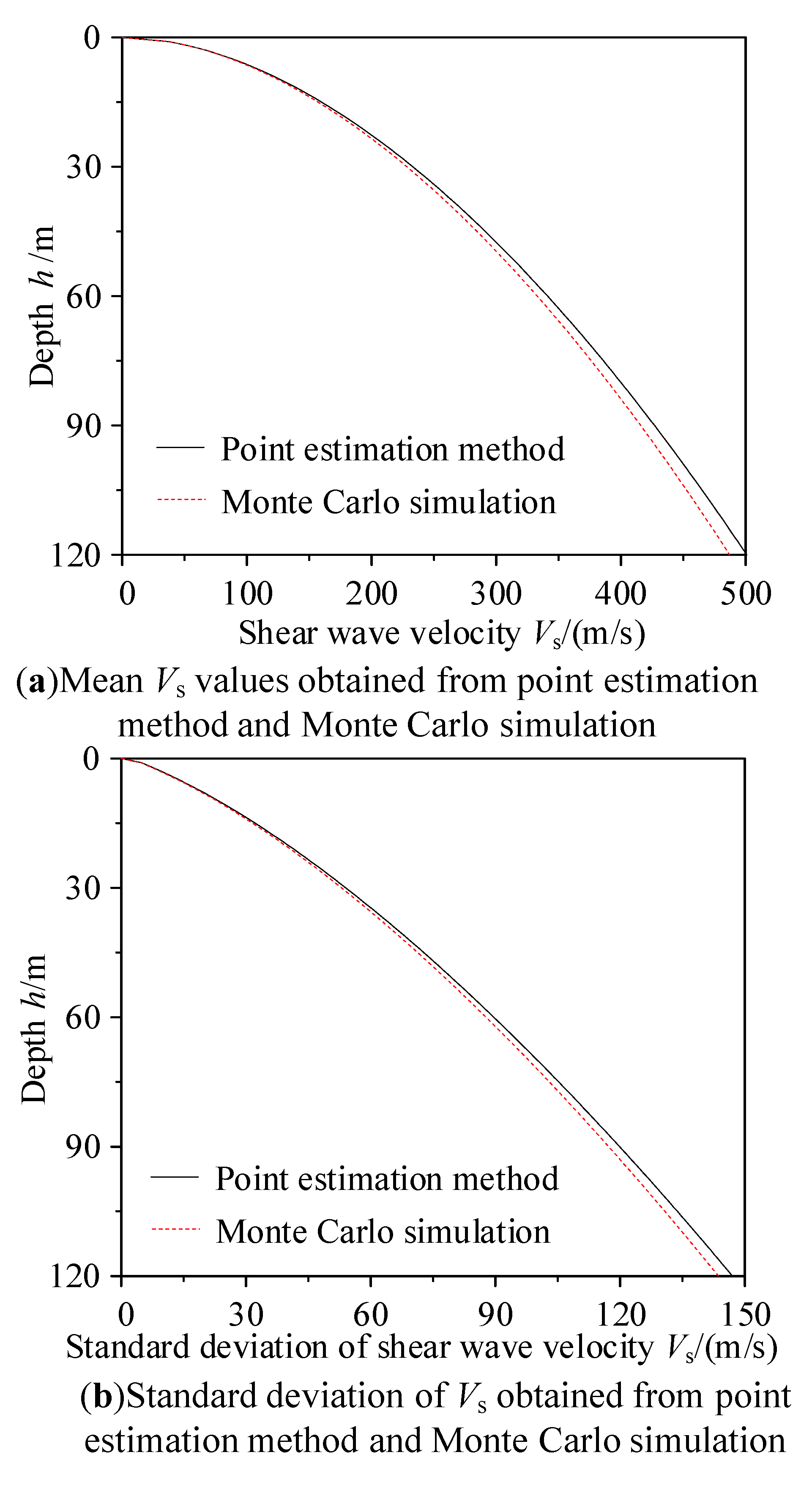
4.3. Comparison with Monte Carlo Simulation Results

The accuracy of the point estimation method can be validated using Monte Carlo simulation. Random sampling of parameters a and b is performed based on the probability distribution curves derived from their maximum posterior mean and maximum posterior variance in Figure 9. Each sampled pair of a and b values is substituted into Equation (8) to calculate the V_s values at various depths. Statistical analysis of V_s values obtained from Monte Carlo simulations at any depth yields the mean and standard deviation of V_s at that depth. To fully capture the distribution of random V_s possibilities, the number of Monte Carlo simulations must reach sufficient value N. The standard deviation ${\sigma }_{V_s}\left(h_{\alpha }\right)$ of V_s at any depth h_α obtained from N random simulations is:

$${\sigma }_{V_s}(h_{\alpha })={\displaystyle \frac{\sqrt{{\sum }_{l=1}^N{\left\{{V_s}^l(h_{\alpha })-\frac{{\sum }_{l=1}^N\left[{V_s}^l\right(h_{\alpha }\left)\right]}{N}\right\}}^2}}{(N-1)}},$$

(28)

In the equation, ${V_s}^l\left(h_{\alpha }\right)$ represents the simulated V_s value at any depth h_α during the l-th random simulation (l = 1, 2, … N). After N simulations, the mean value of the standard deviation ${\sigma }_{V_s}\left(h_{\alpha }\right)$ denoted as E_Aσ, is:

$$E_{A\sigma }={\displaystyle \frac{1}{n}}{\sum }_{\alpha =1}^n\left[{\sigma }_{V_s}\right(h_{\alpha }\left)\right],$$

(29)

In the equation, n = h/Δh, where Δh is the depth interval used to statistically analyze the variability of soil V_s values at different depths. This study sets Δh = 1 m, meaning the variability of soil V_s values is calculated at 1 m intervals. Different values of N yield different E_Aσ, from which the coefficient of variation COV[E_Aσ] can be computed. When COV[E_AE] ≤ 0.1% [37], the statistical characteristics of the fitted parameters for soil shear wave velocity in Table 1 are considered sufficient to indicate that N simulations can comprehensively capture the possible distribution of random V_s values [37]. Taking silty clay as an example, Figure 12 shows the variation in COV[E_Aσ] for random V_s values of silty clay obtained from Monte Carlo simulations with increasing N. When N ≥ 8000, COV[E_Aσ] falls below 0.1%. This study adopts N = 10,000 simulations.

Figure 13 compares the average value and standard deviation of V_s for silty clay at different depths calculated using the point estimation method (Equations (9)–(13)) based on the maximum posterior mean and standard deviation of a and b, with those obtained from Monte Carlo simulation. The differences between them are small, which demonstrates that the results calculated by the point estimation method are reasonable.

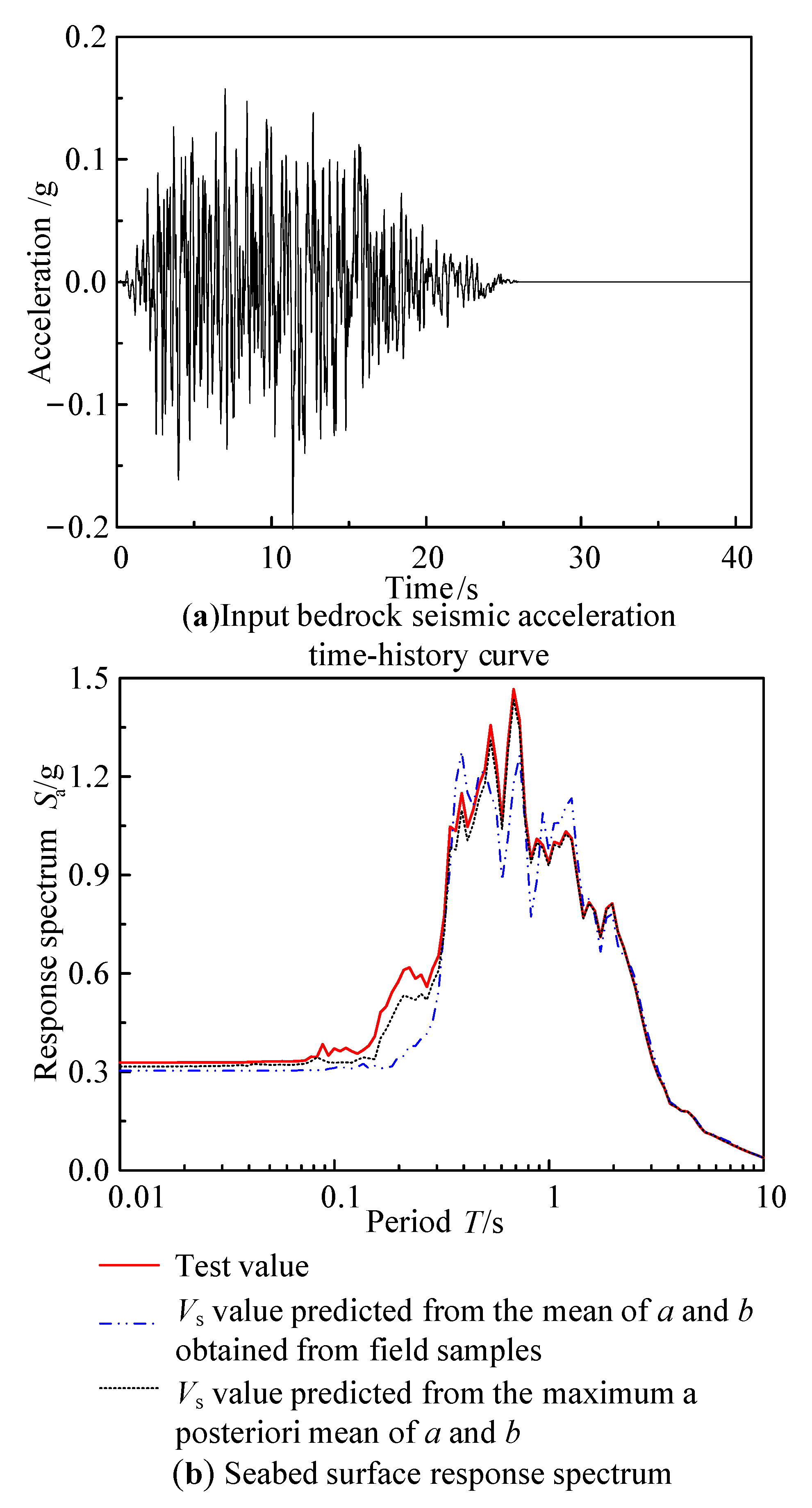
4.4. Impact of V_s Uncertainty On-Site Seismic Response Results

To further compare the influence of soil V_s values predicted by different methods on-site seismic response analysis results, seismic response analysis was conducted for borehole ZK1 in Figure 5. The predicted V_s values for each soil type in borehole ZK1 were sequentially calculated using Equation (8) with (1) the mean values of parameters a and b derived solely from on-site sample data, and (2) the maximum posterior mean values of parameters a and b for each soil type. These predicted V_s values served as input soil shear wave velocities for seismic response analysis.

The stress–strain relationship of soil under dynamic loading is described using the DCZ model (the Davidenkov–Chen–Zhao model) modified with the irregular loading–unloading criteria proposed by Chen et al. [38]. The dynamic shear modulus and damping ratio curves of the soil adopt the recommended values given by Zhang et al. [21].

The information of the magnitude of the design earthquake, the focal depth, the epicentral distance refer to Lv et al. [39].

This paper employs the trigonometric series method to synthesize artificial seismic waves. First, based on the results of seismic safety evaluation, the target response spectrum for the study area is determined. The amplitudes of each frequency component are then determined according to this target response spectrum. Subsequently, a random phase angle is assigned to each frequency component. Following this, all these sine waves are superimposed to generate an initial acceleration time-history with random characteristics.

Since the response spectrum of the initial waveform usually differs from the target spectrum, iterative adjustments are required: Its response spectrum is calculated and compared with the target spectrum, and the amplitudes of each frequency component are repeatedly adjusted based on this comparison until the two satisfactorily match.

To simulate the non-stationary characteristics of real seismic ground motions, the generated stationary wave is finally multiplied by an intensity envelope function, imparting a time-varying characteristic of amplitude that gradually increases, peaks, and then decreases. This method can generate time-histories that both meet engineering spectral requirements and possess the randomness of real seismic ground motions.

This paper employs methods from structural dynamics to compute the response spectrum [40]:

• Input Ground Motion: Select a real recorded or artificially synthesized ground motion acceleration time-history as input.
• Model Establishment: Establish a set of single-degree-of-freedom (SDOF) system models with a fixed damping ratio and different natural vibration periods.
• Dynamic Time-History Analysis: Apply the input ground motion to each SDOF model separately and compute the entire vibration process (displacement, velocity, acceleration) under seismic action through numerical integration.
• Peak Value Extraction: From the full time-history response of each model, identify the absolute maximum value of its response (such as maximum absolute acceleration, maximum relative velocity, or maximum relative displacement).
• Plotting the Spectrum: Use the natural vibration period of each SDOF model as the horizontal coordinate and the corresponding calculated maximum response value as the vertical coordinate. The curve formed by connecting all these points is the (acceleration, velocity, or displacement) response spectrum corresponding to that ground motion.

Figure 14a shows the acceleration time-history curve of the artificially synthesized bedrock seismic wave used for site seismic response analysis, with a peak acceleration of 0.20 g.

The response spectrum corresponding to the red line in Figure 14b is obtained through site seismic response analysis using the measured shear wave velocities of the soil at various depths in borehole ZK1. All the response spectra in Figure 14b are those at the surface of borehole ZK1.

Figure 14b presents the acceleration response spectrum (S_a) values at the surface of borehole ZK1 under this bedrock motion. Compared to the S_a values obtained using V_s predictions based solely on the mean of a and b from on-site samples, the S_a values derived from V_s predictions using the maximum posterior mean of a and b align more closely with the S_a values obtained from measured V_s data. This further demonstrates that combining prior information with on-site sample data enables more accurate prediction of soil V_s values in the study area, thereby enhancing the reliability of site seismic response analysis results.

5. Conclusions

This study utilized collected measured shear wave velocity (V_s) data of soils from a certain sea area in China, dividing the V_s data into one set of on-site samples and six sets of historical data. A power function was employed to establish the relationship between V_s values and depth (h). Bayesian statistical theory was applied to derive the prior and posterior distributions of the mean and variance for parameters a and b in the power function. Using the maximum posterior mean of a and b combined with the point estimation method, the variation in uncertainty in V_s predictions (obtained from the power function) with depth h was characterized. The main conclusions are as follows:

(1)

A power function regression equation was established to relate V_s and h. Prior distributions for the mean and variance of parameters a and b in the power function were derived from six sets of historical data. The prior means of a and b conform to a normal distribution, while their prior variances conform to an inverse gamma distribution.

(2)

The posterior distributions of the mean and variance for a and b were obtained by combining their prior distributions with on-site sample data. Using the maximum posterior mean of a and b with the point estimation method, the variation in the mean and standard deviation of predicted V_s values with h (when using the power function) was derived. The accuracy of the point estimation method results was validated via Monte Carlo simulation.

(3)

Compared to V_s predictions based solely on the mean of a and b from on-site samples, V_s predictions derived from the maximum posterior mean of a and b align more closely with measured V_s values. Consequently, the corresponding site seismic response analysis results also more closely match those calculated using true V_s values.