Research on Aerodynamic Load Simulation Techniques for Floating Vertical-Axis Wind Turbines in Basin Model Test
Abstract
1. Introduction
2. Theoretical Basis
2.1. Similarity Criteria for Model Testing
2.1.1. Description of Similarity Criteria
- Thrust similarity criterion
- TSR similarity criterion
2.1.2. The Phenomenon of Scale Effects
2.2. Aerodynamic Modeling of VAWTs
3. Blade Reconstruction Methodology in Fully Physical Model Tests
3.1. Alternative Solutions
- Increasing air density () by substituting air with a higher−density medium: However, this method is impractical for wind tunnel or wave basin testing due to operational constraints.
- Elevating wind speed () beyond the Froude−scaled value: Although this could augment lift, it would compromise the TSR similarity criterion. Additionally, the resulting increase in wind loading on both the tower and platform would introduce significant distortions in the floating wind turbine system’s dynamic response, leading to substantial measurement inaccuracies.
- Increasing the Reynolds number (Re) through high−pressure wind tunnel testing: This approach presents practical limitations, as most experimental facilities are conventional wind tunnels or wave basins where achieving sufficiently high Reynolds numbers remains technically challenging.
- Enhancing the lift coefficient () by employing airfoils optimized for low–Reynolds–number conditions: While feasible, this method fundamentally modifies the angle–of–attack dependence of both lift and drag coefficients, altering the aerodynamic behavior.
- Increasing chord length (), which scales linearly with aerodynamic loads: However, the associated increase in blade mass would elevate the rotor’s center of gravity, thereby violating Froude scaling requirements for the floating system.
- Adjusting the blade twist angle () to modify the effective angle of attack (), thereby operating at higher lift coefficients: Although this can partially improve rotor thrust, relying solely on twist angle adjustments proves inadequate for achieving target load values.
3.2. Blade Reconstruction Methodology
- Step 1: Scaling ratio determinationGeometric similarity forms the fundamental basis for model testing, requiring strict adherence to consistent scaling relationships. The scaling ratio () is mathematically expressed aswhere and represent corresponding linear dimensions of the model and prototype, respectively, encompassing length parameters, draft measurements, centers of gravity and buoyancy, water depth, and wave height characteristics. The optimal selection of necessitates a comprehensive evaluation of multiple constraints including physical model dimensions, laboratory facility limitations, and specific experimental objectives.
- Step 2: Initial blade parameter calculationApplying Froude scaling principles, the initial model blade parameters are derived from prototype values through the following relationships:where and denote the prototype blade chord length and twist angle, respectively. These equations establish the baseline geometric configuration for subsequent aerodynamic optimization.
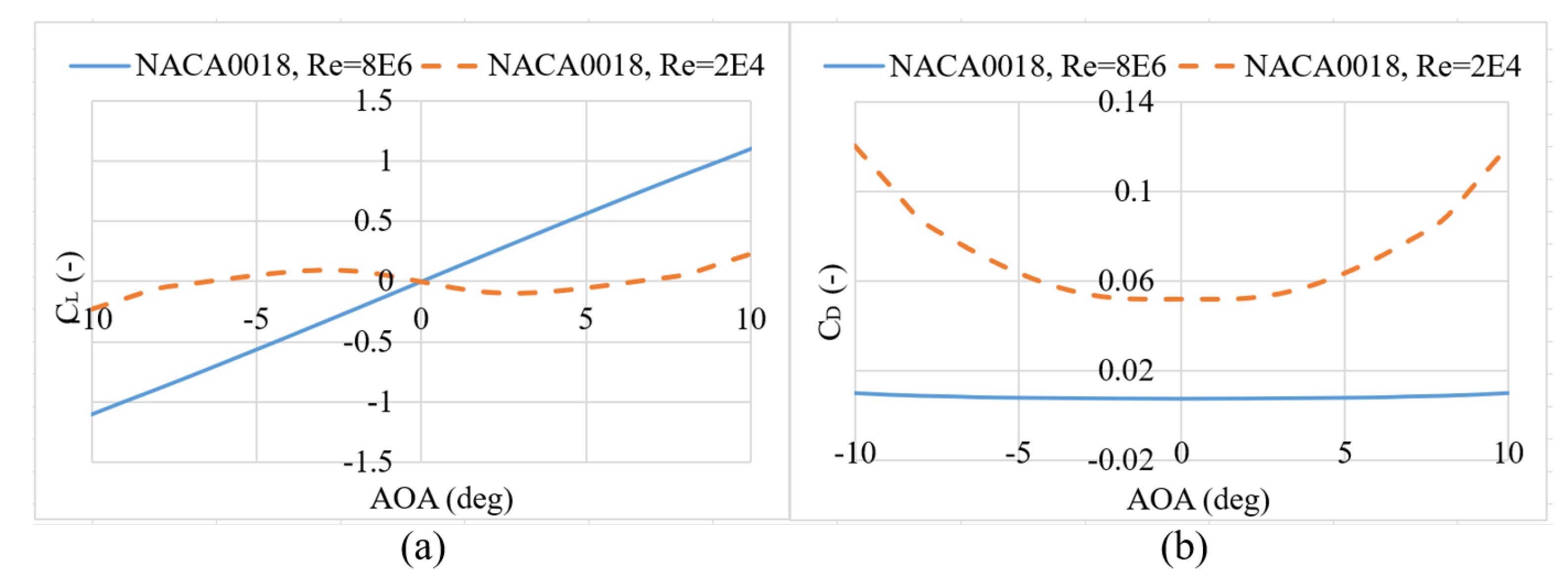
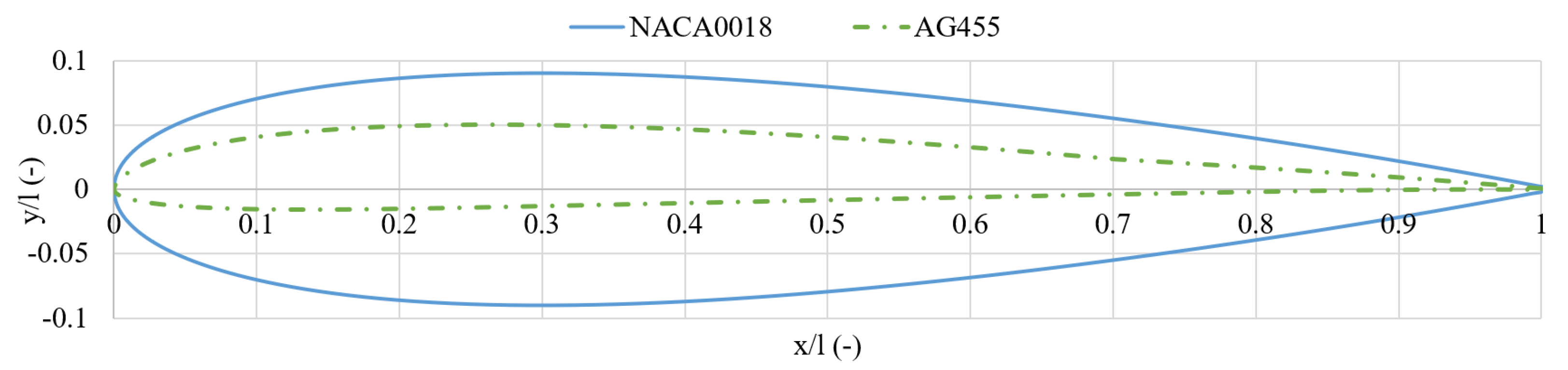
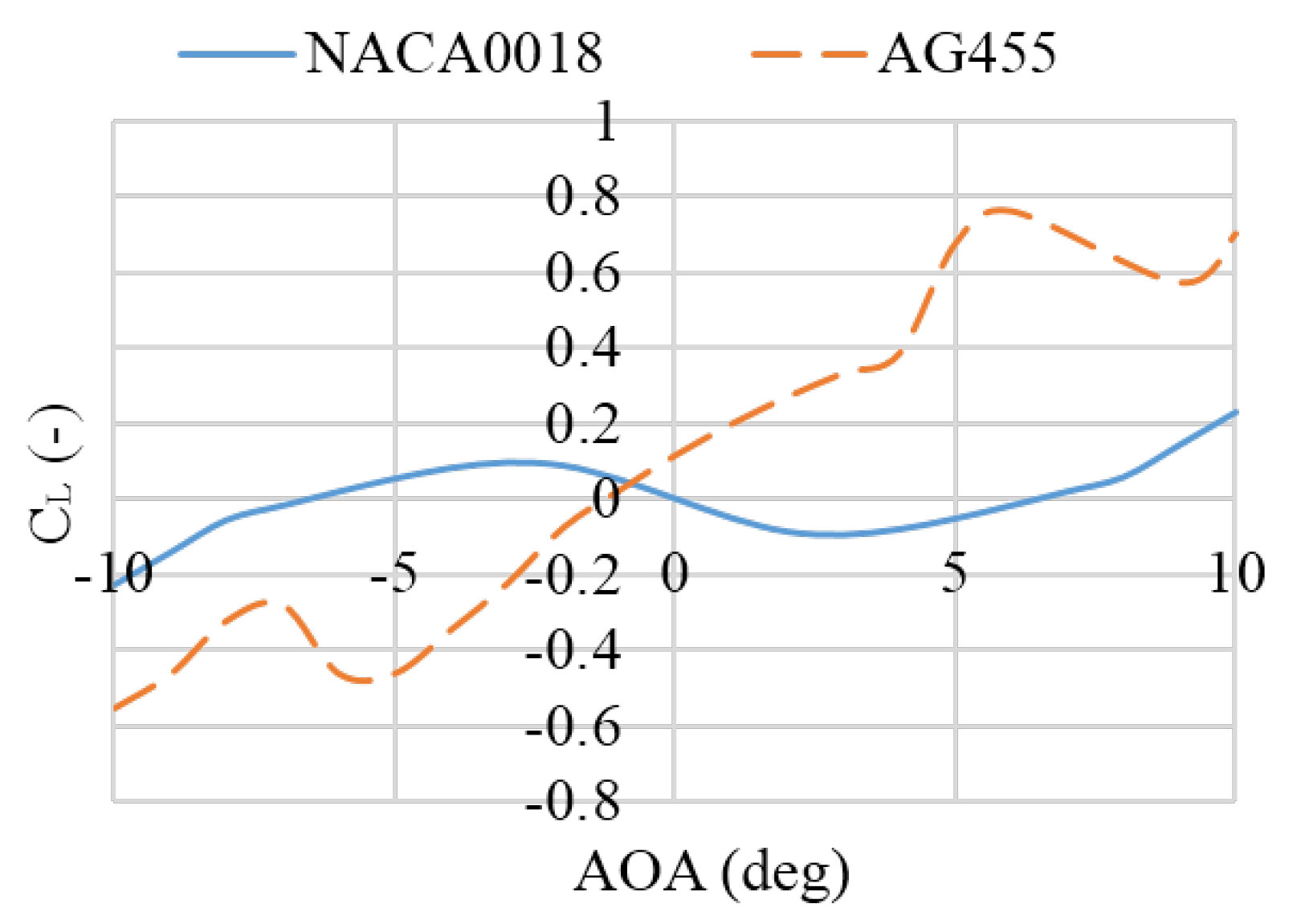
- Step 3: Airfoil profile optimizationFollowing geometric parameter determination, the methodology addresses the critical challenge of maintaining aerodynamic performance at reduced Reynolds numbers through specialized airfoil selection. The significant Reynolds number reduction in scaled testing renders conventional airfoils inadequate for lift generation, necessitating profiles specifically optimized for low−Re conditions. These airfoils must simultaneously achieve high lift coefficients and controlled structural thickness to balance aerodynamic and structural requirements.The comparative analysis between AG455 and NACA0018 airfoils (Figure 4 and Figure 5) demonstrates the superior performance of the AG455 profile in low−Re conditions, exhibiting enhanced lift generation, improved stall characteristics, and better aerodynamic efficiency. Its reduced thickness−to−chord ratio provides additional advantages in weight management and structural integration for scaled models. This airfoil selection critically influences both local blade performance and global system dynamics during testing, ensuring proper simulation of full−scale behavior while accommodating testing constraints.
- Step 4: Taylor series expansion formulationThe thrust coefficient () and side force coefficient () are expanded using a first−order Taylor series approximation about the initial design point ():By substituting the target values and into the equations, a linear system is derived for solving and .
- Step 5: Sensitivity coefficient calculationThe partial derivatives are determined through methodical parameter variation.(1) Baseline coefficients:The initial thrust and side force coefficients (, ) are computed for the geometrically scaled blade (chord , twist ).(2) Chord length sensitivity:
- For fixed , and are evaluated at multiple chord lengths c.
- Least−squares regression yields the functional relationships and , from which and at are extracted.
(3) Twist angle sensitivity:- For fixed , and are evaluated at multiple twist angles .
- Similarly, regression provides and at .
- Step 6: Solution and blade reconstructionThe linear system is solved to determine the optimal chord length () and twist angle (). This completes the blade reconstruction process, ensuring the scaled model achieves target aerodynamic loads while preserving similarity laws.
4. Research on Aerodynamic Load Simulation Devices for Semi−Physical Model Tests
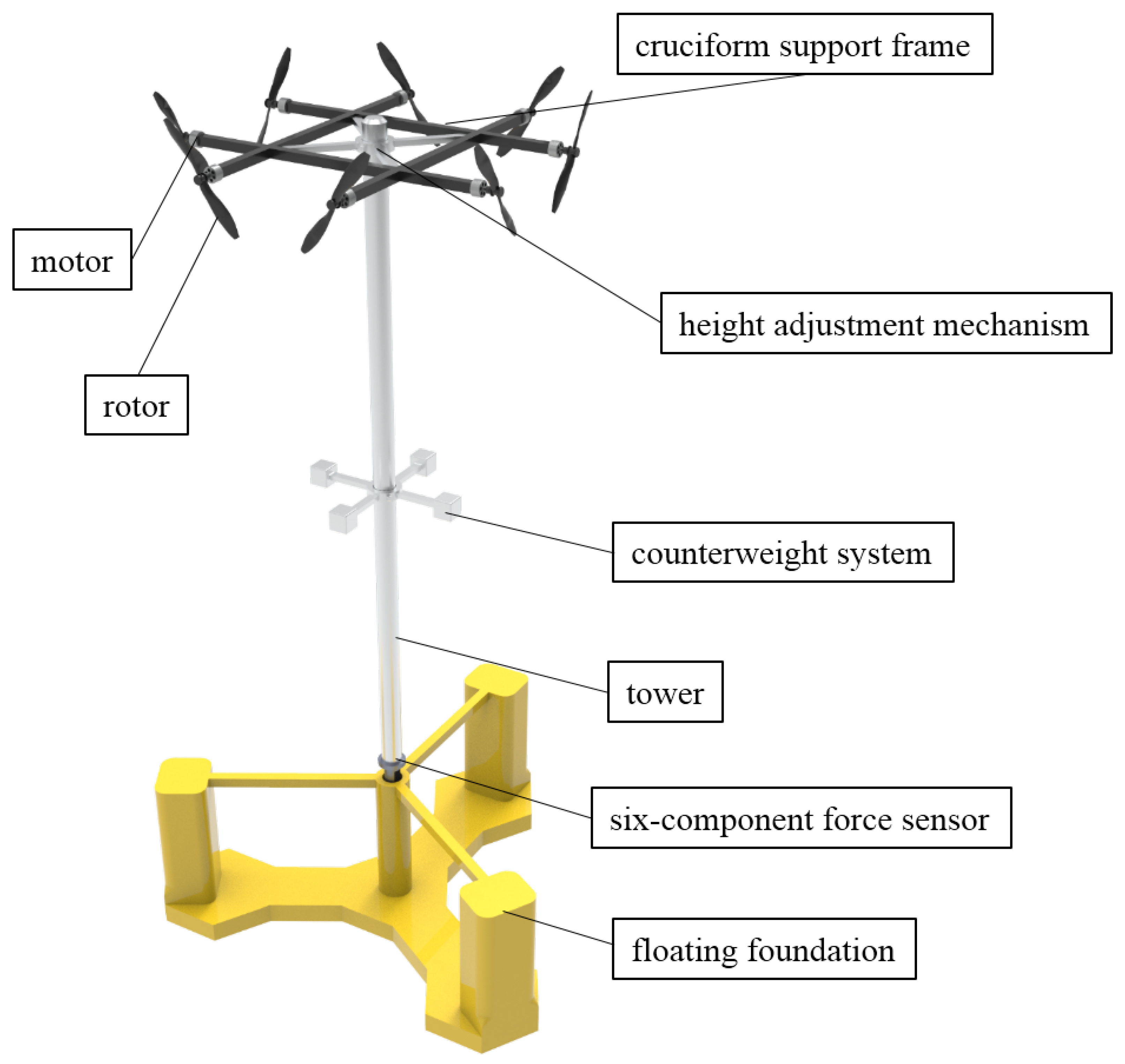
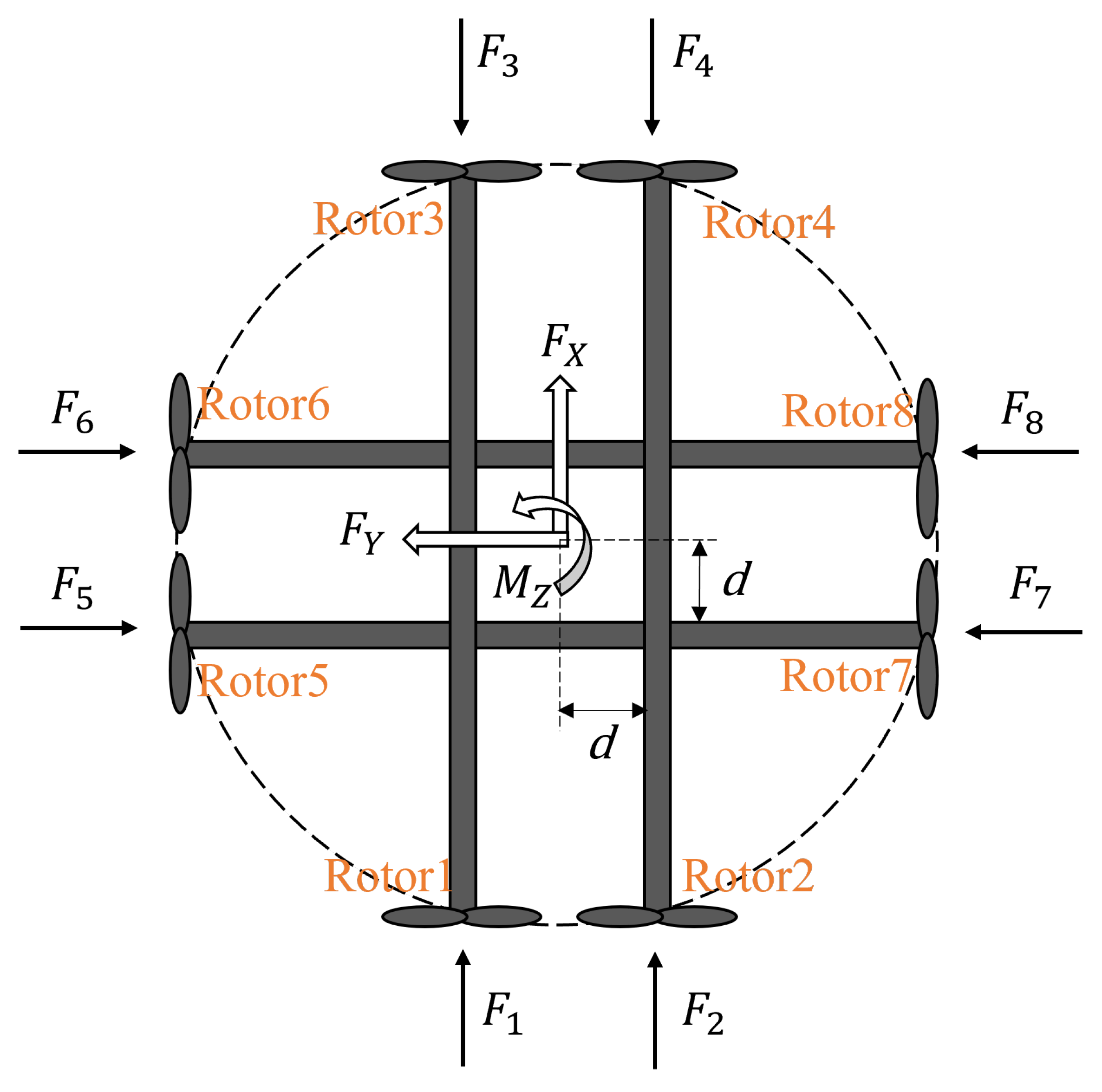
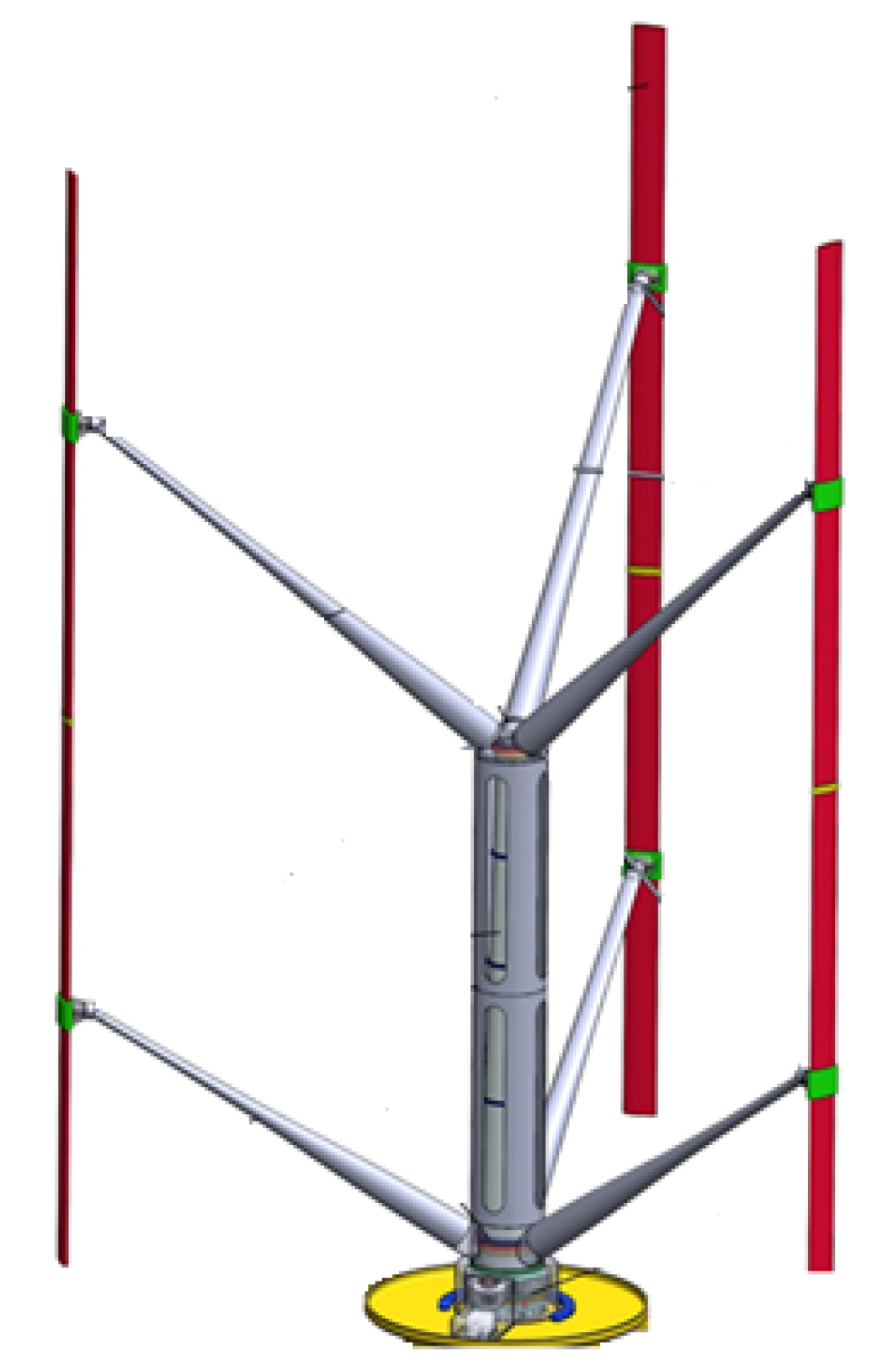
4.1. Physical Structure of the Cruciform−Arranged Rotor System
- Step 1: Connect the tower structure to the supporting column of the floating foundation via the six−component force sensor.
- Step 2: Secure the cruciform support frame to the tower using the height adjustment mechanism, setting the installation height at the aerodynamic force application point:Since the aerodynamic force application height varies under different wind conditions, this adjustment mechanism enables precise simulation of both the aerodynamic force arm and consequent tower base bending moment.
- Step 3: The cruciform support frame consists of four parallel support arms arranged in pairs, with each parallel arm set equidistant from the central point.
- Step 4: Mount the eight rotors to the endpoints of the cruciform frame via their respective motors. The two rotors on each side are installed in opposing rotational directions to create counter−rotation, effectively canceling individual rotor torque effects. Thrust magnitude is determined by rotor speed, with control signal input methods detailed in subsequent steps.
- Step 5: Install the counterweight system onto the tower structure, configuring it to meet three key parameters, namely the target mass (Froude−scaled weight), target center of gravity (vertical positioning), and target moment of inertia (adjustable through support arm length modification).
4.2. Force Allocation Algorithm
- Load Distribution: The target aerodynamic thrust time series along the wind direction, , is achieved by rotors 1−4. The target aerodynamic thrust time series along the crosswind direction, , is achieved by rotors 5−8, with rotors 5 and 6 generating identical aerodynamic thrusts and rotors 7 and 8 generating identical aerodynamic thrusts. The target aerodynamic torque time series about the vertical axis, , is achieved by rotors 1−4.
- Load Equalization: The thrust difference among all eight propellers should be minimized at each time instant. In conventional multi−rotor systems, certain rotors often operate under sustained high loads while others remain idle, leading to localized overheating and accelerated lifespan deterioration. This study enforces uniform load distribution across all rotors through thrust equalization constraints.
- Load temporal smoothness: The thrust variation between adjacent time steps must not exceed prescribed limits to ensure rapid and accurate aerodynamic load response. Traditional approaches require abrupt thrust reversal when load direction changes suddenly, inducing phase lag due to motor inertial delay and consequent load tracking distortion. By constraining inter−step thrust variation rates and leveraging the redundant degrees of freedom inherent in the cruciform configuration, this study fundamentally eliminates thrust discontinuities. When step changes occur in target loads, the algorithm autonomously selects smooth transition sequences for multiple rotor thrust groups while compensating load variations through a coordinated adjustment of remaining rotors, significantly reducing dynamic response time. This capability proves particularly critical for turbulent wind condition simulations. However, conventional methods fail to capture peak loads due to phase lag. The present invention successfully reproduces instantaneous aerodynamic load fluctuations across all wind regimes.
4.3. Control System and Drive System
5. Numerical Verification Case Study
5.1. The Introduction of the Research Object
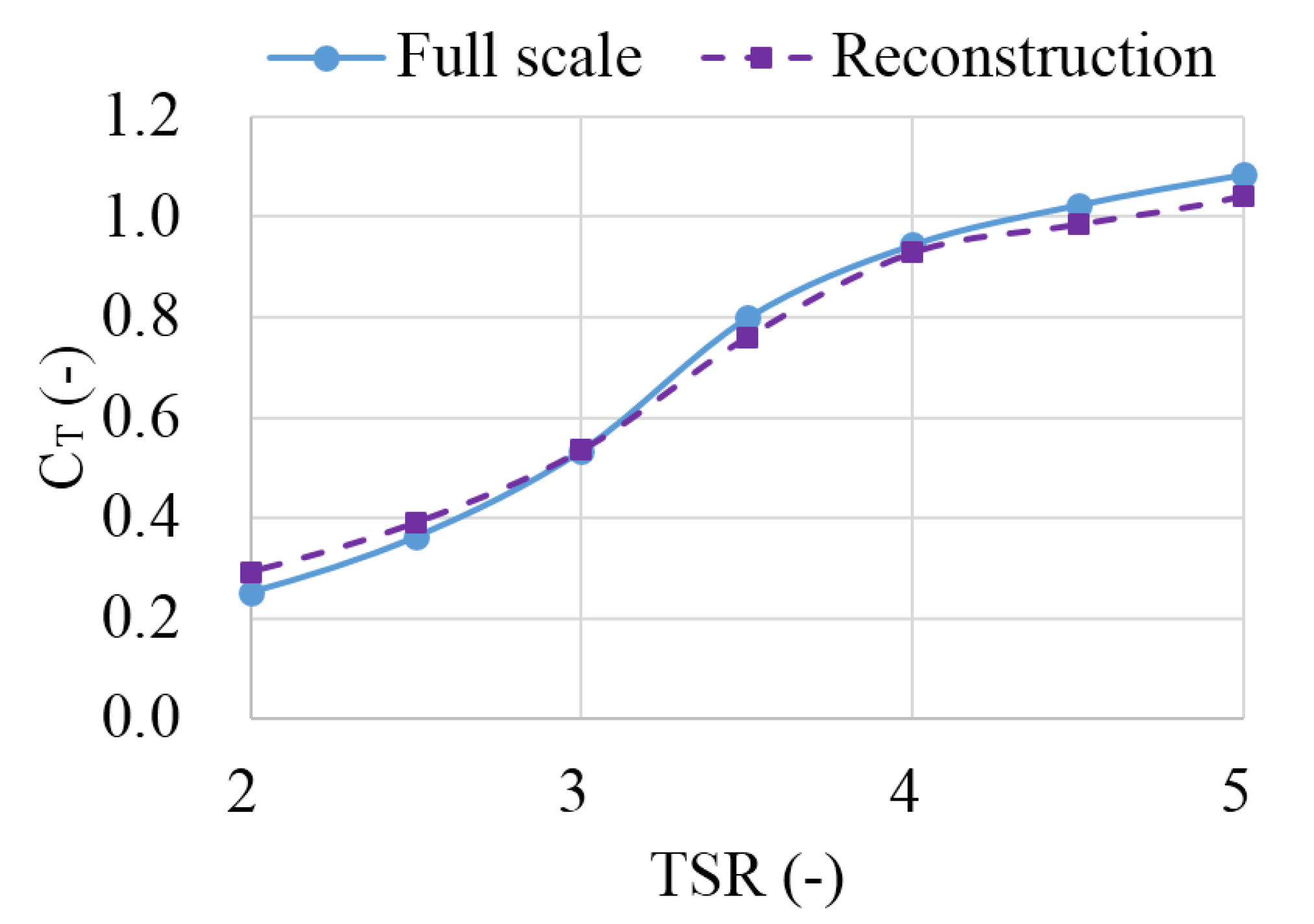
5.2. Numerical Verification in Fully Physical Model Tests
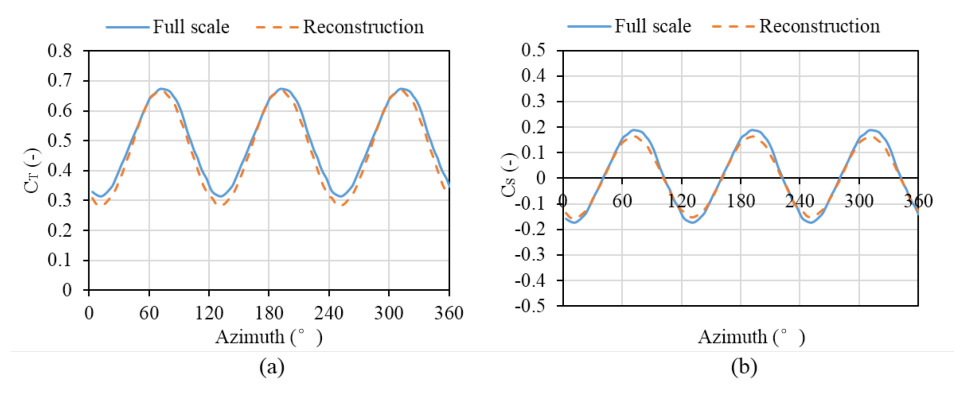
5.3. Numerical Verification in Semi−Physical Model Tests
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Description | SI Unit |
| Angle of attack | deg or rad | |
| Blade twist angle | deg or rad | |
| Density correction factor () | – | |
| Azimuthal angle of rotor rotation | deg or rad | |
| Geometric scaling ratio () | – | |
| Air density | kg/m3 | |
| Rotor angular velocity | rad/s | |
| Kinematic viscosity of the fluid | m2/s | |
| B | Number of blades | – |
| c | Blade chord length | m |
| Drag coefficient | – | |
| Lift coefficient | – | |
| Lateral (side) force coefficient | – | |
| Thrust coefficient | – | |
| D | Drag force per unit blade length | N/m |
| Froude number () | – | |
| , | Forces perpendicular and parallel to the chord | N |
| , | Normal and tangential forces on the actuator cylinder | N |
| , | Aerodynamic thrust in streamwise and crosswind directions | N |
| g | Gravitational acceleration | m/s2 |
| L | Lift force per unit blade length | N/m |
| , | Characteristic length (model and prototype) | m |
| , , | Aerodynamic moments about x, y, and z axes | N·m |
| , | Dimensionless normal and tangential force | – |
| R | Rotor radius | m |
| Reynolds number () | – | |
| T | Aerodynamic thrust | N |
| V | Characteristic velocity | m/s |
| Incoming wind speed | m/s |
Abbreviations
| Abbreviation | Full Form |
| 6−DoF | Six−Degree−of−Freedom |
| AOA | Angle of Attack |
| ESC | Electronic Speed Controller |
| FSR | Froude−Scale Rotor |
| HAWT | Horizontal−Axis Wind Turbine |
| PWM | Pulse Width Modulation |
| Re | Reynolds Number |
| TSR | Tip−Speed Ratio () |
| VAWT | Vertical−Axis Wind Turbine |
References
- Wang, X.; Li, H.; Zhang, W. State-of-the-art floating vertical-axis wind turbines: A review of design and modeling approaches. Renew. Energy 2021, 178, 185–201. [Google Scholar] [CrossRef]
- Liu, C.; Yu, X.; Sun, Z. Aerodynamic load modeling for vertical-axis wind turbines in wind tunnel tests. J. Phys. Conf. Ser. 2022, 2121, 012034. [Google Scholar] [CrossRef]
- Martin, S.; Jensen, P.; Sørensen, J.N. Aerodynamic force simulation devices for semi-physical model tests of vertical-axis wind turbines. Renew. Energy 2021, 172, 821–835. [Google Scholar] [CrossRef]
- Kim, H.; Park, J.; Lee, K. Performance evaluation of floating vertical-axis wind turbines under extreme wind conditions. In Proceedings of the ASME 2022 41st International Conference on Ocean, Offshore and Arctic Engineering (OMAE2022), Hamburg, Germany, 5–10 June 2022; p. V008T10A028. [Google Scholar]
- Nielsen, F.G.; Hanson, T.D.; Skaare, B. Integrated dynamic analysis of floating offshore wind turbines. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Hamburg, Germany, 4–9 June 2006; Volume 47462, pp. 671–679. [Google Scholar]
- Hall, M.; Goupee, A.; Jonkman, J. Development of performance specifications for hybrid modeling of floating wind turbines in wave basin tests. J. Ocean. Eng. Mar. Energy 2018, 4, 1–23. [Google Scholar] [CrossRef]
- Martin, H.R.; Kimball, R.W.; Viselli, A.M.; Goupee, A.J. Methodology for wind/wave basin testing of floating offshore wind turbines. J. Offshore Mech. Arct. Eng. 2014, 136, 020905. [Google Scholar] [CrossRef]
- Abdelghany, E.S.; Sarhan, H.H.; Alahmadi, R.; Farghaly, M.B. Study the Effect of Winglet Height Length on the Aerodynamic Performance of Horizontal Axis Wind Turbines Using Computational Investigation. Energies 2023, 16, 5138. [Google Scholar] [CrossRef]
- Farghaly, M.B.; Abdelghany, E. Study the effect of trailing edge flap deflection on horizontal axis wind turbine performance using computational investigation. Int. J. Renew. Energy Res. 2022, 12, 1942–1953. [Google Scholar] [CrossRef]
- Muller, K.; Sandner, F.; Bredmose, H.; Azcona, J.; Manjock, A.; Pereira, R. Improved tank test procedures for scaled floating offshore wind turbines. In Proceedings of the International Wind Engineering Conference (IWEC), Hannover, Germany, 3–5 September 2014. [Google Scholar]
- Adam, F.; Myland, T.; Dahlhaus, F.; Großmann, J. Scale tests of the GICON®-TLP for wind turbines. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014; Volume 45530, p. V09AT09A011. [Google Scholar]
- De Ridder, E.J.; Otto, W.; Zondervan, G.J.; Huijs, F.; Vaz, G. Development of a scaled-down floating wind turbine for offshore basin testing. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014; Volume 45530, p. V09AT09A027. [Google Scholar]
- Goupee, A.J.; Fowler, M.J.; Kimball, R.W.; Helder, J.; de Ridder, E.J. Additional wind/wave basin testing of the DeepCwind semi-submersible with a performance-matched wind turbine. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014; Volume 45547, p. V09BT09A026. [Google Scholar]
- Yu, W.; Lemmer, F.; Bredmose, H.; Borg, M.; Pegalajar-Jurado, A.; Mikkelsen, R.F.; Larsen, T.S.; Fjelstrup, T.; Lomholt, A.K.; Boehm, L.; et al. The triple spar campaign: Implementation and test of a blade pitch controller on a scaled floating wind turbine model. Energy Procedia 2017, 137, 323–338. [Google Scholar] [CrossRef]
- Azcona, J.; Bouchotrouch, F.; González, M.; Garciandía, J.; Munduate, X.; Kelberlau, F.; Nygaard, T.A. Aerodynamic thrust modelling in wave tank tests of offshore floating wind turbines using a ducted fan. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2014; Volume 524, p. 012089. [Google Scholar]
- Fontanella, A.; Liu, Y.; Azcona, J.; Pires, O.; Bayati, I.; Gueydon, S.; De Ridder, E.J.; Van Wingerden, J.W.; Belloli, M. A hardware-in-the-loop wave-basin scalemodel experiment for the validation of control strategies for floating offshore wind turbines. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2020; Volume 1618, p. 032038. [Google Scholar]
- Bachynski, E.E.; Chabaud, V.; Sauder, T. Real-time hybrid model testing of floating wind turbines: Sensitivity to limited actuation. Energy Procedia 2015, 80, 2–12. [Google Scholar] [CrossRef]
- Hall, M.; Goupee, A.J. Validation of a hybrid modeling approach to floating wind turbine basin testing. Wind Energy 2018, 21, 391–408. [Google Scholar] [CrossRef]
- Wen, B.; Liang, Z.; Zhang, H.; Fan, K.; Wang, Y.; Li, D.; Tian, X.; Peng, Z. A multi-drive aerodynamic load simulator for floating wind turbine model tests: Development, test and application. Ocean. Eng. 2023, 286, 115579. [Google Scholar] [CrossRef]
- Liu, G.; Jiang, Z.; Zhang, H.; Du, Y.; Tian, X.; Wen, B.; Peng, Z. A novel real-time hybrid testing method for Twin-Rotor Floating Wind Turbines with Single-Point Mooring systems. Ocean. Eng. 2024, 312, 119151. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, J.; Grabrick, B.; Jacobson, B.; Nelson, A.; Otte, J. Dynamic response of three floaters supporting vertical axis wind turbines due to wind excitation. J. Fluids Struct. 2018, 80, 316–331. [Google Scholar] [CrossRef]
- Ikoma, T.; Tan, L.; Moritsu, S.; Aida, Y.; Masuda, K. Motion characteristics of a barge-type floating vertical-axis wind turbine with moonpools. Ocean Eng. 2021, 230, 109006. [Google Scholar] [CrossRef]
- Rajeswari, K.; Nallayarasu, S. Experimental and numerical investigation on the suitability of semi-submersible floaters to support vertical axis wind turbine. Ships Offshore Struct. 2021, 17, 1743–1754. [Google Scholar] [CrossRef]
- Zheng, H.; Zheng, X.; Lei, Y.; Li, D.; Ci, X. Experimental validation on the dynamic response of a novel floater uniting a vertical-axis wind turbine with a steel fishing cage. Ocean Eng. 2022, 243, 110257. [Google Scholar] [CrossRef]
- Deng, W.; Guo, Y.; Liu, L.; Li, Y.; Jiang, Y.; Xie, P. Dynamic response analysis of a floating vertical axis wind turbine with helical blades based on the model test. Ocean Eng. 2023, 273, 113930. [Google Scholar] [CrossRef]
- Jiang, Y.; Cheng, Z.; Chen, P.; Chai, W.; Xiao, L. Performance-scaled rotor design method for model testing of floating vertical axis wind turbines in wave basins. Renew. Energy 2023, 219, 119425. [Google Scholar] [CrossRef]
- Jiang, Y.; Chen, P.; Wang, S.; Cheng, Z.; Xiao, L. Dynamic responses of a 5?MW semi-submersible floating vertical-axis wind turbine: A model test study in the wave basin. Ocean. Eng. 2024, 296, 117000. [Google Scholar] [CrossRef]
- Jiang, Y.; Cheng, Z.; Deng, S.; Chen, P.; Liu, L.; Xiao, L. An experimental study on the strain responses of blades and struts of a 5MW semi-submersible floating vertical-axis wind turbine. Mar. Struct. 2025, 102, 103794. [Google Scholar] [CrossRef]
- Cao, Q.; Chen, Y.; Zhang, K.; Zhang, X.; Cheng, X.; Wen, B. Design approach of thrust-matched rotor for basin model tests of floating straight-bladed vertical axis wind turbines. J. Renew. Sustain. Energy 2023, 15, 063308. [Google Scholar] [CrossRef]
- Martin, H.R. Development of a Scale Model Wind Turbine for Testing of Offshore Floating Wind Turbine Systems. Master’s Thesis, The University of Maine, Orono, ME, USA, 2011. [Google Scholar]
- Madsen, H.; Larsen, T.; Paulsen, U.; Vita, L. Implementation of the actuator cylinder flow model in the HAWC2 code for aeroelastic simulations on vertical axis wind turbines. In Proceedings of the 51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013. [Google Scholar]


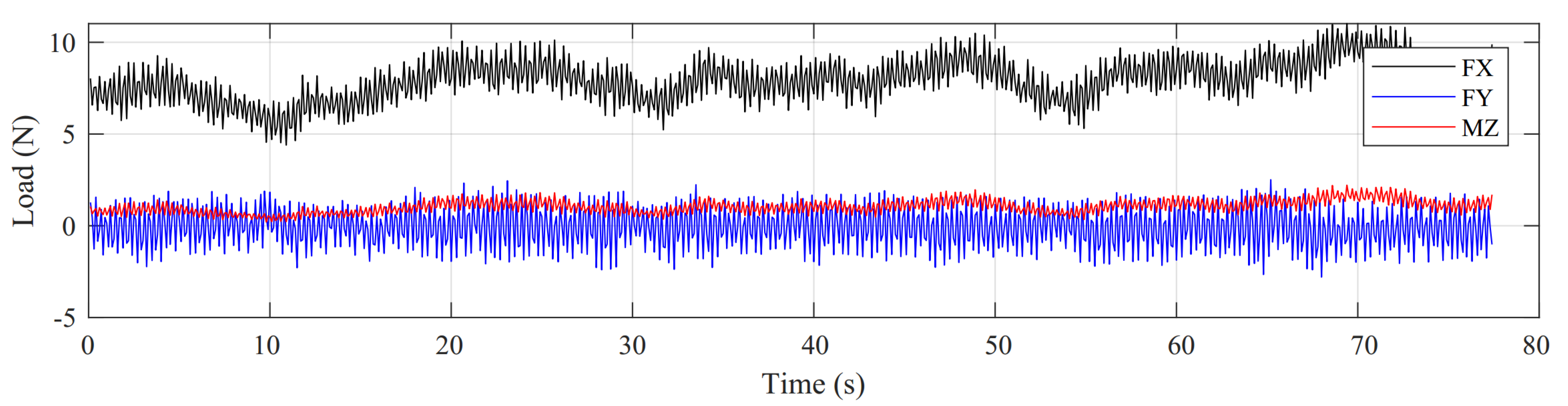
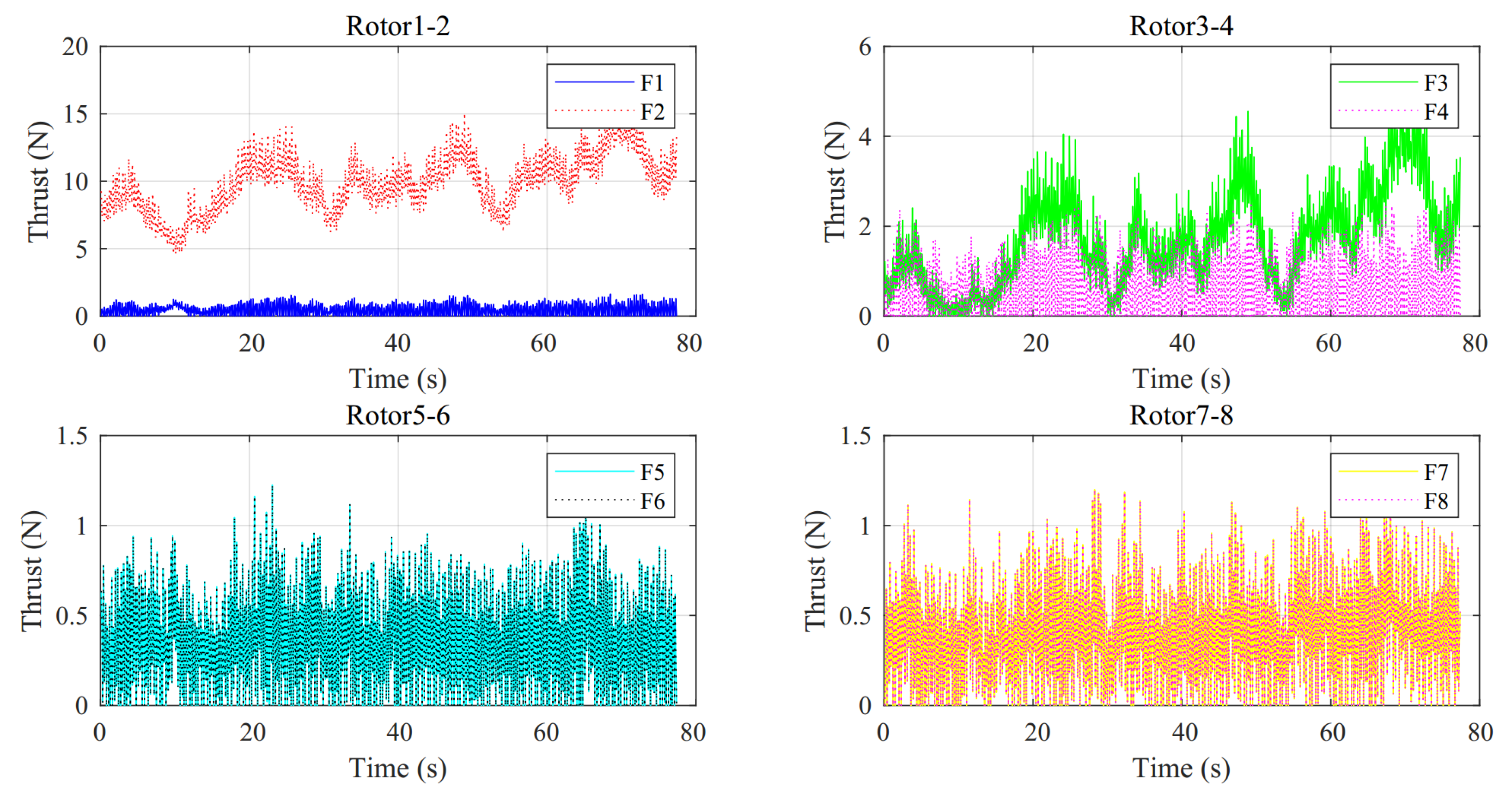
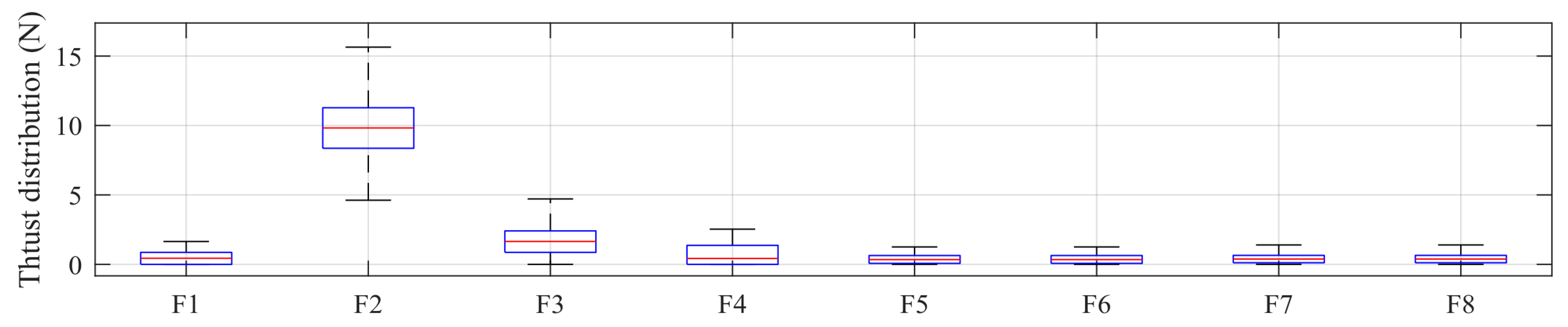
| Parameter | Full−Scale | Model−Scale (1:60) |
|---|---|---|
| Rated power | 10 MW | / |
| Configuration | 3−blade | 3−blade |
| Rotor diameter | 160 m | 0.65 m |
| Blade length | 200 m | 1.33 m |
| Blade airfoil | NACA0018 | AG455 |
| Blade chord | 3.0 m | 0.056 m |
| Blade twist | 0° | −0.6° |
| Rated wind speed | 13.2 m/s | 1.70 m/s |
| Rated rotor speed | 9.68 rpm | 74.98 rpm |
| Wind speed range | 3.0−25.0 m/s | 0.39−3.23 m/s |
| Rotor speed range | 2.2−7.97 rad/s | 17.04−61.74 rad/s |
| TSR range | 2.09−4.80 | 2.90−4.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Q.; Chen, Y.; Zhang, K.; Zhang, X.; Cheng, Z.; Jiang, Z.; Chen, X. Research on Aerodynamic Load Simulation Techniques for Floating Vertical-Axis Wind Turbines in Basin Model Test. J. Mar. Sci. Eng. 2025, 13, 1924. https://doi.org/10.3390/jmse13101924
Cao Q, Chen Y, Zhang K, Zhang X, Cheng Z, Jiang Z, Chen X. Research on Aerodynamic Load Simulation Techniques for Floating Vertical-Axis Wind Turbines in Basin Model Test. Journal of Marine Science and Engineering. 2025; 13(10):1924. https://doi.org/10.3390/jmse13101924
Chicago/Turabian StyleCao, Qun, Ying Chen, Kai Zhang, Xinyu Zhang, Zhengshun Cheng, Zhihao Jiang, and Xing Chen. 2025. "Research on Aerodynamic Load Simulation Techniques for Floating Vertical-Axis Wind Turbines in Basin Model Test" Journal of Marine Science and Engineering 13, no. 10: 1924. https://doi.org/10.3390/jmse13101924
APA StyleCao, Q., Chen, Y., Zhang, K., Zhang, X., Cheng, Z., Jiang, Z., & Chen, X. (2025). Research on Aerodynamic Load Simulation Techniques for Floating Vertical-Axis Wind Turbines in Basin Model Test. Journal of Marine Science and Engineering, 13(10), 1924. https://doi.org/10.3390/jmse13101924






