Wave-Induced Loads and Fatigue Life of Small Vessels Under Complex Sea States

Abstract

The Strait of Messina poses unique challenges for small vessels due to strong currents and complex wave conditions, which critically affect structural integrity and operational safety. This study proposes an integrated methodology that combines seakeeping analysis, a comparison with classification society rules, and fatigue life assessment within a unified and computationally efficient framework. A panel-based approach was used to compute vessel motions and vertical bending moments at different speeds and wave directions. Hydrodynamic loads derived from Response Amplitude Operators (RAOs) were compared with regulatory limits and applied to fatigue analysis. A further innovative aspect is the use of high-resolution bathymetric data from the Strait of Messina, enabling a realistic representation of local currents and sea states and providing a more accurate assessment than studies based on idealized conditions. The results show that forward speed amplifies bending moments, reducing safe wave heights from 2 m at rest to about 0.5 m at 16 knots. Fatigue analysis indicates that aluminum hulls are highly vulnerable to 2–3 m waves, while steel and titanium show no significant damage. The proposed workflow is transferable to other vessel types and supports safer design and operation. The case study of the Strait of Messina, the busiest and most challenging maritime corridor in Italy, confirms the validity and practical importance of the approach. By combining hydrodynamic and structural analyses into a single workflow, this study establishes the foundation for predictive maintenance and real-time structural health monitoring, with significant implications for navigation safety in complex sea environments.

1. Introduction

Structural stresses experienced by small vessel hulls pose significant challenges to both operational stability and structural integrity, particularly when not adequately addressed during the design phase. Despite their limited size, small craft such as fishing boats and recreational vessels often operate under harsh sea conditions, necessitating comprehensive hydrodynamic assessments. As a result, a growing body of literature has focused on elucidating the complex fluid–structure interactions that affect these vessels. Tavakoli et al. [1], for instance, explored the dynamics of a planning hull operating in irregular waves, emphasizing the onset of nonlinear behaviors at higher speeds. Additional research, such as that presented in Refs. [2,3], analyzed how forward speed and wave height affect the seakeeping performance of small fishing and passenger vessels. Iqbal et al. [4] focused on operability and structural reliability under different loading conditions. Their study applied the JONSWAP spectrum to simulate wave environments and evaluated vessel motions against critical safety thresholds. In the context of structural reliability, Hafiz and Sulisetyono [5] employed diffraction theory to analyze wave-induced stresses across multiple hull configurations. Their approach enabled the estimation of peak vertical bending moments (VBMs), revealing the impracticality of certain hull designs under specific sea states. Pacuraru et al. [6] evaluated hydrodynamic performance as a function of hull geometry and speed, demonstrating that drag, sinkage, and trim could be significantly minimized through optimized hull forms, particularly at high speeds. Suastika et al. [7] examined total drag behavior in relation to the implementation of a foil system. Their findings revealed that drag increases at low speeds but decreases as speed rises. This trend is explained by the limited lift generated at lower speeds, which is insufficient to raise the hull above the water. In contrast, at higher speeds, adequate lift is produced, allowing the hull to rise and thereby reducing drag. This reduction in drag at elevated speeds contributes to improved energy savings. Another study [8] combined the ITTC wave spectrum with Response Amplitude Operators (RAOs) to produce a statistical evaluation of vessel responses as a function of wave direction and sailing speed. A polar velocity diagram was used to illustrate vessel responses across five degrees of freedom as a function of sailing speed and wave direction in a specific sea state. Ref. [9], utilized computational fluid dynamics (CFD) to assess resistance by varying the transverse spacing between primary and auxiliary hulls. Results indicated increased hydrodynamic resistance with reduced spacing due to flow interference effects. In the research conducted by Wulandari et al. [10], vessel motion was investigated under wave conditions characterized by the JONSWAP spectrum, which defines the sea state using specific parameters. The study examined RAOs across different wave frequencies and vessel speeds, finding that the peak RAO values increase proportionally with the vessel’s speed. According to the 1987 Nordforsk seakeeping criteria, the results indicated that the vessel can operate safely only at speeds up to 9 knots.

The studies reviewed emphasize that vessel instability in wave conditions is a complex phenomenon to assess, often resulting in poor sailing performance and posing risks of structural damage due to significant dynamic responses and elevated vertical accelerations. In addition, the application of Response Amplitude Operators (RAOs), is often used to assess vessel motions induced by wave excitation forces. The movement of waves induces varying and complex loads on the structure. Low to medium frequency stresses, caused by oscillating wave forces and wave impacts, are critical for the fatigue lifespan of structural components [11]. Another key point is represented by the extensive use of computational hydrodynamics to evaluate the influence of wave height and forward speed to identify critical local areas of the hull subjected to varying sea states, with results subsequently applied in structural reliability assessments. Typically, these structures are coupled through welded joints. These joints, known for being sites of high stress concentrations, are subject to considerable environmental loading from wave pressure and ship movements, resulting in considerable fatigue loads. The combination of stress concentrations and fatigue loads leads to cyclic stress, surpassing the local yield stress which are detectable within a few years of the start of a ship’s service life [12]. For this reason, the fatigue assessment of welded joints is extensively studied during recent decades. The simplest approach is nominal stress, since it is not influenced by local stress changes produced by structural discontinuities. The hot-spot stress approach incorporates all stress effects excluding those caused by the local weld profile, it is well developed for steel and aluminum alloys and less for titanium alloys [13]. The effective notch stress approach considers the local stress increase at the notch formed by the weld toe or the weld root [14].

The present study focuses on a representative pleasure craft operating in the Strait of Messina. The Response Amplitude Operators (RAOs) for translational and rotational motions, as well as vertical bending moments (VBM) were computed for two wave directions and four forward speeds, using sea state conditions characteristic of the region. The resulting hydrodynamic responses were benchmarked against classification society criteria, as well as compared with key insights from existing scientific studies. Furthermore, a fatigue analysis was performed considering the boundary conditions of the examined area, in order to determine, for different materials, the time required to reach structural failure. These results could potentially be applied to real-time stress monitoring by integrating the numerical hydrodynamic approach with finite element analysis and machine learning algorithms. Despite the progress in hydrodynamic and seakeeping analyses of small craft, limited attention has been given to the combined evaluation of wave-induced structural loads and fatigue life. Existing studies rarely link hydrodynamic response with classification society rules and fatigue assessment in a unified framework. A clear scientific gap therefore exists in the literature, as there is a lack of studies that integrate: hydrodynamic simulations, RAOs, classification rules with structural design criteria and fatigue life estimation for small vessels. This research addresses this gap by proposing an integrated methodology designed to generate a comprehensive dataset suitable for both design evaluation and the future implementation of real-time structural monitoring, thus providing a novel and complete approach that uniquely combines these elements into a single, coherent workflow.

2. Methodology

2.1. Hydrodynamic Analysis: Theoretical Basis

Hydrodynamic loads acting on marine structures primarily originate from the kinematics of water particles within waves, vessel motions, and wave–structure interactions. These loads are typically classified into three categories: drag forces, wave excitation forces, and inertia forces. Among these, drag forces are generally negligible in this context, as their contribution becomes significant only under conditions of large wave amplitudes. They are induced by viscosity and are proportional to the square of relative velocity between fluid particle and structure surface. In small amplitude waves, the wave exciting load consists of the first order incident wave force (Froude Krylov force) and the diffraction force which is induced by the disturbance wave due to the existence of a body, the second order forces may be neglected. The wave inertia load is caused by the disturbed waves induced by the body motions. Therefore, considering the analyzed sea state condition, wave excitation and inertia loads are the dominant components considered in the current analysis.

Fluid potential theories are commonly used for solving the wave inertia load and wave exciting load. To analyze the hydrodynamic behavior of the vessel under wave action, three-dimensional panel methods are widely employed. These approaches rely on potential flow theory and involve discretizing the wetted surface of the structure into a mesh of diffraction panels to simulate wave-structure interactions. For smaller structural elements, the Morison equation is commonly used to calculate hydrodynamic forces, with these components also being divided into discrete segments. The computational model employed in this study integrates both the panel method and the Morison equation in a hybrid framework, allowing for a more thorough assessment of hydrodynamic load distribution. For the diffraction analysis, a numerical approach known as the Source Distribution Method is used to calculate first-order wave loads under the assumption of small-amplitude waves and ideal fluid conditions. This method assumes the existence of a spatially dependent velocity potential function. Using linear hydrodynamic theory, the interaction between fluid and structure is modeled by a system of potential flow equations that incorporate both wave diffraction and radiation effects, as detailed in prior studies [15,16]. In this study, the vessel is modeled as a rigid body. In this framework, hydrodynamic loads induced by waves are applied to the hull, while the structural deformations are not coupled back into the fluid model. This assumption is widely used in potential flow-based analyses and provides a computationally efficient first-order prediction of hydrodynamic loads. More advanced formulations including structural flexibility, nonlinear effects, and full two-way FSI are beyond the scope of this work but represent directions for future research. The fluid–structure interaction behavior is described by the following set of equations:

• Laplace equation, applicable everywhere in the fluid domain:

$$∆\phi ={\displaystyle \frac{{\partial }^2\phi }{\partial X^2}}+{\displaystyle \frac{{\partial }^2\phi }{\partial Y^2}}+{\displaystyle \frac{{\partial }^2\phi }{\partial Z^2}}=0$$

(1)

where “$\phi$” is the velocity potential of the fluid, a scalar function from which the velocity field can be derived through the gradient: $\stackrel{\rightharpoonup }{v}=\nabla \phi$, “$∆\phi$” the Laplacian of the potential “$\phi$”, which represents the sum of the second derivatives with respect to the three spatial coordinates.

• Linear free surface equation of zero forward speed case:

$$-{\omega }^2\phi +g{\displaystyle \frac{\partial \phi }{\partial Z}}=0onZ=0$$

(2)

where “$\phi$” is fluid velocity potential, “$\omega$” is wave angular frequency, “g” gravitational acceleration, ${\displaystyle \frac{\partial \phi }{\partial Z}}$ partial derivative of the potential with respect to the vertical coordinate “Z”, Z = 0 is still water level (mean free surface).

• Body surface conditions on the mean wetted body surface:

$${\displaystyle \frac{\partial \phi }{\partial n}}=\left\{\begin{array}{c}-i\omega n_j\mathrm{for\; radiation\; potential}\\ -{\displaystyle \frac{\partial {\phi }_I}{\partial n}}\mathrm{for\; diffraction\; potential}\end{array}\right.$$

(3)

${\displaystyle \frac{\partial \phi }{\partial n}}$ normal derivative of the potential on the body surface, representing the fluid velocity normal to the surface, “${\phi }_I$” represents the velocity potential function describing the initial incoming sinusoidal wave system. “$i$” is imaginary unit ($i^2=-1$) used in the harmonic formulation, “$n_j$” normal velocity of the body in the j-th degree of freedom

• Seabed surface condition at depth of “d”:

$${\displaystyle \frac{\partial \mathsf{\phi }}{\partial Z}}=0onZ=-d$$

(4)

• A suitable radiation condition must be added to these equations so that as $\sqrt{x^2+y^2}\to \infty$ the generalized wave disturbance dies away.

The hydrodynamic problem was solved using ANSYS AQWA (2024), a specialized software package that employs a boundary integration (boundary element), approach to compute the fluid velocity potential under the defined boundary conditions. This method enables an accurate representation of the interaction between waves and the floating structure, capturing the essential hydrodynamic effects required for subsequent structural analyses.

The numerical outputs generated by AQWA were subsequently exported and imported into MATLAB (2024) for post-processing, including RAOs, motions, vertical bending moment calculations, fatigue analyses, and comparison with classification rule-based criteria. In Figure 1 the computational workflow used in this study is shown, which provides a visual summary of the methodology implemented.

A fundamental aspect of this approach is the use of the pulsating Green’s function in the frequency domain [17,18], which satisfies boundary conditions of a linear free surface, seabed, and far-field wave radiation as those given in previously. However, direct evaluation of the frequency domain using this Green’s function is computationally intensive. To overcome this challenge, the present study utilizes a precomputed database of Green’s functions, enabling efficient evaluation of both the function and its first-order derivatives. The low frequency behavior of the Green’s function in this database is defined by Equation (5), as described in [17,18]

$${\omega }_{min}=0.05\sqrt{{\displaystyle \frac{g}{d}}}$$

(5)

where “$d$” is the water depth and g are the gravity acceleration.

Under zero forward-speed conditions, the hydrodynamic loads induced by regular harmonic waves are considered, enabling the analysis of both wave excitation and radiation forces acting on a floating structure. First-order potential theory is employed to model wave diffraction and radiation effects, with the velocity potential in the fluid domain determined using the principle of linear superposition. Once the velocity potential is established, Bernoulli’s equation is applied to compute the hydrodynamic pressure distribution. By integrating this pressure over the wetted surface of the hull, the resulting hydrodynamic forces can be accurately determined. When forward speed is introduced, the governing equations become more complex, necessitating adjustments to the zero-speed formulations to accurately capture vessel–wave interactions. Furthermore, the Source Distribution Method, which utilizes the pulsating Green’s function in the frequency domain, does not inherently consider forward speed in its original formulation. To address this limitation, the translating-pulsating source method is introduced, which, unlike the standard pulsating source approach, incorporates moderate forward speeds into its theoretical framework. Under these conditions, the differences in the computed hydrodynamic responses between the two methods are typically minimal, making the translating-pulsating source method a reliable extension for scenarios involving low to moderate vessel speeds. An important factor introduced under forward-speed conditions is the encounter frequency, which adjusts the wave frequency to reflect the relative motion between the vessel and the incident wave, which can be defined as follows Equation (6):

$${\mathsf{\omega }}_{\mathrm{e}}=\mathsf{\omega }-{\displaystyle \frac{{\mathsf{\omega }}^2\mathrm{U}}{\mathrm{g}}}\cos \mathsf{\beta }$$

(6)

where “$\mathsf{\omega }$” is the wave frequency, “$\mathrm{U}$” is the forward velocity, “$\mathrm{g}$” is the acceleration of gravity, “$\mathsf{\beta }$” is the angle between the incident wave and the ship.

Second-order wave forces can also be estimated through the use of the Quadratic Transfer Function (QTF) matrix, particularly under multi-directional wave conditions. However, such effects are often neglected to reduce computational complexity, especially in moderate sea states where wave amplitudes are relatively small. As the current analysis focuses on the interaction between the fluid and the vessel, a key element is the harmonic response of the structure to a regular wave, expressed by the Response Amplitude Operator (RAO). Derived from the linear equation of hydrodynamic motion [19], RAO represents the dynamic motion response of a structure subjected to wave excitation over a range of frequencies. It serves as a transfer function that relates the wave input to the resulting structural motion, providing a critical tool for predicting the behavior of the vessel under wave loading, as described by the following Equation (7):

$$\mathrm{R}\mathrm{A}\mathrm{O}\left({\omega }_e\right)={\displaystyle \frac{x_p\left({\omega }_e\right)}{{\mu }_{\omega }\left({\omega }_e\right)}}$$

(7)

where $x_p\left({\omega }_e\right)$ is the amplitude of motion and ${\mu }_{\omega }\left({\omega }_e\right)$ is the amplitude of wave.

Ship motions result from external excitations such as wind, currents, and wave action. However, the degree of sensitivity to these excitations varies depending on the type and characteristics of the vessel. The complex hydrodynamic interaction between the ship and the fluid—an inherently infinite-degree-of-freedom system—is commonly simplified by modeling the vessel as a rigid body with six degrees of freedom: three translational (surge, sway, heave) and three rotational (roll, pitch, yaw), often referred to as primary and complementary motions [20]. Generally, smaller motion amplitudes and slower oscillations are associated with better seakeeping performance. Conversely, large and rapid motions indicate poor seakeeping behavior. For this reason, seakeeping is considered a fundamental aspect of naval architecture and vessel design. For the subsequent estimation of total bending moments, the study adopts the empirical formulas provided by the Norwegian classification society (DNV), specifically for hogging (ship bending upward at midship) and sagging (ship bending downward at midship) conditions [21]. These formulae account for the combined effects of still water and wave-induced bending moments as shown in Equations (8) and (9) and are specifically tailored for high-speed light craft, with application to monohull vessels.

$$M_{tothog}=M_{sw}+0.19C_W{L}^{2}B{C}_B$$

(8)

$$M_{totsag}=M_{sw}+0.14C_W{L}^{2}B{(C}_B+0.7)$$

(9)

where “M_sw” is still water bending moment (moment due to static loading conditions without wave effects), “C_W” is Wave coefficient (empirical coefficient related to wave loads), “L” is Ship length between perpendiculars, “B” is Ship breadth, “C_B” is Block coefficient (ratio of the underwater volume of the ship to the volume of a rectangular block with the same length, breadth, and draft) [22].

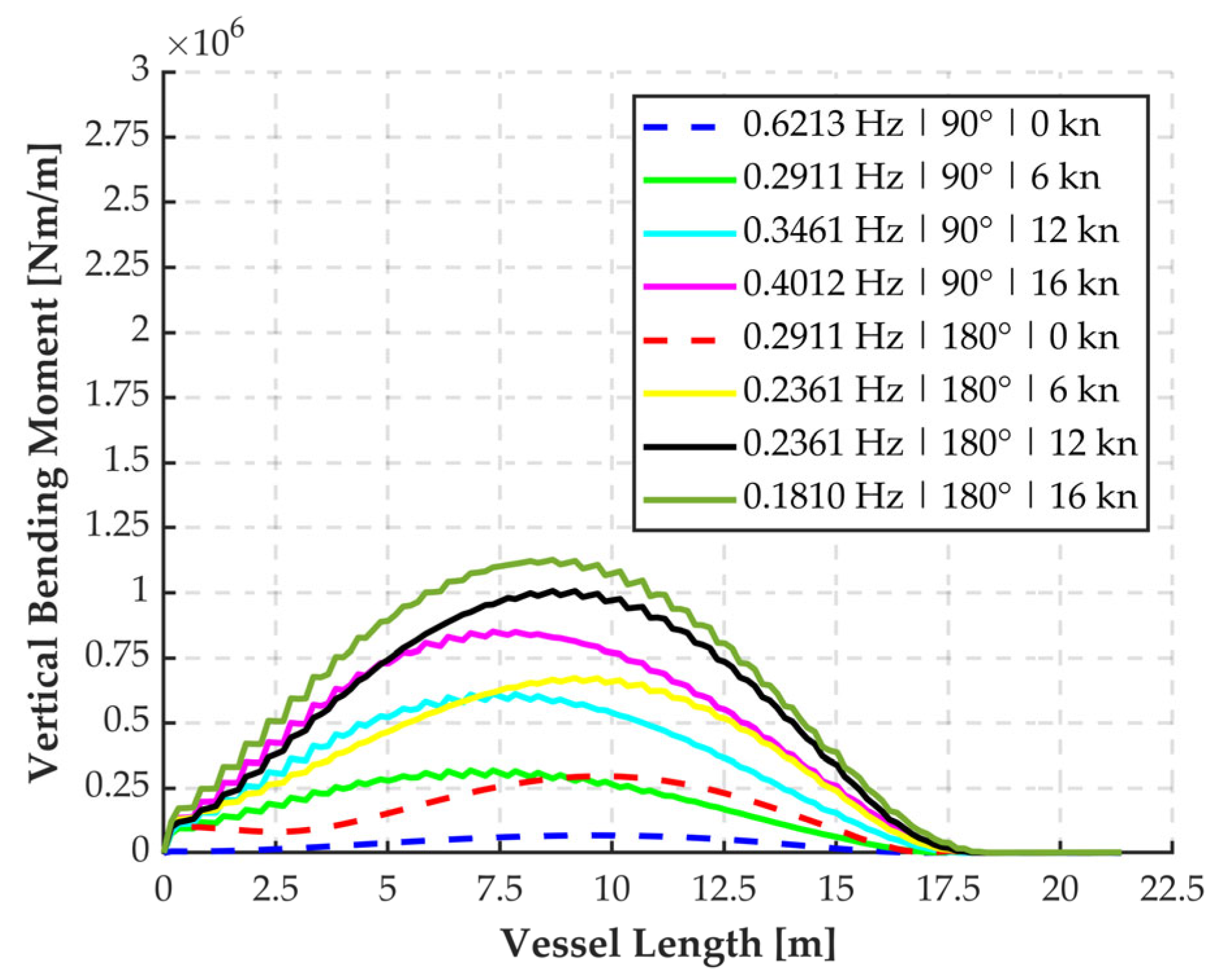
Fatigue analysis was conducted considering the sea states commonly observed in the studied area. The evaluation focused on an operational design life of 20 years. After identifying the most critical sea states according to DNV limits, fatigue life assessment was carried out to determine the time to fatigue failure of the vessel structures. The investigation focused on different materials typically used in ship construction: AA5083, S355, and Ti6Al4V. Further details of the analysis, along with the use of Miner’s rule and Navier’s equation, are provided in Section 3.2.

2.2. Case Study

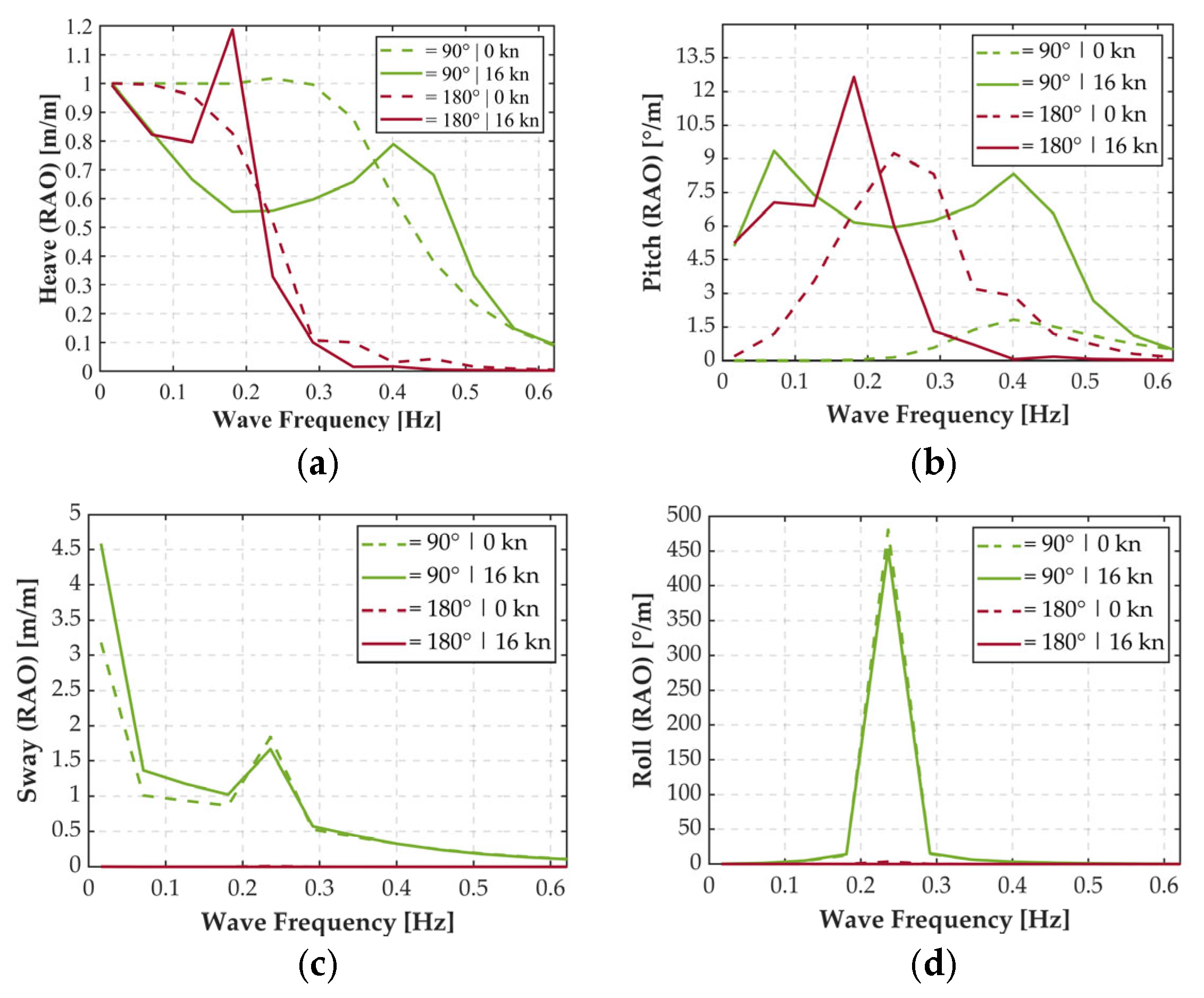
Hydrodynamic simulations were carried out analyzing vessel motions and computing the corresponding Response Amplitude Operators (RAOs) under wave excitation. The analyses were conducted by varying wave train characteristics, both in calm water and under operational conditions. A numerical approach was employed to evaluate the vessel’s seakeeping performance across different scenarios. The simulation results were subsequently compared with bending moment estimates derived from empirical formulas provided by the Norwegian classification society (DNV), enabling a comparative assessment of the numerical and empirical approaches. The outcomes of the motion analysis provide a foundational dataset for further investigations into the vessel’s structural reliability under realistic sea conditions. The principal dimensions of the vessel analyzed are presented in

Table 1. Principal dimensions of the ship.

Parameter	Boat	Unit
Length Over All (LOA)	21.4	m
Breadth (B)	5.5	m
Draft (T)	1.2	m

.

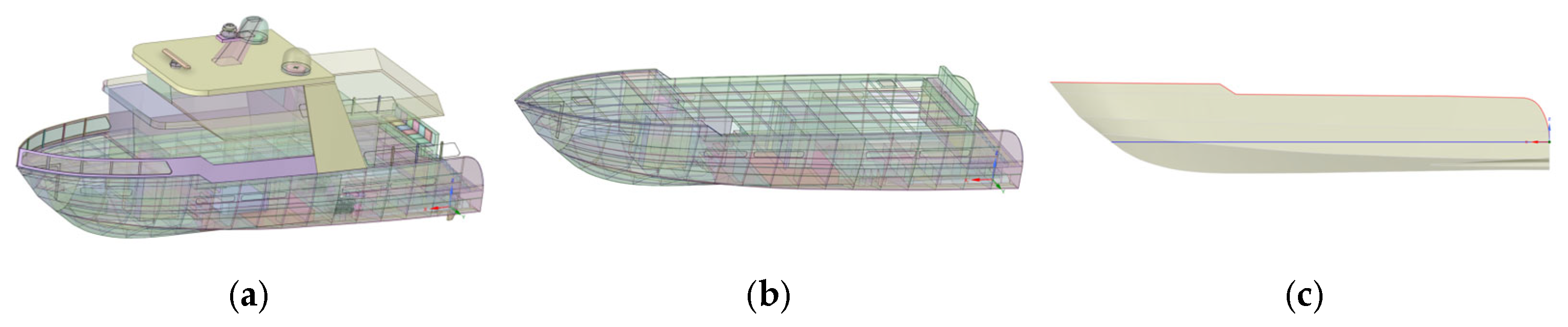
In the considered region, various types of pleasure craft operate or transit. For the analysis, the CAD model of a representative pleasure craft was used, as its main characteristics closely resemble those of the most common private and recreational vessels frequently found in the area. This vessel is shown in Figure 2a. Only the external hull surfaces were included in the hydrodynamic simulations, while all internal structural components, deemed non-essential for this analysis, were excluded. Additionally, all openings in the hull were sealed to ensure they did not influence the simulation results, as illustrated in Figure 2b,c. Subsequently, the hull was divided into two sections using the waterline, located 1.2 m above the baseline (keel line), as the reference plane. This step was necessary to meet the modeling requirements of the hydrodynamic analysis software.

The wetted hull surface was discretized into diffraction panels, and a constant time step of 0.05 s was adopted to ensure numerical stability and accurate resolution of wave–structure interactions.

The vessel was modeled as a rigid-body hull surface, which allows efficient evaluation of global hydrodynamic loads such as vertical bending moments. While this approach does not capture structural flexibility, it provides reliable first-order results suitable for structural assessment at the global scale and a comparison with classification societies rules. Internal structural details were excluded, and hull openings were sealed to avoid spurious effects in the numerical simulations. This simplification preserves the main hydrodynamic characteristics while ensuring robustness of the model.

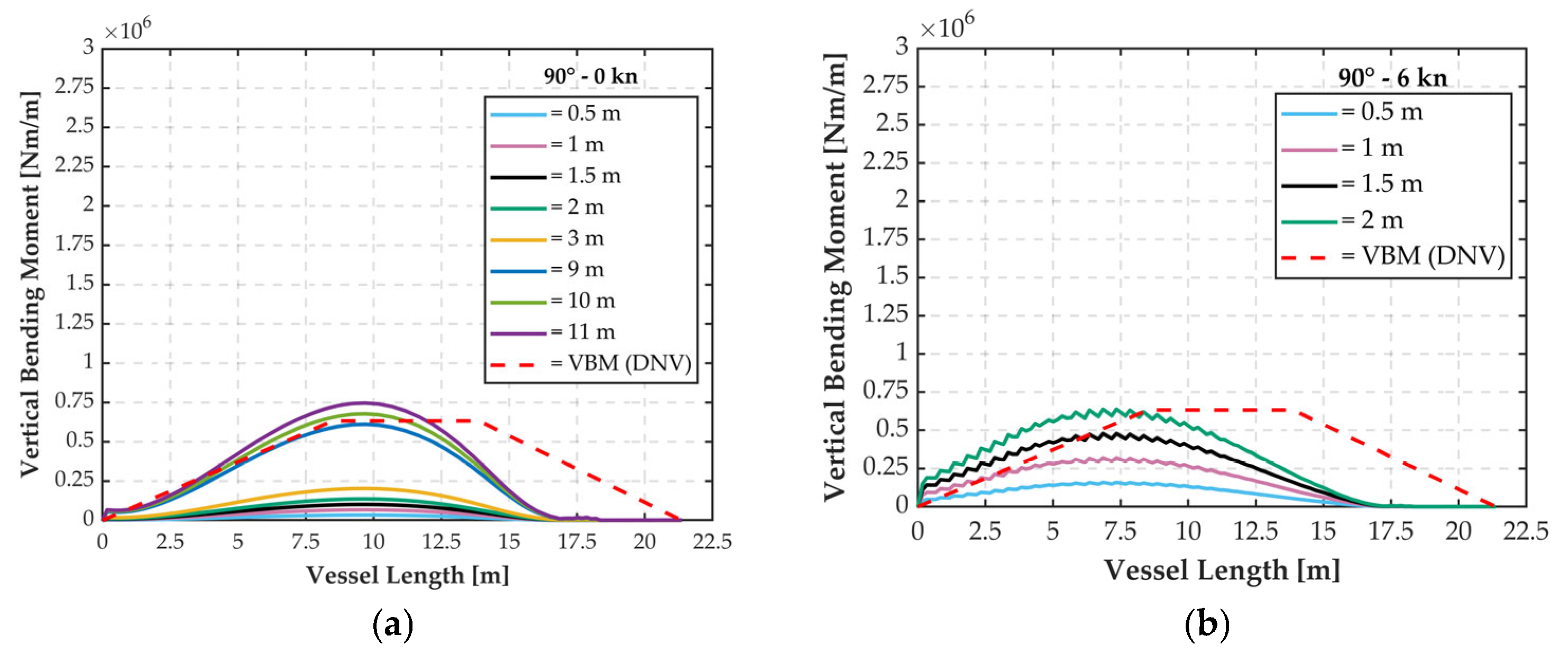
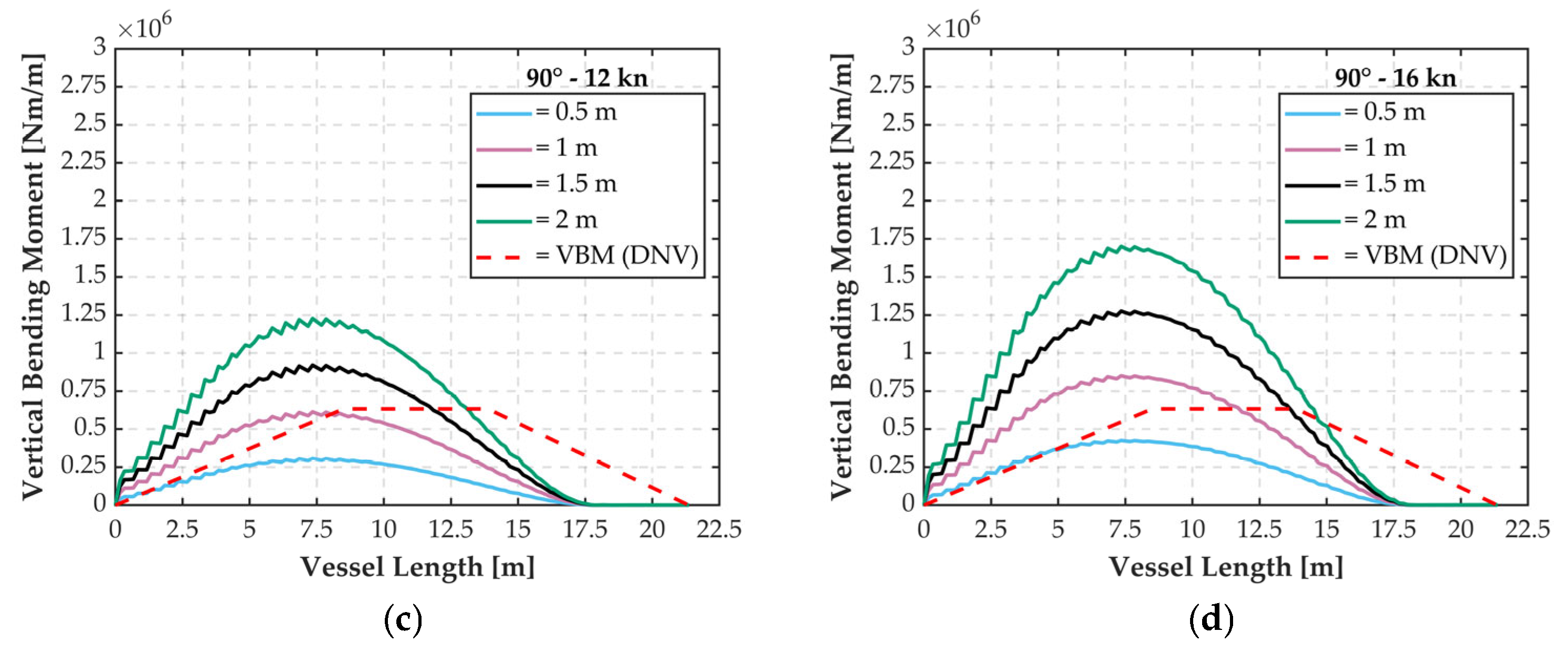
The vessel’s operational area is located in the Strait of Messina, as shown in Figure 3a. The sea conditions in this region can be effectively represented using the JONSWAP (Joint North Sea Wave Project) spectrum. As highlighted in a recent global assessment of its suitability in coastal areas [23], the JONSWAP spectrum has demonstrated good performance in modeling real sea states within the Mediterranean Sea. Although the spectrum describes irregular waves, regular wave components derived from it are employed in this study to analyze the hull’s response. According to data from APAT [24], the average significant wave height in the vessel’s operating area is approximately 2 m. Regarding forward speed, reference is made to the guidelines issued by the Messina Vessel Traffic Service [25], which establish a maximum allowable navigation speed of 16 knots within the Strait. Furthermore, local bathymetric conditions were defined using data from a study by ENEA (the Italian National Agency for New Technologies, Energy, and Sustainable Economic Development) [26] which validated a marine circulation model for the Strait of Messina. This reference provided input parameters for the simulations, including an average sea depth of approximately 100 m, with localized areas reaching depths of up to 250 m, as illustrated in Figure 3b.

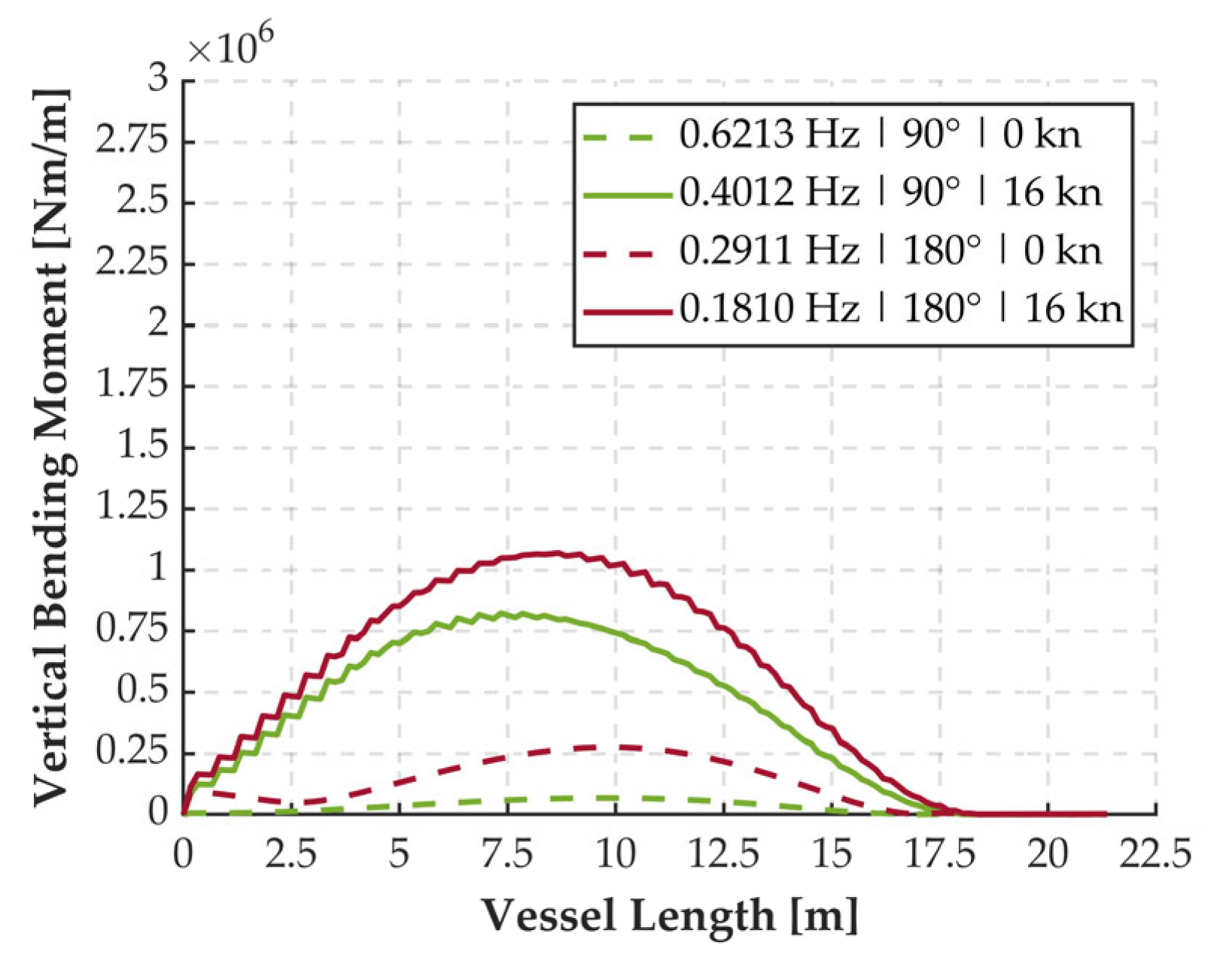
Regarding wave incidence, the most critical directions 180° (head seas) and 90° (beam seas) were considered for the analysis. The corresponding frequency range evaluated is presented in

Table 2. Wave frequencies.

Frequency Number	Wave Frequency (Hz)
1	0.01592
2	0.07095
3	0.12599
4	0.18102
5	0.23606
6	0.29109
7	0.34613
8	0.40116
9	0.4562
10	0.51123
11	0.56627
12	0.62132

.

The gyration radii used in this study are based on the recommendations provided by the International Towing Tank Conference (ITTC) [27] as listed in

Table 3. Radii of gyration of the ship.

Composition	Formula	Value (m)
Kxx	0.34 × B	1.87
Kyy	0.25 × Lpp	4.41
Kzz	0.26 × Lpp	4.59

.

The mesh was chosen for analysis purposes, prioritizing computational efficiency, several analyses were performed by progressively refining the mesh from an element size of 0.5 m down to 0.2 m, observing that the results of the simulations did not differ significantly. Considering the hull dimensions and the required level of accuracy for the hydrodynamic analysis, the computational mesh was suitably refined to ensure both reliability and precision of the results. An illustration of the generated mesh is shown in Figure 4.

Details of the mesh are shown in

Table 4. Mesh characteristics.

Parameters	Value
Element Size	0.5 m
Maximum Allowed Frequency	0.6213 Hz
Total Nodes	1105
Total Elements	1064

.

The mesh was refined using an element size of 0.2 m, resulting in a higher total number of elements. An illustration of the generated mesh is shown in Figure 5. Details of the mesh are shown in

Table 5. Mesh characteristics using smaller elements.

Parameters	Value
Element Size	0.2 m
Maximum Allowed Frequency	0.986 Hz
Total Nodes	5835
Total Elements	5712

.

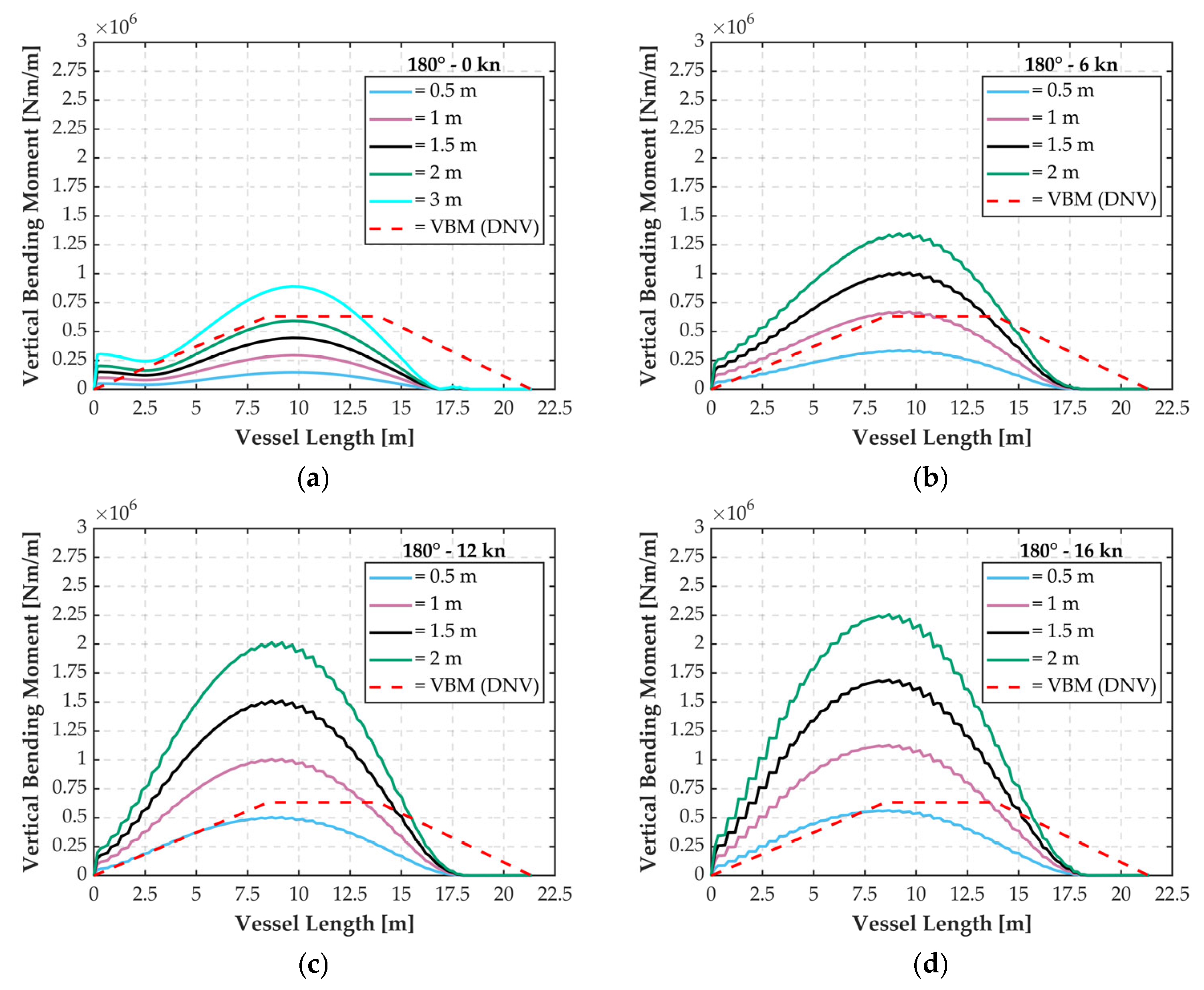
However, the simulation results obtained using the 0.5 m mesh did not show significant deviations when compared to those derived from the finer 0.2 m mesh. For instance, considering the bending moment at 180° without velocity, the 0.5 m mesh produced a value of 2.97 × 10⁵ N·m/m, while the refined 0.2 m mesh resulted in 2.87 × 10⁵ N·m/m. The percentage difference is calculated with the following formula:

$$\mathit{E}\mathit{r}\mathit{r}\mathit{o}\mathit{r}\mathsf{ \%}={\displaystyle \frac{{\mathit{V}}_{\mathbf{0.5}}-{\mathit{V}}_{\mathbf{0.2}}}{{\mathit{V}}_{\mathbf{0.2}}}}\times \mathbf{100}$$

(10)

where ${\mathit{V}}_{\mathbf{0.5}}$ is the value with the coarse mesh and ${\mathit{V}}_{\mathbf{0.2}}$ is the reference value with the finer mesh.

This corresponds to a difference of approximately 3.3%, indicating that the coarser mesh still provides a sufficiently accurate representation for the purposes of this study. The relatively small deviation between the results obtained with the 0.5 m and 0.2 m mesh resolutions demonstrate that the coarser mesh is capable of capturing the structural behavior without significant loss of accuracy. Therefore, in order to reduce computational effort, optimize resource usage, and accelerate the simulation process, the 0.5 m mesh configuration was selected for all subsequent analyses. This choice ensures a good balance between computational efficiency and solution reliability, allowing for parametric studies while maintaining the accuracy of the results.

3. Results and Discussions

3.1. Motions and Vertical Bending Moment Results

Natural modes of a floating structure, such as a ship, describe its fundamental motion responses due to interactions with wave action. These motions are typically expressed in six degrees of freedom and reflect how the structure responds to hydrodynamic forces and moments generated by wave radiation and diffraction. Understanding these modes is crucial for evaluating the dynamic behavior of the structure in marine environments, as they provide insight into possible resonance effects. They are usually identified through hydrodynamic analysis in the frequency domain.

As shown in Figure 6, the main resonance frequencies are: 0.01113 Hz, 0.01895 Hz, 0.02100 Hz, 0.06745 Hz, 0.23789 Hz, 0.42856 Hz, which correspond to the frequencies where the curve exhibits downward peaks. From the graph, it can be observed that the vessel displays multiple resonant behaviors within the frequency range between 0.002 Hz and 9 Hz.

RAOs were then evaluated over a frequency range from 0.01592 Hz to 0.6213 Hz, using ten internal frequencies values. The analysis focused on the bending moment along the “y” axis. Simulations were performed at a forward speed of 16 knots, corresponding to the maximum navigational speed permitted in the Strait of Messina. Two wave incidence angles were considered: 180° (head seas) and 90° (beam seas). For comparative purposes, an identical simulation was carried out without forward speed condition. The results obtained are reported in Figure 7, where the solid lines refer to the results with forward speed, and dashed lines with zero speed.

The maximum bending moment was observed along the vessel’s centerline, with the highest value occurring under forward speed conditions when waves approached from 180°.

The physical boundaries for the analysis presented in Figure 8 were set based on the vessel’s geometry and the surrounding water domain, as defined in the software. In addition to these spatial parameters, the software also requires the specification of several wave characteristics, such as the wave frequency and the sea state type. In particular, the user must define whether the analysis will consider a single, isolated wave or a regular wave train consisting of identical waves. Moreover, the model setup allows for the inclusion of advanced hydrodynamic effects, such as wave diffraction and radiation, which influence the interaction between the incident wave and the vessel’s hull. These effects are essential for accurately predicting the pressure distribution and overall hydrodynamic loads acting on the structure. Figure 8 shows the pressures acting on the structure as a function of the wave, considering a wave height of one meter and a direction of 180°. As can be observed in the following two time steps, “a” and “b”, the maximum pressure moves from bow to stern depending on the position of the wave crest relative to the ship. This difference highlights the dynamic nature of the pressure distribution along the hull as the wave propagates, the image is used for illustrative purposes.

In terms of vessel motions, the RAOs corresponding to translational displacements were analyzed. The results of this analysis are reported in Figure 9.

For heave motion, defined as the vertical translational movement, a higher displacement is observed when waves approach from 180°, particularly under forward speed conditions and in the presence of long waves. However, at frequencies above 0.3 Hz, corresponding to shorter waves, the condition at wave direction of 90° on the motion becomes dominant. A comparable pattern is observed in pitch motion, where the influence of forward speed plays a significant role in shaping the overall motion trends.

For sway motion, which corresponds to the vessel’s lateral translation, the results indicate higher displacement amplitudes under beam sea conditions (90° wave direction) compared to head seas. The influence of waves from 180° is found to be negligible. Similarly, rotational motion along the direction of travel exhibits a more pronounced response for waves approaching from 90°, with a peak amplitude occurring in the 0.2–0.3 Hz frequency range, while the contribution from head-sea conditions is nearly absent.

The bending moments were analyzed at different speeds and for two wave directions 180° (head sea) and 90° (transverse sea) to assess how the ship’s structural response varies under different loading conditions. It is immediately evident from Figure 10 that the bending moment increases progressively with the ship’s speed.

The bending moments are reported for critical wave encounter frequencies those at which the bending moment reaches its maximum value—and for various ship speeds: 0 kn, 6 kn, 12 kn, and 16 kn. The dashed curves correspond to the zero-speed condition, while the solid curves represent the aforementioned operating speeds. The results show that the most critical condition occurs at a speed of 16 kn, although this is an unrealistic scenario for a pleasure craft operating in wave conditions. Nevertheless, in the following sections, this critical frequency and design speed will be examined in detail to enable a comparison with the standardized values defined by DNV, in order to analyze the most severe condition and verify compliance with these regulations. The simulation results for wave-induced vertical bending moments were compared against the design limits specified by the DNV [21] and ABS [28] Classification Society standards. Figure 11 illustrates the distribution of vertical bending moments along the vessel for both 0 kn and 16 kn conditions. Red lines correspond to the maximum vertical bending moment indicated by classification societies. In the case of 180° head waves, the maximum wave-induced bending moment calculated according to classification society rules is M_WS = 632.9 kNm. The VBM curve is obtained by multiplying the wave-induced bending moment by a coefficient, which assumes a unit value between 0.4 L and 0.65 L (with L being the vessel length) and zero value in correspondence with the perpendicular forward and aft. Comparing this term with the results obtained numerically for the most severe condition, in the case of zero forward speed, it occurs for a frequency of 0.29109 Hz (T = 3.43 s). For the case with forward motion, the maximum response shifts to a lower frequency of 0.18102 Hz (T = 5.52 s).

Under zero-speed conditions, as shown in Figure 11a, the standardized vertical bending moment limit is not exceeded for sea states with wave heights up to 2 m. However, higher values than the limit moment are observed for wave heights beyond this threshold. Introducing forward speed into the simulation, illustrated in Figure 11b, shows that the maximum permissible wave height the vessel can safely encounter, based on the vertical bending moment limit defined by classification rules, decreases significantly to around 0.5 m. This underscores the significant impact of forward speed on the vertical bending moment the vessel can withstand in head-sea conditions. For this reason, classification societies generally recommend adjusting vessel speed in response to wave height as bending moments increase.

Since, as previously mentioned, the condition is not realistic, the analysis was further developed by also considering classification society rules, using intermediate speeds of 6 knots and 12 knots. This approach aligns with the recommendation to reduce ship speed as wave height increases. Consequently, the bending moments were compared for the aforementioned speeds and for wave directions of 90° and 180°, across different wave heights. These cross-comparisons were used to build a database, allowing for the estimation of the loads acting on the vessel as a function of the sea state encountered during navigation.

As the vessel speed increases, the vertical bending moment also increases. This trend is evident in how the DNV limit is exceeded at progressively lower wave heights with increasing speed. In fact, by comparing Figure 12a–d, specifically the cases of 90° wave heading at 0 knots and at 16 knots, it can be observed that the limiting wave height corresponding to the standardized threshold decreases from 9 m to approximately 0.75 m.

The results shown in Figure 13a–d indicate that head seas (180°) represent the most critical condition, consistent with findings from other analyses and existing literature. In this case as well, an increase in vessel speed leads to higher bending moments, reaching the most severe condition analyzed, where the DNV limit is not exceeded only for wave heights up to 0.5 m.

Taking into account all analysis results obtained and the vessel’s particular design features and dimensions, it appears more suitable for operation in environments characterized by moderate sea conditions. The lack of stabilization systems may restrict its performance in harsher sea states, implying that its use would be more appropriate during calmer seasons, such as the summer months. In the event of unexpectedly severe sea conditions during transit, the findings suggest that reducing speed or, if necessary, temporarily suspending navigation, could significantly improve operational safety.

3.2. Fatigue Life Analysis for Different Materials

Following the comparison of the vertical bending moment at various speeds and wave directions against the regulatory limits, a fatigue life assessment of the vessel was carried out. For this analysis, the most critical wave direction 180° was considered, along with the design speed of 16 knots. The sea conditions examined are presented in

Table 6. Extreme sea states considered for fatigue life analysis.

	Hs	T	θ
Sea state 1	0.5	5.5	180
Sea state 2	1	5.5	180
Sea state 3	2	5.5	180
Sea state 4	3	5.5	180

and correspond to the sea states previously considered for the bending moment analysis, as well as to the most frequently encountered configurations.

As observed, the wave heights considered exceed the standardized limit set by the classification society, in order to investigate the vessel’s response under the most severe conditions. Moreover, the wave period reported in Table 6 refers to the most critical frequency obtained from the simulation. These sea states are based on 20 years of observational data provided by Campana [29], which also includes the probabilities of occurrence for each sea state, as shown in

Table 7. Probability of analyzed sea state conditions.

	Hs	T	%	Years
Sea state 1	0.5	5.5	30.3	6.06
Sea state 2	1	5.5	44.9	8.98
Sea state 3	2	5.5	20.4	4.08
Sea state 4	3	5.5	3.5	0.70

. From the percentage values, the term “years” corresponds to the amount of time each sea state was observed during the 20-year period.

The fatigue life study was carried out considering the following materials: AA5083, S355, and Ti6Al4V. This selection was based on the primary materials commonly used in the construction of yachts. The 5000 series aluminum alloys are those most widely used in corrosive environments, such as the marine environment [14]. Furthermore, the diversity of the chosen materials aims to investigate the different responses arising from their distinct mechanical and physico-chemical properties. Fatigue damage accumulation was assessed using Equation (11), Miner’s rule:

$$D_i=0.85{\displaystyle \frac{n_i}{N_i}}$$

(11)

Miner’s Rule was employed because of its computational simplicity in estimating cumulative fatigue damage under variable amplitude loading. It is widely recognized as a practical method for preliminary fatigue evaluations, especially in cases involving complex stress spectra such as the one considered here. Nevertheless, it should be emphasized that Miner’s rule is based on the assumption of linear damage accumulation and neglects load sequence effects, making it less accurate for detailed or high-fidelity fatigue analysis. In Equation (11), “i” is the number of sea states considered, “$N_i$” corresponds to the number of cycles to failure of the material under the stress level induced by the respective sea state (number of cycles to failure) and “$n_i$” represents the number of load cycles the ship is subjected to under each sea state (number of applied load cycles) while 0.85 is an empirical correction factor introduced to account for experimental calibration and improve correlation with observed fatigue behavior.

From the simulations, it was possible to determine the bending moment acting on the vessel for the different sea states. Knowing the moment of inertia, the nominal stress can then be obtained using the Navier formula, the following Equation (12):

$$\sigma ={\displaystyle \frac{\mathrm{V}\mathrm{B}\mathrm{M}}{I}}{z}_{NA}$$

(12)

where VBM is the vertical bending moment corresponding to the sea state, I is moment of inertia and z_NA is the distance from neutral axis. The bending moments generated on the vessel under the various sea conditions, along with the corresponding stresses calculated using the previous equation, are reported in

Table 8. Wave-induced stresses.

	Hs	Mw [KNm]	σ [MPa]
Sea state 1	0.5	563.9945	9.08
Sea state 2	1	1127.989	18.15
Sea state 3	2	2255.978	36.30
Sea state 4	3	3383.967	54.45

.

The investigation began by considering Aluminum Alloy 5083, the most commonly used material for such constructions, characterized by a fatigue strength of 36 MPa and a fatigue life of 2 million cycles [30], a common S355 steel and a common titanium alloy that has a fatigue strength of about 100 MPa [13].

The results reported in

Table 9. Fatigue damage accumulation for AA5083, S355 and Ti6Al4V.

			AA5083		S355		Ti6Al4V
	Hs	ni	Ni	Di	Ni	Di	Ni	Di
Sea state 1	0.5	34,746,938	Safe	Safe	Safe	Safe	Safe	Safe
Sea state 2	1	51,489,687	Safe	Safe	Safe	Safe	Safe	Safe
Sea state 3	2	23,393,978	2,000,000	9.942441	Safe	Safe	Safe	Safe
Sea state 4	3	4,013,673	1,820,000	1.874517	Safe	Safe	Safe	Safe

show that sea states with wave heights of 0.5 m and 1 m do not lead to fatigue damage, whereas sea states 3 and 4 result in a cumulative damage of 11.8, corresponding to a fatigue life of approximately 1.7 years. In particular, sea state 3 produces significant damage due to the assumption that the vessel operates continuously for 4 years under wave conditions of 2 m. Considering the type of vessel, typically used during summer months, and the classification society’s limits, such a high damage value is deemed plausible. Moreover, the fatigue resistance of aluminum is significantly lower compared to the other two materials analyzed. Indeed, in the case of S355 steel and Ti6Al4V, it is evident that these materials withstand the analyzed sea states effectively, thanks to their better mechanical properties. The results indicate that aluminum is the most sensitive material to the dynamic loads induced by wave motion, whereas the other two materials are better suited for this type of vessel and the sea states to which it is typically subjected. This analysis was carried out under extreme conditions for the vessel under study. From the analyses performed, we observed that the most critical sea states correspond to sea state 3–4 when using aluminum as the structural material. The following analysis therefore focuses exclusively on aluminum, since both steel and titanium demonstrated good performance under these dynamic load conditions. Given that sea states 3–4 are the most critical for the aluminum structure, a fatigue life analysis was carried out to determine the time to failure when the vessel is subjected to prolonged exposure to these sea conditions. Using Miner’s rule, as previously discussed where fatigue failure is assumed to occur when the cumulative damage reaches a value of 1 we applied the inverse formulation. This allows us to estimate the time to fatigue failure, i.e., the time required for the damage to reach unity under repeated loading conditions. The results are reported in the following

Table 10. Fatigue life for units accumulated damage.

	Hs	T	Di	Time [Days]
Sea state 3	2	5.5	1	127.3
Sea state 4	3	5.5	1	115.8

:

As shown in Table 10, the most severe sea state is 4, which leads to failure after approximately 115.8 days (corresponding to about 3 months and 25 days). For sea state 3, the estimated time to failure is 127.3 days (approximately 4 months and 7 days). This difference is due to the higher wave characteristics associated with sea state 4, which generate greater loads on the structure, accelerating the fatigue process.

4. Discussion

This study presented hydrodynamic simulations of wave-structure interactions under representative sea conditions in the Strait of Messina. Vessel responses were evaluated across a range of wave frequencies and directions, with Response Amplitude Operators (RAOs) calculated for translational and rotational motions, as well as vertical bending moments, to identify critical loading scenarios. These RAOs were calculated using simulation software for both zero-speed and forward-speed conditions.

The maximum vertical bending moments evaluated by the simulations were assessed and compared against the thresholds established by DNV and ABS classification societies. This comparison enabled the identification of sea states that could pose structural risks to navigation in accordance with industry standards. At zero speed, sea states with wave heights up to 2 m remained within acceptable safety limits. However, when forward speed was introduced, the maximum safe wave height decreased to approximately 0.5 m, emphasizing the significant influence of vessel speed on allowable bending moment thresholds. In addition, intermediate forward speeds have been simulated, showing an increase in VBM with the ship’s speed, confirming the trend observed in experimental studies [31,32,33] that focused on VBMs of ship models under different wave conditions, confirming that maximum bending moments occur in forward and head-sea conditions. They also provide RAO–VBM curves that are particularly useful for comparison, supporting our observations regarding the forward bending moment peak and the wave patterns responsible for these maxima. Furthermore, other works and theses [34] explicitly demonstrate the influence of forward speed on VBM, consistently showing that both the bending moments and the associated RAOs increase with vessel speed. These findings justify and reinforce the trends observed in the present study. For example, a comparison with Wulandari study [10] is particularly insightful. In their work, a numerical 3D diffraction based analysis of a crew boat highlights a deterioration of seakeeping and crew comfort above operational speeds, under head-sea conditions with moderate wave heights. While they do not directly assess vertical bending moments (VBM), the increasing dynamic response with forward speed is fully consistent with our findings, where VBM values are amplified beyond similar speed thresholds. This comparison enhances the robustness of our modeling approach and confirms the consistency of the observed trends. The fatigue life assessments were conducted for severe sea states exceeding DNV limits to evaluate the ship’s response under critical conditions. The material investigated were AA5083, S355 and Ti6Al4V. According to the results, fatigue damage occurs for sea states with a significant wave height of up to 2 m when the hull is constructed from aluminum. In contrast, for steel and titanium, the sea conditions considered do not lead to damage accumulation, in good agreement with their mechanical properties.

However, by applying Miner’s inverse rule, it was estimated how long the vessel can withstand the most extreme condition analyzed. On average, fatigue failure is expected to occur after approximately four months of continuous stress in such conditions. The study supports the integration of hydrodynamic simulations with structural models for future fatigue life assessments. Moreover, the findings also highlight the potential for real-time stress monitoring systems that combine simulation data with finite element analysis and machine learning. This framework can also serve as a foundation for extending similar analyses to larger merchant vessels in future studies. The key novelty of this study lies in the development of an integrated procedure that goes beyond a purely hydrodynamic approach. By combining hydrodynamic simulations, classification rules, and fatigue life analysis into a unified and computationally efficient workflow, the methodology provides a comprehensive framework for assessing vessel performance and structural integrity. A further innovative aspect is the use of high-resolution bathymetric data from the Strait of Messina, a maritime area characterized by sudden currents, complex sea states, and heavy traffic. The study demonstrates the applicability of this approach to one of the most challenging real-world scenarios in the Mediterranean, enabling modeling of local currents and complex wave patterns. This combination of methodological integration and context-specific application represents a significant advancement compared to previous works, which typically analyzed seakeeping or structural aspects in isolation under idealized wave conditions. Looking ahead, this integrated approach offers a solid foundation for future developments, including the extension to time-domain simulations, fully coupled FSI analyses, and the incorporation of finite element models and machine learning techniques. These advancements will support the creation of real-time structural health monitoring tools, further enhancing vessel safety and operational decision-making in challenging maritime environments.

The study goes beyond the development of a single case study, offering a scalable framework that can be adapted to different vessel types and operational conditions. Such a framework addresses a scientific gap in the literature, thanks to the combination of these elements into a single workflow and has the potential to be extended to larger merchant vessels, contributing to safer and more efficient and sustainable maritime operations.

The current approach, however, has some limitations, such as the use of linear modeling assumptions and indirect validation. Future research will focus on overcoming these limitations by incorporating nonlinear hydrodynamic effects, experimental data, irregular wave conditions, and full structural coupling (FSI) to further improve prediction accuracy and operational safety but maintaining a good computational efficiency. Moreover, this methodology provides direct support to the structural design process, offering an approach to optimize vessel performance and safety from the early stages of development. In addition, the proposed workflow lays the foundation for the implementation of real-time predictive monitoring systems on board, enabling continuous assessment of structural health and maintenance strategies throughout the vessel’s operational life.

5. Conclusions

This study introduced an integrated and computationally efficient methodology that goes beyond purely hydrodynamic analysis by linking hydrodynamic simulations, classification rules, and fatigue life assessment within a unified framework. A key element is the use of high-resolution bathymetric data from the Strait of Messina, enabling realistic modeling of local currents and complex sea states. This comprehensive approach not only provides practical insights for safer small vessel design and operation but also generates high-quality datasets with significant potential for real-time structural health monitoring. By combining multiple analytical domains into a single workflow, the proposed methodology represents a powerful and highly scalable tool with significant potential. It can be adapted to different types and sizes of vessels, extending beyond small craft to larger ships operating in challenging maritime environments. With the planned future advancements, the method could evolve into an onboard decision-support system, enabling real-time structural health monitoring and predictive maintenance directly during operations.

The main findings are as follows:

• Forward speed strongly amplifies vertical bending moments, reducing safe operating limits from 2 m waves at zero speed to 0.5 m at 16 knots.
• Aluminum hulls are highly sensitive to fatigue under 2–3 m waves, while steel and titanium show no significant fatigue accumulation.
• The methodology reinforces classification rules for small vessels and offers a scalable framework applicable to different vessel types and larger ships.

The case study of the Strait of Messina, which is the busiest maritime corridor in Italy, is particularly relevant, since this area is characterized by sudden and complex sea states that can severely challenge small vessel safety. The results therefore provide both scientific and practical value, highlighting the need for speed management, material selection, and predictive monitoring in such critical waterways.

This research addresses a scientific gap by introducing an integrated workflow that combines hydrodynamic and structural analyses, enhanced by the use of high-resolution bathymetric data to realistically model local currents and sea states. By moving beyond a purely hydrodynamic simulation, this approach establishes the foundation for predictive maintenance and real-time structural health monitoring, with direct implications for navigation safety in highly trafficked and complex environments such as the Strait of Messina.