Optimized Venturi-Ejector Adsorption Mechanism for Underwater Inspection Robots: Design, Simulation, and Field Testing

Abstract

Stable adhesion on non-magnetic, steep, and irregular underwater surfaces (e.g., concrete dams with cracks or biofilms) remains a challenge for inspection robots. This study develops a novel adsorption mechanism based on the synergistic operation of a Venturi-ejector and a composite suction cup. The mechanism utilizes the Venturi effect to generate stable negative pressure via hydrodynamic entrainment and innovatively adopts a composite suction cup—comprising a rigid base and a dual-layer EPDM sponge (closed-cell + open-cell)—to achieve adaptive sealing, thereby reliably applying the efficient negative-pressure generation capability to rough underwater surfaces. Theoretical modeling established the quantitative relationship between adsorption force (F) and key parameters (nozzle/throat diameters, suction cup radius). CFD simulations revealed optimal adsorption at a nozzle diameter of 4.4 mm and throat diameter of 5.8 mm, achieving a peak simulated F of 520 N. Experiments demonstrated a maximum F of 417.9 N at 88.9 W power. The composite seal significantly reduced leakage on high-roughness surfaces (Ra ≥ 6 mm) compared to single-layer designs. Integrated into an inspection robot, the system provided stable adhesion (>600 N per single adsorption device) on vertical walls and reliable operation under real-world conditions at Balnetan Dam, enabling mechanical-arm-assisted maintenance.

1. Introduction

Routine inspection and maintenance of underwater hydraulic structures (e.g., dams, reservoirs, intake structures) are paramount for the safe and efficient operation of hydropower projects. Underwater robots—remotely operated vehicles (ROVs) and autonomous underwater vehicles (AUVs)—have emerged as vital tools for performing these tasks, offering advantages in accessibility and reducing human risk. A critical requirement for many inspection tasks, particularly on vertical or steep surfaces, is the robot’s ability to achieve stable adsorption to the substrate. This adhesion counteracts buoyancy, gravity, and hydrodynamic forces, enabling precise positioning and operation of onboard tools. However, achieving reliable adsorption presents significant challenges on common underwater infrastructure surfaces, which are typically non-magnetic (e.g., concrete, stone) and often irregular, rough, or biofouled.

To address this challenge, researchers domestically and internationally have proposed various adsorption solutions. Current primary adsorption methods for robots include thrust adsorption, biomimetic adsorption, magnetic adsorption, and negative pressure adsorption.

Thrust adsorption presses the robot against the wall using thrust generated by propellers [1]. For example, Mori et al. designed a wall-climbing robot with four thrusters [2]. Chen et al. developed an underwater hull-cleaning robot that generates adsorption force via four vertical thrusters, each capable of a maximum thrust of 260 N [3]. Commercial robots like HullWiper and ROVING BAT also favor thrust adsorption due to its straightforward implementation [4].

Biomimetic adsorption mimics the adhesion mechanisms of organisms like geckos or ivy, utilizing microstructures or intermolecular forces for attachment [5,6] (Krings et al., 2023; Chuang et al., 2017). For instance, Murphy et al. developed the Waalbot II wall-climbing robot employing gecko-inspired microcilia adhesive pads, enabling stable climbing on smooth or rough walls, including inverted surfaces [7]. Xi et al. drew inspiration from the sealing ring structure formed by abalone pedal tentacle contraction, constructing multi-layer sealing rings at the suction cup base, enhancing adsorption force by 15.8% compared to a standard suction cup at 60% vacuum [8]. Cong et al. emulated the microscopic groove structure on the fin surface of the Sichuan rock-climbing loach (Beaufortia kweichowensis), designing non-smooth groove morphologies on the suction cup working surface, achieving a 71.22% increase in maximum adsorption force on PMMA substrates compared to a standard suction cup [9].

Magnetic adsorption and negative pressure adsorption are currently the most widely used methods for underwater robots [10,11]. Magnetic adsorption typically utilizes permanent magnets or electromagnets to generate adhesion. While offering high force-to-weight ratios, this technique is only applicable to ferromagnetic materials. For example, Lee et al. designed the Gunryu III robot, achieving energy-efficient and stable climbing on steel structures using permanent magnet adsorption [12]. Stepson et al. developed a novel magnetic-wheel wall-climbing robot based on a Halbach permanent magnet array for efficient and safe hull inspection [13]. Negative pressure adsorption can be further categorized into contact and non-contact types. Contact negative pressure adsorption creates a vacuum sealed region by pumping out fluid, relying on the pressure differential for adhesion [14]. For example, Souto et al. proposed the Lappa robot, which generates a negative pressure differential within a sealed cavity for attachment [15]. Nassiraei et al. developed a similar suction cup for an underwater cleaning robot [16]. By integrating thrusters with cleaning brushes, they achieved a compact robot structure obtaining 52 N of adsorption force. Based on different hydrodynamic principles, non-contact negative pressure adsorption can be subdivided into two distinct technical pathways: One pathway utilizes the vortex effect, inducing a high-speed rotating flow field within the suction cup cavity to form a low-pressure vortex core at the center via centrifugal force [17]. For example, Liu et al. proposed pump-suction and impeller-type adsorption structures belonging to this category [18]. The other pathway leverages the Bernoulli principle, generating a high-speed outer flow layer between the suction cup and the wall, where increased fluid velocity leads to reduced static pressure [19,20]. For instance, Sakagami et al. developed a wall-climbing robot by adding a negative pressure effect plate around a propeller [21]. Guo et al. designed a hull-cleaning robot using contra-rotating propeller technology. Both designs are based on the Bernoulli principle and demonstrated good performance in actual ship trials [22].

Nevertheless, the aforementioned methods still face common limitations in practical applications: Thrust adsorption suffers from high power consumption and limited payload capacity; biomimetic adsorption involves complex fabrication processes and is prone to contamination; magnetic adsorption is restricted by material limitations; and negative pressure adsorption is sensitive to wall sealing integrity. Consequently, facing the inspection demands of large hydraulic structures with high loads and complex unstructured surfaces, there is an urgent need for a novel underwater adsorption mechanism that simultaneously achieves “strong adsorption force, low energy consumption, and broad adaptability”.

The Venturi ejector, owing to its “zero-mechanical-vacuum-pump” fluid entrainment characteristics, has demonstrated efficient negative pressure generation capabilities in fields such as chemical engineering [23,24] and environmental protection [25,26]. Its core advantages lie in its extremely simple structure, rapid response, low sealing requirements, and ability to form a stable negative pressure zone within milliseconds through jet-entrainment synergy. However, its potential for adhesion on underwater, non-magnetic, irregular walls remains largely unexplored. Addressing this gap, this paper proposes an integrated “Venturi effect-composite suction cup” adhesion system for dam inspection. The innovation of this system lies not only in the suction cup itself but also in its cross-scale synergistic design: The composite suction cup, comprising a rigid base and a flexible sponge layer, ensures both structural strength and adaptive conformity to surface topography; The deep coupling of the submersible pump with the ejector enables dual functions—high-pressure jet driving and negative pressure entrainment—through a single power source; The integrated fluid–structure-control architecture allows the system to provide stable adsorption force on the order of hundreds of Newtons on complex dam surfaces (cracks, exposed aggregate, biofilm) while consuming only around 100 Watts.

The remainder of this paper is structured as follows: Section 2 details the structural design of the Venturi-effect-based composite suction cup and establishes a theoretical model for predicting adsorption force. Section 3 presents the Computational Fluid Dynamics (CFD) simulations conducted to analyze flow field characteristics and optimize key geometric parameters (nozzle diameter, throat diameter, suction cup diameter), followed by a discussion of the results. Section 4 describes the physical experiments performed to validate the theoretical and simulation findings, including laboratory adsorption force tests and field testing on an actual dam surface. Finally, Section 5 summarizes the main conclusions and outlines future work directions.

2. Structural Design and Theoretical Analysis

This section addresses the core challenge of achieving stable adsorption on steep, non-magnetic, and potentially rough underwater surfaces. To this end, a novel composite suction cup structure is proposed, integrating a rigid base for structural integrity, a flexible sponge layer for adaptive sealing on irregular surfaces, and a Venturi ejector driven by a submersible pump for efficient negative pressure generation. The primary goal of the structural design is to combine high adsorption strength with adaptability. To precisely predict the performance of this mechanism and guide its optimization, a mathematical model based on fluid dynamics principles is established to calculate the adsorption force.

2.1. Structural Design

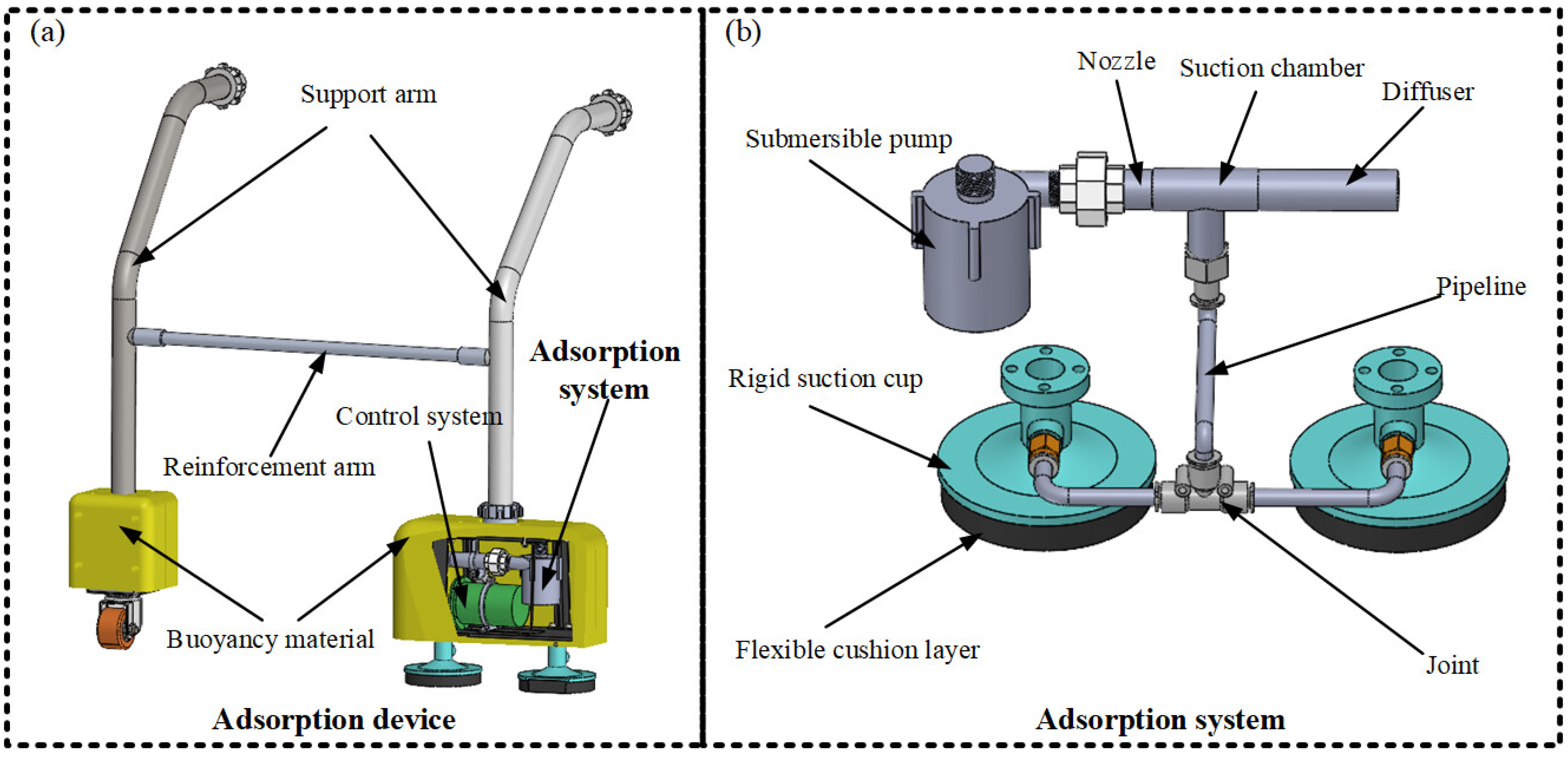
Figure 1a illustrates the three-dimensional model of the underwater inspection robot adsorption device, integrating a support arm, reinforcement arm, buoyancy material, control system and the complete adsorption system. Figure 1b isolates the adsorption system, whose core components include the submersible pump, nozzle, suction chamber, diffuser, pipeline, rigid suction cup and a dual-layer adaptive sealing assembly consisting of closed-cell EPDM sponge and open-cell EPDM sponge—providing structural rigidity while ensuring superior conformance to irregular surfaces.

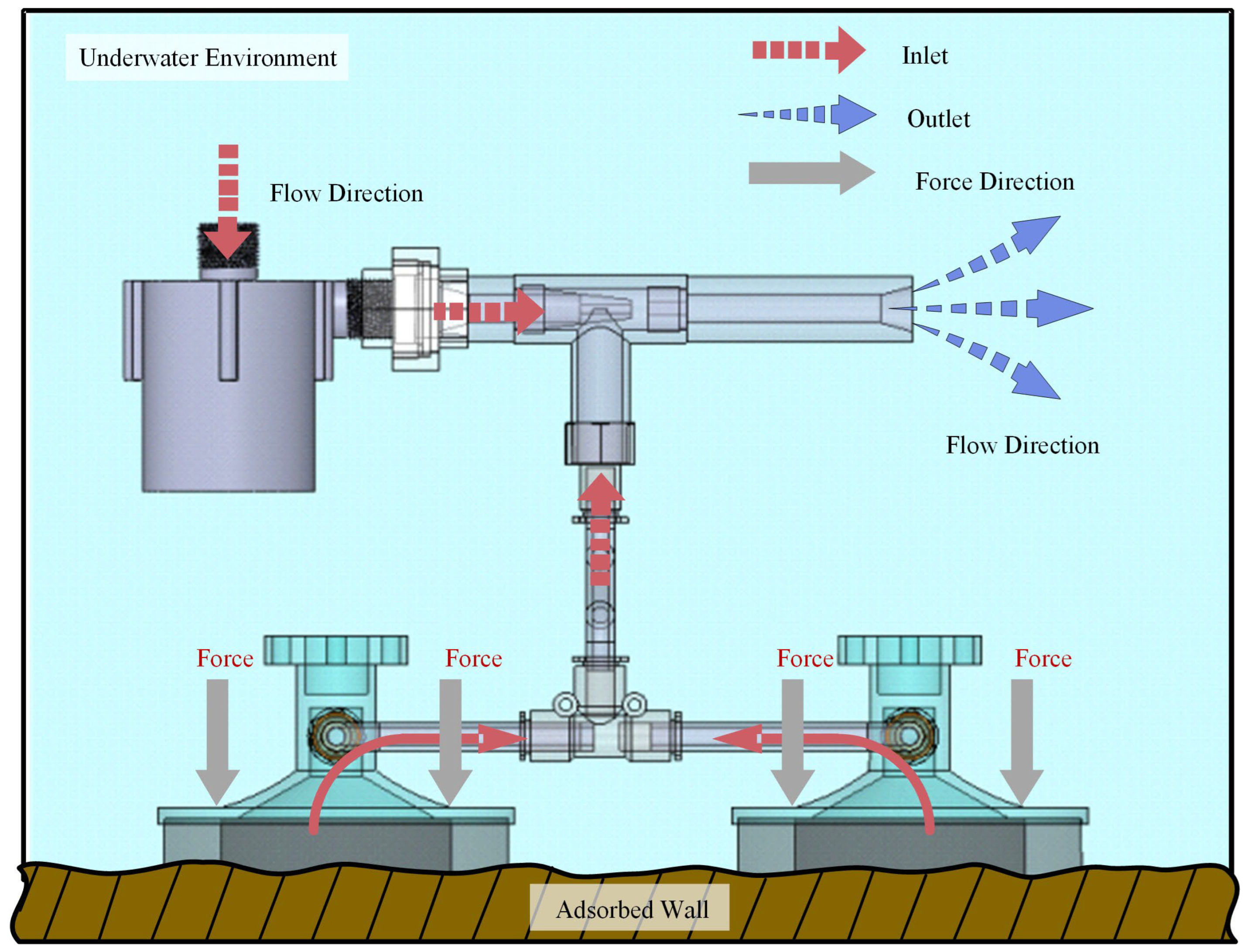
As shown in Figure 2, when the adhesion system approaches the rough concrete dam surface, the submersible pump generates high-pressure water flow. Accelerated by the ejector nozzle, this flow becomes a high-speed jet entering the throat and suction chamber. Significant hydrodynamic effects follow. The jet’s kinetic energy surge causes a sharp pressure drop at the nozzle exit, creating a local low-pressure zone. Simultaneously, the high-speed fluid, via viscous shear and turbulent entrainment, drives the suction chamber fluid out, efficiently evacuating the suction cup to form a stable negative pressure cavity.

Once the negative pressure cavity forms, the suction cup adheres tightly to the dam surface due to the pressure differential. The composite suction cup’s rigid disc ensures structural stability, while the dual-layer sponge assembly provides graded deformation and sealing:

The outer open-cell EPDM sponge, with its high compressibility and interconnected pores, readily conforms to macro-scale surface irregularities and depressions through material flow and pore collapse.

The inner closed-cell EPDM sponge, offering greater structural integrity and elastic recovery, effectively compensates for micro-scale roughness and provides uniform pressure distribution.

This hierarchical structure creates a multi-scale sealing barrier that dynamically adapts to the surface topography, effectively blocking water ingress across diverse and irregular underwater surfaces.

The differential compressibility and mechanical behavior of the two layers enable progressive adaptation. The softer, more compliant open-cell layer absorbs significant variations first, while the stiffer closed-cell layer maintains structural support and ensures consistent sealing pressure. As the seal conforms intimately to the surface asperities, internal fluid exchange diminishes, stabilizing the negative pressure. This creates a lasting adhesion force between the mechanism and the dam, enabling high-strength, stable adhesion on complex and rough engineering surfaces through this mechanical equilibrium.

2.2. Theoretical Analysis

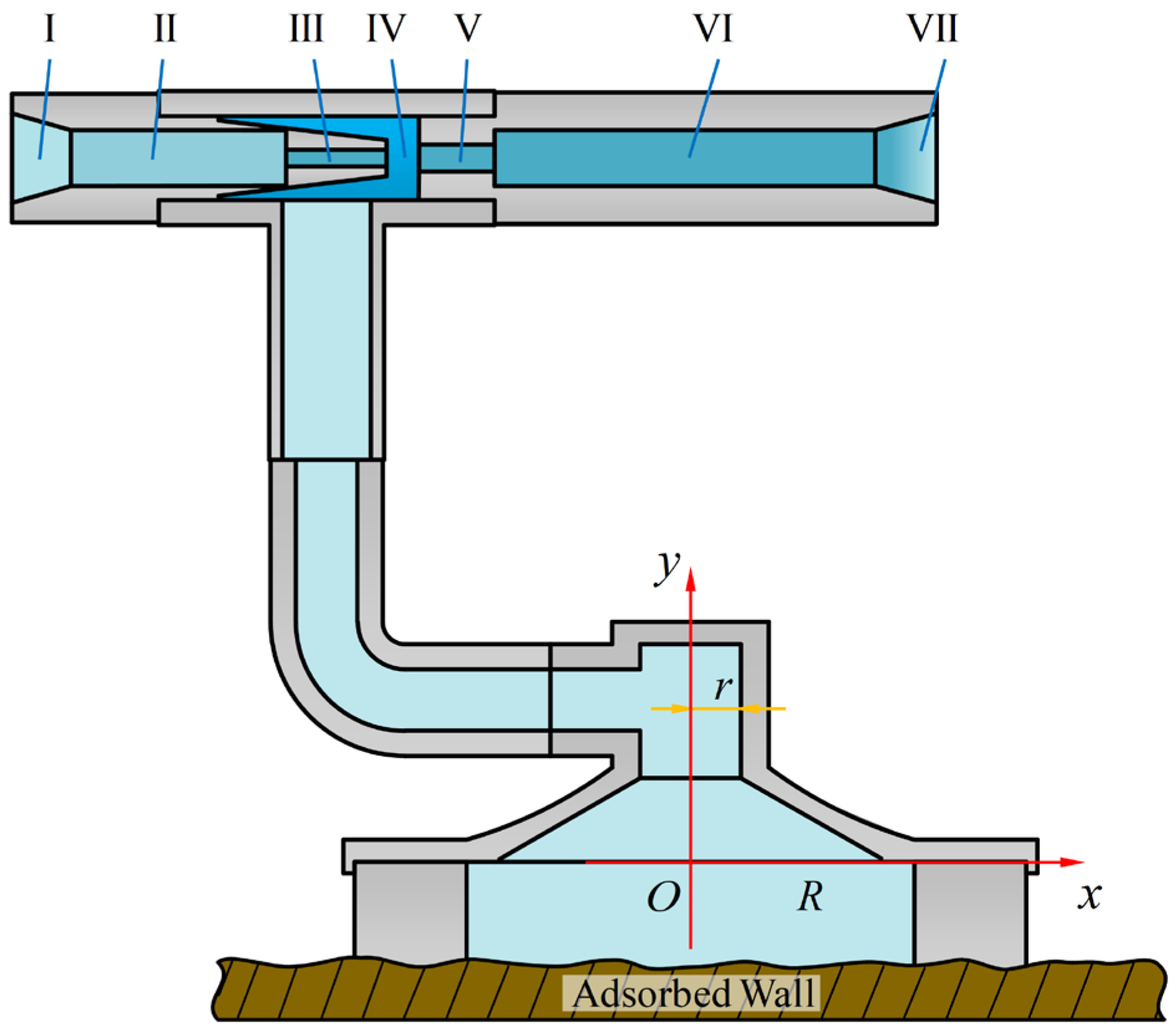
A mathematical model of the adsorption mechanism is established as shown in Figure 3. Here, r represents the radius of the ejector tube, R is the radius of the suction cup of the adsorption mechanism, and D₁ to D₇ correspond to the diameters of the seven transition sections of the ejector. During the operation of the adsorption mechanism, water flows out at high speed from the nozzle of the ejector and enters the throat and suction chamber. Under the Venturi effect, the fluid inside the suction cup is efficiently drawn out. Once the negative pressure stabilizes, the fluid inside the suction cup is considered to be in a static state.

1.

The actual flow velocity v

To determine the negative pressure at the throat, it is necessary to calculate the water flow velocity at the ejector inlet, which is influenced by the pump’s head H and exit velocity v, typically exhibiting a nonlinear relationship as follows:

$$H=a-b{v}^2$$

(1)

where a and b are empirical coefficients specific to the pump.

When the pump is connected to the adsorption system, the total hydraulic resistance loss of the system is given by:

$$h_w={\displaystyle \sum h_j}+{\displaystyle \sum h_f}$$

(2)

Here, h_w denotes the total hydraulic resistance loss, h_j represents the local resistance loss, and h_f signifies the frictional resistance loss along the pipeline.

The local resistance loss can be calculated as:

$$h_j=\zeta {\displaystyle \frac{v^2}{2g}}$$

(3)

where v represents the velocity at the transition section, ζ is the local resistance coefficient, and g is the acceleration due to gravity (9.8 m/s²).

Thus, the total local resistance loss is:

$${\displaystyle \sum h_j=h_{j1}}+h_{j2}+h_{j3}+h_{j4}+h_{j5}+h_{j6}={\displaystyle {\sum }_{i=1}^6{\xi }_i\frac{A_1^2{v}^2}{2g{A}_i^2}}$$

(4)

Here, h_j1 to h_j6 represent the local resistance losses at different sections, and A₁ to A₇ are the areas of the seven transition sections, calculated as A = πD²/4, with v being the velocity at the inlet.

The frictional resistance loss along the pipeline is:

$$h_f=\lambda {\displaystyle \frac{l{v}^2}{2dg}}$$

(5)

where λ is the friction factor, and l is the length of the piping system.

According to the principle that the system’s hydraulic loss equals the pump’s head,

$$H=h_j+h_f$$

(6)

By substituting Equations (1) to (5) into Equation (6), the ejector inlet velocity v can be calculated.

$$v=\sqrt{{\displaystyle \frac{2ga}{{\displaystyle {\sum }_{i=1}^6\frac{A_1^2}{A_i^2}{\xi }_i+\frac{\lambda l}{D}+2g{b}_v}}}}$$

(7)

2.

Negative Pressure in the Suction Chamber p₄

Since sections I and IV are at the same elevation and the frictional resistance loss between them is negligible, applying the Bernoulli equation between these two sections yields [27]:

$${\displaystyle \frac{v^2}{2g}}+H={\displaystyle \frac{p_4}{\rho g}}+{\displaystyle \frac{A_1^2{v}^2}{A_3^{2}2g}}+{\displaystyle {\sum }_{i=1}^3{h}_{ji}}$$

(8)

By solving Equations (1), (3), and (8) simultaneously, the negative pressure p₄ at the throat (section IV) can be determined.

$$p_4={\displaystyle \frac{\rho (1+{\displaystyle {\sum }_{i=4}^6{\xi }_i\frac{A_1^2}{A_i^2}}-\frac{A_1^2}{A_3^2})v^2}{2}}$$

(9)

3.

Adsorption Force F of the Adsorption Mechanism

Given that the height difference between the suction chamber and the interior of the suction cup is negligible, the negative pressure p₄ in the suction chamber is equivalent to the average negative pressure inside the suction cup. Therefore, the adsorption force F generated by the adsorption mechanism is:

$$F=S\times p_4$$

(10)

where S represents the effective area subjected to force, in mm².

By substituting Equations (3) to (9) into Equation (10), the final expression for the adsorption force F is obtained. These analytical relationships provide the basis for the parametric CFD study presented in Section 3.

$$F={\displaystyle \frac{\rho (1+{\displaystyle {\sum }_{i=4}^6{\xi }_i\frac{A_1^2}{A_i^2}}-\frac{A_1^2}{A_3^2})\left(\pi R^2-\pi r^2\right)v^2}{2}}$$

(11)

3. CFD Simulation and Parametric Study Results

This section details the Computational Fluid Dynamics (CFD) methodology [28] employed to analyze the flow dynamics within the Venturi-Ejector Composite Suction Cup (VECSC) and presents the results of the parametric study investigating the influence of key geometric parameters (d, a, b) on the adsorption force F. The goal is to understand the underlying mechanisms, validate the theoretical model, and identify optimal configureurations.

3.1. Simulation Model Setup

Based on the theoretical analysis of the adsorption force, the key parameters affecting the adsorption force F include the pump flow velocity v and head H, the ejector nozzle diameter a, the ejector throat diameter b, and the suction cup inner diameter d. The pump flow velocity v and head H together determine the pressure and velocity at the ejector inlet. An increase in these parameters can significantly enhance the negative pressure in the suction chamber. In this study, a submersible pump with a characteristic curve of H = 18 − 2.909v² (100 W power) was selected. The selection of the spray nozzle diameter a requires a balance between flow loss and the Bernoulli effect: a nozzle that is too small can lead to an increase in the local resistance coefficient, thereby reducing the inlet velocity and weakening the negative pressure generation. Conversely, a nozzle that is too large can weaken the Bernoulli effect, similarly reducing the negative pressure. The throat diameter b has the following effects: a throat that is too small can increase local resistance and reduce the inlet velocity, while a throat that is too large can result in insufficient vacuum in the suction chamber. The suction cup radius r directly determines the area over which the negative pressure acts. A radius that is too small may result in insufficient adsorption force to meet the stability requirements for underwater robot operations, while a radius that is too large is constrained by the overall structural dimensions. To systematically quantify the influence of each parameter on the adsorption force, this study designed the parameter combination scheme shown in

Table 1. Parameter Selection for Simulation Model.

Parameter Category	Parameter Name/Symbol	Values Tested	Unit
Pump Characteristic	Head-Flow Curve	H = 18 − 2.909v2
Ejector Geometry	Nozzle Diameter (a)	3.0, 3.3, 3.5, 3.7, 4.0, 4.2, 4.4, 4.6	mm
Ejector Geometry	Throat Diameter (b)	4.8, 5.0, 5.2, 5.4, 5.6, 5.8, 6.0, 6.2	mm
Suction Cup Geometry	Inner Diameter (d)	50, 60, 70, 80, 90, 100	mm

for multi-condition numerical simulations.

3.2. Boundary Condition Setup and Meshing

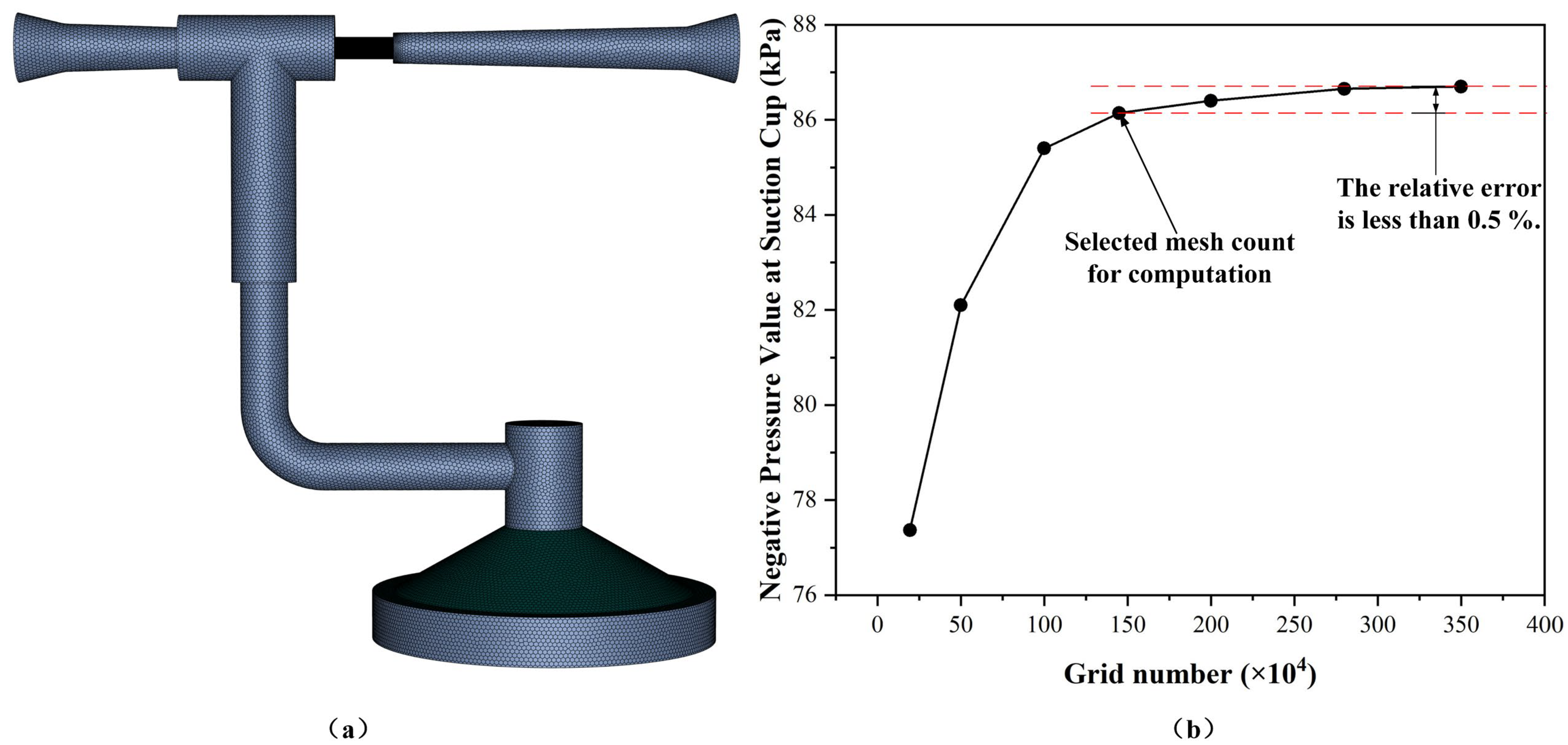
A three-dimensional, steady-state CFD simulation was performed using the Fluent solver (Ansys 2022 R1) to capture the internal flow field within the Venturi-based adsorption structure. The computational domain was confined strictly to the fluid region, comprising the ejector, suction-cup cavity, and connecting pipelines, as illustrated in Figure 4a. The incompressible Navier–Stokes equations were solved in conjunction with the RNG k–ε turbulence model, the latter being selected for its proven accuracy in flows dominated by swirl and high strain rates [29,30]. Enhanced wall treatment was activated to ensure reliable resolution of the near-wall boundary layer.

Pressure–inlet and pressure–outlet conditions were imposed at the domain inlet and outlet, respectively. The inlet pressure was dynamically linked to the experimental pump characteristic curve H = 18 − 2.909v² via a User-Defined Function (UDF) [31,32]. All solid boundaries were treated as no-slip walls. The coupled pressure–velocity scheme was employed, with PRESTO! discretisation for pressure, second-order upwind for momentum, and first-order upwind for turbulent kinetic energy and dissipation rate; gradients were reconstructed using the least-squares cell-based method.

A hybrid mesh of tetrahedra, prisms, and pyramids was generated in Fluent Meshing, with boundary-layer inflation applied in the nozzle contraction, throat, diffuser, and suction chamber to satisfy the turbulence model’s y⁺ requirements. A grid-independence study was conducted by sequentially refining the mesh from 0.5 M to 1.2 M elements [33]. The static pressure monitored at the throat centre varied by only 0.4% between the 0.8 M and 1.2 M cases, confirming that the latter (≈1.2 M cells) achieve an acceptable compromise between accuracy and computational cost. Convergence was declared when the continuity and momentum residuals fell below 10⁻⁵ and the back-flow area fraction at the outlet stabilized at 29.3%, ensuring solution robustness.

3.3. Effect of Suction Cup Inner Diameter on Adsorption Force

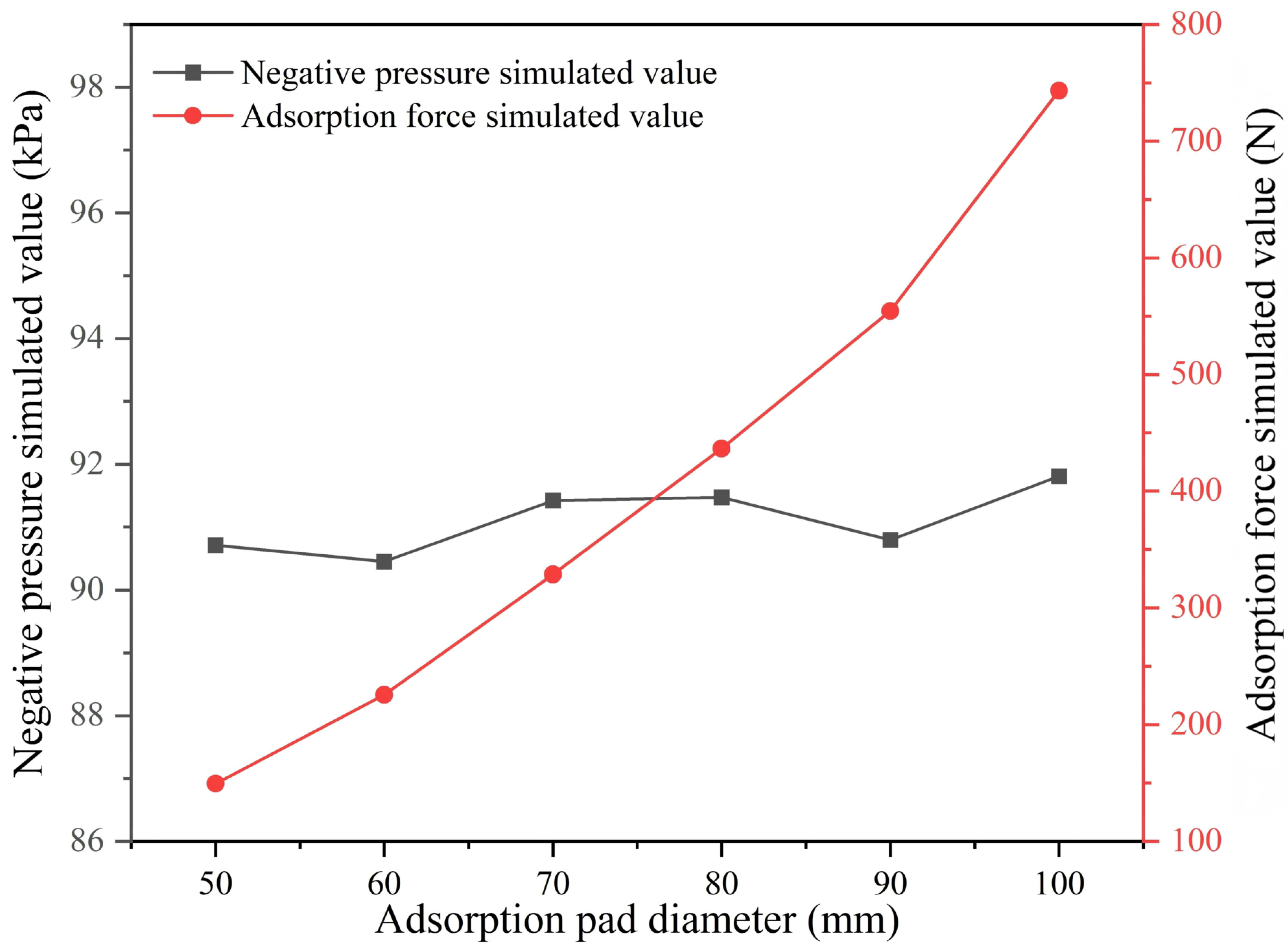
In the design of underwater robot adsorption systems, the inner diameter of the suction cup significantly impacts the adsorption force. This study analyzed the relationship between the suction cup’s inner diameter and the adsorption force under conditions where the ejector nozzle diameter (a) was 3 mm and the throat diameter (b) was 4.8 mm.

As shown in Figure 5, the adsorption force exhibits an upward trend as the inner diameter of the suction cup increases. This is due to the direct increase in the effective negative pressure area caused by the enlargement of the suction cup’s inner diameter. A larger effective area can generate a stronger adsorption force. However, a larger inner diameter is not always better. Once the inner diameter exceeds a certain range, the risk of leakage increases significantly. This not only reduces the adsorption efficiency but can also lead to adsorption failure. For contact negative pressure adsorption, this balance is particularly crucial. If the inner diameter of the suction cup is too small, it becomes difficult to generate sufficient adsorption force to meet the stability requirements for underwater robot operations. Conversely, if the inner diameter is too large, sealing issues can cause the adsorption force to become unstable. Taking into account both the adsorption force and system stability, subsequent research primarily focuses on analyzing and discussing scenarios where the suction cup’s inner diameter is 80 mm.

3.4. Effects of Ejector Nozzle Diameter on Adsorption Force

This study delves into the impact of the ejector nozzle diameter, a critical parameter, on the adsorption force. Based on the established simulation model, with the throat diameter fixed at 5.2 mm, the working conditions corresponding to different nozzle diameters (3.0, 3.3, 3.5, 3.7, 4.0, 4.2, 4.4, 4.6 mm) were named H-H1 to H-H8, respectively, and the influence law of these diameters on adsorption performance was analyzed.

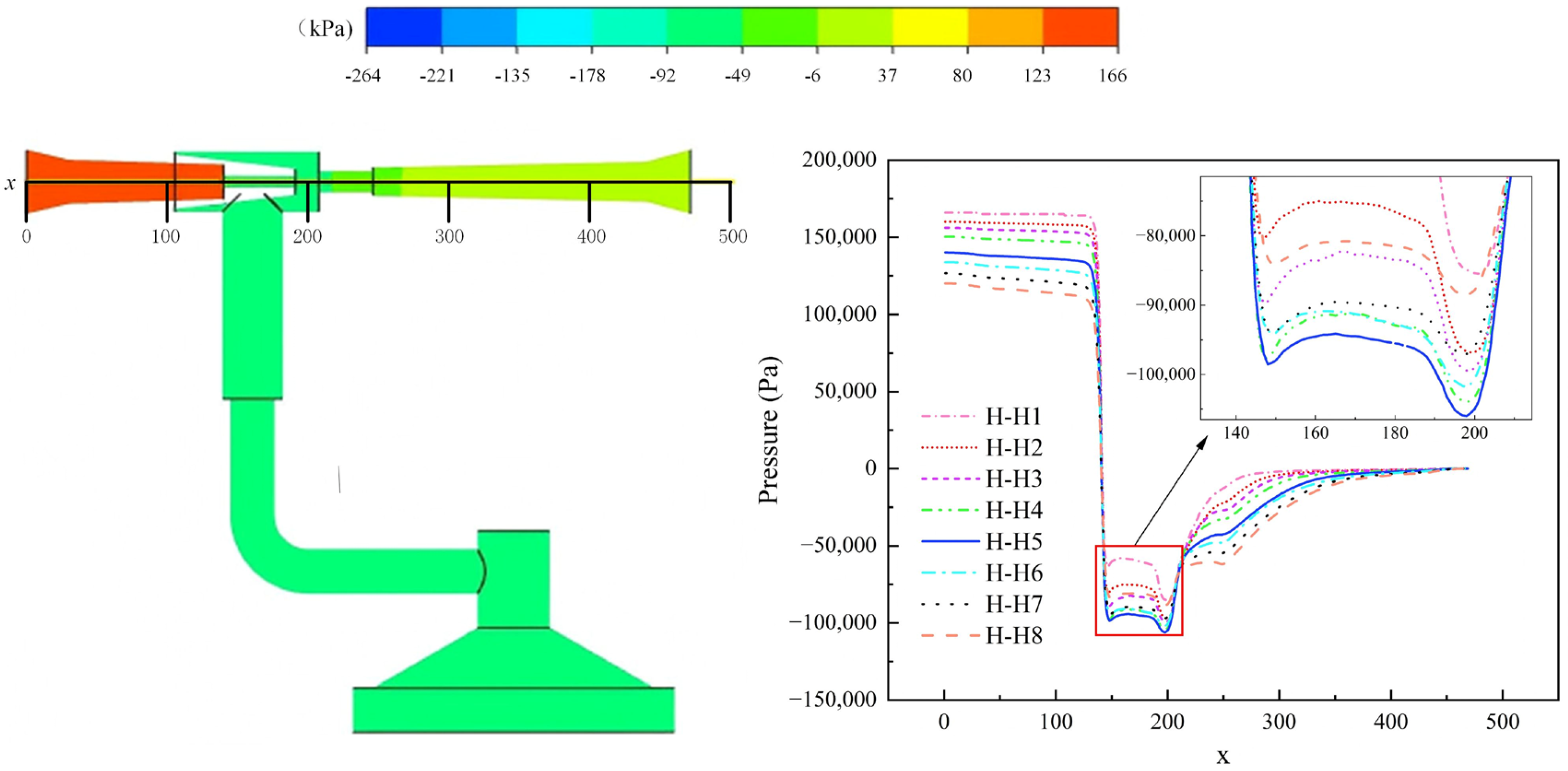
Figure 6 presents the pressure contours and axial pressure curves under working conditions H-H1 to H-H8. When the nozzle diameter is small (e.g., H-H1, 3.0 mm), the pressure at the nozzle exit drops sharply, forming a relatively high negative pressure. This is because a smaller nozzle diameter accelerates the fluid flow. According to Bernoulli’s equation, the increase in flow velocity leads to a significant decrease in static pressure, thereby generating a stronger negative pressure effect inside the suction cup. As the nozzle diameter gradually increases, the negative pressure effect first enhances and then weakens: under the H-H5 working condition (nozzle diameter of 4.0 mm), the negative pressure reaches a maximum value of 103.984 kPa; when the nozzle diameter further increases to the H-H8 working condition (4.6 mm), the negative pressure gradually decreases. This phenomenon indicates that an excessively small nozzle diameter limits the fluid flow due to the excessively large local resistance coefficient, while an excessively large diameter weakens the effect of flow velocity improvement, both of which have adverse effects on negative pressure generation.

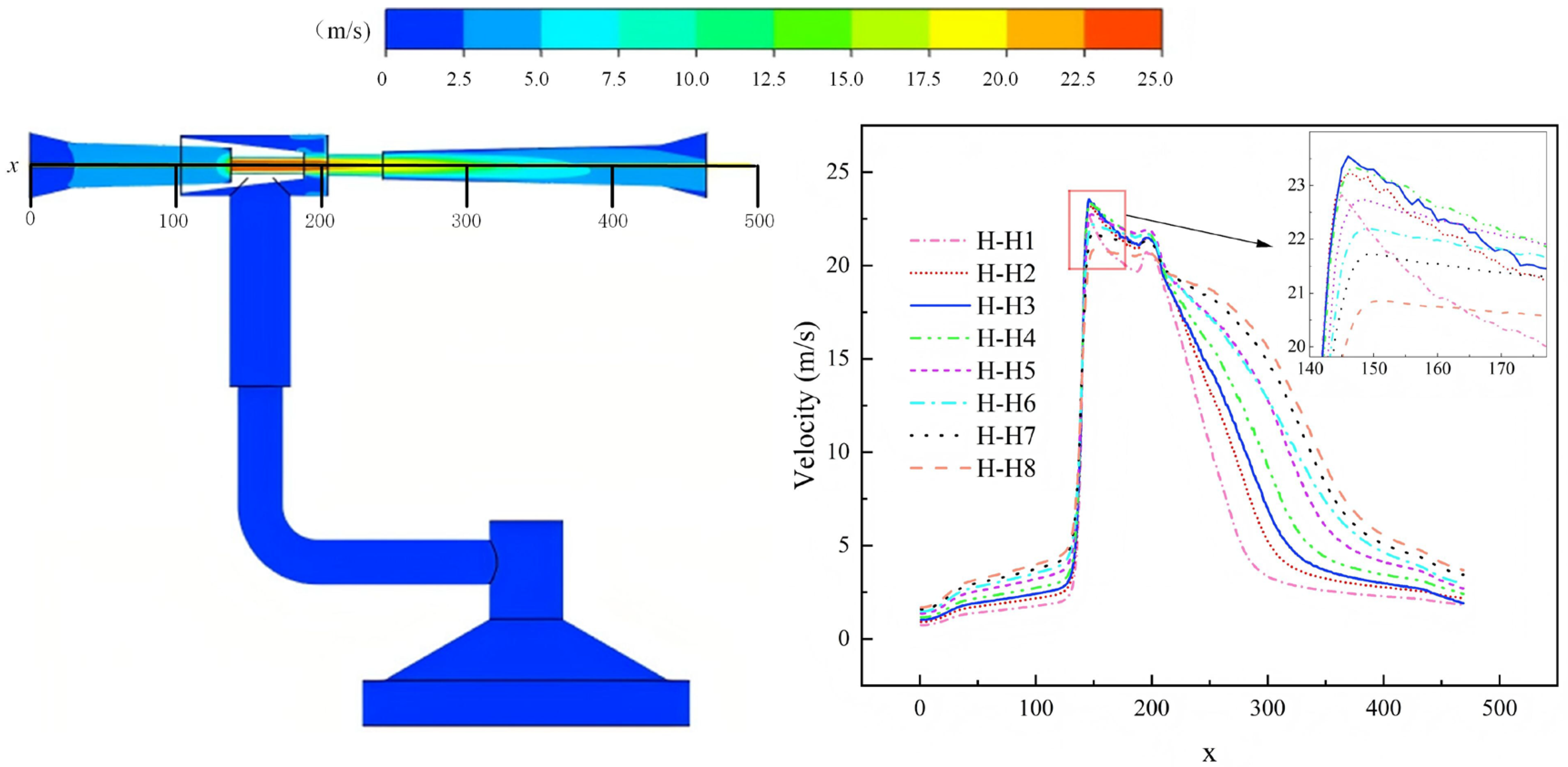
Figure 7 shows the velocity contours and axial velocity curves under working conditions H-H1 to H-H8. Within the range of H-H1 to H-H3 working conditions (nozzle diameters of 3.0–3.5 mm), the smaller nozzle diameter makes the high-speed jet effect at the exit more significant. It drives the fluid flow in the suction chamber through viscous shear and turbulent entrainment, efficiently discharges the fluid in the suction cup, and forms a stable negative pressure cavity. Among them, the axial velocity reaches a peak under the H-H3 working condition (3.5 mm), and the jet driving capacity is the strongest. However, when the nozzle diameter exceeds H-H3, with the increase in diameter (H-H4 to H-H8), the fluid velocity gradually decreases, the viscous shear and turbulent entrainment effects weaken, resulting in a slower fluid renewal rate in the suction chamber and a subsequent decrease in the promoting effect on negative pressure formation.

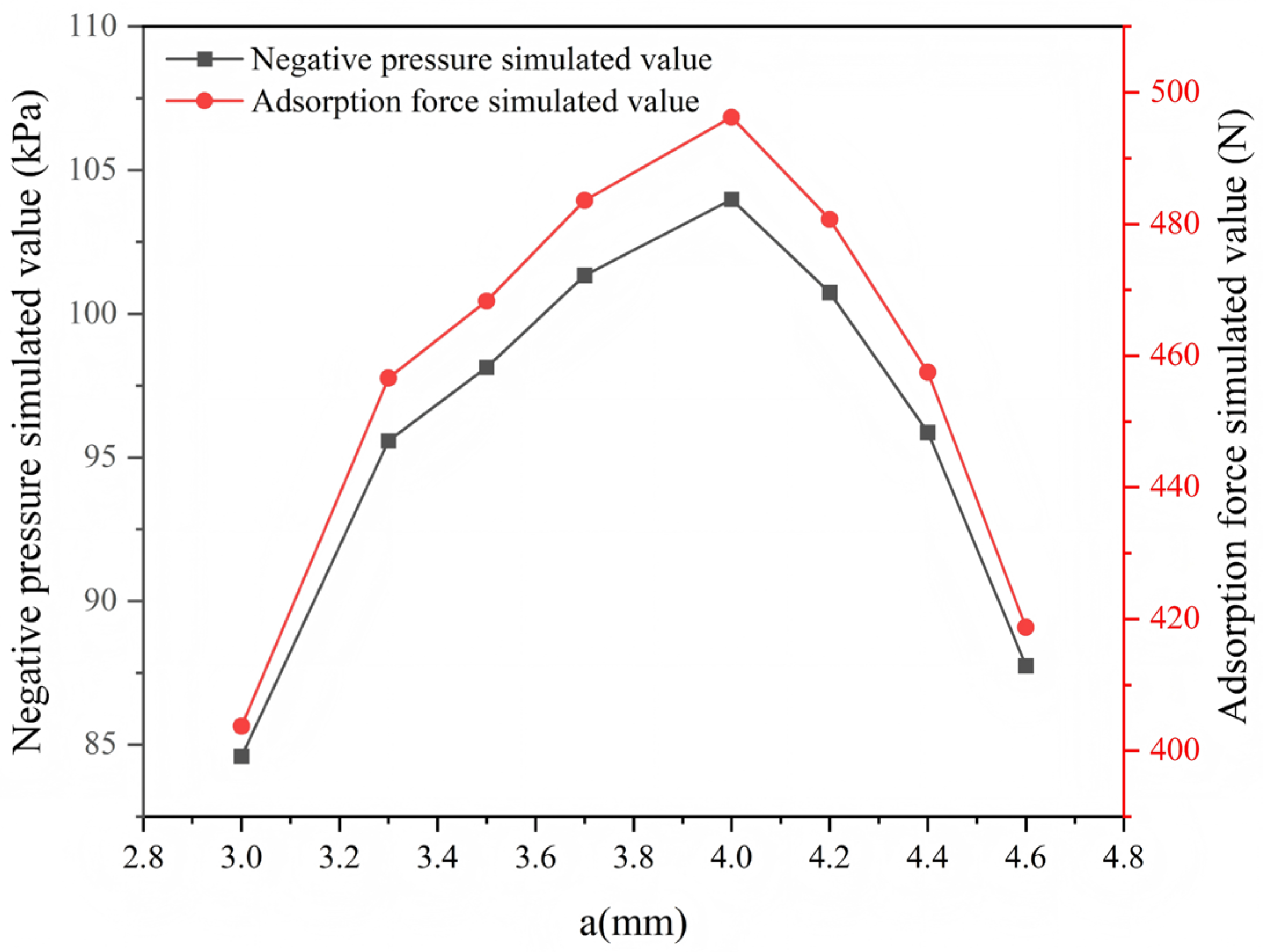
Combined with the correlation curve between nozzle diameter, negative pressure, and adsorption force in Figure 8, it can be seen that there is an obvious nonlinear relationship among the three. When the nozzle diameter is small (H-H1 to H-H3), the enhancing effect of flow velocity improvement on Bernoulli’s effect dominates, and the negative pressure and adsorption force increase with the increase in diameter; when the diameter increases to H-H5 (4.0 mm), the negative pressure reaches a peak, and the adsorption force also increases to a relatively high level; beyond H-H5, the flow velocity improvement effect brought by the decrease in local resistance coefficient can no longer offset the jet intensity attenuation caused by the excessively large diameter, the Bernoulli effect weakens, and both the negative pressure and adsorption force show a downward trend. In conclusion, there exists an optimal nozzle diameter (4.0 mm in this study, corresponding to the H-H5 working condition), at which the local resistance loss is the smallest and the jet intensity is the optimal, enabling the maximization of negative pressure and adsorption force. Figure 6 illustrate the pressure cloud diagrams and axial pressure curves at different nozzle diameters. When the nozzle diameter is small, the pressure at the nozzle exit drops rapidly, creating a high negative pressure. This is due to the smaller nozzle diameter accelerating the fluid flow. According to Bernoulli’s equation, the increase in flow velocity leads to a significant decrease in static pressure, thereby generating a stronger negative pressure effect within the suction cup. However, as the nozzle diameter gradually increases, the negative pressure effect diminishes. Specifically, the negative pressure increases with the nozzle diameter up to 4.0 mm, reaching a maximum value of 103.984 kPa. Beyond this point, further increases in nozzle diameter result in a gradual decrease in negative pressure.

3.5. Effects of Ejector Throat Diameter on Adsorption Force

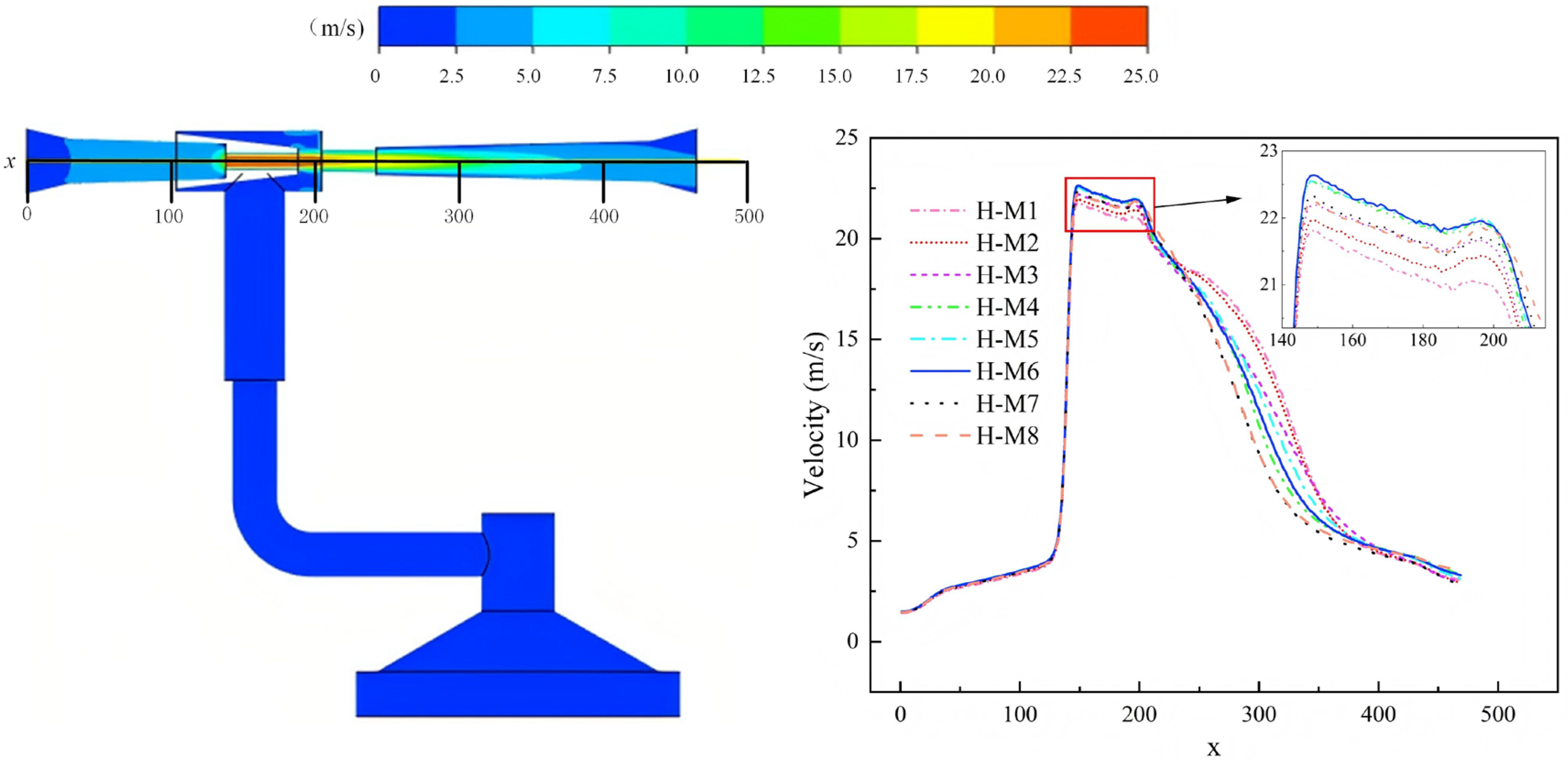
In this section, with the nozzle diameter fixed at 4.2 mm, the working conditions corresponding to throat diameters (4.8, 5.0, 5.2, 5.4, 5.6, 5.8, 6.0, 6.2 mm) were named H-M1 to H-M8, respectively, and the influence law of throat diameter on adsorption force was systematically analyzed.

Figure 9 shows the pressure contours and axial pressure curves under working conditions H-M1 to H-M8. As the throat diameter increases, the negative pressure at the nozzle exit generally first increases and then decreases: under the H-M5 working condition (throat diameter of 5.6 mm), the negative pressure at the nozzle exit reaches the maximum value, and the axial throat area shows a significant negative pressure retention effect. This negative pressure retention capacity shows obvious differences with the change in throat diameter—within the range of H-M1 to H-M5 working conditions (throat diameters of 4.8–5.6 mm), a smaller throat diameter can effectively constrain the fluid flow, maintain a relatively high flow velocity and low pressure in the throat, thereby enhancing the negative pressure retention effect; when the throat diameter exceeds H-M5 (such as H-M6 to H-M8), the constraint effect weakens, the residence time of fluid in the throat is shortened, the negative pressure retention capacity gradually weakens, and even a pressure rebound phenomenon occurs. If the throat diameter is too small (e.g., H-M1, 4.8 mm), although a relatively high negative pressure can be formed, the local resistance loss increases significantly, which in turn affects the smoothness of fluid movement and is not conducive to the stable maintenance of negative pressure.

Figure 10 presents the velocity contours and axial velocity curves under working conditions H-M1 to H-M8. During the H-M1 to H-M6 working conditions (throat diameters of 4.8–5.8 mm), as the throat diameter increases, the fluid velocity in the throat first increases and then tends to be stable. Among them, the axial velocity reaches a peak under the H-M6 working condition (5.8 mm), and at this time, the fluid has the strongest driving capacity for the fluid in the suction chamber, enabling efficient fluid renewal. When the throat diameter further increases to H-M7 to H-M8 (6.0–6.2 mm), the acceleration effect of the throat on the fluid weakens, the flow velocity decreases significantly, the viscous shear and turbulent entrainment effects are weakened accordingly, resulting in a decrease in the fluid renewal rate in the suction chamber and a weakened supporting effect on the formation and stability of negative pressure.

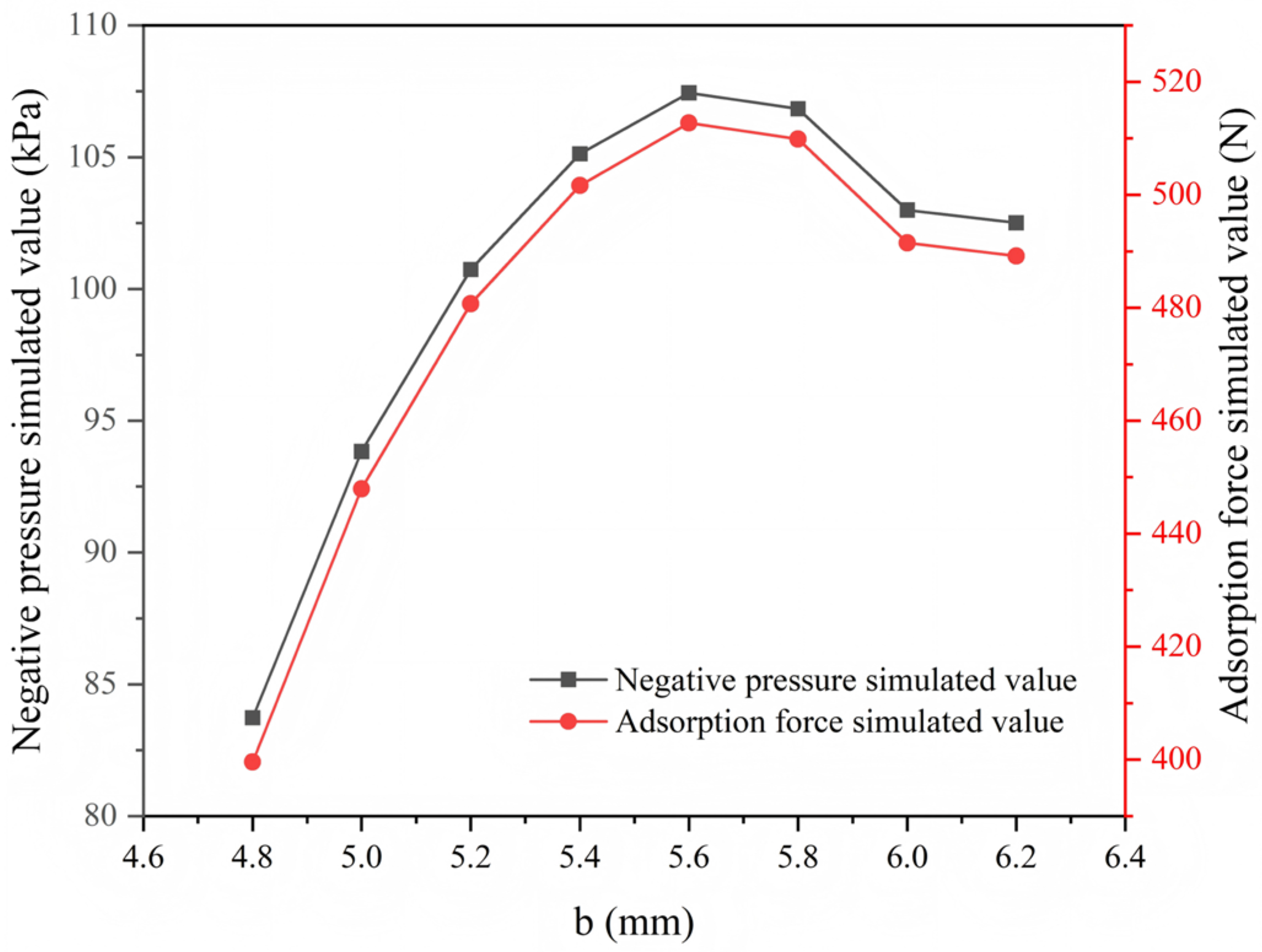
Combined with the relationship curve between throat diameter, negative pressure, and adsorption force in Figure 11, it can be seen that there is also a nonlinear variation characteristic among the three. When the throat diameter is small (H-M1 to H-M5), the effect of reducing local resistance brought by the increase in diameter dominates, the flow velocity improvement promotes the enhancement of Bernoulli’s effect, and the negative pressure and adsorption force gradually increase; under the H-M5 to H-M6 working conditions (5.6–5.8 mm), the negative pressure and adsorption force are maintained at a relatively high level, and the adsorption force under the H-M6 working condition is close to the peak value; when the throat diameter exceeds H-M6, the Bernoulli effect weakens due to the attenuation of flow velocity, and both the negative pressure and adsorption force show a downward trend. It can be concluded that there exists an optimal throat diameter range (5.6–5.8 mm in this study, corresponding to H-M5 to H-M6 working conditions), at which the relatively high flow velocity can be maintained through a reasonable constraint effect, and the local resistance loss can be controlled within a reasonable range, thereby achieving the optimal adsorption performance.

3.6. Synergistic Effects of Ejector Nozzle and Throat Diameters on Adsorption Force

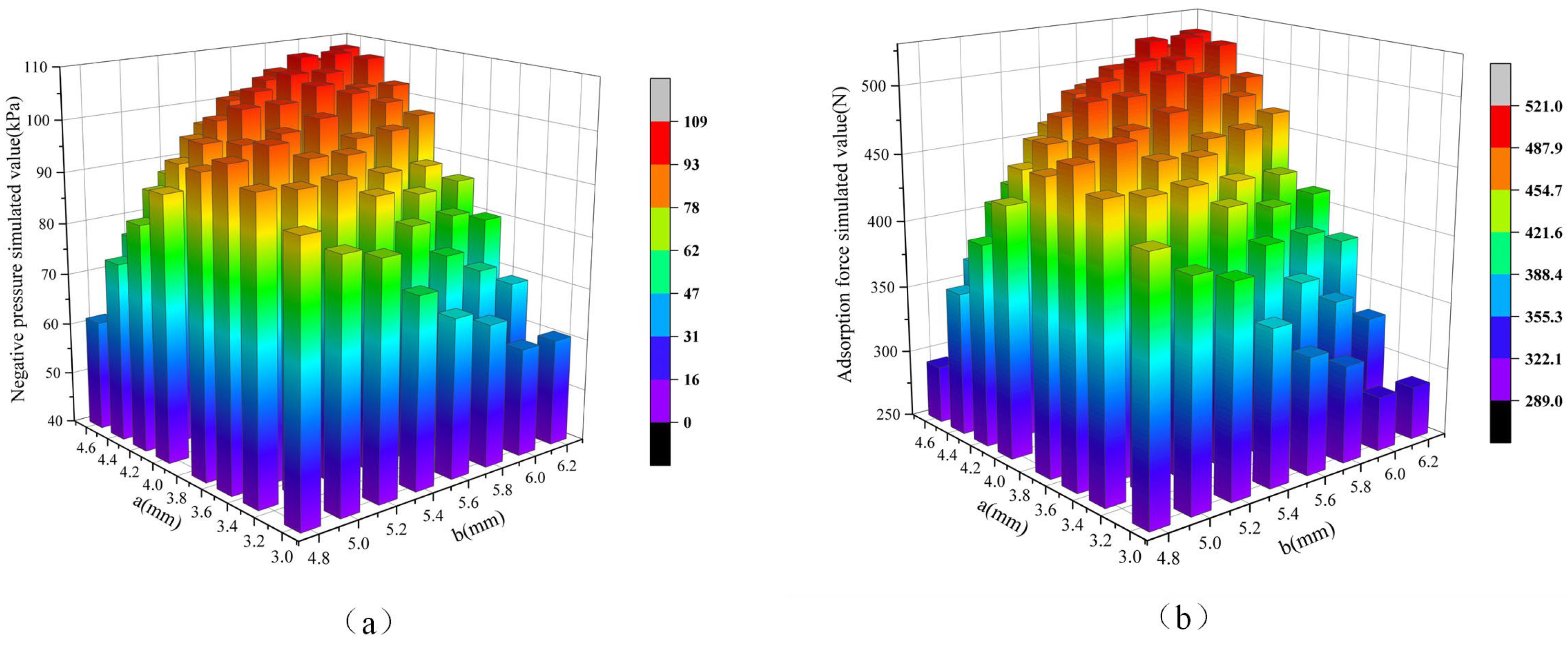
To comprehensively evaluate the performance of the ejector, this study further investigates the combined effects of nozzle and throat diameters. Figure 12a,b illustrate the effects of nozzle-throat diameter combinations on negative pressure and adsorption force, respectively. The results indicate that different combinations of nozzle and throat diameters significantly influence negative pressure and adsorption force. Smaller combinations of nozzle and throat diameters can generate higher negative pressure at the nozzle exit, thereby producing a stronger adsorption force. This is because the smaller nozzle diameter accelerates fluid flow, while the smaller throat diameter effectively constrains fluid flow, maintaining higher fluid velocity and lower pressure within the throat. The combined action of these two factors facilitates negative pressure formation and sustainment.

Specifically, when the nozzle diameter is 4.4 mm and the throat diameter is 5.8 mm (combination a4.4b5.8), the negative pressure simulation value reaches 108.966 kPa, with a corresponding adsorption force of 520 N, representing the optimal adsorption performance in this study. However, when the nozzle and throat diameters exceed a certain range, the adsorption force begins to decline. This is attributed to the fact that overly small nozzle or throat diameters increase local resistance losses, reducing inlet velocity and weakening the Bernoulli effect, thereby generating smaller negative pressure and adsorption force. Similarly, when the nozzle or throat diameter is too large, fluid velocity decreases, weakening the Bernoulli effect and subsequently reducing negative pressure and adsorption force. Therefore, optimizing the combination of nozzle and throat diameters is crucial for enhancing ejector performance. By appropriately matching nozzle and throat diameters, it is possible to achieve a significant fluid velocity and Bernoulli effect with minimal resistance loss, thereby realizing optimal adsorption performance.

4. Performance Experiment

4.1. Experimental Setup

To validate the CFD optimization conclusions from Section 3.6 and comprehensively evaluate the operational performance of the designed adsorption structure, an integrated experimental platform was meticulously constructed (Figure 13a). The platform design strictly followed the nozzle-throat synergy optimization results (Section 3.6, Figure 12), with six representative parameter combinations (H1: a = 3.0 mm, b = 5.0 mm; H2: a = 3.5 mm, b = 5.6 mm; H3: a = 4.0 mm, b = 5.8 mm; H4: a = 4.4 mm, b = 5.8 mm; H5: a = 4.4 mm, b = 6.0 mm; H6: a = 4.6 mm, b = 6.2 mm) fabricated into physical ejector prototypes (Figure 13b). The system comprised four core functional modules:

The adsorption force and negative pressure monitoring unit employed a high-precision dynamometer coupled with a DAQ system to synchronously capture adsorption force (F) and cavity pressure (p).

The surface adaptability validation module simulated real-world underwater engineering complexity using six typical structural surface specimens (Figure 13c), including smooth cement blocks, grid-patterned surfaces, rough curved profiles, irregular granular textures, cracked concrete, and exposed aggregate substrates.

The sealing layer material comparison group investigated the impact of flexible seals on adsorption performance by testing three EPDM variants: open-cell EPDM (high compressibility), closed-cell EPDM (high elastic recovery), and a novel composite EPDM structure (closed-cell + open-cell bilayer, Figure 13d).

The power system utilized two submersible pumps (Q1: characteristic curve H = 18 − 2.909v², rated 100 W; Q2: H = 13 − 4.727v², rated 60 W), with measured average operating powers of 88.938 W and 60.507 W, respectively (Figure 13e).

4.2. Simulation Model Validation

Figure 14 compares the simulated and experimentally measured adsorption forces for the six ejector configurations (H1–H6, now including the optimized H4 configuration with a = 4.4 mm, b = 5.8 mm) under pump Q1. The results demonstrate a consistent trend between the CFD predictions and the experimental measurements, validating the model’s capability in capturing the relative performance variations across different geometric parameters. However, quantitatively, the experimental adsorption forces are systematically lower than the simulated values for all configurations.

Figure 14 compares the simulated and experimentally measured adsorption forces for the six ejector configurations (H1–H6, including the optimized H4 configuration with a nozzle diameter a = 4.4 mm and a throat diameter b = 5.8 mm) under pump Q1. The results demonstrate a strong correlation in the trends between the CFD predictions and the experimental data, validating the reliability of the Computational Fluid Dynamics (CFD) model in predicting the influence of geometric parameters on adsorption performance. Quantitatively, however, the experimental values are systematically lower than the simulated predictions for all configurations. For the optimal H4 configuration, the experimental peak adsorption force (417.9 N) was approximately 19.6% lower than the simulated value (520 N).

This quantitative discrepancy primarily stems from a deviation between the boundary conditions set in the simulations and the actual operational state of the experimental system. The inlet boundary condition for the CFD simulations was defined based on the pump’s performance characteristic under its rated power input. Experimentally, however, the actual operating power of the pump was lower than the rated value, resulting in a downward shift in its overall performance (Head-Flow curve). When coupled with the adsorption system, the actual operating point of the pump was determined by the intersection of this degraded performance curve and the system resistance characteristic, leading to lower actual flow rate and pressure at the ejector inlet than the simulation inputs, consequently reducing the negative pressure generation efficiency. Furthermore, the discrepancies were compounded by: (1) additional turbulent dissipation caused by the microscopic roughness of the machined internal surfaces of the ejector prototypes, which was not fully captured by the hydraulically smooth wall assumption in the CFD model; and (2) the experimental constraint of operating under atmospheric pressure, where the theoretical pressure limit is approximately 100 kPa, with practical limitations such as minor sealing imperfections and potential cavitation at very low pressures preventing the attainment of values closer to the theoretical limit.

Notwithstanding these quantitative differences, the successful identification of the optimal geometric combination (H4) by the CFD model, along with the strong correlation in performance trends, confirms its effectiveness as a tool for design and optimization.

4.3. Adsorption Performance

The relationship between adsorption force (F) and power consumption—core metrics for evaluating underwater adsorption devices—was quantified by comparing experimental results under different power sources. As illustrated in Figure 15, transitioning from the lower-power pump Q2 (60.5 W) to the higher-power pump Q1 (88.9 W) significantly enhanced the negative pressure (p) within the suction cup cavity and the resultant adsorption force (F). This trend was consistent across all tested ejector parameter sets (H1–H6), confirming that increased input power directly strengthens adsorption performance. Notably, under the CFD-optimized H4 configureuration (a = 4.4 mm, b = 5.8 mm), the Q1 pump achieved a peak adsorption force of 417.9N (corresponding to p = 92.17 kPa), markedly exceeding the 360.5 N (p = 80 kPa) obtained with Q2, thereby quantifying the decisive impact of input power intensity on adsorption capability.

The adaptability of the adsorption device to complex underwater engineering surfaces is critical for practical applications. To evaluate this, three flexible sealing materials with distinct mechanical properties—open-cell EPDM, closed-cell EPDM, and composite EPDM—were systematically tested on six representative structural surfaces (Figure 13a) using the optimized H1 configureuration and Q1 power source (

Table 2. Negative pressure retention performance of different EPDM sealing materials on six surface types.

Surface Type	Surface Roughness (Ra, mm)	Open-Cell EPDM (kPa)	Closed-Cell EPDM (kPa)	Composite EPDM (kPa)
Cement Block	0.5–1.5	−77	−76	−77
Square Grid Pattern	1.5–2.5	−77	−78	−77
Rough Arc Surface	≈2.56	−52	−78	−49
Irregular Granular Surface	3.25–8.52	−49	−10	−60
Concrete Joint Surface	≈6.81	−60	−9	−64
Exposed Stone Irregular Surface	6.71–11.49	−33	−8	−64

). On low-roughness surfaces (Ra ≤ 3 mm) with regular topography (e.g., smooth cement blocks, grid-patterned surfaces), all materials provided effective sealing with minimal performance variation, indicating that surface morphology was not a limiting factor for material selection. Even on moderately curved rough surfaces, open-cell and composite EPDM achieved initial conformability due to their superior deformability, whereas closed-cell EPDM required additional preload for stable adsorption.

However, under extreme high-roughness (Ra ≥ 6 mm) or highly irregular conditions (e.g., granular surfaces, cracked concrete, exposed aggregates), material performance diverged sharply, intensifying environmental adaptability challenges. Closed-cell EPDM, reliant on high elasticity and material integrity to maintain sealing, failed to conform to large protrusions or deep cracks due to limited compressive deformation, resulting in complete adsorption failure. In contrast, open-cell EPDM partially preserved adsorption capacity through macro/micro-scale void filling enabled by its high compressibility, yet inherent interconnected pores acted as leakage channels, causing significant force reduction (36.36%, 23.37%, and 57.14% decline on irregular granular, cracked concrete, and exposed aggregate surfaces, respectively).

The composite EPDM pad (closed-cell + open-cell bilayer) demonstrated markedly superior environmental adaptability under these harsh conditions. Its design ingeniously combines the high compression-filling capability of the outer open-cell layer with the sealing integrity of the inner closed-cell layer: the open-cell EPDM preferentially undergoes large-scale deformation to conform to macroscopic roughness, while the closed-cell EPDM provides structural support and blocks potential leakage paths through the open-cell–matrix. This synergy resulted in significantly lower performance loss than monolithic open-cell material, with adsorption force reductions of only 36.36%, 22.07%, and 16.88% on the same irregular surfaces.

4.4. Robotic Application

Based on the optimized parameters identified in Section 3.6 (nozzle-throat optimal combination a = 4.4 mm, b = 5.8 mm), the manufactured prototype of the adsorption unit is shown in Figure 16a. This unit fully retains the core structural features described in Figure 1b: a rigid suction cup body connected via piping to an ejector, with its base covered by an open-cell/closed-cell composite EPDM sponge sealing layer (details in Figure 1b and Figure 13d).

To verify its collaborative performance with the robotic platform, two adsorption units were symmetrically mounted at the ends of the support arms on both sides of the smart inspection robot (referencing the integrated design of support arms and the adsorption system in Figure 1a). During adsorption stability tests conducted in a pool environment (Figure 16b), the robot actively adjusted the angles of the support arms to maintain perpendicular contact between the adsorption units and the pool wall. Test results demonstrated that under rated power (88.9 W), a single adsorption device could stably generate ≥600 N of adsorption force, enabling reliable station-keeping on the vertical pool wall.

To evaluate the effectiveness of the designed adsorption structure in real-world engineering environments, it was integrated into a high-stability intelligent defect-detection robot prototype and tested in a water pool experiment. Subsequently, an in—situ underwater experiment was conducted at the Baihetan Reservoir Dam in Liangshan Autonomous Prefecture, Sichuan Province. On the day of the experiment, the weather was sunny with minor waves on the lake surface due to a southwest wind (Wind Force 2) (Figure 17a). The experiment focused on testing the adhesion stability of the underwater robot on the dam surface (Figure 17b,c). Notably, even with an insulating layer on the Baihetan Dam surface, the adsorption device achieved a negative pressure of 60 kPa, ensuring stable adhesion to the dam surface. This provided a stable platform for underwater inspection and mechanical-arm cleaning operations.

5. Conclusions and Future Work

This study proposes a Venturi-ejector composite adsorption structure for underwater inspection robots. The main conclusions are summarized as follows:

A rigid-flexible composite suction cup with dual-layer EPDM sponge (closed-cell + open-cell) was developed. By synergizing a Venturi ejector with a submersible pump, the system achieved high-strength adsorption (peak 417.9 N) at 88.9 W low power, overcoming limitations on non-magnetic rough surfaces (e.g., concrete dams).

CFD simulations revealed nozzle-throat synergy: Optimal adsorption occurred at nozzle diameter 4.4 mm and throat diameter 5.8 mm, generating 108.966 kPa negative pressure (simulated force 520 N). Experimental validation under H4 configuration (a = 4.4 mm, b = 5.8 mm) confirmed 417.9 N adsorption force (92.17 kPa negative pressure).

The composite seal reduced leakage by >20% versus monolithic open-cell EPDM under high roughness (Ra ≥ 6 mm). On irregular surfaces (exposed aggregate, cracked concrete), adsorption force decline decreased from 36.36% to 16.88%, maintaining 60 kPa negative pressure on dam insulation layers.

Integrated into an inspection robot, the system provided stable adhesion (>600 N per single adsorption device) on vertical walls and reliable operation under real-world conditions at Balnetan Dam, enabling mechanical-arm-assisted maintenance.

Future work will focus on Moreover, the proposed Venturi-ejector adsorption mechanism not only provides a reliable solution for current underwater inspection tasks but also opens up new possibilities for the application of fluid-driven adhesion in other challenging environments, such as marine infrastructure monitoring, underwater welding, and aquaculture facility maintenance. We encourage researchers and engineers to further explore the potential of this mechanism in different operational scenarios and to continue optimizing its performance through advanced materials, adaptive control strategies, and multi-physics modeling. Such efforts will contribute to the broader adoption of intelligent adhesion technologies in unstructured aquatic environments.