1. Introduction
With the global expansion of renewable energy policies, the installation capacity of offshore wind turbines (OWTs) has been increasing rapidly [
1]. In recent years, a clear trend toward larger single turbine capacities exceeding 10 MW has emerged, which contributes to improving power generation efficiency while simultaneously introducing new technical and economic challenges in installation and maintenance phases [
2]. Conventional large-scale OWT installations primarily rely on expensive equipment such as wind turbine installation vessels (WTIVs), heavy-lift crane barges, and multiple auxiliary barges and tugboats. This dependence significantly drives up project costs and delays schedules, while such equipment is not only costly to mobilize but also limited in availability.
In the West Sea and Jeju regions of Korea, severe wave and wind conditions considerably restrict offshore operation periods, imposing substantial seasonal and meteorological constraints [
3]. These limitations result in project delays and higher installation costs. Globally, an imbalance in WTIV availability, coupled with rising fuel and material costs and inflation, has further increased the levelized cost of energy (LCOE) for offshore wind projects, becoming a major barrier to project execution [
4]. Hence, conventional WTIV-based construction methods demand alternative approaches that can enhance both economic feasibility and constructability.
Ramachandran et al. [
5] conducted a combined numerical and experimental investigation of towing dynamics for a fully assembled floating offshore wind turbine (FOWT). Their study compared a potential-flow-based method with a hybrid approach that incorporated Morison’s equation, demonstrating that while the potential-flow model is sufficient under low-speed and mild wave conditions, the hybrid method provides more reliable predictions in higher towing speeds and rougher seas. The results highlighted the capability to accurately estimate platform motions and towline tensions during transportation, thereby offering methodological insights to enhance the safety and feasibility of FOWT towing operations.
In addition to towing-focused studies, hybrid approaches that combine numerical analyses with limited experimental validation have been successfully applied to a range of offshore and marine systems. For instance, Wang et al. [
6] developed a coupled numerical framework for a hybrid floating offshore wind turbine and validated it through scale model tests, demonstrating the effectiveness of such methods in addressing complex offshore engineering problems.
Pengfei Gao et al. [
7] investigated towing resistance and developed a towing scheme for floating offshore wind turbines using CFD-based simulations. Their work validated CFD predictions against experimental and empirical data across a range of drafts and towing speeds, demonstrating that resistance is strongly influenced by draft, speed, and platform configuration. They further recommended maintaining towing speeds under 4 knots to ensure safety, providing practical guidance for safe and efficient towing operations of FOWTs.
Roddier et al. [
8] introduced the floating foundation–based WindFloat system, demonstrating its potential as an alternative to conventional WTIV-dependent installation methods. Their study highlighted how floating platforms can simplify installation procedures and reduce reliance on heavy-lift equipment. However, since WindFloat is specifically designed for floating systems, its direct application to fixed-bottom or jack-up OWTs is limited. Nevertheless, the study is noteworthy in showing that novel installation concepts can fundamentally reshape the cost structure of offshore wind projects.
Yang and Kim [
3] systematically analyzed the restrictive meteorological and oceanic conditions in the West Sea and Jeju waters of Korea and their implications for OWT installation. They emphasized that wave, wind, and current conditions substantially constrain the operational window, with mobilization delays and increased standby costs posing major risks particularly for WTIV-based approaches. Consequently, they concluded that in regions with limited weather windows, installation methods that are more flexible and cost-effective than conventional WTIV-based strategies are required.
Myhr et al. [
9] analyzed the levelized cost of energy (LCOE) for offshore wind projects from a full life-cycle perspective. Their findings indicated that installation methods account for a significant portion of the overall LCOE, with mobilization costs and delays during installation contributing substantially to economic feasibility. This underscores that the development of new installation methodologies is not merely a technical challenge but also an essential task from an economic standpoint.
In summary, previous research has examined offshore wind turbine installation from perspectives such as environmental constraints, towing dynamics, hydrodynamic resistance, floating foundation concepts, and life-cycle economic assessments. While these studies have advanced the understanding of alternative approaches, most still rely on WTIVs or mooring-based systems and therefore fail to resolve the issue of costly equipment dependency. Moreover, practical and cost-effective solutions directly applicable to large-scale (≥10 MW) fixed-bottom or jack-up OWT installations remain limited. To address this gap, the present study proposes a novel anchor-free installation method that eliminates reliance on WTIVs and mooring systems.
Against this background, the present study proposes a new installation method for a jack-up-type 10 MW OWT. In the proposed approach, the entire 10 MW OWT is fabricated onshore, floated off, and transported to the installation site using a tugboat fleet. Upon arrival, the structure is position-controlled through towlines, while the legs of the 10 MW OWT are gradually lowered to penetrate the spudcans into the seabed. This procedure eliminates the need for expensive equipment such as WTIVs or heavy-lift crane barges, enabling installation solely with tugboats. Consequently, the method is expected to reduce installation costs, shorten construction time, and enhance operational flexibility.
The ultimate objective of this study is to analytically verify that the tugboat fleet can provide sufficient pulling capacity to stably maintain the position of a jack-up-type 10 MW OWT. To achieve this, the following procedures are undertaken. First, numerical analyses of the structure under marine environmental conditions are performed to estimate external forces induced by waves, wind, and current. Second, based on the developed model, frequency-domain analyses are conducted to compute the random wave response of the 10 MW OWT. Third, towline tensions are derived from the response results and compared against the towline’s Safe Working Load (SWL) and the tugboats’ Effective Bollard Pull (BPeff). Through this series of numerical calculations, the study proposes a cost-effective and feasible approach that addresses the limitations of conventional WTIV-based installation methods for large jack-up-type 10 MW OWTs.
2. Background
In general, jack-up-type offshore structures are installed through the following procedure. The structure is first assembled onshore and then transported to the installation site by sea. Upon arrival, a mooring system and anchors are deployed to secure a temporary position. Subsequently, three or more legs are gradually lowered, allowing the spudcans to penetrate the seabed, while the pontoon is progressively elevated above the water surface. The buoyancy within the pontoon is then removed, and a preloading process is carried out to ensure sufficient bearing capacity of the spudcans in the seabed. Finally, the upper deck modules and ancillary equipment are installed, completing the installation of the jack-up structure [
10,
11]. This procedure has been validated for its stability and reliability and has been widely applied in offshore plants and offshore wind turbine installations.
While this method ensures stability and benefits from extensive field experience, it also presents several limitations. First, the mandatory mobilization of costly equipment such as WTIVs, crane barges, and large tugboats significantly increases installation expenses [
1,
4]. Second, the installation and removal of the mooring system require considerable time, leading to delays in the overall construction schedule [
12,
13]. Third, in regions such as the West Sea and Jeju waters of Korea, where harsh environmental conditions prevail, the available weather window is limited, which negatively affects project economics [
3]. In particular, for large-scale OWTs exceeding 10 MW, not only the substantial weight but also the large overturning moments generated during towing necessitate the use of even larger equipment, further exacerbating economic challenges.
Meanwhile, the jack-up-type 10 MW OWT considered in this study is installed through a modified procedure. Specifically, instead of employing a mooring system, the tugboat fleet is connected to bollards installed on the pontoon deck of the OWT via towlines, providing the necessary pulling forces in response to waves, wind, and current directions. The tugboats share control forces from different orientations to prevent structural drift and maintain position. Under these conditions, the legs are gradually lowered to allow the spudcans to penetrate the seabed. Finally, the pontoon is elevated above the water surface, securing an air gap and establishing a stable working platform. This anchor-free installation procedure offers significant advantages in terms of cost reduction and construction flexibility compared with conventional methods.
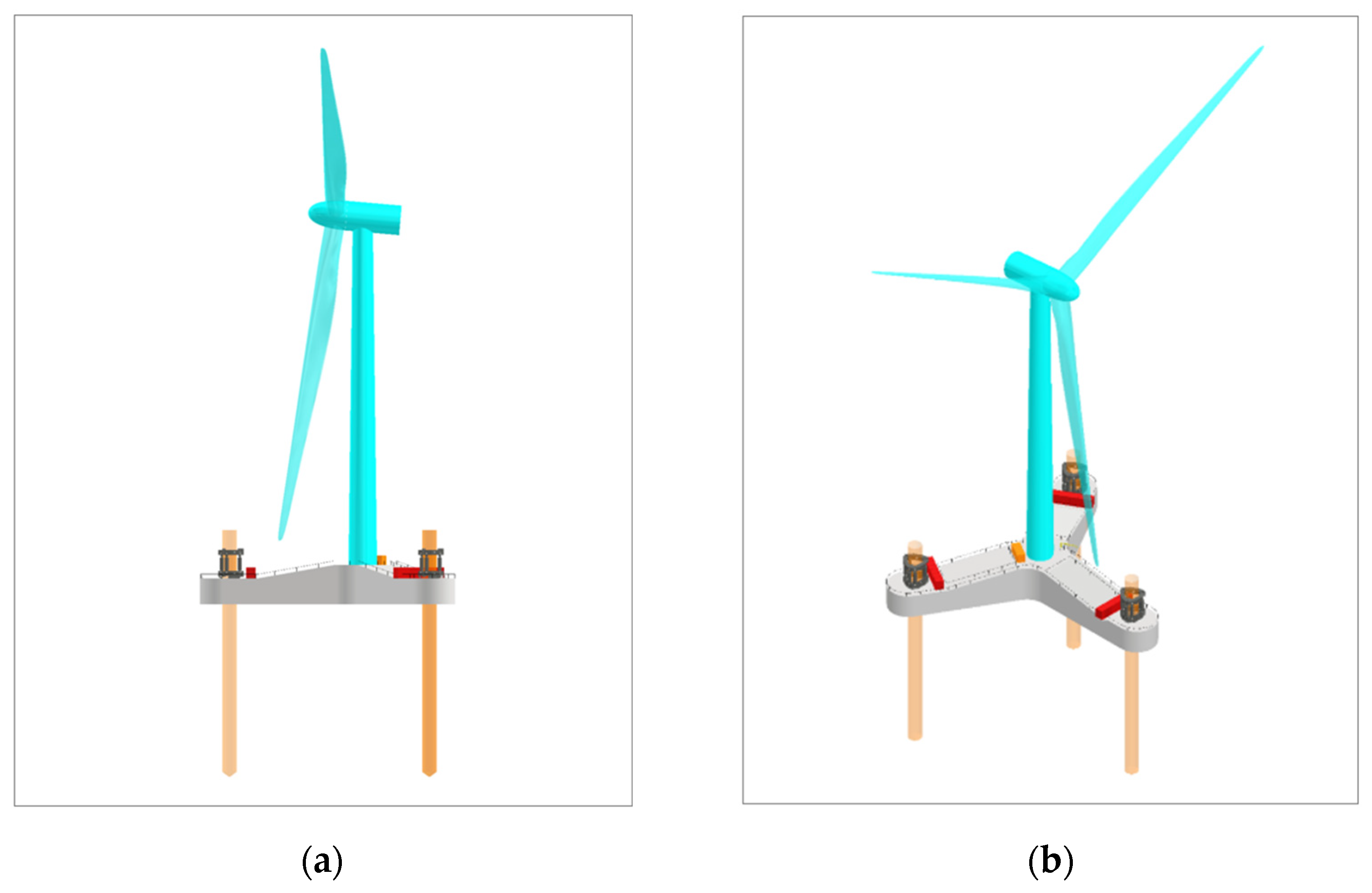
Figure 1 illustrates the configuration of the target structure from various perspectives: (a) front view, (b) side view, (c) top view, and (d) perspective view. The principal particulars, including overall length, leg length, body dimensions, and design draft, are summarized in
Table 1.
Figure 2 conceptually illustrates the installation procedure of the jack-up-type 10 MW OWT, including onshore assembly and float-off, offshore transportation by the tugboat fleet, leg lowering and spudcan penetration, and the final preloading process.
Previous studies have primarily addressed OWT installation stability using mooring-based approaches [
5], while analytical verification of anchor-free installation methods has rarely been reported. In particular, few studies have modeled tugboats as spring elements in frequency-domain analyses and estimated towline tensions based on irregular wave responses. Given that rising installation costs have recently been identified as a major barrier to offshore wind projects [
9], tugboat-based anchor-free installation methods hold considerable potential in terms of cost reduction and operational flexibility.
3. Methodology
3.1. Governing Equations & Numerical Model
The analytical target of this study is a jack-up-type 10 MW OWT system connected to a tugboat fleet via towlines. A numerical model was developed, and motion response analyses were performed in the frequency domain. In the analysis model, the 10 MW OWT was idealized as a six-degree-of-freedom body, incorporating added mass, radiation damping, and hydrostatic restoring coefficients.
The tugboats were not modeled as actual hulls but simplified as fixed points, connected to the bollards installed on the pontoon deck of the OWT via towlines. This approach was adopted because the purpose of this study is to examine the tensions acting on the towlines while the tugboats remain stationed. If the tugboats were modeled as self-propelled hulls, the thrust magnitude and direction would need to be controlled at each simulation step, resulting in significant numerical trial-and-error. Therefore, in this study, towlines were modeled as linear spring elements to provide additional stiffness to the system, thereby incorporating both the six-degree-of-freedom (6-DOF) motion response of the OWT and the restraining effects of the tugboat fleet through the towlines. The equation of motion for the 10 MW OWT in the frequency domain is expressed as Equation (1) [
12].
Here, M denotes the mass matrix of the OWT, A(ω) the added mass matrix, B(ω) the radiation damping matrix, the viscous damping, and C the hydrostatic restoring matrix. Kₜᵤg represents the stiffness matrix idealizing the tugboats as spring elements, while the external force terms include wave, wind, and current loads. The OWT response, ξ(ω), is determined by the interaction between these external forces and the spring stiffness of the tugboats.
The irregular wave response of the OWT was calculated based on the Response Amplitude Operator (RAO). The response spectrum is obtained as the product of the wave spectrum and the RAO, and is expressed as Equation (2).
Here, Sζ(ω) denotes the wave spectrum, and Sξ(ω) represents the response spectrum of the OWT. The time-domain response can be obtained through inverse transformation, from which the towline tension is calculated.
The towline was idealized as a linear spring, and the tension was derived by multiplying the spring stiffness by the displacement difference between the OWT and the tugboat reference point. The tension is expressed as Equation (3).
Here, K
towline (= EA/L) represents the axial stiffness of the towline, and Δξ(ω) denotes the relative displacement between the OWT and the fixed point.
Table 2 summarizes the material properties of the towline used in the present analysis.
Finally, the towline tensions obtained from the frequency-domain analysis are compared with the towline’s Safe Working Load (SWL) and the tugboats’ Effective Bollard Pull (BPeff). By verifying that the calculated tensions remain within the limits of the SWL and BPeff, the safety and feasibility of the proposed installation method are assessed.
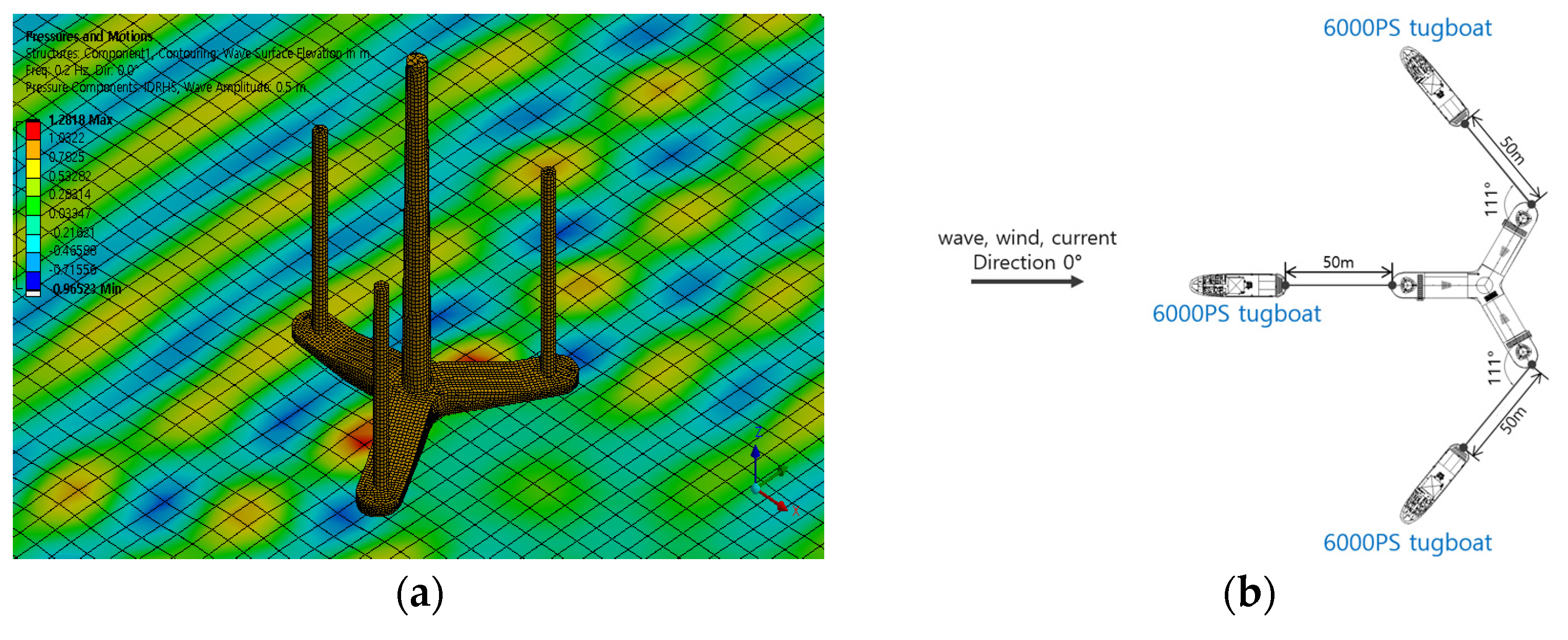
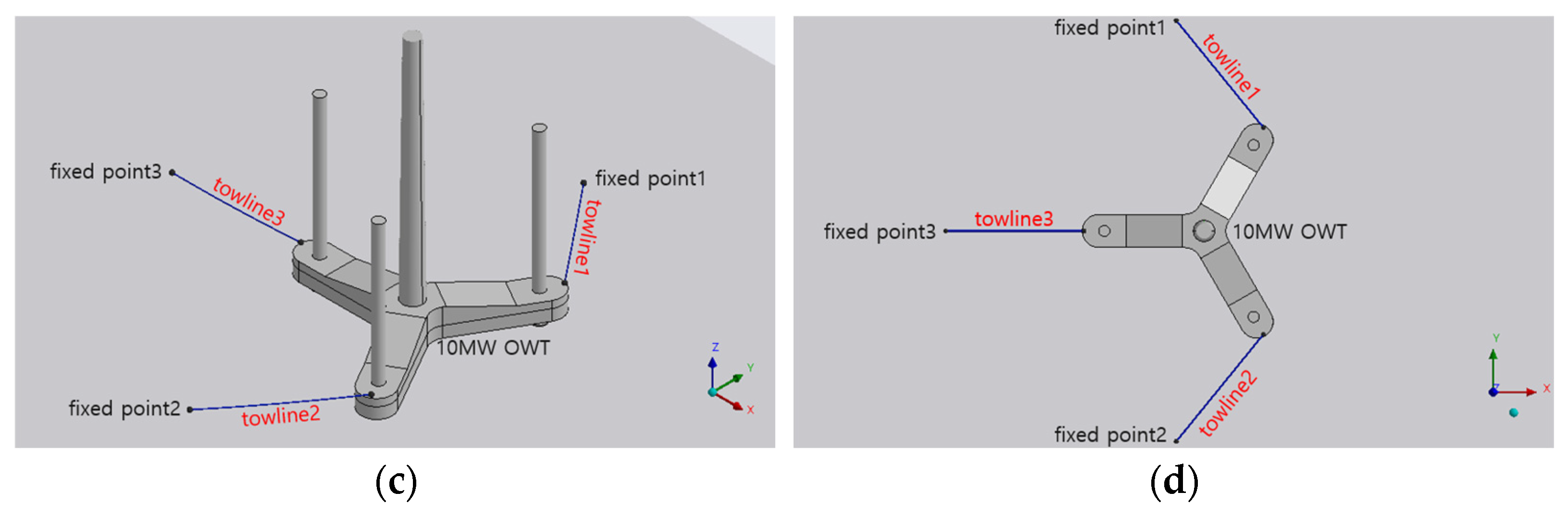
Figure 3 presents the AQWA analysis model developed in this study. (a) shows the hydrodynamic mesh of the 10 MW OWT and the resulting wave elevation, which were used to evaluate wave, radiation, and added mass coefficients. (b) illustrates an example of tugboat arrangement under an environmental load acting from the 0° direction, demonstrating how the tugboats provide restraining effects through towlines connected to bollards on the pontoon deck. (c) depicts a three-dimensional model including the bollard–towline–fixed point connections, while (d) shows the same configuration in a top view. Through this modeling, the interaction between the 10 MW OWT and the towline system was numerically represented, forming the basis for the motion response analysis in the frequency domain.
3.2. Environmental Loads and Analysis Conditions
The environmental loads considered in this study are classified into three components: waves, wind, and current. For the wave conditions, the JONSWAP spectrum was applied with a significant wave height (H
s) of 1.0 m, a peak period (T
p) of 7.0 s, and a peak enhancement factor (γ) of 1.0. Wave directions were set to five cases—0°, 45°, 90°, 135°, and 180°—by applying the uniaxial symmetry of the 10 MW OWT. Wave loads were computed using ANSYS AQWA (2022 R2) [
13], which evaluates both first-order linear wave forces and second-order nonlinear drift forces (QTF). The drift component plays a critical role in assessing the pulling capacity of the tugboats.
Wind and current loads were calculated using MOSES. According to the MOSES (2022) [
14] manual, wind loads are evaluated based on the empirical formula and drag coefficients specified in the ABS Code [
15]. In this study, these formulations were applied to calculate the wind loads acting on the superstructure, nacelle, and tower of the 10 MW OWT. The wind load is expressed as Equation (4).
Here, ρair is the air density, Cd the drag coefficient, Aref the projected area above the water surface, and V the wind velocity. The wind speed was set to 10 m/s, and the wind load calculated in MOSES was divided by the square of the velocity (V2) to derive the velocity-squared-based wind force coefficient. This coefficient was subsequently input into AQWA and used in the frequency-domain analysis.
The current load was estimated based on Morison’s Equation [
16], and the hydrodynamic coefficient library provided in the MOSES manual was employed to calculate the loads acting on the lower pontoon structure of the 10 MW OWT. Since the current was assumed to be steady, the acceleration component was neglected, and only the drag term of Morison’s equation was considered. In this analysis, the current velocity was set to 2 knots (approximately 1.03 m/s). The current load is expressed as Equation (5), and the calculated load was divided by the square of the current velocity (U
2) to derive the velocity-squared-based current force coefficient. This coefficient was subsequently applied as an input parameter in AQWA.
Here, ρseawater is the seawater density, Cc the current drag coefficient, Aref the submerged projected area, and U the current velocity.
The design conditions for determining environmental criteria were adopted from the weather-restricted conditions specified in DNV-ST-N001 [
17] and ISO 19901-6 [
18]. The operational condition (OP
WF) represents the practicable weather condition for construction, obtained by multiplying the design condition (OP
LIM) by the alpha factor (α-factor), whereas OP
LIM denotes the maximum allowable environmental condition for verifying structural safety. The alpha factor is a conservative coefficient introduced to account for uncertainties in weather forecasting and short-term environmental variability. Accordingly, OP
WF is defined as the relaxed value of α × OP
LIM. Thus, the operational condition reasonably reflects the environmental range in which construction activities can be performed while maintaining safety margins.
In this study, α-factors of 0.59 for waves and 0.71 for wind speed were applied. Accordingly, the operational condition (OP
WF) is defined as a relaxed value compared with the design condition (OP
LIM), providing a safety margin that accounts for uncertainties in weather forecasting. The detailed environmental parameters of the operational and design conditions are summarized in
Table 3.
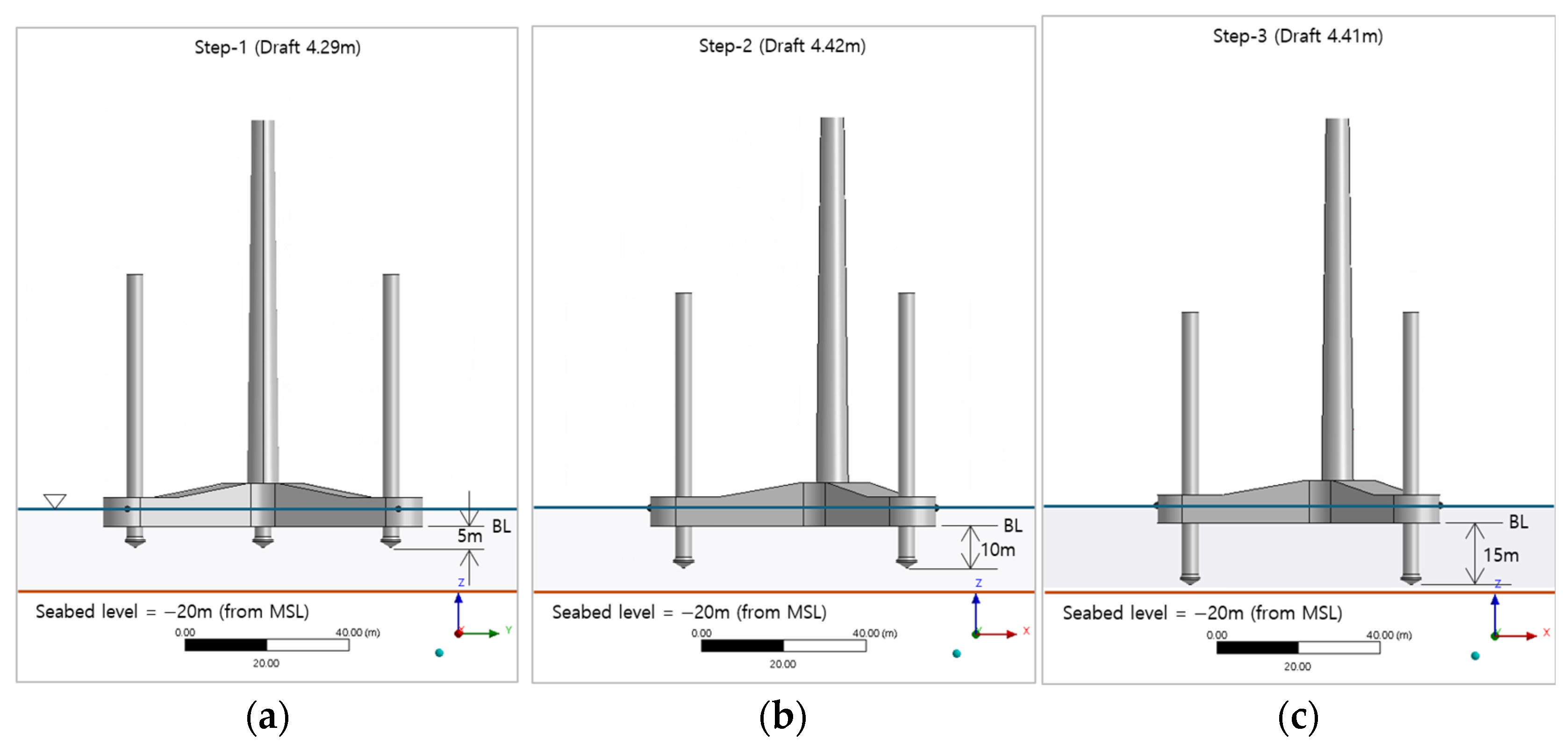
In this analysis, three conditions were applied according to the spudcan lowering stage. Step 1 represents the non-flooded condition, where the spudcan is lowered to –5 m from the baseline (BL, reference baseline at the bottom of the pontoon). Step 2 corresponds to the partially flooded condition with a lowering depth of –10 m, and Step 3 denotes the fully flooded condition with a lowering depth of –15 m. Since the sea surface is located above the BL by the draft, the spudcan penetration depth at each stage is defined with reference to the BL. As the stages progress, the buoyancy and stability characteristics of the pontoon vary, providing an essential basis for analyzing differences in structural dynamic responses during the installation process.
Table 4 summarizes the quantitative stability parameters for each stage, including draft, displacement, GM (metacentric height), and BM (metacentric radius). Correspondingly,
Figure 4 illustrates the spudcan penetration depth relative to the BL and the seabed (–20 m with respect to MSL), thereby visually describing the installation procedure.
In addition, a total of 15 analysis cases were conducted in this study. For each stage condition (Step 1 to Step 3), five environmental load directions—0°, 45°, 90°, 135°, and 180°—were considered. The analysis directions were limited to these five cases because the structure is symmetric about the X-axis, which, in the coordinate system adopted in this study, is defined as the longitudinal axis of the structure. In all cases, the environmental parameters were kept constant, with a significant wave height of 1.0 m, a peak period of 7.0 s, a current velocity of 1.03 m/s, and a wind speed of 10 m/s, as summarized in
Table 5.
3.3. Proposed Anchor-Free Jack-Up Installation Method
This section provides a detailed description of the concept and implementation procedure of the newly proposed anchor-free jack-up installation method. The proposed approach utilizes a tugboat fleet to install a 10 MW OWT in an anchor-free condition, distinguishing itself from conventional methods by enabling installation solely with tugboats, without the need for costly equipment such as WTIVs or heavy-lift crane barges.
The tugboat fleet consists of three vessels, each with a propulsion power of 6000 PS. The rated bollard pull (BP) of each tugboat is approximately 747 kN, and by applying the Tug Efficiency Calculation proposed by DNV (Det Norske Veritas) [
17], an efficiency factor of 80% was considered, yielding an effective bollard pull (BP
eff) of 598 kN. This value accounts for marine resistance, towline inclination, and operational efficiency losses, thereby providing a more realistic towing capacity for practical installation operations, as summarized in
Table 6.
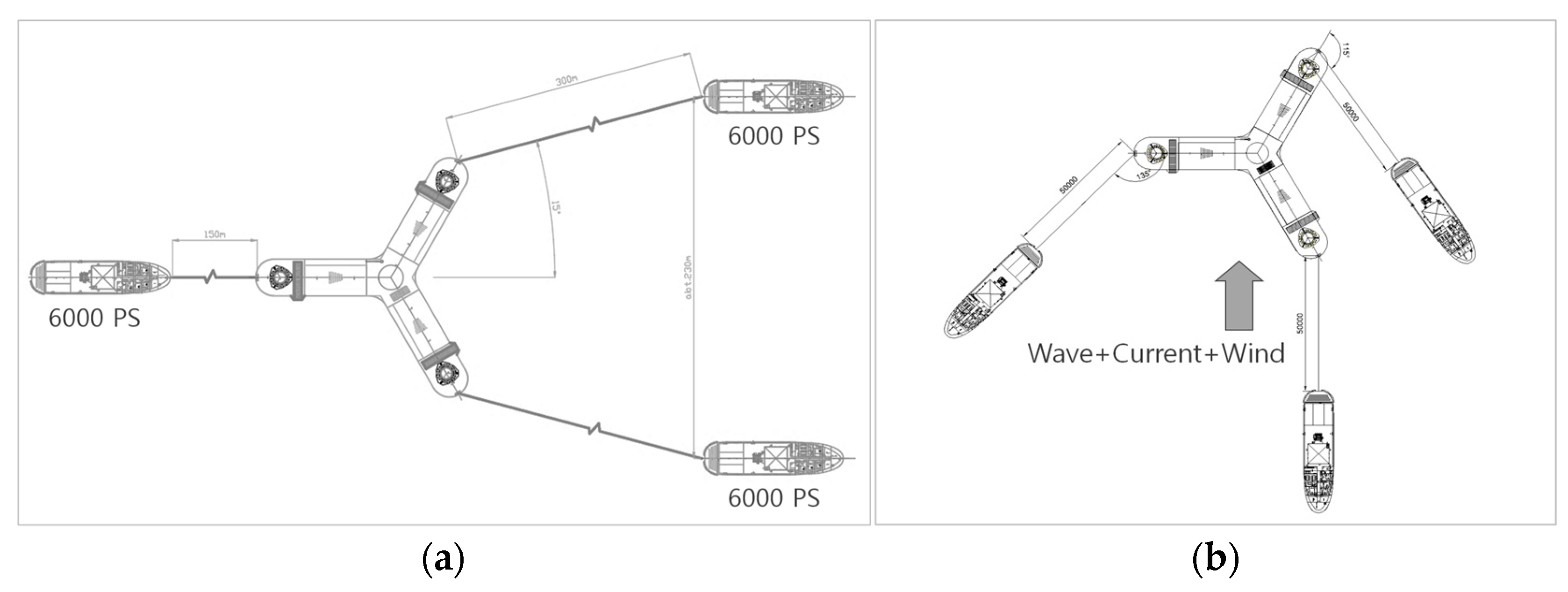
The three tugboats are connected by towlines to three bollards located on the deck of the 10 MW OWT. During the towing stage, two tugboats are positioned symmetrically on the port and starboard sides of the forward section of the OWT to provide direct control against the primary load direction, while the remaining tugboat is positioned at the stern to provide auxiliary stabilization. This arrangement is designed to effectively distribute the external forces induced by waves, wind, and current during marine transportation, thereby minimizing drift and maintaining a safe trajectory.
During the installation stage, the tugboat arrangement is not fixed but is dynamically adjusted in response to the real-time direction and magnitude of the environmental loads. Upon arrival at the site, the towline length is readjusted to approximately 50 m to connect the tugboats with the 10 MW OWT, after which the tugboat fleet first relocates to positions aligned with the environmental load direction to suppress drift.
Figure 5 illustrates the variation in tugboat arrangement under the proposed installation method. (a) shows the basic configuration during the transportation stage, where two tugboats are positioned symmetrically at the bow and one is positioned at the stern. (b) depicts the installation stage, in which the tugboats are repositioned to align with an environmental load acting from the 90° direction. This demonstrates the principle by which the tugboat fleet suppresses drift and maintains the position of the 10 MW OWT.
During the gradual lowering of the spudcans, the tugboats guide the structure to move slowly toward the intended installation position while continuously sharing the pulling force to prevent drift and yaw. In the pre-penetration stage, when the 10 MW OWT is freely floating due to buoyancy, the tugboats actively perform station-keeping by counteracting the environmental loads to suppress drift. Once the spudcans begin to penetrate the seabed, the structural degrees of freedom become constrained, resulting in a significant reduction in drift, and the tugboats provide only auxiliary corrective forces when necessary.
Once the spudcans are sufficiently penetrated, the pontoon is elevated above the water surface, securing a stable working platform. At this stage, the 10 MW OWT structure is restrained by the seabed, and the role of the tugboats is essentially completed, with station-keeping achieved through the bearing capacity of the spudcans.
The numerical analyses conducted in this study are therefore aimed at quantitatively evaluating the pulling forces of the tugboats and verifying whether these forces remain within the limits of the towline’s Safe Working Load (SWL) and the tugboats’ Effective Bollard Pull (BPeff).
To ensure safety, the following procedures are implemented concurrently. First, towline tension and tugboat positions are continuously monitored through a communication system among the tugboats, ensuring that the tension does not exceed the SWL. Second, each tugboat is operated in standby mode to enable immediate response to sudden variations in environmental loads. Third, the lowering speed of the spudcans is adjusted only when drift and yaw remain within allowable limits, and the lowering operation is temporarily suspended if necessary to maintain safety.
The proposed anchor-free installation method offers several advantages compared with conventional WTIV-based approaches. First, the overall installation process can be shortened as the installation and removal of a mooring system are unnecessary. Second, the method delivers significant economic benefits by enabling installation solely with relatively low-cost tugboats, without the mobilization of expensive equipment such as WTIVs or heavy-lift crane barges. Third, by utilizing the maneuverability of tugboats, the method provides superior operational flexibility in responding to changing weather conditions. Accordingly, the proposed method simultaneously satisfies three key requirements—drift suppression, station-keeping, and stable spudcan penetration—and thus can serve as a practical alternative for future large-scale jack-up-type OWT installations.
3.4. Verification Procedure
The validity of the proposed anchor-free installation method was verified through numerical analysis. The objective of the verification was to confirm that the pulling force provided by the tugboat fleet does not exceed the towline’s Safe Working Load (SWL) or the tugboats’ Effective Bollard Pull (BP
eff). To this end, as described in
Section 3.1 and
Section 3.2, MOSES and AQWA were employed to evaluate the external forces induced by waves, wind, and current. The calculated forces were applied under both operational conditions (OP
WF) and design conditions (OP
LIM) to account for a range of environmental scenarios.
The calculated environmental loads were applied as input values for the frequency-domain motion response analysis. The 10 MW OWT was idealized as a six-degree-of-freedom body incorporating added mass, radiation damping, and hydrostatic restoring coefficients, while the tugboats were modeled as fixed points. The towlines were represented as linear spring elements, providing the constraint conditions that connect the tugboats to the OWT. This approach has the advantage of reasonably capturing the restraining effects of the towlines without explicitly modeling the dynamics of the tugboats themselves.
From the analysis, motion responses under irregular wave conditions were obtained, and the resulting towline tensions were calculated. The calculated tensions were then compared with the towline’s Safe Working Load (SWL) and the tugboats’ Effective Bollard Pull (BP
eff = 598 kN) to assess installation feasibility. Furthermore, in this study, the Minimum Breaking Load (MBL) of the towline was set to 1586 kN and conservatively evaluated by comparison with the Required Towline Breaking Load (RTBL) specified in DNV-ST-N001 [
17]. The RTBL is determined based on the bollard pull (BP) of the tugboat and is generally defined as 2.0 × BP in benign areas. In contrast, in other areas, up to 3.0 × BP may be required depending on the conditions, and more specifically, it is calculated as expressed in Equation (6).
The effective bollard pull (BPeff) of the tugboat fleet used in this study was estimated to be 598 kN. Accordingly, the Required Towline Breaking Load (RTBL) based on DNV standards is calculated as approximately 1195 kN in benign areas and about 1585 kN in other areas according to the empirical formulation given in Equation (6). The applied towline has a Minimum Breaking Load (MBL) of 1586 kN, which fully satisfies the benign condition and essentially meets the requirement for other areas. Therefore, the strength of the towline is confirmed to comply with the DNV standard.
Therefore, the final design verification is determined by the pulling force provided by the tugboats. Since the towline already satisfies the RTBL requirement, the design criterion of this study is to demonstrate that the towline tensions do not exceed the Effective Bollard Pull (BPeff = 598 kN). To this end, analyses were conducted for a total of 15 cases, combining the spudcan lowering stages (Step 1, Step 2, Step 3) with the environmental load directions (0°, 45°, 90°, 135°, and 180°). In each case, the calculated towline tension was checked to confirm that it remained within the BPeff limit.
If the calculated towline tension exceeds the BPeff in a particular case, the tugboat arrangement is deemed insufficient to ensure safety. In such cases, the tugboats are re-arranged, and the same procedure is repeated to secure safety. This iterative re-analysis procedure reflects the practical capability to flexibly adjust tugboat arrangements according to environmental load conditions and supports the feasibility of the proposed installation method.
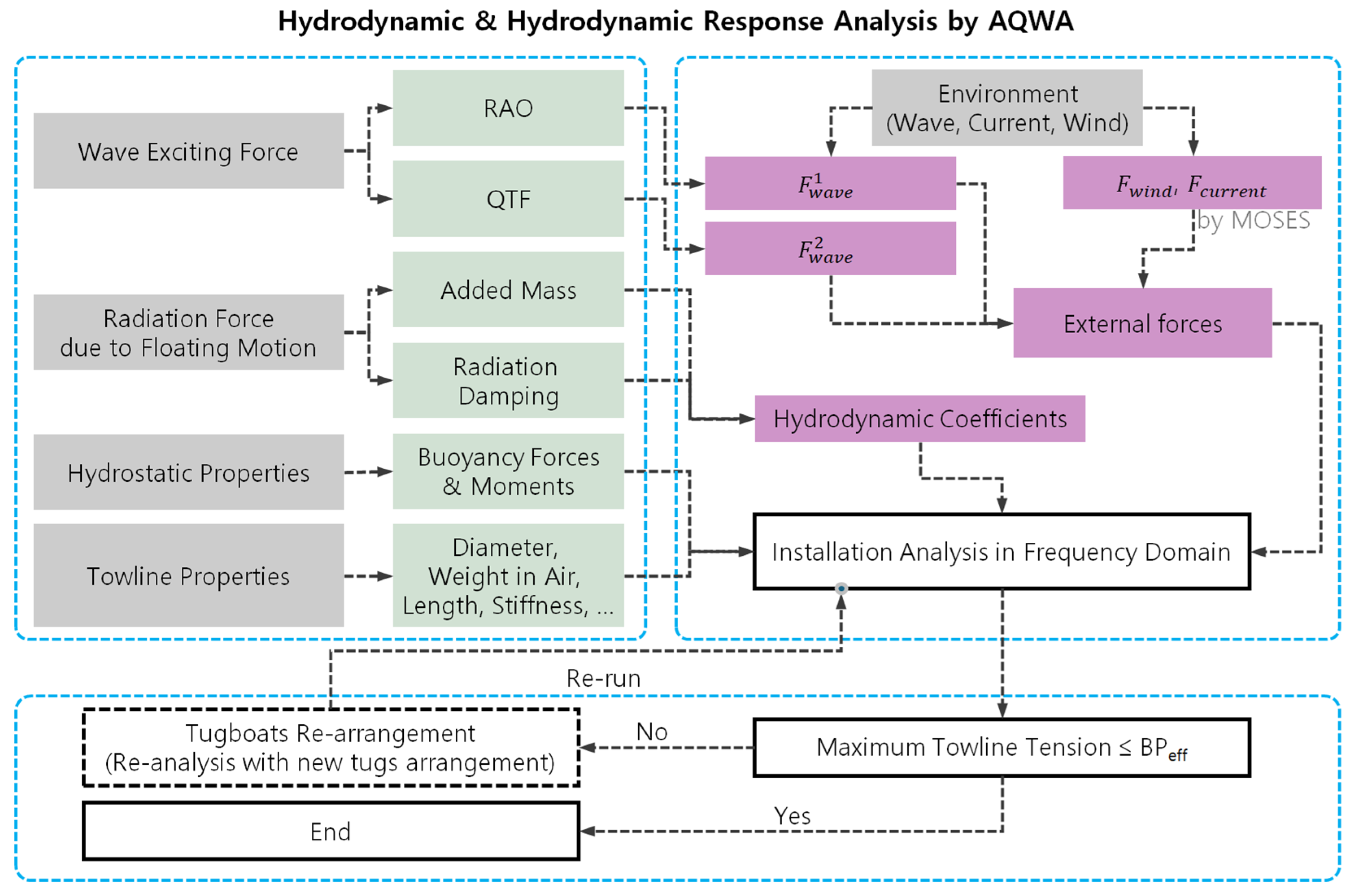
The analysis and verification procedure of this study is illustrated in
Figure 6, which stepwise presents the process from environmental load estimation to towline tension verification, and, if necessary, tugboat re-arrangement and iterative re-analysis.
4. Analysis Setup
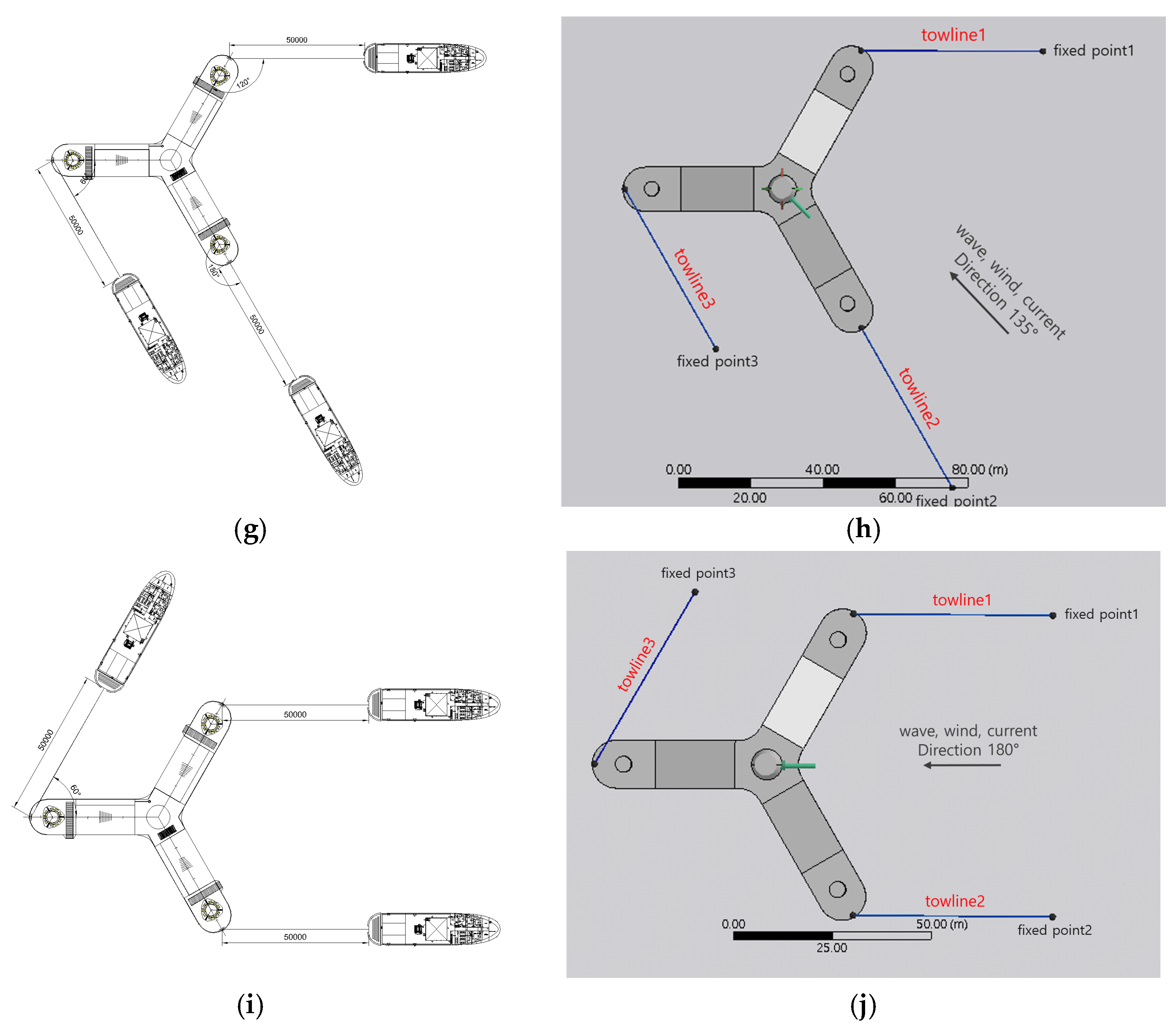
In this study, five environmental load directions (0°, 45°, 90°, 135°, and 180°) were considered to examine the tugboat arrangements and the behavior of the installation system. The tugboat arrangements and an overview of the analysis model for each direction are presented in
Figure 7. This configuration reflects the fact that waves, wind, and current can act from various directions in offshore conditions, and the five representative directions were analyzed to evaluate the tugboat positions and towline connections.
In the analysis coordinate system, the environmental load directions were defined as 0° along the +X-axis, 90° along the +Y-axis, 180° along the –X-axis, and 270° along the –Y-axis, and all environmental loads were applied according to this convention.
Figure 7 presents, for the five directions (0°, 45°, 90°, 135°, and 180°), the tugboat arrangement diagrams on the left and the corresponding analysis model overviews on the right.
5. Results
5.1. Step 1 Results (Spudcan Depth –5 m from BL)
Step 1 corresponds to the initial installation stage, in which the spudcans are lowered to –5 m from the baseline (BL) and the pontoon remains in a non-flooded condition. At this stage, the pontoon draft was calculated to be approximately 4.29 m. Owing to the characteristics of jack-up-type offshore structures, most of the legs are exposed above the water surface in this step, resulting in increased sensitivity to long-period environmental loads.
In addition, due to the relatively high vertical center of gravity (VCG) and limited restoring characteristics, the overall dynamic stability of the system is relatively less favorable in Step 1 compared with Step 2 and Step 3. For this reason, Step 1 is regarded as the most critical condition during the installation process and serves as an important reference stage for verifying the control performance of the tugboat fleet and the distribution of towline tensions.
From the irregular wave response analysis, the towline tensions were found to range between approximately 400 and 500 kN, with the maximum value of 547.4 kN occurring under the 45° environmental load direction. This corresponds to about 91.5% of the tugboat fleet’s Effective Bollard Pull (BPeff = 598 kN). As the calculated tensions in all cases did not exceed either the towline’s Safe Working Load (SWL) or the BPeff, it is confirmed that station-keeping can be achieved solely by the tugboats even in the Spudcan –5 m stage.
The detailed results for each direction are summarized in
Table 7. The 45° condition was identified as the most conservative scenario, while in the 0° condition, the towline tensions were relatively evenly distributed. In contrast, under the 180° condition, the tensions were concentrated on the two towlines aligned with the primary load direction, whereas the remaining towline carried almost no load, showing a distinctly uneven distribution.
These results indicate that, through the iterative re-analysis procedure described in
Section 3.4 and the tugboat re-arrangement, a final configuration ensuring safety was derived. This finding supports the applicability of the proposed anchor-free installation method under actual offshore environmental conditions.
5.2. Step 2 Results (Spudcan Depth –10 m from BL)
Step 2 corresponds to the partially flooded stage, in which the spudcans are lowered to –10 m from the baseline (BL). At this stage, seawater partially enters the pontoon, reducing buoyancy while lowering the vertical center of gravity (VCG) and thereby improving the metacentric height (GM). Consequently, compared with Step 1, the dynamic stability of the structure is enhanced, and the control margin of the tugboat fleet is expected to increase accordingly. Under this condition, the pontoon draft was calculated to be approximately 4.42 m.
From the irregular wave response analysis, as summarized in
Table 8, the towline tensions generally exhibited a more moderate distribution compared with Step 1, with the maximum tension calculated as 515.8 kN under the 45° environmental load condition. This corresponds to approximately 86.3% of the tugboat fleet’s Effective Bollard Pull (BP
eff = 598 kN), slightly lower than the maximum tension observed in Step 1 (547.4 kN, 91.5%). In particular, at 0° and 135° directions, the towline loads tended to be distributed more evenly, whereas under the 90° condition, all three towlines carried relatively high loads but still remained within the BP
eff limit. By contrast, under the 180° condition, similar to Step 1, the tensions were concentrated on two towlines while the remaining one was nearly unloaded (2.4 kN), clearly indicating directional dependence.
The maximum tensions of the three towlines were 457.9 kN (76.6% of BPeff), 515.8 kN (86.3% of BPeff), and 481.2 kN (80.5% of BPeff), respectively, and in all cases neither the towline’s SWL nor the tugboat fleet’s BPeff was exceeded. Therefore, it is confirmed that station-keeping can be achieved solely by the tugboat fleet under the Step 2 condition.
In conclusion, Step 2 represents a stage performed under improved stability due to the partial flooding effect, in which the disadvantages observed in Step 1 are alleviated. The results demonstrate that sufficient safety was secured under the final arrangement conditions derived through the iterative re-analysis procedure. This supports the applicability of the proposed anchor-free installation method as a stable approach even during the intermediate stages of installation.
5.3. Step 3 Results (Spudcan Depth −15 m from BL)
Step 3 corresponds to the fully flooded stage, in which the spudcans are lowered to –15 m from the baseline (BL) and the pontoon is completely filled with seawater. At this stage, buoyancy is significantly reduced and the vertical center of gravity (VCG) is further lowered. As a result, stability is markedly improved compared with the initial stage, and the structural responses to waves and wind are reduced, leading to a substantial enhancement in dynamic stability. Under this condition, the pontoon draft was calculated to be approximately 4.41 m.
From the irregular wave response analysis, as summarized in
Table 9, the towline tensions were generally lower in Step 3 compared with Step 1 and Step 2. The maximum tension was observed under the 45° condition at 519.7 kN, corresponding to approximately 86.9% of the Effective Bollard Pull (BP
eff = 598 kN). Under the 90° condition, the towline tensions were also relatively high (ranging from 450.4 to 477.8 kN), but remained safely within the BP
eff limit. In contrast, at 0° and 135° conditions, the towline tensions were distributed more evenly, while under the 180° condition, the tensions were concentrated on two towlines aligned with the primary load direction, with the remaining towline nearly unloaded (13.7 kN).
The maximum tensions of the three towlines were 450.4 kN (75.3% of BPeff), 519.7 kN (86.9% of BPeff), and 477.8 kN (79.9% of BPeff), respectively. In all cases, neither the towline’s Safe Working Load (SWL) nor the BPeff was exceeded, and compared with Step 1, the maximum tension decreased by approximately 27.7 kN, confirming that the control margin of the tugboat fleet was clearly secured.
In conclusion, Step 3 represents the stage in which the stabilizing effect of full flooding and the reduction in structural responses become evident, indicating that the control burden on the tugboat fleet is somewhat alleviated in the latter part of the installation process. However, as the legs are deeply submerged in this stage, the resistance induced by current increases, and thus, despite the improvement in stability, the towline tensions were found to remain within a range similar to that of Step 2.
These results indicate that the final arrangement conditions derived through the iterative re-analysis procedure ensure sufficient safety even during the final spudcan penetration stage, thereby providing further evidence to reinforce the feasibility of the proposed anchor-free installation method.
5.4. Summary of Results
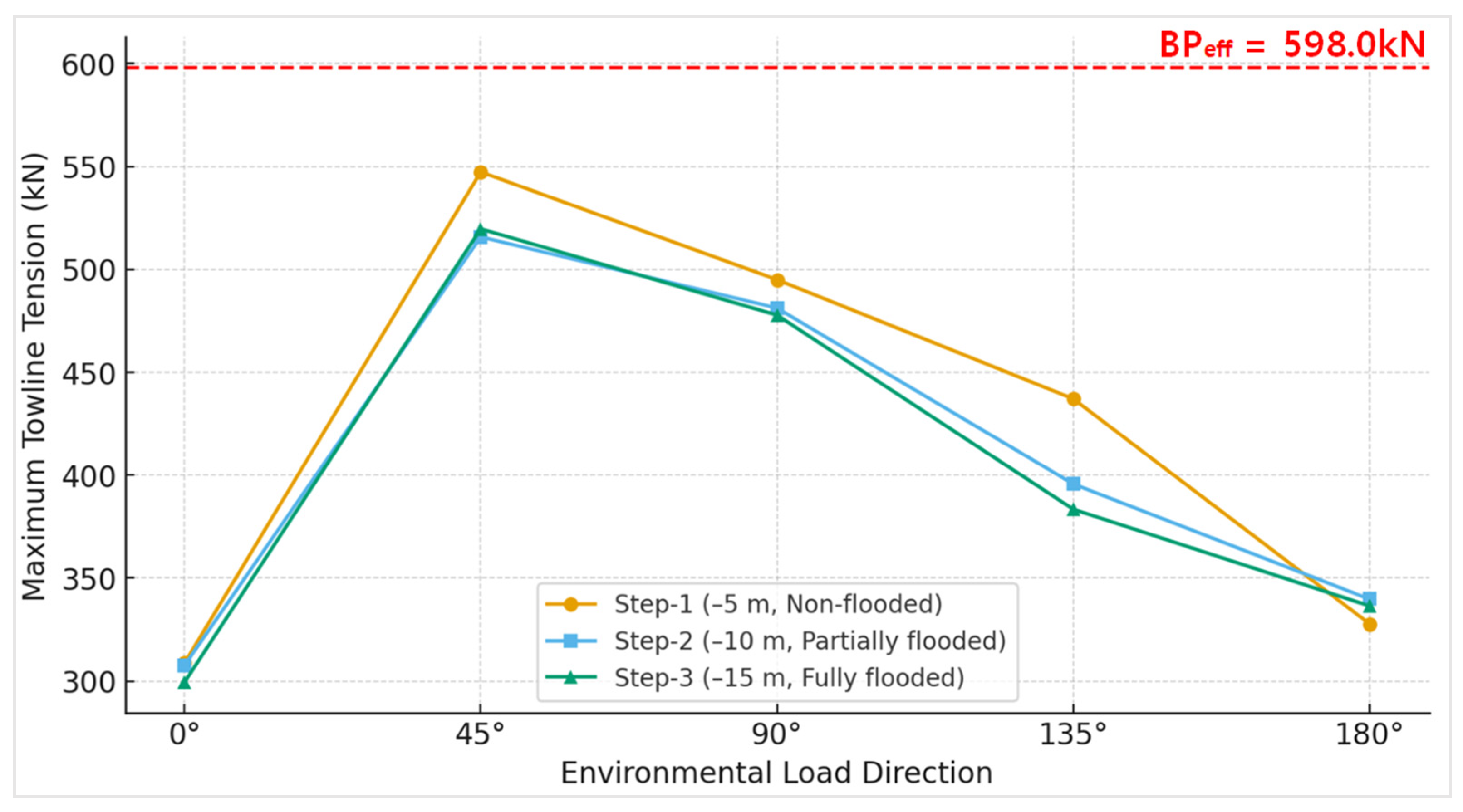
In this study, numerical analyses were performed for three stages corresponding to different spudcan penetration depths: Step 1 (–5 m, non-flooded), Step 2 (–10 m, partially flooded), and Step 3 (–15 m, fully flooded), and the results were compared and analyzed.
Figure 8 summarizes the maximum towline tensions for each stage with respect to the environmental load directions, with the BP
eff of the tugboat fleet (=598 kN) indicated as a reference.
In all stages and directions, the calculated maximum towline tensions did not exceed the BPeff, indicating that sufficient safety margins were secured. The most conservative condition occurred in Step 1 at the 45° direction, where the maximum tension reached 547.4 kN, corresponding to approximately 91.5% of the BPeff. In Step 2 and Step 3, the partial and full flooding effects of the pontoon enhanced stability, resulting in slightly lower maximum tensions of 515.8 kN and 519.7 kN, respectively, compared with Step 1. However, in Step 3, as the legs were deeply submerged, the resistance due to current increased, leading to overall tension levels remaining similar to those in Step 2.
These results demonstrate that the tugboat fleet can provide sufficient station-keeping capability throughout the entire spudcan penetration process and confirm that the final tugboat arrangement derived through the iterative re-analysis and tugboat re-arrangement procedures described in
Section 3.4 satisfies the design criteria under all OP
LIM conditions.
6. Discussion
This study focused on verifying the pulling capacity provided by the tugboat fleet during the installation process of a 10 MW jack-up-type OWT. In conventional mooring-based methods, structural drift and motions are typically suppressed by installing fixed devices such as winches, mooring lines, and anchors. In contrast, this study excluded such restraining devices and evaluated whether the pulling forces provided by the tugboat fleet could maintain the structure in an acceptable station-keeping condition without exceeding the Safe Working Load (SWL) of the towlines and the Effective Bollard Pull (BPeff) of the tugboats. The results numerically demonstrate that an anchor-free installation method relying solely on a tugboat fleet can be a feasible solution for ensuring station-keeping and operational safety.
Although actual installation operations are typically conducted under calm weather conditions, this study considered conservative OP
LIM conditions with α-factors applied to the weather-restricted limits. Nevertheless, in all analysis cases, the towline tensions did not exceed either the SWL or the BP
eff. This indicates that the proposed method satisfies the operational criteria for self-elevating platforms (SEPs) specified in international design codes (DNV-ST-N001 [
17], ISO 19901-6 [
18]) and demonstrates that additional safety margins can be secured for field applications.
Additionally, while this study focused on a water depth of approximately 20 m, the implications of extending the application to deeper waters, such as 40 m, are briefly discussed. An increase in leg length would raise the VCG and reduce the GM during the initial installation stage (Step 1), making the assurance of stability more critical at this stage. Furthermore, as the legs submerge, surface drag and added mass effects may increase, although the pontoon remains the dominant contributor to the overall submerged area. By adjusting the ballast to control the pontoon draft, these additional drag and added mass effects can be mitigated. Ultimately, it is essential to carefully evaluate the loading conditions, including ballast corresponding to the pontoon draft at each stage, to ensure that the station-keeping requirement of the tugboat fleet (based on BPeff) can be maintained without significant variation.
From the perspective of installation equipment, WTIV-based methods not only require the use of expensive vessels but also incur excessive mobilization and standby costs [
9]. In contrast, the anchor-free method proposed in this study relies solely on relatively low-cost tugboats and eliminates the need for mooring installation and removal, thereby offering a significant reduction in construction time. Based on the analysis conditions, the installation of a 10 MW OWT is expected to be completed within 24 h, providing distinct advantages in terms of both economic efficiency and constructability.
The proposed method can be completed within approximately 24 h (1 day) from load-out through launching, transportation, and installation, whereas WTIV-based methods require two separate continuous windows of at least 3 days each for substructure and superstructure installation, resulting in a total operation period of no less than 6 days. Accordingly, the required continuous window is reduced by about 83.3% [ (6 − 1)/6], and even when compared on a per-task basis (3-day blocks), the reduction is approximately 66.6% [(3 − 1)/3]. This difference substantially alleviates the burden of satisfying continuous OPLIM/OPWF conditions and serves as a key factor in enhancing practical applicability in regions with restricted weather windows.
In particular, in regions such as the West Sea and Jeju, where wave, wind, and current conditions are severe and the number of workable days is limited, the proposed method offers even greater potential benefits [
3]. Therefore, the proposed installation approach can be regarded as a practical alternative that improves the economic viability of offshore wind projects and contributes to the broader commercialization of large-scale OWTs.
7. Conclusions
The analysis revealed that the most conservative case occurred in Step 1 at the 45° direction, where the maximum tension reached 547.4 kN, corresponding to approximately 91.5% of the BPeff. In Step 2 and Step 3, the stability enhancement effect from partial and full flooding of the pontoon reduced the maximum tensions to 515.8 kN (86.3% of BPeff) and 519.7 kN (86.9% of BPeff), respectively, compared with Step 1. However, in Step 3, as the legs were deeply submerged, the resistance to current increased, resulting in tension levels remaining similar to those in Step 2. These results demonstrate that station-keeping can be achieved solely by the tugboat fleet at all stages and that the final arrangement derived through the iterative re-analysis and tugboat re-arrangement procedures satisfies the design criteria under all OPLIM conditions.
The proposed anchor-free installation method offers three distinct advantages compared with WTIV-based approaches: (i) reduced installation costs, (ii) shortened construction duration, and (iii) enhanced operational flexibility. In particular, unlike WTIVs and crane barges, tugboats are characterized by lower cost and higher availability, and the absence of mooring installation and removal procedures is favorable for reducing the overall installation time. Based on the analysis conditions, the installation of a jack-up-type 10 MW OWT is expected to be completed within 24 h, providing substantial competitiveness in regions such as the West Sea and Jeju, where weather windows are highly restricted.
In conclusion, the anchor-free installation method proposed in this study is evaluated as an innovative alternative that can overcome the limitations of conventional WTIV-based approaches. Future research should address the applicability to deeper waters, the quantification of uncertainties under diverse environmental conditions, and commercialization validation through full-scale field demonstrations. Through such follow-up studies, the proposed method is expected to evolve into a new standard for next-generation offshore wind turbine installations.
Author Contributions
Conceptualization, J.-H.K., J.Y.S.; methodology, M.H., J.-H.K.; software, A.R.K.; validation, Y.I.P., A.R.K.; formal analysis, M.H., A.R.K.; investigation, A.R.K.; resources, Y.I.P.; data curation, M.H.; writing—original draft preparation, M.H., J.-H.K.; writing—review and editing, Y.I.P., J.-H.K.; visualization, M.H.; supervision, Y.I.P.; project administration, J.Y.S.; funding acquisition, J.Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) grant funded by the Korean Government (MOTIE) (20223030020240, Development of 10MW or higher offshore wind power upper and lower package installation support structure system for LCOE reduction).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
Authors Min Han, A Ra Ko and Jin Young Sung are employed at KOMS Co., Ltd. All authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BL | Base Line (reference baseline at the bottom of pontoon) |
| BM | Metacentric Radius |
| BP | Bollard Pull |
| BPeff | Effective Bollard Pull |
| DNV | Det Norske Veritas |
| Dir | Wave /Load Direction (°) |
| GM | Metacentric Height |
| Hs | Significant Wave Height (m) |
| ISO | International Organization for Standardization |
| KB | Keel to Buoyancy Center |
| LCOE | Levelized Cost of Energy |
| MBL | Minimum Breaking Load |
| OPWF | Operating Weather Forecast Condition |
| OPLIM | Operational Limiting Condition |
| OWT | Offshore Wind Turbine |
| QTF | Quadratic Transfer Function |
| RAO | Response Amplitude Operator |
| RTBL | Required Towline Breaking Load |
| SEP | Self-Elevating Platform |
| SWL | Safety Working Load |
| Tp (s) | Peak Period (second) |
| VCG | Vertical Center of Gravity |
| WTIV | Wind Turbine Installation Vessel |
| γ (gamma) | Peakedness Factor, peak enhancement factor in JONSWAP wave spectrum |
References
- GWEC. Global Offshore Wind Report 2023; Global Wind Energy Council: Brussels, Belgium, 2023. [Google Scholar]
- Musial, W.; Beiter, P.; Spitsen, P.; Nunemaker, J.; Cooperman, A. Offshore Wind Energy Market Report: 2019 Edition; U.S. Department of Energy, Office of Energy Efficiency & Renewable Energy: Washington, DC, USA, 2019. [Google Scholar]
- Yang, K.; Kim, H. Installation Challenges in Korean Offshore Wind Farms. Ocean. Eng. 2020, 217, 107978. [Google Scholar]
- International Renewable Energy Agency (IRENA). Future of Wind: Deployment, Investment, Technology, Grid Integration and Socio-Economic Aspects (A Global Energy Transformation Paper); IRENA: Abu Dhabi, United Arab Emirates, 2022. [Google Scholar]
- Ramachandran, R.C.; Serraris, J.-J.; Hernandez Montfort, J.; de Ridder, E.-J.; Desmond, C.; Murphy, J. Towing Analysis and Validation of a Fully Assembled Floating Offshore Wind Turbine Based on an Experimental Study. J. Mar. Sci. Eng. 2024, 12, 689. [Google Scholar] [CrossRef]
- Wang, L.; Hu, Z.; Ye, L.; Chen, X.; Li, Y. A coupled numerical framework for hybrid floating offshore wind turbine and its validation via scale model tests. Energy 2022, 254, 124301. [Google Scholar]
- Gao, P.; Yuan, X.; Liu, S.; Lin, W.; Chen, M.; Wang, Z.; Tang, Y.; Jiang, X. Towing Resistance and Design of a Towing Scheme for a Floating Wind Turbine. J. Mar. Sci. Eng. 2025, 13, 789. [Google Scholar] [CrossRef]
- Roddier, D.; Cermelli, C.; Aubault, A.; Weinstein, A. WindFloat: A Floating Foundation for Offshore Wind Turbines. J. Renew. Sustain. Energy 2010, 2, 033104. [Google Scholar] [CrossRef]
- Myhr, A.; Bjerkseter, C.; Ågotnes, A.; Nygaard, T.A. Levelised Cost of Energy for Offshore Floating Wind Turbines in a Life Cycle Perspective. Renew. Energy 2014, 66, 714–728. [Google Scholar] [CrossRef]
- Chakrabarti, S. Hydrodynamics of Offshore Structures; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Randolph, M.F.; Gourvenec, S. Offshore Geotechnical Engineering, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Newman, J.N. Marine Hydrodynamics; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- ANSYS Inc. AQWA User Manual, version 2022 R2; ANSYS Inc.: Canonsburg, PA, USA, 2022. [Google Scholar]
- Bentley Systems. MOSES User Manual; Bentley Offshore: Exton, PA, USA, 2022. [Google Scholar]
- American Bureau of Shipping (ABS). Rules for Building and Classing: Floating Offshore Installations at a Fixed Location; ABS: Houston, TX, USA, 2020. [Google Scholar]
- Morison, J.R.; O’Brien, M.P.; Johnson, J.W.; Schaaf, S.A. The Force Exerted by Surface Waves on Piles. Pet. Trans. AIME 1950, 189, 149–157. [Google Scholar] [CrossRef]
- DNV-ST-N001; Marine Operations and Marine Warranty. DNV: Bærum, Norway, 2023.
- ISO 19901-6:2020; Petroleum and Natural Gas Industries–Marine Operations. ISO: Geneva, Switzerland, 2020.
Figure 1.
Configuration of the jack-up-type 10 MW OWT: (a) side view, (b) perspective view.
Figure 1.
Configuration of the jack-up-type 10 MW OWT: (a) side view, (b) perspective view.
Figure 2.
Conceptual installation sequence of the anchor-free jack-up-type 10 MW OWT: (a) loadout and float-off, (b) towing to the site, (c) leg lowering and spudcan penetration, and (d) jacking-up and preloading.
Figure 2.
Conceptual installation sequence of the anchor-free jack-up-type 10 MW OWT: (a) loadout and float-off, (b) towing to the site, (c) leg lowering and spudcan penetration, and (d) jacking-up and preloading.
Figure 3.
AQWA numerical model for the jack-up-type 10MW OWT with towline and fixed-point connections: (a) hydrodynamic mesh & wave elevation result, (b) tugboat arrangement for the case of 0° environmental load direction, (c) 3D model including bollard–towline–fixed point connections, (d) plan view of the towline configuration.
Figure 3.
AQWA numerical model for the jack-up-type 10MW OWT with towline and fixed-point connections: (a) hydrodynamic mesh & wave elevation result, (b) tugboat arrangement for the case of 0° environmental load direction, (c) 3D model including bollard–towline–fixed point connections, (d) plan view of the towline configuration.
Figure 4.
Spudcan positions of the 10 MW OWT by installation steps: (a) Step 1 (Draft 4.29 m, depth –5 m from BL), (b) Step 2 (Draft 4.42 m, depth –10 m from BL), (c) Step 3 (Draft 4.41 m, depth –15 m from BL). BL denotes the pontoon bottom (z = 0), and the seabed level is –20 m from MSL.
Figure 4.
Spudcan positions of the 10 MW OWT by installation steps: (a) Step 1 (Draft 4.29 m, depth –5 m from BL), (b) Step 2 (Draft 4.42 m, depth –10 m from BL), (c) Step 3 (Draft 4.41 m, depth –15 m from BL). BL denotes the pontoon bottom (z = 0), and the seabed level is –20 m from MSL.
Figure 5.
Tugboat arrangement for the proposed anchor-free installation method: (a) transportation stage with symmetric bow and stern arrangement, (b) installation stage under 90° environmental loads showing dynamic repositioning of tugboats.
Figure 5.
Tugboat arrangement for the proposed anchor-free installation method: (a) transportation stage with symmetric bow and stern arrangement, (b) installation stage under 90° environmental loads showing dynamic repositioning of tugboats.
Figure 6.
Verification procedure for the proposed anchor-free installation method.
Figure 6.
Verification procedure for the proposed anchor-free installation method.
Figure 7.
Tugboat arrangements (left) and analysis model schematics (right) under five environmental load directions: (a,b) 0°, (c,d) 45°, (e,f) 90°, (g,h) 135°, (i,j) 180°.
Figure 7.
Tugboat arrangements (left) and analysis model schematics (right) under five environmental load directions: (a,b) 0°, (c,d) 45°, (e,f) 90°, (g,h) 135°, (i,j) 180°.
Figure 8.
Maximum towline tensions under different environmental load directions for Step 1, Step 2, and Step 3, with the effective bollard pull (BPeff = 598 kN) indicated as a reference.
Figure 8.
Maximum towline tensions under different environmental load directions for Step 1, Step 2, and Step 3, with the effective bollard pull (BPeff = 598 kN) indicated as a reference.
Table 1.
Main particulars of the jack-up-type 10MW OWT.
Table 1.
Main particulars of the jack-up-type 10MW OWT.
| Turbine (DTU) | Total Length (m) | Leg Length (m) | Body Arm Length (m) | Body Height (m) | Body Breadth (m) | Towing Draft (m) |
|---|
| 10 MW | 69.1 | Φ4.0 × 60.5 | 36.0 | 10.5 | 12.0 | 4.29 |
Table 2.
Properties of towline used in the numerical model.
Table 2.
Properties of towline used in the numerical model.
| Type | Length (m) | Diameter (mm) | Area (m2) | Weight in Air (kg/m) | Axial Stiffness (kN) | MBL (kN) |
|---|
| Wire | 50 | 50 | 0.0012566 | 9.97 | 101,000 | 1586 |
Table 3.
Environmental conditions for operating (OPWF) and design (OPLIM) cases.
Table 3.
Environmental conditions for operating (OPWF) and design (OPLIM) cases.
| Criteria | Wave Height (Hs) (m) | Wind Speed (m/s) | Current Speed (m/s) | Remarks |
|---|
| OPWF | 0.6 | 7.0 | 1.03 | Operating Weather Forecast Condition |
| OPLIM | 1.0 (α = 0.59) | 10.0 (α = 0.71) | 1.03 | Operational Limiting Condition (Design Condition) |
Table 4.
Principal particulars of the 10 MW OWT by spudcan lowering steps.
Table 4.
Principal particulars of the 10 MW OWT by spudcan lowering steps.
| Items | Step 1 | Step 2 | Step 3 |
|---|
| Spudcan Depth from BL (m) | −5.0 | −10.0 | −15.0 |
| Draft (m) | 4.29 | 4.42 | 4.41 |
| Displacement (t) | 6606 | 6606 | 6606 |
| KB (m) | 2.05 | 2.10 | 2.03 |
| BM (m) | 73.02 | 72.98 | 73.03 |
| VCG (m) | 24.04 | 23.25 | 22.46 |
| GM (m) | 51.03 | 51.83 | 52.60 |
| Kxx (m) | 38.62 | 38.63 | 38.71 |
| Kyy (m) | 38.41 | 38.43 | 38.51 |
| Kzz (m) | 23.29 | 23.29 | 23.29 |
| Leg Status | Non-flooded | Partially Flooded | Fully Flooded |
Table 5.
Analysis conditions (total 15 cases).
Table 5.
Analysis conditions (total 15 cases).
| Step | Analysis No. | Direction | Hs (m) | Tp (s) | Wind (m/s) | Current (m/s) |
|---|
| Step 1 | 1–5 | 0° to 180° at 45° intervals | 1.0 | 7.0 | 10.0 | 1.03 |
| Step 2 | 6–10 | 1.0 | 7.0 | 10.0 | 1.03 |
| Step 3 | 11–15 | 1.0 | 7.0 | 10.0 | 1.03 |
Table 6.
Tugboat particulars and effective Bollard Pull (BPeff).
Table 6.
Tugboat particulars and effective Bollard Pull (BPeff).
| Engine (PS) | LOA (m) | Breadth (m) | Depth (m) | BP (kN) | Tug Efficiency (%) | BPeff (kN) |
|---|
| 6000 | 41.00 | 10.60 | 4.80 | 747 | 80 | 598 |
Table 7.
Towline tensions and comparison with BPeff for Step 1 condition.
Table 7.
Towline tensions and comparison with BPeff for Step 1 condition.
| Step | Analysis No. | Hs (m) | Tp (s) | Dir (°) | Tension (kN) |
|---|
| Towline 1 | Towline 2 | Towline 3 |
|---|
| Step 1 | 1 | 1.0 | 7.0 | 0 | 202.2 | 202.2 | 308.6 |
| 2 | 1.0 | 7.0 | 45 | 131.0 | 547.4 | 168.2 |
| 3 | 1.0 | 7.0 | 90 | 495.0 | 421.8 | 490.9 |
| 4 | 1.0 | 7.0 | 135 | 437.1 | 294.3 | 304.4 |
| 5 | 1.0 | 7.0 | 180 | 327.7 | 326.1 | 14.4 |
| Maximum Tension (kN) | 495.0 | 547.4 | 490.9 |
| BPeff (kN) | 598.0 | 598.0 | 598.0 |
| % of BPeff | 82.78% | 91.54% | 82.09% |
| Check | OK | OK | OK |
Table 8.
Towline tensions and comparison with BPeff for Step 2 condition.
Table 8.
Towline tensions and comparison with BPeff for Step 2 condition.
| Step | Analysis No. | Hs (m) | Tp (s) | Dir (°) | Tension (kN) |
|---|
| Towline 1 | Towline 2 | Towline 3 |
|---|
| Step 2 | 6 | 1.0 | 7.0 | 0 | 200.8 | 200.8 | 307.5 |
| 7 | 1.0 | 7.0 | 45 | 176.8 | 515.8 | 236.3 |
| 8 | 1.0 | 7.0 | 90 | 457.9 | 436.9 | 481.2 |
| 9 | 1.0 | 7.0 | 135 | 395.7 | 265.6 | 219.0 |
| 10 | 1.0 | 7.0 | 180 | 339.5 | 339.7 | 2.4 |
| Maximum Tension (kN) | 457.9 | 515.8 | 481.2 |
| BPeff (kN) | 598.0 | 598.0 | 598.0 |
| % of BPeff | 76.57% | 86.25% | 80.47% |
| Check | OK | OK | OK |
Table 9.
Towline tensions and comparison with BPeff for Step 3 condition.
Table 9.
Towline tensions and comparison with BPeff for Step 3 condition.
| Step | Analysis No. | Hs (m) | Tp (s) | Dir (°) | Tension (kN) |
|---|
| Towline 1 | Towline 2 | Towline 3 |
|---|
| Step 3 | 11 | 1.0 | 7.0 | 0 | 195.1 | 195.1 | 299.3 |
| 12 | 1.0 | 7.0 | 45 | 187.6 | 519.7 | 240.7 |
| 13 | 1.0 | 7.0 | 90 | 450.4 | 440.3 | 477.8 |
| 14 | 1.0 | 7.0 | 135 | 383.4 | 258.1 | 212.6 |
| 15 | 1.0 | 7.0 | 180 | 335.8 | 336.4 | 13.7 |
| Maximum Tension (kN) | 450.4 | 519.7 | 477.8 |
| BPeff (kN) | 598.0 | 598.0 | 598.0 |
| % of BPeff | 75.23% | 86.89% | 79.83% |
| Check | OK | OK | OK |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).