Abstract
Pile-anchor foundations, serving as one of the anchoring solutions to ensure the safety and stability of floating offshore wind turbines, are primarily subjected to inclined loading induced by anchor chain forces, resulting in significantly different bearing behavior compared to conventional vertically loaded pile foundations. However, experimental research on the inclined pullout performance of anchor piles remains insufficient. To address this gap, this study employs a self-developed servo-controlled loading system to investigate the pullout bearing characteristics of anchor piles in dry and saturated sand, considering factors such as pullout angle and loading point depth. The research results show that from the load–displacement curve of the model pile, it can be found that with the increase in displacement, the load it bears first gradually increases to the peak, then decreases, and then gradually stabilizes. The loading angle has a significant impact on the bearing performance of pile-anchor foundations. As the loading angle increases, the failure mode shows pullout failure. When the loading angle increases from 30° to 60°, the bearing performance of the pile foundation decreases by approximately 63%. When the depth of the loading point increases from 0.22 times the pile length to 0.78 times the pile length, the diagonal anchor tensile bearing capacity of the model pile increases by approximately 45%. When the depth of the loading point is the same, the distribution patterns of bending moment and shear force are basically similar. However, the smaller the loading angle, the larger the value. This is because the horizontal load component plays a dominant role. The compression of the piles above and below the loading point, as well as the bending moment, shear force and axial force under saturated sand conditions, are similar to those in dry sand, but their values are reduced by about 50%. It can be seen that the soil conditions have an influence on the bearing characteristics of pile foundations.
1. Introduction
The pile-anchor foundation is a critical component ensuring the stability and reliability of floating wind turbines. In practical engineering applications, the elevation of the anchor chain connection point serves as a key design parameter, significantly influencing the structural response and stability of the foundation. Variations in the connection point location directly affect the loading point elevation, which in turn induces substantial changes in the ultimate bearing capacity and soil failure mechanisms of the pile-anchor foundations. Similarly, differing loading angles profoundly impact both the ultimate bearing capacity and foundation failure modes. For fixed-bottom wind turbine foundations, pile design conventionally considers horizontal, vertical, and moment loads applied at the pile head for bearing capacity analysis [1,2,3,4]. In contrast, floating wind turbine applications lack established design precedents for pile-anchor foundations, with current practices primarily drawing from successful implementations in offshore oil and gas platform anchor systems. The anchor chains and the anchor piles are usually connected at a certain depth below the top of the pile, which makes the force characteristics of the pile-anchor foundations quite different from those of the traditional pile top loading force characteristics [5,6,7,8,9]. Consequently, investigating the bearing behavior of model pile foundations under inclined loading—considering varying pullout angles, loading point elevations, and sand conditions (both dry and saturated)—holds significant engineering importance, and we use a self-developed servo electric cylinder loading device to conduct research on them. After extensive research, we have found that the bearing characteristics of rigid pile-anchor foundations are largely similar to those of the widely studied suction anchor foundations, and the research has become relatively mature. Therefore, this paper focuses on flexible pile-anchor foundations.
Uplift resistance plays a critical role in the bearing behavior of pile foundations, prompting extensive research by scholars [10,11,12,13,14]. Moayedi et al. [15] performed finite element modeling (FEM) to evaluate soil particle movement within a glass box during pile uplift displacement. Their results demonstrate that increasing the number of wings does not invariably enhance pile uplift resistance. Regarding pile groups, Nasr et al. [16], Faizi et al. [17], and Galvis-Castro et al. [18] performed theoretical and experimental studies on single piles and pile groups embedded in sand, investigating the influence of parameters such as pile cross-sectional shape, pile diameter, sand relative density, embedment ratio, and spacing-to-diameter ratio on uplift capacity. Building upon this foundation, Emirler et al. [19] examined the failure mechanisms of pile groups and pile-soil-pile interactions under varying pile cross-sectional shapes, embedment ratios, and spacing-to-diameter ratios.
However, neglecting the horizontal load component poses significant safety risks to foundations, making laboratory model tests investigating pile bearing behavior and failure modes under inclined loading a well-established research focus [20,21,22]. Wang et al. [23] conducted model tests on rock-socketed piles under combined axial-inclined loading, revealing that uplift resistance under inclined loading is significantly lower than under vertical loading, with load–displacement curves exhibiting brittle failure. During inclined tensile loading, soil adjacent to the loaded side remains compressed while the opposite side experiences tension. At ultimate limit state, failure consistently initiates in the soil zone on the loaded side, manifesting as a fan-shaped failure surface at ground level that expands with increasing loading angle, though ultimate bearing capacity decreases [24]. To better predict soil deformation around piles, Li et al. [25,26,27] proposed an energy-based variational method for large-diameter deep foundations (caissons or monopiles) under lateral loading. Huang et al. [28], Santiago et al. [29], and Fu et al. [30] analyzed pile response under inclined loading through centrifuge modeling, while Singh et al. [31], Johnson et al. [32], and Ran et al. [33] performed numerical analyses of bearing characteristics under such conditions. The aforementioned research mainly focuses on the influence characteristics of the horizontal component on pile-soil interaction and the failure modes when oblique loading is applied at the pile top. It provides research accumulation and references for understanding the pile-soil interaction and deformation characteristics under cable-stayed loads. However, whether this research conclusion is applicable when the loading point is located at a certain depth of the pile shaft is not only open to debate but also of great significance.
In the aforementioned studies, loading was applied at the pile head. However, for anchor piles, anchor chains are always connected along the pile shaft to provide enhanced tensile resistance. Ramadan et al. [34] employed centrifuge testing to investigate the mechanical behavior of offshore anchor piles under anchor forces in dense saturated sand. Gui et al. [35] conducted laboratory tests to examine the effects of loading angle, pile diameter, embedment depth, and pile type on the tensile bearing behavior of anchor piles in clay. Luo et al. [36] performed a series of centrifuge model tests on anchor piles under inclined pullout loading, revealing that failure consistently initiates in the loaded-side soil zone at ultimate limit state, manifesting as a fan-shaped failure surface at ground level. As the loading angle increases, horizontal translation of the pile and soil deformation become more pronounced, while tensile bearing capacity improves.
Although the above research has conducted a relatively in-depth discussion on the influence of different loading angles, burial depths, pile diameters and other factors on anchor piles, there are relatively few explorations on the influence of different loading point positions and different sand and soil conditions. Therefore, it is of great significance to study the influence of different loading point positions and different loading angles on the bearing characteristics of flexible pile-anchor foundations in dry and saturated sand. The research results of Sheikhtaheri et al. [37] and Al-Khazaali [38] show that the bearing characteristics of a single pile in saturated sand are the lowest, indicating that the bearing characteristics of the pile decrease with the increase in saturation, which is consistent with the law found in this paper.
Unlike conventional jack or weight loading methods, this study employs a self-developed servo-controlled loading system to investigate the effects of inclined loading angles, loading depths, and sand conditions on the bearing performance of pile-anchor foundations. For the pile-anchor foundations with floating wind turbines as the background, unlike the traditional pile foundation which is loaded at the top of the pile, this study sets up four anchor points at the pile body position for inclined tension loading, simulating the loading characteristics of the pile-anchor foundations in sandy soil under the inclined tension of the anchor chain, and revealing the force mode and failure mechanism at different anchor points. Analyze the differences in the bearing characteristics of single-pile models under different sandy soil conditions.
2. Model Test on Single Pile
2.1. Measurement of Sea Sand Parameters
The sand medium utilized in this experiment originated from a primary marine sand deposit at 50–100 m water depth in an offshore area near Qingdao. Following extraction, the sand underwent sequential pretreatment processes—including high-temperature drying, deionized water rinsing, and graded sieving—to prepare test specimens. Initial dry density (ρ = 1.54 g/cm3) was determined via the ring knife method (GB/T 50123-2019), while maximum and minimum dry densities (ρmax = 1.62 g/cm3; ρmin = 1.46 g/cm3) were established using the graduated cylinder method with vibratory compaction. Relative density Dr = [(ρ − ρmin)/(ρmax − ρmin)] × 100% = 52% classifies the sand as medium dense (40% < Dr ≤ 70%) per GB50021-2001. Triaxial shear tests yielded shear strength parameters of c = 0 kPa, φ = 41.5° for dry sand and c = 0 kPa, φ = 39.3° for saturated sand.
To determine gradation parameters of the sea sand specimen, a measured mass of dried sand was poured into the top sieve and sieved until the passing rate per minute fell below 1% of the retained mass on that sieve. This process yielded eight distinct particle fractions as shown in Figure 1. The retained mass on each sieve and the pan fraction were then weighed. By comparing the cumulative retained mass against the initial specimen mass, the particle size distribution curve was plotted and presented in Figure 2.

Figure 1.
Screening diagram of sea sand.
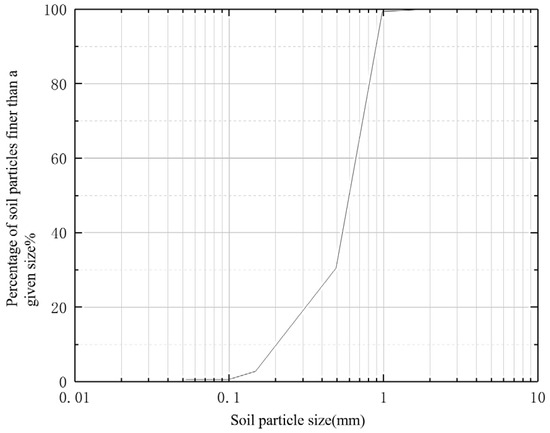
Figure 2.
Gradation curve of sea sand particles.
The particle size distribution curve further yielded gradation parameters for the marine sand specimen, as summarized in Table 1. The sand particles predominantly ranged from 0.5 to 0.9 mm, with a uniformity coefficient Cu = 1.44 indicating poorly graded characteristics, and a curvature coefficient Cv = 1.59 classifying it as poorly graded soil per geotechnical standards.

Table 1.
Relevant gradation parameters of sea sand.
2.2. Experimental Apparatus
As illustrated in Figure 3, the inclined tensile loading test was conducted within a custom-designed model container measuring 1000 mm (length) × 700 mm (width) × 1000 mm (height), with a test sand height of 500 mm. Inclined tensile loading was applied using a self-developed long-stroke, high-capacity servo actuator system capable of generating maximum push/pull forces of 50 kN with a displacement range of 15 cm. The inclined loading was achieved by controlling the extension and retraction of the servo actuator, enabling displacement-controlled inclined tensile loading. The loading speed of the servo electric cylinder is controlled at 0.02 mm/s. The minimum distance between the model pile and the boundary of the model box is 10 cm, which is approximately 8 times the pile diameter.
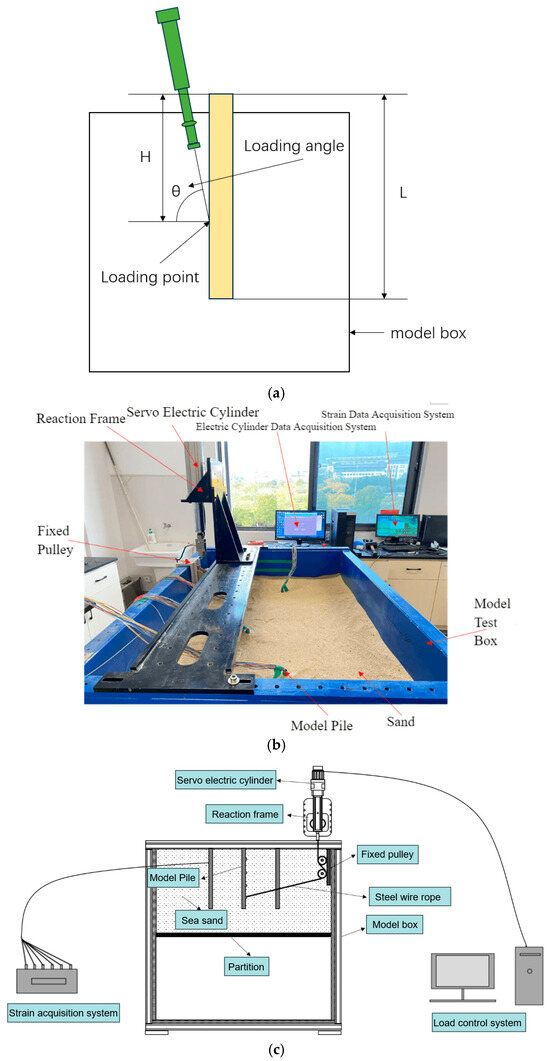
Figure 3.
Loading diagram (a) Schematic diagram of loading angle; (b) Experimental setup photo; (c) Schematic diagram of the loading device.
2.3. Model Experiment Scheme
The experiment comprised 12 test groups under dry sand conditions and 3 test groups under saturated sand conditions, with specific test cases detailed in Table 2 below.

Table 2.
Inclined pullout test matrix of model piles. (Pile Diameter D = 1.2 cm, Pile Length L = 32 cm, Wall Thickness t = 0.6 mm).
2.4. Test Procedure
The specific test steps are as follows: Strain gauges are pasted at the predetermined positions of the model piles. The wires are drilled through the pile body and led out from the top of the pile, and marked for subsequent data processing. The perforation operation should start from a small hole near the bottom of the pile to avoid the pile diameter being too small and hindering the wire extraction. At the predetermined loading depth position, pass the steel wire rope through the pile hole, fix it with an aluminum sleeve and act as a pin to secure it. This aluminum sleeve–steel wire rope combination simulates the anchor system of actual engineering. Then, place the model piles into the model box at different loading depths. When the loading Angle is 30°, the steel wire rope is connected to the electric cylinder joint by passing over the fixed pulley at the set Angle, and the height and position of the pile body are adjusted to meet the 30° requirement. When the loading angles are 45° and 60°, the electric cylinder and the reaction frame are used for inclined pulling loading, and the steel wire rope is directly connected to the servo electric cylinder connection head. Then adjust the height and planar position of the model pile at a fixed Angle. After all the positions are determined, connect the strain gauge sensor of the pile body to the strain acquisition instrument. Finally, complete the layering and sand spreading. The total soil layer height was 50 cm, and it was filled in five times. Before the stratified laying, the relative density Dr of the sea sand was measured to be 52%. As shown in Figure 4a, before layered placement, the relative density Dr of the marine sand was measured to be 52%. The calculated mass of each layer was accurately measured using weighing equipment; as shown in Figure 4b, under the premise of ensuring the same mass, each layer of sand was slowly and evenly poured into the model box using a bucket; as shown in Figure 4c, after pouring each layer of sand, the surface was leveled with a mortar trowel, and the side walls of the model box were tapped with a rubber hammer for correction to ensure the uniformity of each 10 cm layer; as shown in Figure 4d, after completing the sand placement, the test was started after standing for 24 h.

Figure 4.
Diagram of the process of layered paving of sea sand.
For saturated sand, after completing the above operations, we use a water pipe to evenly inject water along the side wall of the model box. We stop injecting water and let it stand for one day to ensure that the sand is fully saturated when all the air bubbles inside the sea sand are expelled and the water level is higher than the height of the sea sand sample (Figure 4e).
3. Analysis of Bearing Characteristics of Pile-Anchor Foundations
3.1. Inclined Loading Test on Single-Pile Model
The inclined tensile loading tests for pile-anchor foundations focused on loading angles and depths as primary variables, with model tests configured at three angles (θ = 30°, 45°, and 60°, defined as the inclination between the steel wire rope and the horizontal plane of the sand foundation) and four loading depths per angle (H = 0.22L, 0.41L, 0.59L, and 0.78L). Given the complexity of shaft-loaded pile experiments and scarce reference data, multiple identical aluminum tube model piles (diameter D = 1.2 cm, length L = 32 cm, wall thickness t = 0.06 cm) were fabricated for batch testing across these parametric combinations.
To ensure the consistency of the soil layer, batch inclined tensile loading tests were conducted on model piles, guaranteeing equal volume and mass for each soil layer according to the layered filling method. Inclined tensile loading tests on single-pile models under dry sand conditions were carried out in three batches. The first batch featured a loading angle of 30°, with four model piles loaded at different depths: H = 0.22L, H = 0.41L, H = 0.59L, and H = 0.78L. The steel wire rope was tensioned via fixed pulleys, and its angle was measured using an electronic inclinometer. The planar position of the model pile relative to the marine sand foundation soil was continuously adjusted until the angle reached approximately 30°. The actuator was then adjusted to 90° and positioned directly above the fixed pulley. The steel wire rope was connected to the actuator connector and clamped securely with aluminum sleeves. Finally, marine sand was placed using the layered filling method. After curing, the pile body strain gauge sensors were connected to the strain acquisition instrument. The instrument was used to conduct resistance testing on the strain gauges. After confirming no errors, the strain acquisition system and actuator loading system were debugged and prepared. Loading and data acquisition commenced after debugging completion. The second and third batches featured loading angles of 45° and 60°, respectively, with the steel wire rope directly connected and tensioned to the servo actuator. The loading angle was measured using the electronic inclinometer, and the planar positions of the model pile, reaction frame backplate, and transverse plate were continuously adjusted to satisfy the requirements for angular loading and boundary conditions. Finally, similarly, marine sand was placed using the layered filling method. After curing, the pile body strain gauge sensors were connected to the strain acquisition instrument. The instrument was used to conduct resistance testing on the strain gauges. After confirming no errors, the strain acquisition system and actuator loading system were debugged and prepared. Loading and data acquisition commenced after debugging completion.
For saturated sand condition tests on single-pile models, three piles at different angles were tested simultaneously in one batch. The first pile was loaded at 30°: the steel wire rope was tensioned via fixed pulleys for load direction change, with its angle measured by an electronic inclinometer. The planar position of the pile relative to the marine sand foundation soil was continuously adjusted until reaching around 30°, thus finalizing its position. The second and third piles were loaded at 45° and 60°, respectively, requiring continuous adjustments to the positions of the piles, reaction frame backplates, and transverse plates to achieve target angles. After positioning all piles, layered placement of marine sand commenced. Post-placement curing was followed by uniform water injection along the container walls using a water pipe. Watering ceased when all air bubbles were expelled from the sand and the water level exceeded the sand surface elevation, after which the system cured for 24 h. Finally, pile strain gauges were connected to the acquisition instrument, resistance was verified, the strain acquisition and actuator systems were synchronized, and loading with data collection proceeded post-calibration.
For single-pile model testing under saturated sand conditions, three piles at different loading angles were completed simultaneously in one batch. The first model pile was loaded at 30°: the steel wire rope was redirected via fixed pulleys and tensioned, with its angle measured using an electronic inclinometer. The planar position of the pile relative to the marine sand foundation soil was continuously adjusted until reaching ≈30°, thus finalizing its position. The second and third piles were loaded at 45° and 60°, respectively, requiring continuous adjustments to the positions of the model piles, reaction frame backplates, and transverse plates to achieve the target loading angles. After positioning all piles, layered placement of marine sand was performed. Following placement, the system underwent curing, after which uniform water injection was applied along the container walls via water pipe until all air bubbles were expelled from the sand and the water level exceeded the sand surface elevation. Watering was then ceased for a 24 h equilibration period. Finally, pile strain gauges were connected to the strain acquisition instrument, resistance was verified, the strain acquisition system and actuator loading system were debugged and synchronized, and loading with data collection commenced post-calibration.
The load–displacement curves, representing the resultant forces and displacements at the loading points, were recorded in real-time by the servo actuator acquisition system. The internal force distribution within the model piles was obtained through real-time strain measurements at designated pile locations via the strain acquisition system. The detailed experimental workflow is illustrated in Figure 5 and Figure 6 below.

Figure 5.
Physical diagram of dry sand model pile test. (a) Angle measurement. (b) Before loading the model pile. (c) After loading the model pile.

Figure 6.
Physical diagram of saturated sand model pile test. (a) Angle measurement. (b) After loading the model pile. (c) After loading the model pile.
3.2. Load–Displacement Curve of Pile-Anchor Foundations
3.2.1. Load–Displacement Curve of Pile-Anchor Foundations in Dry Sand Condition
The pile-anchor foundations had an embedment depth of 32 cm, with loading angles of 30°, 45°, and 60°, and loading depths at H = 0.22L, H = 0.41L, H = 0.59L, and H = 0.78L. Displacement-controlled loading was applied to the model piles by setting an initial minimal actuator displacement to reserve retraction margin for capturing the complete failure process. During loading, the load values were measured by a load cell at the servo actuator connection while displacements at the pile loading point were equated to actuator displacement due to kinematic consistency. The resulting load–displacement curves for model piles in dry sand are presented in Figure 7 below.
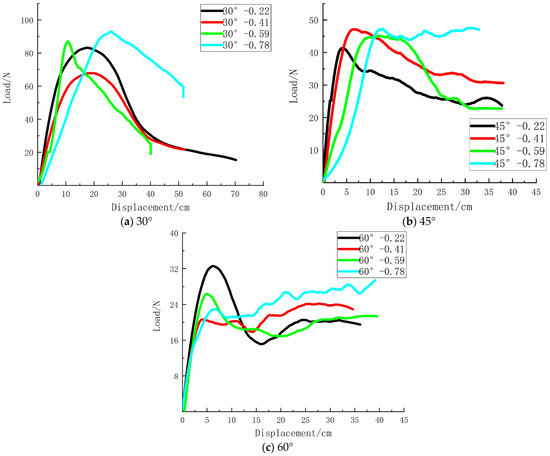
Figure 7.
Load displacement curve.
Analysis of the load–displacement curves in Figure 7 across varying loading depths and angles reveals the following behavioral patterns:
(1) From Figure 7 as a whole, it can be observed that when the model piles undergo cable-stayed loading at the pile shaft position in the marine sand foundation, as the loading depth continues to increase, the slope of the load–displacement curve gradually decreases. All model piles reach the peak bearing capacity within a certain period of time, followed by a decline segment, and after the decline segment, the curve gradually tends to stabilize. The phenomenon may be attributed to the fact that the marine sand foundation is relatively loose, causing the model piles to exhibit a certain amount of rotation during the loading process. The end of this rotation corresponds to the residual strength in the latter stage of the bearing capacity, which is a distinct characteristic that distinguishes this loading method from traditional jack or weight loading. Qpeak and Qres of the model pile are shown in Table 3.

Table 3.
Qpeak and Qres of the model pile under dry sand conditions.
(2) It is not difficult to see from Figure 7 that when the loading angle is 30°, the ultimate bearing capacity of all model piles is relatively high. As the angle increases, the ultimate bearing capacity of the pile foundation decreases to a certain extent. This may be attributed to the fact that during the final stage of this test, the failure mode of the pile foundation was consistently pullout failure, which is controlled by vertical loads. However, the pullout failure also varies with the increase in loading depth. Specifically, the smaller the loading depth, the greater the rotation amount of the model pile and the larger the inclination angle at the top of the pile foundation. In the first half of the loading process, the ultimate bearing capacity of the pile foundation is mainly governed by horizontal loads; in the second half, it is gradually dominated by vertical loads. Therefore, the peak bearing capacity in the first half shows a significant difference due to varying angles, while the difference in residual strength in the second half is not significant. By comparing the three figures above, respectively, it can be seen that in the second half after reaching the ultimate bearing capacity, as the angle increases, the slope of the load–displacement curve also increases. This is because the model piles with a low angle encounter greater soil resistance when pulled out and destroyed, but for large angles, the soil resistance can be said to be very small.
(3) Analysis of Figure 7 reveals distinct bearing capacity characteristics across loading angles: Under smaller loading angles, ultimate capacity is higher when loaded deeper along the pile shaft, likely due to denser soil providing greater soil resistance at lower depths. Conversely, mid-shaft loading induces disturbance-induced loosening of surrounding soil, reducing capacity. At moderate angles, overall capacity stabilizes moderately, with deeper loading points exhibiting higher capacities and shallower points showing lower values, accompanied by significantly different residual strengths. For larger angles, the system demonstrates reduced global capacity with a unique ductile-like response: load–displacement curves initially peak, then decline before rising again to stabilize at ultimate capacity—indicating progressive soil reconsolidation and pile realignment mechanisms.
3.2.2. Load–Displacement Curve of Pile-Anchor Foundations in Saturated Sand Condition
In saturated sand conditions, inclined tensile loading tests were conducted at loading depth H = 0.41L with angles of 30°, 45°, and 60°. Identical loading protocols and data processing methods as those in dry sand were employed. The resulting load–displacement curves for saturated sand are presented below, alongside a comparative analysis with corresponding dry sand curves.
By comparing the load–displacement curves of saturated sand and dry sand, the following rules can be found:
(1) Looking at Figure 8 as a whole, the variation law of the bearing characteristics under saturated sand conditions is consistent with that under dry sand conditions, that is: the ultimate bearing capacity of the model pile in the inclined anchor-tension direction gradually decreases with the increase in the loading angle. Meanwhile, both first increase the bearing capacity to the peak as the anchor-tension displacement increases, and then decrease to a stable stage of bearing capacity reduction. However, compared with dry sand, it is found that the ultimate bearing capacity of pile-anchor foundations under saturated sand conditions is lower. This is because the effective specific gravity of sand soil decreases under saturated conditions, resulting in a reduction in the stiffness of pile-soil interaction resistance and ultimate resistance. The maximum bearing capacity Qpeak of the model pile under saturated sand and dry sand conditions is shown in Table 4 below. It can be seen from the table that the maximum bearing capacity of the model pile under saturated sand conditions is approximately only half of that under dry sand conditions, but this influence gradually weakens as the loading angle increases.
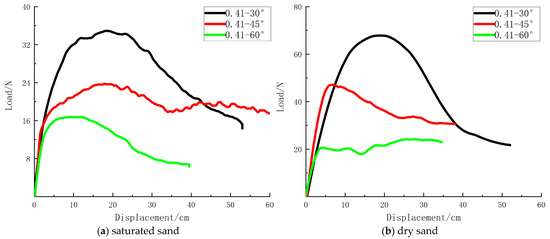
Figure 8.
Comparison of load displacement curves between saturated sand and dry sand.

Table 4.
Qpeak of the model pile under saturated sand and dry sand conditions.
(2) It can be seen from 8a that under the condition of saturated sand, when the loading depth H = 0.41L and the loading angle is 30°, the bearing capacity is relatively high, with a peak bearing capacity of 35.7 N, and then rapidly drops to 15.7 N through a sliding section. When the loading angle is 45°, the bearing capacity decreases somewhat. The peak bearing capacity is 23.8 N. After a downward section, it gradually decreases to 18.7 N and then gradually rises to 20.5 N to reach stability. When the loading angle is 60°, the bearing capacity is relatively low, with a peak bearing capacity of 17.1 N, and then gradually decreases to 7.86 N after a downward section. This is because under the same loading depth conditions, the load components decomposed in the vertical and horizontal directions of the inclined anchor tension load vary with the Angle. When the inclined tension Angle is small, the vertical component load is smaller, while the horizontal bearing capacity of the model pile is higher, thus showing a stronger inclined anchor tension bearing capacity. When the diagonal tension Angle is large, the vertical component load is also significant. However, the pullout bearing capacity of the model pile is limited. Therefore, there may be pullout failure leading to overall diagonal anchor tension failure and showing a relatively low bearing performance.
3.3. Processing of Pile Bending Moment Results
3.3.1. Bending Moment Distribution Patterns at Various Loading Depths
By establishing the constitutive equation of material mechanics and coupling the strain difference with the geometric parameters of the cross-section and the elastic modulus, the bending moment value at a specific position of the pile body is derived:
To study the influence law of the loading point depth at the same loading angle, the bending moment at the maximum peak bearing capacity in Figure 7 was selected for comparison. The initial data results were processed by applying the above Formula (1) to obtain the bending moment data. The relationship curves of the bending moment with the depth of the pile foundation at different loading depths were plotted as shown in Figure 9.
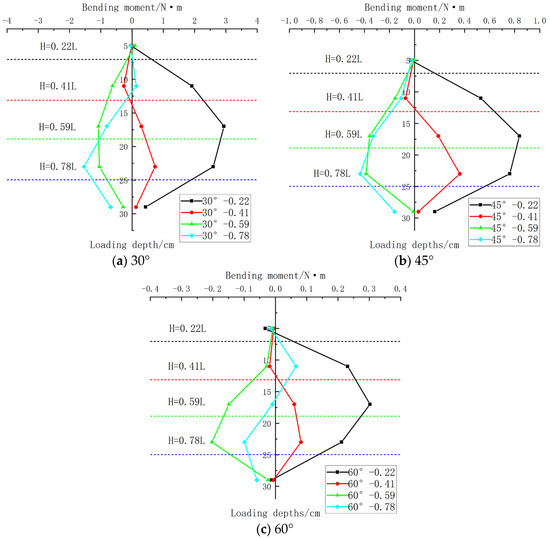
Figure 9.
Comparison of bending moments at different loading depths.
As illustrated in Figure 9, under the same inclined tension loading angle, the bending moment distribution pattern along the pile shaft varies significantly with the depth of the loading point. In contrast, when the loading point depth is fixed, the moment distribution patterns at different inclined tension loading angles are essentially similar, though the magnitude of the bending moment differs.
The variation in the bending moment distribution law is primarily driven by changes in the loading point depth. This is because the anchor tension load applies horizontal forces to both the upper pile segment (above the loading point) and the lower pile segment (below the loading point), thereby inducing corresponding bending moment responses. The specific differences are as follows:
(1) When the loading point is relatively shallow, the soil resistance acting on the upper pile segment is weaker, leading to a smaller negative bending moment. Meanwhile, the lower pile segment is buried deeper, resulting in a larger positive bending moment.
(2) As the loading point depth increases, the length of the upper pile segment extends, subjecting it to greater soil resistance and thus generating a larger negative bending moment. Conversely, the shortened length of the lower pile segment leads to a relatively smaller positive bending moment.
As the loading point moves from the pile top to the pile end, the bending moment distribution pattern along the pile shaft evolves gradually. Notably, the absolute value of the bending moment under deep loading conditions is smaller than that under shallow loading. This phenomenon is attributed to the superior resistance performance of deep foundation soil, which provides stronger lateral restraint compared to shallow soil.
3.3.2. Bending Moment Distribution Pattern Under Different Loading Angles
Based on the aforementioned bending moment processing results, the relationship curves between the bending moment and pile depth under different loading angles were further plotted, as shown in Figure 10.
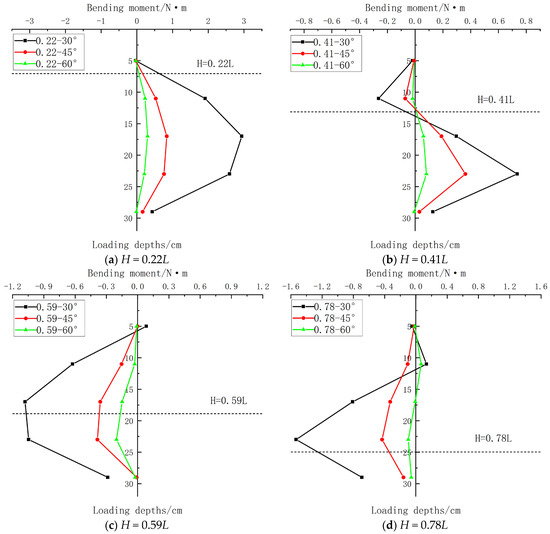
Figure 10.
Comparison of bending moments at different loading angles.
(1) It can be seen from Figure 10 that the variation patterns of the bending moment at the same loading depth but different loading angles are generally similar. As the angle increases, the bending moment overall exhibits a decreasing trend, which also conforms to the deformation behavior of piles under inclined loading. When the loading angle is relatively small, the horizontal load component primarily dominates, resulting in larger bending moment values in the pile. As the loading angle increases, the vertical load component gradually becomes dominant, and the horizontal load component on the pile body decreases, leading to a significant reduction in the bending moment value.
(2) It can be seen from Figure 10a that when loaded at H = 0.22L, the trend of bending moment change is basically consistent, only that as the angle increases, its horizontal load component gradually decreases causing the bending moment value to also decrease; from Figure 10b, it can be seen that when loaded at H = 0.41L, a distinct abrupt change occurs near the loading point, and the bending moment distribution trends above and below the loading point are opposite. The maximum absolute bending moment occurred at a depth of 23 cm, which is only because strain gauges were not installed at pile body positions shallower than 5 cm burial depth, resulting in no bending moment results being extracted; from Figure 10c, it can be seen that when loaded at H = 0.59L, the bending moment variation trends under different angles are basically consistent, and as the angle increases, the absolute value of the bending moment gradually decreases; from Figure 10d, it can be seen that the bending moment distribution characteristics when the loading point depth is at 0.78L are approximately a “mirror-image” relationship along the vertical axis compared to the case when the loading point depth is H = 0.41L, except that the magnitude of the former’s bending moment is smaller.
3.3.3. Processing Results of Pile Bending Moment Under Saturated Sand Condition
Under saturated sand conditions, inclined loading tests at angles of 30°, 45°, and 60° were conducted at a loading depth of H = 0.41L. The loading method and data processing approach were identical to those used in dry sand. The variation in pile bending moment with burial depth under saturated sand conditions is shown in Figure 11 below, with a comparative analysis against the results obtained under dry sand conditions.
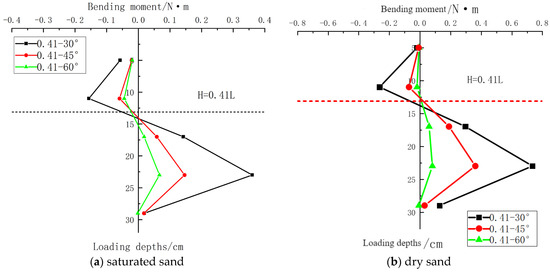
Figure 11.
Comparison of bending moments between saturated sand and dry sand.
According to the comparison in Figure 11, for the same loading depth (H = 0.41L), the bending moment distribution characteristics of the pile-anchor foundations in saturated sand under different loading angles (30°, 45°, and 60°) are entirely consistent with those in dry sand. The pile bending moment gradually decreases as the loading angle increases. This occurs because the bending moment is primarily generated by the horizontal load component acting on the pile. As the angle increases, the horizontal load component progressively diminishes.
Additionally, under identical conditions, the bending moment values of the model pile in saturated sand are approximately half of those observed in dry sand. This reduction is attributed to the lower subgrade reaction of saturated sand compared to dry sand.
3.4. Processing Results of Pile Shear Force
3.4.1. Shear Force Distribution Pattern Under Different Loading Depths
Normally, the pile shear force distribution can be obtained based on the pile bending moment distribution using a specific formula. However, this assumes the bending moment distribution is continuous. In this study, an internal force discontinuity exists at the anchor loading point, meaning the upper and lower segments of the model pile experience different force patterns at the loading point interface. Therefore, following the “Research on Horizontal Test Pile Data Processing Method Based on Akima Interpolation Theory” proposed by Zhu Mingxing et al. [39], this paper employs a new pile shear force calculation method to derive the pile shear force distribution pattern, as shown in Figure 12 below.
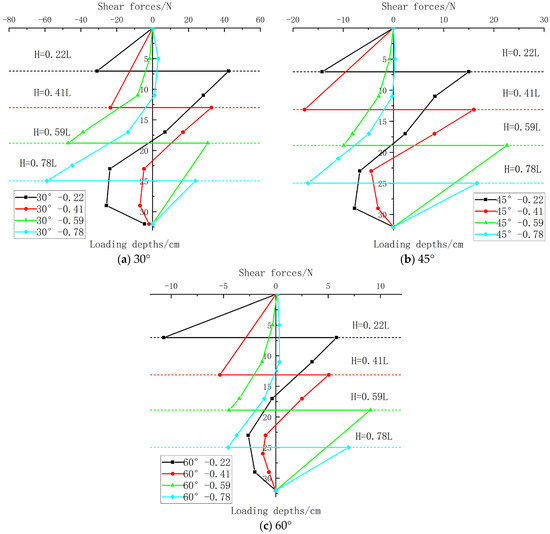
Figure 12.
Comparison of shear forces at different loading depths (a) 30°; (b) 45°; (c) 60°.
According to Figure 12, the characteristics of the pile shear force distribution pattern are very distinct, namely an internal force discontinuity occurs at the loading point interface. For the upper pile segment, the shear force at its tip (the loading point) is maximum and negative. It gradually decreases towards the pile top, reaching zero at the top. For the lower pile segment, the shear force at its top (the loading point) is maximum and positive. It generally attenuates with increasing depth, reaching zero at the pile tip (32 cm depth).
(1) Shear Force Distribution Pattern at 30° Loading Angle
① At loading depth H = 0.22L (=7.04 cm), the maximum negative shear force in the upper segment is −30.93 N at the loading point interface depth. The shear force in the lower segment, starting from 42.36 N at the interface, attenuates with depth. Due to the considerable length of the lower segment, a reverse shear force develops during attenuation with increasing depth, with a maximum negative shear force of −25.7 N at 29 cm depth, finally attenuating to zero at the pile tip.
② At loading depth H = 0.41L (=13.12 cm), the variation pattern is basically consistent with that at H = 0.22L (=7.04 cm), except the magnitudes of the former are smaller than the latter. The maximum negative shear force in the upper segment is −23.49 N at the interface. The lower segment shear force, starting from 32.71 N at the interface, attenuates with depth. Reverse shear force occurs, with a maximum negative value of −7.0 N at 29 cm depth, finally reaching zero at the tip.
③ At loading depth H = 0.59L (=18.88 cm), the entire upper segment exhibits negative shear force distribution, with a maximum of −47 N at the interface. The entire lower segment exhibits positive shear force distribution, with a maximum of 30.7 N at the interface.
④ At loading depth H = 0.78L (=24.96 cm), the situation is basically consistent with that at H = 0.22L (=7.04 cm), but exhibits an “inverted” pattern: The maximum negative shear force in the upper segment is −58.96 N at the interface, gradually attenuating as depth decreases. Positive shear force appears in shallow layers. This is attributed to the longer upper segment length, exhibiting shear distribution characteristics similar to those of semi-rigid or flexible piles. The maximum positive shear force in the lower segment is 23.84 N at the interface.
When the loading angles are 45° and 60°, the shear force distribution law is basically consistent with that at a loading angle of 30°; the only difference is that the overall magnitude of the shear force decreases as the loading angle increases. It can be seen that the shear force decreases gradually with the increase in the loading angle.
3.4.2. Shear Force Distribution Pattern Under Different Loading Angles
Based on the pile shear force distribution results presented in Section 3.4.1, the distribution patterns of shear force with pile depth under different loading angles are obtained, as shown in Figure 13.
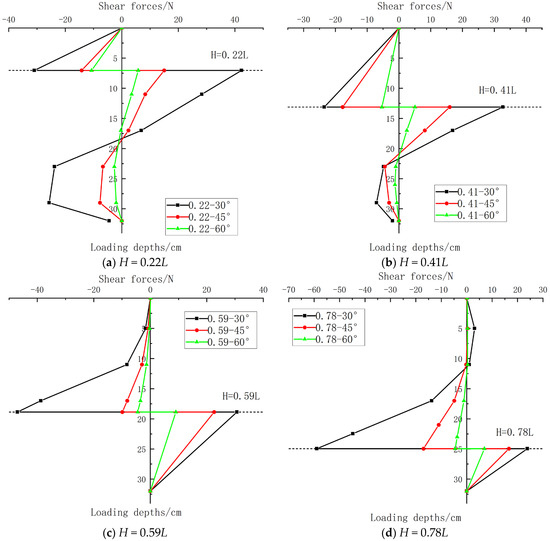
Figure 13.
Comparison of shear forces at different angles.
The shear force-depth distribution curves of the pile under different loading angles consistently exhibit similar trends when loads are applied at H = 0.22L, H = 0.41L, H = 0.59L, and H = 0.78L. The shear force at the pile head is zero, and it gradually increases in the negative direction with increasing embedment depth. The growth rate of negative shear force is more pronounced at smaller loading angles, which results from the reduced horizontal component of oblique tensile forces as the inclination angle increases, causing the bearing capacity control of the model pile to gradually shift to vertical capacity control. At a certain elevation above the loading point, the shear force reaches its negative peak value. At the loading point elevation, the shear force abruptly transitions to positive values and attains its maximum positive value, representing the critical section of maximum shear force in the pile shaft, with the magnitude decreasing as the loading angle increases. Below this point, the shear force rapidly diminishes with increasing depth.
3.4.3. Processing Results of Pile Shear Force Under Saturated Sand Condition
Under saturated sand conditions, inclined loading tests at angles of 30°, 45°, and 60° were conducted at a loading depth of H = 0.41L. The loading method and data processing approach were identical to those used in dry sand. The variation in pile shear force with burial depth under saturated sand conditions is shown in Figure 14 below, with a comparative analysis against the results obtained under dry sand conditions.
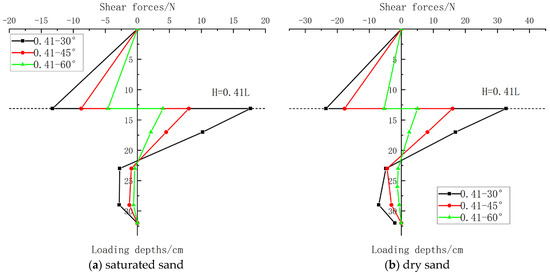
Figure 14.
Comparison of shear forces between saturated sand and dry sand.
From Figure 14, it can be observed that the variation patterns of pile shear force under different soil conditions are fundamentally consistent. However, a comparison of the numerical values reveals that the pile shear force under saturated sand conditions is approximately half of that under dry sand conditions. This consistency aligns with the behavior observed for the pile bending moment, which is attributed to the lower subgrade reaction of saturated sand compared to dry sand.
3.5. Processing Results of Pile Axial Force
3.5.1. Axial Force Distribution Pattern Under Different Loading Depths
Based on the constitutive relationship in material mechanics, the relationship between stress and strain at the monitored cross-sections of the pile can be expressed as:
Then, the axial force N at the cross-section where the strain gauge is attached on the pile shaft is:
Based on the calibration data of the test pile, a mathematical correlation model between axial strain and pile axial force was established using strain measurements from each cross-section. For axial force calculation, the measured strain values are substituted into Equation (2) to solve the stress distribution at each section. Subsequently, the sectional axial force distribution is solved using Equation (3). Figure 15 and Figure 16 show comparative characteristic curves of the axial force distribution under different loading depths for the test pile with a burial depth of 32 cm.
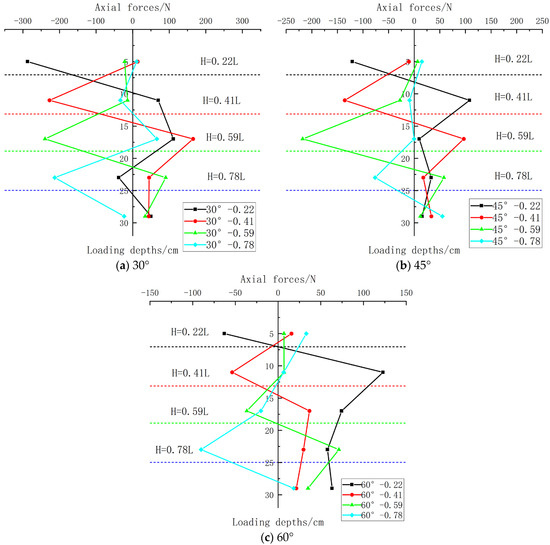
Figure 15.
Comparison of axial forces at different loading depths.
Analysis and comparison of the variation patterns of shear force with depth in the model pile under different loading depths at loading angles of 30°, 45°, and 60° are as follows:
(1) Overall observation of Figure 15 reveals that the axial force variation patterns under different loading depths are fundamentally consistent. A zero-crossing consistently occurs at the loading point, indicating compression in the pile above the loading point and tension below it.
(2) The maximum negative axial forces and maximum positive axial forces in Figure 15 are given in Table 5a–c.

Table 5.
The maximum negative axial forces and maximum positive axial forces.
(3) For loading at the same angle but different depths, the axial force distribution along the pile depth follows a consistent pattern: an abrupt change occurs near the loading point, with the upper segment under compression and the lower segment under tension. The non-zero initial axial force observed at H = 0.22L is likely due to the loading point’s upper location, limited strain gauge coverage, and insufficient data acquisition in shallow zones.
3.5.2. Axial Force Distribution Pattern Under Different Loading Angles
At loading depths of H = 0.22L, H = 0.41L, H = 0.59L, and H = 0.78L, the analysis and comparison of the variation patterns of shear force with depth in the model pile under different loading angles are shown in Figure 16 below:
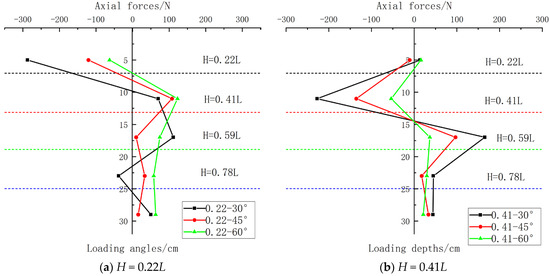
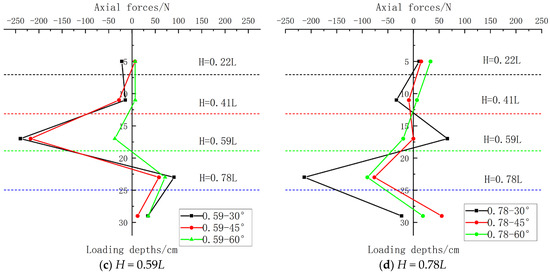
Figure 16.
Comparison of axial forces under different loading angles.
(1) Overall observation of Figure 16 reveals that during inclined loading on the model pile shaft, the axial force distribution along the depth exhibits a distinct pattern, consistently presenting a “lightning-bolt” shape: one segment is positive (indicating compression in the pile) and the other negative (indicating tension). At H = 0.22L and H = 0.78L, incomplete data coverage due to insufficient strain gauge groups results in gaps in the axial force distribution plots. The actual distribution should resemble Figure 16b.
(2) Observation indicates that as the loading angle increases, the pile axial force progressively decreases. This corresponds to the reduction in the pile’s ultimate bearing capacity as the horizontal load component diminishes.
3.5.3. Processing Results of Pile Axial Force Under Saturated Sand Condition
Under saturated sand conditions, inclined loading tests at angles of 30°, 45°, and 60° were conducted at a loading depth of H = 0.41L. The loading method and data processing approach were identical to those used in dry sand. The variation in pile axial force with burial depth under saturated sand conditions is shown in Figure 17 below, with a comparative analysis against the results obtained under dry sand conditions.
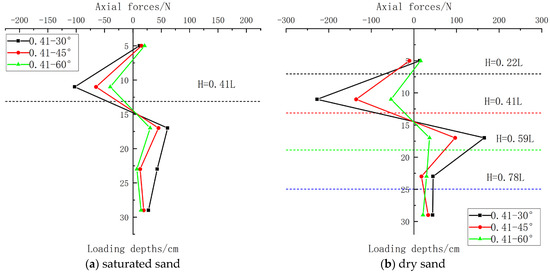
Figure 17.
Comparison of axial forces between saturated sand and dry sand.
From Figure 17, it can be observed that the axial force distribution patterns under different soil conditions are fundamentally consistent. As burial depth increases, the axial force initially rises to a maximum negative value, gradually approaches zero near the loading point, then increases to a maximum positive value before gradually decreasing. The pile axial force progressively diminishes as the loading angle increases. The axial force in saturated sand is approximately half of that observed in dry sand.
4. Conclusions
Based on experimental research on the bearing characteristics of single piles under inclined loading, considering factors such as loading angle, loading depth, and soil conditions, this study analyzed the load–displacement curves of model piles and the distribution patterns of bending moment, shear force, and axial force. The conclusions are as follows:
(1) Analysis of the load–displacement curves reveals that as displacement increases, the load on the model pile initially rises to a peak before decreasing and gradually stabilizing. This behavior may result from pile rotation within the soil during servo-cylinder displacement loading, altering the force mechanism. Rotation ceases when vertical load dominates, leading to post-peak load stabilization. Overall, the ultimate pullout capacity is highest at H = 0.78L.
(2) Loading angle significantly influences pile bearing performance. As the angle increases, vertical load gradually dominates, inducing vertical pullout failure. The bearing capacity decreases by ~63% when the angle increases from 30° to 60°.
(3) Increasing loading depth reduces bearing capacity when loading at the pile mid-depth, likely due to loosening of the soft marine sand around the pile, reducing surrounding soil resistance.
(4) At identical loading depths, bending moment distributions under different angles exhibit similar patterns but differ in magnitude. Variations primarily stem from loading depth changes: inclined loading generates horizontal forces on the upper segment (above the loading point) and lower segment (below), producing corresponding bending responses.
(5) Under insufficient experimental bending moment data, the shear force calculation method based on Akima Interpolation Theory effectively overcomes data limitations, accurately deriving shear distributions in upper/lower pile segments. Shear force trends align with bending moments regarding depth/angle effects. Axial force consistently shows abrupt changes near the loading point, confirming compression above and tension below.
(6) Under different sand conditions, the bearing capacity in saturated sand is about 50% of that in dry sand. Internal force distributions remain consistent but exhibit reduced magnitudes.
In the practical application of anchor piles, a low cable-stayed angle means that a longer anchor chain is required, which increases costs. However, the foundation bearing performance of a high cable-stayed angle is not as good as that of a low angle. Therefore, this paper provides certain references for the trade-off in designing the cable-stayed angle of anchor piles. This study provides a relatively comprehensive analysis for the research on flexible pile-anchor foundations under the conditions of saturated sand and dry sand, considering the influences of different loading points and different loading angles. However, the current research does not take into account the foundation bearing characteristics of flexible piles under cyclic loads, and these factors will be the key focus areas of future research.
Author Contributions
Conceptualization, B.L., J.S. and M.Z.; Methodology, J.S. and X.L.; Validation, Y.W.; Formal analysis, Y.W., H.D. and J.C.; Resources, B.L. and H.D.; Data curation, P.L. and J.C.; Writing—original draft, Y.W. and P.L.; Writing—review & editing, M.Z., X.L., J.C. and H.O.; Supervision, H.D., M.Z. and H.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China Youth Science Fund Project grant number 52201324, CCCC Highway Consultants Co., Ltd. “Unveiling List and Assuming Command” Program for Key Technology R&D Program grant number 2023-ZJKJ-01 and the Research on Key Technologies of Far-reaching Offshore Wind Power grant number SW-2023-039.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors are grateful to Wang T and Jing L for their assistance.
Conflicts of Interest
Authors Bo Liu and Huiyuan Deng were employed by CCCC Highway Consultants Co., Ltd. Author Jiaqing Shu was employed by Jiangsu Electric Power Design and Research Institute Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The authors declare that this study received funding from CCCC Highway Consultants Co., Ltd. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.
Abbreviations
| E | Elastic modulus of the model pile |
| I | Moment of inertia of the model pile |
| Δε | Bending strain at the cross-section |
| D | Spacing between tension-compression strain measurement points |
| M | Bending moment at the tested pile cross-section |
| ε | Average strain at the tested cross-section |
| σ | Stress at the cross-section |
| A | Cross-sectional area of the model pile |
| N | Axial force at the tested pile cross-section |
| Dr | Relative Density of Soil |
| ρ | Dry Density |
| ρmax | Maximum Dry Density |
| ρmin | Minimum Dry Density |
| φ | Angle of Internal Friction |
| Cu | Uniformity Coefficient |
| Cv | Curvature Coefficient |
| c | Cohesion |
| V | Shear Force |
References
- Lopez-Olocco, T.; Liang, G.; Medina-Manuel, A.; Ynocente, L.S.; Jiang, Z.; Souto-Iglesias, A. Experimental comparison of a dual-spar floating wind farm with shared mooring against a single floating wind turbine under wave conditions. Eng. Struct. 2023, 292, 116475. [Google Scholar] [CrossRef]
- Zhai, J.; Yin, Q.; Ji, C. Performance-based design of environmental parameters for offshore wind turbine foundations. Ocean. Eng. 2024, 309, 118520. [Google Scholar] [CrossRef]
- Li, H.; Lian, J.; Liu, R.; Wang, H.; Yang, X. Research on the equivalent stiffness of bucket foundations for offshore wind power. Ocean. Eng. 2024, 302, 117596. [Google Scholar] [CrossRef]
- OuYang, H.; Dai, G.; Qin, W.; Zhang, C.; Zhu, W.; Gong, W. Experimental study on the mechanical behaviors and particle breakage characteristics of calcareous sand from South China Sea under repeated one-dimensional impacts. Acta Geotech. 2022, 17, 3927–3946. [Google Scholar] [CrossRef]
- Nazari, M.; Vermeulen, O.; Llistar, L.V.; Nystrøm, P.R. A Mechanical-Empirical Model for Anchoring Capacity of Inclined Pile in Clay Used for Deep Water Floating Wind Turbines. Int. J. Offshore Polar Eng. 2024, 34, 374–382. [Google Scholar] [CrossRef]
- Peng, Y.; Yin, Z.Y. Micromechanical analysis of suction pile-granular soil interaction under inclined pulling load of mooring line: Mooring depth effect. Mar. Struct. 2023, 92, 103499. [Google Scholar] [CrossRef]
- Ramadan, M.I.; Butt, S.D.; Popescu, R. Offshore anchor piles under mooring forces: Numerical modeling. Can. Geotech. J. 2013, 50, 189–199. [Google Scholar] [CrossRef]
- Qin, W.; Ye, C.; Gao, J.; Dai, G.; Wang, D.; Dong, Y. Pore water pressure of clay soil around large-diameter open-ended thin-walled pile (LOTP) during impact penetration. Comput. Geotech. 2025, 180, 107065. [Google Scholar] [CrossRef]
- Qin, W.; Gao, J.; Chang, K.; Dai, G.; Wei, H. Set-up effect of large-diameter open-ended thin-walled pipe piles driven in clay. Comput. Geotech. 2023, 159, 105459. [Google Scholar] [CrossRef]
- Saathoff, J.E.; Achmus, M. Estimation of capacity decrease due to accumulated excess pore pressures around cyclically loaded offshore foundations in sand. Ocean. Eng. 2024, 294, 116733. [Google Scholar] [CrossRef]
- He, L.; Chen, X.; Wang, Z.; Han, Y.; Su, T.; Dai, G.; Zhang, E.; Long, Z. A case study on the bearing characteristics of a bottom uplift pile in a layered foundation. Sci. Rep. 2022, 12, 22457. [Google Scholar] [CrossRef]
- Qin, W.; Cai, S.; Dai, G.; Wang, D.; Chang, K. Soil resistance during driving of offshore large-diameter open-ended thin-wall pipe piles driven into clay by impact hammers. Comput. Geotech. 2023, 153, 105085. [Google Scholar] [CrossRef]
- Li, W.; Li, X.; Wang, T.; Yin, Q.; Zhu, M. The Simplified Method of Head Stiffness Considering Semi-Rigid Behaviors of Deep Foundations in OWT Systems. Buildings 2024, 14, 1803. [Google Scholar] [CrossRef]
- Li, X.; Dai, G.; Zhang, F.; Gong, W. Energy-based analysis of laterally loaded caissons with large diameters under small-strain conditions. Int. J. Geomech. 2022, 22, 05022005. [Google Scholar] [CrossRef]
- Moayedi, H.; Mosallanezhad, M. Uplift resistance of belled and multi-belled piles in loose sand. Measurement 2017, 109, 346–353. [Google Scholar] [CrossRef]
- Nasr, A.M. Uplift behavior of vertical piles embedded in oil-contaminated sand. J. Geotech. Geoenviron. Eng. 2013, 139, 162–174. [Google Scholar] [CrossRef]
- Faizi, K.; Armaghani, D.J.; Sohaei, H.; Rashid, A.S.A.; Nazir, R. Deformation model of sand around short piles under pullout test. Measurement 2015, 63, 110–119. [Google Scholar] [CrossRef]
- Galvis-Castro, A.C.; Tovar-Valencia, R.D.; Salgado, R.; Prezzi, M. Compressive and tensile shaft resistance of nondisplacement piles in sand. J. Geotech. Geoenviron. Eng. 2019, 145, 04019041. [Google Scholar] [CrossRef]
- Emirler, B.; Tolun, M.; Yildiz, A. Investigation on determining uplift capacity and failure mechanism of the pile groups in sand. Ocean. Eng. 2020, 218, 108145. [Google Scholar] [CrossRef]
- Kong, G.Q.; Liu, Z.P.; Wang, L.H.; Liu, H.L.; Yang, Q. Experimental studies on the behavior of a single shaped pile under oblique pullout loads. Acta Geotech. 2023, 18, 4733–4746. [Google Scholar] [CrossRef]
- Liu, K.; Xu, C.; Xu, H.; Zhu, W.; Nie, Z. Experimental Study on Load-Transfer Mechanism and Failure Mode of Batter Pile under Oblique Uplift Loading. Int. J. Geomech. 2022, 22, 04022231. [Google Scholar] [CrossRef]
- Kong, G.Q.; Cao, Z.H.; Zhou, H.; Sun, X.J. Analysis of piles under oblique pullout load using transparent-soil models. Geotech. Test. J. 2015, 38, 725–738. [Google Scholar] [CrossRef]
- Wang, Q.; Hu, Z.; Ji, Y.; Ma, J.; Chen, W. Model test of rock-socketed pile under axial and oblique tension loading in combined composite ground. Int. J. Geomech. 2022, 22, 04022182. [Google Scholar] [CrossRef]
- Wang, Z.; Luo, G.; Kong, G.; Zhang, Y.; Lu, J.; Chen, Y.; Yang, Q. Centrifuge model tests on anchor pile of single point mooring system under oblique pullout load using transparent sand. Ocean. Eng. 2022, 264, 112441. [Google Scholar] [CrossRef]
- Li, X.; Dai, G.; Zhu, M.; Zhu, W.; Zhang, F. Investigation of the soil deformation around laterally loaded deep foundations with large diameters. Acta Geotech. 2024, 19, 2293–2314. [Google Scholar] [CrossRef]
- Qin, W.; Cai, S.; Dai, G.; Wei, H. Analytical solutions of soil plug behaviors in open-ended pile driven by impact load. Acta Geotech. 2023, 18, 4183–4194. [Google Scholar] [CrossRef]
- Liu, H.; Zhu, M.; Li, X.; Dai, G.; Yin, Q.; Liu, J.; Ling, C. Experimental study on shear behavior of interface between different soil materials and concrete under variable normal stress. Appl. Sci. 2022, 12, 11213. [Google Scholar] [CrossRef]
- Huang, T.; O’Loughlin, C.; Gaudin, C.; Tian, Y.; Lu, T. Drained response of rigid piles in sand under an inclined tensile load. Geotech. Lett. 2020, 10, 30–37. [Google Scholar] [CrossRef]
- Santiago, P.C.; Saboya, F.; Tibana, S.; Reis, R.M.; Borges, R.G. Centrifuge modelling of a combined pile-type anchor subjected to general inclined loading. Mar. Struct. 2020, 74, 102815. [Google Scholar] [CrossRef]
- Fu, Y.; Zhang, X.; Li, Y.; Gu, H.; Sun, J.; Liu, Y.; Lee, F.H. Holding capacity of dynamically installed anchors in normally consolidated clay under inclined loading. Can. Geotech. J. 2017, 54, 1257–1271. [Google Scholar] [CrossRef]
- Singh, T.; Pal, M.; Arora, V.K. Modeling oblique load carrying capacity of batter pile groups using neural network, random forest regression and M5 model tree. Front. Struct. Civ. Eng. 2019, 13, 674–685. [Google Scholar] [CrossRef]
- Johnson, K.; Lemcke, P.; Karunasena, W.; Sivakugan, N. Modelling the load–deformation response of deep foundations under oblique loading. Environ. Model. Softw. 2006, 21, 1375–1380. [Google Scholar] [CrossRef]
- Ran, Y.; Wang, X.; Zhu, Y. Experimental and numerical study on dynamic response of concrete filled steel tubular pile subjected to oblique impact. In Structures; Elsevier: Amsterdam, The Netherlands, 2022; Volume 39, pp. 917–927. [Google Scholar]
- Ramadan, M.I.; Butt, S.D.; Popescu, R. Offshore anchor piles under mooring forces: Centrifuge modeling. Can. Geotech. J. 2013, 50, 373–381. [Google Scholar] [CrossRef]
- Gui, F.; Kong, J.; Feng, D.; Qu, X.; Zhu, F.; You, Y. Uplift resistance capacity of anchor piles used in marine aquaculture. Sci. Rep. 2021, 11, 20321. [Google Scholar] [CrossRef]
- Luo, G.; Wang, Z.; Kong, G.; Zhang, Y.; Yang, Q.; Zhou, Y.; Li, P.; Wang, M. Centrifuge model tests on an anchor pile under cyclic oblique pullout load using transparent sand. Mar. Georesour. Geotechnol. 2025, 43, 437–447. [Google Scholar] [CrossRef]
- Sheikhtaheri, M. Experimental and Numerical Modeling Studies for Interpreting and Estimating the p–δ Behavior of Single Model Piles in Unsaturated Sands. Doctoral Dissertation, Université d’Ottawa/University of Ottawa, Ottawa, ON, Canada, 2014. [Google Scholar]
- Al-Khazaali, M.; Vanapalli, S.K. Experimental investigation of single model pile and pile group behavior in saturated and unsaturated sand. J. Geotech. Geoenviron. Eng. 2019, 145, 04019112. [Google Scholar] [CrossRef]
- Zhu, M.; Yin, Q.; Gong, W.; Dai, G.; Lu, H. Research on Horizontal Test Pile Data Processing Method Based on Akima Interpolation Theory. J. Geotech. Eng. 2020, 42, 80–84. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).