Optimized Line-of-Sight Active Disturbance Rejection Control for Depth Tracking of Hybrid Underwater Gliders in Disturbed Environments
Abstract
1. Introduction
- Addressing the HUG longitudinal plane motion control problem, its kinematics and dynamic models are combined for control. Kinematically, LOS guidance transforms the depth control problem into a line-of-sight distance tracking problem. To address error accumulation issues with the traditional LOS look-ahead distance, an OLOS method is proposed to adaptively adjust the look-ahead distance.
- Dynamically, active disturbance rejection control (ADRC) is employed. A tracking differentiator optimized with the tangent Sigmoid function (TSTD) enhances the disturbance–observation capability of the extended state observer (ESO) within the ADRC framework for unknown system dynamics and environmental disturbances. Aiming at HUG motion characteristics, control performance during attitude transitions is improved, drift error caused by overshoot is reduced, and adaptability to the marine environment is enhanced.
- The proposed control method is validated through experiments. Comparative experimental results show the effectiveness of the proposed control method in depth tracking control and disturbance rejection under specified requirements, demonstrating significant performance improvements.
2. Mathematical Model of Hybrid Drive Underwater Glider
2.1. Working Principle of Hybrid Drive Underwater Glider
2.2. Kinematics and Dynamics Models
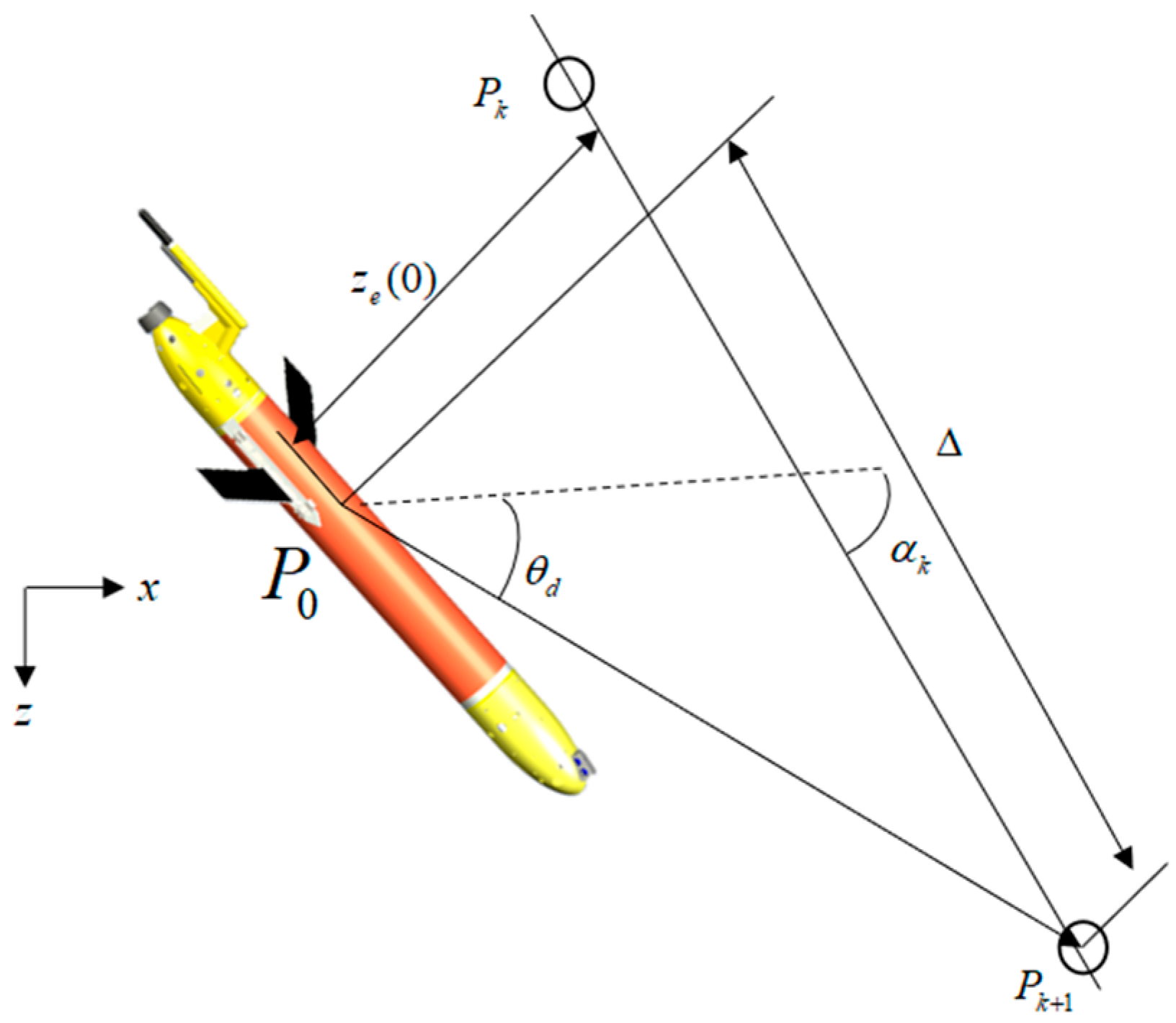
3. Optimization of LOS Guidance
3.1. LOS Guidance
3.2. Optimize LOS Guidance
- (1)
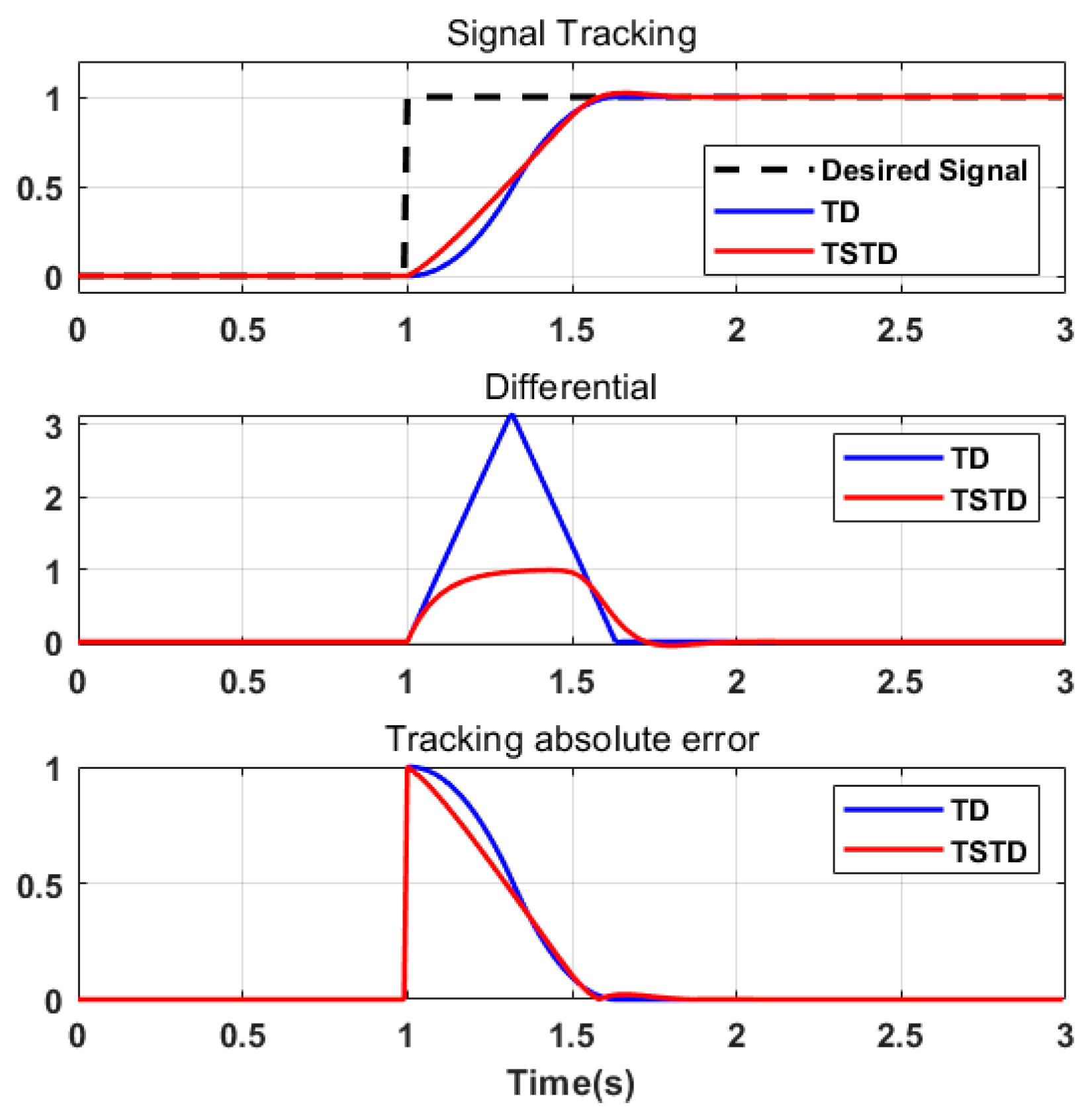
- Fast Transient Response: With , the system exhibits high-gain behavior, driving toward zero exponentially. This phase minimizes the settling time during large initial errors.
- (2)
- Overshoot Suppression: As , increasing Δ reduces the control aggressiveness. The smooth transition to ensures bounded control inputs, thereby attenuating oscillations and suppressing overshoot.
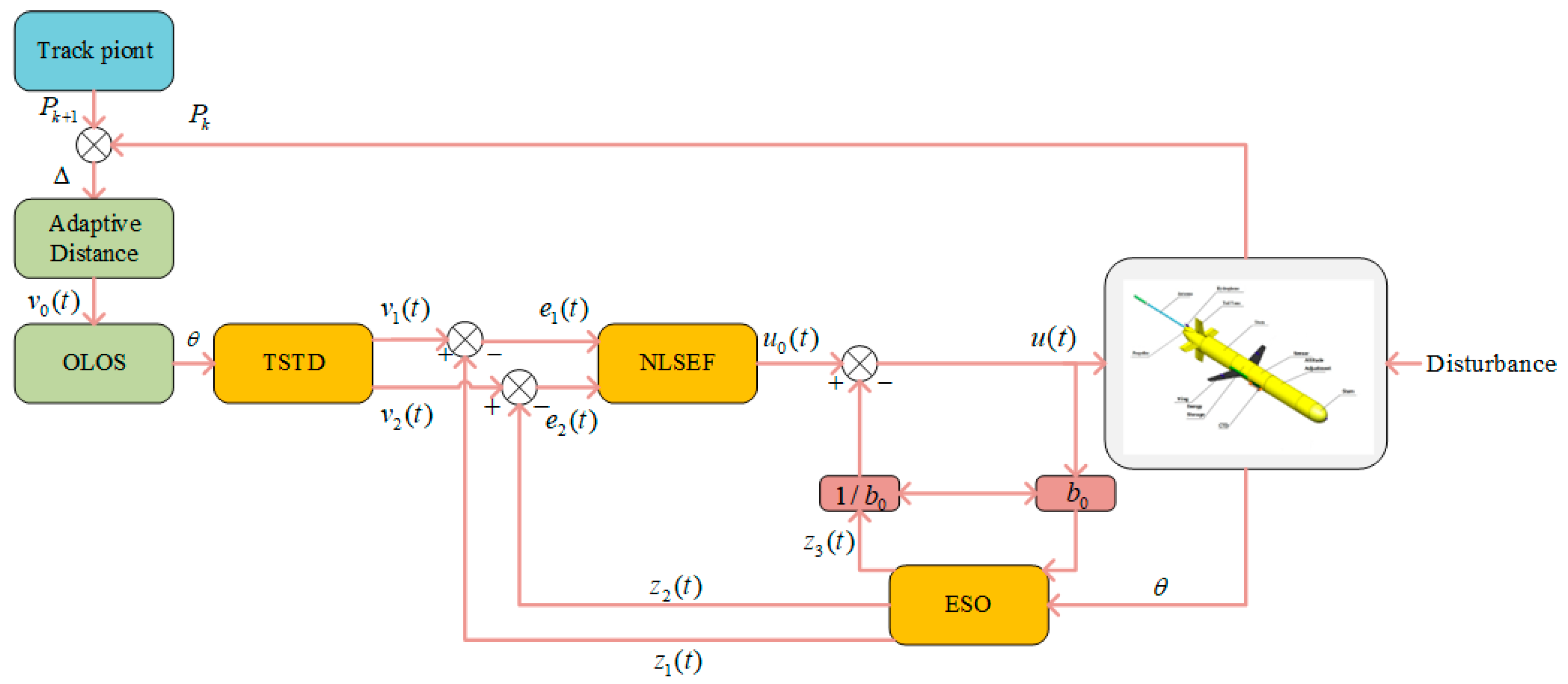
4. ADRC System
4.1. TSTD
4.2. ESO
4.3. NLSEF
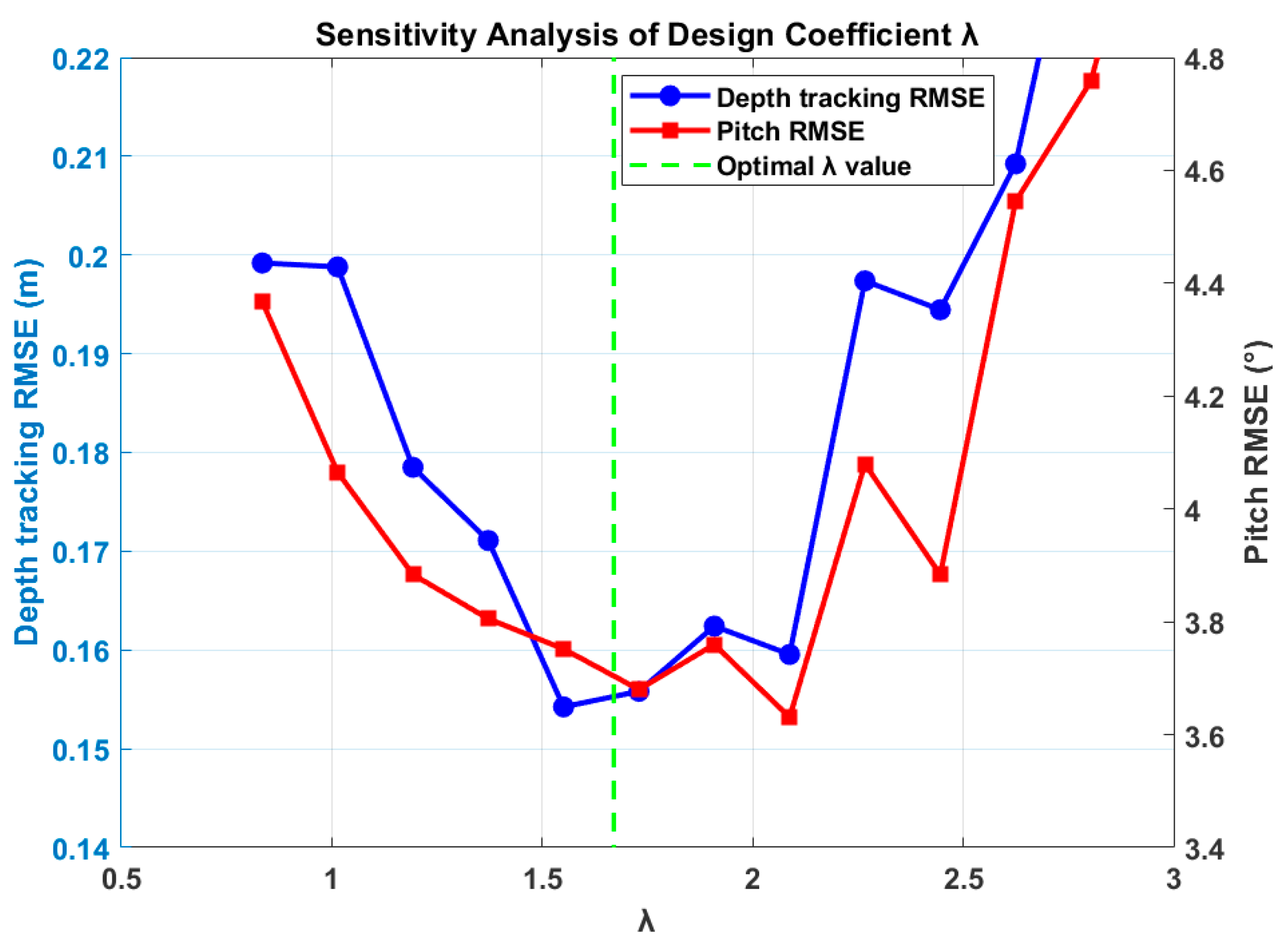
- Baseline tuning: PID gains (, in Formula (45)) initialized via the Ziegler–Nichols method.
- ESO optimization: Observer gains () adjusted using the Lyapunov stability criterion (Theorem 1), with , , ensuring .
- calibration: , selected to balance chattering suppression and disturbance sensitivity.
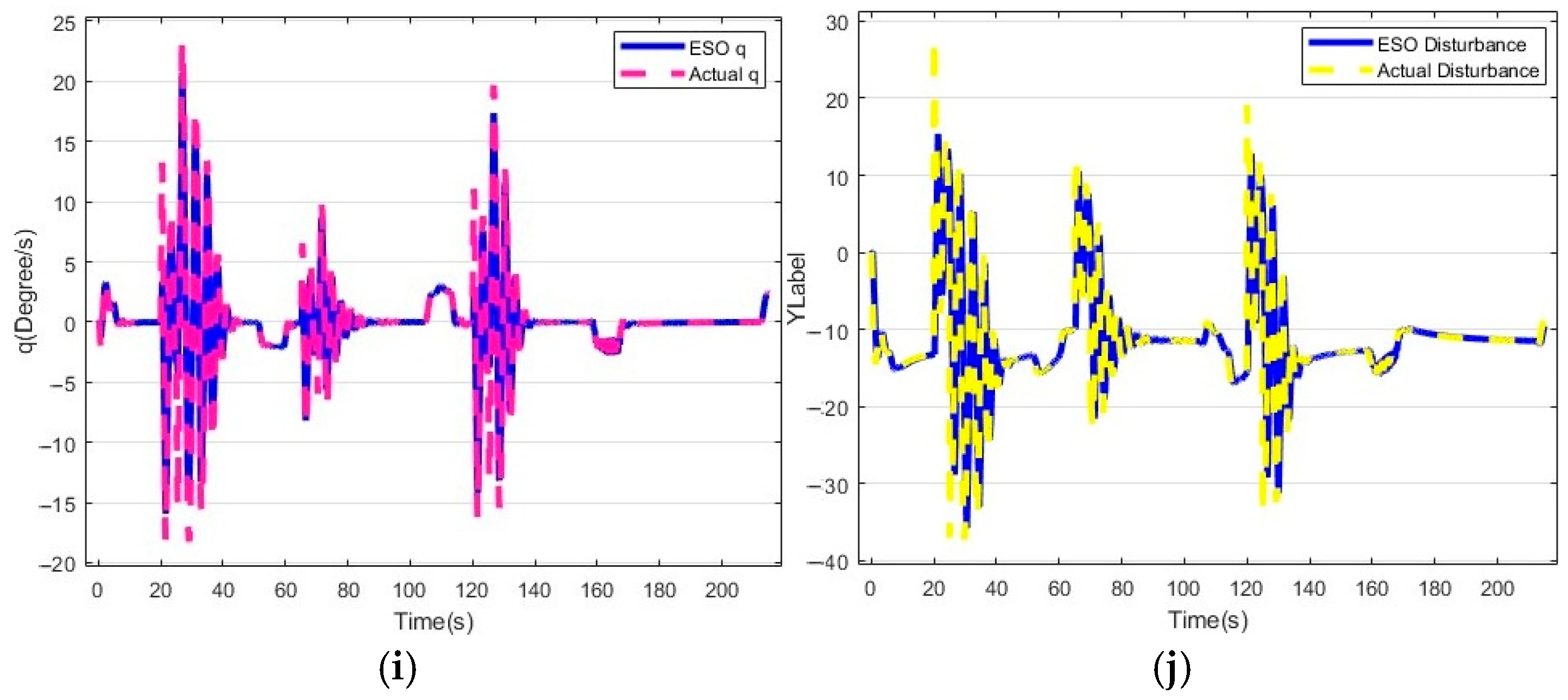
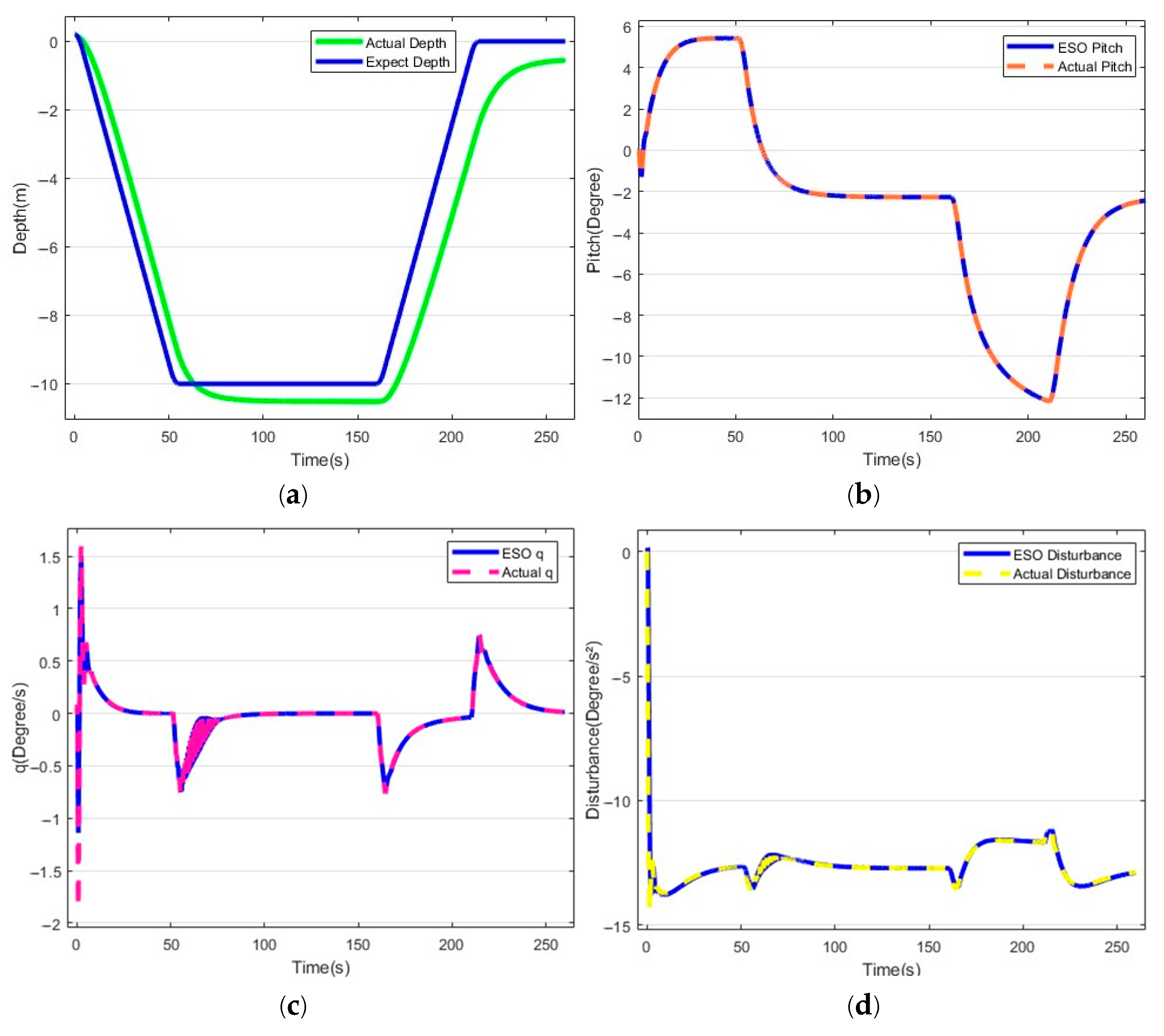
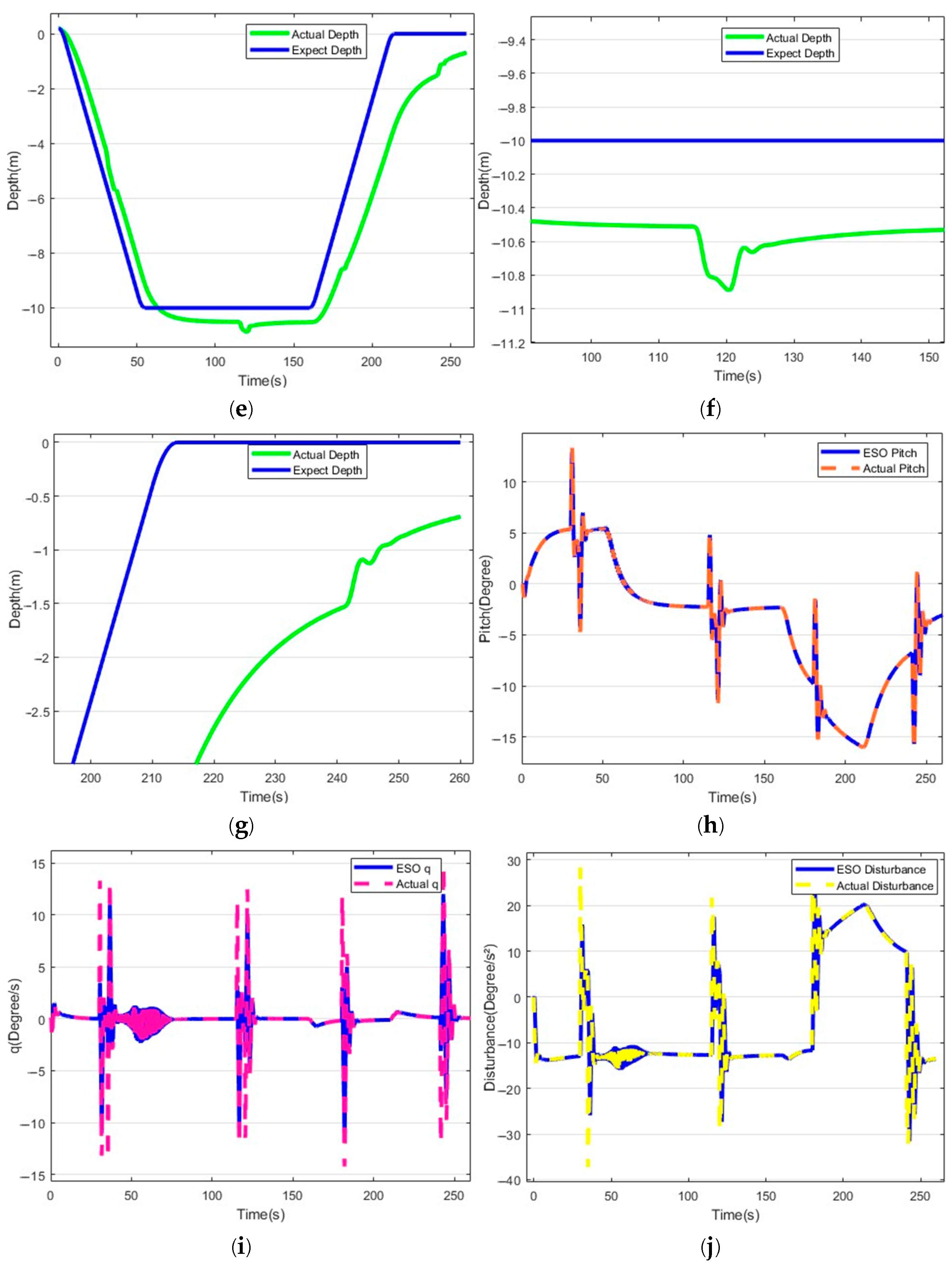
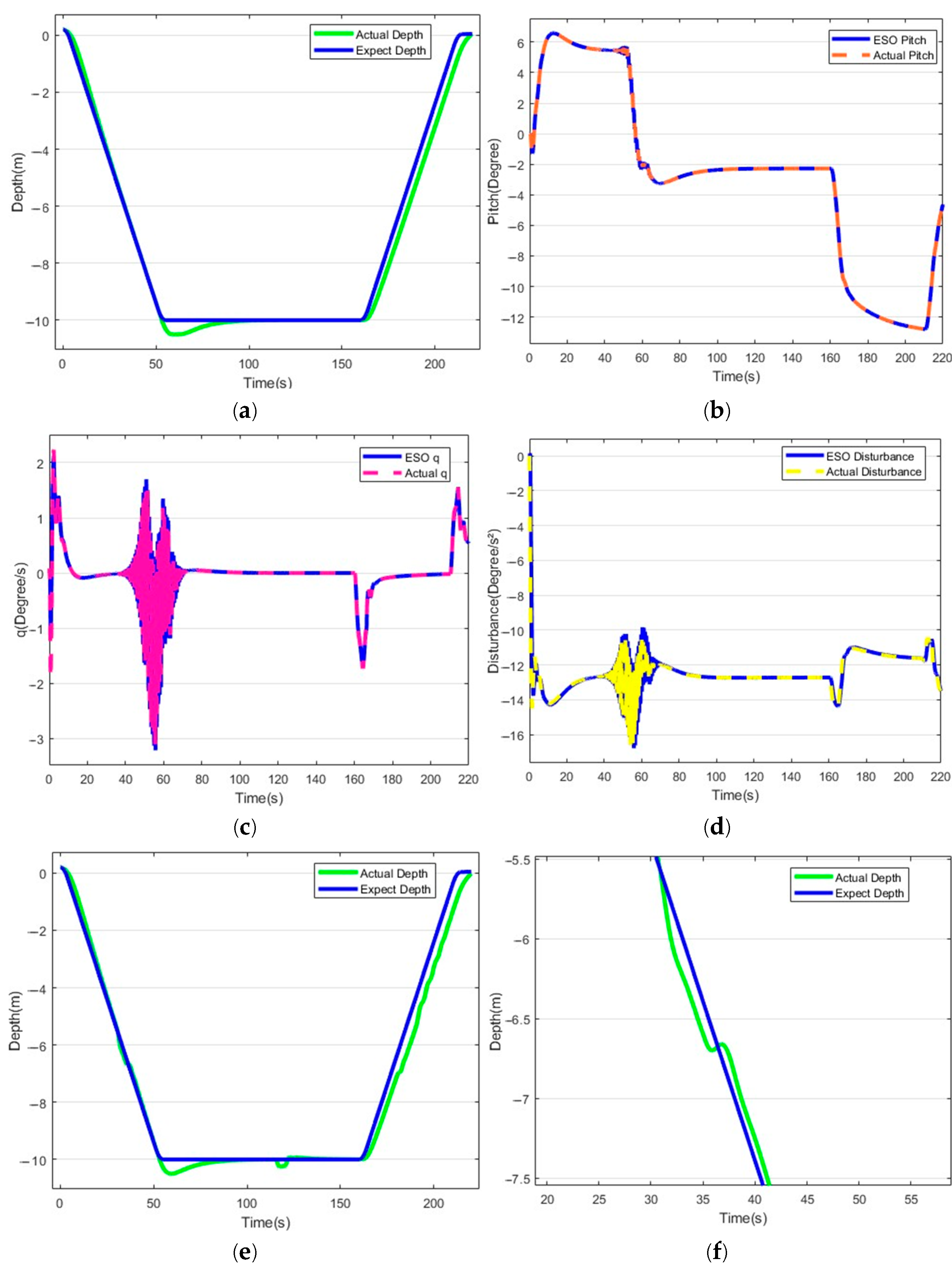
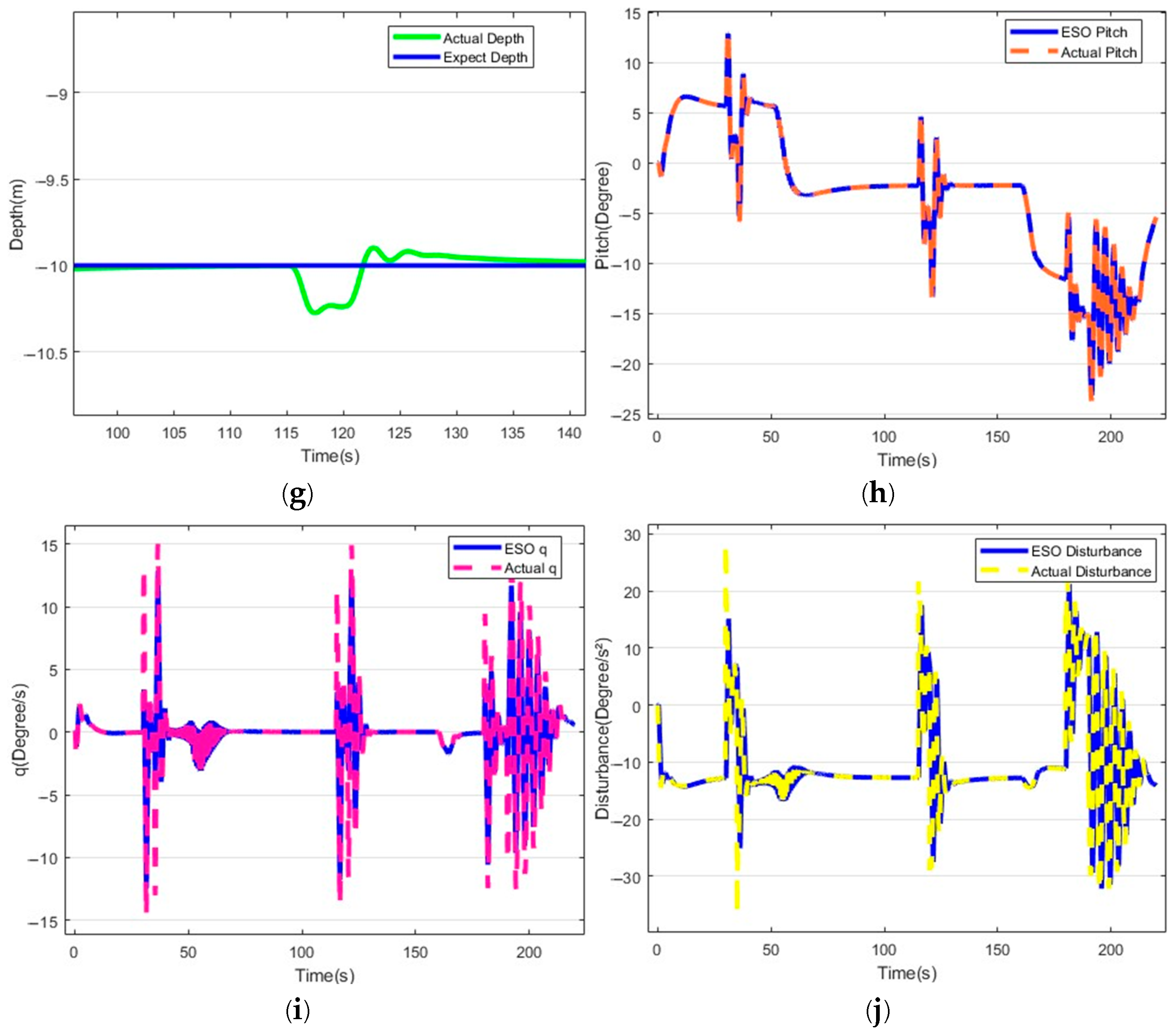
5. Comparative Experiment Results
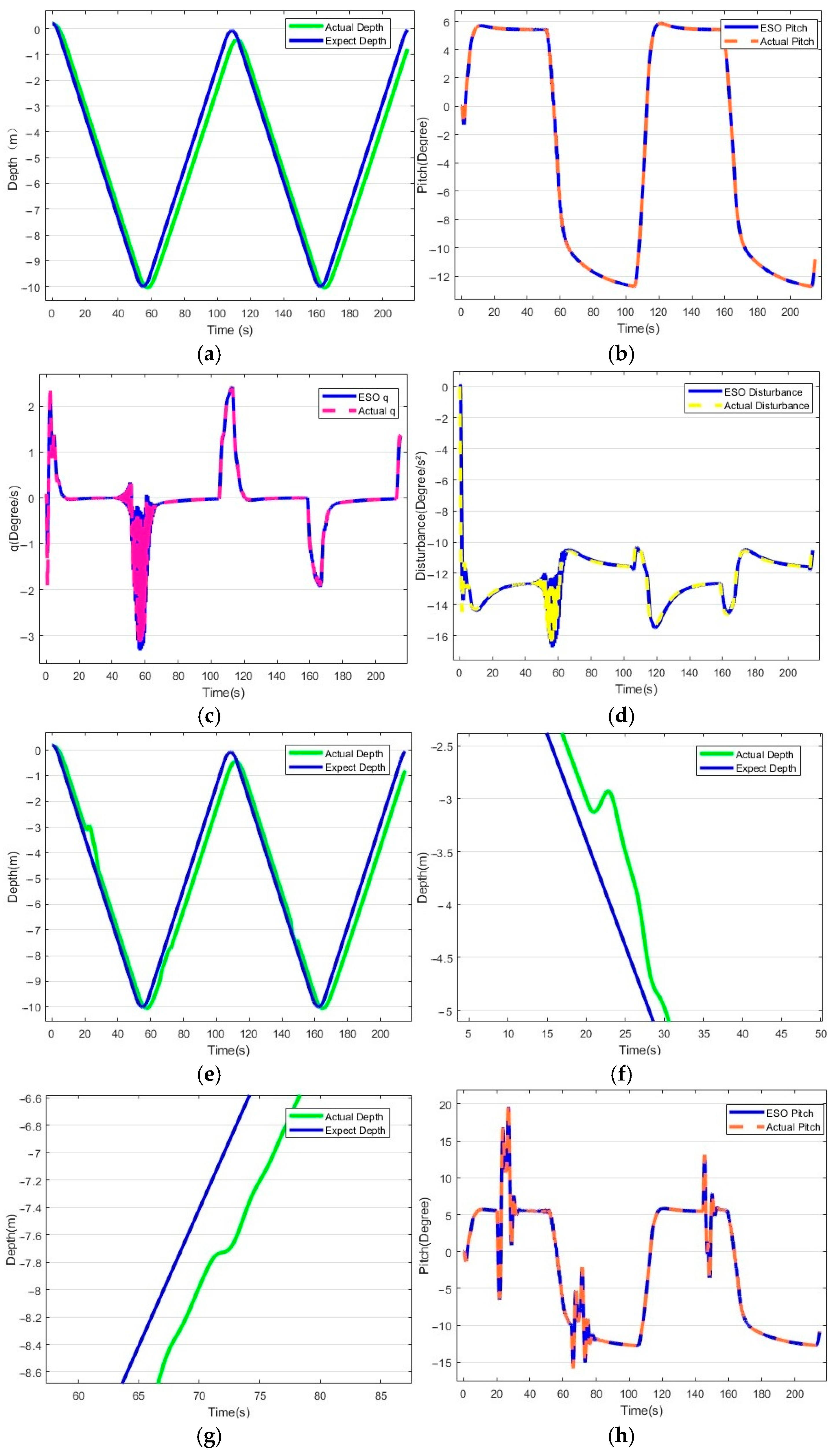
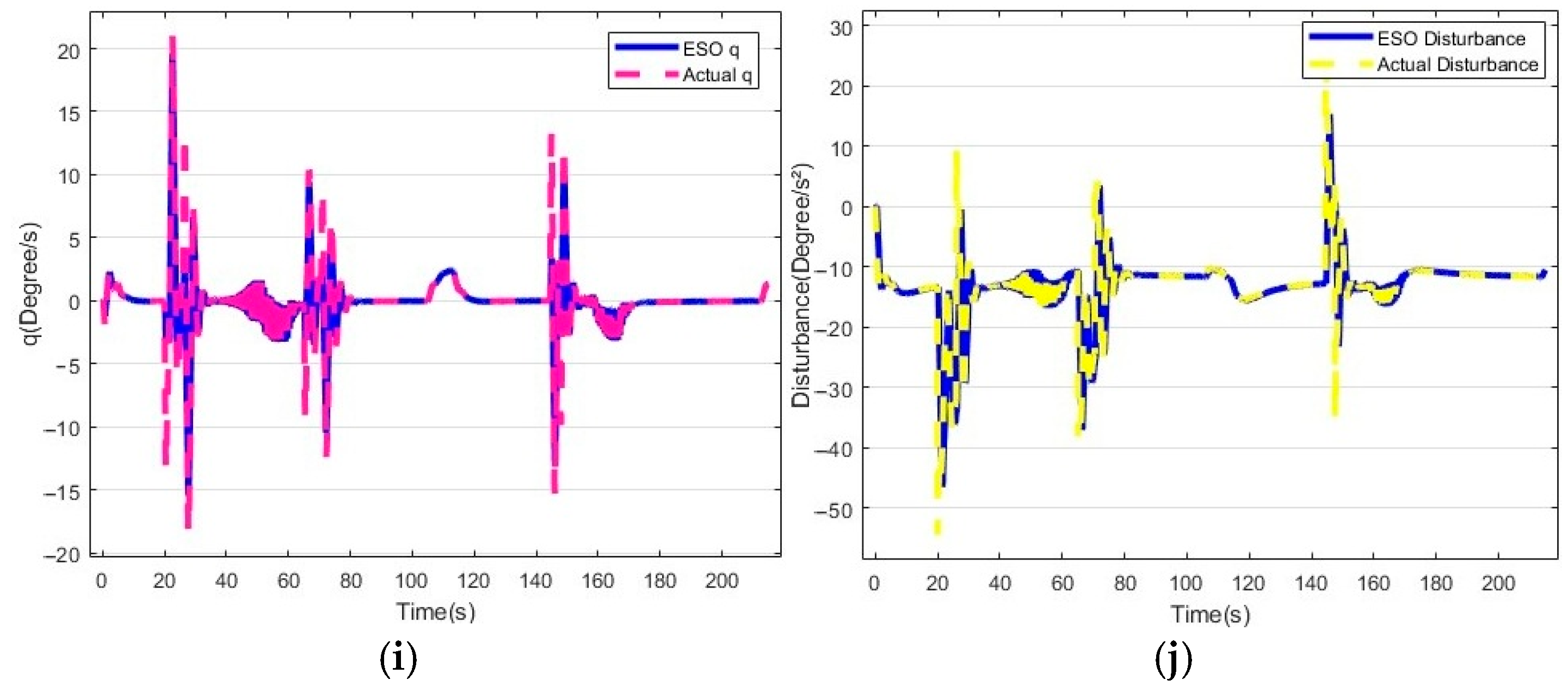
5.1. Routine Gliding Exercise Test
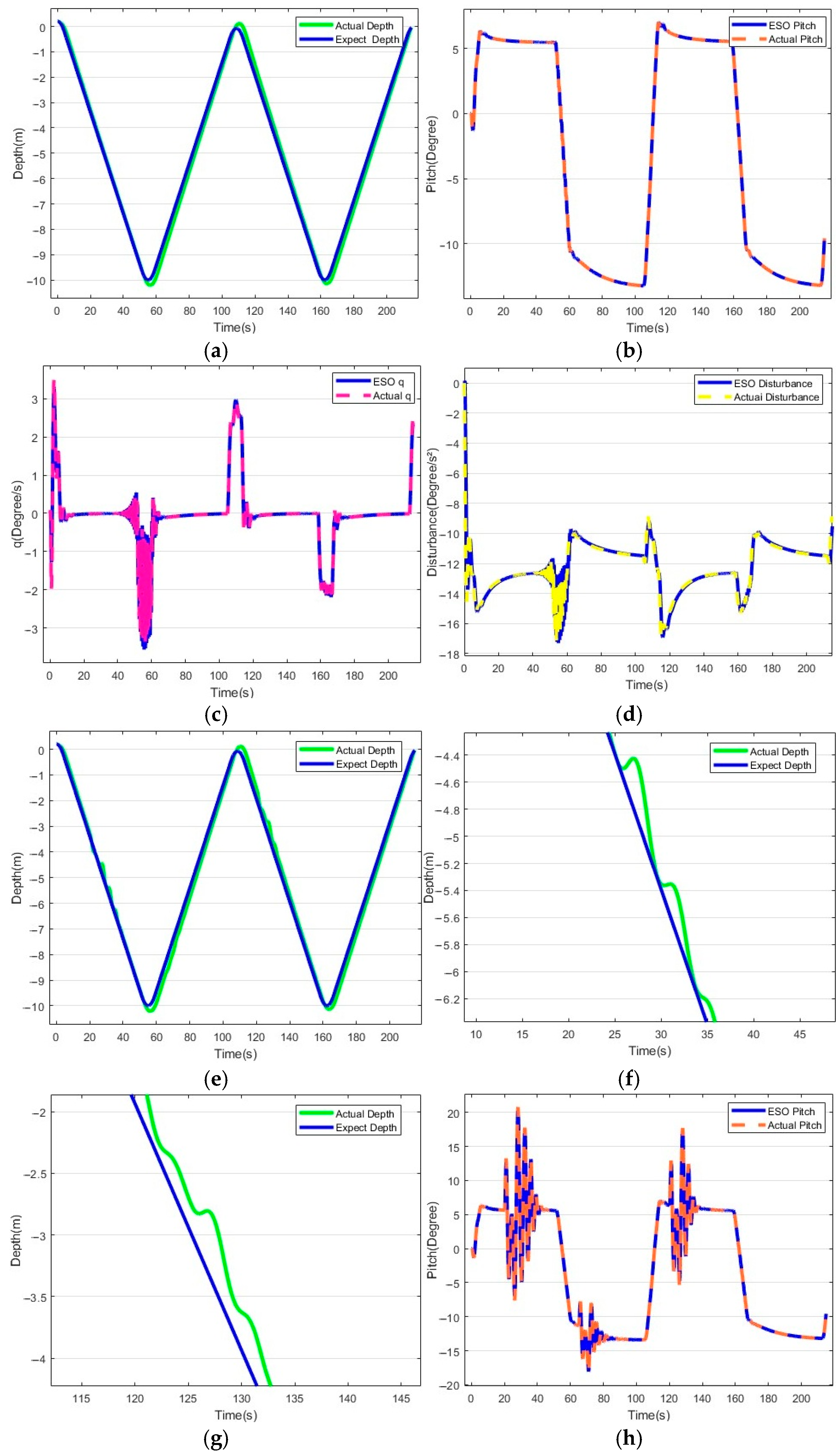
5.2. Hybrid Drive Exercise Test
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, J.; Li, W.; Liu, Q.; Luo, B.; Cui, W. Current Status and Technical Challenges in the Development of Biomimetic Robotic Fish-Type Submersible. Ocean-Land-Atmos. Res. 2024, 3, 0036. [Google Scholar] [CrossRef]
- Webb, D.C.; Simonetti, P.J.; Jones, C.P. SLOCUM: An underwater glider propelled by environmental energy. IEEE J. Ocean. Eng. 2001, 26, 447–452. [Google Scholar] [CrossRef]
- Eriksen, C.C.; Osse, T.J.; Light, R.D.; Wen, T.; Lehman, T.W.; Sabin, P.L.; Ballard, J.W.; Chiodi, A.M. Seaglider: A long-range autonomous underwater vehicle for oceanographic research. IEEE J. Ocean. Eng. 2001, 26, 424–436. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C.; Yang, M.; Liang, Y.; Han, W.; Yang, S. Glide performance analysis of underwater glider with sweep wings inspired by swift. Front. Mar. Sci. 2022, 9, 1048328. [Google Scholar] [CrossRef]
- Chu, F.S.; Si, Z.S.; Pang, C.G.; Yu, J.C. Thermal Lag Correction From a GLIDER Payload CTD for Poor Temperature Data. Pure Appl. Geophys. 2020, 177, 3039–3051. [Google Scholar]
- Liu, Z.; Xu, J.; Yu, J. Real-time quality control of data from Sea-Wing underwater glider installed with Glider Payload CTD sensor. Acta Oceanol. Sin. 2020, 39, 134–144. [Google Scholar]
- Zhou, H.; Zeng, Z.; Yu, C.; Yao, B.; Lian, L. Adaptive robust sliding mode control of autonomous underwater glider with input constraints for persistent virtual mooring. Appl. Ocean Res. 2020, 95, 102027. [Google Scholar]
- Wang, Y.; Guo, Y.; Yang, S.; Sun, T.; Wang, X.; Zhou, H. Design, Hydrodynamic Analysis, and Testing of a Bio-inspired Movable Bow Mechanism for the Hybrid-driven Underwater Glider. J. Bionic Eng. 2023, 20, 1493–1513. [Google Scholar]
- Eichhorn, M. Optimal Routing Strategies for Autonomous Underwater Vehicles in Time-Varying Environment. Robot. Auton. Syst. 2015, 67, 33–43. [Google Scholar] [CrossRef]
- Zhou, M.; Bachmayer, R.; Deyoung, B. Surveying a Floating Iceberg with the USV SEADRAGON. Front. Mar. Sci. 2021, 8, 549566. [Google Scholar] [CrossRef]
- Zhang, Y.; Hobson, B.W.; Kieft, B.; Godin, M.A.; Ravens, T.; Ulmgren, M. Adaptive Zigzag Mapping of a Patchy Field by a Long-Range Autonomous Underwater Vehicle. IEEE J. Ocean. Eng. 2024, 49, 403–415. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Y.; Wang, Y.; Zhang, H.; Zhang, L. Dynamic modeling and motion control strategy for deep-sea hybrid-driven underwater gliders considering hull deformation and seawater density variation. Ocean Eng. 2017, 143, 66–78. [Google Scholar] [CrossRef]
- Yang, C.; Peng, S.; Fan, S. Performance and Stability Analysis for ZJU Glider. Mar. Technol. Soc. J. 2014, 48, 88–103. [Google Scholar] [CrossRef]
- Isa, K.; Arshad, M.R.; Ishak, S. A hybrid-driven underwater glider model, hydrodynamics estimation, and an analysis of the motion control. Ocean Eng. 2014, 81, 111–129. [Google Scholar] [CrossRef]
- Liu, F.; Lan, T.; Wei, Z.; Sun, X.; Zhang, S.; Sang, H.; Huang, F. Adaptive propeller rudder controller for the wave glider with a propeller-rudder control system. Ocean Eng. 2023, 289, 116129. [Google Scholar] [CrossRef]
- Fan, S.S.; Yang, C.J.; Peng, S.L.; Li, K.H.; Xie, Y.; Zhang, S.Y. Underwater glider design based on dynamic model analysis and prototype development. J. Zhejiang Univ. Sci. C 2013, 14, 583–599. [Google Scholar] [CrossRef]
- Bhatta, P.; Leonard, N.E. Nonlinear gliding stability and control for vehicles with hydrodynamic forcing. Automatica 2008, 44, 1240–1250. [Google Scholar] [CrossRef]
- Su, Z.Q.; Zhou, M.; Han, F.F.; Zhu, Y.W.; Song, D.L.; Guo, T.T. Attitude control of underwater glider combined reinforcement learning with active disturbance rejection control. J. Mar. Sci. Technol. 2019, 24, 686–704. [Google Scholar] [CrossRef]
- Zhou, H.; Fu, J.; Zeng, Z.; Yu, C.; Wei, Z.; Yao, B.; Lian, L. Adaptive robust tracking control for underwater gliders with uncertainty and time-varying input delay. Ocean Eng. 2021, 240, 109945. [Google Scholar] [CrossRef]
- Caharija, W.; Pettersen, K.Y.; Gravdahl, J.T.; Børhaug, E. Integral LOS guidance for horizontal path following of underactuated autonomous underwater vehicles in the presence of vertical ocean currents. In Proceedings of the American Control Conference (ACC), Maui, HI, USA, 10–13 December 2012. [Google Scholar]
- Zhang, H. An Improved ELOS Guidance Law for Path Following of Underactuated Unmanned Surface Vehicles. Sensors 2024, 24, 5384. [Google Scholar]
- Xiu, Y.; Li, D.; Zhang, M.; Deng, H.; Law, R.; Huang, Y.; Wu, E.Q.; Xu, X. Finite-Time Sideslip Differentiator-Based LOS Guidance for Robust Path Following of Snake Robots. IEEE/CAA J. Autom. Sin. 2023, 10, 239–253. [Google Scholar] [CrossRef]
- Lefeber, E.; Pettersen, K.Y.; Nijmeijer, H. Tracking control of an underactuated ship. IEEE Trans. Control Syst. Technol. 2003, 11, 52–61. [Google Scholar] [CrossRef]
- Fossen, T.I.; Lekkas, A.M. Direct and indirect adaptive integral line-of-sight path-following controllers for marine craft exposed to ocean currents. Int. J. Adapt. Control Signal Process. 2017, 31, 445–463. [Google Scholar] [CrossRef]
- Leonard, N.E. Model-Based Feedback Control of Autonomous Underwater Gliders. IEEE J. Ocean. Eng. 2001, 26, 633–645. [Google Scholar] [CrossRef]
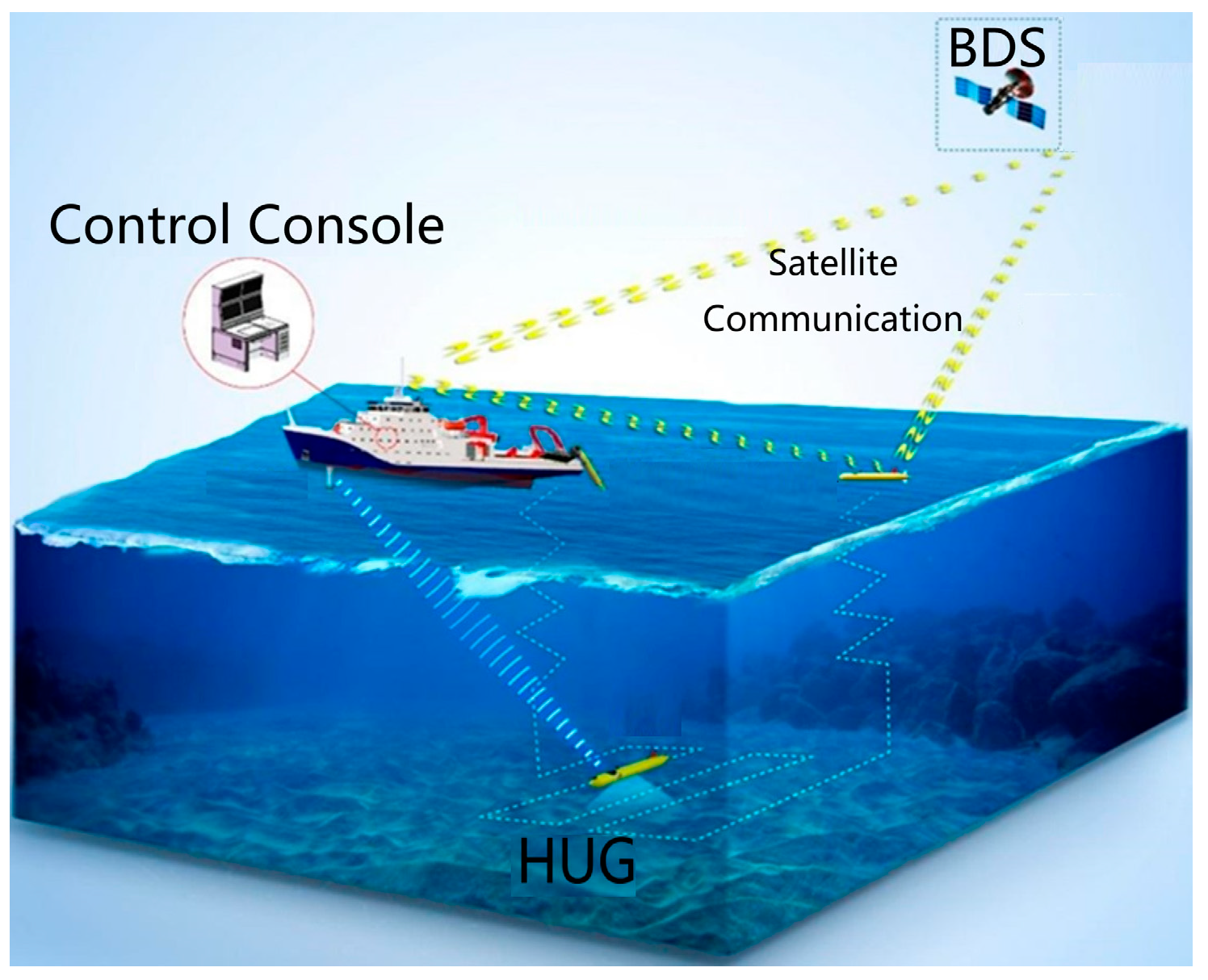
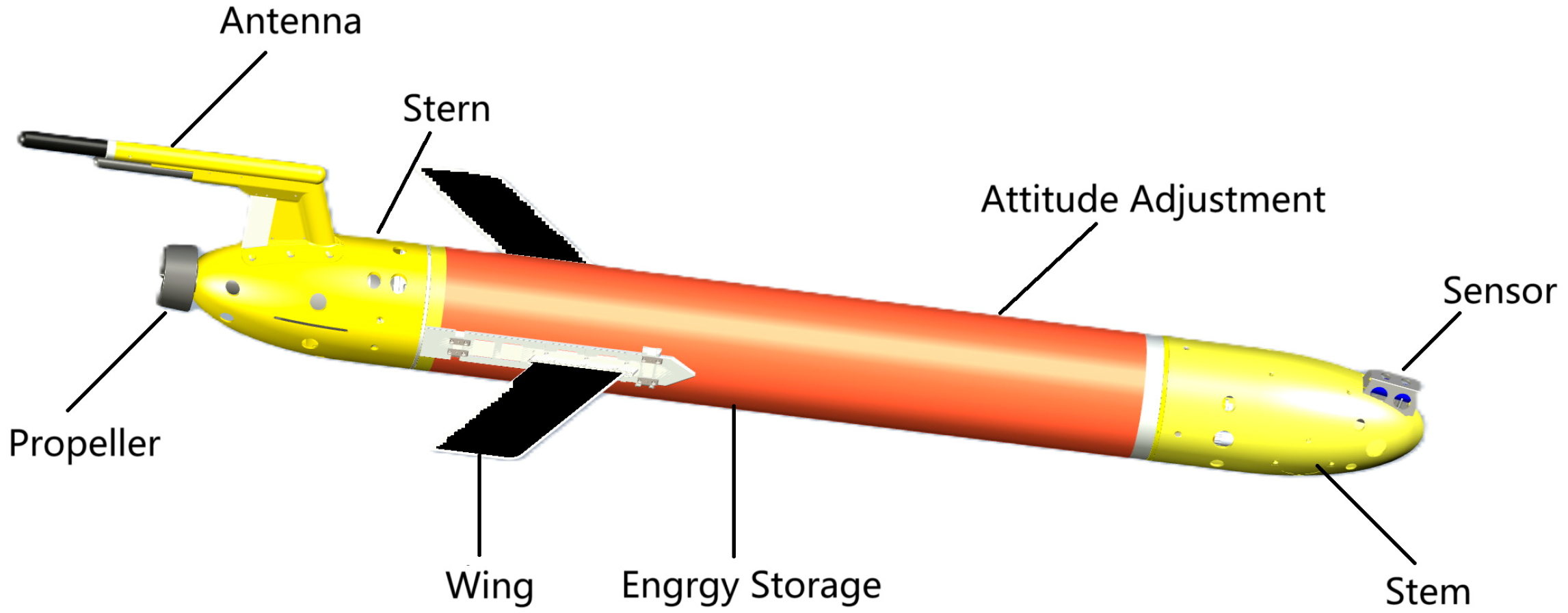
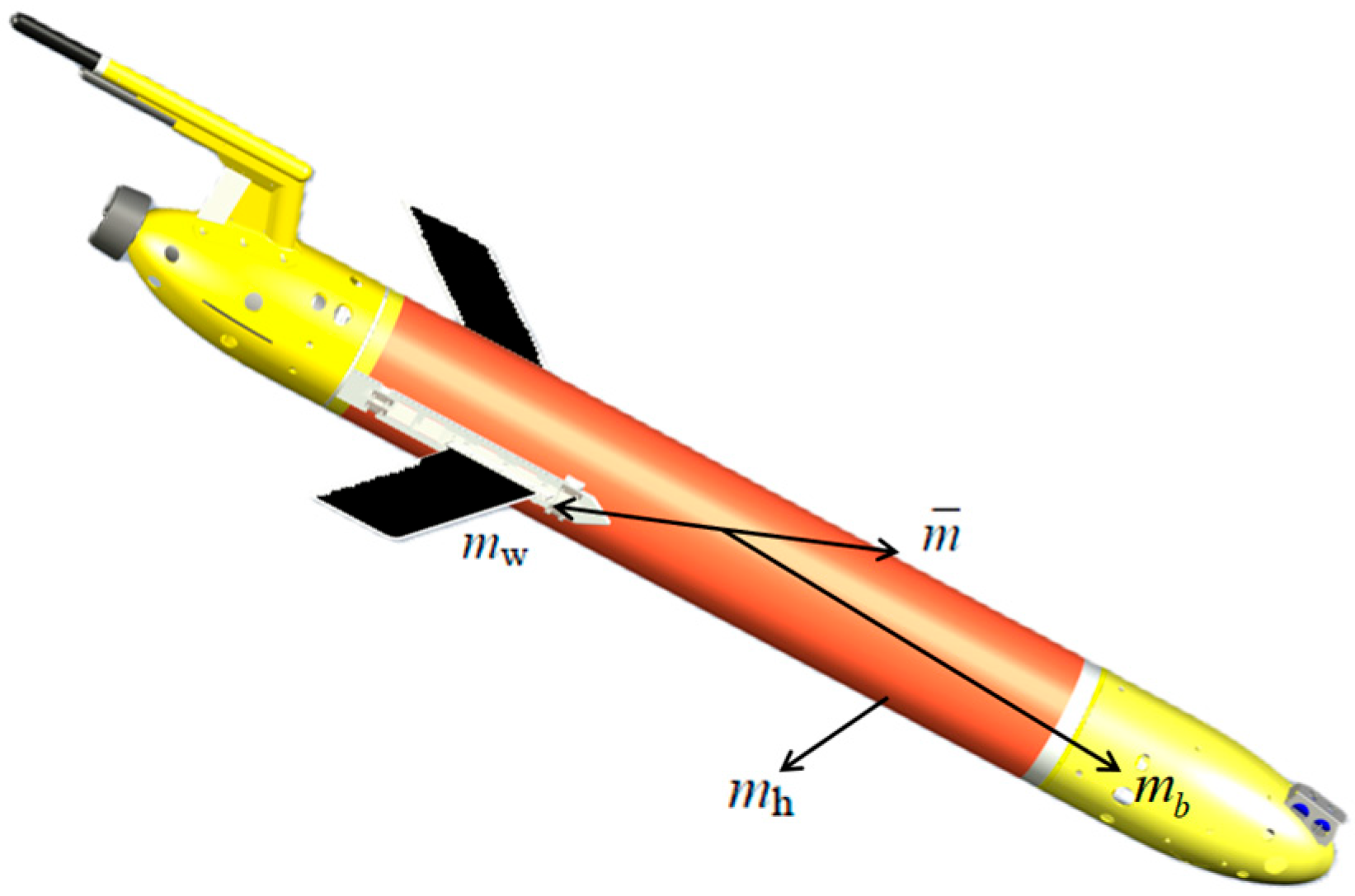
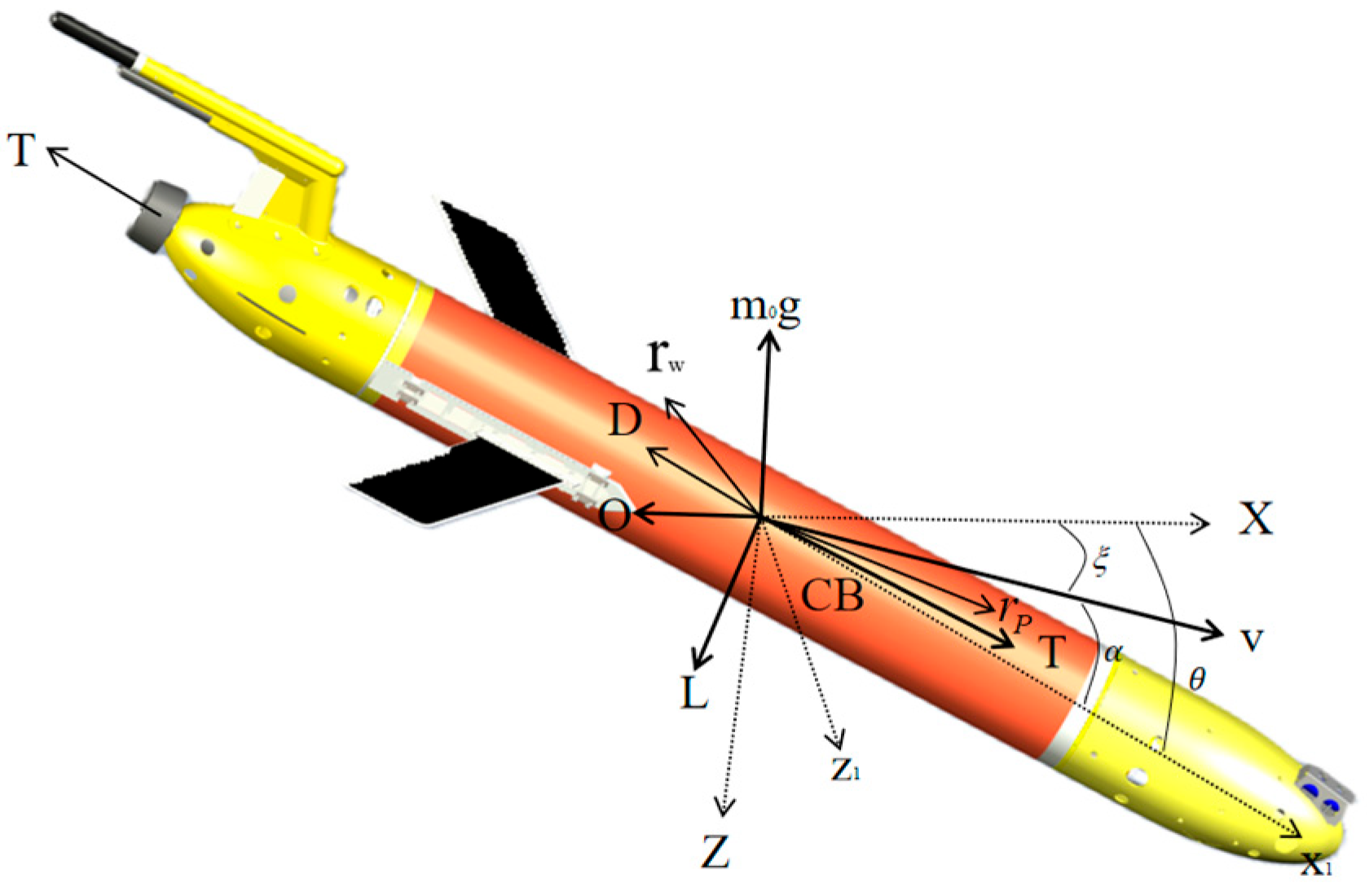

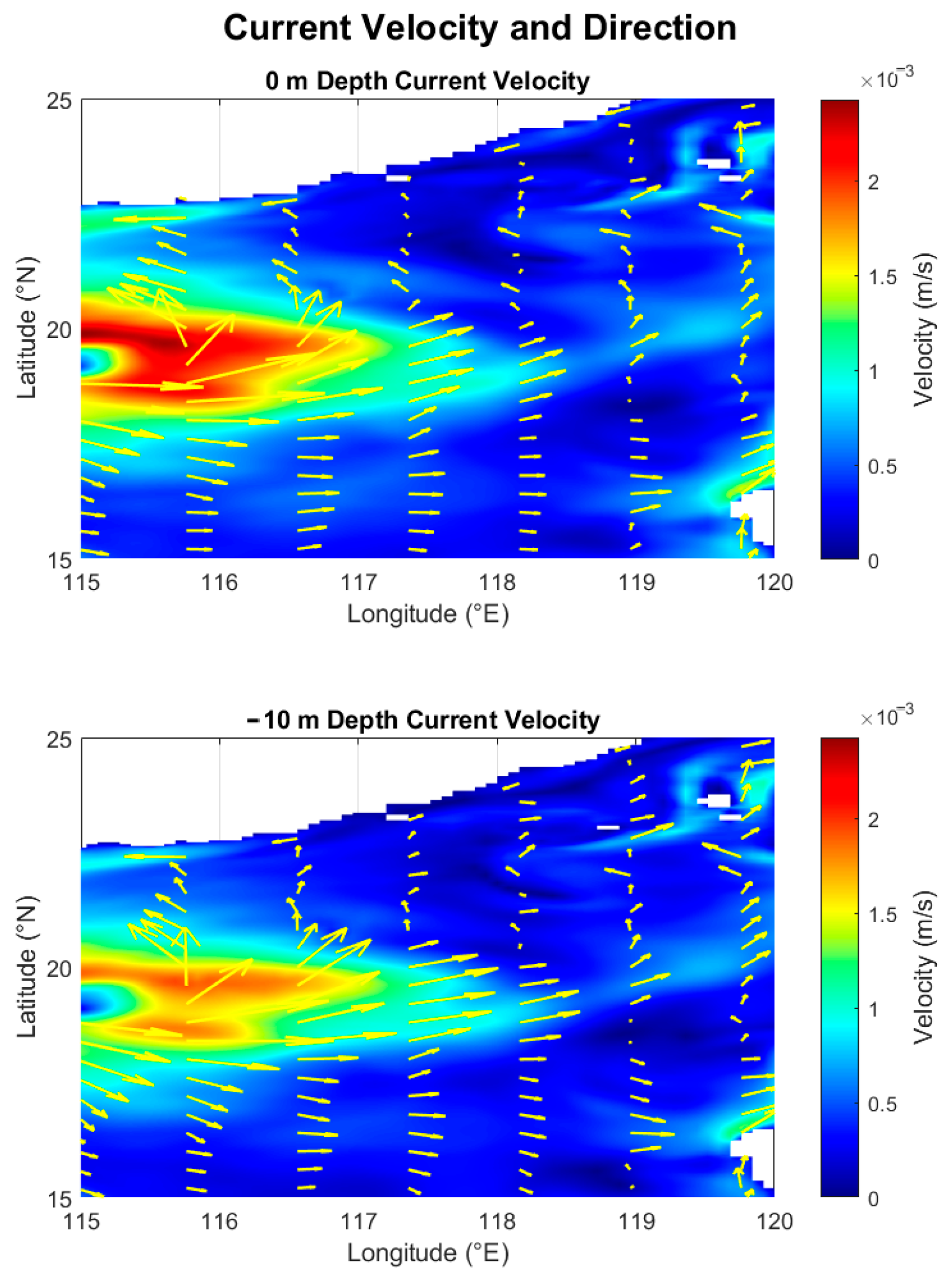
| Name | Numerical |
|---|---|
| length | 1.8 m |
| 45 kg | |
| 15 kg | |
| 20 kg | |
| 1025 kg/m3 | |
| 3.6 m | |
| 10.8 m |
| Performance Index | ADRC | OLOS-ADRC | |
|---|---|---|---|
| Time | Error | 7 s | 3 s |
| Depth | Error | −0.5 m | 0.2 m |
| Attitude Angle error | Undisturbed | 3.1° | 2.1° |
| Disturbed | 4.5° | 3.3° |
| Performance Index | ADRC | OLOS-ADRC | |
|---|---|---|---|
| Time | Error | 7 s | 1 s |
| Depth keeping | Error | 0.6 m | 0.1 m |
| Disturbed adjustment | Length | 0.5 m | 0.3 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Zhou, H.; Xu, P.; Jin, Y.; Tian, Z.; Zhao, Y. Optimized Line-of-Sight Active Disturbance Rejection Control for Depth Tracking of Hybrid Underwater Gliders in Disturbed Environments. J. Mar. Sci. Eng. 2025, 13, 1835. https://doi.org/10.3390/jmse13101835
Zhao Y, Zhou H, Xu P, Jin Y, Tian Z, Zhao Y. Optimized Line-of-Sight Active Disturbance Rejection Control for Depth Tracking of Hybrid Underwater Gliders in Disturbed Environments. Journal of Marine Science and Engineering. 2025; 13(10):1835. https://doi.org/10.3390/jmse13101835
Chicago/Turabian StyleZhao, Yan, Hefeng Zhou, Pan Xu, Yongping Jin, Zhangfu Tian, and Yun Zhao. 2025. "Optimized Line-of-Sight Active Disturbance Rejection Control for Depth Tracking of Hybrid Underwater Gliders in Disturbed Environments" Journal of Marine Science and Engineering 13, no. 10: 1835. https://doi.org/10.3390/jmse13101835
APA StyleZhao, Y., Zhou, H., Xu, P., Jin, Y., Tian, Z., & Zhao, Y. (2025). Optimized Line-of-Sight Active Disturbance Rejection Control for Depth Tracking of Hybrid Underwater Gliders in Disturbed Environments. Journal of Marine Science and Engineering, 13(10), 1835. https://doi.org/10.3390/jmse13101835






