Abstract
To enhance the adaptability of automated guided vehicles (AGVs) in port operations, this paper proposes a novel collaborative transport strategy for dual AGVs. This study focuses on reducing formation completion time, improving motion safety, and enhancing pose accuracy at the docking point for no-load dual AGVs, which is the first phase of the transport strategy. To implement this strategy, the sizes of the existing AGVs are adjusted, and a hybrid collaborative control framework is designed. This framework includes a feedback mechanism based on the leader–follower formation model, along with a closed-loop controller utilizing the sliding mode control algorithm. Finally, simulation and physical tests based on real port data verify the proposed strategy’s effectiveness. The results show it significantly enhances the dual AGVs’ motion safety and docking accuracy, providing new insights for smart port development.
1. Introduction
Automated guided vehicles (AGVs) play a pivotal role in modern port logistics by enhancing operational efficiency and reducing labor costs [1]. However, the growing demand for greater flexibility and adaptability in container transport presents significant challenges [2,3], which arise from three main factors: (1) Low Utilization: Ports commonly handle both 20-feet (ft) and 40 ft containers. Although current AGVs can transport either a single 40 ft container or two 20 ft containers simultaneously, they often end up transporting only one 20 ft container, leading to an underutilization of transport resources. (2) Poor Flexibility: the typical 15-m length of current AGVs requires ample operating space, which can cause traffic congestion and disrupt other machinery operations. (3) Poor Adaptability: As container sizes increase and port space decreases, current AGVs struggle to accommodate containers longer than 40 ft.
Therefore, the port industry urgently needs innovative transportation solutions to overcome these challenges and improve operational efficiency [4]. Inspired by the cooperative behavior seen in biological systems, such as bird flocks and fish schools, multi-robot collaborative transport offers a promising solution [5,6]. For example, two small AGVs can work together to transport containers of 40 ft or longer, while a single AGV is typically limited to transporting only one 20 ft container at a time. Currently, multi-robot collaborative transport can be categorized into two main approaches, force-feedback-based methods [7,8] and formation-based methods [9,10]. Compared to force-feedback methods, formation-based methods do not rely on high-precision force sensors and feature simpler control algorithms, making them more suitable for real-time onboard applications [11]. (1) Formation-based collaborative transport is especially well suited for dual AGV operations in smart port environments, and (2) the transport process of dual AGVs can be divided into two phases; first, operating in formation to the loading area without a load, and second, transporting the container to the unloading area. This paper focuses on the no-load formation phase of dual AGV operations. The following sections provide an in-depth review of the current research on formation control.
From the perspective of the topological relationships among formation members, mainstream formation control strategies can be categorized into virtual structure methods [12], behavior-based methods [13], graph-theoretic methods [14], leader–follower methods [15,16], and other related frameworks [17]. Among these, the leader–follower method is the most widely adopted method due to its simplicity, scalability, and ease of engineering implementation. For example, [18] proposed an adaptive robust formation control strategy based on non-singular terminal sliding mode control (SMC), which was successfully applied to joint formation scenarios involving unmanned aerial vehicles (UAVs) and unmanned ground vehicles (UGVs). While the study validated the effectiveness of this approach in a simulated environment, it highlighted the significant potential of the leader–follower method for heterogeneous multi-agent cooperative systems. Similarly, [19] introduced a distributed model predictive control (MPC) strategy to assess the formation performance of multiple mobile robots in dynamic, disturbed environments, demonstrating the effectiveness of the proposed scheme through integrated simulation experiments. Through a literature review, it was found that current research on leader–follower formation control focuses on three main areas: (1) enhancing the robustness of multi-robot systems by addressing challenges such as robust control, fault-tolerant control, and distributed control techniques aimed at maintaining formation stability despite disturbances and system faults in complex environments [20,21]; (2) improving communication and coordination efficiency, with approaches like graph-theoretic methods, game-theoretic frameworks, and distributed optimization, which focus on minimizing communication overhead while maintaining real-time performance and effective coordination [22,23]; and (3) advancing adaptive control and learning strategies using techniques like deep reinforcement learning (DRL), adaptive control, and online learning to achieve real-time adaptive behavior in dynamic environments, thereby enhancing the system’s overall adaptability [24,25].
However, several critical research areas remain underexplored, hindering the advancement of leader–follower-based formation control strategies. The main challenges are as follows: (1) Current research lacks robust feedback mechanisms, and formation schemes overly rely on the leader’s state information, which can lead to formation instability and safety risks [26,27,28]. For example, in container port operations, discrepancies between sensor measurements and the actual state of the leader AGV can result in positional errors, collisions, and conflicts among the AGVs’ formation; (2) Existing studies often lack rigorous theoretical analyses of key performance metrics, such as formation establishment time, system responsiveness, and control precision, limiting their applicability in high-performance scenarios [29,30,31]. For example, in dual AGV port operations, the limited operational space requires frequent starts, stops, and accelerations, along with stringent precision requirements at loading and unloading points to minimize the alignment time between cranes and AGVs, optimizing container loading efficiency. Failure to meet these control standards may result in collisions, excessive road occupancy, and delays in alignment, all of which severely impact container trans-shipment efficiency; (3) Much of the research focuses on simulation environments, with insufficient attention to real-world industrial scenarios, limiting the practical relevance and generalizability of the proposed solutions [32,33,34].
To address the challenges outlined above, this paper introduces three key innovations: (1) The traditional leader–follower formation strategy is enhanced with a feedback mechanism that mitigates the issue of state interaction between follower and leader AGVs. This enhancement improves the coupling between formation members, thereby increasing system stability, robustness, and fault tolerance; (2) An SMC controller is developed, incorporating position and orientation errors as constraints and applying an exponential convergence law to accelerate error convergence. This design improves the response time and accuracy of the formation control system while minimizing high-frequency oscillations and ensuring smoother operation; (3) In the context of container port operations, the time and distance required to establish a stable formation are evaluated to assess the feasibility and efficiency of the proposed strategy and controller for practical port applications. Additionally, accuracy metrics for parking position and the orientation of AGVs formation on straight and curved paths are developed, demonstrating the approach’s effectiveness and practicality through simulations and real-world experiments.
The remainder of this paper is organized as follows: Section 2 introduces the horizontal transportation technology used in smart container ports and the novel transportation strategy proposed in this study. Section 3 develops the kinematic model of a single AGV, followed by the dual AGV formation model and its associated feedback mechanism. Section 4 details the design of the SMC controller and demonstrates its stability using Lyapunov’s second method. Section 5 and Section 6 evaluate the no-load formation conditions through simulations and experiments, validating the effectiveness of the proposed approach. Finally, Section 7 concludes the paper by summarizing the research findings and discussing potential directions for future work.
2. Preliminary Knowledge
The AGV plays a central role in horizontal transportation tasks at smart container ports, transporting containers of various specifications between the storage yard and the quayside operation area, as illustrated in Figure 1.
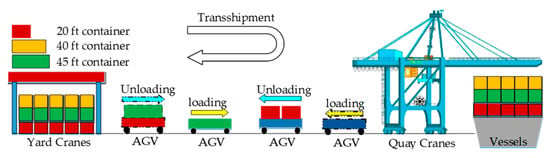
Figure 1.
Diagram of the horizontal transport process at the smart container ports.
Currently, AGVs in container ports typically have a length exceeding 15 m and are designed to transport either a 40 ft or 45 ft container or two 20 ft containers simultaneously. The dimensions of standard containers are specified in Table 1.

Table 1.
The size specifications of standard containers.
Under the new transportation strategy, small AGVs are employed to transport individual 20 ft containers, while dual small AGVs form a longitudinal formation to transport 40 ft containers, as illustrated in Figure 2. A key aspect of this dual AGV operation is the no-load formation maneuver leading to the handling point, which is the primary focus of this study.
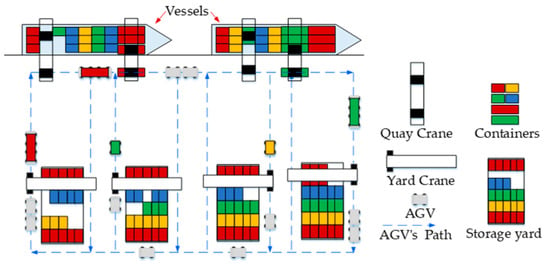
Figure 2.
Diagram of the new transportation strategy at the smart container ports.
3. System Modeling
3.1. The Kinematic Model of a Single AGV
Currently, smart container ports typically employ Ackermann-steered, electrically driven AGVs that operate under nonholonomic constraints. The kinematic model for these vehicles is assumed as follows: (1) The wheels experience no lateral slip, with only the front wheels being steerable and the rear wheels providing propulsion; (2) The steering angles of both front wheels are always identical; (3) Load transfer between the front and rear axles is neglected, restricting the model to planar motion.
In Figure 3, xoy represents the global coordinate system, and L denotes the wheelbase of the AGV. Points and represent the centers of the front and rear axles, respectively. denotes the steering angle of the front wheels, and represents the orientation of the AGV in the inertial frame. denotes the longitudinal velocity, and represents the angular velocity about the point . Based on the geometric relationships outlined, the i-th AGV in a fleet of N AGVs satisfies the following nonholonomic constraint equation:
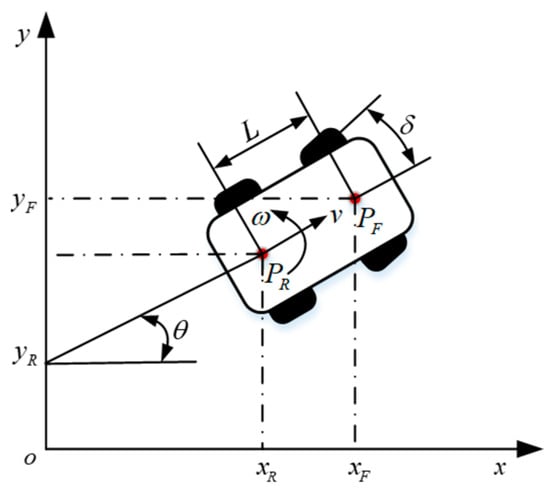
Figure 3.
Kinematic model of the single AGV.
The kinematic model of the i-th AGV is as follows:
In Equation (2), the relationship between the angular velocity , wheelbase , linear velocity , and the steering angle of the front wheels is expressed as follows:
Since and represent the input parameters of the dual AGVs’ formation control system, the subsequent controller design is primarily focused on calculating these two variables. Additionally, the geometric relationship between points and is described as follows:
3.2. Feedback Mechanism of the Formation
To improve the fault tolerance and robustness of the leader–follower formation strategy, a feedback mechanism for the formation is proposed in the following section. Typically, the desired path points for the leader AGV are communicated to its onboard controller via the higher-level control system. The leader AGV uses this onboard controller to perform path tracking and transmits the desired positions to the follower AGV based on the formation model. Both AGVs maintain the formation by tracking their respective desired positions. In this approach, the leader AGV only needs to send the desired positions to the follower at predefined intervals, without actively monitoring its tracking performance. However, in this study, both the leader and follower AGVs periodically transmit their motion states to the upper-level controller, which assesses whether the formation tracking error exceeds a specified threshold and makes decisions accordingly. Formation maintenance and calibration are then carried out as each AGV follows the commands from the upper controller.
As shown in Figure 4, the upper controller of the management system sends preset desired points to the onboard controller of the leader AGV. These desired points are expressed as follows:
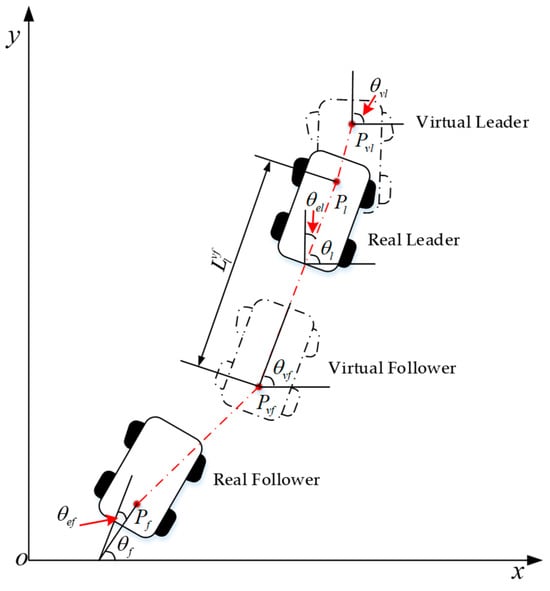
Figure 4.
Formation model of the dual AGVs.
During the formation task, the leader AGV is expected to follow the desired trajectory, as described in Equation (5). In this context, and represent the desired position and orientation of the leader AGV, respectively. To improve the formation control accuracy, the center point of the front and rear axles are selected as the reference points for the leader (virtual leader) and follower (virtual follower) AGVs. The point in Equation (5) is designated as the control point for the virtual leader AGV, which is used for tracking by the leader AGV. The parameter represents the position and orientation errors between the leader AGV’s control point and the tracking point . The parameter defines the error threshold for the leader AGV’s position and orientation tracking. The following inequalities must be satisfied to ensure that the tracking error of the leader AGV complies with the formation constraints:
In Equation (6), denotes the position error threshold of the leader AGV, which restricts the allowable range of position deviation, while denotes the posture error threshold, which limits the permissible range of orientation deviation between the leader and virtual leader AGVs.
The control point is computed from the control point , and the following geometric relationship between the two points is satisfied:
In Equation (7), denotes the distance between the control point and the control point . represents the leader AGV’s heading angle, which defines the body posture of the leader AGV. During the dual AGVs’ formation movement, the AGVs track the motion points and , respectively. The following inequalities must be satisfied for the follower AGV’s trajectory tracking error to meet the formation requirements:
In Equation (8), represents the relative position error between control points and . The parameter is the position error threshold for the follower AGV, which defines the maximum allowable position deviation. Similarly, denotes the body posture error between the follower AGV and the virtual follower, while represents the posture error threshold, which constrains the maximum allowable deviation in the follower’s orientation. When the inequalities in Equation (8) are satisfied, it indicates that both the position and posture errors of the follower AGV have converged within acceptable bounds during the formation movement.
In Figure 4, the upper controller uses consistent criteria to track errors in the dual AGVs. Taking the follower AGV as an example, if the tracking error exceeds the threshold (i.e., when Equation (8) is violated), the controller will check the posture error. If the position error is too large and is negative (indicating the control point is ahead), the controller will command the leader AGV to accelerate. If the position error is within limits but the posture error is too high, the controller will adjust the leader AGV’s angular velocity based on the follower’s heading. For example, if the follower AGV is misaligned to the left while the leader AGV is turning right, the controller will reduce the leader’s clockwise rotation to correct the posture. If a fault is detected in either AGV during operation, the controller will issue a stop command to both AGVs, ensuring smooth deceleration and safe parking.
To facilitate the design of the subsequent closed-loop feedback controller, the tracking error of the control point relative to the point for the follower AGV is analyzed. In Figure 5, represents the vehicle coordinate system, with the follower AGV’s body orientation along the axis, the axis perpendicular to the axis, and as the origin. The position and posture errors of the follower AGV’s control point relative to the virtual follower AGV’s control point can be expressed as follows:
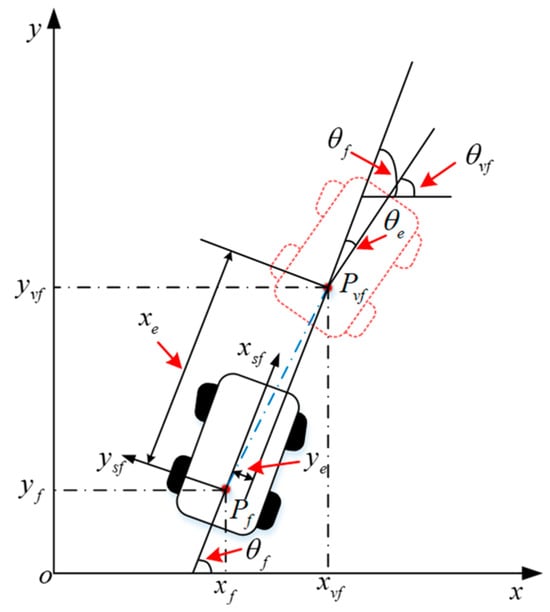
Figure 5.
Tracking error model of the follower AGV.
In Equation (9), for simplicity, we replace , , and with , , and , and we use these terms in the following sections. represents the projection of the position and posture errors on the follower AGV’s body coordinate system.
4. Innovative Controller Design
The dual AGV formation system has nonlinear dynamics and a strong coupling between its components. SMC is a robust nonlinear control method with advantages such as high disturbance rejection, simple design, and independence from system parameters and external disturbances. It does not require online identification and can achieve fast response times, making it ideal for dual AGV formation control. In the SMC algorithm, the system’s trajectory starts from an arbitrary position and moves towards the sliding mode surface in a finite amount of time. The key steps include determining the switching function based on error dynamics and calculating the control law. To reduce chattering and improve convergence time, a suitable convergence function must also be designed.
In the formation strategy above, both the leader and follower AGVs use the same control algorithms, turning the dual AGV formation control into a trajectory-tracking problem for each AGV. Using the follower AGV as an example, the controller is designed based on the desired position and posture , the desired velocity , and the actual position and posture . The goal is to design an SMC controller that uses position and posture errors , switching between functions and convergence laws, to calculate the control output . Finally, continuous feedback optimization ensures the tracking error converges to zero in a finite amount of time. The control principles are shown in Figure 6.
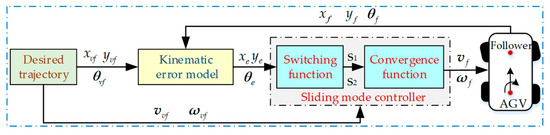
Figure 6.
Block diagram of the SMC system.
The differential equation for the error in the AGV’s control system can be derived by taking the time derivative of Equation (9):
During the collaborative movement of the dual AGVs, both position and posture constraints must be maintained simultaneously. Therefore, the heading angle error , lateral error , and longitudinal error are chosen as control parameters. The SMC switching functions are designed as follows:
To enhance the rate of error convergence in the dual AGV control system, an exponential convergence law is implemented, as given by the following equation:
In Equation (12), the convergence velocity is gradually reduced from a large value to zero based on the initial error, which reduces the convergence time and ensures the system trajectory reaches the sliding surface with minimal velocity. To minimize chattering, a continuous function is employed in place of the discontinuous function in Equation (12), as defined below:
In Equation (13), where is a small positive constant, combining Equations (10)–(13) leads to the following equation:
By combining the equations above, the system’s control laws can be derived as follows:
Considering the physical constraints of the AGV, the control output must satisfy the following conditions:
To prove the stability of the system, we construct the following Lyapunov function:
Taking the first-order derivative of Equation (18) yields the following equation:
In Equation (19), , , , , and are all positive values larger than zero. Therefore, Equation (19) can be expressed as follows:
When , and if and only if the condition is satisfied, according to Lyaounov’s second method, the SMC system is asymptotically stable.
5. Simulations and Analysis
Simulations are conducted in MATLAB to validate the effectiveness of the transportation strategy in the first phase and the implementation approach proposed in this study. The simulation examines two typical operating conditions: straight-line movement and the turning maneuvers of dual AGVs in an unloaded formation.
First, to evaluate the feedback mechanism for dual AGVs, performance is compared between formation strategies with and without it. In one test, the AGVs start synchronously at a set distance and move together in a straight line while maintaining the desired separation. However, due to a fault in the follower AGV, the AGVs do not start simultaneously. The analysis then examines how the feedback mechanism influences the results.
Second, motion distance and time are key indicators for evaluating the performance of the formation strategy and controller, particularly when the AGVs start independently and quickly form a stable formation after receiving a task. The faster they achieve a stable formation within a limited area, the more efficient the transportation. This indicator also helps assess whether the proposed scheme is suitable for real-world applications.
Third, in container transport, an AGV’s route includes both straight-line and turning movements. Therefore, the simulation in this paper incorporates both motion types to evaluate the effectiveness of the proposed scheme. The position and orientation accuracy of the dual AGVs after reaching the target point are used to assess whether the formation reduces the adaptation time between the spreader and AGVs. Based on real-world operations in smart container ports, the required parking accuracy is set at less than 0.02 m for position and 0.035 rad for orientation.
Several key parameters are kept constant to the simulations described above. and represent the control point of the leader and follower AGVs, respectively, while, , , , and are the linear and angular velocities of the dual AGVs. The controller parameters include the sampling frequency and other values like for tuning. To make the test more realistic and avoid actuator saturation, the AGV’s linear and angular accelerations are limited. Specifically, linear acceleration is restricted to −6 m/s2 to 1 m/s2, and angular acceleration is limited to −0.25 rad/s2 to +0.25 rad/s2. The AGV specifications are as follows: wheelbase m, a total length of 6.2 m, and overhangs of 0.6 m at the front and rear. For the simulations, a 40 ft container with a length of 12.2 m is used. To balance the forces on the AGVs, the container is placed with its ends aligned with the front and rear axles of the AGVs. The distance between the dual AGVs in the simulation is set to 1 m, measured between the overhangs. Further details are shown in Figure 7.
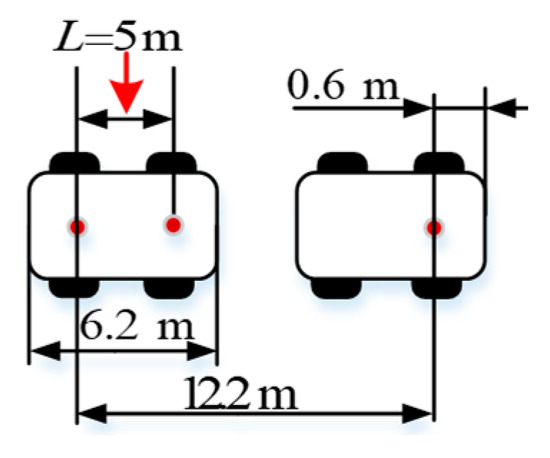
Figure 7.
Longitudinal formation of no-load dual AGVs.
5.1. Simulation with the Formation Feedback Mechanism
At the start of the simulation, the two AGVs are parked in their assigned positions, with the actual control points of the leader and follower AGVs represented by and , respectively. Due to an actuator failure, the follower AGV is delayed in starting and does not synchronize with the leader AGV. The actuator fault on the follower AGV is resolved after 5 s. As the longitudinal error between the AGVs increases, a clear distinction in formation behavior is observed, depending on the presence or absence of a feedback mechanism. The simulation duration is 25 s, with the AGVs moving in a straight line throughout. In the first 10 s, the leader AGV accelerates uniformly from rest with a constant acceleration of . Afterward, it moves at a constant velocity for 5 s, followed by a constant deceleration phase with an acceleration of over the next 10 s. Throughout the simulation, the SMC controller and leader–follower strategy control the follower AGV’s motion. The relevant system parameters, including , , and , are defined. The simulation results are shown in Figure 8.
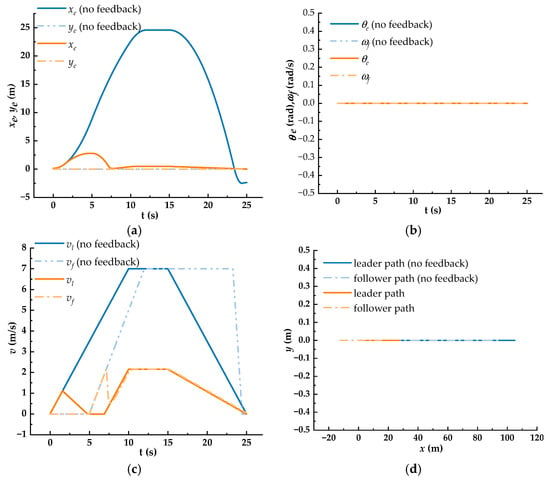
Figure 8.
Performance testing of the feedback mechanism. (a) Lateral and longitudinal errors; (b) heading angle error and angular velocity; (c) comparison curves of linear velocity; (d) comparison curves of the path.
In Figure 8a, the simulation without the feedback mechanism shows that, due to the follower AGV remaining stationary for the first 5 s, its longitudinal error increases. The error exceeds 20 m until the leader AGV begins decelerating, at which point it starts to decrease. Eventually, the error stabilizes at −2.37 m, indicating a collision between the AGVs. In contrast, with the feedback mechanism (Figure 8a), the longitudinal error is kept within the set thresholds of 2.5 m and −0.1 m. When the error exceeds these limits, the upper controller adjusts the leader AGV’s velocity to bring the error back within the threshold range, allowing the longitudinal error to decrease quickly once it surpasses the upper threshold. The lateral and heading angle errors in Figure 8a,b remain zero throughout the simulation, demonstrating that the formation strategy ensures precise straight-line motion, due to the effective control of the SMC controller. In Figure 8c, the velocities of the leader and follower AGVs fluctuate several times with the feedback mechanism, whereas without the feedback mechanism, their velocities follow the planned trajectory exactly. This difference arises because the feedback mechanism ensures the longitudinal error stays within the set thresholds. Figure 8d shows the motion paths of the AGVs. In the simulation without the feedback mechanism, the follower AGV’s parking accuracy is poor, with a longitudinal error of −2.3 m, indicating a collision. With the feedback mechanism, the AGVs’ parking accuracy improves, and the longitudinal error decreases to −0.01 m. The results presented above provide two key insights: (1) the formation feedback mechanism developed in this study enhances the completion rate, safety, and precision of the formation control tasks; and (2) the control strategy that incorporates this formation feedback mechanism exhibits significant fault tolerance and demonstrates superior environmental adaptability compared to strategies that do not employ such a mechanism.
Additionally, the situation in which the angle error exceeds the threshold aligns closely with the simulation principles outlined earlier. Therefore, a separate comparative analysis of the feedback mechanism is unnecessary, as the behavior under these conditions is consistent with the previous results.
5.2. Simulation with the Dual AGVs’ Form Maintains the Formation
Due to the limited horizontal transport area within the smart container ports, the dual AGVs must quickly form a stable formation in a short time. Generally, the average working velocity of an AGV in a smart port is approximately 7 m/s. Therefore, the maximum velocity of the follower AGV is set to 10 m/s, with the normal working velocity being 7 m/s. The simulation scenarios are as follows: Two AGVs park in different locations and, upon receiving a transport task, begin to form and maintain their formation while moving. At the initial time, the position and posture of the leader and follower AGVs are and , respectively. Both the leader and follower AGVs have a velocity of zero. The desired formation of the dual AGVs is the same as shown in Figure 7. In the simulation, during the first 10 s, the leader AGV accelerates uniformly with an acceleration of 0.7 m/s2. Subsequently, the leader AGV maintains a velocity of 7 m/s while moving in a straight line, and the entire simulation lasts for 300 s. The movement of the follower AGV is guided by the formation strategy and controller. Other parameters are set as follows: , , and . The relevant simulation results are shown in Figure 9.
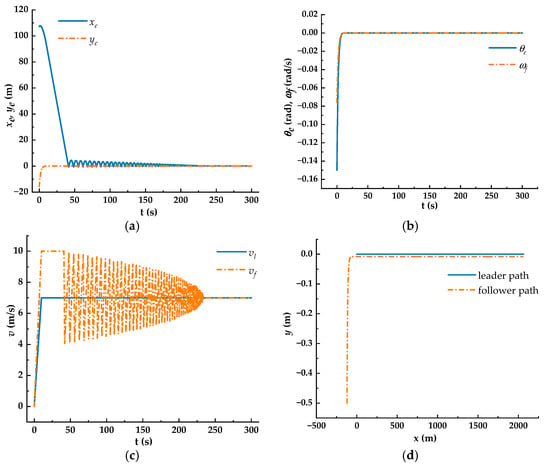
Figure 9.
Dual AGVs form and keep the formation (). (a) Lateral and longitudinal errors; (b) heading angle error and angular velocity; (c) comparison curves of linear velocity; (d) comparison curves of the path.
In Figure 9a, the lateral and longitudinal position errors of the follower AGV are m and m during the initial phase. As the leader AGV moves, the lateral and longitudinal errors begin to decrease. For example, the lateral error stably converges to at the 12th s, indicating a fast error convergence speed of the control system. The longitudinal error stably converges to m at the 230th s, indicating that the follower AGV moves for 230 s (approximately 1680 m) before the formation stabilizes. It is suitable for formation tasks where the dual AGVs are far away from the handling point. When the AGVs are close to the handling point, the leader AGV can move at low velocity or remain stationary, allowing the follower AGV to catch up and reduce the distance required for the dual AGVs to achieve a stable formation. Figure 9b shows that the heading angle error quickly decreased after the follower AGV started to move and finally stabilized at zero at the 9th s. In addition, the angular velocity of the follower AGV also converged to zero at the 9th s. The change in angular velocity compensates for the position and posture errors at the initial time. In Figure 9c, to achieve longitudinal and lateral errors of less than 0.01 m, the linear velocity of the follower AGV approaches that of the leader AGV. Eventually, the velocities of the dual AGVs are aligned at the 230th s, indicating that it took 230 s for the formation to stabilize. Figure 9d shows the motion paths of the leader and follower AGVs, demonstrating that the dual AGVs maintained good straightness throughout the simulation.
The simulation results shown In Figure 9 Indicate that the formation stability time Is too long, which is not ideal for actual transport operations. In practice, the longitudinal error of the formation can be allowed to increase within a certain range, as long as stability is maintained. Therefore, another simulation is conducted, adjusting the convergence threshold of the longitudinal error to less than 0.05 m, to test the time required for the dual AGVs to transition from standstill to a stable formation. Some parameters are readjusted as follows: and . The new simulation results are shown in Figure 10.
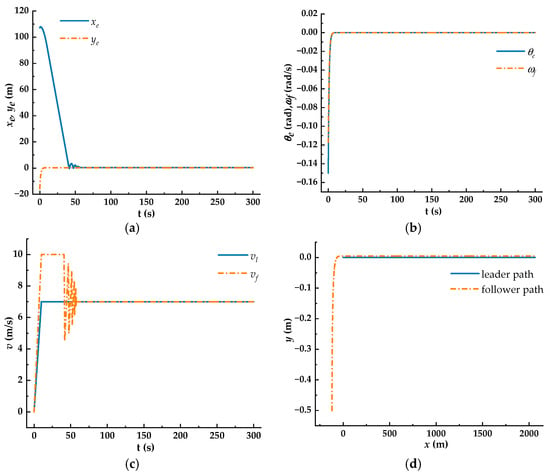
Figure 10.
Dual AGVs form and keep the formation (). (a) Lateral and longitudinal errors; (b) heading angle error and angular velocity; (c) comparison curves of linear velocity; (d) comparison curves of the path.
In Figure 10a, the lateral and longitudinal errors of the follower AGV stably converge to m and m, respectively, where converges at the 10th s, and converges at the 57th s. This indicates that the follower AGV’s motion lasts for 57 s (approximately 469 m) before the dual AGV formation stabilizes, yielding results significantly better than before. Figure 10b shows that the heading angle error of the follower AGV steadily converges to zero at the 11th s, along with the angular velocity. The convergence times of these two parameters are similar to those observed in the previous simulation. Figure 10c shows that the time required for the dual AGVs to achieve consistent linear velocity is reduced. At the 57th s, the motion state of the dual AGVs becomes synchronized. Figure 10d demonstrates that the formation of the dual AGVs maintains good straightness throughout the simulation, highlighting the stability of the SMC controller proposed in this study.
5.3. Simulation in Turning Condition
This part simulates the movement of the dual AGVs between the quay cranes and the yard cranes. Specifically, the two AGVs, running near the terminal front and close to each other, quickly form a formation after receiving a transport task and work together to reach the handling point. This simulation involves a combination of turning and straight-line motions. The relevant simulation parameters are set as follows: , , , , and . The initial position and posture of the dual AGVs are and , respectively. The simulation lasts for 30 s. During the first 5 s, the leader AGV guides the follower AGV to move in a straight line at a constant velocity of 4 m/s. Then, the dual AGVs turn at a constant angular velocity for 20 s. Finally, the leader AGV moves in a straight line with uniform deceleration for the last 5 s. To validate the superiority of the proposed control method, a comparative analysis is conducted with the incremental PID control method used in state-of-the-art automated container ports. For clarity, the control method proposed in this paper is referred to as Con1, while the incremental PID control method is denoted as Con2. Con2 employs a distributed control architecture for the longitudinal and lateral control of the AGVs. The gain parameters for the longitudinal PID controller are as follows: proportional gain , integral gain , and derivative gain . For the lateral PID controller, the parameters are as follows: proportional gain , integral gain , and derivative gain . The corresponding simulation results are shown in Figure 11.
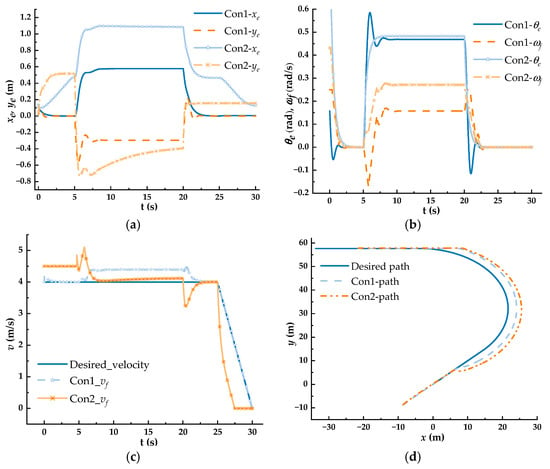
Figure 11.
Simulation performance under various turning conditions. (a) Lateral and longitudinal errors; (b) heading angle error and angular velocity; (c) comparison curves of linear velocity; (d) comparison curves of the path.
Figure 11a compares the positional accuracy of the two port AGV control methods: Con1, the centralized SMC control method proposed herein; and Con2, the incremental PID control method used in leading ports. It presents the longitudinal and lateral motion errors of the AGVs over time.
For the longitudinal error, Con1 remains close to zero during the first 0–5 s, indicating a capacity to maintain precise initial formation. As the formation enters a curve at 6 s, the error gradually increases, stabilizing at 0.45 m by 8.5 s. After transitioning to a straight path at 20.6 s, the error decreases and converges to 0.015 m by 23 s, remaining constant until the vehicles stop. In contrast, Con2’s longitudinal error increases during the 0–5 s interval, indicating poor longitudinal consistency and formation space instability. The error rises from 5 to 8.5 s while performing the curve, stabilizes at 1.1 m from 8.5 to 20.6 s, and then decreases upon entering the straight path, with slower convergence and lower precision than Con1. At the stopping point, the error is 0.12 m.
For the lateral error, Con1 shows negligible error during the first 5 s, reflecting excellent motion consistency. Between 5 and 20.6 s, the error briefly increases before stabilizing, and then rapidly converges to zero after 20.6 s, aligning with the longitudinal error trend and indicating effective motion coordination. At the stopping point, Con1’s lateral error is 0.013 m. For Con2, the lateral error fluctuates significantly, peaking at 0.76 m during the turn, reflecting poor formation retention. At the stopping point, the lateral error is 0.128 m, substantially higher than Con1’s.
The steady-state errors observed for both Con1 and Con2 between 8.5 and 20.6 s are due to the nonholonomic constraints of the AGVs, which prevent access to certain turning positions. These errors, however, remain within an acceptable range.
Figure 11b shows the steady-state heading angle error of Con1, which primarily occurs during the initial straight segment, the turning segment, and the straight segment following the turn of the simulated AGV formation. The data indicate that as the road conditions change, the heading angle error of Con1 adjusts quickly and converges within a short period, demonstrating the excellent real-time performance and stability of the proposed formation control method. At the turning points, the maximum heading angle error between formations is 0.45 rad, and at the stopping points, it is 0.025 rad, meeting the precision requirements for AGVs at automated port loading and unloading points.
The yaw rate of Con1 remains stable throughout, with only minor fluctuations during turns, indicating that the proposed method effectively reduces system oscillations, ensuring smooth AGV formation operation.
In contrast, Con2 performs less favorably. Its heading angle error and yaw rate show significant fluctuations during the initial phase, indicating an overshoot. Although Con2 exhibits good convergence in subsequent straight, turning, and deceleration segments, its steady-state heading angle error and yaw rate are higher than Con1. This suggests that Con2 uses a more aggressive control strategy, potentially leading to higher energy consumption and safety risks. However, at the stopping points, the heading angle error is 0.032 rad, still meeting the docking precision requirements for port AGVs, indicating that Con2 also meets the operational requirements for lateral control.
Figure 11c shows the velocity variations in Con1 and Con2. The data reveal that Con1 exhibits smaller fluctuations and smoother velocity changes throughout the simulation. Except for the turning segment between 5 and 20.6 s, where its longitudinal velocity exceeds that of the leading AGV, while Con1 maintains a high consistency with the leading AGV’s longitudinal velocity during other phases. This demonstrates that Con1’s longitudinal velocity control is stable and can effectively track the velocity changes in the leading AGV.
In contrast, Con2 operates at a relatively high velocity from the outset. As it attempts to correct formation errors, its velocity fluctuates several times, eventually stopping at 27 s. The data show that Con2 performs poorly in longitudinal velocity control, with frequent fluctuations in formation error and unstable AGV operation, posing significant safety risks. Furthermore, this aggressive operational mode likely leads to higher energy consumption compared to Con1.
Figure 11d illustrates the operational paths of the AGV formation under Con1 and Con2. The data indicate that while both methods maintain formation stability and operational accuracy to some extent, Con1 outperforms Con2 in all aspects.
Specifically, Con1 demonstrates superior performance in the following ways: During linear motion, the dual AGVs maintain high path coherence. Although the follower AGV’s larger turning radius slightly reduces coherence during turning, this does not compromise its overall formation performance. The simulation results demonstrate that the Con1 method enables two AGVs, despite initial positional deviations, to rapidly achieve formation within 5 s. Throughout the operation of the dual AGV formation, a high formation consistency is preserved. In particular, at the docking points, the positional error between the AGVs is minimized to 0.016 m, while the attitude error is strictly constrained to 1.8°. This precise coordination not only enhances the efficiency of the loading spreader’s docking process but also mitigates the occurrence of AGV load imbalance, which may result from improper container placement during the loading procedure.
The simulation results Indicate the following: (1) The dual AGV formation control strategy and its associated controllers proposed in this study meet the operational requirements for horizontal transportation in automated container ports, thereby demonstrating their potential for practical application in real-world scenarios; (2) During the experiments, variations in road curvature and AGV velocity did not significantly affect the responsiveness, control precision, or task completion rate of the control system. The system consistently exhibited high performance, underscoring the low sensitivity of the designed formation control system to changes in environmental parameters and highlighting its robust performance.
6. Experiments and Analysis
To demonstrate the engineering application of the scheme proposed in this study, several physical experiments are presented. A brief overview of the experimental setup is first provided. In these experiments, two AGVs developed by our robotics lab are used. Figure 12a,b show the top and bottom views of the AGV, respectively. For a single AGV, the master controller is a Raspberry Pi, which manages the data interaction between the leader and follower AGVs, sensor data fusion and decoding, command distribution, and other functions. The slave controller, an STM32, handles sensor data collection and motor control. The upper controller, a computer, is responsible for path planning and decision-making during formation tasks. Both the upper controller and the Raspberry Pi run the Ubuntu 18.04 operating system and the robot operating system (ROS).

Figure 12.
The hardware system structure of a single AGV. (a) Top view; (b) bottom view.
The upper controller (computer) communicates with the single AGV via the network port of the Raspberry Pi, while the master controller interfaces with the slave controller through serial ports. Data interactions between controllers are managed through publishing and subscribing to topics and services in ROS. The communication topology between the AGVs is shown in Figure 13.
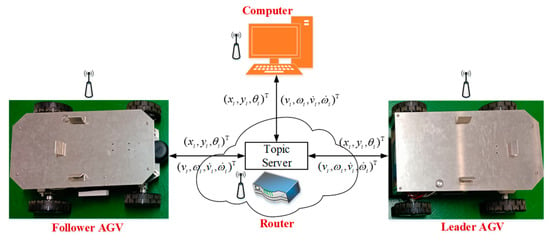
Figure 13.
Schematic of a hybrid communication network.
Due to space limitations of the experimental setup, a container scaled to 1/15th of a standard 40 ft container was designed. Accordingly, the AGV size was also adjusted. The dimensions of the scaled-down 40 ft container are 0.81 m in length, 0.16 m in width, and 0.17 m in height. The wheelbase of a single AGV is m, and its total length is 0.42 m. Based on the no-load formation experiments, the parameter is set to m. The system’s sampling frequency during the experiments is , and other relevant parameters are specified in the corresponding experiment sections. To validate the simulation results, the experiments focus on testing the formation feedback mechanism and evaluating parking position accuracy under various working conditions.
6.1. Experiment with the Formation Feedback Mechanism
In the experiment, the initial pose of the leader and follower AGVs are , , respectively. The leader AGV starts from rest and accelerates uniformly in a straight line for 5 s. It then continues at a constant velocity of 0.2 m/s for 10 s before decelerating uniformly in a straight line for 5 s, bringing its velocity to zero. Due to a failure in the follower AGV, it starts 5 s later than the leader AGV. The maximum velocity of the dual AGVs is limited to 0.2 m/s, and the formation feedback mechanism is activated when the longitudinal error between the two AGVs exceeds 1.5 m or falls below −0.1 m. In this experiment, when the upper controller detects that the distance between the dual AGVs exceeds the upper threshold, it commands the leader AGV to decelerate uniformly until the distance is within the threshold. Similarly, when the distance falls below the lower threshold, the upper controller sends a uniform acceleration command to the leader AGV until the distance is within the range. The parameters of the controller in the experiment are as follows: , , , , and . The experimental results, both with and without a feedback mechanism, are shown in Figure 14.
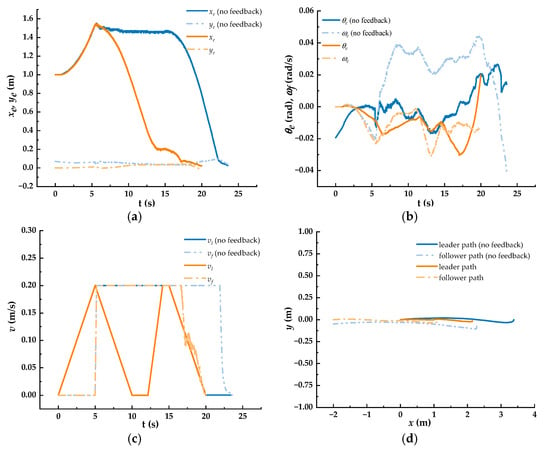
Figure 14.
The experiment with and without a feedback mechanism. (a) Lateral and longitudinal errors; (b) heading angle error and angular velocity; (c) comparison curves of linear velocity; (d) comparison curves of the path.
In Figure 14a, to clearly highlight the differences between the experiments and prevent potential damage due to AGV collision, the longitudinal error is set to m in both experiments, with and without the feedback mechanism. It can be observed that in the experiment with the feedback mechanism, the longitudinal error quickly decreased after the lateral error exceeded the 1.5 m threshold, and by the 20th s, it stably converged to 0. In contrast, in the experiment without the feedback mechanism, the longitudinal error only began to decrease once the leader AGV stopped, and by the 25th s, it converged to zero. These results indicate that the feedback mechanism in the dual AGV formation enhances the efficiency of maintaining a stable formation. In Figure 14b, it can be seen that the heading angle error and the angular velocity fluctuations of the follower AGV are more prolonged in the experiment without the feedback mechanism. This suggests that the feedback mechanism helps make the dual AGVs’ motion smoother, especially when the system has significant initial errors. Figure 14c shows that the leader AGV reduces its linear velocity when the follower AGV’s longitudinal tracking error exceeds the predefined threshold. This feedback mechanism effectively shortens the time needed to achieve a stable formation. Figure 14d shows the paths of both the leader and follower AGVs. Under identical initial error conditions, it is clear that the dual AGV system without a feedback mechanism requires a longer path to reach the desired formation. This is primarily due to the leader AGV’s failure to decelerate in response to the follower AGV’s increasing tracking error. Additionally, inherent mechanical imperfections in the self-developed AGVs, such as manufacturing tolerances and assembly errors, cause deviations from the desired straight-line path.
6.2. Experiment in Turning Condition
The turning maneuver experiment is a key test for evaluating the feasibility and effectiveness of the proposed dual AGV formation strategy, as it involves both linear and curvilinear motion. The initial pose of the dual AGVs are set as follows: and , respectively. The experiment begins with the leader AGV starting from rest and linearly accelerating to a velocity of 0.2 m/s over a 5 s interval. The AGV then maintains a constant linear velocity while executing a 10 s turning maneuver with an angular velocity of . Afterward, the leader AGV transitions to a linear motion phase for 10 s at a constant velocity of 0.2 m/s, followed by a 5 s deceleration phase to a complete stop. The motion of the follower AGV is fully controlled by the formation strategy and controller, as shown in Figure 15.
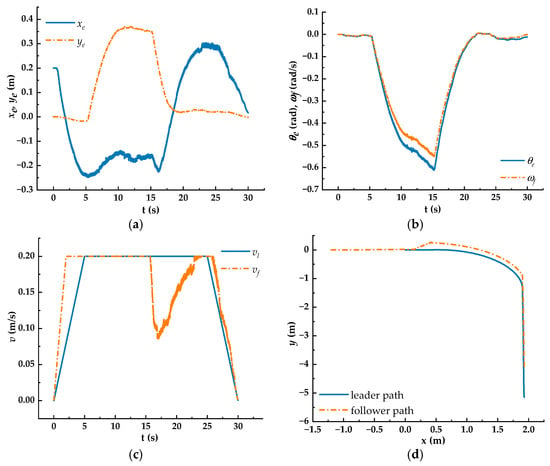
Figure 15.
Experiment performance under turning conditions. (a) Lateral and longitudinal errors; (b) heading angle error and angular velocity; (c) comparison curves of linear velocity; (d) comparison curves of the path.
Figure 15a shows that both the longitudinal and lateral tracking errors converge to zero during the linear motion phase. Although the errors increase during the turning maneuver, they remain within bounds and eventually stabilize at a steady-state value. These experimental results are consistent with the simulation findings presented in the previous section. The increased tracking errors during the turning maneuver can be attributed to the nonholonomic constraints of the AGV’s kinematic model, which limits its lateral maneuverability. Figure 15b shows that both the longitudinal and lateral tracking errors are significant during the turning maneuver but converge to near-zero values during the linear motion phase, consistent with the simulation results. Additionally, due to the inherent mechanical imperfections of the experimental AGV, the controller requires a small control input to compensate for these errors, even during the linear motion phase. This highlights the controller’s sensitivity and precision. As shown in Figure 15c, the follower AGV experiences a noticeable decrease in linear velocity during the turning maneuver. This reduction is due to the inter-AGV distance falling below the predefined threshold. Figure 15d reveals that the follower AGV follows a trajectory with a larger turning radius than the leader AGV. Despite this difference, the dual AGV system successfully maintains formation throughout the experiment. Foremost, in the parking area, the poses of dual AGVs are and , respectively. The experimental data show a separation of 1.016 m between the AGVs during the parking maneuver. Additionally, the pose accuracy between the AGVs is 0.01 rad. This level of precision allows for quick adaptation between the spreader and the AGVs at the handing point.
7. Conclusions
The study focuses on the small-sized dual AGV collaborative transportation strategy. This strategy addresses the long-standing challenge of low transport efficiency in automated container ports, caused by limited AGV flexibility and adaptability. By improving AGV performance during the no-load stage, particularly in formation control, this approach provides valuable insights into enhancing port throughput, reducing operational costs, and shortening ship waiting times, thereby potentially increasing port competitiveness in the global shipping market.
Specifically, our hybrid collaborative control framework, which combines the leader–follower model with an SMC algorithm, achieves higher pose accuracy at docking points. This precision reduces the alignment time between AGVs and loading equipment, thereby improving loading efficiency. Additionally, the reduced formation completion time optimizes port resource utilization, enabling a more efficient scheduling of container handling tasks.
For researchers in freight logistics, intelligent transportation systems (ITSs), and AGV development, our study offers practical insights. In freight logistics, dual-agent cooperation can optimize the transport of large or specialized cargo, where single-vehicle approaches often fall short. In an ITS, our algorithms can be integrated into port traffic management systems to improve coordination and traffic flow. AGV researchers can build on our control algorithms, adapting them for different AGV models or more complex port scenarios.
Future research could explore the scalability of the dual AGV system, such as extending the cooperative model to multiple AGV clusters to manage the exponential growth of container traffic in megaports. Enhancing the adaptability of control algorithms to extreme weather conditions, such as strong winds or heavy rain, is another potential direction. Additionally, future studies should focus on quantifying the improvements in efficiency brought by the proposed strategy, analyzing the exact time and energy savings and assessing the overall impact on port operation efficiency. This could include real-world testing and comprehensive simulations to provide more detailed insights into the potential benefits for port logistics.
Author Contributions
Conceptualization, W.L. and Q.Z.; methodology, Q.Z. and W.L.; software, Q.Z. and L.G.; validation, W.L.; formal analysis, Q.Z. and X.Q.; investigation, Q.Z. and W.L.; resources, W.L. and Q.Z.; data curation, Q.Z.; writing—original draft preparation, Q.Z.; writing—review and editing, Q.Z. and W.L.; visualization, Q.Z., W.L., L.G., and X.Q.; supervision, W.L.; project administration, W.L. and Q.Z.; funding acquisition, W.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grants 62173263), the Innovation Research Team Project of Natural Science Foundation of Hainan, China (621CXTD1013), and the National Key Research and Development Program of China (2019YFB1600400).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author. The data are not publicly available due to the limitations of the study phase.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kon, W.K.; Abdul Rahman, N.S.F.; Md Hanafiah, R.; Abdul Hamid, S. The Global Trends of Automated Container Terminal: A Systematic Literature Review. Marit. Bus. Rev. 2021, 6, 206–233. [Google Scholar] [CrossRef]
- Lau, Y.; Chen, Q.; Poo, M.C.-P.; Ng, A.K.Y.; Ying, C.C. Maritime Transport Resilience: A Systematic Literature Review on the Current State of the Art, Research Agenda and Future Research Directions. Ocean Coast. Manag. 2024, 251, 107086. [Google Scholar] [CrossRef]
- Pjevcevic, D.; Nikolic, M.; Vidic, N.; Vukadinovic, K. Data Envelopment Analysis of AGV Fleet Sizing at a Port Container Terminal. Int. J. Prod. Res. 2017, 55, 4021–4034. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, W.-F.; Zhou, J.-L. No-Load Formation Control of Dual AGVs Based on Container Terminals. In Proceedings of the 2022 IEEE International Conference on Networking, Sensing and Control (ICNSC), Shanghai, China, 15–18 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Rizzo, C.; Lagrana, A.; Serrano, D. GEOMOVE: Detached AGVs for Cooperative Transportation of Large and Heavy Loads in the Aeronautic Industry. In Proceedings of the 2020 IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC), Ponta Delgada, Portugal, 15–17 April 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 126–133. [Google Scholar] [CrossRef]
- Huzaefa, F.; Liu, Y.-C. Force Distribution and Estimation for Cooperative Transportation Control on Multiple Unmanned Ground Vehicles. IEEE Trans. Cybern. 2023, 53, 1335–1347. [Google Scholar] [CrossRef]
- Flixeder, S.; Glück, T.; Kugi, A. Force-Based Cooperative Handling and Lay-up of Deformable Materials: Mechatronic Design, Modeling, and Control of a Demonstrator. Mechatronics 2017, 47, 246–261. [Google Scholar] [CrossRef]
- Rosenfelder, M.; Ebel, H.; Eberhard, P. Force-Based Organization and Control Scheme for the Non-Prehensile Cooperative Transportation of Objects. Robotica 2024, 42, 611–624. [Google Scholar] [CrossRef]
- Chen, Q.; Sun, Y.; Zhao, M.; Liu, M. Consensus-Based Cooperative Formation Guidance Strategy for Multiparafoil Airdrop Systems. IEEE Trans. Autom. Sci. Eng. 2021, 18, 2175–2184. [Google Scholar] [CrossRef]
- Su, Y.-H.; Bhowmick, P.; Lanzon, A. A Robust Adaptive Formation Control Methodology for Networked Multi-UAV Systems with Applications to Cooperative Payload Transportation. Control Eng. Pract. 2023, 138, 105608. [Google Scholar] [CrossRef]
- Er, M.J.; Li, Z. Formation Control of Unmanned Surface Vehicles Using Fixed-Time Non-Singular Terminal Sliding Mode Strategy. J. Mar. Sci. Eng. 2022, 10, 1308. [Google Scholar] [CrossRef]
- Guo, J.; Liu, Z.; Song, Y.; Yang, C.; Liang, C. Research on Multi-UAV Formation and Semi-Physical Simulation With Virtual Structure. IEEE Access 2023, 11, 126027–126039. [Google Scholar] [CrossRef]
- Wen, J.; Yang, J.; Li, Y.; He, J.; Li, Z.; Song, H. Behavior-Based Formation Control Digital Twin for Multi-AUG in Edge Computing. IEEE Trans. Netw. Sci. Eng. 2023, 10, 2791–2801. [Google Scholar] [CrossRef]
- Chen, F.; Ren, W. Multi-Agent Control: A Graph-Theoretic Perspective. J. Syst. Sci. Complex. 2021, 34, 1973–2002. [Google Scholar] [CrossRef]
- He, S.; Wang, M.; Dai, S.-L.; Luo, F. Leader-Follower Formation Control of USVs With Prescribed Performance and Collision Avoidance. IEEE Trans. Ind. Inform. 2019, 15, 572–581. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, D.; Yang, S.; Shan, M. A Practical Leader-Follower Tracking Control Scheme for Multiple Nonholonomic Mobile Robots in Unknown Obstacle Environments. IEEE Trans. Control Syst. Technol. 2019, 27, 1685–1693. [Google Scholar] [CrossRef]
- Chang, X.; Jiao, J.; Li, Y.; Hong, B. Multi-Consensus Formation Control by Artificial Potential Field Based on Velocity Threshold. Front. Neurosci. 2024, 18, 1367248. [Google Scholar] [CrossRef]
- Ullah, N.; Mehmood, Y.; Aslam, J.; Ali, A.; Iqbal, J. UAVs-UGV Leader-Follower Formation Using Adaptive Non-Singular Terminal Super Twisting Sliding Mode Control. IEEE Access 2021, 9, 74385–74405. [Google Scholar] [CrossRef]
- Jiang, C.; Guo, Y. Incorporating Control Barrier Functions in Distributed Model Predictive Control for Multirobot Coordinated Control. IEEE Trans. Control Netw. Syst. 2024, 11, 547–557. [Google Scholar] [CrossRef]
- Trinh, M.H.; Tran, Q.V.; Vu, D.V.; Nguyen, P.D.; Ahn, H.-S. Robust Tracking Control of Bearing-Constrained Leader-Follower Formation. Automatica 2021, 131, 109733. [Google Scholar] [CrossRef]
- Xuan-Mung, N.; Hong, S.K. Robust Adaptive Formation Control of Quadcopters Based on a Leader-Follower Approach. Int. J. Adv. Robot. Syst. 2019, 16, 172988141986273. [Google Scholar] [CrossRef]
- Liu, X.; Ge, S.S.; Goh, C.-H. Vision-Based Leader-Follower Formation Control of Multiagents With Visibility Constraints. IEEE Trans. Control Syst. Technol. 2019, 27, 1326–1333. [Google Scholar] [CrossRef]
- He, J.; Liao, J. Formation Tracking Control with Disturbance Rejection in Leader-Follower Multi-Agent Systems under Dynamic Event-Triggered Mechanism. Eng. Appl. Artif. Intell. 2024, 133, 108441. [Google Scholar] [CrossRef]
- Khodamipour, G.; Khorashadizadeh, S.; Farshad, M. Adaptive Formation Control of Leader-Follower Mobile Robots Using Reinforcement Learning and the Fourier Series Expansion. ISA Trans. 2023, 138, 63–73. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Liu, H.; Xie, F.; Huang, H. Adaptive Distributed Control for Leader-Follower Formation Based on a Recurrent SAC Algorithm. Electronics 2024, 13, 3513. [Google Scholar] [CrossRef]
- Gao, Z.; Guo, G. Fixed-Time Leader-Follower Formation Control of Autonomous Underwater Vehicles With Event-Triggered Intermittent Communications. IEEE Access 2018, 6, 27902–27911. [Google Scholar] [CrossRef]
- Wang, Y.; Shan, M.; Yue, Y.; Wang, D. Vision-Based Flexible Leader-Follower Formation Tracking of Multiple Nonholonomic Mobile Robots in Unknown Obstacle Environments. IEEE Trans. Control Syst. Technol. 2020, 28, 1025–1033. [Google Scholar] [CrossRef]
- Li, Z.; Yuan, Y.; Ke, F.; He, W.; Su, C.-Y. Robust Vision-Based Tube Model Predictive Control of Multiple Mobile Robots for Leader-Follower Formation. IEEE Trans. Ind. Electron. 2020, 67, 3096–3106. [Google Scholar] [CrossRef]
- Shen, H.; Yin, Y.; Qian, X. Fixed-Time Formation Control for Unmanned Surface Vehicles with Parametric Uncertainties and Complex Disturbance. J. Mar. Sci. Eng. 2022, 10, 1246. [Google Scholar] [CrossRef]
- Li, K.; Shen, Z.; Jing, G.; Song, Y. Angle-Constrained Formation Control under Directed Non-Triangulated Sensing Graphs. Automatica 2024, 163, 111565. [Google Scholar] [CrossRef]
- Wang, S.; Wang, H.; Li, Y.; Li, Q. Distributed Finite-Time Neuroadaptive Fault-Tolerant Formation Control for Multi-Robot Systems. Appl. Ocean. Res. 2024, 150, 104067. [Google Scholar] [CrossRef]
- Du, Z.; Zhang, H.; Wang, Z.; Yan, H. Model Predictive Formation Tracking-Containment Control for Multi-UAVs With Obstacle Avoidance. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 3404–3414. [Google Scholar] [CrossRef]
- Wang, C.; Sun, Y.; Ma, X.; Chen, Q.; Gao, Q.; Liu, X. Multi-Agent Dynamic Formation Interception Control Based on Rigid Graph. Complex Intell. Syst. 2024, 10, 5585–5598. [Google Scholar] [CrossRef]
- Guo, T.; Liu, Y.; Hu, H.-X. Adaptive Connectivity-Preserving Formation Control with a Dynamic Event-Triggering Mechanism. J. Frankl. Inst. 2025, 362, 107331. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).