An Equivalent Linear Method to Predict Nonlinear Bending Mechanics of Dredging Floating Hose String
Abstract
1. Introduction
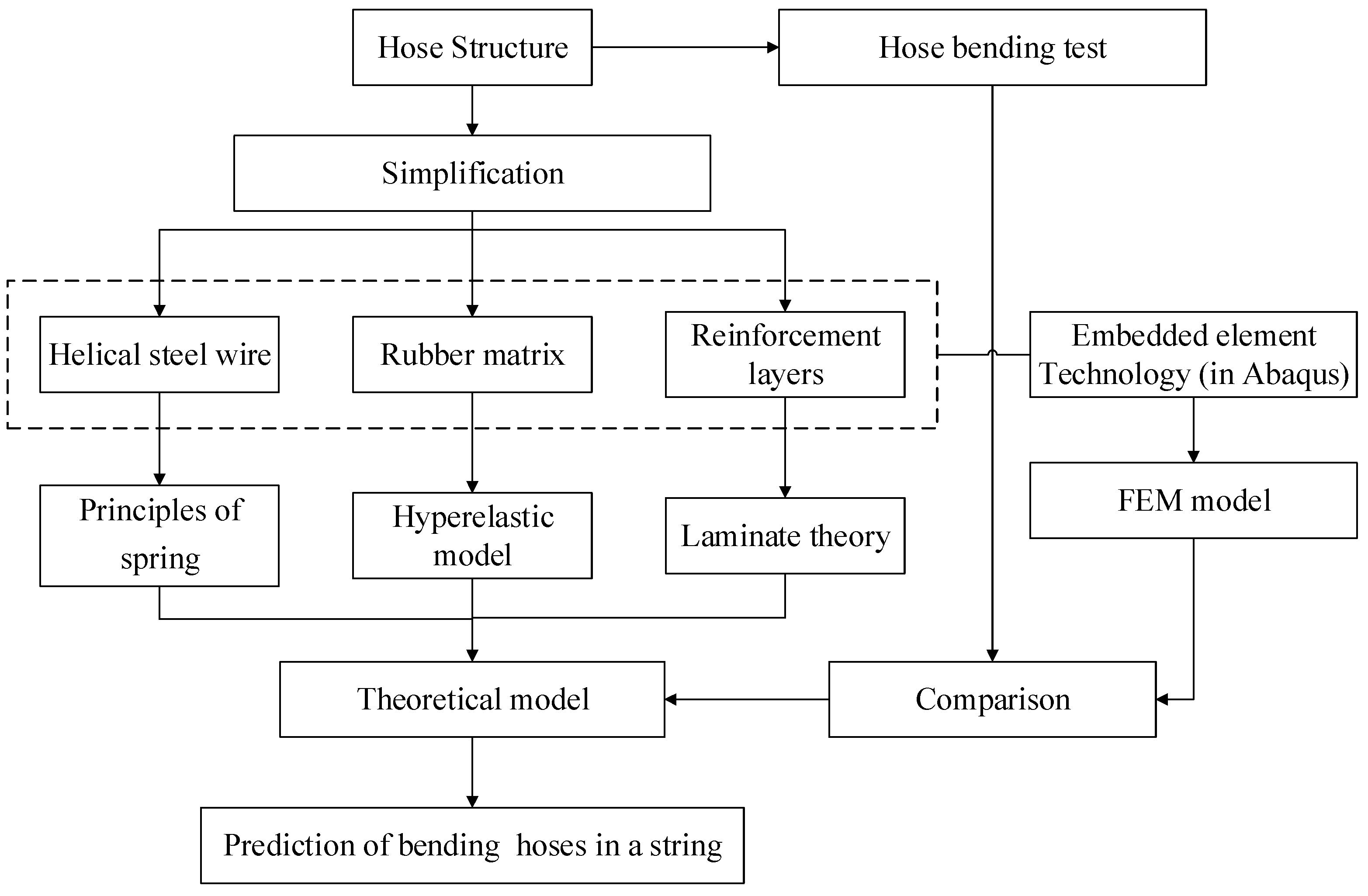
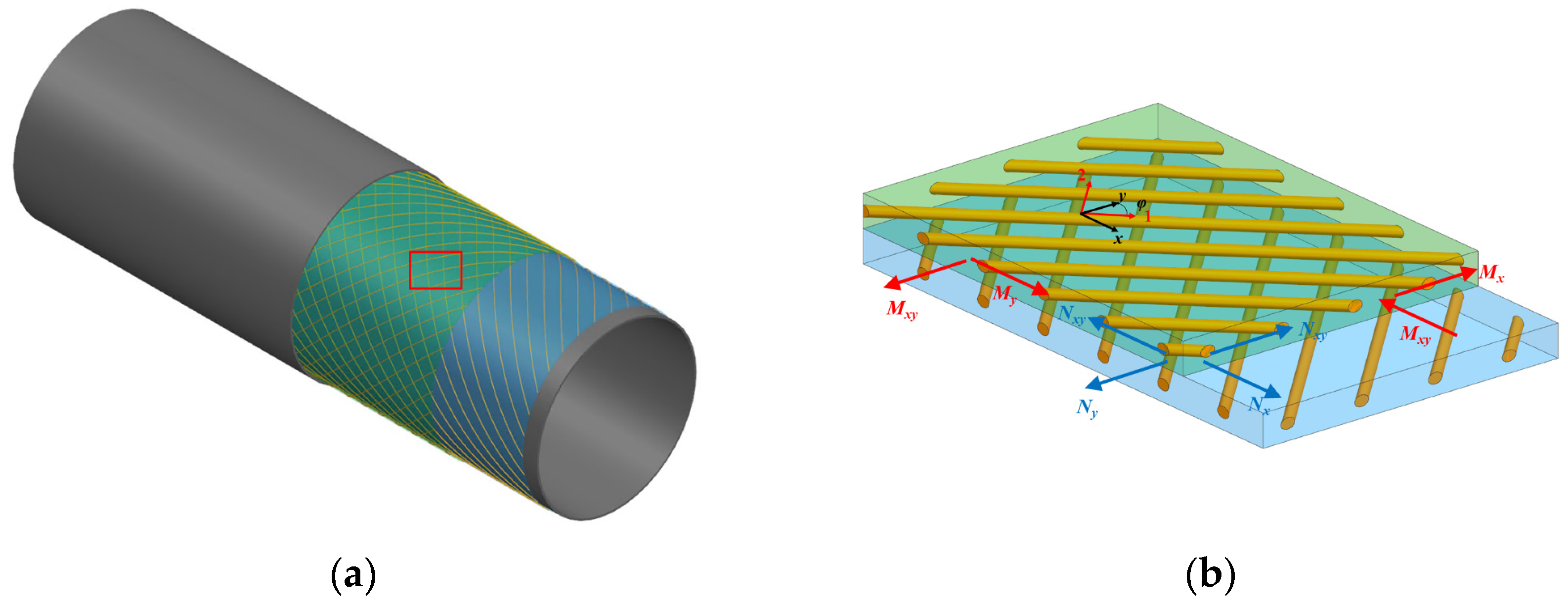
2. Hose Structure and Assumption
- (a)
- The whole hose is divided into three main components based on the structure and material characteristics of the floating hose, including the rubber matrix, cord reinforcement layer, and helical steel wire. There are no material defects in any group of structures. The floating body and other outer structures do not bear loads when the hose bends.
- (b)
- The adhesion assumption, wherein each layer maintains adhesion without separation under external forces.
- (c)
- The cord layer is considered a linear elastic material within a small deformation range.
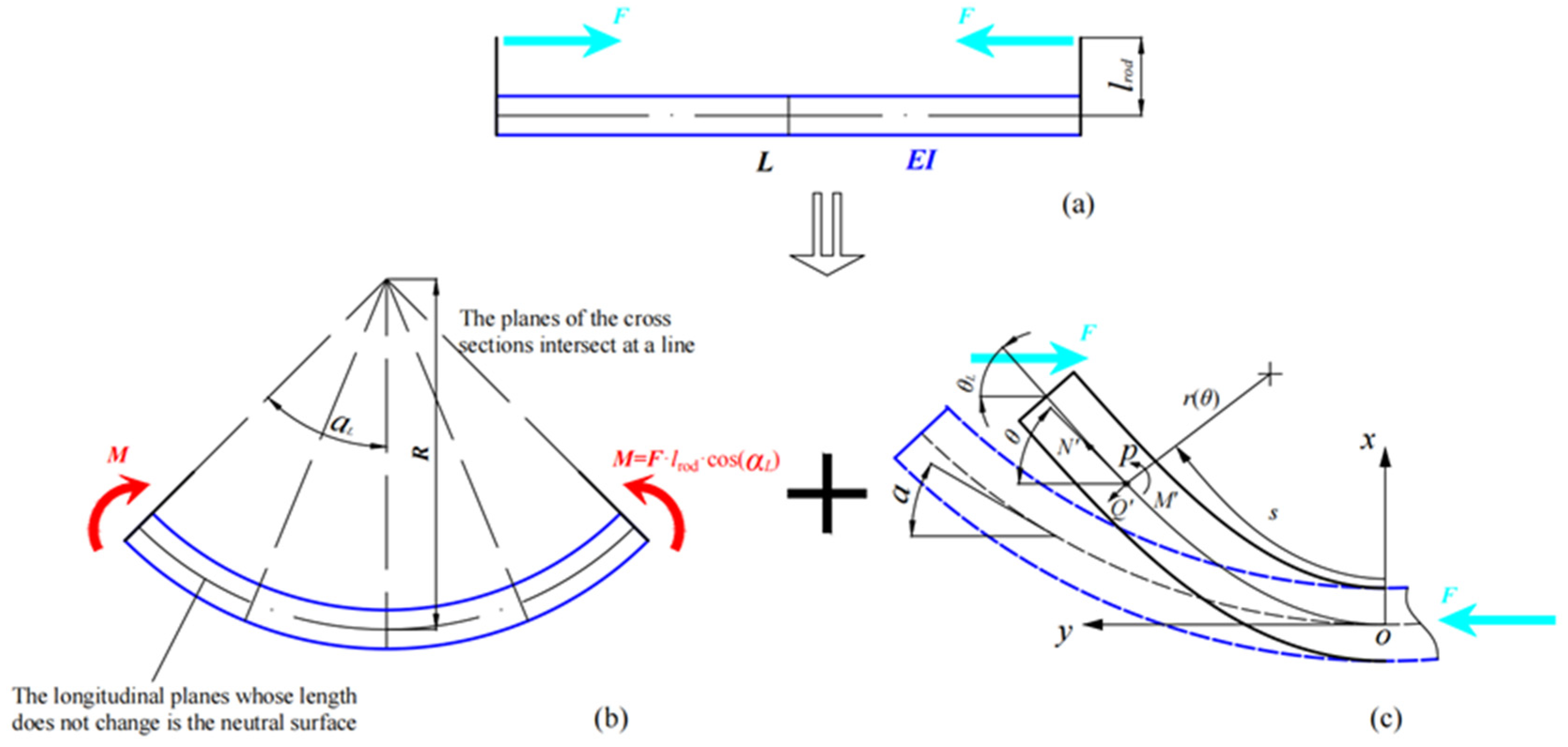
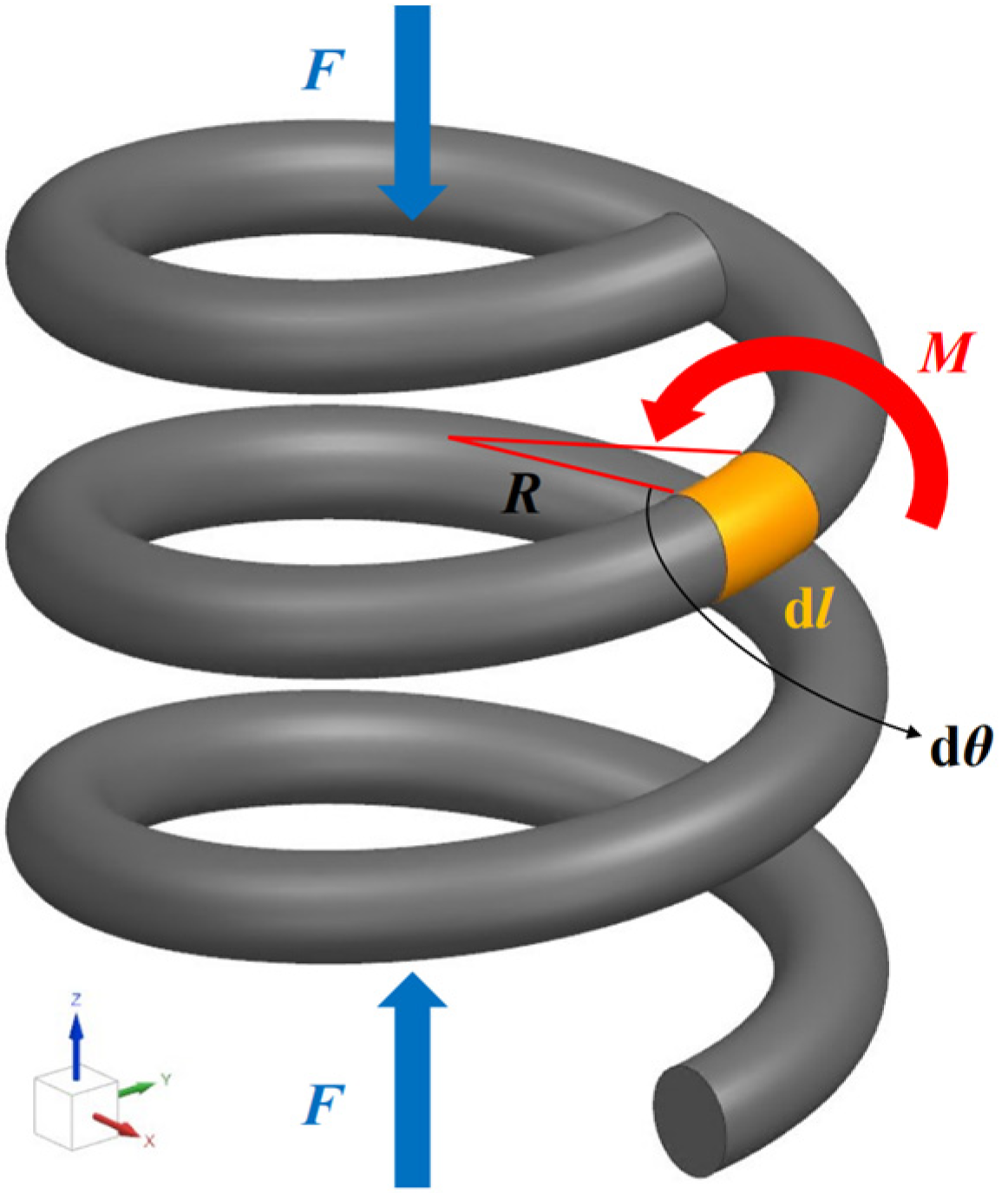
3. Theoretical Analysis Solution
3.1. The Constitutive of Rubber Matrix
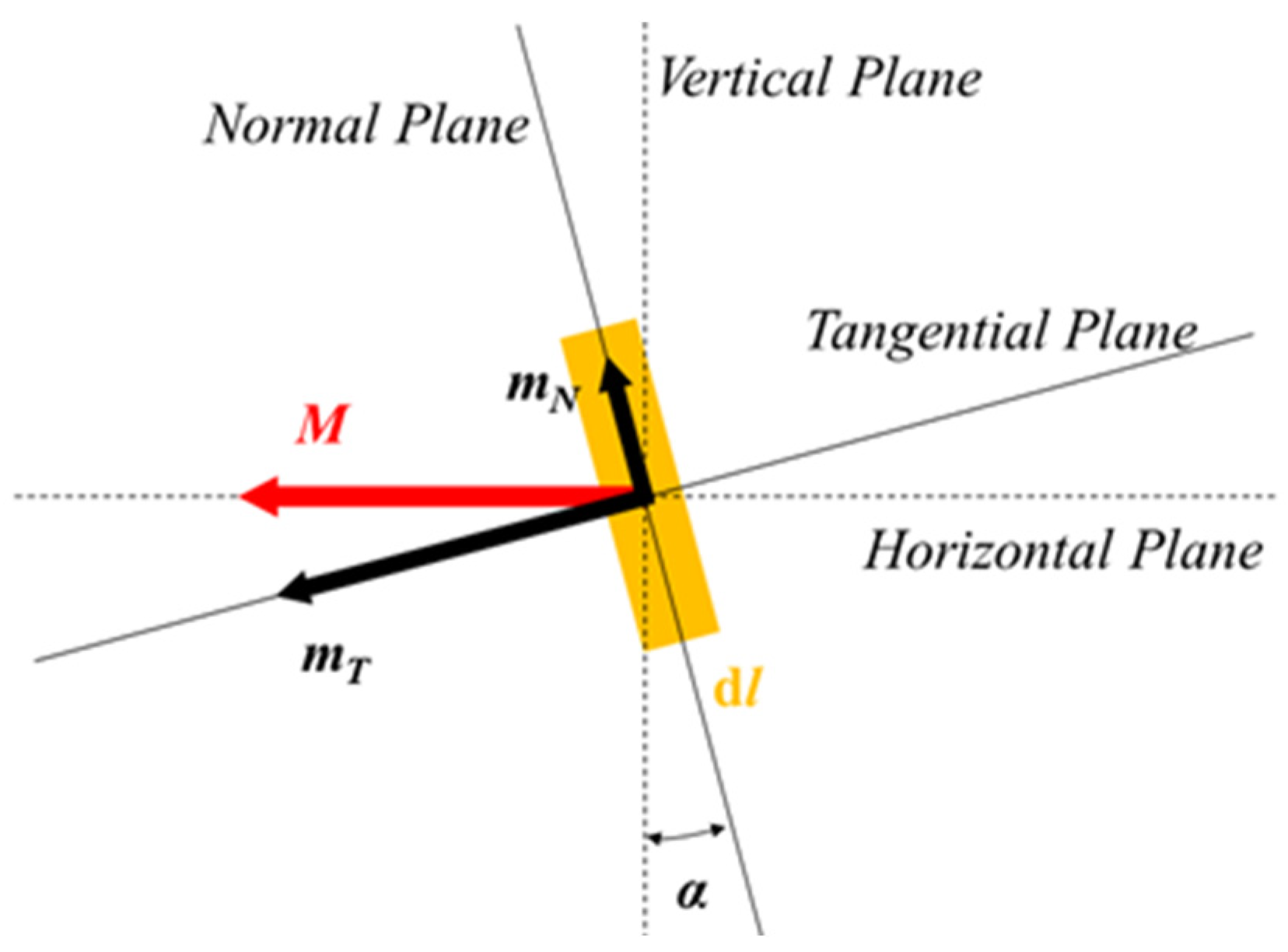
3.2. The Constitutive of Helical Steel Wire
3.3. Composite Reinforced Layers
3.4. Material Parameters
4. Case Study
4.1. Numerical Model
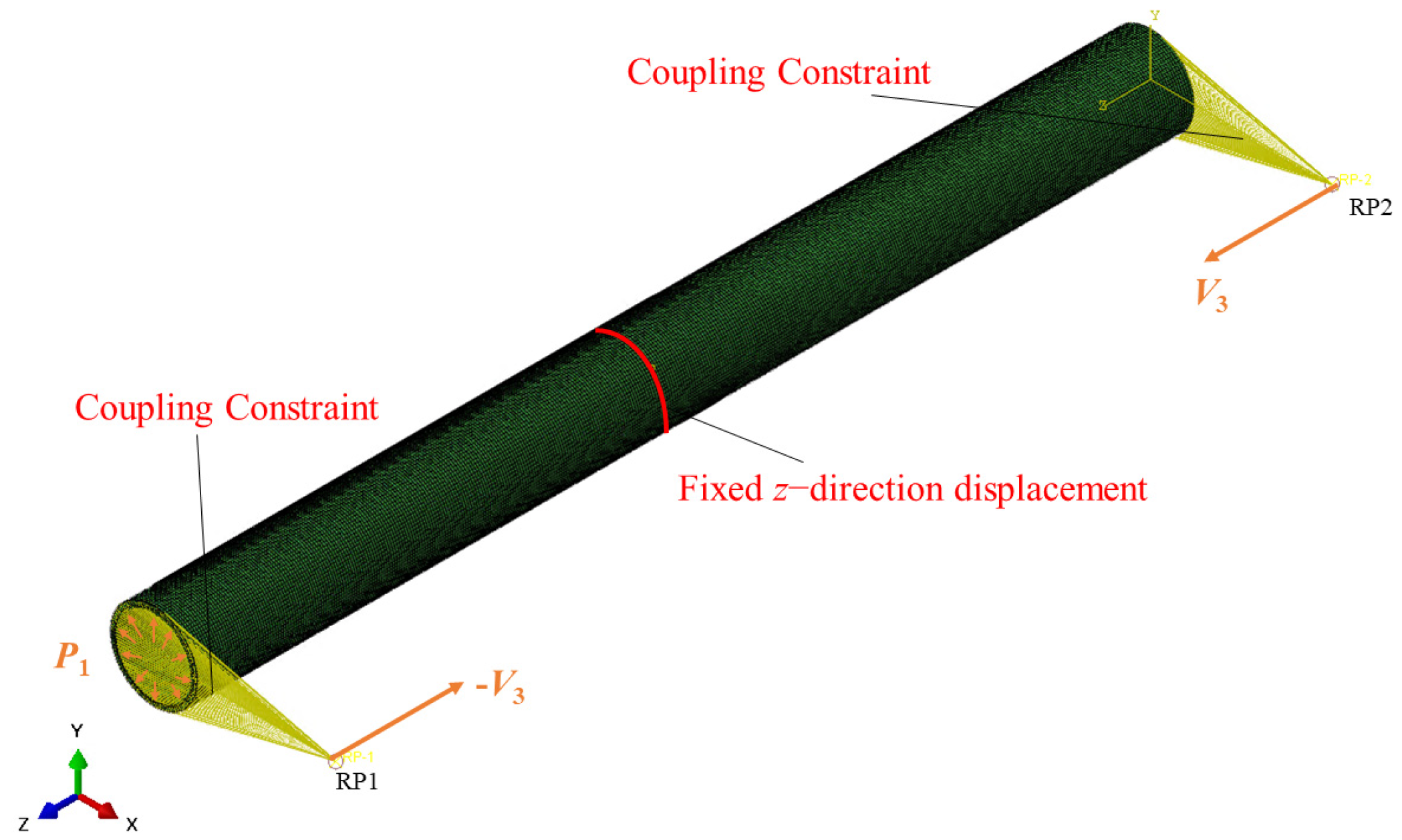
4.1.1. Finite Element Modeling Setup
4.1.2. Loads and Boundary Conditions
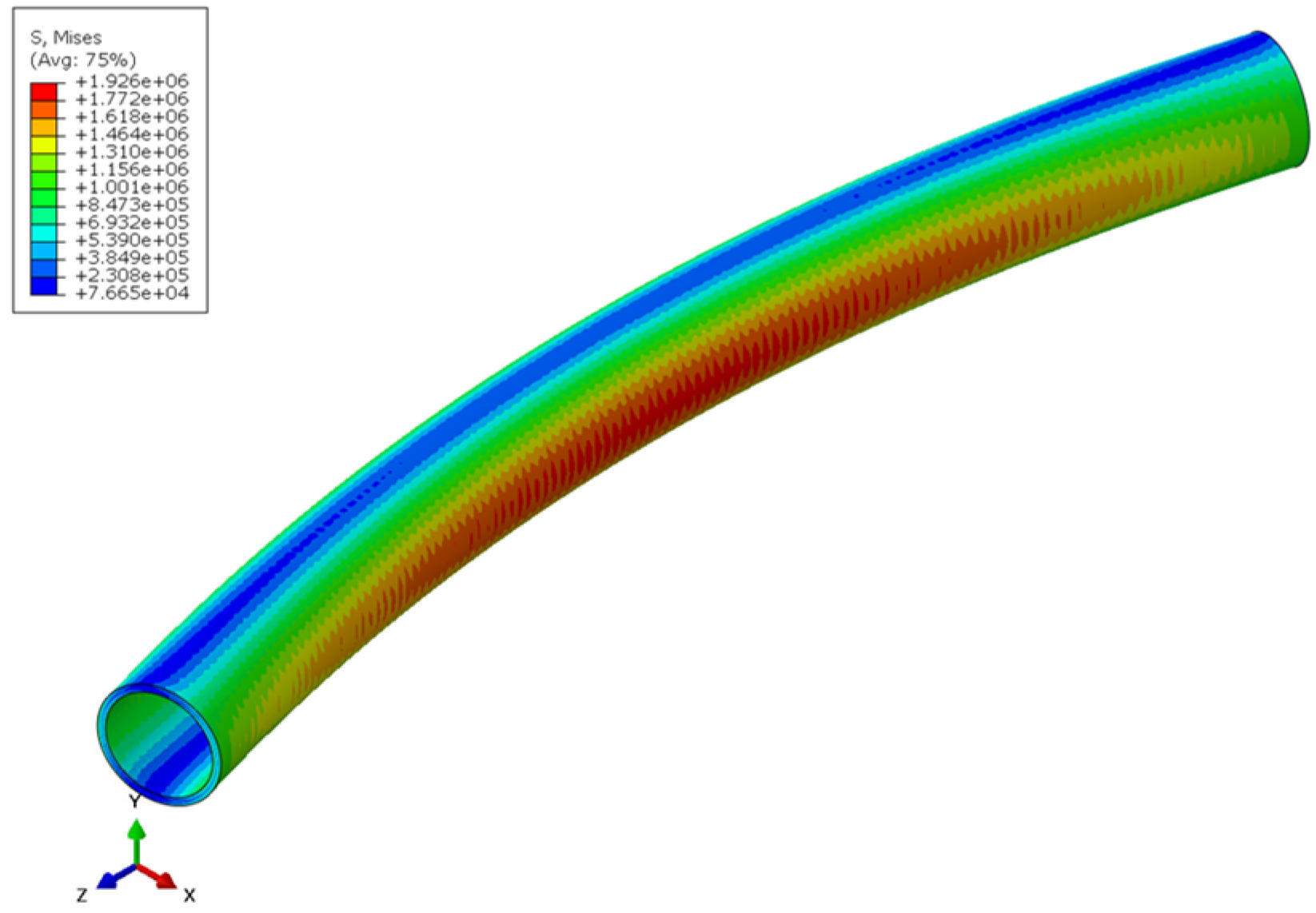
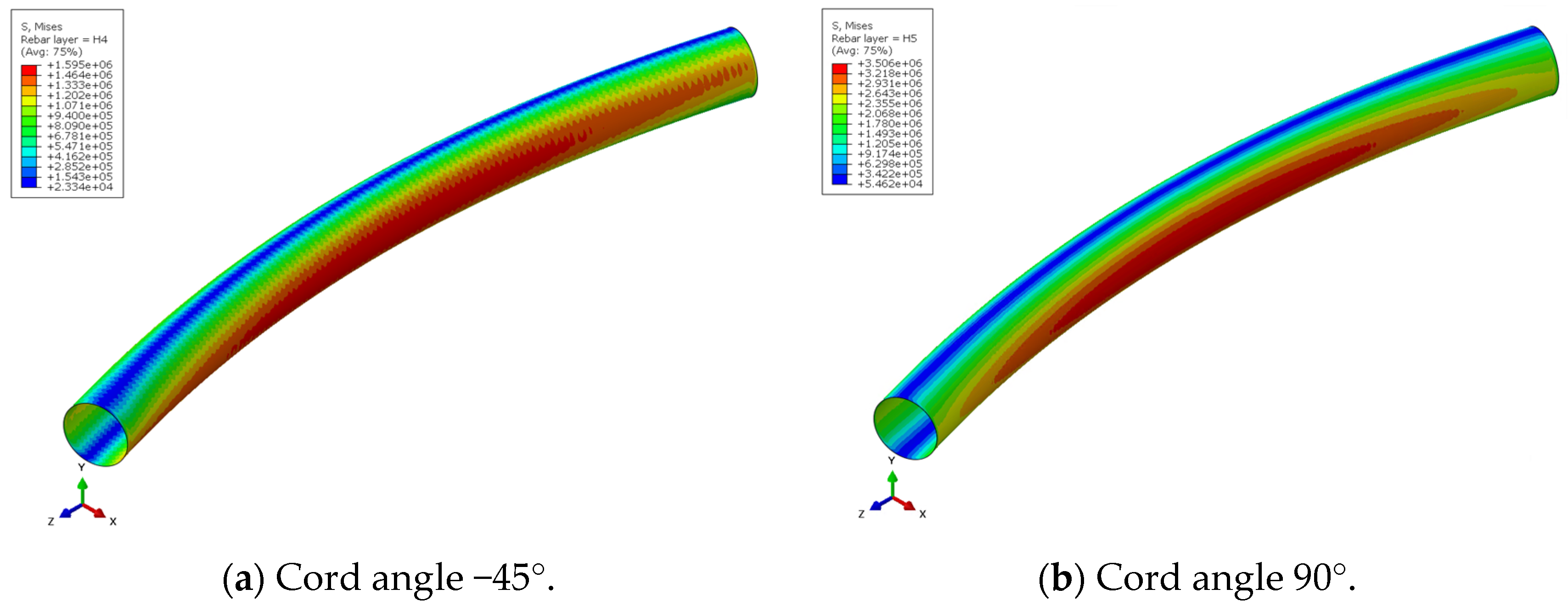
4.1.3. Stress and Deformation
4.2. Hose Bending Test Setup
4.3. Comparison
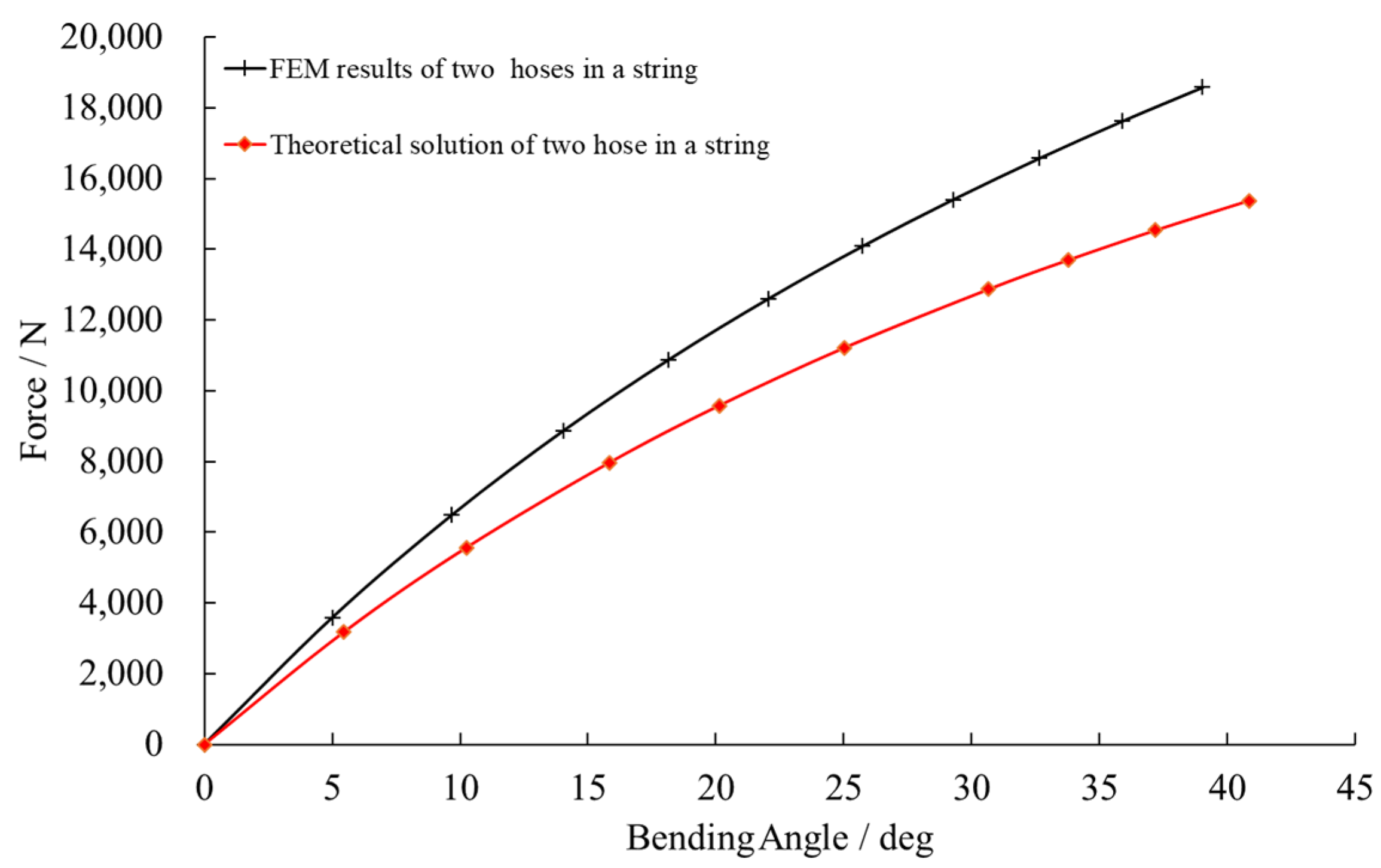
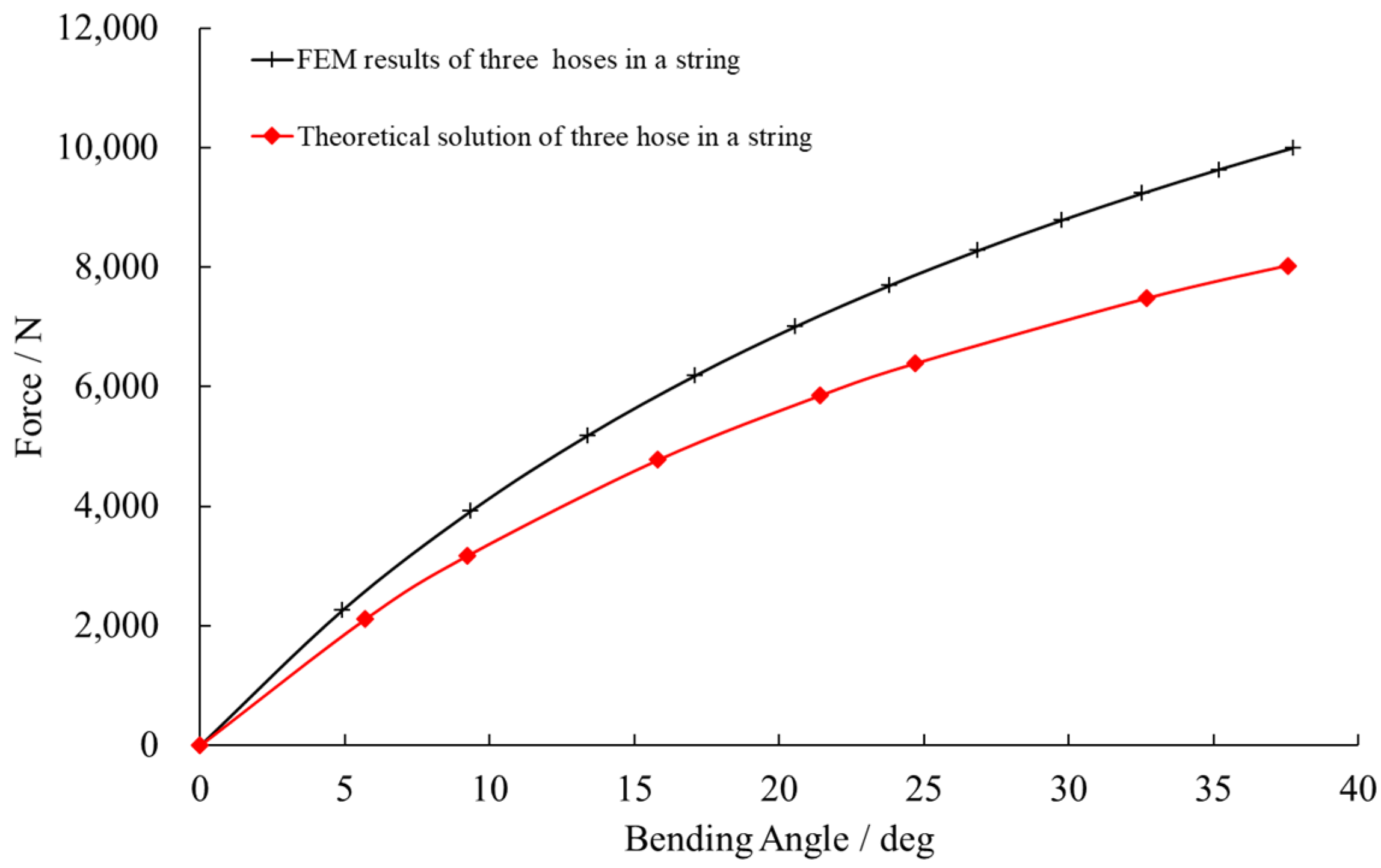
4.4. Hose String Bending
4.4.1. Flange Connection
4.4.2. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Orion Market Research. Global Dredging Hose Market Size, Share and Trends Analysis Report, by Type (Floating Dredge Hose and Non-Floating Dredge Hose) and Forecast, 2020–2026; 2020. Available online: https://www.omrglobal.com/industry-reports/floating-dredging-hose-market (accessed on 24 January 2024).
- JSA. JIS F 3995. Rubber Sleeves for Dredge Discharge Pipes; Japanese Standards Association (JSA): Tokyo, Japan, 2000. [Google Scholar]
- OCIMF. Guide to Manufacturing and Purchasing Hoses for Offshore Moorings (GMPHOM), 5th ed.; Oil Companies International Marine Forum (OCIMF), Witherby Seamanship International Ltd.: Livingstone, UK, 2009. [Google Scholar]
- API. API 17K. Specification for Bonded Flexible Pipe, 3rd ed.; American Petroleum Institute (API): Houston, TX, USA, 2017. [Google Scholar]
- ISO 28017:2018; Rubber Hoses and Hose Assemblies, Wire or Textile Reinforced, for Dredging Applications. International Organization for Standardization (ISO): Geneva, Switzerland, 2018.
- Amaechi, C.V.; Wang, F.C.; Jae, I.A.; Aboshio, A.; Odijie, A.C.; Ye, J.Q. A literature review on the technologies of bonded hoses for marine applications. Ships Offshore Struct. 2022, 17, 2819–2850. [Google Scholar] [CrossRef]
- Tonatto, M.L.P.; Tita, V.; Forte, M.M.C.; Amico, S.C. Multi-scale analyses of a floating marine hose with hybrid polyaramid/polyamide reinforcement cords. Mar. Struct. 2018, 60, 279–292. [Google Scholar] [CrossRef]
- Zhou, Y.; Duan, M.L.; Ma, J.M.; Sun, G.M. Theoretical analysis of reinforcement layers in bonded flexible marine hose under internal pressure. Eng. Struct. 2018, 168, 384–398. [Google Scholar] [CrossRef]
- Gao, P.; Li, C.C.; Wang, H.; Gao, Q.; Li, Y. A simplified method to predict the crush behavior of offshore bonded rubber hose. J. Mar. Sci. Eng. 2023, 11, 406. [Google Scholar] [CrossRef]
- Gao, Q.; Zhang, P.; Duan, M.; Yang, X.B.; Shi, W.; An, C.; Li, Z. Investigation on structural behavior of ring-stiffened composite offshore rubber hose under internal pressure. Appl. Ocean Res. 2018, 79, 7–19. [Google Scholar] [CrossRef]
- Bedford, A.; Liechti, K.M. Mechanics of Materials, 2nd ed.; Springer: Cham, Switzerland, 2020; pp. 361–367. [Google Scholar]
- Hackett, R.M. Strain-Energy Functions. In Hyperelasticity Primer, 1st ed.; Springer: Cham, Switzerland, 2016; pp. 19–25. [Google Scholar]
- Rivlin, R.S. Large elastic deformations of isotropic materials IV. further developments of the general theory. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 241, 379–397. [Google Scholar]
- Mooney, M. A theory of large elastic deformations. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Yeoh, O.H. Characterization of elastic properties of carbon-black-filled rubber vulcanizates. Rubber Chem. Technol. 1990, 63, 792–805. [Google Scholar] [CrossRef]
- Ogden, R.W. Large deformation isotropic elasticity: On the correlation of theory and experiment for incompressible rubberlike solids. Proc. R. Soc. Lond. Ser. A 1972, 328, 567–583. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef]
- Gent, A.N. A new constitutive relation for rubber. Rubber Chem. Technol. 1996, 69, 59–61. [Google Scholar] [CrossRef]
- Kobelev, V. Principles of Spring Design. In Durability of Springs, 2nd ed.; Springer: Cham, Switzerland, 2021; pp. 1–9. [Google Scholar]
- Teodorescu, P.P. Mathematical Models in Mechanics of Deformable Solids. In Treatise on Classical Elasticity. Springer, Theory and Related Problems, 1st ed.; Springer: Dordrecht, London, UK, 2013; pp. 138–155. [Google Scholar]
- Halpin, J.C.; Tsai, S.W.; Halpin, J.C.; Tsai, S.W. Effect of Environmental Factors on Composite Materials; Air Force Technical Report AFML-TR 67-423; 1967. Available online: https://www.semanticscholar.org/paper/Effects-of-Environmental-Factors-on-Composite-Halpin/1a8502fad082b55755965085de1b6dad8edcbca2 (accessed on 24 January 2024).
- Yi, X.S.; Du, S.; Zhang, L.T. Composite Structure Design and Analysis. In Composite Materials Engineering, Volume 1: Fundamentals of Composite Materials, 1st ed.; Chemical Industry Press: Beijing, China, 2018; pp. 383–395. [Google Scholar]
- Yu, L.; Li, Y.; Xia, L.J.; Ding, J.H.; Yang, Q. Research on mechanics of ship-launching airbags I-material constitutive relations by numerical and experimental approaches. Appl. Ocean Res. 2015, 52, 222–233. [Google Scholar] [CrossRef]
- ISO 23529:2016; Rubber–General Procedures for Preparing and Conditioning Test Pieces for Physical Test Methods. Physical tests. International Organization for Standardization: Geneva, Switzerland, 2016.
- GB/T 528-2009; Rubber, Vulcanized or Thermoplastic—Determination of Tensile Stress-Strain Properties. National Standard Committee Rubber Rubber Physical and Chemical Test Methods Technical Committee: Shenyang, China, 2009.
- Amaechi, C.V.; Chesterton, C.; Butler, H.O.; Gu, Z.; Odijie, A.C.; Wang, F.; Hou, X.; Ye, J. Finite element modelling on the mechanical behaviour of marine bonded composite hose (MBCH) under burst and bollapse. J. Mar. Sci. Eng. 2022, 10, 151. [Google Scholar] [CrossRef]
- GB/T 37221-2018; Self-Floating Rubber Hoses and Hose Assemblies for Dredging Applications and Rubber and Plastics Hoses and Tubing—Measurement of Flexibility and Stiffness—Part 1: Bending Tests at Ambient Temperatures. China Petroleum and Chemical Industry Federation: Beijing, China, 2018.








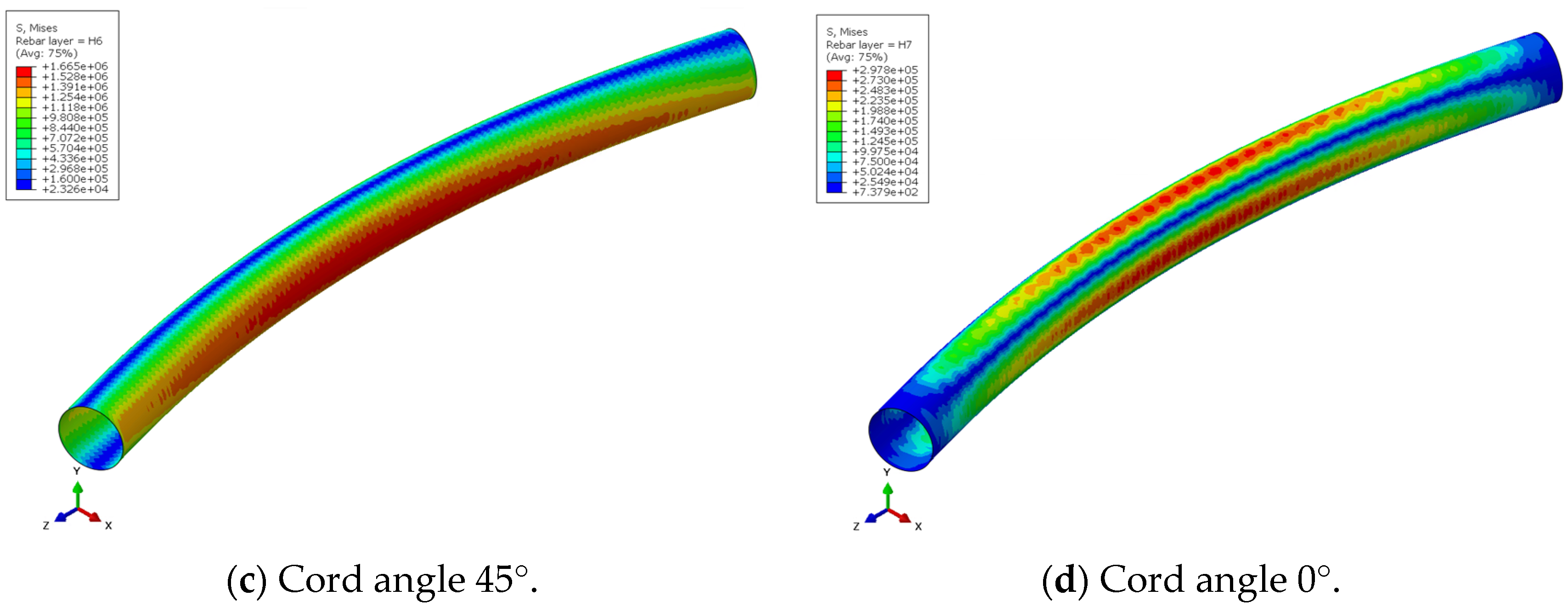
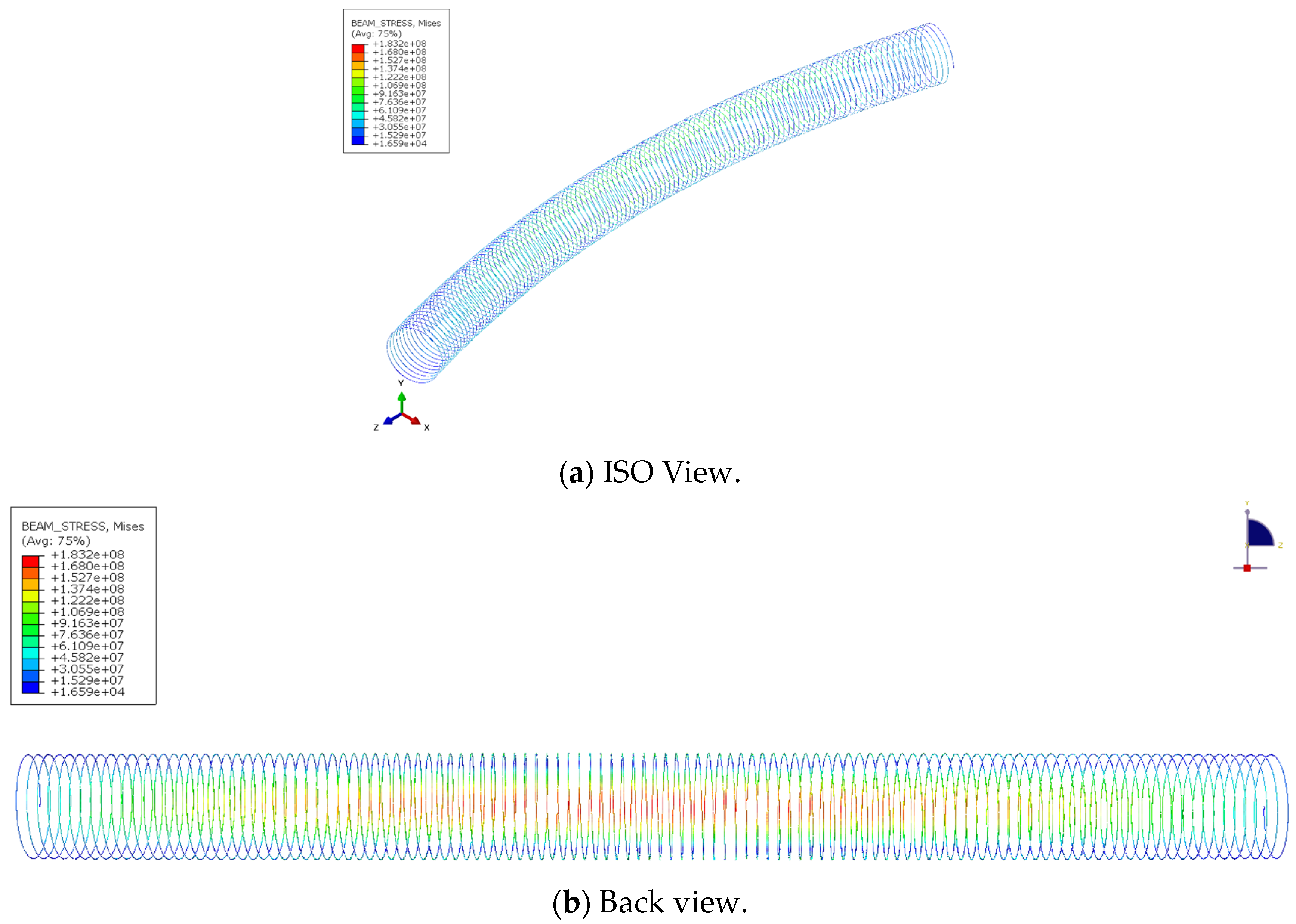

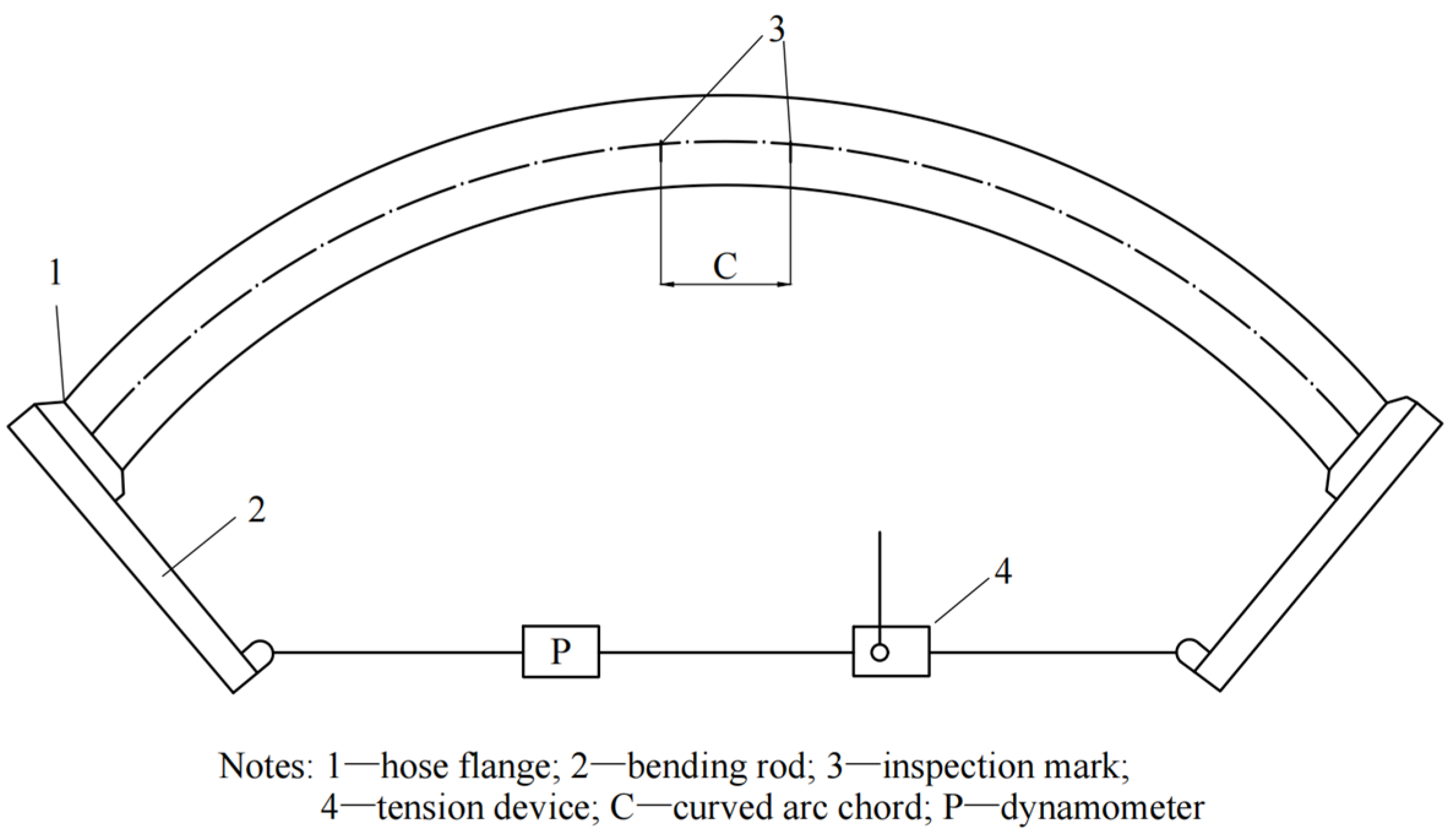




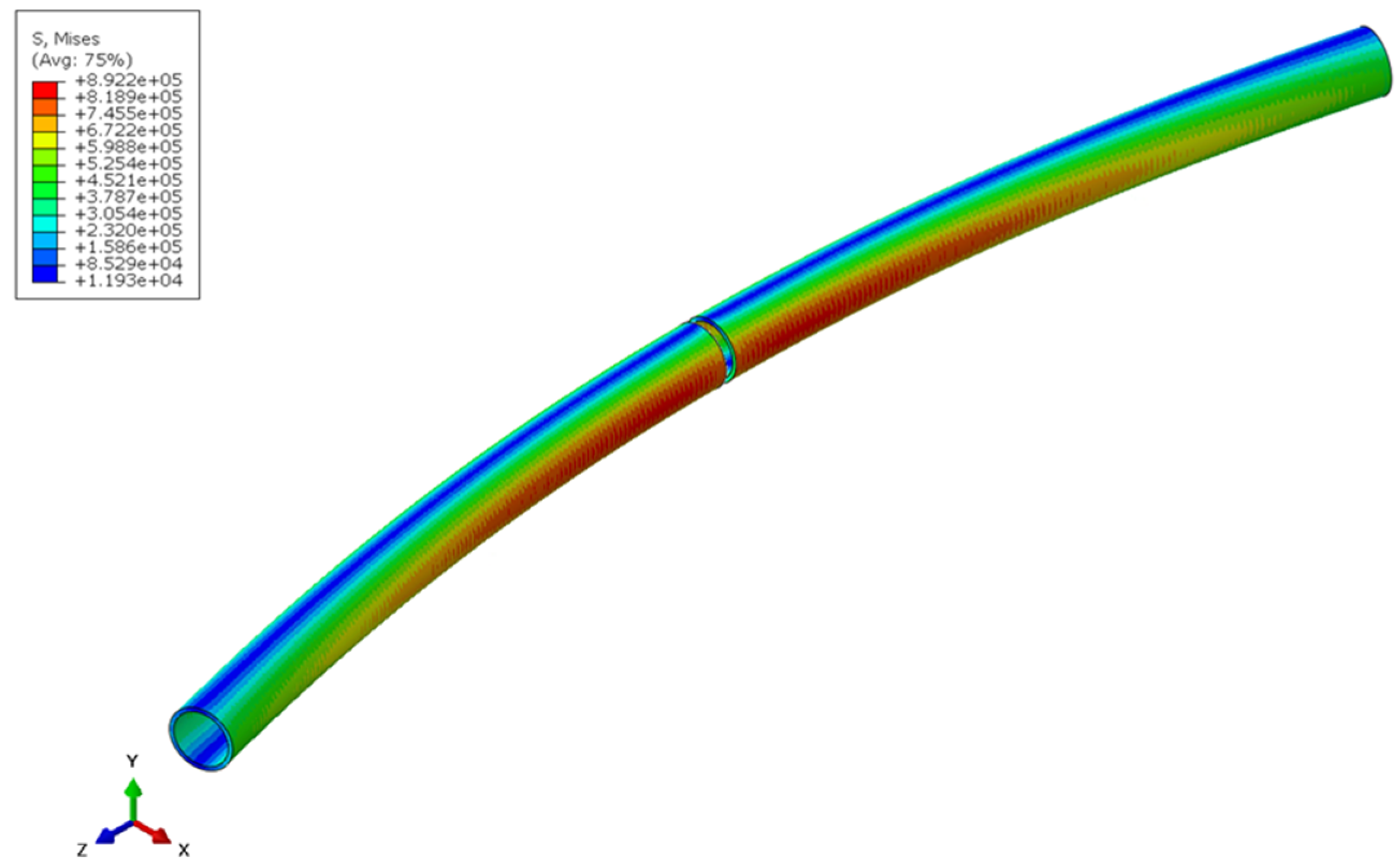

| Material | Parameters |
|---|---|
| Rubber | C10 = 9.68 MPa; C20 = 0.46 MPa; C30 = 0.21 MPa |
| Steel (Helical wire) | Young’s modulus = 140 GPa; Poisson’s ratio = 0.3 |
| Steel (Flange) | Young’s modulus = 206 GPa; Poisson’s ratio = 0.3 |
| Cord | Tensile modulus = 1313 MPa; Poisson’s ratio = 0.3 |
| Parameter | Value |
|---|---|
| Nominal inner radius/mm | 450 |
| Outer radius/mm | 518 |
| Winding angle of 1st reinforcement layer | [90°/45°/0°/−45°/90°/45°/0°] |
| Winding angle of 2nd reinforcement layer | [45°/−45°] |
| Mean helix radius/mm | 480 |
| Helix wire diameter/mm | 12 |
| Pitch of helix/mm | 100 |
| Length of the model/mm | 11,900 |
| Component | Element Type | No. of Elements | No. of Nodes |
|---|---|---|---|
| Rubber matrix | C3D8H | 77,224 | 116,130 |
| Reinforcement (2 layers) | S4R | 42,552 | 42,660 |
| Reinforcement (14 layers) | S4R | 37,824 | 37,920 |
| Helical steel wire | B31 | 11,867 | 11,868 |
| Flange (string bending) | C3D8R | 1456 | 2496 |
| Composition | (EI)rubber | (EI)reinforcement | (EI)wire | (EI)total |
|---|---|---|---|---|
| Value/N·m2 | 953,632 | 903,652 | 584 | 1,857,868 |
| Proportion | 51.33% | 48.64% | 0.03% | - |
| Angle | Force by Theory | Force by FEM | Average Force by Test | Error 1 | Error 2 |
|---|---|---|---|---|---|
| (1) | (2) | (3) | ((1)–(3))/(3) | ((2)–(3))/(3) | |
| 10° | 11,758 | 14,358 | 14,602 | −19.47% | −1.67% |
| 25° | 26,597 | 32,316 | 27,578 | −3.56% | 17.18% |
| 35° | 35,070 | 42,275 | 35,467 | −1.12% | 19.20% |
| 45° | 42,639 | 50,724 | 43,927 | −2.93% | 15.47% |
| 50° | 46,138 | 54,367 | 45,223 | 2.02% | 20.22% |
| 55° | 49,460 | 58,412 | 47,856 | 3.35% | 22.06% |
| 60° | 52,631 | 62,947 | 57,200 | −7.99% | 10.05% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Yu, L.; Li, X.; Liu, J. An Equivalent Linear Method to Predict Nonlinear Bending Mechanics of Dredging Floating Hose String. J. Mar. Sci. Eng. 2024, 12, 421. https://doi.org/10.3390/jmse12030421
Liu J, Yu L, Li X, Liu J. An Equivalent Linear Method to Predict Nonlinear Bending Mechanics of Dredging Floating Hose String. Journal of Marine Science and Engineering. 2024; 12(3):421. https://doi.org/10.3390/jmse12030421
Chicago/Turabian StyleLiu, Jingjing, Long Yu, Xiaoyan Li, and Jing Liu. 2024. "An Equivalent Linear Method to Predict Nonlinear Bending Mechanics of Dredging Floating Hose String" Journal of Marine Science and Engineering 12, no. 3: 421. https://doi.org/10.3390/jmse12030421
APA StyleLiu, J., Yu, L., Li, X., & Liu, J. (2024). An Equivalent Linear Method to Predict Nonlinear Bending Mechanics of Dredging Floating Hose String. Journal of Marine Science and Engineering, 12(3), 421. https://doi.org/10.3390/jmse12030421






