Numerical Simulation of Offshore Suction Bucket Foundation Pullout Characteristics under Undrained Conditions
Abstract
1. Introduction
2. Numerical Simulation
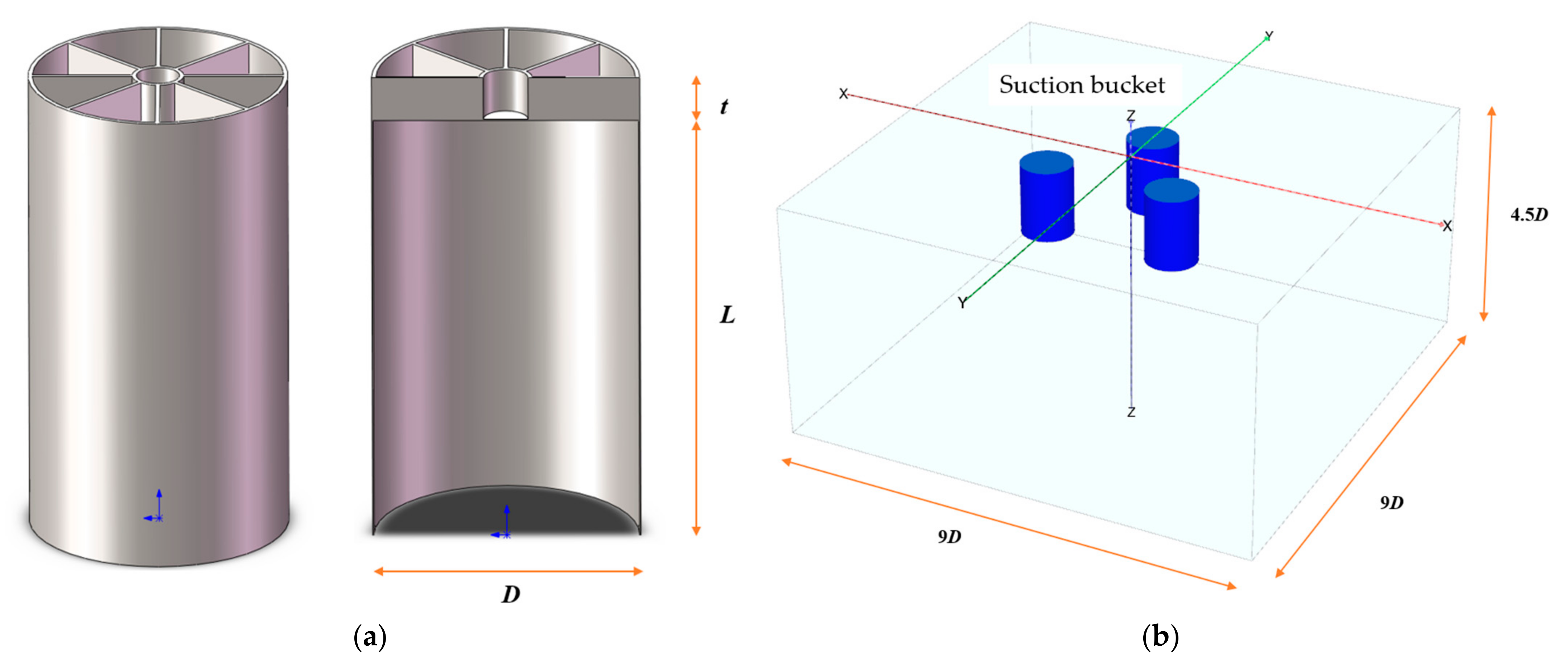
2.1. Finite Element Model
2.2. Soil Material Model
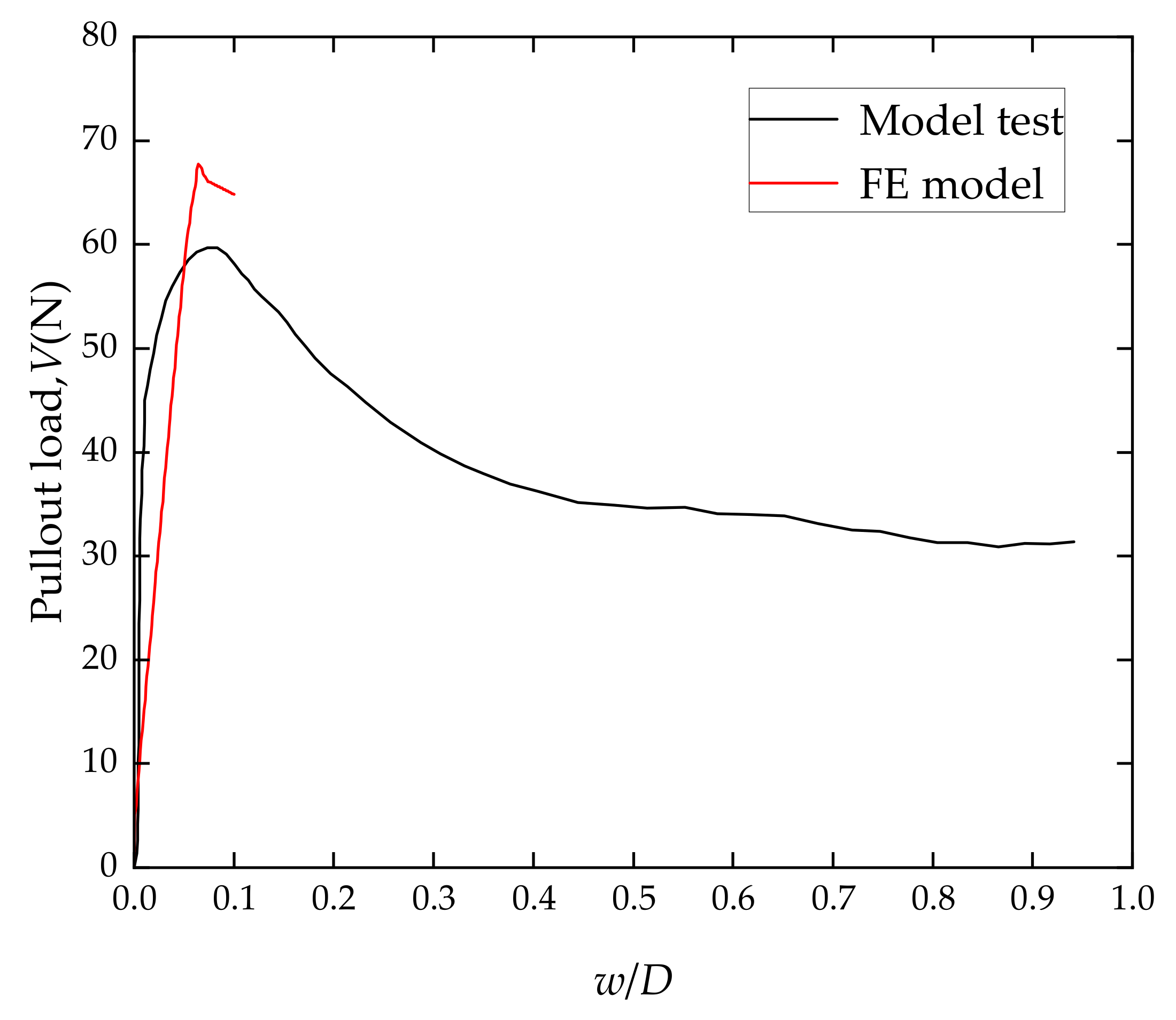
2.3. Validation of the Numerical Model
3. Results and Discussion
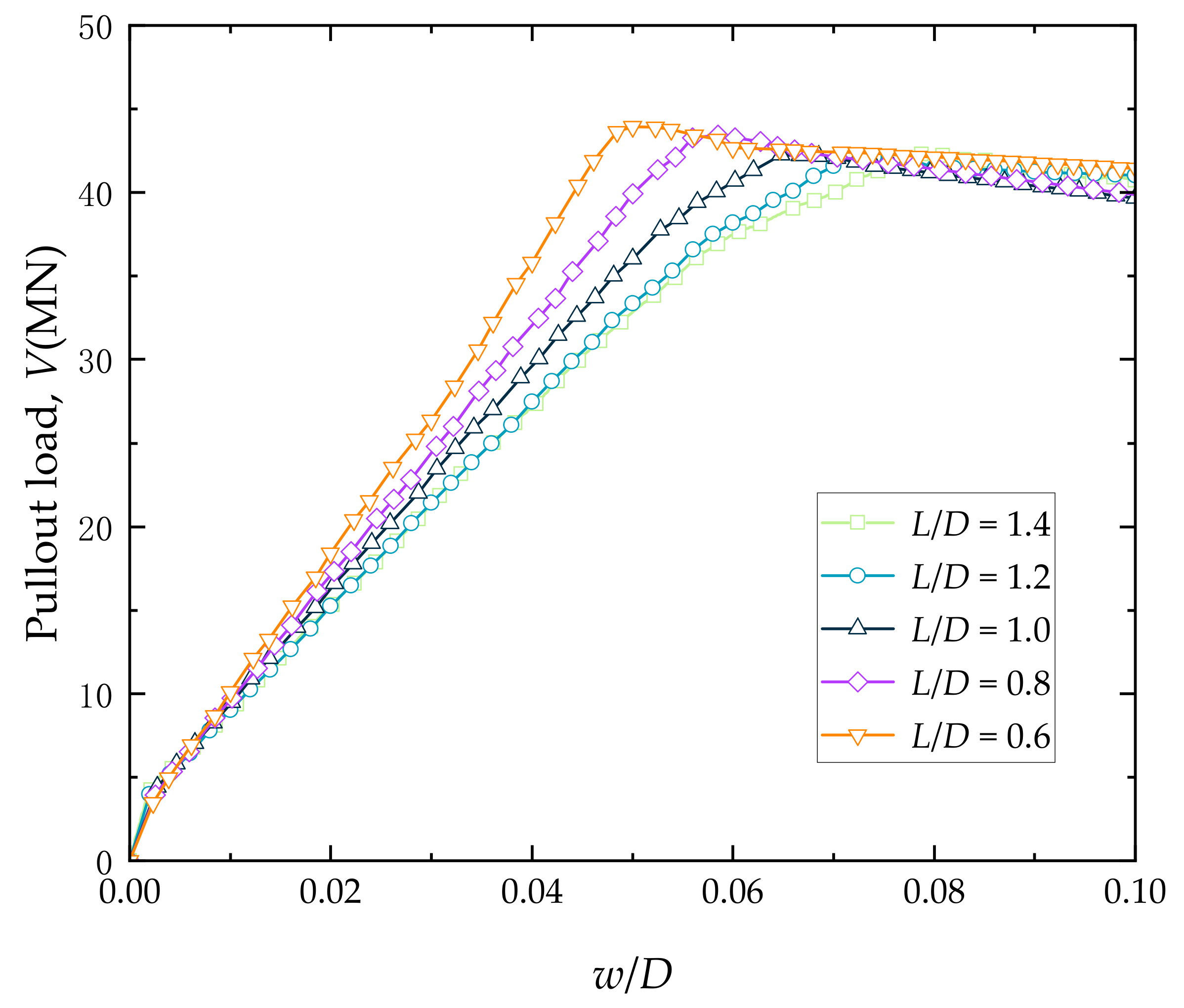
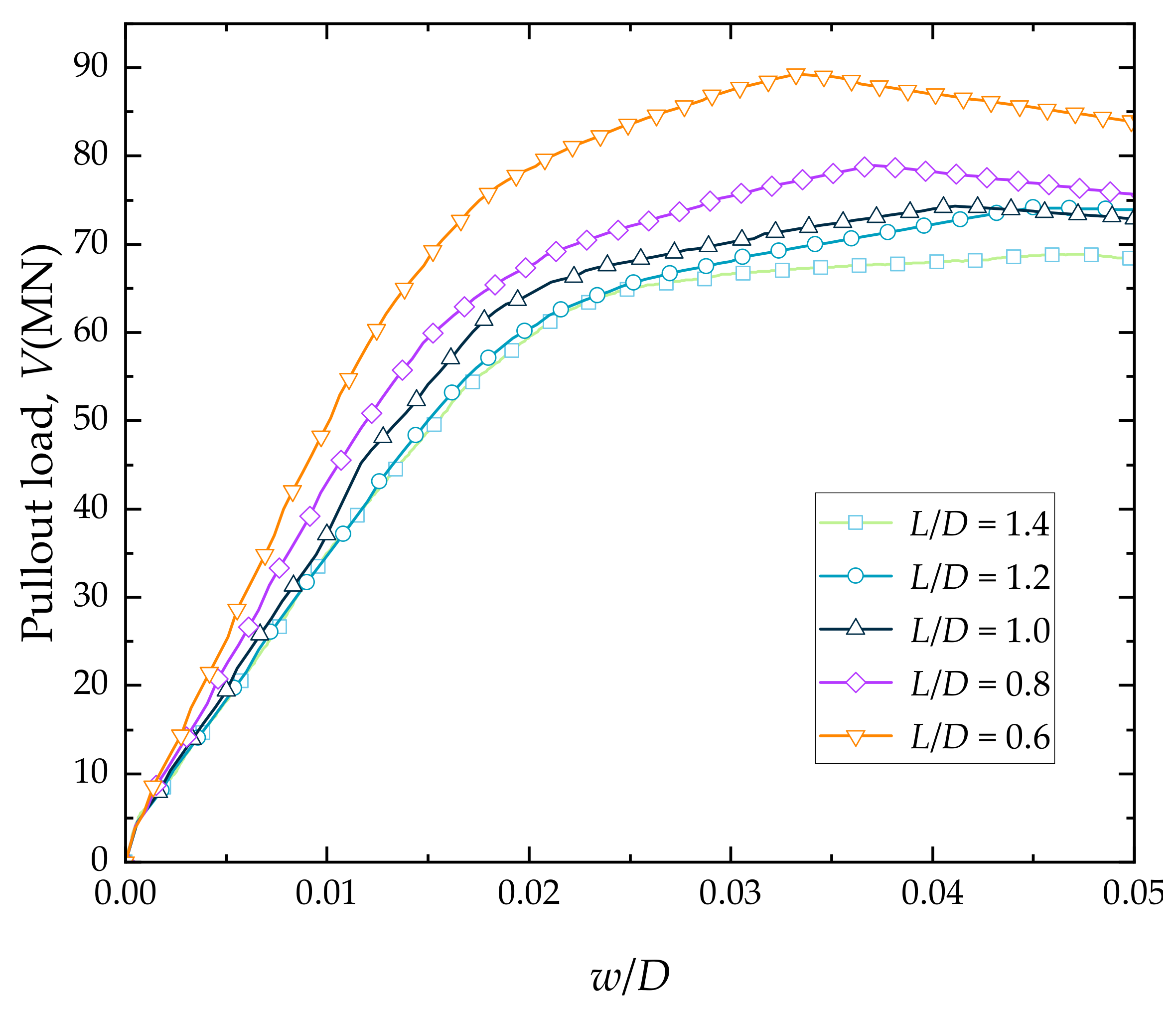
3.1. Study on the Pullout Capacity of the Bucket
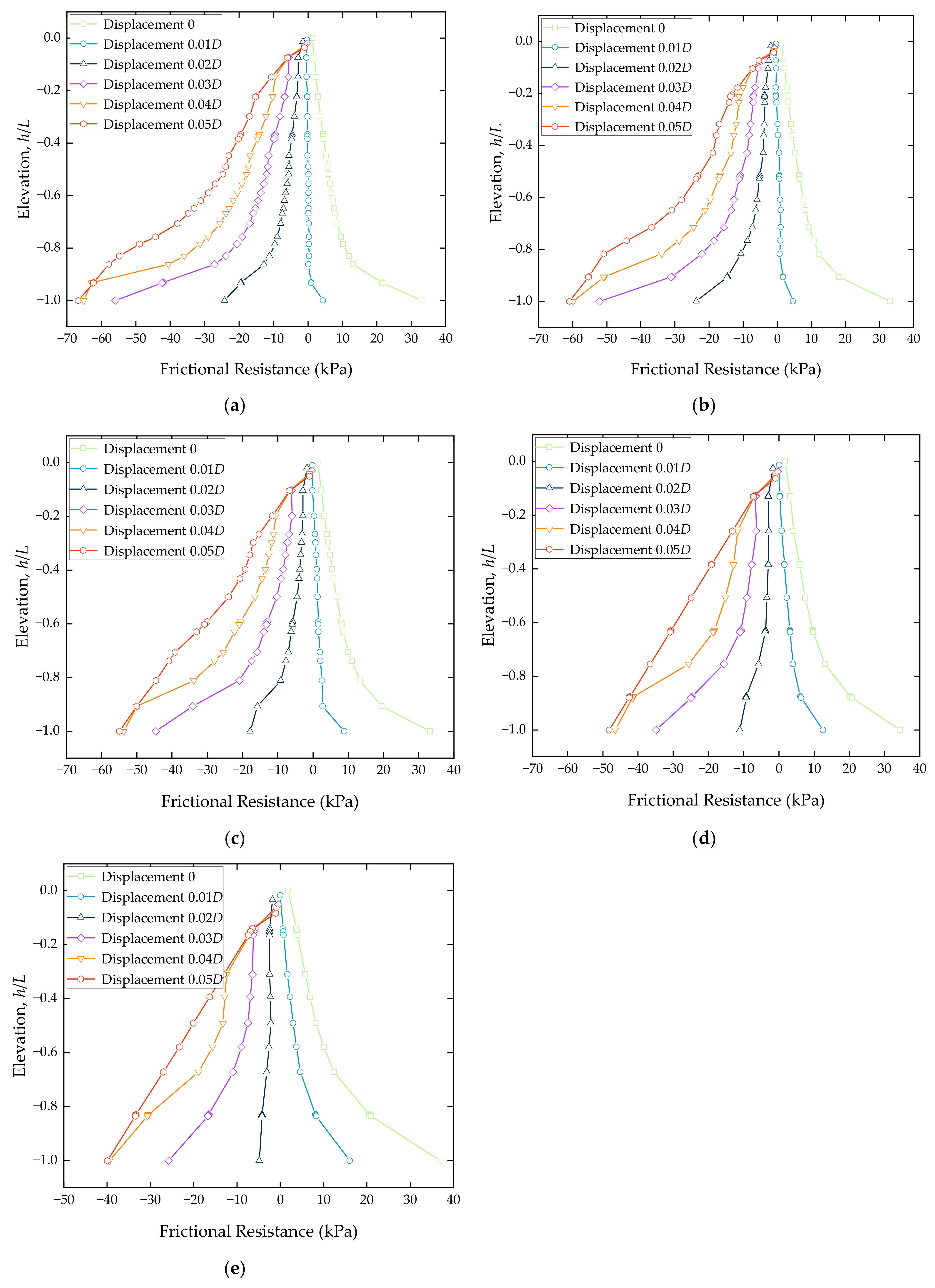
3.2. Study of the Frictional Resistance of the Bucket
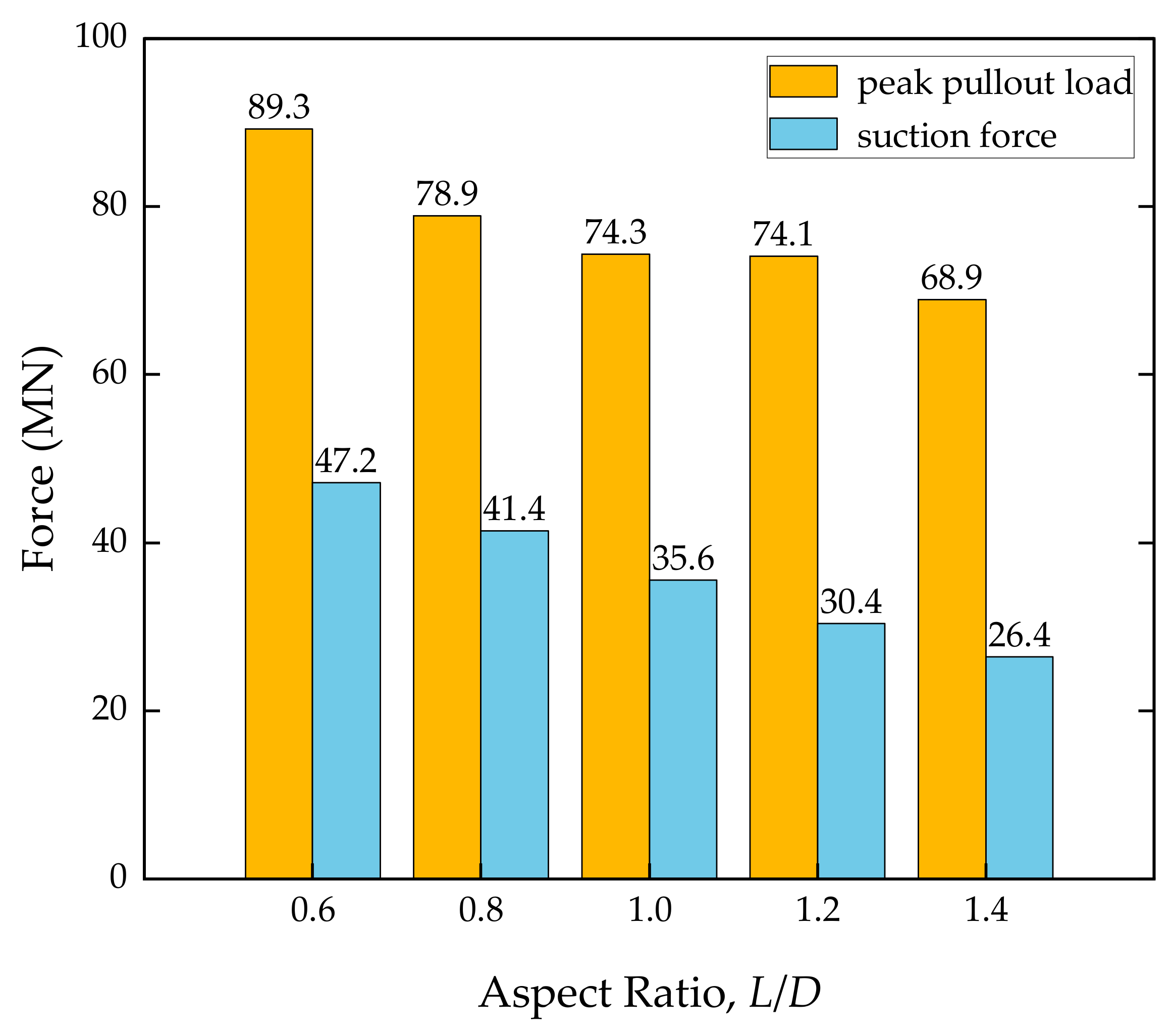
3.3. Suction Pressure Study of a Bucket
4. Conclusions
- (1)
- The behavior of the suction bucket during pullout in both sand and clay shows a similar trend. Initially, the pullout resistance rapidly increases with displacement, reaching a maximum value before gradually decreasing with further displacement. This behavior is characterized by a peak pullout load.
- (2)
- A smaller L/D ratio leads to a larger peak pullout load and higher initial stiffness. There is a 4.4% increase in peak pullout load in sand and a 29.6% increase in peak pullout load in soft clay when the L/D ratio decreases from 1.4 to 0.6. The soil failure displacement at the time of reaching the peak pullout load decreases with a reduction in L/D.
- (3)
- During the initial stage of pullout, the suction bucket foundation experiences upward-directed frictional resistance, with the highest amount of frictional resistance located at the foundation’s base. As the foundation moves upward, the frictional resistance on the outer wall of the bucket gradually changes from upward to downward. This change is observed more quickly in the lower part of the foundation. During the pullout process of 0.01D~0.02D, there is a situation where the upper frictional resistance on the bucket foundation is upward and the lower frictional resistance is downward.
- (4)
- During the process of removing the suction bucket, the suction pressure gradually increases until the soil fails. The suction force at the lower part of the bucket lid is one of the main factors affecting its pullout resistance. At L/D = 1.4, the suction force accounts for 38.3% of the peak pullout load, and this proportion increases as L/D decreases. At L/D = 0.6, the suction force constitutes more than 50% of the peak pullout load.
- (5)
- The displacement of soil failure at the ultimate pullout load exhibits a lagging trend compared to the displacement when the frictional resistance of the bucket wall begins to stabilize. This lag is due to the sustained increase in suction even as the frictional resistance stabilizes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Global Wind Energy Council. GWECs Global Offshore Wind Report 2022. Available online: https://gwec.net/gwecs-global-offshore-wind-report/ (accessed on 5 January 2024).
- Byrne, B.W.; Houlsby, G.T. Foundations for offshore wind turbines. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2003, 361, 2909–2930. [Google Scholar] [CrossRef]
- Xiaochun, S.; Riqing, X.; Xiaonan, G.; Guoxiang, C.; Zhongli, Y. Development of bucket foundation. China Civ. Eng. J. 2000, 33, 68–92. [Google Scholar] [CrossRef]
- Feld, T.; Rasmussen, J.L.; Sørensen, P.H. Structural and Economic Optimization of Offshore Wind Turbine Support Structure and Foundation In AAU Geotechnical Engineering Papers: Foundation Engineering Paper; Geotechnical Engineering Group: Aalborg, Denmark, 1999; Volume R 9904. [Google Scholar]
- Wang, Y.; Zhu, X.; Lv, Y.; Yang, Q. Large deformation finite element analysis of the installation of suction caisson in clay. Mar. Georesources Geotechnol. 2018, 36, 883–894. [Google Scholar] [CrossRef]
- Shen, K.; Guo, Z.; Wang, L.; Rui, S.; He, B. Investigation on seepage erosion and safety mechanism of suction caisson installation. In Proceedings of the 1st Vietnam Symposium on Advances in Offshore Engineering: Energy and Geotechnics; Springer: Singapore, 2018. [Google Scholar] [CrossRef]
- Guo, W.; Chu, J.; Kou, H. Model tests of soil heave plug formation in suction caisson. Proc. Inst. Civ. Eng. Geotech. Eng. 2016, 169, 214–223. [Google Scholar] [CrossRef]
- Byrne, B.W.; Houlsby, G.T. Assessing novel foundation options for offshore wind turbines. In Proceedings of the World Maritime Technology Conference, London, UK, 6–10 March 2016. [Google Scholar]
- Byrne, B.; Houlsby, G.; Martin, C.; Fish, P. Suction caisson foundations for offshore wind turbines. Wind Eng. 2002, 26, 145–155. [Google Scholar] [CrossRef]
- Houlsby, G.T.; Kelly, R.B.; Huxtable, J.; Byrne, B.W. Field trials of suction caissons in clay for offshore wind turbine foundations. Géotechnique 2005, 55, 287–296. [Google Scholar] [CrossRef]
- Houlsby, G.T.; Ibsen, L.B.; Byrne, B.W. Suction caissons for wind turbines In Frontiers in Offshore Geotechnics: ISFOG; CRC Press: Boca Raton, FL, USA, 2005; pp. 75–93. [Google Scholar]
- Kim, D.J.; Choo, Y.W.; Kim, J.H.; Kim, S.; Kim, D.S. Investigation of monotonic and cyclic behavior of tripod suction bucket foundations for offshore wind towers using centrifuge modeling. J. Geotech. Geoenviron. Eng. 2014, 140, 04014008. [Google Scholar] [CrossRef]
- Hung, L.C.; Lee, S.; Tran, N.X.; Kim, S.R. Experimental investigation of the vertical pullout cyclic response of bucket foundations in sand. Appl. Ocean Res. 2017, 68, 325–335. [Google Scholar] [CrossRef]
- Hong, S.; Vicent, S.; Gu, K.Y.; Kim, S.R. Effect of drainage condition on the pullout characteristics of bucket foundations in sand. Ocean Eng. 2022, 260, 111994. [Google Scholar] [CrossRef]
- Vicent, S.; Kim, S.R.; Bong, T. Effect of loading rate on the pullout capacity of offshore bucket foundations in sand. Ocean Eng. 2020, 210, 107427. [Google Scholar] [CrossRef]
- Ssenyondo, V.; Hong, S.; Bong, T.; Kim, S.R. Effects of embedment depth on the pullout capacity of bucket foundations in sand. Ocean Eng. 2021, 237, 109643. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, M.; Lou, Z. A study on the mechanism of interaction between bucket foundation and soil under vertical loadings. China Civ. Eng. J. 2005, 38, 97–101. [Google Scholar]
- Sun, X.; Luan, M.; Tang, X. Study of horizontal bearing capacity of bucket foundation on saturated soft clay ground. Rock Soil Mech. 2010, 31, 667–672. [Google Scholar] [CrossRef]
- Shen, K.; Zhang, Y.; Klinkvort, R.T.; Sturm, H.; Jostad, H.P.; Sivasithamparam, N.; Gou, Z. Numerical simulation of suction bucket under vertical tension loading. In Proceedings of the 8th International Conference on Offshore Site Investigation and Geotechnics, London, UK, 12–14 September 2017. [Google Scholar]
- Asakereh, A.; Kamali, A.H. Evaluation of Influencing Factors on the Pull-out Behavior of Suction Caissons. J. Struct. Eng. Geo-Tech. 2018, 8, 11–18. [Google Scholar]
- Dai, J.L. Centrifugal and Numerical Study on Uplift Behaviour of Suction Caissons in Soft Clay; Zhejiang University: Hangzhou, China, 2020. [Google Scholar] [CrossRef]
- Kim, S.R.; Oh, M. Group effect on bearing capacities of tripod bucket foundations in undrained clay. Ocean Eng. 2014, 79, 1–9. [Google Scholar] [CrossRef]
- Senders, M. Suction Caissons in Sand as Tripod Foundations for Offshore Wind Turbines; University of Western Australia: Perth, Australia, 2009. [Google Scholar] [CrossRef]
- Vaitkunaite, E.; Nielsen, B.N.; Ibsen, L.B. Bucket foundation response under various displacement rates. Int. J. Offshore Polar Eng. 2016, 26, 116–124. [Google Scholar] [CrossRef]
- Kulczykowski, M. Experimental investigation of skirted foundation in sand subjected to rapid uplift. Arch. Hydro-Eng. Environ. Mech. 2020, 67, 17–34. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, Y.; Ma, Z.; Andersen, K.H.; Jostad, H.P. Design considerations of suction caisson foundations for offshore wind turbines in Southern China. Appl. Ocean Res. 2020, 104, 102358. [Google Scholar] [CrossRef]
- Puyang, Z.; Lianshuo, X.; Conghuan, L. Pull-Up Resistance Characteristics of Three-Bucket Jacket Foundation in Clay. Adv. New Renew. Energy 2023, 11, 506–511. [Google Scholar]
- Iskander, M.; El-Gharbawy, S.; Olson, R. Performance of suction caissons in sand and clay. Can. Geotech. J. 2002, 39, 576–584. [Google Scholar] [CrossRef]
- Nabipour, M.; Matin, N.H. An investigation into the pull-out failure mechanisms of suction caissons. Int. J. Marit. Technol. 2015, 4, 21–35. Available online: http://ijmt.ir/article-1-327-en.html (accessed on 11 January 2024).


| Bucket Parameters | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Skirt length, L (m) | 16.75 | 15.00 | 13.50 | 11.80 | 9.75 |
| Diameter, D (m) | 11.45 | 12.50 | 13.5 | 14.75 | 16.25 |
| Side wall thickness, t1 (mm) | 50 | 50 | 50 | 50 | 50 |
| Head wall thickness, t2 (mm) | 500 | 500 | 500 | 500 | 500 |
| Aspect ratio, L/D | 1.4 | 1.2 | 1.0 | 0.8 | 0.6 |
| Sand Material Parameters | Value |
|---|---|
| Saturated unit weight, γsat (kN/m3) | 20 |
| Poisson’s ratio, v′ | 0.35 |
| Initial elastic modulus, E (kPa) | 1000 |
| Stiffness increment, E′inc (kPa/m) | 1000 |
| Initial undrained shear strength, Su (kPa) | 1 |
| Strength increment, Su,inc (kPa/m) | 4 |
| Clay Material Parameters | Value |
|---|---|
| Natural unit weight, γunsat (kN/m3) | 16 |
| Saturated unit weight, γsat (kN/m3) | 17 |
| Shear modulus in drained triaxial test, E50ref (kPa) | 2000 |
| Shear modulus in consolidation test, Eoedref (kPa) | 2000 |
| Unload/Reload modulus, Eurref (kPa) | 10,000 |
| Unload Poisson’s ratio, v′ | 0.2 |
| Stress exponent, m | 0.5 |
| Cohesion, c′ (kPa) | 5 |
| Friction angle, φ′ (°) | 25 |
| Dilatancy angle, Ψ′ (°) | 0 |
| Overconsolidation ratio, OCR | 1.5 |
| Preconsolidation stress, POP | 1 |
| Permeability, k (m/s) | 6.944 × 10−6 |
| Maximum Pullout Load, V (MN) | Failure Displacement, w/D | |
|---|---|---|
| Foundation 1 (L/D = 1.4) | 42.079 | 0.078 |
| Foundation 2 (L/D = 1.2) | 42.164 | 0.072 |
| Foundation 3 (L/D = 1.0) | 42.261 | 0.064 |
| Foundation 4 (L/D = 0.8) | 43.446 | 0.057 |
| Foundation 5 (L/D = 0.6) | 43.955 | 0.049 |
| Maximum Pullout Load, V (MN) | Failure Displacement, w/D | |
|---|---|---|
| Foundation 1 (L/D = 1.4) | 68.883 | 0.047 |
| Foundation 2 (L/D = 1.2) | 74.122 | 0.045 |
| Foundation 3 (L/D = 1.0) | 74.334 | 0.041 |
| Foundation 4 (L/D = 0.8) | 78.944 | 0.037 |
| Foundation 5 (L/D = 0.6) | 89.266 | 0.033 |
| Displacement, w/D | |
|---|---|
| Foundation 1 (L/D = 1.4) | 0.024 |
| Foundation 2 (L/D = 1.2) | 0.022 |
| Foundation 3 (L/D = 1.0) | 0.019 |
| Foundation 4 (L/D = 0.8) | 0.018 |
| Foundation 5 (L/D = 0.6) | 0.017 |
| Displacement, w/D | Suction Pressure (kPa) | |
|---|---|---|
| Foundation 1 (L/D = 1.4) | 0.047 | −240.22 |
| Foundation 2 (L/D = 1.2) | 0.045 | −247.88 |
| Foundation 3 (L/D = 1.0) | 0.041 | −248.50 |
| Foundation 4 (L/D = 0.8) | 0.037 | −242.67 |
| Foundation 5 (L/D = 0.6) | 0.033 | −227.59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, P.; Chen, Y.; Lai, Z.; Liu, H.; Zhu, R. Numerical Simulation of Offshore Suction Bucket Foundation Pullout Characteristics under Undrained Conditions. J. Mar. Sci. Eng. 2024, 12, 419. https://doi.org/10.3390/jmse12030419
Chen P, Chen Y, Lai Z, Liu H, Zhu R. Numerical Simulation of Offshore Suction Bucket Foundation Pullout Characteristics under Undrained Conditions. Journal of Marine Science and Engineering. 2024; 12(3):419. https://doi.org/10.3390/jmse12030419
Chicago/Turabian StyleChen, Pengyu, Yong Chen, Zongyuan Lai, Hanqiu Liu, and Ronghua Zhu. 2024. "Numerical Simulation of Offshore Suction Bucket Foundation Pullout Characteristics under Undrained Conditions" Journal of Marine Science and Engineering 12, no. 3: 419. https://doi.org/10.3390/jmse12030419
APA StyleChen, P., Chen, Y., Lai, Z., Liu, H., & Zhu, R. (2024). Numerical Simulation of Offshore Suction Bucket Foundation Pullout Characteristics under Undrained Conditions. Journal of Marine Science and Engineering, 12(3), 419. https://doi.org/10.3390/jmse12030419




_Zhu.png)


