Research on the Internal Flow Difference between Peak and Valley Conditions of Water Jet Propulsion Pump during Working at Hump Region
Abstract
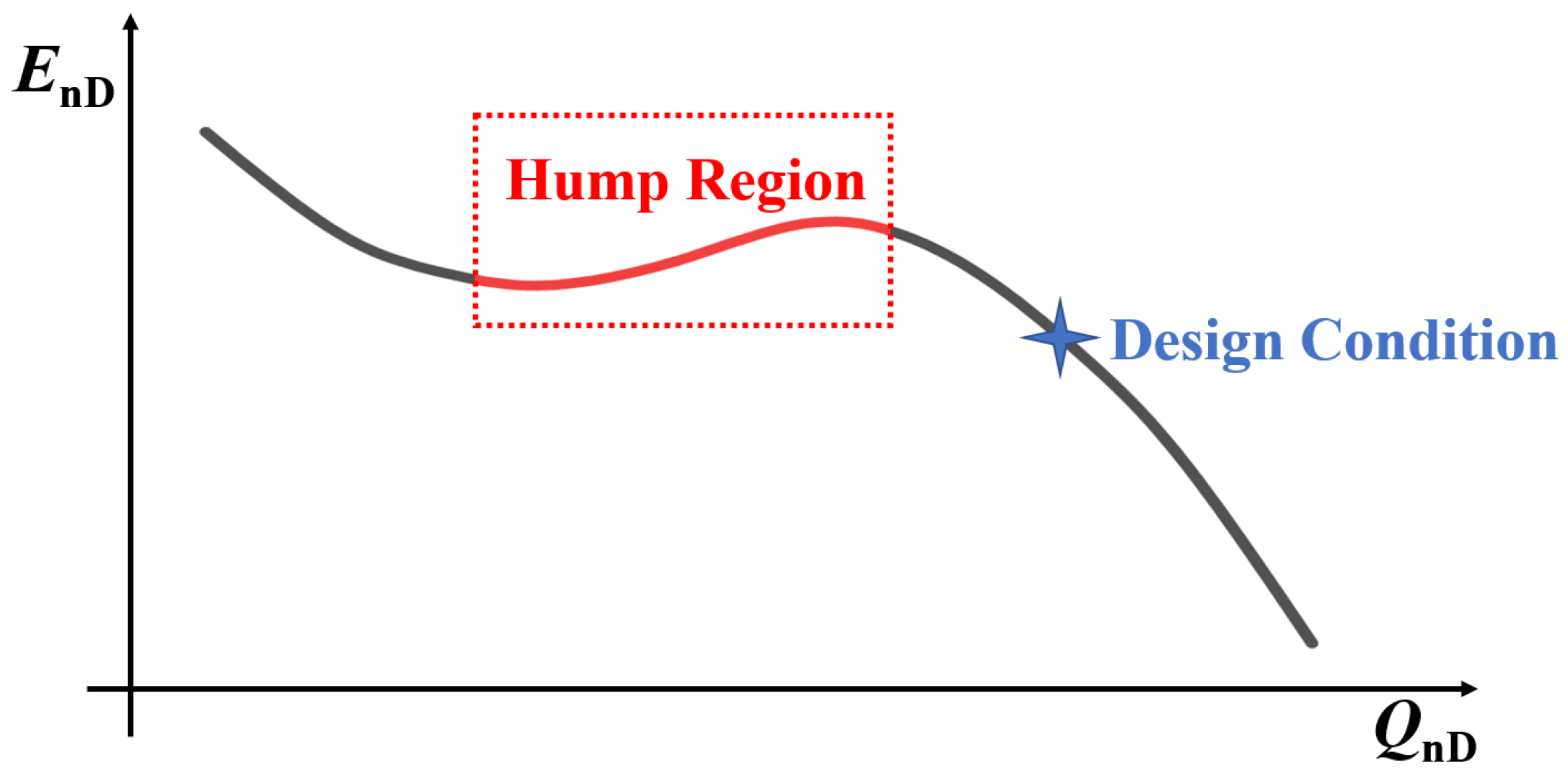
1. Introduction
2. Experimental Model and Test Platform
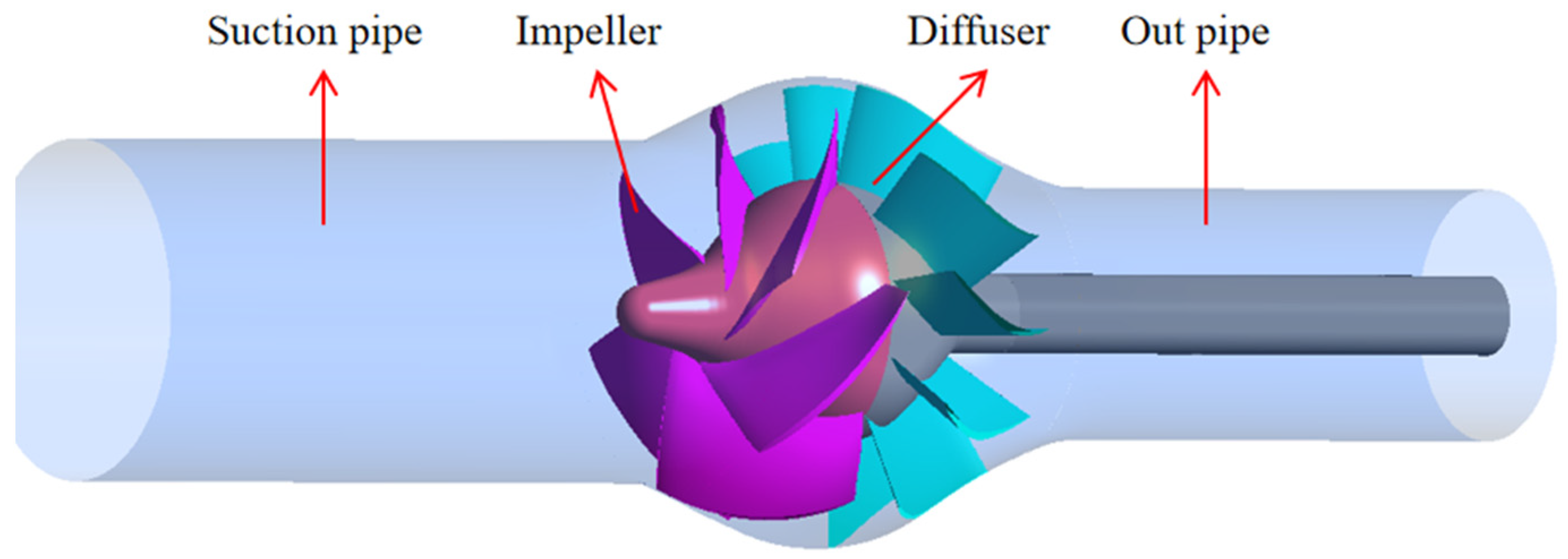
2.1. Experimental Pump Structure and Parameters
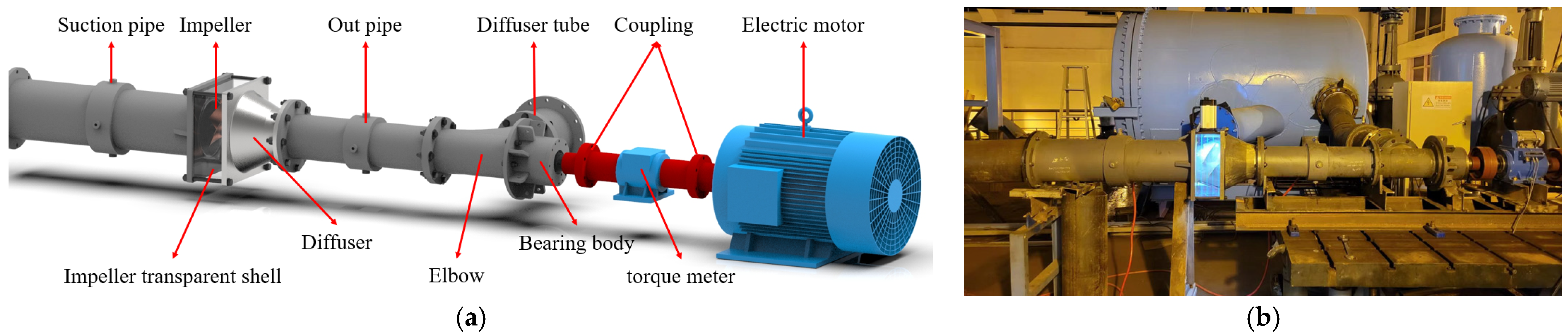
2.2. Test Platform and Method
2.2.1. Experimental Testing Method and Apparatus
2.2.2. Experimental Principles and Methods
3. Numerical Simulation Method
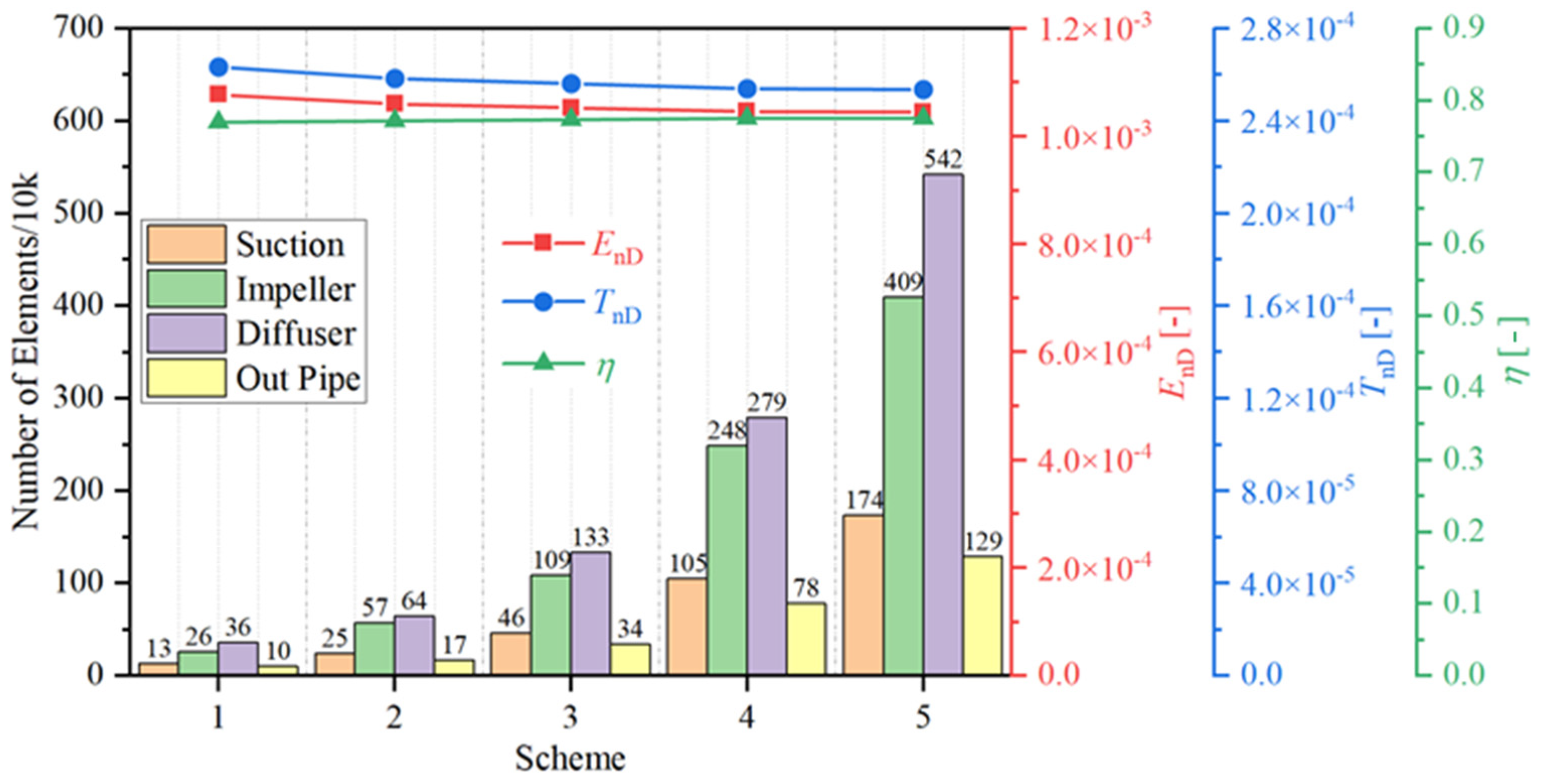
3.1. Grid Generation
3.2. Calculation Setting
3.2.1. Governing Equations
- (1)
- Continuity equation
- (2)
- Momentum conservation equation
- (3)
- Turbulence model functions
3.2.2. Turbulence Model
3.2.3. Boundary Conditions
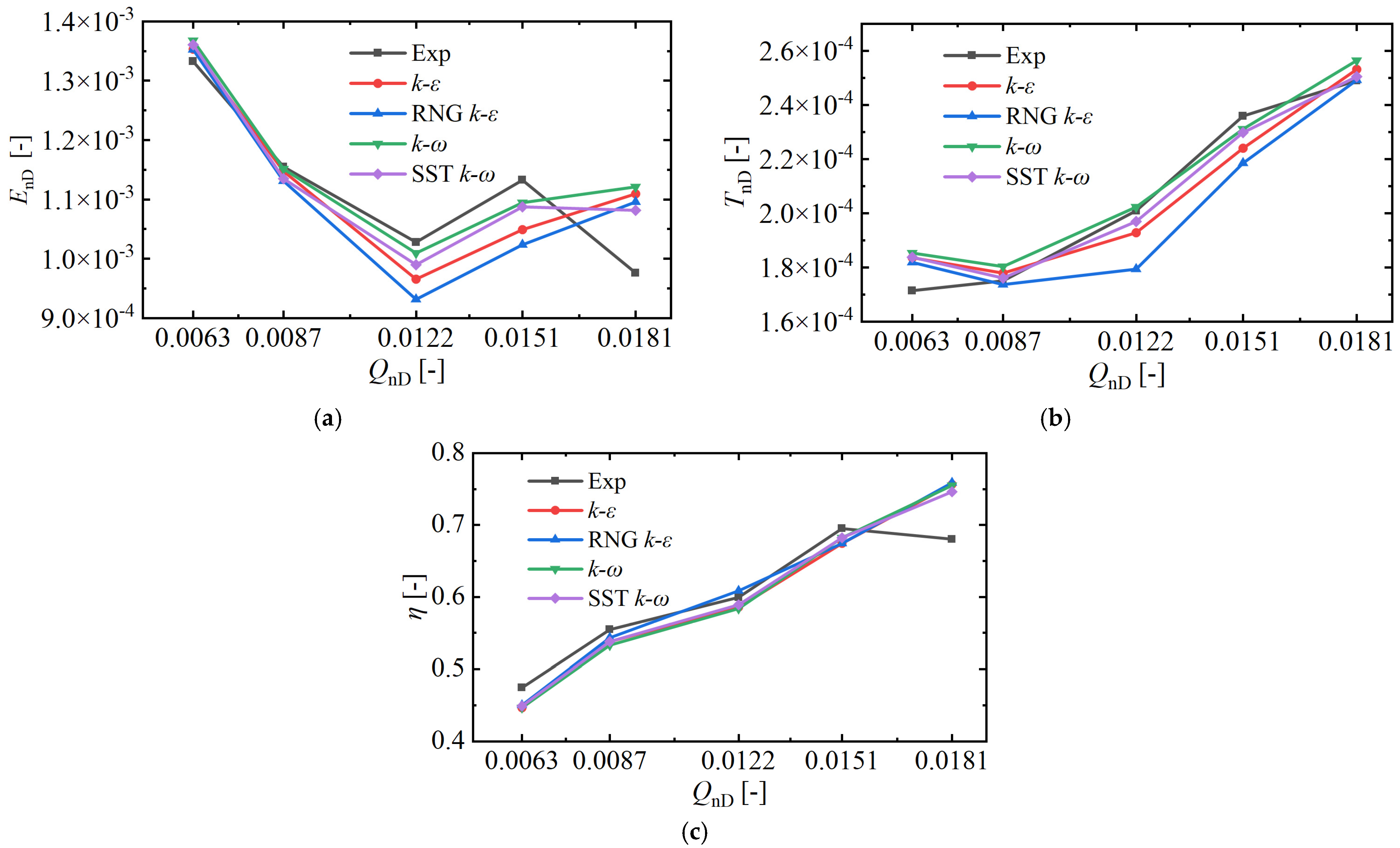
3.3. Grid Independence Verification
4. Results and Analysis
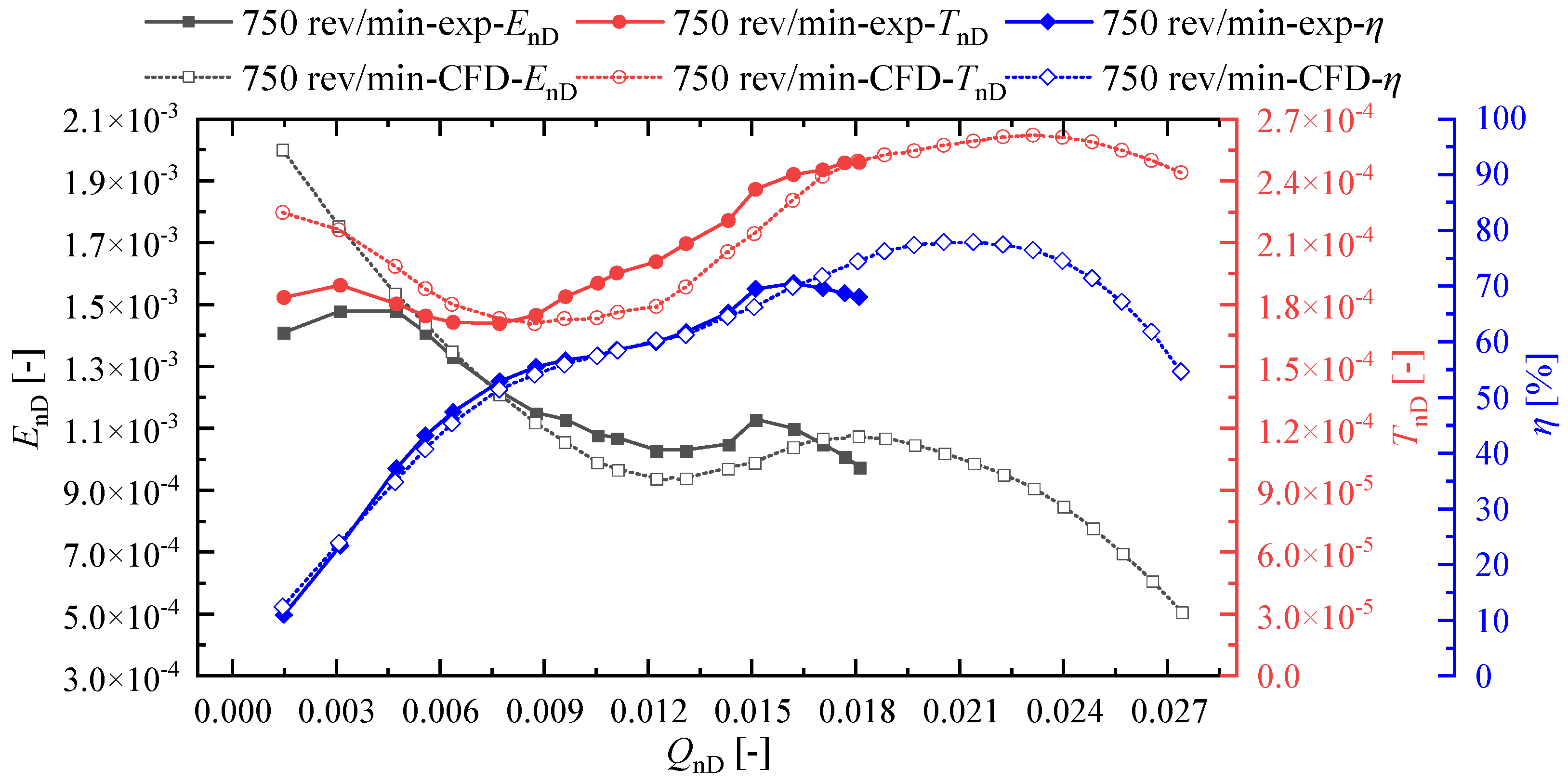
4.1. Comparison of Experimental and Numerical Simulation Results of Hydraulic Performance Curves
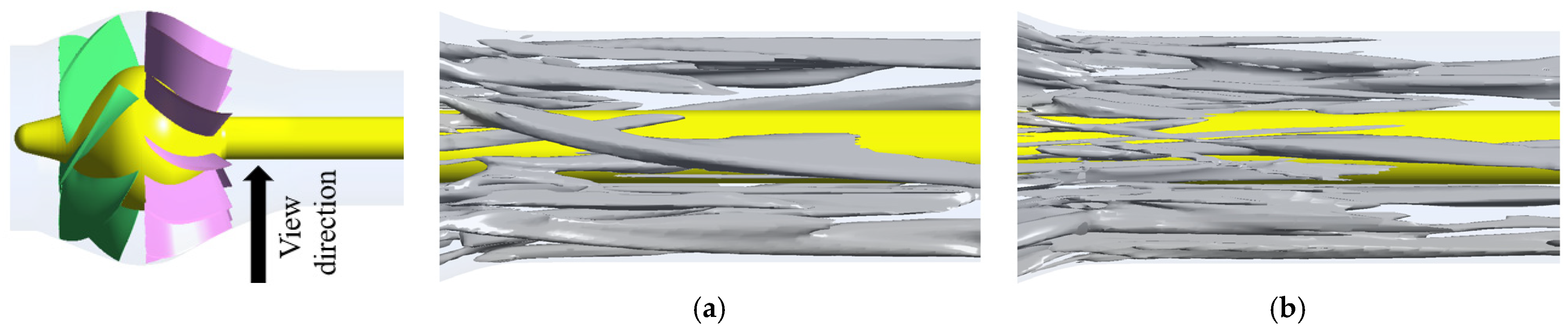
4.2. Cavitation Flow Structure of Water Jet Propulsion Pump under Hump–Peak–Valley Condition
4.3. Entropy Generation Distribution
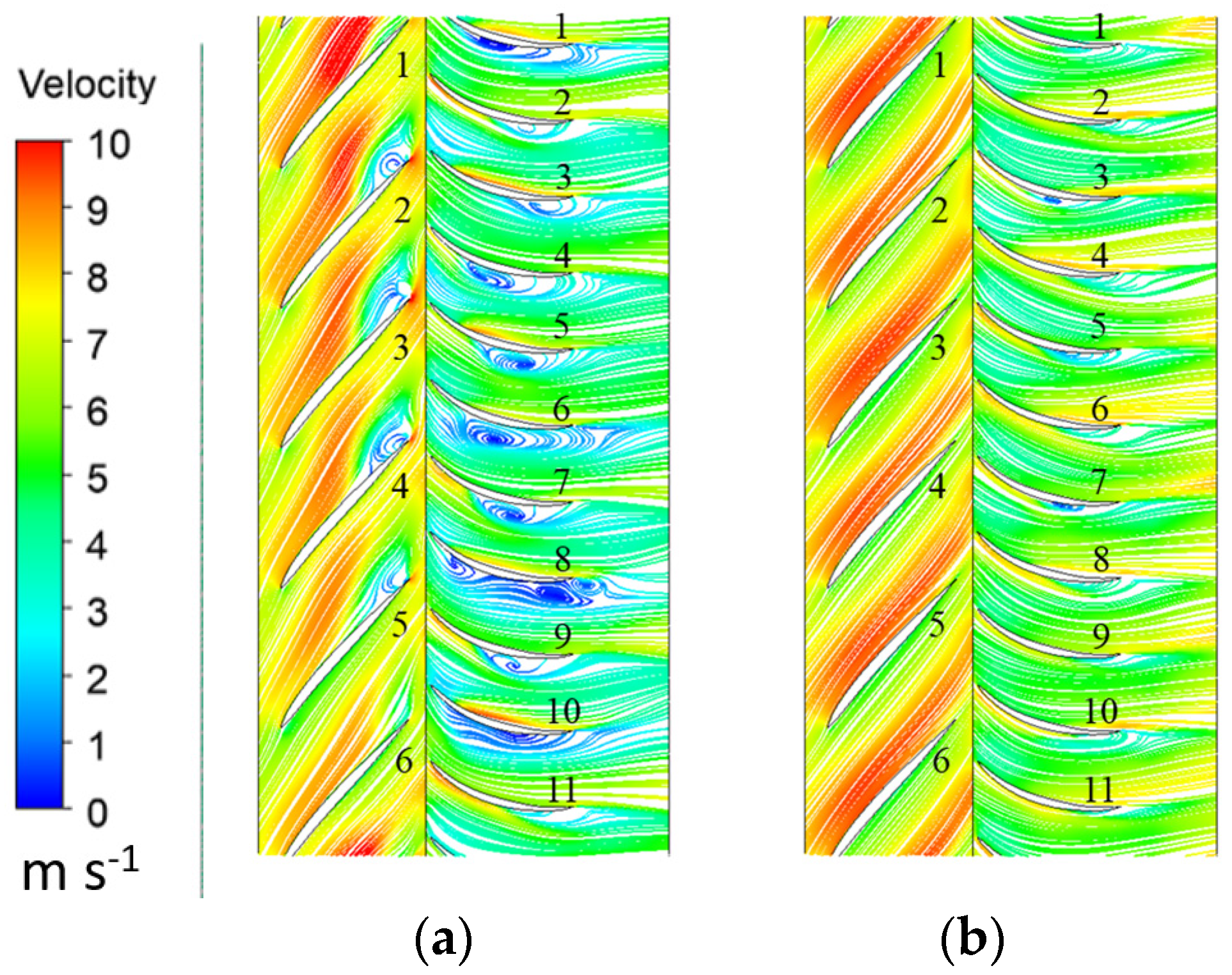
4.4. Vorticity and Turbulence Distributions
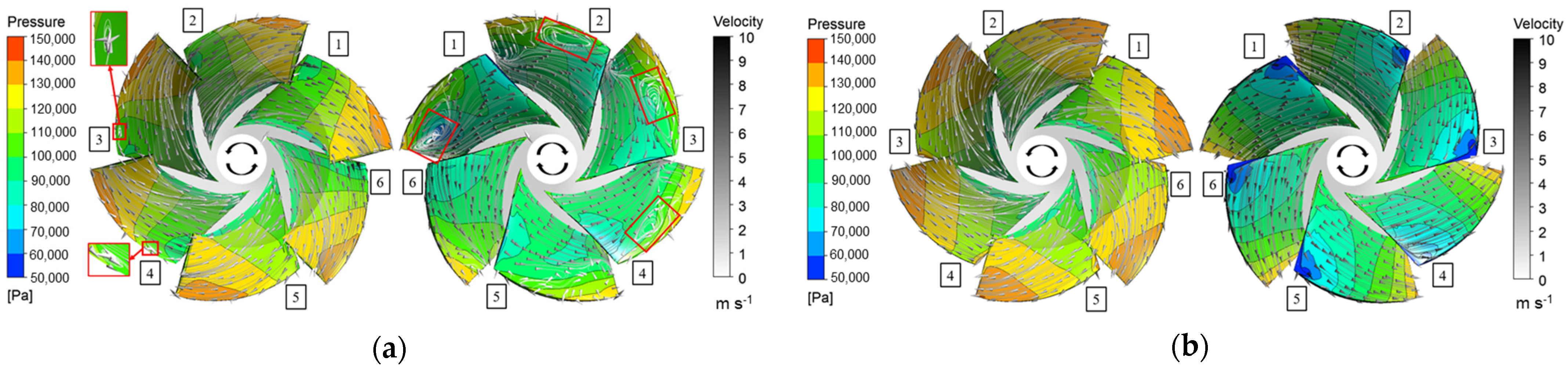
4.5. Pressure and Velocity Distributions
4.6. Discussion
5. Conclusions
- (1)
- When we tested the water jet propulsion pump, we found significant vibrations in the pump, especially at small flow points that deviated from the design conditions. The performance curve of the pump was obtained by experimentation. A pronounced hump was found. According to the vibration phenomenon found in our experiment, the mechanism of vibration needs to be revealed.
- (2)
- Compared to the peak flow condition, the valley flow condition exhibits a higher intensity of vortex cores near the hub region within the impeller. The valley flow condition also has a greater number of small-scale vortex cores near the hub region within the diffuser. The intensity of vortex cores near the shroud region is approximately the same, but the overall intensity is higher. The valley flow condition has a lower overall intensity of vortex cores within the outlet pipe.
- (3)
- The regions with high turbulent kinetic energy in the impeller region are mainly located near the shroud under both valley and peak flow conditions. In the diffuser region, there are regions with high turbulent kinetic energy at different circumferential heights, but the distribution patterns vary. As the circumferential height increases, the turbulent kinetic energy at the inlet of the diffuser increases, while it decreases at the outlet. Additionally, during the valley flow condition, there are regions with high turbulent kinetic energy near the hub within the clearance between the impeller and diffuser. This indicates a higher turbulent intensity in that region. Overall, under the valley flow condition, the impeller and diffuser regions exhibit higher turbulent kinetic energy compared to when under the peak flow condition.
- (4)
- Comparing with the valley and peak pressure and velocity distributions shows that in the valley condition, the streamline of the pressure surface of the impeller blade is relatively smooth and uniform overall, but there are flow separation and vortex flow structures on the suction surface. The scale of the vortex structure in the channel is not uniformly distributed. Under the peak condition, the streamlines on the pressure surface and the suction surface of the impeller blade are relatively smooth and uniform, the flow is regular, and only a small backflow vortex appears on the back of the diffuser.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yan, Z.; Luyi, W.; Jinqing, Z.; Yun, Z. Influence of multi-parameter optimization design on hydraulic performance of water-jet propulsion assembly. J. Drain. Irrig. Mach. Eng. 2021, 39, 655–662. (In Chinese) [Google Scholar]
- Park, W.G.; Jang, J.H.; Chun, H.H.; Kim, M.C. Numerical flow and performance analysis of water-jet propulsion system. Ocean Eng. 2005, 32, 1740–1761. [Google Scholar] [CrossRef]
- Long, Y.; Zhu, R.; Wang, D. A cavitation performance prediction method for pumps PART1-Proposal and feasibility. Nucl. Eng. Technol. 2020, 52, 2471–2478. [Google Scholar]
- Long, Y.; An, C.; Zhu, R.; Chen, J. Research on hydrodynamics of high velocity regions in a water-jet pump based on experimental and numerical calculations at different cavitation conditions. Phys. Fluids 2021, 33, 045124. [Google Scholar] [CrossRef]
- Long, Y.; Zhang, Y.; Chen, J.; Zhu, R.; Wang, D. A cavitation performance prediction method for pumps: Part2-sensitivity and accuracy. Nucl. Eng. Technol. 2021, 53, 3612–3624. [Google Scholar]
- Long, Y.; Zhang, M.; Zhou, Z.; Zhong, J.; An, C.; Chen, Y.; Wan, C.; Zhu, R. Research on cavitation wake vortex structures near the impeller tip of a water-jet pump. Energies 2023, 16, 1576. [Google Scholar] [CrossRef]
- Mu, J.; Wang, L. Approach to the criterion of hump on centrifugal pump performance curve. Trans. Chin. Soc. Agric. Mach. 2004, 35, 74–76. (In Chinese) [Google Scholar]
- Huang, S.; Song, Y.; Yin, J.; Xu, R.; Wang, D. Research on pressure pulsation characteristics of a reactor coolant pump in hump region. Ann. Nucl. Energy 2022, 178, 109325. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, D.; Ran, H.; Xu, R.; Song, Y.; Gong, B. RANS CFD analysis of hump formation mechanism in double-suction centrifugal pump under part load condition. Energies 2021, 14, 6815. [Google Scholar] [CrossRef]
- Wang, Y.-Q.; Ding, Z.-W. Optimization design of hump phenomenon of low specific speed centrifugal pump based on CFD and orthogonal test. Sci. Rep. 2022, 12, 12121. [Google Scholar] [CrossRef]
- Yang, J.; Feng, X.; Liu, X.; Peng, T.; Chen, Z.; Wang, Z. The suppression of hump instability inside a pump turbine in pump mode using water injection control. Processes 2023, 11, 1647. [Google Scholar] [CrossRef]
- Yang, J.; Pavesi, G.; Liu, X.; Xie, T.; Liu, J. Unsteady flow characteristics regarding hump instability in the first stage of a multistage pump-turbine in pump mode. Renew. Energy 2018, 127, 377–385. [Google Scholar] [CrossRef]
- Li, W.; Ping, Y.; Shi, W.; Ji, L.; Li, E.; Ma, L. Research progress in rotating stall in mixed-flow pumps with guide vane. J. Drain. Irrig. Mach. Eng. 2019, 37, 737–745. (In Chinese) [Google Scholar]
- Li, E.; Li, W.; Shi, W.; Ma, L.; Yang, Z. Research on stall discrimination of a mixed-flow water jet pump in hump region. J. Cent. South Univ. (Sci. Technol.) 2020, 51, 2643–2652. (In Chinese) [Google Scholar]
- Ye, W.; Ikuta, A.; Chen, Y.; Miyagawa, K.; Luo, X. Numerical simulation on role of the rotating stall on the hump characteristic in a mixed flow pump using modified partially averaged Navier-Stokes model. Renew. Energy 2020, 166, 91–107. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Y.; Liu, C.; Han, W. Study on unsteady internal flow characteristics in hump zone of mixed flow pump turbine. J. Gansu Sci. 2017, 29, 54–58. (In Chinese) [Google Scholar]
- Yang, J.; Yuan, S.; Pavesi, G.; Chun, L.; Zhou, Y. Study of hump instability phenomena in pump turbine at large partial flow conditions on pump mode. J. Mech. Eng. 2016, 52, 170–178. (In Chinese) [Google Scholar] [CrossRef]
- Pavesi, G.; Yang, J.; Cavazzini, G.; Ardizzon, G. Experimental analysis of instability phenomena in a high-head reversible pump-turbine at large partial flow condition. In Proceedings of the 11th European Conference—Turbomachinery Fluid Dynamics and Thermodynamics, Madrid, Spain, 23–27 March 2015. [Google Scholar]
- Pavesi, G.; Cavazzini, G.; Ardizzon, G. Numerical analysis of the transient behaviour of a variable speed pump-turbine during a pumping power reduction scenario. Energies 2016, 9, 534. [Google Scholar] [CrossRef]
- Ješe, U.; Fortes-Patella, R.; Dular, M. Numerical study of pump-turbine instabilities under pumping mode off-design condi-tions. In Proceedings of the ASME-JSME-KSME Joint Fluids Engineering Conference, Seoul, Republic of Korea, 26–31 July 2015. [Google Scholar]
- Braun, O.; Kueny, J.L.; Avellan, F. Numerical analysis of flow phenomena related to the unstable energy-discharge characteristic of a pump-turbine in pump mode. In Proceedings of the 2005 ASME Fluid Engineering Division Summer Meeting and Exhibition, Houston, TX, USA, 19–23 June 2005. [Google Scholar]
- Liu, Y.; Wang, D.; Ran, H. Computational research on the formation mechanism of double humps in pump–turbines. Eng. Appl. Comput. Fluid Mech. 2021, 15, 1542–1562. [Google Scholar] [CrossRef]
- Li, D. Investigation on Flow Mechanism and Transient Characteristics in Hump Region of a Pump-Turbine. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2017. (In Chinese). [Google Scholar]
- Chen, J. Experimental Investigation of Hysteresis Characteristics in the Hump and S-Shaped Region of a Pump-Turbine. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2017. (In Chinese). [Google Scholar]
- GB/T 3216-2016; Rotodynamic Pumps–Hydraulic Performance Acceptance Tests—Grades 1, 2 and 3. Standards Press of China: Beijing, China, 2016.
- GB/T 13006-2013; NPSH for Centrifugal, Mixed Flow, and Axial Flow Pumps. Standards Press of China: Beijing, China, 2016.
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Menter, F.R. Zonal two-equation k-ω turbulence model for aerodynamic flows. In Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference, Orlando, FL, USA, 6–9 July 1993; pp. 1993–2906. [Google Scholar]
- Menter, F.R.; Kunts, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Xu, S.; Long, X.P.; Ji, B.; Li, G.B.; Song, T. Vortex dynamic characteristics of unsteady tip clearance cavitation in a water-jet propulsion pump determined with different vortex identification methods. J. Mech. Sci. Technol. 2019, 33, 5901–5912. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| Maximum design rotating speed | 1500 r/min |
| Flow rate under maximum design rotating speed | 1660 m3/h |
| Head under maximum design rotating speed | ≥17 m |
| Impeller inlet diameter | 250 mm |
| Impeller blade number | 6 |
| Diffuser blade number | 11 |
| Diffuser outlet diameter | 183 mm |
| Impeller blade inlet angle | 31° |
| Impeller blade outlet angle | 44° |
| Blade tip clearance | 1 mm |
| Operation Condition | Entropy Generation/(W·K−1) | Entropy Generation Proportion/% | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Suction Pipe | Impeller | Diffuser | Out Pipe | Total | Suction Pipe | Impeller | Diffuser | Out Pipe | |
| Valley | 0.18 | 2.70 | 3.05 | 1.77 | 7.70 | 2.4 | 35.1 | 39.6 | 23.0 |
| Peak | 0.27 | 2.42 | 2.12 | 2.75 | 7.57 | 3.6 | 31.9 | 28.1 | 36.3 |
| Operation Condition | Entropy Generation/(W·K−1) | Entropy Generation Proportion/% | |||||
|---|---|---|---|---|---|---|---|
| Direct Dissipation | Turbulent Dissipation | Wall Dissipation | Total | Direct Dissipation | Turbulent Dissipation | Wall Dissipation | |
| Valley | 0.02 | 2.29 | 0.40 | 2.70 | 0.6 | 84.7 | 14.8 |
| Peak | 0.02 | 1.73 | 0.66 | 2.42 | 1.0 | 71.5 | 27.5 |
| Operation Condition | Entropy Generation/(W·K−1) | Entropy Generation Proportion/% | |||||
|---|---|---|---|---|---|---|---|
| Direct Dissipation | Turbulent Dissipation | Wall Dissipation | Total | Direct Dissipation | Turbulent Dissipation | Wall Dissipation | |
| Valley | 0.01 | 2.31 | 0.72 | 3.05 | 0.5 | 75.8 | 23.7 |
| Condition | 0.02 | 1.42 | 0.69 | 2.12 | 0.8 | 66.7 | 32.5 |
| Operation Condition | Entropy Generation/(W·K−1) | Entropy Generation Proportion/% | |||||
|---|---|---|---|---|---|---|---|
| Direct Dissipation | Turbulent Dissipation | Wall Dissipation | Total | Direct Dissipation | Turbulent Dissipation | Wall Dissipation | |
| Valley | 0.01 | 1.26 | 0.50 | 1.77 | 0.3 | 71.5 | 28.2 |
| Peak | 0.01 | 1.65 | 1.09 | 2.75 | 0.4 | 60.1 | 39.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, H.; Long, Y.; Zhong, J. Research on the Internal Flow Difference between Peak and Valley Conditions of Water Jet Propulsion Pump during Working at Hump Region. J. Mar. Sci. Eng. 2024, 12, 258. https://doi.org/10.3390/jmse12020258
Han H, Long Y, Zhong J. Research on the Internal Flow Difference between Peak and Valley Conditions of Water Jet Propulsion Pump during Working at Hump Region. Journal of Marine Science and Engineering. 2024; 12(2):258. https://doi.org/10.3390/jmse12020258
Chicago/Turabian StyleHan, Hanqiao, Yun Long, and Jinqing Zhong. 2024. "Research on the Internal Flow Difference between Peak and Valley Conditions of Water Jet Propulsion Pump during Working at Hump Region" Journal of Marine Science and Engineering 12, no. 2: 258. https://doi.org/10.3390/jmse12020258
APA StyleHan, H., Long, Y., & Zhong, J. (2024). Research on the Internal Flow Difference between Peak and Valley Conditions of Water Jet Propulsion Pump during Working at Hump Region. Journal of Marine Science and Engineering, 12(2), 258. https://doi.org/10.3390/jmse12020258







