Study on the Sealing Performance of Flexible Pipe End-Fittings Considering the Creep Behavior of PVDF Material at Different Temperatures
Abstract
1. Introduction
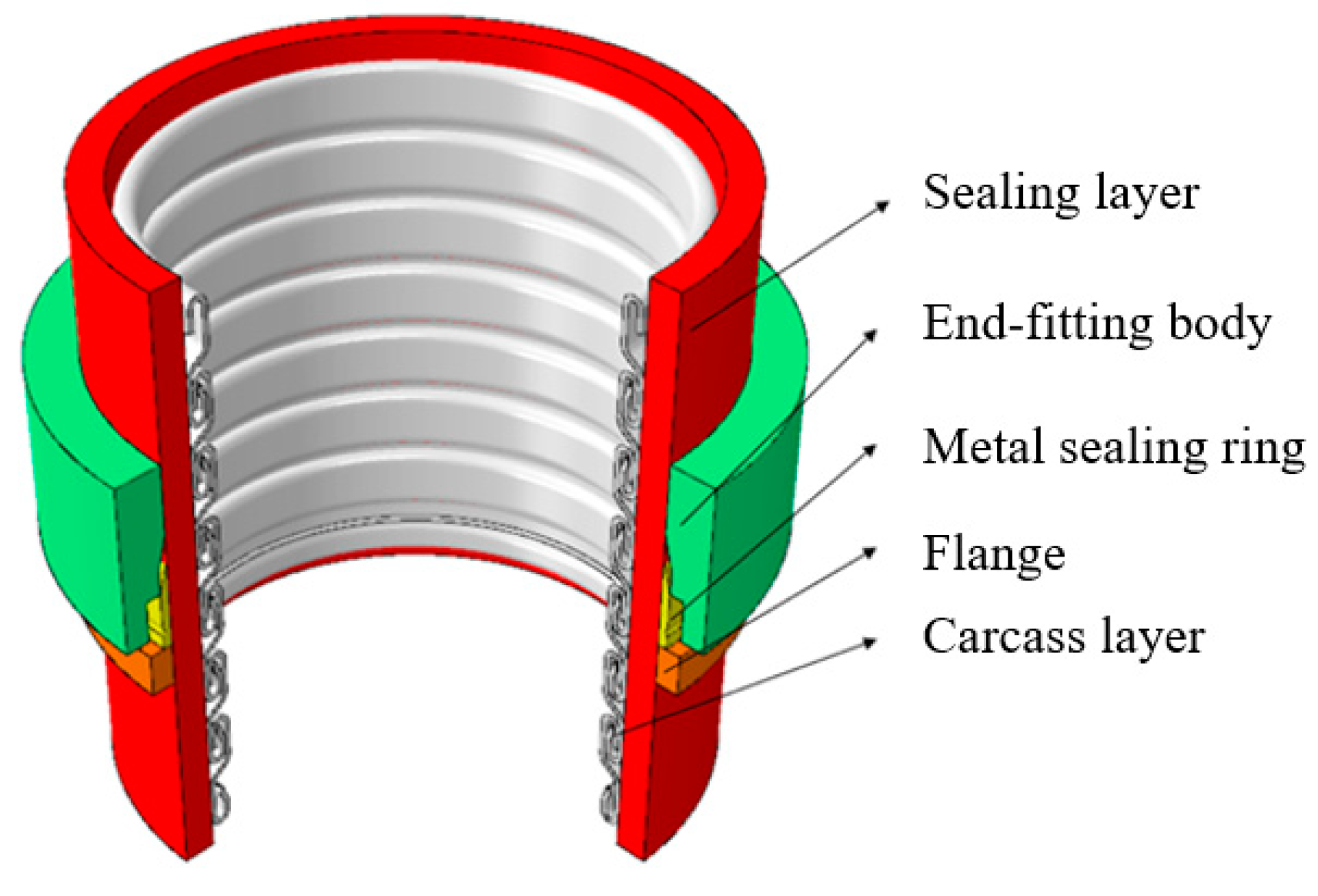
2. Materials and Methods
2.1. PVDF Compression Test
2.2. PVDF Compression Creep Test
3. Results and Discussion
3.1. Time Hardening Model
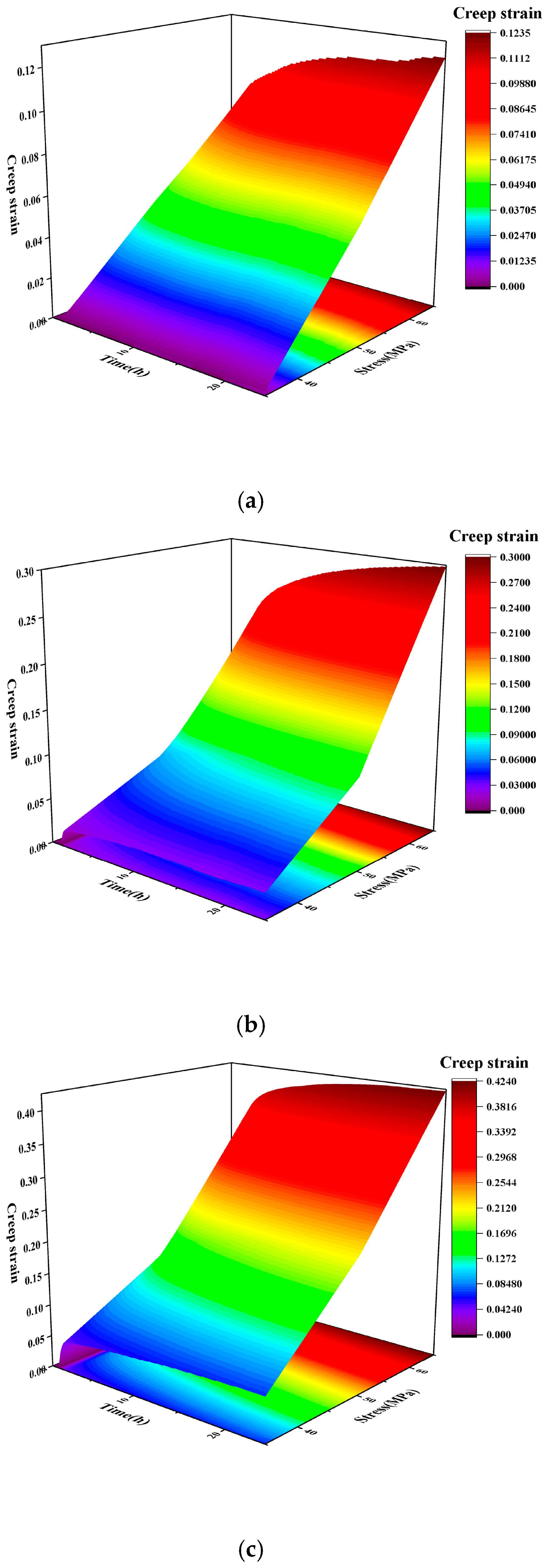
3.2. Creep Analysis
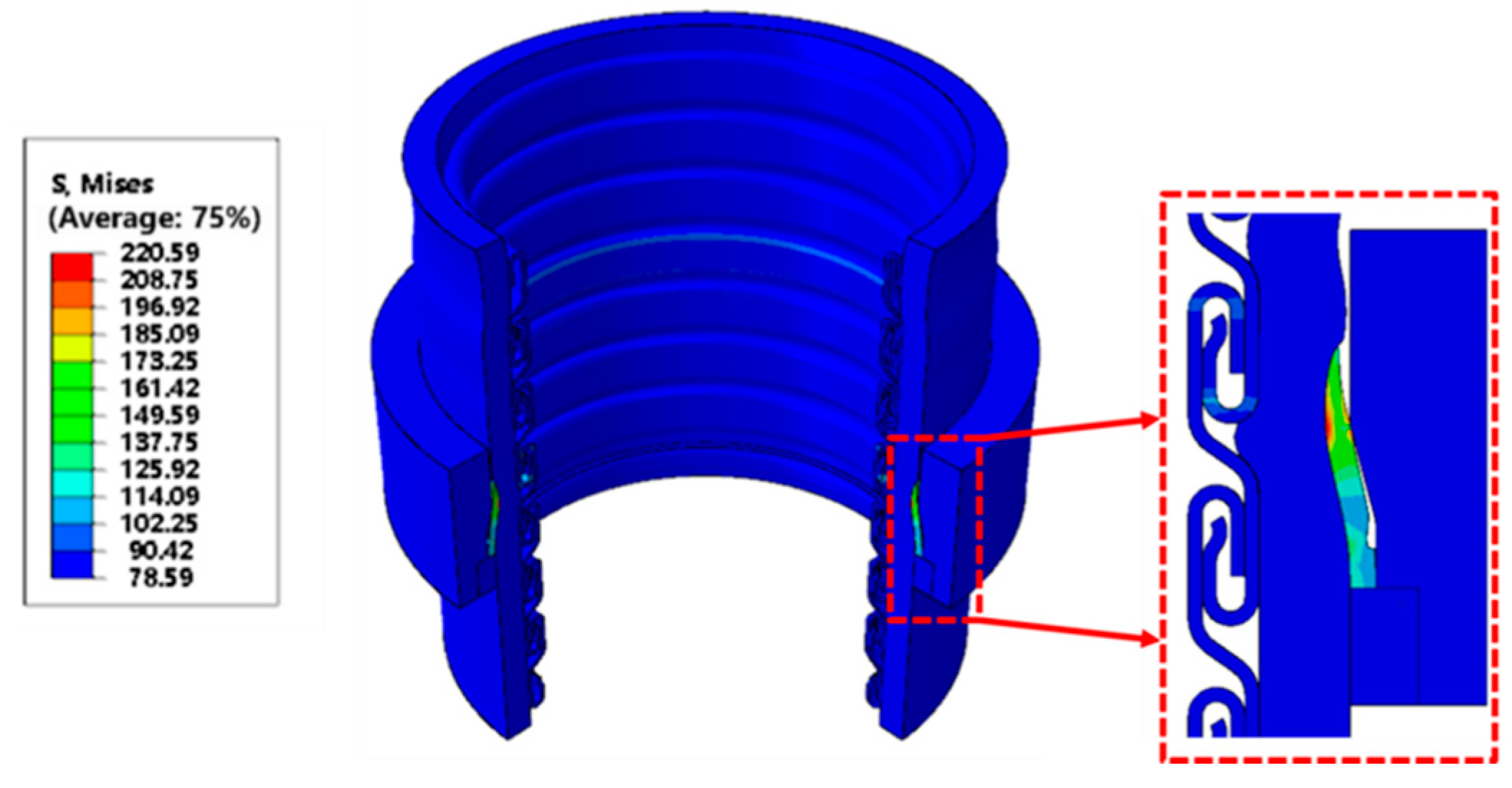
3.2.1. Sealing Layer Stress Analysis
3.2.2. Analysis of Thickness Reduction of Sealing Layer
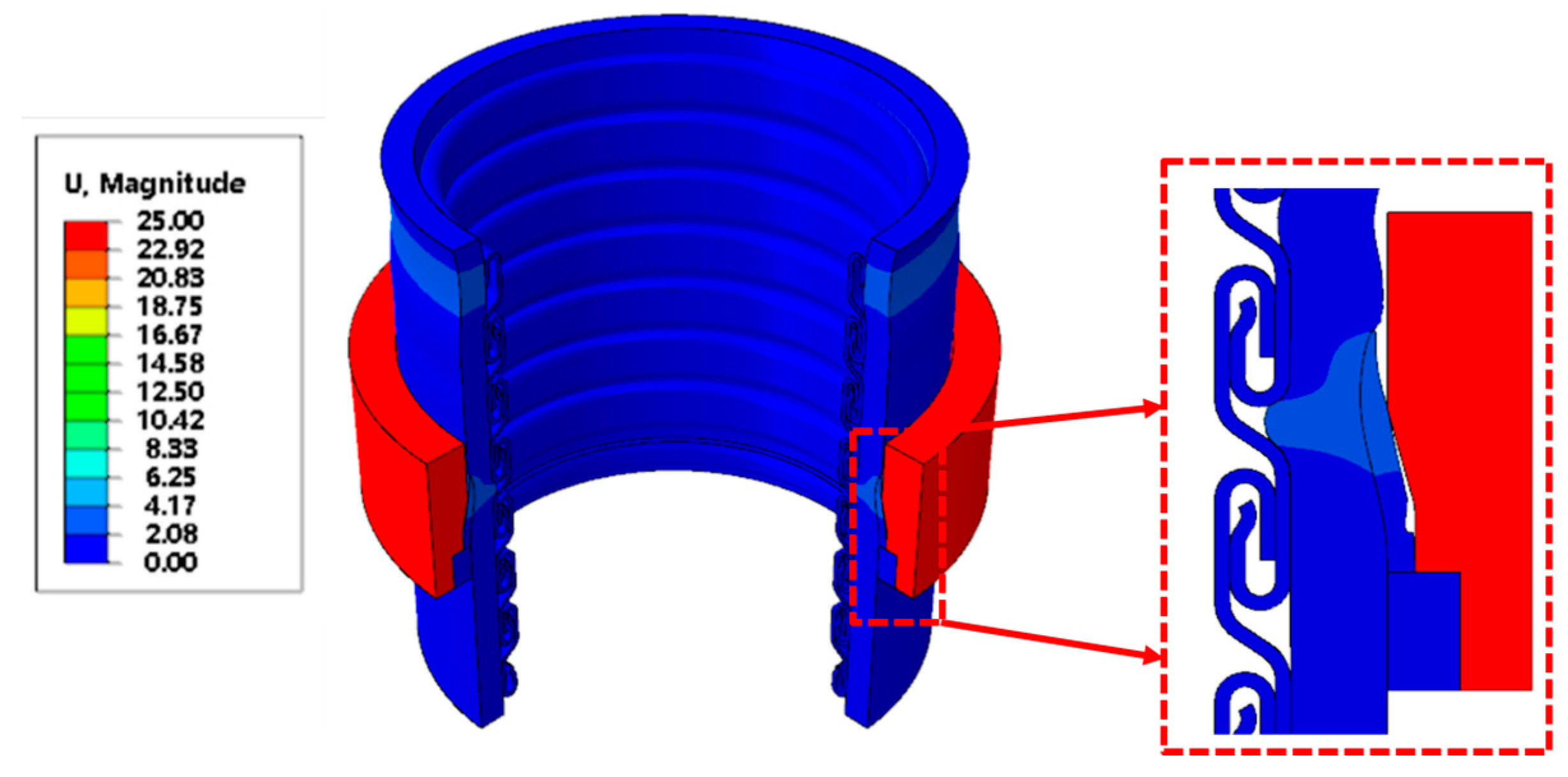
3.2.3. Sealing Performance Analysis of End-Fitting
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, H.L.; Vaz, M.A.; Caire, M. A finite element model for unbonded flexible pipe under combined axisymmetric and bending loads. Mar. Struct. 2020, 74, 102826. [Google Scholar] [CrossRef]
- Dahl, C.S.; Andersen, B.; Groenne, M. Developments in Managing Flexible Risers and pipelines, a Supplier’s Perspective. In Offshore Technology Conference; OTC: Houston, TX, USA, 2011. [Google Scholar]
- Fernando, P.; Nott, G.; Graham, E.; Roberts, A.; Sheldrake, T.; Brunskill, H.; Zhou, L.; Lewis, R. Experimental Evaluation of the Metal-Tometal Seal Design For High-Pressure Flexible Pipes. In Offshore Technology Conference; OTC: Houston, TX, USA, 2012. [Google Scholar]
- Zhang, T.; Lu, Q.Z.; Yan, J.; Wang, S.C.; Yue, Q.J.; Wu, S.H.; Lu, H.L.; Chen, J.L. Numerical Study on Flexible Pipe End Fitting Progressive Failure Behavior Based on Cohesive Zone Model. J. Mar. Sci. Eng. 2023, 11, 116. [Google Scholar] [CrossRef]
- Fernando, U.S.; Karabelas, G. Analysis of End fitting Barrier Seal Performance in High Pressure Unbonded Flexible Pipes. In Proceedings of the 33rd ASME International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014. [Google Scholar]
- Li, X.; Du, X.; Wan, J.; Xiao, H. Structure analysis of flexible pipe end fitting seal system. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, St. John’s, NL, Canada, 11–16 July 1999. [Google Scholar]
- Zhou, C.L.; Zheng, J.Y.; Gu, C.H.; Zhao, Y.Z.; Liu, P.F. Sealing performance analysis of rubber O-ring in high-pressure gaseous hydrogen based on finite element method. Int. J. Hydrogen Energy 2017, 42, 11996–12004. [Google Scholar] [CrossRef]
- Chen, K.; Zhang, M.; Fu, S.; Zhao, B.; Luo, C. A numerical model for stress relaxation analysis of sealing systems in nonbonded pipe end fittings. J. Ocean. Eng. Sci. 2023; in press. [Google Scholar] [CrossRef]
- Persson, B.; Yang, C. Theory of the leak-rate of seals. J. Phys. Condens. Matter. 2008, 20, 315011. [Google Scholar] [CrossRef]
- Lorenz, B.; Persson, B. Leak rate of seals: Comparison of theory with experiment. Europhys. Lett. 2009, 86, 44006. [Google Scholar] [CrossRef]
- Lorenz, B.; Persson, B. Leak rate of seals: Effective-medium theory and comparison with experiment. Phys. J. E 2010, 31, 159–167. [Google Scholar] [CrossRef] [PubMed]
- Slee, A.J.; Stobbart, J.; Gethin, D.T.; Hardy, S.J. Case Study on a Complex Seal Design for a High Pressure Vessel Application. In Proceedings of the ASME Pressure Vessels and Piping Conference, Anaheim, CA, USA, 20–24 July 2014. [Google Scholar]
- Gorash, Y.; Dempster, W.; Nicholls, W.D.; Hamilton, R. Fluid pressure penetration for advanced FEA of metal-to-metal seals. Proc. Appl. Math. Mech. 2015. [Google Scholar] [CrossRef]
- Tang, L.; He, W.; Zhu, X.; Zhou, Y. Sealing Performance of the End Fitting of a Marine Unbonded Flexible Pipe under Pressure Penetration. J. Appl. Comput. Mech. 2020, 6, 543–553. [Google Scholar]
- Saneian, M.; Bai, Y. Evaluation of the Inner Liner in Unbounded Flexible Pipelines in the Sealing System of End-Fitting. In Proceedings of the ASME 2024 43rd International Conference on Ocean, Offshore and Arctic Engineering, Singapore, 9–14 June 2024. [Google Scholar]
- Shen, Y.; Zhao, J.; Tan, Z.; Sheldrake, T. Analysis of the Creep Behaviour of the Polymer Barrier Layer in Unbonded Flexible Pipes Under Different Fluid Temperatures. In Proceedings of the ASME 2012 31st International Conference on Ocean, Offshore and Arctic Engineering, Rio de Janeiro, Brazil, 1–6 July 2012. [Google Scholar]
- de Lima, H.F.; Vaz, M.A.; da Costa, M.F.; Gomez, A.A.; de Oliveira, G.L. Creep behavior of in-service flexible flowline polyamide 11. Polym. Test. 2020, 81, 106205. [Google Scholar] [CrossRef]
- Zhang, J. Creep Behavior Analysis of Unbonded Flexible Riser Lining; China University of Petroleum: Beijing, China, 2023. [Google Scholar]
- Amjadi, M.; Fatemi, A. Creep behavior and modeling of high-density polyethylene (HDPE). Polym. Test. 2021, 94, 107031. [Google Scholar] [CrossRef]
- Spathis, G.; Kontou, E. Creep failure time prediction of polymers and polymer composites. Compos. Sci. Technol. 2012, 72, 959–964. [Google Scholar] [CrossRef]
- Lai, J.; Bakker, A. Analysis of the non-linear creep of high-density polyethylene. Polymer 1995, 36, 93–99. [Google Scholar] [CrossRef]
- Dargahi, A.; Schultz, R.; Runka, J.; Ashrafizadeh, H.; Xu, B.; Naguib, H.E. Nonlinear creep characteristics of extruded Poly (vinylidene fluoride-co-hexafluoropropylene) with high β-phase content under extreme conditions: Design, characterization, and modeling. Mater. Des. 2023, 232, 112124. [Google Scholar] [CrossRef]
- Zheng, Y.Y.; Zhou, J.X.; Ling, X.; Yang, Z.; Yang, S.S.; Wang, Y.N. Creep Property Assessment of Type 304 by Small Punch Creep Test. In Proceedings of the 2nd International Conference SSTT on Determinational of Mechanical Properties of Materials by Small Punch and other Miniature Testing Techniques, Ostrava, Czech Republic, 2–4 October 2012. [Google Scholar]
- GB/T 1041-2008; Determination of Compression Properties of Plastics. China Standard Press: Beijing, China, 2008.
- GB/T 11546-2008; Determination of Creep Properties of Plastics. China Standard Press: Beijing, China, 2008.
- Zhao, Y.; Ji, H.; An, X.; Li, Y. Numerical simulation of creep and stress relaxation of smooth specimens was carried out by ABAQUS. J. Chin. People ’s Armed Police Acad. Eng. 2001, 17, 14–15. [Google Scholar]
- American Petroleum Institute. In API SPEC 17J Specification for Unbonded Flexible Pipe; American Petroleum Institute: Washington, DC, USA, 2014.
















| Parameter | Value | Unit | ||
|---|---|---|---|---|
| 25 °C | 40 °C | 55 °C | ||
| Modulus of elasticity | 870 | 680 | 550 | MPa |
| Compression Deformation Rate | >3 | >3 | >3 | % |
| Yield strength | 110 | 88 | 70 | MPa |
| Compressive strength | 160 | 130 | 105 | MPa |
| T/°C | A | m | n |
|---|---|---|---|
| 25 | 1.58 × 10−11 | −0.76 | 1.13 |
| 40 | 1.72 × 10−9 | −0.83 | 1.20 |
| 55 | 3.21 × 10−7 | −0.93 | 1.42 |
| Parameter | Value | Unit |
|---|---|---|
| Elastic modulus | 210 | GPa |
| Yield strength | 400 | MPa |
| Failure Criteria | Thickness Thinning Criterion/year | Critical Pressure Criterion/year | |
|---|---|---|---|
| T/°C | |||
| 25 | 10.9th | 6.4th | |
| 40 | 3.2th | 4.9th | |
| 55 | 1.5th | 3.0rd | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Q.; Xu, S.; Zhang, T.; Yin, Y.; Lu, H.; Yan, J. Study on the Sealing Performance of Flexible Pipe End-Fittings Considering the Creep Behavior of PVDF Material at Different Temperatures. J. Mar. Sci. Eng. 2024, 12, 2362. https://doi.org/10.3390/jmse12122362
Lu Q, Xu S, Zhang T, Yin Y, Lu H, Yan J. Study on the Sealing Performance of Flexible Pipe End-Fittings Considering the Creep Behavior of PVDF Material at Different Temperatures. Journal of Marine Science and Engineering. 2024; 12(12):2362. https://doi.org/10.3390/jmse12122362
Chicago/Turabian StyleLu, Qingzhen, Shengjie Xu, Tao Zhang, Yuanchao Yin, Hailong Lu, and Jun Yan. 2024. "Study on the Sealing Performance of Flexible Pipe End-Fittings Considering the Creep Behavior of PVDF Material at Different Temperatures" Journal of Marine Science and Engineering 12, no. 12: 2362. https://doi.org/10.3390/jmse12122362
APA StyleLu, Q., Xu, S., Zhang, T., Yin, Y., Lu, H., & Yan, J. (2024). Study on the Sealing Performance of Flexible Pipe End-Fittings Considering the Creep Behavior of PVDF Material at Different Temperatures. Journal of Marine Science and Engineering, 12(12), 2362. https://doi.org/10.3390/jmse12122362






