Investigating Tidal Stream Turbine Array Performance Considering Effects of Number of Turbines, Array Layouts, and Yaw Angles
Abstract
:1. Introduction
2. Numerical Model
2.1. Governing Equations
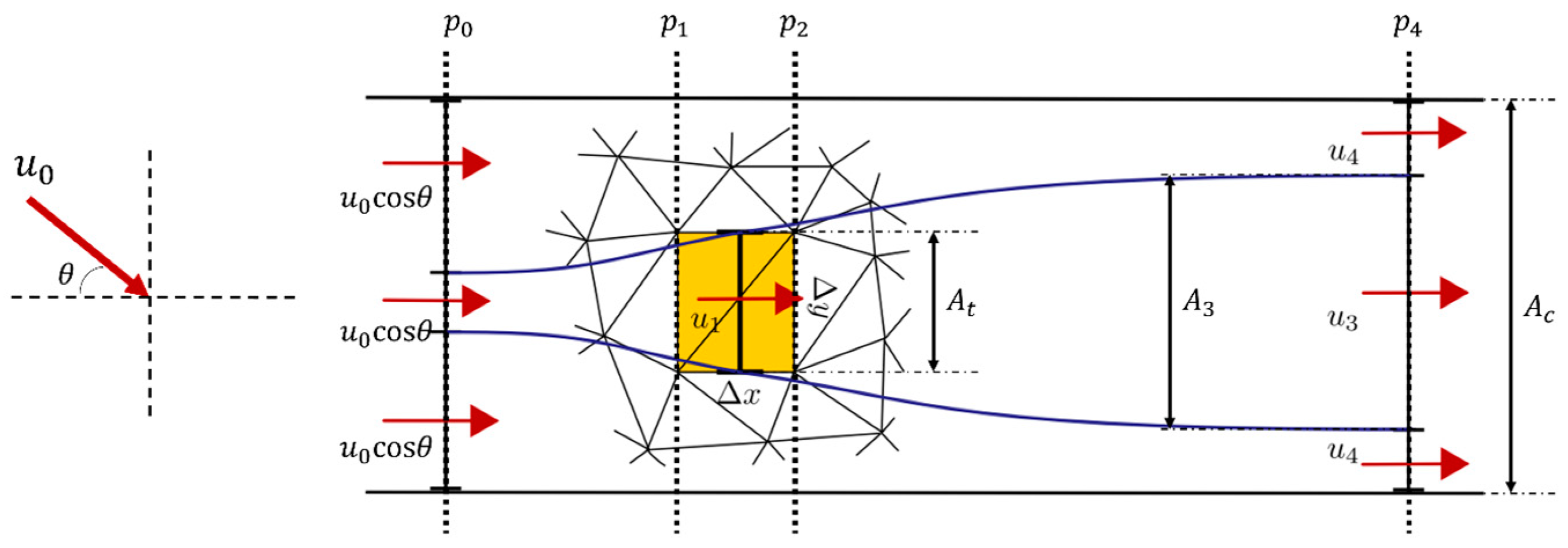
2.2. Yawed Turbine Model
2.3. Optimization Model
- Input the initial values of coordinates and yaw angles for each turbine, forming the parameter vector .
- Solve the shallow water equation with the turbine-related information vector, and obtain the corresponding elevation field, , and velocity field, .
- Evaluate the functional of interest and compute the functional gradient .
- Check if fulfils the optimization termination criteria. If so, stop and output the parameter vector, , and the functional of interest, . Otherwise, proceed to step 5.
- Improve parameter vector to using the quasi-Newton method and go to step 2 with .
2.4. Computational Domain and Its Meshing
2.5. Solver Options and Boundary Conditions
2.6. Model Validation
2.6.1. Hydrodynamic Model Validation Data Sources
2.6.2. Turbine Model Validation Data Sources
2.6.3. Validation Metrics
2.7. Studying Cases
2.7.1. Scenario 1
2.7.2. Scenario 2
2.7.3. Scenario 3
3. Results and Discussion
3.1. Model Validation Results
3.1.1. Tidal Stream Model Validation
3.1.2. Yawed Turbine Model Validation
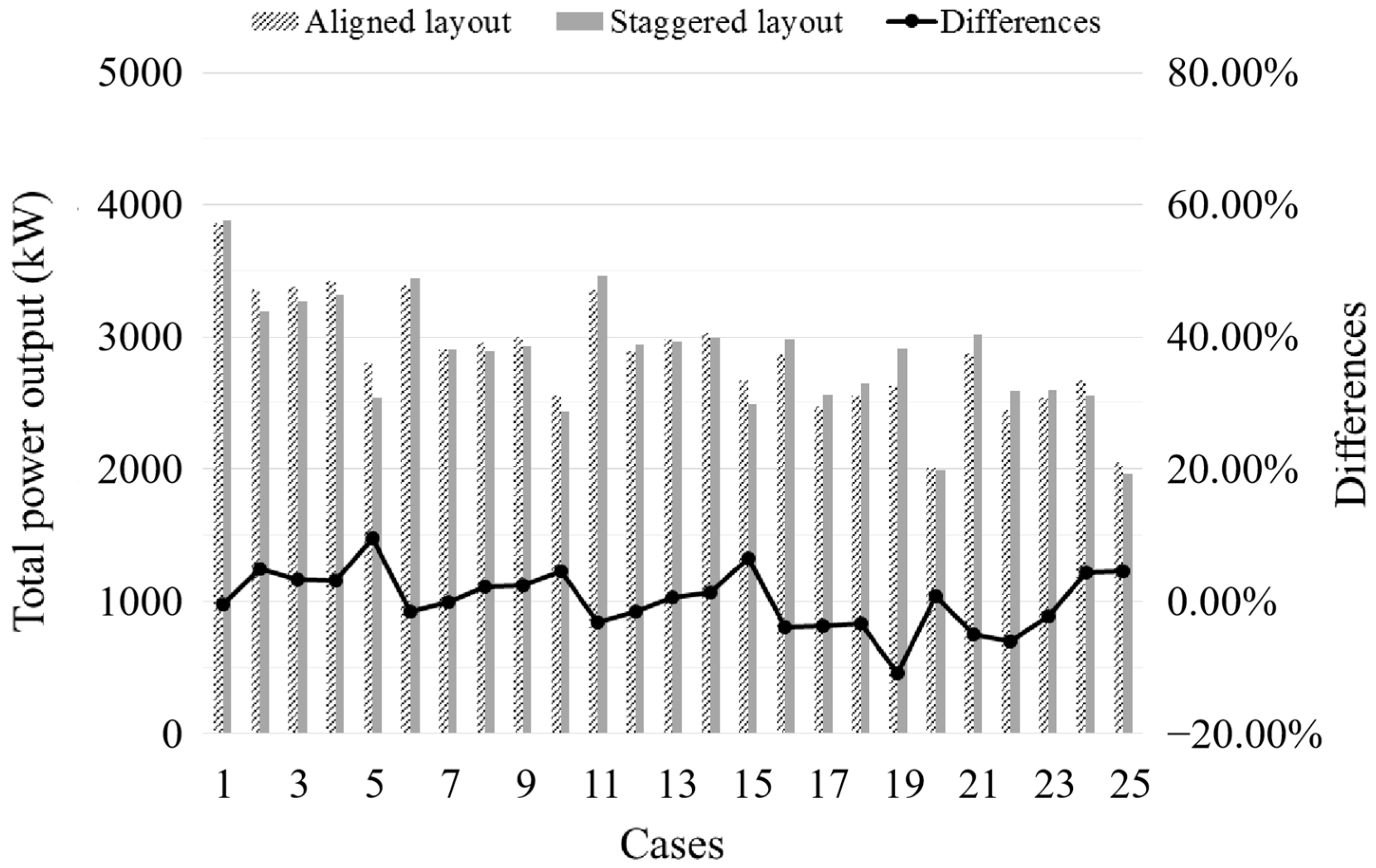
3.2. Effects of the Number of Turbines
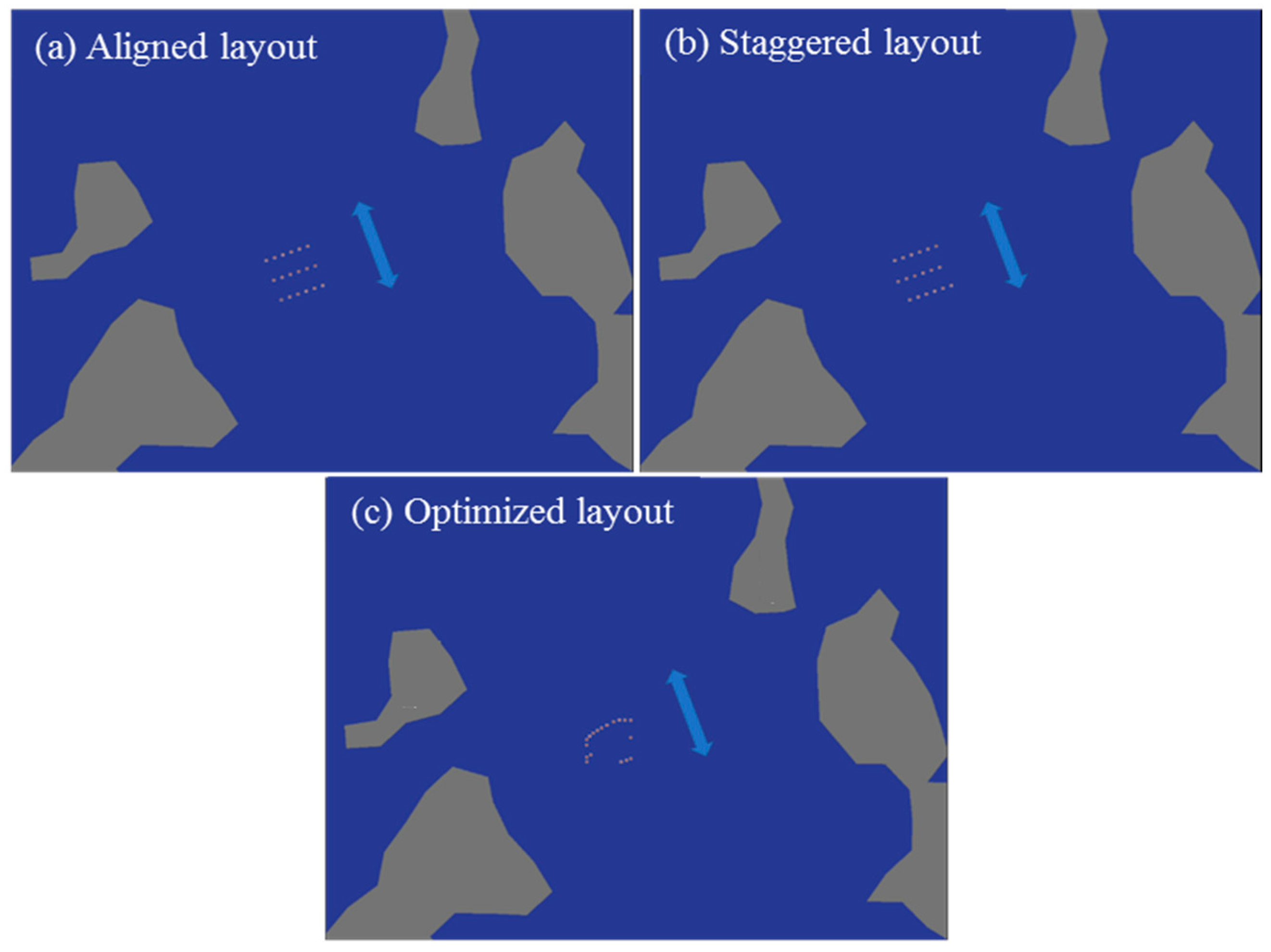
3.3. Effects of Array Layout
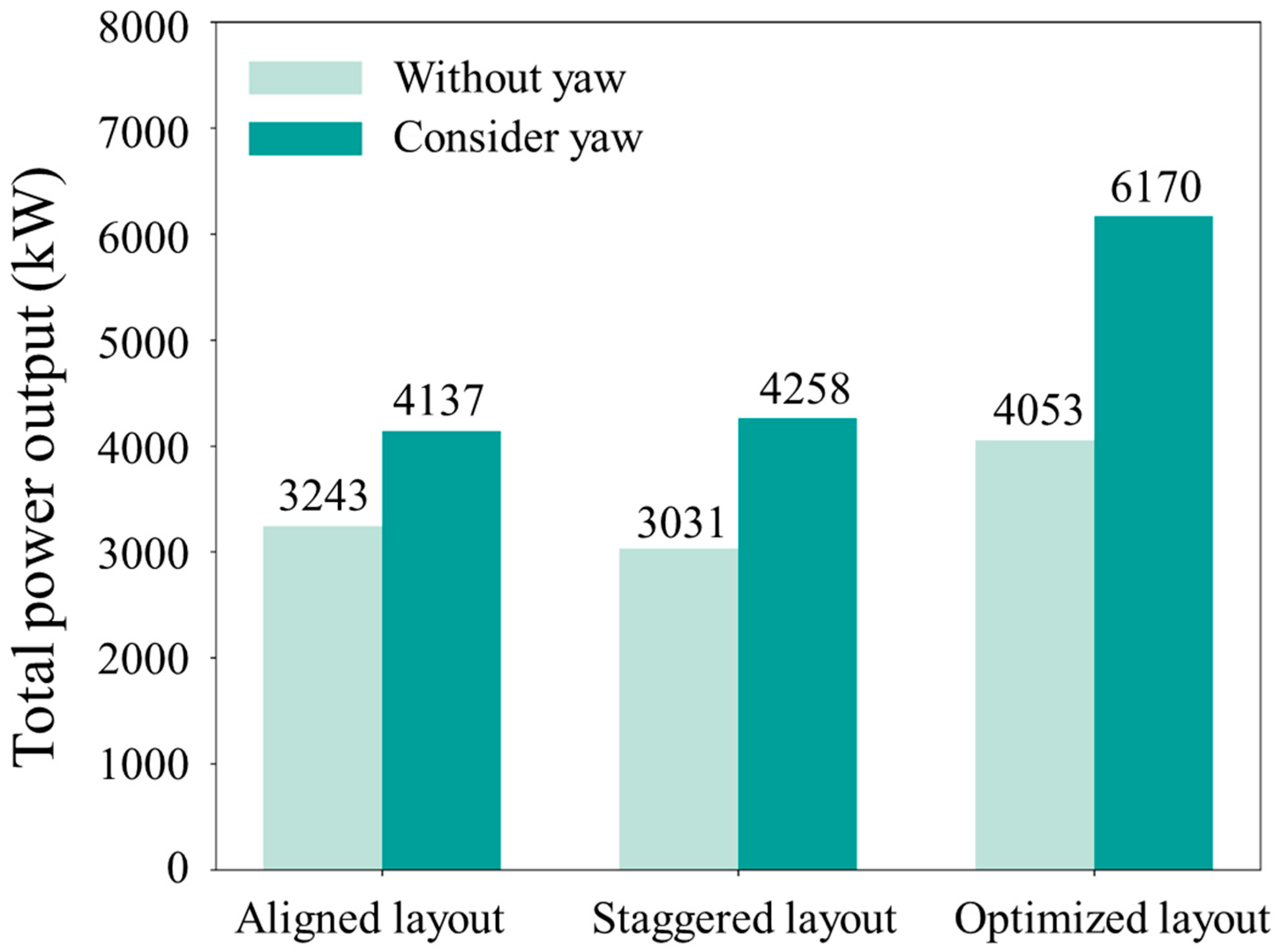
3.4. Effects of Yaw Angle
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Free surface displacement | |
| Time | |
| Total water depth | |
| Depth-averaged velocity vector | |
| Kinematic viscosity | |
| Coriolis frequency | |
| Natural bottom shear stress | |
| Dimensionless friction coefficient | |
| Number of turbines | |
| Thrust coefficient of the i-th turbine in Thetis | |
| Two-dimensional bump function | |
| Coordinates of the i-th turbine | |
| Radius of the turbine. | |
| Thrust coefficient of the turbine | |
| Turbine cross-sectional area | |
| Upstream velocity | |
| Normal component of velocity | |
| Yaw angle | |
| Actual area where the thrust force is applied | |
| Cross-section area | |
| Function of interest | |
| Partial differential equations | |
| Fields of tidal elevation and tidal velocity | |
| Low bounds of the turbine deploying area | |
| Up bounds of the turbine deploying area | |
| Minimum distance constrains | |
| Vector of coordinates and yaw angles for each turbine | |
| Regression score | |
| Measured value of the i-th sample | |
| Simulated value of the i-th sample | |
| Total number of samples | |
| Mean value over all samples | |
| Aligned layout achieving the highest power output with 20 turbines | |
| Aligned layout resulting in the lowest power output with 20 turbines | |
| Staggered layout achieving the highest power output with 20 turbines | |
| Staggered layout resulting in the lowest power output with 20 turbines | |
| Aligned layout simulated using OpenTidalFarm | |
| Staggered layout simulated using OpenTidalFarm | |
| Optimized layout simulated using OpenTidalFarm | |
| Aligned layout simulated using Thetis | |
| Staggered layout simulated using Thetis | |
| Optimized layout simulated using Thetis |
| PDE | Partial Differential Equations |
| TDA | Turbine Deploying Area |
| RMSE | Root Mean Squared Error |
| POPT | Power Output Per Turbine |
| IPO | Instantaneous Power Output |
References
- Dong, Y.; Yan, Y.; Xu, S.; Zhang, X.; Zhang, X.; Chen, J.; Guo, J. An Adaptive Yaw Method of Horizontal-Axis Tidal Stream Turbines for Bidirectional Energy Capture. Energy 2023, 282, 128918. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, J.; Lin, Y.; Si, Y.; Huang, C.; Yang, J.; Huang, B.; Li, W. Present Situation and Future Prospect of Renewable Energy in China. Renew. Sustain. Energy Rev. 2017, 76, 865–871. [Google Scholar] [CrossRef]
- Melikoglu, M. Current Status and Future of Ocean Energy Sources: A Global Review. Ocean Eng. 2018, 148, 563–573. [Google Scholar] [CrossRef]
- Zheng, J.; Dai, P.; Zhang, J. Tidal Stream Energy in China. Procedia Eng. 2015, 116, 880–887. [Google Scholar] [CrossRef]
- Azlan, F.; Kurnia, J.C.; Tan, B.T.; Ismadi, M.-Z. Review on Optimisation Methods of Wind Farm Array under Three Classical Wind Condition Problems. Renew. Sustain. Energy Rev. 2021, 135, 110047. [Google Scholar] [CrossRef]
- Vennell, R. The Energetics of Large Tidal Turbine Arrays. Renew. Energy 2012, 48, 210–219. [Google Scholar] [CrossRef]
- Vennell, R.; Funke, S.W.; Draper, S.; Stevens, C.; Divett, T. Designing Large Arrays of Tidal Turbines: A Synthesis and Review. Renew. Sustain. Energy Rev. 2015, 41, 454–472. [Google Scholar] [CrossRef]
- Malki, R.; Williams, A.J.; Croft, T.N.; Togneri, M.; Masters, I. A Coupled Blade Element Momentum—Computational Fluid Dynamics Model for Evaluating Tidal Stream Turbine Performance. Appl. Math. Model. 2013, 37, 3006–3020. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, B.; Lin, J.; Wang, S. Experimental Study of Wake Structure behind a Horizontal Axis Tidal Stream Turbine. Appl. Energy 2017, 196, 82–96. [Google Scholar] [CrossRef]
- Divett, T.; Vennell, R.; Stevens, C. Optimization of Multiple Turbine Arrays in a Channel with Tidally Reversing Flow by Numerical Modelling with Adaptive Mesh. Phil. Trans. R. Soc. A. 2013, 371, 20120251. [Google Scholar] [CrossRef]
- Draper, S.; Nishino, T. Centred and Staggered Arrangements of Tidal Turbines. J. Fluid Mech. 2014, 739, 72–93. [Google Scholar] [CrossRef]
- Nash, S.; Olbert, A.; Hartnett, M. Towards a Low-Cost Modelling System for Optimising the Layout of Tidal Turbine Arrays. Energies 2015, 8, 13521–13539. [Google Scholar] [CrossRef]
- Lo Brutto, O.A.; Thiébot, J.; Guillou, S.S.; Gualous, H. A Semi-Analytic Method to Optimize Tidal Farm Layouts—Application to the Alderney Race (Raz Blanchard), France. Appl. Energy 2016, 183, 1168–1180. [Google Scholar] [CrossRef]
- Lo Brutto, O.A.; Nguyen, V.T.; Guillou, S.S.; Thiébot, J.; Gualous, H. Tidal Farm Analysis Using an Analytical Model for the Flow Velocity Prediction in the Wake of a Tidal Turbine with Small Diameter to Depth Ratio. Renew. Energy 2016, 99, 347–359. [Google Scholar] [CrossRef]
- Wu, G.; Wu, H.; Wang, X.; Zhou, Q.; Liu, X. Tidal Turbine Array Optimization Based on the Discrete Particle Swarm Algorithm. China Ocean Eng 2018, 32, 358–364. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, H.; Kang, H.-S.; Li, H. Layout Optimization of a Tidal Current Turbine Array Based on Quantum Discrete Particle Swarm Algorithm. J. Mar. Sci. Eng. 2023, 11, 1994. [Google Scholar] [CrossRef]
- Funke, S.W.; Farrell, P.E.; Piggott, M.D. Tidal Turbine Array Optimisation Using the Adjoint Approach. Renew. Energy 2014, 63, 658–673. [Google Scholar] [CrossRef]
- Funke, S.W.; Farrell, P.E. A Framework for Automated PDE-Constrained Optimisation. arXiv 2013, arXiv:1302.3894. [Google Scholar]
- Funke, S. The Automation of PDE-Constrained Optimisation and Its Applications. Ph.D. Thesis, Imperial College London, London, UK, 2013. [Google Scholar]
- Culley, D.M.; Funke, S.W.; Kramer, S.C.; Piggott, M.D. Integration of Cost Modelling within the Micro-Siting Design Optimisation of Tidal Turbine Arrays. Renew. Energy 2016, 85, 215–227. [Google Scholar] [CrossRef]
- Du Feu, R.J.; Funke, S.W.; Kramer, S.C.; Hill, J.; Piggott, M.D. The Trade-off between Tidal-Turbine Array Yield and Environmental Impact: A Habitat Suitability Modelling Approach. Renew. Energy 2019, 143, 390–403. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, J.; Tong, L.; Guo, Y.; Zhang, P. Investigation of Array Layout of Tidal Stream Turbines on Energy Extraction Efficiency. Ocean Eng. 2020, 196, 106775. [Google Scholar] [CrossRef]
- Qian, Y.; Zhang, Y.; Sun, Y.; Zhang, H.; Zhang, Z.; Li, C. Experimental and Numerical Investigations on the Performance and Wake Characteristics of a Tidal Turbine under Yaw. Ocean Eng. 2023, 289, 116276. [Google Scholar] [CrossRef]
- Zhang, Y.; Peng, B.; Zheng, J.; Zheng, Y.; Tang, Q.; Liu, Z.; Xu, J.; Wang, Y.; Fernandez-Rodriguez, E. The Impact of Yaw Motion on the Wake Interaction of Adjacent Floating Tidal Stream Turbines under Free Surface Condition. Energy 2023, 283, 129071. [Google Scholar] [CrossRef]
- Galloway, P.W.; Myers, L.E.; Bahaj, A.S. Experimental and Numerical Results of Rotor Power and Thrust of a Tidal Turbine Operating at Yaw and in Waves. In Proceedings of the World Renewable Energy Congress, Linköping, Sweden, 8–13 May 2011; p. 2246e2253. [Google Scholar]
- Zhang, C.; Zhang, J.; Angeloudis, A.; Zhou, Y.; Kramer, S.C.; Piggott, M.D. Physical Modelling of Tidal Stream Turbine Wake Structures under Yaw Conditions. Energies 2023, 16, 1742. [Google Scholar] [CrossRef]
- Li, C.; Zhang, Y.; Zheng, Y.; Qian, Y.; Fernandez-Rodriguez, E.; Benini, E. Research on the Effect of Yawing Motion on Tidal Turbine Performance Based on Actuator-Line Method. Ocean Eng. 2023, 279, 114345. [Google Scholar] [CrossRef]
- Modali, P.K. On Performance and Wake Characteristics of a Tidal Turbine under Yaw; Lehigh University: Bethlehem, PA, USA, 2016. [Google Scholar]
- Badoe, C.E.; Li, X.; Williams, A.J.; Masters, I. Output of a Tidal Farm in Yawed Flow and Varying Turbulence Using GAD-CFD. Ocean Eng. 2024, 294, 116736. [Google Scholar] [CrossRef]
- Kramer, S.C.; Piggott, M.D. A Correction to the Enhanced Bottom Drag Parameterisation of Tidal Turbines. Renew. Energy 2016, 92, 385–396. [Google Scholar] [CrossRef]
- Zhang, C.; Kramer, S.C.; Angeloudis, A.; Zhang, J.; Lin, X.; Piggott, M.D. Improving Tidal Turbine Array Performance through the Optimisation of Layout and Yaw Angles. Int. J. Mar. Ene. 2022, 5, 273–280. [Google Scholar] [CrossRef]
- Schwedes, T.; Ham, D.A.; Funke, S.W.; Piggott, M.D. Mesh Dependence in PDE- Constrained Optimisation; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Zhang, J.; Zhang, C.; Angeloudis, A.; Kramer, S.C.; He, R.; Piggott, M.D. Interactions between Tidal Stream Turbine Arrays and Their Hydrodynamic Impact around Zhoushan Island, China. Ocean Eng. 2022, 246, 110431. [Google Scholar] [CrossRef]
- Zhang, C.; Cheng, X.; Angeloudis, A.; Kramer, S.C.; Wu, C.; Chen, Y.; Piggott, M.D. Economics-Constrained Tidal Turbine Array Layout Optimisation at the Putuoshan–Hulu Island Waterway. Ocean Eng. 2024, 314, 119618. [Google Scholar] [CrossRef]
- Egbert, G.D.; Erofeeva, S.Y. Efficient Inverse Modeling of Barotropic Ocean Tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef]
- O’Doherty, D.M.; Mason-Jones, A.; Morris, C.; O’Doherty, T.; Byrne, C.; Prickett, P.W.; Grosvenor, R.I. Others Interaction of Marine Turbines in Close Proximity. In Proceedings of the 9th european wave and tidal energy conference (EWTEC), Southampton, UK, 5–9 September 2011; pp. 10–14. [Google Scholar]














| Scenario 1 | (m) | (m) | The Number of Turbines | The Number of Columns | The Number of Rows |
|---|---|---|---|---|---|
| Case 1 | 40 | 40 | 30 | 6 | 5 |
| Case 2 | 40 | 45 | 24 | 6 | 4 |
| Case 3 | 40 | 50 | 24 | 6 | 4 |
| Case 4 | 40 | 55 | 24 | 6 | 4 |
| Case 5 | 40 | 60 | 18 | 6 | 3 |
| Case 6 | 45 | 40 | 25 | 5 | 5 |
| Case 7 | 45 | 45 | 20 | 5 | 4 |
| Case 8 | 45 | 50 | 20 | 5 | 4 |
| Case 9 | 45 | 55 | 20 | 5 | 4 |
| Case 10 | 45 | 60 | 15 | 5 | 3 |
| Case 11 | 50 | 40 | 25 | 5 | 5 |
| Case 12 | 50 | 45 | 20 | 5 | 4 |
| Case 13 | 50 | 50 | 20 | 5 | 4 |
| Case 14 | 50 | 55 | 20 | 5 | 4 |
| Case 15 | 50 | 60 | 15 | 5 | 3 |
| Case 16 | 55 | 40 | 20 | 4 | 5 |
| Case 17 | 55 | 45 | 16 | 4 | 4 |
| Case 18 | 55 | 50 | 16 | 4 | 4 |
| Case 19 | 55 | 55 | 16 | 4 | 4 |
| Case 20 | 55 | 60 | 12 | 4 | 3 |
| Case 21 | 60 | 40 | 20 | 4 | 5 |
| Case 22 | 60 | 45 | 16 | 4 | 4 |
| Case 23 | 60 | 50 | 16 | 4 | 4 |
| Case 24 | 60 | 55 | 16 | 4 | 4 |
| Case 25 | 60 | 60 | 12 | 4 | 3 |
| Tides | Types | RMSE | |||
|---|---|---|---|---|---|
| Case OB1 | Case OB2 | Case OB1 | Case OB2 | ||
| All 2013.08.15 ~2013.08.25 | (m) | 0.125 | 0.148 | 0.985 | 0.978 |
| Neap tide 2013.08.16 10:00 ~2013.08.17 11:00 | (m/s) | 0.217 | 0.157 | 0.159 | 0.558 |
) | 42.2 | 43.9 | --- | --- | |
| Intermediate tide 2013.08.19 14:00 ~2013.08.20 15:00 | (m/s) | 0.367 | 0.156 | 0.106 | 0.839 |
) | 23.8 | 20.7 | --- | --- | |
| Spring tide 2013.08.23 10:00 ~2013.08.24 11:00 | (m/s) | 0.468 | 0.170 | −0.064 | 0.859 |
) | 21.5 | 29.1 | --- | --- | |
| Yaw Angle | 1D | 2D | 4D | 6D | 8D | 10D |
|---|---|---|---|---|---|---|
| 0° | 0.30 | 0.24 | 0.17 | 0.12 | 0.07 | 0.06 |
| 10° | 0.22 | 0.19 | 0.08 | 0.04 | 0.01 | 0.01 |
| 20° | 0.18 | 0.14 | 0.07 | 0.04 | 0.02 | 0.01 |
| 30° | 0.16 | 0.11 | 0.05 | 0.04 | 0.03 | 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Zhang, K.; Cheng, X.; Lin, X.; Zhang, J.; Wu, C.; Ren, Z. Investigating Tidal Stream Turbine Array Performance Considering Effects of Number of Turbines, Array Layouts, and Yaw Angles. J. Mar. Sci. Eng. 2024, 12, 2325. https://doi.org/10.3390/jmse12122325
Zhang C, Zhang K, Cheng X, Lin X, Zhang J, Wu C, Ren Z. Investigating Tidal Stream Turbine Array Performance Considering Effects of Number of Turbines, Array Layouts, and Yaw Angles. Journal of Marine Science and Engineering. 2024; 12(12):2325. https://doi.org/10.3390/jmse12122325
Chicago/Turabian StyleZhang, Can, Kai Zhang, Xiaoming Cheng, Xiangfeng Lin, Jisheng Zhang, Chengsheng Wu, and Zhihao Ren. 2024. "Investigating Tidal Stream Turbine Array Performance Considering Effects of Number of Turbines, Array Layouts, and Yaw Angles" Journal of Marine Science and Engineering 12, no. 12: 2325. https://doi.org/10.3390/jmse12122325
APA StyleZhang, C., Zhang, K., Cheng, X., Lin, X., Zhang, J., Wu, C., & Ren, Z. (2024). Investigating Tidal Stream Turbine Array Performance Considering Effects of Number of Turbines, Array Layouts, and Yaw Angles. Journal of Marine Science and Engineering, 12(12), 2325. https://doi.org/10.3390/jmse12122325






