Acoustic Propagation and Transmission Loss Analysis in Shallow Water of Northern Arabian Sea
Abstract
1. Introduction
- Provided novel data by quantifying environmental parameters, such as temperature, conductivity, water density, salinity, sound velocity, and depth using the conductivity temperature and depth (CTD) apparatus, enabling the determination of the sound speed profile in the northern Arabian Sea.
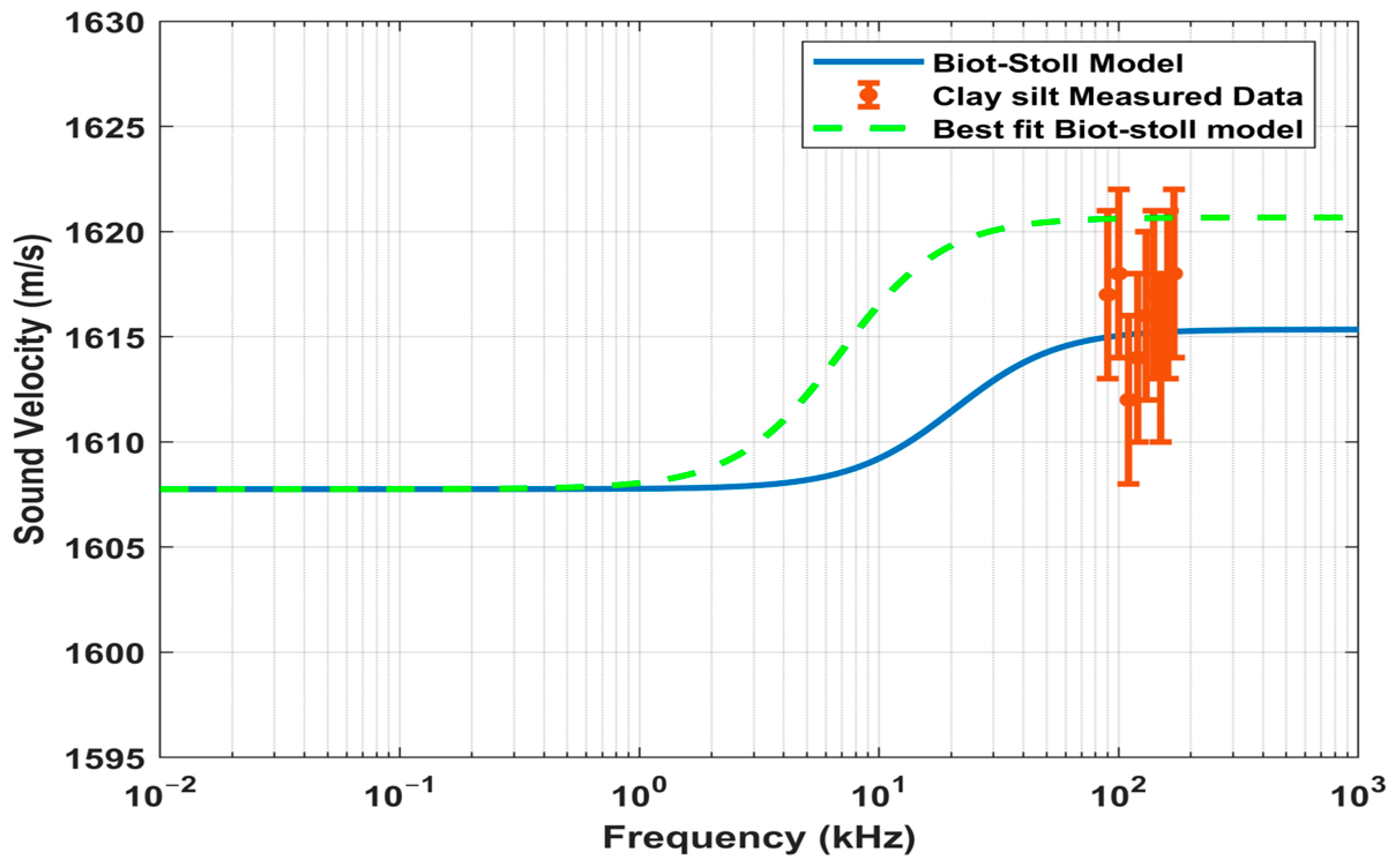
- Physical characteristics of sediment samples collected from the northern Arabian Sea were identified as clayey silt through categorization and sieve analysis. Additionally, bulk density, mean grain size, grain density, mass density, porosity, and acoustic properties, including sound speed and attenuation in sediment, were measured and analyzed from the laboratory experiments.
- Established the understanding of sound propagation characteristics within the low-frequency range of 50–500 Hz, highlighting the impact of the ocean floor on acoustic propagation, which is crucial for the advancement of underwater acoustic applications and the optimization of sonar system performance.
2. Materials and Methods
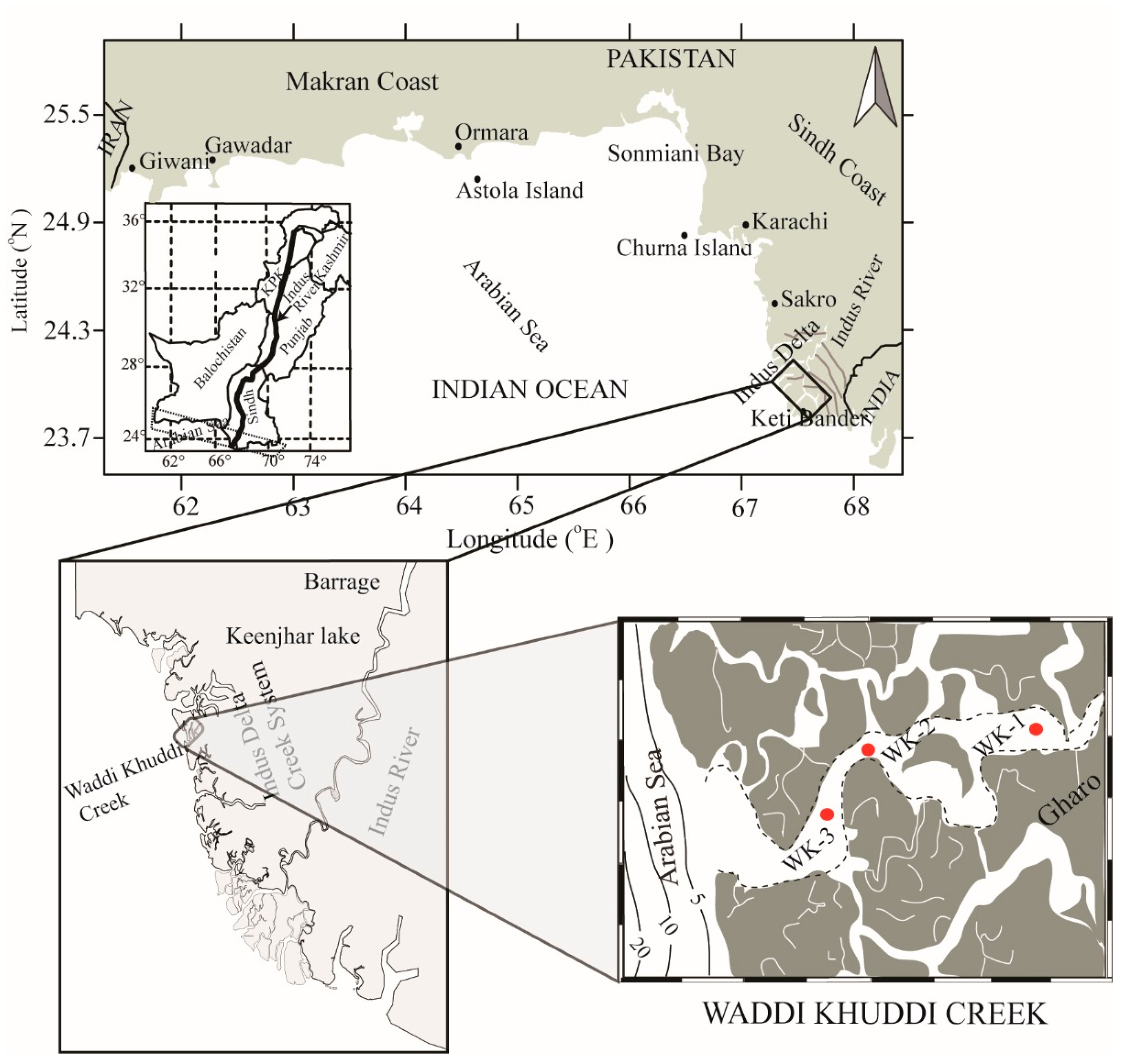
2.1. Study Site
2.2. Physical Properties of Novel Sediment Sample
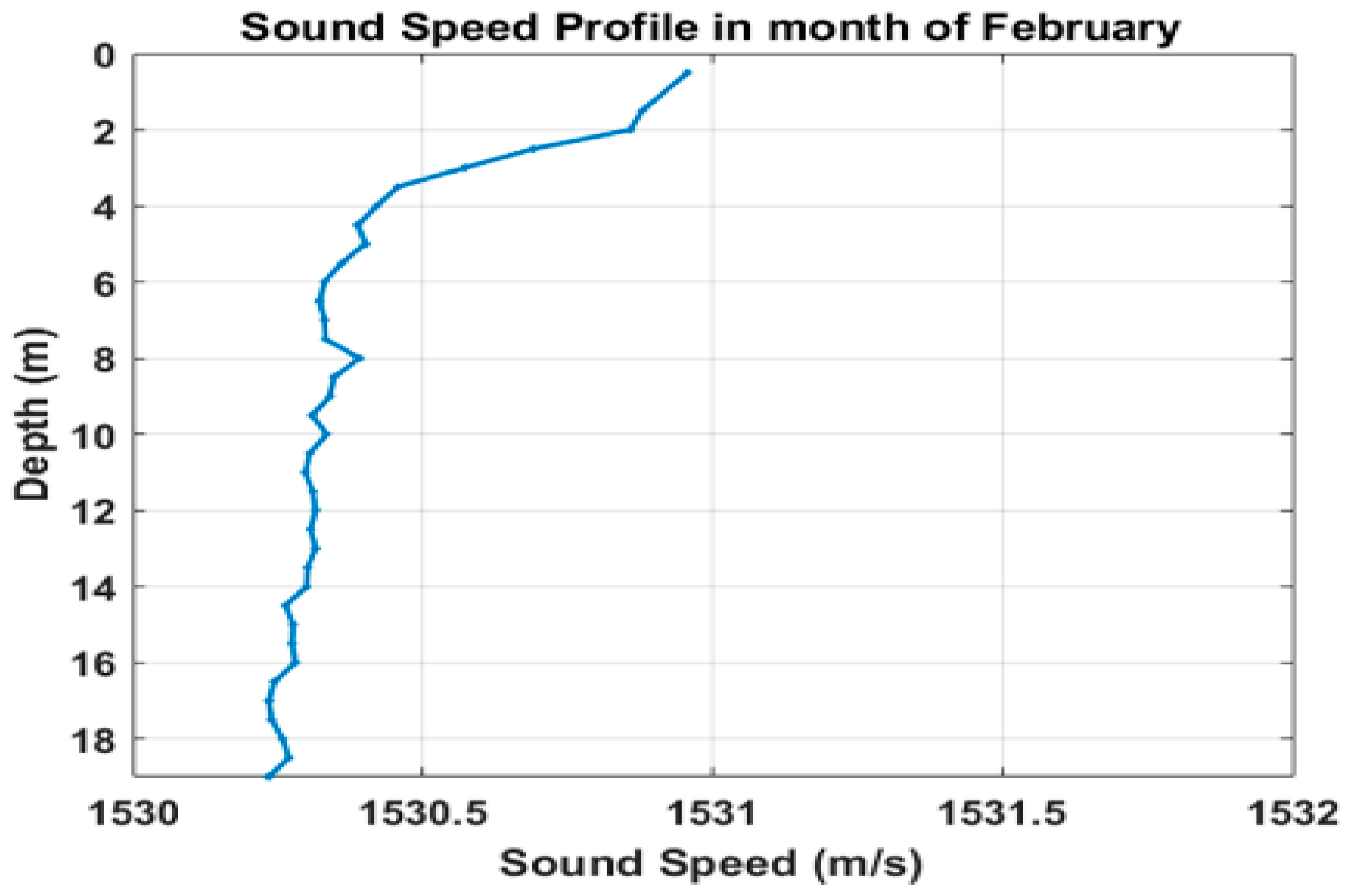
2.3. Sound Speed Profile
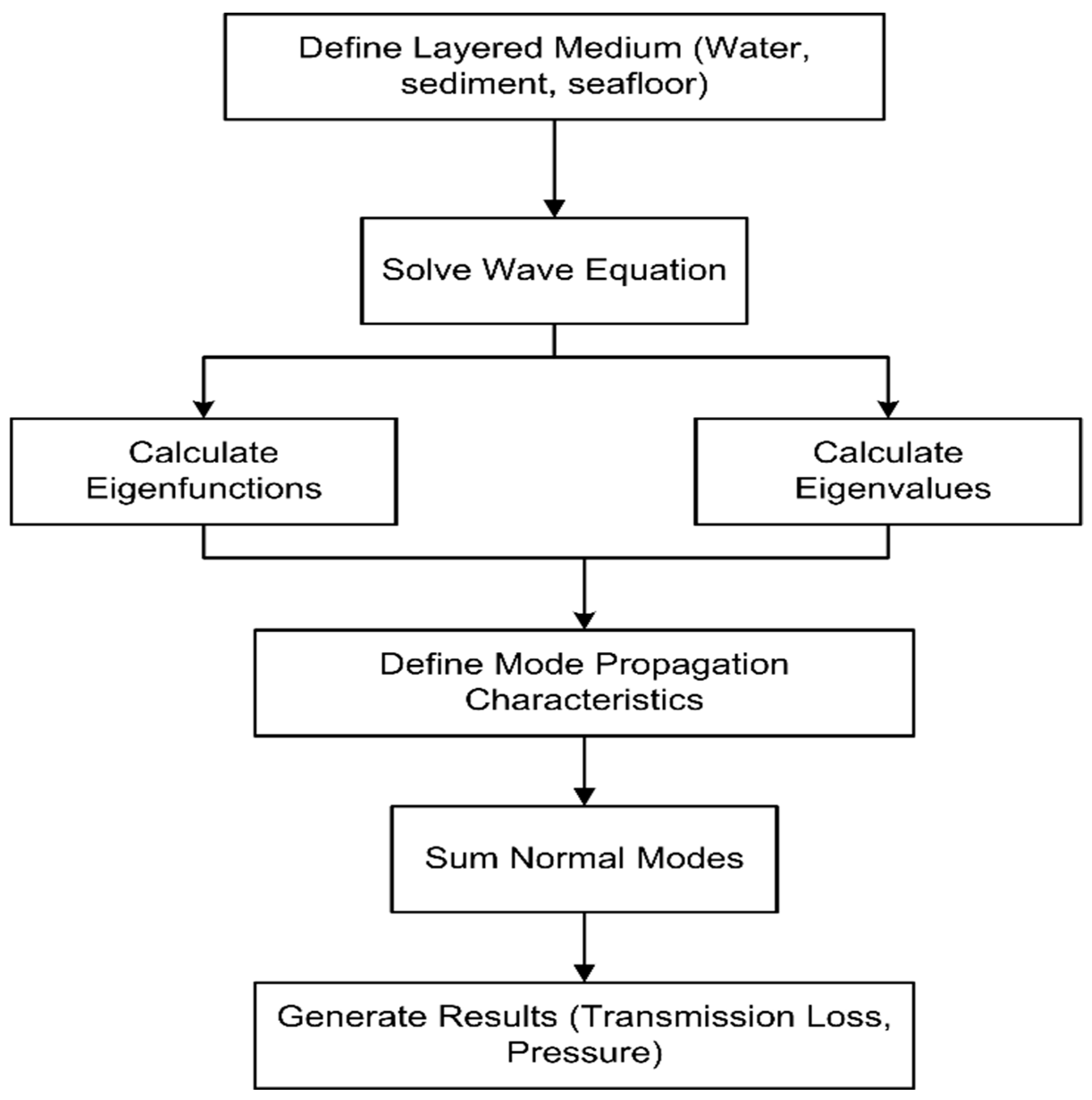
2.4. Normal Mode Program Kraken C
3. Normal Mode Theoretical Framework
4. Simulation Results
4.1. Shallow Water Propagation Modeling
4.2. Identification and Analysis of Environmental Parameters
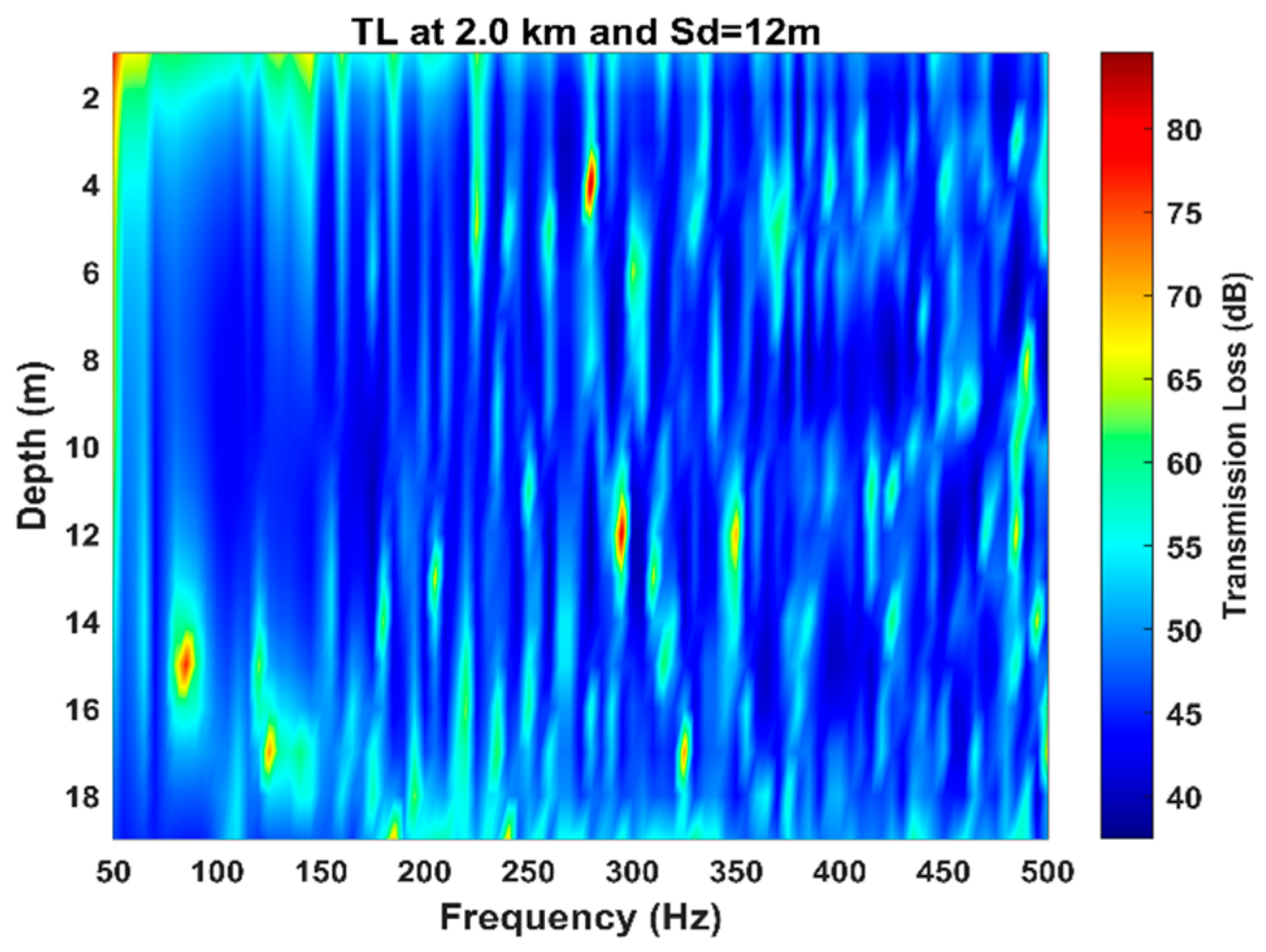
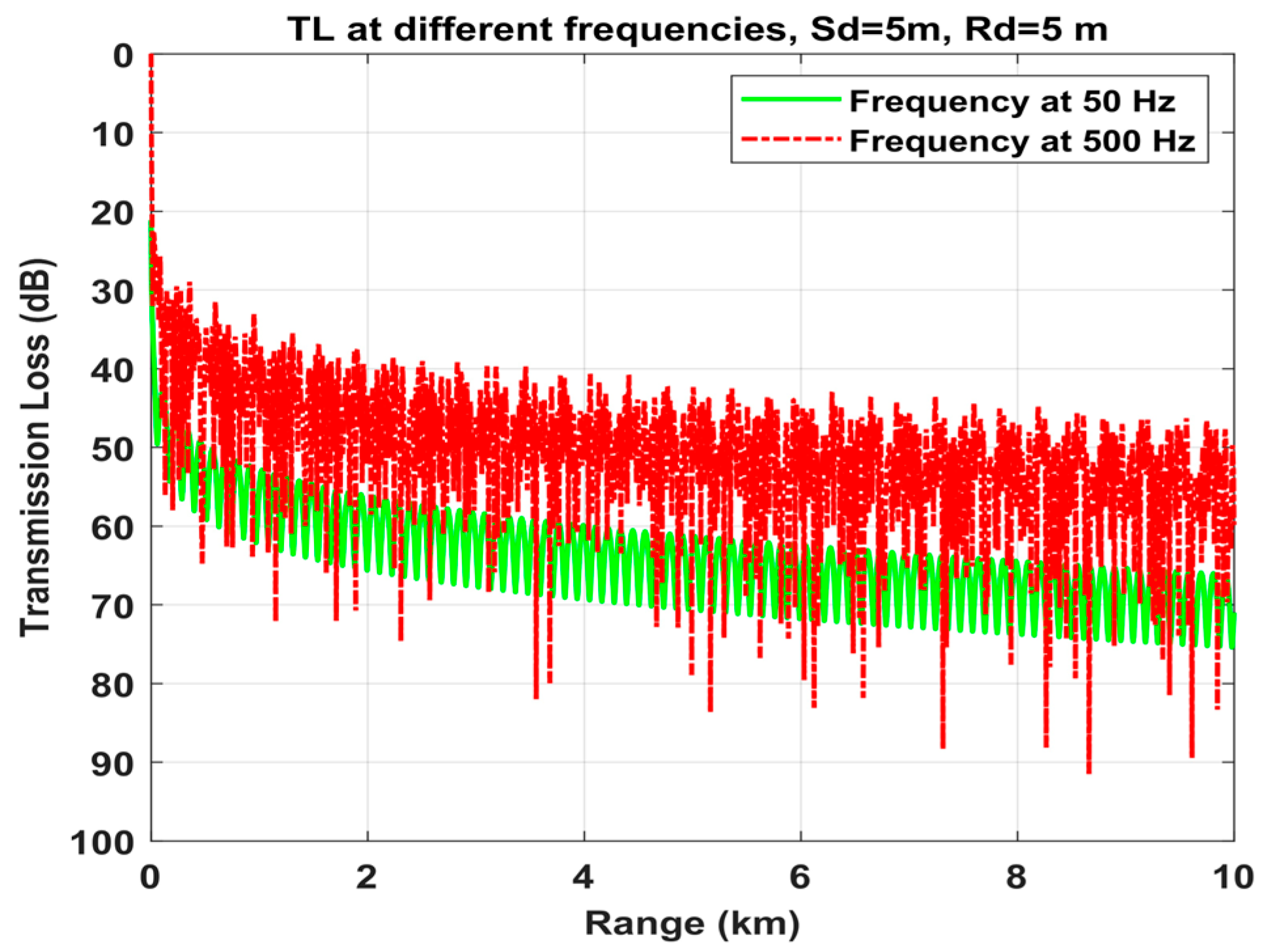
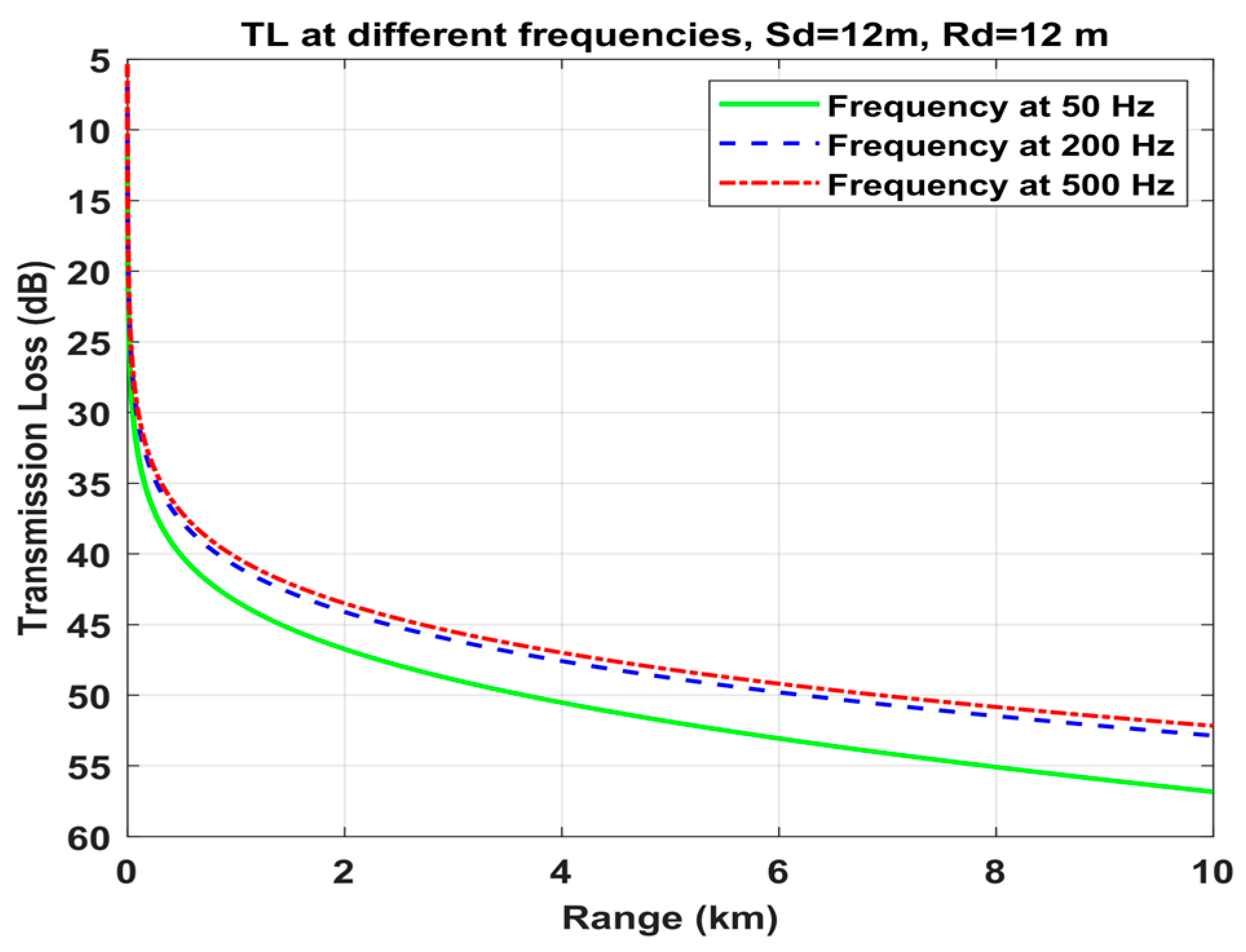
4.2.1. Wave Frequency Influence
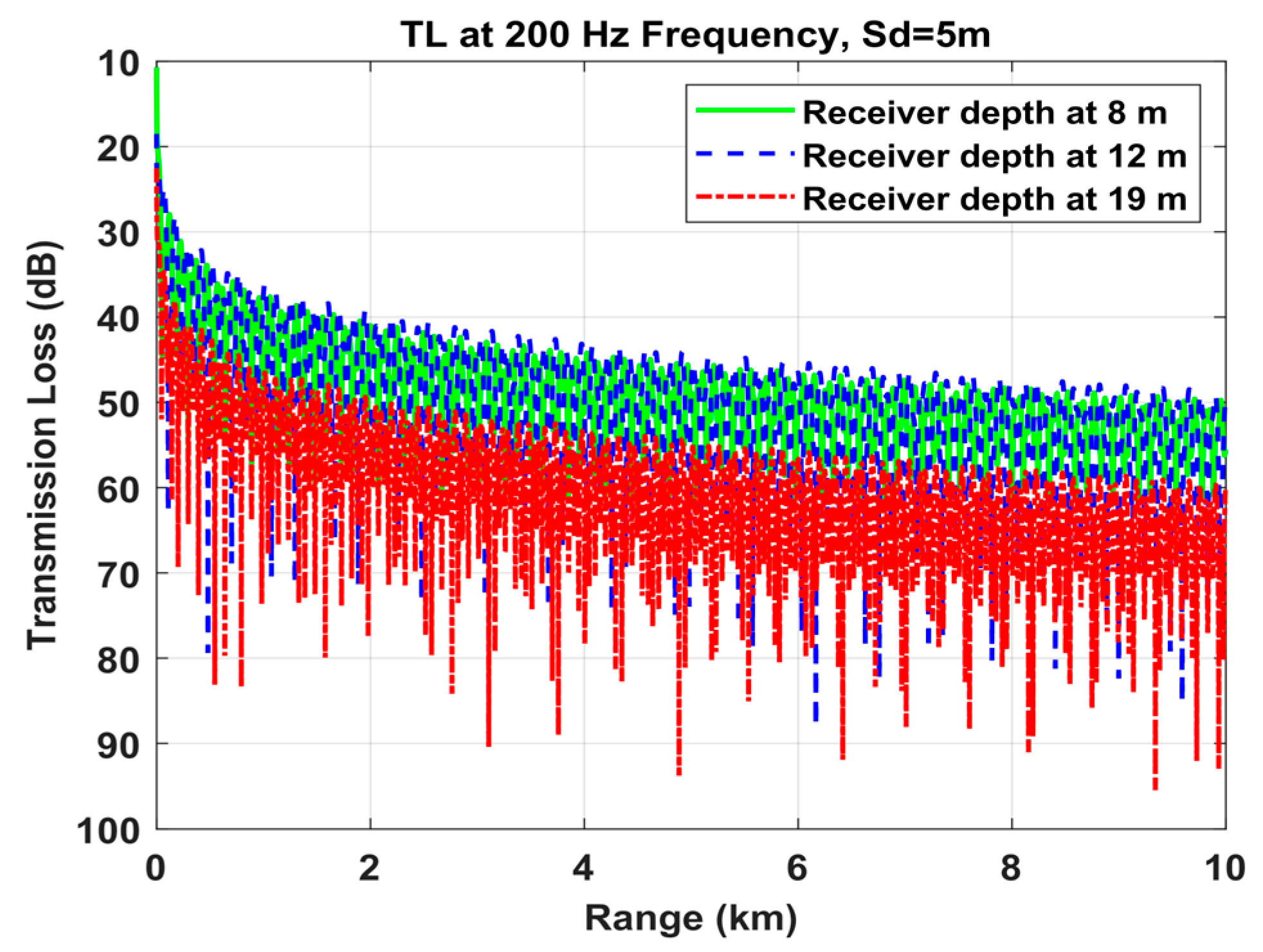
4.2.2. Influence of Source and Receiver Depths
4.2.3. Bottom Roughness
4.2.4. Incoherent Transmission Loss
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Venkateswara Rao, C.; Ravi Sankar, M.; SR Charan, P.; Bavya Sri, V.; Bhaavan Sri Sailesh, A.; Sri Uma Suseela, M.; Padmavathy, N. Analysis of acoustic channel model characteristics in deep-sea water. In Proceedings of the International Conference on Cognitive Computing and Cyber Physical Systems, Bhimavaram, India, 26–27 November 2022; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Zhu, H.; Xue, Y.; Ren, Q.; Liu, X.; Wang, J.; Cui, Z.; Zhang, S.; Fan, H. Inversion of shallow seabed structure and geoacoustic parameters with waveguide characteristic impedance based on Bayesian approach. Front. Mar. Sci. 2023, 10, 1104570. [Google Scholar] [CrossRef]
- Ewing, J.; Carter, J.A.; Sutton, G.H.; Barstow, N. Shallow water sediment properties derived from high-frequency shear and interface waves. J. Geophys. Res. Solid Earth 1992, 97, 4739–4762. [Google Scholar] [CrossRef]
- Tolstoy, I.; Clay, C. Ocean acoustics: An evaluation. Rev. Geophys. 1966, 4, 33–40. [Google Scholar] [CrossRef]
- Su, X.; Qin, J.; Yu, X. Interference Pattern Anomaly of an Acoustic Field Induced by Bottom Elasticity in Shallow Water. J. Mar. Sci. Eng. 2023, 11, 647. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Q.; Wang, W.; Zhang, Y.; Yan, H.; Zhu, H. Effects of inclined sea bottom on acoustic propagation characteristics in shallow ocean fronts. In Proceedings of the CAIBDA 2022, 2nd International Conference on Artificial Intelligence, Big Data and Algorithms, Nanjing, China, 17–19 June 2022; VDE: Frankfurt am Main, Germany, 2022. [Google Scholar]
- Jensen, F.B. Numerical models in underwater acoustics. In Hybrid Formulation of Wave Propagation and Scattering; Springer: Berlin/Heidelberg, Germany, 1984; pp. 295–335. [Google Scholar]
- Kexin, L.; Chitre, M. Ocean Acoustic Propagation Modeling Using Scientific Machine Learning. In Proceedings of the OCEANS 2021: San Diego–Porto, San Diego, CA, USA, 20–23 September 2021; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar]
- Pekeris, C.L. Theory of Propagation of Explosive Sound in Shallow Water; Generic Publications: Homebush West, Australia, 1948. [Google Scholar]
- Jensen, F.; Ferla, M.S. The SACLANTCEN Normal-Mode Acoustic Propagation Model, SACLANTCEN SM-121; SACLANT ASW Research Centre: La Qpezia, Italy, 1979. [Google Scholar]
- Porter, M.B. The KRAKEN Normal Mode Program; Naval Research Laboratory: Washington, DC, USA, 1992. [Google Scholar]
- Etter, P.C. Underwater Acoustic Modeling and Simulation; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Jensen, F.B.; Kuperman, W.A.; Porter, M.B.; Schmidt, H. Normal Modes. In Computational Ocean Acoustics; Springer: New York, NY, USA, 2011; pp. 337–455. [Google Scholar]
- Bhatti, A.A.; Khan, S.; Yiwang, H. Numerical Simulation of Shallow Water Propagation using Normal Mode Theory. In Proceedings of the 2019 16th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 8–12 January 2019; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Shaikh, S.; Huang, Y.W. Influences analysis of environmental parameters on sound propagation in shallow water. Appl. Mech. Mater. 2014, 556, 4815–4819. [Google Scholar] [CrossRef]
- Jensen, F.B.; Kuperman, W.A.; Porter, M.B.; Schmidt, H.; McKay, S. Computational ocean acoustics. Comput. Phys. 1995, 9, 55–56. [Google Scholar] [CrossRef]
- Valle-Molina, C.; Stokoe, K.H. Seismic measurements in sand specimens with varying degrees of saturation using piezoelectric transducers. Can. Geotech. J. 2012, 49, 671–685. [Google Scholar] [CrossRef]
- Rogers, A.K.; Yamamoto, T.; Carey, W. Experimental investigation of sediment effect on acoustic wave propagation in the shallow ocean. J. Acoust. Soc. Am. 1993, 93, 1747–1761. [Google Scholar] [CrossRef]
- Noufal, K.; Sanjana, M.; Latha, G. Acoustic propagation in shallow waters of south east Arabian Sea using Normal mode approach. Indian J. Geo Mar. Sci. 2017, 46, 2175–2181. [Google Scholar]
- Meyer, V.; Audoly, C. A comparison between experiments and simulation for shallow water short range acoustic propagation. In Proceedings of the ICSV 24 24th International Congress on Sound and Vibration, London, UK, 23–27 July 2017. [Google Scholar]
- Bonnel, J.; Flamant, J.; Dall’Osto, D.R.; Le Bihan, N.; Dahl, P.H. Polarization of ocean acoustic normal modes. J. Acoust. Soc. Am. 2021, 150, 1897–1911. [Google Scholar] [CrossRef]
- Sanjana, M.; Latha, G.; Thirunavukkarasu, A.; Raguraman, G. Acoustic propagation affected by environmental parameters in coastal waters. Indian J. Geo Mar. Sci. 2014, 43, 17–21. [Google Scholar]
- Shaikh, S.; Huang, Y.-W.; Zhang, Z.-C.; Zuberi, H.H. Fine Sand and Clay Sediment Acoustic Properties of the Novel Sediment Sample from the Arabian Sea: Experimental Investigations and Biot–Stoll Model Validation. China Ocean Eng. 2024, 38, 169–180. [Google Scholar] [CrossRef]
- Folk, R.L. Petrology of Sedimentary Rocks; Hemphill Publishing Company: Sutton, UK, 1980. [Google Scholar]
- Kimura, M. Prediction of tortuosity, permeability, and pore radius of water-saturated unconsolidated glass beads and sands. J. Acoust. Soc. Am. 2018, 143, 3154–3168. [Google Scholar] [CrossRef] [PubMed]
- Udden, J.A. Mechanical composition of clastic sediments. Bull. Geol. Soc. Am. 1914, 25, 655–744. [Google Scholar] [CrossRef]
- Wentworth, C.K. A scale of grade and class terms for clastic sediments. J. Geol. 1922, 30, 377–392. [Google Scholar] [CrossRef]
- Jackson, D.; Richardson, M. High-Frequency Seafloor Acoustics; Springer Science & Business Media: Cham, Switzerland, 2007. [Google Scholar]
- Avnimelech, Y.; Ritvo, G.; Meijer, L.E.; Kochba, M. Water content, organic carbon and dry bulk density in flooded sediments. Aquac. Eng. 2001, 25, 25–33. [Google Scholar] [CrossRef]
- Yu, S. Geoacoustic Parameter Inversion Based on Backscattering Strength; Harbin Engineering University: Harbin, China, 2014; (In Chinese with an English Abstract). [Google Scholar]
- Danielson, R.; Sutherland, P. Porosity. In Methods of Soil Analysis: Part 1 Physical and Mineralogical Methods; American Society of Agronomy, Inc.: Madison, WI, USA, 1986; Volume 5, pp. 443–461. [Google Scholar]
- Azeez, A.; Revichandran, C.; Muraleedharan, K.; John, S.; Seena, G.; Nair, R.C.; Manju, K. Sound speed variation in the coastal waters off Cochin and signature of subsurface maxima. Ocean Dyn. 2021, 71, 923–933. [Google Scholar]
- Qiao, G.; Ismail, A.; Aatiq, M. A Study on Multi-Path Channel Response of Acoustic Propagation in Northwestern Arabian Sea. Res. J. Appl. Sci. Eng. Technol. 2013, 4619–4628. [Google Scholar] [CrossRef]
- Mackenzie, K.V. Nine-term equation for sound speed in the oceans. J. Acoust. Soc. Am. 1981, 70, 807–812. [Google Scholar] [CrossRef]
- Ismail, A.; Gang, Q.; Khan, R.; Kabir, J.; Pasha, B.; Masood, A.; Malik, A.; Khan, A. Variability of channel response and acoustic system performance: Simulation study. In Proceedings of the 2013 10th International Bhurban Conference on Applied Sciences & Technology (IBCAST), Islamabad, Pakistan, 15–19 January 2013; IEEE: Piscataway, NJ, USA, 2013. [Google Scholar]
- Frisk, G.V. Ocean and Seabed Acoustics: A Theory of Wave Propagation; Pearson Education: London, UK, 1994. [Google Scholar]
- Ma, X.; Wang, Y.; Zhu, X.; Liu, W.; Lan, Q.; Xiao, W. A spectral method for two-dimensional ocean acoustic propagation. J. Mar. Sci. Eng. 2021, 9, 892. [Google Scholar] [CrossRef]
- Ma, X.; Wang, Y.; Zhu, X.; Liu, W.; Xiao, W.; Lan, Q. A high-efficiency spectral method for two-dimensional ocean acoustic propagation calculations. Entropy 2021, 23, 1227. [Google Scholar] [CrossRef] [PubMed]
- Ahmed Alanazi, M.; Ali, I. Simulations and analysis of underwater acoustic wave propagation model based on Helmholtz equation. Appl. Math. Sci. Eng. 2024, 32, 2338397. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, M.; Xue, H.; Gong, Y.; Qiu, B. Prediction method of underwater acoustic transmission loss based on deep belief net neural network. Appl. Sci. 2021, 11, 4896. [Google Scholar] [CrossRef]








| Parameters | Symbol | Unit | Measured Values |
|---|---|---|---|
| Silt concentration | - | % | 13.4 |
| Clay concentration | - | % | 86.6 |
| Mean grain diameter | d | mm | 0.012 |
| Mean grain size | Phi (φ) | - | 6.4 |
| Sediment grain density | g/cm3 | 1.685 | |
| Sediment bulk density | g/cm3 | 0.539 | |
| Porosity | - | 0.680 | |
| Sediment density | g/cm3 | 1.24 |
| Parameters | Symbol | Unit | Range Values |
|---|---|---|---|
| Channel depth | H | m | 19.0 |
| Range | r | km | 10 |
| Speed of sound in water | m/s | See Figure 4 | |
| Water density | 1.025 | ||
| Speed of sound in sediment | m/s | 1607.75–1607.83 | |
| Sediment attenuation | dB/km-Hz | 0.02 | |
| P-wave speed in basement | m/s | 4000 | |
| S-wave speed in basement | m/s | 2000 | |
| Density in basement | 1.9 | ||
| P-wave attenuation in basement | dB/km-Hz | 0.005 | |
| S-wave attenuation in basement | dB/km-Hz | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shaikh, S.; Huang, Y.; Alharbi, A.; Bilal, M.; Shaikh, A.S.; Zuberi, H.H.; Dars, M.A. Acoustic Propagation and Transmission Loss Analysis in Shallow Water of Northern Arabian Sea. J. Mar. Sci. Eng. 2024, 12, 2256. https://doi.org/10.3390/jmse12122256
Shaikh S, Huang Y, Alharbi A, Bilal M, Shaikh AS, Zuberi HH, Dars MA. Acoustic Propagation and Transmission Loss Analysis in Shallow Water of Northern Arabian Sea. Journal of Marine Science and Engineering. 2024; 12(12):2256. https://doi.org/10.3390/jmse12122256
Chicago/Turabian StyleShaikh, Shahabuddin, Yiwang Huang, Ayman Alharbi, Muhammad Bilal, Abdul Sami Shaikh, Habib Hussain Zuberi, and Muhammad Ayoob Dars. 2024. "Acoustic Propagation and Transmission Loss Analysis in Shallow Water of Northern Arabian Sea" Journal of Marine Science and Engineering 12, no. 12: 2256. https://doi.org/10.3390/jmse12122256
APA StyleShaikh, S., Huang, Y., Alharbi, A., Bilal, M., Shaikh, A. S., Zuberi, H. H., & Dars, M. A. (2024). Acoustic Propagation and Transmission Loss Analysis in Shallow Water of Northern Arabian Sea. Journal of Marine Science and Engineering, 12(12), 2256. https://doi.org/10.3390/jmse12122256








