Ship Trajectory Prediction in Complex Waterways Based on Transformer and Social Variational Autoencoder (SocialVAE)
Abstract
1. Introduction
- The encoder module of SocialVAE, initially utilizing an RNN, uses a substituted Transformer Encoder. This replacement effectively addresses the inherent limitations of RNNs in capturing long-term temporal dependencies.
- The original RNN-based decoder module of SocialVAE is replaced with a Multilayer Perceptron (MLP). This modification significantly enhances computational efficiency and robustness by simplifying the decoding process.
- A ship collision avoidance mechanism is introduced into the model by augmenting the loss function with distance constraints between ships during trajectory prediction. It effectively captures the interactive behaviors associated with collision avoidance.
- A ship trajectory prediction model called ShipTrack-TVAE is proposed, which integrates the advantages of SocialVAE and Transformer architectures. It is superior in ship trajectory forecasting under dynamic conditions and uncertainties compared to other baseline models.
2. Methodology
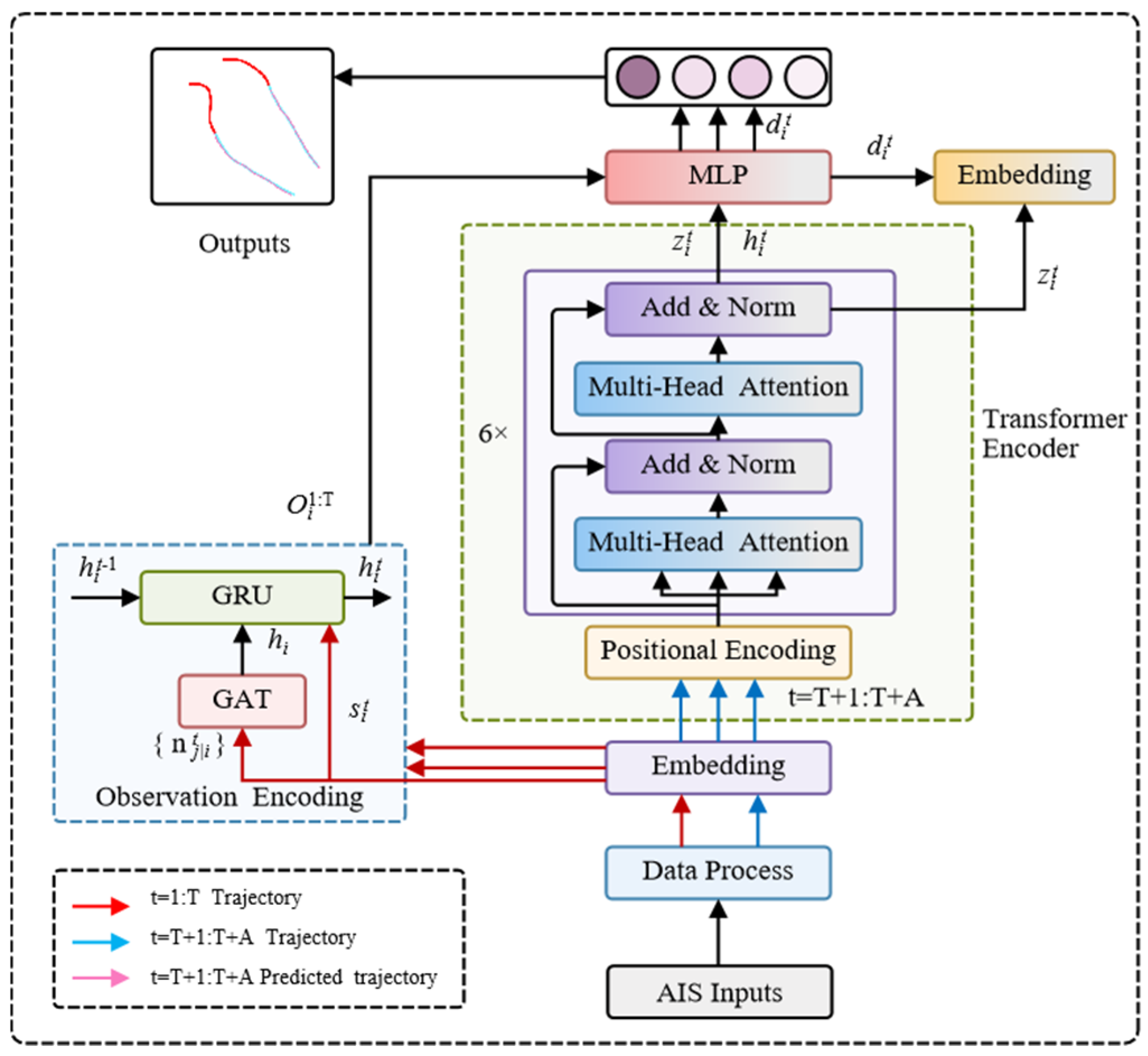
2.1. Model Architecture
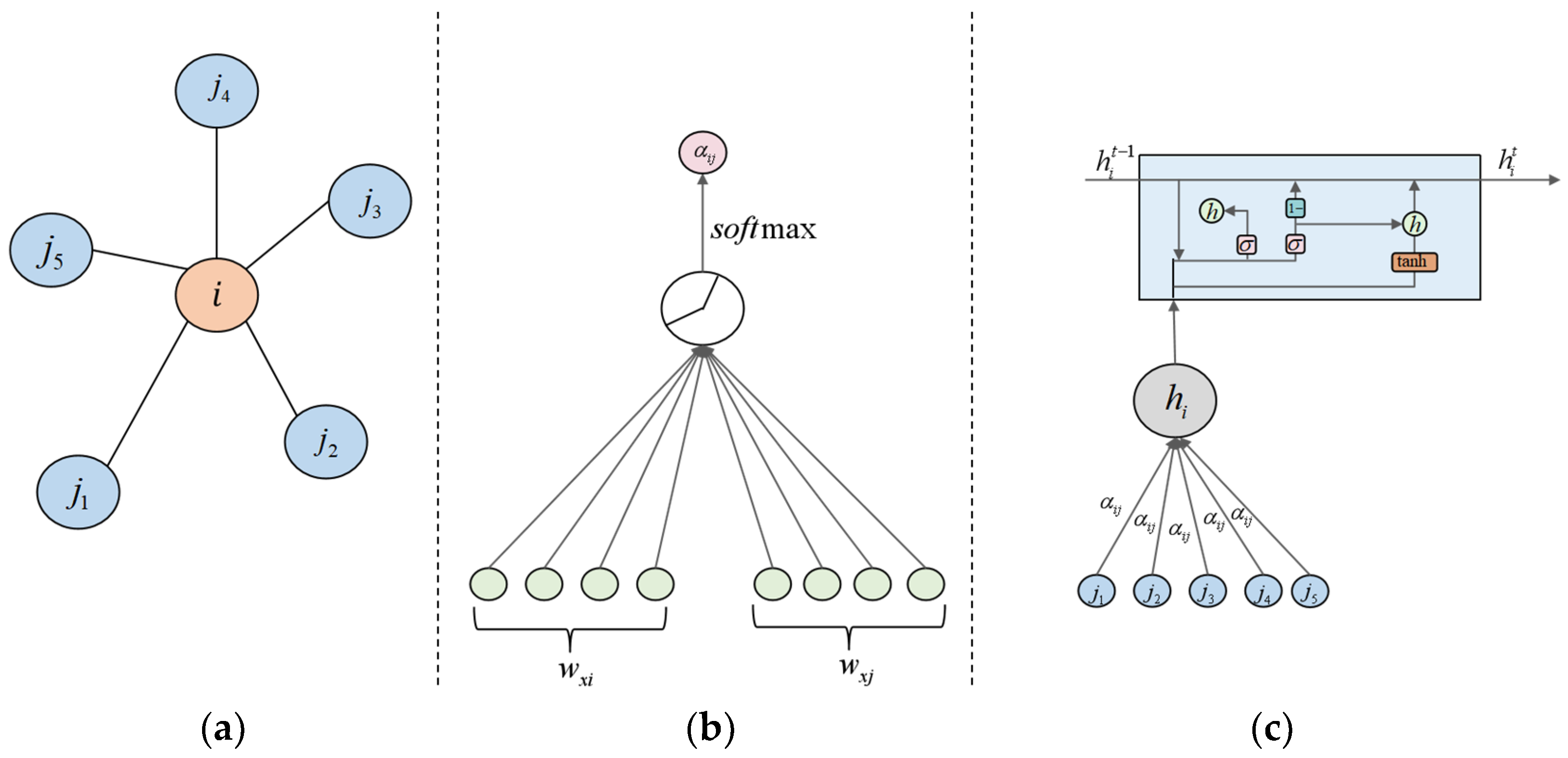
2.2. Observation Encoding
2.3. Transformer Encoder
2.4. Decoder
2.5. Loss Function
3. Experimental Results and Analysis
3.1. Data Collection and Preprocessing
3.2. Network Parameter Setting
3.3. Evaluation Metrics and Comparison Baselines
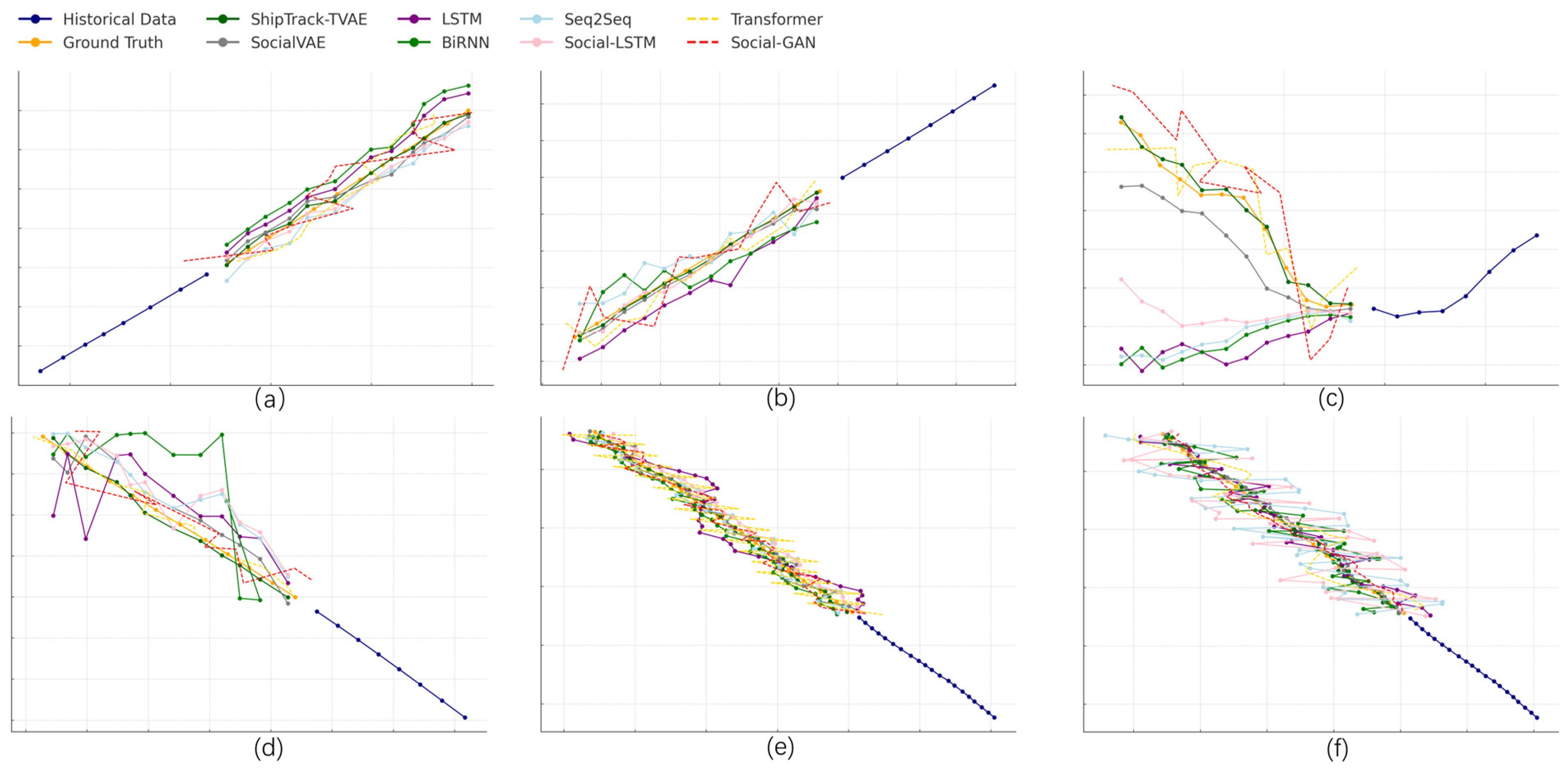
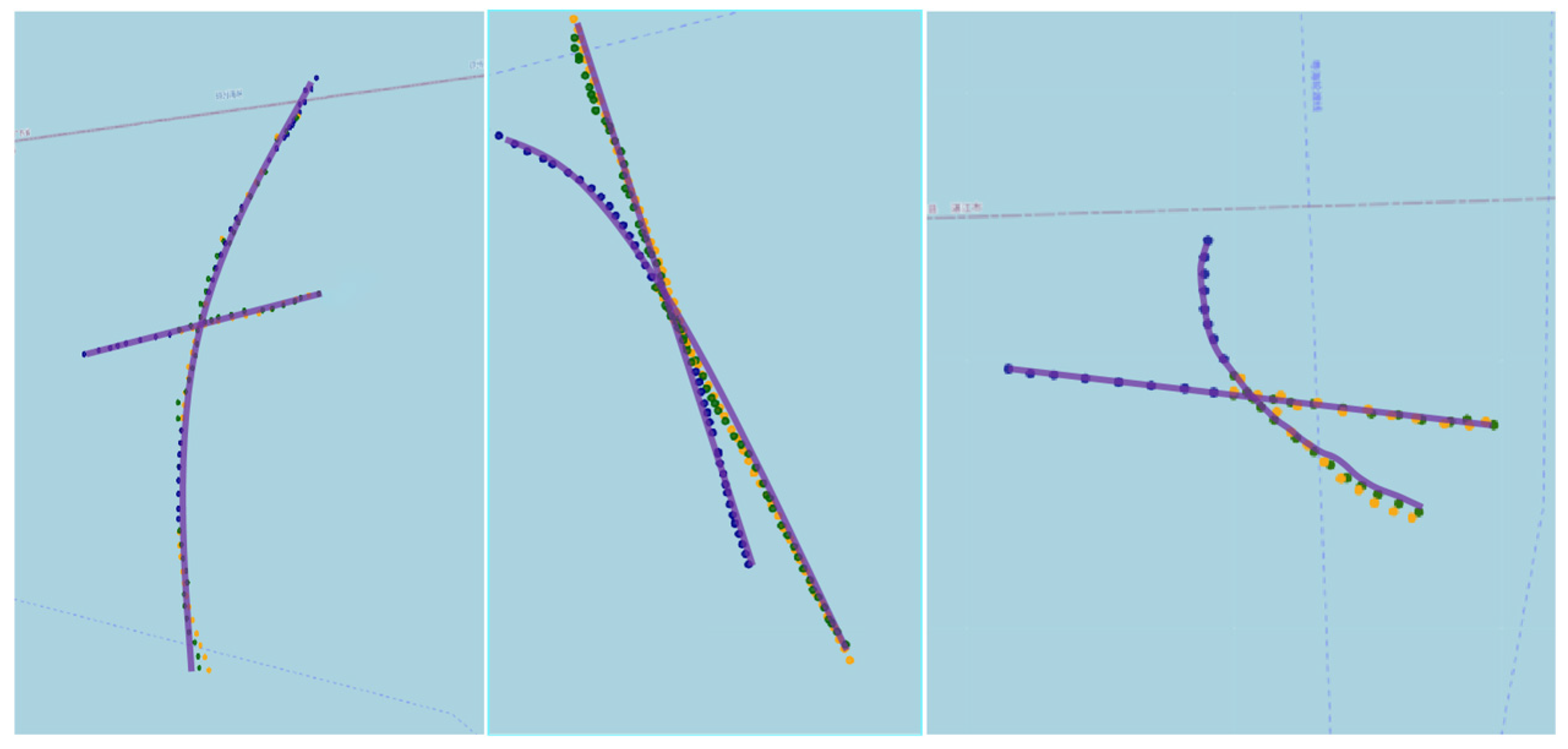
3.4. Comparative Test
3.5. Ablation Experiment
3.6. Analysis of Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ADE | Average Displacement Error |
| AIS | Automatic Identification System |
| APE | ambient pressure error |
| BiRNN | Bidirectional Recurrent Neural Network |
| FDE | Final Displacement Error |
| GAT | Graph Attention Network |
| GAN | Generative Adversarial Network |
| GCN | Graph Convolutional Network |
| GL-STGCNN | Graph Learning Spatio Temporal Graph Convolutional Neural Network |
| KL | Kullback Leibler (Divergence) |
| LSTM | Long Short-Term Memory |
| MMSI | Maritime Mobile Service Identity |
| MLP | Multilayer Perceptron |
| probability density function | |
| RNN | recurrent neural network |
| Seq2Seq | Sequence to Sequence |
| Social-STGCNN | Social Spatio Temporal Graph Convolutional Neural Network |
| TVAE | Transformer Variational Autoencoder |
| VAE | Variational Autoencoder |
| MSTFormer | Motion-Inspired Spatial–Temporal Transformer |
| VTS | Vessel Traffic System |
| CPI | Comprehensive Performance Index |
References
- Lehtola, V.; Montewka, J.; Goerlandt, F.; Guinness, R.; Lensu, M. Finding safe and efficient shipping routes in ice-covered waters: A framework and a model. Cold Reg. Sci. Technol. 2019, 165, 102795. [Google Scholar] [CrossRef]
- Felski, A.; Jaskólski, K.; Banyś, P. Comprehensive Assessment of Automatic Identification System (AIS) Data Application to Anti-collision Manoeuvring. J. Navig. 2015, 68, 697–717. [Google Scholar] [CrossRef]
- Murray, B.; Perera, L.P. An AIS-based deep learning framework for regional ship behavior prediction. Reliab. Eng. Syst. Saf. 2021, 215, 107819. [Google Scholar] [CrossRef]
- Dalsnes, B.R.; Hexeberg, S.; Flåten, A.L.; Eriksen, B.-O.H.; Brekke, E.F. The Neighbor Course Distribution Method with Gaussian Mixture Models for AIS-Based Vessel Trajectory Prediction. In Proceedings of the 2018 21st International Conference on Information Fusion (FUSION), Cambridge, UK, 10–13 July 2018; pp. 580–587. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, G.; Hu, C.; Ma, X. Wavelet Analysis Based Hidden Markov Model for Large Ship Trajectory Prediction. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 2913–2918. [Google Scholar] [CrossRef]
- Tang, H.; Yin, Y.; Shen, H. A model for vessel trajectory prediction based on long short-term memory neural network. J. Mar. Eng. Technol. 2022, 21, 136–145. [Google Scholar] [CrossRef]
- Suo, Y.; Chen, W.; Claramunt, C.; Yang, S. A Ship Trajectory Prediction Framework Based on a Recurrent Neural Network. Sensors 2020, 20, 5133. [Google Scholar] [CrossRef]
- Sun, Q.; Tang, Z.; Gao, J.; Zhang, G. Short-term ship motion attitude prediction based on LSTM and GPR. Appl. Ocean Res. 2022, 118, 102927. [Google Scholar] [CrossRef]
- Zhang, X.; Fu, X.; Xiao, Z.; Xu, H.; Qin, Z. Vessel Trajectory Prediction in Maritime Transportation: Current Approaches and Beyond. IEEE Trans. Intell. Transp. Syst. 2022, 23, 19980–19998. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, J.; Fang, L.; Jiang, Q.; Zhou, B. Multimodal Motion Prediction With Stacked Transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 7577–7586. [Google Scholar] [CrossRef]
- Jiang, D.; Shi, G.; Li, N.; Ma, L.; Li, W.; Shi, J. TRFM-LS: Transformer-Based Deep Learning Method for Vessel Trajectory Prediction. J. Mar. Sci. Eng. 2023, 11, 880. [Google Scholar] [CrossRef]
- Qiang, H.; Guo, Z.; Xie, S.; Peng, X. MSTFormer: Motion Inspired Spatial-temporal Transformer with Dynamic-aware Attention for long-term Vessel Trajectory Prediction. arXiv 2023. [Google Scholar] [CrossRef]
- Lin, Z.; Li, F.; Zeng, L.; Hao, J.; Pan, M. Ship trajectory prediction model based on improved SocialVAE. In Proceedings of the 5th International Conference on Computer Information and Big Data Applications, Wuhan China, 26–28 April 2024; Association for Computing Machinery: New York, NY, USA; pp. 1145–1149. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, L.; Zhu, M.; Chen, S.; Zhang, H.; Zeng, Z. A Bi-directional LSTM Ship Trajectory Prediction Method based on Attention Mechanism. In Proceedings of the 2021 IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 March 2021; pp. 1987–1993. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, H.; Cui, F.; Liu, Y.; Liu, Z.; Dong, J. Research into Ship Trajectory Prediction Based on An Improved LSTM Network. J. Mar. Sci. Eng. 2023, 11, 1268. [Google Scholar] [CrossRef]
- Cui, Z.; Pan, M.; Lin, Z.; Liu, Z. A GAN based multi-vessel trajectory prediction method. J. Dalian Marit. Univ. 2023, 49, 51–60. [Google Scholar] [CrossRef]
- Wu, Y.; Yv, W.; Zeng, G.; Shang, Y.; Liao, W. GL-STGCNN: Enhancing Multi-Ship Trajectory Prediction with MPC Correction. J. Mar. Sci. Eng. 2024, 12, 882. [Google Scholar] [CrossRef]
- Suo, Y.; Ding, Z.; Zhang, T. The Mamba Model: A Novel Approach for Predicting Ship Trajectories. J. Mar. Sci. Eng. 2024, 12, 1321. [Google Scholar] [CrossRef]
- Xu, P.; Hayet, J.-B.; Karamouzas, I. SocialVAE: Human Trajectory Prediction using Timewise Latents. arXiv 2022. [Google Scholar] [CrossRef]
- Gao, W.; Liu, J.; Zhi, J.; Wang, J. Improved SocialVAE: A Socially-Aware Ship Trajectory Prediction Method for Port Operations. In Proceedings of the 2023 2nd International Conference on Machine Learning, Cloud Computing and Intelligent Mining (MLCCIM), Hubei, China, 25–29 July 2023; pp. 420–424. [Google Scholar] [CrossRef]
- Xu, B.; Wang, X.; Li, S.; Li, J.; Liu, C. Social-CVAE: Pedestrian Trajectory Prediction Using Conditional Variational Auto-Encoder. In Proceedings of the Neural Information Processing; Luo, B., Cheng, L., Wu, Z.-G., Li, H., Li, C., Eds.; Springer Nature: Singapore, 2024; pp. 476–489. [Google Scholar] [CrossRef]
- Liu, Z.; Li, S.; Hao, J.; Hu, J.; Pan, M. An Efficient and Fast Model Reduced Kernel KNN for Human Activity Recognition. J. Adv. Transp. 2021, 2021, 2026895. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is All you Need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Yang, Z.; Dai, Z.; Yang, Y.; Carbonell, J.; Salakhutdinov, R.R.; Le, Q.V. XLNet: Generalized Autoregressive Pretraining for Language Understanding. arXiv 2019, arXiv:1906.08237. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. arXiv 2018. [Google Scholar] [CrossRef]
- Xue, H.; Wang, S.; Xia, M.; Guo, S. G-Trans: A hierarchical approach to vessel trajectory prediction with GRU-based transformer. Ocean Eng. 2024, 300, 117431. [Google Scholar] [CrossRef]
- Huang, Z.-T.; Luo, Y.; Han, L.; Wang, K.; Yao, S.-S.; Su, H.-X.; Chen, S.; Cao, G.-Y.; De Fries, C.M.; Chen, Z.-S.; et al. Patterns of cardiometabolic multimorbidity and the risk of depressive symptoms in a longitudinal cohort of middle-aged and older Chinese. J. Affect. Disord. 2022, 301, 1–7. [Google Scholar] [CrossRef]
- Murray, B.; Perera, L.P. A dual linear autoencoder approach for vessel trajectory prediction using historical AIS data. Ocean Eng. 2020, 209, 107478. [Google Scholar] [CrossRef]
- Pellegrini, S.; Ess, A.; Schindler, K.; van Gool, L. You’ll never walk alone: Modeling social behavior for multi-target tracking. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 21 September–4 October 2009; pp. 261–268. [Google Scholar] [CrossRef]
- Alahi, A.; Goel, K.; Ramanathan, V.; Robicquet, A.; Fei-Fei, L.; Savarese, S. Social LSTM: Human Trajectory Prediction in Crowded Spaces. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 961–971. [Google Scholar] [CrossRef]
- Inoue, K.; Hara, K.; Kaneko, M.; Masuda, K. Assessment of the Correlation of Safety between Ship Handling and Environment. J. Jpn. Inst. Navig. 1996, 95, 147–153. [Google Scholar] [CrossRef]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Wang, X.; Li, S.; Cao, Y.; Xin, T.; Yang, L. Dynamic speed trajectory generation and tracking control for autonomous driving of intelligent high-speed trains combining with deep learning and backstepping control methods. Eng. Appl. Artif. Intell. 2022, 115, 105230. [Google Scholar] [CrossRef]
- Forti, N.; Millefiori, L.M.; Braca, P.; Willett, P. Prediction oof Vessel Trajectories from AIS Data via Sequence-to-Sequence Recurrent Neural Networks. In Proceedings of the ICASSP 2020–2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 8936–8940. [Google Scholar] [CrossRef]
- Mohamed, A.; Qian, K.; Elhoseiny, M.; Claudel, C. Social-STGCNN: A Social Spatio-Temporal Graph Convolutional Neural Network for Human Trajectory Prediction. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 14412–14420. [Google Scholar] [CrossRef]







| Parameters | Setting |
|---|---|
| The number of encoder layers | 6 |
| The number of multi-heads | 8 |
| Learning rate | 0.0001 |
| Batch size | 64 |
| Max epoch | 100 |
| Number of observed neighbors | 5 |
| Prediction horizon | 35 |
| Observation horizon | 20 |
| Step | Metrics | ShipTrack-TVAE | SocialVAE | BiRNN | LSTM | Seq2Seq | Social-STGCNN | Social-GAN | Transformer |
|---|---|---|---|---|---|---|---|---|---|
| 12 | ADE | 0.0118 | 0.0135 | 0.183 | 0.0565 | 0.0328 | 0.0257 | 0.0437 | 0.0187 |
| FDE | 0.0206 | 0.0249 | 0.234 | 0.146 | 0.774 | 0.0505 | 0.0955 | 0.0361 | |
| APE | 0.23 | 0.30 | 0.44 | 0.36 | 0.34 | 0.31 | 0.35 | 0.30 | |
| 35 | ADE | 0.0275 | 0.0327 | 0.479 | 0.0931 | 0.0794 | 0.0564 | 0.0853 | 0.0381 |
| FDE | 0.0423 | 0.0593 | 0.913 | 0.231 | 0.173 | 0.119 | 0.191 | 0.0693 | |
| APE | 0.24 | 0.32 | 0.46 | 0.39 | 0.36 | 0.34 | 0.38 | 0.33 | |
| 80 | ADE | 0.0472 | 0.0604 | 0.583 | 0.265 | 0.168 | 0.135 | 0.212 | 0.0725 |
| FDE | 0.0903 | 0.1099 | 1.234 | 0.596 | 0.474 | 0.505 | 0.563 | 0.1179 | |
| APE | 0.27 | 0.35 | 0.51 | 0.41 | 0.39 | 0.37 | 0.40 | 0.36 |
| Step | Metrics | ShipTrack-TVAE | SocialVAE | BiRNN | LSTM | Seq2Seq | Social-STGCNN | Social-GAN | Transformer |
|---|---|---|---|---|---|---|---|---|---|
| 12 | Training Time (s/epoch) | 250 | 220 | 150 | 170 | 200 | 180 | 230 | 240 |
| Inference Speed (s/step) | 0.016 | 0.013 | 0.010 | 0.011 | 0.012 | 0.010 | 0.012 | 0.014 | |
| 35 | Training Time (s/epoch) | 290 | 250 | 170 | 190 | 230 | 200 | 260 | 280 |
| Inference Speed (s/step) | 0.019 | 0.015 | 0.012 | 0.013 | 0.014 | 0.012 | 0.014 | 0.016 | |
| 80 | Training Time (s/epoch) | 370 | 320 | 220 | 250 | 300 | 260 | 340 | 360 |
| Inference Speed (s/step) | 0.024 | 0.020 | 0.015 | 0.016 | 0.018 | 0.015 | 0.018 | 0.021 |
| Model | ADE (Step = 20) | FDE (Step = 20) | APE (Step = 20) | ADE (Step = 35) | FDE (Step = 35) | APE (Step = 35) | ADE (Step = 80) | FDE (Step = 80) | APE (Step = 80) |
|---|---|---|---|---|---|---|---|---|---|
| SocialVAE (Base) | 0.0135 | 0.0249 | 0.30 | 0.0327 | 0.0593 | 0.32 | 0.0604 | 0.1099 | 0.35 |
| Base + Transformer | 0.0125 | 0.0225 | 0.29 | 0.0301 | 0.0516 | 0.30 | 0.0545 | 0.1001 | 0.33 |
| Base + Transformer + Collision (Ours) | 0.0118 | 0.0206 | 0.23 | 0.0275 | 0.0423 | 0.24 | 0.0472 | 0.0903 | 0.27 |
| (Nautical Miles) | ADE (Step = 12) | FDE (Step = 12) | APE (Step = 12) | ADE (Step = 35) | FDE (Step = 35) | APE (Step = 35) | ADE (Step = 80) | FDE (Step = 80) | APE (Step = 80) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.0118 | 0.0206 | 0.23 | 0.0275 | 0.0423 | 0.24 | 0.0472 | 0.0903 | 0.27 |
| 1.5 | 0.0121 | 0.0210 | 0.24 | 0.0280 | 0.0430 | 0.25 | 0.0480 | 0.0920 | 0.28 |
| 2 | 0.0125 | 0.0215 | 0.25 | 0.0288 | 0.0440 | 0.26 | 0.0492 | 0.0945 | 0.29 |
| 2.5 | 0.0130 | 0.0223 | 0.27 | 0.0300 | 0.0455 | 0.28 | 0.0508 | 0.0970 | 0.30 |
| 3 | 0.0138 | 0.0235 | 0.29 | 0.0315 | 0.0480 | 0.30 | 0.0528 | 0.1005 | 0.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Pan, M.; Liu, Z.; Li, S.; Chen, Y.; Wei, Y. Ship Trajectory Prediction in Complex Waterways Based on Transformer and Social Variational Autoencoder (SocialVAE). J. Mar. Sci. Eng. 2024, 12, 2233. https://doi.org/10.3390/jmse12122233
Wang P, Pan M, Liu Z, Li S, Chen Y, Wei Y. Ship Trajectory Prediction in Complex Waterways Based on Transformer and Social Variational Autoencoder (SocialVAE). Journal of Marine Science and Engineering. 2024; 12(12):2233. https://doi.org/10.3390/jmse12122233
Chicago/Turabian StyleWang, Pengyue, Mingyang Pan, Zongying Liu, Shaoxi Li, Yuanlong Chen, and Yang Wei. 2024. "Ship Trajectory Prediction in Complex Waterways Based on Transformer and Social Variational Autoencoder (SocialVAE)" Journal of Marine Science and Engineering 12, no. 12: 2233. https://doi.org/10.3390/jmse12122233
APA StyleWang, P., Pan, M., Liu, Z., Li, S., Chen, Y., & Wei, Y. (2024). Ship Trajectory Prediction in Complex Waterways Based on Transformer and Social Variational Autoencoder (SocialVAE). Journal of Marine Science and Engineering, 12(12), 2233. https://doi.org/10.3390/jmse12122233






