Spatial Sequential Matching Enhanced Underwater Single-Photon Lidar Imaging Algorithm
Abstract
:1. Introduction
2. Methods
2.1. The Experiment System and Layout
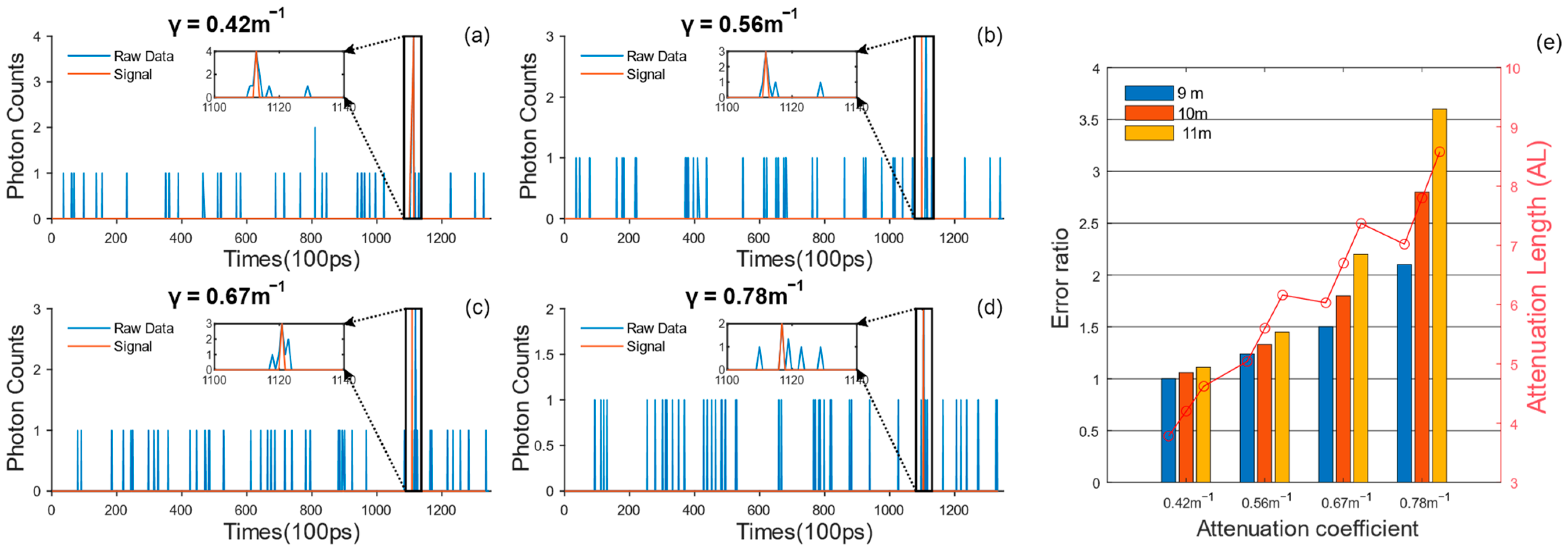
2.2. Attenuation Measurement and Evaluation Metrics
2.3. Noise and Echo Signal Distribution Characteristics
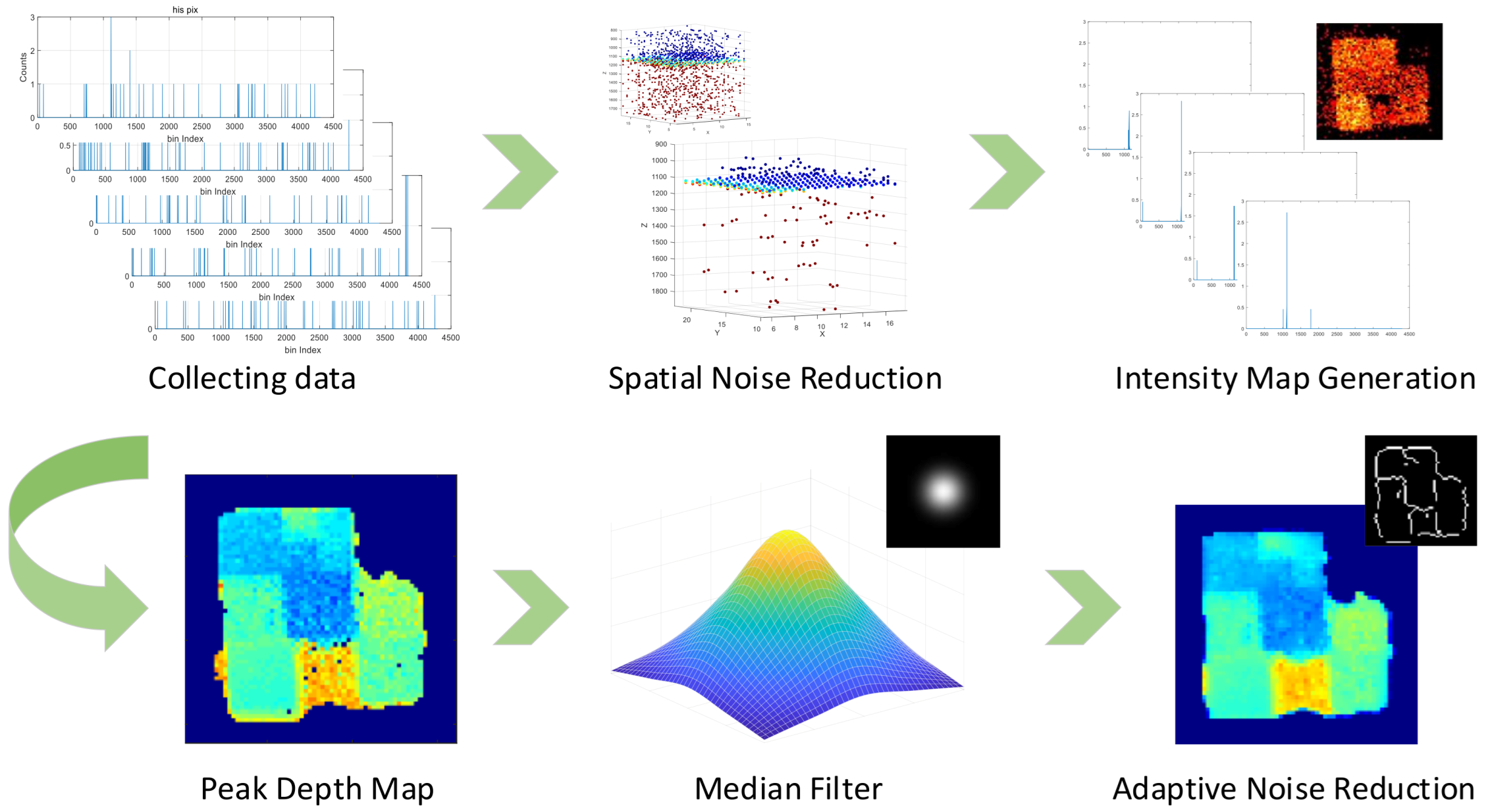
2.4. Reconstruction Algorithm
| Algorithm 1 SSME algorithm interpretation |
| Input: scan_resolution, bins, bin_width, data_histogram |
| Output: Intensity_map, Depth_map |
| //Data preprocessing and filtering |
| for all in do |
| end for |
| //Matched filtering and mask generation |
| for all in do |
| end for |
| //Depth value extraction and masking |
| for all in do |
| end for |
| //Denoising and adaptive TV smoothing |
| for all do |
| end for |
2.4.1. Data Preprocessing
2.4.2. Peak Depth Based on Matched Filtering
2.4.3. Optimizing Reconstruction Results
3. Results
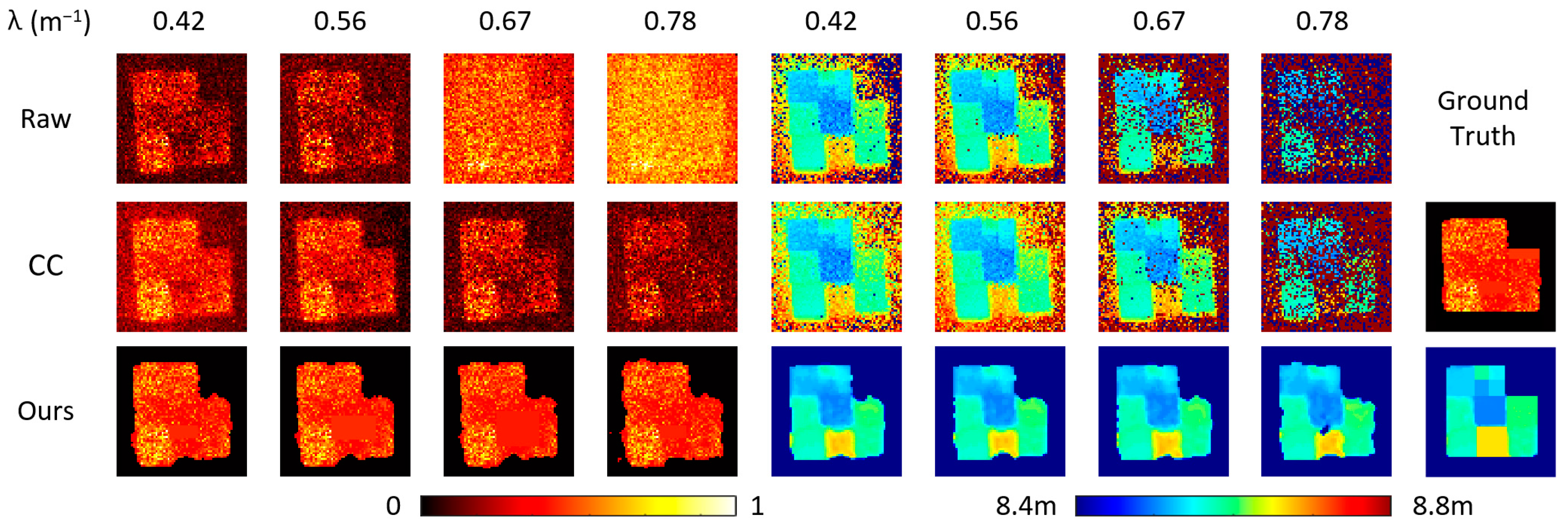
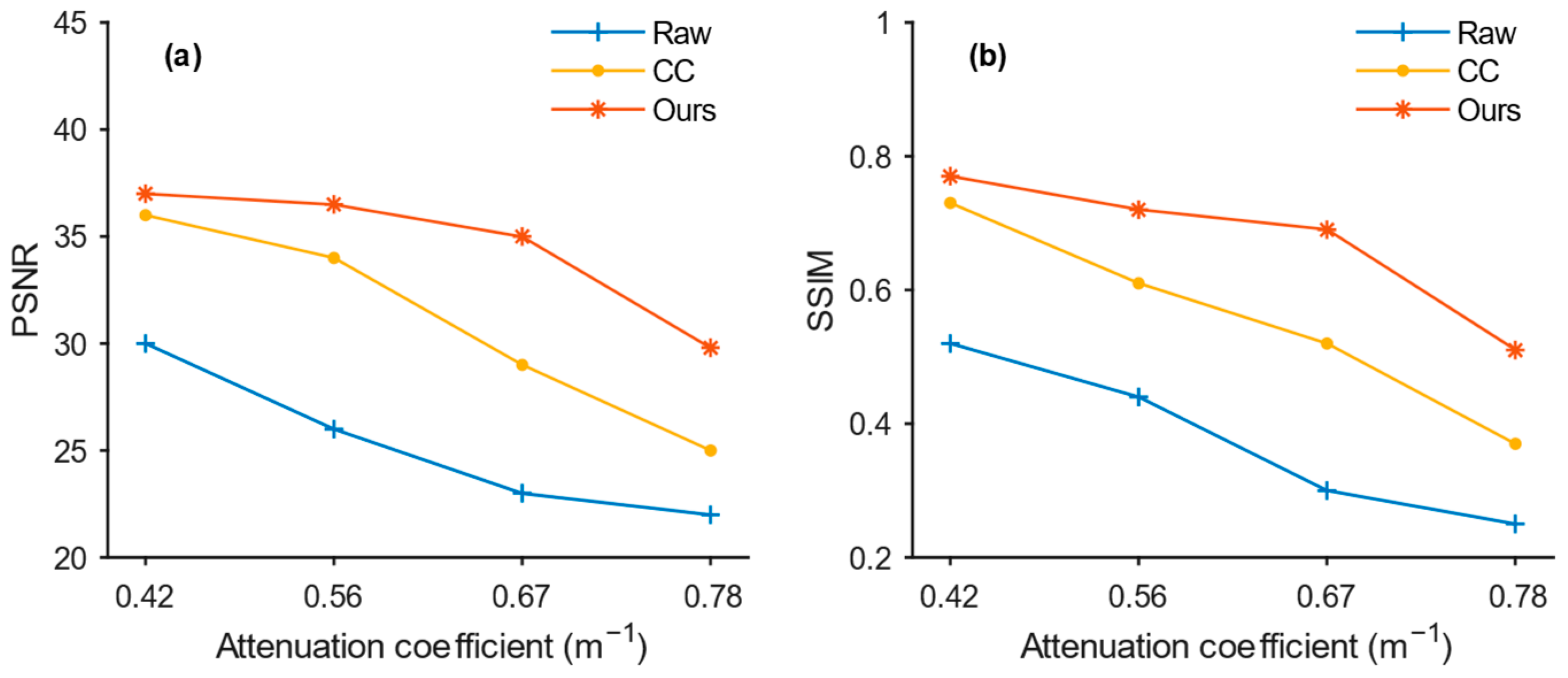
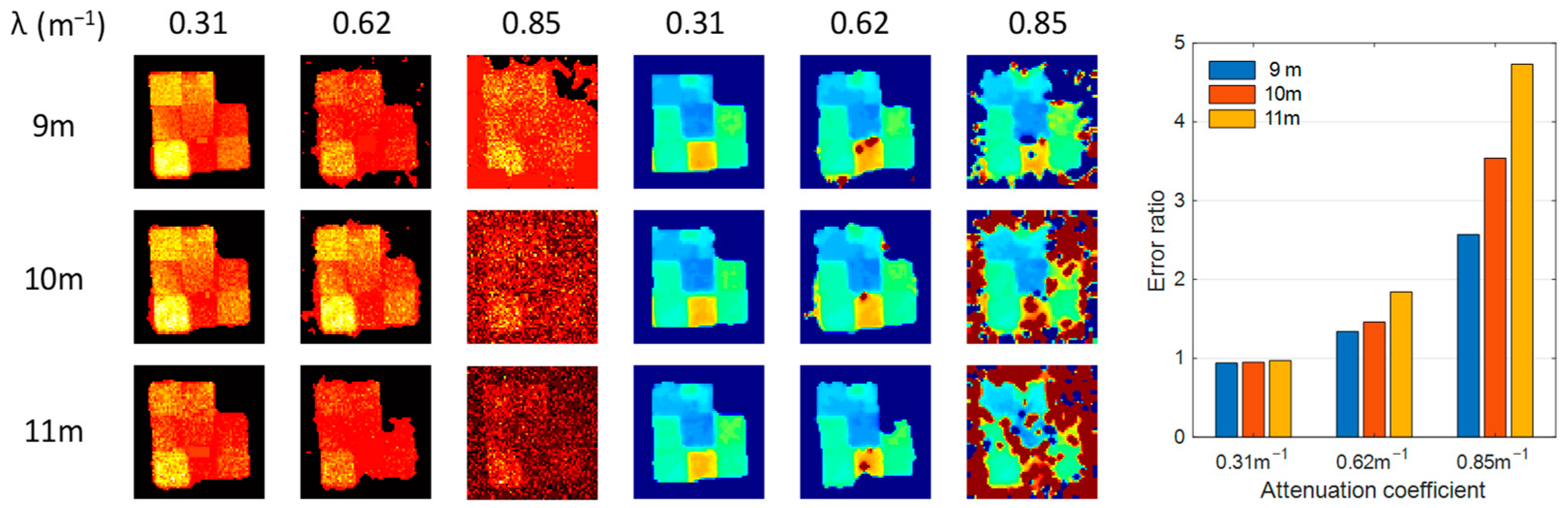
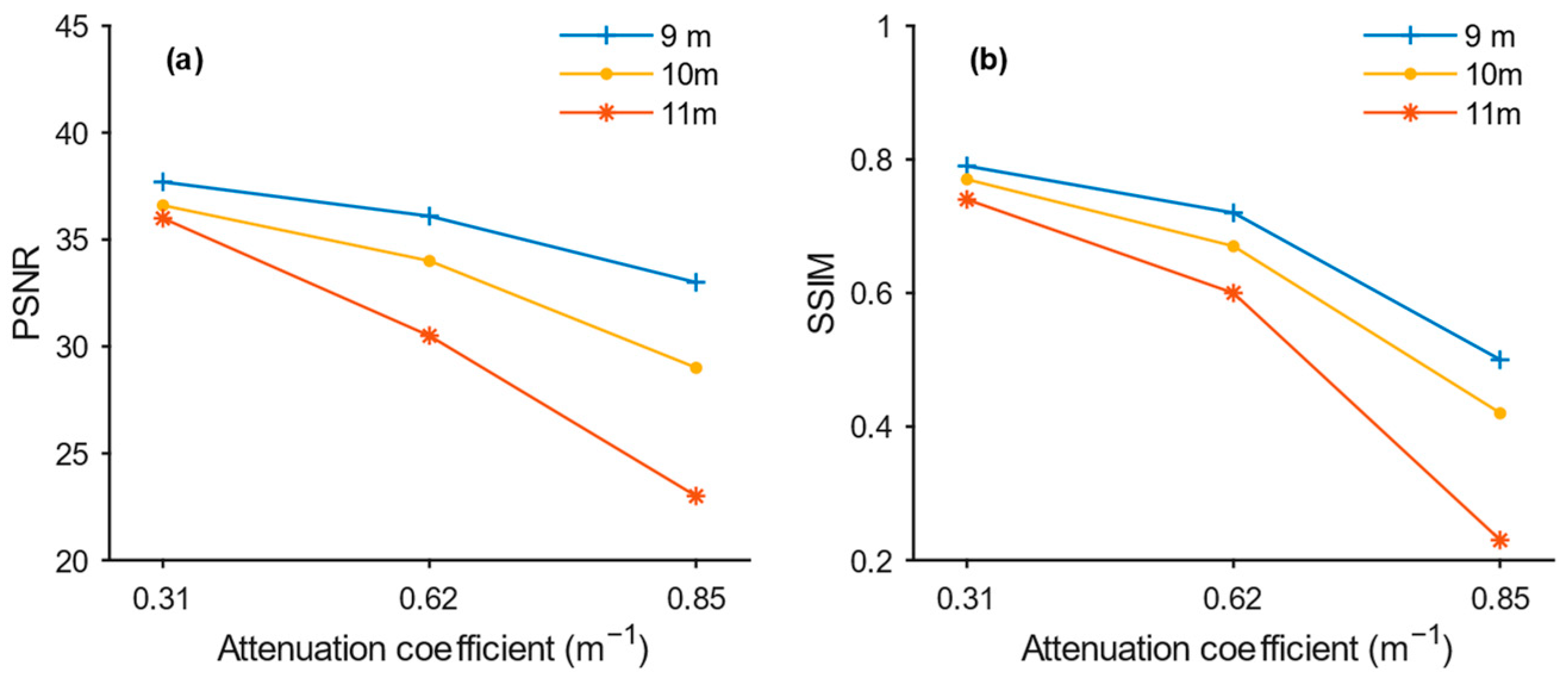
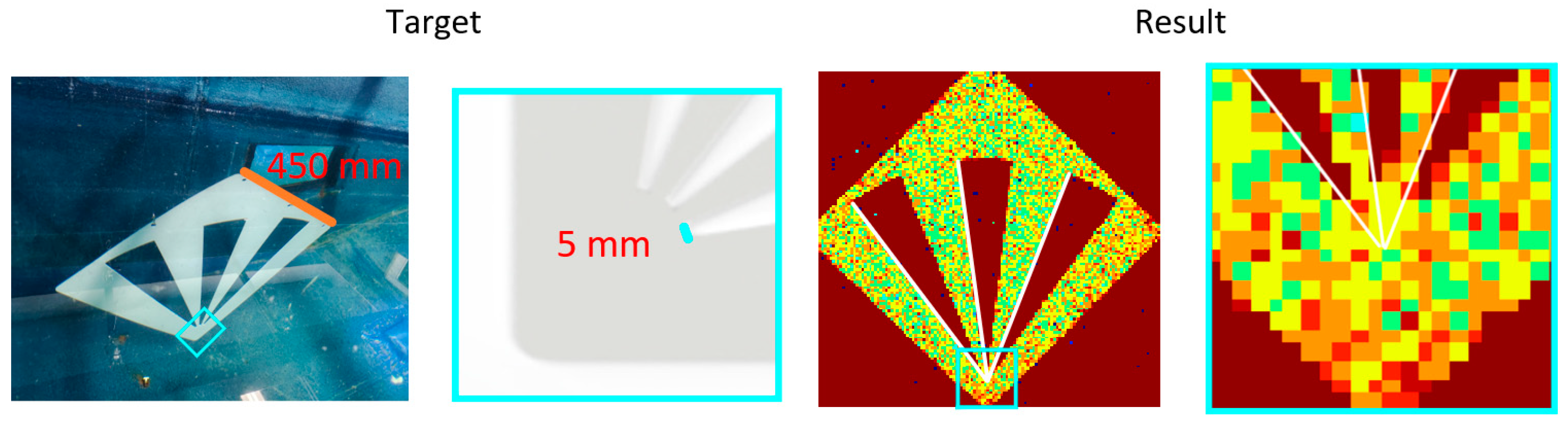
3.1. Depth Error and Reconstruction Results Under Different Turbidity
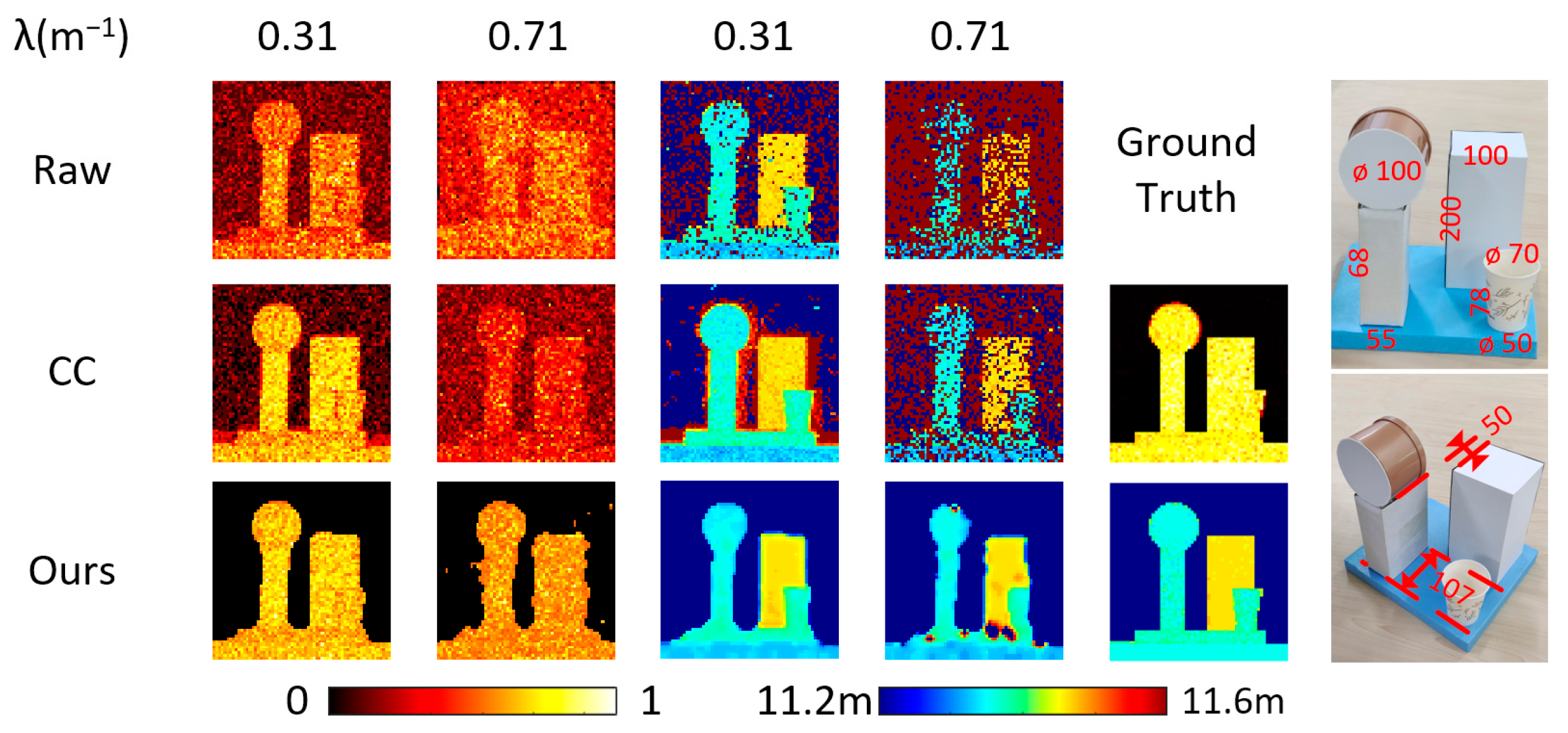
3.2. Image Reconstruction Performance Outside the Test Target
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McManamon, P.F. LiDAR Technologies and Systems; SPIE: Bellingham, WA, USA, 2019; ISBN 978-1-5106-2539-6. [Google Scholar]
- Molebny, V.; McManamon, P.; Steinvall, O.; Kobayashi, T.; Chen, W. Laser Radar: Historical Prospective—From the East to the West. Opt. Eng. 2017, 56, 031220. [Google Scholar] [CrossRef]
- Tobin, R.; Halimi, A.; McCarthy, A.; Soan, P.J.; Buller, G.S. Robust Real-Time 3D Imaging of Moving Scenes through Atmospheric Obscurant Using Single-Photon LiDAR. Sci. Rep. 2021, 11, 11236. [Google Scholar] [CrossRef] [PubMed]
- Maccarone, A.; McCarthy, A.; Ren, X.; Warburton, R.E.; Wallace, A.M.; Moffat, J.; Petillot, Y.; Buller, G.S. Underwater Depth Imaging Using Time-Correlated Single-Photon Counting. Opt. Express 2015, 23, 33911. [Google Scholar] [CrossRef]
- Hadfield, R.H.; Leach, J.; Fleming, F.; Paul, D.J.; Tan, C.H.; Ng, J.S.; Henderson, R.K.; Buller, G.S. Single-Photon Detection for Long-Range Imaging and Sensing. Optica 2023, 10, 1124–1141. [Google Scholar] [CrossRef]
- Acconcia, G.; Ceccarelli, F.; Gulinatti, A.; Rech, I. Timing Measurements with Silicon Single Photon Avalanche Diodes: Principles and Perspectives [Invited]. Opt. Express 2023, 31, 33963–33999. [Google Scholar] [CrossRef] [PubMed]
- Rapp, J.; Tachella, J.; Altmann, Y.; McLaughlin, S.; Goyal, V.K. Advances in Single-Photon Lidar for Autonomous Vehicles: Working Principles, Challenges, and Recent Advances. IEEE Signal Process. Mag. 2020, 37, 62–71. [Google Scholar] [CrossRef]
- Pawlikowska, A.M.; Halimi, A.; Lamb, R.A.; Buller, G.S. Single-Photon Three-Dimensional Imaging at up to 10 Kilometers Range. Opt. Express 2017, 25, 11919. [Google Scholar] [CrossRef]
- Li, Z.-P.; Huang, X.; Cao, Y.; Wang, B.; Li, Y.-H.; Jin, W.; Yu, C.; Zhang, J.; Zhang, Q.; Peng, C.-Z.; et al. Single-Photon Computational 3D Imaging at 45 Km. Photon. Res. 2020, 8, 1532. [Google Scholar] [CrossRef]
- McCarthy, A.; Collins, R.J.; Krichel, N.J.; Fernández, V.; Wallace, A.M.; Buller, G.S. Long-Range Time-of-Flight Scanning Sensor Based on High-Speed Time-Correlated Single-Photon Counting. Appl. Opt. 2009, 48, 6241. [Google Scholar] [CrossRef]
- Tobin, R.; Halimi, A.; McCarthy, A.; Ren, X.; McEwan, K.J.; McLaughlin, S.; Buller, G.S. Long-Range Depth Profiling of Camouflaged Targets Using Single-Photon Detection. Opt. Eng. 2017, 57, 031303. [Google Scholar] [CrossRef]
- Chan, S.; Warburton, R.E.; Gariepy, G.; Leach, J.; Faccio, D. Non-Line-of-Sight Tracking of People at Long Range. Opt. Express 2017, 25, 10109–10117. [Google Scholar] [CrossRef] [PubMed]
- Faccio, D.; Velten, A.; Wetzstein, G. Non-Line-of-Sight Imaging. Nat. Rev. Phys. 2020, 2, 318–327. [Google Scholar] [CrossRef]
- Cao, R.; de Goumoens, F.; Blochet, B.; Xu, J.; Yang, C. High-Resolution Non-Line-of-Sight Imaging Employing Active Focusing. Nat. Photon. 2022, 16, 462–468. [Google Scholar] [CrossRef]
- Maccarone, A.; Mattioli Della Rocca, F.; McCarthy, A.; Henderson, R.; Buller, G.S. Three-Dimensional Imaging of Stationary and Moving Targets in Turbid Underwater Environments Using a Single-Photon Detector Array. Opt. Express 2019, 27, 28437. [Google Scholar] [CrossRef]
- Satat, G.; Tancik, M.; Raskar, R. Towards Photography through Realistic Fog. In Proceedings of the 2018 IEEE International Conference on Computational Photography (ICCP), Pittsburgh, PA, USA, 4–6 May 2018; pp. 1–10. [Google Scholar]
- Zhang, Y.; Li, S.; Sun, J.; Zhang, X.; Liu, D.; Zhou, X.; Li, H.; Hou, Y. Three-Dimensional Single-Photon Imaging through Realistic Fog in an Outdoor Environment during the Day. Opt. Express 2022, 30, 34497. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Li, S.; Jiang, P.; Sun, J.; Liu, D.; Yang, X.; Zhang, X.; Zhang, H. Depth Imaging through Realistic Fog Using Gm-APD Lidar. In Proceedings of the Sixteenth National Conference on Laser Technology and Optoelectronics, Shanghai, China, 3–6 June 2021; Volume 11907, pp. 146–154. [Google Scholar]
- Satat, G.; Tancik, M.; Gupta, O.; Heshmat, B.; Raskar, R. Object Classification through Scattering Media with Deep Learning on Time Resolved Measurement. Opt. Express 2017, 25, 17466–17479. [Google Scholar] [CrossRef]
- McCarthy, A.; Ren, X.; Della Frera, A.; Gemmell, N.R.; Krichel, N.J.; Scarcella, C.; Ruggeri, A.; Tosi, A.; Buller, G.S. Kilometer-Range Depth Imaging at 1550 Nm Wavelength Using an InGaAs/InP Single-Photon Avalanche Diode Detector. Opt. Express 2013, 21, 22098–22113. [Google Scholar] [CrossRef]
- Kijima, D.; Kushida, T.; Kitajima, H.; Tanaka, K.; Kubo, H.; Funatomi, T.; Mukaigawa, Y. Time-of-Flight Imaging in Fog Using Multiple Time-Gated Exposures. Opt. Express 2021, 29, 6453–6467. [Google Scholar] [CrossRef]
- Yang, F.; Sua, Y.M.; Louridas, A.; Lamer, K.; Zhu, Z.; Luke, E.; Huang, Y.-P.; Kollias, P.; Vogelmann, A.M.; McComiskey, A. A Time-Gated, Time-Correlated Single-Photon-Counting Lidar to Observe Atmospheric Clouds at Submeter Resolution. Remote Sens. 2023, 15, 1500. [Google Scholar] [CrossRef]
- Li, Y.; Xue, Y.; Tian, L. Deep Speckle Correlation: A Deep Learning Approach toward Scalable Imaging through Scattering Media. Optica 2018, 5, 1181. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Vellekoop, I.M.; Mosk, A.P. Focusing Coherent Light through Opaque Strongly Scattering Media. Opt. Lett. 2007, 32, 2309–2311. [Google Scholar] [CrossRef] [PubMed]
- Yaqoob, Z.; Psaltis, D.; Feld, M.S.; Yang, C. Optical Phase Conjugation for Turbidity Suppression in Biological Samples. Nat. Photonics 2008, 2, 110–115. [Google Scholar] [CrossRef] [PubMed]
- Popoff, S.M.; Lerosey, G.; Carminati, R.; Fink, M.; Boccara, A.C.; Gigan, S. Measuring the Transmission Matrix in Optics: An Approach to the Study and Control of Light Propagation in Disordered Media. Phys. Rev. Lett. 2010, 104, 100601. [Google Scholar] [CrossRef] [PubMed]
- Bertolotti, J.; Van Putten, E.G.; Blum, C.; Lagendijk, A.; Vos, W.L.; Mosk, A.P. Non-Invasive Imaging through Opaque Scattering Layers. Nature 2012, 491, 232–234. [Google Scholar] [CrossRef]
- Sun, Y.; Shi, J.; Sun, L.; Fan, J.; Zeng, G. Image Reconstruction through Dynamic Scattering Media Based on Deep Learning. Opt. Express 2019, 27, 16032. [Google Scholar] [CrossRef]
- Liu, D.; Sun, J.; Gao, S.; Ma, L.; Jiang, P.; Guo, S.; Zhou, X. Single-Parameter Estimation Construction Algorithm for Gm-APD Ladar Imaging through Fog. Opt. Commun. 2021, 482, 126558. [Google Scholar] [CrossRef]
- Rong, T.; Wang, Y.; Zhu, Q.; Wang, C.; Zhang, Y.; Li, J.; Zhou, Z.; Luo, Q. Sequential Two-Mode Fusion Underwater Single-Photon Lidar Imaging Algorithm. J. Mar. Sci. Eng. 2024, 12, 1595. [Google Scholar] [CrossRef]
- Duntley, S.Q. Light in the Sea*. J. Opt. Soc. Am. 1963, 53, 214–233. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Z.; Huang, M.; Xie, J.; Jia, F.; Liu, L.; Zhao, Y. Non-Invasive Imaging through Scattering Media with Unaligned Data Using Dual-Cycle GANs. Opt. Commun. 2022, 525, 128832. [Google Scholar] [CrossRef]
- Toublanc, D. Henyey–Greenstein and Mie Phase Functions in Monte Carlo Radiative Transfer Computations. Appl. Opt. 1996, 35, 3270–3274. [Google Scholar] [CrossRef]
- Collister, B.L.; Zimmerman, R.C.; Hill, V.J.; Sukenik, C.I.; Balch, W.M. Polarized Lidar and Ocean Particles: Insights from a Mesoscale Coccolithophore Bloom. Appl. Opt. 2020, 59, 4650–4662. [Google Scholar] [CrossRef] [PubMed]
- Shin, Y.; Nam, S.-W.; An, C.-K.; Powers, E.J. Design of a Time-Frequency Domain Matched Filter for Detection of Non-Stationary Signals. In Proceedings of the 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing, Salt Lake City, UT, USA, 7–11 May 2001; Volume 6, pp. 3585–3588. [Google Scholar]
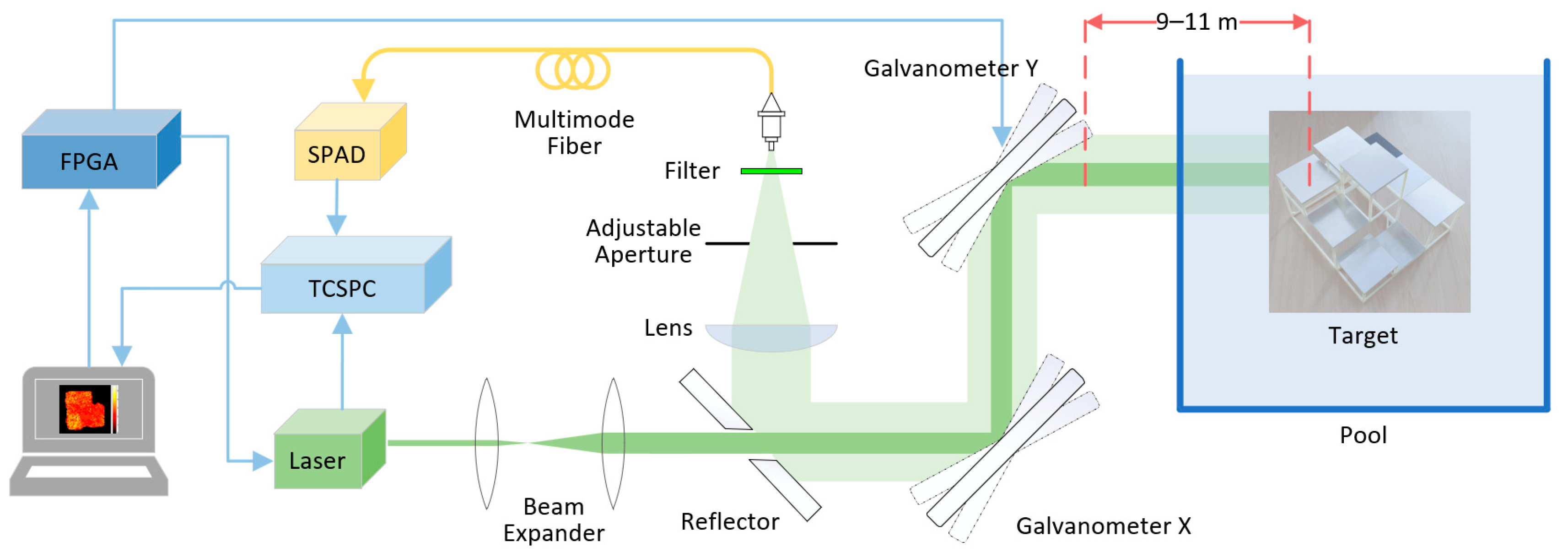


| Parameter | Comment |
|---|---|
| Environment | • Unfiltered tap water • Unfiltered tap water with different concentrations of Maalox |
| Target stand-off distance | ~9, 10, 11 m in water |
| Laser system | sub-nanosecond passively Q-switched laser MCC-532-5-030 |
| Illumination wavelength | 532 nm |
| Laser repetition rate | 5 kHz |
| Average optical power | 150 mW |
| Single pulse energy | ~30 μJ |
| Laser spot diameter at target | ~8 mm diameter |
| Optical field of view | ~42 mm diameter at 9 m |
| Single pixel emission times used in these experiments | 10 times/pixel 50 times/pixel 500 times/pixel |
| Histogram length | 150 bins |
| Bin width | 100 picoseconds |
| Detectors | Single-Photon Avalanche Diode Detector SPCM-AQRH-14-FC, 1 pixel |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Q.; Wang, Y.; Wang, C.; Rong, T.; Li, B.; Ying, X. Spatial Sequential Matching Enhanced Underwater Single-Photon Lidar Imaging Algorithm. J. Mar. Sci. Eng. 2024, 12, 2223. https://doi.org/10.3390/jmse12122223
Zhu Q, Wang Y, Wang C, Rong T, Li B, Ying X. Spatial Sequential Matching Enhanced Underwater Single-Photon Lidar Imaging Algorithm. Journal of Marine Science and Engineering. 2024; 12(12):2223. https://doi.org/10.3390/jmse12122223
Chicago/Turabian StyleZhu, Qiguang, Yuhang Wang, Chenxu Wang, Tian Rong, Buxiao Li, and Xiaotian Ying. 2024. "Spatial Sequential Matching Enhanced Underwater Single-Photon Lidar Imaging Algorithm" Journal of Marine Science and Engineering 12, no. 12: 2223. https://doi.org/10.3390/jmse12122223
APA StyleZhu, Q., Wang, Y., Wang, C., Rong, T., Li, B., & Ying, X. (2024). Spatial Sequential Matching Enhanced Underwater Single-Photon Lidar Imaging Algorithm. Journal of Marine Science and Engineering, 12(12), 2223. https://doi.org/10.3390/jmse12122223





