Modeling of Three-Dimensional Ocean Current Based on Ocean Current Big Data for Underwater Vehicles
Abstract
1. Introduction
2. Methods
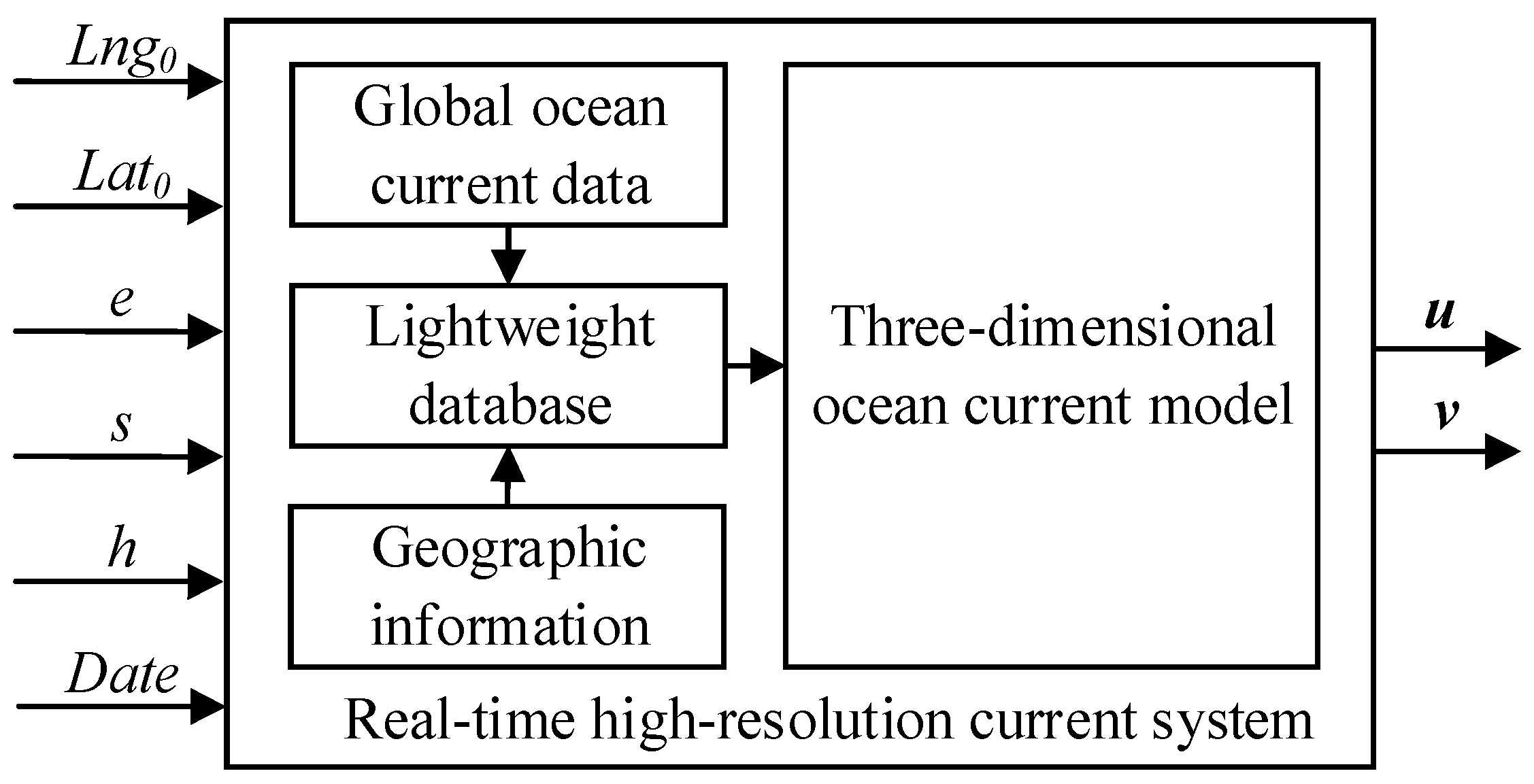
2.1. Real-Time High-Resolution Current System
2.1.1. Current Modeling
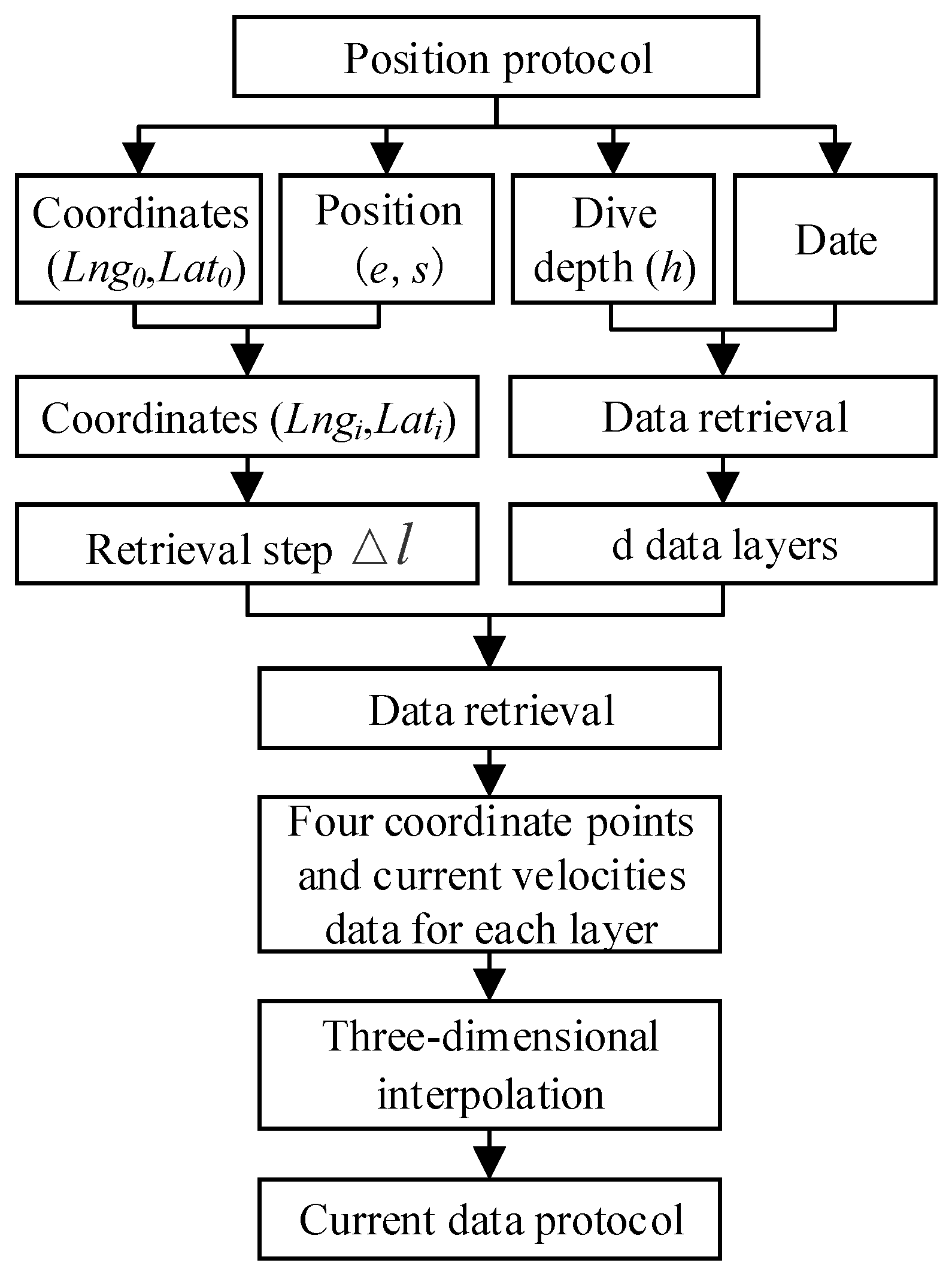
2.1.2. System Workflow
2.2. Processing Global Ocean Current Data
2.2.1. Current Data Reconstruction
2.2.2. Fast-Access Retrieval of Target Data
2.2.3. Current Velocity Position
2.3. Three-Dimensional Current Modeling
Three-Dimensional Interpolation of the Current Data
- Three-dimensional trilinear interpolation
- Three-dimensional Newton and bilinear interpolation
- Three-dimensional spline and bilinear interpolation
3. Results and Discussion
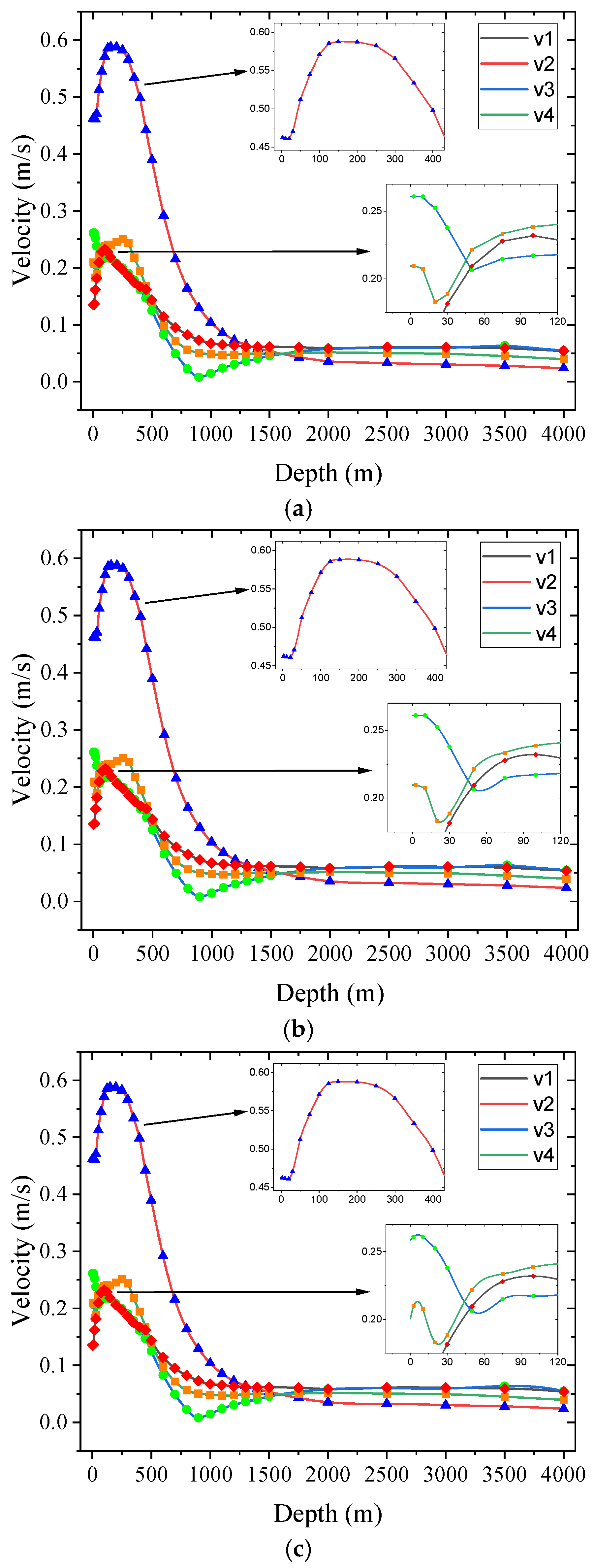
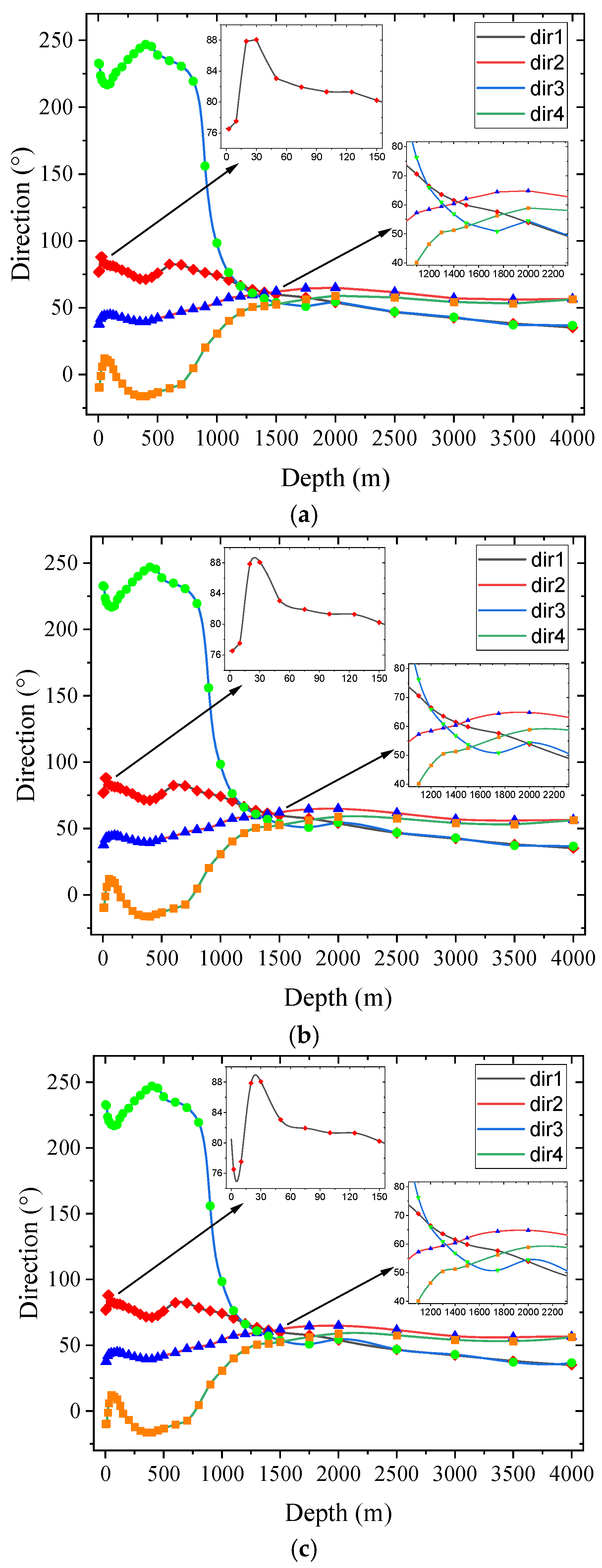
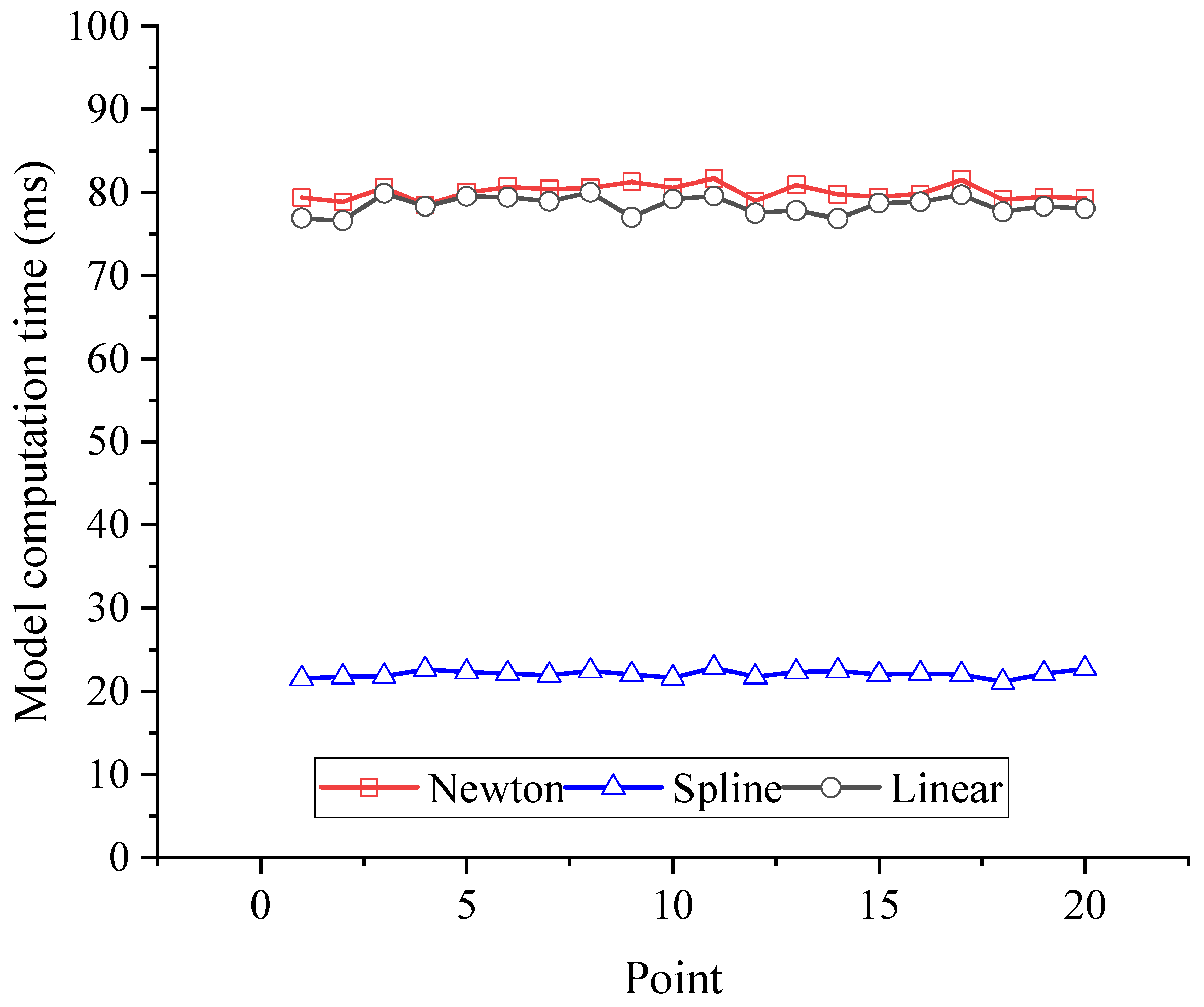
3.1. Effect Comparison of Different Interpolation Methods
3.2. Interpolation Results Comparison
3.3. Property Comparison of Multiple Current Models
3.4. Profiling Float Trajectories Under the Influence of Currents
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xie, J.; Zhu, J. Estimation of the surface and mid-depth currents from Argo floats in the Pacific and error analysis. J. Mar. Syst. 2008, 73, 61–75. [Google Scholar] [CrossRef]
- Zhao, D.; Zhang, S.; Gao, S.; Zhong, X. Review on the influence of underwater vehicles motion and load under current. Chin. J. Ship Res. 2024, 19, 1–16. [Google Scholar]
- Politi, E.; Dimitrakopoulos, G. Comparison of Evolutionary Algorithms for AUVs for Path Planning in Variable Conditions. In Proceedings of the 2019 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 5–7 December 2019. [Google Scholar]
- Hu, W. Numerical Simulation of Course-Keeping for Autonomous Underwater Vehicle Under Current Disturbance. Master’s Thesis, Dalian Maritime University, Dalian, China, 2024. [Google Scholar]
- Men, T.; Wang, Y.; Guan, S.; Ding, J. Research on water outlet location prediction of underwater glider based on ocean current. Ship Sci. Technol. 2023, 45, 66–73. [Google Scholar]
- Zang, W.; Nie, Y.; Song, D.; Guo, T.; Li, K. Research on Constraining Strategies of Underwater Glider’s Trajectory Under the Influence of Ocean Currents Based on DQN Algorithm OCEANS. In Proceedings of the 2019 MTS/IEEE SEATTLE, Seattle, WA, USA, 27–31 October 2019. [Google Scholar]
- Alvarez, A.; Caiti, A.; Onken, R. Evolutionary path planning for autonomous underwater vehicles in a variable ocean. IEEE J. Ocean. Eng. 2004, 29, 418–429. [Google Scholar] [CrossRef]
- Wang, X. Research on Virtual Mooring Control of Underwater Gliders. Master’s Thesis, Tianjin University, Tianjin, China, 2020. [Google Scholar]
- Lan, W. Research on Underwater Glider Formation Path Planning Under the Influence of Ocean Current. Ph.D. Thesis, Dalian Maritime University, Dalian, China, 2023. [Google Scholar]
- Ma, Y.; Wang, Y.; Guan, S.; Wang, N.; Ding, J. Motion Control Simulation of Underwater Gliders in Kuroshio. J. Unmanned Undersea Syst. 2024, 32, 1–7. [Google Scholar]
- Gao, W. Study on path planning of an underwater glider in the complex marine environment. Master’s Thesis, Tianjin University, Tianjin, China, 2022. [Google Scholar]
- Li, Y.; He, X.; Lu, Z.; Jing, P.; Su, Y. Comprehensive Ocean Information-Enabled AUV Motion Planning Based on Reinforcement Learning. Remote Sens. 2023, 15, 3077. [Google Scholar] [CrossRef]
- Yao, X.; Cui, M.; Wang, L.; Li, Y.; Zhou, C.; Su, M.; Hu, G. Three-Dimensional Velocity Field Interpolation Based on Attention Mechanism. Appl. Sci. 2023, 13, 13045. [Google Scholar] [CrossRef]
- Wu, H.; Niu, W.; Wang, S.; Yan, S. A feedback control strategy for improving the motion accuracy of underwater gliders in currents: Performance analysis and parameter optimization. Ocean. Eng. 2022, 252, 111250. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, L.; Liang, Y.; Niu, W.; Yang, M.; Yang, S. Modelling and analysis of depth-averaged currents for underwater gliders. Ocean. Eng. 2024, 312, 119086. [Google Scholar] [CrossRef]
- Jing, G.; Lei, L.; Gang, Y. Dynamic modeling and experimental analysis of an underwater glider in the ocean. Appl. Math. Model. 2022, 108, 392–407. [Google Scholar] [CrossRef]
- Lan, W.; Jin, X.; Chang, X.; Zhou, H. Based on Deep Reinforcement Learning to path planning in uncertain ocean currents for Underwater Gliders. Ocean. Eng. 2024, 301, 117501. [Google Scholar] [CrossRef]
- Hu, H.; Zhang, Z.; Li, L.; Peng, X. Energy-optimal motion planning of underwater gliders accounting for seabed Topography and ocean currents. Ocean. Eng. 2023, 288, 116008. [Google Scholar] [CrossRef]
- Li, X.; Yu, S. Three-dimensional path planning for AUVs in ocean currents environment based on an improved compression factor particle swarm optimization algorithm. Ocean. Eng. 2023, 280, 114610. [Google Scholar] [CrossRef]
- Lan, W.; Jin, X.; Chang, X.; Wang, T.; Zhou, H.; Tian, W.; Zhou, L. Path planning for underwater gliders in time-varying ocean current using deep reinforcement learning. Ocean. Eng. 2022, 262, 112226. [Google Scholar] [CrossRef]
- Qiu, B.; Wang, M.; Li, H.; Ma, L.; Li, X.; Zhu, Z.; Zhou, F. Development of hybrid neural network and current forecasting model based dead reckoning method for accurate prediction of underwater glider position. Ocean. Eng. 2023, 285, 115486. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, Y.; Wan, X.; Ming, Y.; Yang, S. Position prediction of underwater gliders based on a new heterogeneous model ensemble method. Ocean. Eng. 2024, 309, 118312. [Google Scholar] [CrossRef]
- Zhao, Y.; Lin, L.; Wang, Q.; Wen, P.; Yang, D. Trajectory prediction of sea targets based on geodetic distance similarity calculation. J. Compute. Appl. 2023, 43, 3594–3598. [Google Scholar]









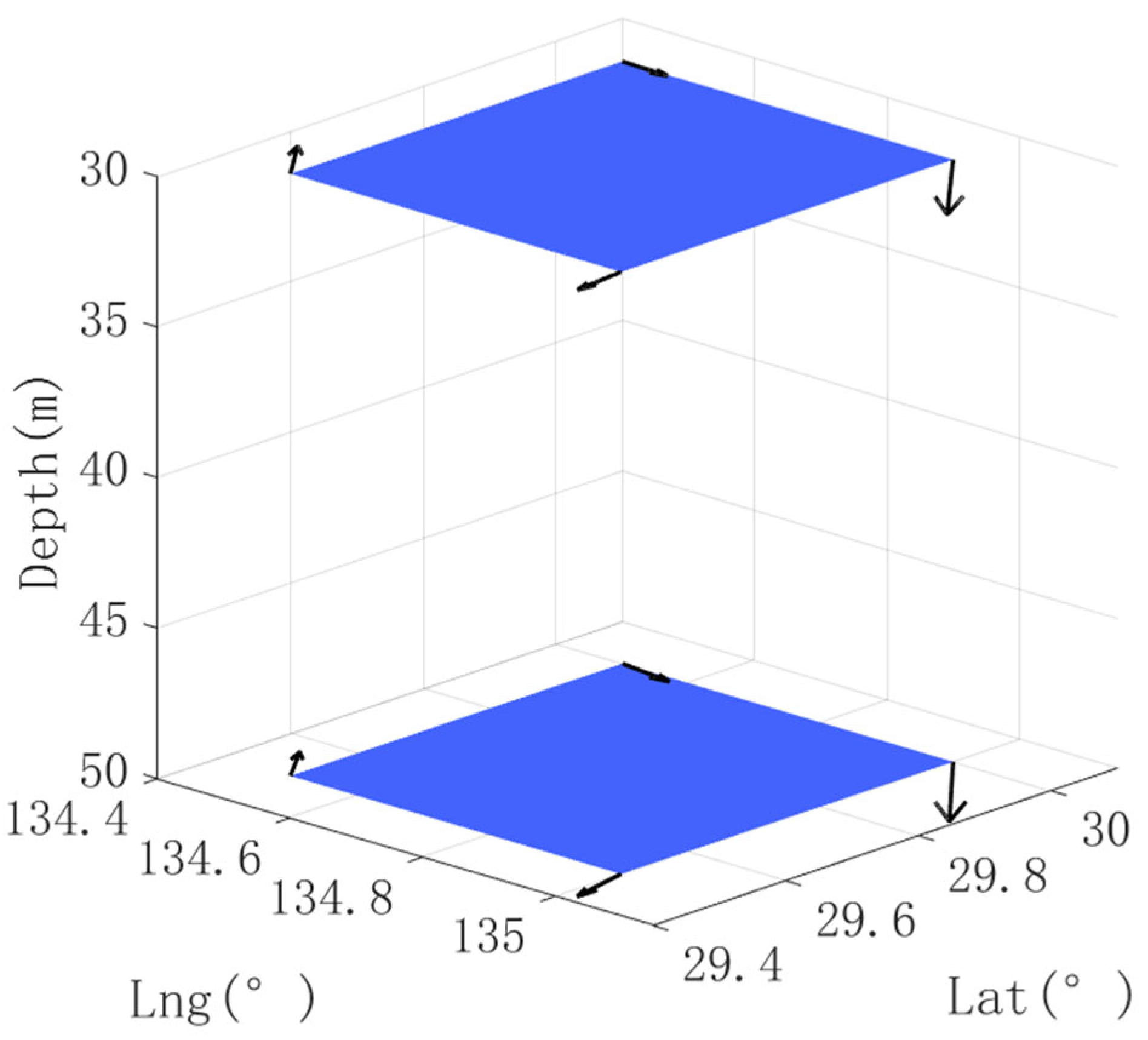

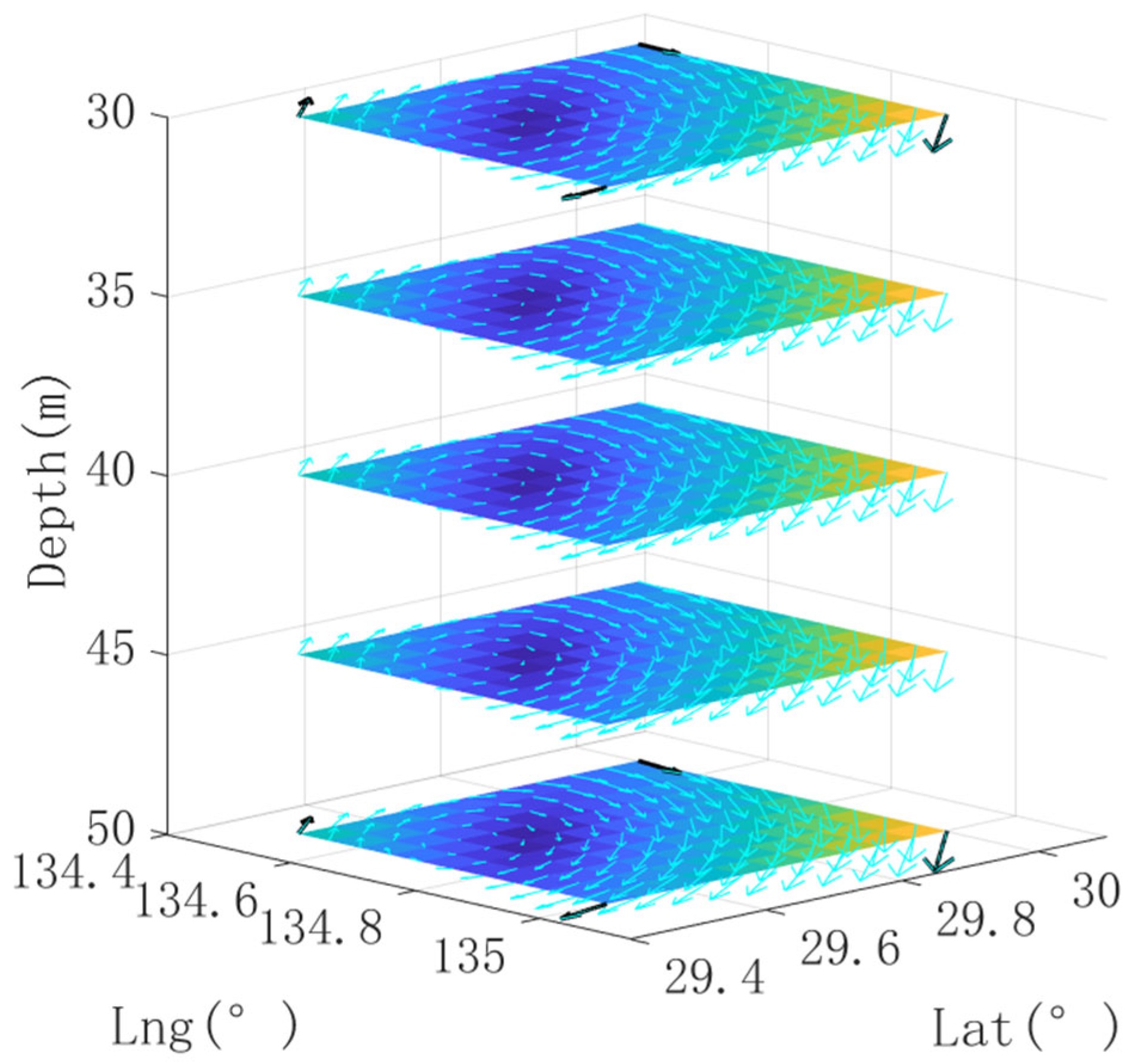



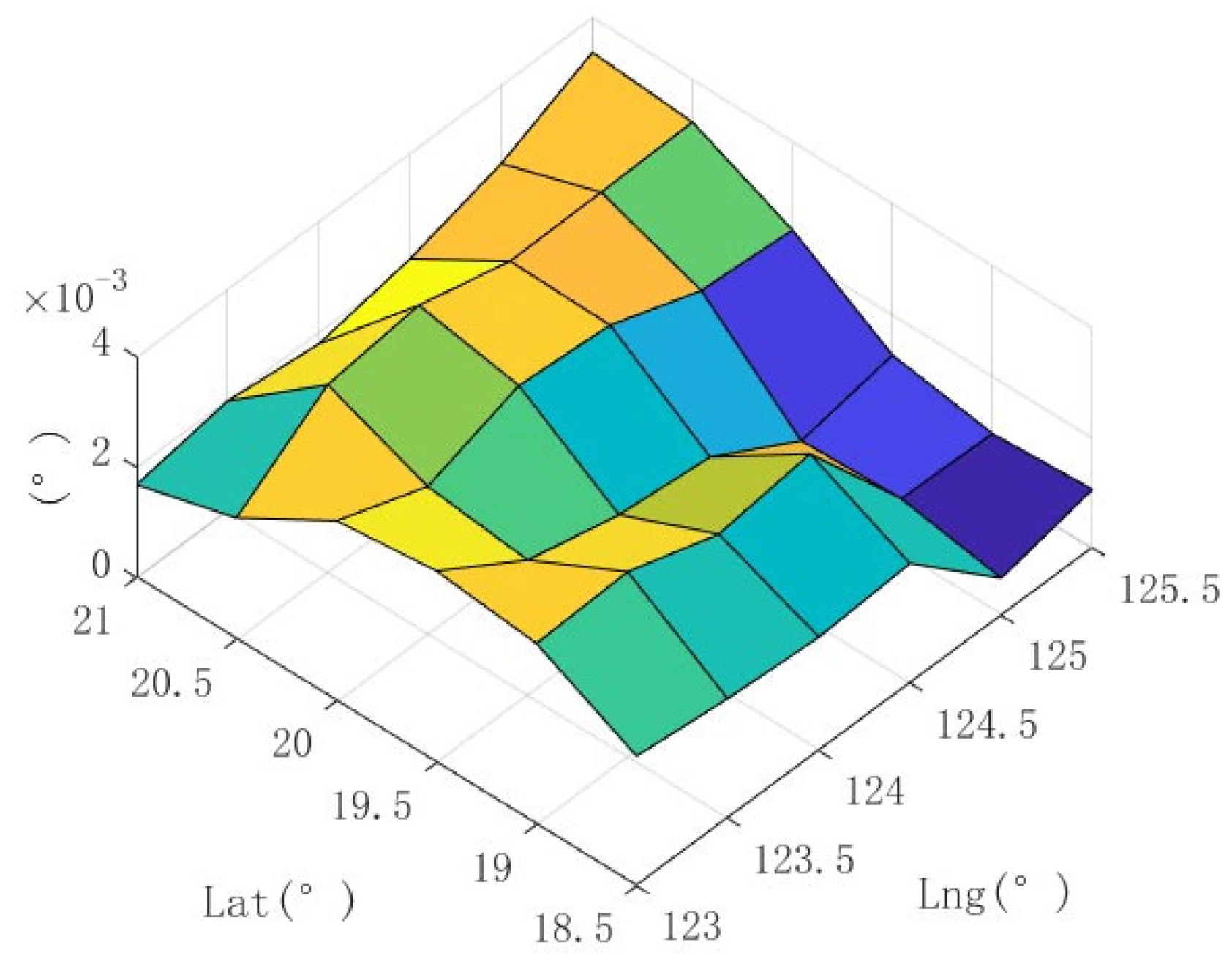
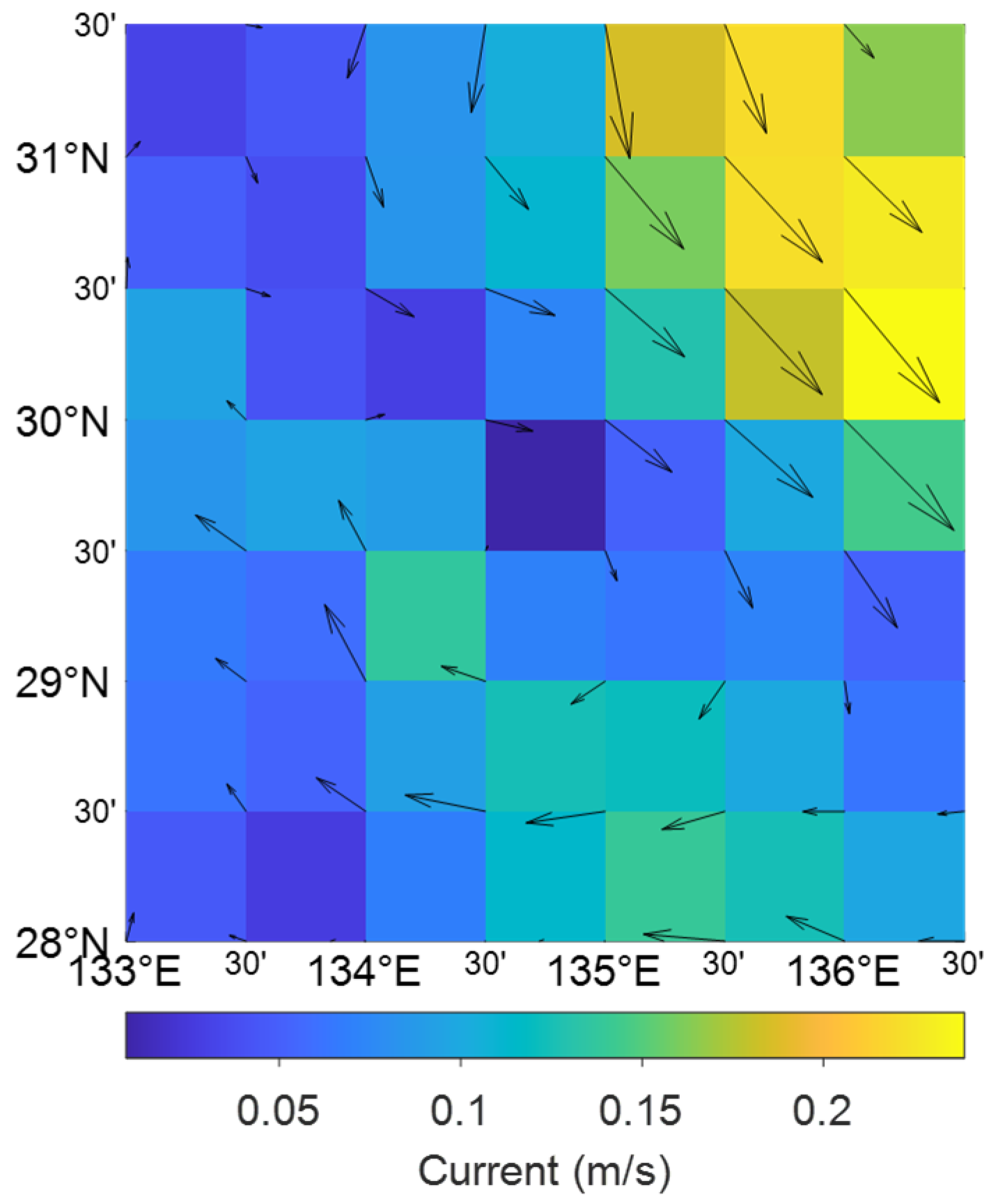





| No | Symbols List | Value |
|---|---|---|
| 1 | The Earth’s average radius R | 6,371,393 m |
| 2 | The step size of retrieval ∆l | 0.5° |
| No | Symbols List | Explanation |
|---|---|---|
| 1 | uh1m, uh2m, uh3m, uh4m | Current velocities along the i-axis at depth hm near the real-time position |
| 2 | vh1m, vh2m, vh3m, vh4m. | Current velocities along the j-axis at depth hm near the real-time position |
| 3 | uh1(m+1), uh2(m+1), uh3(m+1), uh4(m+1) | Current velocities along the i-axis at depth h(m+1) near the real-time position |
| 4 | vh1(m+1), vh2(m+1), vh3(m+1), vh4(m+1) | Current velocities along the j-axis at depth h(m+1) near the real-time position |
| 5 | uh1, uh2, uh3, uh4 | Current velocities along the i-axis at depth h when interpolated along the k-axis |
| 6 | vh1, vh2, vh3, vh4 | Current velocities along the j-axis at depth h when interpolated along the k-axis |
| 7 | ue1, ue2, ue3, ue4 | Current velocities along the i-axis at depth h |
| 8 | ve1, ve2, ve3, ve4 | Current velocities along the j-axis at depth h |
| 9 | u | Current velocities at the real-time position |
| 10 | v | Current velocities at the real-time position |
| No | Symbols List | Explanation |
|---|---|---|
| 1 | uh1m, uh2m, uh3m, uh4m | Current velocities along the i-axis at depth hm near the real-time position |
| 2 | vh1m, vh2m, vh3m, vh4m | Current velocities along the j-axis at depth hm near the real-time position |
| 3 | uh1(m+1), uh2(m+1), uh3(m+1), uh4(m+1) | Current velocities along the i-axis at depth h(m+1) near the real-time position |
| 4 | vh1(m+1), vh2(m+1), vh3(m+1), vh4(m+1) | Current velocities along the j-axis at depth h(m+1) near the real-time position |
| 5 | uh1(m+2), uh2(m+2), uh3(m+2), uh4(m+2) | Current velocities along the i-axis at depth h(m+2) near the real-time position |
| 6 | vh1(m+2), vh2(m+2), vh3(m+2), vh4(m+2) | Current velocities along the j-axis at depth h(m+2) near the real-time position |
| 7 | uh1(m+3), uh2(m+3), uh3(m+3), uh4(m+3) | Current velocities along the i-axis at depth h(m+3) near the real-time position |
| 8 | uh1(m+3), uh2(m+3), uh3(m+3), uh4(m+3) | Current velocities along the j-axis at depth h(m+3) near the real-time position |
| 9 | uh1, uh2, uh3, uh4 | Current velocities along the i-axis at depth h when interpolated along the k-axis |
| 10 | vh1, vh2, vh3, vh4 | Current velocities along the j-axis at depth h when interpolated along the k-axis |
| 11 | ue1, ue2, ue3, ue4 | Current velocities along the i-axis at depth h |
| 12 | ve1, ve2, ve3, ve4 | Current velocities along the j-axis at depth h |
| 13 | u | Current velocities at the real-time position |
| 14 | v | Current velocities at the real-time position |
| No | Symbols List | Explanation |
|---|---|---|
| 1 | n | Number of data layers |
| 2 | uh11, uh21, uh31, uh41 | Current velocities along the i-axis at depth h1 |
| 3 | vh11, vh21, vh31, vh41 | Current velocities along the j-axis at depth h1 |
| 4 | uh1(m+1), uh2(m+1), uh3(m+1), uh4(m+1) | Current velocities along the i-axis at depth h(m+1) near the real-time position |
| 5 | vh1(m+1), vh2(m+1), vh3(m+1), vh4(m+1) | Current velocities along the j-axis at depth h(m+1) near the real-time position |
| 6 | uh1(m+2), uh2(m+2), uh3(m+2), uh4(m+2) | Current velocities along the i-axis at depth h(m+2) near the real-time position |
| 7 | vh1(m+2), vh2(m+2), vh3(m+2), vh4(m+2) | Current velocities along the j-axis at depth h(m+2) near the real-time position |
| 8 | uh1n, uh2n, uh3n, uh4n | Current velocities along the i-axis at depth hn near the real-time position |
| 9 | uh1n, uh2n, uh3n, uh4n | Current velocities along the j-axis at depth hn near the real-time position |
| 10 | uh1, uh2, uh3, uh4 | Current velocities along the i-axis at depth h when interpolated along the k-axis |
| 11 | vh1, vh2, vh3, vh4 | Current velocities along the j-axis at depth h when interpolated along the k-axis |
| 12 | ue1, ue2, ue3, ue4 | Current velocities along the i-axis at depth h |
| 13 | ve1, ve2, ve3, ve4 | Current velocities along the j-axis at depth h |
| 14 | u | Current velocities at the real-time position |
| 15 | v | Current velocities at the real-time position |
| No | Current Model | Modeling | High Resolution | Different Currents | Data Authenticity | Data Updatability |
|---|---|---|---|---|---|---|
| 1 | A stream function | Calculating the function (2D) | √ | |||
| 2 | Uniform current field | Nearest-neighbor interpolation (2D) | √ | |||
| 3 | 3D current field | Bilinear interpolation (2D) | √ | |||
| 4 | 3D velocity field | 3D interpolation | √ | √ | ||
| 5 | 3D-OCM | 3D interpolation | √ | √ | √ | √ |
| No | Symbols List | Value |
|---|---|---|
| 1 | Mass | 54.7 kg |
| 2 | Surface volume | 0.052884 m3 |
| 3 | Surface density | 1025.32 kg/m3 |
| 4 | Volume at 100 m | 0.052734 m3 |
| 5 | Density at 100 m | 1026.66 kg/m3 |
| 6 | Wetted area | 0.77 m2 |
| 7 | Dive resistance coefficient | 0.77 |
| 8 | Float resistance coefficient | 0.46 |
| 9 | Dive depth | 100 m |
| 10 | Oil volume change | 100 mL |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, Y.; Li, X.; Li, H.; Zou, Y.; Yang, Y.; Xu, J. Modeling of Three-Dimensional Ocean Current Based on Ocean Current Big Data for Underwater Vehicles. J. Mar. Sci. Eng. 2024, 12, 2219. https://doi.org/10.3390/jmse12122219
Wen Y, Li X, Li H, Zou Y, Yang Y, Xu J. Modeling of Three-Dimensional Ocean Current Based on Ocean Current Big Data for Underwater Vehicles. Journal of Marine Science and Engineering. 2024; 12(12):2219. https://doi.org/10.3390/jmse12122219
Chicago/Turabian StyleWen, Yicheng, Xingfei Li, Hongyu Li, Yanchao Zou, Yiguang Yang, and Jiayi Xu. 2024. "Modeling of Three-Dimensional Ocean Current Based on Ocean Current Big Data for Underwater Vehicles" Journal of Marine Science and Engineering 12, no. 12: 2219. https://doi.org/10.3390/jmse12122219
APA StyleWen, Y., Li, X., Li, H., Zou, Y., Yang, Y., & Xu, J. (2024). Modeling of Three-Dimensional Ocean Current Based on Ocean Current Big Data for Underwater Vehicles. Journal of Marine Science and Engineering, 12(12), 2219. https://doi.org/10.3390/jmse12122219






