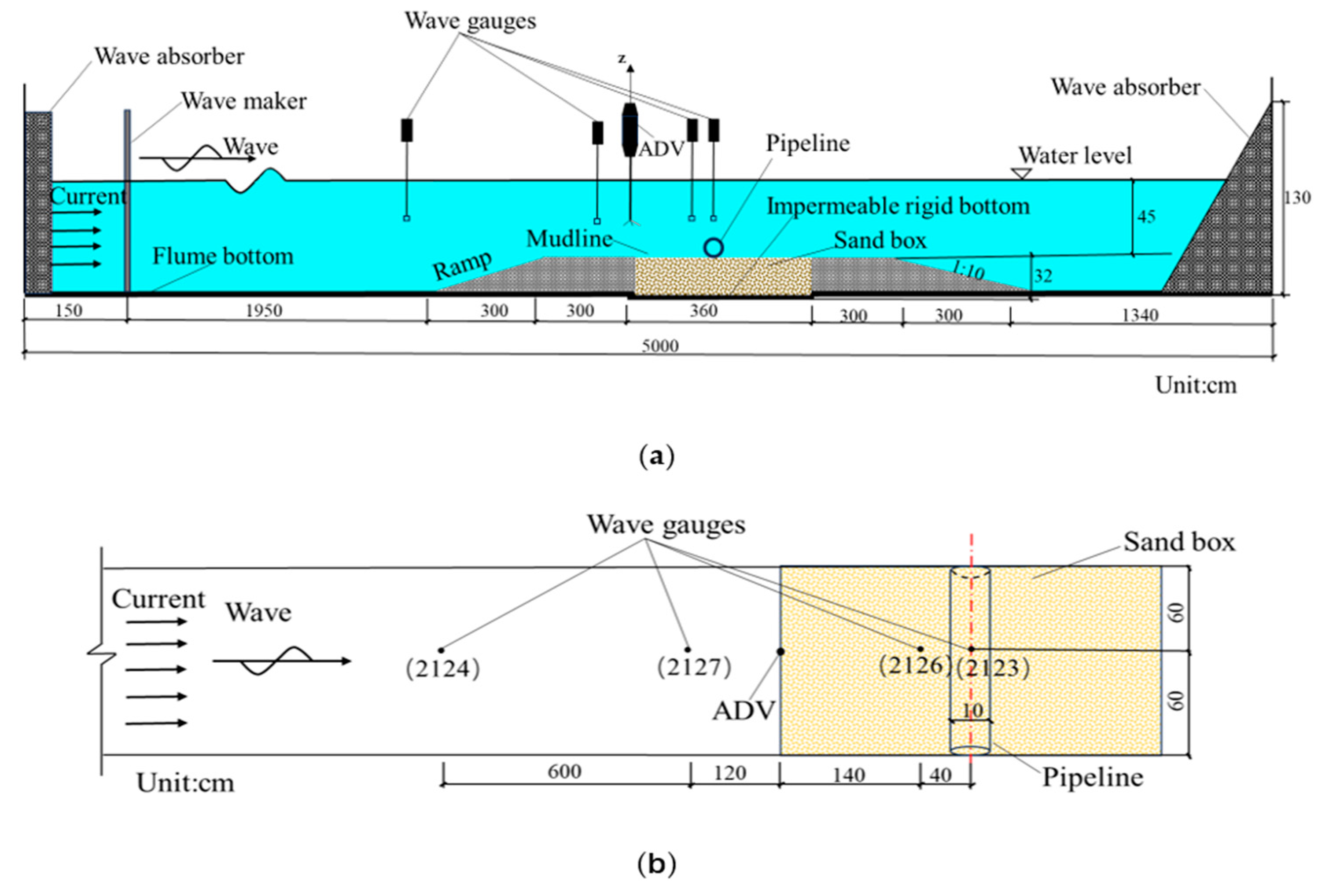
1. Introduction
With the continuous development and advancement of marine engineering, submarine pipelines play a crucial role in the transportation of oil and gas resources across oceans. These pipelines are lifelines deep beneath the sea, consistently delivering precious marine resources to various parts of the world, meeting the enormous demand for energy. However, at the same time, damage and failure incidents of submarine pipelines occur from time to time. These incidents not only pose potential threats to the marine environment, but could also disrupt the normal transportation of marine resources, potentially leading to significant safety accidents [
1,
2]. Therefore, the stability of pipelines has become a global hotspot among both coastal and geotechnical engineers [
3]. Research results show that seabed deformation due to wave (current) action, seabed liquefaction [
4,
5,
6,
7], and accidents caused by fishing activities or falling objects [
8,
9] are among the major factors in the failure of submarine pipelines. It is widely recognized that an increase in pore pressure will lead to a decrease in effective stress, which directly leads to the weakening of soil strength and the enhancement of compressibility. Under the action of waves and currents, these changes can significantly affect the stability of the ocean’s structure. Therefore, it is critically important to delve into the dynamic response of the seabed surrounding submarine pipelines under the influence of waves (and currents), as well as to develop protection strategies for submarine pipelines and the surrounding seafloor.
The effect of the liquefaction potential of seafloor soil on the instability of marine structures cannot be ignored. The dynamic wave pressure generated by the wave and current load is applied to the seafloor surface, resulting in significant changes in the size and distribution of pore water pressure and effective stress inside the seabed. The soil at the bottom of the sea is in a saturated condition (above the water table), and at a point, in the interior of the soil, the effective stress conditions may instantly change or even be cancelled out by an increase in pore water pressure (u
0 + Δu) due to an external and instantaneous stress (u
0 is the initial effective stress). When the upward component of pore pressure is greater than the gravity of soil particles, the soil particles are in a suspended state, resulting in soil liquefaction, and then the seabed surface loses all bearing strength, resulting in structural instability. Therefore, in order to better protect the pipeline from the impact of soil instability, the pipeline can be buried at a certain depth. Sudhan et al. [
10] conducted a simulation study on a pipeline buried under the seabed, examining the mechanism of pore water pressure surrounding the pipeline under different wave conditions and burial depth ratios. Zhou et al. [
11] modeled pipelines in three semi-buried or resting soils considering the isotropic action of regular waves, and found that the superposition of water flow in the same direction of the waves increased pore pressure and thus increased the probability of seafloor liquefaction. Based on the study of codirectional regular wave flow, Chen et al. [
12] extensively examined the impact of wave flow inversion on pore pressure around pipelines in trenches and seabed liquefaction. The experimental results revealed that when the direction of the current aligns with the wave propagation, the risk of liquefaction around the pipe significantly increases; conversely, if the current direction opposes the wave propagation, this helps to reduce the likelihood of soil liquefaction. Zhai et al. [
13] conducted a series of regular wave tests and numerical modeling analyses, adding variables such as sand grain size and pipeline diameter on the basis of varying different backfill depths. However, only the wave-induced pore pressures within the circular area around the buried sandy seabed pipeline were analyzed, which has certain limitations. Sun et al. [
14] not only demonstrated the pore pressure values on the surface of a partially buried pipeline through flume tests, but also systematically evaluated the variations in pore pressure within the gully sediment stratum surrounding the pipeline and its immediate vicinity. The findings indicated that a deeper gully depth and a thicker buried stratum can significantly reduce the pore water pressure across the entire trench zone, meaning that the greater the burial depth of the pipeline, the less it is affected by seabed instability; thereby, enhanced shelter can be used as a measure to protect submarine pipelines from the effects of transient seafloor liquefaction. On the other hand, Gao et al. [
15] explored pore pressure variations due to waves in the pulverized bed around buried pipelines and partially/fully backfilled pipelines. The measured data not only confirm that residual pore pressure is the primary cause of liquefaction in pulverized soil, but also demonstrate that full backfilling, as an economically effective protective method, significantly reduces liquefaction risks and ensures the safety and stability of pipelines in pulverized seabed. This conclusion further enhances the significance of adapting the construction of marine infrastructure in different soil circumstances.
In addition to adjusting the buried depth of the pipeline, the use of the rock berm protection method can also be considered [
16]. Sekiguchi et al. [
17] conducted four experiments (two test plots had gravel covering the entire soil surface, and the remaining two test plots had gravel only covering part of the soil surface) to explore the effects of varying the thickness and width of gravel cover on fine sand sediments. The experimental results indicate that using gravel/stone block/riprap covering may be an effective measure to protect soil (whether hydraulically filled or naturally deposited) from liquefaction. Subsequently, Sumer et al. [
18] carried out an experimental study on stone covering (including the influence of the intermediate filter layer) on the silt seabed under the action of continuous waves and analyzed in depth the effects of stone accumulation density and the number of stone layers on the distribution depth of pore pressure across the entire soil layer. As the experimental data indicate, under the action of continuous waves, the presence of covered stone decreases the liquefaction potential, which is mainly related to the density of stone accumulation and the quantity of stone layers. Moreover, the sinking displacement of stone in soil can be effectively reduced by increasing the filter layer. The studies above are all focused on covering the seabed surface with stone layers, and do not consider the existence of structures such as pipelines. Later, Sumer et al. [
19] studied the stability of rock berm (three different berm materials were used, respectively) laid above a pipeline in a trench under the action of large waves and obtained a critical mobility number corresponding to the initial movement of the rock berm, according to the experimental results. In addition to covering the upper part of the pipeline with a stone safeguarding layer, Tauqeer and Yin et al. [
20,
21] calculated the load carrying capacity and discussed the geometric optimization of three shapes of GRP protective covers via the finite element method (FEM), with the aim of addressing the problem of submarine pipelines subjected to the load of fishing activities and the impact of falling objects. This laid a foundation for the selection and use of a GRP shield (a subsea protection cover designed by PJNC company to protect offshore oil and gas pipelines from falling objects, manufactured from concreate as well as Glass-Reinforced Plastic (“GRP”); it is low cost, lightweight, and easy to install). The above pipeline protection measures are based on the concept of covering pipelines with rigid protective layers to withstand the influence of ocean currents and heavy load impacts. In addition, covering them with flexible protective pads is also an effective protection method. Geotextiles are engineering synthetic materials widely used in marine and civil engineering. They can prevent fine soil particles from passing through while allowing water and other fluids to flow smoothly, which is crucial for preventing soil erosion and protecting infrastructure. Therefore, geotextiles can be used as protective layers to prevent waves or other biological damage to marine infrastructure. Additionally, this structure can resist chemical corrosion (this experiment utilizes this property of geotextiles). Furthermore, the reinforcing effect of geotextiles gives them a certain tensile strength, enhancing the overall strength and stability of the soil, especially in weak foundations or areas that need reinforcement [
22,
23,
24]. Aside from covering pipelines with protective layers, there are also structural support measures (specifically including grout bag support, underwater pile support, and riprap support) to prevent pipe instability and failure due to overhanging spans caused by topography. Xie et al. [
25] and Zhang et al. [
26] have conducted comprehensive reviews and detailed analyses of the experimental research and progress in the field of pipeline protection.
The aforementioned research on protective pipeline coverings mainly focuses on the stability of the protective measures. Only a few studies focus on the mechanisms of changes in hydrodynamic motion around submarine pipelines and submarine response under the action of protective measures. Hence, a comprehensive set of scale model pipeline tests are performed in this study in a wave flume to investigate both wave dynamics and seabed reactions in the vicinity of pipelines, considering scenarios with and without the application of geotextiles and stone cover protection. The protective effect of the measures, i.e., the geotextiles and stones, on pore pressure is comprehensively examined under various wave and current conditions. To the best of the author’s knowledge, this is the first experimental study of wave-current-induced pore pressure around geotextile and stone coverings that protect pipelines. In
Section 2, the experimental arrangements and workflow are thoroughly described.
Section 3 examines and analyzes both the hydrodynamic characteristics of the flow fields and the spatial distribution of seafloor pore pressure around the protective pipeline. Eventually, the crucial discoveries of this paper are concluded in
Section 4.
3. Results and Discussion
This study primarily investigates the hydrodynamic alterations surrounding a submarine pipeline and seabed pore pressure under the impact of regular waves with or without current. The experimental outcomes are contrasted with the protective efficacy of geotextiles and stone covers on the pipeline. In this experiment, the intersection point between the seabed surface and the pipeline centerline is designated as the coordinate origin, with the x-axis positive direction aligned with the wave propagation direction and the z-axis positive direction extending upwards from the seabed surface. In subsequent analyses, ƞ denotes the wave profile and |pw| signifies the maximum dynamic wave pressure. Additionally, the time–history variation curve of pore pressure (denoted as ps) and the vertical depth variation in seabed pore pressure under regular wave–current action are considered, as well as the pore pressure variation patterns at different positions of the pipeline (front, bottom, and back). It should be mentioned that the pore pressure here refers to the excess pore pressure, which means it needs to be subtracted from the static pore pressure. Furthermore, to more intuitively observe the changes in pore pressure within the seabed, the relevant data were nondimensionalized. The equation p0 = γw·h is the static pore pressure on the seabed surface, where γw is the specific weight of the water and h is the water depth. The impact of wave factors such as wave height (H), wave period (T), and wave velocity (U) on seabed pore pressure distribution around the pipeline are analyzed.
3.1. Hydrodynamic Properties Surrounding the Pipeline Under Wave and Current Influence
3.1.1. The Wave Profile Surrounding the Pipeline
In the experiment, the wave-height gauge WHG2123 was used to measure the wave surface change above the pipe with or without protection.
Figure 6 shows the time-series change curve of the wave front at the top of the pipe with or without protection under the influence of regular waves (and currents). It can be seen from the figure that the fluctuation ranges depending on whether or not there is protection, under the regular wave condition monitored by WHG2123, are [−37.25,59.51] and [−43.47,65.57], respectively. The addition of forward flow significantly accelerates the wave propagation, and the fluctuation range at the top of the unprotected pipe is significantly reduced (the fluctuation range is [−43.73,56.76], which is 7.84% lower than that under the condition of no current), while the fluctuation range of the geotextile- and stone-covered pipe is increased by 5.18%. This is because the existence of geotextile and stone cover increases the height of the structure to a certain extent, resulting in an increase in the fluctuation range. When the wave flow is reversed, the current will inhibit the wave propagation, the wave period will decrease, and the fluctuation amplitude of the pipe with or without protection will increase significantly. The fluctuation amplitudes of the pipe with and without protection are [−55.07,95.63] and [−54.12,86.88], respectively. Compared with the no-current condition, the fluctuation amplitude increased by 35.81% and 29.30%, respectively. It can be seen from the experiment that the effect of the reverse current on the wave is significant and cannot be ignored.
3.1.2. Dynamic Wave Pressures Around the Pipeline
Figure 7 illustrates the spatial distribution of dynamic wave pressure on the pipe surface, with and without geotextile and stone cover protection, under the influence of regular waves with varying wave characteristics. The maximum dynamic wave pressure is selected as the ordinate. When waves act alone, wave height is positively correlated with wave pressure, meaning that higher wave heights result in greater wave pressures. Due to the obstruction of wave energy propagation by the pipe, the maximum wave pressure at the pipe’s bottom stagnation point is higher than at the top stagnation point, particularly at the 270° point on the pipe’s surface. In comparison to the unprotected single pipe, the maximum wave pressure measured on the geotextile- and stone-protected pipe is reduced by 38.24%, and the distribution of wave pressure along the pipe’s surface is more uniform, especially under the action of waves with higher wave heights. In the absence of protection, the wave pressure on the pipe surface is also positively correlated with the wave period. When the wave period reaches its maximum of T = 1.8 s, the wave pressure at 270° on the pipe surface reaches its peak. However, when the period is T = 1.8 s, the maximum dynamic wave pressure at 270° on the geotextile- and stone-covered pipe surface decreases, and the dynamic wave pressure at 270° on the geotextile- and stone-covered pipe surface is reduced by 41.56% under the action of a T = 1.8 s wave period.
Figure 8 illustrates the spatial distribution of dynamic wave pressure on the surface of the pipe with and without geotextile and stone protection under the combined action of regular waves and varying current rates (U). When the wave and current act in the same direction, taking the flow rate U = 0.2 m/s as an example, the maximum wave pressure value of the pipe under the protection of geotextiles and stones is reduced by 24.03% compared with that of the pipe without protection. When the wave and the flow act in the opposite direction, for example, U = −0.2 m/s, compared with the unprotected pipe, the maximum wave pressure value of the pipe under the protection of geotextiles and stones is reduced by 40.51%, and the protection effect on the bottom of the pipe is obvious. These comprehensive results show that the effect of geotextiles and stones acting as hydrodynamic protection around the pipe is remarkable, considering wave action with a large wave height and wave period, as well as wave–current action.
3.2. Seabed Response Around the Pipeline Under Wave–Current Action
Figure 9 shows the time series of pore pressure induced by waves (and currents) beneath the bottom of the pipeline, resulting in either exposure to hydrodynamic actions or backfilling with geotextile and stone cover. The pore pressure in this paper is the excess pore pressure
ps after subtracting the hydrostatic pressure. Due to the energy dissipation caused by sediment particles, the pore pressure attenuates gradually in the seabed depth direction. The pore pressure amplitude at different layers of the geotextile- and stone-covered protected pipeline is much smaller than that of the unprotected pipeline. Meanwhile, it can be seen from the figure that the influence of the current direction on the pore pressure in the seabed is obvious. Compared with the reverse current, the maximum pore pressure amplitudes at p31, p32, p33, and p34 of the unprotected pipeline increase by 0.04 kPa, 0.05 kPa, 0.07 kPa, and 0.09 kPa, respectively, under the wave condition with forward current. The maximum pore pressure amplitudes at p31, p32, p33, and p34 of the geotextile- and stone-covered pipeline, on the other hand, are increased by 0.04 kPa, 0.05 kpa, 0.07 kPa, and 0.06 kPa, respectively. This demonstrates that the forward current can promote wave conduction along the seabed depth with regard to that under the reverse current condition; as a consequence, the pore pressure in the profile of seabed depth becomes larger when the current and the wave travel in the same direction. This is ascribed as the reason that the forward current enhances the permeability of wave energy into the seabed. Moreover, the protective effect of the geotextile and stone cover means that the current has little effect on the pore pressure on the seabed surface, particularly below z = −0.12 m (p33), which is also reflected in
Section 3.4.3.
3.3. Influence of Protection Layer Properties on Seabed Response
Figure 10 shows the distribution and variation patterns of excess pore pressure within the seabed at different positions around the pipelines with and without the protection of geotextiles and stone cover, with four layers of pore pressure sensors arranged at four depth directions of z = −0.03 m, −0.06 m, −0.12 m, and −0.18 m. |
ps|/
p0 represents the dimensionless maximum excess pore pressure caused by waves (current). Considering the wave-alone situation, as seen in
Figure 10a, the pore pressure underneath the unprotected pipeline is obviously smaller than the pore pressure at the far end of the seabed. The attenuation of wave energy along the propagation approach caused by the porosity property of the seabed contributes to this phenomenon. Furthermore, as the depth of the seabed near the pipeline increases, the rate of pore pressure dissipation gradually slows down, indicating that the pipeline has a certain protective effect on the surrounding area. Comparing
Figure 10a,b, the pore pressure around the geotextile- and stone-covered protected pipeline does not change obviously in comparison to that in the vicinity of the exposed pipeline, and the pore pressure amplitudes of the front, bottom, and back of the pipelines are roughly the same.
When the wave superimposes a forward current, as seen in
Figure 10c,d, the change in velocity has a significant effect on the amplitude of the pore pressure around the fully exposed pipeline, and the influence degree of current on the pore pressure amplitude decreases with the depth of the seabed. This is mainly due to the obstructing effect of the pipeline on the fluid field, which reduces the wave pressure exerted on the seabed surface behind the pipe, thus weakening the infiltration effect of current flow on the pore pressure on the seabed. However, the protection layer of the geotextile and stones embedded on the pipeline blocks the current propagation, leading to the pore pressure amplitude not changing significantly. As seen in
Figure 10e,f, when waves are superimposed by a reverse current, the impact of velocity change on the amplitude of pore pressure around the unprotected pipeline is smaller than that under the condition of the wave and current in the same direction. However, the amplitude of the pore pressure in front, at the bottom, and at the back of the protected pipeline is much smaller than that within the seabed around the unprotected pipeline. That is, the sheltering function of the geotextile and stone coverage serves as the pipe’s protection measure; this is obvious when the current travels against the wave.
3.4. Influence of Wave and Current Parameters on Seabed Response
3.4.1. Impact of Wave Height Parameters
The influence of waves with diverse wave heights on the seabed pore pressure around the unprotected pipe is discussed. The fixed period T = 1.6 s.
Figure 11 shows the vertical distribution of excess pore pressure in the seabed around the bottom of the pipes with and without protection versus various wave heights (z/h represents the dimensionless vertical depth of the seabed). With the increase in soil depth, pore pressure gradually dissipates. The effect of wave height on the pore pressure at the bottom of the unprotected pipe is concentrated in the upper seabed z/h = −0.09, and the effect of geotextile and stone load on the pore pressure at the bottom of the protected pipe is concentrated in the upper seabed z/h = −0.38. Due to the positive correlation between wave energy and wave height, the pore pressure amplitudes of the seabed in both cases (with and without geotextile- and stone-covered protective pipe) increase with the increase in wave height and reach the maximum value when H = 0.14 m. With regard to the pore pressure of w7(z/h = 0) near the seabed surface, as the wave height increases from 0.08 m to 0.14 m at an interval of 0.02 m, the percentage increases in pore pressure measured under the unprotected pipe are 33.70%, 21.95%, and 14.67%, respectively, while the percentage increases in pore water pressure measured for the geotextile- and stone-covered pipe are 22.58%, 21.05%, and 14.13%, respectively. Thus, the effect of wave height on pore pressure amplitude decreases with the increase in wave height. Moreover, compared with the unprotected pipe, the pore pressure measured for the protected pipe (w7) decreased by 32.61%, 38.21%, 38.67%, and 38.95%, respectively, when the wave height increased. The effect of geotextile and stone protection on wave height and pore pressure amplitude increases with the increase in wave height. That is, the greater the wave height, the better the wave protection effect.
3.4.2. Impact of Wave Period Parameters
The responses of the seabed around the pipelines to waves with diverse wave periods are discussed. The fixed wave height H = 0.1 m.
Figure 12 shows the vertical distribution of excess pore pressure in the seabed around the bottom of the pipes with and without protection at various wave periods. The results show that, under wave load, the pore pressure amplitude at the bottom of the pipe without protection increases with the increase in the wave period. Meanwhile, the attenuation rate of pore pressure versus the depth of the seabed becomes slower with the increase in the wave period. When the period increases from 1.2 s to 1.8 s at an interval of 0.2 s, the increases in pore pressure around the unprotected pipe are 26.04%, 2.48%, and 1.61%, respectively, whereas the increment percentages of pore water pressure measured for the geotextile- and stone-protected pipeline are 37.50%, 15.15%, and 0, respectively. The effect of wave period on pore pressure amplitude also decreases with the increase in wave period, and the effect of wave period on pore pressure amplitude is much smaller than that of wave height on pore pressure. Similarly, the wave protection effect of the geotextile and stones on the pipe is more significant with a greater wave period.
3.4.3. Impact of Current Parameters
We further analyzed the effect of the superposed regular wave with different current rates on the seabed pore pressure around the unprotected pipe (note that the forward flow is positive, the reverse flow is negative, and the symbol only represents the direction, not the size). The fixed wave height H = 0.1 m and the period T = 1.6 s.
Figure 13 shows the vertical distribution of excess pore pressure at the bottom of the unprotected pipe at different current rates. The presence of water flow will affect the wave action and make the decay rate of pore pressure in the vertical direction change irregularly, especially in the countercurrent action.
When the wave–current action increases from U = 0 m/s to U = 0.2 m/s, the pore pressure amplitude at the bottom of the pipe increases by 27.64% and 7.89% in the case of the unprotected and geotextile- and stone-protected pipes, respectively. However, when the reverse action of wave–current increases from U = 0 m/s to U = −0.2 m/s, the measured pore pressure amplitude of the pipe bottom increases by 49.59% and 2.63% in the case of the unprotected and geotextile- and stone-protected pipes, respectively. When the current rates are U = 0 m/s, U = 0.2 m/s, and U = −0.2 m/s, the pore pressure amplitude measured for the geotextile- and stone-protected pipe decreases by 38.21%, 47.77%, and 57.60%, respectively, compared with that measured for the unprotected pipe. Therefore, this shows that geotextile and stone cover protection still has a significant protective effect on the pipe under the combined action of wave and current load, and the applicability to the sea condition of wave and reversed current is the most obvious, making this approach the best choice for pipe protection measures.
4. Conclusions
In this paper, wave–current flume experiments were conducted to study the dynamic wave pressure and pore pressure around submarine pipelines with and without geotextile and stone cover under the influence of regular waves and regular wave–current combined action. The protective effects of geotextiles and stones were compared and analyzed. Based on the summary analysis of the experimental results, the following conclusions can be drawn:
- (1)
Compared with the unprotected pipeline, the dynamic wave pressure on the surface of the protected pipeline decreases when the wave and current are superimposed. The change is smaller when the wave height and the wave period become larger, which indicates that the protection effect of geotextiles and stones covering the pipeline is more significant when the wave height and wave period are larger and the water and current are superimposed.
- (2)
The pore pressure driven by wave (and current) load decreases continuously with the seabed depth profile, and the pore pressure amplitude in the seabed around the geotextile- and stone-covered pipeline is smaller than that around the unprotected pipeline. In addition, the protective effect of the geotextile and stone covering layer makes the effect of current on pore pressures below z = −0.12 m on the seabed surface small. Compared with the single wave load, the forward current can promote the wave propagation speed; the velocity of wave propagation is inhibited by the reverse current. As a result, the common current promotes pore pressure conduction through the depth of the seabed, enhancing the greater permeability of waves into the seabed compared to the opposite current. That is, when waves act in the same direction as ocean currents, pipelines are more vulnerable to potential instability on the seabed.
- (3)
Under the combined action of waves and current, the pore pressure amplitudes of the front, bottom, and back of the geotextile- and stone-covered protected pipeline are basically the same, and the pore pressure is much smaller than that of the unprotected pipeline. However, the amplitude of the pore pressure around the unprotected pipe varies greatly, especially when the wave current is acting in the same direction.
- (4)
The pore pressure amplitude increases with the increase in wave height and period. The presence of current will affect the wave profile and make the attenuation rate of vertical pore pressure change irregularly. The effect of the geotextile and stone covering reduces the pore pressure around the pipeline, and the protective effect is more obvious when the current superposition wave is larger and the wave period is longer.
In this study, the wave tests only consider the protective effect of geotextiles and stones covering a submarine pipeline under the action of regular waves and regular wave–current action. However, in a real marine environment, the effects of random waves and random current characteristics cannot be ignored. Therefore, it is necessary to further study the protection effect of geotextiles and stones covering a submarine pipeline under random wave–current conditions. In terms of submarine pipeline protection, it is necessary to increase the research on other pipeline protection measures, such as covering the pipeline surface with protective pads or rigid protective covers. In addition, this experiment only compares and measures wave-induced pore pressure around protected and unprotected pipelines, but the relationship between local erosion and pore pressure around geotextile- and stone-covered pipelines is not available in the literature. In addition, this paper only focuses on physical modeling and does not carry out numerical simulation. The effect of the geotextile- and stone-covered pipeline on seabed response and liquefaction potential under different seabed parameters, as well as regular spectra and random spectra, can be further studied by numerical simulation in the future.