Enhanced Control Strategies for Underactuated AUVs Using Backstepping Integral Sliding Mode Techniques for Ocean Current Challenges
Abstract
1. Introduction
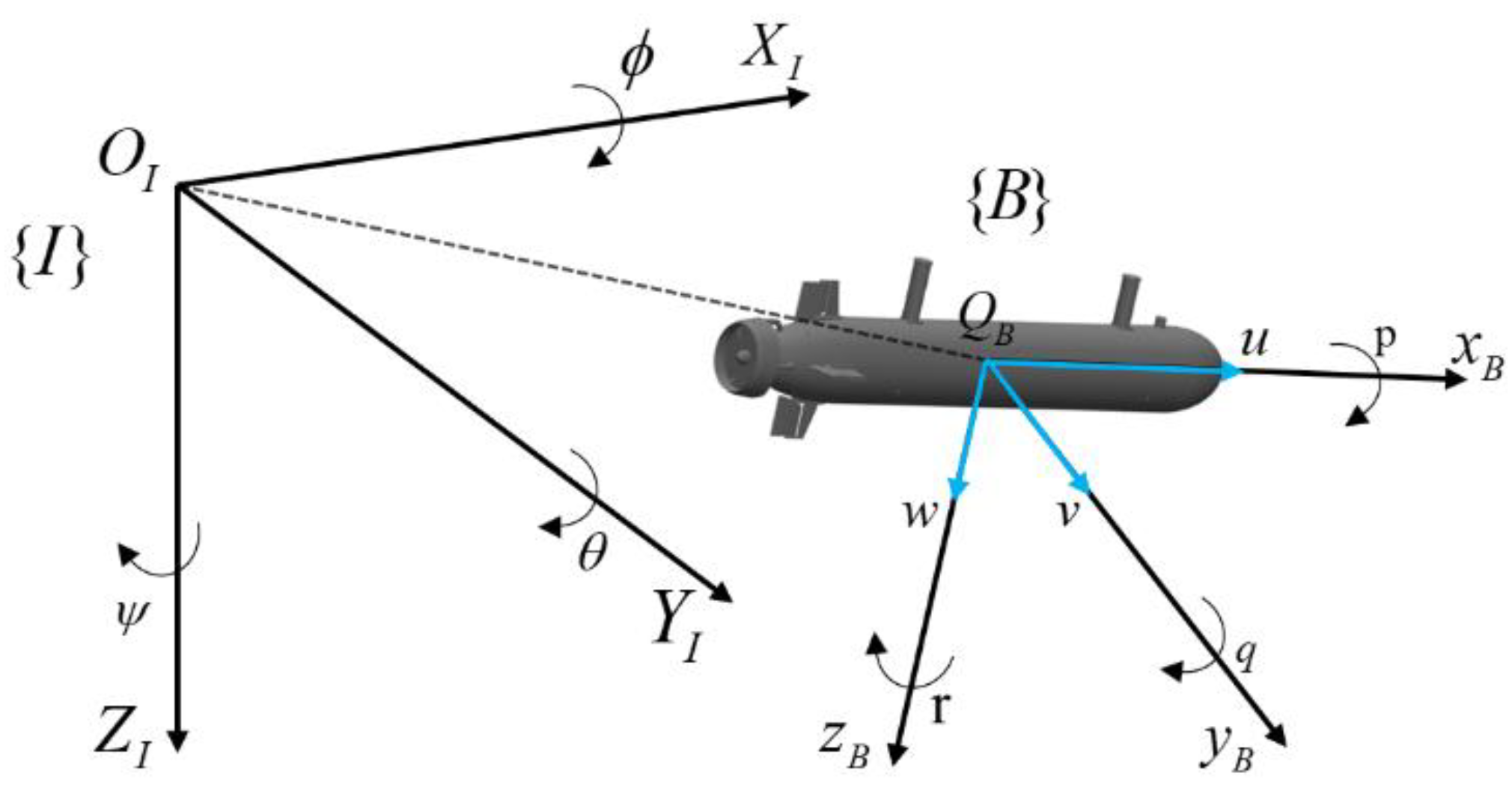
2. Preliminaries and AUV Modeling
2.1. Model Analysis and Simplification
2.2. Rudder Force Model
2.3. Ocean Current Disturbance Model
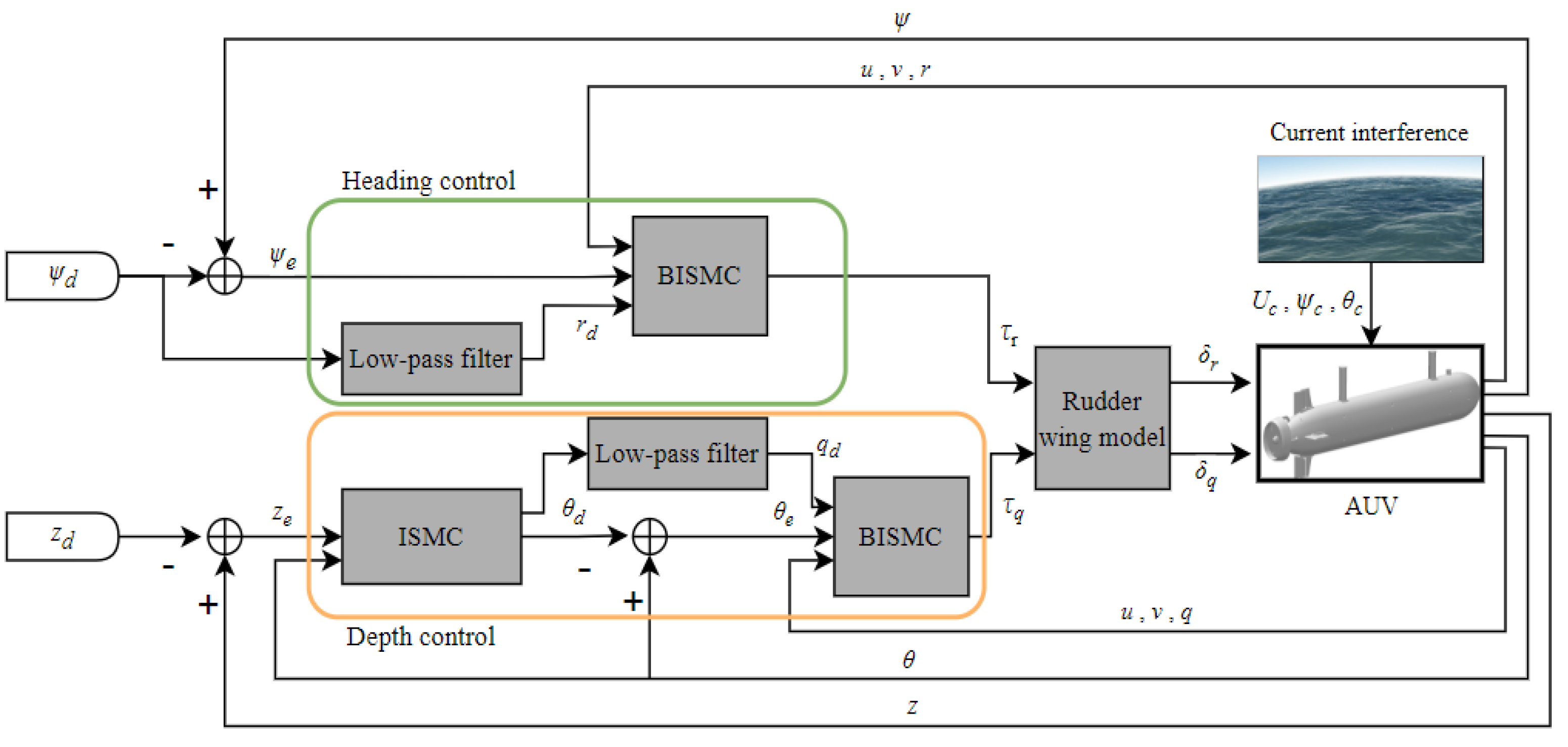
3. Backstepping Integral Sliding Mode Controller Design
3.1. Heading Controller Design
3.2. Depth Controller Design
3.3. Lyapunov Stability Verification
4. Simulation Verification
4.1. Parameters of the Underactuated AUV
4.2. Simulation Model Validation
4.3. Case Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Liu, J.; Yu, J.; Liu, D. Single Neural Network-Based Asymptotic Adaptive Control for an Autonomous Underwater Vehicle with Uncertain Dynamics. Ocean Eng. 2023, 286, 115553. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, K. Backstepping-Based Adaptive Control of Underactuated AUV Subject to Unknown Dynamics and Zero Tracking Errors. Ocean Eng. 2024, 302, 117640. [Google Scholar] [CrossRef]
- Min, F.; Yang, F.; Wang, G.; Ye, X. Research on the Heading Control of Underwater Vehicle Under Hover Condition. IEEE Access 2020, 8, 220908–220920. [Google Scholar] [CrossRef]
- Xia, Y.; Xu, K.; Li, Y.; Xu, G.; Xiang, X. Improved Line-of-Sight Trajectory Tracking Control of under-Actuated AUV Subjects to Ocean Currents and Input Saturation. Ocean Eng. 2019, 174, 14–30. [Google Scholar] [CrossRef]
- Liu, L.; Wang, D.; Peng, Z. ESO-Based Line-of-Sight Guidance Law for Path Following of Underactuated Marine Surface Vehicles With Exact Sideslip Compensation. IEEE J. Ocean. Eng. 2017, 42, 477–487. [Google Scholar] [CrossRef]
- Shen, C.; Shi, Y.; Buckham, B. Trajectory Tracking Control of an Autonomous Underwater Vehicle Using Lyapunov-Based Model Predictive Control. IEEE Trans. Ind. Electron. 2018, 65, 5796–5805. [Google Scholar] [CrossRef]
- Kim, J.; Joe, H.; Yu, S.; Lee, J.S.; Kim, M. Time-Delay Controller Design for Position Control of Autonomous Underwater Vehicle Under Disturbances. IEEE Trans. Ind. Electron. 2016, 63, 1052–1061. [Google Scholar] [CrossRef]
- Lin, Y.-H.; Yu, C.-M.; Wu, I.-C.; Wu, C.-Y. The Depth-Keeping Performance of Autonomous Underwater Vehicle Advancing in Waves Integrating the Diving Control System with the Adaptive Fuzzy Controller. Ocean Eng. 2023, 268, 113609. [Google Scholar] [CrossRef]
- Cervantes, I.; Alvarez-Ramirez, J. On the PID Tracking Control of Robot Manipulators. Syst. Control Lett. 2001, 42, 37–46. [Google Scholar] [CrossRef]
- Silva, G.J.; Datta, A.; Bhattacharyya, S.P. New Results on the Synthesis of PID Controllers. IEEE Trans. Autom. Control 2002, 47, 241–252. [Google Scholar] [CrossRef]
- Yao, X.; Meng, L.; Niu, X. LQR Pitch Control Strategy of AUVs Based on the Optimum of Sailing Resistance. Chin. J. Ship Res. 2017, 12, 111–119. Available online: http://www.ship-research.com/en/article/doi/10.3969/j.issn.1673-3185.2017.03.016?viewType=HTML (accessed on 17 June 2024).
- Al Makdah, A.A.R.; Daher, N.; Asmar, D.; Shammas, E. Three-Dimensional Trajectory Tracking of a Hybrid Autonomous Underwater Vehicle in the Presence of Underwater Current. Ocean Eng. 2019, 185, 115–132. [Google Scholar] [CrossRef]
- Repoulias, F.; Papadopoulos, E. Planar Trajectory Planning and Tracking Control Design for Underactuated AUVs. Ocean Eng. 2007, 34, 1650–1667. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Rawlings, J.B.; Rao, C.V.; Scokaert, P.O.M. Constrained Model Predictive Control: Stability and Optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Naeem, W.; Sutton, R.; Chudley, J. Model Predictive Control of an Autonomous Underwater Vehicle with a Fuzzy Objective Function Optimized Using a GA. IFAC Proc. Vol. 2004, 37, 433–438. [Google Scholar] [CrossRef]
- Habibnejad Korayem, M.; Ghobadi, N.; Fathollahi Dehkordi, S. Designing an Optimal Control Strategy for a Mobile Manipulator and Its Application by Considering the Effect of Uncertainties and Wheel Slipping. Optim. Control Appl. Methods 2021, 42, 1487–1511. [Google Scholar] [CrossRef]
- Monnet, D.; Ninin, J.; Clement, B. A Global Optimization Approach to H∞ Synthesis with Parametric Uncertainties Applied to AUV control. IFAC-PapersOnLine 2017, 50, 3953–3958. [Google Scholar] [CrossRef]
- Joe, H.; Kim, M.; Yu, S. Second-Order Sliding-Mode Controller for Autonomous Underwater Vehicle in the Presence of Unknown Disturbances. Nonlinear Dyn. 2014, 78, 183–196. [Google Scholar] [CrossRef]
- Konar, S.; Patil, M.D.; Vyawahare, V.A. Design of a Fractional Order Sliding Mode Controller for Depth Control of AUV. In Proceedings of the 2018 Second International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 14–15 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1342–1345. [Google Scholar]
- Yu, H. Globally Finite-Time Stable Three-Dimensional Trajectory-Tracking Control of Underactuated UUVs. Ocean Eng. 2019, 189, 106329. [Google Scholar] [CrossRef]
- Nhut Thanh, P.N.; Tam, P.M.; Huy Anh, H.P. A New Approach for Three-Dimensional Trajectory Tracking Control of under-Actuated AUVs with Model Uncertainties. Ocean Eng. 2021, 228, 108951. [Google Scholar] [CrossRef]
- Dai, X.; Xu, H.; Ma, H.; Ding, J.; Lai, Q. Dual Closed Loop AUV Trajectory Tracking Control Based on Finite Time and State Observer. Math. Biosci. Eng. 2022, 19, 11086–11113. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Liu, J.; Yu, J. Adaptive Asymptotic Tracking Control for Autonomous Underwater Vehicles with Non-Vanishing Uncertainties and Input Saturation. Ocean Eng. 2023, 276, 114280. [Google Scholar] [CrossRef]
- Wu, J.; Liu, J.; Chen, K. Backstepping Sliding Mode Control for Three-Dimensional Trajectory Tracking of AUV under Time-Varying Disturbance. Ship Sci. Technol. 2022, 44, 82–87. [Google Scholar]
- Qiao, L.; Zhang, W. Double-Loop Integral Terminal Sliding Mode Tracking Control for UUVs with Adaptive Dynamic Compensation of Uncertainties and Disturbances. IEEE J. Ocean Eng. 2019, 44, 29–53. [Google Scholar] [CrossRef]
- Van, M. Adaptive Neural Integral Sliding-Mode Control for Tracking Control of Fully Actuated Uncertain Surface Vessels. Int. J. Robust Nonlinear Control 2019, 29, 1537–1557. [Google Scholar] [CrossRef]
- Yu, C.; Wang, R.; Zhang, X.; Li, Y. Experimental and Numerical Study on Underwater Radiated Noise of AUV. Ocean Eng. 2020, 201, 107111. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, Z.; Wan, L. Robust Prescribed-Time ESO-Based Practical Predefined-Time SMC for Benthic AUV Trajectory-Tracking Control with Uncertainties and Environment Disturbance. J. Mar. Sci. Eng. 2024, 12, 1014. [Google Scholar] [CrossRef]
- Fang, K.; Fang, H.; Zhang, J.; Yao, J.; Li, J. Neural Adaptive Output Feedback Tracking Control of Underactuated AUVs. Ocean Eng. 2021, 234, 109211. [Google Scholar] [CrossRef]
- Ioannou, P.A.; Sun, J. Robust Adaptive Control.; PTR Prentice-Hall: New Jersey, NJ, USA, 1996; pp. 75–76. [Google Scholar]














| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 1000 (kg/m3) | −21.01 | ||
| 11 (kg) | 3.834 | ||
| 1.2 (m) | −26.08 | ||
| 106.0 (N) | −96.22 | ||
| 107.9 (N) | −41.9 | ||
| 0.016 (kg · m2) | −21.01 | ||
| 0.8 (kg · m2) | −3.834 | ||
| 0.8 (kg · m2) | −2.918 | ||
| 0.0296 | −112.4 | ||
| −0.683 | 2.107 | ||
| −1.428 | 1.591 | ||
| −26.08 | −1.325 | ||
| −1.279 | −2.918 | ||
| −26.08 | −56.21 | ||
| −1.279 | −2.107 | ||
| −26.08 | −1.591 | ||
| −96.22 | −1.325 | ||
| −0.419 |
| BC | SMC | BISMC | |||
|---|---|---|---|---|---|
| Parameter | Value | Parameter | Value | Parameter | Value |
| k1 | 2 | c1 | 1 | k1 | 2 |
| k2 | 10 | E | 6 | τ | 0.025 |
| P | 2 | c1 | 0.5 | ||
| E | 6 | ||||
| P | 2 | ||||
| M | 5 | ||||
| BC | SMC | ISMC | BISMC | ||||
|---|---|---|---|---|---|---|---|
| Parameter | Value | Parameter | Value | Parameter | Value | Parameter | Value |
| k1 | 1.5 | c1 | 2 | c1 | 1 | k1 | 1.5 |
| k2 | 6 | c2 | 4 | E1 | 10 | τ | 0.025 |
| k3 | 2 | E | 10 | P1 | 3 | c2 | 0.5 |
| P | 3 | M1 | 5 | E2 | 10 | ||
| P2 | 3 | ||||||
| M2 | 5 | ||||||
| Performance Metrics | BC | SMC | BISMC | BC | SMC | BISMC | BC | SMC | BISMC |
|---|---|---|---|---|---|---|---|---|---|
| IAE | |||||||||
| ψe | 248.5 | 239.7 | 210 | 287.5 | 248 | 210 | 286.1 | 248.1 | 210 |
| ze | 246.5 | 239.2 | 233.9 | 394.8 | 369.6 | 266.1 | 395.3 | 370.8 | 251.7 |
| AVE | |||||||||
| ψe | 2.07 | 1.998 | 1.75 | 2.395 | 2.067 | 1.75 | 2.384 | 2.068 | 1.75 |
| ze | 1.232 | 1.196 | 1.17 | 1.974 | 1.848 | 1.33 | 1.977 | 1.854 | 1.259 |
| ITAE | |||||||||
| ψe (104) | 1.682 | 1.623 | 1.412 | 2.136 | 1.736 | 1.412 | 2.128 | 1.736 | 1.412 |
| ze (104) | 2.593 | 2.493 | 2.464 | 4.325 | 4.002 | 2.795 | 4.353 | 4.040 | 2.661 |
| Performance Metrics | BC | SMC | BISMC |
|---|---|---|---|
| IAE | |||
| ψe | 249.7 | 239.6 | 211.7 |
| ze | 275 | 270.5 | 269.4 |
| AVE | |||
| ψe | 2.081 | 1.997 | 1.765 |
| ze | 1.375 | 1.353 | 1.348 |
| ITAE | |||
| ψe (104) | 1.706 | 1.621 | 1.428 |
| ze (104) | 2.909 | 2.852 | 2.845 |
| ASSE | |||
| ψe | 0.584 | 0.098 | 0.129 |
| ze | 0.518 | 0.114 | 0.199 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Q.; Yuan, J.; Dong, Z.; Chai, Z.; Wan, L. Enhanced Control Strategies for Underactuated AUVs Using Backstepping Integral Sliding Mode Techniques for Ocean Current Challenges. J. Mar. Sci. Eng. 2024, 12, 2201. https://doi.org/10.3390/jmse12122201
Chen Q, Yuan J, Dong Z, Chai Z, Wan L. Enhanced Control Strategies for Underactuated AUVs Using Backstepping Integral Sliding Mode Techniques for Ocean Current Challenges. Journal of Marine Science and Engineering. 2024; 12(12):2201. https://doi.org/10.3390/jmse12122201
Chicago/Turabian StyleChen, Qingdong, Jianping Yuan, Zhihui Dong, Zhuohui Chai, and Lei Wan. 2024. "Enhanced Control Strategies for Underactuated AUVs Using Backstepping Integral Sliding Mode Techniques for Ocean Current Challenges" Journal of Marine Science and Engineering 12, no. 12: 2201. https://doi.org/10.3390/jmse12122201
APA StyleChen, Q., Yuan, J., Dong, Z., Chai, Z., & Wan, L. (2024). Enhanced Control Strategies for Underactuated AUVs Using Backstepping Integral Sliding Mode Techniques for Ocean Current Challenges. Journal of Marine Science and Engineering, 12(12), 2201. https://doi.org/10.3390/jmse12122201





