Dynamic Response and Fatigue Analysis of a New Marine Gravitational Energy Storage System Under Wave Loads
Abstract
:1. Introduction
2. Materials and Methods
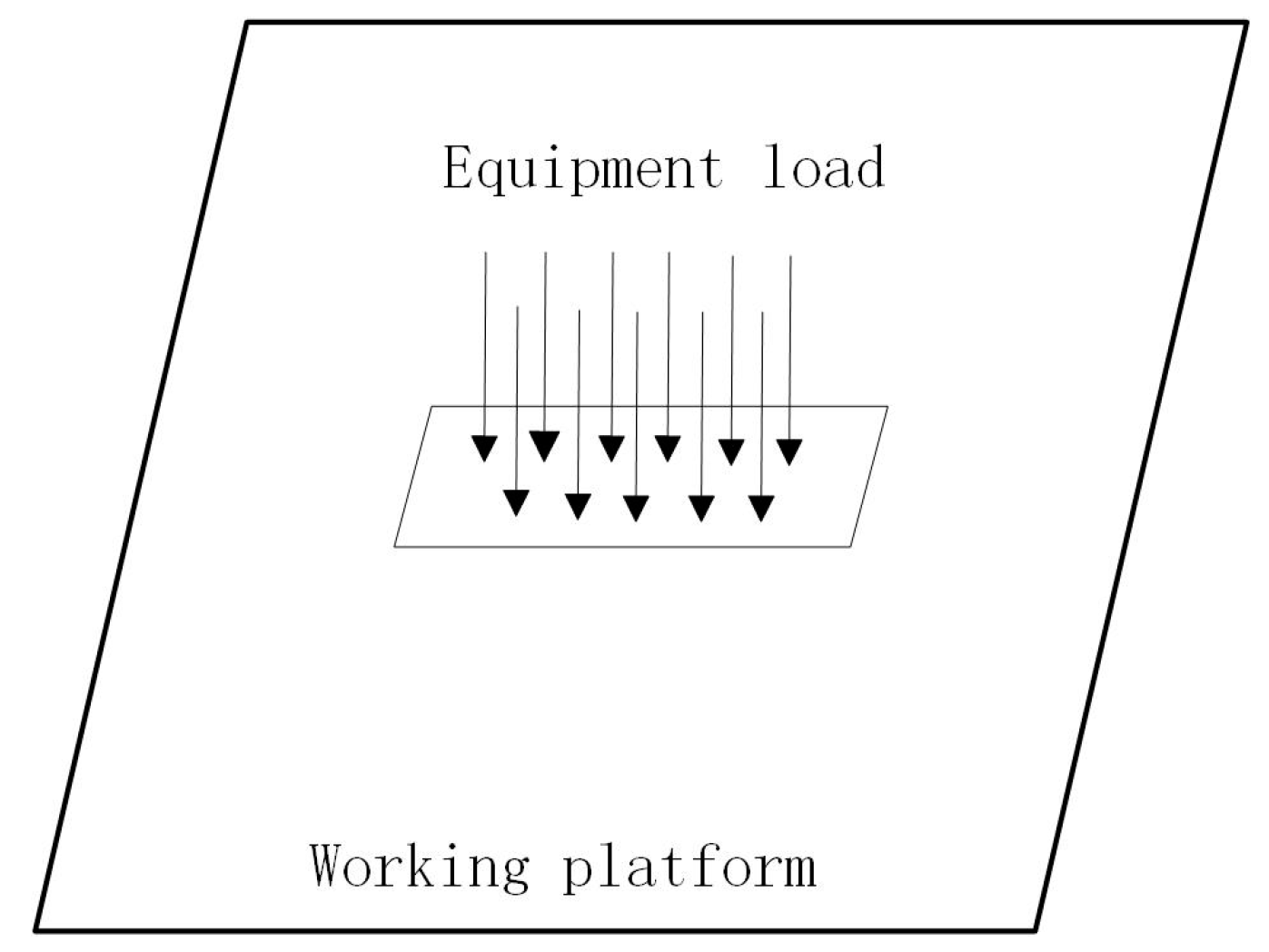
2.1. Basic Principles of Gravitational Energy Storage
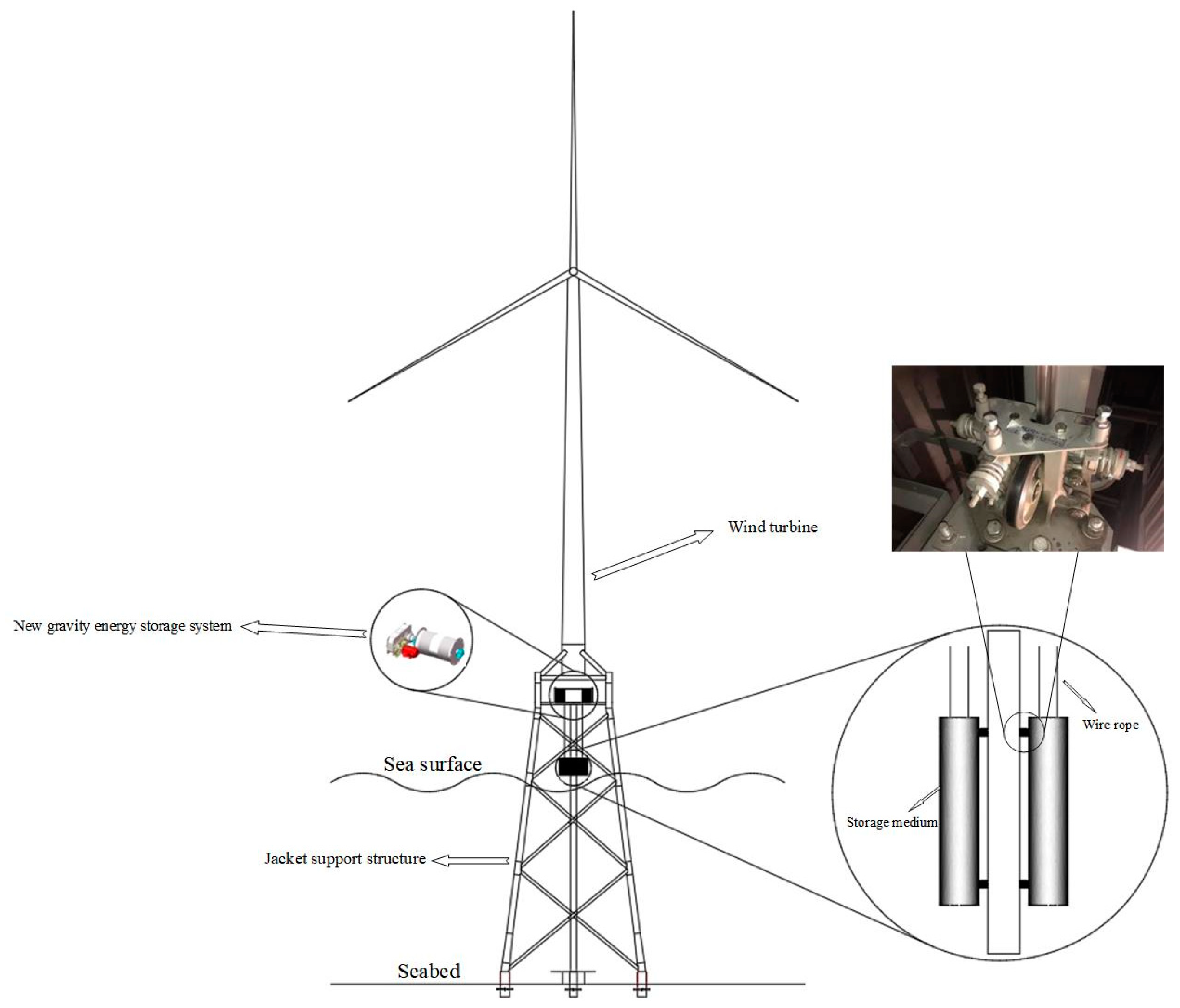
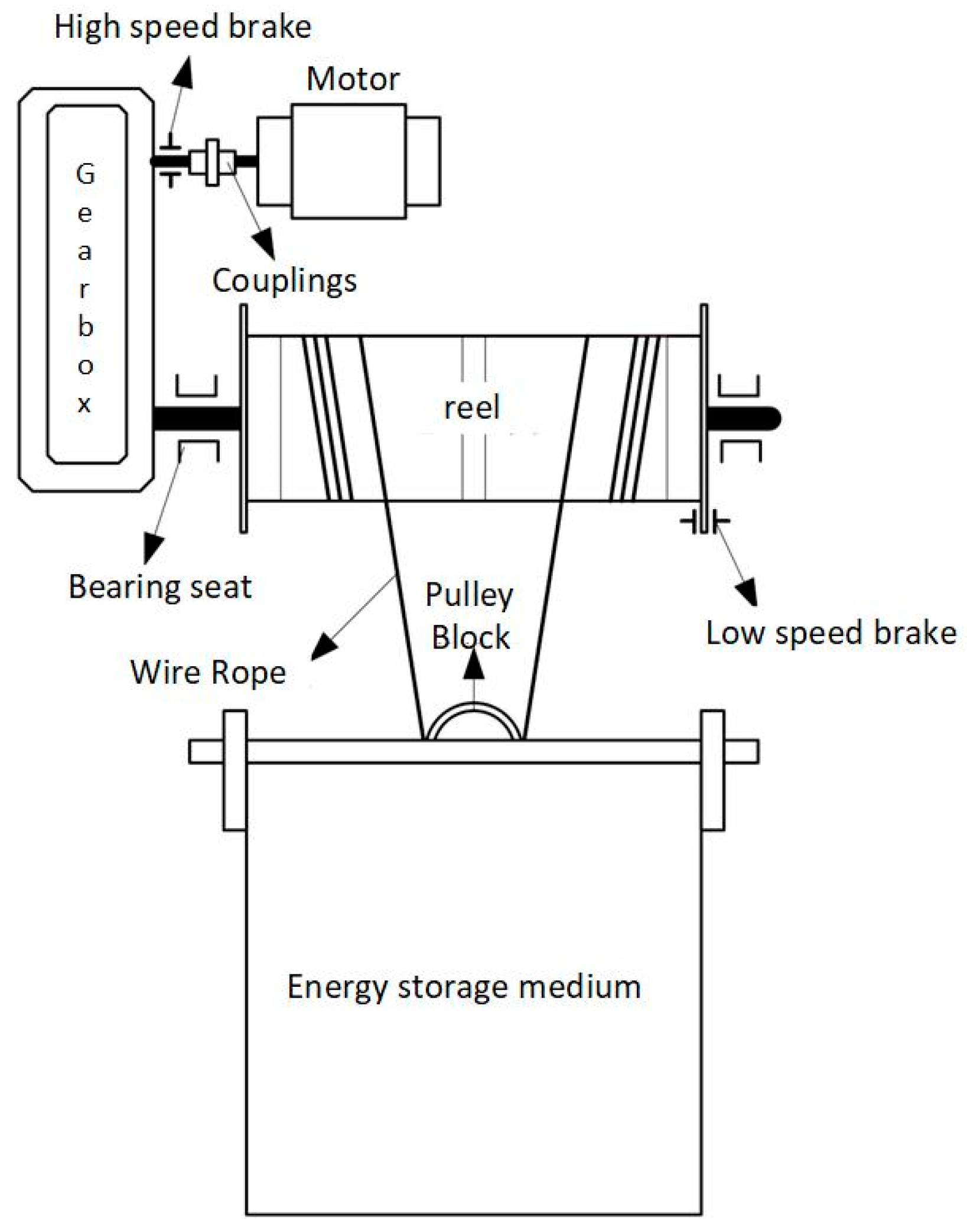
2.2. Design of a New Marine Gravitational Energy Storage System
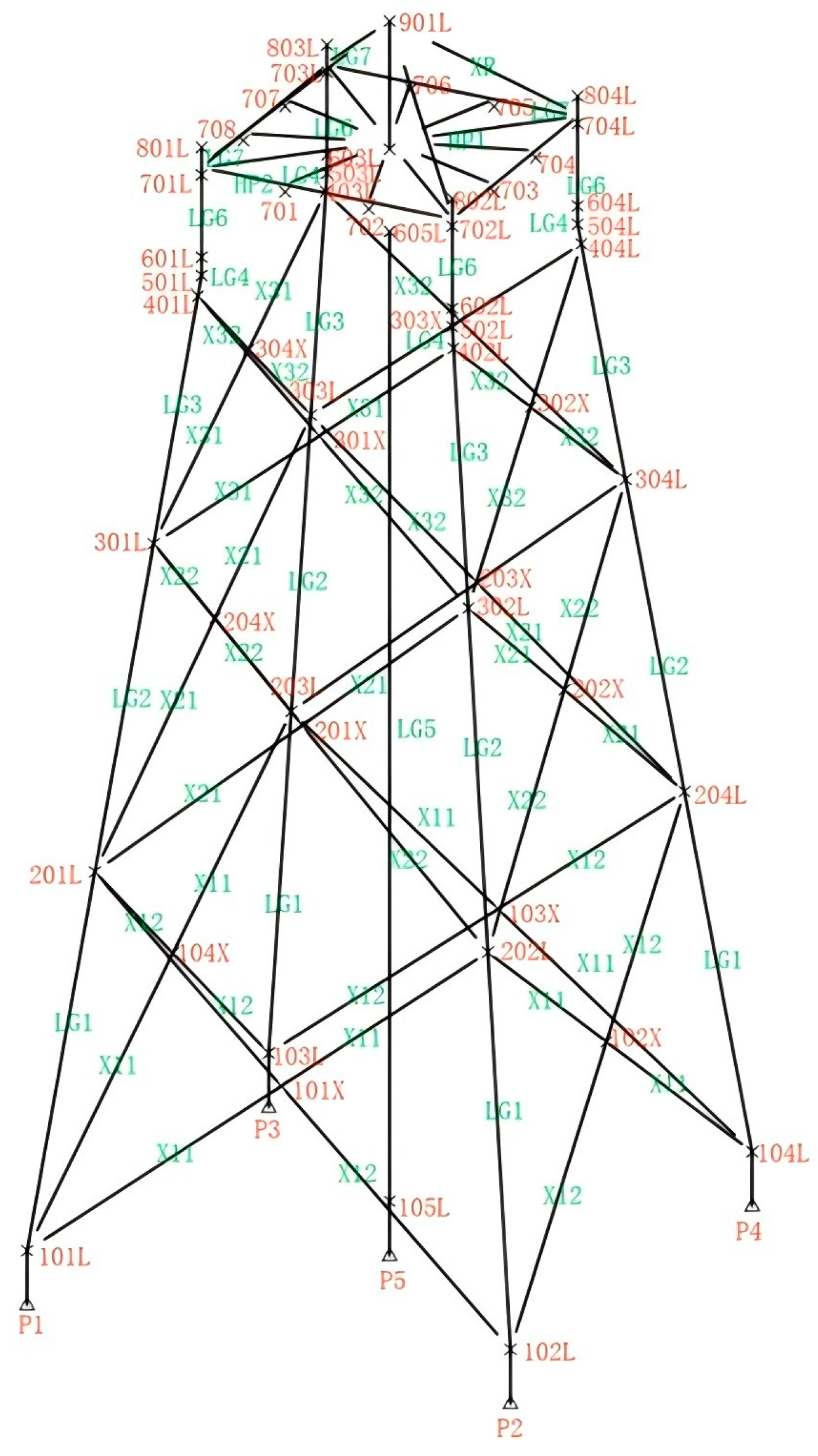
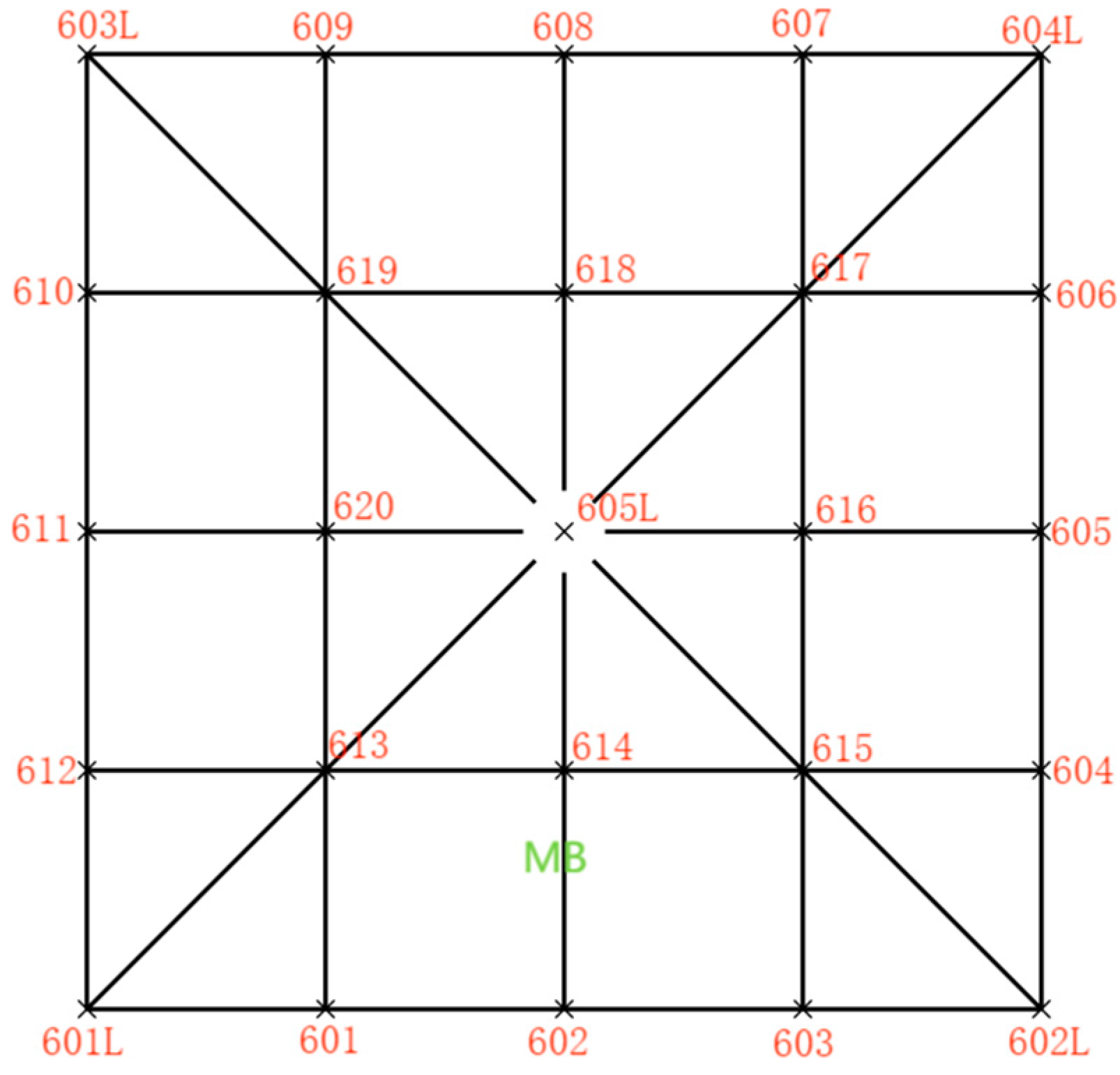
2.3. Design and Establishment of the Model
2.4. Environmental Parameters
2.4.1. Soil Parameters
2.4.2. Marine Environmental Parameters
2.4.3. Parameters of Upper Wind Turbine
- (1)
- Basic Parameters of Wind Turbine
- (2)
- Parameters of wind turbine tower
- (3)
- Peak load of wind turbine
3. Numerical Simulation Analysis
3.1. Static Analysis
3.1.1. Analysis Method
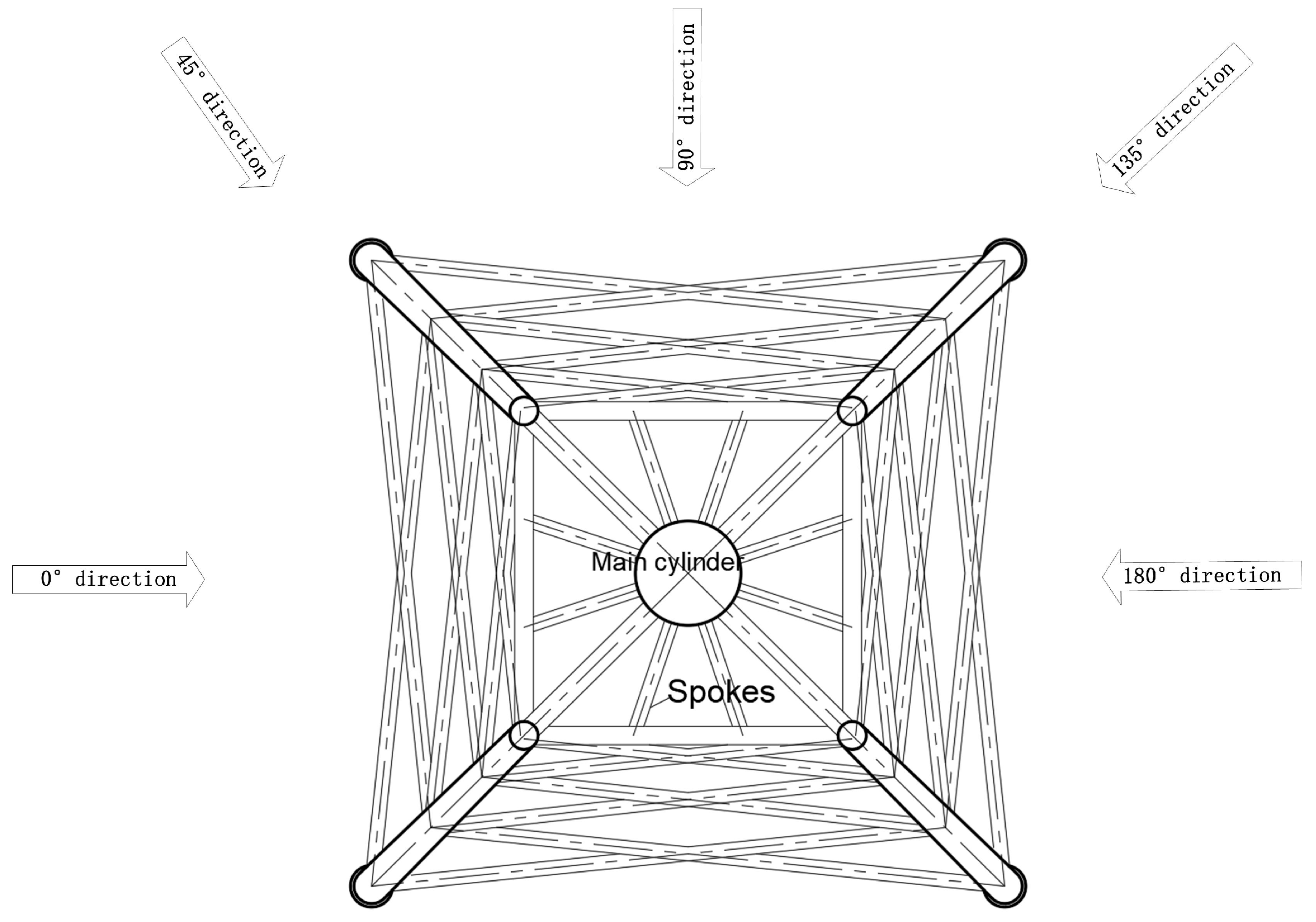
3.1.2. Load Conditions and Combinations
3.1.3. Static Analysis Results
- Calibration of Structural Strength
- 2.
- Calibration of bearing capacity of pile foundation
- 3.
- Calibration of structural deformation
3.2. Modal Analysis
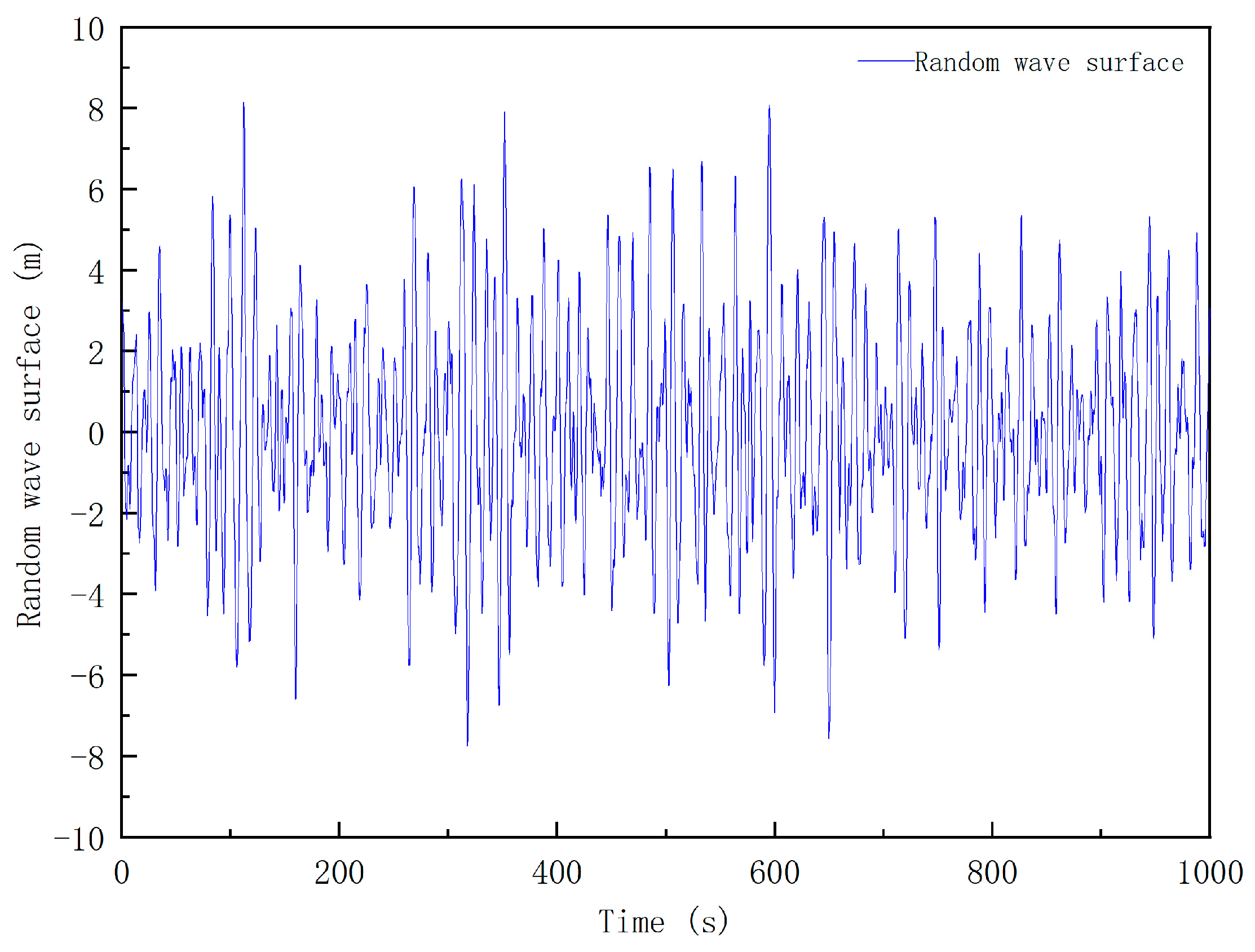
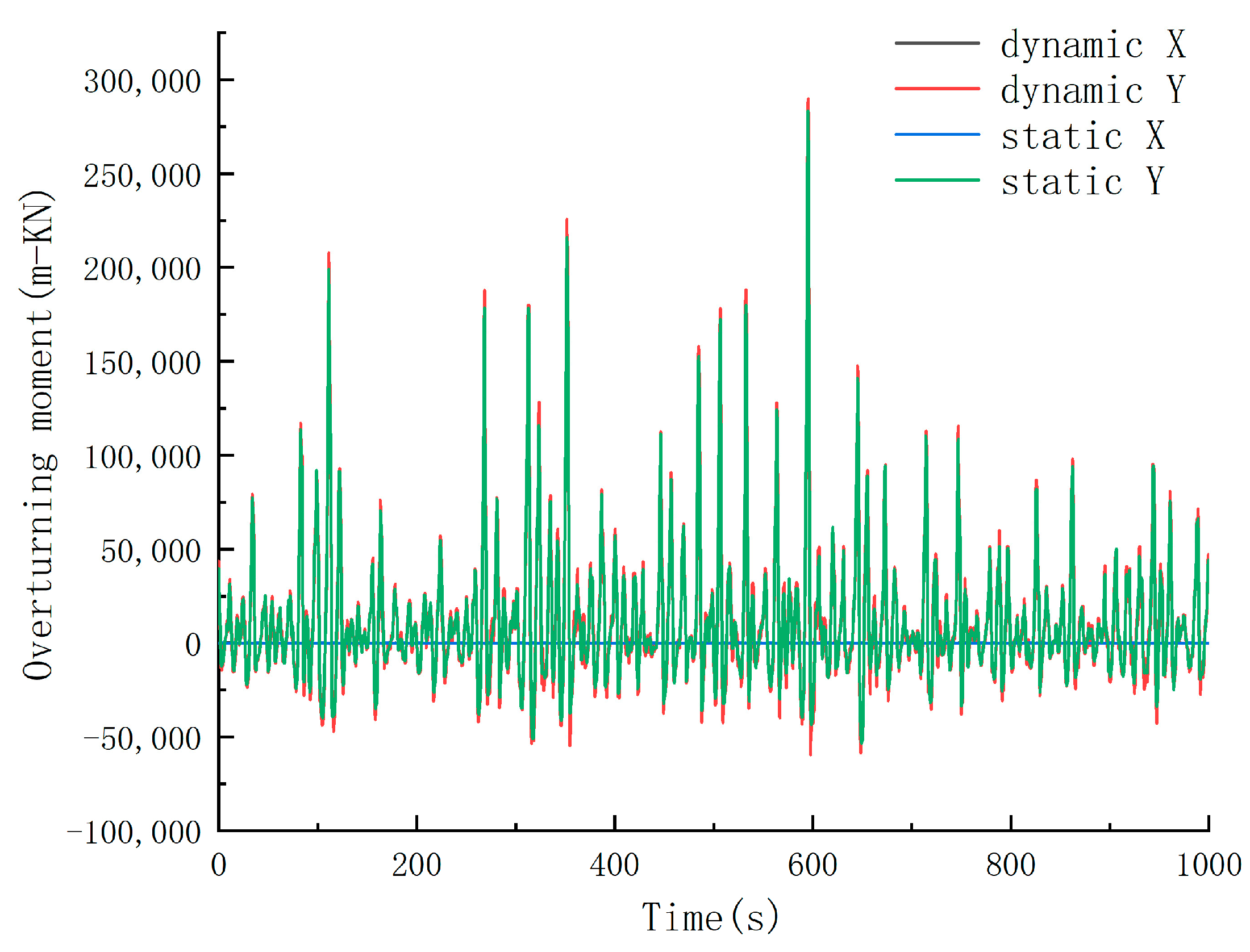
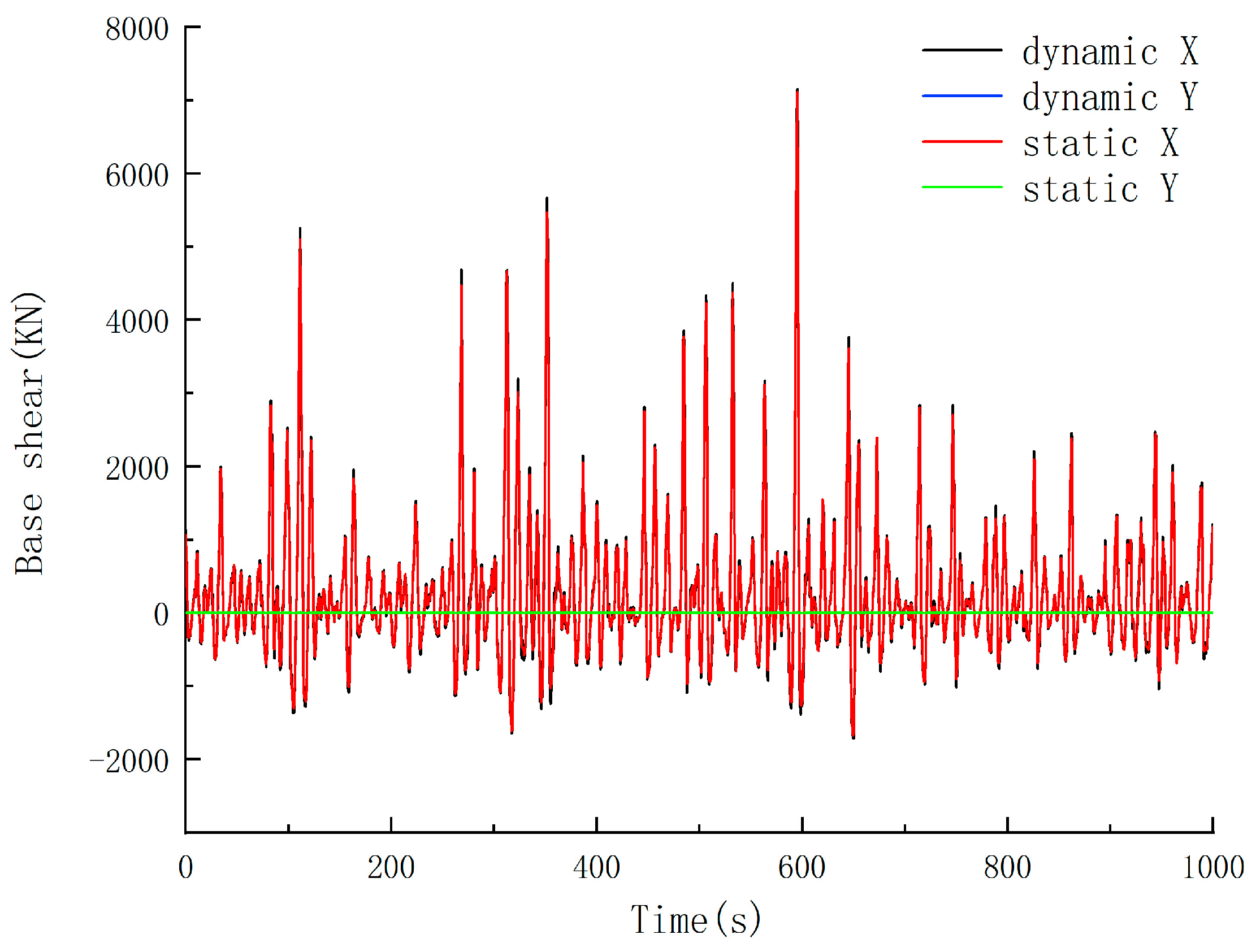
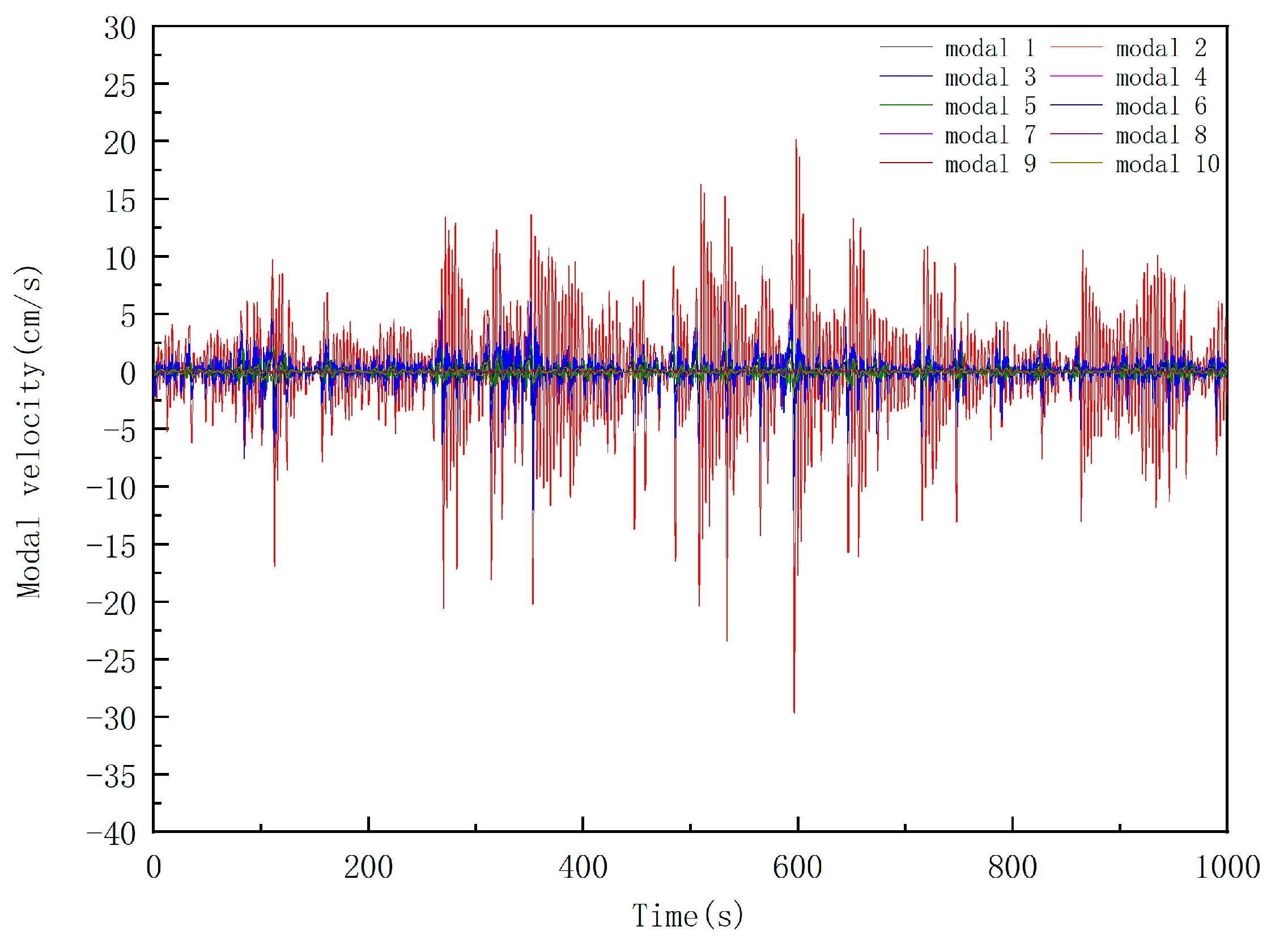
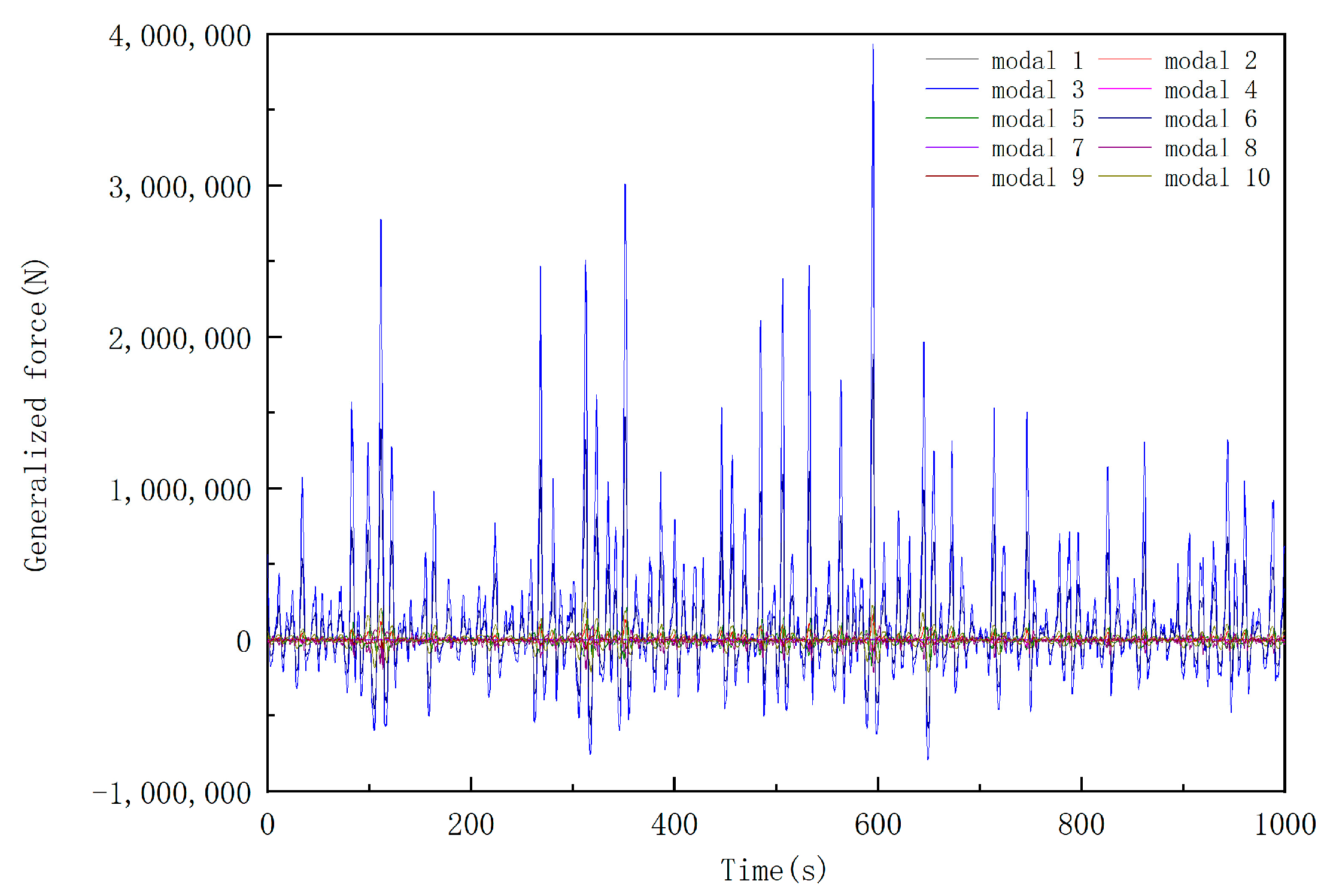
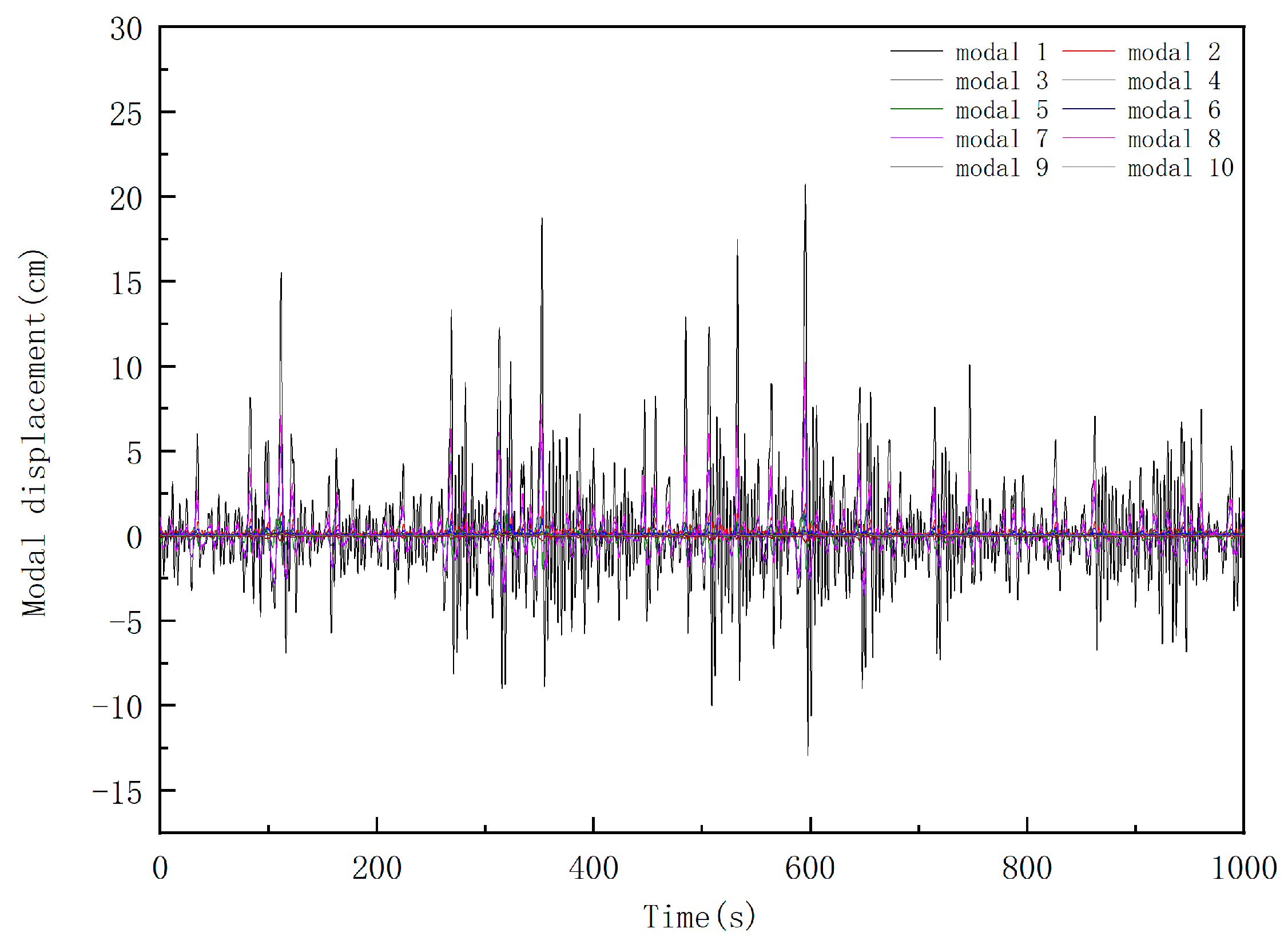
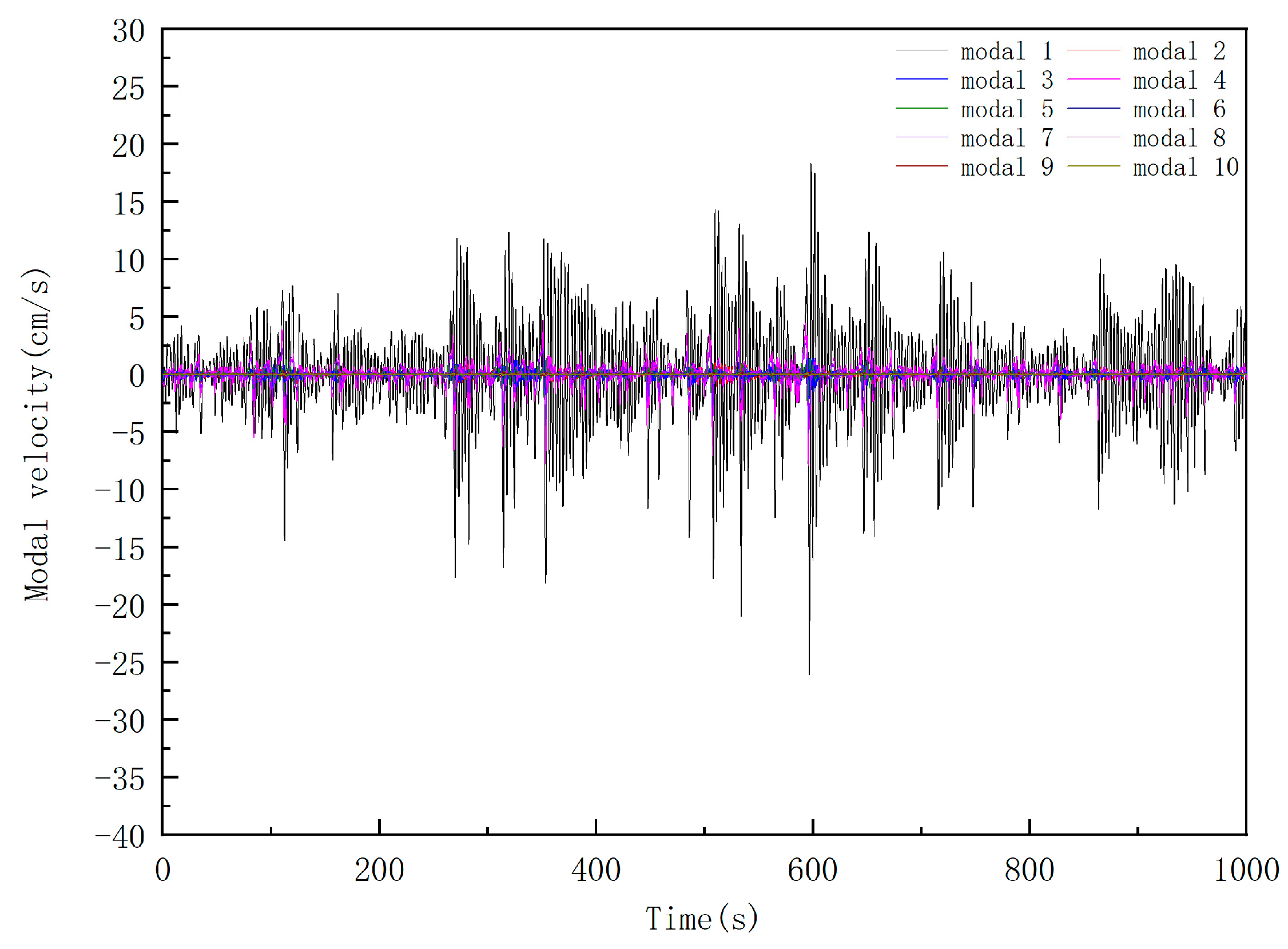
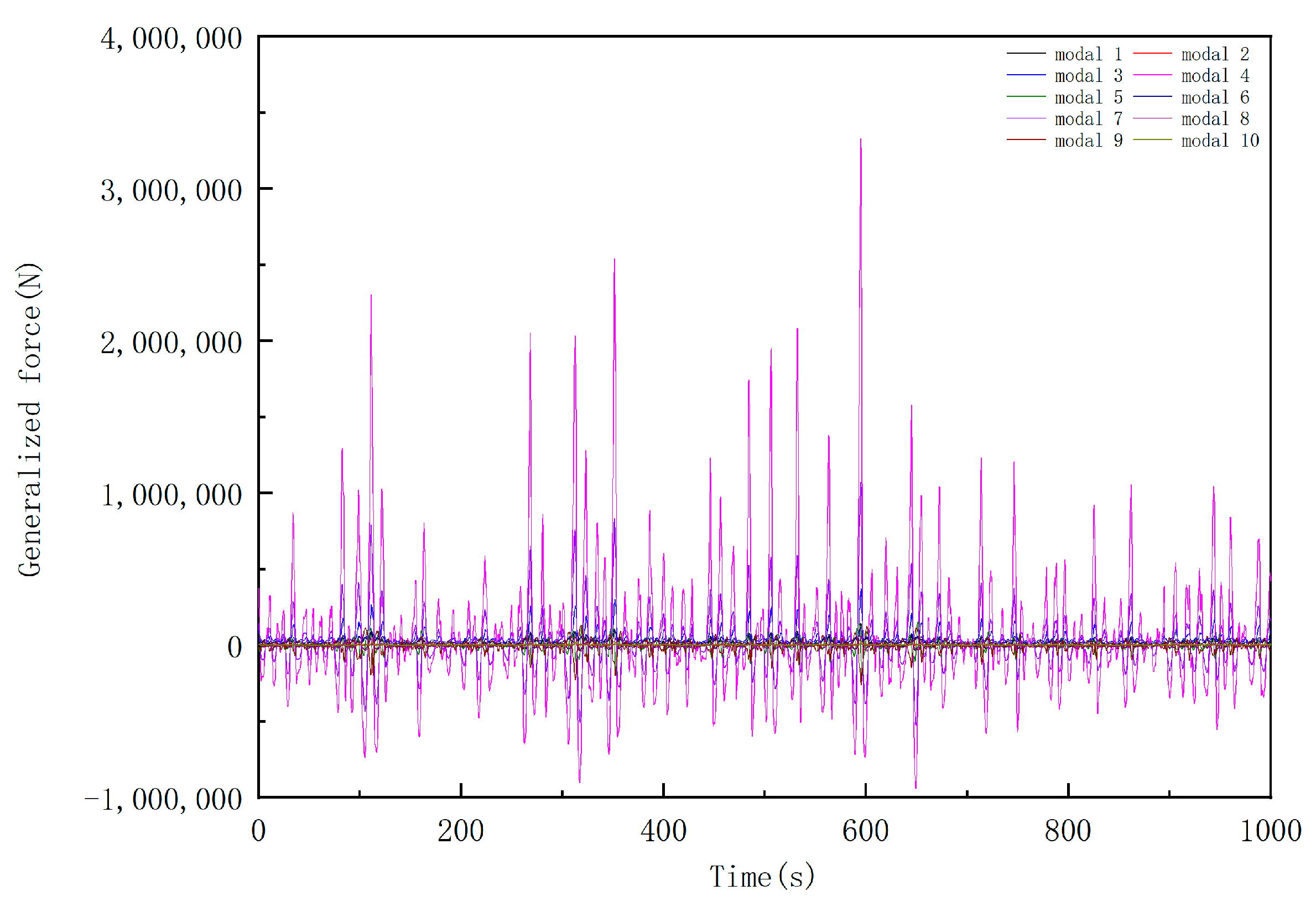
3.3. Dynamic Response Analysis of Random Waves
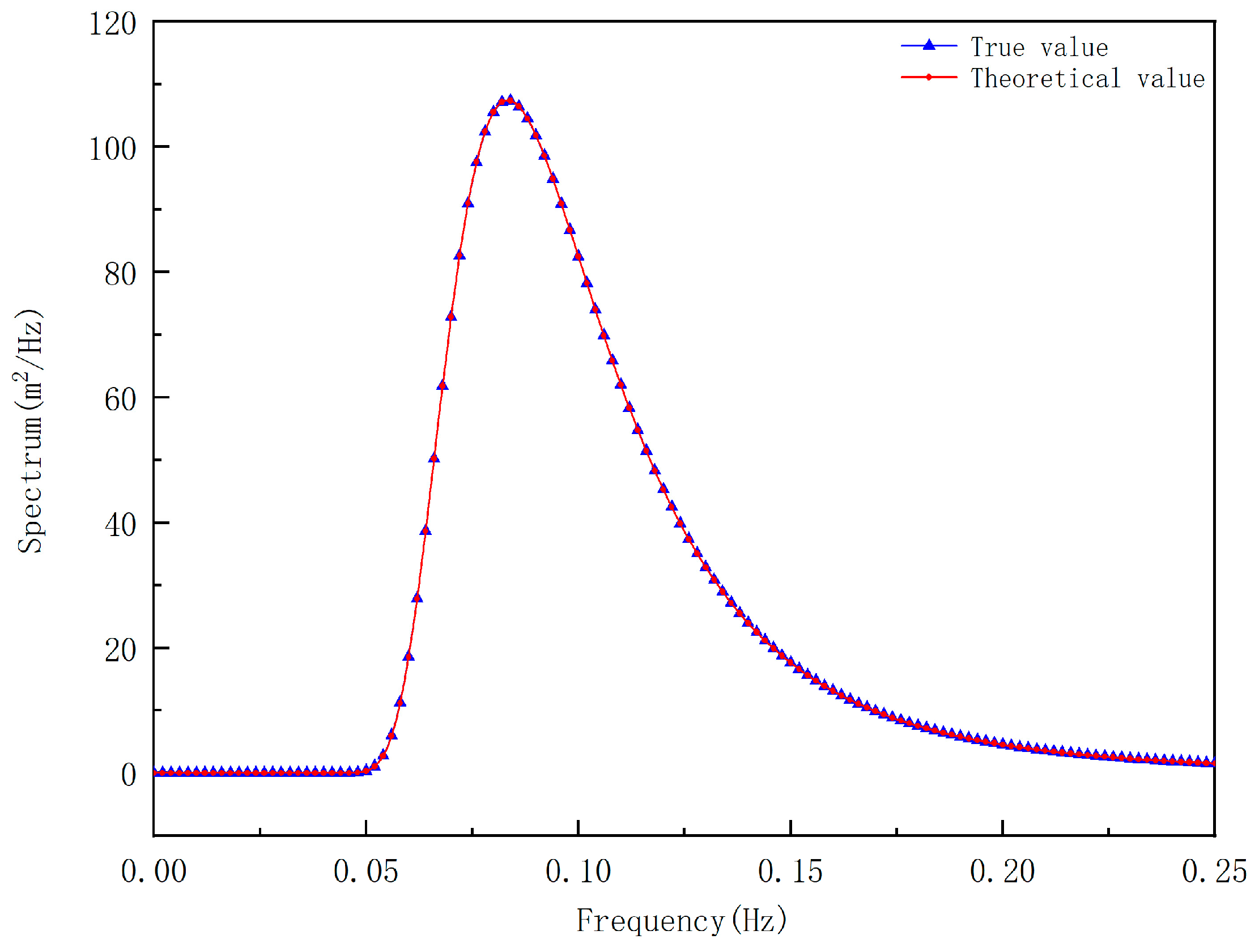
3.4. Wave Spectra and Fatigue Analysis
3.4.1. Wave Conditions
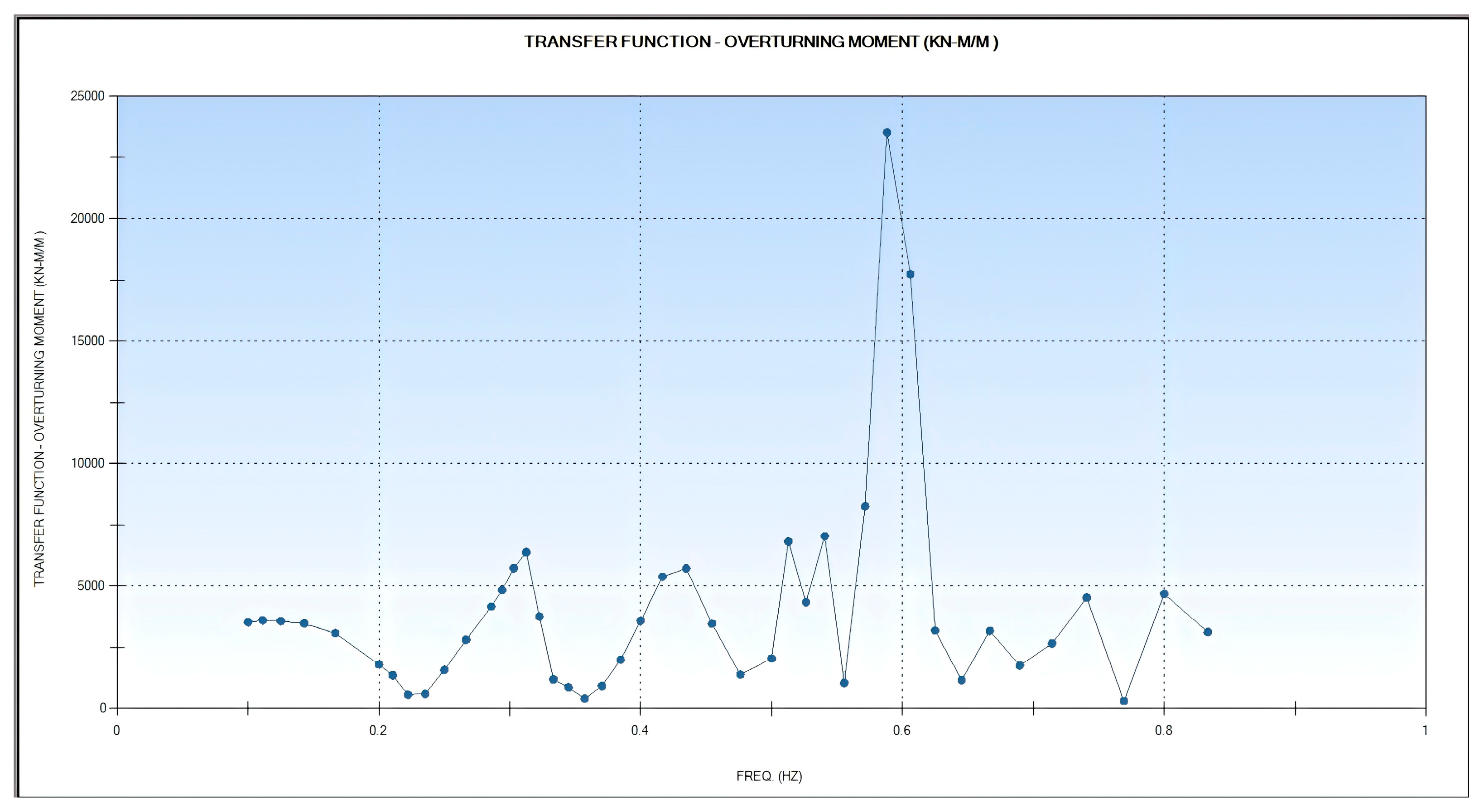
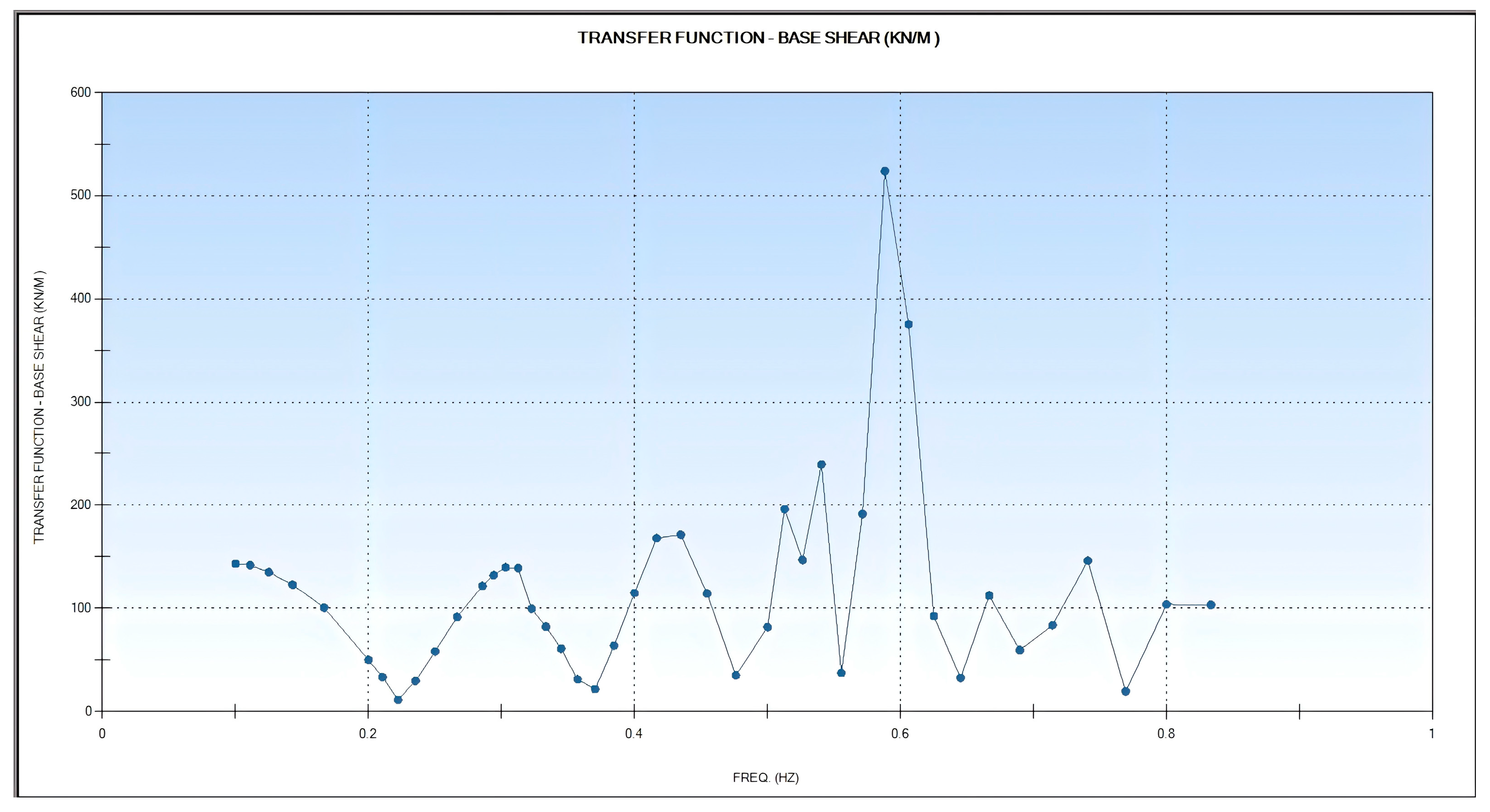
3.4.2. Calculation of Transfer Function
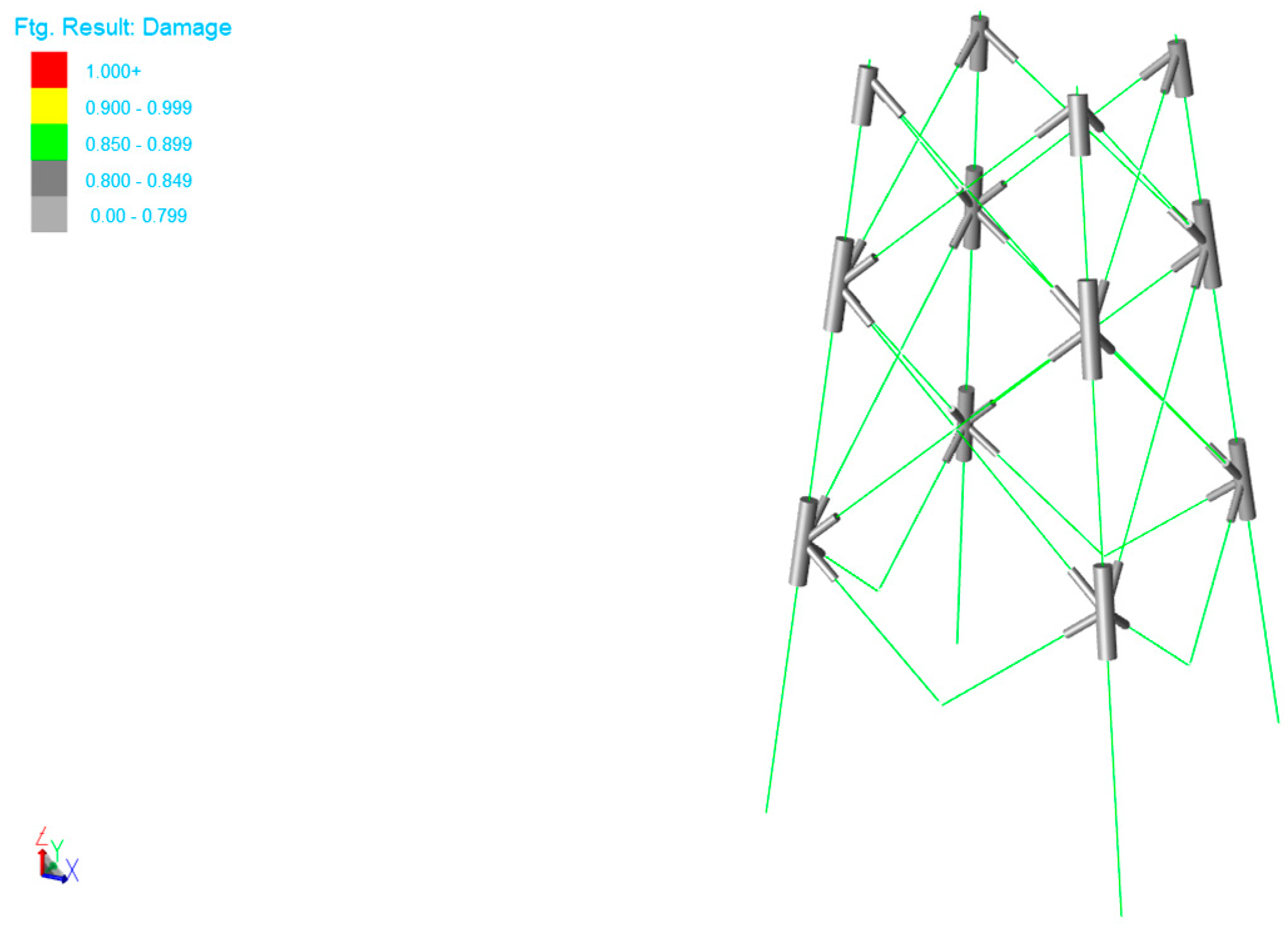
3.4.3. Fatigue Analysis Results
4. Conclusions
- In the static analysis, all structural UC values meet the requirements. Among them, the member bars with larger UC values are mainly those that connect the main conductor pipe and the main cylinder.
- In the modal analysis, the first- and second-order natural frequencies of the support structure are not within the hazard range and meet the safety requirements.
- In the analysis of random wave dynamic response, it is concluded that the first- and fourth-order modes are the greatest contributor to the dynamic response.
- In the fatigue analysis, all nodes are within a reasonable range, in which the damage values of 301L, 302L, 303L, and 304L are generally greater than those of other nodes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.; Carriveau, R.; Ting, D.S.K.; Xiong, W.; Wang, Z. A review of marine renewable energy storage. Int. J. Energy Res. 2019, 43, 6108–6150. [Google Scholar] [CrossRef]
- Amir, M.; Deshmukh, R.G.; Khalid, H.M.; Said, Z.; Raza, A.; Muyeen, S.; Nizami, A.-S.; Elavarasan, R.M.; Saidur, R.; Sopian, K. Energy storage technologies: An integrated survey of developments, global economical/environmental effects, optimal scheduling model, and sustainable adaption policies. J. Energy Storage 2023, 72, 108694. [Google Scholar] [CrossRef]
- Rekioua, D. Energy storage systems for photovoltaic and wind systems: A review. Energies 2023, 16, 3893. [Google Scholar] [CrossRef]
- Berrada, A. Financial and economic modeling of large-scale gravity energy storage system. Renew. Energy 2022, 192, 405–419. [Google Scholar] [CrossRef]
- Tong, W.; Lu, Z.; Sun, J.; Zhao, G.; Han, M.; Xu, J. Solid gravity energy storage technology: Classification and comparison. Energy Rep. 2022, 8, 926–934. [Google Scholar] [CrossRef]
- Tong, W.; Lu, Z.; Chen, W.; Han, M.; Zhao, G.; Wang, X.; Deng, Z. Solid gravity energy storage: A review. J. Energy Storage 2022, 53, 105226. [Google Scholar] [CrossRef]
- Botha, C.; Kamper, M. Capability study of dry gravity energy storage. J. Energy Storage 2019, 23, 159–174. [Google Scholar] [CrossRef]
- Du, Y.M.; Kong, D.Q.; Wang, S.L.; Zhu, B. Fatigue analysis of jacket foundations for offshore wind turbines. Rock Soil Mech. 2024, 44, 8. [Google Scholar]
- Zhu, R.H.; Tian, Z.; Long, Z. Jacket Foundation Design for 200 MW offshore Demonstration Wind Farm Project of Zhuhai Guishan. Wind 2013, 9, 94–98. [Google Scholar]
- Lavassani, S.H.H.; Gavgani, S.A.M.; Doroudi, R. Optimal control of jacket platforms vibrations under the simultaneous effect of waves and earthquakes considering fluid-structure interaction. Ocean Eng. 2023, 280, 114593. [Google Scholar] [CrossRef]
- Othman, N.A.; Mohd, M.H. Response of the offshore jacket platform at its ultimate strength under operating and extreme loads: A Malaysian waters case study. Ships Offshore Struct. 2024, 1–22. [Google Scholar] [CrossRef]
- Sui, H.; Zhang, J.; Liu, F.; Ma, Z.; Gu, C.; Qiu, H.; Wu, R.; Song, H.; Song, H. Dynamic response analysis and vibration reduction of a 10-MW jacket offshore wind turbines under the combined wind and ice loads. Ocean Eng. 2024, 303, 117553. [Google Scholar] [CrossRef]
- Hunt, J.D.; Zakeri, B.; Jurasz, J.; Tong, W.; Dąbek, P.B.; Brandão, R.; Patro, E.R.; Đurin, B.; Filho, W.L.; Wada, Y.; et al. Underground gravity energy storage: A solution for long-term energy storage. Energies 2023, 16, 825. [Google Scholar] [CrossRef]
- Tong, W.; Lu, Z.; Zhao, H.; Han, M.; Zhao, G.; Hunt, J.D. The structure and control strategies of hybrid solid gravity energy storage system. J. Energy Storage 2023, 67, 107570. [Google Scholar] [CrossRef]
- Hou, H.; Xu, T.; Wu, X.; Wang, H.; Tang, A.; Chen, Y. Optimal capacity configuration of the wind-photovoltaic-storage hybrid power system based on gravity energy storage system. Appl. Energy 2020, 271, 115052. [Google Scholar] [CrossRef]
- Ameur, A.; Berrada, A.; Emrani, A. Dynamic forecasting model of a hybrid photovoltaic/gravity energy storage system for residential applications. Energy Build. 2022, 271, 112325. [Google Scholar] [CrossRef]
- Botha, C.D.; Kamper, M.J. Linear electric machine-based gravity energy storage for wind farm integration. In Proceedings of the 2020 International SAUPEC/RobMech/PRASA Conference, Cape Town, South Africa, 29–31 January 2020; pp. 1–6. [Google Scholar]
- Yi, C.; Wang, Z.; Zhang, G.; Su, Y. Design and Analysis of a Novel offshore Gravity Energy Storage Support Structure Based Wind Power Jacket Foundation. Smart Syst. Green Energy 2024, 6, 1–9. [Google Scholar]
- Bauduin, C.; Bakker, K.; Frank, R. Use of finite element methods in geotechnical ultimate limit state design. In Proceedings of the 16th International Conference on Soil Mechanics and Geotechnical Engineering, Osaka, Japan, 12–16 September 2005; pp. 2775–2779. [Google Scholar]
- Wang, S.; Moan, T. Methodology of load effect analysis and ultimate limit state design of semi-submersible hulls of floating wind turbines: With a focus on floater column design. Mar. Struct. 2024, 93, 103526. [Google Scholar] [CrossRef]
- Saadian, R.; Taheri, A. Fatigue damage analysis of an existing fixed offshore platform using spectral method for life extension. J. Mar. Sci. Technol. 2018, 23, 877–887. [Google Scholar] [CrossRef]
- Wang, N.; Liang, R.; Li, L.; Liu, Z.; Zhao, Z. Research on complex multimodal vibration characteristics of offshore platform. Rev. Adv. Mater. Sci. 2023, 62, 20220311. [Google Scholar] [CrossRef]
- Józefiak, K.; Zbiciak, A.; Maślakowski, M.; Piotrowski, T. Numerical modelling and bearing capacity analysis of pile foundation. Procedia Eng. 2015, 111, 356–363. [Google Scholar] [CrossRef]
- Kuwajima, K.; Hyodo, M.; Hyde, A.F. Pile bearing capacity factors and soil crushabiity. J. Geotech. Geoenvironmental Eng. 2009, 135, 901–913. [Google Scholar] [CrossRef]
- FD003-2007; Design Regulations on Subgrade and Foundation for Wind Turbine Generator System. China Renewable Energy Engineering Institute: Beijing, China, 2007.
- Ren, J.; Sun, X. Prediction of ultimate bearing capacity of pile foundation based on two optimization algorithm models. Buildings 2023, 13, 1242. [Google Scholar] [CrossRef]
- Moarefzadeh, M.; Melchers, R. Nonlinear wave theory in reliability analysis of offshore structures. Probabilistic Eng. Mech. 2006, 21, 99–111. [Google Scholar] [CrossRef]
- DNV-OS-J101; Design of Offshore WindTurbine Structures. Det Norske Veritas AS: Oslo, Norway, 2013.
- Qu, K.; Wen, B.; Ren, X.; Kraatz, S.; Sun, W.; Deng, B.; Jiang, C. Numerical investigation on hydrodynamic load of coastal bridge deck under joint action of solitary wave and wind. Ocean Eng. 2020, 217, 108037. [Google Scholar] [CrossRef]
- Nessim, M.; Hong, H.; Swail, V.; Henderson, C. Design criteria for offshore structures under combined wind and wave loading. J. Offshore Mech. Arct. Eng. 1995, 117, 1–11. [Google Scholar] [CrossRef]
- Taira, K.; Brunton, S.L.; Dawson, S.T.; Rowley, C.W.; Colonius, T.; McKeon, B.J.; Schmidt, O.T.; Gordeyev, S.; Theofilis, V.; Ukeiley, L.S. Modal analysis of fluid flows: An overview. AIAA J. 2017, 55, 4013–4041. [Google Scholar] [CrossRef]
- Ti, Z.; Zhang, M.; Li, Y.; Wei, K. Numerical study on the stochastic response of a long-span sea-crossing bridge subjected to extreme nonlinear wave loads. Eng. Struct. 2019, 196, 109287. [Google Scholar] [CrossRef]
- Chao, Z.; Hao, H.; Bi, K.; Yan, X. Dynamic amplification factors for a system with multiple-degrees-of-freedom. Earthq. Eng. Eng. 2020, 19, 363–375. [Google Scholar] [CrossRef]





| GES | PHES | Li-Ion | NaS | |
|---|---|---|---|---|
| IRR | 14.16% | 13.46% | 16.27% | 16.40% |
| Payback Period (year) | 6 | 8 | 4 | 4 |
| Soil Layer Number | Name | Layer Thickness (m) | Effective Unit Weight (kN/m3) | Cu Value (kPa) |
|---|---|---|---|---|
| ① | Mucky clay | 5.0 | 16.5 | 35 |
| ② | Silty clay | 9.5 | 17. 3 | 70 |
| ③ | Sandy silt | 7.2 | 17. 2 | 85 |
| ④ | Clay | 11.5 | 17.4 | 45 |
| ⑤ | Viscous silt | 11.2 | 17.6 | 50 |
| ⑥ | Silt | 13.3 | 18.2 | - |
| ⑦ | Viscous silt | 12.5 | 18.5 | 80 |
| ⑧ | Clay | 13.8 | 18.7 | 120 |
| Water Level | Recurrence Interval (Years) | Wave Height H (m) | Cycle T (s) | Water Height Hw (m) | Average Wind Speed (m/s) |
|---|---|---|---|---|---|
| Extremely high water level | 50 | 13.7 | 12.7 | 42.08 | 37.5 |
| 5 | 10.3 | 11.6 | 42.08 | 28.4 | |
| Extremely low water level | 50 | 13.1 | 12.4 | 40.98 | 37.5 |
| 5 | 10.1 | 11.3 | 40.98 | 28.4 | |
| Designed high water level | 1 | 5.9 | 10.6 | 38.02 | 20.1 |
| Designed low water level | 1 | 5.5 | 10.4 | 37.90 | 20.1 |
| Wind Turbine Parameters | Value |
|---|---|
| Wind turbine grade | IEC II A |
| Rated power | 5 MW |
| Blade diameter | 110 m |
| Total weight of rotor and cabin | 170 t |
| The position of the overall center of gravity of the rotors and cabin | (1.1 m, 0, 1.8 m) |
| 1P, 3P frequency range | 0.109~0.266 Hz, 0.356~0.798 Hz |
| Segment Name | Top Diameter (m) | Bottom Diameter (m) | Wall Thickness (mm) | Height (m) | Mass of Flange Accessories (kg) |
|---|---|---|---|---|---|
| Upper section | 3.07 | 3.9 | 20 | 32.1 | 4865.4 |
| Middle section | 3.9 | 4.5 | 28 | 30.8 | 7468.6 |
| Lower section | 4.5 | 4.5 | 51 | 14.9 | 18,708.7 |
| Load Conditions | Fx (kN) | Fy (kN) | Fz (kN) | Mx (kN·m) | My (kN·m) | Mz (kN·m) |
|---|---|---|---|---|---|---|
| Extreme conditions | −935 | −72 | −4540 | 3280 | −86,100 | −1145 |
| Normal operating conditions | 510 | −22 | −4640 | 4130 | 45,410 | 472 |
| Wheel Height (m) | Allowed Settlement Value | Allowed Tilt Rate tan θ | |
|---|---|---|---|
| High-Compression Clay | Low- and Medium-Compression Clay and Sandy Soil | ||
| Hl < 60 | 300 | 100 | 0.006 |
| 60 < Hl ≤ 80 | 200 | 0.005 | |
| 80 < Hl ≤ 100 | 150 | 0.004 | |
| 100 > Hl | 100 | 0.003 | |
| Water Level | Recurrence Interval (Years) | Wave Height H (m) | Cycle T (s) | Water Height Hw (m) | ||
|---|---|---|---|---|---|---|
| Extremely high water level | 50 | 13.7 | 12.7 | 42.08 | 0.0087 | 0.026 |
| 5 | 10.3 | 11.6 | 42.08 | 0.0078 | 0.032 | |
| Extremely low water level | 50 | 13.1 | 12.4 | 40.98 | 0.0087 | 0.027 |
| 5 | 10.1 | 11.3 | 40.98 | 0.0081 | 0.032 | |
| Designed high water level | 1 | 5.9 | 10.6 | 38.02 | 0.0054 | 0.035 |
| Designed low water level | 1 | 5.5 | 10.4 | 37.90 | 0.0052 | 0.036 |
| Designed Working Conditions | Load Combinations | Wind Turbine Load | Types of Environmental Loads and Corresponding Recurrence Intervals | |||
|---|---|---|---|---|---|---|
| Wind | Wave | Current | Water Level | |||
| Extreme working conditions | E_1 | Extreme load | 50 | 5 | 5 | Extremely high water level |
| E_2 | 50 | 5 | 5 | Extremely low water level | ||
| E_3 | 5 | 50 | 5 | Extremely high water level | ||
| E_4 | 5 | 50 | 5 | Extremely low water level | ||
| E_5 | 5 | 5 | 50 | Extremely high water level | ||
| E_6 | 5 | 5 | 50 | Extremely low water level | ||
| Normal operating conditions | N_1 | Normal operating load | 1 | 1 | 1 | Designed water level |
| N_2 | 1 | 1 | 1 | Designed water level | ||
| Designed Working Conditions | Partial Coefficient of Load | Combination Value Coefficient | Structural Importance Coefficient | Pile Foundation Resistance Coefficient | ||
|---|---|---|---|---|---|---|
| Fixed Load | Variable Load | Environmental Load | ||||
| Extreme working conditions | 1.0/0.9 | 1.0/0.9 | 1.35 | 0.7 | 1.1 | 1.25 |
| Normal operating conditions | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.5 |
| Member Bar Group Number | Member Bars | Working Conditions | UC Value | Member Bar Group Number | Member Bars | Working Conditions | UC Value | Allowable Value |
|---|---|---|---|---|---|---|---|---|
| BR1 | 701L-901L | E_4 (180°) | 0.71 | X32 | 304L-303X | E_4 (0°) | 0.24 | 1 |
| FL | 901L-705L | E_4 (0°) | 0.31 | LG1 | 103L-203L | E_4 (135°) | 0.61 | |
| MB | 620-605L | E_4 (180°) | 0.81 | LG2 | 203L-303L | E_4 (135°) | 0.49 | |
| HP1 | 705L-704L | E_4 (180°) | 0.47 | LG3 | 301L-401L | E_4 (180°) | 0.46 | |
| HP2 | 701L-706 | E_4 (180°) | 0.26 | LG4 | 401L-501L | E_4 (180°) | 0.35 | |
| X11 | 101L-101X | E_4 (180°) | 0.22 | LG5 | 605L-105L | E_4 (180°) | 0.54 | |
| X12 | 104L-103X | E_4 (0°) | 0.37 | LG6 | 603L-703L | E_4 (135°) | 0.32 | |
| X21 | 201L-201X | E_4 (0°) | 0.2 | PL1 | 103L-P3 | E_4 (135°) | 0.17 | |
| X22 | 204L-203X | E_4 (0°) | 0.34 | PL2 | 105L-P5 | E_4 (180°) | 0.07 | |
| X31 | 301L-301X | E_4 (180°) | 0.14 |
| Node Number | Strength UC Value | Structure UC Value | Working Conditions | Node Number | Strength UC Value | Structure UC Value | Working Conditions | Allowable Value |
|---|---|---|---|---|---|---|---|---|
| 101L | 0.289 | 0.414 | E_4 (180°) | 703L | 0.487 | 0.590 | E_4 (180°) | 1 |
| 102L | 0.104 | 0.414 | E_4 (0°) | 704L | 0.313 | 0.590 | E_4 (45°) | |
| 103L | 0.301 | 0.414 | E_4 (90°) | 701 | 0.216 | 0.811 | E_4 (180°) | |
| 104L | 0.108 | 0.414 | E_4 (45°) | 702 | 0.153 | 0.811 | E_4 (90°) | |
| 201L | 0.126 | 0.690 | E_4 (180°) | 703 | 0.156 | 0.811 | E_4 (180°) | |
| 202L | 0.159 | 0.690 | E_4 (0°) | 704 | 0.159 | 0.811 | E_4 (180°) | |
| 203L | 0.167 | 0.690 | E_4 (90°) | 705 | 0.146 | 0.811 | E_4 (90°) | |
| 204L | 0.166 | 0.690 | E_4 (0°) | 706 | 0.256 | 0.811 | E_4 (135°) | |
| 301L | 0.234 | 0.674 | E_4 (0°) | 707 | 0.226 | 0.811 | E_4 (45°) | |
| 302L | 0.164 | 0.674 | E_4 (45°) | 708 | 0.253 | 0.811 | E_4 (180°) | |
| 303L | 0.233 | 0.674 | E_4 (0°) | 101X | 0.106 | 0.566 | E_4 (180°) | |
| 304L | 0.146 | 0.674 | E_4 (45°) | 102X | 0.087 | 0.566 | E_4 (180°) | |
| 401L | 0.329 | 0.689 | E_4 (45°) | 103X | 0.098 | 0.566 | E_4 (90°) | |
| 402L | 0.261 | 0.689 | E_4 (180°) | 104X | 0.070 | 0.566 | E_4 (135°) | |
| 403L | 0.269 | 0.689 | E_4 (0°) | 201X | 0.143 | 0.572 | E_4 (180°) | |
| 404L | 0.261 | 0.689 | E_4 (45°) | 202X | 0.095 | 0.572 | E_4 (45°) | |
| 501L | 0.424 | 0.299 | E_4 (180°) | 203X | 0.147 | 0.572 | E_4 (90°) | |
| 502L | 0.128 | 0.299 | E_4 (180°) | 204X | 0.112 | 0.572 | E_4 (180°) | |
| 503L | 0.391 | 0.299 | E_4 (180°) | 301X | 0.126 | 0.567 | E_4 (180°) | |
| 504L | 0.132 | 0.299 | E_4 (135°) | 302X | 0.083 | 0.567 | E_4 (135°) | |
| 701L | 0.509 | 0.590 | E_4 (180°) | 303X | 0.137 | 0.567 | E_4 (0°) | |
| 702L | 0.277 | 0.590 | E_4 (0°) | 304X | 0.131 | 0.567 | E_4 (0°) |
| Pile Head Node Number | Maximum Tensile Load of Pile Foundation (kN) | Limit Uplift Bearing Capacity of Pile Foundation (kN) | Working Conditions | Maximum Uplift Bearing Capacity Ratio | Allowable Value |
|---|---|---|---|---|---|
| P1 | 0 | 17,775.5 | / | / | 1 |
| P2 | 1581 | 17,775.5 | E_4 (135°) | 0.11 | |
| P3 | 0 | 17,775.5 | / | / | |
| P4 | 968.3 | 17,775.5 | E_4 (180°) | 0.07 | |
| P5 | 0 | 14,704.9 | / | / |
| Pile Head Node Number | Maximum Compression Load of Pile Foundation (kN) | Limit Compression Bearing Capacity of Pile Foundation (kN) | Working Conditions | Maximum Uplift Bearing Capacity Ratio | Allowable Value |
|---|---|---|---|---|---|
| P1 | 8948.6 | 16,322.4 | E_4 (180°) | 0.69 | 1 |
| P2 | 3277.4 | 16,322.4 | E_4 (0°) | 0.25 | |
| P3 | 9290.5 | 16,322.4 | E_4 (135°) | 0.71 | |
| P4 | 3780.0 | 16,322.4 | E_4 (45°) | 0.29 | |
| P5 | 3568.0 | 13,526.7 | E_4 (90°) | 0.33 |
| Pile Head Node Number | Maximum Lateral Displacement on the Mud Surface (mm) | Working Conditions | Maximum Vertical Settlement (mm) | Working Conditions | Maximum Angle on the Mud Surface (°) | Working Conditions |
|---|---|---|---|---|---|---|
| P1 | 2.6 | N_2 (180°) | 3.2 | N_2 (180°) | 0.29 | N_2 (180°) |
| P2 | 6.3 | N_2 (0°) | 6.0 | N_2 (0°) | 0.45 | N_2 (0°) |
| P3 | 2.6 | N_2 (135°) | 3.2 | N_2 (135°) | 0.3 | N_2 (90°) |
| P4 | 6.0 | N_2 (0°) | 6.0 | N_2 (45°) | 0.41 | N_2 (0°) |
| P5 | 0.2 | N_2 (0°) | 4.4 | N_2 (0°) | 0.05 | N_2 (0°) |
| Modal | Frequency (Hz) | Cycle (s) |
|---|---|---|
| 1 | 0.326 | 3.323 |
| 2 | 0.327 | 2.872 |
| 3 | 1.296 | 0.772 |
| 4 | 1.296 | 0.771 |
| 5 | 2.201 | 0.454 |
| 6 | 2.339 | 0.428 |
| 7 | 2.368 | 0.422 |
| 8 | 2.393 | 0.418 |
| 9 | 2.454 | 0.408 |
| 10 | 2.902 | 0.345 |
| Parameters | Selected Parameters |
|---|---|
| Cycle | 12 s |
| Significant wave height | 10 m |
| Wave iteration time | 1000 s |
| Analysis time step size | 1 s |
| Structural damping | 3.0% |
| Calculation Items | Overturning Moment (m-kN) | Base Shear (kN) | ||
|---|---|---|---|---|
| Direction | X | Y | X | Y |
| Static method | 112.8264 | 283,279.9 | 7111.258 | 8.4123 |
| Dynamic method | 174.8481 | 289,771.6 | 7151.915 | 10.2785 |
| DAF | 1.550 | 1.023 | 1.006 | 1.222 |
| Wave Direction | 0° | 30° | 60° | 90° | 120° | 150° | 180° |
|---|---|---|---|---|---|---|---|
| Probability | 15 | 12 | 13 | 11 | 20 | 10 | 19 |
| HS (m) | 0–1 | 1–3 | 3–6 | |
|---|---|---|---|---|
| TP (s) | ||||
| 0–1.5 | 15.0 | 10.0 | 10.0 | |
| 1.5–3 | 10.0 | 19.0 | 11.0 | |
| 3–5 | 5.0 | 8.0 | 5.0 | |
| 5–8 | 2.0 | 3.0 | 2.0 | |
| Node Number | Maximum Damage Value | Minimum Damage Value |
|---|---|---|
| 404L | 0.076 | 0.036 |
| 403L | 0.082 | 0.034 |
| 402L | 0.076 | 0.035 |
| 401L | 0.082 | 0.044 |
| 304L | 0.484 | 0.038 |
| 303L | 0.797 | 0.040 |
| 302L | 0.795 | 0.042 |
| 301L | 0.624 | 0.043 |
| 204L | 0.029 | 0.155 × 10−2 |
| 203L | 0.036 | 0.535 × 10−3 |
| 202L | 0.026 | 0.168 × 10−2 |
| 201L | 0.033 | 0.815 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Huang, D.; He, H.; Yang, F.; Li, W.; Chen, Y. Dynamic Response and Fatigue Analysis of a New Marine Gravitational Energy Storage System Under Wave Loads. J. Mar. Sci. Eng. 2024, 12, 2196. https://doi.org/10.3390/jmse12122196
Wang Z, Huang D, He H, Yang F, Li W, Chen Y. Dynamic Response and Fatigue Analysis of a New Marine Gravitational Energy Storage System Under Wave Loads. Journal of Marine Science and Engineering. 2024; 12(12):2196. https://doi.org/10.3390/jmse12122196
Chicago/Turabian StyleWang, Ziheng, Dazhi Huang, Hongkun He, Feifei Yang, Wenhao Li, and Yi Chen. 2024. "Dynamic Response and Fatigue Analysis of a New Marine Gravitational Energy Storage System Under Wave Loads" Journal of Marine Science and Engineering 12, no. 12: 2196. https://doi.org/10.3390/jmse12122196
APA StyleWang, Z., Huang, D., He, H., Yang, F., Li, W., & Chen, Y. (2024). Dynamic Response and Fatigue Analysis of a New Marine Gravitational Energy Storage System Under Wave Loads. Journal of Marine Science and Engineering, 12(12), 2196. https://doi.org/10.3390/jmse12122196





