Hydrodynamic Performance Investigations of OWC and Hybrid System: Geometry of OWC and Rectangular Submerged Breakwater
Abstract
1. Introduction
2. Numerical Model
2.1. Governing Equation
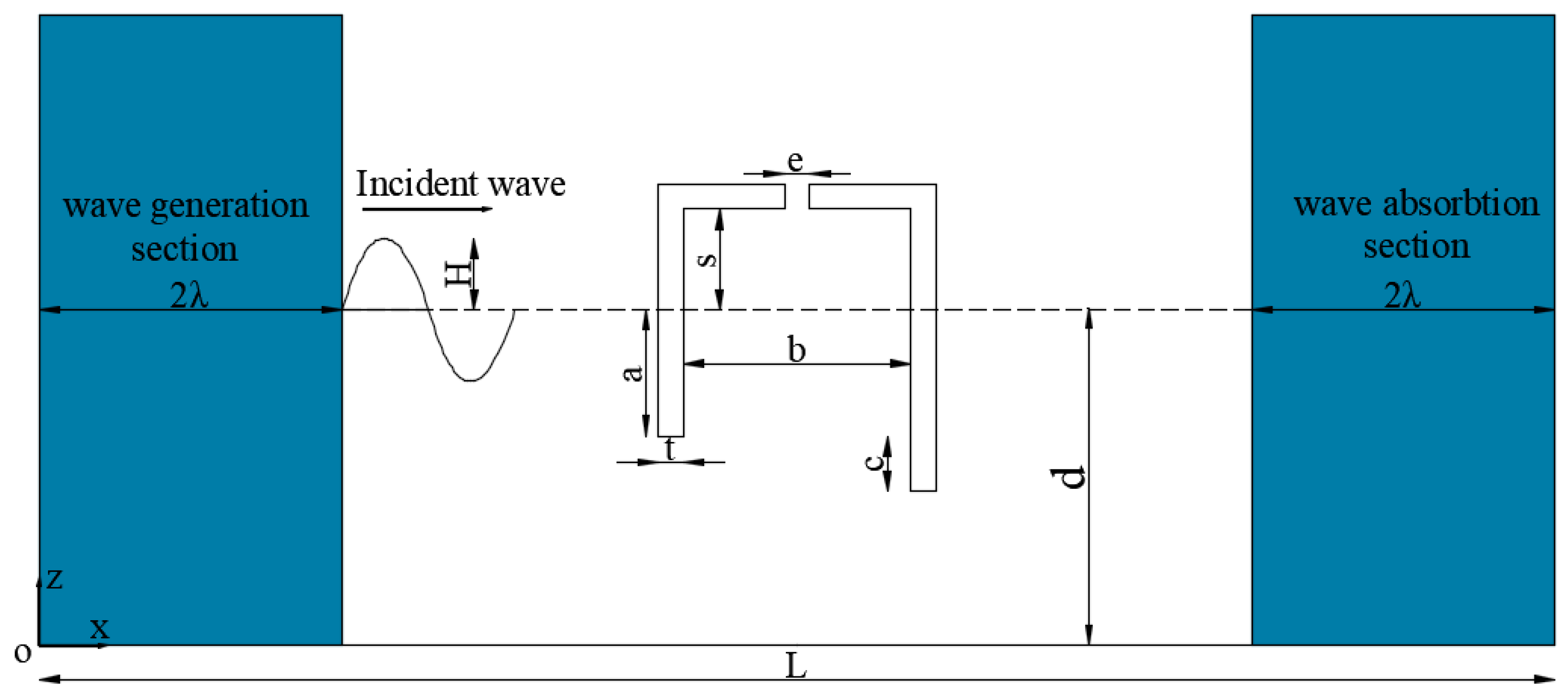
2.2. Wave Generation and Absorption
2.3. Model Validation
2.4. Performance Coefficient of OWC
3. Results
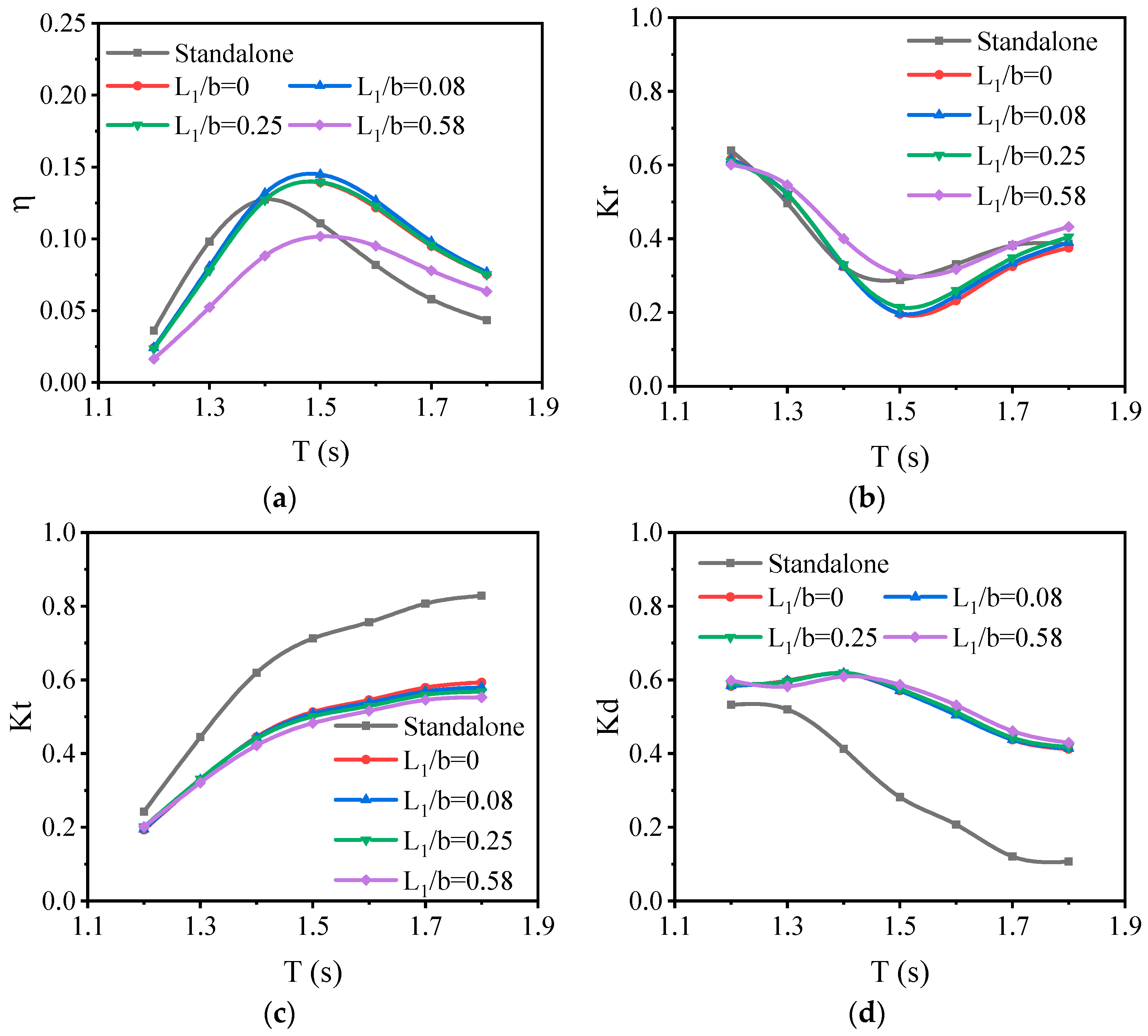
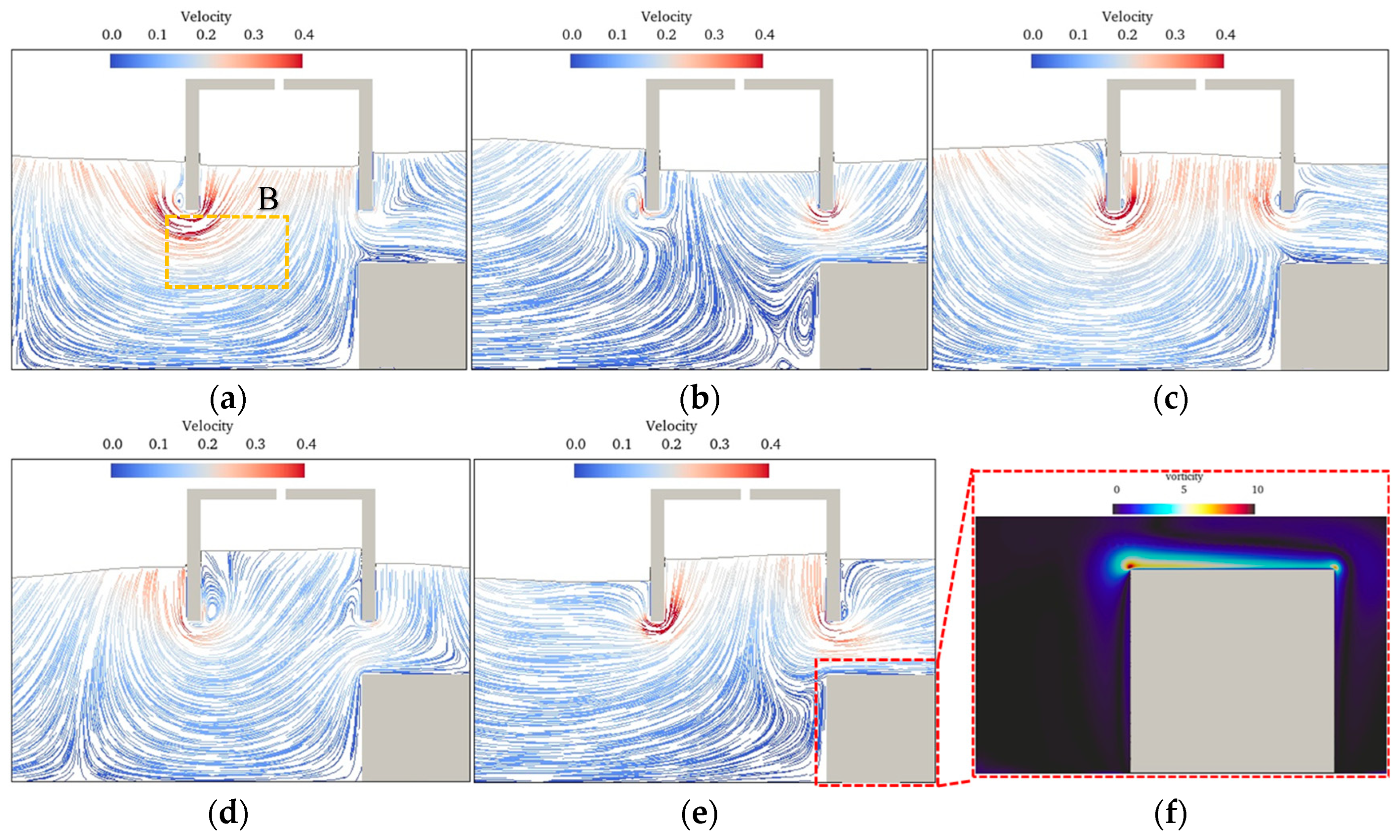
3.1. Effect of OWC Geometry
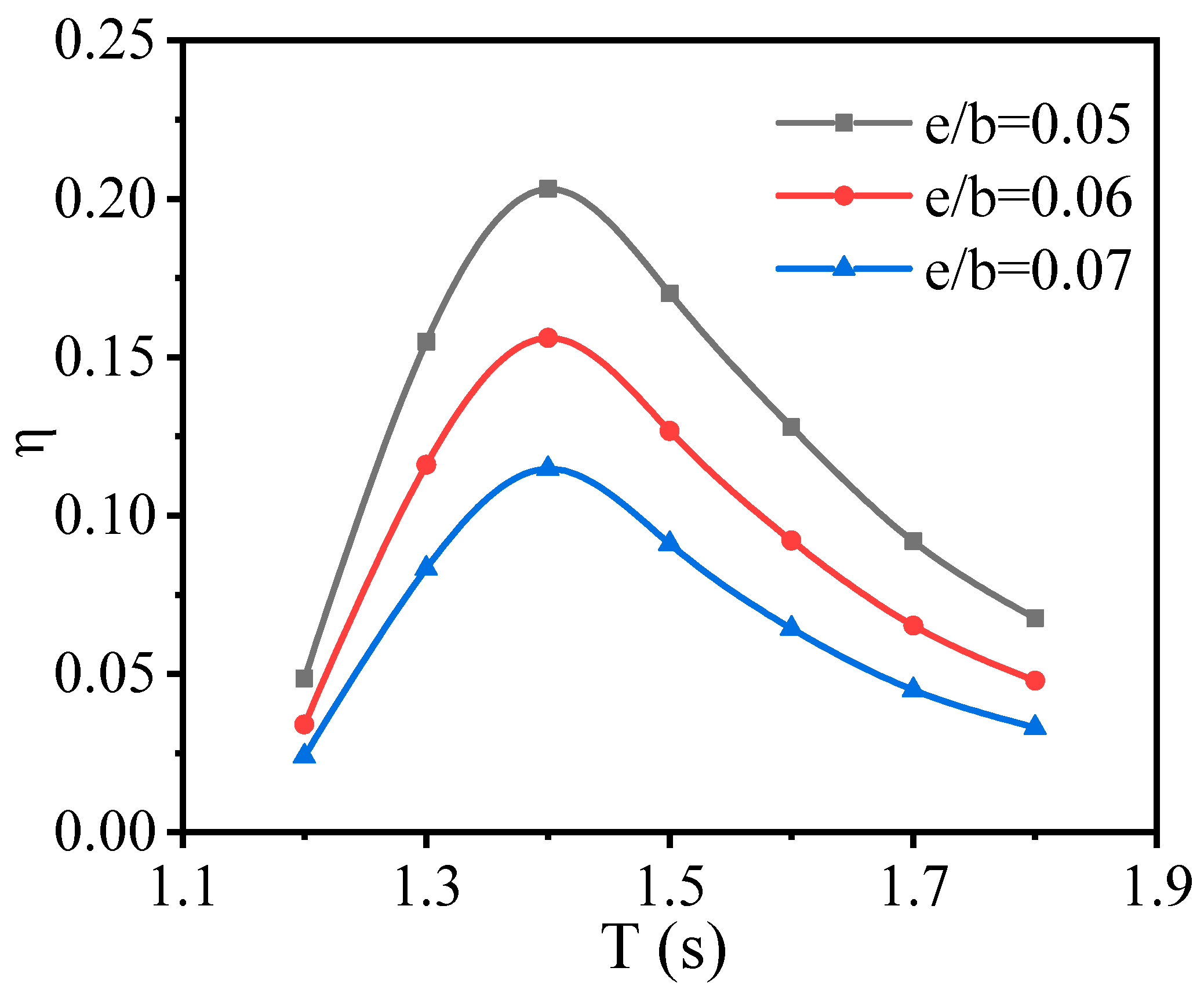
3.1.1. Effect of Opening Height
3.1.2. Effect of Draft
3.1.3. Effect of Chamber Width
3.1.4. Effect of PTO Damping and Water Column Motion
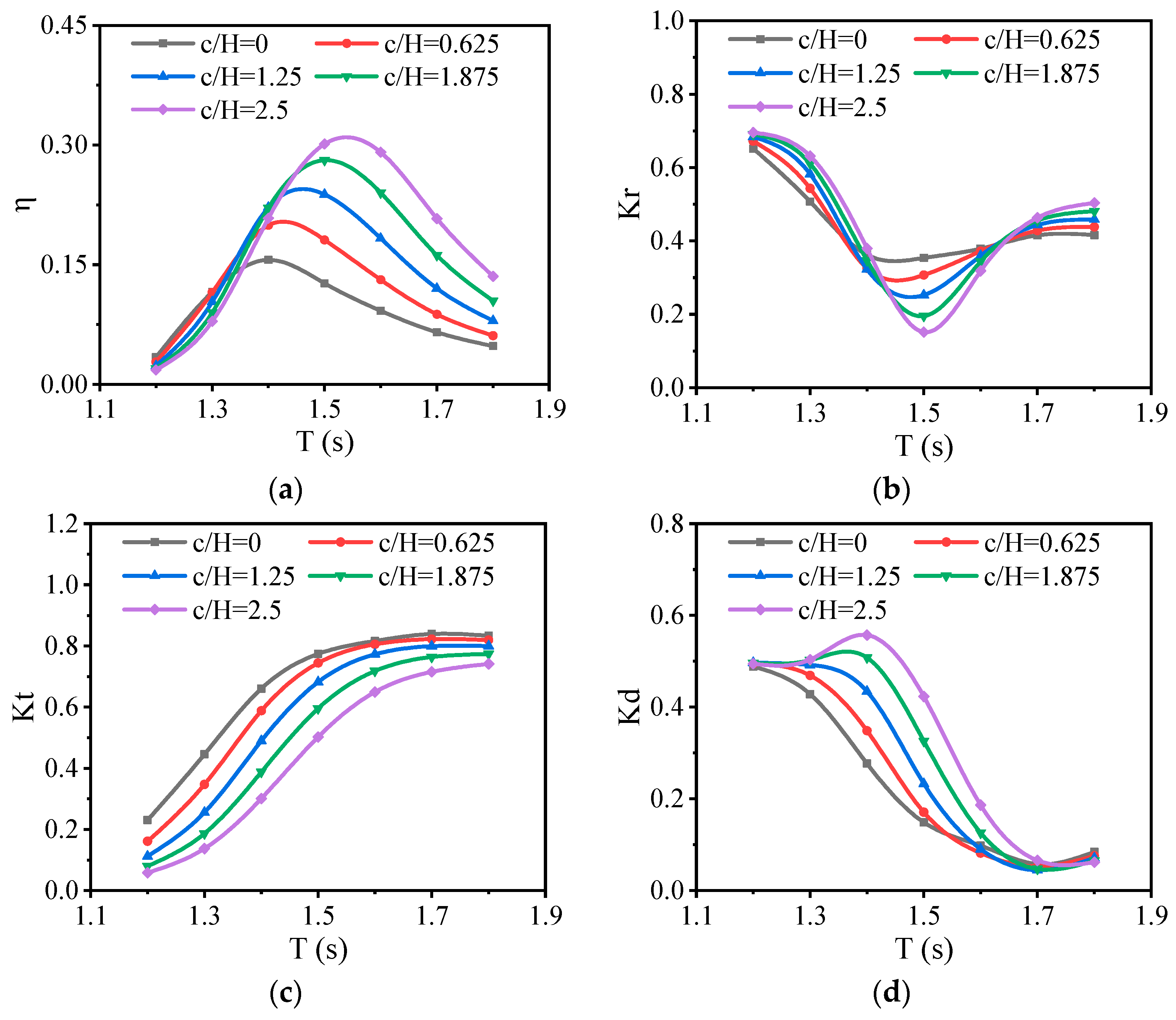
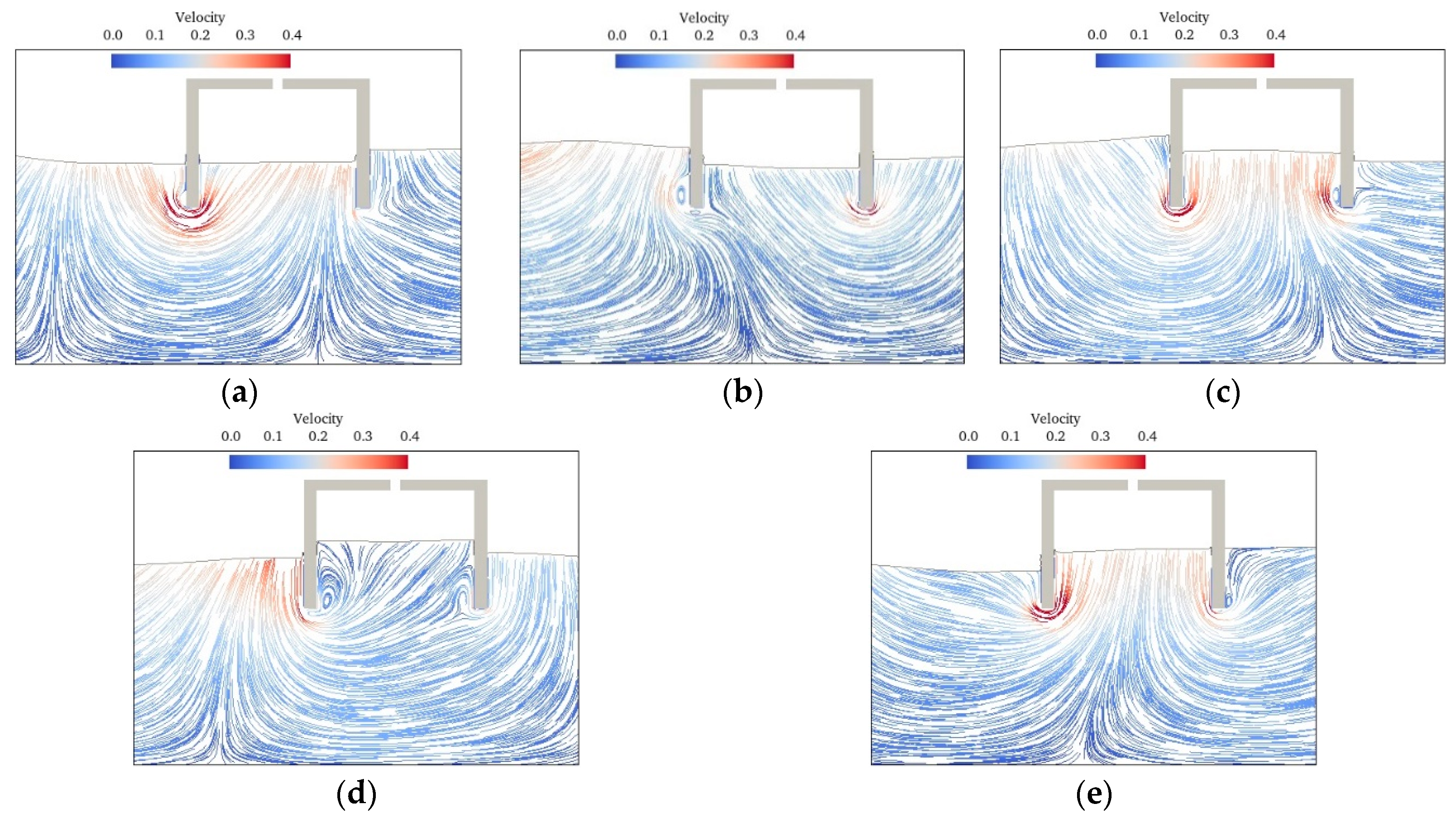
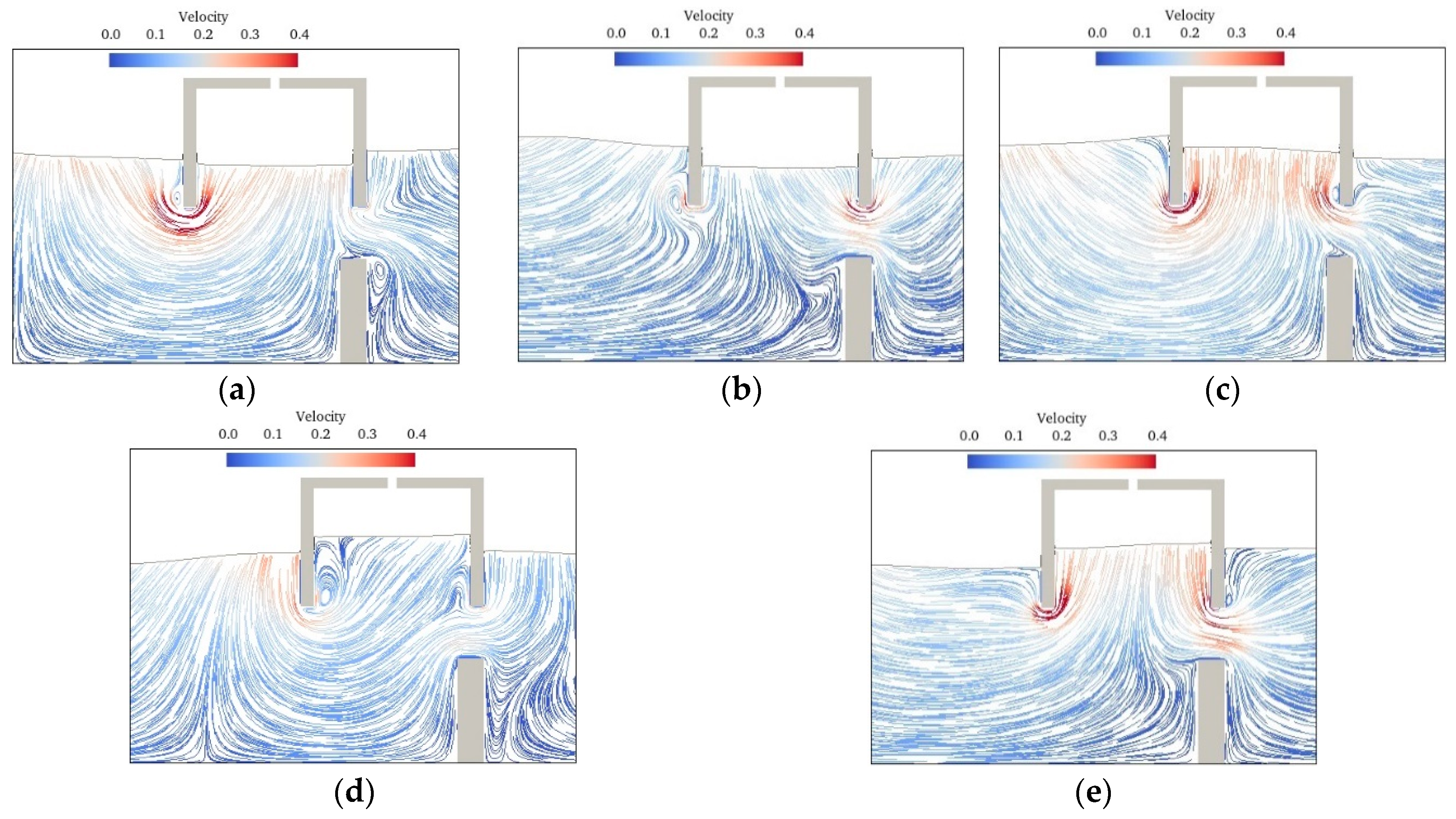
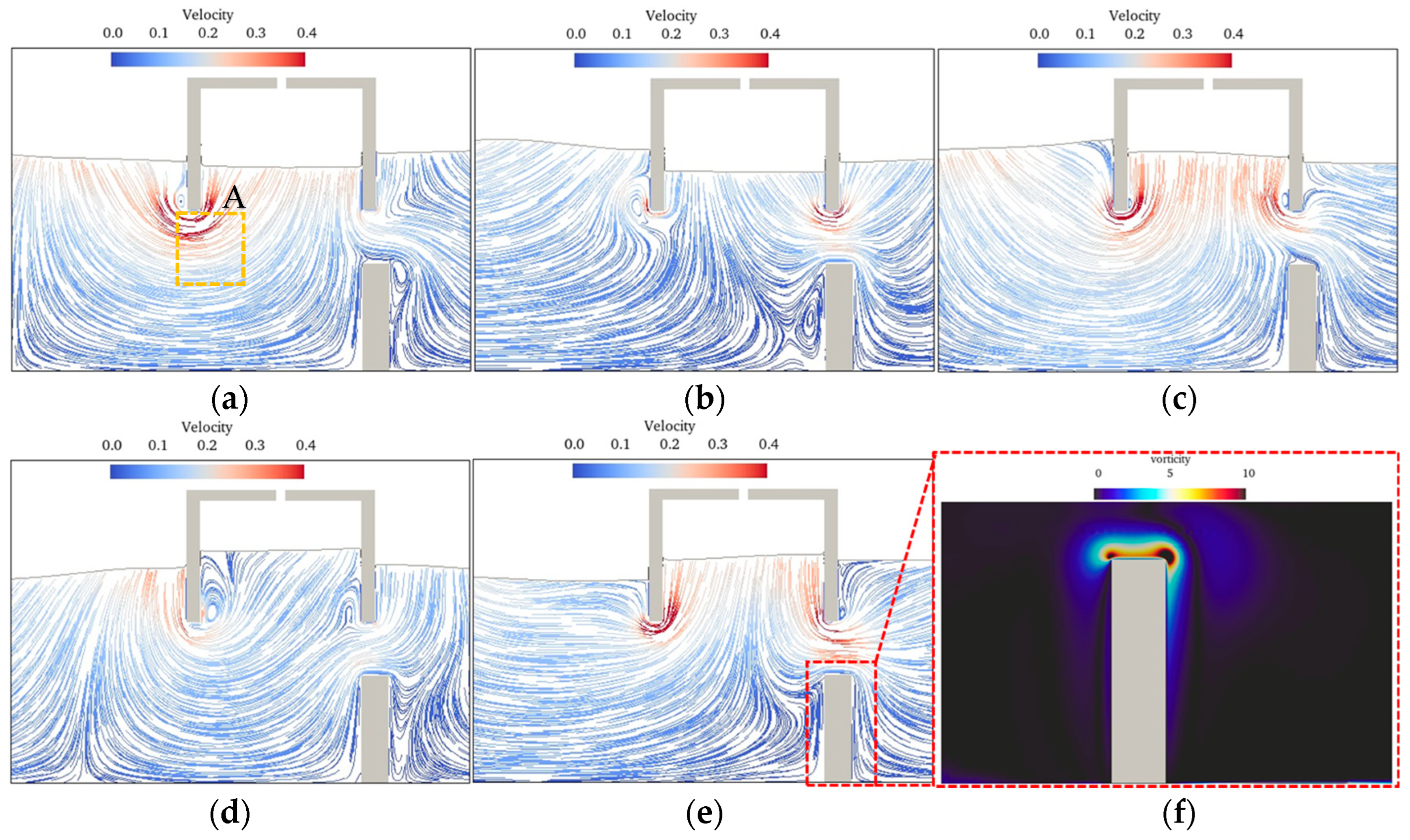
3.2. Effect of Submerge Breakwater on OWC
4. Conclusions
- (1)
- Increasing the opening height enhances the energy conversion efficiency of the OWC under long wave periods. For different wave periods, there is an optimal draft for the OWC to maximize the energy conversion efficiency. Meanwhile, the optimal draft for the OWC increases with the wave period. Increasing PTO damping does not change the resonance period of the OWC, while the free surface elevation inside the chamber reduces.
- (2)
- The inclination of the water column is low under both short and long waves, and the wave period corresponding to the maximum inclination is slightly greater than the resonance period of the OWC. Around the maximum inclination of the water column, multi-point measurements of the wave elevation in the chamber are necessary to reduce measurement errors caused by the spatial non-uniformity of the water column.
- (3)
- Compared to a standalone OWC, the submerged breakwater-OWC hybrid system exhibits a higher energy conversion efficiency in medium-to-long waves and superior wave attenuation performance.
- (4)
- When the submerged breakwater length L1 in the hybrid system is optimal and the back wall of the breakwater is aligned with the back wall of the OWC, the energy conversion efficiency is the highest. Future studies could explore the relationship between the OWC air chamber width and optimal breakwater dimensions, further optimizing the hydrodynamic performance of the integrated system.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Clément, A.; McCullen, P.; Falcão, A.; Fiorentino, A.; Gardner, F.; Hammarlund, K.; Lemonis, G.; Lewis, T.; Nielsen, K.; Petroncini, S.; et al. Wave energy in Europe: Current status and perspectives. Renew. Sust. Energy Rev. 2002, 6, 405–431. [Google Scholar] [CrossRef]
- Crespo, A.J.C.; Altomare, C.; Domínguez, J.M.; González-Cao, J.; Gómez-Gesteira, M. Towards simulating floating offshore oscillating water column converters with Smoothed Particle Hydrodynamics. Coast. Eng. 2017, 126, 11–26. [Google Scholar] [CrossRef]
- Evans, D.V.; Porter, R. Hydrodynamic characteristics of an oscillating water column device. Appl. Ocean Res. 1995, 17, 155–164. [Google Scholar] [CrossRef]
- Mustapa, M.A.; Yaakob, O.B.; Ahmed, Y.M.; Rheem, C.; Koh, K.K.; Adnan, F.A. Wave energy device and breakwater integration: A review. Renew. Sustain. Energy Rev. 2017, 77, 43–58. [Google Scholar] [CrossRef]
- Elhanafi, A.; Macfarlane, G.; Fleming, A.; Leong, Z. Experimental and numerical investigations on the hydrodynamic performance of a floating–moored oscillating water column wave energy converter. Appl. Energy 2017, 205, 369–390. [Google Scholar] [CrossRef]
- Gao, J.; Lyu, J.; Wang, J.; Zhang, J.; Liu, Q.; Zang, J.; Zou, T. Study on Transient Gap Resonance with Consideration of the Motion of Floating Body. China Ocean Eng. 2022, 36, 994–1006. [Google Scholar] [CrossRef]
- Chen, J.; Wen, H.; Wang, Y.; Wang, G. A correlation study of optimal chamber width with the relative front wall draught of onshore OWC device. Energy 2021, 225, 120307. [Google Scholar] [CrossRef]
- Samak, M.M.; Elgamal, H.; Elmekawy, A.M.N. The contribution of L-shaped front wall in the improvement of the oscillating water column wave energy converter performance. Energy 2021, 226, 120421. [Google Scholar] [CrossRef]
- Çelik, A.; Altunkaynak, A. Experimental investigations on the performance of a fixed-oscillating water column type wave energy converter. Energy 2019, 188, 116071. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y. Hydrodynamic performance of an offshore Oscillating Water Column device mounted over an immersed horizontal plate: A numerical study. Energy 2021, 222, 119964. [Google Scholar] [CrossRef]
- Ning, D.Z.; Wang, R.Q.; Zhang, C.W. Numerical Simulation of a Dual-Chamber Oscillating Water Column Wave Energy Converter. Sustainability 2017, 9, 1599. [Google Scholar] [CrossRef]
- Mirzaei, H.; Moghim, M.N.; Movahedian, B. Numerical Solution of Hydrodynamic Efficiency Equations for an Oscillating Water Column Wave Energy Converter Using the Method of Fundamental Solutions. Eng. Anal. Bound. Elem. 2024, 158, 270–288. [Google Scholar] [CrossRef]
- Kharati-Koopaee, M.; Fathi-Kelestani, A. Assessment of oscillating water column performance: Influence of wave steepness at various chamber lengths and bottom slopes. Renew. Energy 2020, 147, 1595–1608. [Google Scholar] [CrossRef]
- Mora, A.; Bautista, E.; Méndez, F. Influence of a tapered and slender wave collector on the increment of the efficiency of an oscillating water column wave-energy converter. Ocean Eng. 2017, 129, 20–36. [Google Scholar] [CrossRef]
- Rezanejad, K.; Bhattacharjee, J.; Soares, C.G. Analytical and Numerical Study of Nearshore Multiple Oscillating Water Columns. J. Offshore Mech. Arct. 2016, 138, 021901. [Google Scholar] [CrossRef]
- Zheng, S.; Antonini, A.; Zhang, Y.; Greaves, D.; Miles, J.; Iglesias, G. Wave power extraction from multiple oscillating water columns along a straight coast. J. Fluid Mech. 2019, 878, 445–480. [Google Scholar] [CrossRef]
- Boccotti, P.; Filianoti, P.; Fiamma, V.; Arena, F. Caisson breakwaters embodying an OWC with a small opening—Part II: A small-scale field experiment. Ocean Eng. 2007, 34, 820–841. [Google Scholar] [CrossRef]
- Wang, C.; Ma, T.; Zhang, Y. Semi-analytical study on an integrated-system with separated heaving OWC and breakwater: Structure size optimization and gap resonance utilization. Ocean Eng. 2022, 245, 110319. [Google Scholar] [CrossRef]
- Han, Z.; Liu, Z.; Shi, H. Numerical study on overtopping performance of a multi-level breakwater for wave energy conversion. Ocean Eng. 2018, 150, 94–101. [Google Scholar] [CrossRef]
- Martins-Rivas, H.; Mei, C.C. Wave power extraction from an oscillating water column along a straight coast. Ocean Eng. 2009, 36, 426–433. [Google Scholar] [CrossRef]
- Martins-Rivas, H.; Mei, C.C. Wave power extraction from an oscillating water column at the tip of a breakwater. J. Fluid Mech. 2009, 626, 395–414. [Google Scholar] [CrossRef]
- Elhanafi, A.; Macfarlane, G.; Fleming, A.; Leong, Z. Scaling and air compressibility effects on a three-dimensional offshore stationary OWC wave energy converter. Appl. Energy 2017, 189, 1–20. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Fuhrman, D.R.; Madsen, P.A.; Bingham, H.B. Numerical simulation of lowest-order short-crested wave instabilities. J. Fluid Mech. 2006, 563, 415. [Google Scholar] [CrossRef]
- Jacobsen, N.G.; Fuhrman, D.R.; Fredsøe, J. A wave generation toolbox for the open-source CFD library: OpenFoam®. Int. J. Numer. Methods Fluids 2012, 70, 1073–1088. [Google Scholar] [CrossRef]
- Xie, G.; Hu, C.; Zhao, T.; Ma, Y.; Ni, W. Coupled hydrodynamic performance investigations of a hybrid system with oscillating water column and submerged breakwater. Ocean Eng. 2023, 283, 115205. [Google Scholar] [CrossRef]
- Iturrioz, A.; Guanche, R.; Lara, J.L.; Vidal, C.; Losada, I.J. Validation of OpenFOAM® for Oscillating Water Column three-dimensional modeling. Ocean Eng. 2015, 107, 222–236. [Google Scholar] [CrossRef]
- He, F.; Huang, Z. Hydrodynamic performance of pile-supported OWC-type structures as breakwaters: An experimental study. Ocean Eng. 2014, 88, 618–626. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, B.; Zang, J.; Vogel, C.; Fan, T.; Chen, C. Effects of narrow gap wave resonance on a dual-floater WEC-breakwater hybrid system. Ocean Eng. 2021, 225, 108762. [Google Scholar] [CrossRef]
- Çelik, A.; Altunkaynak; Çelik, A.; Altunkaynak, A. Experimental and analytical investigation on chamber water surface fluctuations and motion behaviours of water column type wave energy converter. Ocean Eng. 2018, 150, 209–220. [Google Scholar] [CrossRef]


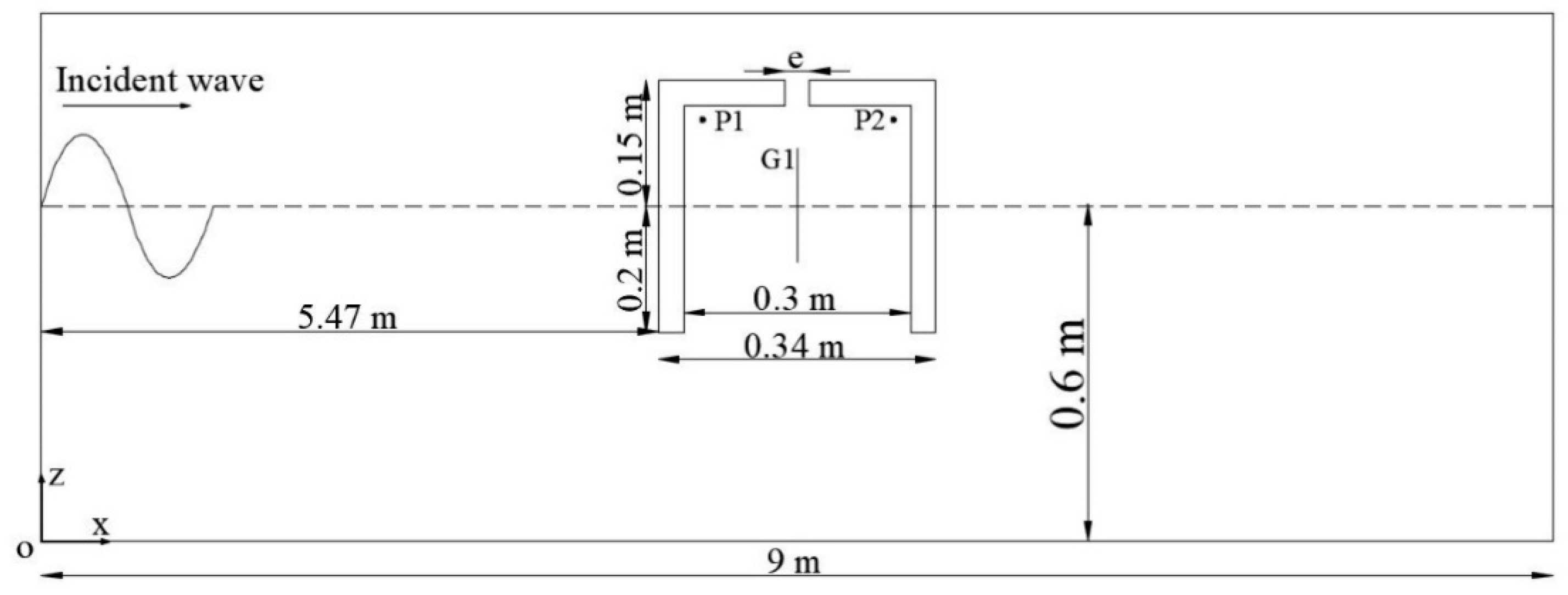
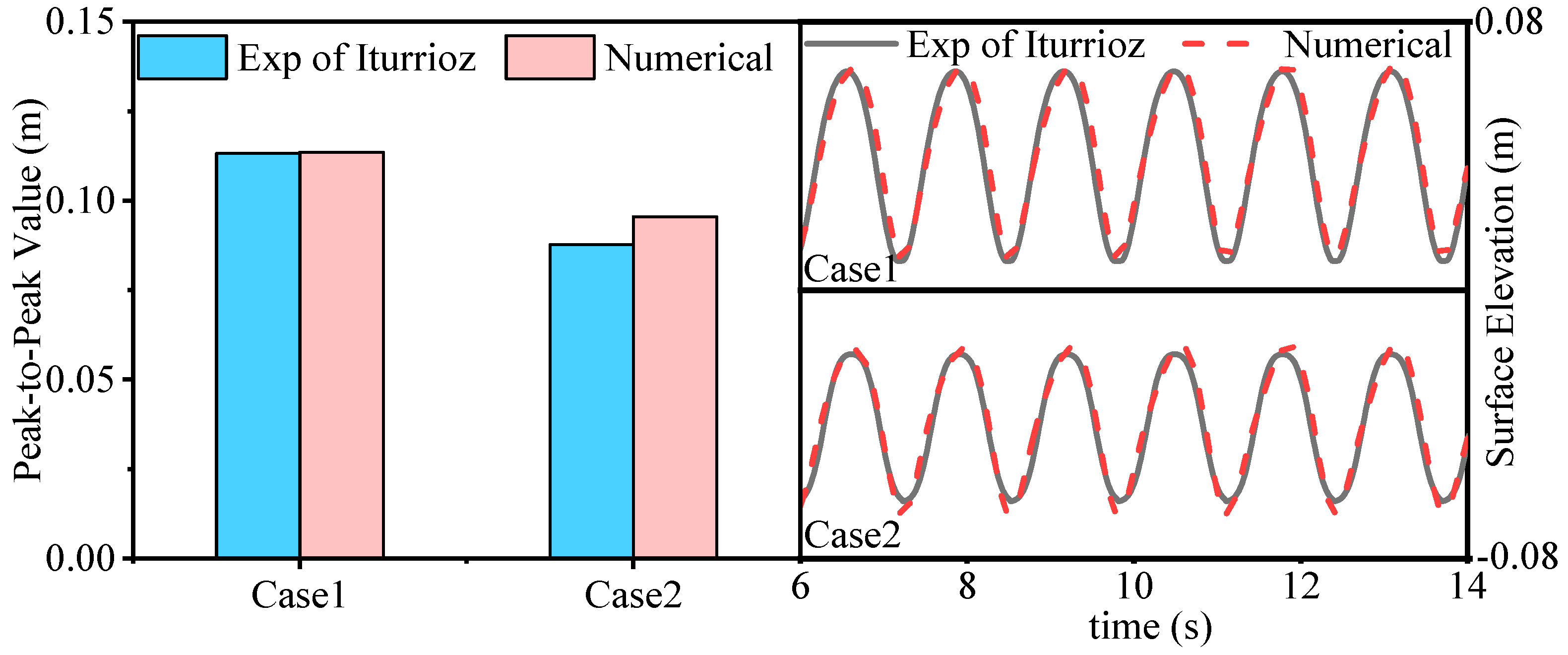
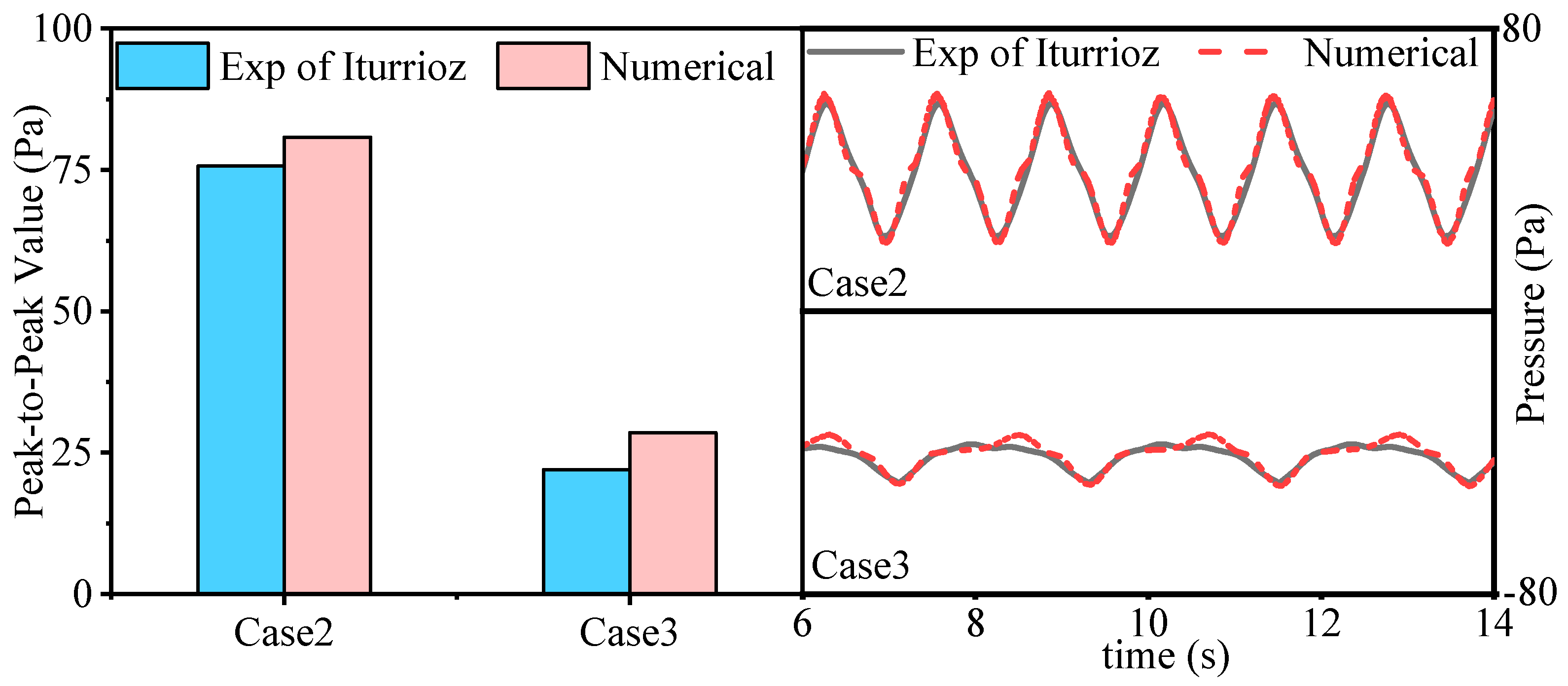
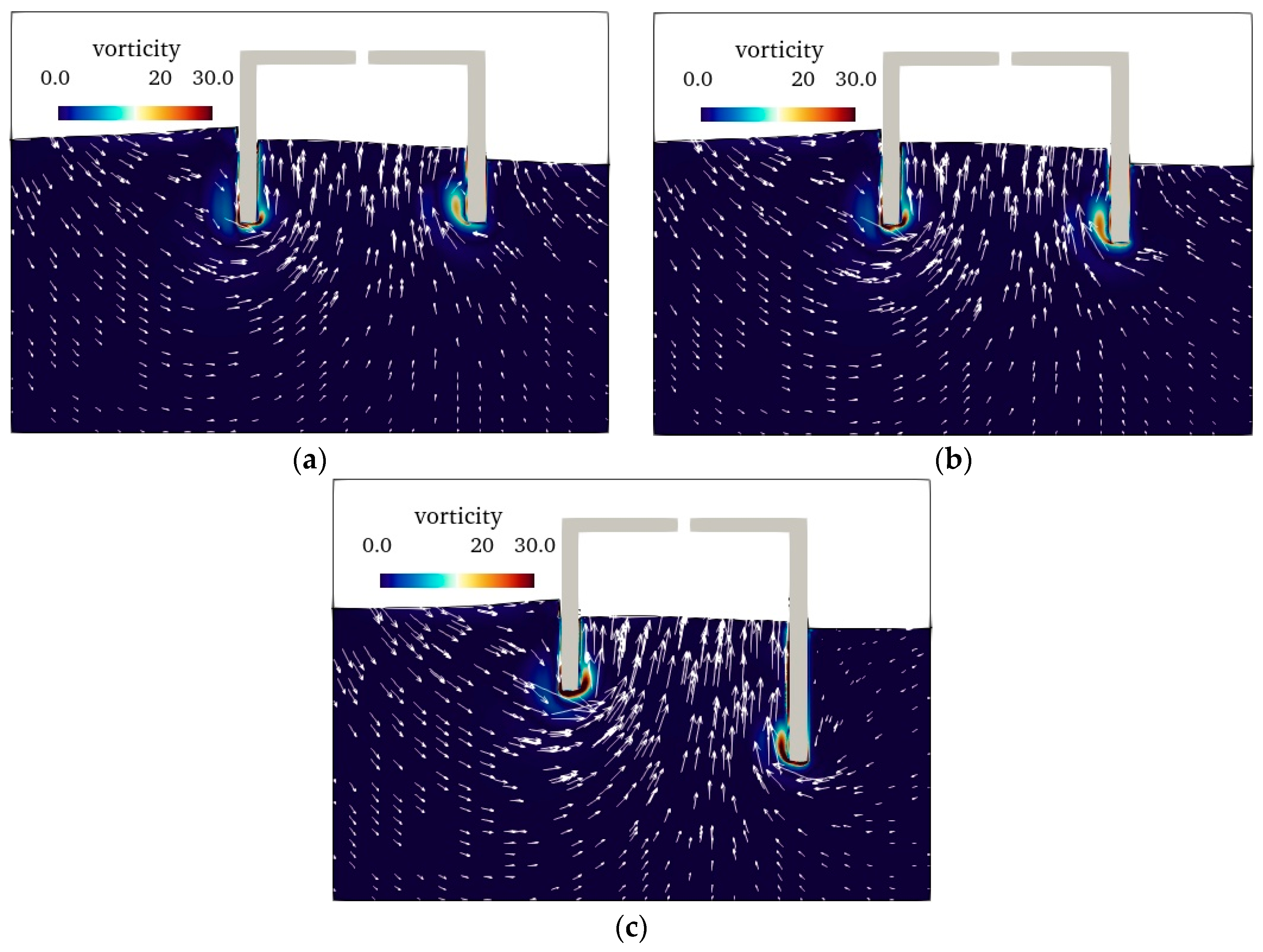


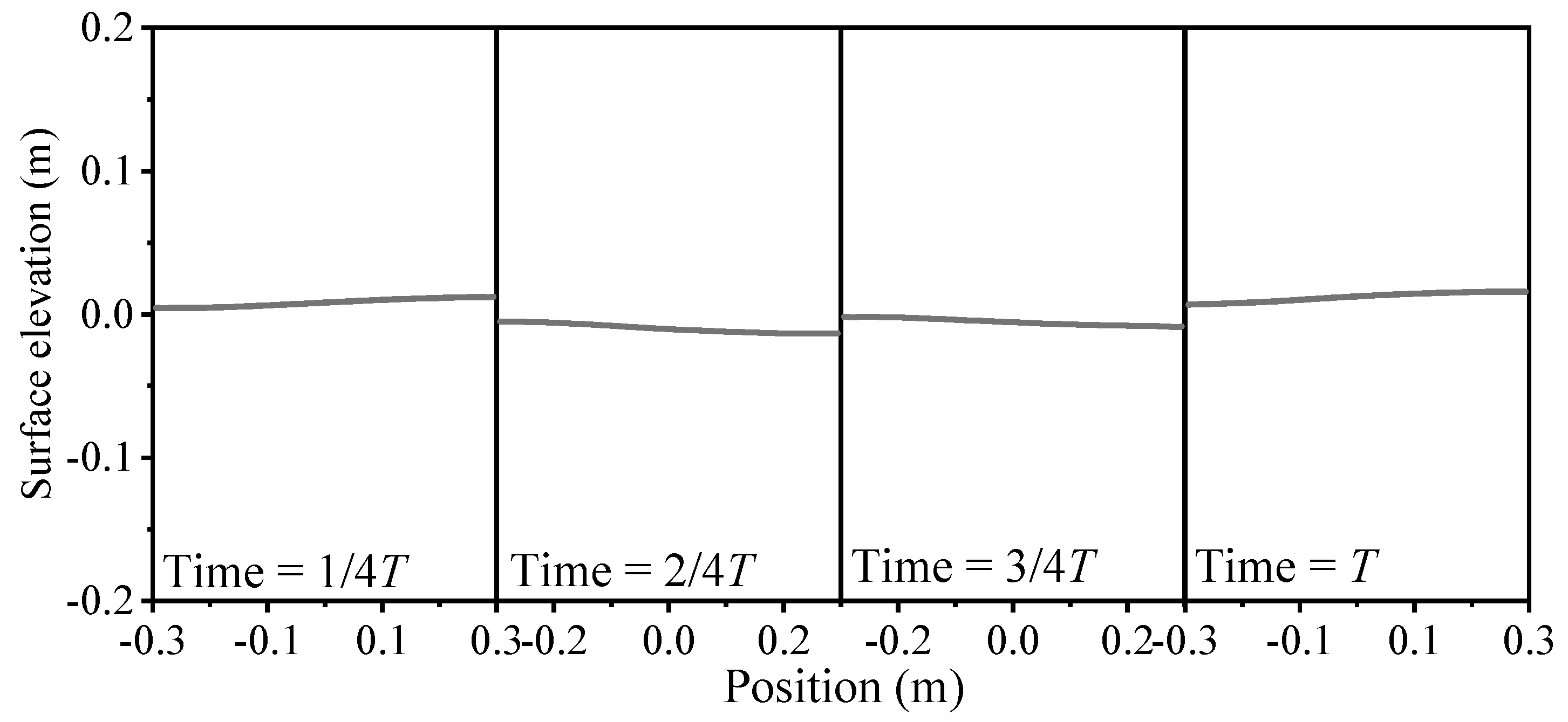
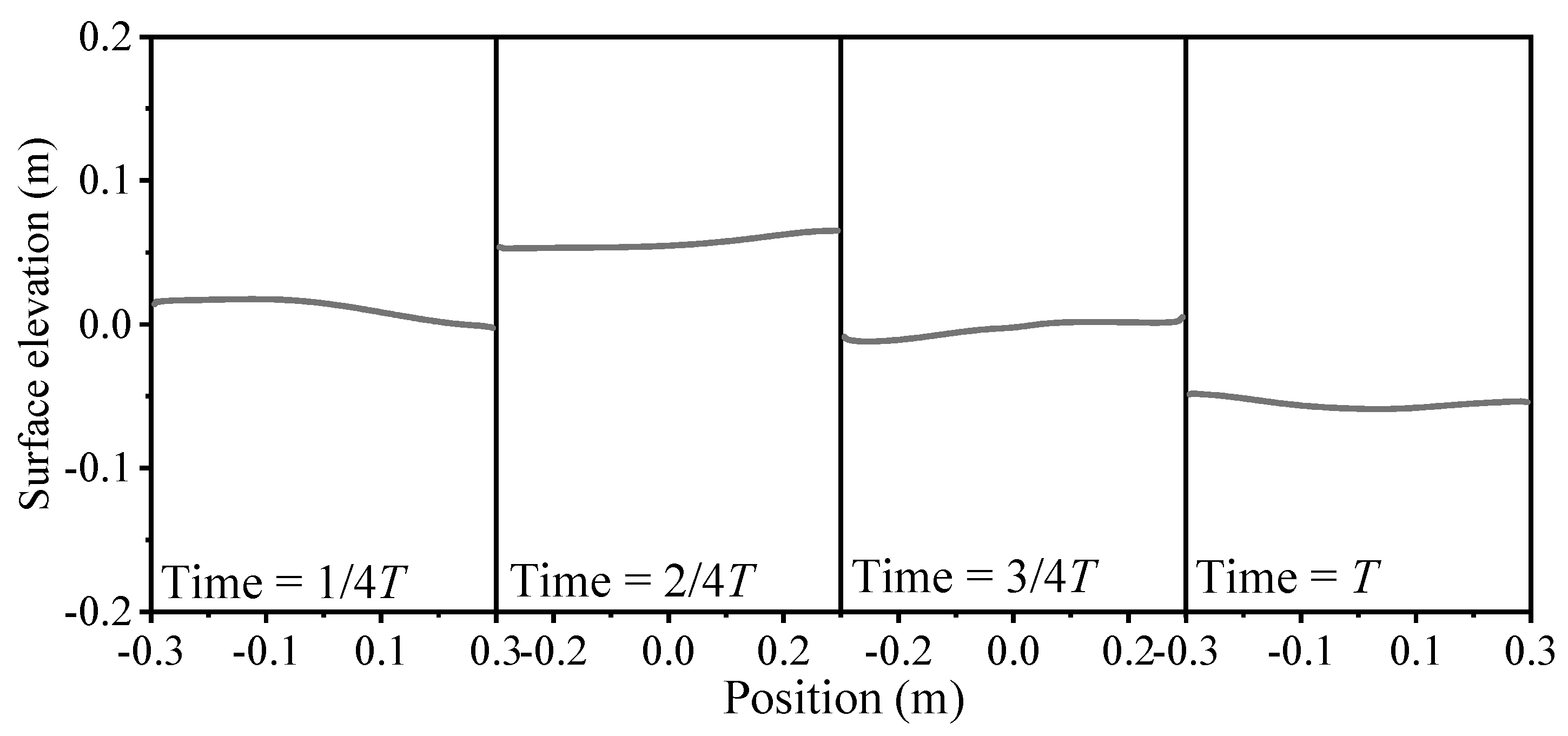

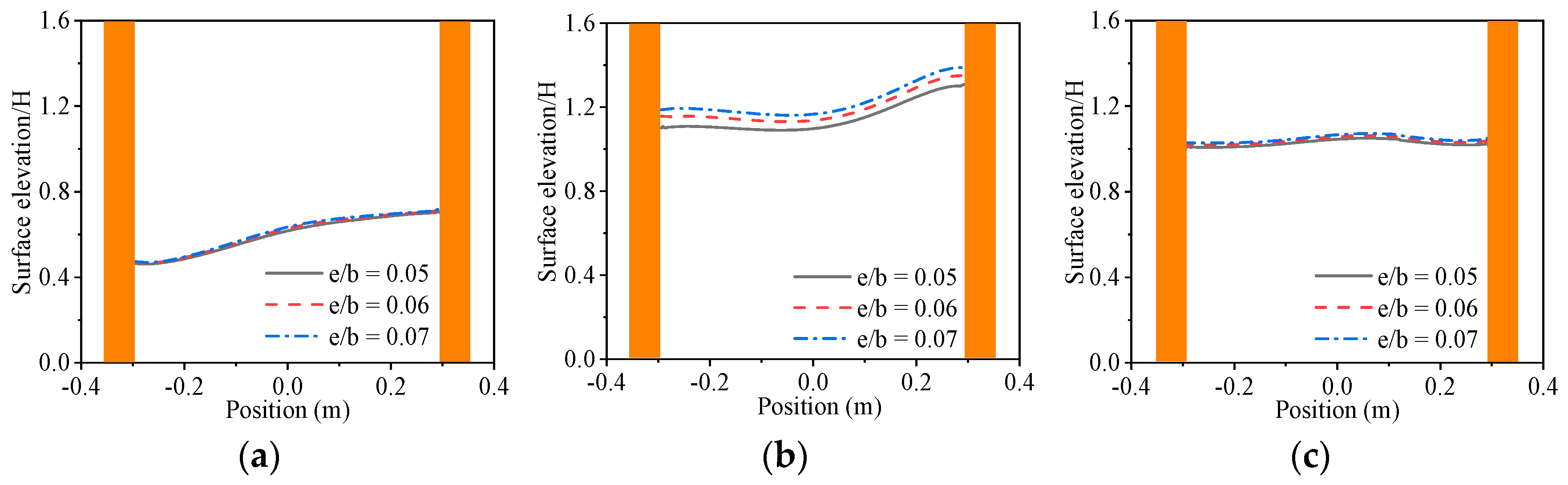
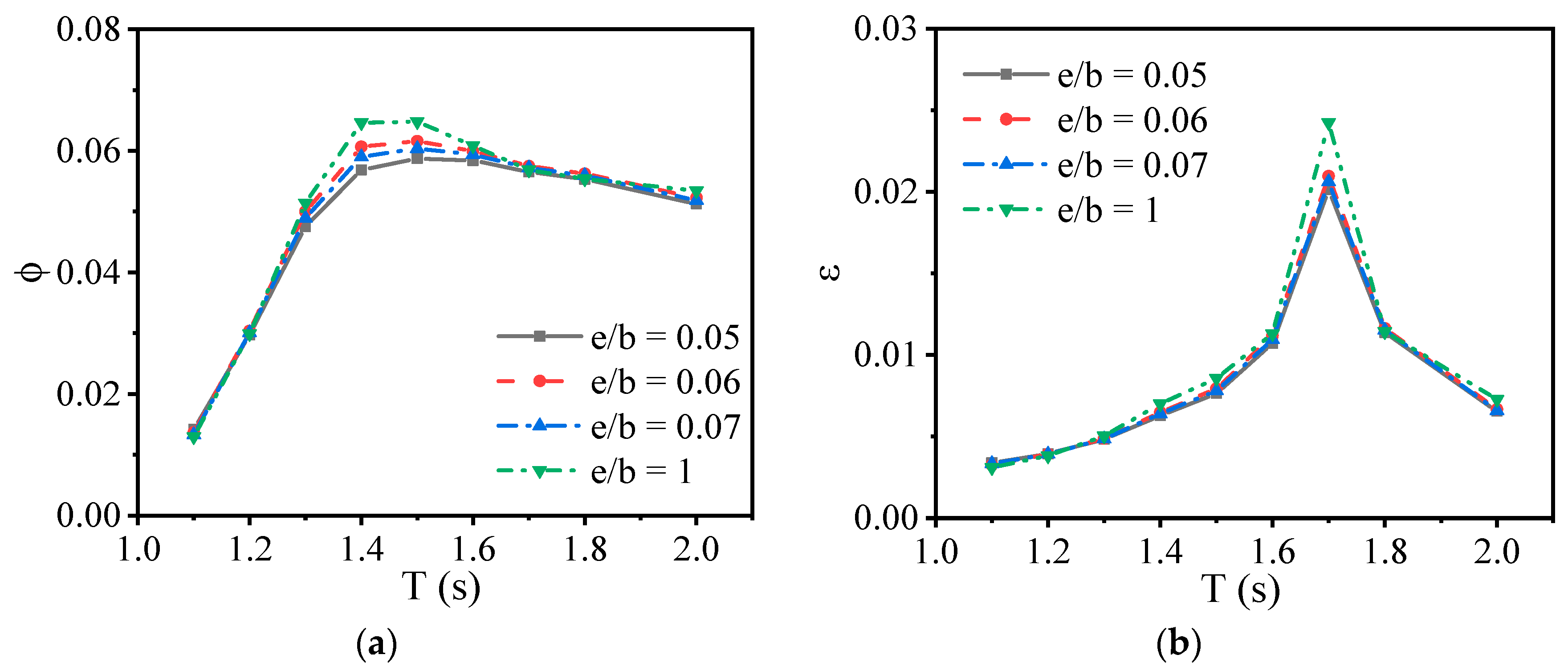



| Case | H (m) | T (s) | e (m) |
|---|---|---|---|
| 1 | 0.08 | 1.3 | 0.05 |
| 2 | 0.08 | 1.3 | 0.009 |
| 3 | 0.08 | 2.2 | 0.009 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, G.; Hu, C.; Li, D.; Ma, Y.; Zhang, X.; Zhu, Y. Hydrodynamic Performance Investigations of OWC and Hybrid System: Geometry of OWC and Rectangular Submerged Breakwater. J. Mar. Sci. Eng. 2024, 12, 2191. https://doi.org/10.3390/jmse12122191
Xie G, Hu C, Li D, Ma Y, Zhang X, Zhu Y. Hydrodynamic Performance Investigations of OWC and Hybrid System: Geometry of OWC and Rectangular Submerged Breakwater. Journal of Marine Science and Engineering. 2024; 12(12):2191. https://doi.org/10.3390/jmse12122191
Chicago/Turabian StyleXie, Guangci, Chao Hu, Dong Li, Yong Ma, Xu Zhang, and Yuanyao Zhu. 2024. "Hydrodynamic Performance Investigations of OWC and Hybrid System: Geometry of OWC and Rectangular Submerged Breakwater" Journal of Marine Science and Engineering 12, no. 12: 2191. https://doi.org/10.3390/jmse12122191
APA StyleXie, G., Hu, C., Li, D., Ma, Y., Zhang, X., & Zhu, Y. (2024). Hydrodynamic Performance Investigations of OWC and Hybrid System: Geometry of OWC and Rectangular Submerged Breakwater. Journal of Marine Science and Engineering, 12(12), 2191. https://doi.org/10.3390/jmse12122191







