Simulation Method and Application of Non-Stationary Random Fields for Deeply Dependent Seabed Soil Parameters
Abstract
1. Introduction
1.1. Soil Liquefaction Risk and Impact
1.2. Spatial Variability of Geotechnical Parameters
1.3. Depth-Dependent Non-Stationary Stochastic Field
1.4. Site Characterization and Methodology
2. Stochastic Simulation Method for Vs-Structure
2.1. Trend Function and Its Uncertainty
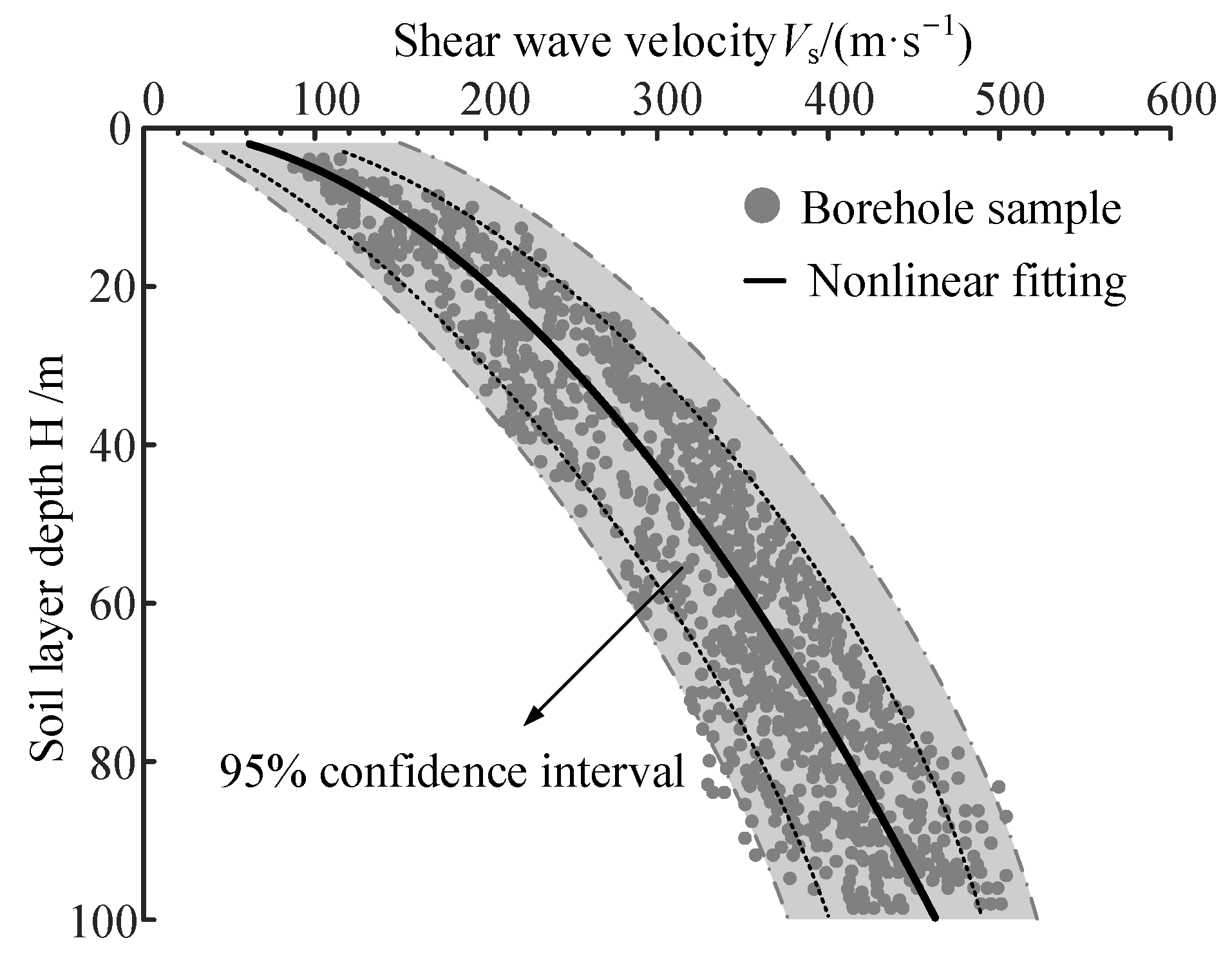
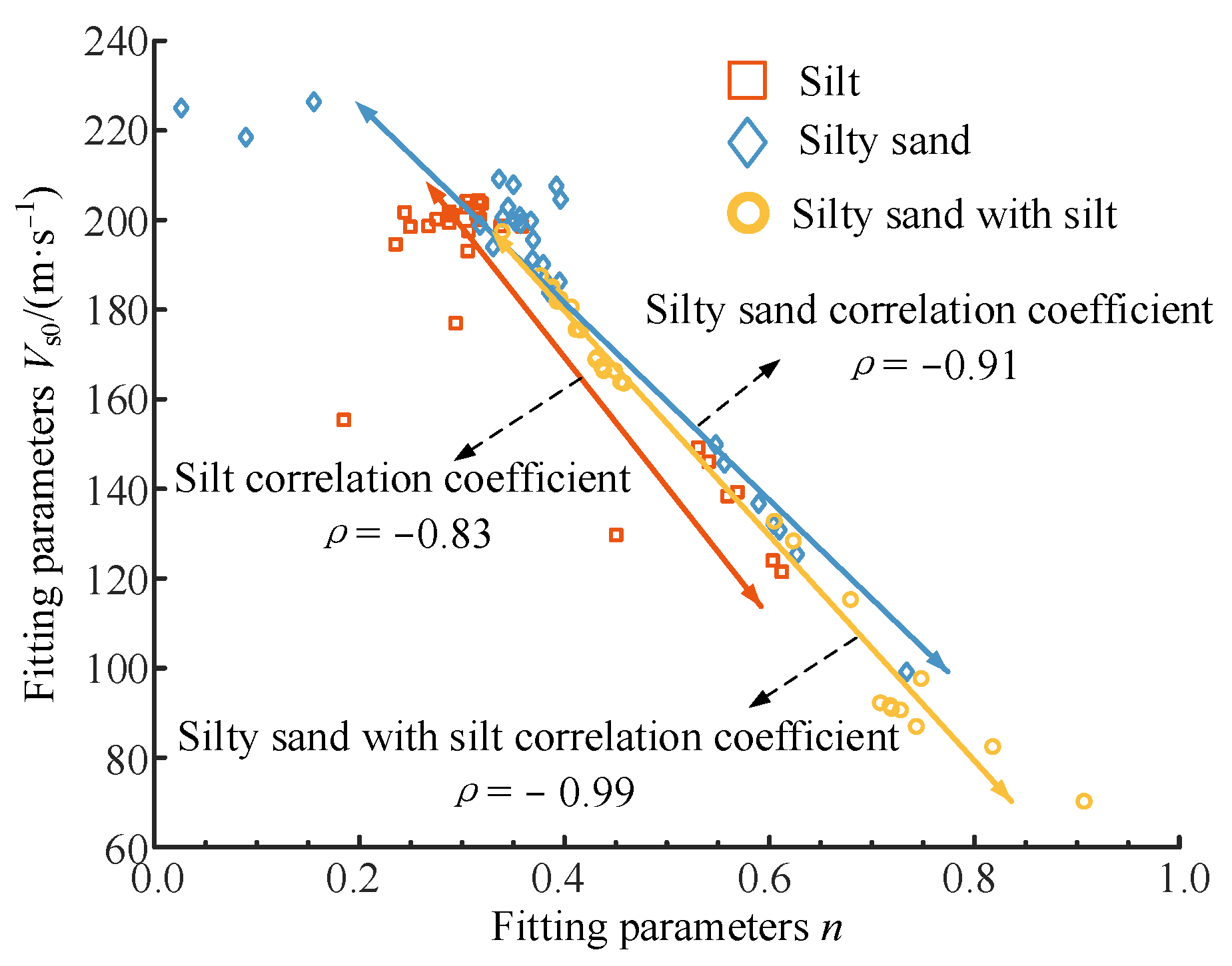
2.1.1. Determination of Trend Functions
2.1.2. Solution for the Mean and Standard Deviation of Soil Vs Varying with h
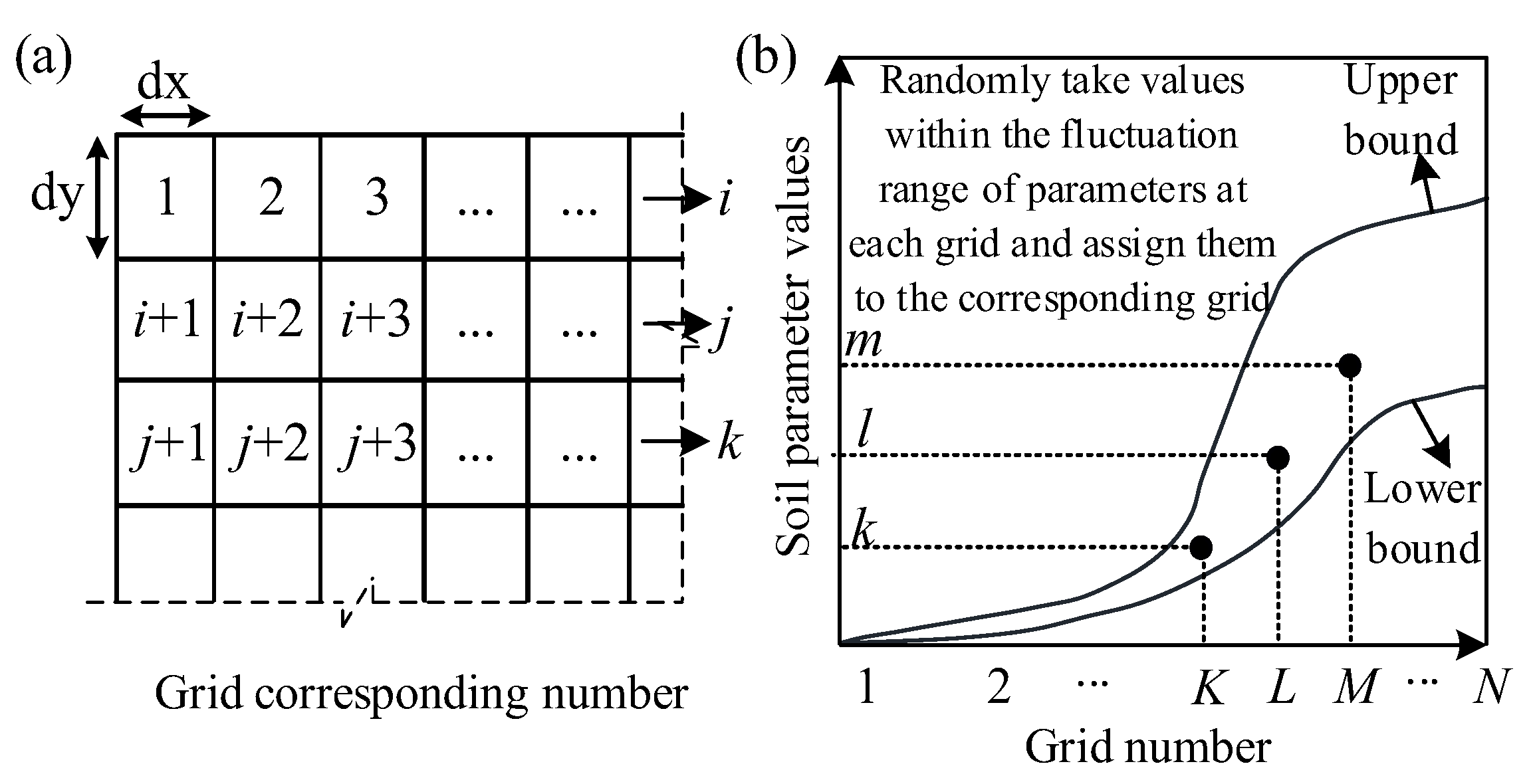
2.2. Simulation of the Random Vs-Structure Field
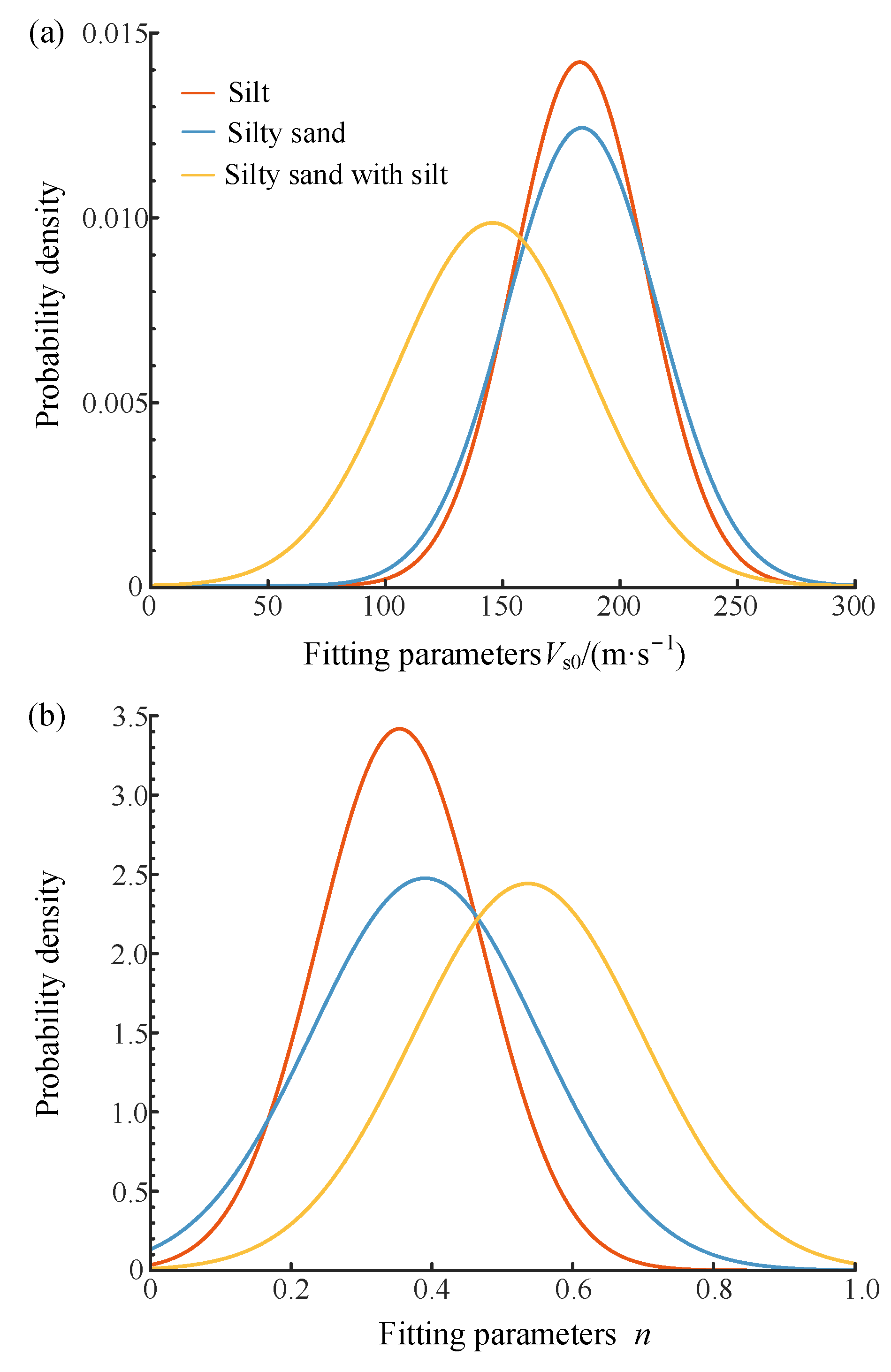
2.2.1. Simulating the Variability of Parameter Vs0 Using Random Variables
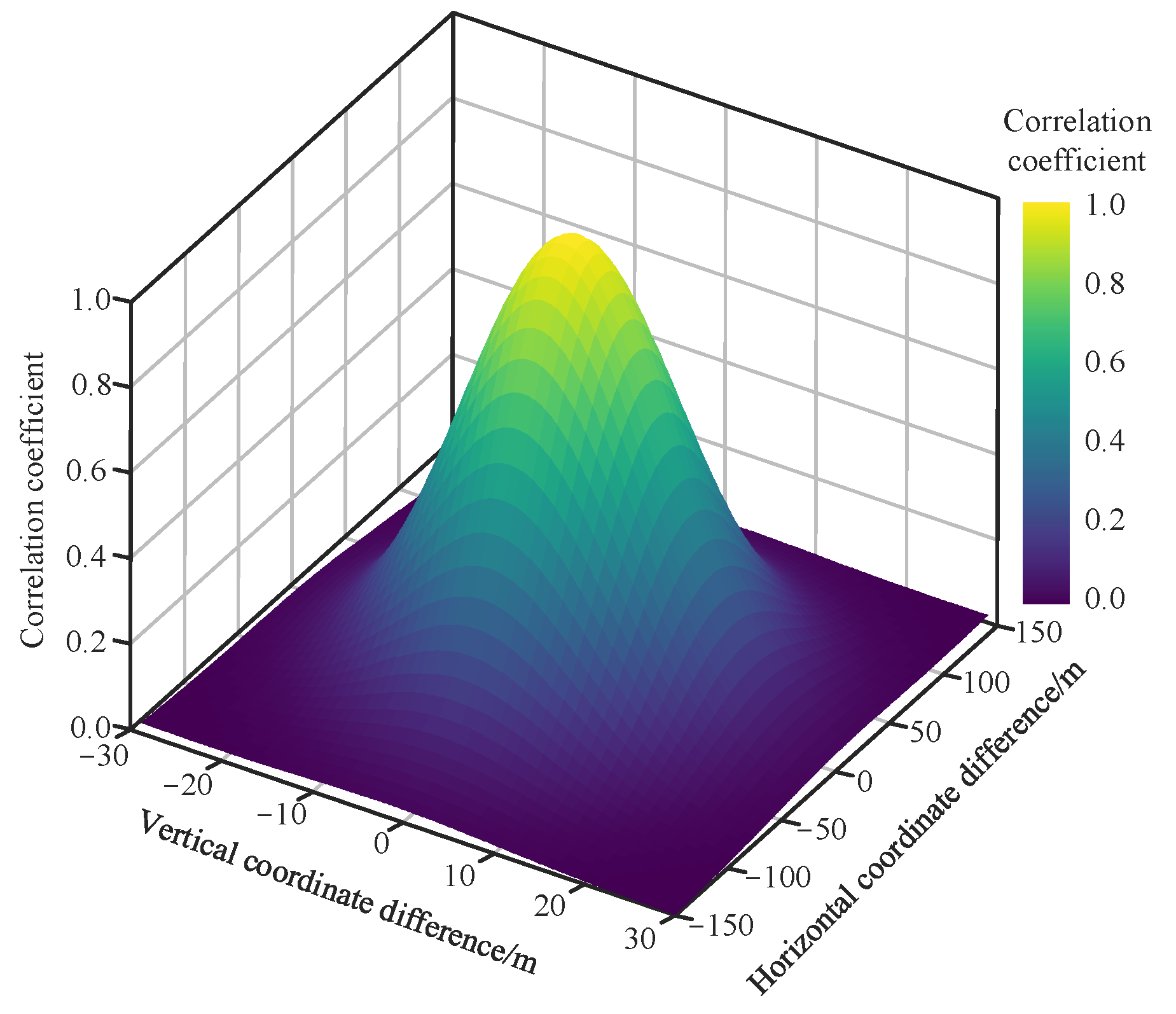
2.2.2. Simulating the Variability of Parameter n Using a Stationary Random Field
2.2.3. Acquisition of the Random Vs-Structure Non-Stationary Random Field
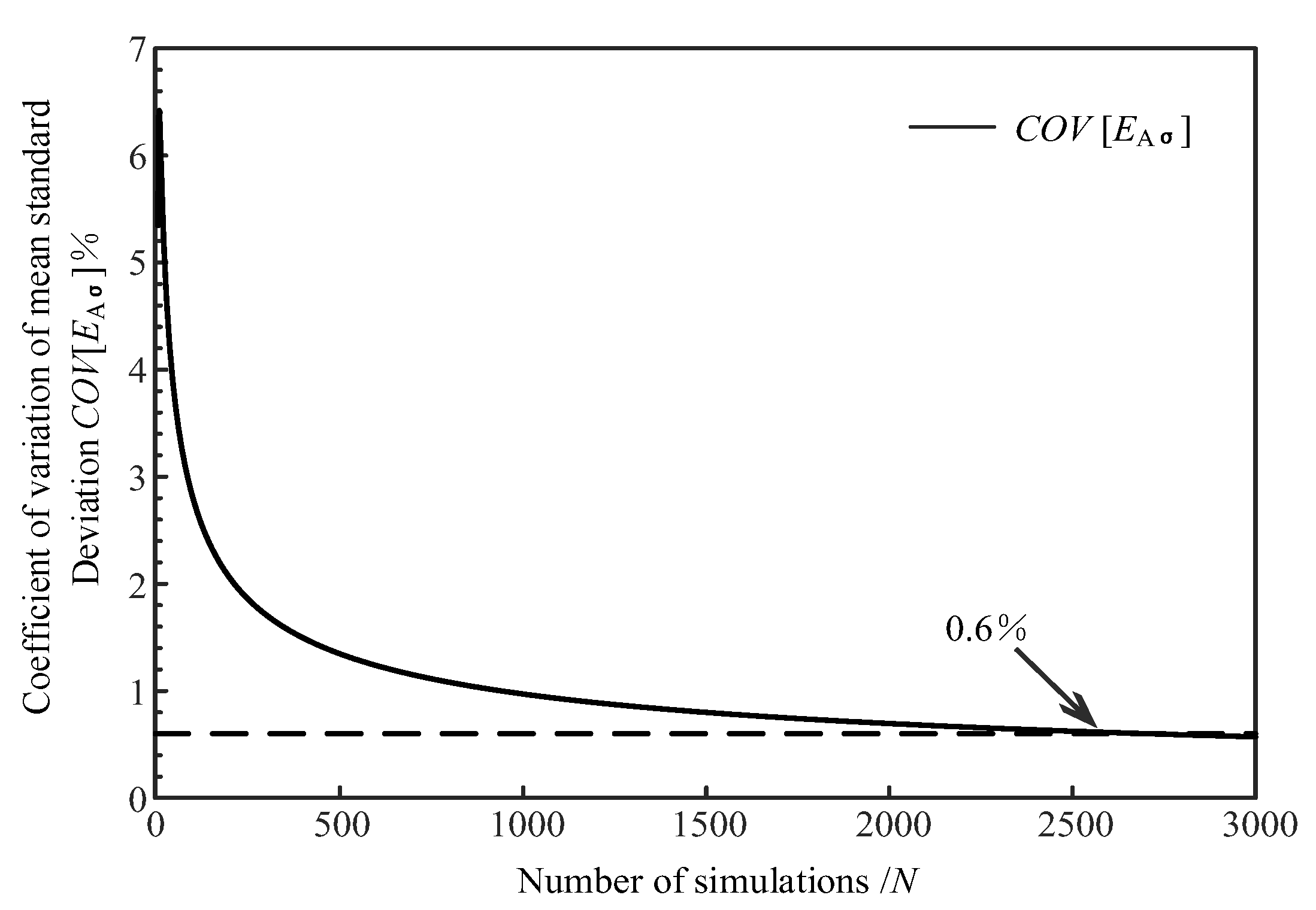
2.3. Determining the Number of Simulations N for the Random Field
3. Results
3.1. Location of the Study Area
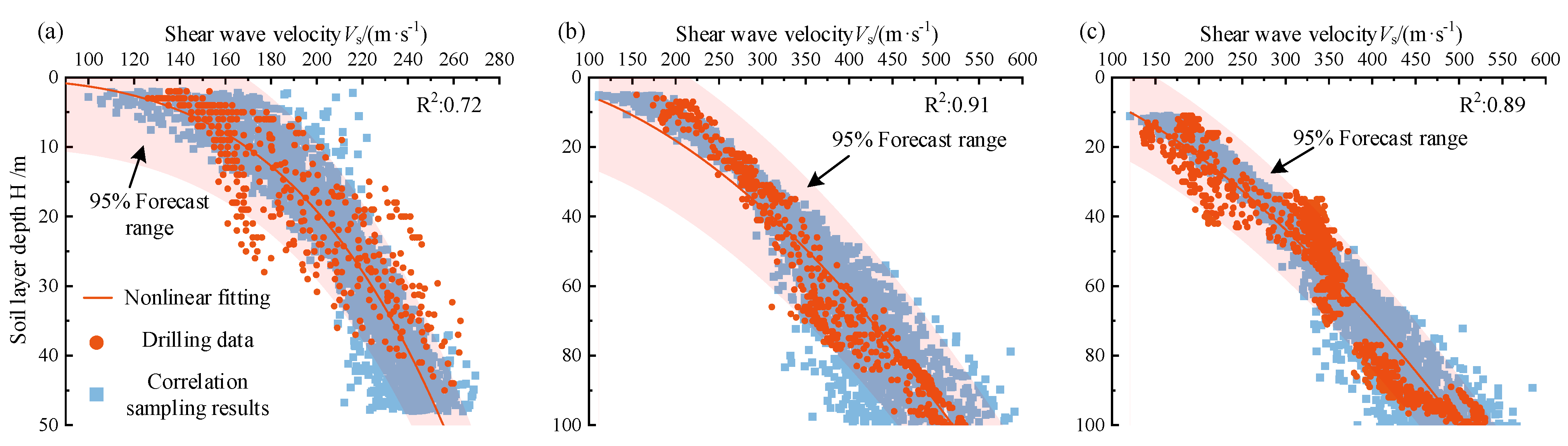
3.2. Statistical Characteristics of Measured Vs Data
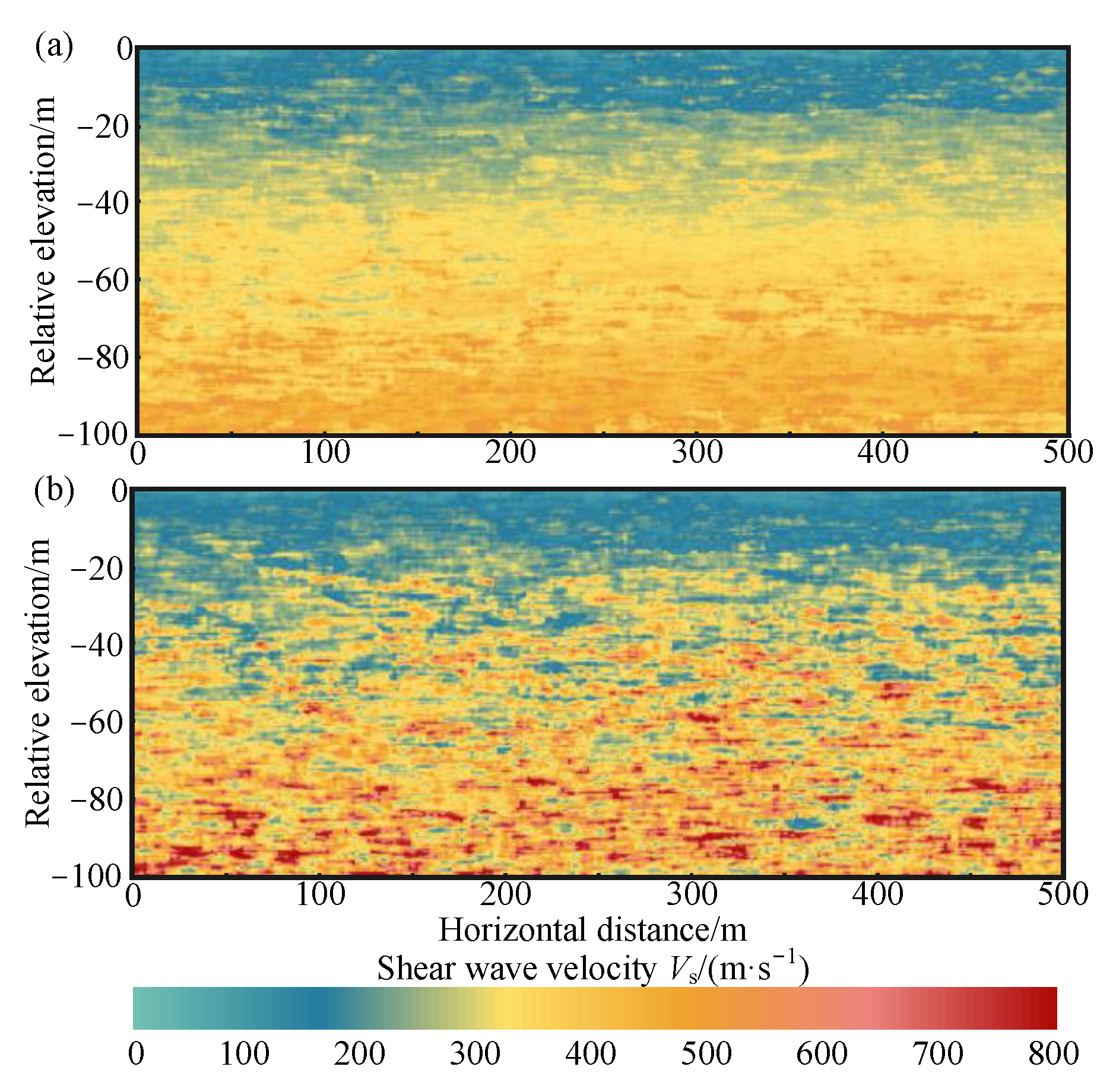
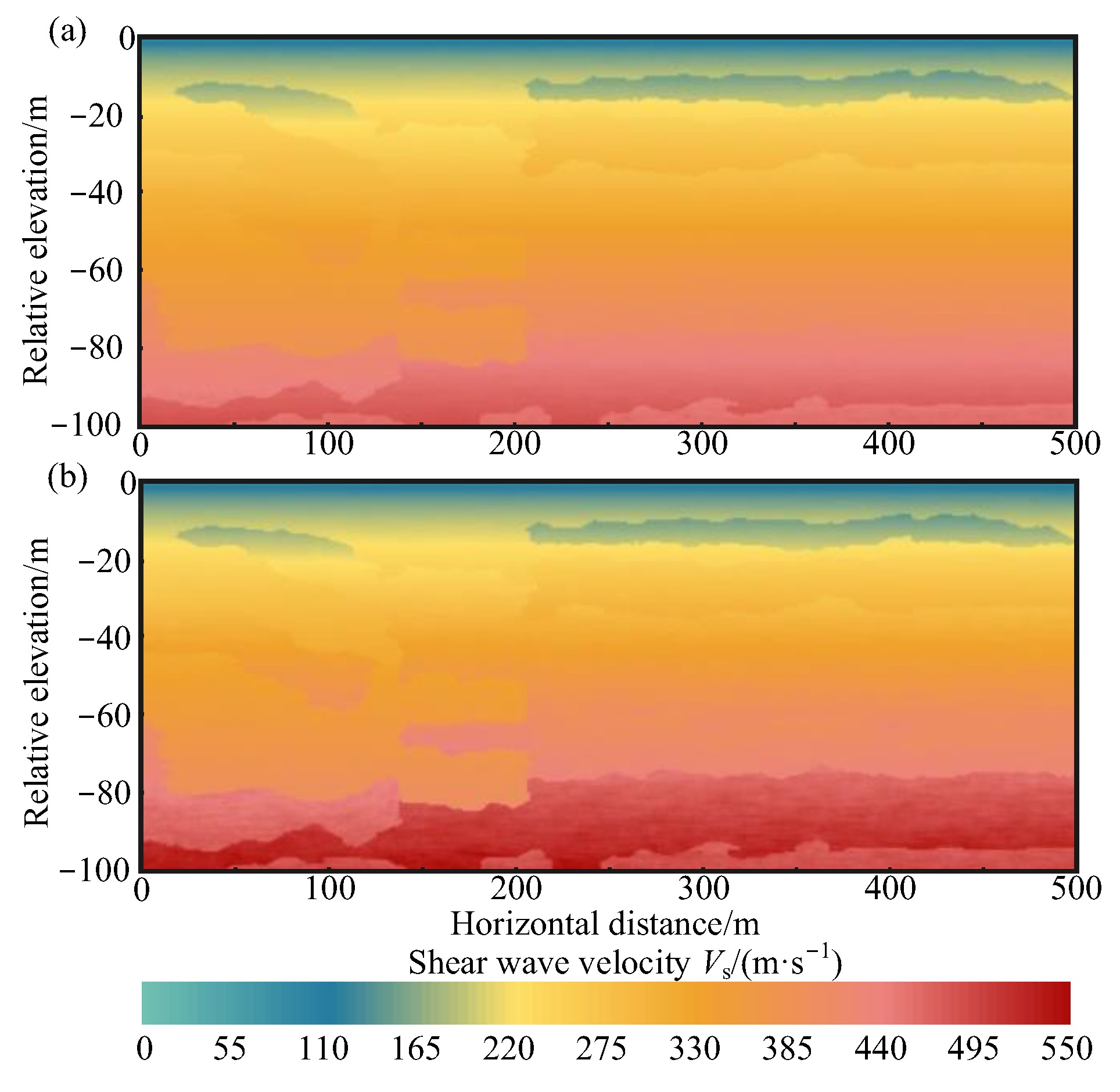
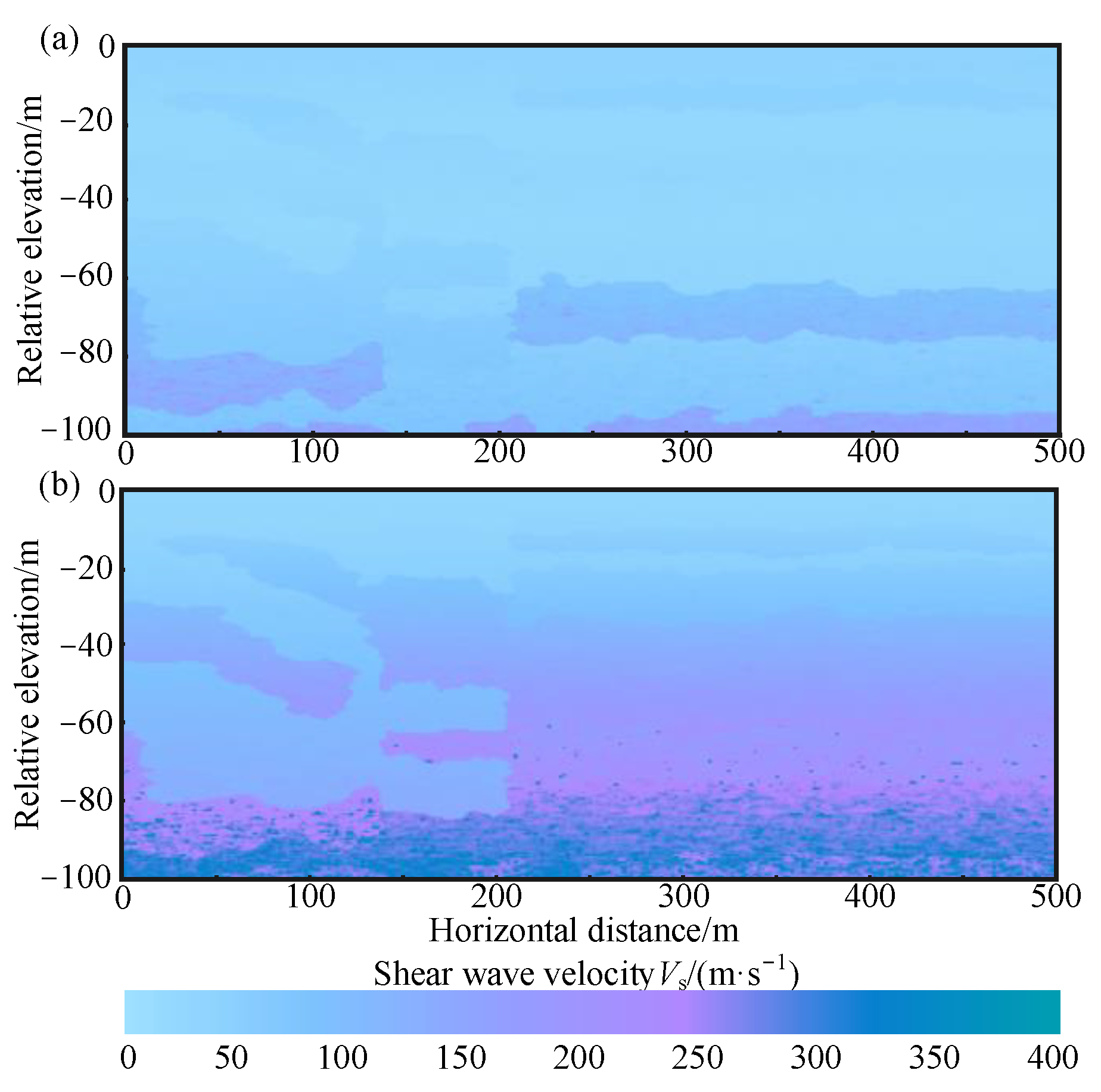
3.3. Simulation of the Non-Stationary Vs-Structure Random Field in the Study Area
4. Discussion
4.1. Liquefaction Discriminant Method for Soil Based on Shear Wave Velocity
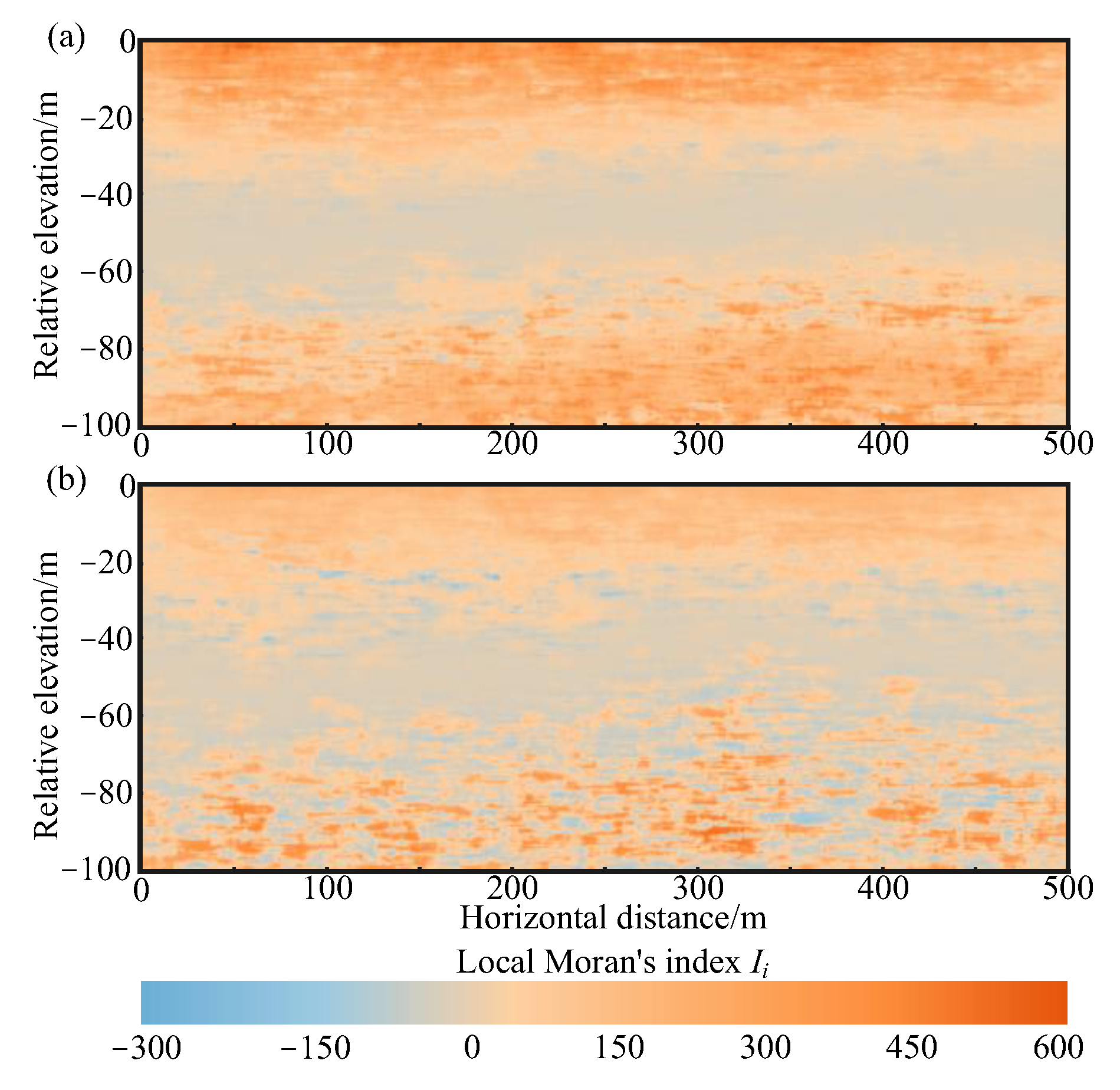
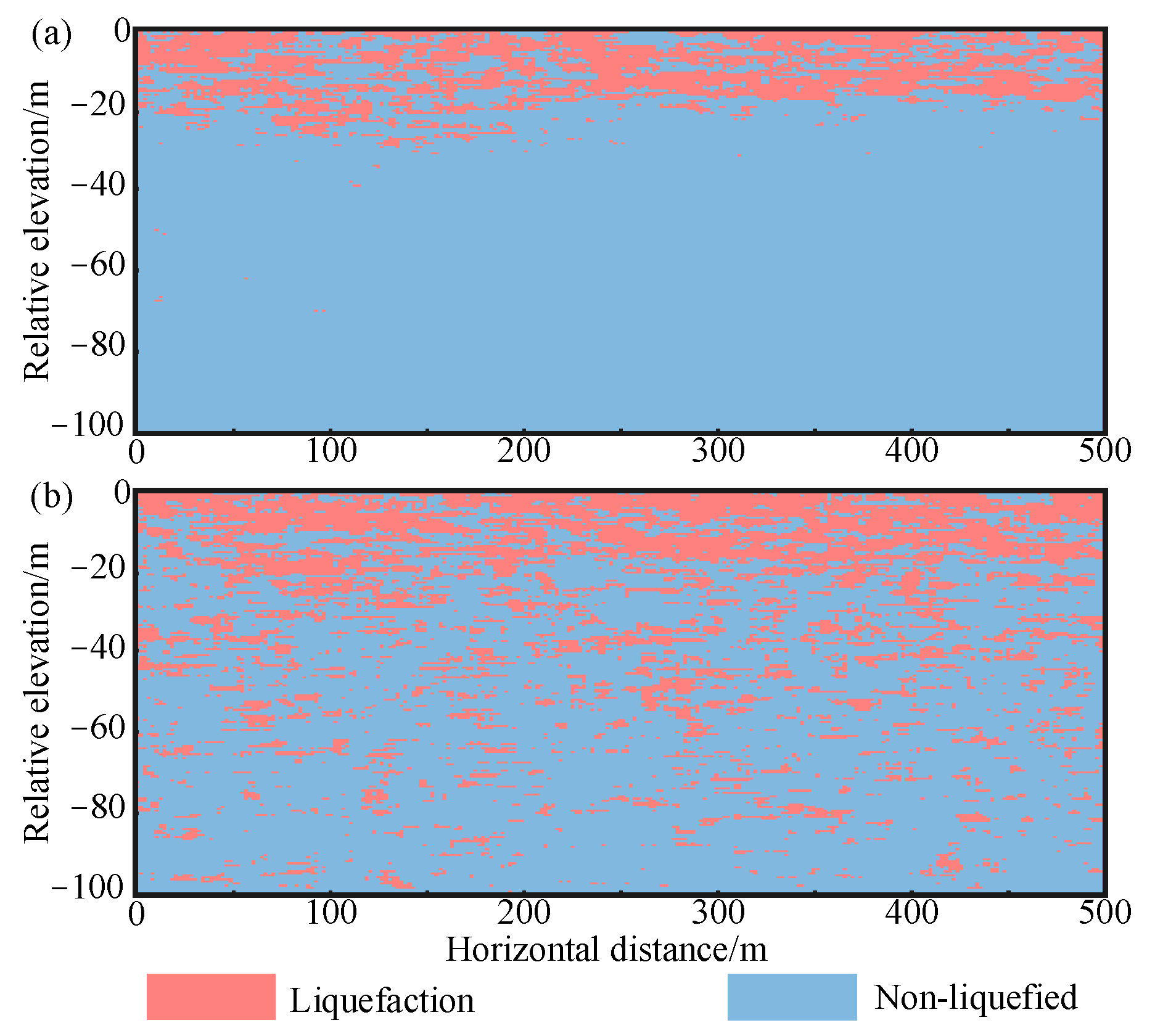
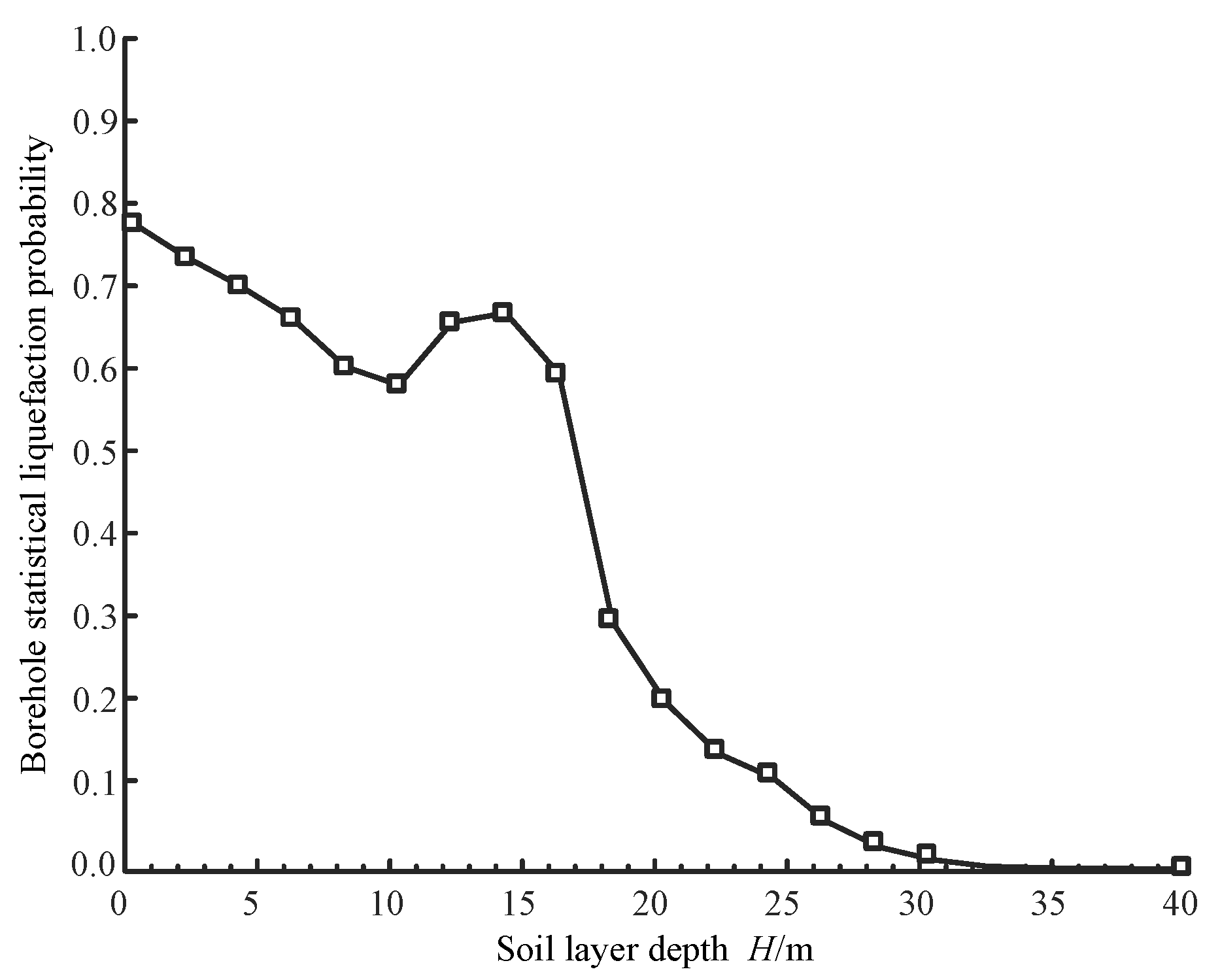
4.2. Liquefaction Discriminant Results in the Study Area
4.3. Verification of Liquefaction Discriminant Accuracy
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Notation | |
| Vs | Shear wave velocity |
| h | Depth |
| Effective overburden pressure | |
| Pa | Standard atmospheric pressure |
| Effective unit weight of the soil | |
| Vs0 | Shear wave velocity of the soil at a fixed depth |
| n | Associated with the soil’s coefficient of uniformity |
| , | Mean values of Vs0, n |
| , | Standard deviations of Vs0, n |
| E[Vs(h)] | Mean values of Vs at different depths |
| p±± | Weight function |
| ρ | Correlation coefficient |
| The second-order moments of Vs | |
| μv, σv | Mean and standard deviation of Vs0 |
| μlnV, σlnV | Log mean and standard deviation of Vs0 |
| δx, δy | Autocorrelation distances in the horizontal and vertical directions |
| R | Autocorrelation coefficient matrix |
| U | Sampling matrix |
| X, Y | Standardized positronic distribution sampling matrix |
| L | Cholesky’s decomposition of the lower triangular matrix |
| μlnn, σlnn | Log mean and standard deviation of n |
| H | Lognormal random field |
| Simulated values of Vs at grid point uα in the lth stochastic simulation | |
| COV[EAσ] | Vs mean standard deviation coefficient of variation |
| Ii | Localized Moran index |
| σv | Soil overburden pressure |
| Effective soil overburden pressure | |
| amax | Peak horizontal ground acceleration |
| g | Gravitational acceleration |
| γd | Soil shear stress reduction factor |
| Kσ, Cσ | Effective overburden pressure correction factor |
| α(z), β(z) | Cyclic stress ratio depth correction factor |
| MSF | Magnitude calibration factor |
| Vs1 | Modified shear wave velocity |
| Fs | Factor of safety for liquefaction potential of soils |
| PL(uα) | Probability of soil liquefaction |
References
- Zhang, Y.; Zhao, K.; Peng, Y.J.; Chen, G.X. Dynamic shear modulus and damping ratio characteristics of undisturbed marine soils in the Bohai Sea, China. Earthq. Eng. Eng. Vib. 2022, 21, 297–312. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Hyodo, M.; Goda, K.; Tazoh, T.; Taylor, C.A. Liquefaction of soil in the Tokyo Bay area from the 2011 Tohoku (Japan) earthquake. Soil Dyn. Earthq. Eng. 2011, 31, 1618–1628. [Google Scholar] [CrossRef]
- Orense, R.P.; Pender, M.J.; Wotherspoon, L.M. Analysis of soil liquefaction during the recent Canterbury (New Zealand) earthquakes. Geotech. Eng. J. Seags Agssea 2012, 43, 8–17. [Google Scholar]
- Sonmez, B.; Ulusay, R. Liquefaction potential at Izmit Bay: Comparison of predicted and observed soil liquefaction during the Kocaeli earthquake. Bull. Eng. Geol. Environ. 2008, 67, 1–9. [Google Scholar] [CrossRef]
- Andrus, R.D.; Stokoe II, K.H. Liquefaction resistance of soils from shear-wave velocity. J. Geotech. Geoenviron. 2000, 126, 1015–1025. [Google Scholar] [CrossRef]
- Chen, G.X.; Kong, M.Y.; Khoshnevisan, S.; Chen, W.Y.; Li, X.J. Calibration of Vs-based empirical models for assessing soil liquefaction potential using expanded database. Bull. Eng. Geol. Environ. 2019, 78, 945–957. [Google Scholar] [CrossRef]
- Liu, W.X.; Juang, C.H.; Chen, Q.S.; Chen, G.X. Dynamic site response analysis in the face of uncertainty–an approach based on response surface method. Int. J. Numer. Anal. Met. 2021, 45, 1854–1867. [Google Scholar] [CrossRef]
- Al-Jeznawi, D.; Sadik, L.; Al-Janabi, M.A.Q.; Alzabeebee, S.; Hajjat, J.; Keawsawasvong, S. Developing Vs-NSPT Prediction Models Using Bayesian Framework. Transp. Infrastruct. Geotechnol. 2024, 11, 1777–1798. [Google Scholar] [CrossRef]
- Esfehanizadeh, M.; Nabizadeh, F.; Yazarloo, R. Correlation between standard penetration (NSPT) and shear wave velocity (VS) for young coastal sands of the Caspian Sea. Arab. J. Geosci. 2015, 8, 7333–7341. [Google Scholar] [CrossRef]
- Hossain, M.B.; Rahman, M.M.; Haque, M.R. Empirical correlation between shear wave velocity (Vs) and uncorrected standard penetration resistance (SPT-N) for Dinajpur District, Bangladesh. J. Nat. 2021, 3, 25–29. [Google Scholar] [CrossRef]
- Kishida, T.; Tsai, C. Prediction Model of Shear Wave Velocity by Using SPT Blow Counts Based on the Conditional Probability Framework. J. Geotech. Geoenviron. 2017, 143, 4016108. [Google Scholar] [CrossRef]
- Dobry, R.; Abdoun, T.; Stokoe, K.H.; Moss, R.E.S.; Hatton, M.; El, G.H. Liquefaction Potential of Recent Fills versus Natural Sands Located in High-Seismicity Regions Using Shear-Wave Velocity. J. Geotech. Geoenviron. 2015, 141, 4014112. [Google Scholar] [CrossRef]
- Chen, G.X.; Zhu, J.; Qiang, M.Y.; Gong, W.P. Three-dimensional site characterization with borehole data—A case study of Suzhou area. Eng. Geol. 2018, 234, 65–82. [Google Scholar] [CrossRef]
- Wang, R.H.; Li, D.Q.; Wang, M.Y.; Liu, Y. Deterministic and Probabilistic Investigations of Piping Occurrence during Tunneling through Spatially Variable Soils. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2021, 7, 4021009. [Google Scholar] [CrossRef]
- Hussien, M.N.; Karray, M. Shear wave velocity as a geotechnical parameter: An overview. Can. Geotech. J. 2015, 53, 252–272. [Google Scholar] [CrossRef]
- Jha, S.K.; Ching, J.Y. Simplified reliability method for spatially variable undrained engineered slopes. Soils Found. 2013, 53, 708–719. [Google Scholar] [CrossRef]
- Jiang, S.H.; Huang, J.S. Efficient slope reliability analysis at low-probability levels in spatially variable soils. Comput. Geotech. 2016, 75, 18–27. [Google Scholar] [CrossRef]
- Jiang, S.H.; Huang, J.S.; Griffiths, D.V.; Deng, Z.P. Advances in reliability and risk analyses of slopes in spatially variable soils: A state-of-the-art review. Comput. Geotech. 2022, 141, 104498. [Google Scholar] [CrossRef]
- Liu, L.L.; Cheng, Y.M.; Pan, Q.J.; Dias, D. Incorporating stratigraphic boundary uncertainty into reliability analysis of slopes in spatially variable soils using one-dimensional conditional Markov chain model. Comput. Geotech. 2020, 118, 103321. [Google Scholar] [CrossRef]
- Zhu, B.; Pei, H.F.; Yang, Q. Reliability analysis of submarine slope considering the spatial variability of the sediment strength using random fields. Appl. Ocean. Res. 2019, 86, 340–350. [Google Scholar] [CrossRef]
- Liu, W.X.; Chen, Q.S.; Wang, C.F.; Chen, G.X. Spatially correlated multiscale Vs30 mapping and a case study of the Suzhou site. Eng. Geol. 2017, 220, 110–122. [Google Scholar] [CrossRef]
- Liu, W.X.; Juang, C.H.; Peng, Y.J.; Chen, G.X. Regional characterization of vs30 with hybrid geotechnical and geological data. Undergr. Space 2023, 11, 218–231. [Google Scholar] [CrossRef]
- Lyu, B.; Hu, Y.; Wang, Y. Data-Driven Development of Three-Dimensional Subsurface Models from Sparse Measurements Using Bayesian Compressive Sampling: A Benchmarking Study. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2023, 9, 4023010. [Google Scholar] [CrossRef]
- Phoon, K.K.; Kulhawy, F.H. Characterization of geotechnical variability. Can. Geotech. J. 1999, 36, 612–624. [Google Scholar] [CrossRef]
- Vanmarcke, E.H. Probabilistic modeling of soil profiles. J. Geotech. Eng. Div. 1977, 103, 1227–1246. [Google Scholar] [CrossRef]
- Carle, S.F.; Fogg, G.E. Modeling Spatial Variability with One and Multidimensional Continuous-Lag Markov Chains. Math. Geol. 1997, 29, 891–918. [Google Scholar] [CrossRef]
- Carle, S.F.; Fogg, G.E. Integration of soft data into geostatistical simulation of categorical variables. Front. Earth Sci. 2020, 8, 565707. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Fenton, G.A. Probabilistic slope stability analysis by finite elements. J. Geotech. Geoenviron. 2004, 130, 507–518. [Google Scholar] [CrossRef]
- Griffiths, D.; Yu, X. Another look at the stability of slopes with linearly increasing undrained strength. Geotechnique 2015, 65, 824–830. [Google Scholar] [CrossRef]
- Li, N.; Zhang, Y.; Huang, L. Real-Time Slope Monitoring System and Risk Communication among Various Parties: Case Study for a Large-Scale Slope in Shenzhen, China. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2021, 7, 4021051. [Google Scholar] [CrossRef]
- Zhang, Z.; Niu, Q.; Liu, X.; Zhang, Y.; Zhao, T.S.; Liu, M. Durability Life Prediction of Reinforced Concrete Structure Corroded by Chloride Based on the Gamma Process. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2021, 7, 4021061. [Google Scholar] [CrossRef]
- Zhou, M.L.; Shadabfar, M.; Xue, Y.D.; Zhang, Y.; Huang, H. Probabilistic Analysis of Tunnel Roof Deflection under Sequential Excavation Using ANN-Based Monte Carlo Simulation and Simplified Reliability Approach. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2021, 7, 4021043. [Google Scholar] [CrossRef]
- Gong, W.P.; Juang, C.H.; Martin, J.R.; Tang, H.M.; Wang, Q.Q.; Huang, H.W. Probabilistic analysis of tunnel longitudinal performance based upon conditional random field simulation of soil properties. Tunn. Undergr. Space Technol. 2018, 73, 1–14. [Google Scholar] [CrossRef]
- Gong, W.P.; Zhao, C.; Juang, C.H.; Zhang, Y.J.; Tang, H.M.; Lu, Y.C. Coupled characterization of stratigraphic and geo-properties uncertainties—A conditional random field approach. Eng. Geol. 2021, 294, 106348. [Google Scholar] [CrossRef]
- Li, D.Q.; Qi, X.H.; Phoon, K.K.; Zhang, L.M.; Zhou, C.B. Effect of spatially variable shear strength parameters with linearly increasing mean trend on reliability of infinite slopes. Struct. Saf. 2014, 49, 45–55. [Google Scholar] [CrossRef]
- Liu, W.X.; Chen, Q.S.; Juang, C.H.; Chen, G.X. Uncertainty propagation of soil property in dynamic site response under different site conditions. Int. J. Numer. Anal. Met. 2023, 47, 1521–1538. [Google Scholar] [CrossRef]
- Lumb, P. The variability of natural soils. Can. Geotech. J. 1966, 3, 74–97. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; Li, D.Q. Investigation of slope failure mode evolution during large deformation in spatially variable soils by random limit equilibrium and material point methods. Comput. Geotech. 2019, 111, 301–312. [Google Scholar] [CrossRef]
- Jiang, S.H.; Huang, J.S. Modeling of non-stationary random field of undrained shear strength of soil for slope reliability analysis. Soils Found. 2018, 58, 185–198. [Google Scholar] [CrossRef]
- Fu, C.J.; Wang, J.G.; Zhao, T.L. Analytical Calculation of Instantaneous Liquefaction of a Seabed around Buried Pipelines Induced by Cnoidal Waves. J. Mar. Sci. Eng. 2023, 11, 1319. [Google Scholar] [CrossRef]
- Ma, J.Y.; Zhao, H.Y.; Jeng, D.S. Numerical Modeling of Composite Load-Induced Seabed Response around a Suction Anchor. J. Mar. Sci. Eng. 2024, 12, 189. [Google Scholar] [CrossRef]
- Wu, Q.; Lu, Q.R.; Guo, Q.Z.; Zhao, K.; Chen, P.; Chen, G.X. Experimental Investigation on Small-Strain Stiffness of Marine Silty Sand. J. Mar. Sci. Eng. 2020, 8, 360. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Cui, L.; Zhai, H.L.; Jeng, D.S. Assessment of Wave–Current-Induced Liquefaction under Twin Pipelines Using the Coupling Model. J. Mar. Sci. Eng. 2023, 11, 1372. [Google Scholar] [CrossRef]
- Poom, L.; Af Wåhlberg, A. Accuracy of conversion formula for effect sizes: A Monte Carlo simulation. Res. Synth. Methods 2022, 13, 508–519. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.J.; Wu, S.C.; Zhang, Z.X.; Huang, S.G. Reliability analysis of rock slopes considering the uncertainty of joint spatial distributions. Comput. Geotech. 2023, 161, 105566. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, G.X.; Zhao, K.; Peng, Y.J.; Jiang, Z.J.; Yang, W.B. Prediction uncertainty characteristics of dynamic shear modulus ratio and damping ratio of marine soil. Eng. Mech. 2023, 40, 161–171. [Google Scholar] [CrossRef]
- Rosenblueth, E. Two-point estimates in probabilities. Appl. Math. Model. 1981, 5, 329–335. [Google Scholar] [CrossRef]
- Andrus, R.D.; Chung, R.M.; Juang, C.H.; Stokoe, K.H. Guidelines for Evaluating Liquefaction Resistance Using Shear Wave Velocity Measurement and Simplified Procedures; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2003. [Google Scholar]
- Hardin, B.O.; Black, W.L. Sand stiffness under various triaxial stresses. J. Soil. Mech. Found. Div. 1966, 92, 27–42. [Google Scholar] [CrossRef]
- Hardin, B.O.; Richart, F.E. Elastic Wave Velocities in Granular Soils. J. Soil. Mech. Found. Div. 1963, 89, 33–65. [Google Scholar] [CrossRef]
- Menq, F.; Stokoe, K. Linear dynamic properties of sandy and gravelly soils from large-scale resonant tests. In Deformation Characteristics of Geomaterials/Comportement Des Sols Et Des Roches Tendres; Swets and Zeitlinger: Lisse, The Netherlands, 2003. [Google Scholar]
- Wichtmann, T.; Triantafyllidis, T. Influence of the grain-size distribution curve of quartz sand on the small strain shear modulus G max. J. Geotech. Geoenviron. 2009, 135, 1404–1418. [Google Scholar] [CrossRef]
- Chen, Z.H.; Huang, K.H. Layered non-stationary random field model for reliability analysis of soil slopes. Chin. J. Geotech. Eng. 2020, 42, 1247–1256. [Google Scholar] [CrossRef]
- Hoffman, Y. Gaussian Fields and Constrained Simulations of the Large-Scale Structure; Springer: Berlin/Heidelberg, Germany, 2008; pp. 565–583. [Google Scholar]
- Li, J.; Liu, Y.; Fu, Q.L.; Dai, M.N.; Wei, P.F. Study on soil disturbance area under shield tunneling based on field shear wave velocity test. J. Zhejiang Univ. Technol. 2023, 51, 146–151. [Google Scholar]
- Wilson, S.D.; Brown, F.R.; Schwarz, S.D. In Situ Determination of Dynamic Soil Properties; Dynamic Geotechnical Testing; ASTM International: West Conshohocken, PA, USA, 1978. [Google Scholar] [CrossRef]
- Cami, B.; Javankhoshdel, S.; Phoon, K.K.; Ching, J.Y. Scale of Fluctuation for Spatially Varying Soils: Estimation Methods and Values. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2020, 6, 3120002. [Google Scholar] [CrossRef]




| Soil Type | Depth (m) | Vs (m/s) | SPT | γ (kN/m3) | Compaction | Gmax (kPa) |
|---|---|---|---|---|---|---|
| Silt | 0–20 | 81–161 | 1–14 | 18.7–19.3 | Loose | 14.5–24.3 |
| 20–40 | 158–248 | 6–27 | 19.3–20.1 | Medium Dense | 32.4–53.8 | |
| 40–60 | 220–365 | - | 18.9–20.3 | Medium Dense | 53.5–79.2 | |
| 60–80 | - | - | 19.5–20.2 | Dense | 68.8–84.9 | |
| 80–100 | - | - | - | Dense | - | |
| Silty sand | 0–20 | 120–181 | 2–10 | - | - | - |
| 20–40 | 169–275 | 7–38 | 19.4–19.8 | Medium Dense | 45.8–53.8 | |
| 40–60 | 255–393 | - | 19.8–20.2 | Dense | 53.6–57.9 | |
| 60–80 | 304–460 | - | 19.5–20.1 | Dense | 94.6–96.2 | |
| 80–100 | 345–510 | - | 19.7–20.3 | Dense | 94.4–114.8 | |
| Silty sand with silt | 0–20 | 135–245 | 3–26 | 19.7–20.0 | Loose | 24.7–25.1 |
| 20–40 | 136–318 | 3–60 | 19.9–20.4 | Medium Dense | 22.3–47.5 | |
| 40–60 | 266–405 | - | - | - | - | |
| 60–80 | 334–464 | - | - | - | - | |
| 80–100 | 392–530 | - | 20.4–21.0 | Dense | 98.7–110.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Xu, G.; Pan, F.; Zhang, Y.; Huang, J.; Zhou, Z. Simulation Method and Application of Non-Stationary Random Fields for Deeply Dependent Seabed Soil Parameters. J. Mar. Sci. Eng. 2024, 12, 2183. https://doi.org/10.3390/jmse12122183
Zhang Z, Xu G, Pan F, Zhang Y, Huang J, Zhou Z. Simulation Method and Application of Non-Stationary Random Fields for Deeply Dependent Seabed Soil Parameters. Journal of Marine Science and Engineering. 2024; 12(12):2183. https://doi.org/10.3390/jmse12122183
Chicago/Turabian StyleZhang, Zhengyang, Guanlan Xu, Fengqian Pan, Yan Zhang, Junpeng Huang, and Zhenglong Zhou. 2024. "Simulation Method and Application of Non-Stationary Random Fields for Deeply Dependent Seabed Soil Parameters" Journal of Marine Science and Engineering 12, no. 12: 2183. https://doi.org/10.3390/jmse12122183
APA StyleZhang, Z., Xu, G., Pan, F., Zhang, Y., Huang, J., & Zhou, Z. (2024). Simulation Method and Application of Non-Stationary Random Fields for Deeply Dependent Seabed Soil Parameters. Journal of Marine Science and Engineering, 12(12), 2183. https://doi.org/10.3390/jmse12122183





