Numerical Study of the Hydrodynamic Performance of a Dual-Chamber Oscillating Water Column Wave Energy Converter Device
Abstract
1. Introduction
2. Materials and Methods
2.1. Viscous Flow Model
2.2. Numerical Model Setup
2.3. Numerical Results Validation
2.3.1. Convergence Test for Numerical Computational Grids
2.3.2. Verification
3. Results and Discussion
3.1. Dual-Chamber OWC Wave Surface and Pressure
3.2. Dual-Chamber OWC Energy Conversion Efficiency
3.3. Dual-Chamber OWC Wave Energy Absorption
3.4. Dual-Chamber OWC Wave Forces on Front Wall
3.5. Dual-Chamber OWC Internal Flow Field
4. Conclusions
- (1)
- Compared to the single-chamber setup, the dual-chamber OWC’s energy conversion efficiency was noticeably higher. In the resonance zone, energy conversion efficiency increased by about 25% in the dual-chamber OWC.
- (2)
- Compared to the single-chamber OWC, the dual-chamber OWC had a wider resonance bandwidth, particularly within the wavenumber range of kh = 2–3. This wider resonance range can be attributed to the presence of two or more resonant frequencies in the dual-chamber configuration, which leads to a more consistent improvement in efficiency compared to the single-chamber design.
- (3)
- Compared to the single-chamber arrangement, the dual-chamber OWC had increased internal chamber pressure and wave surface elevation. Higher chamber pressure and larger oscillation amplitudes indicate enhanced internal wave motion, which enables the dual-chamber OWC to absorb more wave energy and increase energy conversion efficiency.
- (4)
- Although the single-chamber OWC captured more wave energy per unit chamber than the individual sub-chambers of the dual-chamber OWC, the dual-chamber system demonstrated alternating peaks in energy capture over multiple cycles. This behavior was likely due to the asymmetric oscillations of the water surface within the chambers.
- (5)
- Two vortices of equal size and opposite directions were generated near the air vents of the chamber. These vortices merged to form a stable vortex (vortex E) that remained in the rear chamber without dissipating against the rear wall. This persistent vortex enhances the energy conversion efficiency by maintaining continuous air movement within the chamber thereby significantly influencing the surface wave behavior.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qing, L.U.; Shi, H.-d. Progress and future trend of wave energy technology in China. Coast. Eng. 2022, 41, 1–12. [Google Scholar]
- Falnes, J. Radiation impedance matrix and optimum power absorption for interacting oscillators in surface waves. Appl. Ocean Res. 1980, 2, 75–80. [Google Scholar] [CrossRef]
- John Ashlin, S.J.; Sundar, V.; Sannasiraj, S.A. Effects of bottom profile of an oscillating water column device on its hydrodynamic characteristics. Renew. Energy 2016, 96, 341–353. [Google Scholar] [CrossRef]
- Ning, D.Z.; Wang, R.Q.; Zou, Q.P.; Teng, B. An experimental investigation of hydrodynamics of a fixed OWC Wave Energy Converter. Appl. Energy 2016, 168, 636–648. [Google Scholar] [CrossRef]
- Deng, Z.; Ou, Z.; Ren, X.; Zhang, D.; Si, Y. Theoretical analysis of an asymmetric offshore-stationary oscillating water column device with bottom plate. J. Waterw. Port Coast. Ocean Eng. 2020, 146, 04020013. [Google Scholar] [CrossRef]
- Nader, J.R.; Zhu, S.P.; Cooper, P.; Stappenbelt, B. A finite-element study of the efficiency of arrays of oscillating water column wave energy converters. Ocean Eng. 2012, 43, 72–81. [Google Scholar] [CrossRef]
- Evans, D.V. The oscillating water column wave-energy device. IMA J. Appl. Math. 1978, 22, 423–433. [Google Scholar] [CrossRef]
- Evans, D.V.; Porter, R. Hydrodynamic characteristics of an oscillating water column device. Appl. Ocean Res. 1995, 17, 155–164. [Google Scholar] [CrossRef]
- Josset, C.; Clément, A.H. A time-domain numerical simulator for oscillating water column wave power plants. Renew. Energy 2007, 32, 1379–1402. [Google Scholar] [CrossRef]
- Gomes, R.; Henriques, J.; Gato, L.; Falcão, A. Hydrodynamic optimization of an axisymmetric floating oscillating water column for wave energy conversion. Renew. Energy 2012, 44, 328–339. [Google Scholar] [CrossRef]
- Zhou, Y.; Ning, D.; Liang, D.; Cai, S. Nonlinear hydrodynamic analysis of an offshore oscillating water column wave energy converter. Renew. Sustain. Energy Rev. 2021, 145, 111086. [Google Scholar] [CrossRef]
- Dezhi, N.; Jin, S.H.I.; Bin, T.; Haitao, Z. Numerical simulation of a land-based oscillating water column wave energy conversion device. J. Harbin Eng. Univ. 2014, 7, 789–794. [Google Scholar]
- Zhu, J.L.; Tang, P.; Zhang, H.S.; Zheng, P.B. Numerical study of hydrodynamic characteristics of a three-dimensional oscillating water column wave-power device. J. Mar. Sci. Eng. 2024, 12, 1161. [Google Scholar] [CrossRef]
- Hsieh, M.-F.; Lin, H.; Dorrell, D.G.; Hsieh, M.-J.; Lin, C.-C. Development of a wave energy converter using a two chamber oscillating water column. IEEE Trans. Sustain. Energy 2012, 3, 482–497. [Google Scholar] [CrossRef]
- Rezanejad, K.; Bhattacharjee, J.; Guedes Soares, C.G. Analytical and numerical study of dual-chamber oscillating water columns on stepped bottom. Renew. Energy 2015, 75, 272–282. [Google Scholar] [CrossRef]
- Ning, D.; Wang, R.; Chen, L.; Sun, K. Experimental investigation of a land-based dual-chamber OWC wave energy converter. Renew. Sustain. Energy Rev. 2019, 105, 48–60. [Google Scholar] [CrossRef]
- Elhanafi, A.; Macfarlane, G.; Ning, D. Hydrodynamic performance of single–chamber and dual–chamber offshore–stationary Oscillating water Column devices using CFD. Appl. Energy 2018, 228, 82–96. [Google Scholar] [CrossRef]
- He, F.; Leng, J.; Zhao, X. An experimental investigation into the wave power extraction of a floating box-type breakwater with dual pneumatic chambers. Appl. Ocean Res. 2017, 67, 21–30. [Google Scholar] [CrossRef]
- Ning, D.; Zhou, Y.; Zhang, C. Hydrodynamic modeling of a novel dual-chamber OWC wave energy converter. Appl. Ocean Res. 2018, 78, 180–191. [Google Scholar] [CrossRef]
- Ning, D.; Zhou, Y.; Mayon, R.; Johanning, L. Experimental investigation on the hydrodynamic performance of a cylindrical dual-chamber Oscillating water Column device. Appl. Energy 2020, 260, 114252. [Google Scholar] [CrossRef]
- Taherian Haghighi, A.T.; Nikseresht, A.H.; Hayati, M. Numerical analysis of hydrodynamic performance of a dual-chamber Oscillating water Column. Energy 2021, 221, 119892. [Google Scholar] [CrossRef]
- Rezanejad, K.; Guedes Soares, C. Hydrodynamic investigation of a novel concept of oscillating water column type wave energy converter device. J. Offshore Mech. Arct. Eng. 2021, 143, 042003. [Google Scholar] [CrossRef]
- Rezanejad, K.; Gadelho, J.F.M.; Xu, S.; Guedes Soares, C. Experimental investigation on the hydrodynamic performance of a new type floating Oscillating water Column device with dual-chambers. Ocean Eng. 2021, 234, 109307. [Google Scholar] [CrossRef]
- Xu, S.; Guedes Soares, C.G. Experimental investigation on short-term fatigue damage of slack and hybrid mooring for wave energy converters. Ocean Eng. 2020, 195, 106618. [Google Scholar] [CrossRef]
- Xu, S.; Rezanejad, K.; Gadelho, J.F.M.; Guedes Soares, C. Influence of the power take-off damping of a dual chamber floating oscillating water column on the mooring fatigue damage. Ocean Eng. 2022, 249, 110832. [Google Scholar] [CrossRef]
- Falcão, A.F.D.O. Wave energy utilization: A review of the technologies. Renew. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Morris-Thomas, M.T.; Irvin, R.J.; Thiagarajan, K.P. An investigation into the hydrodynamic efficiency of an oscillating water column. J. Offshore Mech. Arct. Eng. 2007, 129, 273–278. [Google Scholar] [CrossRef]
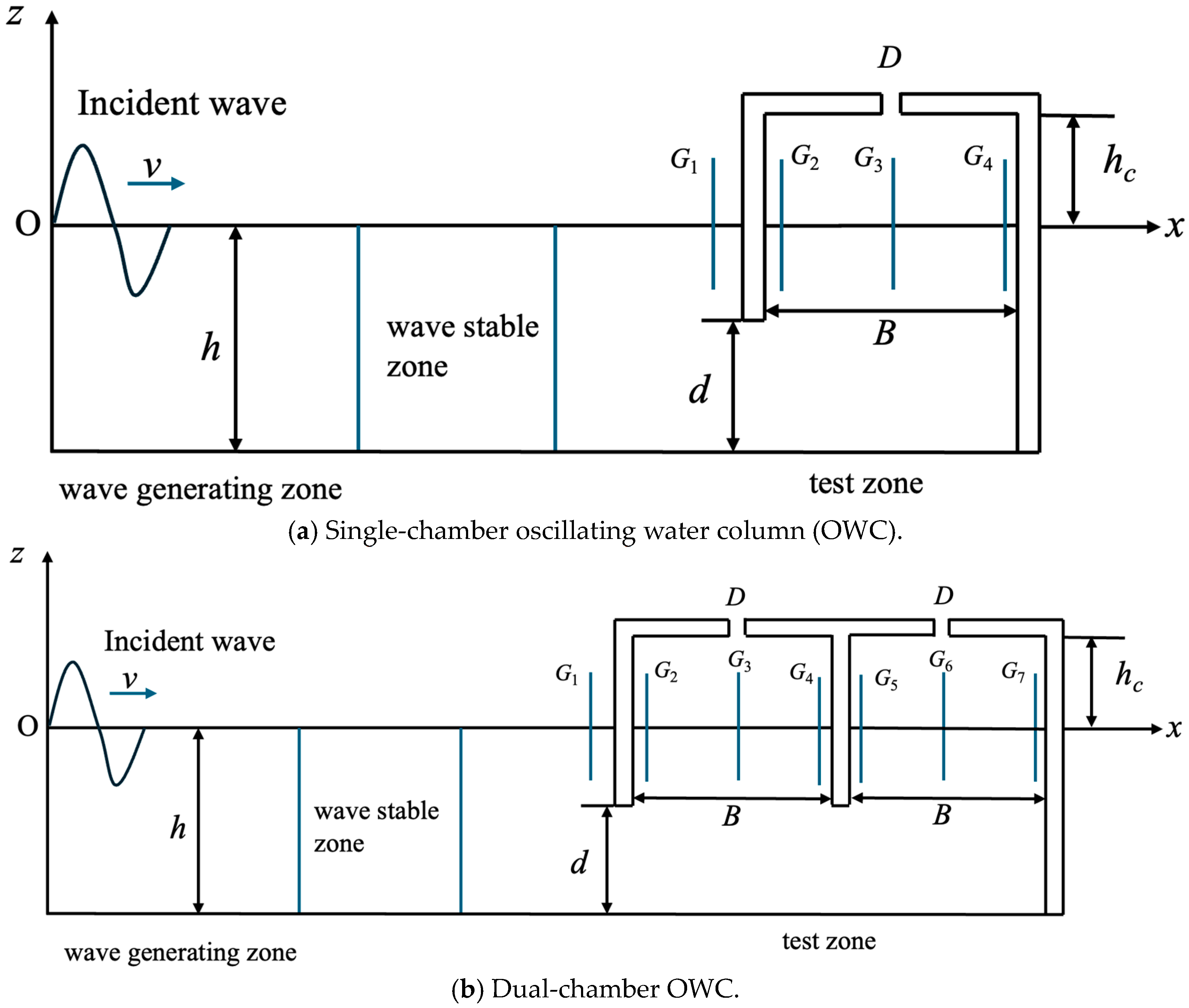


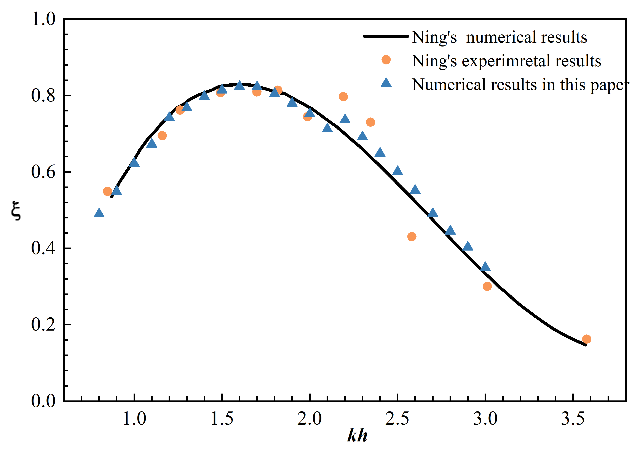













| T (s) | 0.9 | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 | 1.9 |
| kh | 2.23 | 2.06 | 1.91 | 1.79 | 1.70 | 1.61 | 1.54 | 1.48 | 1.42 | 1.37 | 1.33 |
| T (s) | 2.0 | 2.1 | 2.2 | 2.3 | 2.4 | 2.5 | 2.6 | 2.7 | 2.8 | 2.9 | 3.0 |
| kh | 1.29 | 1.26 | 1.22 | 1.20 | 1.17 | 1.14 | 1.12 | 1.10 | 1.08 | 1.06 | 1.04 |
| Chamber Type | Chamber Width B (m) | Chamber Height hc (m) | Wave Height H (m) | Wave Period T (s) | Holes Width D (m) | |
|---|---|---|---|---|---|---|
| Case 1 | single-chamber | 0.55 | 0.02 | 0.06 | 0.8–3.0 | 0.064 |
| Case 2 | single-chamber | 0.55 | 0.02 | 0.03 | 0.8–3.0 | 0.064 |
| Case 3 | dual-chamber | 0.55 | 0.02 | 0.06 | 0.8–3.0 | 0.064 |
| Case 4 | dual-chamber | 0.55 | 0.02 | 0.03 | 0.8–3.0 | 0.064 |
| Case 5 | dual-chamber | 0.255 | 0.02 | 0.06 | 0.8–3.0 | 0.064 |
| Case 6 | dual-chamber | 0.255 | 0.02 | 0.03 | 0.8–3.0 | 0.064 |
| Case 7 | single-chamber | 0.55 | 0.02 | 0.06 | 0.8–3.0 | 0.160 |
| Case 8 | single-chamber | 0.55 | 0.025 | 0.06 | 0.8–3.0 | 0.064 |
| Grid | Mesh 1 | Mesh 2 | Mesh 3 |
|---|---|---|---|
| grid subdivision | 60 | 80 | 120 |
| grid size (m) | 0.04 | 0.031 | 0.02 |
| Total grids (×104) | 9.1 | 12.2 | 18.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, P.; Xu, Q.; Jiang, S.; Zhu, J.; Zhang, H. Numerical Study of the Hydrodynamic Performance of a Dual-Chamber Oscillating Water Column Wave Energy Converter Device. J. Mar. Sci. Eng. 2024, 12, 2176. https://doi.org/10.3390/jmse12122176
Tang P, Xu Q, Jiang S, Zhu J, Zhang H. Numerical Study of the Hydrodynamic Performance of a Dual-Chamber Oscillating Water Column Wave Energy Converter Device. Journal of Marine Science and Engineering. 2024; 12(12):2176. https://doi.org/10.3390/jmse12122176
Chicago/Turabian StyleTang, Peng, Qing Xu, Shengchao Jiang, Junlin Zhu, and Hongsheng Zhang. 2024. "Numerical Study of the Hydrodynamic Performance of a Dual-Chamber Oscillating Water Column Wave Energy Converter Device" Journal of Marine Science and Engineering 12, no. 12: 2176. https://doi.org/10.3390/jmse12122176
APA StyleTang, P., Xu, Q., Jiang, S., Zhu, J., & Zhang, H. (2024). Numerical Study of the Hydrodynamic Performance of a Dual-Chamber Oscillating Water Column Wave Energy Converter Device. Journal of Marine Science and Engineering, 12(12), 2176. https://doi.org/10.3390/jmse12122176





