Trans-Media Motion Control of a Hybrid Aerial Underwater Vehicle Considering Actuator Dynamic Input Saturation
Abstract
1. Introduction
2. Trans-Media Model of HAUV
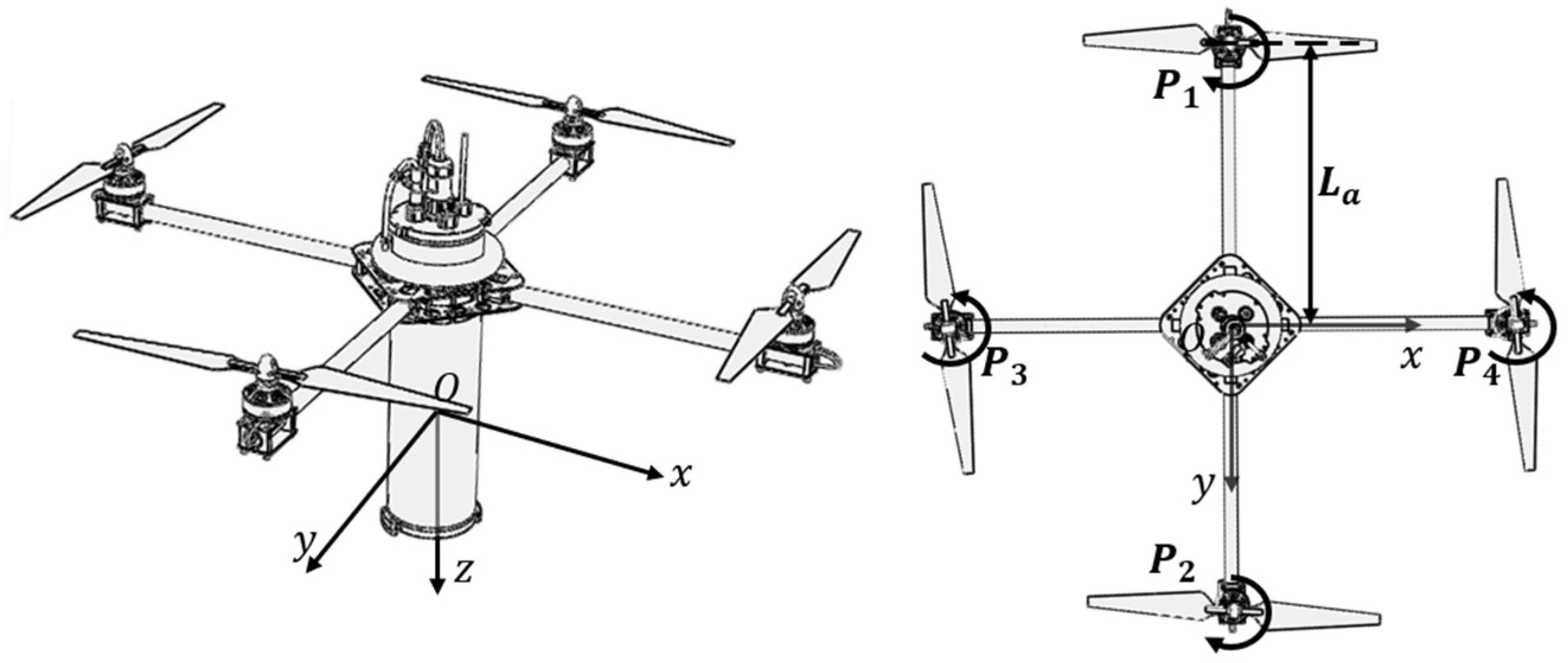
2.1. Coordinate System and Coordinate Transformation
2.2. Trans-Media Dynamic Model of HAUV Body
2.3. Input Saturation of Trans-Media Thrusters
2.4. Environment Model
3. Control Design
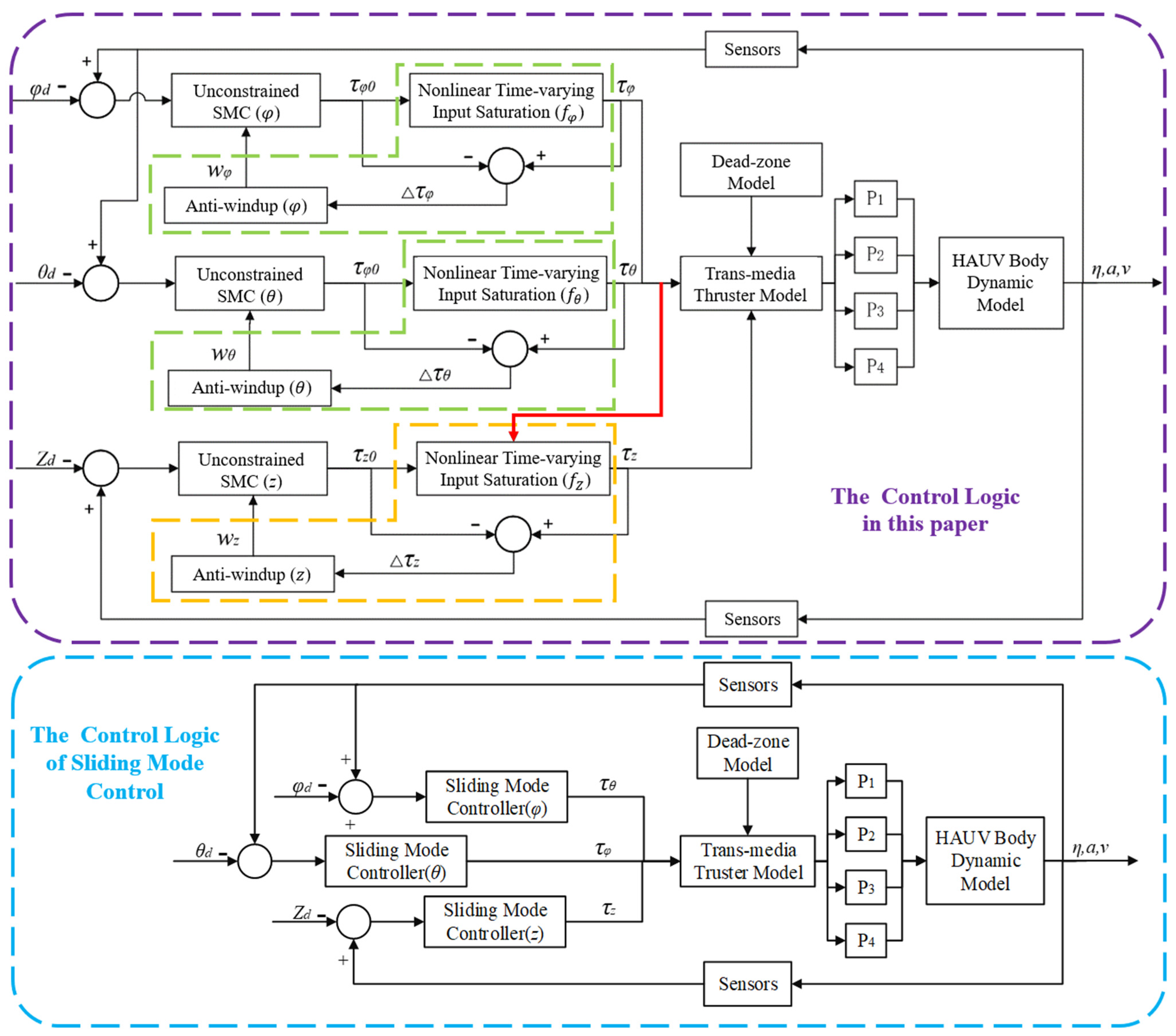
3.1. Control Strategy
3.2. Controller Design
3.3. Stability Analysis
4. Simulation
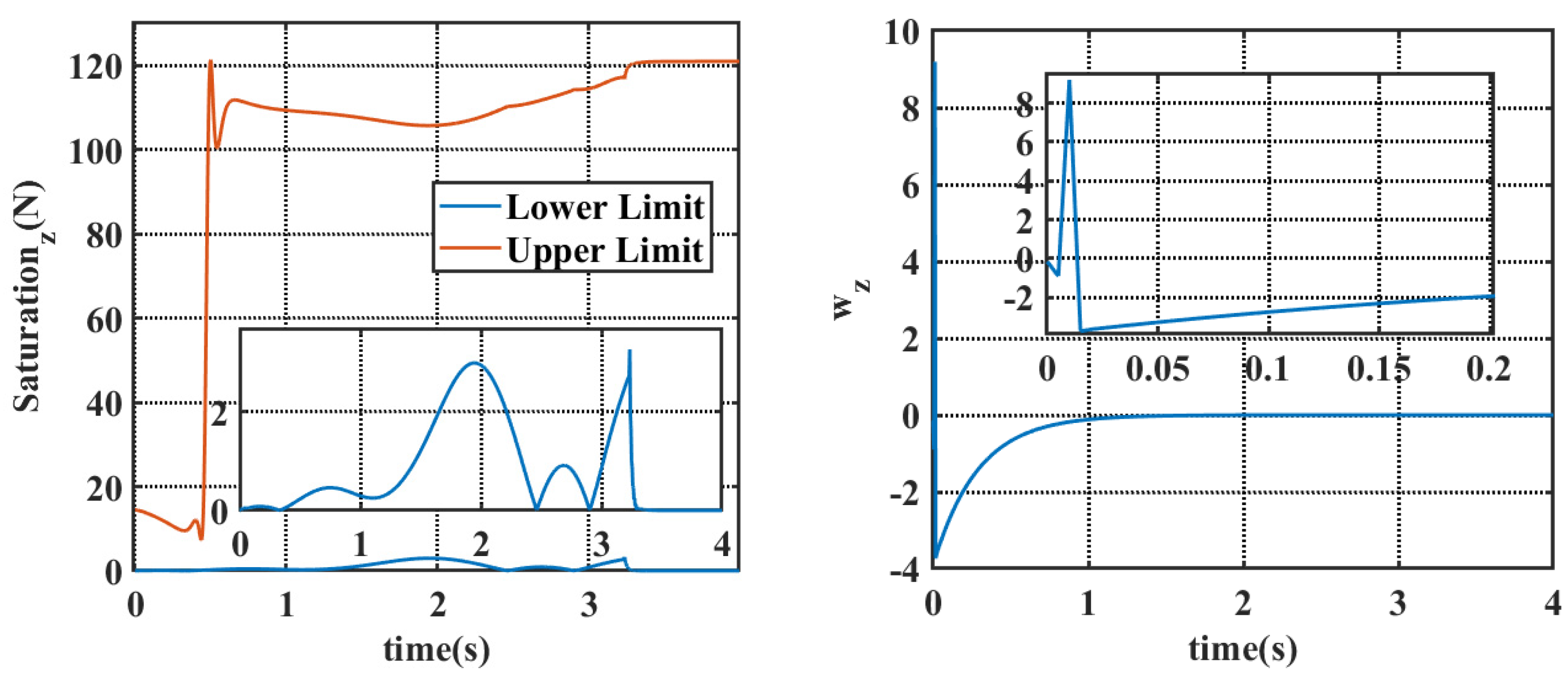
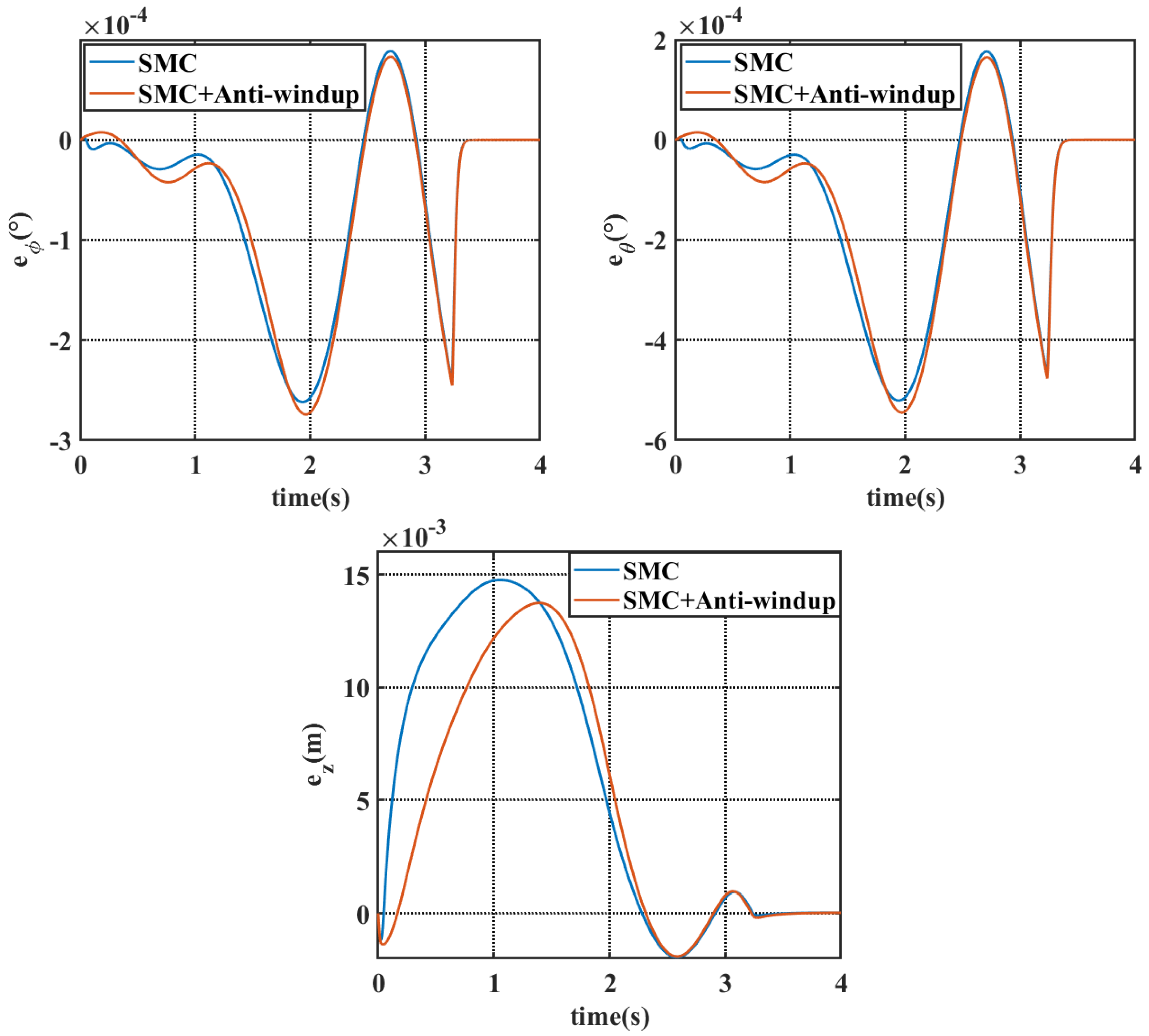
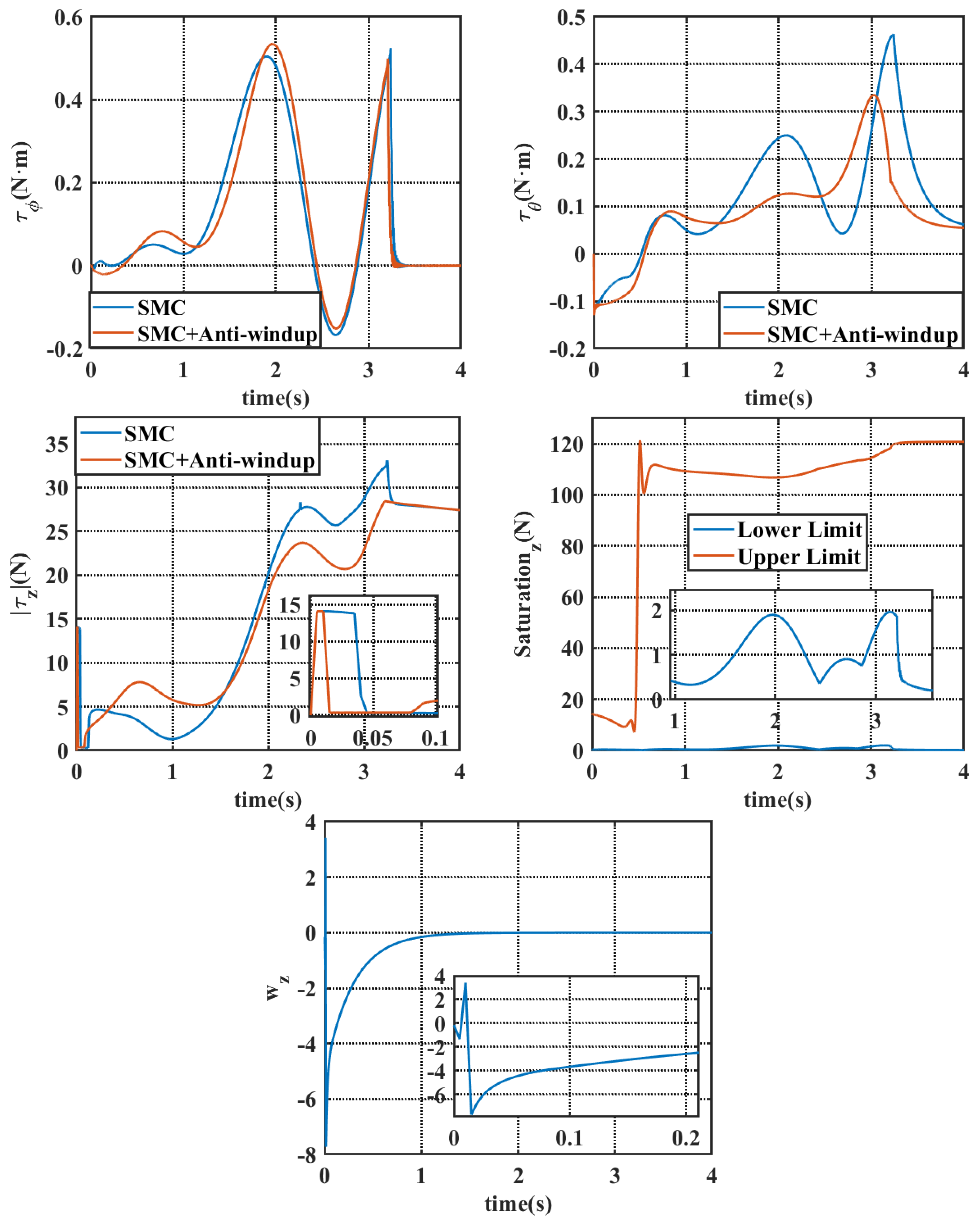
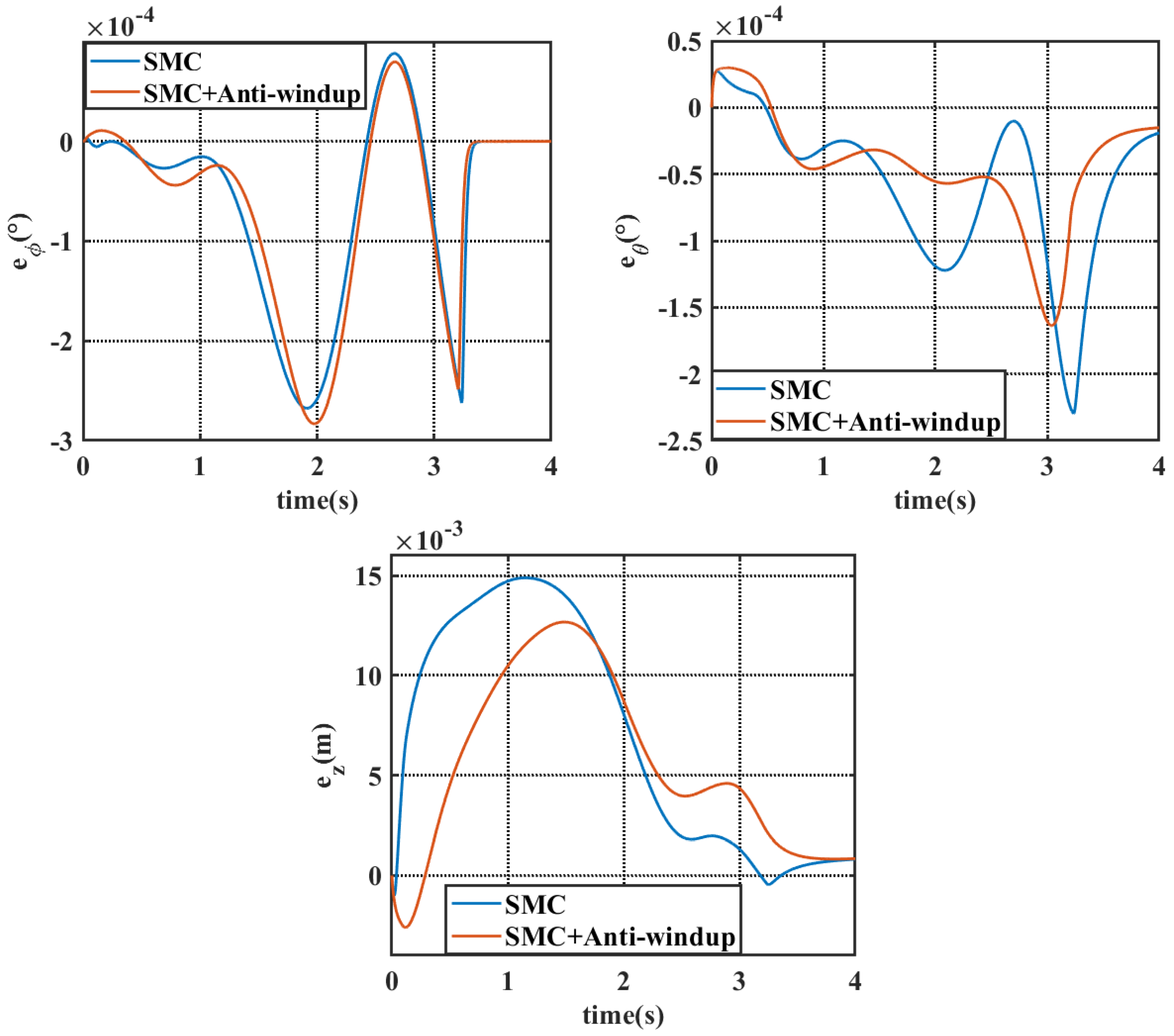
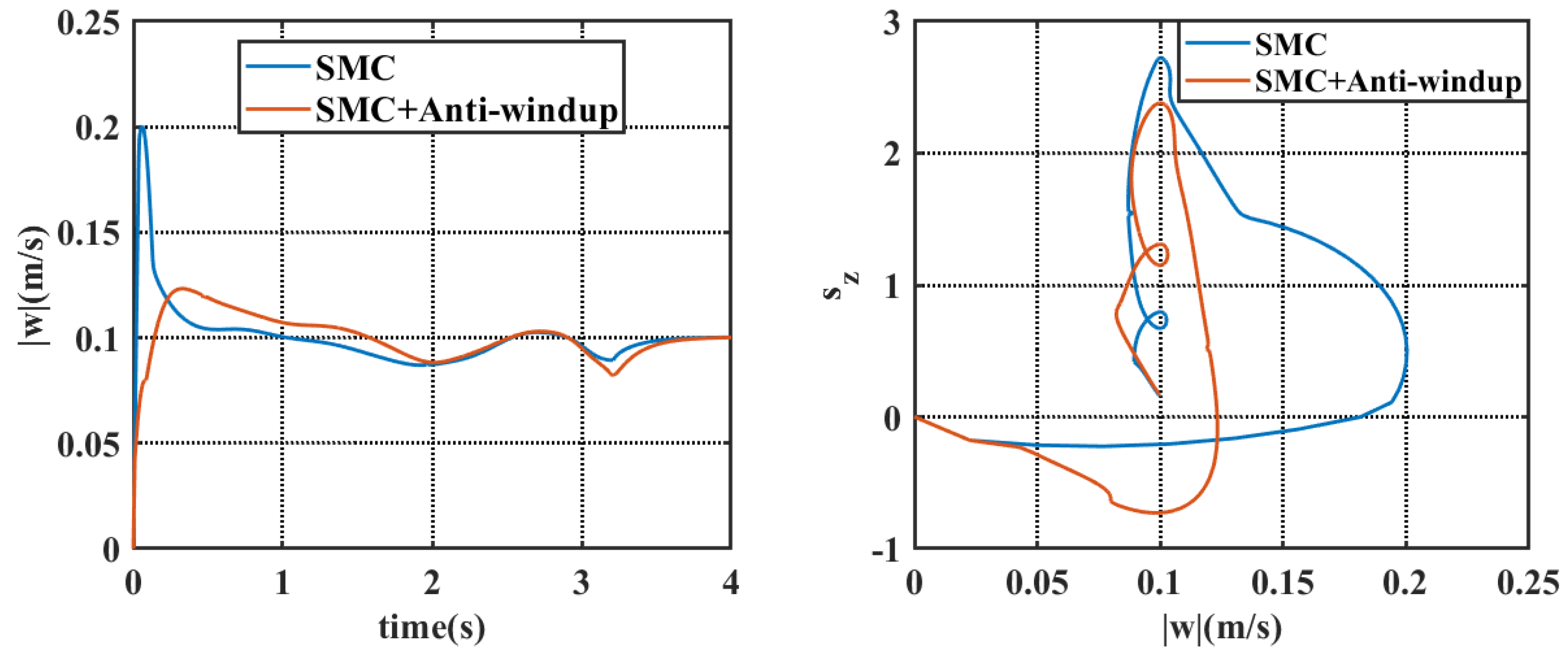
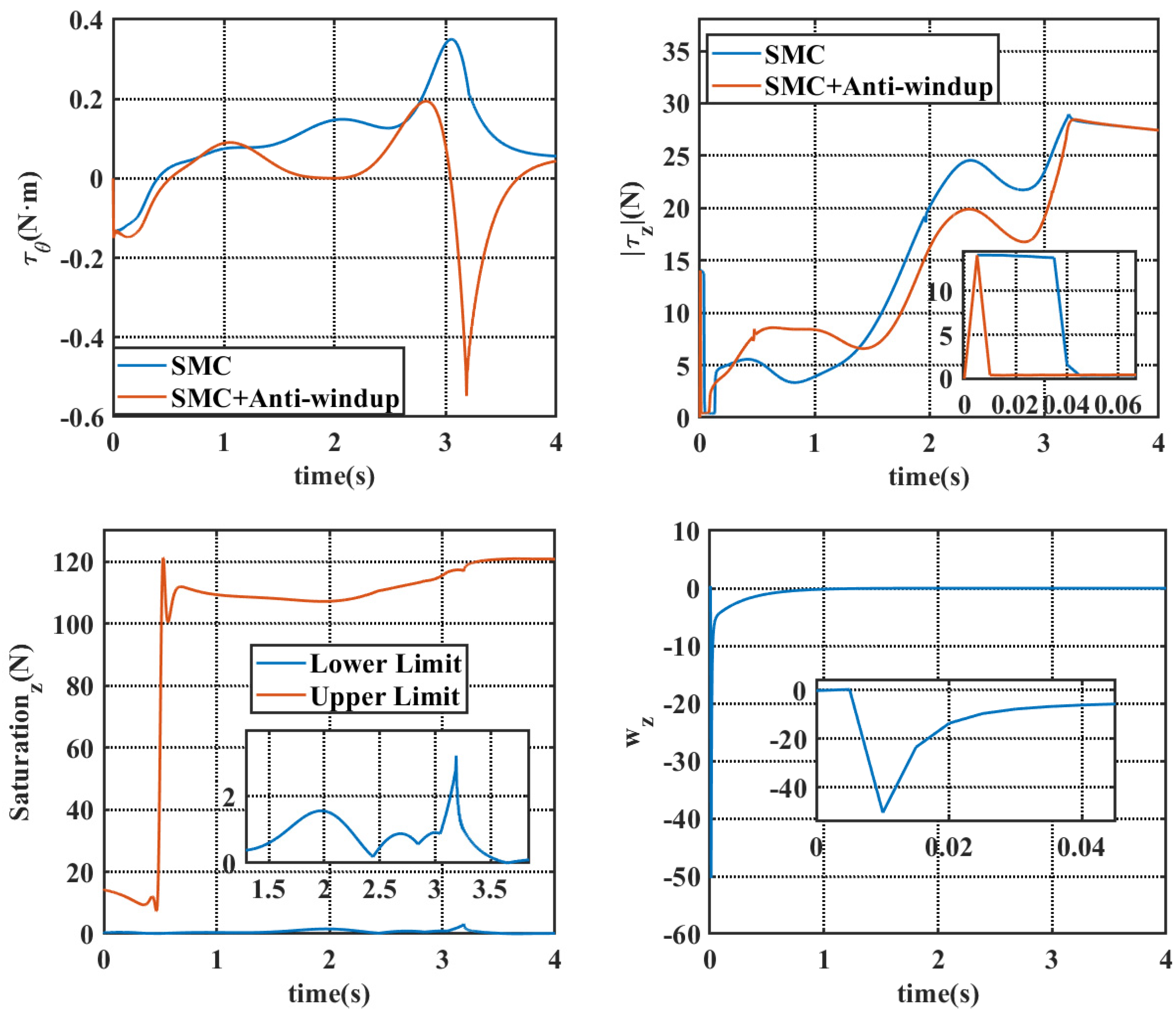
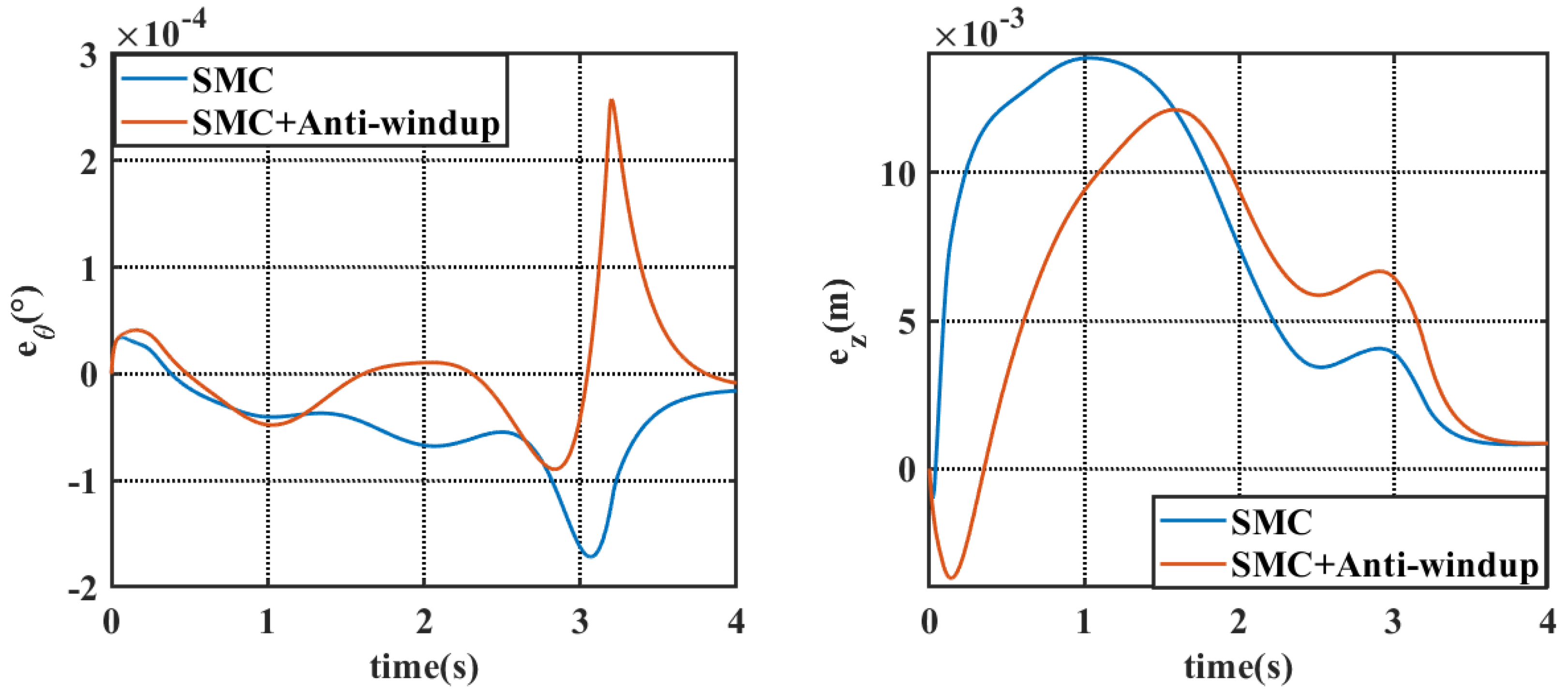
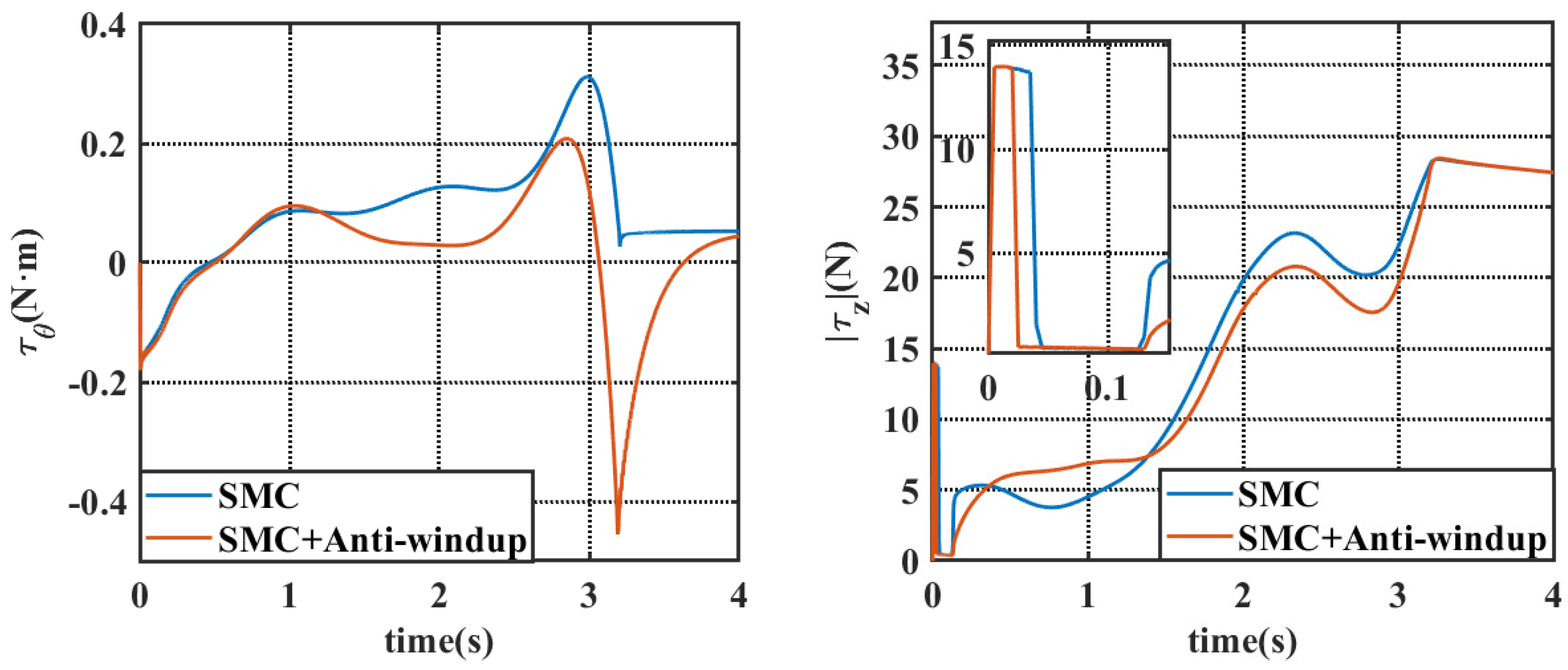
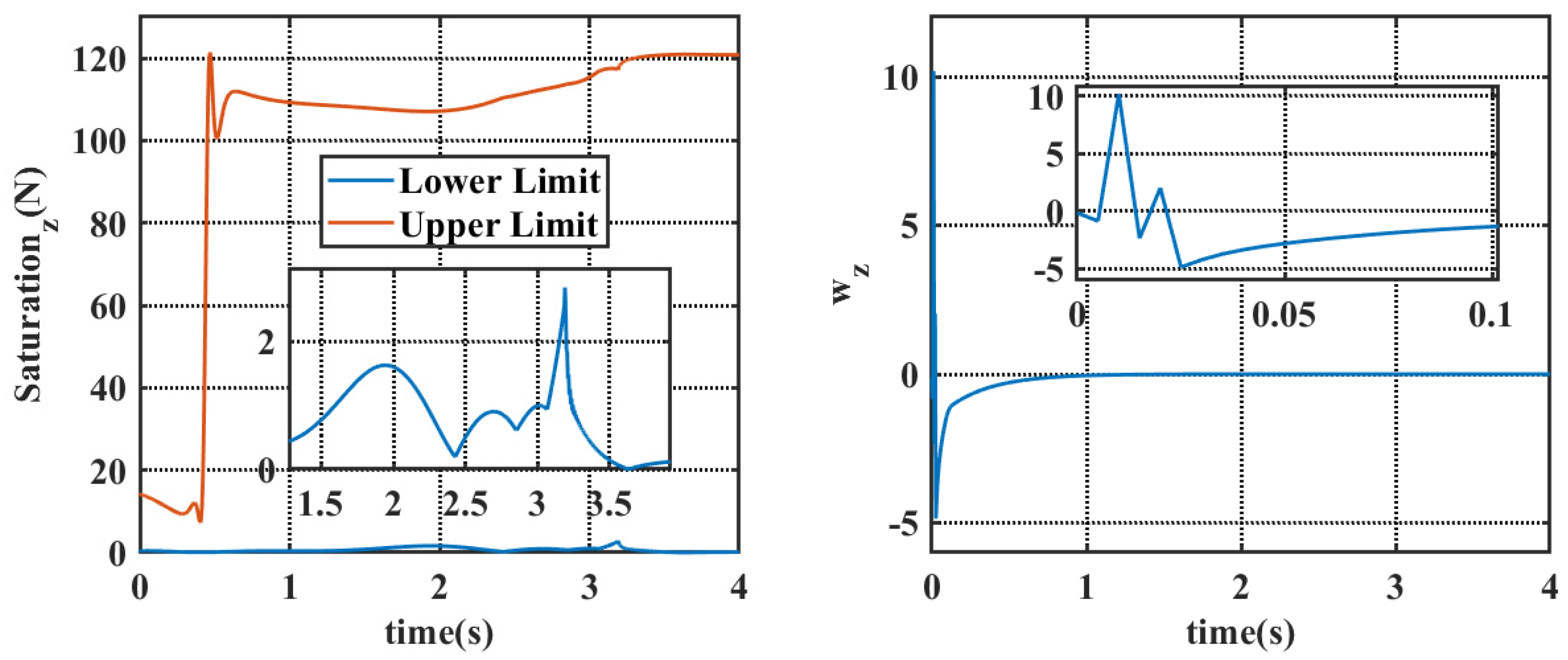
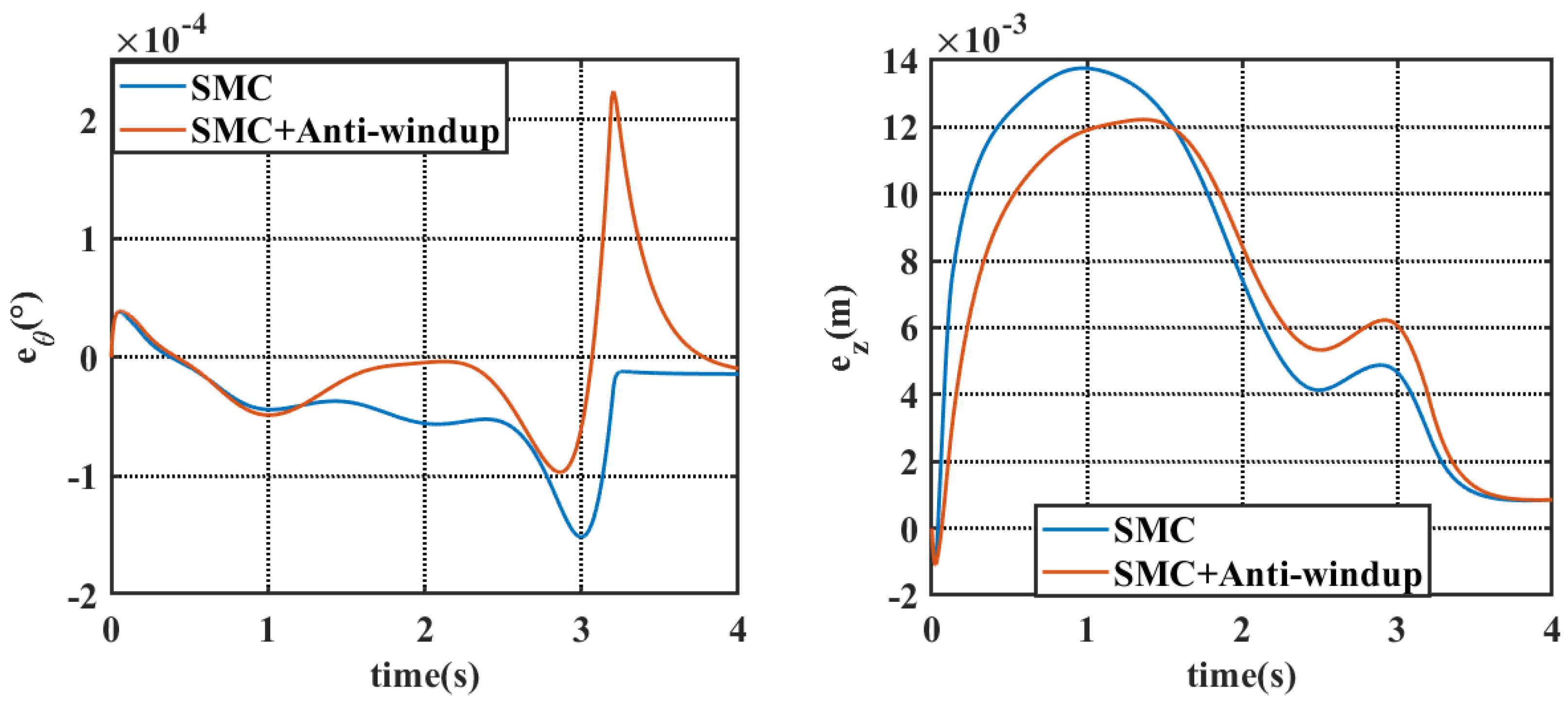
4.1. Simulation Results Under Static Water Conditions
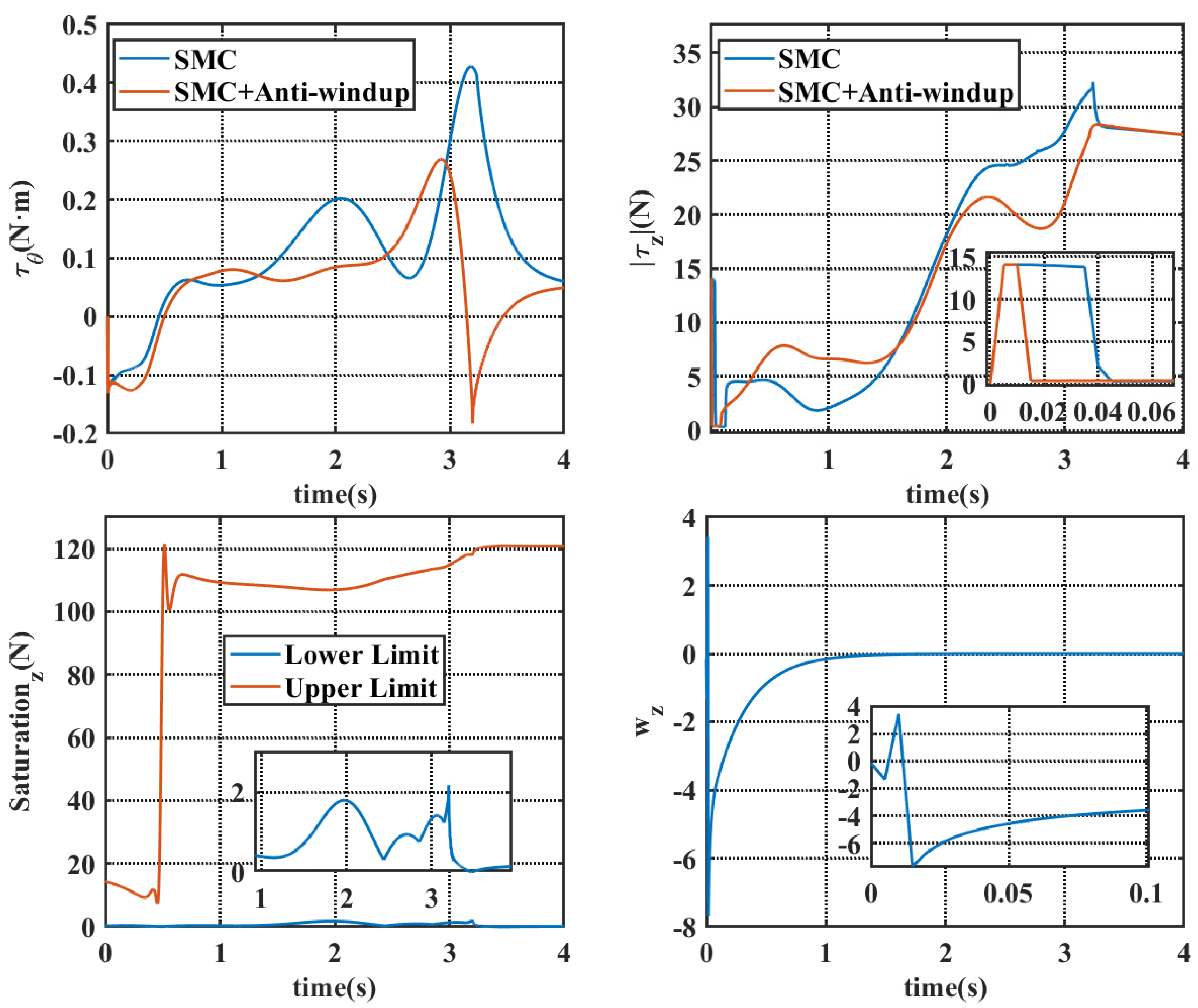
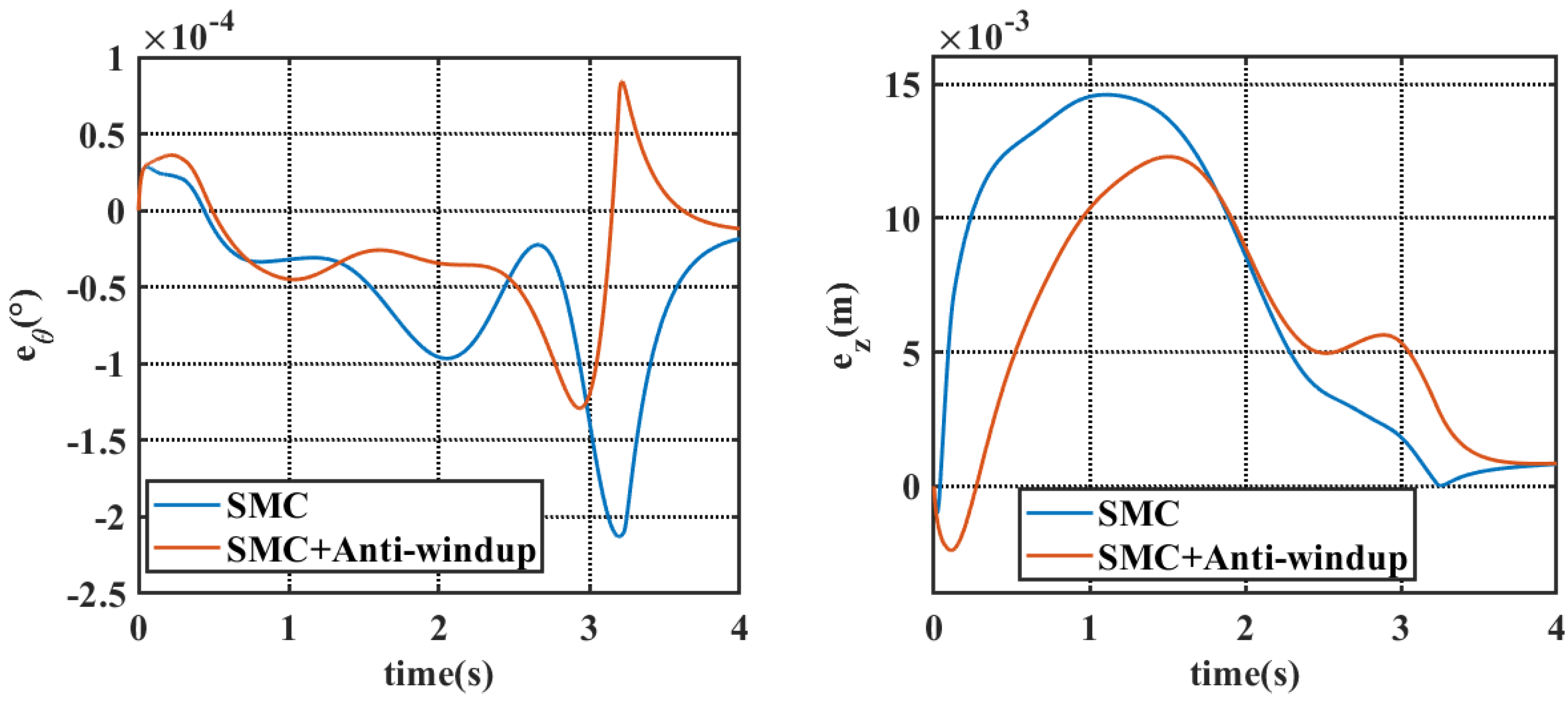
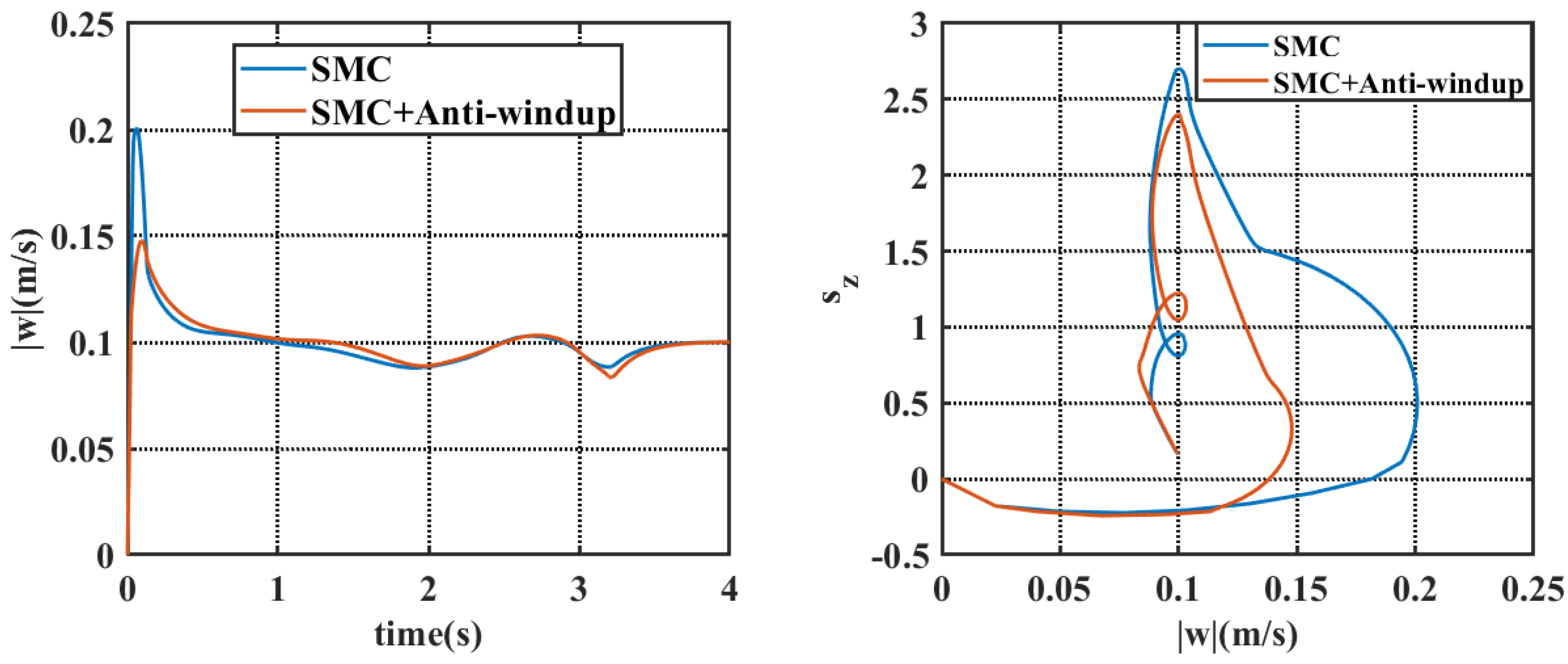
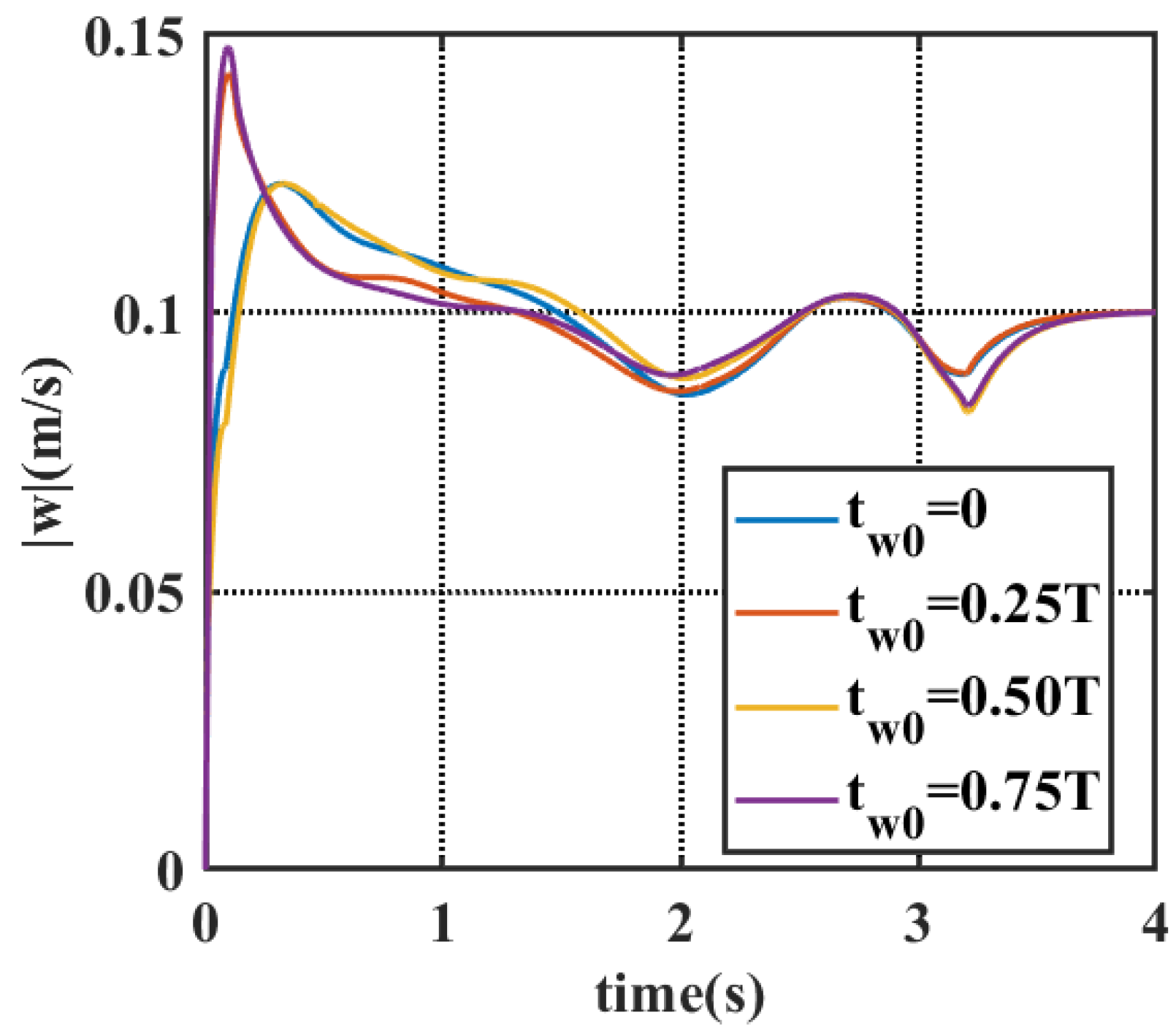
4.2. Simulation Results Under Wind, Wave, and Current Conditions
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Variable | Definition |
|---|---|
| Generalized position vector in fixed coordinate system | |
| Generalized force vector in fixed coordinate system | |
| Generalized speed vector in satellite coordinates | |
| Generalized speed transformation matrix | |
| System inertia matrix | |
| Rigid-body Coriolisand centripetal matrix | |
| Vector of gravitational/buoyancy forces and moments | |
| Trans-media hydrodynamic vector | |
| Disturbance vector | |
| The upper limit of dynamic input saturation in the pitch degree of freedom | |
| The upper limit of dynamic input saturation in the roll degree of freedom | |
| The upper limit of dynamic input saturation in the heave degree of freedom | |
| Maximum trans-media thrust of the i-th trans-media thruster | |
| Length of the multi-rotor HAUV arm | |
| Input saturation function | |
| Sliding mode variable at the i-th degree of freedom | |
| Anti-windup adaptive compensation variable | |
| Model uncertainty adaptive compensation variable at the i-th degree of freedom | |
| Generalized position tracking error at the i-th degree of freedom | |
| constants | |
| Generalized expected position at the i-th degree of freedom | |
| a time-varying unknown disturbance |
Appendix B
References
- Yang, X.; Wang, T.; Liang, J.; Yao, G.; Liu, M. Survey on the novel hybrid aquatic–aerial amphibious aircraft: Aquatic unmanned aerial vehicle (AquaUAV). Prog. Aerosp. Sci. 2015, 74, 131–151. [Google Scholar] [CrossRef]
- Zimmerman, S.; Abdelkefi, A. Review of marine animals and bioinspired robotic vehicles: Classifications and characteristics. Prog. Aerosp. Sci. 2017, 93, 95–119. [Google Scholar] [CrossRef]
- Narayanan, A.; Rajeshirke, P.; Sharma, A.; Pestonjamasp, K. Survey of the emerging bio-inspired Unmanned Aerial Underwater Vehicles. IOP Conf. Ser. Mater. Sci. Eng. 2020, 810, 012078. [Google Scholar] [CrossRef]
- Farinha, A.; Tria, J.; Zufferey, R.; Armanini, S.F.; Kovac, M. Challenges in control and autonomy of unmanned aerial-aquatic vehicles. In Proceedings of the 2021 29th Mediterranean Conference on Control and Automation (MED), Puglia, Italy, 22–25 June 2021; pp. 937–942. [Google Scholar]
- Ma, Z.; Chen, D.; Li, G.; Jing, X.; Xiao, S. Configuration design and trans-media control status of the hybrid aerial underwater vehicles. Appl. Sci. 2022, 12, 765. [Google Scholar] [CrossRef]
- Tan, Y.; Chen, B. Survey on the development of aerial–aquatic hybrid vehicles. Unmanned Syst. 2021, 9, 263–282. [Google Scholar] [CrossRef]
- Yao, G.; Li, Y.; Zhang, H.; Wang, T.; Sun, F.; Yang, X. Review of hybrid aquatic-aerial vehicle (HAAV): Classifications, current status, applications, challenges and technology perspectives. Prog. Aerosp. Sci. 2023, 139, 100902. [Google Scholar] [CrossRef]
- Miranda Pinheiro, P.; Dias de Oliveira Evald, P.J.; Bedin Grando, R.; Alves Neto, A.; Drews, P.L.J., Jr. Hybrid Unmanned Aerial Underwater Vehicles: Asurvey on Concepts and Technologies. SSRN 2023, 4424715. [Google Scholar]
- Zheng, T. Current status and prospect of aquatic-aerial unmanned vehicles. Highlights Sci. Eng. Technol. 2023, 46, 125–133. [Google Scholar] [CrossRef]
- Alzu’Bi, H.; Mansour, L.; Rawashdeh, O. Loon Copter: Implementation of a hybrid unmanned aquatic-aerial quadcopter with active buoyancy control. J. Robot. Syst. 2018, 35, 764–778. [Google Scholar] [CrossRef]
- Drews, P.L.J.; Neto, A.A.; Campos, M.F. Hybrid unmanned aerial underwater vehicle: Modeling and simulation. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 4637–4642. [Google Scholar]
- Horn, A.C.; Pinheiro, P.M.; Silva, C.B.; Neto, A.A.; Drews, P.L.J., Jr. A study on configuration of propellers for multirotor-like hybrid aerial-aquatic vehicles. In Proceedings of the 2019 19th International Conference on Advanced Robotics (ICAR), Belo Horizonte, Brazil, 2–6 December 2019; pp. 173–178. [Google Scholar]
- Sun, X.; Cao, J.; Li, Y.; Wang, B. Design and field test of a foldable wing unmanned aerial–underwater vehicle. J. Field Robot. 2023, 41, 347–373. [Google Scholar] [CrossRef]
- Maia, M.; Soni, P.; Diez, F. Demonstration of an aerial and submersible vehicle capable of flight and underwater navigation with seamless air-water transition. arXiv 2015, arXiv:1507.01932. [Google Scholar]
- Chen, Q.; Zhu, D.; Liu, Z. Attitude control of aerial and underwater vehicles using single-input FUZZY P+ID controller. Appl. Ocean Res. 2020, 107, 102460. [Google Scholar] [CrossRef]
- Neto, A.A.; Mozelli, L.A.; Drews, P.L.J., Jr.; Campos, M.F.M. Attitude control for a hybrid unmanned aerial underwater vehicle: A robust switched strategy with global stability. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 395–400. [Google Scholar]
- Ma, Z.; Feng, J.; Yang, J. Research on vertical air–water trans-media control of hybrid unmanned aerial underwater vehicles based on adaptive sliding mode dynamical surface control. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418770531. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, Y.; Meng, Y.; Yu, S.; Zhuang, Y. System modeling and simulation of an unmanned aerial underwater vehicle. J. Mar. Sci. Eng. 2019, 7, 444. [Google Scholar] [CrossRef]
- Lu, D.; Xiong, C.; Zeng, Z.; Lian, L. Adaptive dynamic surface control for a hybrid aerial underwater vehicle with parametric dynamics and uncertainties. IEEE J. Ocean. Eng. 2019, 45, 740–758. [Google Scholar] [CrossRef]
- Lu, D.; Guo, Y.; Xiong, C.; Zeng, Z.; Lian, L. Takeoff and landing control of a hybrid aerial underwater vehicle on disturbed water’s surface. IEEE J. Ocean. Eng. 2021, 47, 295–311. [Google Scholar] [CrossRef]
- Wei, T.; Li, J.; Zeng, Z.; Lian, L. Trans-media resistance investigation of hybrid aerial underwater vehicle base on hydrodynamic experiments and machine learning. Ocean Eng. 2022, 266, 112808. [Google Scholar] [CrossRef]
- Wei, T.; Zhou, Z.; Wang, Y.; Zeng, Z.; Lian, L. Hydrodynamic study of hybrid aerial underwater vehicle in the wind, wave, and current environment. In Proceedings of the 2023 IEEE Underwater Technology (UT), Tokyo, Japan, 6–9 March 2023. [Google Scholar]
- Cui, R.; Zhang, X.; Cui, D. Adaptive sliding-mode attitude control for autonomous underwater vehicles with input nonlinearities. Ocean Eng. 2016, 123, 45–54. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, T.; Bi, Y.; Zeng, Z.; Lian, L.; Dan, Y. Trans-Media Motion Control of a Hybrid Aerial Underwater Vehicle Considering Actuator Dynamic Input Saturation. J. Mar. Sci. Eng. 2024, 12, 2169. https://doi.org/10.3390/jmse12122169
Wei T, Bi Y, Zeng Z, Lian L, Dan Y. Trans-Media Motion Control of a Hybrid Aerial Underwater Vehicle Considering Actuator Dynamic Input Saturation. Journal of Marine Science and Engineering. 2024; 12(12):2169. https://doi.org/10.3390/jmse12122169
Chicago/Turabian StyleWei, Tongjin, Yuanbo Bi, Zheng Zeng, Lian Lian, and Yangwen Dan. 2024. "Trans-Media Motion Control of a Hybrid Aerial Underwater Vehicle Considering Actuator Dynamic Input Saturation" Journal of Marine Science and Engineering 12, no. 12: 2169. https://doi.org/10.3390/jmse12122169
APA StyleWei, T., Bi, Y., Zeng, Z., Lian, L., & Dan, Y. (2024). Trans-Media Motion Control of a Hybrid Aerial Underwater Vehicle Considering Actuator Dynamic Input Saturation. Journal of Marine Science and Engineering, 12(12), 2169. https://doi.org/10.3390/jmse12122169








