Abstract
In recent years, hybrid unmanned aerial underwater vehicles (HAUVs), which are capable of air–water trans-media motion, have been increasingly developed. For most HAUVs, air–water trans–media motion is a relatively dangerous and difficult process. Therefore, it is of great significance to study the particular process. This paper presents the first study on the kinematic stability of the air–water trans–media motion of HAUVs. First, a simplified dynamic model of HAUVs is proposed, including the hydrodynamic forces and the time–varying buoyancy. Then, based on the proposed model and the Hurwitz method, this paper derives the air–water trans–media kinematic stability criterion for HAUVs. This criterion can be applied to most air–water trans–media motions that satisfy the assumptions in this paper. Finally, this paper takes “Nezha”, a novel HAUV, as an example to analyze its air–water trans–media kinematic stability. The results show that the proposed criterion is effective in judging the vehicle’s design, including the geometry and thruster power, which are important factors in the performance of the trans–media process.
1. Introduction
The ocean is rich in resources, but human understanding of the ocean is far from complete. Therefore, autonomous underwater vehicles (AUVs) and unmanned aerial vehicles (UAVs) have been successively used to observe various phenomena in the ocean and collect valuable ocean data. However, AUVs and UAVs can operate only in underwater or aerial domains. Therefore, in recent years, hybrid unmanned aerial underwater vehicles (HAUVs), which can fly in the air, navigate the water and which has the ability to repeat air–water trans–media motions (Figure 1), have been attracting increasing interest worldwide.
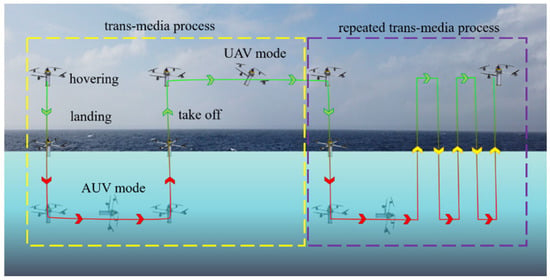
Figure 1.
Sketch of the moving process of an HAUV.
At present, a variety of HAUVs have been designed by many research institutes worldwide. Maia et al. [1,2] designed a fully operational HAUV, which achieved the goal of air–water trans–media motion control. A fixed–wing HAUV was developed and achieved air–water trans–media motion successfully [3]. Alzu’bi H et al. [4] designed an HAUV with active buoyancy control capable of aerial flight, water–surface operation and subaquatic diving. A new HAUV consisting of a passively flooding and draining wing was developed which positively affected air–water trans–media buoyancy adjustment [5,6]. Lu et al. [7] developed an HAUV that combined both underwater glider (UG) and UAV modes to achieve air–water trans–media motion while increasing the working endurance successfully. Zongcheng et al. [8] designed a morphing HAUV and simulated the control behavior of the vehicle in the water–exit process. In these studies, all kinds of HAUVs successfully achieved at least one air–water trans–media motion. However, as far as we know, the success rate of air–water trans–media motion is not high.
For most HAUVs, air–water trans–media motion is a relatively dangerous and challenging process. Therefore, most of the current research on HAUVs does not consider disturbances. However, during the air–water trans–media process, the HAUV is disturbed by wind, wave and current in the natural environment. These disturbances have significant negative effects on the actual air–water trans–media motion of HAUVs, such as capsizing the vehicle, damaging the propeller and so on. In other words, the disturbance of the natural environment is an important cause of the loss or damage of the HAUV. Therefore, it is of great importance to study trans–media kinematic stability to ensure the safety of HAUVs in the air–water trans–media process. However, there is no trans–media kinematic stability criterion to design HAUVs.
As for other marine vehicles, there are several kinematic stability criteria to guide the design. The study of marine vehicle kinematic stability began in the middle of the 20th century. Based on Newton’s second law, Abkowitz et al. [9,10] deduced and developed a set of classical six–degree–of–freedom kinematic stability analysis methods for ocean vehicles. Then, the kinematic stability analysis method was proposed based on Lyapunov stability theory [11]. Leonard et al. [12] analyzed the stability of the vertical plane motion of a bottom–heavy underwater vehicle. The kinematic stability of a survey–style AUV and the formula for critical speed were studied [13]. Chen et al. [14] studied the kinematic stability of an autonomous underwater helicopter in six degrees of freedom and carried out the simulation verification. Ayyangar et al. [15] studied the dynamic stability of a positively buoyant AUV in the vertical plane for a level flight. The kinematic stability of the underwater dynamic docking device was analyzed [16].
At present, there is no relevant research on a kinematic stability analysis of the air–water trans–media motion of HAUVs. However, it plays an important role in the overall design and trajectory control. Based on the existing maneuverability theory, a kinematic stability analysis method for the air–water trans–media motion of HAUVs is proposed in this paper. This method can be used as a design criterion to evaluate the kinematic stability of an HAUV in the air–water trans–media process. Moreover, the kinematic stability verified by this method is an important prerequisite for the controller design of HAUV. The main contributions of the manuscript can be summarized as follows:
- (1)
- Based on the model of underwater vehicle maneuverability and the recent research results on air–water trans–media hydrodynamics, a simplified model for the air–water trans–media process is proposed.
- (2)
- Based on the Hurwitz method, the criterion of kinematic stability for the air–water trans–media motion of HAUVs is derived in this paper.
- (3)
- Based on the criterion proposed in this paper, the kinematic stability of an instance of HAUV, named Nezha, is analyzed.
The remainder of this study is organized as follows: Section 2 presents the Nezha system and trans–media process. Section 3 proposes an air–water trans–media model and simplification. Section 4 derives the criterion of kinematic stability for the air–water trans–media motion of HAUVs. Section 5 takes Nezha as an example to analyze its kinematic stability. Finally, Section 6 summarizes the key conclusions of this work.
2. Nezha System and Trans–Media Process
2.1. System Configuration
A novel HAUV (named Nezha), capable of aerial flight, diving and repeated transitions between aerial and underwater environments, was proposed in our previous studies. The conceptual design of Nezha is shown in Figure 2. In Figure 2, the coordinate system is established to describe the position of the center of gravity. is in the bottom center of the HAUV. Nezha consists of a waterproof cylinder main fuselage and four lightweight struts supporting four motor/propeller combinations. Nezha uses the motor with 550 rpm/V motor KV and APC 14 × 55 propeller. The physical parameters of the vehicle are listed in Table 1.
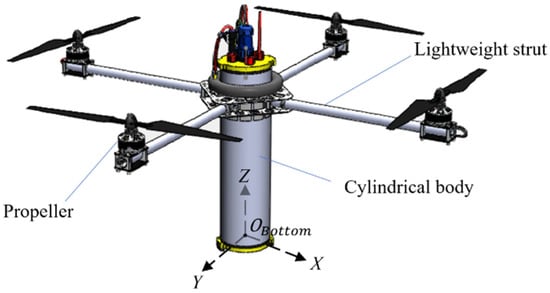
Figure 2.
Diagram of the overall structure of Nezha.

Table 1.
The physical parameters of Nezha.
2.2. Trans–Media Motion Process
Nezha has three main operation stages: the AUV stage, UAV stage, and air–water trans–media stage. As highlighted by the green box in Figure 3, the water–entry process of Nezha starts when the bottom touches the water and ends at an upright free–floating position at the surface, while the water–exit process is the opposite. Unlike the HAUVs launched underwater with significant initial velocity, Nezha moves slowly in the trans–media stage (less than 0.5 m/s).
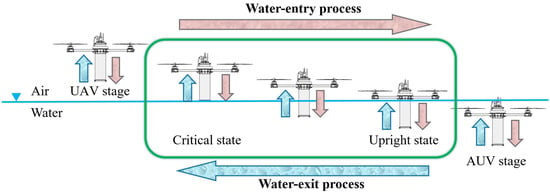
Figure 3.
Diagram of the trans–media process.
There are significant features in the trans–media stage resulting in unstable motion and even failures of water–exit or water–entry for Nezha:
- (1)
- In the process of air–water trans–media motion, a negative restoring moment occurs to accelerate the capsizing of the HAUV. In other words, the HAUV is not statically stable according to the classical theory. However, the classical static stability analysis does not include the thrust provided by the thrusters, which is necessary for the HAUV during the air–water trans–media process. Because there is no thrust, there is no air–water trans-media process. In this paper, the thrust and torque provided by the thrusters are taken into account in the static stability analysis.
- (2)
- The vehicle is subjected to disturbances of wind, wave and current in the air–water trans-media process in reality. These disturbances are superimposed with the overturning moment mentioned above, and consequently a severer negative force is experienced by the vehicle. In this paper, these disturbances are simplified. The influence of these disturbances on HAUV is considered roughly through the change of motion state, such as .
- (3)
- The hydrodynamic coefficients of Nezha are time–varying when the vehicle travels through the water’s surface, which greatly influences the dynamic stability of the vehicle during the air–water trans–media process.
Therefore, it is necessary to theoretically study the air–water trans–media kinematic stability of HAUV.
2.3. Definition of Kinematic Stability
The definition of kinematic stability is sourced from the field of ships. Kinematic stability measures the ability of an HAUV to return to the original state after being disturbed. The detailed description of kinematic stability is shown in Figure 4. After the initial disturbance, it is assumed that the change of attitude of HAUV is , the change of angular velocity is and the change of the position is . According to the response of HAUV, the kinematic stability can be classified into two types, as follows:
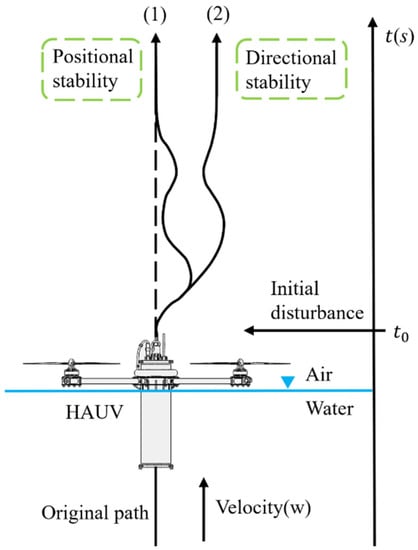
Figure 4.
The definition of kinematic stability.
- (1)
- Positional stability: After the initial disturbance, if .
- (2)
- Directional stability: After the initial disturbance, if .
3. Model and Simplification
As is shown in Figure 5, two coordinate frames are established, i.e., a geodetic coordinate frame (E) and a body coordinate frame (O). Point O coincides with the center of mass of the vehicle. We define the coordinates of point O as (), which represents the position of the vehicle in the geodetic coordinate frame. The attitude of the vehicle with respect to the geodetic coordinate frame is defined as (). and denote linear and angular velocities respectively in the body coordinate frame. is the external force vector of the vehicle expressed in the body coordinate frame, while is the moment vector of the vehicle expressed in the body coordinate frame. The dynamics variables in this paper are explained in Table 2.
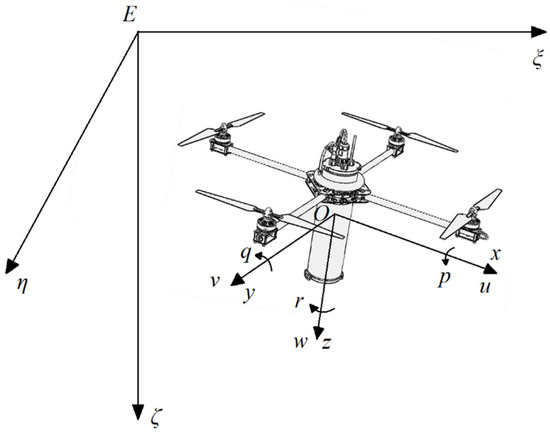
Figure 5.
The definitions of coordinate frames.

Table 2.
The nomenclature of the hydrodynamics variables.
There are some assumptions for the simplification of the following theoretical analysis:
- (1)
- Since the rate of change of acceleration in the trans–media process of Nezha is very low, we believe that the motion of Nezha in the trans–media process satisfies the “slow–motion” hypothesis.
- (2)
- According to previous research [17,18,19], the hydrodynamic coefficients of the HAUV in the trans–media process are assumed to be a linear variation with the draft depth.
Since the vertical motion is slow, the change of buoyancy of Nezha is immediately rebalanced by the lift of the propeller. Therefore, in building the trans–media model of HAUV, we mainly consider the influence of hydrodynamic force on kinematic stability.
Consider trans–media motions in two vertical planes separately, i.e., the plane and the plane. The model in the plane is as follows:
where means that the corresponding terms change with . If there is no , it means the hydrodynamic value of the HAUV at the initial time during the water–exit process. Hydrodynamic parameters are expanded by the Taylor series expansion. Only the linear term is retained in the Taylor expansion of hydrodynamic resistance, ignoring the higher–order term and the coupling term.
The model in plane can be established by following the above method and thus is given below:
The Taylor series expansion is as follows:
4. Trans–Media Kinematic Stability Criterion
Based on the established model for HAUV maneuverability, the criterion for trans–media kinematic stability is derived in this section.
4.1. Trans–Media Kinematic Stability Criterion in ξEζ Plane
4.1.1. Static Stability
For static stability in the plane, the static force analysis is shown in Figure 6. Assuming that other motion parameters remain unchanged, only the change of is considered after environmental disturbance.
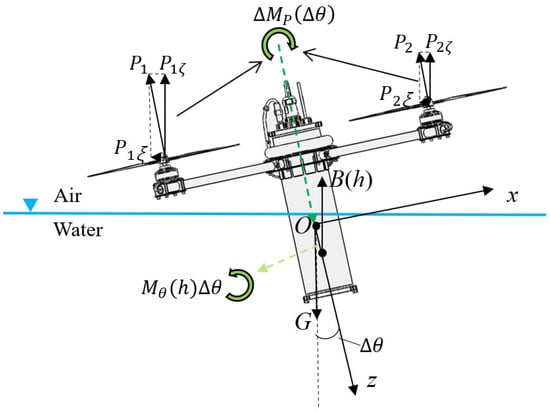
Figure 6.
Static force analysis in the ξEζ plane.
Since the thrust and torque provided by the thrusters are the necessary conditions for HAUV air–water trans–media motion, the maximum torque provided by the thrusters is introduced into the static stability analysis in this paper. is the torque, which the propeller needs to provide, varying with . It should be noted that the mentioned in this paper is an embodiment of the maximum capability of the propellers, which does not involve specific dynamic changes. is the torque generated by the differential rotation of the propellers before the disturbance. In the process of checking, we mainly use the upper limit of .
are the force provided by the propellers, whose components in the directions of and are , and and . Because are small, their effects can be ignored in order to simplify the calculation. is the force of gravity. is the buoyancy, which varies with . By static force analysis, the restoring moment is , and the air–water trans–media motion is stable when the following conditions are met:
4.1.2. Dynamical Stability
Based on Equation (2), the HAUV is assumed to be disturbed in a uniform vertical motion () in the trans–media process. The perturbations in surge and pitch motions are defined as . The dynamical force analysis is shown in Figure 7.
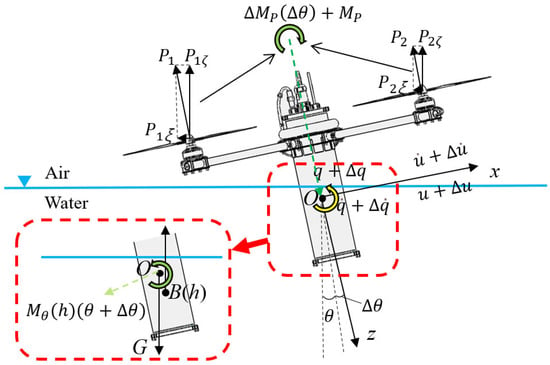
Figure 7.
Dynamical force analysis in the plane.
Subtracting Equation (6) by Equation (2) yields the following perturbation equations:
According to the general solution of the inhomogeneous differential equation, we get the solution to and . By dimensionless and , we get the following formula:
The symbol represents the dimensionless value of the corresponding variable.
Let , and consider the dimensionless disturbance . Plug in this boundary condition, and we get :
By substituting and arranging Equations (7)–(11), we get a differential equation with respect to the perturbation term .
Rewrite Equation (12) in the following form:
To avoid repetition, the expression of can be found in the Appendix A.
If , the solution to Equation (13) does not converge to zero. Thus, is required. When , Equation (13) is an homogeneous differential equation, and its convergence of solution can be judged by the Hurwitz method.
The characteristic equation of Equation (13) is as follows:
According to the Hurwitz method, the motion is stable when the following conditions are met:
As the values of the hydrodynamics variables change with the depth of draft, it is necessary to ensure that the values of meet the requirements in Equation (15) during the air–water trans–media process. The continuous change of draft depth in the air–water trans–media process is discretized. If the value of at each discrete depth meets the requirement of Equation (15), the trans–media motion is stable. It is found that represents the criterion of static stability in the plane, which also verifies the correctness of the derivation. In other words, dynamic stability is built on static stability.
The Hurwitz method states that the perturbations will converge to zero when . However, for the air–water trans–media motion, the time is limited. Therefore, it cannot guarantee that the perturbations of the system will be eliminated in the air–water trans–media process, but it can ensure that the perturbations are bounded instead of getting worse. Therefore, the air–water trans–media process is stable in the presence of disturbance.
When the air–water trans–media stage is over, the dynamic stability of the HAUV in a single medium can be judged by the same criterion except for those hydrodynamic coefficients, which are not time–varying, and which in the corresponding media are used instead. If the vehicle can satisfy the kinematic stability criterion throughout the moving process, we consider that the HAUV has global kinematic stability.
Equation (15) is only applicable to the stability of the HAUV at a small linear angle. Equation (15) is not enough to conclude the dynamic stability of the HAUV at the large angle of the heel. Part of the HAUV’s propeller will slam into the water at large angles. The slamming of the propeller will result in a significant decrease in the speed of the propeller and then lead to a significant decrease in the thrust generated. According to the previous HAUV lake test experience, there are two main situations under large angles: (1) the HAUV fails to generate enough thrust, failing water exit. (2) The thrust generated by some thrusters drops significantly because of the slamming, while the thrust generated by the remaining thrusters remains the same. This creates a negative capsizing moment, which will capsize the HAUV. Therefore, the HAUV studied in this paper is unstable at large angles.
4.2. Trans–Media Kinematic Stability Criterion in the Plane
4.2.1. Static Stability
For static stability in ηEζ plane, static force analysis is shown in Figure 8. Assuming that other motion parameters remain unchanged, only the change of is considered after environmental disturbance.
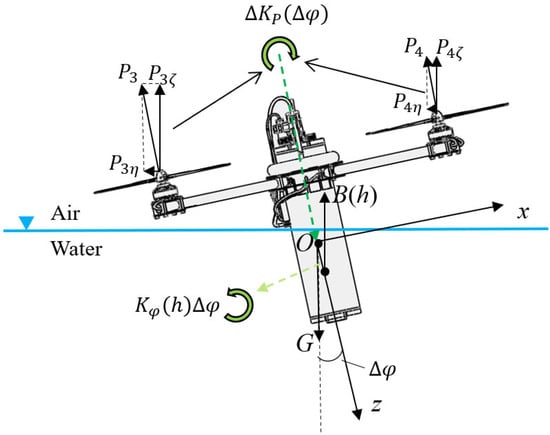
Figure 8.
Static force analysis in the plane.
is the torque, which the propeller needs to provide, varying with . It should be noted that the mentioned in this paper is an embodiment of the maximum capability of the propellers, which does not involve specific dynamic changes. is the torque generated by the differential rotation of the propellers before the disturbance. In the process of checking, we mainly use the upper limit of for checking. are the force provided by the propellers. are the components in the direction and . As in Section 4.1.1, we ignore the effects of . is the force of gravity. is the buoyancy, which varies with .
By static force analysis, the restoring moment is , and the air–water trans–media motion is stable when the following conditions are met:
4.2.2. Dynamical Stability
As for the motion assumption in Section 4.1.2, we define the disturbance as in the plane. As shown in Figure 9, we carry out the force analysis in the plane.
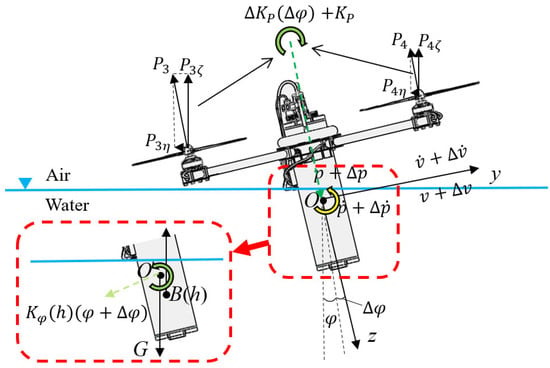
Figure 9.
The diagram of force analysis in the plane.
If we subtract Equation (4) from Equation (17), we get the perturbation term equation:
The derivation process on plane is the same as that on plane . Let t = 0 and consider the dimensionless disturbance . The derivation results are given as follows:
The motion in the plane is stable when the following conditions are met:
represents the criterion of static stability in the plane.
5. Trans–Media Kinematic Stability Analysis
Based on the proposed trans–media kinematic stability criterion, the kinematic stability of the air–water trans–media process for Nezha was analyzed numerically. In addition, the trans–media motion of Nezha was decomposed into the plane and the plane, respectively, to study the vehicle’s trans–media kinematic stabilities in both directions.
5.1. Trans–Media Kinematic Stability Analysis in the Plane
The trans–media kinematic stability of HAUV with different and different (the velocity of uniform vertical motion) in the air–water trans–media process was simulated and analyzed. The simulation parameters in the plane were as follows: . As shown in Figure 10, the air–water trans–media kinematic stability under different speeds was checked. The value of , which are always greater than zero, increases with the draft depth . The value of decreases first and then increases as increases. The changing trend of is mainly affected by the restoring moment, specifically including the impact of HAUV buoyancy and the restoring arm. The change of can be divided into three stages:
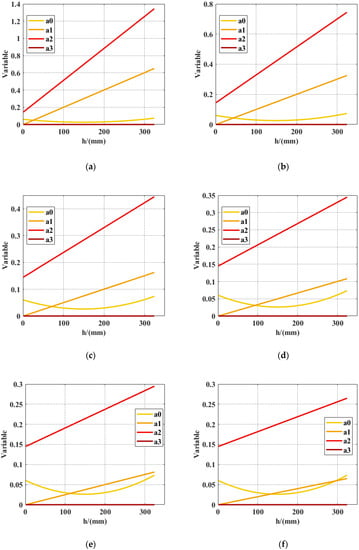
Figure 10.
(a) Criterion variables at ; (b) Criterion variables at ; (c) Criterion variables at ; (d) Criterion variables at ; (e) Criterion variables at ; (f) Criterion variables at .
- (1)
- 0 < h ≤ 0.148 m: The impact of the restoring moment is negative, and the negative effect gradually increases. In this process, the buoyancy increases, and the restoring arm decreases gradually. The change of buoyancy plays a major role.
- (2)
- 0.148 m < h ≤ 0.296 m: The effect of the restoring moment is negative, but the negative effect gradually decreases. In this process, buoyancy increases, and the restoring arm decreases. The change of the restoring arm plays a major role.
- (3)
- 0.296 m < h ≤ 0.323 m: The effect of the restoring moment is positive, and the positive effect gradually increases. In this process, the buoyancy and the restoring arm increase.
Moreover, the value of is always greater than 0. This indicates that with an increase in the draft depth, the trans–media kinematic stability of the HAUV is enhanced, which is consistent with the actual air–water trans–media process. The value of is equal to 0 in the trans–media process, which is consistent with the results of the above theoretical proof in Section 4. It was found that all the requirements in Equation (15) were satisfied within the velocity range of [0.05 m/s,0.5 m/s]. Therefore, Nezha has kinematic stability in the plane.
5.2. Trans–Media Kinematic Stability Analysis in Plane
The kinematic stability of the HAUV was simulated with a different and a different in the air–water trans–media process. The simulation parameters in plane were as follows:. As shown in Figure 11, the air–water trans–media kinematic stability under different speeds was checked. As the velocity increases, the air–water trans–media kinematic stability becomes less stable. However, in the actual HAUV trans–media process, we want this process to be as short as possible since this stage is a transient phase. Therefore, it requires balancing the trans–media process’s stability and time. This also guides the actual control of the HAUV trans–media motion.
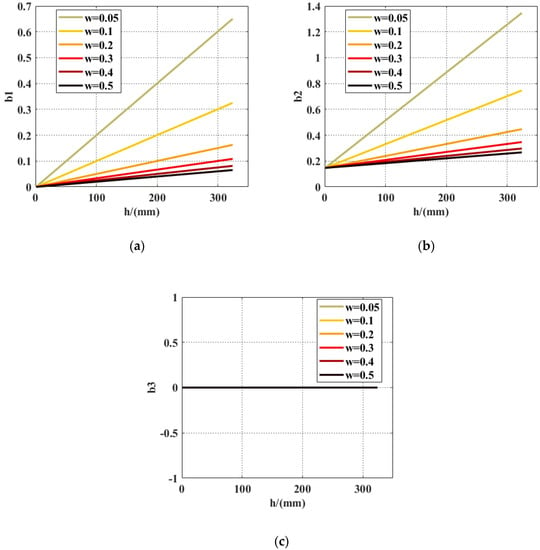
Figure 11.
(a) The change curve of at different air–water trans–media velocities; (b) The change curve of at different air–water trans–media velocities; (c) The change curve of at different air–water trans–media velocities–.
The value of b3 is equal to 0 in the trans–media process, satisfying Criterion (24) derived above. It was found that the requirements in Criterion (24) were satisfied within the velocity range of [0.05 m/s,0.5 m/s].
We then analyzed the criterion in detail. mainly represents the static stability of the HAUV in the air–water trans–media process, which is the premise of dynamic stability. The main influencing parameters of are the restoring moment and , which represent the static stability of the HAUV and the adjustment ability of the propellers under the corresponding , respectively.
As its definition indicates, is independent of . Whether satisfies the criterion depends on the value of . Values of varying with under different upper limits of propeller regulation are given in Figure 12. When is greater than 0.04, the HAUV has kinematic stability throughout the air–water trans–media process. When is less than 0.04, the HAUV has partial kinematic stability. As shown in Figure 12, when , has a part with a value of less than zero with the change of . In this part, the HAUV has no kinematic stability because the propeller cannot provide enough thrust: HAUV will capsize when HAUV is slightly disturbed.
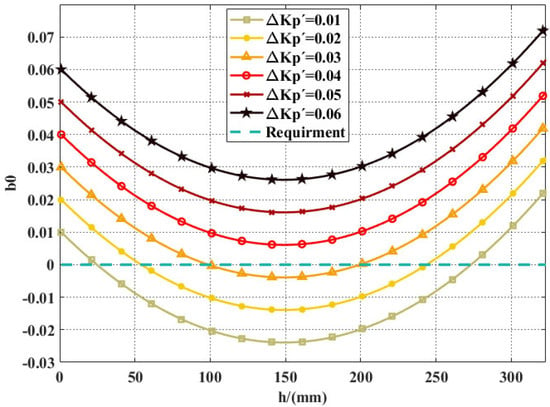
Figure 12.
The variation of as a function of h at different upper limits of propeller regulation.
As for Nezha, is specifically set to 0.06, and consequently the stability requirement of is satisfied. Nezha has kinematic stability on both the plane and the plane. Nezha therefore has kinematic stability in the air–water trans–media process.
This provides some basis for the design of HAUVs in the future. When selecting the propeller, one should ensure that the ( is the density of water) value meets the requirements of the criteria. Therefore, is an important standard for designing the maximum thrust of the propellers. Only in this way can the air–water trans–media motion of the HAUV be controlled to overcome the external disturbance. On the contrary, as long as the kinematic stability criterion proposed in this paper is not satisfied, the kinematic stability cannot be guaranteed no matter what control law is applied. Therefore, the kinematic stability criterion proposed in this paper is an essential premise for motion control design.
6. Conclusions
In this paper, the air–water trans–media kinematic stability of HAUVs was analyzed under the assumptions of “slow–motion” and linear hydrodynamic variation with the draft depth. First, by following the model of classic underwater vehicle maneuverability and some recent research achievements in the field of hydrodynamics, this paper presented a model that is suitable for HAUV maneuverability. Then, the criterion of air–water trans–media kinematic stability of HAUVs was derived based on the model. This criterion provides a theoretical basis for the design of future HAUVs and provides an important prerequisite for the design of air–water trans–media motion control laws for HAUVs. Moreover, the criterion can be applied to most air–water trans–media motions that satisfy the assumptions in this paper. Finally, this criterion was used to analyze the air–water trans–media kinematic stability of Nezha, and the air–water trans–media process’s kinematic stability was analyzed with different draft depths and velocities. Furthermore, the influence of the propellers on the kinematic stability was analyzed.
Some interesting research subjects are worthy of further study in the future, including the complex behavior of the hydrodynamic characteristics during the air–water trans–media process for an HAUV and its effects on the vehicle’s kinematic stability. For example, the hydrodynamics of the vehicle change nonlinearly when the vehicle travels through the water’s surface in nature, although the variation trend is the same as that of linear change.
Author Contributions
T.W., D.L. and Z.Z. contributed to conceptualization, methodology, formal analysis and writing—original draft preparation; L.L. and Z.Z. contributed to supervision, project administration and funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the National Natural Science Foundation of China under grant 41706108. It was also funded in part by: the Science and Technology Commission of Shanghai Municipality Project 20dz1206600, the Natural Science Foundation of Shanghai under Grant 20ZR1424800 and the Shanghai Jiao Tong University Scientific and Technological Innovation Funds under Grant 2019QYB04.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
References
- Maia, M.M.; Mercado, D.A.; Diez, F.J. Design and implementation of multirotor aerial–underwater vehicles with experimental results. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017. [Google Scholar]
- Ravell, D.A.M.; Maia, M.M.; Diez, F.J. Modeling and control of unmanned aerial/underwater vehicles using hybrid control. Control. Eng. Pract. 2018, 76, 112–122. [Google Scholar] [CrossRef]
- Moore, J.; Fein, A.; Setzler, W. Design and Analysis of a Fixed–Wing Unmanned Aerial–Aquatic Vehicle. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018. [Google Scholar]
- Alzu’bi, H.; Mansour, I.; Rawashdeh, O. Loon Copter: Implementation of a hybrid unmanned aquatic–aerial quadcopter with active buoyancy control. J. Field Robot. 2018, 35, 764–778. [Google Scholar] [CrossRef]
- Stewart, W.; Weisler, W.; Anderson, M.; Bryant, M.; Peters, K. Dynamic Modeling of Passively Draining Structures for Aerial–Aquatic Unmanned Vehicles. IEEE J. Ocean. Eng. 2020, 45, 840–850. [Google Scholar] [CrossRef]
- Weisler, W.; Stewart, W.; Anderson, M.B.; Peters, K.J.; Gopalarathnam, A.; Bryant, M. Testing and Characterization of a Fixed Wing Cross–Domain Unmanned Vehicle Operating in Aerial and Underwater Environments. IEEE J. Ocean. Eng. 2018, 43, 969–982. [Google Scholar] [CrossRef]
- Lu, D.; Xiong, C.; Zeng, Z.; Lian, L. A Multimodal Aerial Underwater Vehicle with Extended Endurance and Capabilities. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019. [Google Scholar]
- Zongcheng, M.; Danqiang, C.; Guoshuai, L.; Junjie, Z. Constrained adaptive backstepping take-off control for a morphing hybrid aerial underwater vehicle. Ocean Eng. 2020, 213, 107666. [Google Scholar] [CrossRef]
- Abkowitz, M.A. Lectures on Ship Hydrodynamics–Steering and Manoeuvrability; Report Hy–5; Hydro–and Aerodynamic Laboratory: Lyngby, Denmark, 1964. [Google Scholar]
- Gertler, M.; Hagen, G.R. Standard Equations of Motion for Submarine Simulation; David w Taylor Naval Ship Research and Development Center: Bethesda, MD, USA, 1967. [Google Scholar]
- Fossen, T.I. Guidance and Control of Ocean Vehicles. Doctors Thesis, University of Trondheim, Trondheim, Norway, 1994. [Google Scholar]
- Leonard, N.E. Stability of a bottom–heavy underwater vehicle. Automatica 1997, 33, 331–346. [Google Scholar] [CrossRef] [Green Version]
- Palmer, A.R. Analysis of the Propulsion and Manoeuvring Characteristics of Survey–Style AUVs and the Development of a Multi–Purpose AUV; University of Southampton: Southampton, UK, 2009. [Google Scholar]
- Chen, C.-W.; Jiang, Y.; Huang, H.-C.; Ji, D.-X.; Sun, G.-Q.; Yu, Z.; Chen, Y. Computational fluid dynamics study of the motion stability of an autonomous underwater helicopter. Ocean Eng. 2017, 143, 227–239. [Google Scholar] [CrossRef]
- Ayyangar, V.; Krishnankutty, P.; Korulla, M.; Panigrahi, P. Stability analysis of a positively buoyant underwater vehicle in vertical plane for a level flight at varying buoyancy, BG and speeds. Ocean Eng. 2018, 148, 331–348. [Google Scholar] [CrossRef]
- Meng, L.; Lin, Y.; Gu, H.; Bai, G.; Su, T.-C. Study on dynamic characteristics analysis of underwater dynamic docking device. Ocean Eng. 2019, 180, 1–9. [Google Scholar] [CrossRef]
- Zhang, Q.; Hu, J.-H.; Feng, J.-F.; Xu, B.-W.; Liu, A. Motion law and density influence of a submersible aerial vehicle in the water–exit process. Fluid Dyn. Res. 2018, 50, 065516. [Google Scholar] [CrossRef]
- Ma, Z.; Feng, J.; Yang, J. Research on vertical air–water trans–media control of Hybrid Unmanned Aerial Underwater Vehicles based on adaptive sliding mode dynamical surface control. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418770531. [Google Scholar] [CrossRef] [Green Version]
- Ma, Z.; Hu, J.; Feng, J.; Liu, A.; Chen, G. A longitudinal air–water trans–media dynamic model for slender vehicles under low–speed condition. Nonlinear Dyn. 2019, 99, 1195–1210. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).