Concentric Compressive Behavior and Design of Stainless Steel–Concrete Double-Skin Composite Tubes Influenced by Dual Hydraulic Pressures
Abstract
1. Introduction
2. Finite Element Simulation
2.1. FE Model
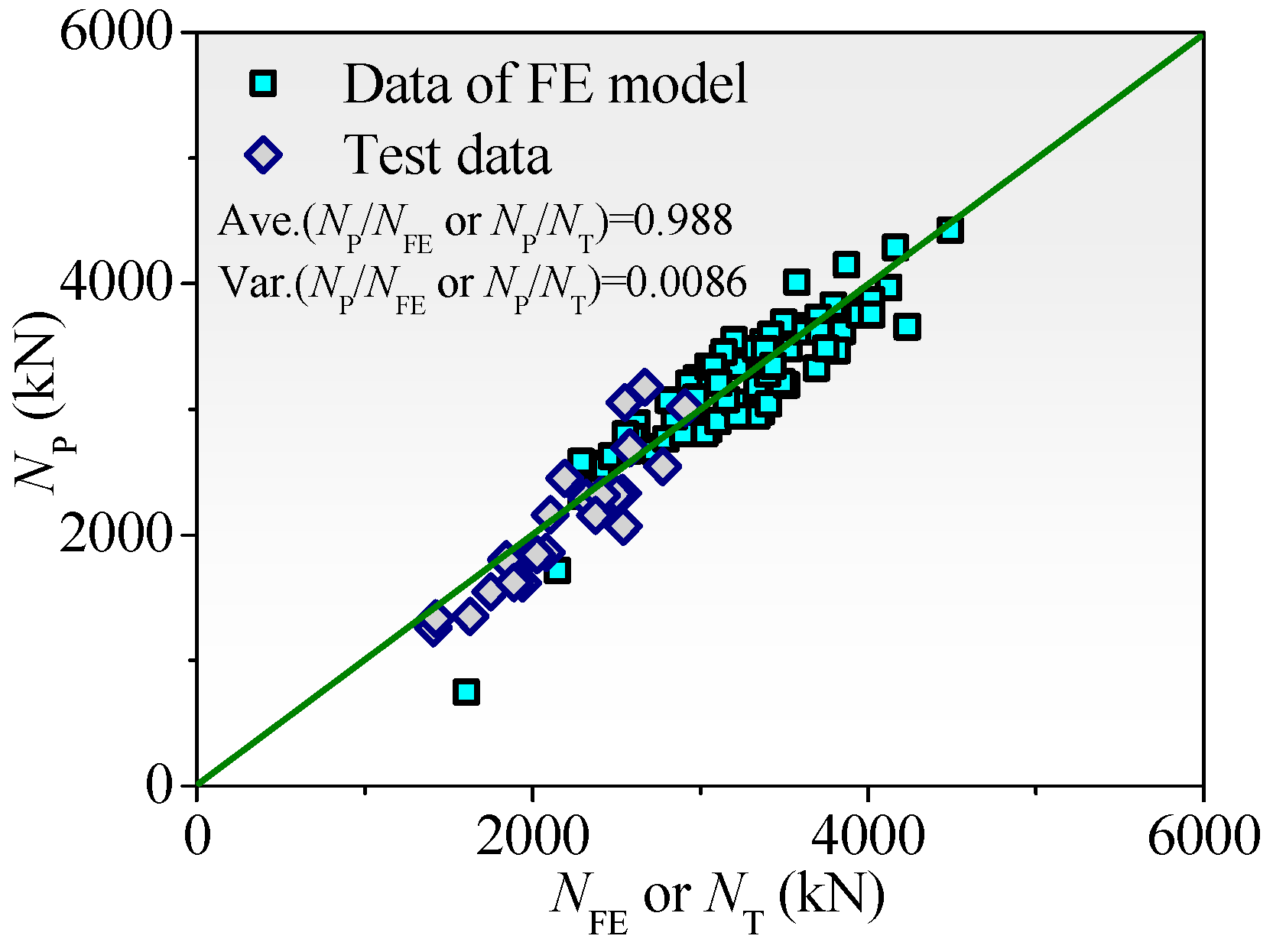
2.2. Validation of FE Model
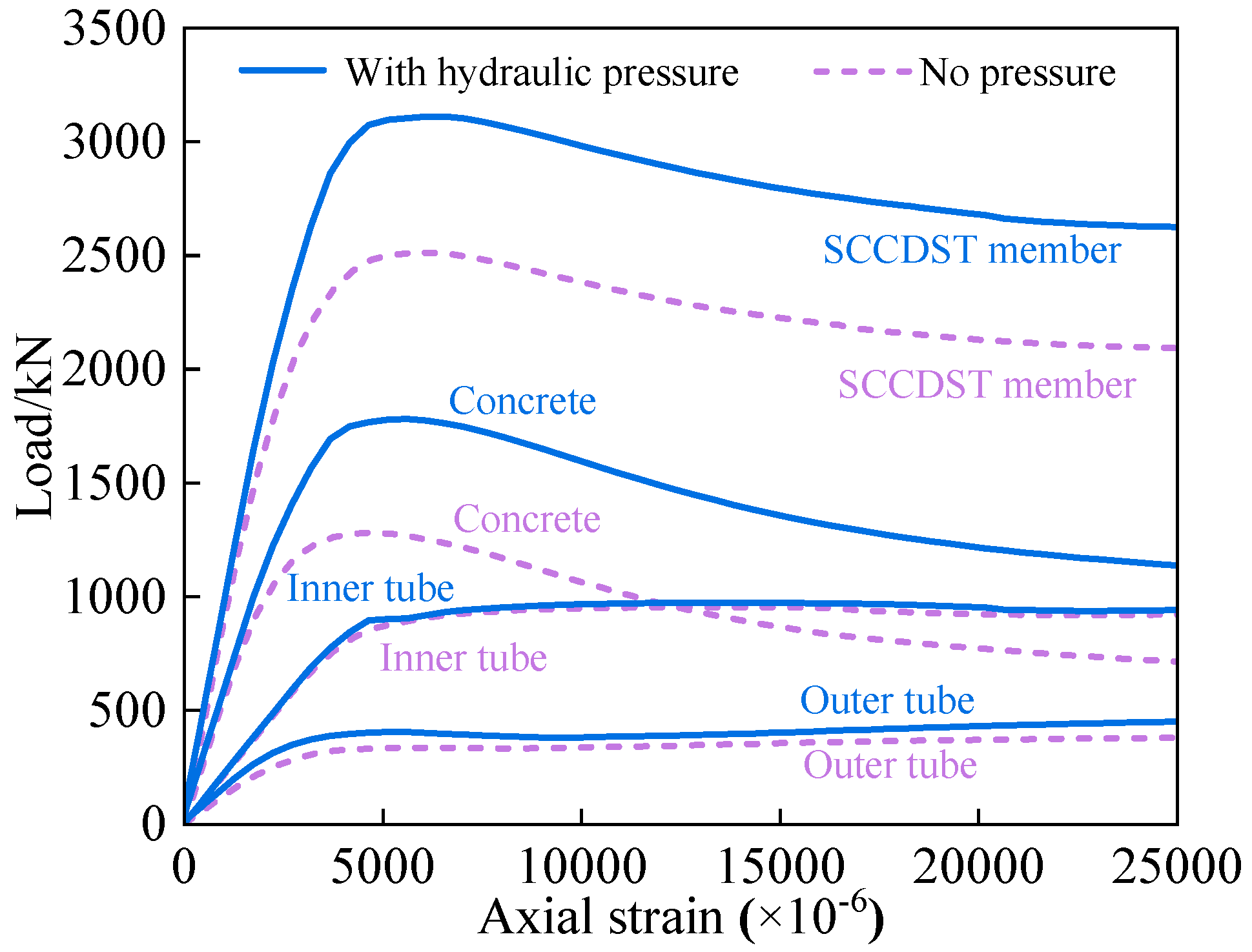
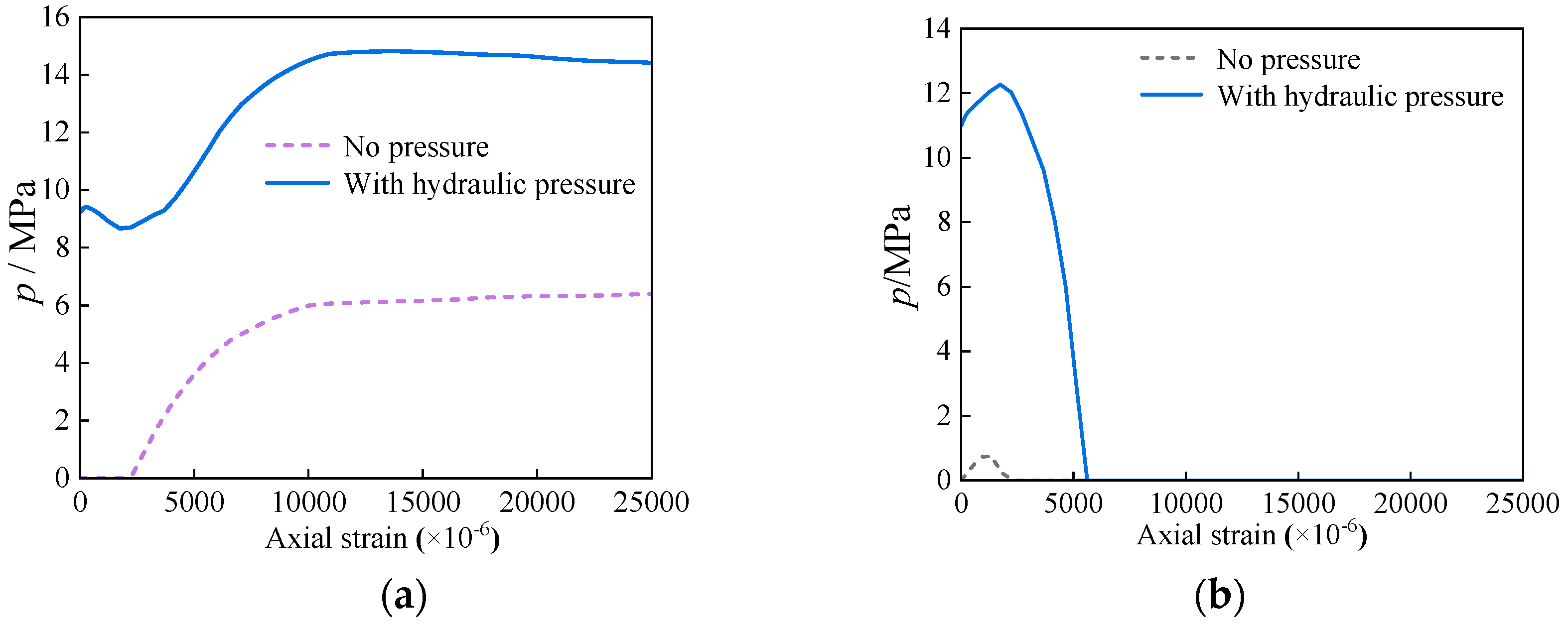
3. Full-Range Analysis of Compressive Performance
4. Parametric Study
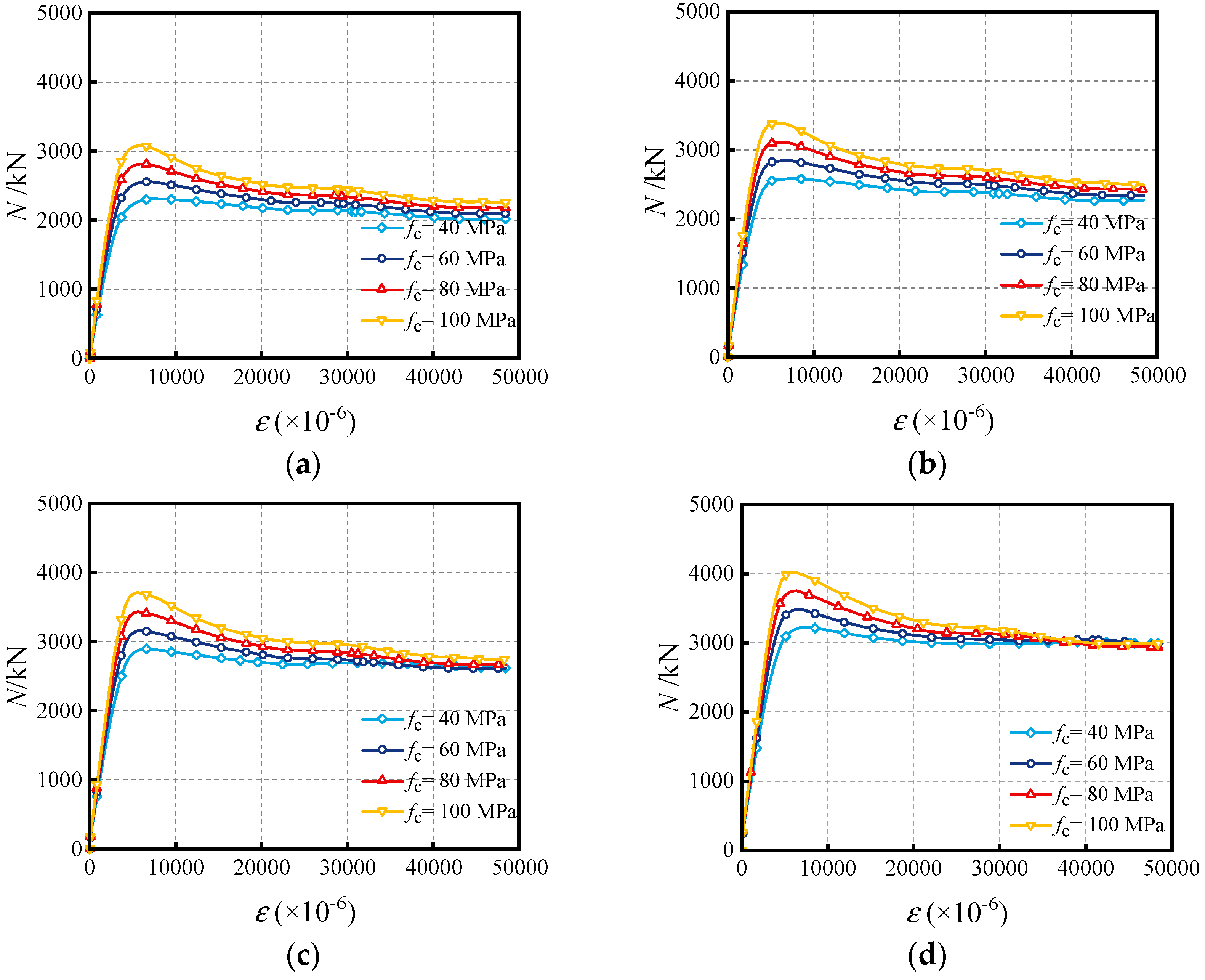
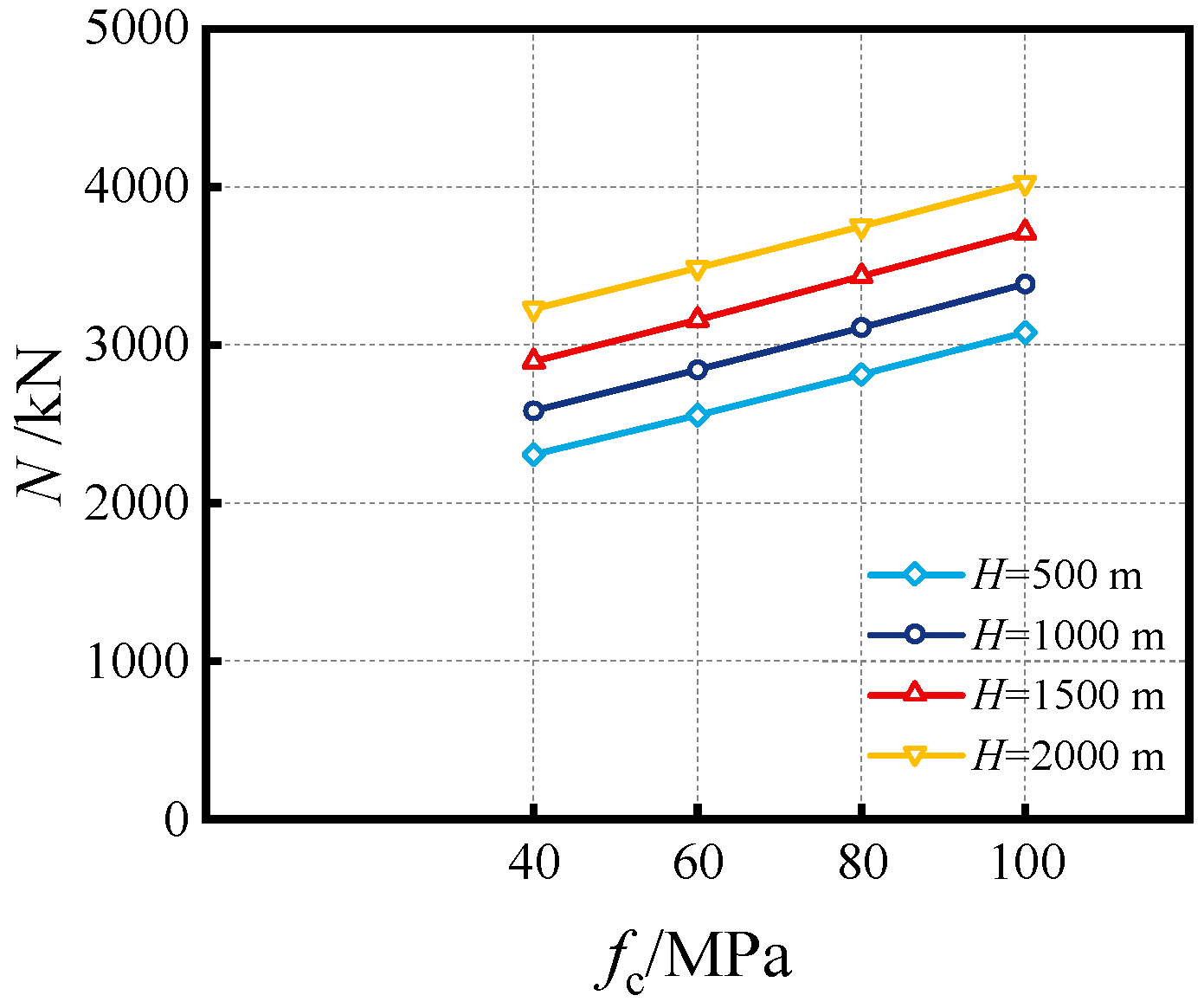
4.1. Influence of Compressive Concrete Strength (fc)
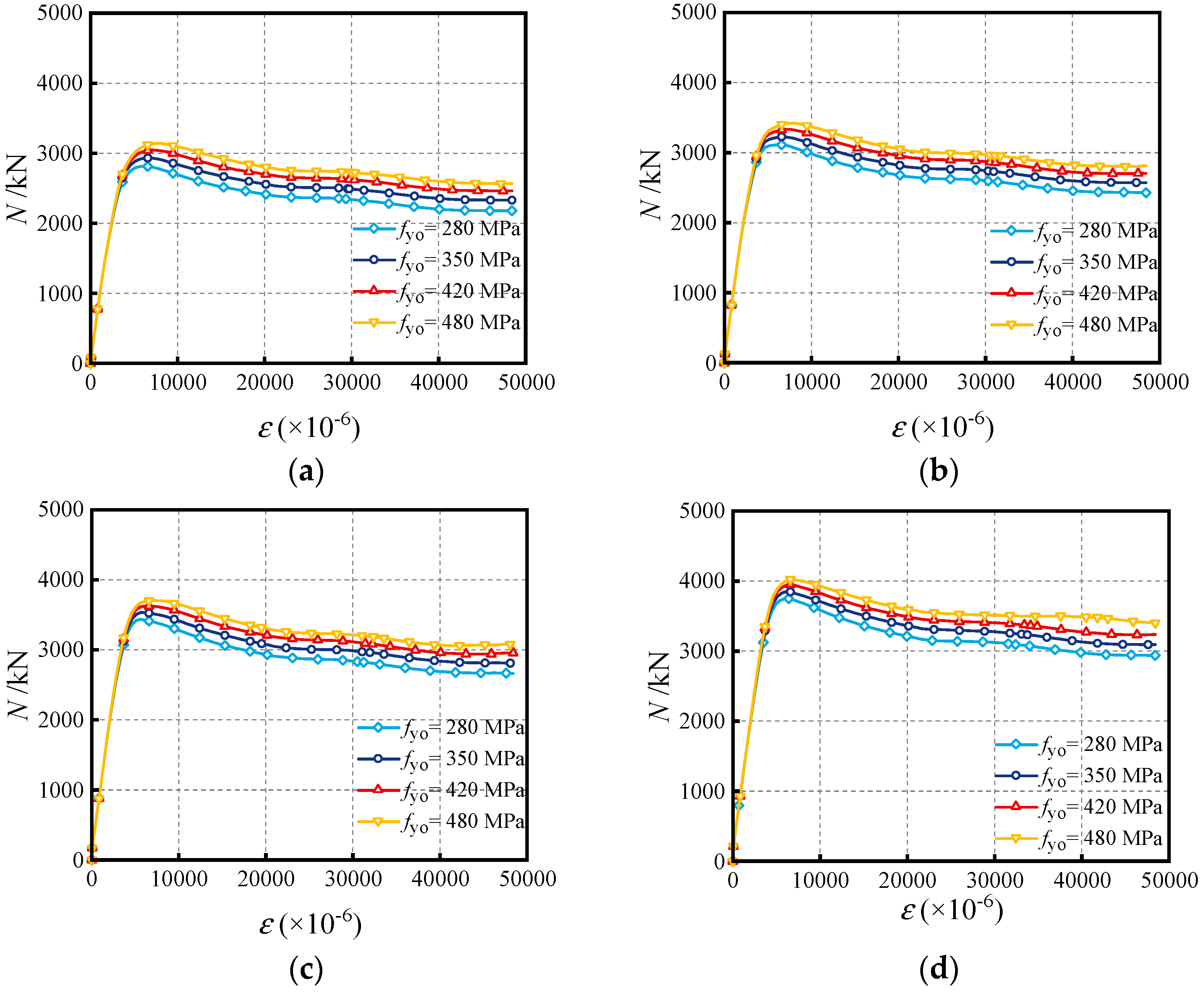
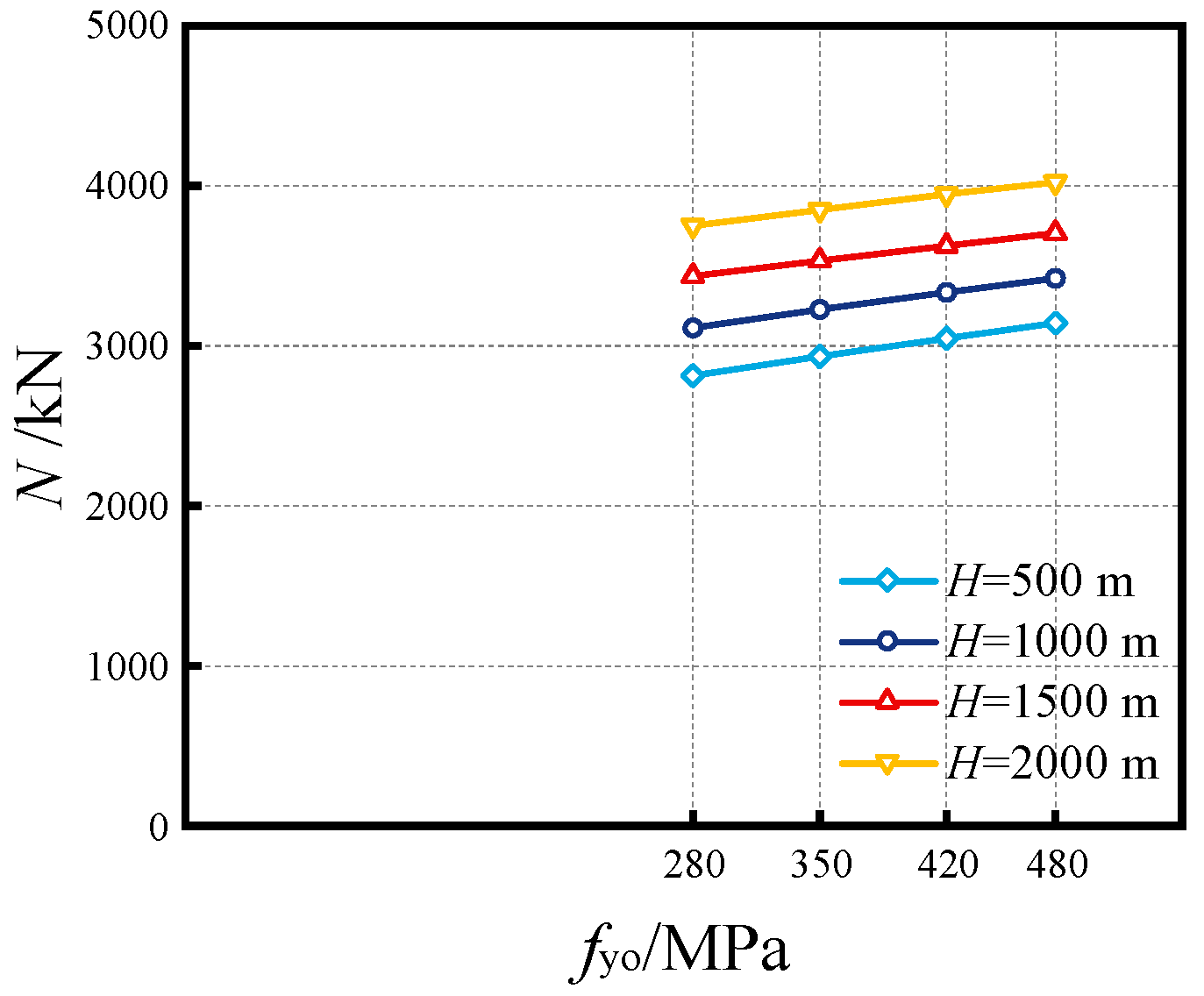
4.2. Influence of Yield Strength of Outer Tube (fyo)
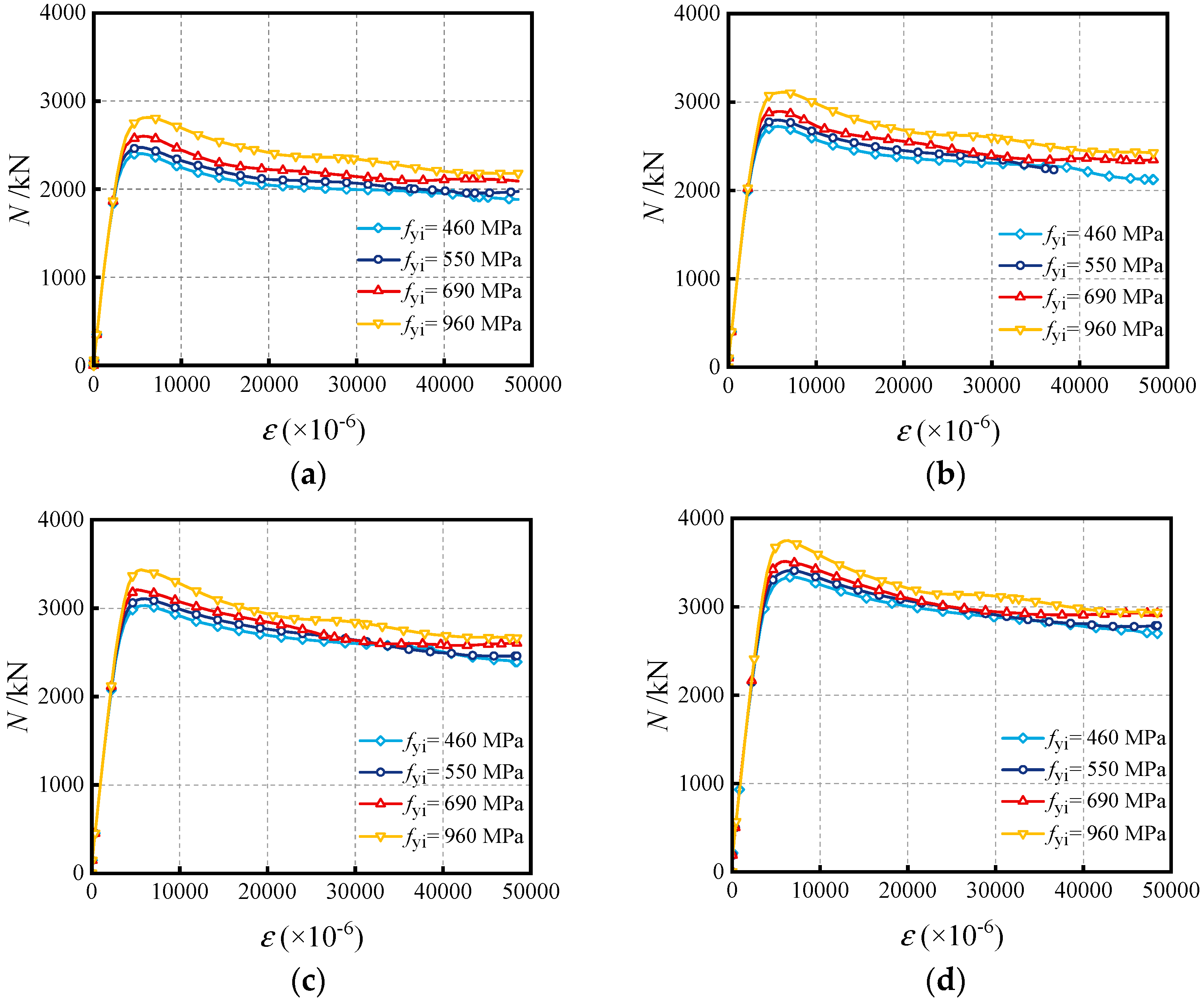
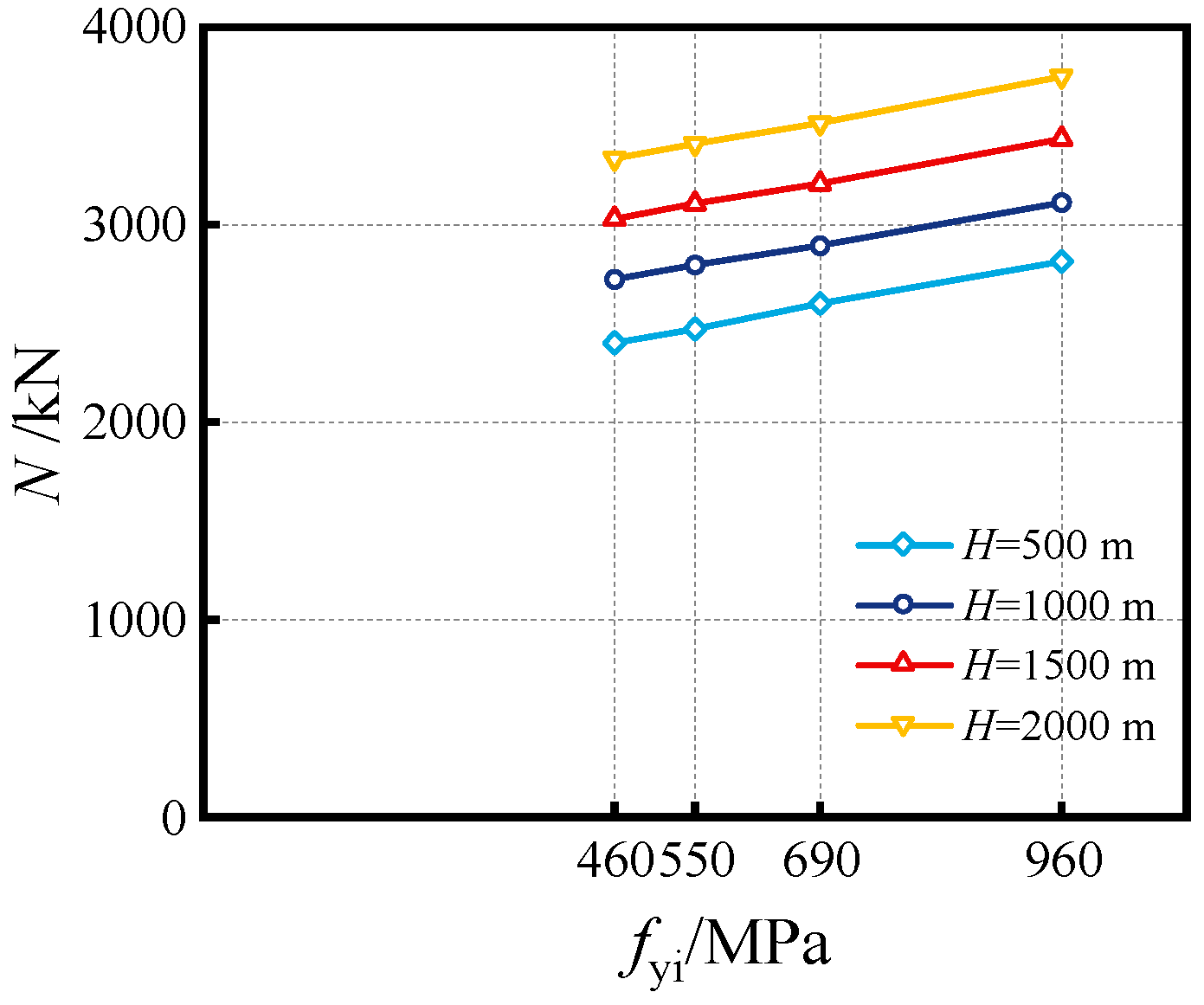
4.3. Influence of Yield Strength of Inner Tube (fyi)
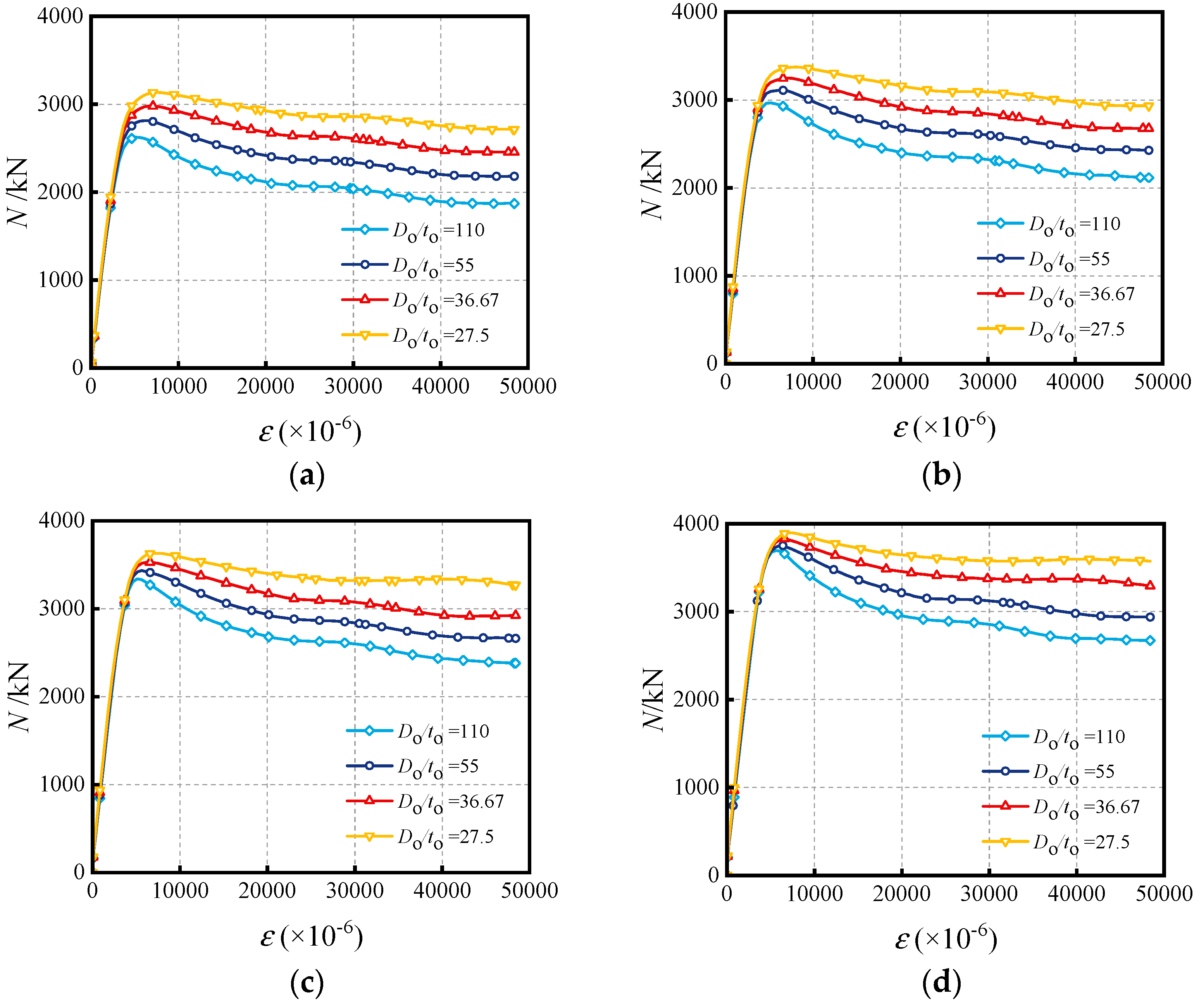
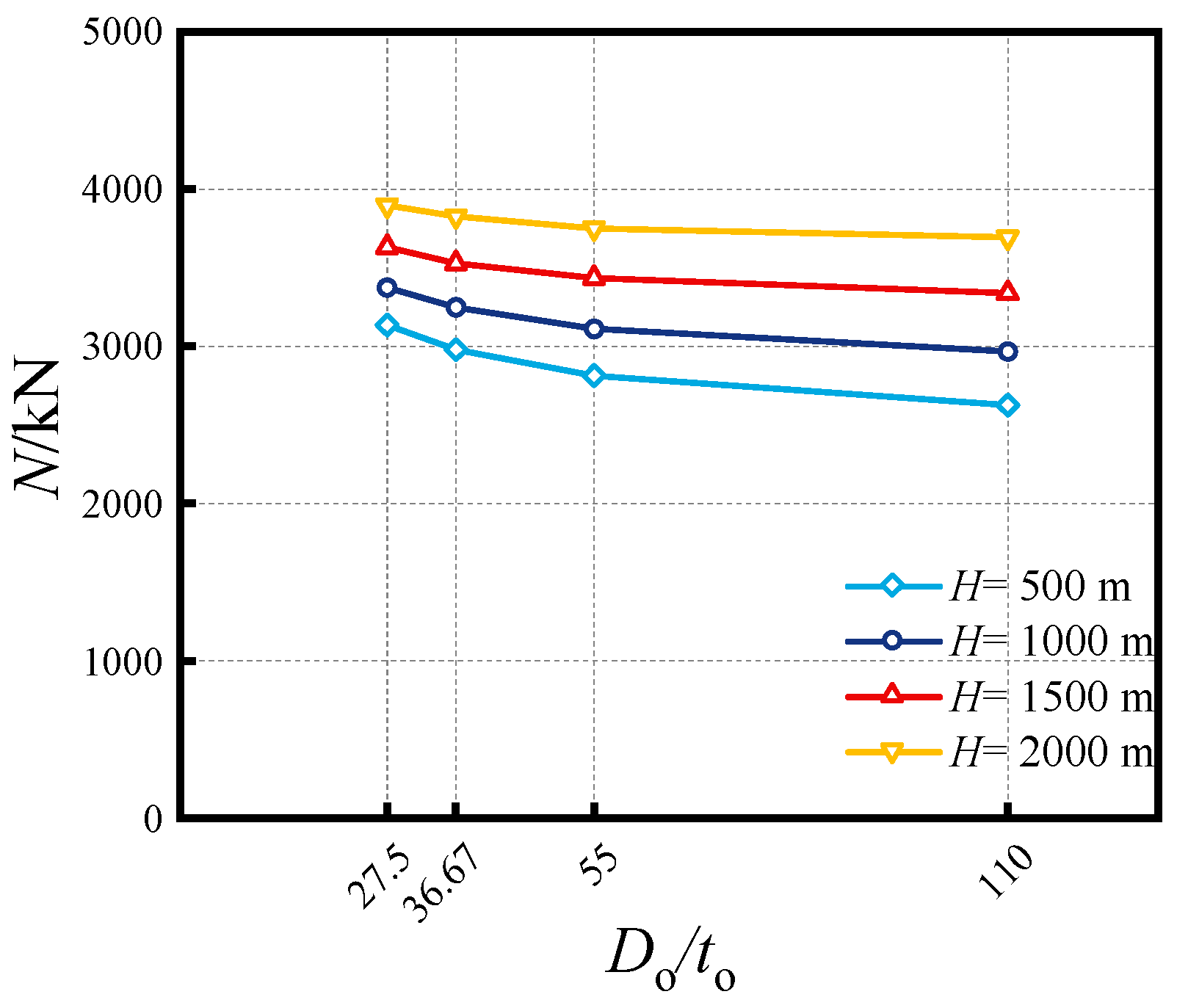
4.4. Influence of Do/to Ratio
4.5. Influence of Di/ti Ratio
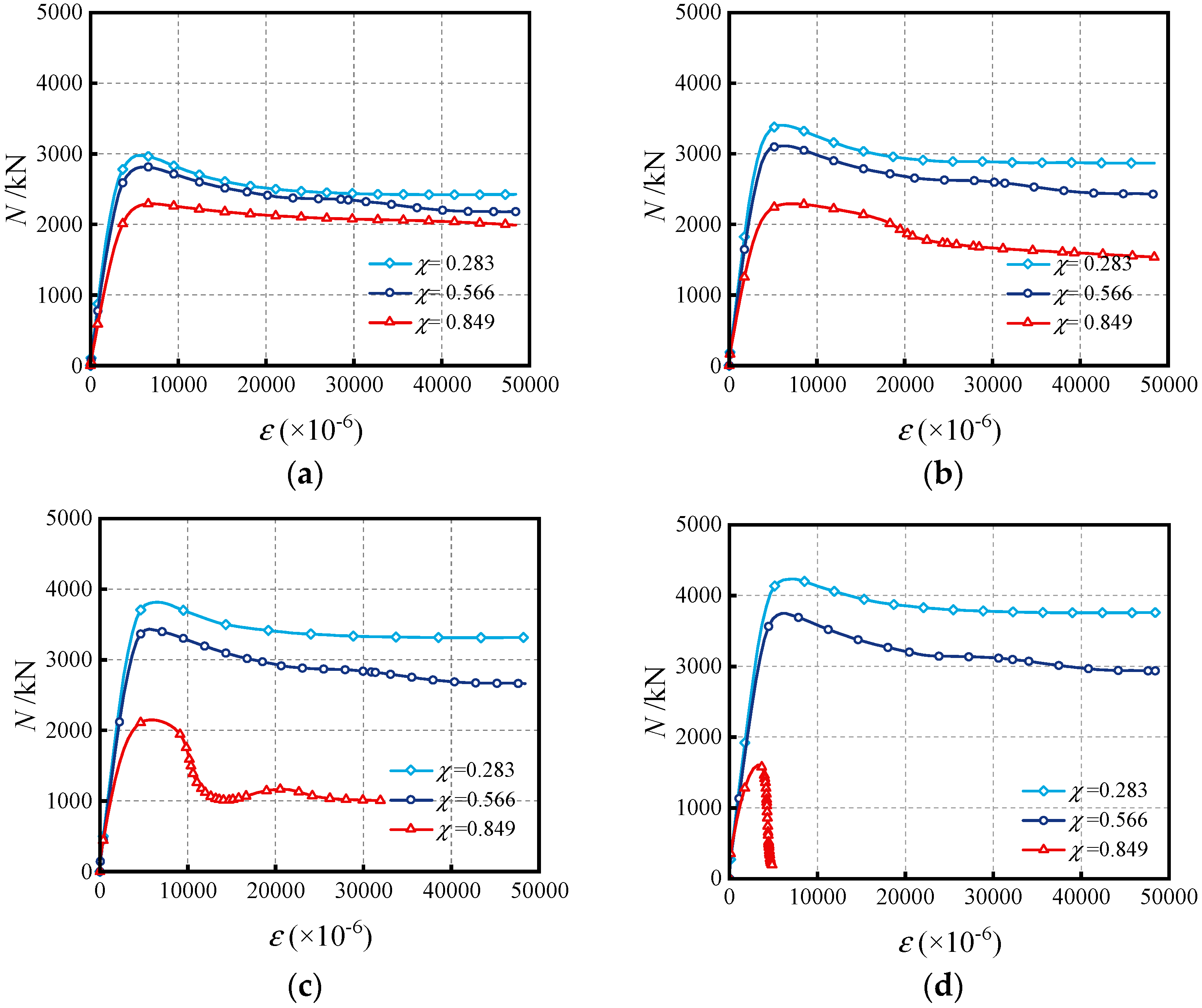
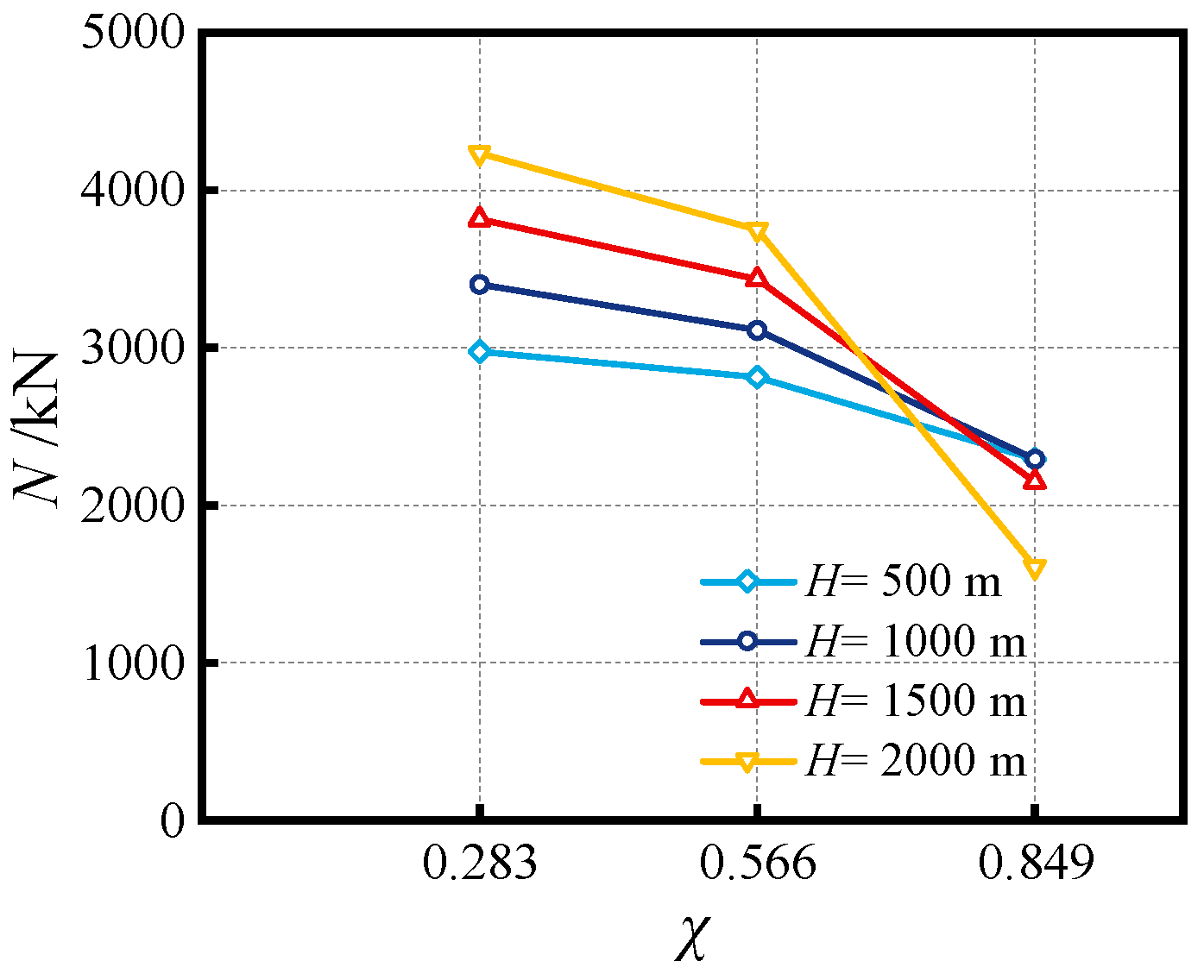
4.6. Influence of Hollow Ratio (χ)
5. Strength Model of Axial Bearing Capacity
6. Conclusions
- (1)
- The verified FE model is employed to analyze the concentric compressive mechanism of the SSCDS composite tube in an environment of dual hydraulic pressures. The full-range mechanism reveals that the application of dual hydraulic pressures enhances the confinement of the sandwich concrete, leading to an elevated axial compressive strength when compared to the unpressurized benchmark. The dual hydraulic pressures results in an uneven distribution of stress within the sandwich concrete along the radial axis, leading to a condition of increased non-uniformity in constraint;
- (2)
- The effects of critical parameters are analyzed, encompassing the impact of the Do/to ratio, Di/ti ratio, fyo, fyi, fc and χ at various water depths. Increasing material strengths of fyo, fyi and fc can enhance the compressive capacity, while enhancing the diameter-to-thickness ratio (Do/to, Di/ti) can decrease the capacity. The synergistic effect of external hydraulic pressure and internal fluid pressure can augment the confinement efficacy of SSCDS composite tubes, thereby enhancing their axial load-bearing capacity. As the hollow ratio increases, the augmentation of bearing capacity diminishes with greater water depths;
- (3)
- A practical methodology that integrates the effects of dual hydraulic pressures has been developed and validated for the members of SSCDS composite tubes. It serves as an initial framework for the safety assessment of deep-water engineering applications (e.g., submarine pipeline).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, R.; Chen, B.Q.; Guedes Soares, C. Design Equation of Buckle Propagation Pressure for Pipe-in-Pipe Systems. J. Mar. Sci. Eng. 2023, 11, 622. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, J.; Duan, M.; Sun, C.; Wang, X. Experimental and numerical study of lateral indentation for pipe-in-pipe structures. J. Mar. Sci. Eng. 2023, 11, 98. [Google Scholar] [CrossRef]
- Fan, J.; Chang, X.; Chen, B.; Yang, Y.; Li, Y. Stability and modal evolution characteristics of pipe-in-pipe system with internal intermediate support. Eng. Struct. 2024, 304, 117577. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, R.; Lam, D.; Hou, C.C.; Zhang, R. Behaviours of circular CFDST with stainless steel external tube: Slender columns and beams. Thin Wall. Struct. 2021, 158, 107172. [Google Scholar] [CrossRef]
- Tien, C.M.T.; Manalo, A.; Dixon, P.; Tafsirojjaman, T.; Karunasena, W.; Flood, W.W.; Ahmadi, H.; Kiriella, S.; Salah, A.; Wham, B.P. Effects of the legacy pipe ends on the behaviour of pipe-in-pipe repair systems under internal pressure. Eng. Fail. Anal. 2023, 144, 106957. [Google Scholar] [CrossRef]
- Mohammed, A.I.; Bartzas, K.; Johnson, C.; Spence, S.; Skyes, P.; Kidd, G.; McConnachie, J.; Njuguna, J. Structural response of a compliant pipe-in-pipe under frictionless and frictional conditions of the seabed. Ocean Eng. 2023, 276, 114020. [Google Scholar] [CrossRef]
- Sun, M.M.; Fang, H.Y.; Wang, N.N.; Du, X.M.; Zhao, H.S.; Zhai, K.J. Limit state equation and failure pressure prediction model of pipeline with complex loading. Nat. Commun. 2024, 15, 4473. [Google Scholar] [CrossRef]
- Pagoulatou, M.; Sheehan, T.; Dai, X.H.; Lam, D. Finite element analysis on the capacity of circular concrete-filled double-skin steel tubular (CFDST) stub columns. Eng. Struct. 2014, 72, 102–112. [Google Scholar] [CrossRef]
- Tran, V.L.; Kim, S.E. Efficiency of three advanced data-driven models for predicting axial compression capacity of CFDST columns. Thin Wall. Struct. 2020, 152, 106744. [Google Scholar] [CrossRef]
- Wang, W.D.; Fan, J.H.; Shi, Y.L.; Xian, W. Research on mechanical behaviour of tapered concrete-filled double skin steel tubular members with large hollow ratio subjected to bending. J. Constr. Steel Res. 2021, 182, 106689. [Google Scholar] [CrossRef]
- Shi, Y.L.; Zhang, C.F.; Xian, W.; Wang, W.D. Research on mechanical behavior of tapered concrete-filled double skin steel tubular members under eccentric compression. J. Build. Struct. 2021, 42, 155–164. (In Chinese) [Google Scholar]
- Li, W.; Li, W.J.; Xu, L.F.; Wang, F.C. Performance of CFDST beams using high-strength steel under bending. Structures 2021, 34, 2644–2655. [Google Scholar] [CrossRef]
- Ci, J.; Ahmed, M.; Tran, V.L.; Jia, H.; Chen, S. Axial compressive behavior of circular concrete-filled double steel tubular short columns. Adv. Struct. Eng. 2022, 25, 259–276. [Google Scholar] [CrossRef]
- Fan, J.H.; Wang, W.D.; Shi, Y.L.; Ji, S.H. Torsional behaviour of tapered CFDST members with large void ratio. J. Build. Eng. 2022, 52, 104434. [Google Scholar] [CrossRef]
- Lu, G.; Su, M.; Zhou, X.; Deng, X.; Bai, Y.; Wang, Y. Numerical analysis on torsional behavior of rectangular and square CFDST members. J. Constr. Steel Res. 2022, 193, 107294. [Google Scholar] [CrossRef]
- Wang, X.T.; Peng, X.; Zhang, J.P.; Yan, C.Z.; Li, X.G.; Yan, F.J. An experimental study on the flexural behavior of tapered high-strength thin-walled concrete-filled double skin steel tubular members. Prog. Steel Build. Struct. 2022, 24, 24–33. (In Chinese) [Google Scholar]
- Zheng, Y.; Wang, C.; Chen, M. Flexural strength and stiffness of circular double-skin and double-tube concrete-filled steel tubes. Mar. Struct. 2022, 81, 103126. [Google Scholar] [CrossRef]
- Deng, R.; Zhou, X.H.; Wang, Y.H.; Bai, J.L.; Deng, X.W. Experimental study on tapered concrete-filled double skin steel tubular columns under torsion. Thin Wall. Struct. 2022, 177, 109444. [Google Scholar] [CrossRef]
- Cheng, Z.; Wang, F.; Zhang, D. Analytical model for axially compressed circular concrete-filled double skin steel tubes (CFDSTs): Insights from concrete non-uniformly confined states. Thin Wall. Struct. 2023, 192, 111106. [Google Scholar] [CrossRef]
- Yilmaz, B.C.C.; Binbir, E.; Guzelbulut, C.; Yildirim, H.; Celik, O.C. Circular concrete-filled double skin steel tubes under concentric compression: Tests and FEA parametric study. Compos. Struct. 2023, 309, 116765. [Google Scholar] [CrossRef]
- Han, L.H.; Ren, Q.X.; Li, W. Tests on stub stainless steel–concrete–carbon steel double-skin tubular (DST) columns. J. Constr. Steel Res. 2011, 67, 437–452. [Google Scholar] [CrossRef]
- Wang, F.; Young, B.; Gardner, L. Compressive testing and numerical modelling of concrete-filled double skin CHS with austenitic stainless steel outer tubes. Thin Wall. Struct. 2019, 141, 345–359. [Google Scholar] [CrossRef]
- Wang, F.; Young, B.; Gardner, L. CFDST sections with square stainless steel outer tubes under axial compression: Experimental investigation, numerical modelling and design. Eng. Struct. 2020, 207, 110189. [Google Scholar] [CrossRef]
- Le, T.T.; Patel, V.I.; Liang, Q.Q.; Huynh, P. Axisymmetric simulation of circular concrete-filled double-skin steel tubular short columns incorporating outer stainless-steel tube. Eng. Struct. 2021, 227, 111416. [Google Scholar] [CrossRef]
- Zhou, F.; Lama, L.; Zhao, K. Design of stainless steel CHS-concrete infill-carbon steel CHS double-skin stub columns. Eng. Struct. 2023, 278, 115479. [Google Scholar] [CrossRef]
- Wang, F.C.; Han, L.H. Analytical behavior of carbon steel-concrete-stainless steel double-skin tube (DST) used in submarine pipeline structure. Mar. Struct. 2019, 63, 99–116. [Google Scholar] [CrossRef]
- Wang, J.T.; Yang, K.L.; Sun, J.Y. Compressive Behavior of Stainless Steel–Concrete–Carbon Steel Double-Skin Tubular (SCCDST) Members Subjected to External Hydraulic Pressure. J. Mar. Sci. Eng. 2024, 12, 406. [Google Scholar] [CrossRef]
- Shi, Y.J.; Wang, M.; Wang, Y.Q. Study on constitutive model of structural steel under cyclic loading. Eng. Mech. 2012, 29, 92–98. (In Chinese) [Google Scholar] [CrossRef]
- Patel, V.I.; Hassanein, M.F.; Thai, H.T.; Al Abadi, H.; Paton-Cole, V. Behaviour of axially loaded circular concrete-filled bimetallic stainless-carbon steel tubular short columns. Eng. Struct. 2017, 147, 583–597. [Google Scholar] [CrossRef]
- Han, L.H. Concrete Filled Steel Tubular Structures—Theory and Practice; Science Press: Beijing, China, 2016. (In Chinese) [Google Scholar]
- T/CCES 7-2020; China Civil Engineering Society. Technical Specification for Concrete-Filled Double Skin Steel Tubular Structures. China Architecture & Building Press: Beijing, China, 2020. (In Chinese)
- T/CECS 952-2021; China Association for Engineering Construction Standardization. Technical Specification for Concrete-Filled Stainless Steel Tubular Structures. China Architecture & Building Press: Beijing, China, 2022. (In Chinese)
- Sakino, K.; Nakahara, H.; Morino, S.; Nishiyama, I. Behavior of centrally loaded concrete-filled steel-tube short columns. J. Struct. Eng. 2004, 130, 180–188. [Google Scholar] [CrossRef]
- Richart, F.E.; Brandtzæg, A.; Brown, R.L. A Study of the Failure of Concrete Under Combined Compressive Stresses; University of Illinois, Bulletin: Champaign, IL, USA, 1928. [Google Scholar]
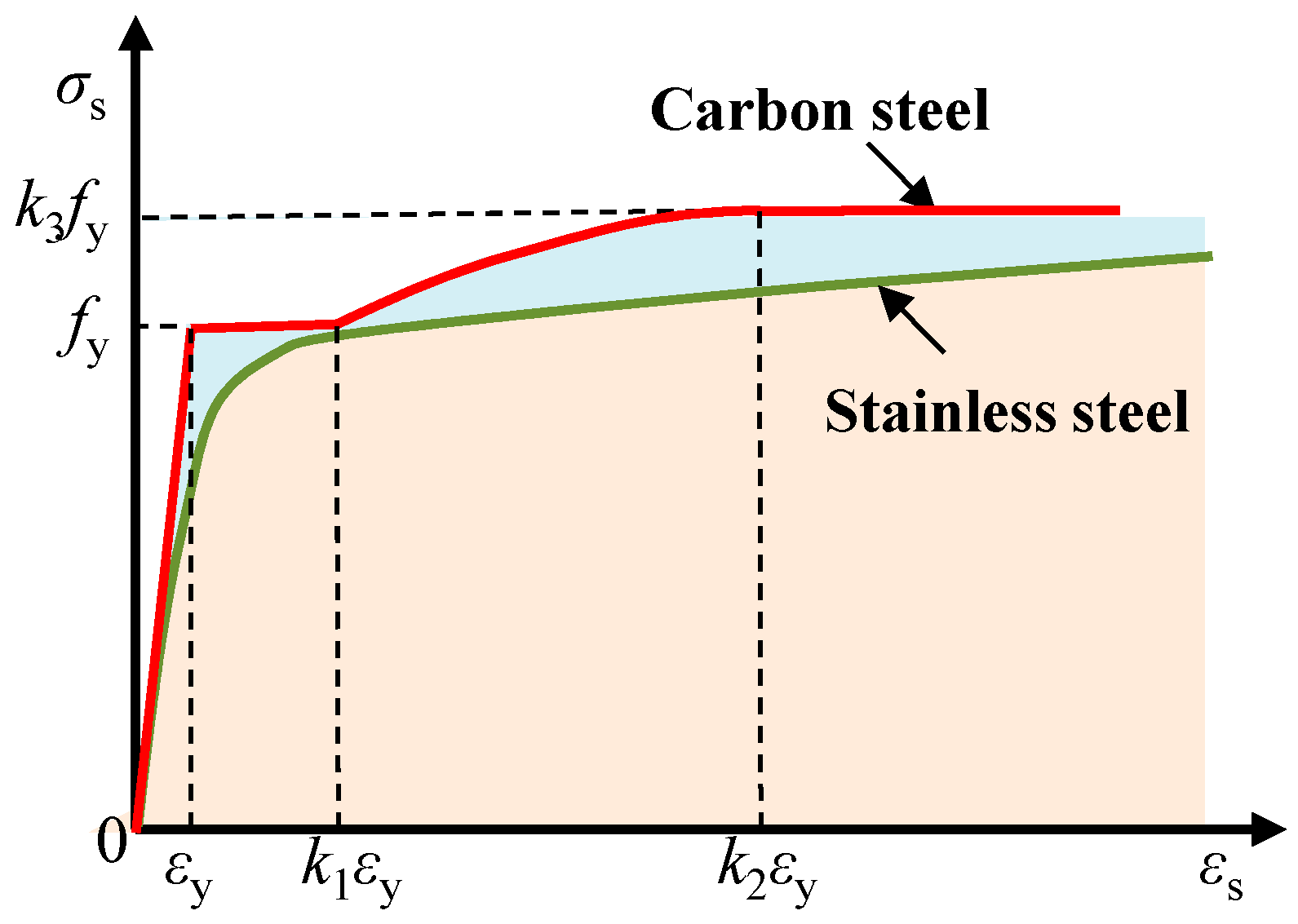

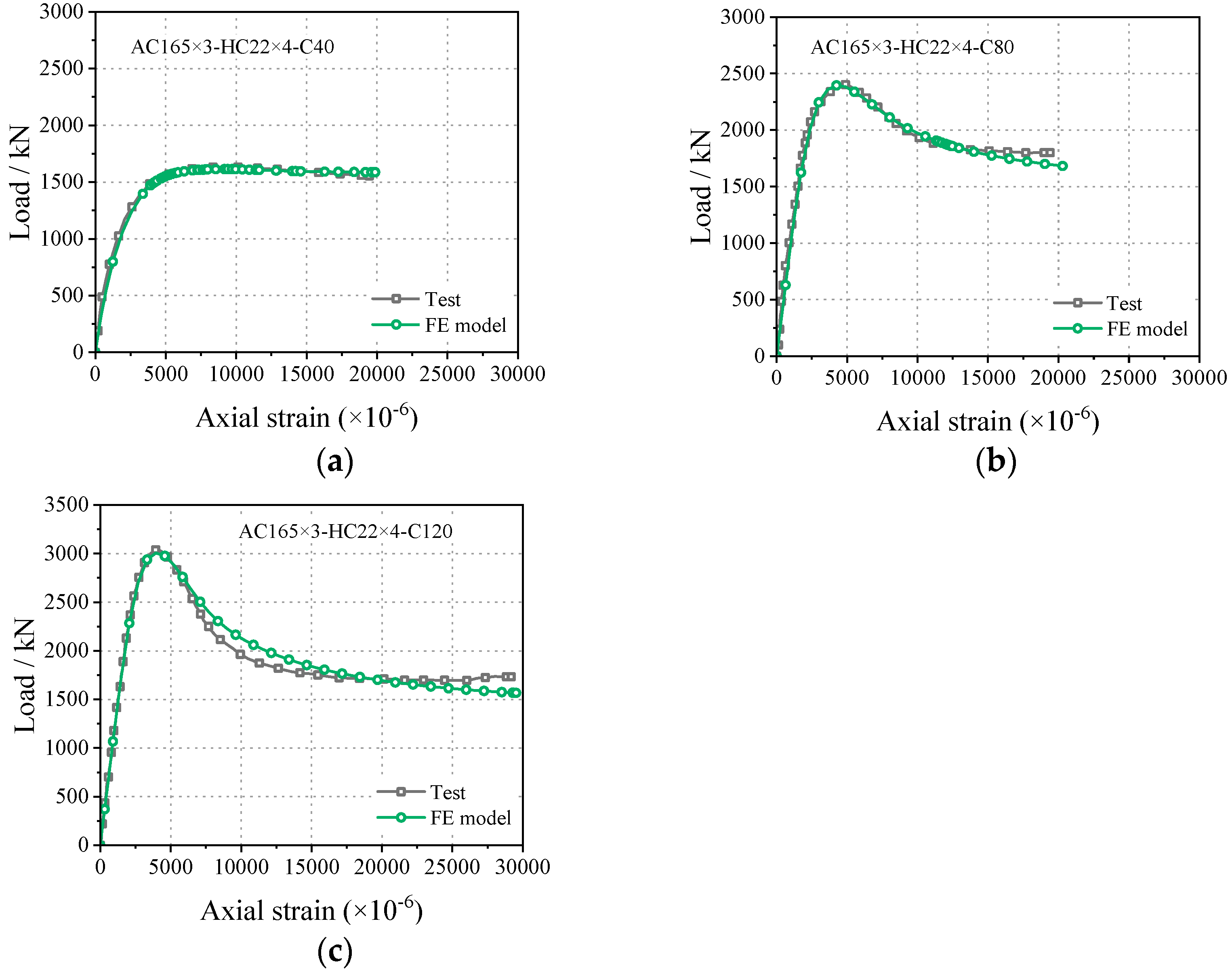




| Specimen [21] | Length/mm | Outer Tube/mm | Inner Tube/mm | Material Strength/MPa | Test Strength NT/kN | Simulated Strength NFE/kN | NFE/NT | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Do | to | Di | ti | fyo | fyi | fc | |||||
| AC140×3-HC22×4-C40 | 350 | 140.2 | 2.92 | 22.1 | 4.09 | 300 | 794 | 40.5 | 1410 | 1398.48 | 0.9918 |
| AC140×3-HC22×4-C80 | 350 | 140.2 | 2.91 | 22.1 | 4.10 | 300 | 794 | 79.9 | 1845 | 1845.94 | 1.0005 |
| AC140×3-HC22×4-C120 | 350 | 140.2 | 2.89 | 22.1 | 4.08 | 300 | 794 | 115.6 | 2321 | 2322.87 | 1.0008 |
| AC140×3-HC32×6-C40 | 350 | 140.3 | 2.89 | 32.0 | 5.48 | 300 | 619 | 40.5 | 1423 | 1470.33 | 1.0333 |
| AC140×3-HC32×6-C80 | 350 | 140.2 | 2.92 | 31.9 | 5.27 | 300 | 619 | 79.9 | 2012 | 2016.15 | 1.0021 |
| AC140×3-HC32×6-C120 | 350 | 140.1 | 2.91 | 31.9 | 5.36 | 300 | 619 | 115.6 | 2537 | 2513.09 | 0.9906 |
| AC140×3-HC38×8-C40 | 350 | 140.1 | 2.91 | 38.1 | 7.63 | 300 | 433 | 40.5 | 1626 | 1562.52 | 0.9610 |
| AC140×3-HC38×8-C80 | 350 | 140.1 | 2.90 | 38.0 | 7.51 | 300 | 433 | 79.9 | 2083 | 2078.90 | 0.9980 |
| AC140×3-HC38×8-C120 | 350 | 140.2 | 2.90 | 37.9 | 7.39 | 300 | 433 | 115.6 | 2500 | 2537.38 | 1.0150 |
| AC140×3-HC55×11-C40 | 350 | 140.2 | 2.90 | 55.1 | 10.62 | 300 | 739 | 40.5 | 2543 | 2541.38 | 0.9994 |
| AC140×3-HC55×11-C80 | 350 | 140.1 | 2.90 | 55.2 | 10.76 | 300 | 739 | 79.9 | 2775 | 2572.60 | 0.9919 |
| AC140×3-HC89×4-C40 | 350 | 140.1 | 2.87 | 89.0 | 3.89 | 300 | 1029 | 40.5 | 2025 | 2008.07 | 0.9916 |
| AC140×3-HC89×4-C80 | 350 | 140.1 | 2.86 | 89.1 | 3.91 | 300 | 1029 | 79.9 | 2107 | 2157.63 | 1.0240 |
| AC140×3-HC89×4-C120 | 350 | 140.2 | 2.88 | 89.1 | 3.91 | 300 | 1029 | 115.6 | 2195 | 2152.46 | 0.9806 |
| AC165×3-HC22×4-C40 | 413 | 165.3 | 2.94 | 22.0 | 4.14 | 276 | 794 | 40.5 | 1750 | 1613.74 | 0.9221 |
| AC165×3-HC22×4-C80 | 413 | 165.2 | 2.94 | 22.1 | 4.09 | 276 | 794 | 79.9 | 2413 | 2374.28 | 0.9840 |
| AC165×3-HC22×4-C120 | 413 | 165.3 | 2.94 | 22.1 | 4.04 | 276 | 794 | 115.6 | 2911 | 2914.87 | 1.0013 |
| AC165×3-HC32×6-C40 | 413 | 165.3 | 2.93 | 31.9 | 5.35 | 276 | 619 | 40.5 | 1943 | 1914.14 | 0.9851 |
| AC165×3-HC32×6-C40R | 413 | 165.3 | 2.94 | 31.9 | 5.39 | 276 | 619 | 40.5 | 1891 | 1853.36 | 0.9801 |
| AC165×3-HC32×6-C80 | 413 | 165.3 | 2.94 | 31.8 | 5.25 | 276 | 619 | 79.9 | 2550 | 2577.29 | 1.0107 |
| AC165×3-HC89×4-C40 | 413 | 165.5 | 2.92 | 89.0 | 3.92 | 276 | 1029 | 40.5 | 2375 | 2330.04 | 0.9811 |
| AC165×3-HC89×4-C80 | 413 | 165.4 | 2.91 | 89.1 | 3.91 | 276 | 1029 | 79.9 | 2580 | 2598.90 | 1.0073 |
| AC165×3-HC89×4-C120 | 413 | 165.2 | 2.92 | 88.9 | 3.88 | 276 | 1029 | 115.6 | 2671 | 2685.27 | 1.0053 |
| Mean | 0.9938 | ||||||||||
| Variance | 0.0005 | ||||||||||
| Water Depths (H)/m | Do/to | Di/ti | fyo/MPa | fyi/MPa | fc/MPa | χ |
|---|---|---|---|---|---|---|
| 500; 1000; 1500; 2000 | 110; 55; 36.67; 27.5 | 45; 22.5; 15; 11.25 | 280; 350; 420; 480 | 460; 550; 690; 960 | 40; 60; 80; 100 | 0.283; 0.566; 0.849 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.-T.; Yang, Y.; Yang, K.-L.; Hu, D.-L.; Xu, L.-B.; Li, J.-X. Concentric Compressive Behavior and Design of Stainless Steel–Concrete Double-Skin Composite Tubes Influenced by Dual Hydraulic Pressures. J. Mar. Sci. Eng. 2024, 12, 2140. https://doi.org/10.3390/jmse12122140
Wang J-T, Yang Y, Yang K-L, Hu D-L, Xu L-B, Li J-X. Concentric Compressive Behavior and Design of Stainless Steel–Concrete Double-Skin Composite Tubes Influenced by Dual Hydraulic Pressures. Journal of Marine Science and Engineering. 2024; 12(12):2140. https://doi.org/10.3390/jmse12122140
Chicago/Turabian StyleWang, Jian-Tao, Yang Yang, Kai-Lin Yang, Deng-Long Hu, Long-Bo Xu, and Jun-Xin Li. 2024. "Concentric Compressive Behavior and Design of Stainless Steel–Concrete Double-Skin Composite Tubes Influenced by Dual Hydraulic Pressures" Journal of Marine Science and Engineering 12, no. 12: 2140. https://doi.org/10.3390/jmse12122140
APA StyleWang, J.-T., Yang, Y., Yang, K.-L., Hu, D.-L., Xu, L.-B., & Li, J.-X. (2024). Concentric Compressive Behavior and Design of Stainless Steel–Concrete Double-Skin Composite Tubes Influenced by Dual Hydraulic Pressures. Journal of Marine Science and Engineering, 12(12), 2140. https://doi.org/10.3390/jmse12122140






