Experimental Investigation on Wave and Bed Profile Evolution in a Sandbar-Lagoon Coast with Submerged Vegetation
Abstract
1. Introduction
2. Methodology
2.1. Experimental Setup
2.2. Data Processing
3. Results
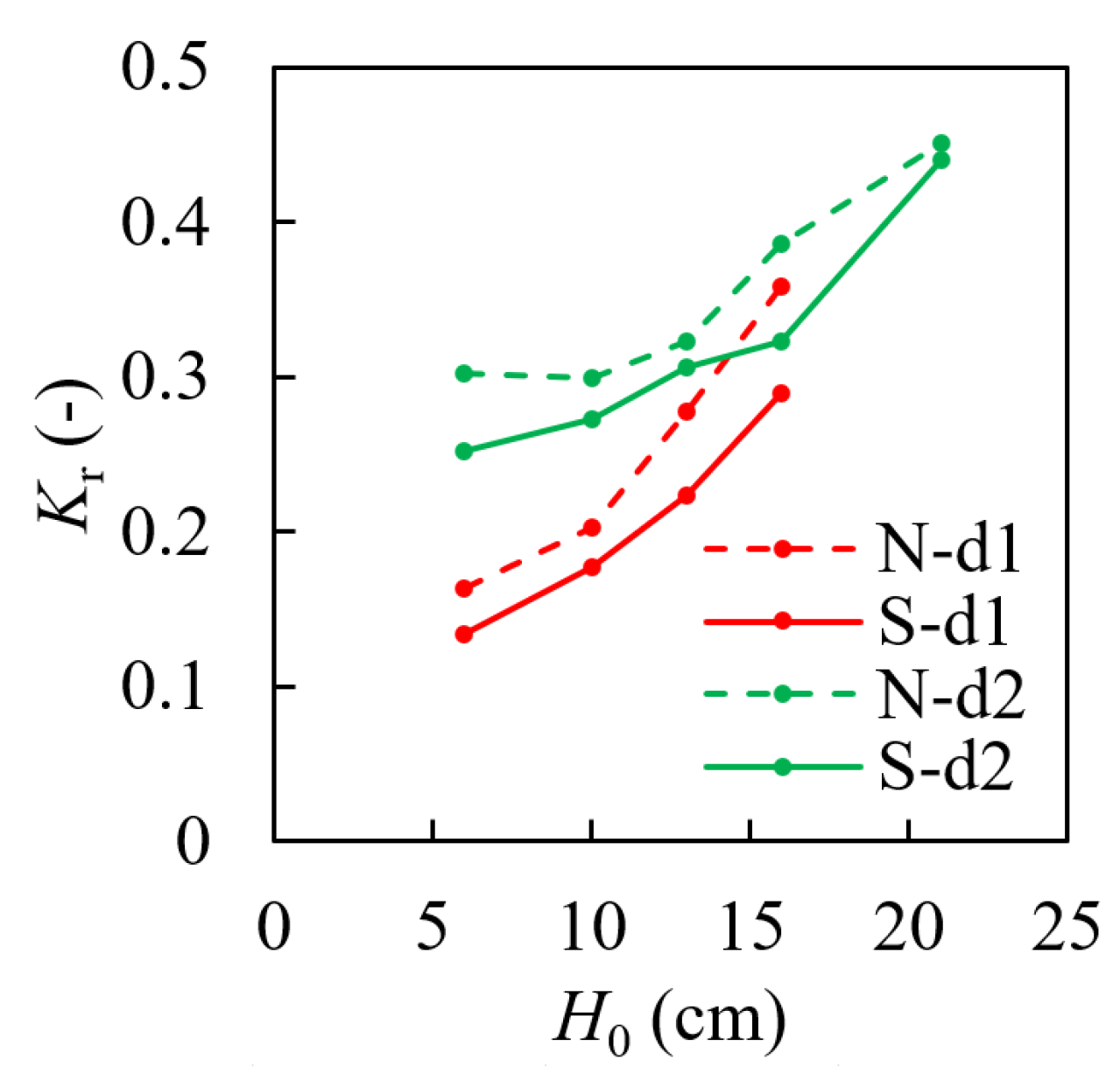
3.1. Wave Propagation
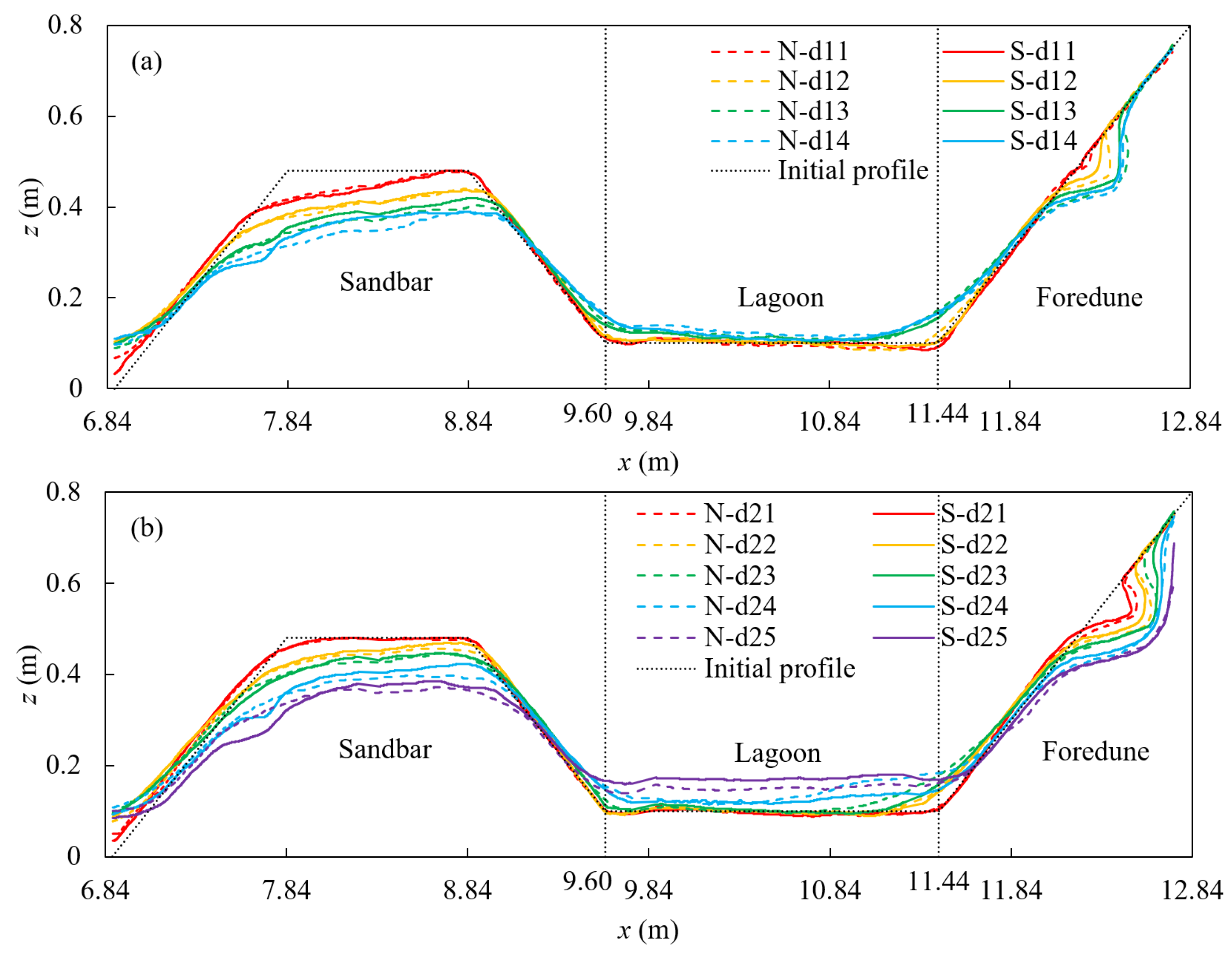
3.2. Bed Profiles
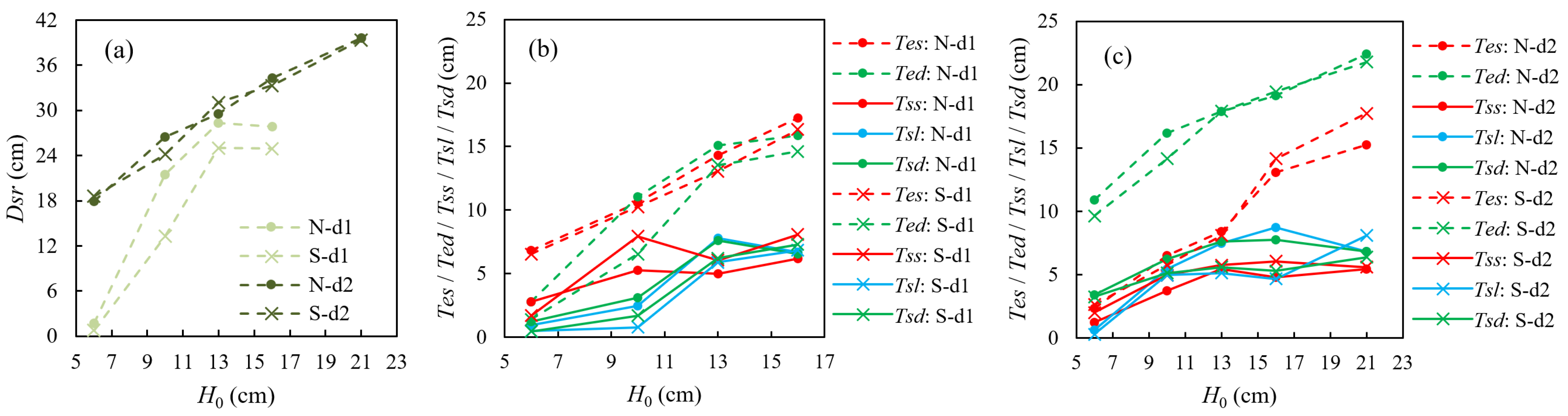
3.3. Sediment Transport
4. Discussion
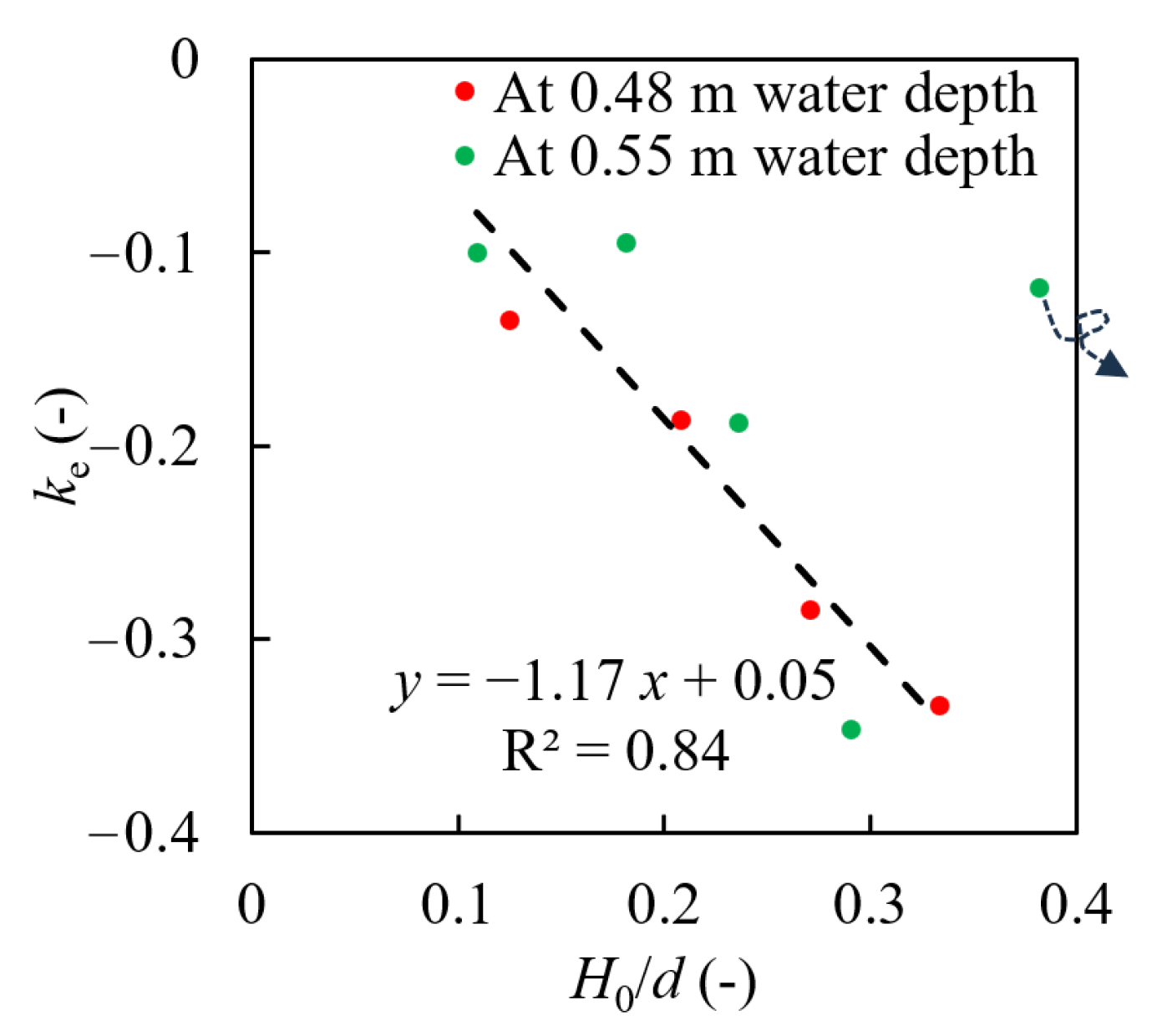
4.1. Linear Relationship Between the Change Ratio in Wave Energy and the Relative Incident Wave Height
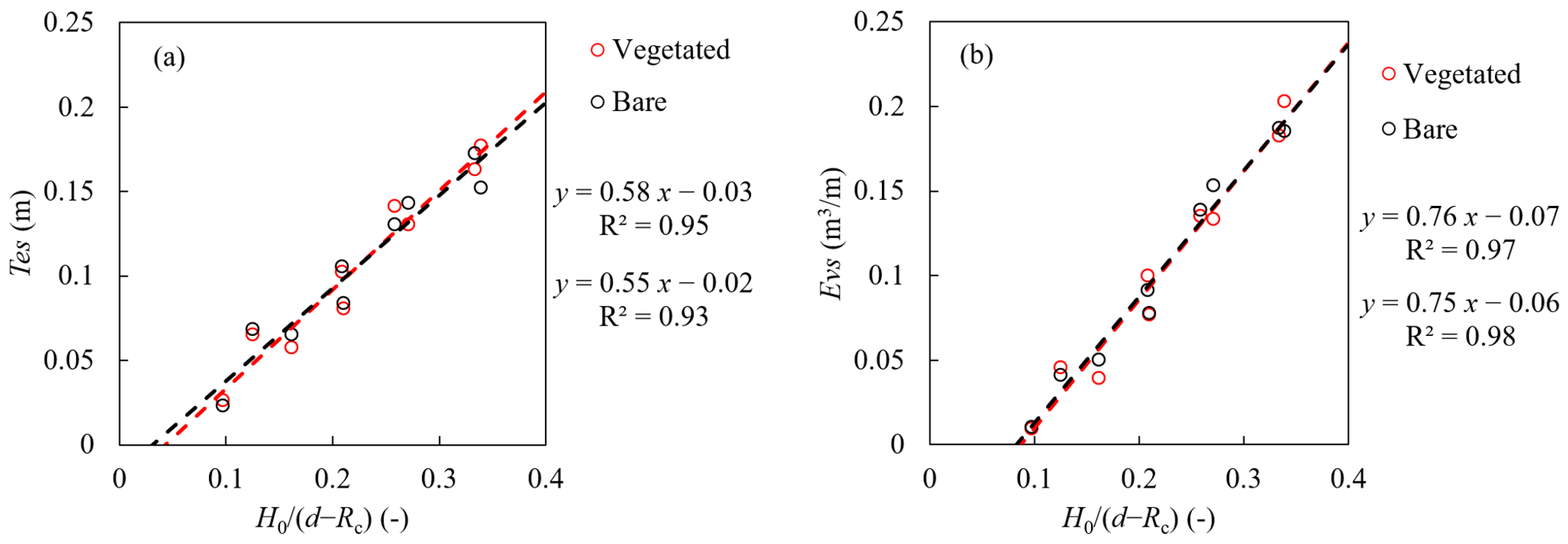
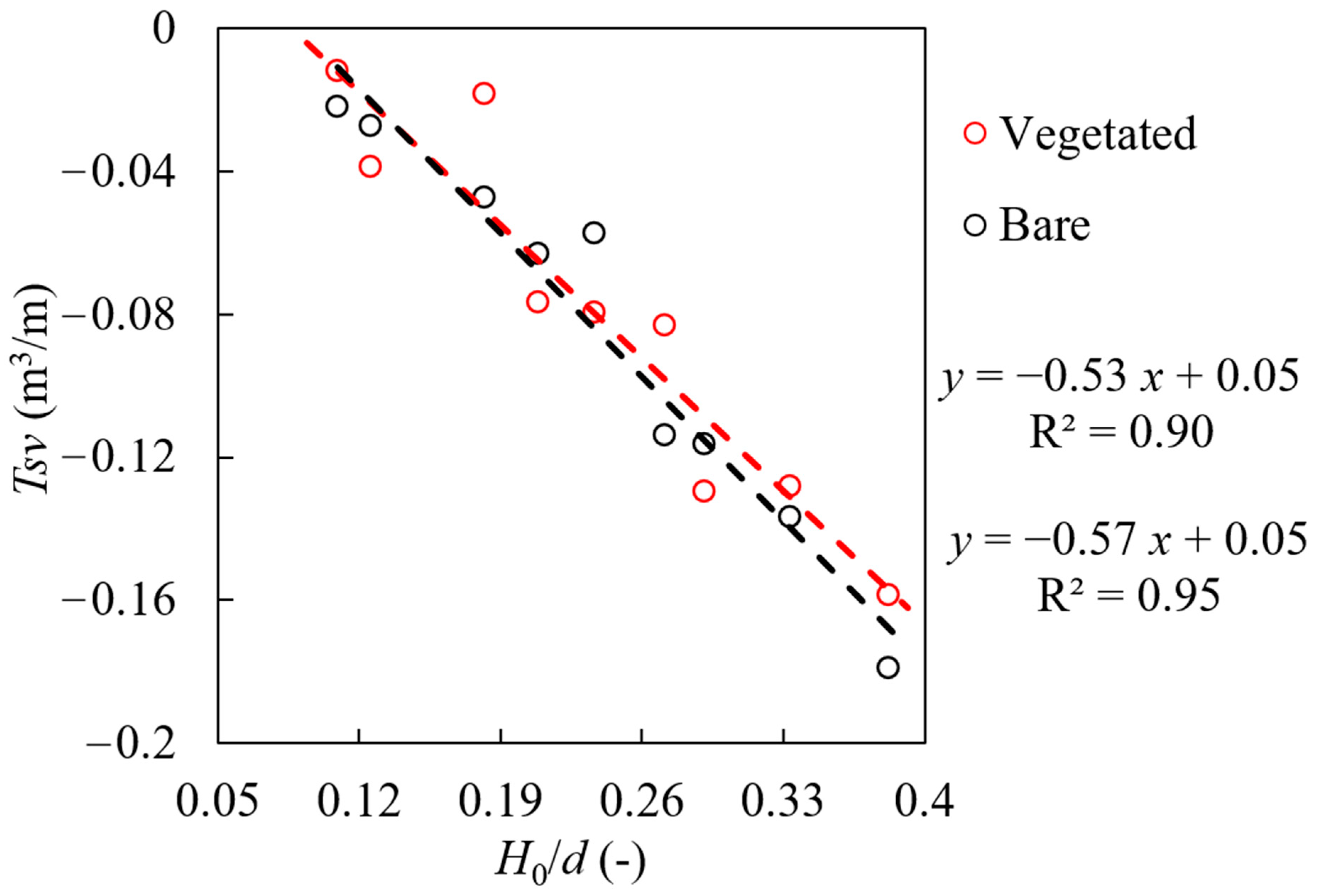
4.2. Mathematical Expressions for Sediment Transport
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Costanza, R.; D’arge, R.; Groot, R.D.; Farber, S.; Grasso, M.; Hannon, B.; Limburg, K.; Naeem, S.; O’neill, R.V.; Paruelo, J.; et al. The value of the world’s ecosystem services and natural capital. Nature 1997, 387, 253–260. [Google Scholar] [CrossRef]
- Clara, I.; Dyack, B.; Rolfe, J.; Newton, A.; Borg, D.; Povilanskas, R.; Brito, A.C. The value of coastal lagoons: Case study of recreation at the Ria de Aveiro, Portugal in comparison to the Coorong, Australia. J. Nat. Conserv. 2018, 43, 190–200. [Google Scholar] [CrossRef]
- Suresh, K.; Khanal, U.; Wilson, C. Stakeholders’ use and preservation valuation of lagoon ecosystems. Econ. Anal. Policy 2021, 71, 123–137. [Google Scholar] [CrossRef]
- Morris, R.L.; Konlechner, T.M.; Ghisalberti, M.; Swearer, S.E. From grey to green efficacy of eco-engineering solutions for nature-based coastal defence. Glob. Chang. Biol. 2018, 24, 1827–1842. [Google Scholar] [CrossRef]
- Kuang, C.P.; Cong, X.; Fan, J.D.; Li, H.Y. Review of physical experiments on mechanisms of coastal protection by vegetation. J. Tongji Univ. (Nat. Sci.) 2024, 52, 378–387. [Google Scholar]
- Zhu, L.H.; Zou, Q.P. Three-layer analytical solution for wave attenuation by suspended and nonsuspended vegetation canopy. In Proceedings of the 35th International Conference on Coastal Engineering Proceeding, Antalya, Turkey, 17–20 November 2016. [Google Scholar] [CrossRef]
- Zhu, L.; Huguenard, K.; Zou, Q.; Fredriksson, D.W.; Xie, D. Aquaculture farms as nature-based coastal protection: Random wave attenuation by suspended and submerged canopies. Coast. Eng. 2020, 160, 103737. [Google Scholar] [CrossRef]
- Chen, H.; Zou, Q. Eulerian–lagrangian flow-vegetation interaction model using immersed boundary method and openfoam. Adv. Water Resour. 2019, 126, 176–192. [Google Scholar] [CrossRef]
- Anderson, M.E.; Smith, J.M. Wave attenuation by flexible, idealized salt marsh vegetation. Coast. Eng. 2014, 83, 82–92. [Google Scholar] [CrossRef]
- Maza, M.; Lara, J.; Losada, I.; Ondiviela, B.; Trinogga, J.; Bouma, T. Large-scale 3-D experiments of wave and current interaction with real vegetation. Part 2: Experimental analysis. Coast. Eng. 2015, 106, 73–86. [Google Scholar] [CrossRef]
- Wang, X.Y.; Xie, W.M.; Zhang, D.; He, Q. Wave and vegetation effects on flow and suspended sediment characteristics: A flume study. Estuar. Coast. Shelf Sci. 2016, 182, 1–11. [Google Scholar] [CrossRef]
- Rupprecht, F.; Möller, I.; Paul, M.; Kudella, M.; Spencer, T.; Wesenbeeck, B.K.V.; Wolters, G.; Jensen, K.; Bouma, T.J.; Miranda-lange, M.; et al. Vegetation-wave interactions in salt marshes under storm surge conditions. Ecol. Eng. 2017, 100, 301–315. [Google Scholar] [CrossRef]
- Lei, J.R.; Nepf, H. Wave damping by flexible vegetation: Connecting individual blade dynamics to the meadow scale. Coast. Eng. 2019, 147, 138–148. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, P.; Nepf, H. A simple wave damping model for flexible marsh plants. Limnol. Oceanogr. 2021, 66, 4182–4196. [Google Scholar] [CrossRef]
- Maza, M.; Lara, J.L.; Losada, I.J. A paradigm shift in the quantification of wave energy attenuation due to saltmarshes based on their standing biomass. Sci. Rep. 2022, 12, 13883. [Google Scholar] [CrossRef]
- Mendez, F.J.; Losada, I.J. An empirical model to estimate the propagation of random breaking and nonbreaking waves over vegetation fields. Coast. Eng. 2004, 51, 103–118. [Google Scholar] [CrossRef]
- Zhao, Y.; Peng, Z.; He, Q.; Ma, Y.X. Wave attenuation over combined salt marsh vegetation. Ocean Eng. 2023, 267, 113234. [Google Scholar] [CrossRef]
- Liu, C.; Shan, Y. Impact of an emergent model vegetation patch on flow adjustment and velocity. Proc. Inst. Civ. Eng.—Water Manag. 2021, 175, 55–66. [Google Scholar] [CrossRef]
- Liu, C.; Shan, Y.; Nepf, H. Impact of stem size on turbulence and sediment resuspension under unidirectional flow. Water Resour. Res. 2021, 57, e2020WR028620. [Google Scholar] [CrossRef]
- Tinoco, R.O.; Coco, G. A laboratory study on sediment resuspension within arrays of rigid cylinders. Adv. Water Resour. 2016, 92, 1–9. [Google Scholar] [CrossRef]
- Yi, Y.J.; Tang, Y.J.; Tang, C.H.; Zhang, S.H. Effect of stem-generated turbulence on sediment resuspension within rigid vegetation canopies in waves. J. Lake Sci. 2020, 32, 1827–1836. [Google Scholar]
- Xu, Y.; Nepf, H. Suspended sediment concentration profile in a Typha latifolia canopy. Water Resour. Res. 2021, 57, e2021WR029902. [Google Scholar] [CrossRef]
- Marin-diaz, B.; Bouma, T.J.; Infantes, E. Role of eelgrass on bed-load transport and sediment resuspension under oscillatory flow. Limnol. Oceanogr. 2019, 65, 426–436. [Google Scholar] [CrossRef]
- Lou, S.; Chen, M.; Ma, G.F.; Liu, S.G.; Wang, H. Sediment suspension affected by submerged rigid vegetation under waves, currents and combined wave-current flows. Coast. Eng. 2022, 173, 104082. [Google Scholar] [CrossRef]
- Yagci, O.; Celik, M.F.; Kitsikoudis, V.; Kirca, V.O.; Hodoglu, C.; Valyrakis, M.; Duran, Z.; Kaya, S. Scour patterns around isolated vegetation elements. Adv. Water Resour. 2016, 97, 251–265. [Google Scholar] [CrossRef]
- Yamasaki, T.N.; Jiang, B.; Janzen, J.G.; Nepf, H.M. Feedback between vegetation, flow, and deposition: A study of artificial vegetation patch development. J. Hydrol. 2021, 598, 126232. [Google Scholar] [CrossRef]
- Shan, Y.; Zhao, T.; Liu, C.; Nepf, H. Turbulence and bed load transport in channels with randomly distributed emergent patches of model vegetation. Geophys. Res. Lett. 2020, 47, e2020GL087055. [Google Scholar] [CrossRef]
- Zhang, J.; Lei, J.; Huai, W.; Nepf, H. Turbulence and particle deposition under steady flow along a submerged seagrass meadow. J. Geophys. Res. Ocean. 2020, 125, e2019JC015985. [Google Scholar] [CrossRef]
- Hu, Z.; Lei, J.; Liu, C.; Nepf, H. Wake structure and sediment deposition behind models of submerged vegetation with and without flexible leaves. Adv. Water Resour. 2018, 118, 28–38. [Google Scholar] [CrossRef]
- Bennett, W.G.; Horrillo-caraballo, J.M.; Fairchild, T.P.; van Veelenkarun, T.J.; Karunarathna, H. Saltmarsh vegetation alters tidal hydrodynamics of small estuaries. Appl. Ocean Res. 2023, 138, 103678. [Google Scholar] [CrossRef]
- Zhu, Q.; Wiberg, P.L.; Reidenbach, M.A. Quantifying seasonal seagrass effects on flow and sediment dynamics in a back-barrier bay. J. Geophys. Res. Ocean. 2021, 126, e2020JC016547. [Google Scholar] [CrossRef]
- Nardin, W.; Lera, S.; Nienhuis, J. Effect of offshore waves and vegetation on the sediment budget in the Virginia Coast Reserve (VA). Earth Surf. Process. Landf. 2020, 45, 3055–3068. [Google Scholar] [CrossRef]
- Garzon, J.L.; Miesse, T.; Ferreira, C.M. Field-based numerical model investigation of wave propagation across marshes in the Chesapeake Bay under storm conditions. Coast. Eng. 2019, 146, 32–46. [Google Scholar] [CrossRef]
- Yin, K.; Xu, S.; Huang, W.; Li, R.; Xiao, H. Modeling beach profile changes by typhoon impacts at Xiamen coast. Nat. Hazards 2019, 95, 783–804. [Google Scholar] [CrossRef]
- Feagin, R.A.; Lozada-bernard, S.M.; Ravens, T.M.; Ller, I.M.; Yeager, K.M.; Baird, A.H. Does vegetation prevent wave erosion of salt marsh edges? Proc. Natl. Acad. Sci. USA 2009, 106, 10109–10113. [Google Scholar] [CrossRef]
- Feagin, R.; Furman, M.; Salgado, K.; Martinez, M.; Innocenti, R.; Eubanks, K.; Figlus, J.; Huff, T.; Sigren, J.; Silva, R. The role of beach and sand dune vegetation in mediating wave run up erosion. Estuar. Coast. Shelf Sci. 2019, 219, 97–106. [Google Scholar] [CrossRef]
- Feagin, R.A.; Innocenti, R.A.; Bond, H.; Wengrove, M.; Huff, T.P.; Lomonaco, P.; Tsai, B.; Puleo, J.; Pontiki, M.; Figlus, J.; et al. Does vegetation accelerate coastal dune erosion during extreme events? Sci. Adv. 2023, 9, eadg7135. [Google Scholar] [CrossRef]
- Cong, X.; Kuang, C.P.; Zheng, Y.H.; Han, X.J.; Fan, J.D.; Zhao, F.; Yu, L. Experimental observation on wave propagation and geomorphological evolution in a sandbar-lagoon system. Appl. Ocean Res. 2023, 141, 103785. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, C.; Cai, Y.; Xie, M.; Qi, H.; Wang, Y. Wave dissipation and sediment transport patterns during shoreface nourishment towards equilibrium. J. Mar. Sci. Eng. 2021, 9, 535. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, C.; Dai, W.Q.; Chen, D.K.; Sui, T.T.; Xie, M.X.; Chen, S.G. Laboratory investigation on morphology response of submerged artificial sandbar and its impact on beach evolution under storm wave condition. Mar. Geol. 2022, 443, 106668. [Google Scholar] [CrossRef]
- Pan, Y.; Yin, S.; Chen, Y.P.; Yang, Y.B.; Xu, C.Y.; Xu, Z.S. An experimental study on the evolution of a submerged berm under the effects of regular waves in low-energy conditions. Coast. Eng. 2022, 176, 104169. [Google Scholar] [CrossRef]
- Pan, Y.; Qu, X.K.; Yang, Y.B.; Zhang, J.B.; Wang, G.; Yin, S.; Chen, Y.P. Laboratory experiments on the evolution of a submerged berm driven by low-energy irregular waves. Coast. Eng. 2023, 182, 104301. [Google Scholar] [CrossRef]
- Marmoush, R.Y.; Mulligan, R.P. A three-dimensional laboratory investigation of beach morphology change during a storm event. Geomorphology 2020, 363, 107224. [Google Scholar] [CrossRef]
- Pye, K.; Blott, S. Assessment of beach and dune erosion and accretion using LiDAR: Impact of the stormy 2013–14 winter and longer term trends on the Sefton Coast, UK. Geomorphology 2016, 266, 146–167. [Google Scholar] [CrossRef]
- Casamayor, M.; Alonso, I.; Valiente, N.G.; Sánchez-garcía, M. Seasonal response of a composite beach in relation to wave climate. Geomorphology 2022, 408, 108245. [Google Scholar] [CrossRef]
- Wang, J.; You, Z.J.; Liang, B.; Wang, Z.; Yang, B. The physical processes of sandy beach evolution under storm and non-storm wave conditions simulated in wave flume. Mar. Geol. 2023, 462, 107065. [Google Scholar] [CrossRef]
- Keijsers, J.G.S.; de Groot, A.V.; Riksen, M.J.P.M. Vegetation and sedimentation on coastal foredunes. Geomorphology 2015, 228, 723–734. [Google Scholar] [CrossRef]
- Durán, O.; Moore, L.J. Vegetation controls on the maximum size of coastal dunes. Proc. Natl. Acad. Sci. USA 2013, 110, 17217–17222. [Google Scholar] [CrossRef]
- Odériz, I.; Knöchelmann, N.; Silva, R.; Feagin, R.A.; Martínez, M.L.; Mendoza, E. Reinforcement of vegetated and unvegetated dunes by a rocky core: A viable alternative for dissipating waves and providing protection? Coast. Eng. 2020, 158, 103675. [Google Scholar] [CrossRef]
- Astudillo, C.; Gracia, V.; Cáceres, I.; Sierra, J.P.; Sanchez-arcilla, A. Beach profile changes induced by surrogate Posidonia Oceanica: Laboratory experiments. Coast. Eng. 2022, 175, 104144. [Google Scholar] [CrossRef]
- Lee, J.; Jeong, Y.; Jeong, J.; Hur, D. An experimental study on the effect of cross-sectional changes in rigid and flexible submerged vegetation on beach erosion control. J. Coast. Res. 2024, 116, 643–647. [Google Scholar] [CrossRef]
- Gong, S.P.; Xu, S.D.; Li, M.X.; Wang, Y.R.; Yin, K.; Chen, Y.M. Experimental study on wave attenuation and beach profile evolution under the protection of submerged flexible vegetation. J. Hydrol. 2024, 638, 131478. [Google Scholar] [CrossRef]
- Gong, S.P.; Xu, S.D.; Yin, K.; Chen, Y.M.; Chen, J.; Lei, J.R. Experimental study on wave attenuation and cross-shore profiles by submerged flexible vegetation. Ocean Eng. 2024, 307, 118218. [Google Scholar] [CrossRef]
- Cong, X.; Kuang, C.P.; Huang, G.W.; Zou, Q.P.; Han, X.J.; Shen, C.; Gu, J. Experimental study on the morphodynamic evolution of sandbar-lagoon system with emergent vegetation. Coast. Eng. 2023, 184, 104340. [Google Scholar] [CrossRef]
- Kuang, C.P.; Cong, X.; Gong, L.X.; Liu, J.T.; Han, X.J.; Xing, W. Cross-shore profile evolution induced by real emergent vegetation in a sandbar-lagoon coast: Laboratory experiments. Geomorphology 2024, 468, 109500. [Google Scholar] [CrossRef]
- Ma, Y.; Kuang, C.P.; Han, X.J.; Niu, H.B.; Zheng, Y.H.; Shen, C. Experimental study on the influence of an artificial reef on cross-shore morphodynamic processes of a wave-dominated beach. Water 2020, 12, 2947. [Google Scholar] [CrossRef]
- Yin, S.; Pan, Y.; Chen, Y.P. Scale design based on local curve fitting method for low-energy sandy beach. Hydro-Sci. Eng. 2017, 4, 43–51. [Google Scholar]
- Zhou, Y.; Jiang, Z.J.; Qiu, G.L.; Zhang, P.D.; Xu, S.C.; Zhang, X.M.; Liu, S.L.; Li, W.T.; Wu, Y.C.; Yue, S.D.; et al. Distribution status, degradation reasons and protection countermeasures of seagrass resources in China. Oceanol. Limnol. Sin. 2023, 54, 1248–1257. [Google Scholar]
- Zhi, K.T.; Yang, J.; Yin, Z.Q.; Wang, Y.; Li, X.L.; Chen, L.; Wei, H.F.; Wang, Y.J.; Yu, L.J.; Sun, Q.; et al. Distribution characteristics of seagrass, algae, and attached organisms in the seagrass beds of Changshan Islands, Dalian. Mar. Fish. 2024, 46, 297–306. [Google Scholar]
- Zhu, G.; Ren, B.; Dong, P.; Wang, G.; Chen, W. Experimental investigation on the infragravity wave on different reef systems under irregular wave action. Ocean Eng. 2021, 226, 108851. [Google Scholar] [CrossRef]
- Goda, Y.; Suzuki, Y. Estimation of incident and reflected waves in random wave experiments. In Proceedings of the 15th International Conference on Coastal Engineering, Honolulu, HI, USA, 11–17 July 1976; pp. 828–845. [Google Scholar]
- Zou, Q.; Peng, Z. Evolution of wave shape over a low-crested structure. Coast. Eng. 2011, 58, 478–488. [Google Scholar] [CrossRef]
- Sun, J.W.; van prooijen, B.; Wang, X.Y.; Xie, W.M.; Xu, F.; He, Q.; Wang, Z.B. Conditional effects of tides and waves on sediment supply to salt marshes. J. Geophys. Res. Earth Surf. 2024, 129, e2024JF007686. [Google Scholar] [CrossRef]





| Test Names | H0 (m) | T0 (s) | Vegetation Density (shoots/m2) | |
|---|---|---|---|---|
| d = 0.48 m | d = 0.55 m | |||
| N-d11 | N-d21 | 0.06 | 1.33 | 0 |
| N-d12 | N-d22 | 0.10 | 1.60 | 0 |
| N-d13 | N-d23 | 0.13 | 1.68 | 0 |
| N-d14 | N-d24 | 0.16 | 1.80 | 0 |
| - | N-d25 | 0.21 | 2.12 | 0 |
| S-d11 | S-d21 | 0.06 | 1.33 | 2500 |
| S-d12 | S-d22 | 0.10 | 1.60 | 2500 |
| S-d13 | S-d23 | 0.13 | 1.68 | 2500 |
| S-d14 | S-d24 | 0.16 | 1.80 | 2500 |
| - | S-d25 | 0.21 | 2.12 | 2500 |
| Test Names | Change Ratios of the Short-Wave Height (-) | Change Ratios of the Long-Wave Height (-) | Change Ratios of the Total Wave Energy (-) | |||
|---|---|---|---|---|---|---|
| Wa | W7 | Wa | W7 | Wa | W7 | |
| S-d11 | −4.54% | −55.91% | −36.89% | 70.28% | −13.54% | 42.17% |
| S-d12 | −7.72% | −15.53% | −28.80% | −5.24% | −18.68% | −21.17% |
| S-d13 | −12.54% | −20.77% | −25.88% | 0.08% | −28.48% | −23.57% |
| S-d14 | −12.26% | −11.06% | −39.17% | −12.60% | −33.44% | −22.71% |
| Average | −9.27% | −25.81% | −32.69% | −8.92% | −23.54% | −22.48% |
| S-d21 | −5.11% | −6.86% | −5.53% | −14.15% | −9.99% | −14.07% |
| S-d22 | −3.95% | −7.24% | −19.23% | −13.08% | −9.51% | −16.01% |
| S-d23 | −9.29% | −6.70% | −12.51% | −6.49% | −18.83% | −12.70% |
| S-d24 | −13.84% | −3.91% | −42.39% | −11.44% | −34.69% | −10.08% |
| S-d25 | −3.57% | −8.20% | −15.04% | −7.98% | −11.82% | −15.58% |
| Average | −7.15% | −6.58% | −18.94% | −10.63% | −16.97% | −13.69% |
| Test Names | Shoreline Receding Distance (-) | Maximum Erosion Thickness (-) | Maximum Deposition Thickness (-) | |||
|---|---|---|---|---|---|---|
| Sandbar | Foredune | Sandbar | Lagoon | Foredune | ||
| S-d11 | −54.55% | −4.55% | −50.00% | −38.89% | −50.00% | −62.50% |
| S-d12 | −38.32% | −2.94% | −40.85% | 50.00% | −68.04% | −45.00% |
| S-d13 | −11.63% | −8.70% | −10.31% | 21.88% | −24.00% | −18.37% |
| S-d14 | −10.42% | −5.41% | −7.84% | 30.37% | 2.33% | 11.90% |
| Average | −28.73% | −5.40% | −27.25% | 34.08% | −47.35% | −41.96% |
| S-d21 | 3.49% | 13.33% | −11.43% | 62.50% | −50.00% | −4.55% |
| S-d22 | −8.88% | −11.90% | −12.50% | 33.33% | −8.57% | −17.50% |
| S-d23 | 5.04% | −3.70% | 0.00% | 5.71% | −31.25% | −26.53% |
| S-d24 | −2.97% | 8.33% | 1.63% | 25.81% | −46.43% | −32.00% |
| S-d25 | −0.59% | 16.33% | −2.78% | 2.86% | 18.18% | −6.82% |
| Average | −4.15% | −7.80% | −6.68% | 26.04% | −34.06% | −17.48% |
| Test Names | Change Ratios of Erosion Volume (-) | Change Ratios of Deposition Volume (-) | Change Ratios of Lagoon Deposition Volume (-) | ||
|---|---|---|---|---|---|
| Sandbar | Foredune | Sandbar | Foredune | ||
| S-d11 | 10.66% | −61.51% | −42.96% | −82.20% | −55.03% |
| S-d12 | 9.49% | −48.32% | −7.61% | −44.55% | −50.77% |
| S-d13 | −12.94% | −29.37% | 8.91% | −3.43% | −4.06% |
| S-d14 | −2.41% | −18.92% | 16.98% | 48.48% | −20.37% |
| Average | −7.67% | −39.53% | 12.95% | −43.39% | −32.56% |
| S-d21 | −10.48% | −15.03% | 69.13% | 3.15% | −3.09% |
| S-d22 | −21.31% | −17.68% | 47.73% | −1.51% | 30.08% |
| S-d23 | −1.09% | 8.21% | −10.83% | −17.04% | −44.30% |
| S-d24 | −2.70% | −10.32% | 3.61% | −29.99% | −29.63% |
| S-d25 | 9.53% | −6.36% | 21.72% | 31.10% | 28.15% |
| Average | −8.90% | −12.35% | 35.55% | −16.18% | −25.67% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, W.; Cong, X.; Kuang, C.; Wang, D.; An, Z.; Zou, Q. Experimental Investigation on Wave and Bed Profile Evolution in a Sandbar-Lagoon Coast with Submerged Vegetation. J. Mar. Sci. Eng. 2024, 12, 2126. https://doi.org/10.3390/jmse12122126
Xing W, Cong X, Kuang C, Wang D, An Z, Zou Q. Experimental Investigation on Wave and Bed Profile Evolution in a Sandbar-Lagoon Coast with Submerged Vegetation. Journal of Marine Science and Engineering. 2024; 12(12):2126. https://doi.org/10.3390/jmse12122126
Chicago/Turabian StyleXing, Wei, Xin Cong, Cuiping Kuang, Dan Wang, Zhenzhen An, and Qingping Zou. 2024. "Experimental Investigation on Wave and Bed Profile Evolution in a Sandbar-Lagoon Coast with Submerged Vegetation" Journal of Marine Science and Engineering 12, no. 12: 2126. https://doi.org/10.3390/jmse12122126
APA StyleXing, W., Cong, X., Kuang, C., Wang, D., An, Z., & Zou, Q. (2024). Experimental Investigation on Wave and Bed Profile Evolution in a Sandbar-Lagoon Coast with Submerged Vegetation. Journal of Marine Science and Engineering, 12(12), 2126. https://doi.org/10.3390/jmse12122126








