A Novel Denoising Method for Ship-Radiated Noise
Abstract
:1. Introduction
2. Basic Theories
2.1. SVMD
2.2. FuDE
3. Proposed Denoising Methods for SN
- SVMD adaptively decomposed SN into certain IMFs.
- The FuDE of each IMF was calculated.
- According to the FuDE-based dual-threshold analysis, both high threshold (Hth) and low threshold (Lth) were obtained.
- The IMFs could be classified into three categories based on the high and low thresholds, including signal IMFs, noise–signal IMFs and noise IMFs.
- The denoised signal was obtained by reconstructing the signal IMFs and denoised noise–signal IMFs, and the noise IMFs were discarded.
4. Denoising Experiment for Simulation Signals
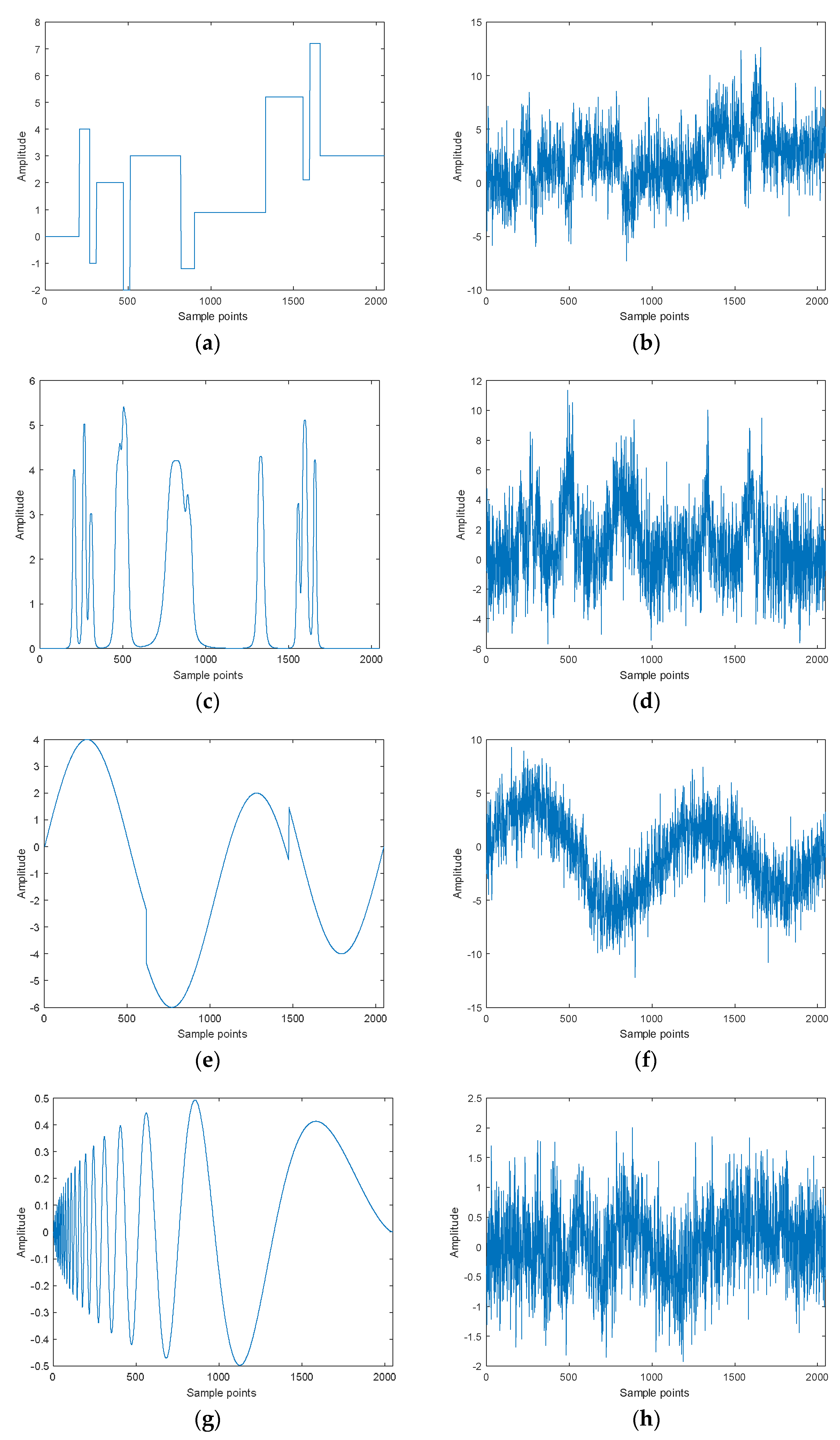
4.1. Four Types of Test Signals
4.2. Denoising Experiment of Test Signals
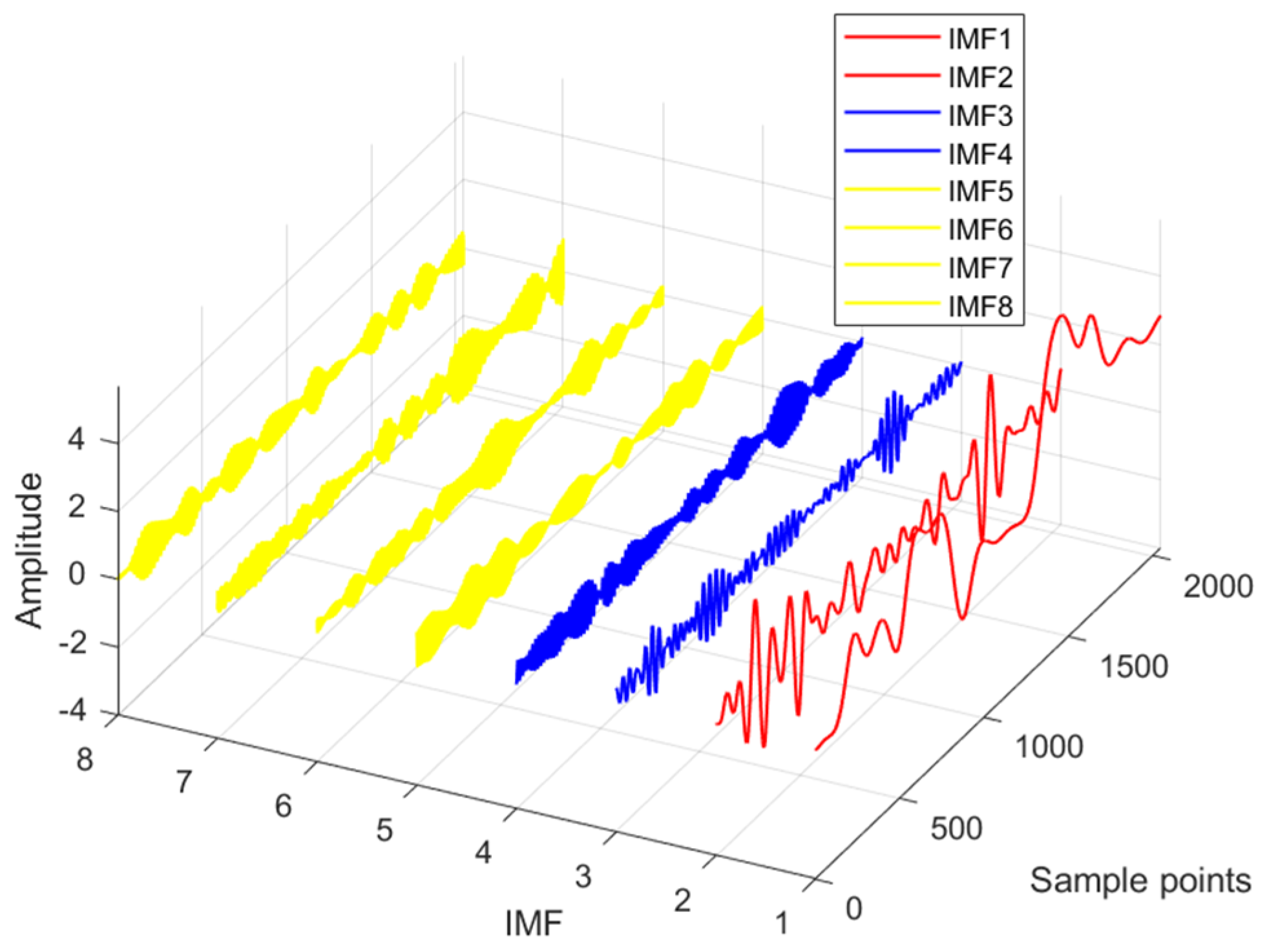
4.2.1. SVMD of Simulation Signals
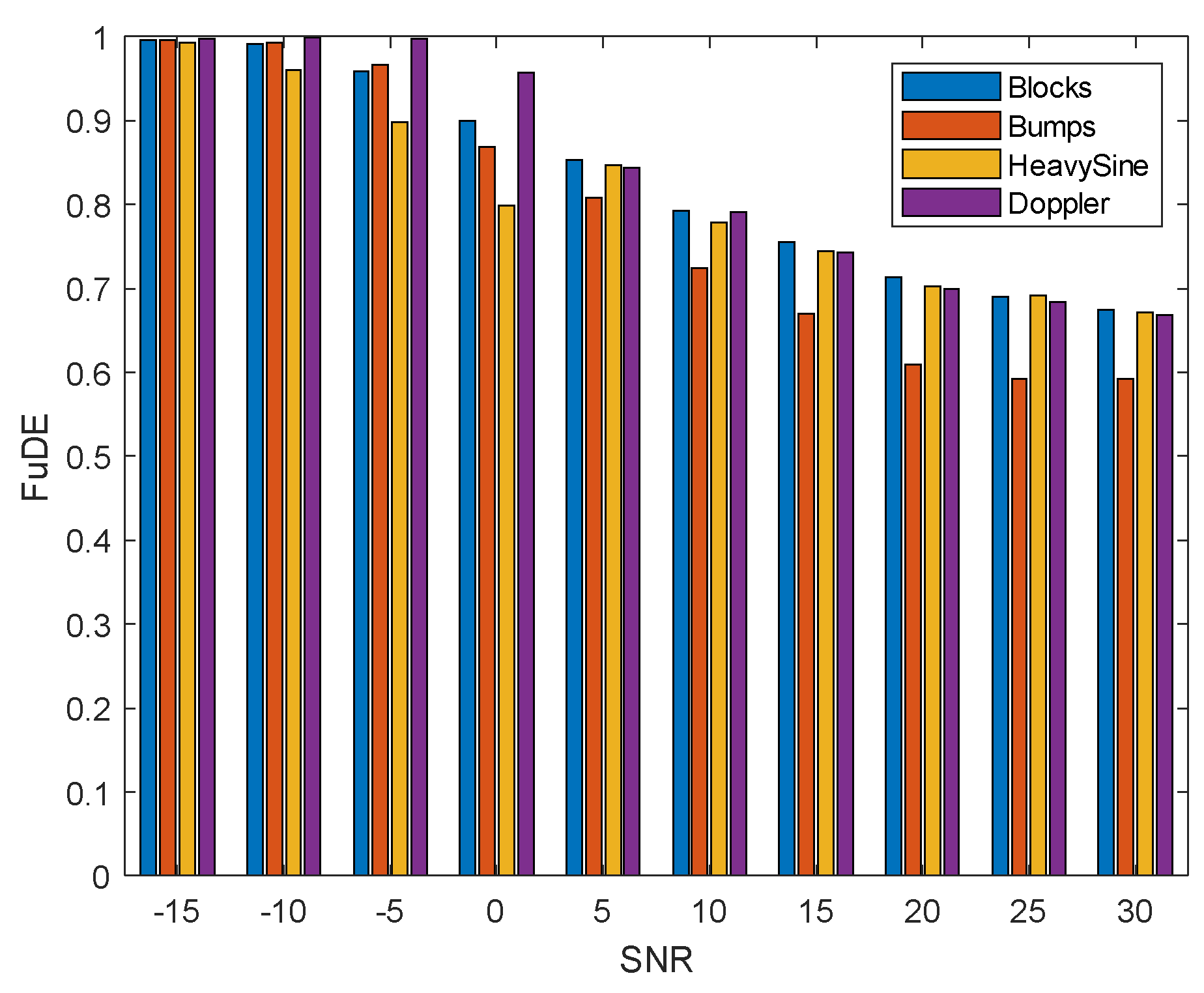
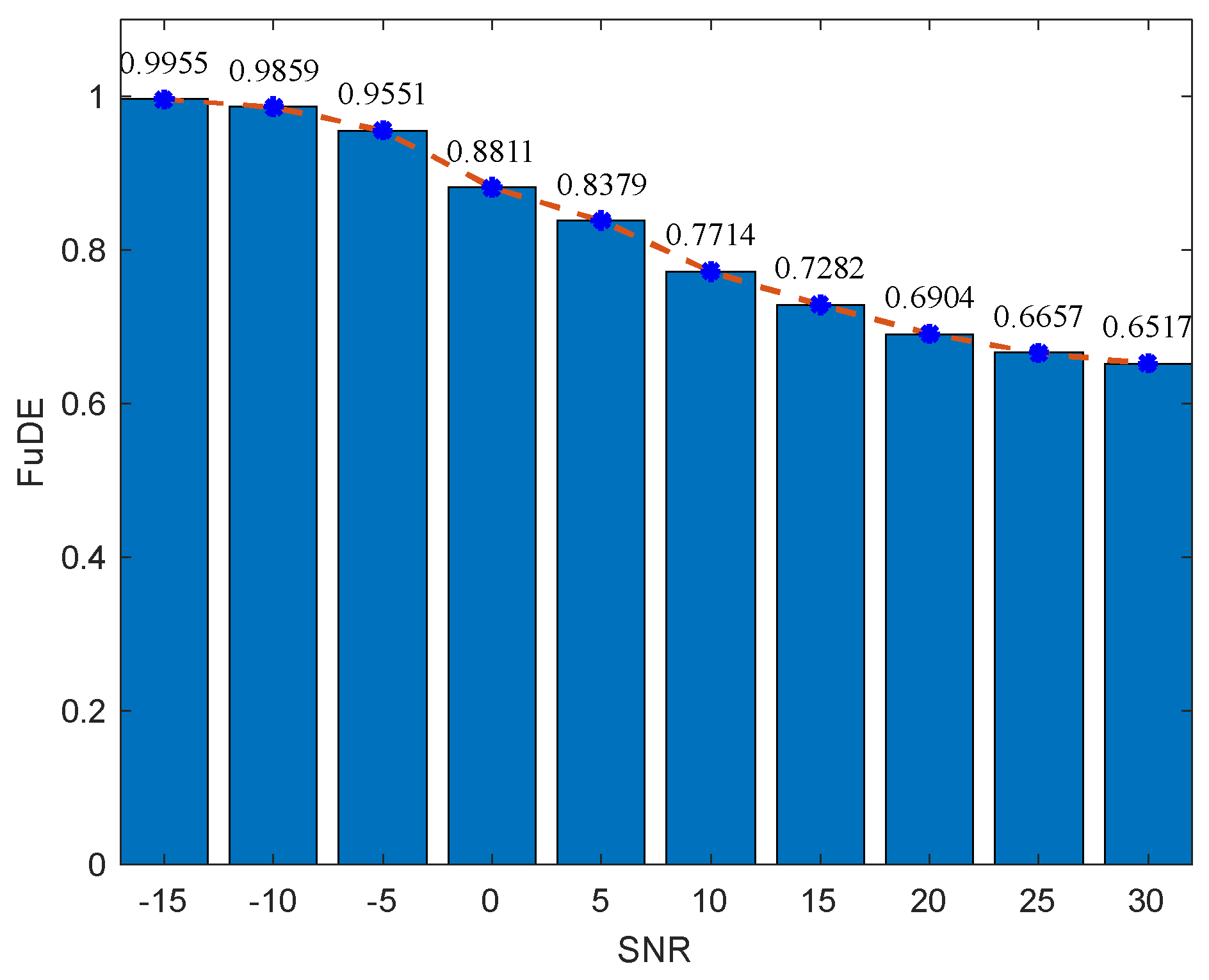
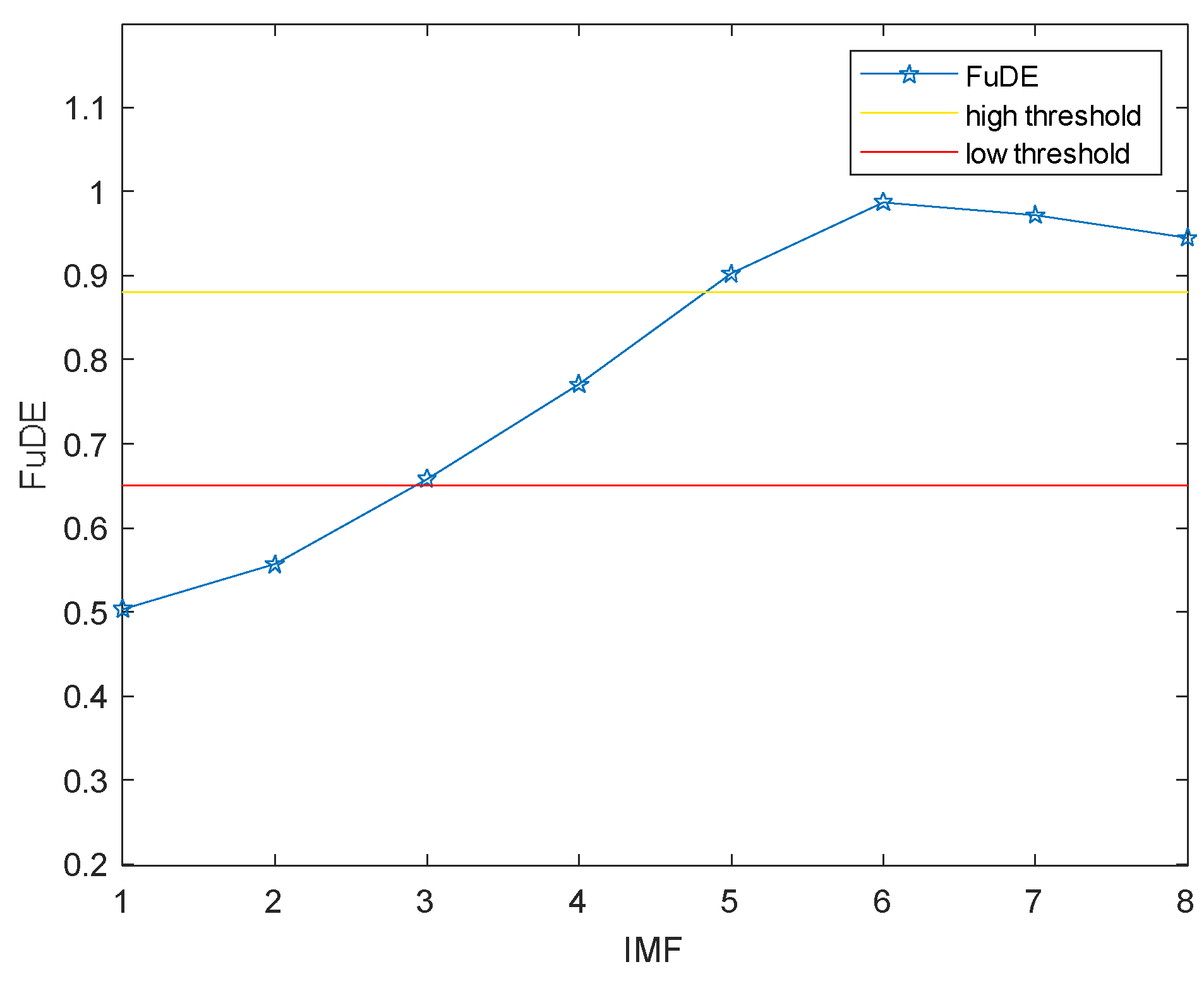
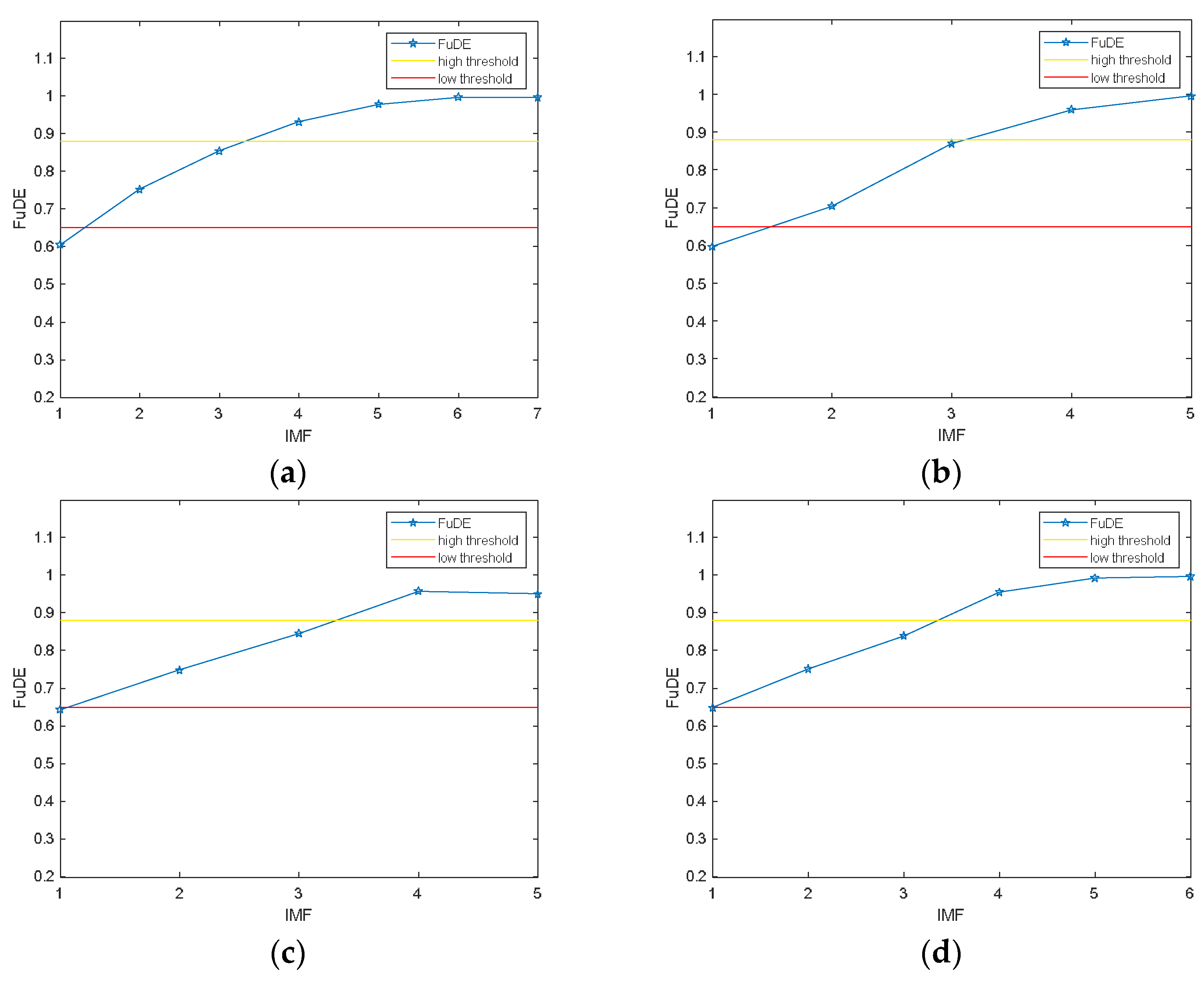
4.2.2. FuDE-Based Dual-Threshold Analysis and IMF Classification
4.2.3. Denoising and Reconstruction
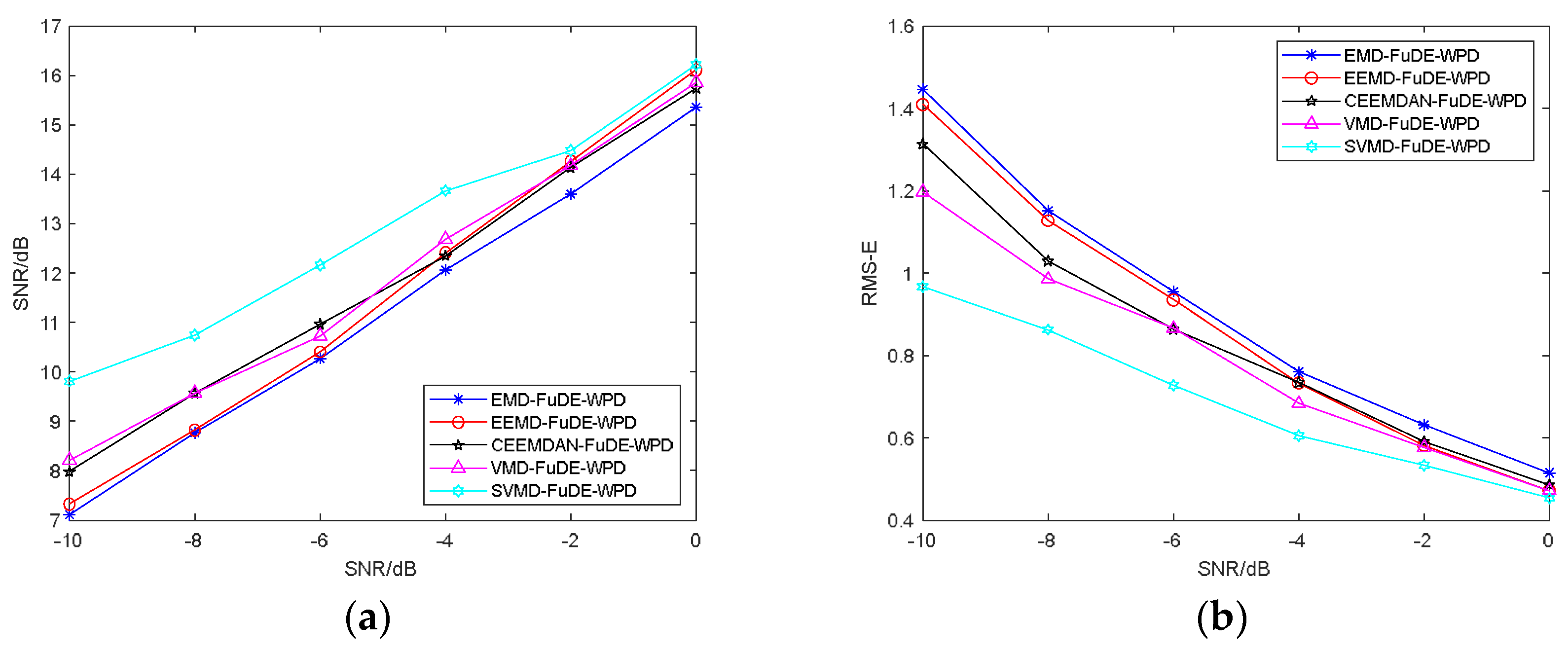
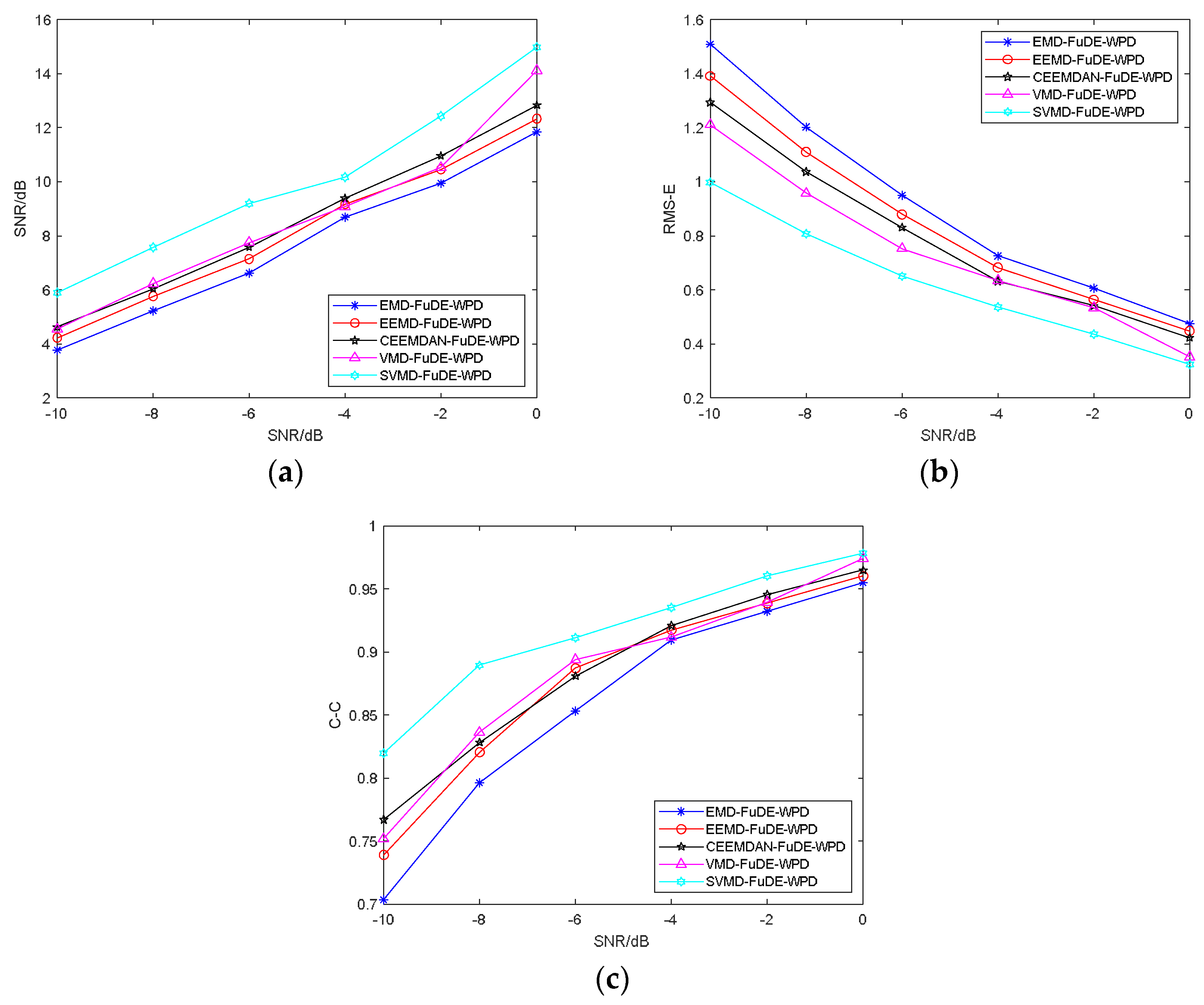
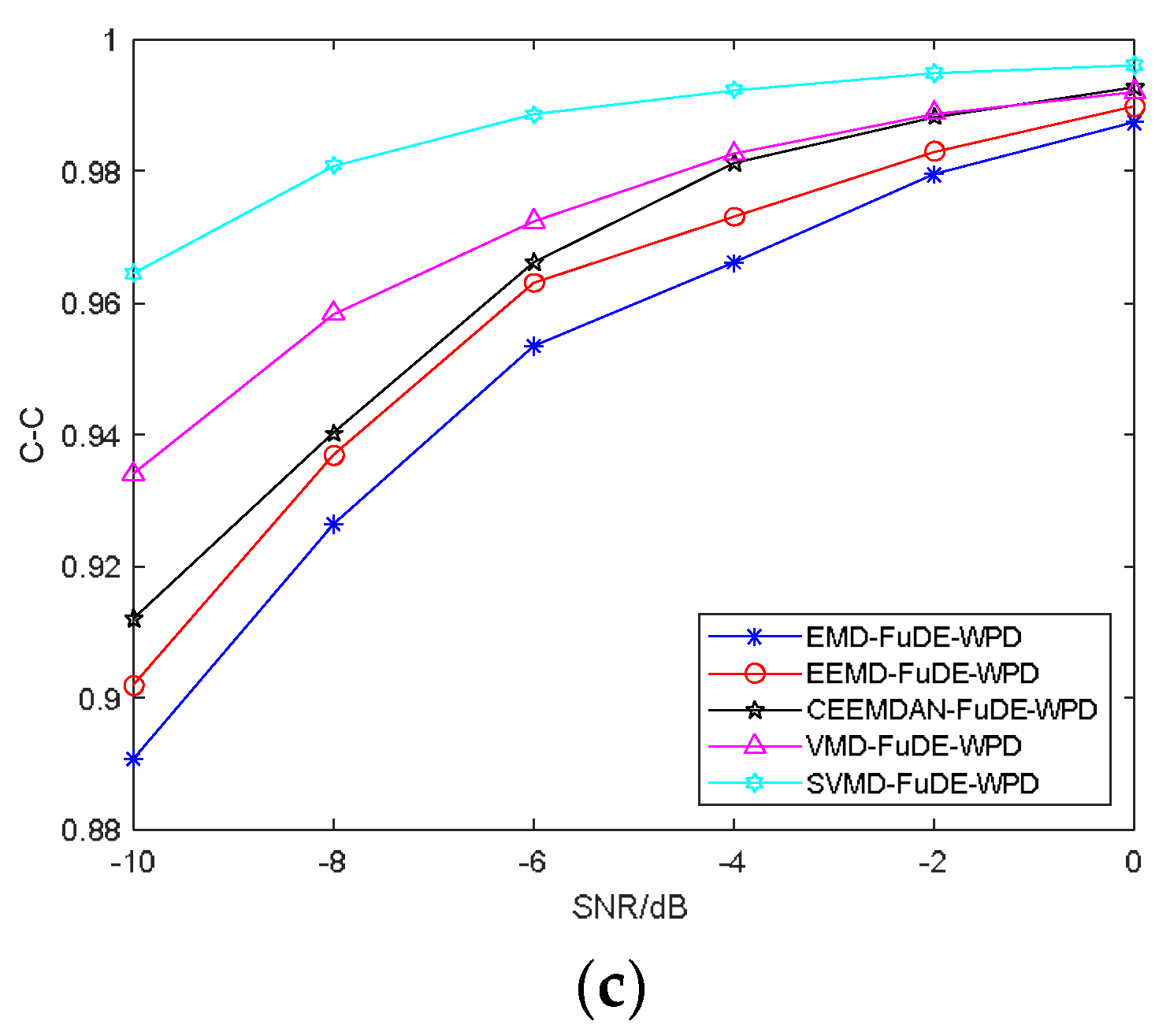
4.3. Comparation of Denoising Methods
4.3.1. Evaluation Metrics
4.3.2. Comparative Analysis
5. Experiment and Analysis of SN
5.1. Four Types of SNs and Evaluation Criterion
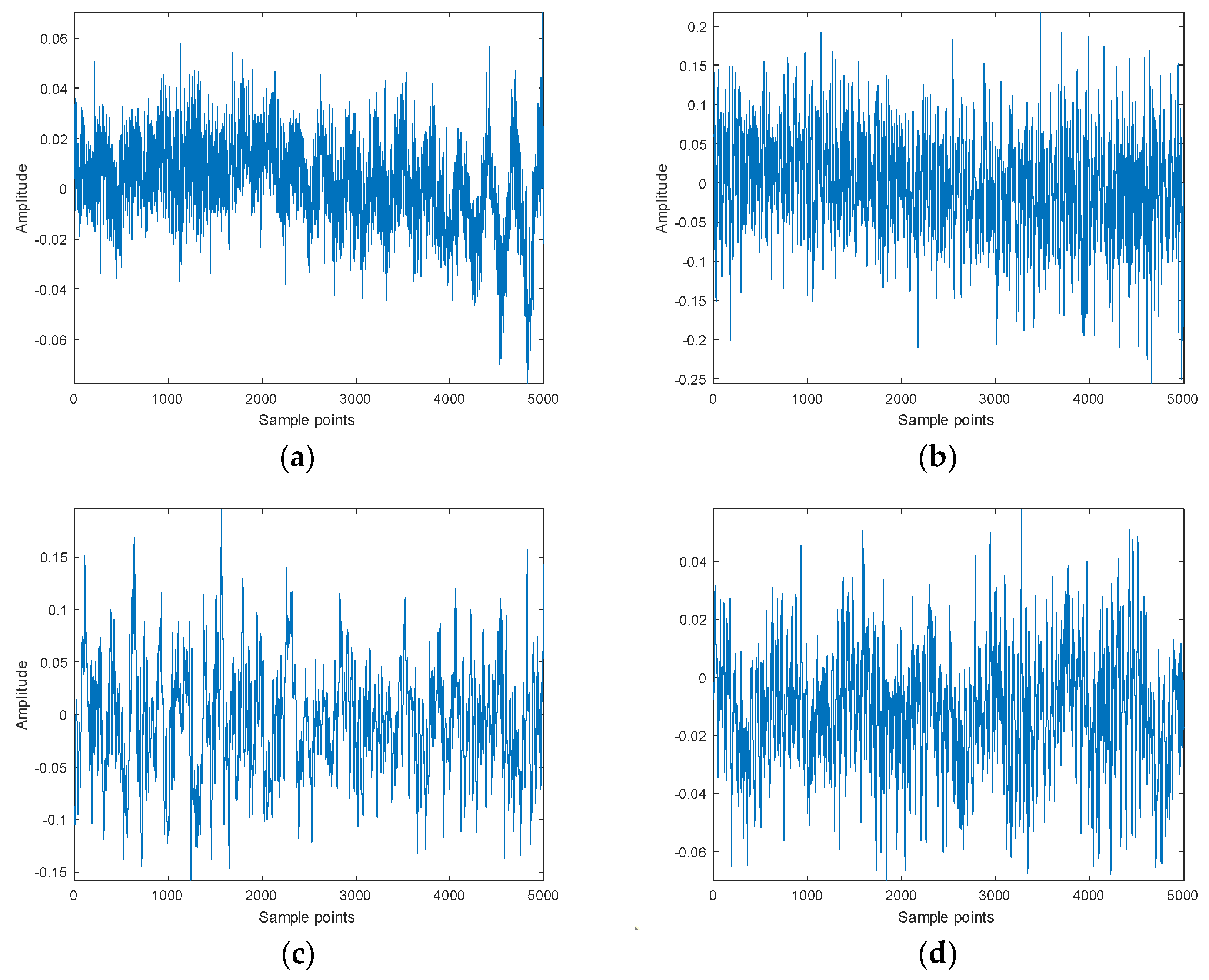
5.1.1. Four Types of SNs
5.1.2. Evaluation Criterion
5.2. Denoising Experiment of SN
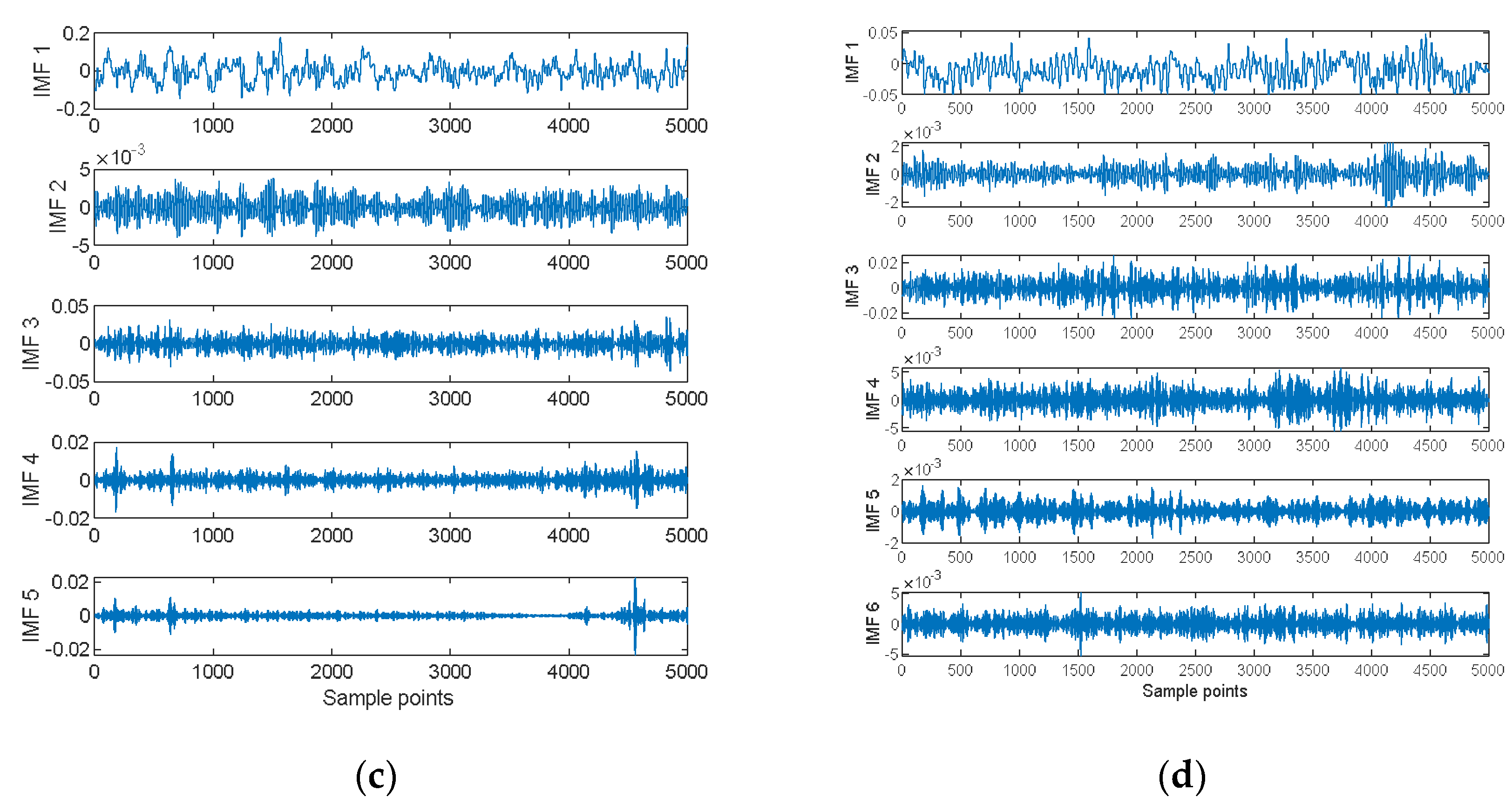
5.2.1. Decomposed SN via SVMD
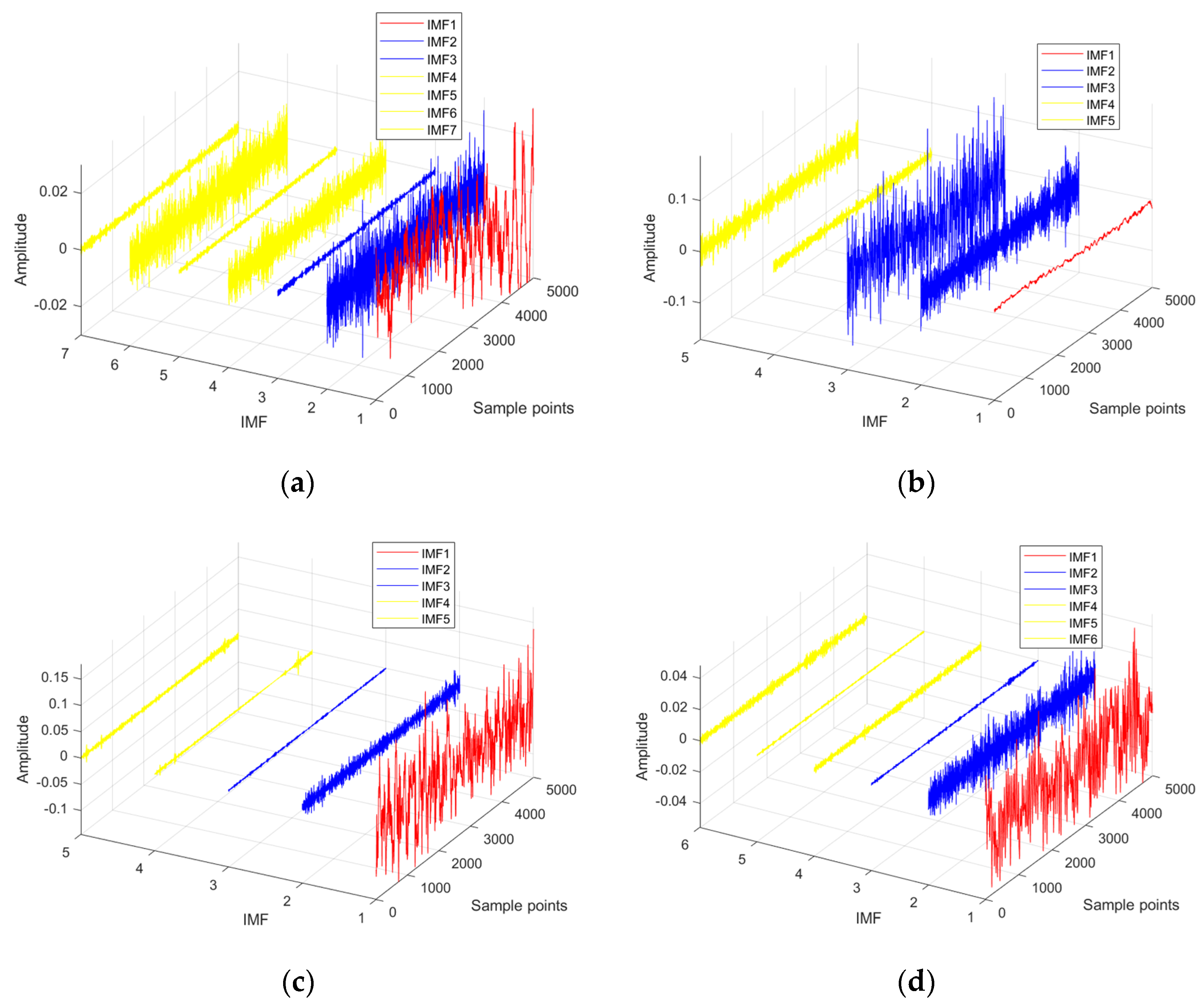
5.2.2. Classification and Reconstruction of IMF
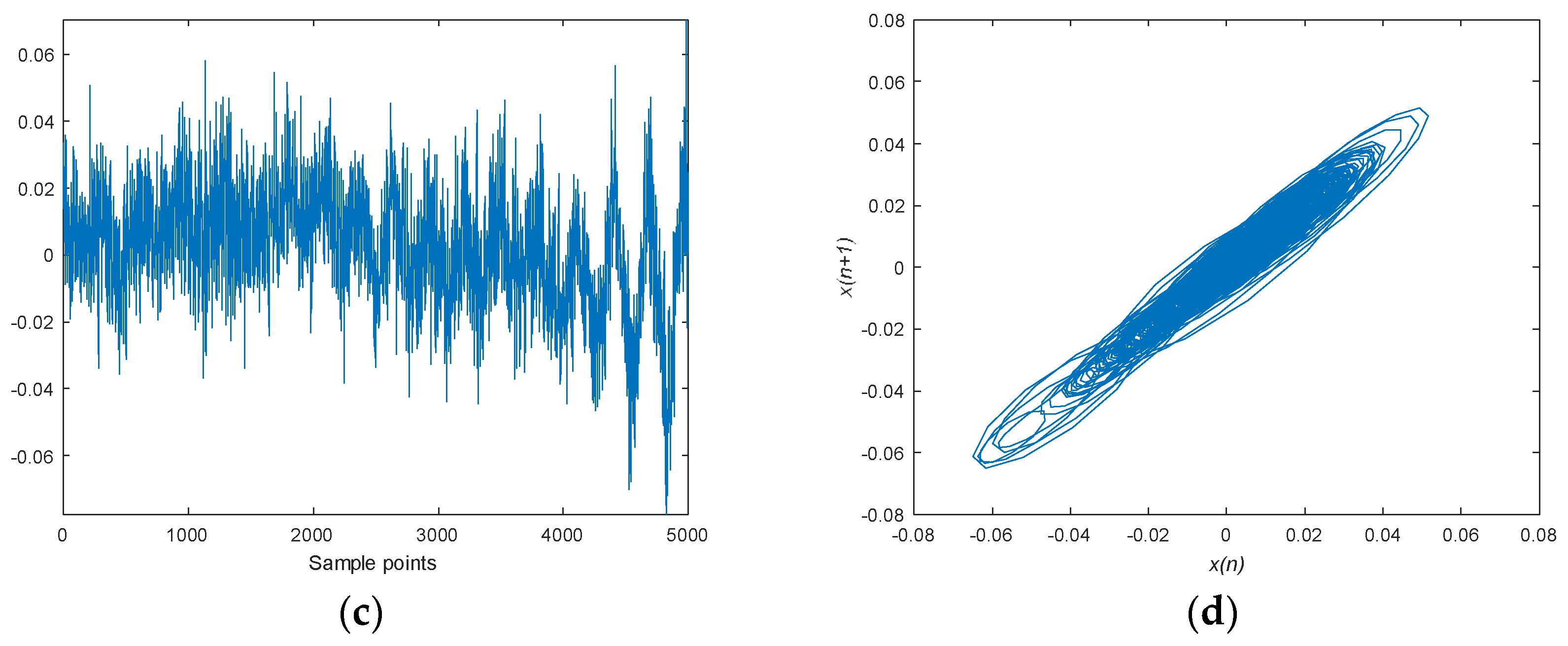
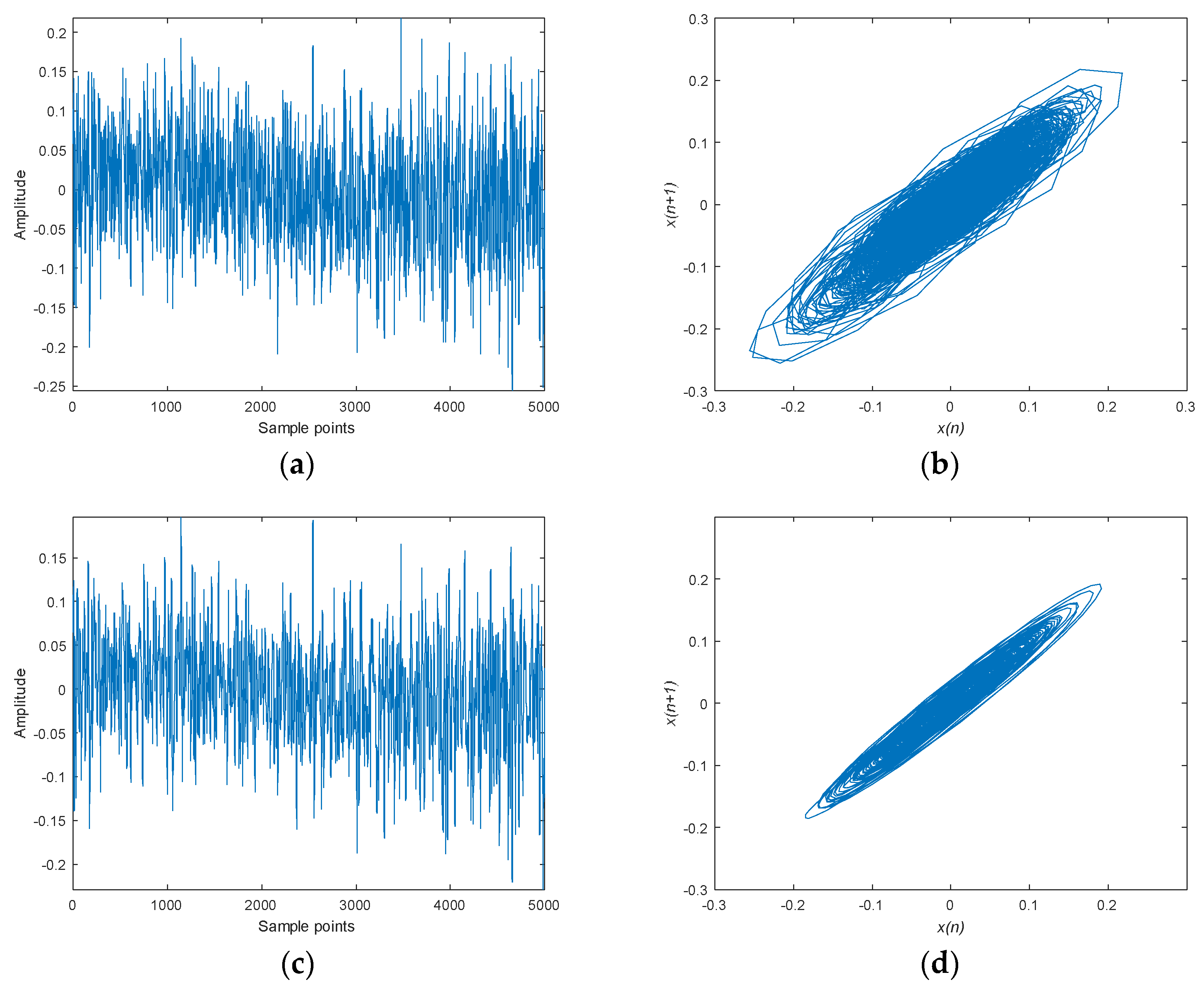
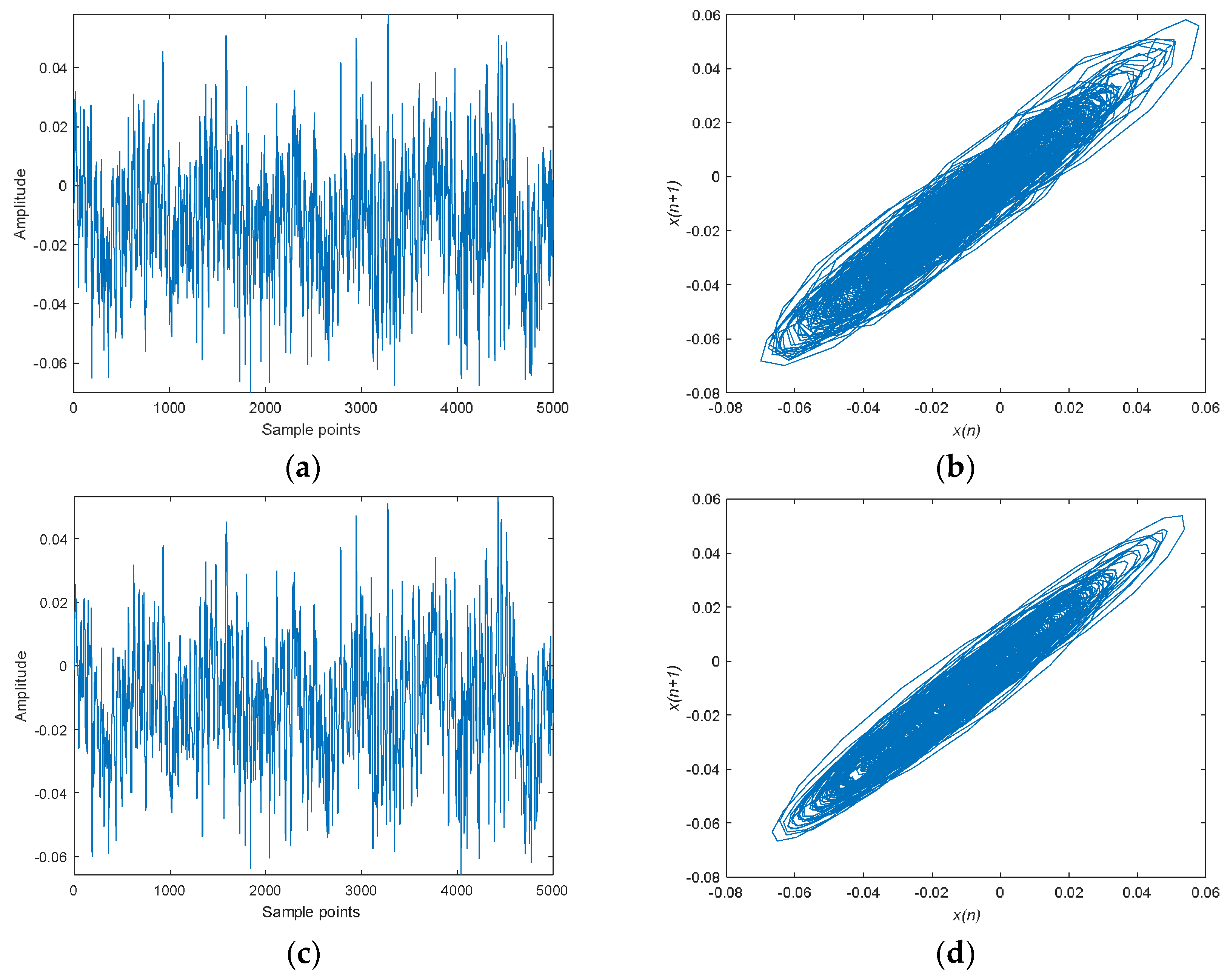
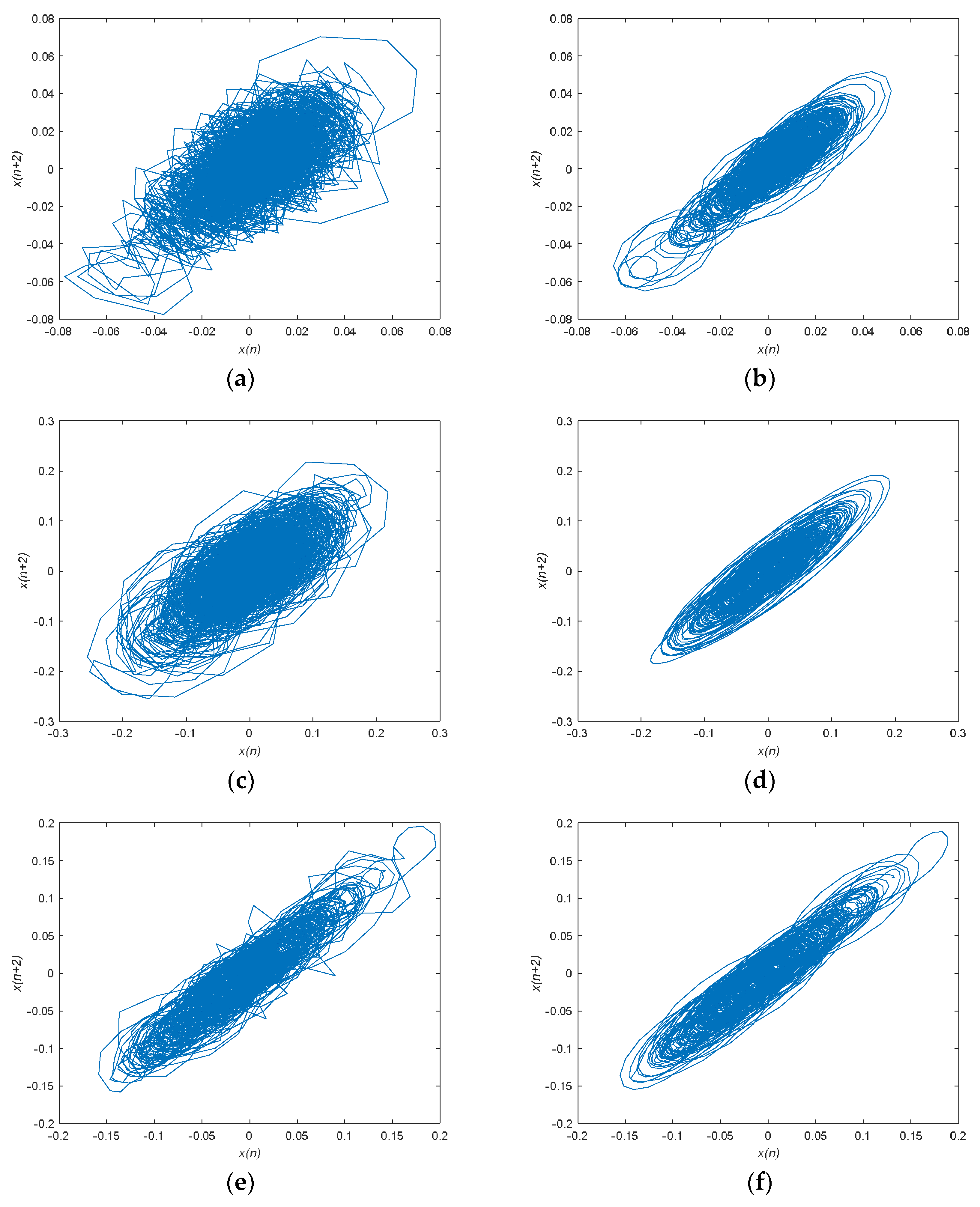
5.2.3. Denoising Result and Analysis
6. Conclusions
- (1)
- SVMD-FuDE-WPD was proposed as the denoising method for SN; SVMD can resolve the parameter selection problem of VMD and suppresses the mode mixing of EMD, and the FuDE-based dual-threshold analysis precisely classifies IMF into three categories.
- (2)
- Compared with EMD-FuDE-WPD, EEMD-FuDE-WPD, CEEMDAN-FuDE-WPD and VMD-FuDE-WPD, the proposed method has the lowest RMS-E as well as the highest SNR and C-C, which shows a better denoising performance.
- (3)
- The SVMD-FuDE-WPD method leads to much smoother and more regular attractor trajectories, more distinct waveforms of SN, and lower DE and PE values, which prove that the proposed method performs effectively at denoising SN.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Niu, F.; Hui, J.; Zhao, A.; Cheng, Y.; Chen, Y. Application of SN-EMD in Mode Feature Extraction of Ship Radiated Noise. Math. Probl. Eng. 2018, 20, 2184612. [Google Scholar] [CrossRef]
- Siddagangaiah, S.; Li, Y.; Guo, X.; Yang, K. On the dynamics of ocean ambient noise: Two decades later. Chaos 2015, 25, 103117. [Google Scholar] [CrossRef] [PubMed]
- Tucker, J.D.; Azimi-Sadjadi, M.R. Coherence-based underwater target detection from multiple disparatesonar platforms. IEEE J. Ocean Eng. 2011, 36, 37–51. [Google Scholar] [CrossRef]
- Jiang, J.; Shi, T.; Huang, M.; Xiao, Z. Multi-Scale Spectral Feature Extraction for Underwater Acoustic Target Recognition. Measurement 2020, 166, 108227. [Google Scholar] [CrossRef]
- Baskar, V.V.; Rajendran, V.; Logashanmugam, E. Study of different denoising methods for underwater acoustic signal. J. Mar. Sci. Technol. 2015, 23, 414–419. [Google Scholar]
- Siddagangaiah, S.; Li, Y.; Guo, X.; Chen, X.; Zhang, Q.; Yang, K.; Yang, Y. A Complexity-Based Approach for the Detection of Weak Signals in Ocean Ambient Noise. Entropy 2016, 18, 101. [Google Scholar] [CrossRef]
- Cawley, R.; Hsu, G.H. Local-geometric project ion method for noise reduction in chaotic maps and flows. Phys. Rev. A 1992, 46, 3057–3082. [Google Scholar] [CrossRef]
- Buchris, Y.; Amar, A.; Benesty, J.; Cohen, I. Incoherent synthesis of sparse arrays for frequency-invariant beamforming. IEEE/ACM Trans. Audio Speech Lang. Process. 2018, 27, 482–495. [Google Scholar] [CrossRef]
- Zhao, X.; Ye, B. Selection of effective singular values using difference spectrum and its application to fault diagnosis of headstock. Mech. Syst. Signal Process. 2011, 25, 1617–1631. [Google Scholar] [CrossRef]
- Li, Y.; Tang, B.; Geng, B.; Jiao, S. Fractional Order Fuzzy Dispersion Entropy and Its Application in Bearing Fault Diagnosis. Fractal Fract. 2022, 6, 544. [Google Scholar] [CrossRef]
- Li, Y.; Jiao, S.; Geng, B. Refined composite multiscale fluctuation-based dispersion Lempel–Ziv complexity for signal analysis. ISA Trans. 2023, 133, 273–284. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Geng, B.; Tang, B. Simplified coded dispersion entropy: A nonlinear metric for signal analysis. Nonlinear Dyn. 2023, 111, 9327–9344. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Boudraa, A.O.; Cexus, J.C. EMD-Based signal filtering. IEEE Trans. Instrum. Meas. 2007, 56, 2196–2202. [Google Scholar] [CrossRef]
- Kopsinis, Y.; McLaughlin, S. Development of EMD-based denoising methods inspired by wavelet thresholding. IEEE Trans. Signal Process. 2009, 57, 13511362. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Yang, H.; Li, Y.A.; Li, G.H. Noise reduction method of ship radiated noise with ensemble empirical mode decomposition of adaptive noise. Noise Control Eng. J. 2016, 64, 230–242. [Google Scholar]
- Li, Y.; Wang, L. A novel noise reduction technique for underwater acoustic signals based on complete ensemble empirical mode decomposition with adaptive noise, minimum mean square variance criterion and least mean square adaptive filter. Def. Technol. 2020, 16, 543–554. [Google Scholar] [CrossRef]
- Yan, H.; Xu, T.; Wang, P.; Zhang, L.; Hu, H.; Bai, Y. MEMS Hydrophone Signal Denoising and Baseline Drift Removal Algorithm Based on Parameter-Optimized Variational Mode Decomposition and Correlation Coefficient. Sensors 2019, 19, 4622. [Google Scholar] [CrossRef] [PubMed]
- Nazari, M.; Sakhaei, S.M. Successive Variational Mode Decomposition. Signal Process. 2020, 174, 107610. [Google Scholar] [CrossRef]
- Li, Y.; Tang, B.; Jiao, S. SO-slope entropy coupled with SVMD: A novel adaptive feature extraction method for ship-radiated noise. Ocean Eng. 2023, 280, 114677. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, Y.; Jiang, S.; Jin, X.; Wei, Y. Rolling Bearing Fault Diagnosis Based on Successive Variational Mode Decomposition and the EP Index. Sensors 2022, 22, 3889. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zhang, Y.; Li, G. Fault-Diagnosis Method for Rotating Machinery Based on SVMD Entropy and Machine Learning. Algorithms 2023, 16, 304. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, T.; Zhang, L.; Qiao, L. Epileptic seizure prediction using successive variational mode decomposition and transformers deep learning network. Front. Neurosci. 2022, 16, 982541. [Google Scholar] [CrossRef] [PubMed]
- Vashishtha, G.; Chauhan, S.; Singh, M.; Kumarn, R. Bearing defect identification by swarm decomposition considering permutation entropy measure and opposition-based slime mould algorithm. Measurement 2021, 178, 109389. [Google Scholar] [CrossRef]
- Vashishtha, G.; Chauhan, S.; Yadav, N.; Yadav, N.; Kumar, N.; Kumar, R. A two-level adaptive chirp mode decomposition and tangent entropy in estimation of single-valued neutrosophic cross-entropy for detecting impeller defects in centrifugal pump. Appl. Acoust. 2022, 197, 108905. [Google Scholar] [CrossRef]
- Figlus, T.; Gnap, J.; Skrúcaný, T.; Šarkan, B.; Stoklosa, J. The use of denoising and analysis of the acoustic signal entropy in diagnosing engine valve clearance. Entropy 2016, 18, 253. [Google Scholar] [CrossRef]
- Li, G.; Yang, Z.; Yang, H. Noise Reduction Method of Underwater Acoustic Signals Based on Uniform Phase Empirical Mode Decomposition, Amplitude-Aware Permutation Entropy, and Pearson Correlation Coefficient. Entropy 2018, 20, 918. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Chen, X.; Yu, J. Denoising and Feature Extraction Algorithms Using NPE Combined with VMD and Their Applications in Ship-Radiated Noise. Symmetry 2017, 9, 256. [Google Scholar] [CrossRef]
- Li, G.; Yang, Z.; Yang, H. A Denoising Method of Ship Radiated Noise Signal Based on Modified CEEMDAN, Dispersion Entropy, and Interval Thresholding. Electronics 2019, 8, 597. [Google Scholar] [CrossRef]
- Rostaghi, M.; Khatibi, M.M.; Ashory, M.R.; Azami, H. Fuzzy Dispersion Entropy: A Nonlinear Measure for Signal Analysis. IEEE Trans. Fuzzy Syst. 2022, 30, 3785–3796. [Google Scholar] [CrossRef]
- Ma, H.; Xu, Y.; Wang, J.; Song, M.; Zhang, S. SVMD coupled with dual-threshold criteria of correlation coefficient: A self-adaptive denoising method for ship-radiated noise signal. Ocean Eng. 2023, 281, 114931. [Google Scholar] [CrossRef]
- National Park Service. Available online: https://www.nps.gov/glba/learn/nature/soundclips.htm (accessed on 28 February 2023).
- Yang, S.; Li, Z. Classification of ship-radiated signals via chaotic features. Electron. Lett. 2003, 39, 395–397. [Google Scholar] [CrossRef]
- Yang, H.; Cheng, Y.; Li, G. A denoising method for ship radiated noise based on Spearman variational mode decomposition, spatial-dependence recurrence sample entropy, improved wavelet threshold denoising, and Savitzky-Golay filter. Alex. Eng. J. 2021, 60, 3379–3400. [Google Scholar] [CrossRef]












| SNR (dB) | Parameter | Denoising Methods | ||||
|---|---|---|---|---|---|---|
| EMD- FuDE-WPD | EEMD-FuDE-WPD | CEEMDAN-FuDE-WPD | VMD-FuDE-WPD | Proposed | ||
| −10 | SNR (dB) | 7.1123 | 7.3263 | 7.9787 | 8.2092 | 9.8129 |
| RMS-E- | 1.4452 | 1.4090 | 1.3131 | 1.1964 | 0.9669 | |
| C-C | 0.7951 | 0.8161 | 0.8345 | 0.8347 | 0.8775 | |
| −8 | SNR (dB) | 8.7669 | 8.8213 | 9.5679 | 9.5642 | 10.7419 |
| RMS-E | 1.1512 | 1.1267 | 1.0290 | 0.9847 | 0.8622 | |
| C-C | 0.8608 | 0.8651 | 0.8822 | 0.8794 | 0.9019 | |
| −6 | SNR (dB) | 10.2715 | 10.4009 | 10.9614 | 10.7204 | 12.1555 |
| RMS-E | 0.9554 | 0.9346 | 0.8634 | 0.8651 | 0.72627 | |
| C-C | 0.9006 | 0.9016 | 0.9164 | 0.9051 | 0.9317 | |
| −4 | SNR (dB) | 12.0612 | 12.4051 | 12.3482 | 12.6794 | 13.6665 |
| RMS-E | 0.7595 | 0.7328 | 0.7335 | 0.6829 | 0.6046 | |
| C-C | 0.9318 | 0.9396 | 0.9359 | 0.9384 | 0.9522 | |
| −2 | SNR (dB) | 13.5964 | 14.2625 | 14.1302 | 14.1702 | 14.4824 |
| RMS-E | 0.6311 | 0.5819 | 0.5913 | 0.5770 | 0.5322 | |
| C-C | 0.9520 | 0.9588 | 0.9567 | 0.9373 | 0.9631 | |
| 0 | SNR (dB) | 15.3607 | 16.1055 | 15.7362 | 15.8557 | 16.2097 |
| RMS-E | 0.5149 | 0.4716 | 0.4857 | 0.4717 | 0.4529 | |
| C-C | 0.9676 | 0.9726 | 0.9581 | 0.9714 | 0.9738 | |
| SNR (dB) | Parameters | Denoising Methods | ||||
|---|---|---|---|---|---|---|
| EMD- FuDE-WPD | EEMD-FuDE-WPD | CEEMDAN-FuDE-WPD | VMD-FuDE-WPD | Proposed | ||
| −10 | SNR (dB) | 3.7562 | 4.2255 | 4.6239 | 4.5349 | 5.8977 |
| RMS-E | 1.5080 | 1.3910 | 1.2937 | 1.2107 | 0.9976 | |
| C-C | 0.7035 | 0.7389 | 0.7668 | 0.7516 | 0.8194 | |
| −8 | SNR (dB) | 5.2223 | 5.7629 | 6.0370 | 6.2175 | 7.5599 |
| RMS-E | 1.2024 | 1.1100 | 1.0366 | 0.9570 | 0.8072 | |
| C-C | 0.7963 | 0.8204 | 0.8281 | 0.8361 | 0.8893 | |
| −6 | SNR (dB) | 6.6256 | 7.1416 | 7.5747 | 7.7470 | 9.1989 |
| RMS-E | 0.9502 | 0.8791 | 0.8301 | 0.7525 | 0.6495 | |
| C-C | 0.8530 | 0.8869 | 0.8808 | 0.8937 | 0.9110 | |
| −4 | SNR (dB) | 8.6903 | 9.1641 | 9.3790 | 9.0854 | 10.1697 |
| RMS-E | 0.7249 | 0.6824 | 0.6305 | 0.6344 | 0.5358 | |
| C-C | 0.9093 | 0.9174 | 0.9208 | 0.9115 | 0.9353 | |
| −2 | SNR (dB) | 9.9321 | 10.4520 | 10.9616 | 10.5184 | 12.4269 |
| RMS-E | 0.6063 | 0.5637 | 0.5403 | 0.5329 | 0.4360 | |
| C-C | 0.9322 | 0.9385 | 0.9452 | 0.9393 | 0.9603 | |
| 0 | SNR (dB) | 11.8321 | 12.3313 | 12.8301 | 14.1153 | 14.9826 |
| RMS-E | 0.4732 | 0.4477 | 0.4226 | 0.3519 | 0.3230 | |
| C-C | 0.9550 | 0.9601 | 0.9648 | 0.9741 | 0.9780 | |
| SNR (dB) | Parameters | Denoising Methods | ||||
|---|---|---|---|---|---|---|
| EMD- FuDE-WPD | EEMD-FuDE-WPD | CEEMDAN-FuDE-WPD | VMD-FuDE-WPD | Proposed | ||
| −10 | SNR (dB) | 7.1206 | 7.6017 | 8.3059 | 9.2277 | 11.9972 |
| RMS-E | 1.4862 | 1.4138 | 1.2932 | 1.1304 | 0.8092 | |
| C-C | 0.8907 | 0.9019 | 0.9120 | 0.9340 | 0.9646 | |
| −8 | SNR (dB) | 8.7535 | 9.4141 | 9.6216 | 11.1875 | 14.6590 |
| RMS-E | 1.1932 | 1.1116 | 1.0725 | 0.8899 | 0.5843 | |
| C-C | 0.9265 | 0.9369 | 0.9402 | 0.9584 | 0.9809 | |
| −6 | SNR (dB) | 10.7013 | 11.4311 | 12.1106 | 12.9648 | 16.6854 |
| RMS-E | 0.9351 | 0.8554 | 0.8033 | 0.7098 | 0.4550 | |
| C-C | 0.9535 | 0.9631 | 0.9662 | 0.9725 | 0.9886 | |
| −4 | SNR (dB) | 12.8621 | 13.0554 | 14.7153 | 14.9012 | 18.4936 |
| RMS-E | 0.7186 | 0.6975 | 0.5821 | 0.5641 | 0.3672 | |
| C-C | 0.9661 | 0.9731 | 0.9813 | 0.9826 | 0.9924 | |
| −2 | SNR (dB) | 14.2346 | 15.0312 | 16.6148 | 16.7928 | 20.2769 |
| RMS-E | 0.6128 | 0.5544 | 0.4604 | 0.4476 | 0.2999 | |
| C-C | 0.9795 | 0.9830 | 0.9883 | 0.9888 | 0.9950 | |
| 0 | SNR (dB) | 16.3358 | 17.2349 | 18.7690 | 18.3044 | 21.2527 |
| RMS-E | 0.4771 | 0.4257 | 0.3585 | 0.3777 | 0.2598 | |
| C-C | 0.9874 | 0.9898 | 0.9928 | 0.9921 | 0.9962 | |
| SNR (dB) | Parameters | Denoising Methods | ||||
|---|---|---|---|---|---|---|
| EMD- FuDE-WPD | EEMD-FuDE-WPD | CEEMDAN-FuDE-WPD | VMD-FuDE-WPD | Proposed | ||
| −10 | SNR (dB) | 1.4928 | 1.6554 | 2.0722 | 2.2558 | 3.0188 |
| RMS-E | 0.4347 | 0.4223 | 0.3678 | 0.3410 | 0.3007 | |
| C-C | 0.5335 | 0.5562 | 0.6103 | 0.6333 | 0.6951 | |
| −8 | SNR (dB) | 2.1155 | 2.6804 | 2.7758 | 3.0444 | 4.1249 |
| RMS-E | 0.3476 | 0.3255 | 0.3001 | 0.2796 | 0.2494 | |
| C-C | 0.6181 | 0.6727 | 0.6825 | 0.7088 | 0.7791 | |
| −6 | SNR (dB) | 3.1346 | 3.5160 | 3.8485 | 4.1854 | 4.5290 |
| RMS-E | 0.2822 | 0.2627 | 0.2437 | 0.2173 | 0.2191 | |
| C-C | 0.7083 | 0.7423 | 0.7609 | 0.7315 | 0.8001 | |
| −4 | SNR (dB) | 4.2189 | 4.9282 | 5.1783 | 5.4913 | 6.3261 |
| RMS-E | 0.2225 | 0.2011 | 0.1906 | 0.1774 | 0.1627 | |
| C-C | 0.7854 | 0.8215 | 0.8319 | 0.8440 | 0.8714 | |
| −2 | SNR (dB) | 6.3355 | 6.4252 | 6.3921 | 7.0159 | 8.7687 |
| RMS-E | 0.1589 | 0.1599 | 0.1592 | 0.1406 | 0.1164 | |
| C-C | 0.8743 | 0.8757 | 0.8757 | 0.8853 | 0.9270 | |
| 0 | SNR (dB) | 8.0902 | 7.8850 | 7.8137 | 8.6208 | 10.1565 |
| RMS-E | 0.1258 | 0.1288 | 0.1288 | 0.1120 | 0.0949 | |
| C-C | 0.9179 | 0.9115 | 0.9127 | 0.9314 | 0.9495 | |
| SN Signal | Status | DE | PE |
|---|---|---|---|
| SN-1 | Original | 0.8601 | 1.6513 |
| Denoised | 0.7179 | 1.0502 | |
| SN-2 | Original | 0.8030 | 1.4610 |
| Denoised | 0.6979 | 1.0403 | |
| SN-3 | Original | 0.6981 | 1.3301 |
| Denoised | 0.6705 | 1.1163 | |
| SN-4 | Original | 0.7450 | 1.3877 |
| Denoised | 0.7124 | 1.1892 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zhang, C.; Zhou, Y. A Novel Denoising Method for Ship-Radiated Noise. J. Mar. Sci. Eng. 2023, 11, 1730. https://doi.org/10.3390/jmse11091730
Li Y, Zhang C, Zhou Y. A Novel Denoising Method for Ship-Radiated Noise. Journal of Marine Science and Engineering. 2023; 11(9):1730. https://doi.org/10.3390/jmse11091730
Chicago/Turabian StyleLi, Yuxing, Chunli Zhang, and Yuhan Zhou. 2023. "A Novel Denoising Method for Ship-Radiated Noise" Journal of Marine Science and Engineering 11, no. 9: 1730. https://doi.org/10.3390/jmse11091730
APA StyleLi, Y., Zhang, C., & Zhou, Y. (2023). A Novel Denoising Method for Ship-Radiated Noise. Journal of Marine Science and Engineering, 11(9), 1730. https://doi.org/10.3390/jmse11091730







