The Effect of a Linear Free Surface Boundary Condition on the Steady-State Wave-Making of Shallowly Submerged Underwater Vehicles
Abstract
1. Introduction
2. Numerical Methods
2.1. Boundary Element Method
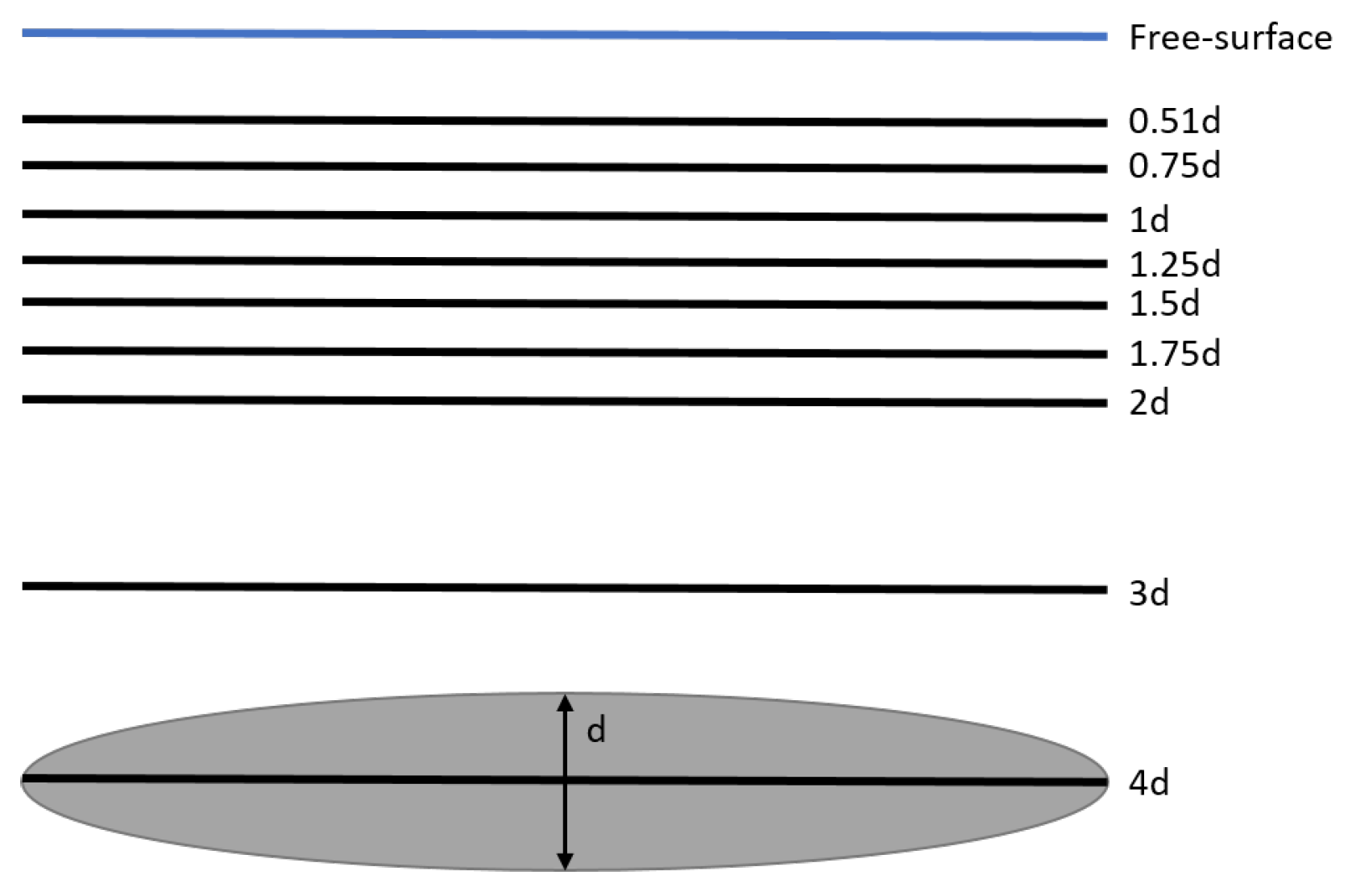
2.2. RANSE CFD
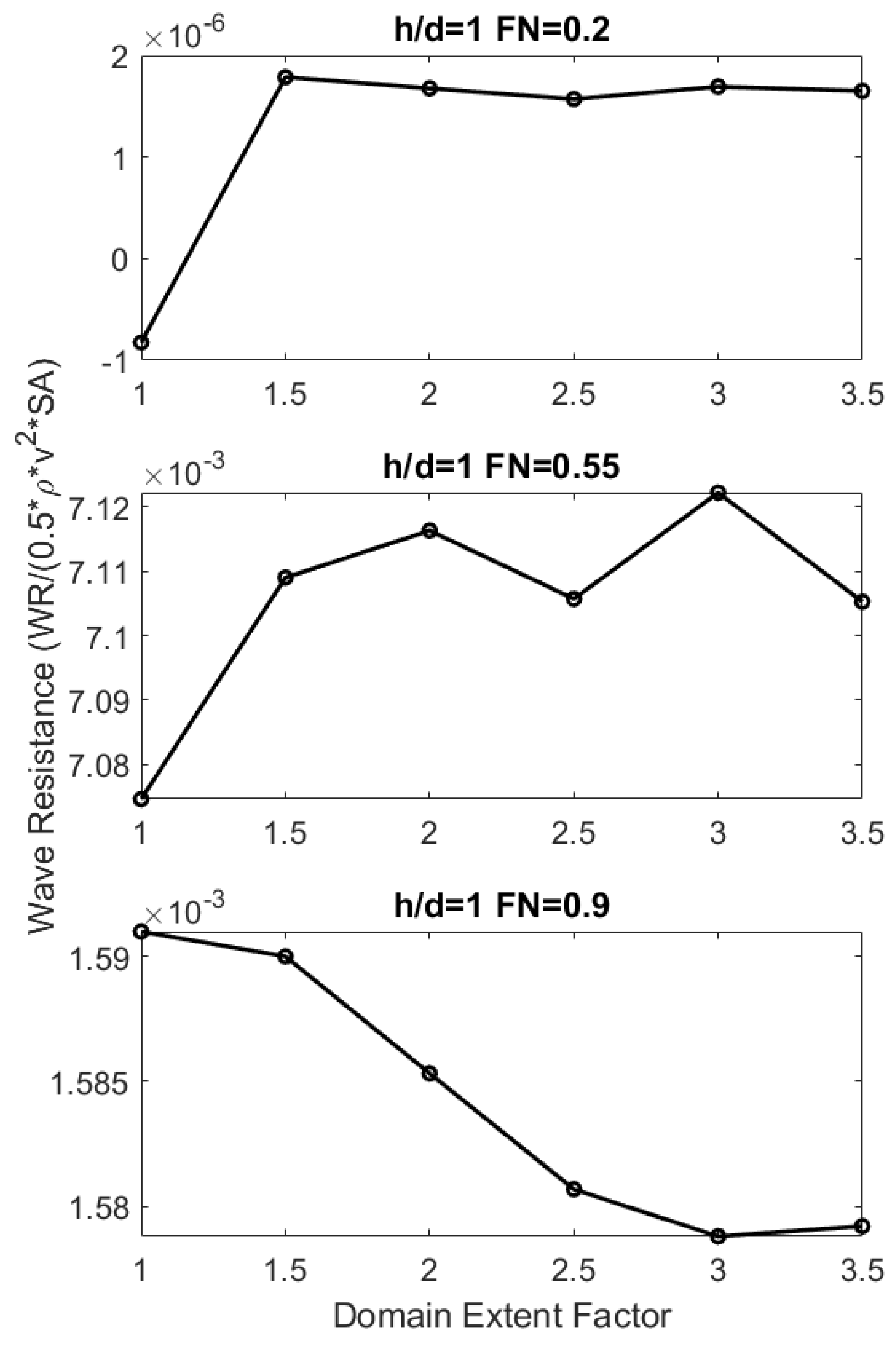
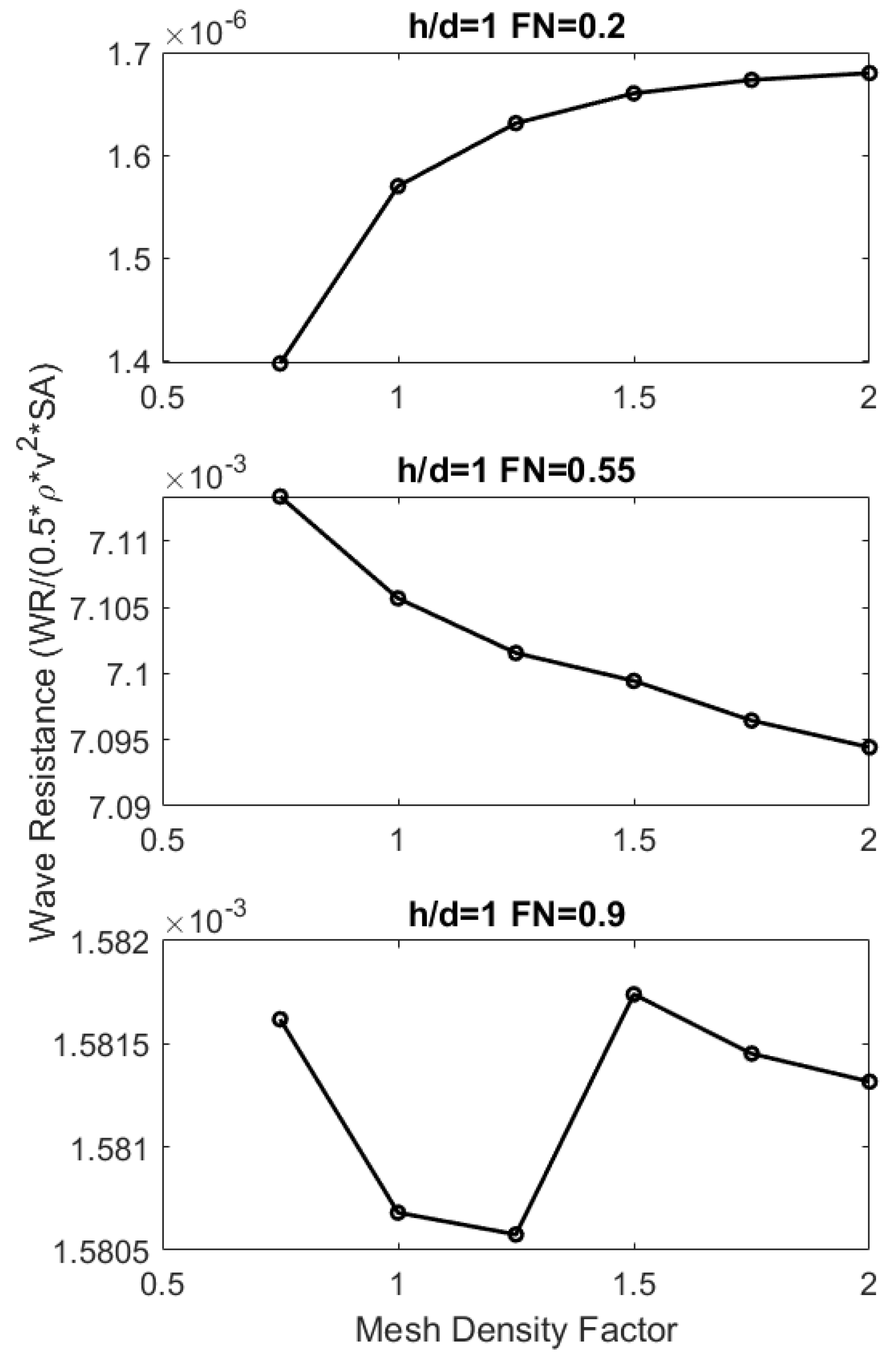
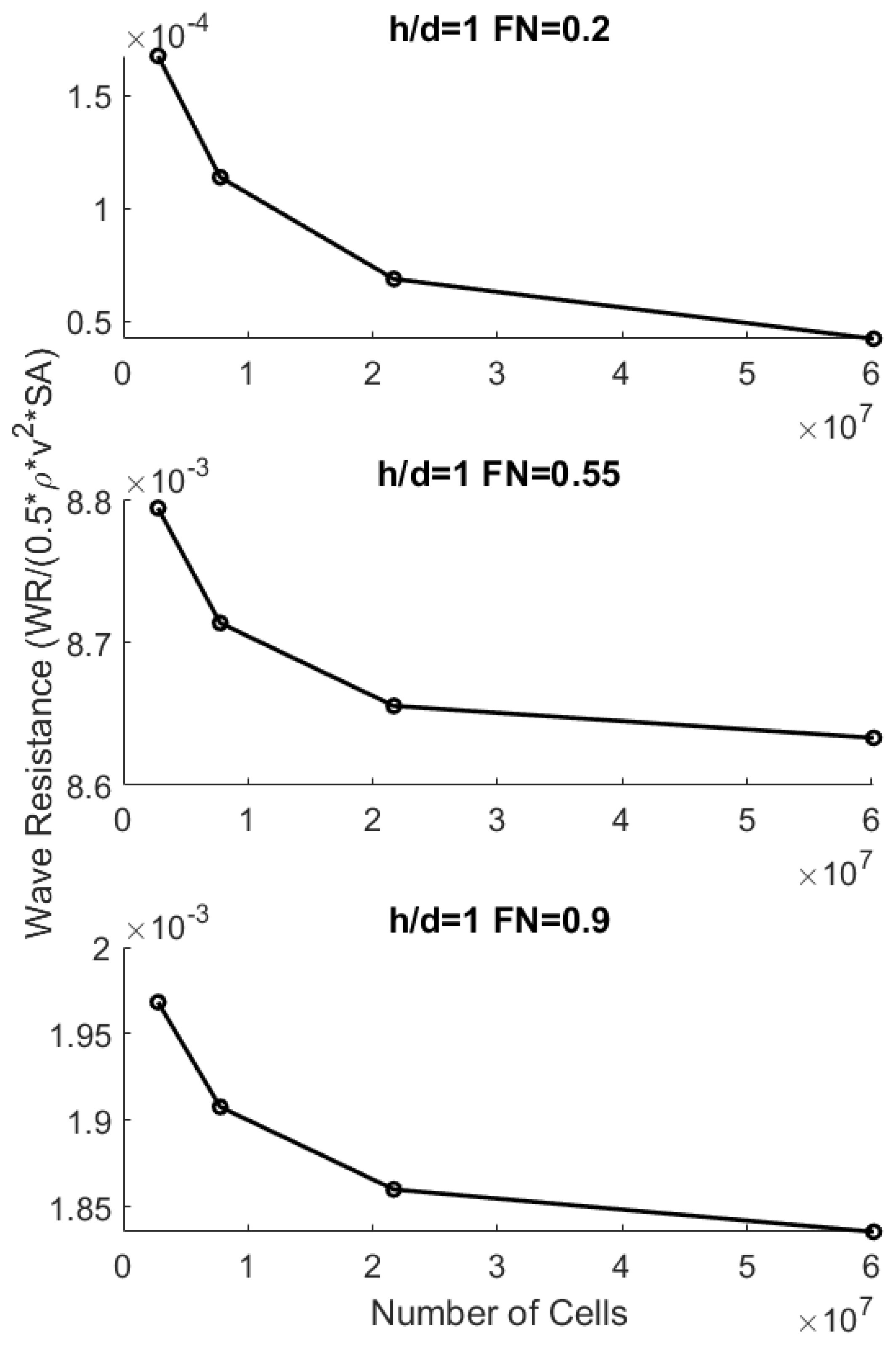
2.3. Simulation Validation
3. Results and Discussion
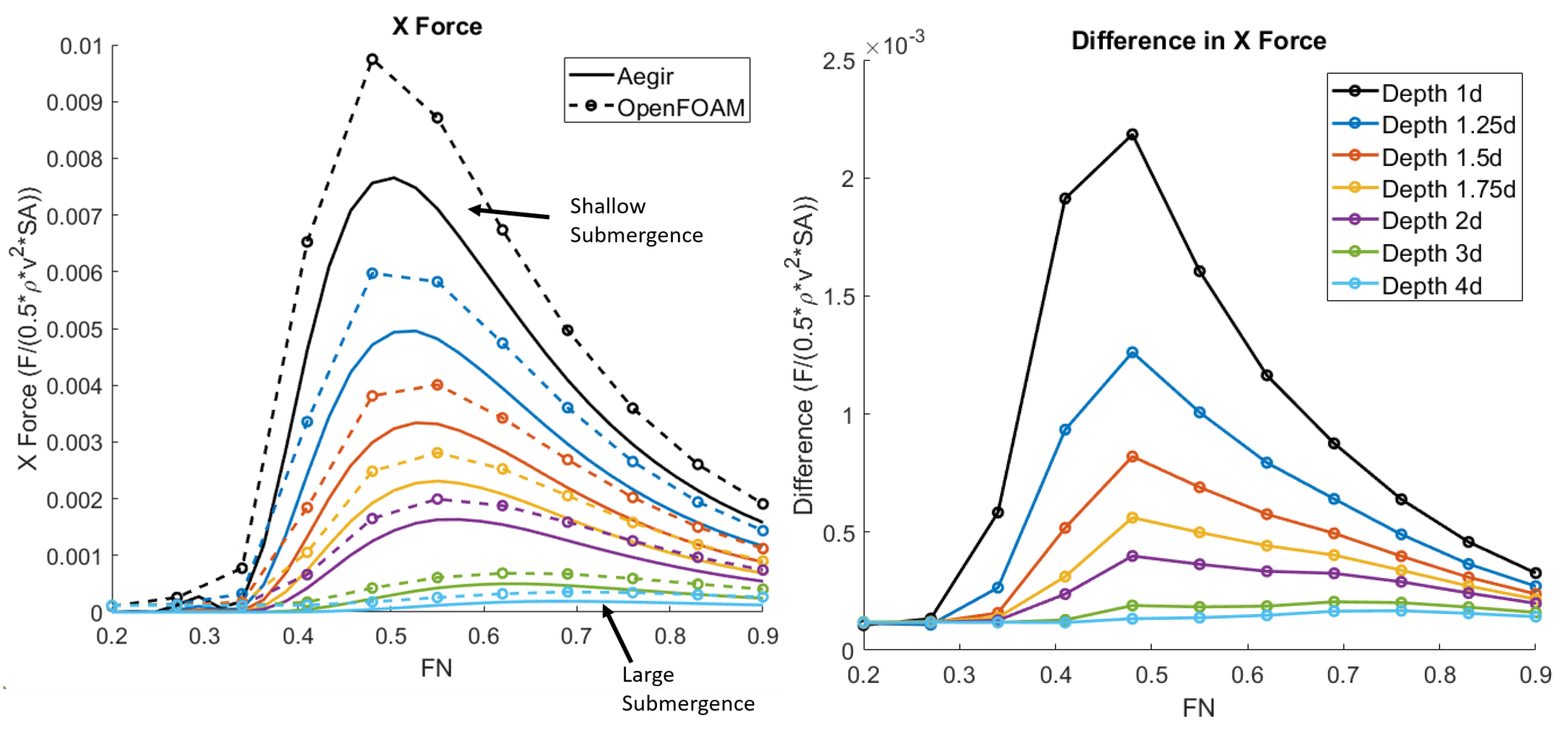
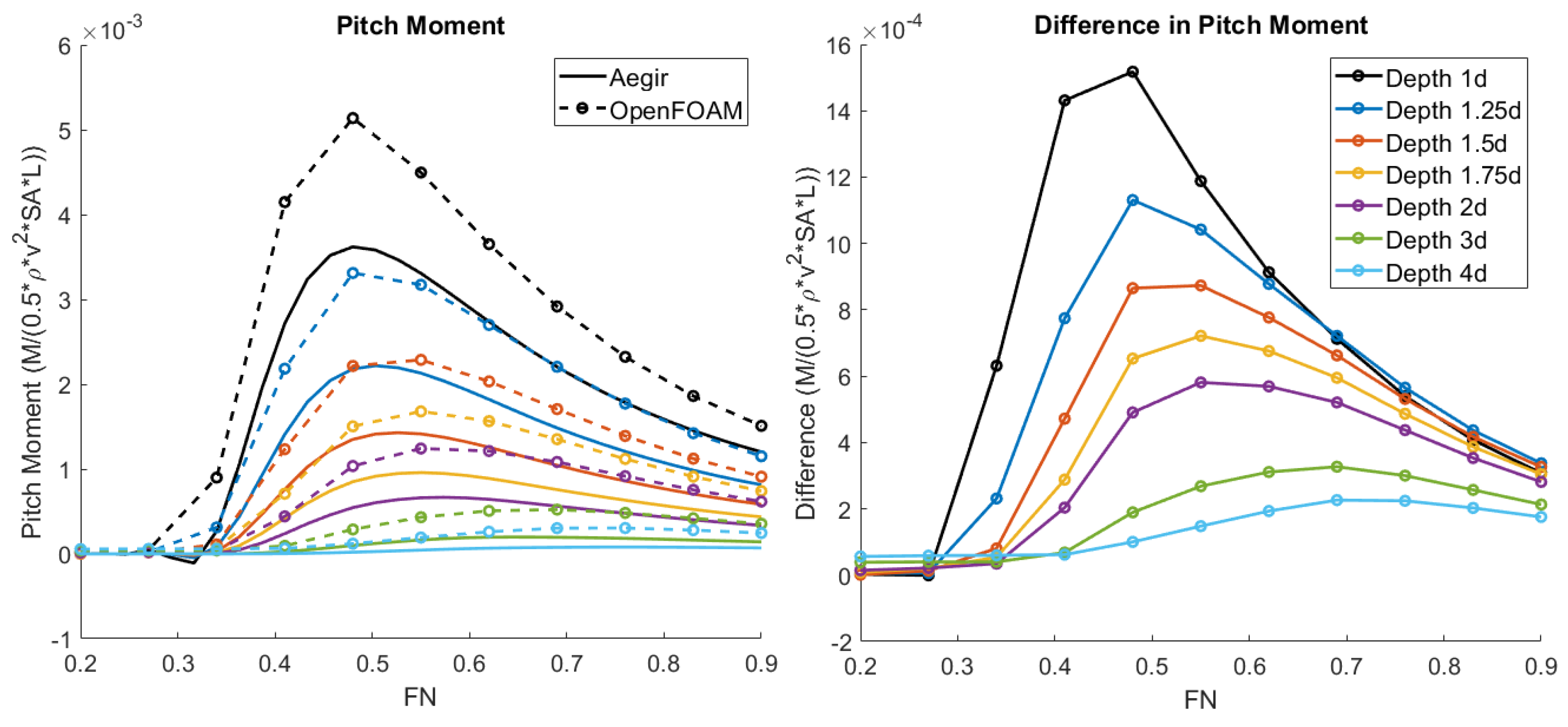
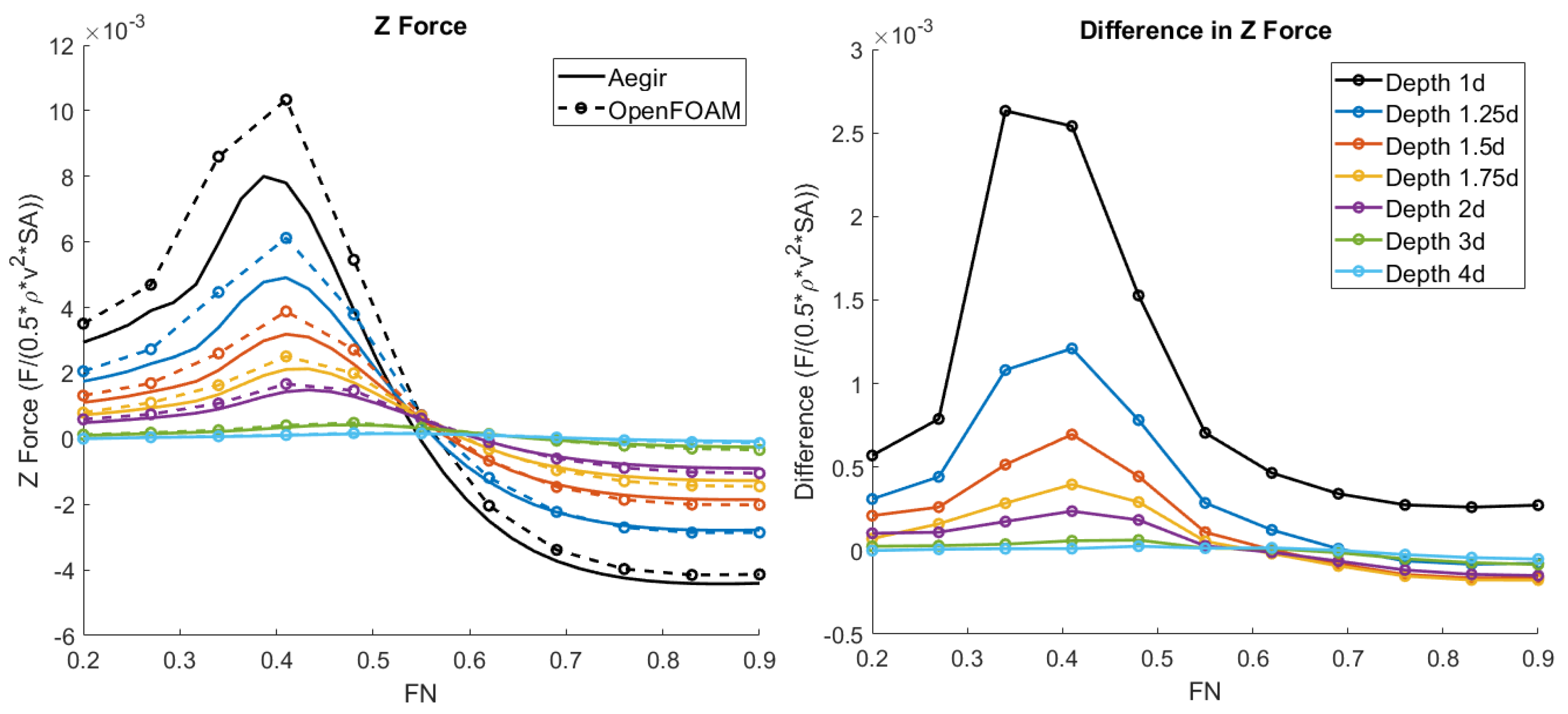
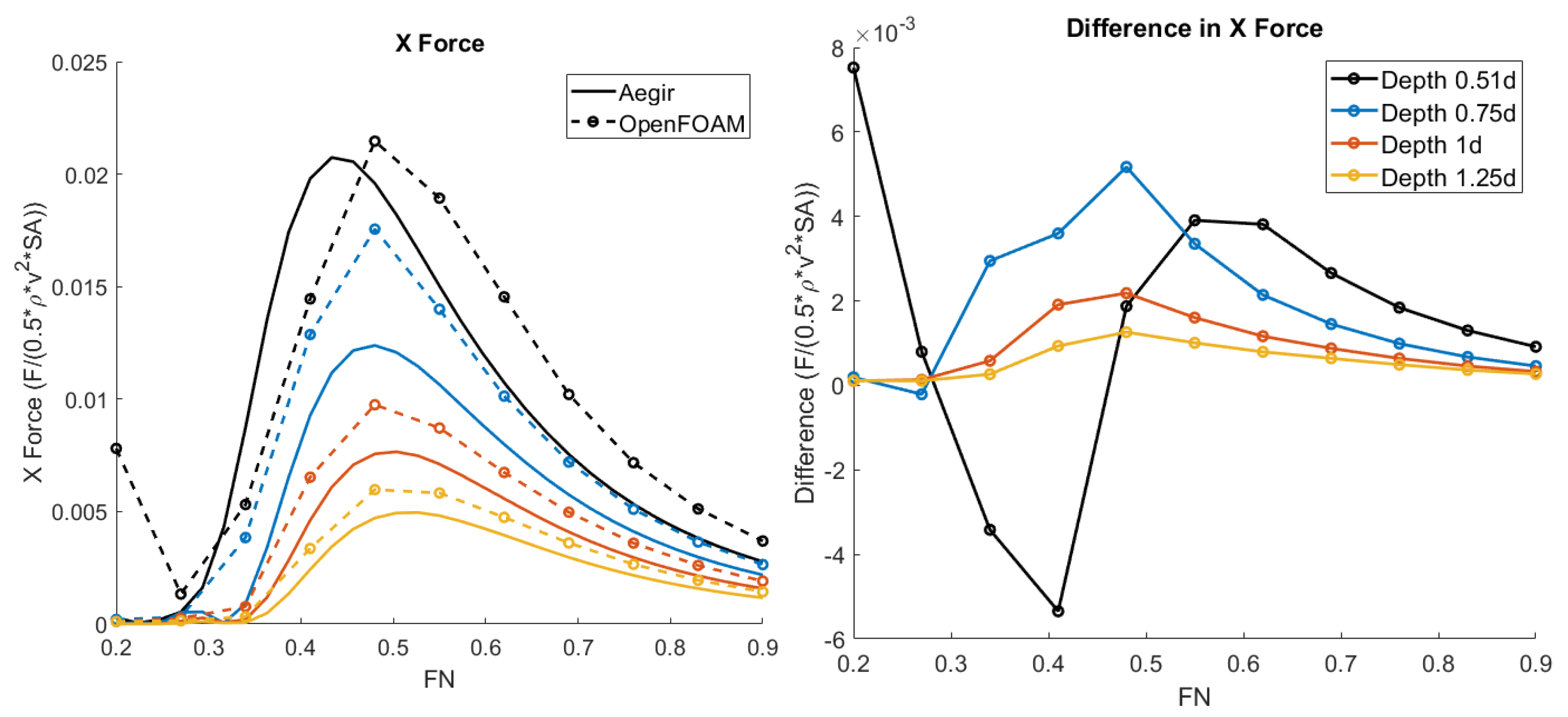
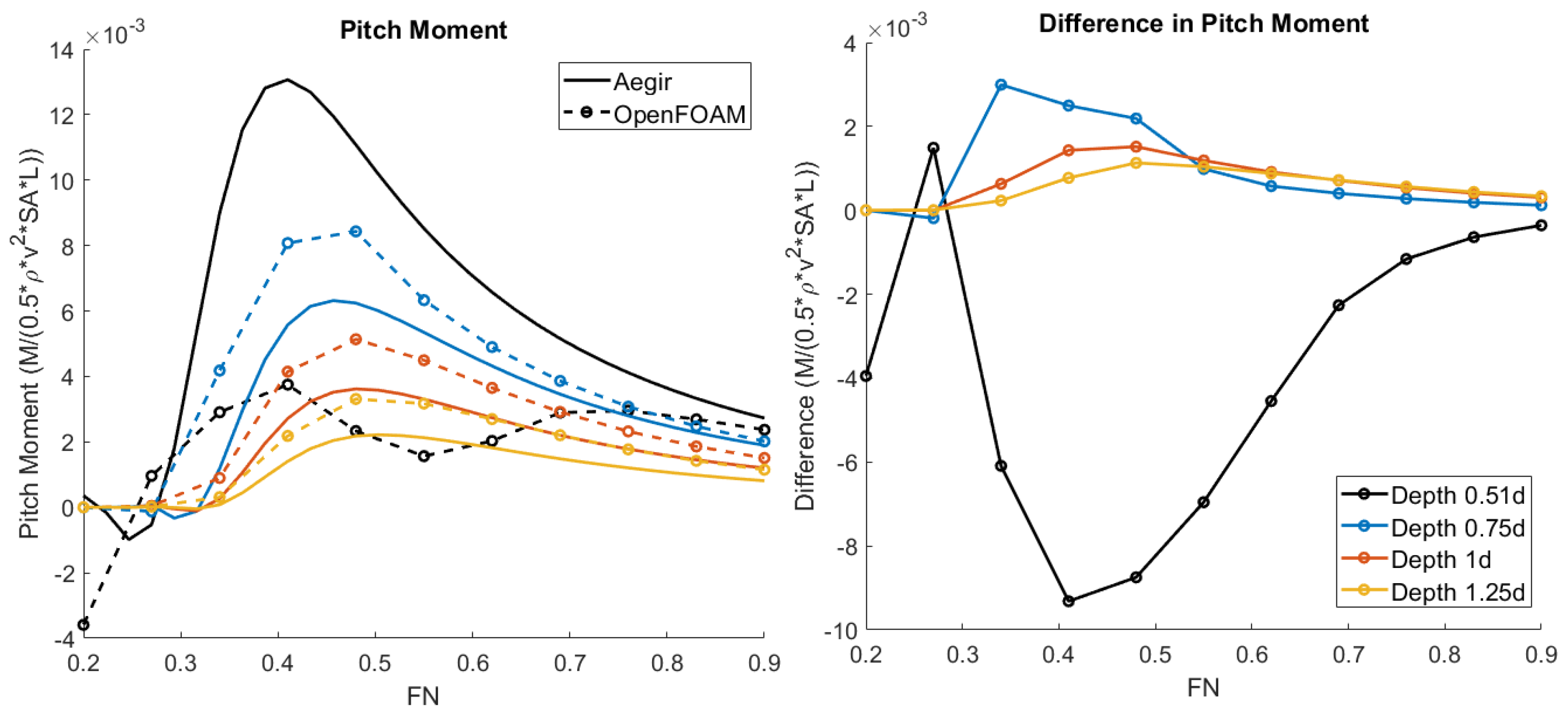
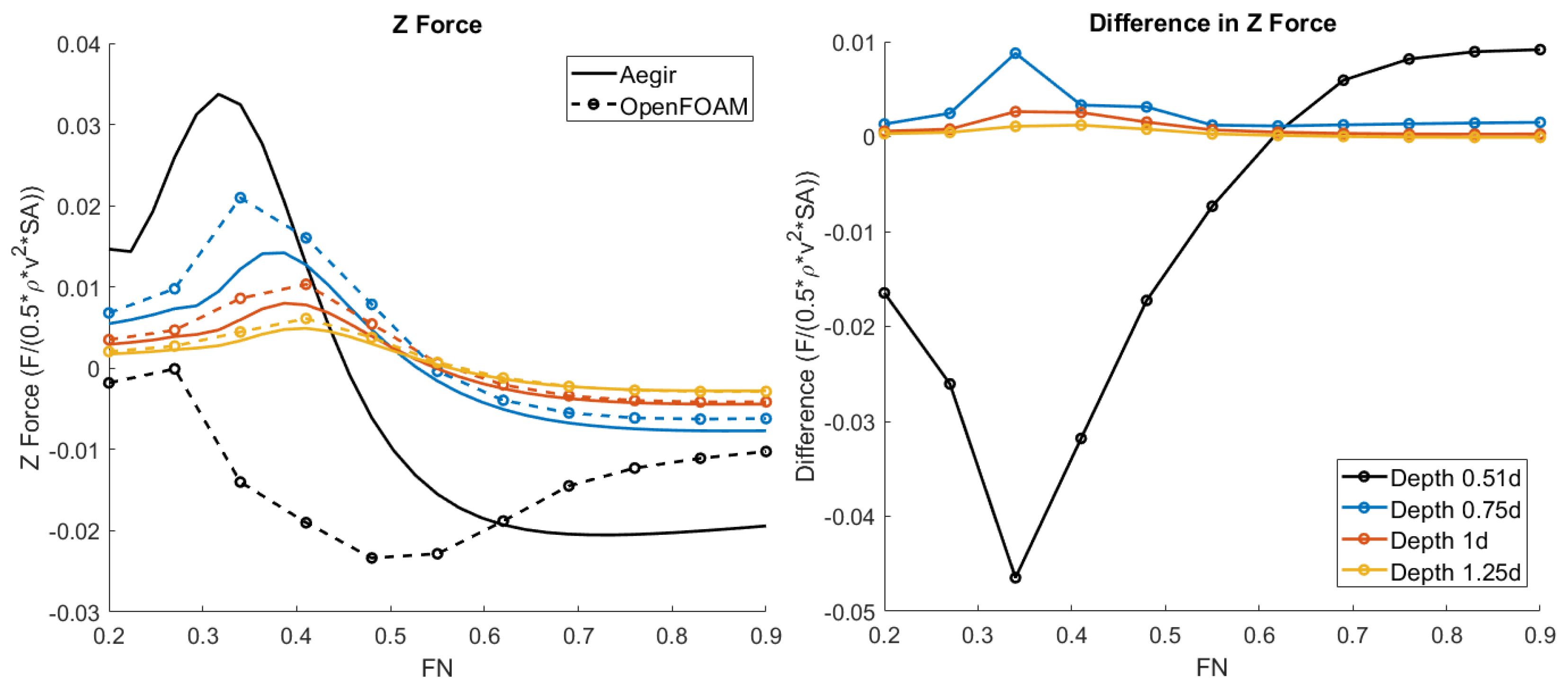
3.1. Forces and Moments
3.2. Wave Pattern and Longitudinal Wave Profile
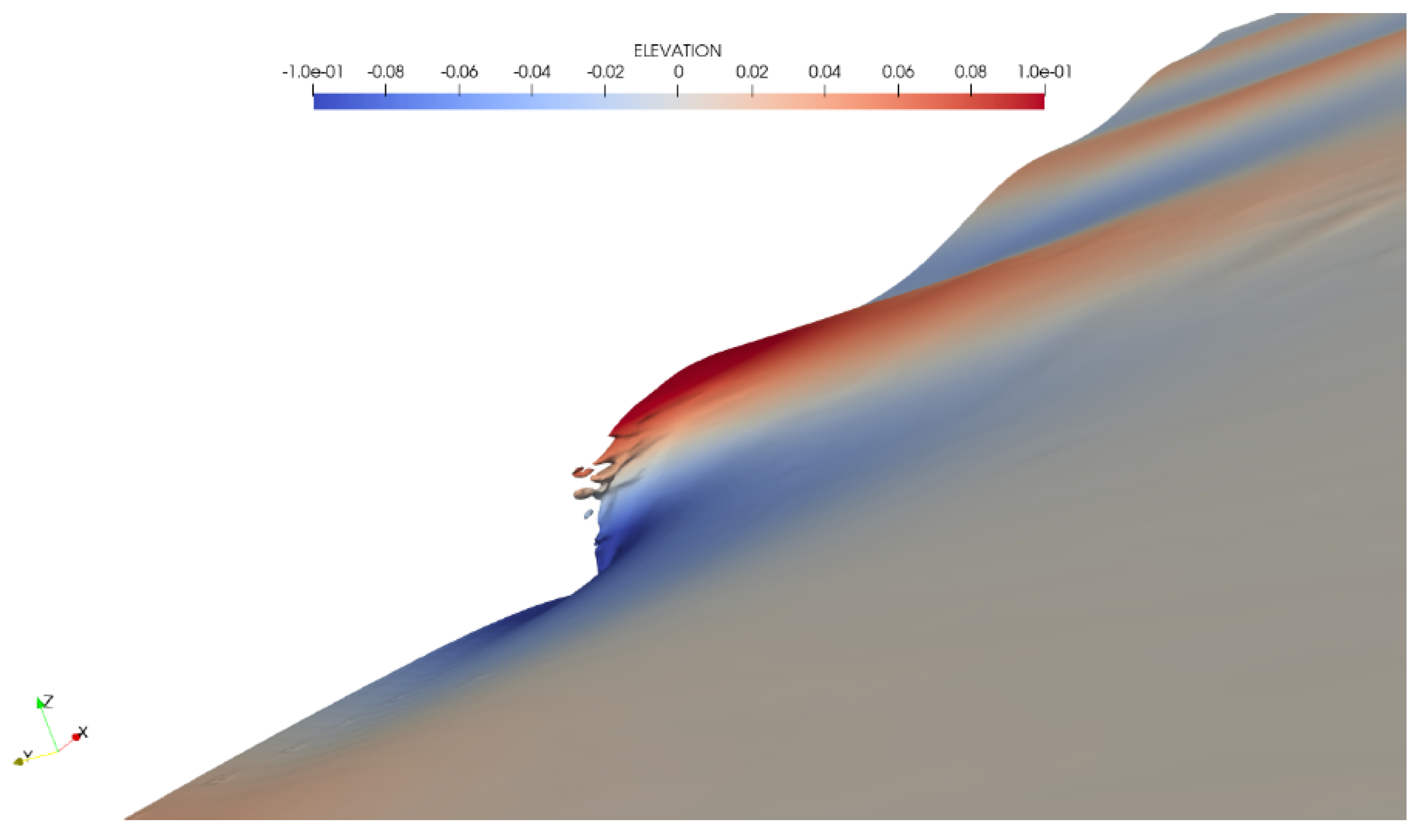
3.3. Breaking Waves
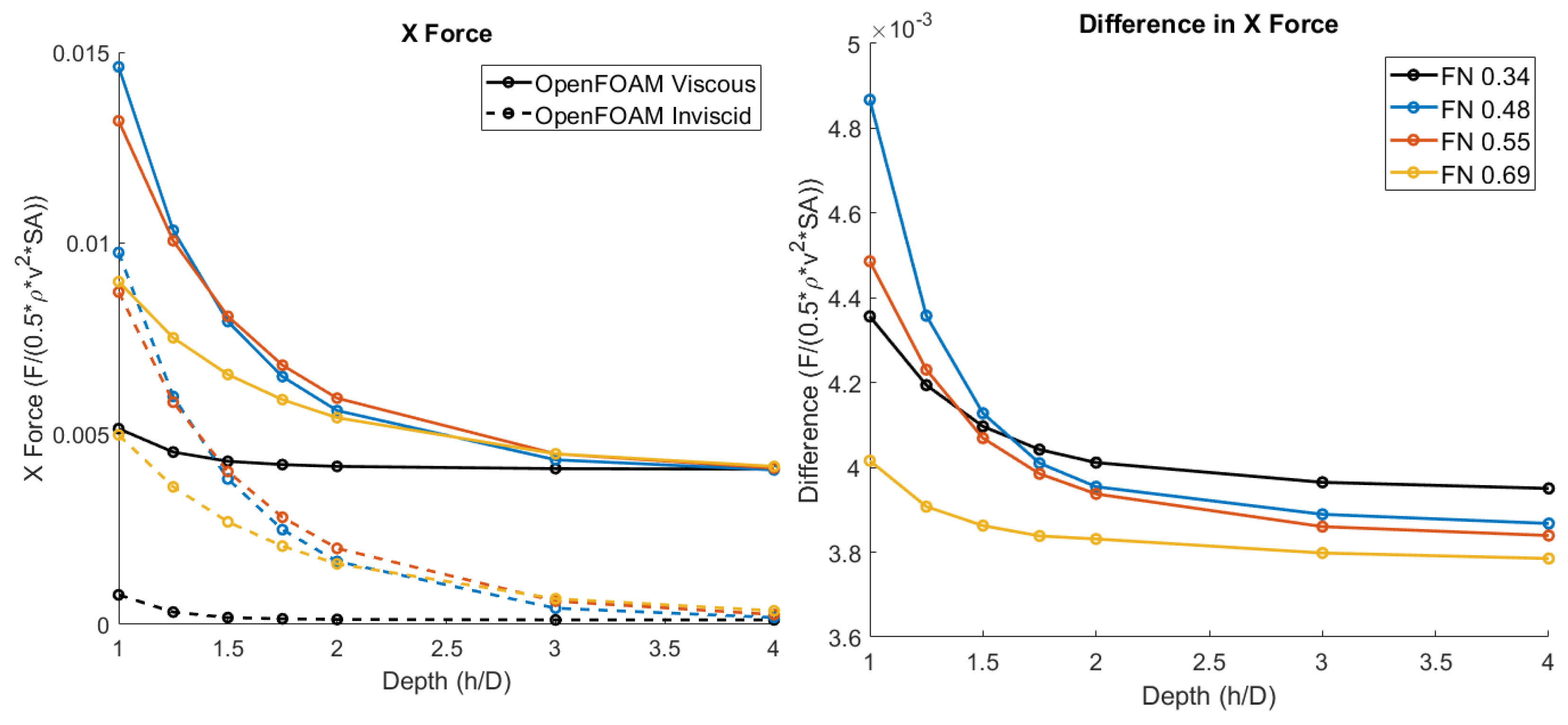
3.4. Viscous Effects
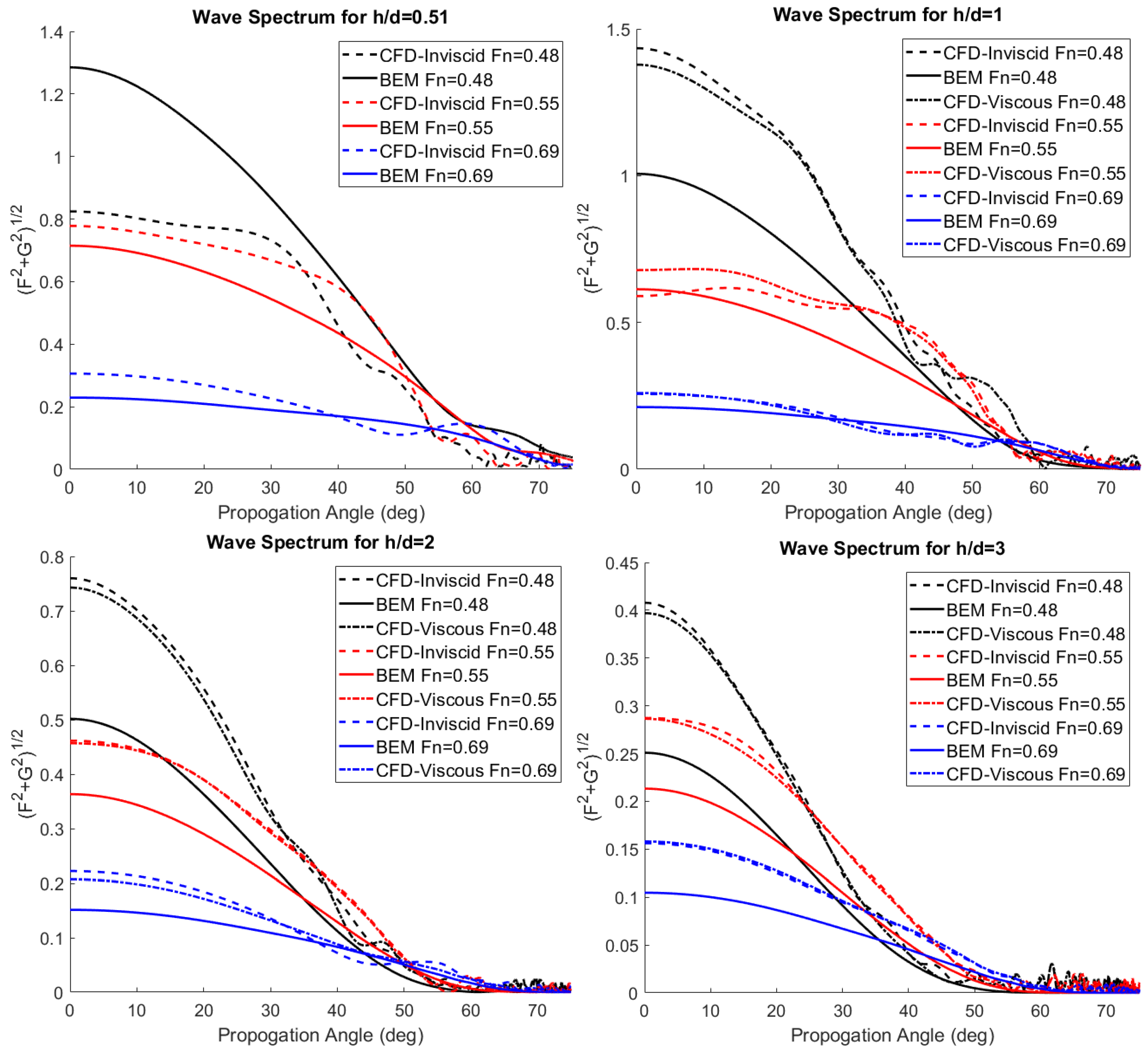
3.5. Wave Spectrum
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Battista, T. Lagrangian Mechanics Modeling of Free Surface-Affected Marine Craft. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 2018. [Google Scholar]
- Valentinis, F.; Battista, T.; Woolsey, C. A Maneuvering Model for an Underwater Vehicle Near a Free Surface—Part III: Simulation and Control Under Waves. IEEE J. Ocean. Eng. 2023, 1–26. [Google Scholar] [CrossRef]
- Valentinis, F.; Donaire, A.; Perez, T. Energy-Based Motion Control of a Slender Hull Unmanned Underwater Vehicle. Ocean Eng. 2015, 104, 604–616. [Google Scholar] [CrossRef]
- Woolsey, C.A.; Techy, L. Cross-Track Control of a Slender, Underactuated AUV Using Potential Shaping. Ocean Eng. 2009, 36, 82–91. [Google Scholar] [CrossRef]
- Battista, T.; Valentinis, F.; Woolsey, C. A Maneuvering Model for an Underwater Vehicle Near a Free Surface—Part I: Motion Without Memory Effects. IEEE J. Ocean. Eng. 2020, 45, 212–226. [Google Scholar] [CrossRef]
- Battista, T.; Valentinis, F.; Woolsey, C. A Maneuvering Model for an Underwater Vehicle Near a Free Surface—Part II: Incorporation of the Free Surface Memory. IEEE J. Ocean. Eng. 2023, 1–12. [Google Scholar] [CrossRef]
- Jung, S.; Brizzolara, S.; Woolsey, C. An Approach for Computing Parameters for a Lagrangian Nonlinear Maneuvering and Seakeeping Model of Submerged Vessel Motion. IEEE J. Ocean. Eng. 2021, 46, 749–764. [Google Scholar] [CrossRef]
- Jung, S.; Brizzolara, S.; Woolsey, C.A. Parameter Computation for a Lagrangian Mechanical System Model of a Submerged Vessel Moving near a Free Surface. Ocean Eng. 2021, 230, 108988. [Google Scholar] [CrossRef]
- Raven, H.C. A Solution Method for the Nonlinear Wave Resistance Problem. Ph.D. Thesis, Delft University of Technology, Delft, NL, USA, 1996. [Google Scholar]
- White, P.F.; Piro, D.J.; Knight, B.G.; Maki, K.J. A Hybrid Numerical Framework for Simulation of Ships Maneuvering in Waves. J. Ship Res. 2022, 66, 159–171. [Google Scholar] [CrossRef]
- Abdul Khader, M.H. Effects of Wave Drag on Submerged Bodies. La Houille Blanche, 1979; pp. 465–470. Available online: https://www.shf-lhb.org/articles/lhb/pdf/1979/05/lhb1979044.pdf (accessed on 1 April 2023).
- Chey, Y.H. The Consistent Second-Order Wave Theory and Its Application to a Submerged Spheroid. J. Ship Res. 1970, 14, 23–50. [Google Scholar] [CrossRef]
- Tuck, E.; Scullen, D. A Comparison of Linear and Nonlinear Computations of Waves Made by Slender Submerged Bodies. J. Eng. Math. 2002, 42, 255–264. [Google Scholar] [CrossRef]
- Lambert, W.; Brizzolara, S. On the Effect of Non-Linear Boundary Conditions on the Wave Disturbance and Hydrodynamic Forces of Underwater Vehicles Travelling Near the Free-Surface. In Proceedings of the ASME 2020 39th International Conference on Ocean, Offshore and Arctic Engineering, Online, 3–7 August 2020; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2020. [Google Scholar]
- Lambert, W.; Brizzolara, S.; Woolsey, C. On the Effect of Free-Surface Linearization on the Predicted Hydrodynamic Response of Underwater Vehicles Travelling Near the Free-Surface. In Proceedings of the OMAE 2022, Hamburg, Germany, 5–11 June 2022. [Google Scholar]
- Kring, D.C.D.C. Time Domain Ship Motions by a Three-Dimensional Rankine Panel Method. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1994. [Google Scholar]
- Lambert, W.B.; Brizzolara, S. Wave Resistance Reduction for Ships Traveling in Fleet Formation. In Proceedings of the SNAME Maritime Convention, Virtual, 29 September 2020. [Google Scholar]
- Rosenthal, B.; Datla, R.; Greeley, D.; Kring, D.; Keipper, T.; Milewski, B. Optimization Validation of a High-Speed Boat. In Proceedings of the 2013 Summer Computer Simulation Conference (SCSC’13), Toronto, ON, Canada, 7–10 July 2013; Society for Modeling & Simulation International: Vista, CA, USA, 2013; pp. 1–8. [Google Scholar]
- Gouveia, R.; Fitzpatrick, S.; Costa, A.; Kring, D. Time Domain Simulation of Lifting Bodies Acting at or Near the Free Surface With Vortex Particle Wakes. J. Fluids Eng. 2019, 141, 041201. [Google Scholar] [CrossRef]
- Brizzolara, S. Automatic Optimisation of a New Fast Catamaran with Bulbous Bow. In Proceedings of the International Conference on High-Performance Marine Vehicles (HIPER 2004), Rome, Italy, 27–29 September 2004; pp. 116–128. [Google Scholar]
- Brizzolara, S.; Vernengo, G.; Bonfiglio, L.; Bruzzone, D. Comparative Performance of Optimum High Speed SWATH and Semi-SWATH in Calm Water and in Waves. In Proceedings of the SNAME Maritime Convention and 5th World Maritime Technology Conference, Providence, RI, USA, 3–7 November 2015. [Google Scholar]
- Doyle, W.J.; Schambach, L.S.; Smith, M.V.; Field, C.; Hart, C.J. Verification, Validation, and Best Practices for a High-Order, Potential-Flow Boundary Element Method. In Proceedings of the SNAME 13th International Conference on Fast Sea Transportation, Washington, DC, USA, 1–4 September 2015. [Google Scholar]
- Weller, H.; Tabor, G.; Jasak, H.; Fureby, C. A Tensorial Approach to Computational Continuum Mechanics Using Object Orientated Techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Lyu, W.; el Moctar, O. Numerical and Experimental Investigations of Wave-Induced Second Order Hydrodynamic Loads. Ocean Eng. 2017, 131, 197–212. [Google Scholar] [CrossRef]
- Weinblum, G.; Amtsberg, H.; Bock, W. Tests on Wave Resistance of Immersed Bodies of Revolution; Technical Report; Defense Technical Information Center: Potomac, VA, USA, 1950. [Google Scholar]
- Hoerner, S.F. Fluid Dynamic Drag: Practical Information on Aerodynamic Drag and Hydrodynamic Resistance, 2nd ed.; Hoerner Fluid Dynamics: Bakersfield, CA, USA, 1965; Chapter 6C. [Google Scholar]
- Menter, F.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Devolder, B.; Troch, P.; Rauwoens, P. Performance of a buoyancy-modified k-ω and k-ω SST turbulence model for simulating wave breaking under regular waves using OpenFOAM. Coast. Eng. 2018, 138, 49–65. [Google Scholar] [CrossRef]
- Eggers, K.W.H. An Assessment of Some Experimental Methods for Determining the Wavemaking Characteristics of a Ship Form. Trans. SNAME 1967, 75, 112–157. [Google Scholar]
- Brizzolara, S.; Bruzzone, D.; Cassella, P.; Scamardella, I.; Zotti, I. Wave Resistance and Wave Patterns for High-Speed Crafts; Validation of Numerical Results by Model Test. In Proceedings of the 22nd Symposium on Naval Hydrodynamics, Washington, DC, USA, 9–14 August 1998; pp. 69–83. [Google Scholar]
- Janson, C.E.; Spinney, D. A Comparison of Four Wave Cut Analysis Methods for Wave Resistance Prediction. Ship Technol. Res. 2004, 51, 173–184. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lambert, W.; Brizzolara, S.; Woolsey, C. The Effect of a Linear Free Surface Boundary Condition on the Steady-State Wave-Making of Shallowly Submerged Underwater Vehicles. J. Mar. Sci. Eng. 2023, 11, 981. https://doi.org/10.3390/jmse11050981
Lambert W, Brizzolara S, Woolsey C. The Effect of a Linear Free Surface Boundary Condition on the Steady-State Wave-Making of Shallowly Submerged Underwater Vehicles. Journal of Marine Science and Engineering. 2023; 11(5):981. https://doi.org/10.3390/jmse11050981
Chicago/Turabian StyleLambert, William, Stefano Brizzolara, and Craig Woolsey. 2023. "The Effect of a Linear Free Surface Boundary Condition on the Steady-State Wave-Making of Shallowly Submerged Underwater Vehicles" Journal of Marine Science and Engineering 11, no. 5: 981. https://doi.org/10.3390/jmse11050981
APA StyleLambert, W., Brizzolara, S., & Woolsey, C. (2023). The Effect of a Linear Free Surface Boundary Condition on the Steady-State Wave-Making of Shallowly Submerged Underwater Vehicles. Journal of Marine Science and Engineering, 11(5), 981. https://doi.org/10.3390/jmse11050981





