Hydrodynamic Shape Design and Self-Propulsion Analysis of a Hybrid-Driven AUG
Abstract
1. Introduction
2. Numerical Method
2.1. Governing Equations
2.2. Turbulence Model
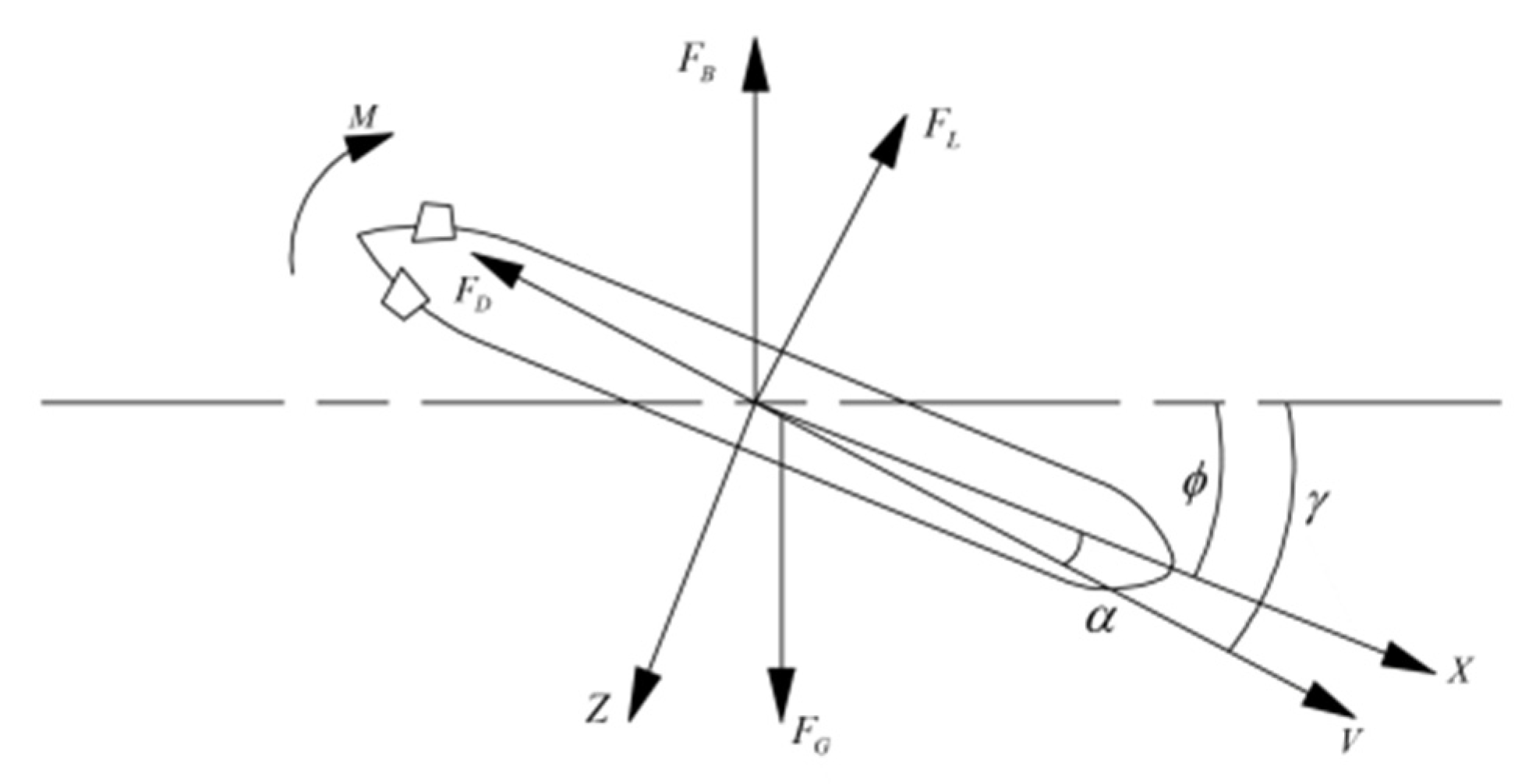
2.3. Dimensionless Parameters for Simulation and Test of AUG
2.4. Dimensionless Parameters for Simulation and Test of Propeller
2.5. Self-Propulsion Parameters of the AUG
3. Hydrodynamic Shape Optimization Design of the Hybrid-Driven AUG
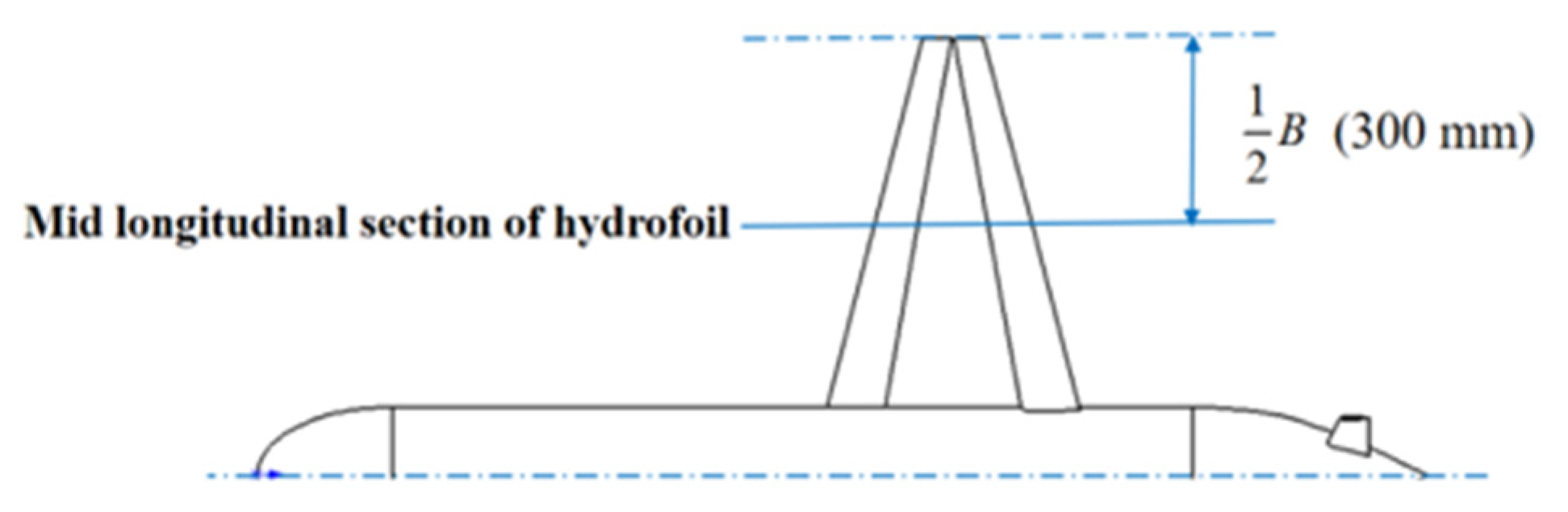
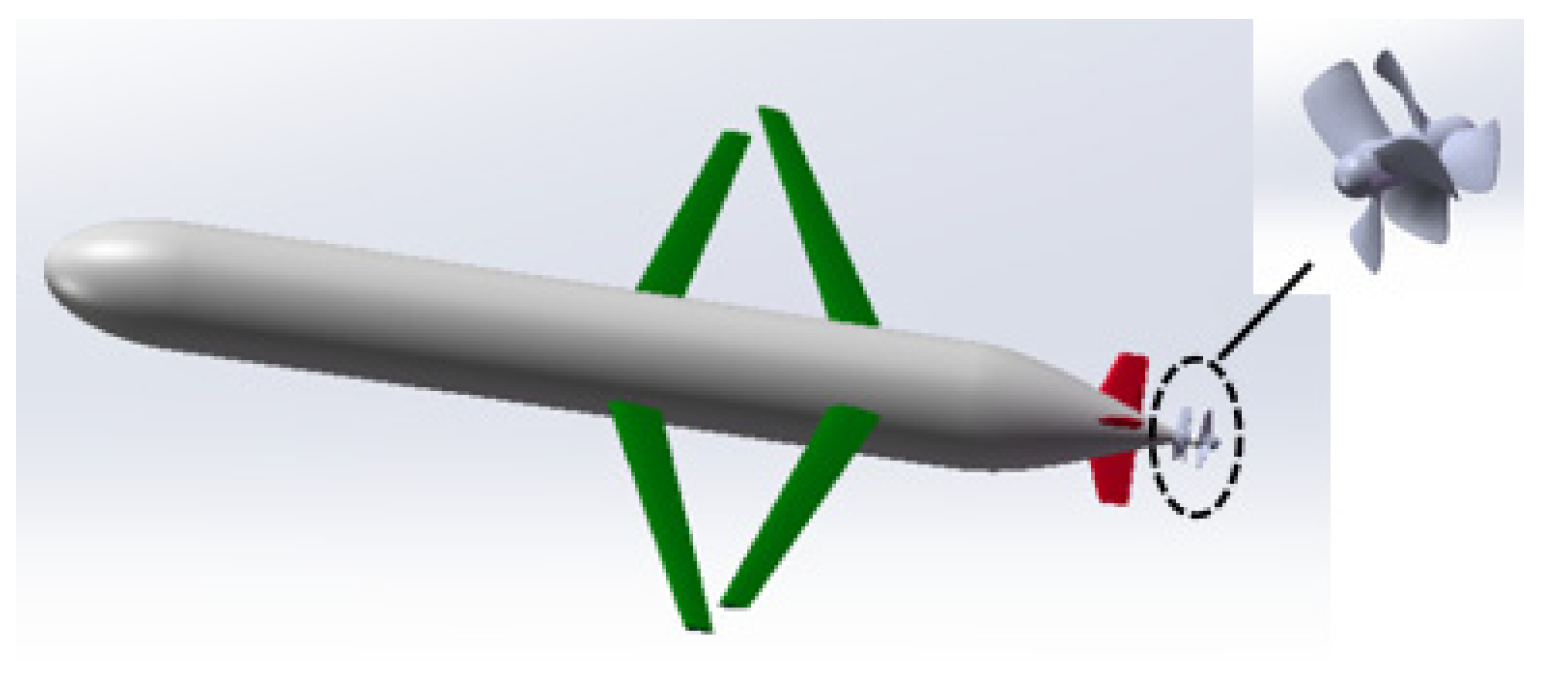
3.1. Main Dimension Parameters of the Hybrid-Driven AUG
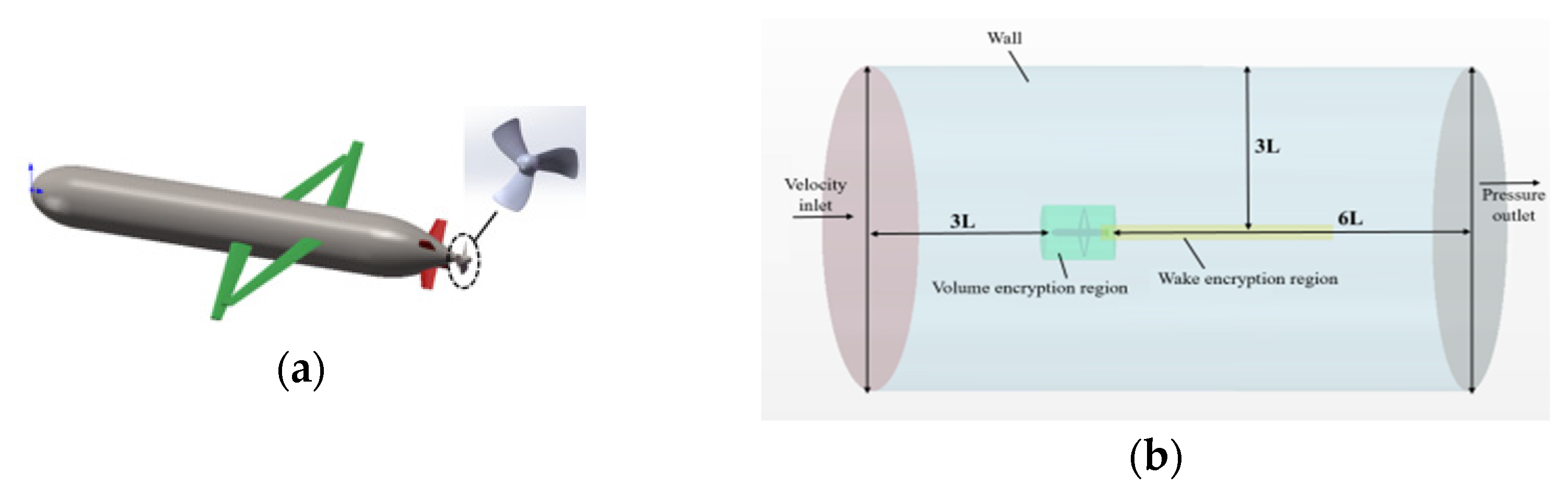
3.2. Simulation Settings
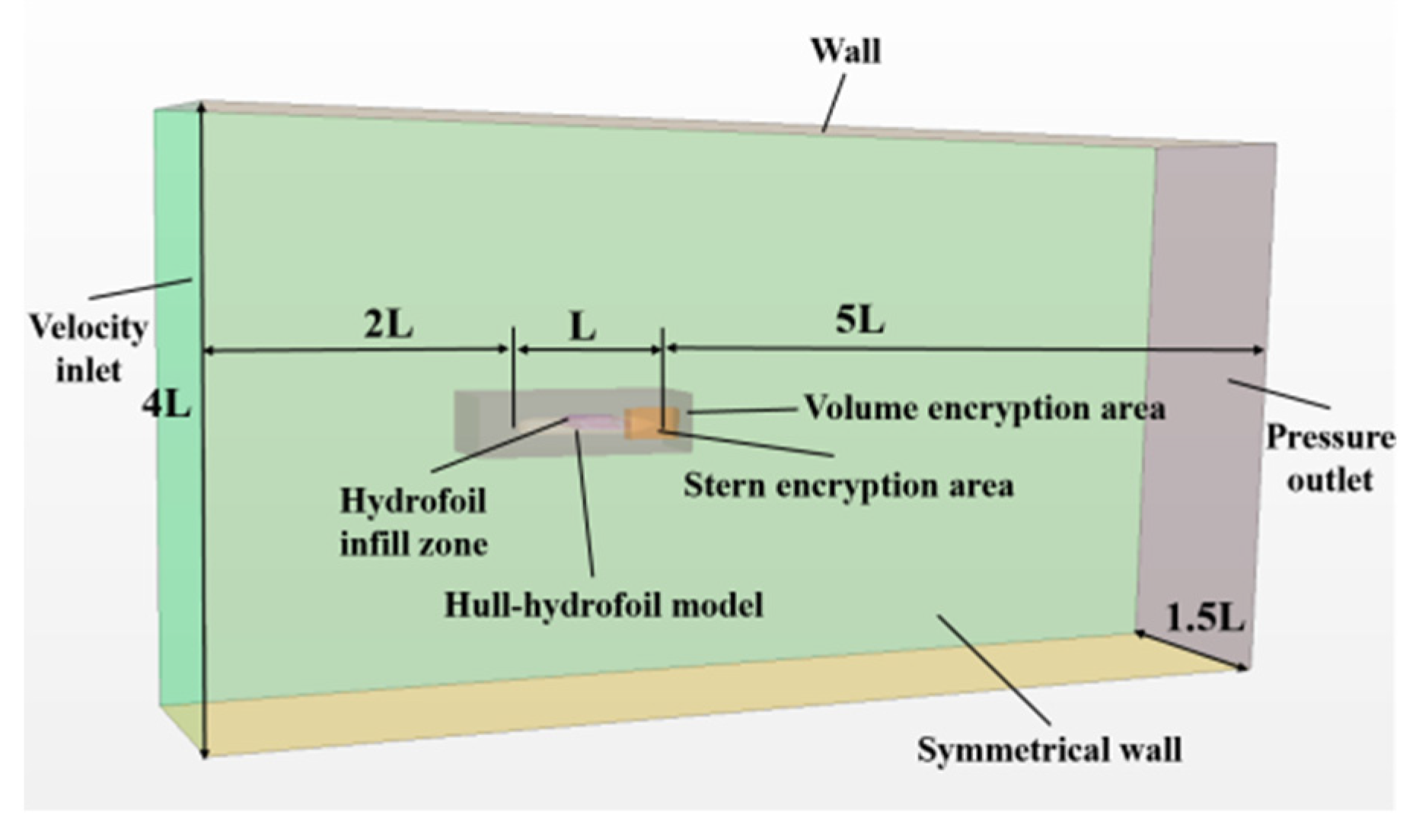
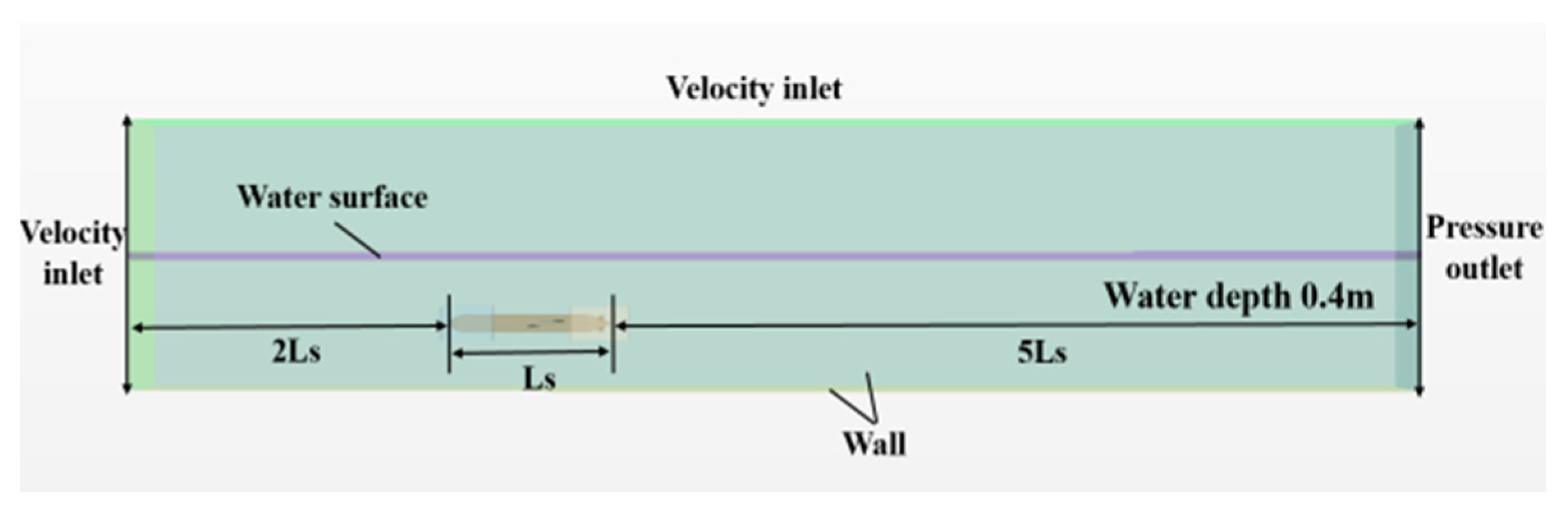
3.2.1. Calculation Domain
3.2.2. Mesh Strategy
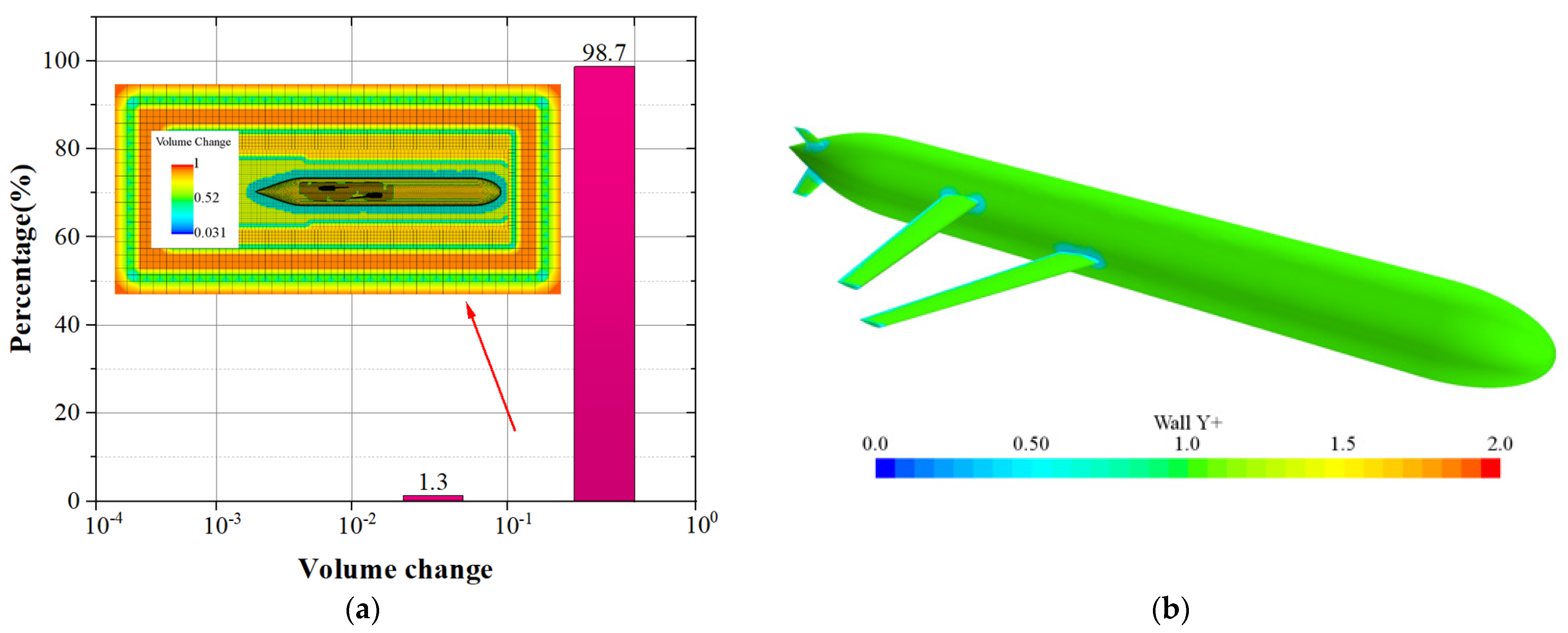
3.2.3. Mesh Independence Analysis
3.3. Type Selection Design for Hull Line
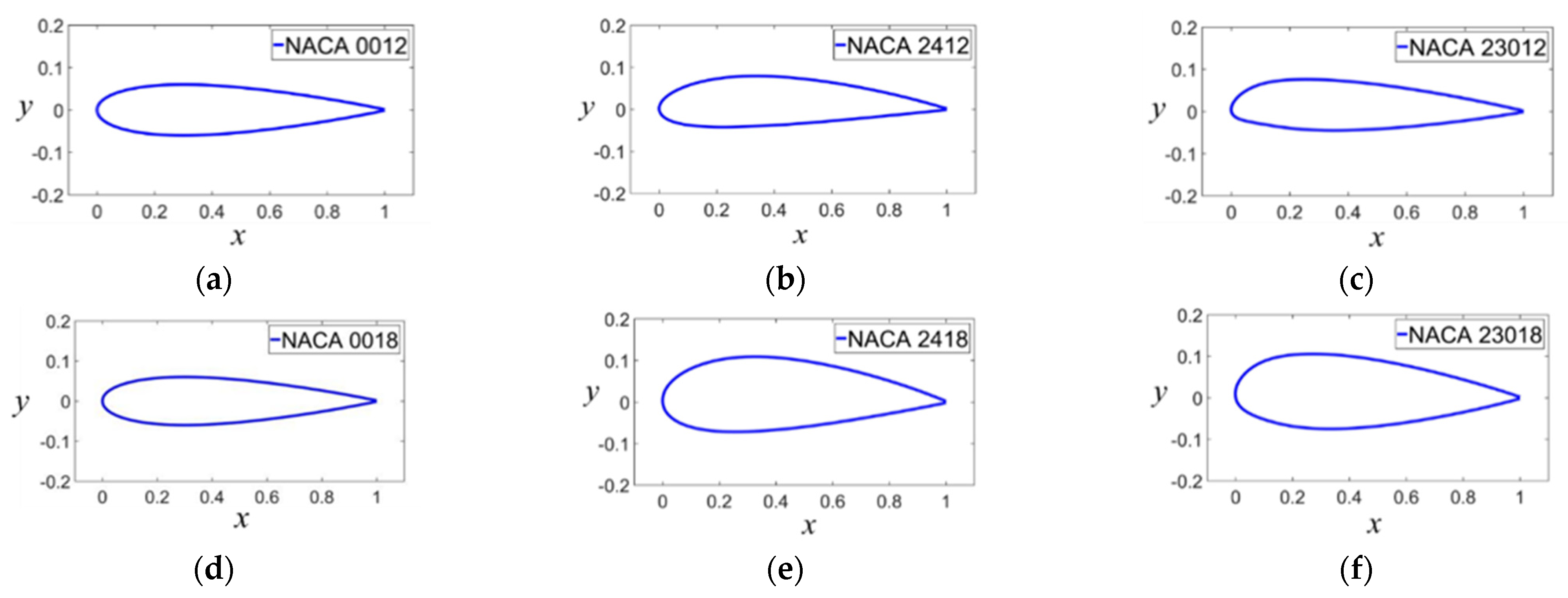
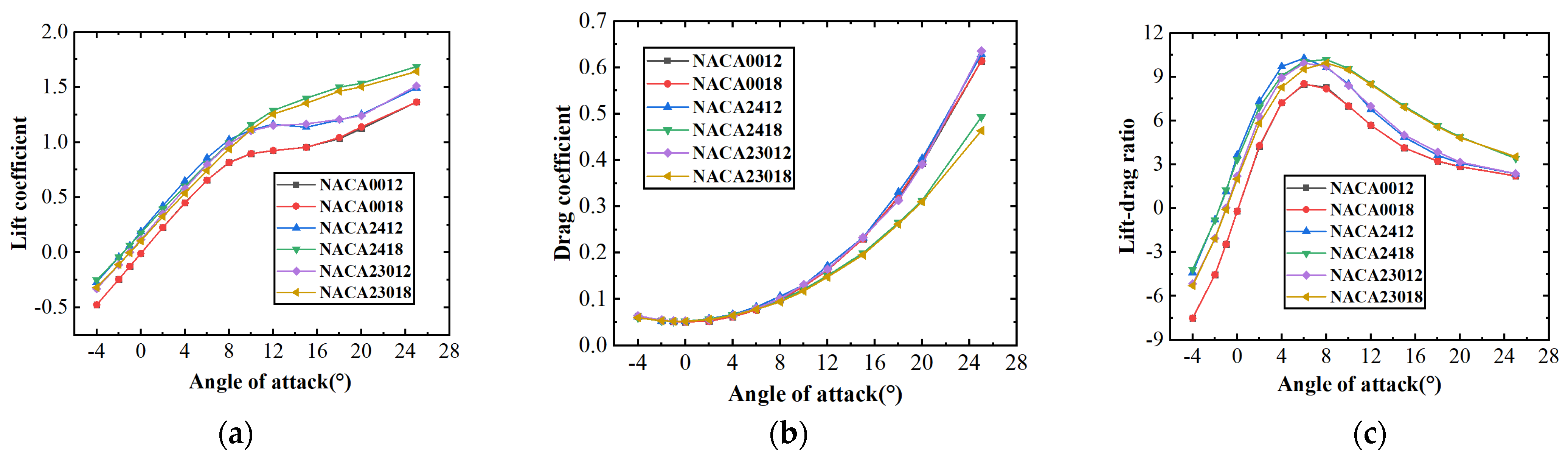
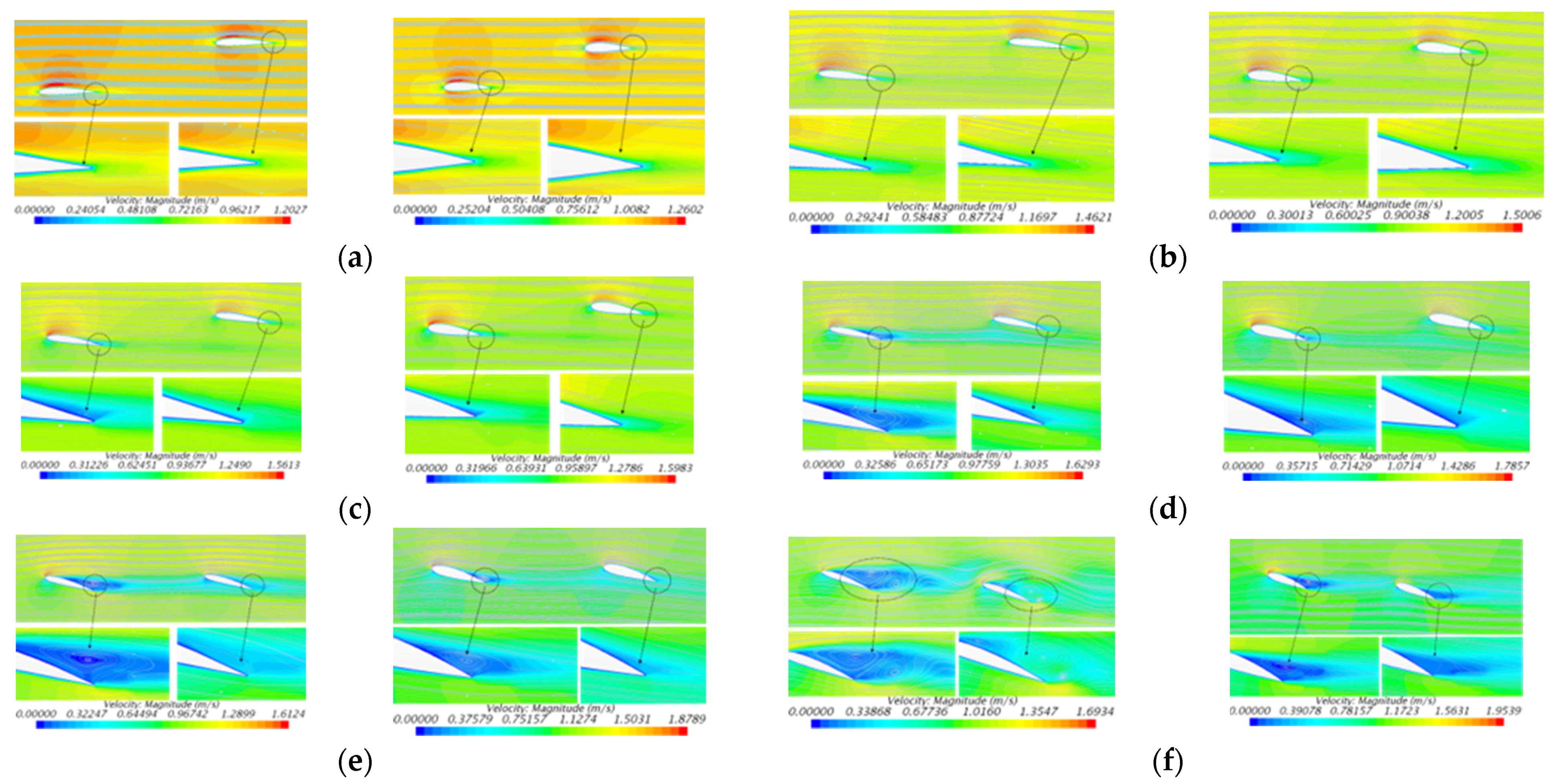
3.4. Selection and Design of Hydrofoil Profile
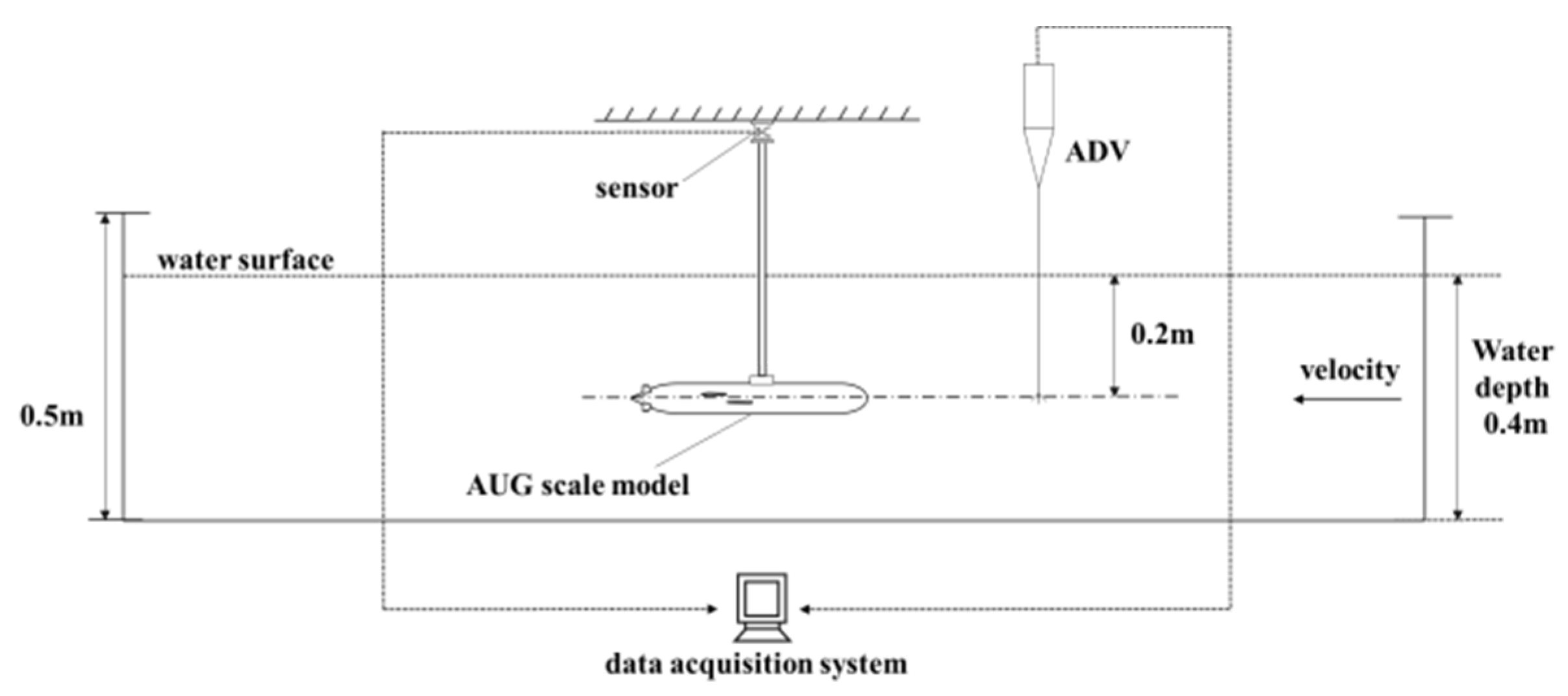
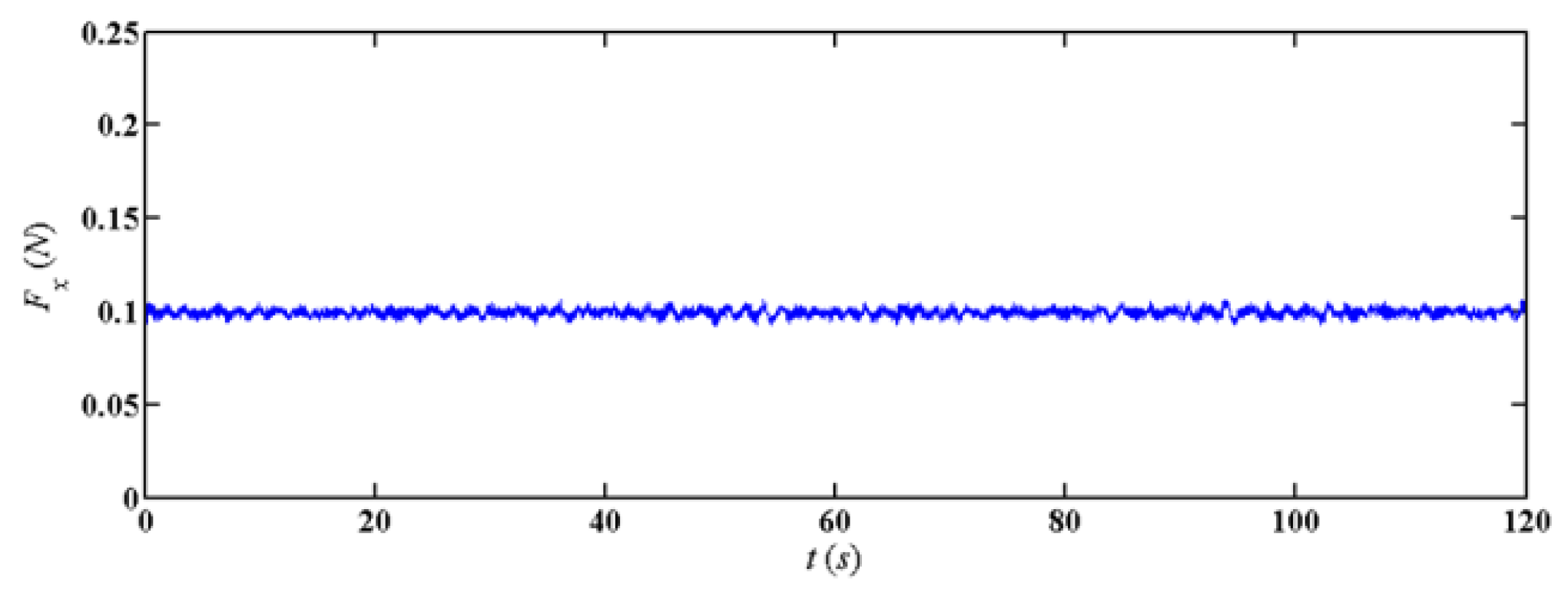
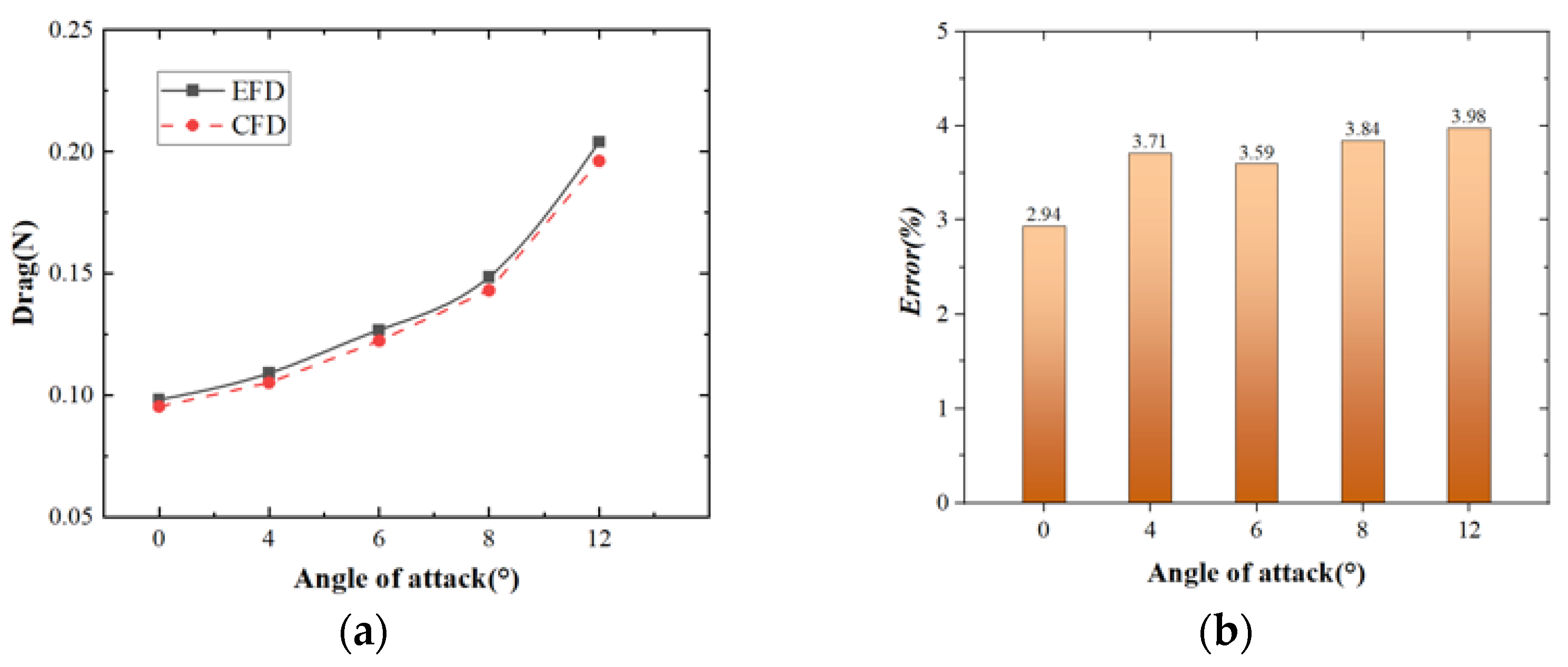
3.5. Verification of the Numerical Simulation for the Hybrid-Driven AUG without Propeller
4. Self-Propulsion Analysis of the Hybrid-Driven AUG
4.1. Test and Simulation of a Single Propeller
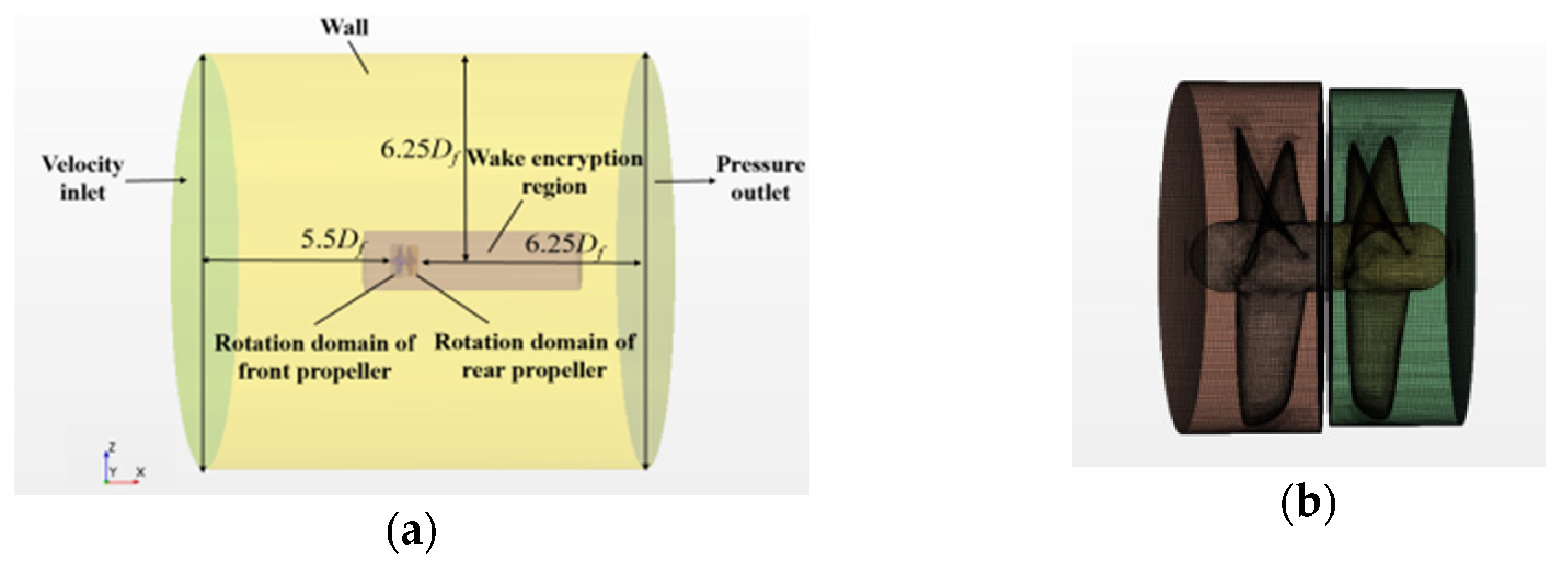
4.2. Simulation of 715 CRP
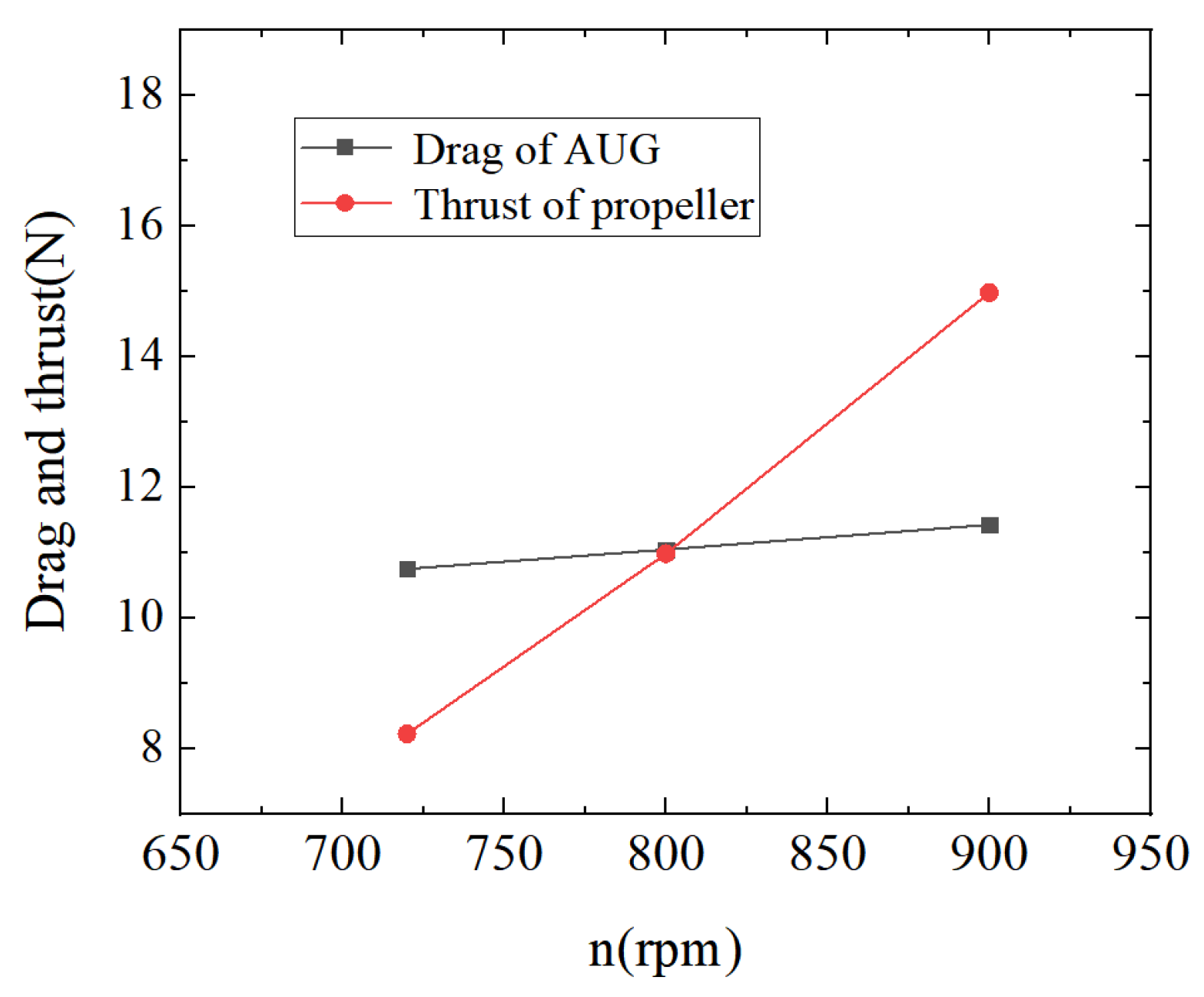
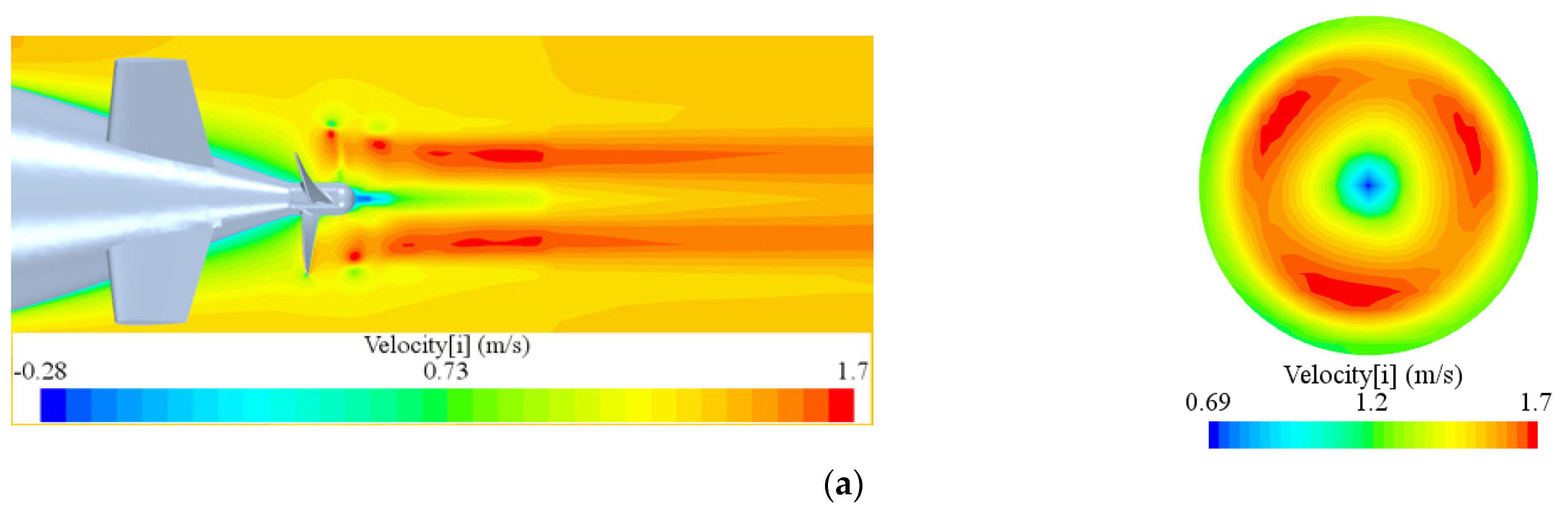
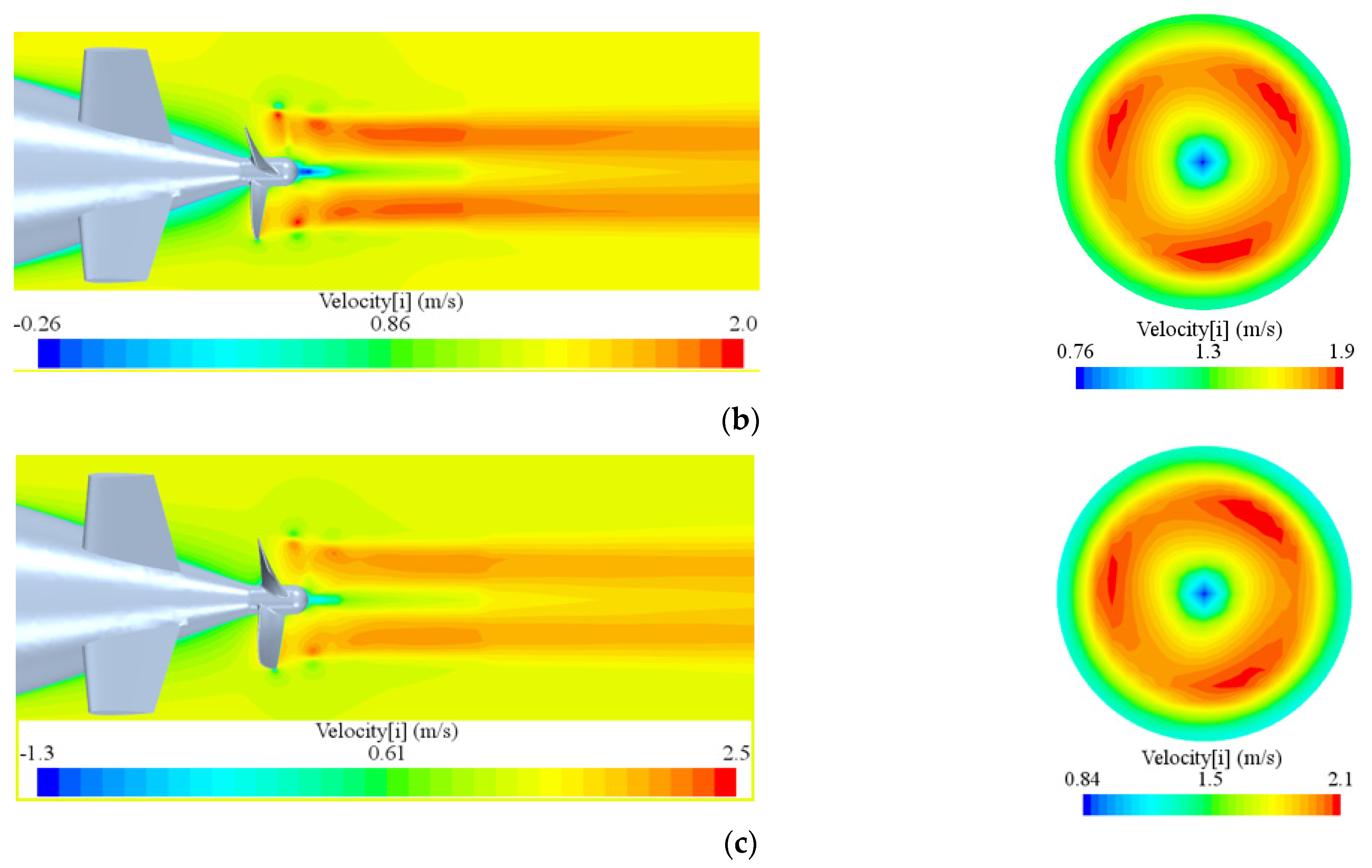
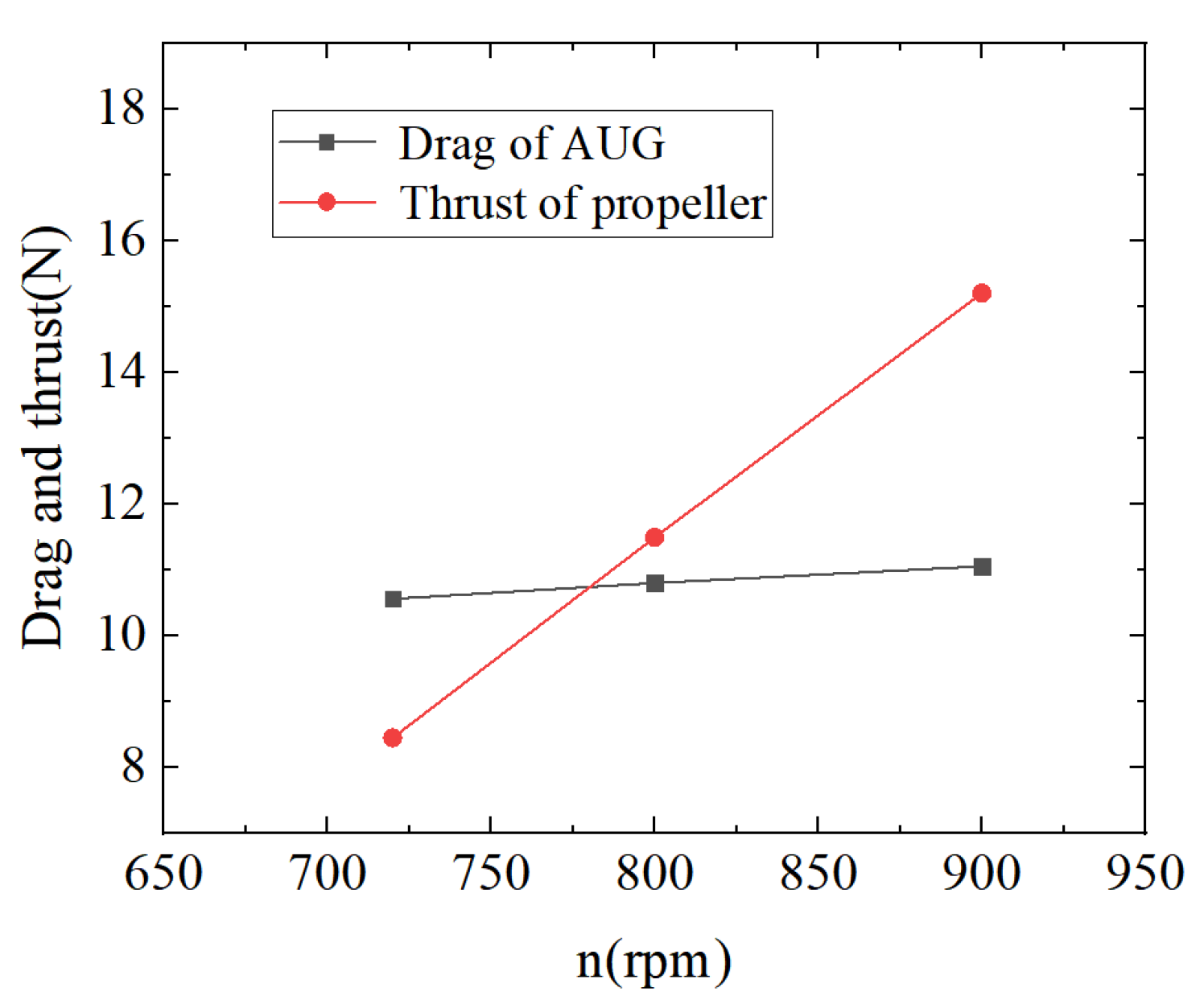
4.3. Self-Propulsion Simulation of the Hybrid-Driven AUG with the Single Propeller
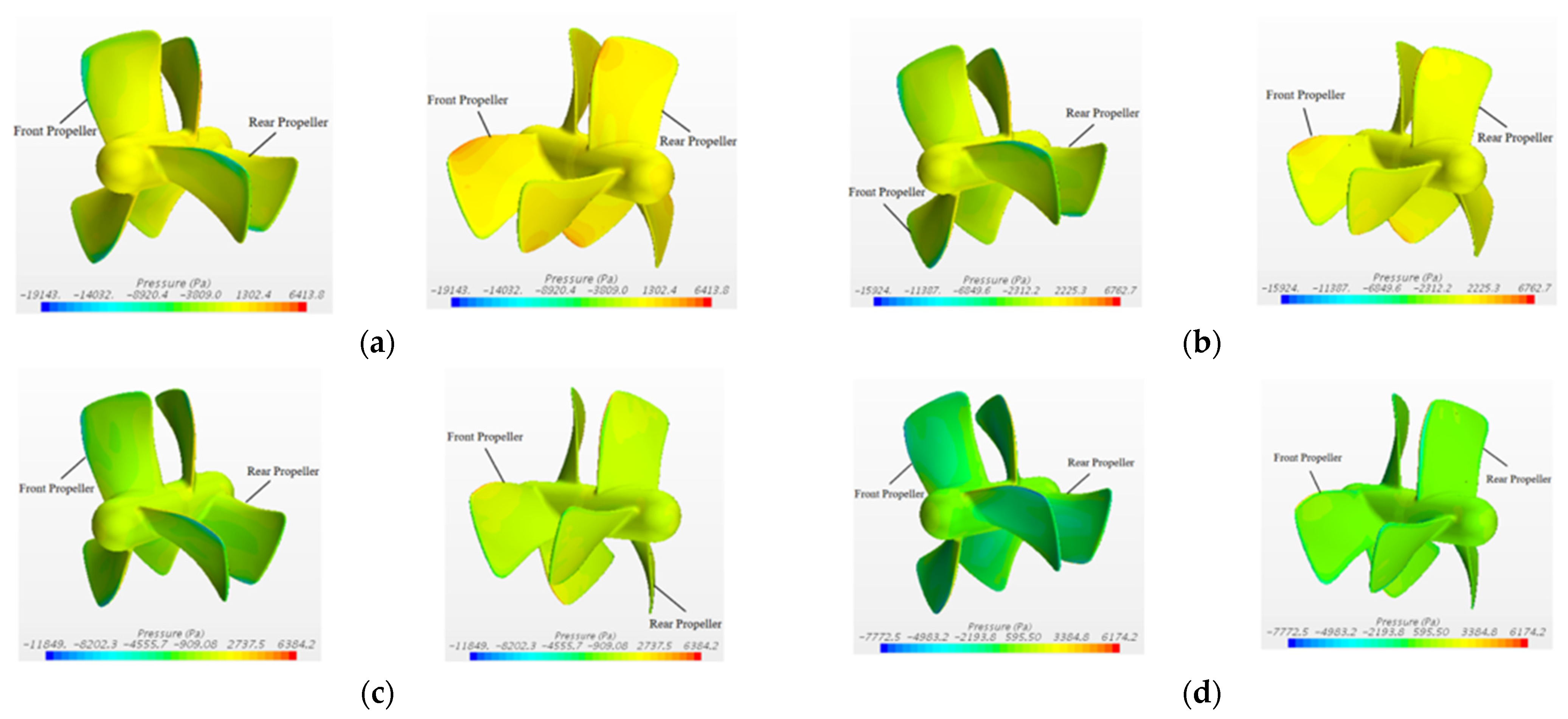
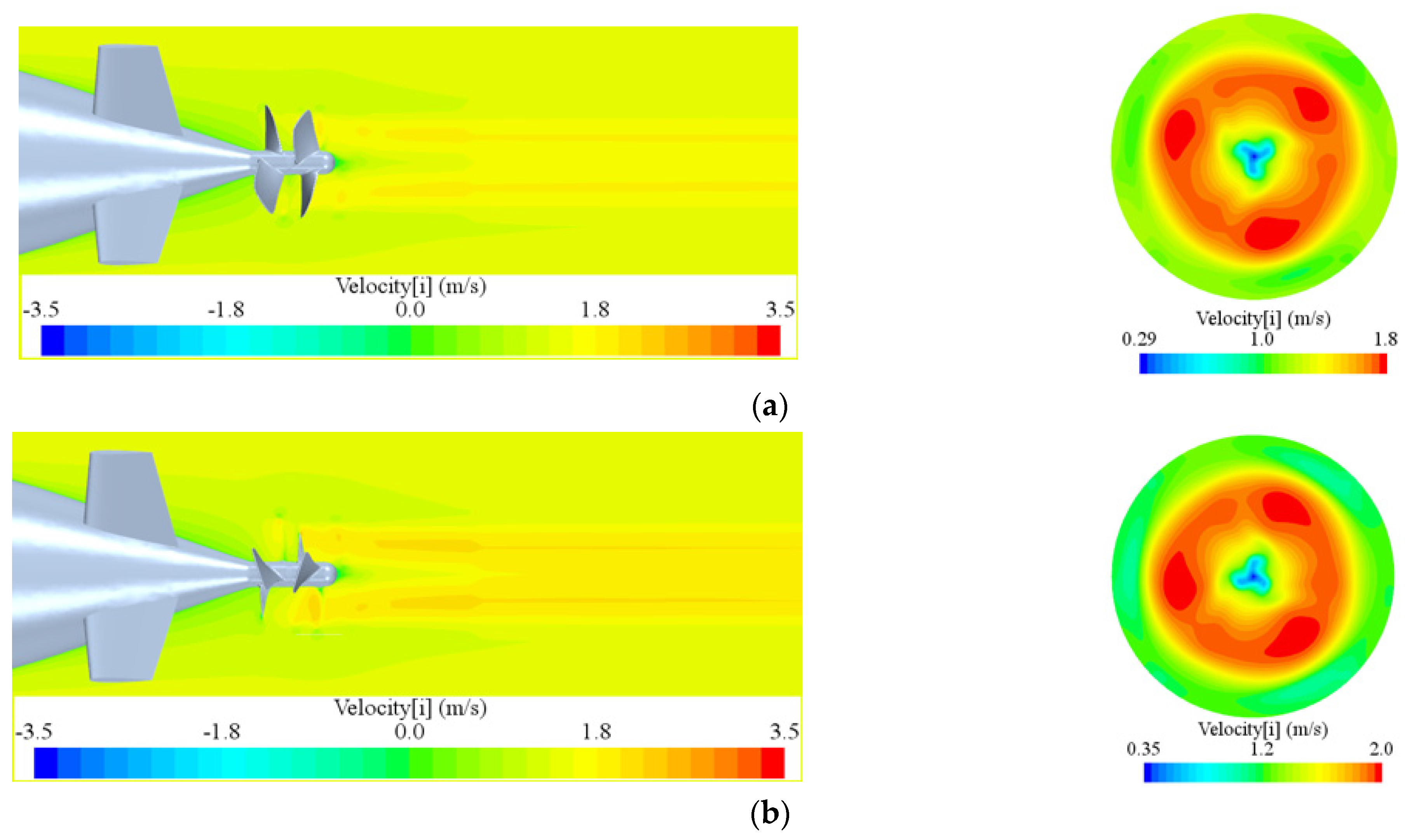
4.4. Self-Propulsion Simulation of the Hybrid-Driven AUG with the CRP
4.5. The Self-Propulsion Comparation of AUGs with Different Hull Lines Matched with CRP
5. Conclusions
- In this paper, numerical simulations of the rhomboid wings with different hydrodynamic shapes were conducted under the condition of straight-line motion and oblique motions (i.e., the gliding motion). Comparing the hydrodynamic coefficients, the hydrodynamic shape of the rhomboid wing was optimized. Through comprehensive comparison, the AUG with a hull line shape (p = 2; θ = 15°) and hydrofoil NACA2418 presented the best performance, where the lift–drag ratio increased by 22.5% compared with the initial model at an 8° angle of attack for the designed working condition.
- The drag tests and numerical simulations of the scale model of the hybrid-driven AUG with the optimized hydrodynamic shape were carried out without the propeller. Compared with the experimental results, the reliability of the numerical method was verified.
- The open water performance tests and corresponding simulations of the Whale715 propeller were conducted to verify the CFD simulation results in this paper. The results showed that the SST k-ω turbulence model could accurately predict the propeller hydrodynamic performance.
- Based on the open water simulations and tests for the Whale715 single propeller and its relative contra-rotating propeller, the self-propulsion performance of the hybrid-driven AUG with the single propeller and CRP was analyzed, respectively, at the designed speed. The results showed that the overall torque of the hybrid-driven AUG with the CRP was notably reduced by 92.3% compared with that of the AUG with a single propeller. Due to the greater thrust output, the hybrid-driven AUG with the CRP could reach the self-propulsion point at a lower propeller rotation speed. In addition, the self-propulsion performance with the CRP for the AUGs with various hull lines was compared, which indicated that the hybrid-driven AUG under the optimization design mainly based on the premise of the gliding motion might not show an excellent behavior during the self-propulsion motion with the straight-line route.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Parameter | Unit | Symbol | Parameter | Unit |
| J | Advance speed coefficient | [-] | L | Effective maximum length of AUG | [m] |
| KT | Thrust coefficient | [-] | Ls | Effective maximum length of S-AUG | [m] |
| KQ | Torque coefficient | [-] | Dh | Maximum diameter of the hull | [m] |
| T | Thrust of propeller | [N] | B | Wingspan of the hydrofoil | [m] |
| Q | Torque of propeller | [N-m] | a | Length of the bow | [m] |
| TB | Propeller thrust under the self-propulsion condition | [N] | b | Length of AUG parallel middle body | [m] |
| Q0 | Propeller torque in open water test | [N-m] | c | Length of the stern | [m] |
| QB | Propeller torque under the self-propulsion condition | [N-m] | Ct | Chord length of the hydrofoil tip | [m] |
| ηo | Propulsion efficiency of propeller in the open water condition | [-] | Cr | Chord length of the hydrofoil root | [m] |
| ηR | Shaft transmission efficiency | [-] | p | Sharpness factor | [-] |
| ηH | Hull efficiency | [-] | θ | Angle of run | [°] |
| PB | Brake horsepower | [W] | α | Angle of attack | [°] |
| PE | Effective horsepower | [W] | S | Wet surface area of the hydrofoil | [m2] |
| PS | Motor horsepower | [W] | S-AUG | Scale model of AUG | [-] |
| D | Propeller diameter | [m] | CD | Drag coefficient | [-] |
| Df | Diameter of front propeller | [m] | CL | Lift coefficient | [-] |
| Da | Diameter of rear propeller | [m] | FD | Drag of AUG | [N] |
| n | Rotation speed of propeller | [rps] | FL | Lift of AUG | [N] |
| VA | Advance speed of propeller | [m/s] | ▽ | Displacement of AUG | [m3] |
| Tf | Thrust of front propeller | [N] | V | Navigation speed of AUG | [m/s] |
| Ta | Thrust of rear propeller | [N] | ρ | Water density | [kg/m3] |
| Tc | Thrust of CRP | [N] | KTf | Thrust coefficient of front propeller | [-] |
| Qf | Torque of front propeller | [N-m] | KTa | Thrust coefficient of rear propeller | [-] |
| Qa | Torque of rear propeller | [N-m] | KQf | Torque coefficient of front propeller | [-] |
| Qc | Torque of CRP | [N-m] | KQa | Torque coefficient of rear propeller | [-] |
| U | Voltage | [V] | QPC | Quasi-propulsive coefficient | [-] |
| I | Current | [A] | Pressure | Pressure distribution of blade surface | [Pa] |
References
- Rudnick, D.L.; Davis, R.E.; Eriksen, C.C.; Fratantoni, D.M.; Perry, M.J. Underwater Glider for Ocean Research. Mar. Technol. Soc. J. 2004, 38, 73–84. [Google Scholar] [CrossRef]
- Liu, Y.J.; Liu, J.; Pan, G.; Huang, Q.G.; Guo, L.M. Dynamic Analysis of an Autonomous Underwater Glider with Single- and Two-Stage Vibration Isolators. J. Mar. Sci. Eng. 2022, 10, 162. [Google Scholar] [CrossRef]
- Li, Y.C.; Ma, Z. Numerical investigation on novel conceptual design of hybrid-driven autono-mous underwater glider with active twin flapping foils. Ocean Eng. 2020, 214, 107867. [Google Scholar] [CrossRef]
- Li, Y.C.; Hu, J.X.; Zhao, Q.Z.; Pan, Z.Y.; Ma, Z. Hydrodynamic Performance of Autonomous Underwater Gliders with Active Twin Undulatory Wings of Different Aspect Ratios. J. Mar. Sci. Eng. 2020, 8, 476. [Google Scholar] [CrossRef]
- Shen, X.R.; Wang, Y.H.; Yang, S.Q.; Liang, Y.; Li, H.Z. Development of underwater gliders: An overview and prospect. J. Unmanned Undersea Syst. 2018, 26, 89–106. [Google Scholar]
- Ebata, S.; Yasuda, T.; Minagawa, H.; Miyamoto, Y.; Satofuka, N. A Study of Cross-Sectional Shape of Wing for Underwater Glider at Low Reynolds Number Region. Trans. Jpn. Soc. Mech. Eng. 2013, 79, 1886–1899. [Google Scholar] [CrossRef]
- Singh, Y.; Bhattacharyya, S.K.; Idichandy, V.G. CFD Approach to Modelling, Hydrodynamic Analysis and Motion Characteristics of a Laboratory Underwater Glider with Experimental Results. J. Ocean Eng. Sci. 2017, 2, 90–119. [Google Scholar] [CrossRef]
- Chen, C.W.; Feng, Z.; Liang, X. Hydrodynamic Analysis of Underwater Glider with Diamond Wing in Unsteady and Nonuniform Flow Field. J. Mar. Sci. Technol. 2018, 26, 787–802. [Google Scholar]
- Shankar, R.V.S.; Vijayakumar, R. Numerical Study of the Effect of Wing Position on Autonomous Underwater Glider. Def. Sci. J. 2020, 70, 214–220. [Google Scholar] [CrossRef]
- Jay, A. The potential for Autonomous Underwater Gliders in large lake research. J. Great Lakes Res. 2013, 39, 8–13. [Google Scholar]
- Paul, M.K.; Tom, H.; Joel, H. Autonomous underwater glider observations in southern Lake Ontario and Niagara River plume. Aquat. Ecosyst. Health Manag. 2022, 25, 102–113. [Google Scholar]
- Jenkins, S.A.; Humphreys, D.E.; Sherman, J. Underwater Glider System Study; Scripps Institution of Oceanography Technical Report; Office of Naval Research: Arlington, VA, USA, 2003. [Google Scholar]
- Madureira, L.; Sousa, A.; Sousa, J.; Gonçalves, G. Low Cost Autonomous Underwater Vehicles for New Concepts of Coastal Field Studies. J. Coast. Res. 2009, 2, 59–62. [Google Scholar]
- Bachmayer, R.; Leonard, N.E.; Gravery, J.; Fiorelli, E.; Paley, D. Underwater gliders: Recent developments and future applications. In Proceedings of the IEEE Proceeding of International Symposium on Underwater Technology, Taipei, Taiwan, 20 May 2004. [Google Scholar]
- Griffiths, G.; Jones, C.P.; Ferguson, J.; Bose, N. Undersea glider. J. Ocean. Technol. 2007, 2, 64–75. [Google Scholar]
- Yamamoto, I. Research and development of past, present, and future AUV technologies. Under-Water Technol. 2006, 69, 28–29. [Google Scholar]
- Wood, S.; Allen, T.; Kuhn, S. Autonomous Underwater Vehicle: Powered Glider; Technical Report; Florida Institute of Technology: Melbourne, FL, USA, 2007. [Google Scholar]
- Wood, S.; Allen, T.; Kuhn, S.; Caldwell, J. The development of an autonomous underwater powered glider for deep-sea biological, chemical and physical oceanography. In Proceedings of the OCEANS 2007—Europe, Aberdeen, UK, 18–21 June 2007; pp. 1–6. [Google Scholar]
- Jones, C.; Allsup, B.; Webb, D. Glider Expanding the Capabilities. Mar. Technol. Soc. 2011, 58. [Google Scholar]
- Liu, F.; Wang, Y.H.; Wang, S.X. Development of the Hybrid Underwater Glider Petrel-II. Sea Technol. 2014, 55, 51–54. [Google Scholar]
- Nathan, C.; Pablo, M.C. Submarine propeller computations and application to self-propulsion of DARPA Sub-off. Ocean Eng. 2013, 60, 68–80. [Google Scholar]
- Rattanasiri, P.; Wilson, P.A.; Phillips, A.B. Numerical investigation of a pair of self-propelled AUVs operating in tandem. Ocean Eng. 2015, 100, 126–137. [Google Scholar] [CrossRef]
- Zhang, R.C.; Dong, X.J.; Wang, Z.; Huang, Y.; Yu, J.C. Numerical design and validation of propeller for long-range AUV. Shipbuild. China 2019, 60, 147–159. [Google Scholar]
- Liu, J.X.; Wang, M.; Yu, F.; Gao, S.; Yan, T.H.; He, B. Numerical study on the hull–propeller inter-action of autonomous underwater vehicle. Ocean Eng. 2023, 271, 113777. [Google Scholar] [CrossRef]
- Huang, Y.S.; Dong, X.Q. Design of wake-adapted contra-rotating propellers for high-speed underwater vehicles. Appl. Ocean. Res. 2019, 2, 91–97. [Google Scholar] [CrossRef]
- Kingan, M.J.; Parry, A.B. Acoustic theory of the many-bladed contra-rotating propeller: The effects of sweep on noise enhancement and reduction. J. Sound Vib. 2020, 3, 468–472. [Google Scholar] [CrossRef]
- Wang, Z.; Xiong, Y. Effect of Time Step Size and Turbulence Model on the Open Water Hydrodynamic Performance Prediction of Contra-Rotating Propellers. China Ocean Eng. 2013, 27, 193–204. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Xiong, Y.; Qi, W.J. Numerical prediction of contra-rotating propellers’ open water performance. J. Huazhong Univ. Ence. Technol. 2012, 40, 77–80+88. [Google Scholar]
- Hu, J.; Wang, Y.Z.; Zhang, W.P.; Chang, X.; Zhao, W. Tip vortex prediction for contra-rotating propeller using large eddy simulation. Ocean Eng. 2019, 194, 106410.1–106410.17. [Google Scholar] [CrossRef]
- Paik, K.J.; Hwang, S.; Jung, J.; Lee, T.; Lee, T.T.; Ahn, H.; Van, S.H. Investigation on the wake evolution of contra-rotating propeller using RANS computation and SPIV measurement. Int. J. Nav. Archit. Ocean Eng. 2015, 7, 595–609. [Google Scholar] [CrossRef]
- He, D.; Wan, D.; Yu, X. Numerical Investigations of Open-Water Performance of Contra-Rotating Propellers. In Proceedings of the 27th International Ocean and Polar Engineering Conference, San Francisco, CA, USA, 25–30 June 2017. [Google Scholar]
- Tang, J.P. ANSYS FLUNET 16.0 Learning Manual; People’s Posts and Telecommunications Press: Jiangsu, China, 2016; pp. 14–37. [Google Scholar]
- Wang, F.J. Principle and Application of CFD Software for Computational Fluid Dynamics Analysis; Qsinghua University Press: Beijing, China, 2004; pp. 12–18. [Google Scholar]
- Zhou, L.D. Research Progress and Application in Ship and Ocean Engineering Computer Fluid Dynamics. Acta Aerodyn. Amica Sin. 1998, 1, 122–131. [Google Scholar]
- Sun, C.; Song, B.; Peng, W. Parametric Geometric Model and Shape Optimization of an Underwater Glider with Blended-wing-body. Int. J. Nav. Archit. Ocean Eng. 2015, 7, 995–1006. [Google Scholar] [CrossRef]
- Divsalar, K.; Shafaghat, R.; Farhadi, M.; Alamian, R. Numerical Simulation of Hydrodynamic Properties of Alex Type Gliders. Int. J. Eng. 2020, 33, 1387–1396. [Google Scholar]
- Musa, O.; Xiong, C.; Zhou, C.; Gong, L. Assessment of the Modified Rotation/Curvature Correction SST Turbulence Model for Simulating Swirling Reacting Unsteady Flows in a Solid-fuel Ramjet Engine. Acta Astronaut. 2016, 129, 241–252. [Google Scholar] [CrossRef]
- Sheng, Z.B.; Liu, Y.Z. Ship Principle; Shanghai Jiaotong University Press: Shanghai, China, 2004; pp. 17–48. [Google Scholar]
- Ghassemi, H.; Taherinasab, M. Numerical calculations of the hydrodynamic performance of the contra-rotating propeller (CRP) for high speed vehicle. Pol. Marit. Res. 2013, 20, 13–20. [Google Scholar] [CrossRef]
- Yu, J.C.; Zhang, A.Q.; Jin, W.M.; Chen, Q.; Tian, Y.; Liu, C.J. Development and Experiments of the Sea-Wing Underwater Glider. China Ocean Eng. 2011, 25, 721–736. [Google Scholar] [CrossRef]
- Bertram, V. Practical Ship Hydrodynamics; Elsvier: Amsterdam, The Netherlands, 2012; p. 3. [Google Scholar]
- Adapco. STAR-CCM+ Theory Guide; CD-ADAPCO: Melville, NY, USA, 2021. [Google Scholar]
- Myring, D.F. A Theoretical Study of Body Drag in Subcritical Axisymmetric Flow. Aeronaut. Quartely 1976, 27, 186–194. [Google Scholar] [CrossRef]













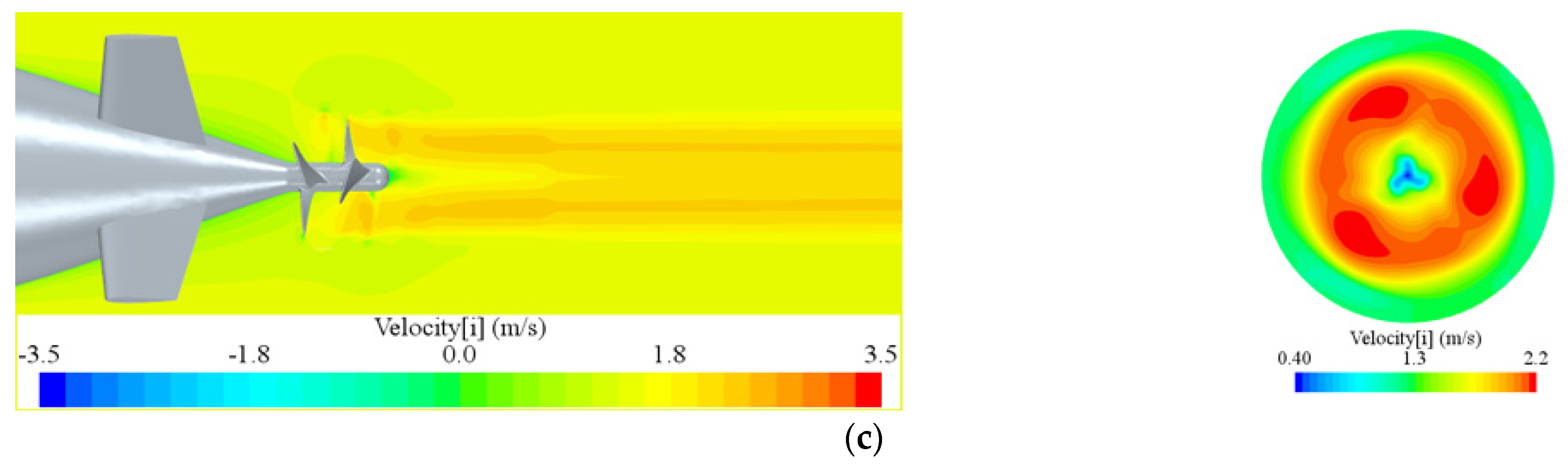
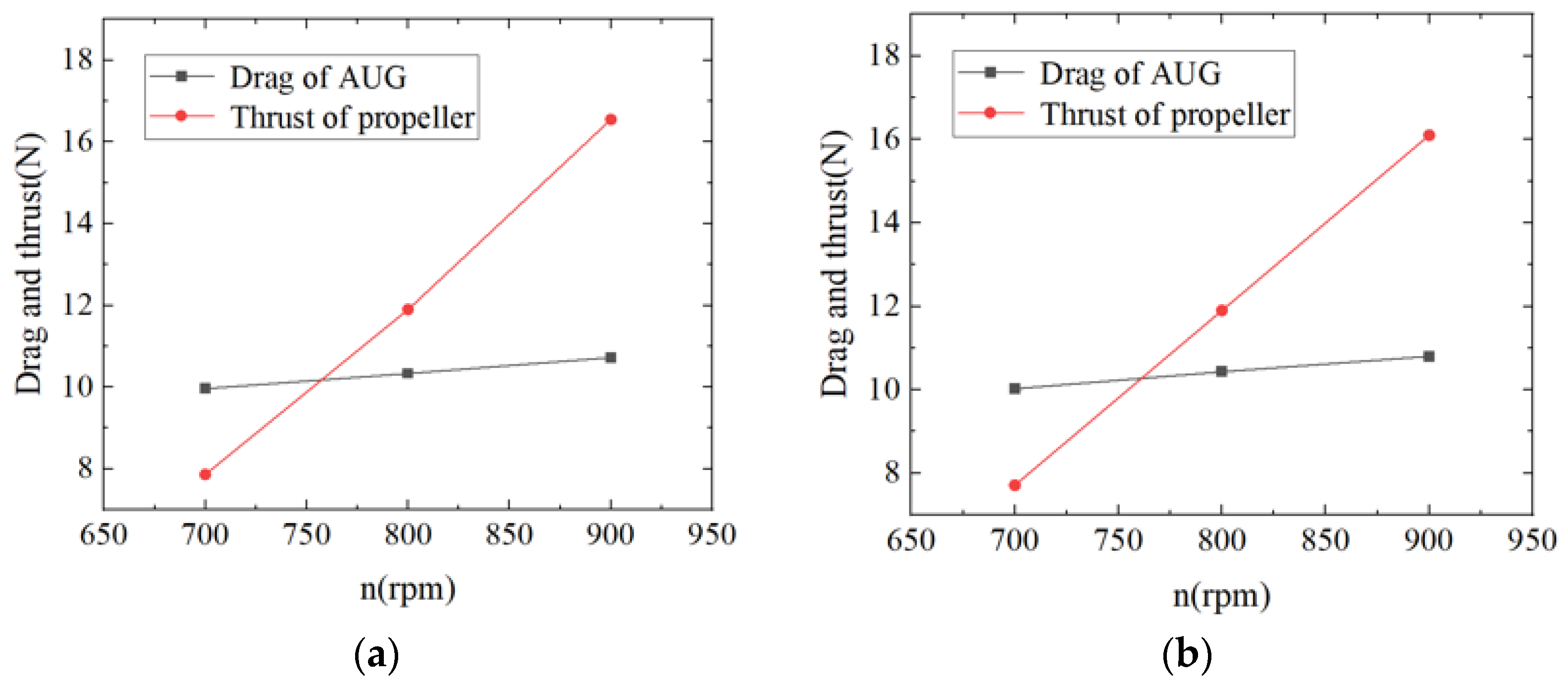
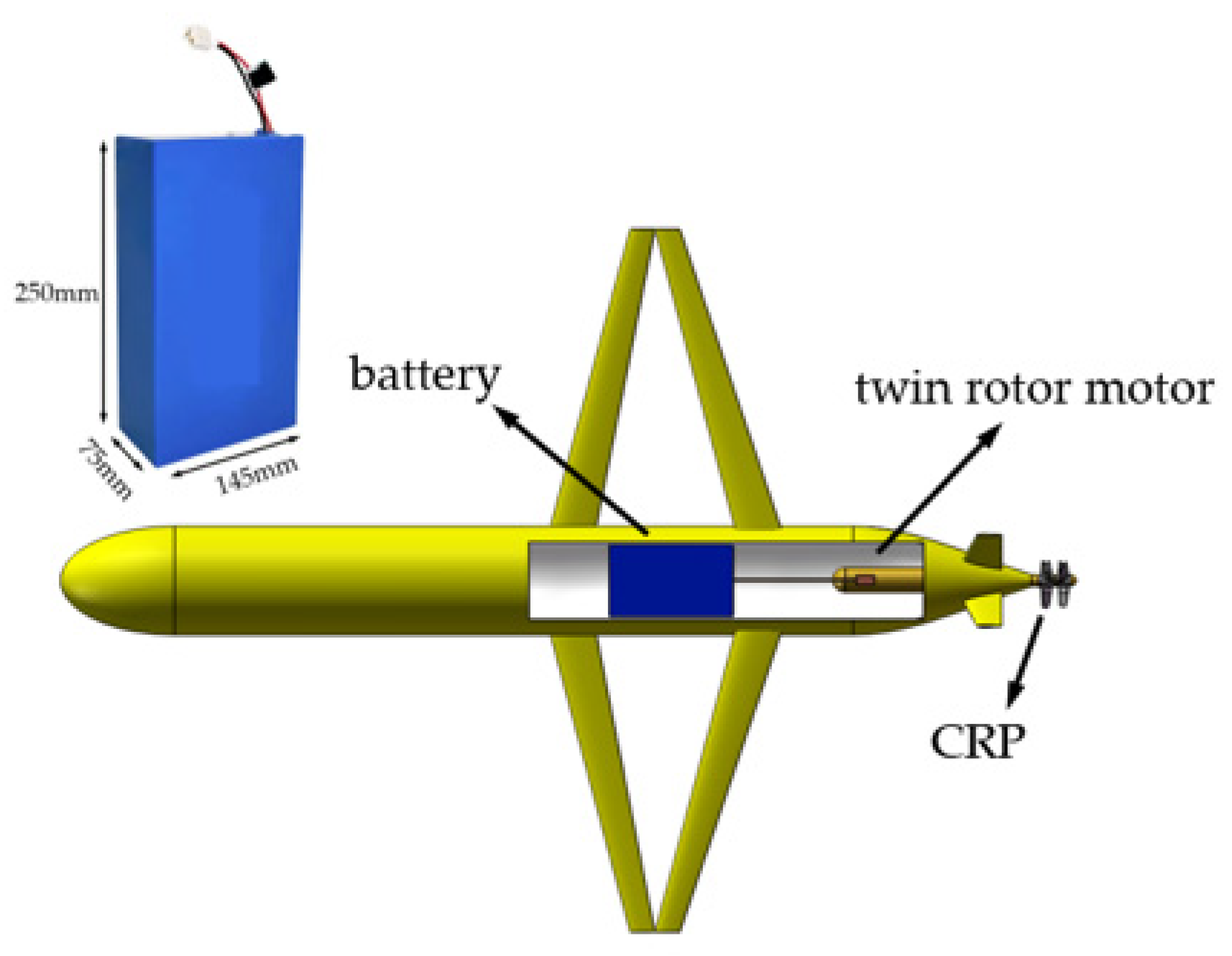
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Effective maximum length | L | 2.00 | [m] |
| Maximum diameter of the hull | Dh | 0.22 | [m] |
| Length of the bow | L1 | 0.23 | [m] |
| Length of the stern | L2 | 0.40 | [m] |
| Wingspan of the hydrofoil | B | 0.60 | [m] |
| Chord length of the hydrofoil tip | Ct | 0.05 | [m] |
| Chord length of the hydrofoil root | Cr | 0.10 | [m] |
| Wet surface area of the hydrofoil | S | 0.18 | [m2] |
| Displacement volume | ▽ | 0.0646 | [m3] |
| Parameter | Front Propeller | Rear Propeller |
|---|---|---|
| Diameter | 112 mm | 108 mm |
| Direction of rotation | Dextral rotation | Levo rotation |
| Number of blades | 3 | 3 |
| V (m/s) | n (rpm) | FD (N) | T (N) | Q (N-m) |
|---|---|---|---|---|
| 1.4 | 800 | 11.044 | 10.980 | 0.247 |
| V (m/s) | n (rpm) | FD (N) | Propeller Thrust (N) | Propeller Torque (N-m) | ||||
|---|---|---|---|---|---|---|---|---|
| Tf | Ta | T | Qf | Qa | Q | |||
| 1.4 | 780 | 10.73 | 6.11 | 4.57 | 10.68 | 0.129 | −0.110 | 0.019 |
| Hull Line | V (m/s) | VA (m/s) | n (rpm) | J | FD (N) | TB (N) | Q0 (N-m) | QB (N-m) | PE (W) | ηR | η0 | ηH | PB (W) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p = 2; θ = 15° | 1.4 | 1.040 | 780 | 0.7143 | 10.73 | 10.68 | 0.205 | 0.239 | 15.022 | 0.860 | 0.48525 | 1.350 | 26.664 |
| p = 2; θ = 25° | 1.4 | 0.995 | 755 | 0.7060 | 10.14 | 10.01 | 0.194 | 0.220 | 14.196 | 0.882 | 0.48509 | 1.425 | 23.284 |
| p = 3; θ = 25° | 1.4 | 0.999 | 760 | 0.7040 | 10.20 | 10.00 | 0.198 | 0.215 | 14.280 | 0.921 | 0.48505 | 1.429 | 22.369 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.-W.; Zhou, Z.-Y.; Chen, X.-P.; Zhou, X.-J. Hydrodynamic Shape Design and Self-Propulsion Analysis of a Hybrid-Driven AUG. J. Mar. Sci. Eng. 2023, 11, 886. https://doi.org/10.3390/jmse11040886
Chen C-W, Zhou Z-Y, Chen X-P, Zhou X-J. Hydrodynamic Shape Design and Self-Propulsion Analysis of a Hybrid-Driven AUG. Journal of Marine Science and Engineering. 2023; 11(4):886. https://doi.org/10.3390/jmse11040886
Chicago/Turabian StyleChen, Chen-Wei, Zhao-Ye Zhou, Xu-Peng Chen, and Xiao-Jing Zhou. 2023. "Hydrodynamic Shape Design and Self-Propulsion Analysis of a Hybrid-Driven AUG" Journal of Marine Science and Engineering 11, no. 4: 886. https://doi.org/10.3390/jmse11040886
APA StyleChen, C.-W., Zhou, Z.-Y., Chen, X.-P., & Zhou, X.-J. (2023). Hydrodynamic Shape Design and Self-Propulsion Analysis of a Hybrid-Driven AUG. Journal of Marine Science and Engineering, 11(4), 886. https://doi.org/10.3390/jmse11040886






