Towards Digital Twinning of Fabrication Lines in Shipyards
Abstract
1. Introduction
Brief Literature Review
2. Mathematical Modeling
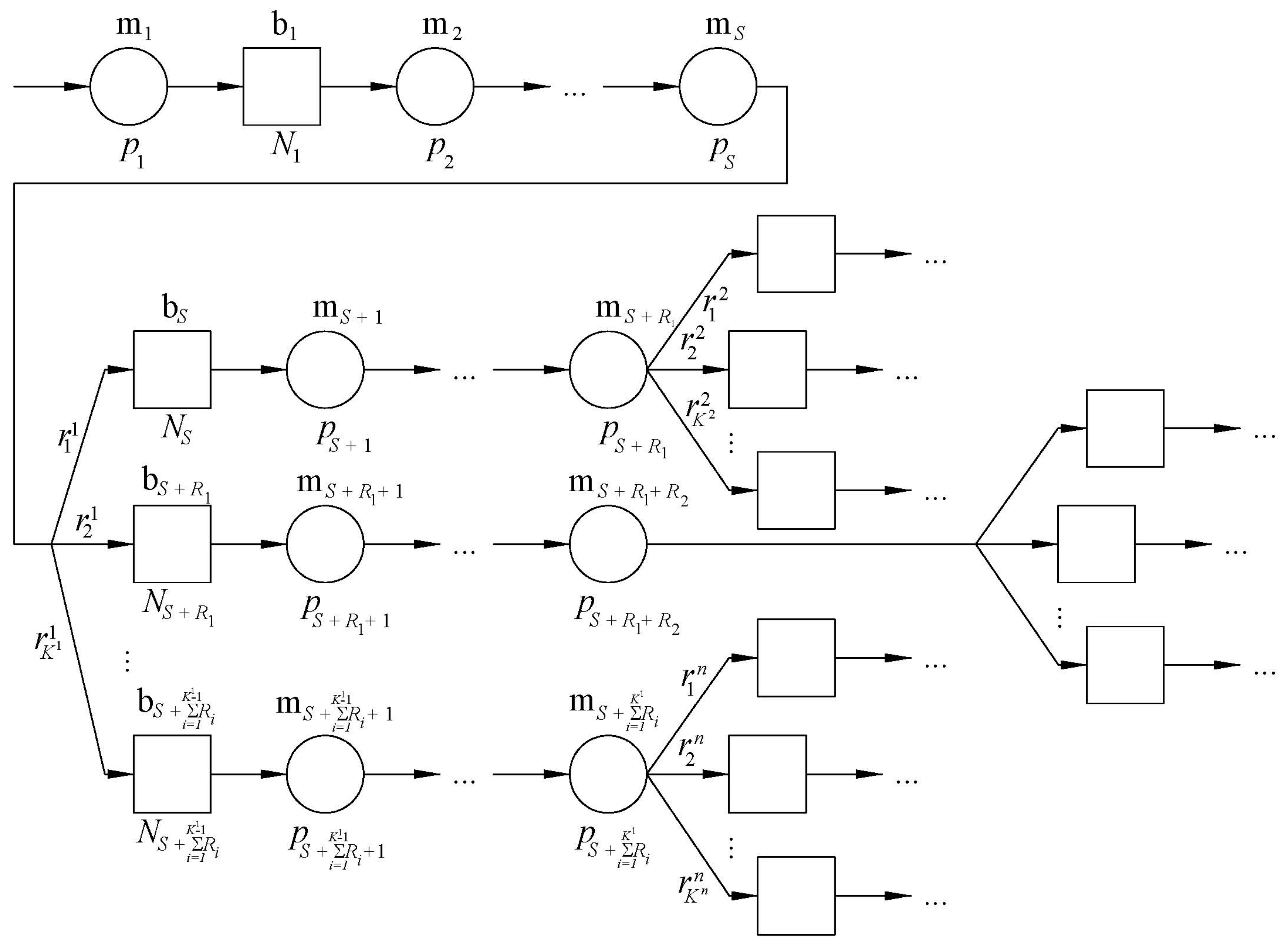
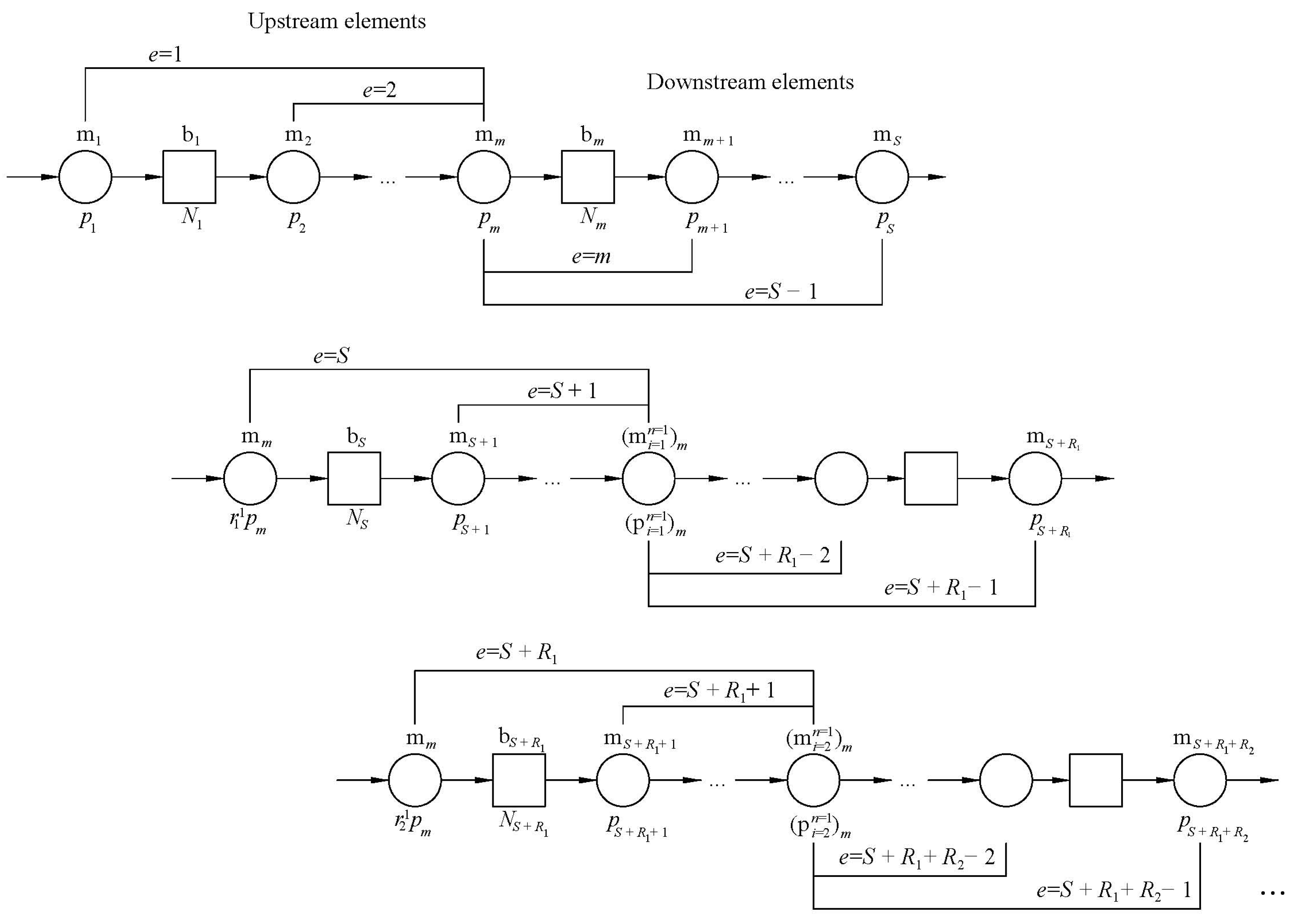
2.1. The Finite-State Method
2.2. Key Performance Indicators
2.3. Digital Threading
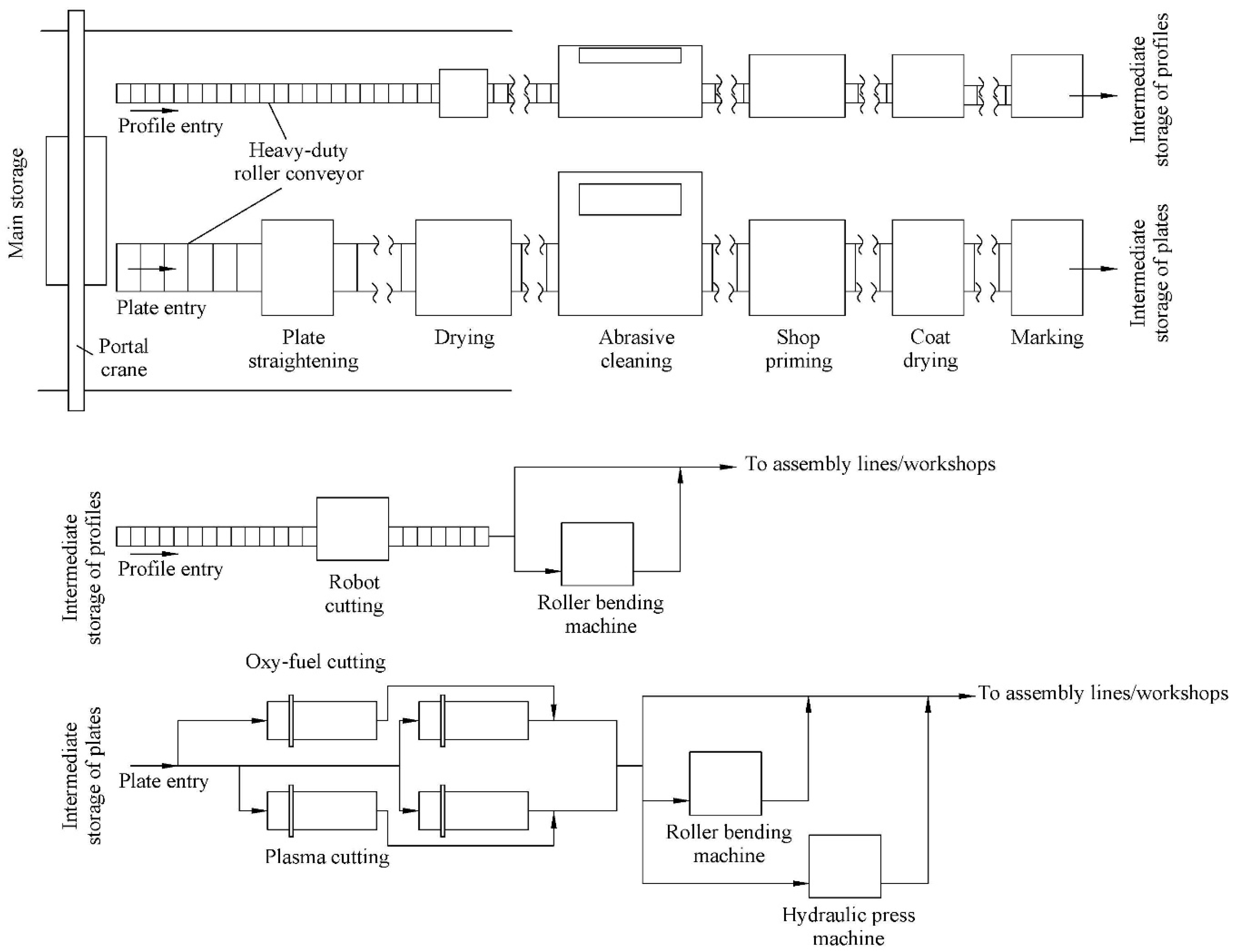
3. Application of the Developed Theory
Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mourtzis, D. Simulation in the design and operation of manufacturing systems: State of the art and new trends. Int. J. Prod. Res. 2020, 58, 1927–1949. [Google Scholar] [CrossRef]
- Dolgui, A.; Sgarbossa, F.; Simonetto, M. Design and management of assembly systems 4.0: Systematic literature review and research agenda. Int. J. Prod. Res. 2021, 60, 184–210. [Google Scholar] [CrossRef]
- Hadžić, N.; Ložar, V.; Opetuk, T.; Andrić, J. The Bernoulli splitting line: Analytical and semi-analytical evaluation of the steady-state performance. Int. J. Prod. Res. 2021, 60, 5912–5936. [Google Scholar] [CrossRef]
- Dain, O.; Ginsberg, M.; Keenan, E.; Pyle, J.; Smith, T.; Stoneman, A.; Pardoe, I. Stochastic Shipyard Simulation with Simyard. In Proceedings of the 2006 Winter Simulation Conference, Monterey, CA, USA, 3–6 December 2006; pp. 1770–1778. [Google Scholar] [CrossRef]
- Ljubenkov, B.; Đukić, G.; Kuzmanić, M. Simulation Methods in Shipbuilding Process Design. J. Mech. Eng. 2008, 54, 131–139. Available online: https://www.sv-jme.eu/article/simulation-methods-in-shipbuilding-process-design/ (accessed on 13 December 2022).
- Hadjina, M. Simulation Modelling Based Methodology for Shipbuilding Production Process Design. Strojarstvo 2009, 51, 547–553. Available online: https://hrcak.srce.hr/50589 (accessed on 14 December 2022).
- Hadžić, N.; Ložar, V.; Opetuk, T.; Andrić, J. A Finite State Method in improvement and design of lean Bernoulli serial production lines. Comput. Ind. Eng. 2021, 158, 107449. [Google Scholar] [CrossRef]
- Hadžić, N.; Ložar, V.; Opetuk, T.; Kunkera, Z. The Bernoulli Assembly Line: The Analytical and Semi-Analytical Evaluation of Steady-State Performance. Appl. Sci. 2022, 12, 12447. [Google Scholar] [CrossRef]
- Grieves, M.W. Product lifecycle management: The new paradigm for enterprises. Int. J. Prod. Dev. 2005, 2, 71–84. [Google Scholar] [CrossRef]
- Grieves, M.W. Product Lifecycle Management; McGraw-Hill: Nova Iorque, Brazil, 2006. [Google Scholar]
- Grieves, M.W. Virtually Perfect: Driving Innovative and Lean Products through Product Lifecycle Management; Space Coast Press: Cocoa Beach, FL, USA, 2011. [Google Scholar]
- Tuegel, E.J.; Ingraffea, A.R.; Eason, T.G.; Spottswood, S.M. Reengineering Aircraft Structural Life Prediction Using a Digital Twin. Int. J. Aerosp. Eng. 2011, 2011, 154798. [Google Scholar] [CrossRef]
- Cerrone, A.; Hochhalter, J.D.; Heber, G.; Ingraffea, A.R. On the Effects of Modeling As-Manufactured Geometry: Toward Digital Twin. Int. J. Aerosp. Eng. 2014, 3, 39278. [Google Scholar] [CrossRef]
- Rosen, R.; Von Wichert, G.; Lo, G.; Bettenhausen, K.D. About The Importance of Autonomy and Digital Twins for the Future of Manufacturing. IFAC-PapersOnLine 2015, 48, 567–572. [Google Scholar] [CrossRef]
- Boschert, S.; Rosen, R. Digital Twin—The Simulation Aspect. Mechatron. Futures 2016, 59–74. [Google Scholar] [CrossRef]
- Coraddu, A.; Oneto, L.; Baldi, F.; Cipollini, F.; Atlar, M.; Savio, S. Data-driven ship digital twin for estimating the speed loss caused by the marine fouling. Ocean. Eng. 2019, 186, 106063. [Google Scholar] [CrossRef]
- Wang, M.M.; Wang, C.Y.; Hnydiuk-Stefan, A.; Feng, S.Z.; Atilla, I.; Li, Z. Recent progress on reliability analysis of offshore wind turbine support structures considering digital twin solutions. Ocean. Eng. 2021, 232, 109168. [Google Scholar] [CrossRef]
- Kutzke, D.T.; Carter, J.B.; Hartman, B.T. Subsystem selection for digital twin development: A case study on an unmanned underwater vehicle. Ocean. Eng. 2021, 223, 108629. [Google Scholar] [CrossRef]
- Lee, J.H.; Nam, Y.S.; Kim, Y.; Liu, Y.M.; Lee, J.; Yang, H. Real-time digital twin for ship operation in waves. Ocean. Eng. 2022, 266, 112867. [Google Scholar] [CrossRef]
- Wasserman, S. What is the Digital Twin and Why Should Simulation and IoT Experts Care? 2017. Available online: https://www.engineering.com/story/what-is-the-digital-twin-and-why-should-simulation-and-iot-experts-care (accessed on 10 January 2023).
- Kritzinger, W.; Karner, M.; Traar, G.; Henjes, J.; Sihn, W. Digital Twin in manufacturing: A categorical literature review and classification. IFAC-PapersOnLine 2018, 51, 1016–1022. [Google Scholar] [CrossRef]
- Mourtzis, D.; Vlachou, E.; Giannoulis, C.; Siganakis, E.; Zogopoulos, V. Applications for Frugal Product Customization and Design of Manufacturing Networks. Procedia CIRP 2016, 52, 228–233. [Google Scholar] [CrossRef]
- Gebhardt, M.; Kopyto, M.; Birkel, H.; Hartman, E. Industry 4.0 technologies as enablers of collaboration in circular supply chains: A systematic literature review. Int. J. Prod. Res. 2021, 60, 6967–6995. [Google Scholar] [CrossRef]
- Polini, W.; Corrado, A. Digital twin of composite assembly manufacturing process. Int. J. Prod. Res. 2020, 58, 5238–5252. [Google Scholar] [CrossRef]
- Li, J.J.; Zhou, G.H.; Zhang, C. A twin data and knowledge-driven intelligent process planning framework of aviation parts. Int. J. Prod. Res. 2021, 60, 5217–5234. [Google Scholar] [CrossRef]
- Zheng, X.; Lu, J.; Kiritsis, D. The emergence of cognitive digital twin: Vision, challenges and opportunities. Int. J. Prod. Res. 2021, 60, 7610–7632. [Google Scholar] [CrossRef]
- Coelho, F.; Relvas, S.; Barbosa-Póvoa, A.P. Simulation-based decision support tool for in-house logistics: The basis for a digital twin. Comput. Ind. Eng. 2021, 153, 107094. [Google Scholar] [CrossRef]
- Psarommatis, F.; Sousa, J.; Mendonça, J.P.; Kiritsis, D. Zero-defect manufacturing the approach for higher manufacturing sustainability in the era of industry 4.0: A position paper. Int. J. Prod. Res. 2022, 60, 73–91. [Google Scholar] [CrossRef]
- Psarommatis, F.; May, G. A literature review and design methodology for digital twins in the era of zero defect manufacturing. Int. J. Prod. Res. 2022, 1–21. [Google Scholar] [CrossRef]
- Dornelles, J.A.; Ayala, N.F.; Frank, A.G. Smart Working in Industry 4.0: How digital technologies enhance manufacturing workers’ activities. Comput. Ind. Eng. 2022, 163, 107804. [Google Scholar] [CrossRef]
- Segura, A.; Diez, H.V.; Barandiaran, I.; Arbelaiz, A.; Álvarez, H.; Simões, B.; Posada, J.; García-Alonso, A.; Ugarte, R. Visual computing technologies to support the Operator 4.0. Comput. Ind. Eng. 2022, 139, 105550. [Google Scholar] [CrossRef]
- Papandopulos, C.T.; Li, J.; O’Kelly, M.E.J. A classification and review of timed Markov models of manufacturing systems. Comput. Ind. Eng. 2019, 128, 219–244. [Google Scholar] [CrossRef]
- Li, J.; Meerkov, S.M. Production System Engineering; Springer: New York, NY, USA, 2009. [Google Scholar]
- Gershwin, S.B. An Efficient Decomposition Method for the Approximate Evaluation of Tandem Queues with Finite Storage Space and Blocking. Oper. Res. 1987, 35, 291–305. [Google Scholar] [CrossRef]
- Jacobs, D.; Meerkov, S.M. Asymptotically reliable serial production lines with a quality control system. Comput. Math. Appl. 1991, 21, 85–90. [Google Scholar] [CrossRef]
- Ložar, V.; Hadžić, N.; Opetuk, T.; Slapničar, V. Accuracy of Semi-Analytical and Numerical Approaches in Evaluation of Serial Bernoulli Production Lines. Mathematics 2021, 9, 1461. [Google Scholar] [CrossRef]
- Hadžić, N. Analytical solution of the serial Bernoulli production line steady-state performance and its application in the shipbuilding process. Int. J. Prod. Res. 2019, 56, 1052–1065. [Google Scholar] [CrossRef]
- Aminuddin, N.A.B.; Garza-Reyes, J.A.; Kumar, V.; Antony, J.; Rocha-Lona, L. An analysis of managerial factors affecting the implementation and use of overall equipment effectiveness. Int. J. Prod. Res. 2016, 54, 4430–4447. [Google Scholar] [CrossRef]
- Foulloy, L.; Olivine, V.; Berrah, L. A fuzzy temporal approach to the Overall Equipment Effectiveness measurement. Comput. Ind. Eng. 2019, 127, 103–115. [Google Scholar] [CrossRef]
- Caprce, J.D.; Da Silva, C.T.; Rigo, P.; Pires, F.C.M. Discrete Even Production Simulation and Optimisation of Ship Block Erection Process. In Proceedings of the 10th International Conference on Computer Applications and Information Technology in the Maritime Industries 2011, Como, Italy, 20–21 June 2011; pp. 271–282. [Google Scholar]
- Son, M.J.; Kim, T.W. Job Assignment Simulation of Ship Hull Production Design in Consideration of Mid-Term Schedule. J. Soc. Nav. Archit. Korea 2013, 50, 334–342. [Google Scholar] [CrossRef]
- Hadjina, M.; Fafandjel, N.; Matulja, T. Shipbuilding production process design methodology using computer simulation. Brodogradnja 2015, 66, 77–91. Available online: https://hrcak.srce.hr/140058 (accessed on 14 December 2022).
- Wang, C.; Mao, P.; Mao, Y.; Shin, J.G. Research on scheduling and optimization under uncertain conditions in panel block production line in shipbuilding. Int. J. Nav. Archit. Ocean. Eng. 2016, 8, 398–408. [Google Scholar] [CrossRef]
- Oliveira, A.; Gordo, J.M. Lean tools applied to a shipbuilding panel line assembling process. Brodogradnja 2018, 69, 53–64. Available online: https://hrcak.srce.hr/207743 (accessed on 14 December 2022). [CrossRef]
- Stanić, V.; Hadjina, M.; Fafandjel, N.; Matulja, T. Toward Shipbuilding 4.0–An Industry 4.0 changing the face of the shipbuilding industry. Brodogradnja 2018, 69, 111–128. Available online: https://hrcak.srce.hr/201162 (accessed on 14 December 2022). [CrossRef]
- Vidal-Balea, A.; Blanco-Novoa, O.; Fraga-Lamas, P.; Vilar-Montesions, M.; Fernández-Caramés, M. Creating Collaborative Augmented Reality Experiences for Industry 4.0 Training and Assistance Applications: Performance Evaluation in the Shipyard of the Future. Appl. Sci. 2020, 10, 9073. [Google Scholar] [CrossRef]
- Choi, T.; Seo, Y. A Real-Time Physical Progress Measurement Method for Schedule Performance Control Using Vision, an AR Marker and Machine Learning in a Ship Block Assembly Process. Sensors 2020, 20, 5386. [Google Scholar] [CrossRef] [PubMed]
- Bilen, U.; Helvacioglu, S. Data driven performance evaluation in shipbuilding. Brodogradnja 2020, 71, 39–51. [Google Scholar] [CrossRef]
- Lee, Y.G.; Ju, S.H.; Woo, J.H. Simulation-based planning system for shipbuilding. Int. J. Comput. Integr. Manuf. 2020, 33, 626–641. [Google Scholar] [CrossRef]
- Hadžić, N.; Ložar, V.; Opetuk, T.; Cajner, H. Improvability of the fabrication line in a shipyard. Brodogradnja 2021, 72, 13–28. [Google Scholar] [CrossRef]
- Price, J.R.; Trost, C.S.; Bespolka, C.; Xie, T. Productivity Management Insights and Lessons from Naval Ship Repair. Nav. Eng. J. 2021, 133, 77–90. [Google Scholar]
- Wu, Q.; Mao, Y.; Chen, J.; Wang, C. Application Research of Digital Twin-Driven Ship Intelligent Manufacturing System: Pipe Machining Production Line. J. Mar. Sci. Eng. 2021, 9, 338. [Google Scholar] [CrossRef]
- Pang, T.Y.; Pelaez Restrepo, J.D.; Cheng, C.T.; Yasin, A.; Lim, H.; Miletic, M. Developing a Digital Twin and Digital Thread Framework for an ‘Industry 4.0’ Shipyard. Appl. Sci. 2021, 11, 1097. [Google Scholar] [CrossRef]
- Incontrol Simulation Solutions (2021) Enterprise Dynamics Tutorial; InControl: Utrecht, The Netherlands, 2021.

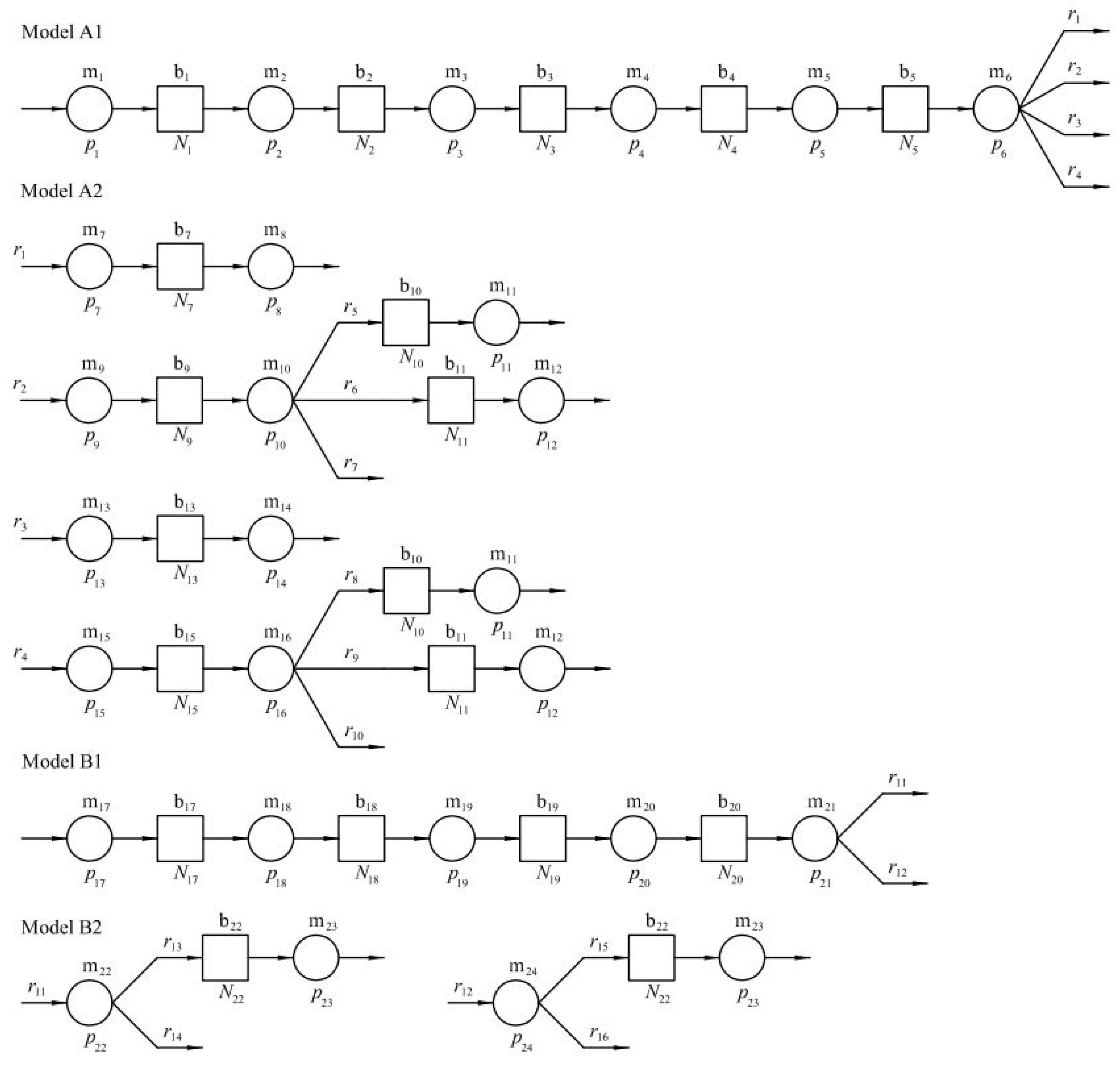



| i | mi | Model | Operation | pi |
|---|---|---|---|---|
| 1 | m1 | A1 | Plate straightening | 0.90 |
| 2 | m2 | Drying | 0.91 | |
| 3 | m3 | Abrasive cleaning | 0.98 | |
| 4 | m4 | Shop priming | 0.80 | |
| 5 | m5 | Coat drying | 0.91 | |
| 6 | m6 | Marking | 0.96 | |
| 7 | m7 | A2 | Plasma tracing and cutting | 0.70 |
| 8 | m8 | Plasma marking | 0.77 | |
| 9 | m9 | Plasma tracing and cutting | 0.71 | |
| 10 | m10 | Plasma marking | 0.77 | |
| 11 | m11 | Plate-forming–roller-bending machine | 0.85 | |
| 12 | m12 | Plate forming–hydraulic press | 0.85 | |
| 13 | m13 | Oxy-fuel tracing and cutting | 0.70 | |
| 14 | m14 | Oxy-fuel marking | 0.77 | |
| 15 | m15 | Oxy-fuel tracing and cutting | 0.71 | |
| 16 | m16 | Oxy-fuel marking | 0.77 | |
| 17 | m17 | B1 | Drying | 0.91 |
| 18 | m18 | Abrasive cleaning | 0.98 | |
| 19 | m19 | Shop priming | 0.80 | |
| 20 | m20 | Coat drying | 0.91 | |
| 21 | m21 | Marking | 0.96 | |
| 22 | m22 | B2 | Oxy-fuel manual cutting | 0.77 |
| 23 | m23 | Stiffener-forming–roller-bending machine | 0.93 | |
| 24 | m24 | Oxy-fuel robotic cutting | 0.81 |
| BC * | b1 | b2 | b3 | b4 | b5 | b7 | b9 | b10 | b11 | b13 | b15 | b17 | b18 | b19 | b20 | b22 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ni | 4 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 8 | 8 | 8 | 8 | 4 |
| Splitting Rate | r1 | r2 | r3 | r4 | r5 | r6 | r7 | r8 | r9 | r10 | r11 | r12 | r13 | r14 | r15 | r16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ri | 0.5 | 0.5 | 0 | 0 | 0.05 | 0.05 | 0.9 | 0 | 0 | 0 | 1 | 0 | 0.2 | 0.8 | 0 | 0 |
| A1 | PR6 | WIP1 | WIP2 | WIP3 | WIP4 | WIP5 | RT6 | |||||
| MM | 0.78 | 3.35 | 0.93 | 0.98 | 0.81 | 0.81 | 8.82 | |||||
| NM | 0.80 | 4.00 | 1.00 | 1.00 | 0.00 | 0.00 | 7.50 | |||||
| A2 | PR8 | WIP7 | RT8 | |||||||||
| MM | 0.64 | 1.18 | 1.84 | |||||||||
| NM | 0.70 | 0.00 | n/a | |||||||||
| PR11 | PR12 | PR10r3 | WIP9 | WIP10 | WIP11 | RT11 | RT12 | RT10r3 | ||||
| MM | 0.04 | 0.04 | 0.64 | 1.20 | 0.04 | 0.04 | 31 | 31 | 1.87 | |||
| NM | 0.04 | 0.04 | 0.63 | 0.00 | 0.00 | 0.00 | n/a | n/a | n/a | |||
| B1 | PR21 | WIP17 | WIP18 | WIP19 | WIP20 | RT21 | ||||||
| MM | 0.80 | 7.35 | 7.91 | 1.45 | 0.99 | 22.12 | ||||||
| NM | 0.80 | 7.98 | 9.99 | 0.00 | 0.00 | 22.46 | ||||||
| B2 | PR22r14 | PR23 | WIP22 | RT22r14 | RT23 | |||||||
| MM | 0.15 | 0.62 | 0.17 | / | 0.27 | |||||||
| NM | 0.15 | 0.62 | 0.00 | / | n/a |
| A1 | BL1 | BL2 | BL3 | BL4 | BL5 | ST2 | ST3 | ST4 | ST5 | ST6 | |
| MM | 0.17 | 0.24 | 0.27 | 0.08 | 0.03 | 0.00 | 0.07 | 0.01 | 0.17 | 0.19 | |
| NM | 0.10 | 0.11 | 0.18 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.11 | 0.16 | |
| A2 | BL7 | ST8 | |||||||||
| MM | 0.06 | 0.13 | |||||||||
| NM | 0.00 | 0.07 | |||||||||
| BL9 | BL10 | ST10 | ST11 | ST12 | |||||||
| MM | 0.06 | 0.00 | 0.12 | 0.81 | 0.81 | ||||||
| NM | 0.00 | 0.00 | 0.07 | 0.81 | 0.81 | ||||||
| B1 | BL17 | BL18 | BL19 | BL20 | ST18 | ST19 | ST20 | ST21 | |||
| MM | 0.11 | 0.18 | 0.00 | 0.00 | 0.00 | 0.00 | 0.11 | 0.16 | |||
| NM | 0.11 | 0.18 | 0.00 | 0.00 | 0.00 | 0.00 | 0.11 | 0.16 | |||
| B2 | BL22 | BL23 | ST23 | ||||||||
| MM | 0.00 | 0.00 | 0.78 | ||||||||
| NM | 0.00 | 0.00 | 0.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hadžić, N.; Ložar, V.; Opetuk, T.; Keser, R. Towards Digital Twinning of Fabrication Lines in Shipyards. J. Mar. Sci. Eng. 2023, 11, 1053. https://doi.org/10.3390/jmse11051053
Hadžić N, Ložar V, Opetuk T, Keser R. Towards Digital Twinning of Fabrication Lines in Shipyards. Journal of Marine Science and Engineering. 2023; 11(5):1053. https://doi.org/10.3390/jmse11051053
Chicago/Turabian StyleHadžić, Neven, Viktor Ložar, Tihomir Opetuk, and Robert Keser. 2023. "Towards Digital Twinning of Fabrication Lines in Shipyards" Journal of Marine Science and Engineering 11, no. 5: 1053. https://doi.org/10.3390/jmse11051053
APA StyleHadžić, N., Ložar, V., Opetuk, T., & Keser, R. (2023). Towards Digital Twinning of Fabrication Lines in Shipyards. Journal of Marine Science and Engineering, 11(5), 1053. https://doi.org/10.3390/jmse11051053








