Study of the Master Bay Plan Problem Based on a Twin 40-Foot Quay Crane Operation
Abstract
1. Introduction
2. Literature Review
2.1. Master Bay Plan Problem
2.2. Collaborative Scheduling of Ship Stowage and QC
2.3. Problem Description
2.3.1. Master Bay Plan Problem
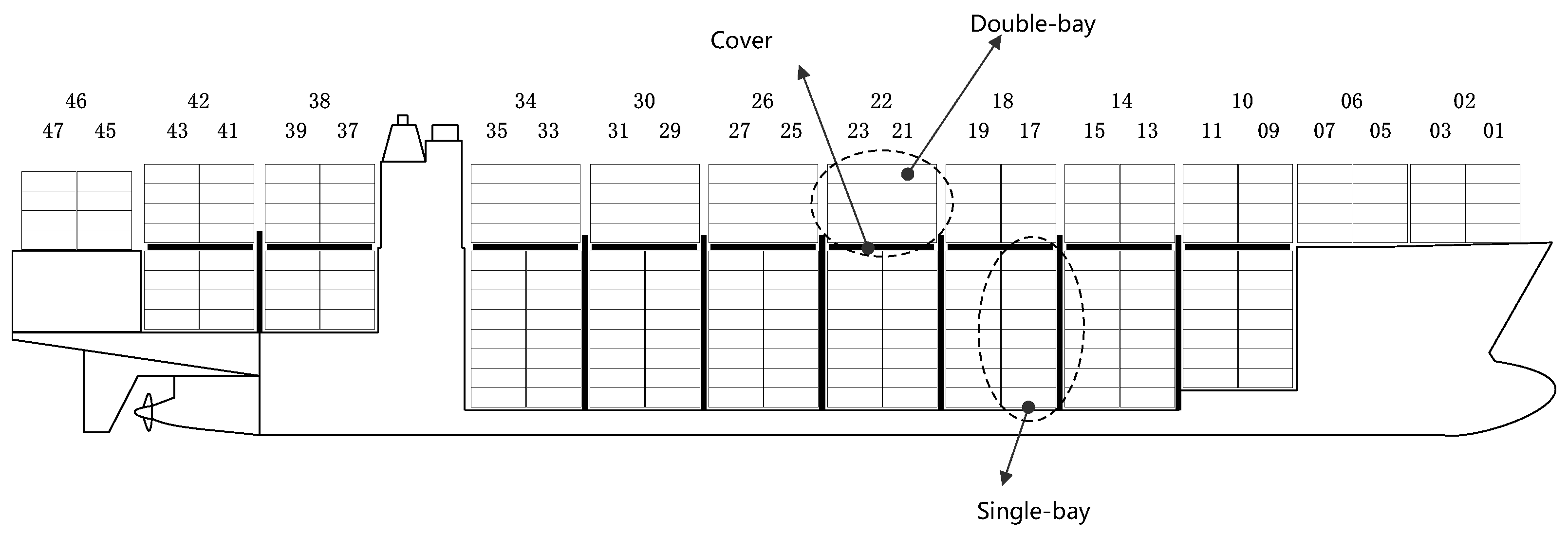
2.3.2. Container Ship
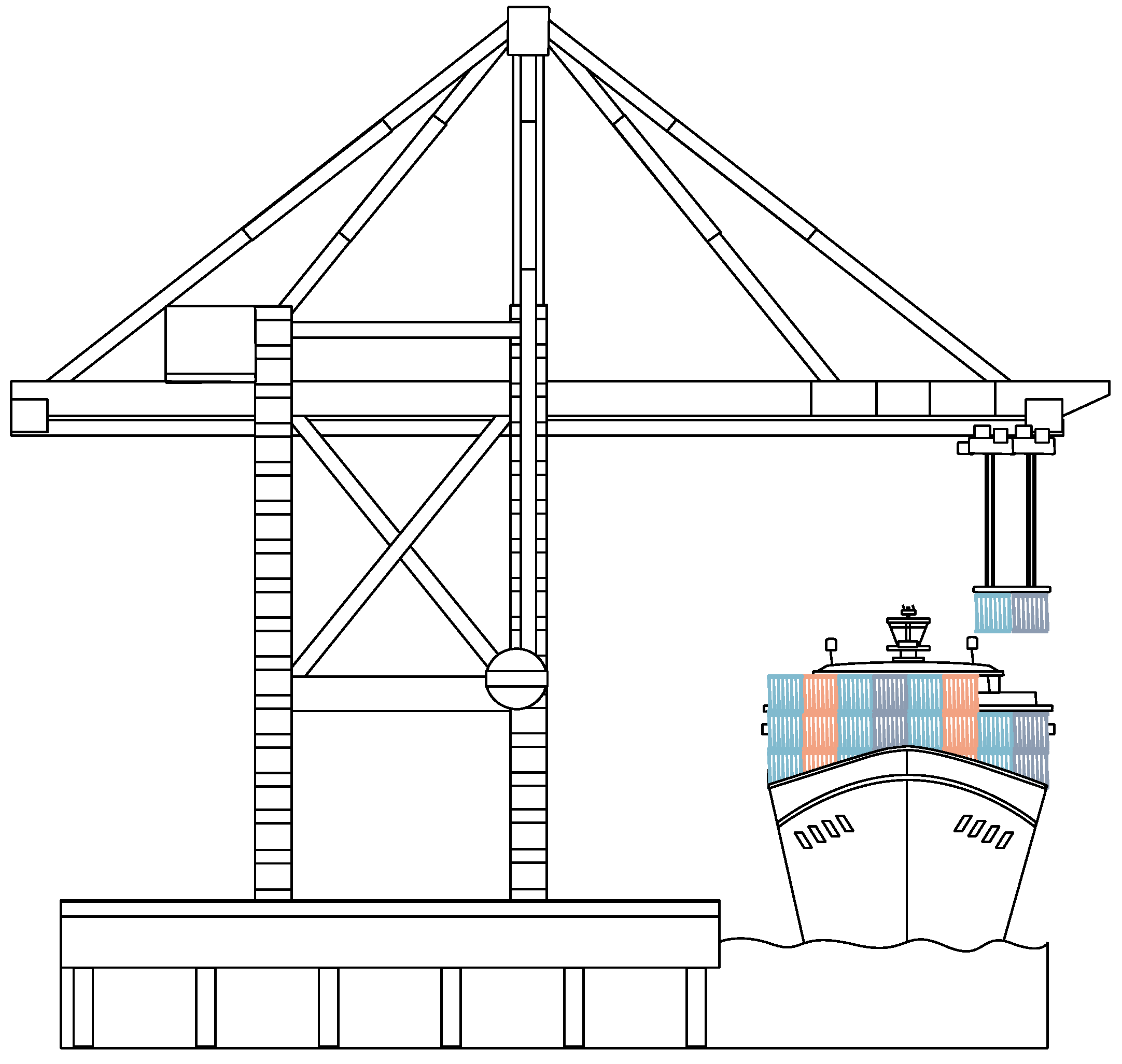
2.3.3. Twin 40-Foot QC
2.3.4. Rehandling Operation
3. Materials and Methods
3.1. MP-MBPP Model
3.1.1. Assumption
- 1
- The attribute information of the containers to be loaded and unloaded at each port of call on the route is known, such as the type, size, destination port, and quantity of the containers.
- 2
- The structure of the container ship is known, including the number of bays, the capacity of each bay, the bay number, etc.
- 3
- Only standard 20-foot and 40-foot containers are considered, and oversize, refrigerated, and dangerous containers are ignored.
- 4
- The ship only loads at the origin port and unloads at the destination port.
- 5
- At any given time, all containers to be loaded on the ship must not exceed the maximum loading capacity of the ship in terms of weight, and the total quantity of containers should not exceed the maximum number of container slots on the ship.
- 6
- Starting from the bow, every two adjacent bays form a double-bay, and both can accommodate 40-foot containers.
- 7
- The average additional loading and unloading time caused by container rehandling is represented as , the time required for the crane to move one bay distance is , and the average time required for the crane to load or unload a container is .
- 8
- The cranes are uniform and are twin 40-foot QCs.
3.1.2. Sets
- B: Index set of single bays,
- F: Index set of double-bays, ,
- O: Index set of double-bay serial numbers,
- P: Index set of ports,
- R: Index set of columns in the bay,
- L: Index set of tiers in the bay,
- : Subset of tiers in the bay, when
- C: Index set of containers in the route,
- Q: Index set of QCs,
- T: Index set of ship berthing times,
3.1.3. Parameters
- : Number of slots in the double-bay f,
- : Number of slots in the single-bay b of the double-bay f,,
- : Number of slots assigned to the container groups from the origin port i to the destination port j in the double-bay f,,
- : Number of 20-foot slots assigned to the container groups from the origin port i to the destination port j in the double-bay f,,
- : Number of 40-foot slots assigned to the container groups from the origin port i to the destination port j in the double-bay f,,
- : Number of 20-foot slots assigned to the container groups from the origin port i to the destination port j in the single bay b of the double-bay f,,,
- : Number of 40-foot slots assigned to the container groups from the origin port i to the destination port j in the single bay b of the double-bay f,,,
- : Number of containers from the origin port i to the destination port j,
- : Number of 20-foot containers from the origin port i to the destination port j,
- : Number of 40-foot containers from the origin port i to the destination port j,
- : Number of vacant slots of the single bay b in the double-bay f when arriving at the port j,,,
- : Denotes the double-bay where the QC q is located at the moment of t,,
- : Denotes the number of double-bays where the QC q is located at the moment of t,,,
- : Denotes the serial number of the double-bay where the QC q is located at the moment of t,,,,
- : Denotes the number of containers that the QC q is loading or unloading at time t,,
3.1.4. Variables
- : , if the double-bay f is assigned to containers from the origin port i to the destination port j at moment t, otherwise ,,,
- : , if the single bay b in the double-bay f is assigned to containers from the origin port i to the destination port j at moment t, otherwise ,,,,
- : , if the column r of the single bay b in the double-bay f is assigned to containers from the origin port i to the destination port j at moment t, otherwise ,,,,,
- : , if the tier l in column r of the single bay b in the double-bay f is assigned at moment t, otherwise ,,,,,
- : , if the tier l in column r of the single bay b in the double-bay f is assigned to containers from the origin port i to the destination port j at moment t, otherwise ,,,,,,
- : , if the tier l in column r of the single bay b in the double-bay f is assigned to a container c at moment t, otherwise ,,,,,,
- : , if the tier l in column r of the single bay b in the double-bay f is assigned to a 20-foot container c at moment t, otherwise ,,,,,,
- : , if the tier l in column r of single-bay b in the double-bay f is assigned to a 40-foot container c at moment t, otherwise ,,,,,,
- : , if , otherwise ,,,,,
3.1.5. Objective & Constraints
3.2. Stowage Strategies and Solution Algorithm
- 1
- The origin of the container is the same as Port A, and the destination is before Port B;
- 2
- The destination of the container is the same as Port B, and the origin is after Port A;
- 3
- The loading and unloading ports of the container are both before Port B;
- 4
- The loading and unloading ports of the container are both after Port A.
3.2.1. New Strategies of MP-MBPP
- Strategy S1: Double-bays are selected sequentially, starting from the center of the ship and moving towards both ends, with non-adjacent bays selected first. After reaching the bow or stern, the remaining double-bays are selected using the same rule from the center of the ship, forming the set of twice-selected double-bays, denoted as , where is the rounded-up value. This strategy prioritizes safety distance for QC operations and non-crossing constraints by assigning containers with the same destination port to non-adjacent double-bays. This approach aims to balance the workload of the QCs and reduce waiting time.
- Strategy S2: This strategy does not specify the order of double-bays, but assigns a random number within a certain range to the double-bays where the container group is located. Then, these double-bays are sorted in descending order based on these numbers to obtain the latest position of the double-bays on the ship. Particle swarm optimization is then used for iterative optimization.
- Rule R1: This strategy prioritizes non-empty bays with the goal of minimizing the number of occupied bays. Firstly, double-bay 1 is used to load container group . If the capacity of double-bay 1 is greater than the number of containers in the group , it is used to load container group , and then container group is selected according to the order of the container group until its capacity or weight limit is exceeded. Then, the next sorted ship double-bay set is considered. This ensures that each double-bay is filled before moving on to the next one.
- Rule R2: Due to the consistent berthing structure of the selected vessel in this paper, the double-bays of the vessel are not sorted before loading the container groups. Instead, specific double-bays are designated for each container group, and the number of containers to be loaded throughout the entire route is determined in advance. According to this rule, the double-bays are loaded in sequence based on the sorting of container groups. Once a double-bay is loaded with a container group, the next double-bay in the set of double-bays on the vessel is considered for other container groups, i.e., ensuring that the 20-foot containers of the destination port can be loaded. In addition, when the destination port of a group of containers is close to the current port in the ranking (under the condition that the loading constraints are satisfied for the empty container slots in the loaded container double-bay), the 40-foot container of the destination port closer to the current loading port is given priority to be loaded.
- 1
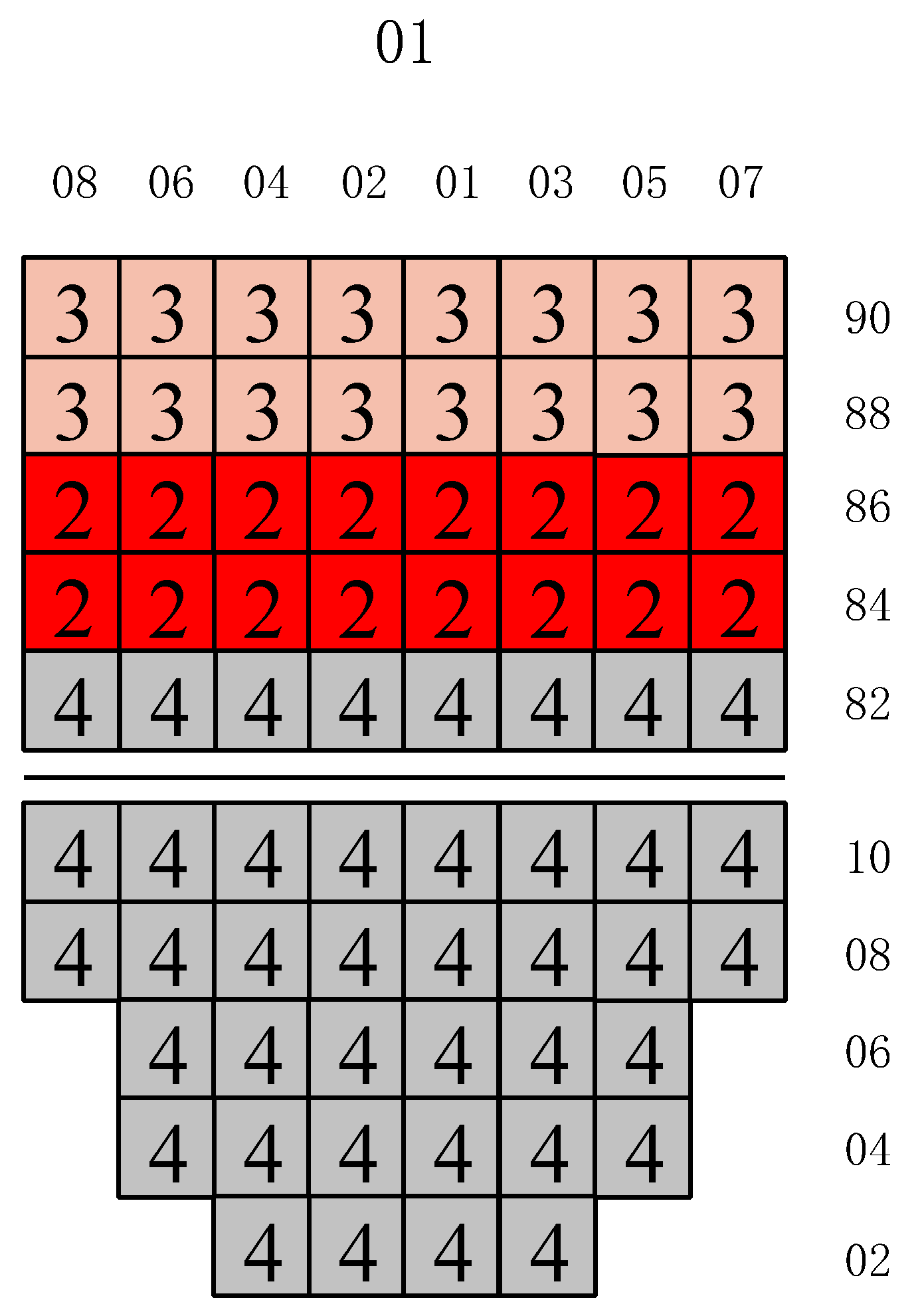
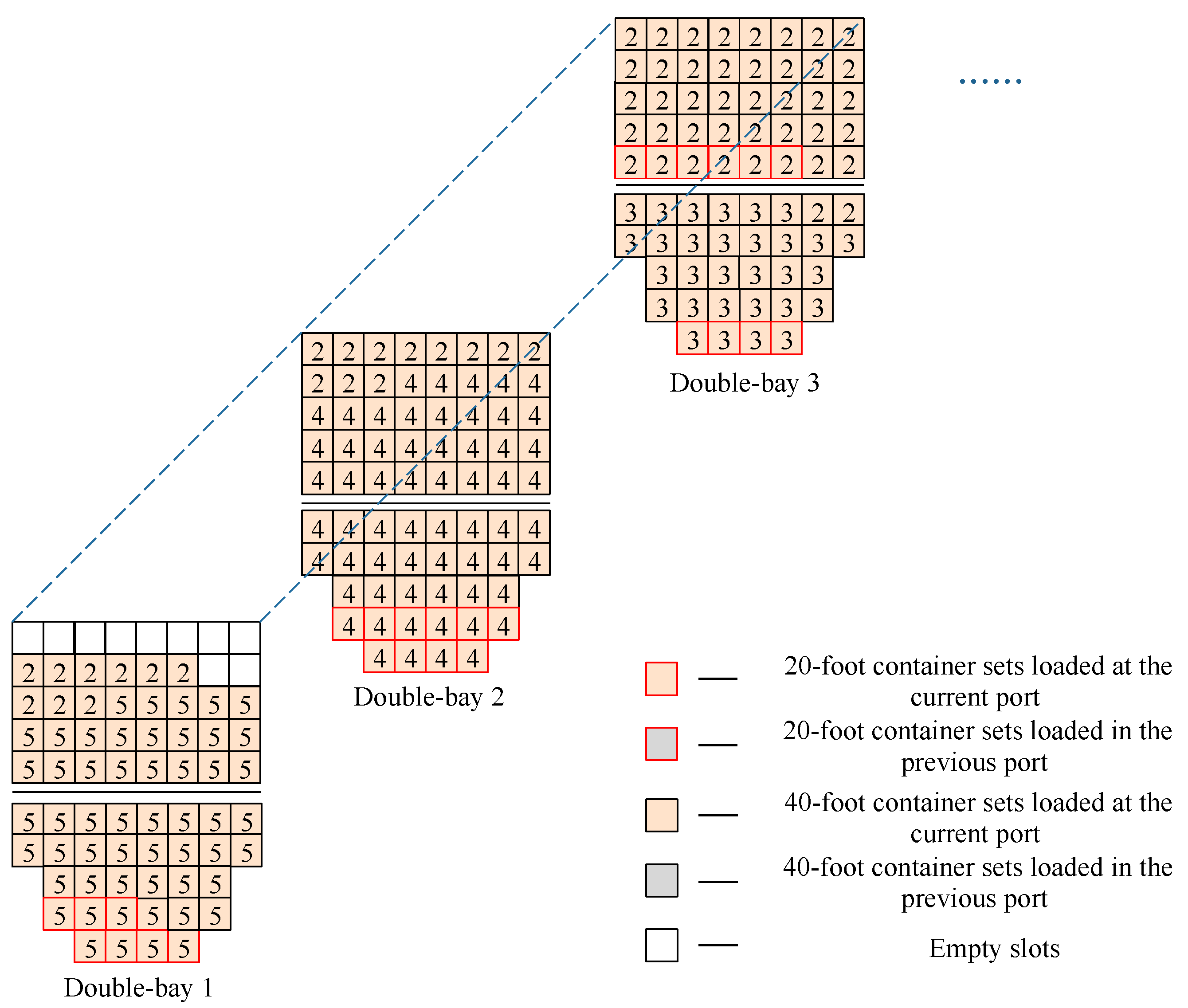
- If the lower deck stowage of the previous destination is not fully loaded, the 40-foot container of the subsequent destination is loaded into the hold first, followed by the 20-foot container of the subsequent destination on the deck. As shown in Figure 9, after the ship loads containers with destination port 4, the hold is not yet full, so the 20-foot containers of destination port 3 need to be loaded. However, priority is given to loading 40-foot containers first to partially fill the hold before loading 20-foot containers.
- 2
- If the upper deck stowage of the previous destination is not fully loaded, the next double-bay in the sorted set of ship double-bays is selected. The 20-foot containers of the subsequent destination are loaded into that double-bay and then loading continues according to rule R1, as shown in Figure 10. At the current port, priority is given to loading the 20-foot containers, but if there is an empty space above the previous double-bay on the upper deck and 40-foot containers have already been loaded on that deck, the next double-bay is selected for loading.
3.2.2. Operation of Twin 40-Foot QCs
- 1
- Loading rule: When only loading operations are required at the current port, the assigned QCs will load containers from the center of the ship to the sides.
- 2
- Loading and unloading rule: When both loading and unloading operations are required or only unloading operations are required at the current port, one crane will load and unload containers from the bow to the stern of the ship, while another crane will load and unload containers from the middle to the stern of the ship.At the same time, the ”Load as you unload” rule is used. Specifically, twin 40-foot QCs are assigned to the double-bays that require unloading; after unloading the imported containers in the double-bay, they will continue to load the exported containers allocated to the same double-bay. After completing the loading and unloading tasks in the double-bay, the twin 40-foot QCs will move to the nearest double-bay to continue loading or unloading operation.
3.2.3. Particle Swarm Optimization
4. Computational Results
4.1. Instance of Shipping Line
4.2. Analysis of Results
4.2.1. Different Strategies for Double-Bay
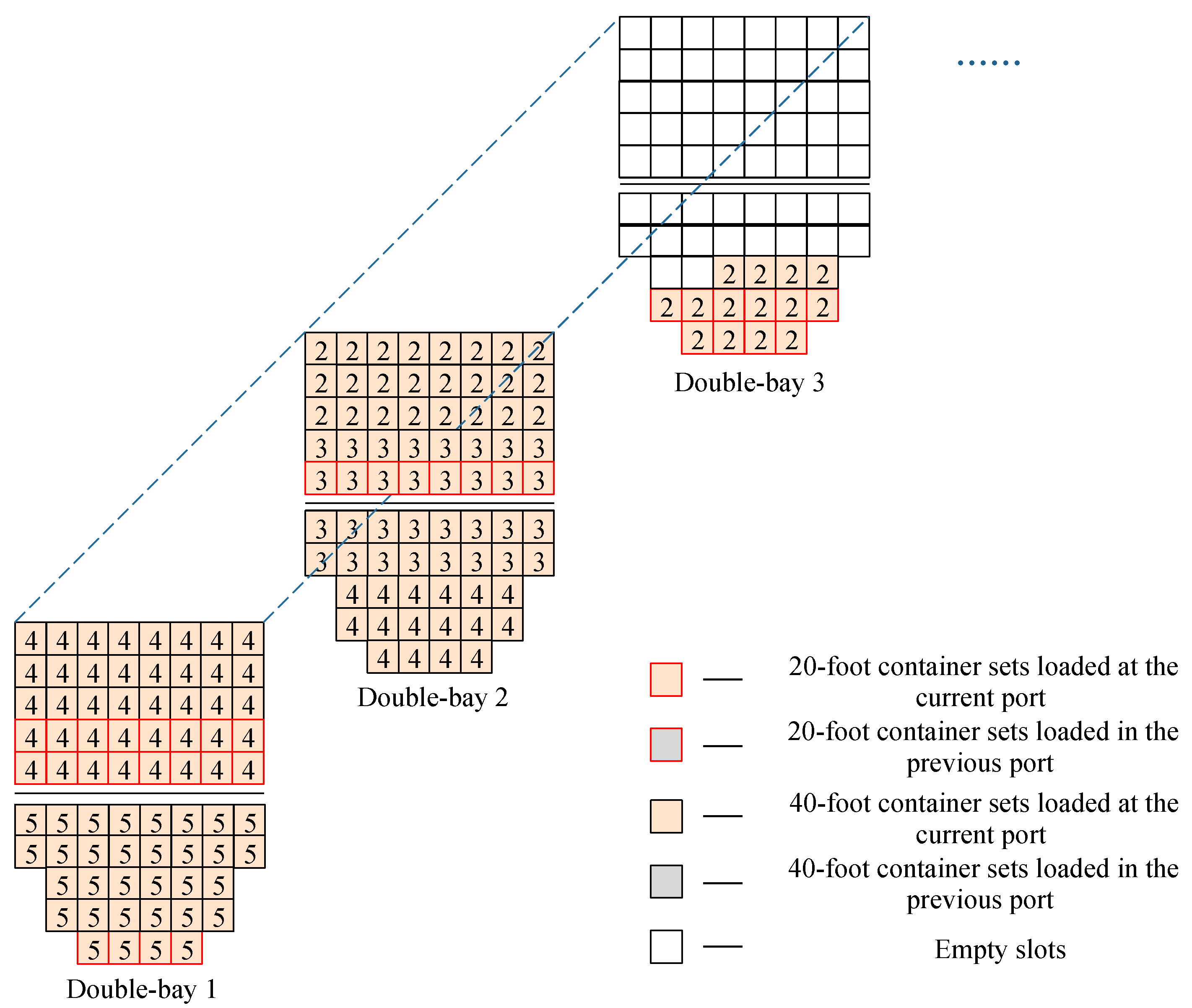
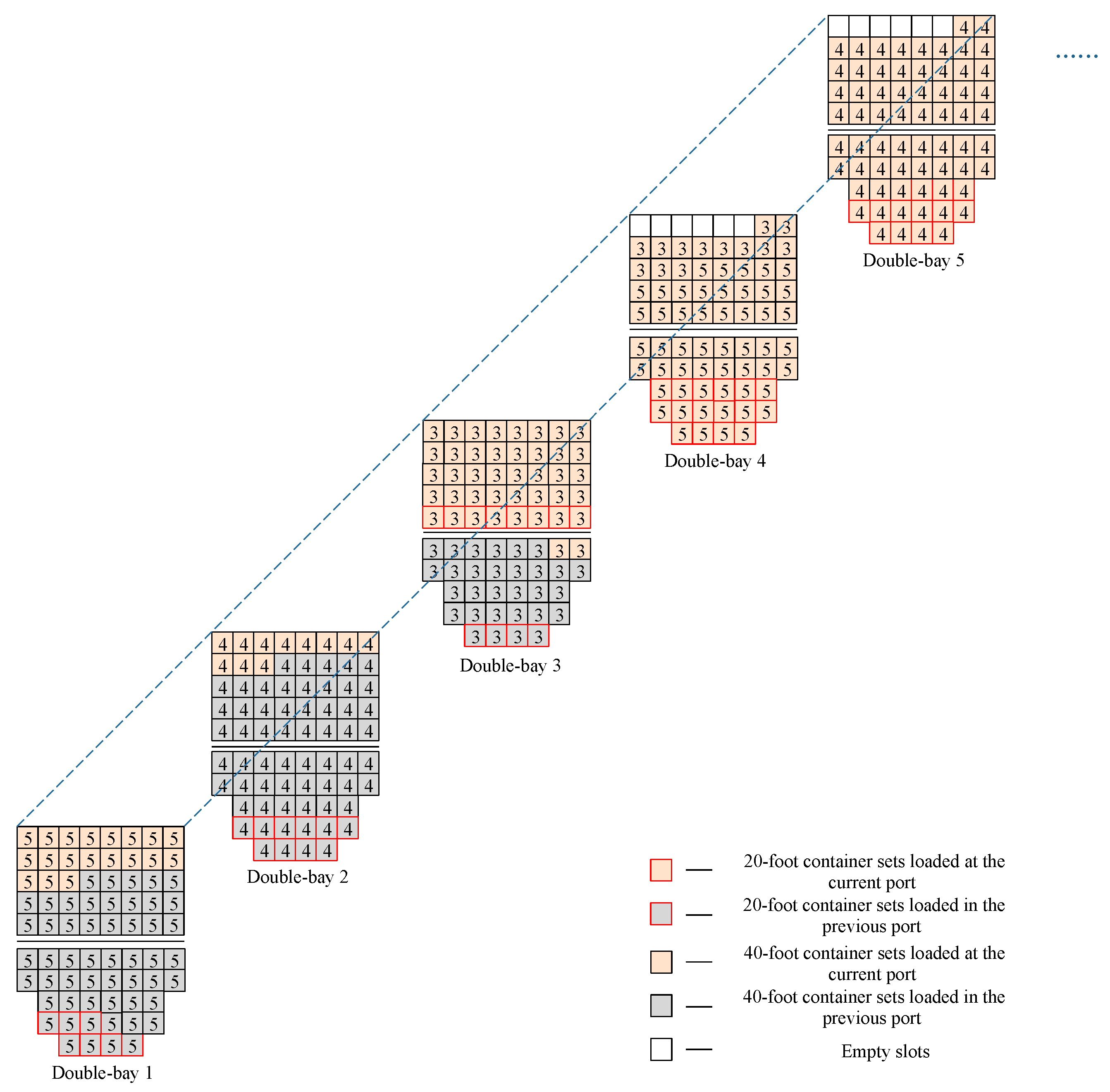
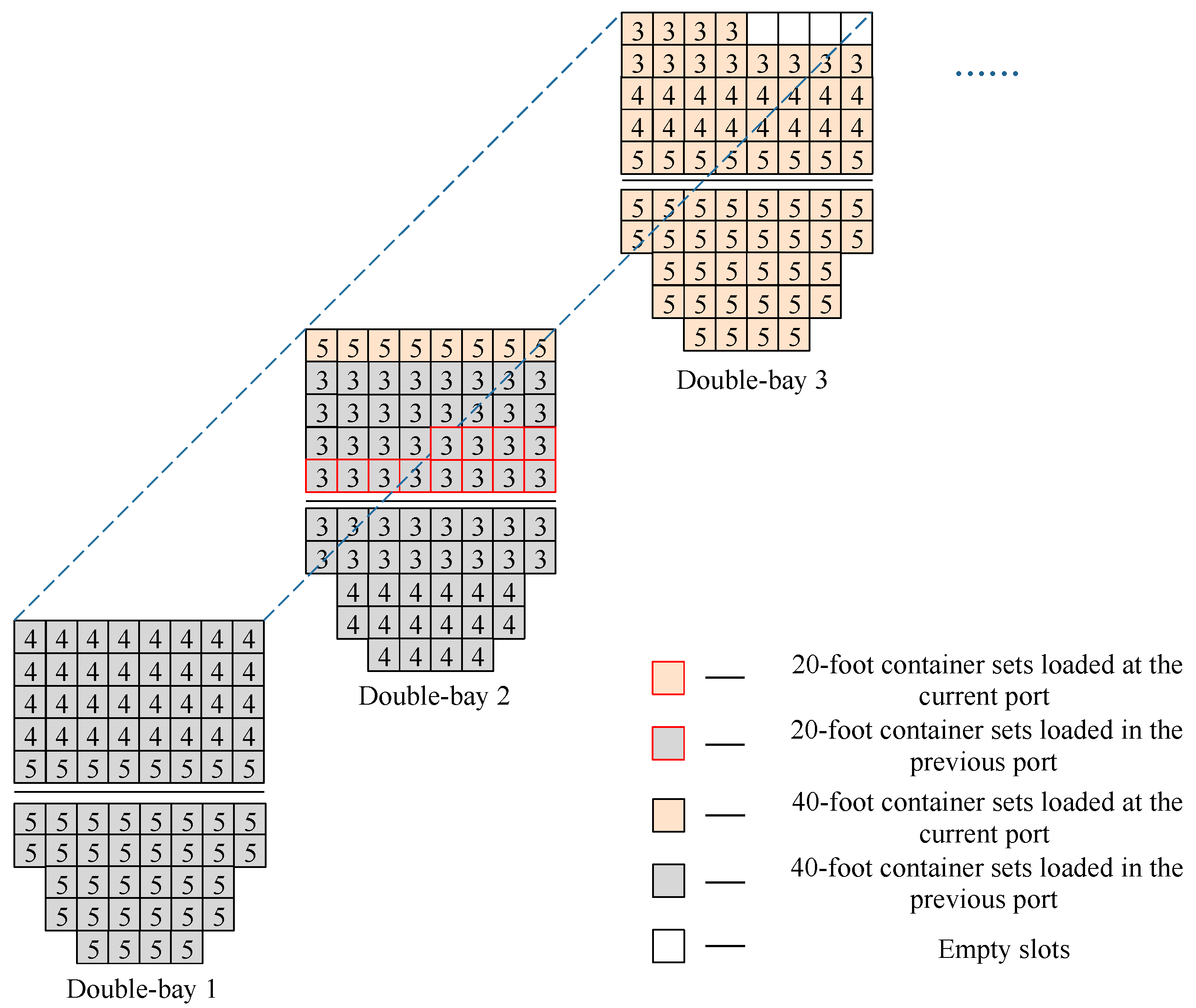
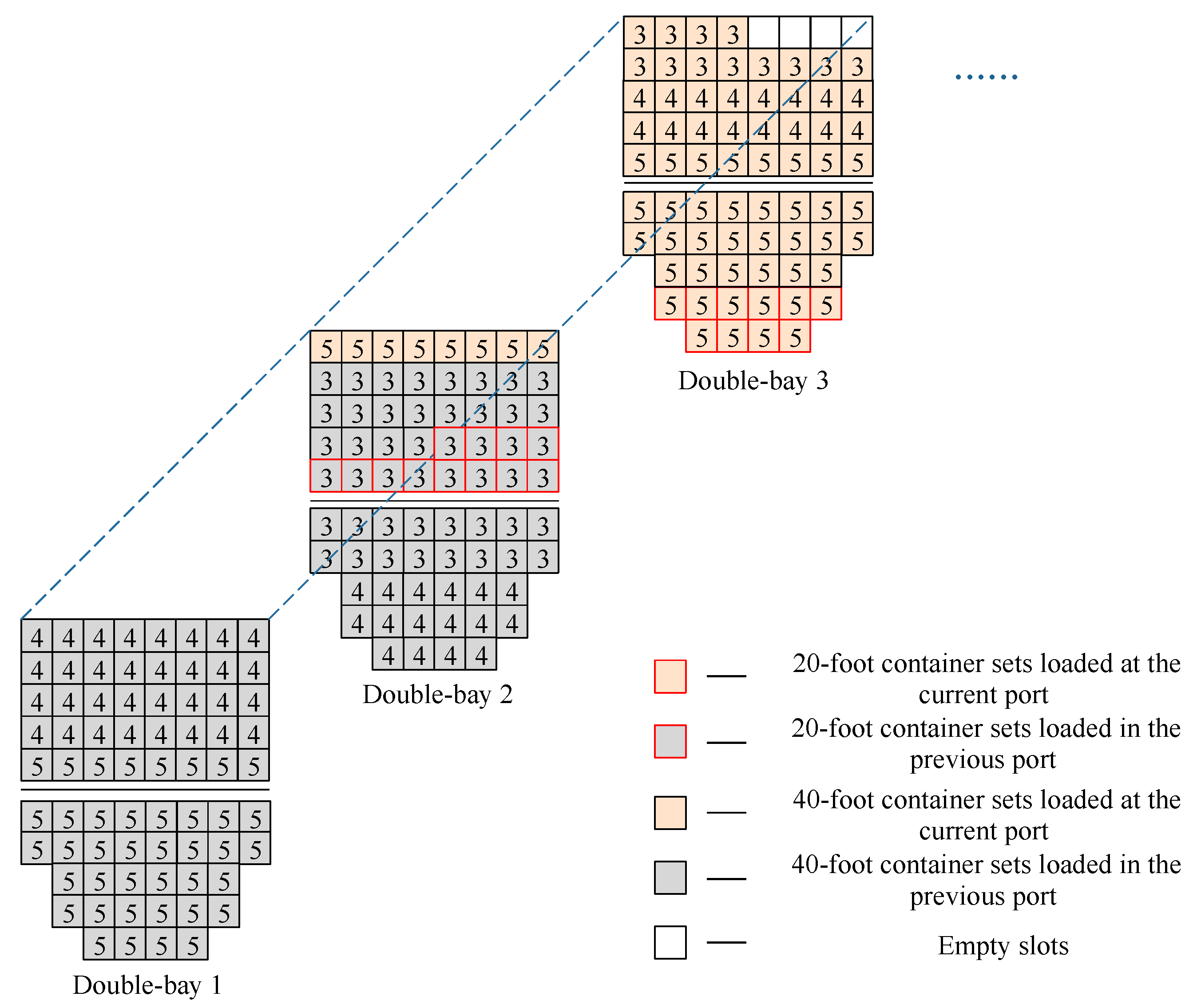
4.2.2. Stowage of the Double-Bay and Single Bay
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Le, P.T.W.; Kwon, O.K.; Ruan, X. Sustainability Challenges in Maritime Transport and Logistics Industry and Its Way Ahead. Sustainability 2019, 11, 1331. [Google Scholar] [CrossRef]
- Kim, S.; Kim, C. Analysis of the Impact of COVID-19 on Port Operation. J. Korean Navig. Port Res. 2021, 45, 155–164. [Google Scholar]
- Sung, L.J.; Hun, P.S. Study on the Recent Global Shipping Environment Change and Domestic Countermeasure. J. Marit. Bus. 2021, 49, 99–122. [Google Scholar]
- Tai, Z.; Guo, J.; Guan, Y.; Shi, Q. Impact of COVID-19 on Port Production and Operation Based on System Dynamics: A Case Study of Shanghai Port in China. J. Adv. Transp. 2021, 2021, 9689391. [Google Scholar] [CrossRef]
- Beskovnik, B.; Zanne, M.; Golnar, M. Dynamic Changes in Port Logistics Caused by the COVID-19 Pandemic. J. Mar. Sci. Eng. 2022, 10, 1473. [Google Scholar] [CrossRef]
- Caballini, C.; Ghiara, H.; Persico, L. Analysis of the impacts of COVID-19 on selected categories of goods passing through the ports of Genoa and Savona, Italy. Case Stud. Transp. Policy 2022, 10, 851–869. [Google Scholar] [CrossRef] [PubMed]
- Jin, L.; Chen, J.; Chen, Z.; Yu, B. Impact of COVID-19 on China’s international liner shipping network based on AIS data. Transp. Policy 2022, 121, 90–99. [Google Scholar] [CrossRef]
- Kim, B.; Kim, G.; Kang, M. Study on Comparing the Performance of Fully Automated Container Terminals during the COVID-19 Pandemic. Sustainability 2022, 14, 9415. [Google Scholar] [CrossRef]
- Yap, W.Y.; Yang, D. Hub port choice and shipping connectivity in Southeast Asia during COVID-19 pandemic: Implications for post-pandemic competition landscape. Marit. Policy Manag. 2022. [Google Scholar] [CrossRef]
- Bandyopadhyay, A.; Bhatnagar, S. Impact of COVID-19 on ports, multimodal logistics and transport sector in India: Responses and policy imperatives. Transp. Policy 2023, 130, 15–25. [Google Scholar] [CrossRef]
- Medda, F.; Liu, Q. Determinants and strategies for the development of container terminals. J. Product. Anal. 2013, 40, 83–98. [Google Scholar] [CrossRef]
- Chang, Y.M.; Hamedi, M.; Haghani, A. Solving integrated problem of stowage planning with crane split by an improved genetic algorithm based on novel encoding mode. Meas. Control 2023, 56, 172–191. [Google Scholar] [CrossRef]
- Chen, J.H. A note on: A flexible crane scheduling methodology for container terminals. Flex. Serv. Manuf. J. 2019, 31, 34–40. [Google Scholar] [CrossRef]
- Iris, C.; Pacino, D. A Survey on the Ship Loading Problem; Springer International Publishing: New York, NY, USA, 2015; pp. 238–251. [Google Scholar]
- Wilson, I.D.; Roach, P.A. Container stowage planning: A methodology for generating computerised solutions. J. Oper. Res. Soc. 2000, 51, 1248–1255. [Google Scholar] [CrossRef]
- Pacino, D.; Delgado, A.; Jensen, R.M. Fast generation of near-optimal plans for eco-efficient stowage of large container vessels. In Proceedings of the 2nd International Conference on Computational Logistics, Hamburg, Germany, 19–22 September 2011. [Google Scholar]
- Ambrosino, D.; Sciomachen, A.; Tanfani, E. Stowing a containership: The master bay plan problem. Transp. Res. Part Policy Pract. 2004, 38, 81–99. [Google Scholar] [CrossRef]
- Ambrosino, D.; Sciomachen, A.; Tanfani, E. A decomposition heuristics for the container ship stowage problem. J. Heuristics 2006, 12, 211–233. [Google Scholar] [CrossRef]
- Ambrosino, D.; Paolucci, M.; Sciomachen, A. Experimental evaluation of mixed integer programming models for the multi-port master bay plan problem. Flex. Serv. Manuf. J. 2015, 27, 263–284. [Google Scholar] [CrossRef]
- Ting, S.C.; Tzeng, G.H. Bi-criteria approach to container ship slot allocation in liner shipping. Marit. Econ. Logist. 2016, 18, 141–157. [Google Scholar] [CrossRef]
- Bilican, M.S.; Evren, R.; Karatas, D.M. A Mathematical Model and Two-Stage Heuristic for the Container Stowage Planning Problem With Stability Parameters. IEEE Access 2020, 8, 113392–113413. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Y.; Ji, S.; Zheng, L.; Xu, J. Multi-stage hierarchical decomposition approach for stowage planning problem in inland container liner shipping. J. Oper. Res. Soc. 2020, 71, 381–399. [Google Scholar] [CrossRef]
- Ambrosino, D.; Sciomachen, A. A shipping line stowage-planning procedure in the presence of hazardous containers. Marit. Econ. Logist. 2021, 23, 49–70. [Google Scholar] [CrossRef]
- Iris, Ç.; Pacino, D.; Ropke, S.; Larsen, A. Integrated Berth Allocation and Quay Crane Assignment Problem: Set partitioning models and computational results. Transp. Res. Part Logist. Transp. Rev. 2015, 81, 75–97. [Google Scholar] [CrossRef]
- Iris, Ç.; Lam, J.S.L. Recoverable robustness in weekly berth and quay crane planning. Transp. Res. Part Methodol. 2019, 122, 365–389. [Google Scholar] [CrossRef]
- Wilson, I.D.; Roach, P.A.; Ware, J.A. Container stowage pre-planning: Using search to generate solutions, a case study. Knowl. Based Syst. 2001, 14, 137–145. [Google Scholar] [CrossRef]
- Sciomachen, A.; Tanfani, E. A 3D-BPP approach for optimising stowage plans and terminal productivity. Eur. J. Oper. Res. 2007, 183, 1433–1446. [Google Scholar] [CrossRef]
- Lee, D.H.; Wang, H.Q.; Miao, L.X. Quay crane scheduling with handling priority in port container terminals. Eng. Optim. 2008, 40, 179–189. [Google Scholar] [CrossRef]
- Shen, Y.F.; Zhao, N.; Mi, W.J. Group-Bay Stowage Planning Problem for Container Ship. Pol. Marit. Res. 2016, 23, 152–159. [Google Scholar]
- Iris, Ç.; Christensen, J.; Pacino, D.; Ropke, S. Flexible ship loading problem with transfer vehicle assignment and scheduling. Transp. Res. Part Methodol. 2018, 111, 113–134. [Google Scholar] [CrossRef]
- Pacino, D. Crane Intensity and Block Stowage Strategies in Stowage Planning; Springer International Publishing: New York, NY, USA, 2018; pp. 191–206. [Google Scholar]
- Azevedo, A.T.; Neto, L.L.D.; Chaves, A.A.; Moretti, A.C. Solving the 3D stowage planning problem integrated with the quay crane scheduling problem by representation by rules and genetic algorithm. Appl. Soft Comput. 2018, 65, 495–516. [Google Scholar] [CrossRef]
- Steenken, D.; Voss, S.; Stahlbock, R. Container terminal operation and operations research—A classification and literature review. OR Spectr. 2004, 26, 3–49. [Google Scholar]
- Wang, S.A. Essential elements in tactical planning models for container liner shipping. Transp. Res. Part Methodol. 2013, 54, 84–99. [Google Scholar] [CrossRef]
- Jingjing, Y.; Guolei, T.; Da, L. Optimal Number of Quay Cranes in Container Terminals with Twin-40-Feet Quay Cranes. In Proceedings of the 10th International Conference on Computer Modeling and Simulation, Sydney, Australia, 8–10 January 2018. [Google Scholar]
- Fan, H.Y. A modification to particle swarm optimization algorithm. Eng. Comput. 2002, 19, 970–989. [Google Scholar] [CrossRef]
- Mahfouf, M.; Chen, M.Y.; Linkens, D.A. Adaptive weighted particle swarm optimisation for multi-objective optimal design of alloy steels. In Proceedings of the Parallel Problem Solving from Nature-PPSN VIII: 8th International Conference, Birmingham, UK, 18–22 September 2004; pp. 762–771. [Google Scholar]




| The number of Double-Bay | 02 | 06 | 10 | 14 | 18 | 22 | 26 | 30 | 34 |
|---|---|---|---|---|---|---|---|---|---|
| The priority of Bay | 3.43 | −2.51 | 0.33 | 1.37 | 9.78 | −5.32 | 8.67 | 6.65 | −7.34 |
| The number of Double-Bay | 18 | 26 | 30 | 02 | 14 | 10 | 06 | 22 | 34 |
|---|---|---|---|---|---|---|---|---|---|
| The priority of Bay | 9.78 | 8.67 | 6.65 | 3.43 | 1.37 | 0.33 | −2.51 | −5.32 | −7.34 |
| Cargo Volume (20ft) | Destination Ports | |||||||
|---|---|---|---|---|---|---|---|---|
| B | C | D | E | F | G | Total | ||
| Starting Ports | A | 214 | 303 | 210 | 98 | 139 | 244 | 1208 |
| B | - | 58 | 291 | 125 | 126 | 210 | 810 | |
| C | - | - | 48 | 290 | 330 | 80 | 749 | |
| D | - | - | - | 20 | 52 | 34 | 106 | |
| E | - | - | - | - | 120 | 0 | 120 | |
| F | - | - | - | - | - | 165 | 165 | |
| Cargo Volume (40ft) | Destination Ports | |||||||
|---|---|---|---|---|---|---|---|---|
| B | C | D | E | F | G | Total | ||
| Starting Ports | A | 13 | 11 | 0 | 0 | 6 | 15 | 45 |
| B | - | 10 | 16 | 18 | 0 | 0 | 44 | |
| C | - | - | 4 | 6 | 20 | 10 | 40 | |
| D | - | - | - | 0 | 40 | 0 | 40 | |
| E | - | - | - | - | 8 | 10 | 18 | |
| F | - | - | - | - | - | 8 | 8 | |
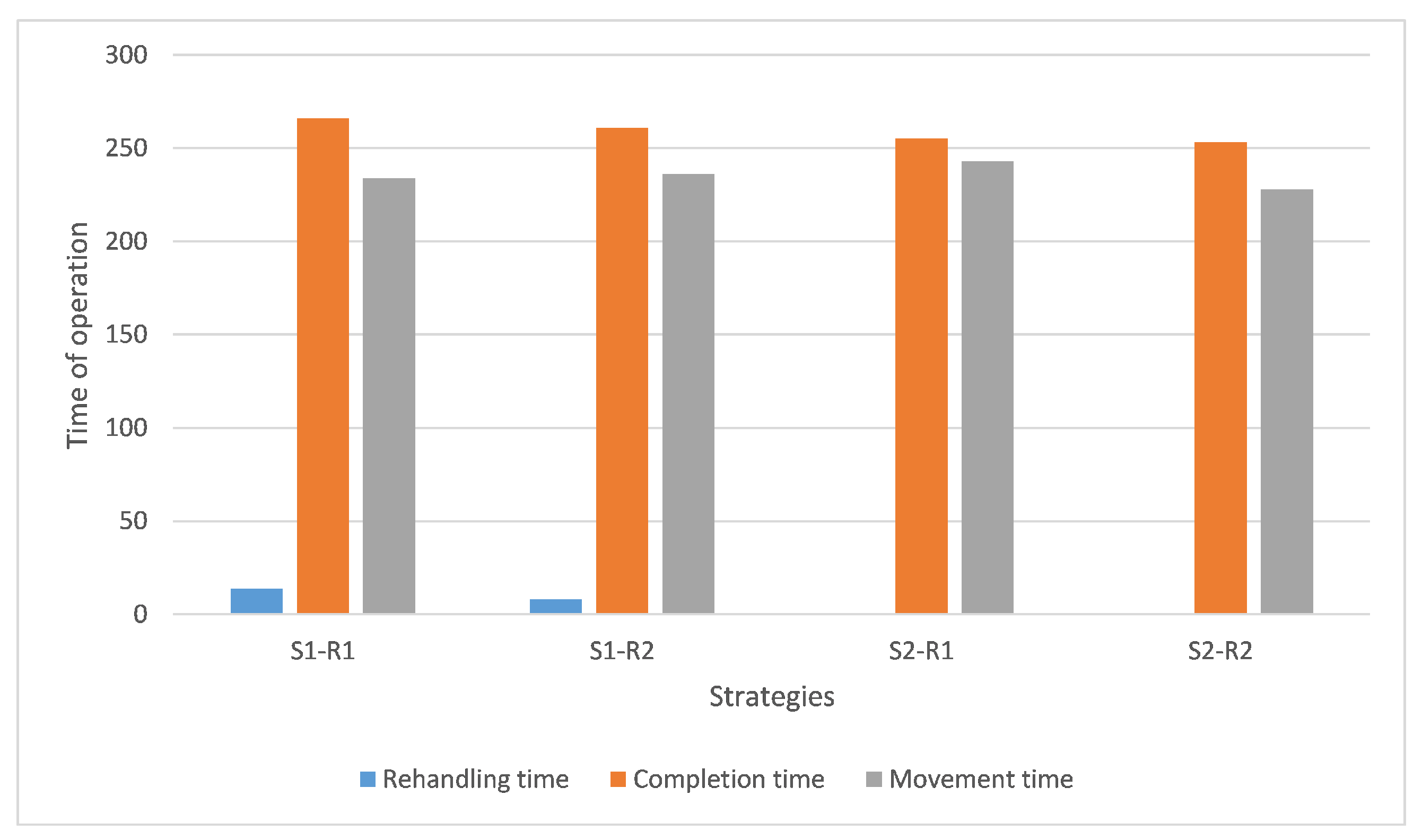
| Strategies | S1-R1 | S1-R2 | S2-R1 | S2-R2 |
|---|---|---|---|---|
| Max/min | 1131 | 1195 | 1214 | 1145 |
| Min/min | 1128 | 1134 | 1206 | 1119 |
| Avg/min | 1129.5 | 1164.5 | 1210 | 1122 |
| Gap/% | − | 3.1% | 7.13% | −0.66% |
| QC | Movement Time /min | Loading/Unloading Time /min | Completion Time /min | Berthing Time /min | |
|---|---|---|---|---|---|
| Port A | 1 | 16 | 130 | 146 | |
| 2 | 24 | 195 | 219 | 219 | |
| Port B | 1 | 20 | 101 | 121 | |
| 2 | 16 | 185 | 201 | 201 | |
| Port C | 1 | 12 | 152 | 164 | |
| 2 | 24 | 156 | 180 | 180 | |
| Port D | 1 | 0 | 87 | 87 | |
| 2 | 32 | 108 | 140 | 140 | |
| Port E | 1 | 8 | 99 | 107 | |
| 2 | 4 | 87 | 91 | 107 | |
| Port F | 1 | 20 | 140 | 160 | |
| 2 | 8 | 136 | 144 | 160 | |
| Port G | 1 | 32 | 102 | 134 | |
| 2 | 12 | 103 | 115 | 134 |
| QC | Movement Time /min | Loading/Unloading Time /min | Completion Time /min | Berthing Time /min | |
|---|---|---|---|---|---|
| Port A | 1 | 18 | 408 | 426 | |
| 2 | 22 | 419 | 441 | 441 | |
| Port B | 1 | 26 | 462 | 488 | |
| 2 | 20 | 287 | 307 | 488 | |
| Port C | 1 | 32 | 510 | 542 | |
| 2 | 10 | 341 | 351 | 542 | |
| Port D | 1 | 16 | 268 | 284 | |
| 2 | 26 | 172 | 198 | 284 | |
| Port E | 1 | 20 | 254 | 274 | |
| 2 | 20 | 294 | 314 | 314 | |
| Port F | 1 | 14 | 336 | 350 | |
| 2 | 10 | 392 | 402 | 402 | |
| Port G | 1 | 6 | 230 | 236 | |
| 2 | 10 | 294 | 304 | 304 |
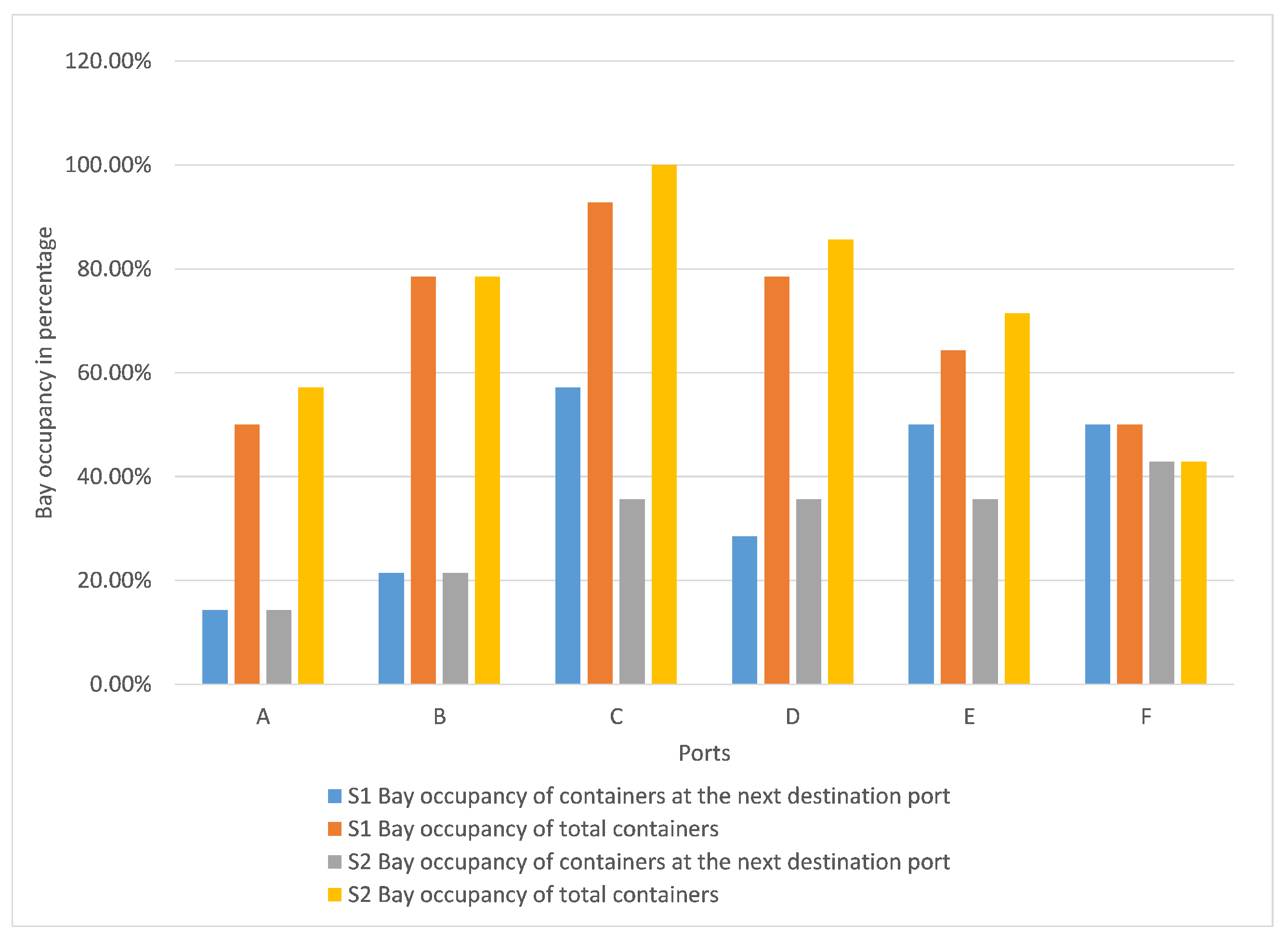
| Ports | A | B | C | D | E | F | G | Total |
|---|---|---|---|---|---|---|---|---|
| Single bay/min | 441 | 488 | 542 | 284 | 314 | 402 | 304 | 2775 |
| Double-bay/min | 219 | 201 | 180 | 140 | 107 | 160 | 134 | 1141 |
| Difference ratio/% | 50.34 | 58.81 | 66.79 | 50.7 | 65.92 | 60.2 | 55.92 | 58.89 |
| Ports | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| Single Bay | 19/28 | 24/28 | 27/28 | 22/28 | 18/28 | 9/28 |
| Double-bay | 16/28 | 22/24 | 28/28 | 24/28 | 20/28 | 12/28 |
| Strategies | S-1 | S1-R1 | S1-R2 | S2-R1 | S2-R2 |
|---|---|---|---|---|---|
| Max/min | 1532 | 1131 | 1195 | 1214 | 1145 |
| Min/min | 1506 | 1128 | 1134 | 1206 | 1119 |
| Avg/min | 1519 | 1129.5 | 1164.5 | 1210 | 1122 |
| Gap/% | - | −25.6% | −23.33% | −20.3% | −26.13% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Yu, H.; Zhu, X. Study of the Master Bay Plan Problem Based on a Twin 40-Foot Quay Crane Operation. J. Mar. Sci. Eng. 2023, 11, 807. https://doi.org/10.3390/jmse11040807
Yang Y, Yu H, Zhu X. Study of the Master Bay Plan Problem Based on a Twin 40-Foot Quay Crane Operation. Journal of Marine Science and Engineering. 2023; 11(4):807. https://doi.org/10.3390/jmse11040807
Chicago/Turabian StyleYang, Yongsheng, Haizhou Yu, and Xiaolin Zhu. 2023. "Study of the Master Bay Plan Problem Based on a Twin 40-Foot Quay Crane Operation" Journal of Marine Science and Engineering 11, no. 4: 807. https://doi.org/10.3390/jmse11040807
APA StyleYang, Y., Yu, H., & Zhu, X. (2023). Study of the Master Bay Plan Problem Based on a Twin 40-Foot Quay Crane Operation. Journal of Marine Science and Engineering, 11(4), 807. https://doi.org/10.3390/jmse11040807





