A Novel Method for Imputing Missing Values in Ship Static Data Based on Generative Adversarial Networks
Abstract
1. Introduction
2. Methodology
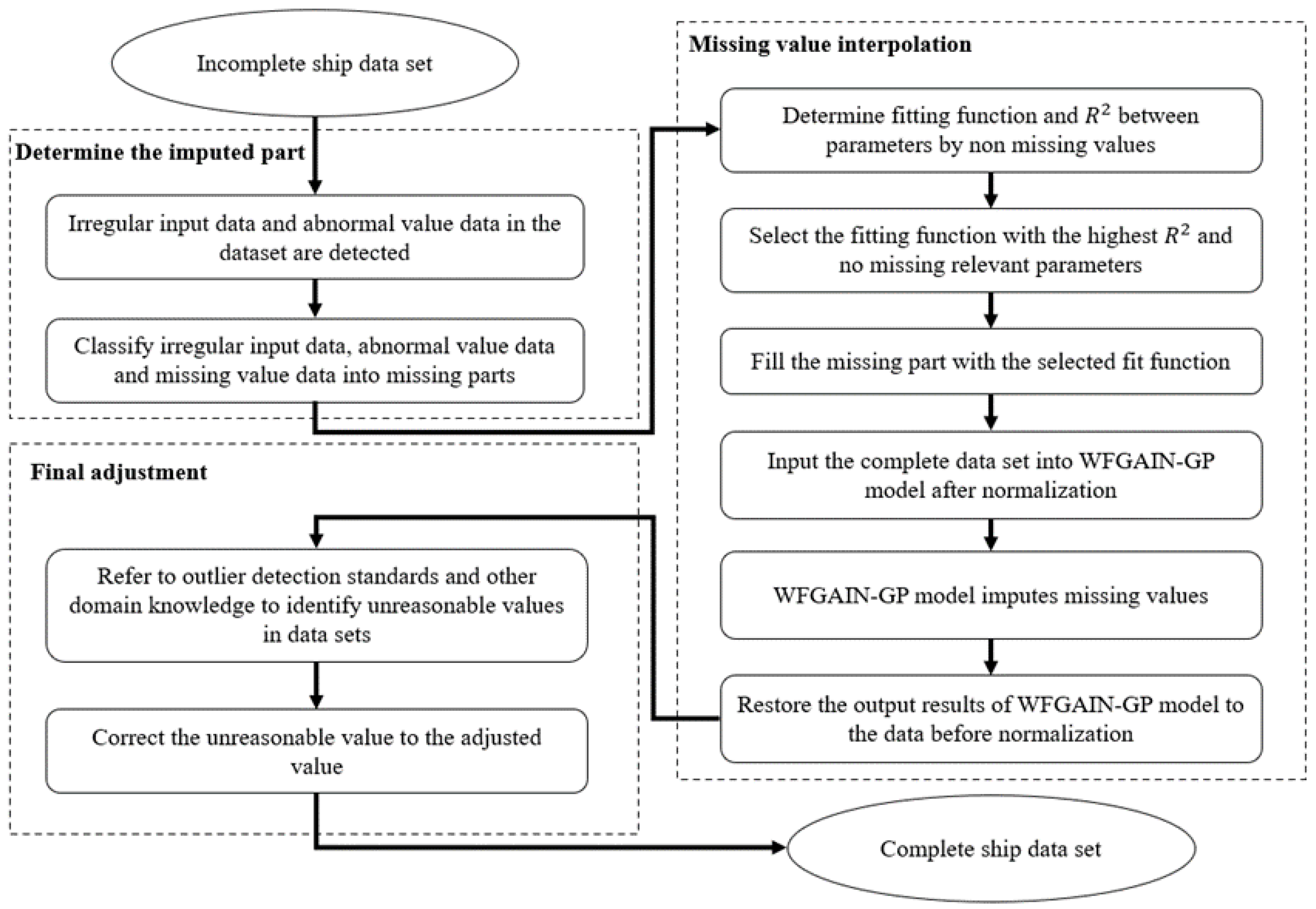
2.1. Missing Data Handling Process
| Algorithm 1: Determining the portion of data that needs to be imputed | |
| 1: | for do |
| 2: | for do |
| 3: | if is irregular input data, missing value data, or abnormal value data |
| 4: | Set to null. |
| 5: | = 0 |
| 6: | Else |
| 7: | = 1 |
| 8: | end if |
| 9: | end for |
| 10: | end for |
| where is the data value of the th parameter in the th ship case. is the mask value of the th parameter in the th ship case. | |
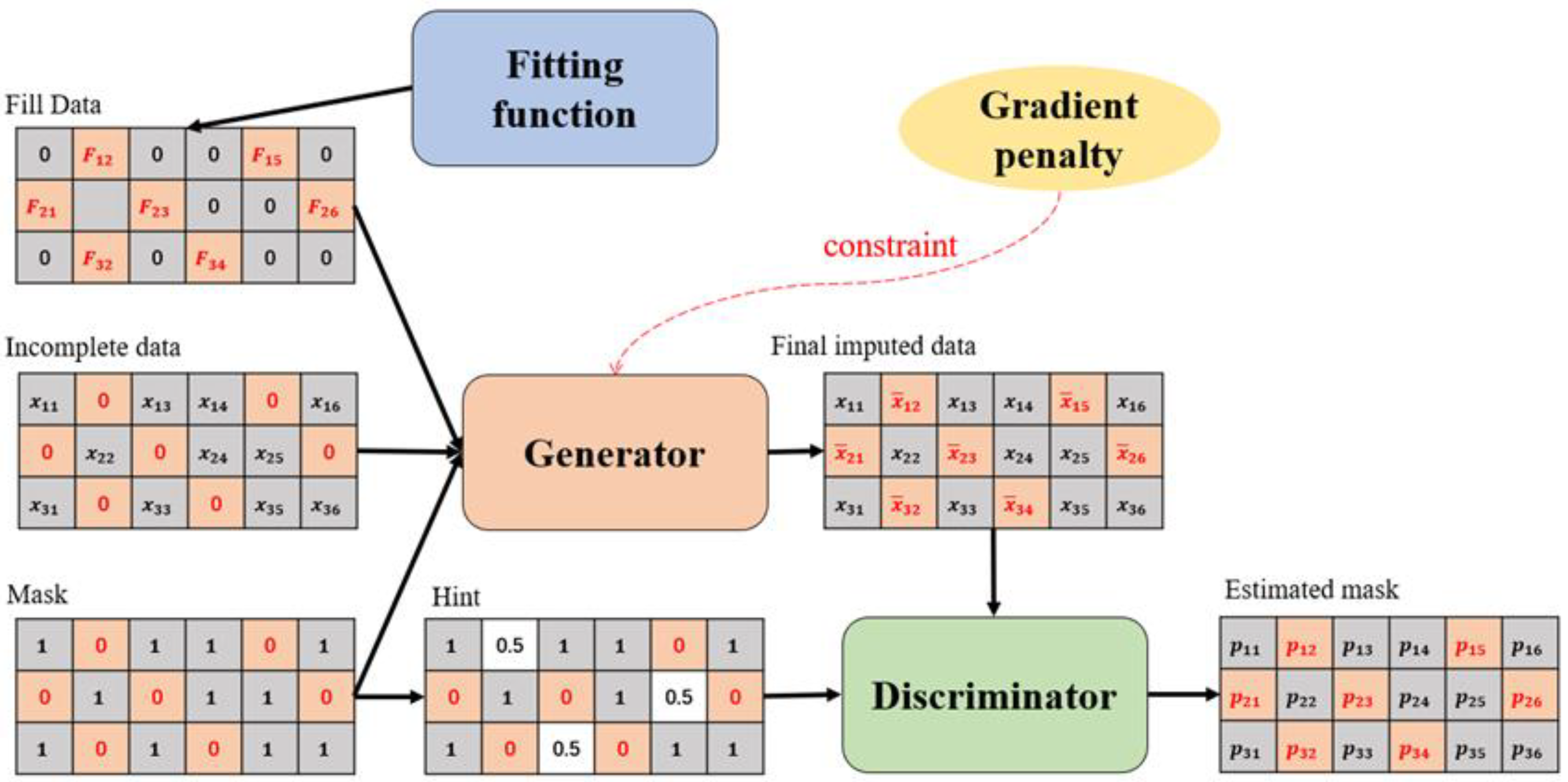
| Algorithm 2: Impute missing values | |
| 1: | /*Temporary filling */ |
| 2: | for do |
| 3: | for do |
| 4: | if is null |
| 5: | Determine the available with the maximum value. |
| 6: | Set to the of . |
| 7: | Else |
| 8: | Set to the . |
| 9: | end if |
| 10: | end for |
| 11: | end for |
| 12: | /*Imputation*/ |
| 13: | Input: Incomplete dataset , Mask vector . |
| 14: | for number of training iterations do |
| 15: | for k steps do |
| 16: | Train the discriminator D. |
| 17: | end for |
| 18: | Train the Generator G. |
| 19: | end for |
| 20: | Output: Complete dataset |
| where is the data value of the th parameter in the th ship case. is the mask value of the mask vector . is the fitted value of the polynomial fitting function . belongs to the imputed complete dataset after temporary filling. | |
| Algorithm 3: Adjusting predicted values with ship domain knowledge | |
| 1: | for do |
| 2: | for do |
| 3: | if = 0 and is abnormal value data |
| 4: | Re-estimate the value of . or replace with the . |
| 5: | end if |
| 6: | end for |
| 7: | end for |
| where is the data value of the th parameter in th ship case. is the mask value of the th parameter in th ship case. is the fitted value of the polynomial fitting function . | |
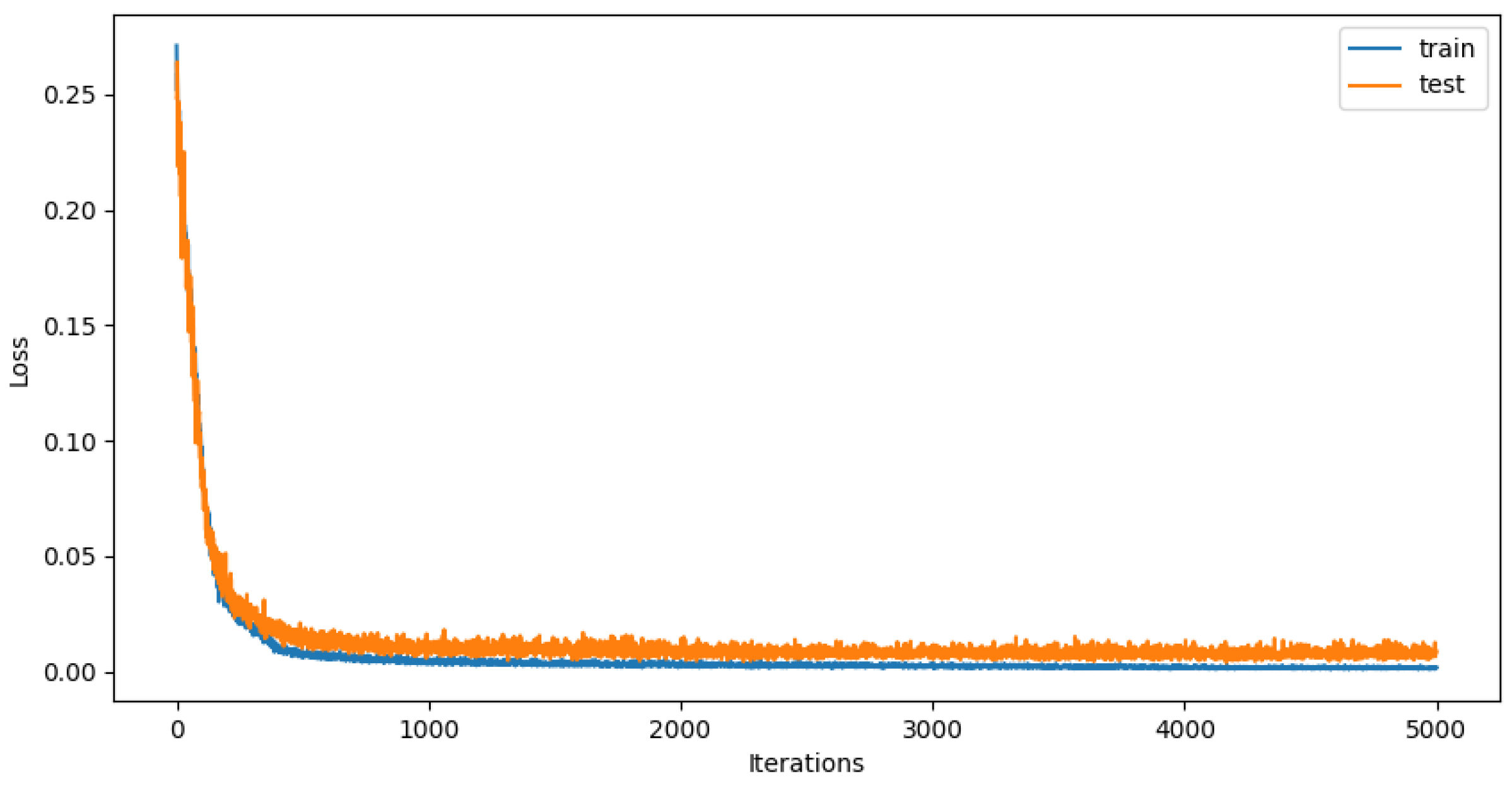
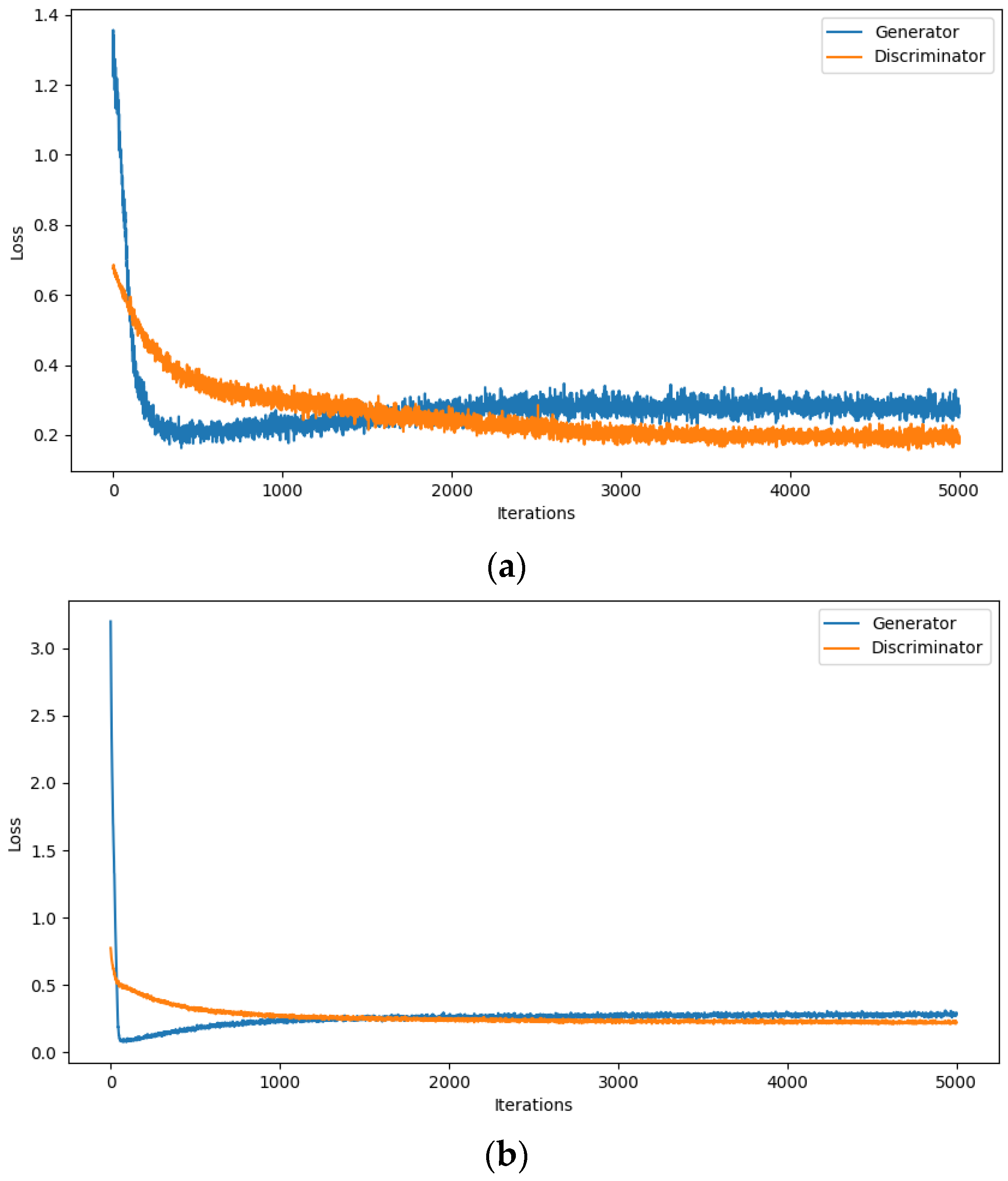
2.2. WFGAIN-GP
- Removes the sigmoid activation function in the last layer of D.
- Removes the log from the loss functions of G and D.
- After updating the parameters of D each time, truncates so that their absolute values do not exceed a fixed constant.
- Uses RMSProp or SGD instead of momentum-based optimization algorithms.
- Therefore, based on the third modification, the new and are defined as follows:
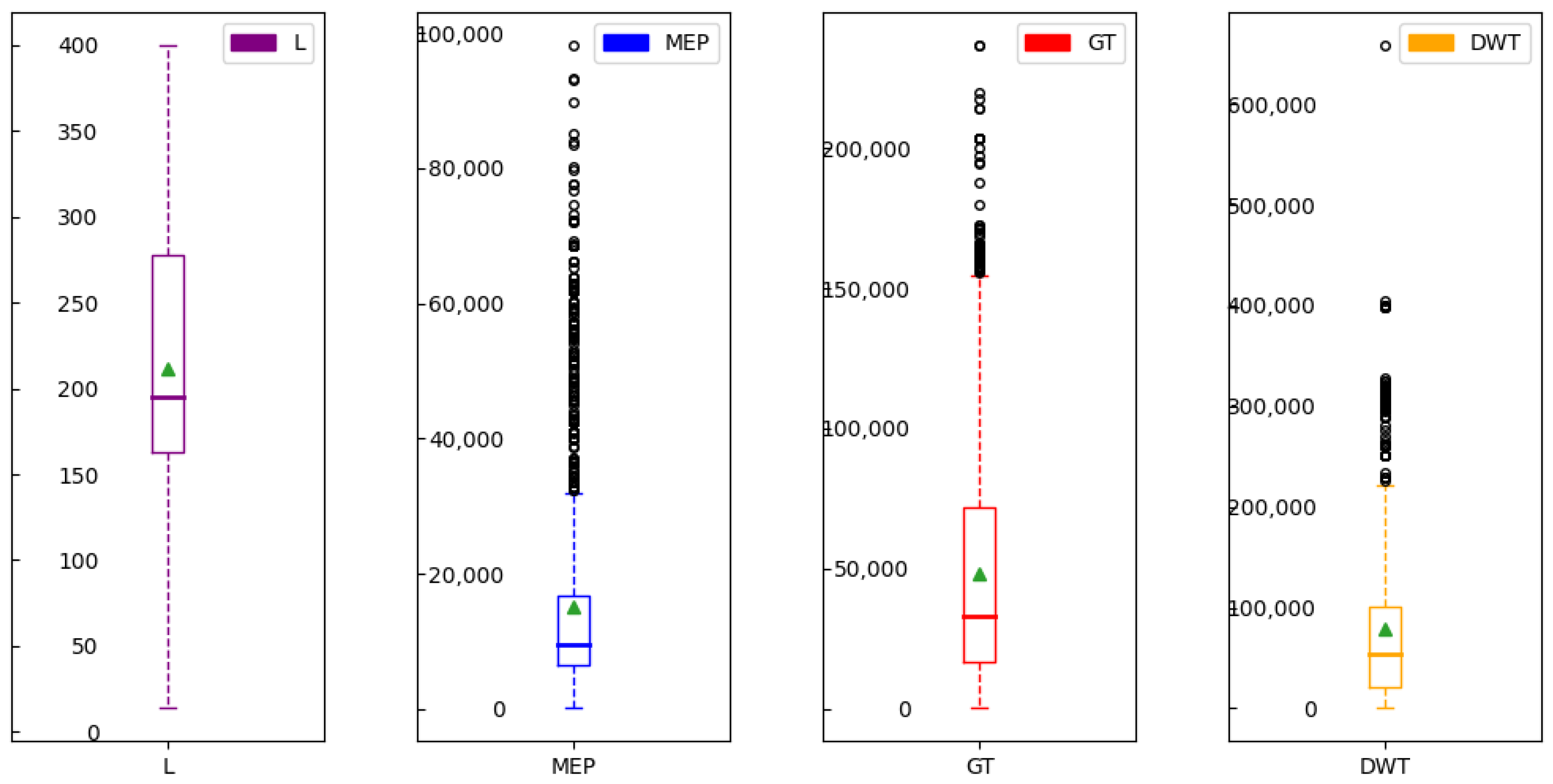
2.3. Detection of Outliers
2.4. Experimental Evaluation Criteria
3. Case Study
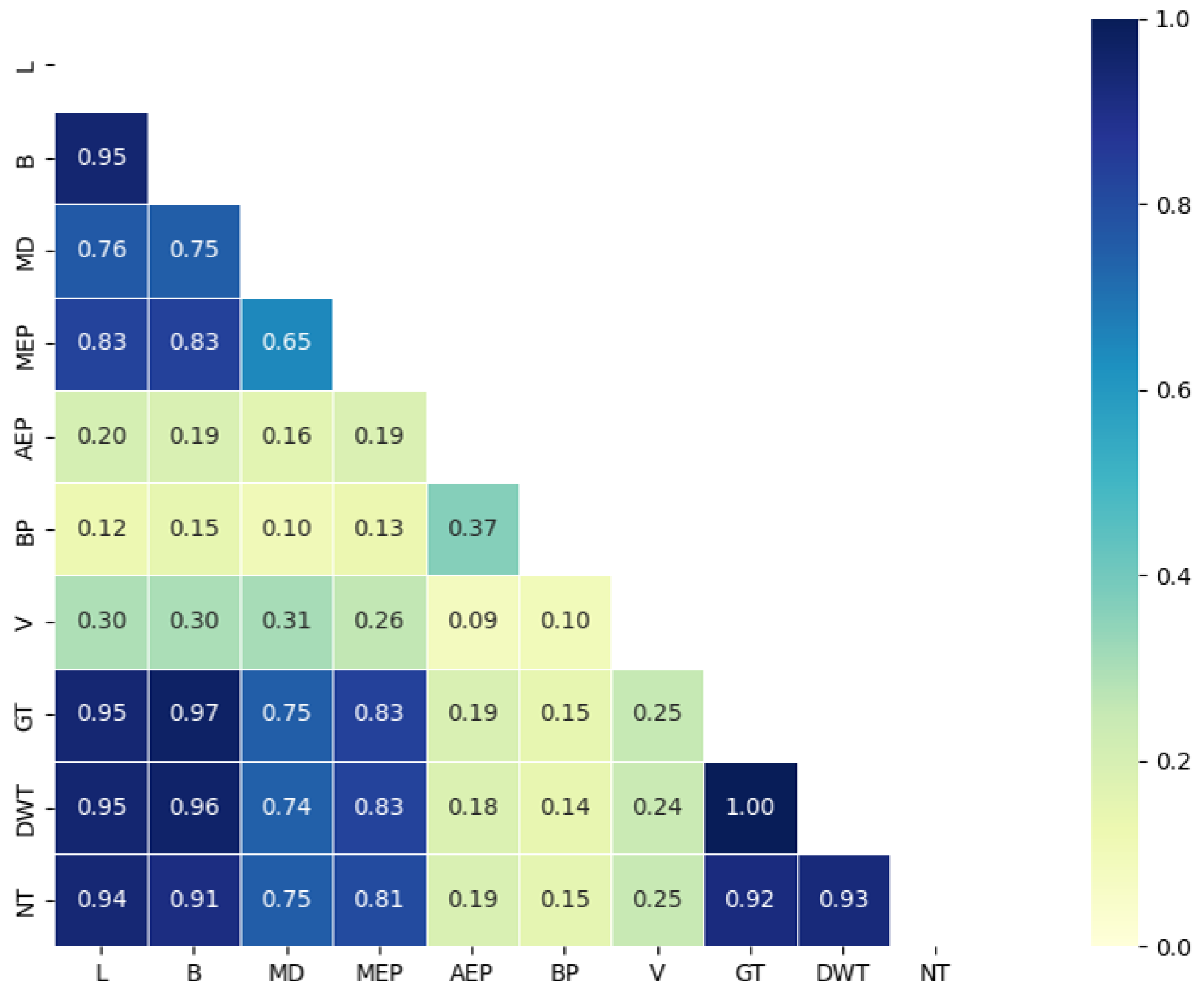
3.1. Ship Database Analysis
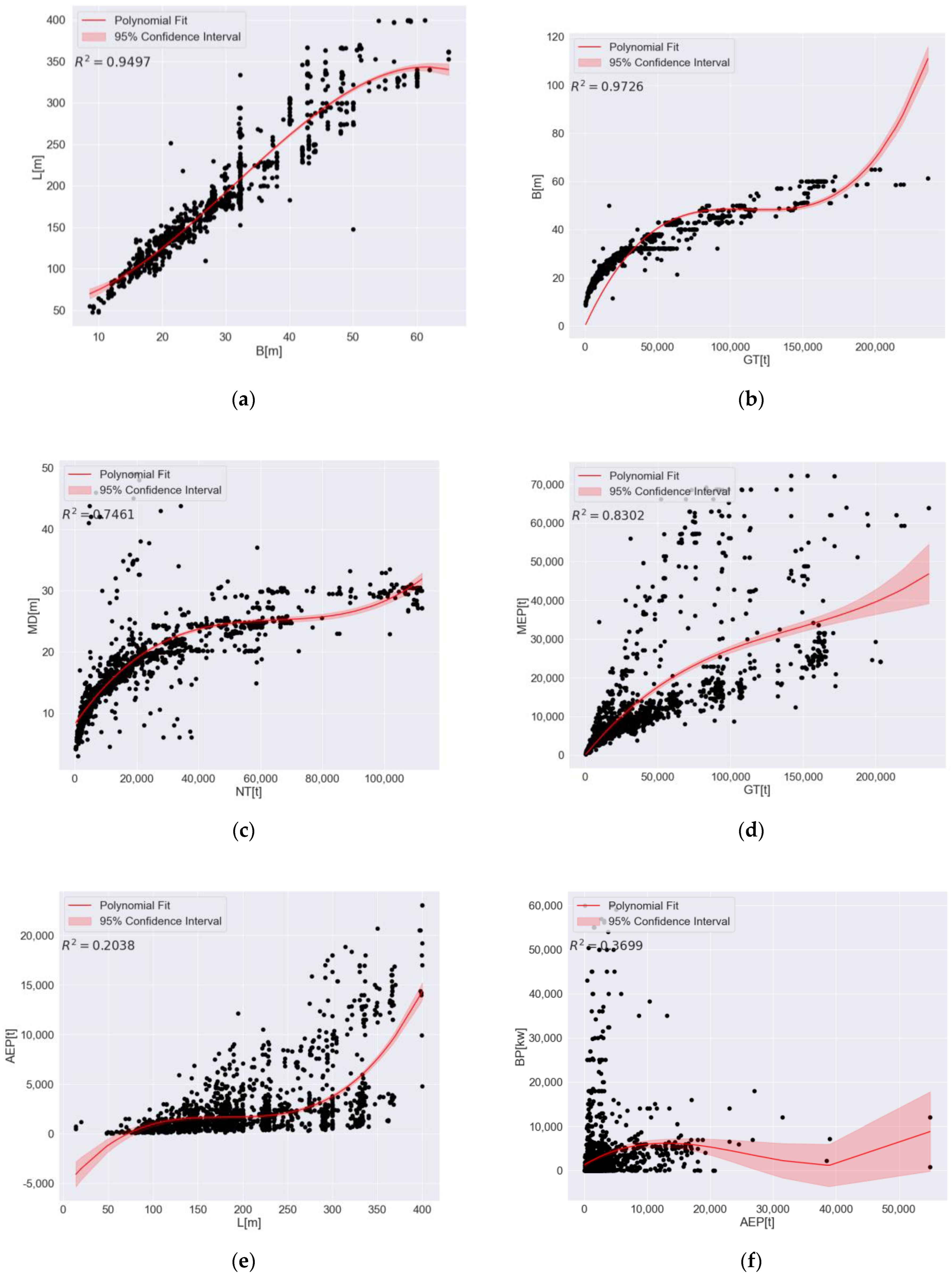
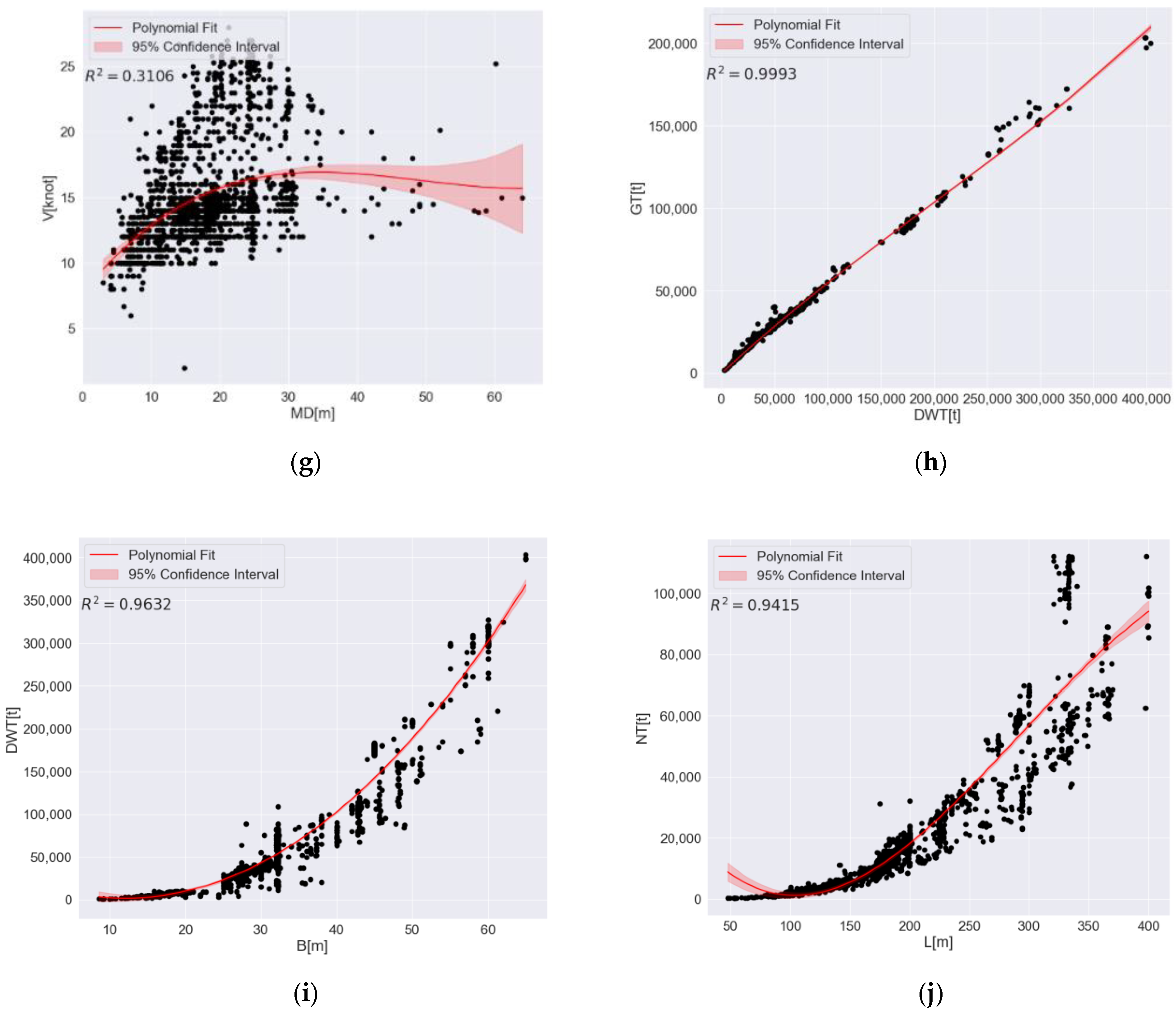
3.2. Polynomial Fit Analysis
3.3. Comparative Experimental Analysis
3.4. Analysis of Different Characteristic Dimensions
3.5. Imputation of Real Missing Values
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Ship Principal Parameters | Valid Data | Missing Data | Mean | Median | Minimum | Maximum | Std. Dev | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|---|
| L [m] | 3090 | 52 | 255.3 | 400.0 | 263.2 | 50.0 | 83.8 | −0.14 | −1.06 |
| B [m] | 2950 | 192 | 36.1 | 61.5 | 32.3 | 11.3 | 10.6 | 0.22 | −0.70 |
| MD [m] | 2434 | 708 | 18.8 | 29.9 | 19.1 | 4.0 | 5.9 | −0.02 | −0.77 |
| MEP [kw] | 2844 | 298 | 37,619.9 | 122,650.0 | 36,560.0 | 933.0 | 24,093.1 | 0.33 | −0.81 |
| AEP [kw] | 1972 | 1170 | 6436.3 | 88,180.0 | 4000.0 | 80.0 | 6700.6 | 3.25 | 25.24 |
| BP [kw] | 2595 | 547 | 2585.6 | 7000.0 | 2000.0 | 7.5 | 2056.0 | 0.42 | −1.16 |
| V [knot] | 1673 | 1469 | 20.9 | 28.8 | 22.0 | 5.0 | 4.0 | −1.09 | 1.08 |
| GT [t] | 3142 | 0 | 64,360.0 | 236,583.0 | 47,914.0 | 967.0 | 53,233.8 | 1.02 | 0.41 |
| DWT [t] | 3129 | 13 | 70,955.8 | 658,129.0 | 58,255.0 | 1.0 | 54,083.5 | 1.17 | 4.11 |
| NT [t] | 3141 | 1 | 33,180.7 | 130,371.0 | 24,504.0 | 468.0 | 27,406.6 | 0.90 | 0.13 |
| Ship Principal Parameters | Valid Data | Missing Data | Mean | Median | Minimum | Maximum | Std. Dev | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|---|
| L [m] | 4954 | 46 | 211.7 | 228 | 40.8 | 340 | 91.1 | −0.17 | −1.2 |
| B [m] | 4739 | 252 | 36.1 | 32.3 | 7 | 60.1 | 17.4 | −0.01 | −1.32 |
| MD [m] | 4289 | 702 | 16.2 | 18.8 | 3 | 29.8 | 8.1 | −0.05 | −1.29 |
| MEP [kw] | 4542 | 449 | 14,727.8 | 12,500 | 800 | 62,749 | 9597.4 | 0.65 | 0.28 |
| AEP [kw] | 3663 | 1328 | 1768.6 | 1110 | 60 | 33,351 | 2333.8 | 6.17 | 59.04 |
| BP [kw] | 3019 | 1972 | 1426.2 | 720 | 10 | 7100 | 1637.8 | 1.3 | 0.93 |
| V [knot] | 3694 | 1297 | 13.6 | 14 | 6 | 48 | 2.4 | 2.43 | 39 |
| GT [t] | 4987 | 4 | 63,034.3 | 42,884 | 424 | 170,611 | 59,140.4 | 0.71 | −0.97 |
| DWT [t] | 4983 | 8 | 116,425.6 | 74,993 | 498 | 380,000 | 114,894.9 | 0.77 | −0.93 |
| NT [t] | 4990 | 1 | 38,544.4 | 22,259.5 | 60 | 112,281 | 39,900.4 | 0.85 | −0.85 |
| Static Database (Container Ship) | Static Database (Oil Tanker) | ||||
|---|---|---|---|---|---|
| 205.440 | 91 | 0.000 | 514.417 | 131 | 0.000 |
Appendix B
| Algorithm | RMSE | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Container Ship | Oil Tanker | |||||||||||
| 10% | 20% | 30% | 40% | 50% | 60% | 10% | 20% | 30% | 40% | 50% | 60% | |
| MF | 0.225 | 0.232 | 0.241 | 0.249 | 0.268 | 0.291 | 0.254 | 0.268 | 0.288 | 0.297 | 0.329 | 0.344 |
| PF | 0.273 | 0.283 | 0.312 | 0.337 | 0.342 | 0.359 | 0.289 | 0.307 | 0.323 | 0.347 | 0.356 | 0.381 |
| GAIN | 0.215 | 0.221 | 0.235 | 0.246 | 0.258 | 0.269 | 0.232 | 0.242 | 0.249 | 0.255 | 0.263 | 0.270 |
| WFGAIN-GP | 0.216 | 0.219 | 0.238 | 0.243 | 0.255 | 0.273 | 0.241 | 0.243 | 0.251 | 0.262 | 0.267 | 0.275 |
| RMSE | ||||||||
|---|---|---|---|---|---|---|---|---|
| Ship Principal Parameters | Container Ship | Oil Tanker | ||||||
| MF | PF | GAIN | WFGAIN-GP | MF | PF | GAIN | WFGAIN-GP | |
| L [m] | 0.166 | 0.185 | 0.989 | 0.109 | 0.175 | 0.227 | 0.105 | 0.101 |
| B [m] | 0.135 | 0.194 | 0.109 | 0.117 | 0.156 | 0.235 | 0.128 | 0.108 |
| MD [m] | 0.197 | 0.201 | 0.115 | 0.103 | 0.199 | 0.216 | 0.119 | 0.115 |
| MEP [kw] | 0.211 | 0.336 | 0.178 | 0.188 | 0.230 | 0.356 | 0.204 | 0.196 |
| AEP [kw] | 0.347 | 0.450 | 0.296 | 0.293 | 0.358 | 0.483 | 0.278 | 0.281 |
| BP [kw] | 0.312 | 0.443 | 0.255 | 0.234 | 0.327 | 0.455 | 0.251 | 0.245 |
| V [knot] | 0.175 | 0.225 | 0.143 | 0.131 | 0.133 | 0.163 | 0.103 | 0.106 |
| GT [t] | 0.323 | 0.417 | 0.269 | 0.278 | 0.337 | 0.454 | 0.291 | 0.289 |
| DWT [t] | 0.296 | 0.363 | 0.268 | 0.250 | 0.319 | 0.408 | 0.263 | 0.267 |
| NT [t] | 0.244 | 0.298 | 0.207 | 0.192 | 0.266 | 0.369 | 0.197 | 0.189 |
References
- Sirimanne, S.N.; Hoffman, J.; Juan, W.; Asariotis, R.; Assaf, M.; Ayala, G.; Benamara, H.; Chantrel, D.; Hoffmann, J. Review of maritime transport 2019. In Proceedings of the United Nations Conference on Trade and Development, Geneva, Switzerland, 24–25 September 2019. [Google Scholar]
- Imtiaz, S.A.; Shah, S.L. Treatment of missing values in process data analysis. Can. J. Chem. Eng. 2008, 86, 838–858. [Google Scholar] [CrossRef]
- Khatibisepehr, S.; Huang, B.; Khare, S. Design of inferential sensors in the process industry: A review of Bayesian methods. J. Process Control 2013, 23, 1575–1596. [Google Scholar] [CrossRef]
- Wang, Z.; Claramunt, C.; Wang, Y. Extracting global shipping networks from massive historical automatic identification system sensor data: A bottom-up approach. Sensors 2019, 19, 3363. [Google Scholar] [CrossRef] [PubMed]
- Jaskólski, K.; Marchel, Ł.; Felski, A.; Jaskólski, M.; Specht, M. Automatic Identification System (AIS) Dynamic Data Integrity Monitoring and Trajectory Tracking Based on the Simultaneous Localization and Mapping (SLAM) Process Model. Sensors 2021, 21, 8430. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Chen, X. Inference of single vessel behaviour with incomplete satellite-based AIS data. J. Navig. 2013, 66, 813–823. [Google Scholar] [CrossRef]
- Mao, S.; Tu, E.; Zhang, G.; Rachmawati, L.; Rajabally, E.; Huang, G.B. An automatic identification system (AIS) database for maritime trajectory prediction and data mining. In Proceedings of the ELM-2016, Singapore, 13–15 December 2016; Springer International Publishing: Cham, Switzerland, 2018; pp. 241–257. [Google Scholar]
- Dobrkovic, A.; Iacob, M.E.; van Hillegersberg, J. Maritime pattern extraction and route reconstruction from incomplete AIS data. Int. J. Data Sci. Anal. 2018, 5, 111–136. [Google Scholar] [CrossRef]
- Gutierrez-Torre, A.; Berral, J.L.; Buchaca, D.; Guevara, M.; Soret, A.; Carrera, D. Improving maritime traffic emission estimations on missing data with CRBMs. Eng. Appl. Artif. Intell. 2020, 94, 103793. [Google Scholar] [CrossRef]
- Guo, S.; Mou, J.; Chen, L.; Chen, P. Improved kinematic interpolation for AIS trajectory reconstruction. Ocean Eng. 2021, 234, 109256. [Google Scholar] [CrossRef]
- Gao, D.W.; Zhu, Y.S.; Zhang, J.F.; He, Y.K.; Yan, K.; Yan, B.R. A novel MP-LSTM method for ship trajectory prediction based on AIS data. Ocean Eng. 2021, 228, 108956. [Google Scholar] [CrossRef]
- Cheliotis, M.; Gkerekos, C.; Lazakis, I.; Theotokatos, G. A novel data condition and performance hybrid imputation method for energy efficient operations of marine systems. Ocean Eng. 2019, 188, 106220. [Google Scholar] [CrossRef]
- Gao, J.; Cai, Z.; Yu, W.; Sun, W. Trajectory Data Compression Algorithm Based on Ship Navigation State and Acceleration Variation. J. Mar. Sci. Eng. 2023, 11, 216. [Google Scholar] [CrossRef]
- Ekinci, S.; Çelebi, U.B.; Bal, M.; Amasyali, M.F.; Boyaci, U.K. Predictions of oil/chemical tanker main design parameters using computational intelligence techniques. Appl. Soft Comput. 2011, 11, 2356–2366. [Google Scholar] [CrossRef]
- Chen, D.; Wang, X.; Li, Y.; Lang, J.; Zhou, Y.; Guo, X.; Zhao, Y. High-spatiotemporal-resolution ship emission inventory of China based on AIS data in 2014. Sci. Total Environ. 2017, 609, 776–787. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Wen, Y.; Zhang, Y.; Zhou, C.; Zhang, F.; Yang, T. Dynamic calculation of ship exhaust emissions based on real-time AIS data. Transp. Res. Part D Transp. Environ. 2020, 80, 102277. [Google Scholar] [CrossRef]
- Abramowski, T.; Cepowski, T.; Zvolenský, P. Determination of regression formulas for key design characteristics of container ships at preliminary design stage. New Trends Prod. Eng. 2018, 1, 247–257. [Google Scholar] [CrossRef]
- Gurgen, S.; Altin, I.; Ozkok, M. Prediction of main particulars of a chemical tanker at preliminary ship design using artificial neural network. Ships Offshore Struct. 2018, 13, 459–465. [Google Scholar] [CrossRef]
- Kim, Y.; Steen, S.; Muri, H. A novel method for estimating missing values in ship principal data. Ocean Eng. 2022, 251, 110979. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. arXiv 2014, arXiv:1406.2661. [Google Scholar] [CrossRef]
- Arjovsky, M.; Bottou, L. Towards principled methods for training generative adversarial networks. arXiv 2017, arXiv:1701.04862. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the International Conference on Machine Learning, PMLR, Honolulu, HI, USA, 23–29 July 2017; pp. 214–223. [Google Scholar]
- Sun, J.; Bhattarai, B.; Chen, Z.; Kim, T.K. Secgan: Parallel conditional generative adversarial networks for face editing via semantic consistency. arXiv 2021, arXiv:2111.09298. [Google Scholar]
- Pei, H.; Ren, K.; Yang, Y.; Liu, C.; Qin, T.; Li, D. Towards generating real-world time series data. In Proceedings of the 2021 IEEE International Conference on Data Mining (ICDM), Auckland, New Zealand, 7–10 December 2021; IEEE: New York, NY, USA, 2021; pp. 469–478. [Google Scholar]
- Shi, Y.; Han, L.; Han, L.; Chang, S.; Hu, T.; Dancey, D. A latent encoder coupled generative adversarial network (le-gan) for efficient hyperspectral image super-resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 3193441. [Google Scholar] [CrossRef]
- Poudevigne-Durance, T.; Jones, O.D.; Qin, Y. MaWGAN: A generative adversarial network to create synthetic data from datasets with missing data. Electronics 2022, 11, 837. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Mohammadi, S.; Zamani, H.; Gandomi, M.; Gandomi, A.H. A hybrid imputation method for multi-pattern missing data: A case study on type II diabetes diagnosis. Electronics 2021, 10, 3167. [Google Scholar] [CrossRef]
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A.C. Improved training of wasserstein gans. In Advances in Neural Information Processing Systems; MIT: Cambridge, MA, USA, 2017; Volume 30. [Google Scholar]
- Radford, A.; Metz, L.; Chintala, S. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv 2015, arXiv:1511.06434. [Google Scholar]
- Yoon, J.; Jordon, J.; Schaar, M. Gain: Missing data imputation using generative adversarial nets. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 5689–5698. [Google Scholar]
- Wang, Y.; Li, D.; Li, X.; Yang, M. PC-GAIN: Pseudo-label conditional generative adversarial imputation networks for incomplete data. Neural Netw. 2021, 141, 395–403. [Google Scholar] [CrossRef]
- Neves, D.T.; Alves, J.; Naik, M.G.; Proenca, A.J.; Prasser, F. From missing data imputation to data generation. J. Comput. Sci. 2022, 61, 101640. [Google Scholar] [CrossRef]
- Dong, W.; Fong, D.; Yoon, J.; Wan, E.; Bedford, L.; Tang, E.; Lam, C. Generative adversarial networks for imputing missing data for big data clinical research. BMC Med. Res. Methodol. 2021, 21, 78. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, P.; Yu, Y.; Li, X.; Biancardo, S.A.; Zhang, J. Missing data repairs for traffic flow with self-attention generative adversarial imputation net. IEEE Trans. Intell. Transp. Syst. 2021, 23, 7919–7930. [Google Scholar] [CrossRef]
- International Maritime Organization (IMO). Fourth Greenhouse Gas Study. 2020. Available online: https://www.imo.org/en/OurWork/Environment/Pages/Fourth-IMO-Greenhouse-Gas-Study-2020.aspx (accessed on 16 January 2023).
- Rubin, D.B. Inference and missing data. Biometrika 1976, 63, 581–592. [Google Scholar] [CrossRef]
- Little, R.J. A test of missing completely at random for multivariate data with missing values. J. Am. Stat. Assoc. 1988, 83, 1198–1202. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Tong, Y.; Yu, L.; Li, S.; Liu, J.; Qin, H.; Li, W. Polynomial fitting algorithm based on neural network. ASP Trans. Pattern Recognit. Intell. Syst. 2021, 1, 32–39. [Google Scholar] [CrossRef]


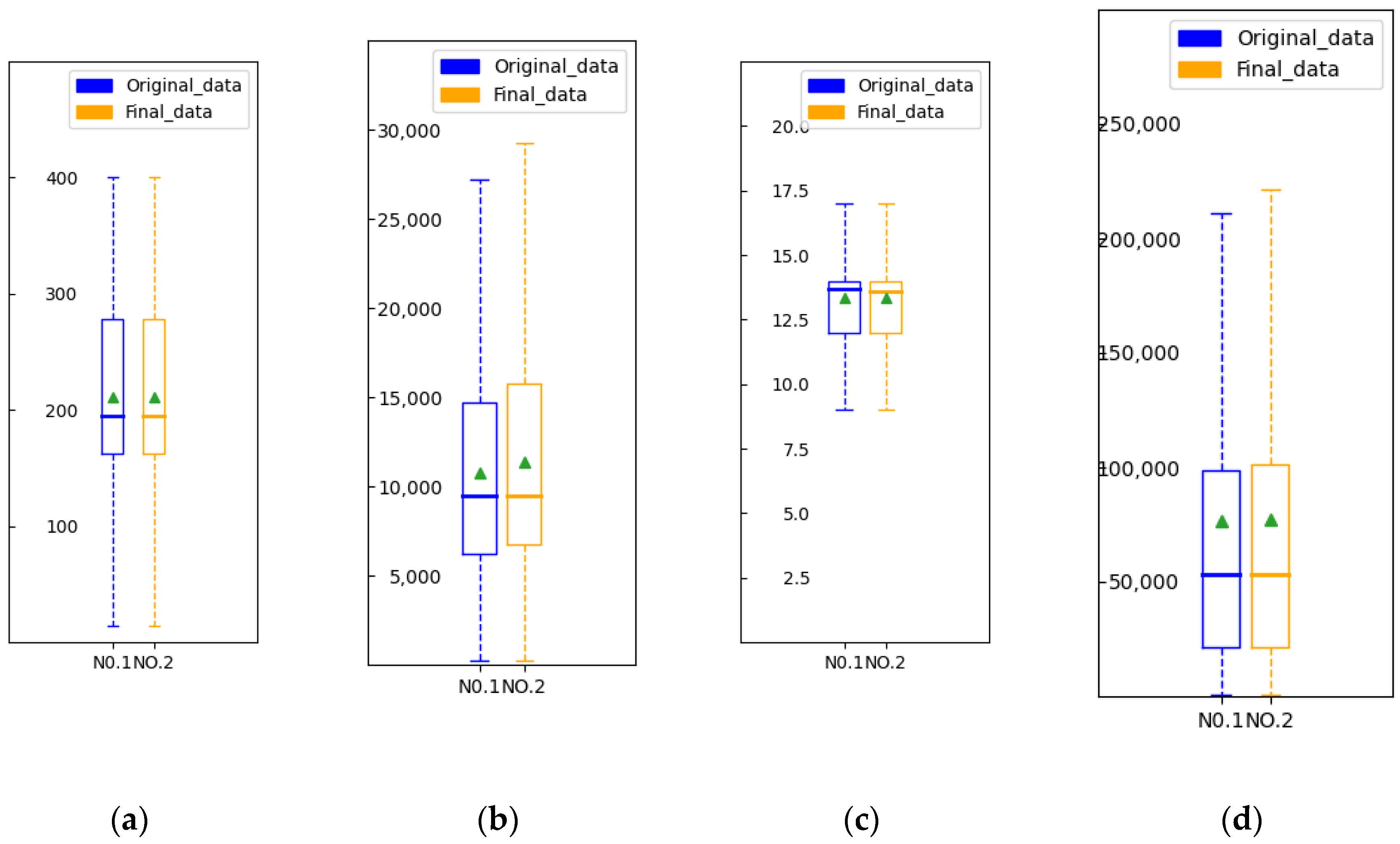
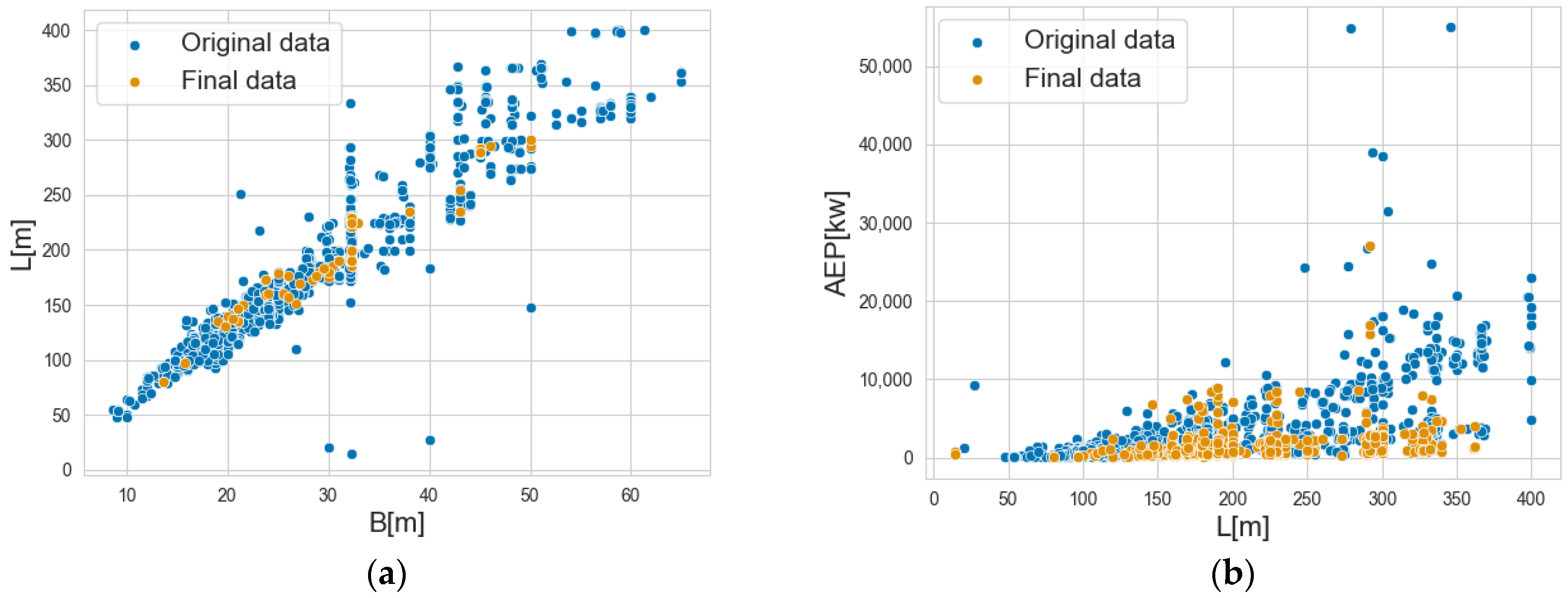
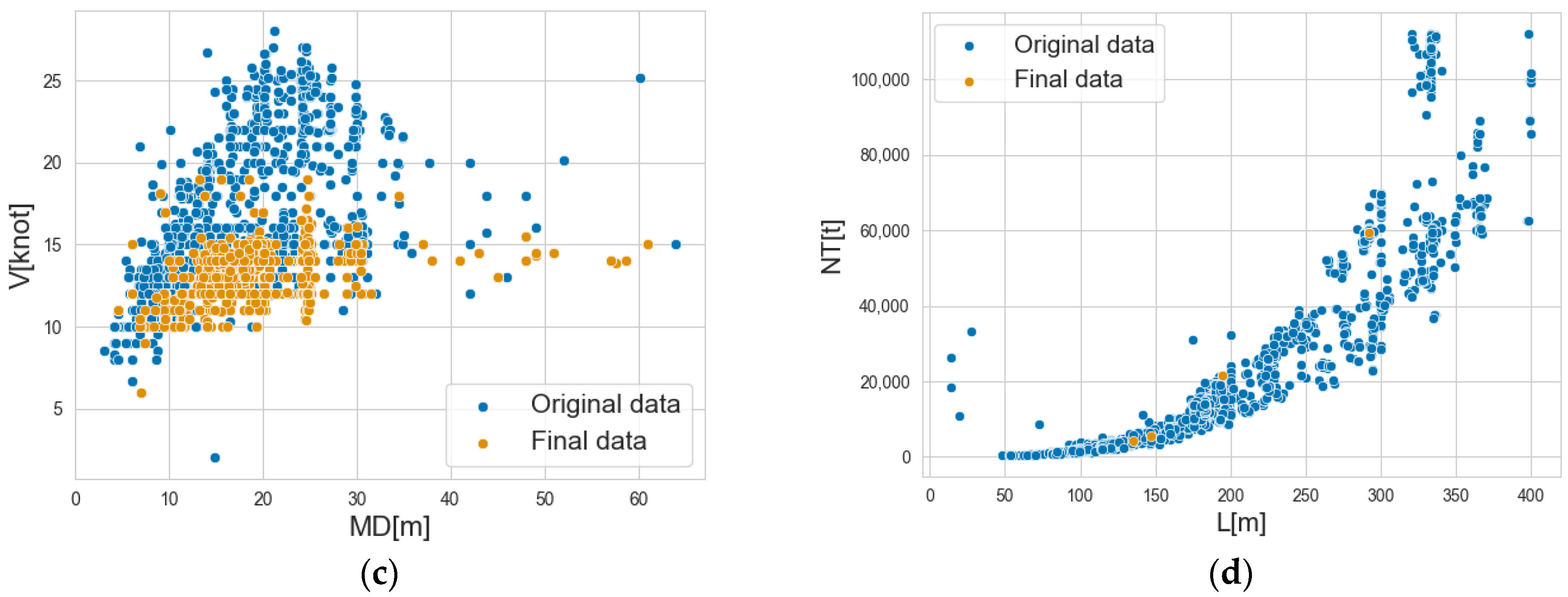
| Attribute Column Name | The Upper Limit of the Range | The Lower Limit of the Range |
|---|---|---|
| L [m] | 500 | 1 |
| B [m] | 80 | 1 |
| MD [m] | 50 | 1 |
| MEP [kw] | 150,000 | 750 |
| AEP [kw] | 100,000 | 60 |
| BP [kw] | 7200 | 7.2 |
| V [knot] | 50 | 5 |
| GT [t] | 1,000,000 | 400 |
| DWT [t] | 800,000 | 1 |
| NT [t] | 1,000,000 and ≤GT | 1 |
| Ship Principal Parameters | Valid Data | Missing Data | Mean | Median | Minimum | Maximum | Std. Dev | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|---|
| L [m] | 8085 | 82 | 211.0 | 199.9 | 32.3 | 362.0 | 54.7 | 0.24 | 0.08 |
| B [m] | 7660 | 507 | 33.6 | 32.3 | 8.8 | 65.0 | 9.00 | 0.62 | 1.05 |
| MD [m] | 6948 | 1219 | 18.1 | 18.3 | 2.7 | 29.9 | 4.73 | −0.32 | 0.11 |
| MEP [kw] | 7785 | 382 | 10,228.4 | 9070.0 | 750 | 100,000.0 | 5844.20 | 3.84 | 40.80 |
| AEP [kw] | 5128 | 3039 | 1322.6 | 920.0 | 75.0 | 27,000.0 | 1342.22 | 6.52 | 79.83 |
| BP [kw] | 6871 | 1296 | 1011.7 | 885.0 | 7.2 | 7200.0 | 985.97 | 2.30 | 8.91 |
| V [knot] | 5050 | 3117 | 13.1 | 13.0 | 6.0 | 24.0 | 1.45 | 0.16 | 2.49 |
| GT [t] | 8160 | 7 | 44,836.5 | 34,773.0 | 436 | 371,066 | 34,037.11 | 1.78 | 4.44 |
| DWT [t] | 8140 | 27 | 82,416.5 | 61,003.5 | 1.0 | 766,044.0 | 68,444.74 | 1.90 | 5.56 |
| NT [t] | 8163 | 4 | 25,923.7 | 20,020.0 | 101 | 216,496 | 18,567.55 | 1.15 | 1.38 |
| Number of Missing Parameters | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of ships | 3348 | 1333 | 3252 | 82 | 151 | 1 | 0 | 0 | 0 | 0 | 0 |
| Percentage | 40.99% | 16.32% | 39.82% | 1.00% | 1.85% | 0.01% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% |
| Static database (Bulk cargo ship) | 1075.646 | 218 | 0.000 |
| Parameter | Coefficient of the Polynomial Function | ||||
|---|---|---|---|---|---|
| y | x | ||||
| L | B | ||||
| B | GT | ||||
| MD | NT | ||||
| MEP | GT | ||||
| AEP | L | ||||
| BP | AEP | ||||
| V | MD | ||||
| GT | DWT | ||||
| DWT | B | ||||
| NT | L | ||||
| Algorithm | RMSE | |||||
|---|---|---|---|---|---|---|
| 10% | 20% | 30% | 40% | 50% | 60% | |
| MF | 0.204 | 0.216 | 0.224 | 0.231 | 0.248 | 0.263 |
| PF | 0.214 | 0.223 | 0.236 | 0.243 | 0.265 | 0.291 |
| GAIN | 0.201 | 0.207 | 0.213 | 0.224 | 0.233 | 0.246 |
| WFGAIN-GP | 0.199 | 0.204 | 0.214 | 0.219 | 0.231 | 0.244 |
| Algorithm | MAPE | |||||
|---|---|---|---|---|---|---|
| 10% | 20% | 30% | 40% | 50% | 60% | |
| MF | 12.42 | 16.02 | 25.56 | 31.85 | 47.67 | 59.21 |
| PF | 13.52 | 16.87 | 29.86 | 37.46 | 51.63 | 66.58 |
| GAIN | 12.09 | 14.94 | 23.81 | 30.58 | 44.19 | 54.74 |
| WFGAIN-GP | 11.87 | 14.58 | 23.97 | 29.67 | 43.72 | 54.21 |
| Algorithm | AUROC | |||||
|---|---|---|---|---|---|---|
| 10% | 20% | 30% | 40% | 50% | 60% | |
| MF | 0.765 | 0.749 | 0.731 | 0.705 | 0.652 | 0.624 |
| GAIN | 0.765 | 0.748 | 0.733 | 0.716 | 0.684 | 0.651 |
| WFGAIN-GP | 0.768 | 0.752 | 0.739 | 0.711 | 0.692 | 0.663 |
| Ship Principal Parameters | L [m] | B [m] | MD [m] | MEP [kw] | AEP [kw] | BP [kw] | V [knot] | GT [t] | DWT [t] | NT [t] |
|---|---|---|---|---|---|---|---|---|---|---|
| Missing rate (%) | 1.01 | 6.62 | 17.54 | 4.91 | 59.26 | 18.86 | 61.72 | 0.08 | 0.33 | 0.04 |
| Algorithm | RMSE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| L [m] | B [m] | MD [m] | MEP [kw] | AEP [kw] | BP [kw] | V [knot] | GT [t] | DW [t] | NT [t] | |
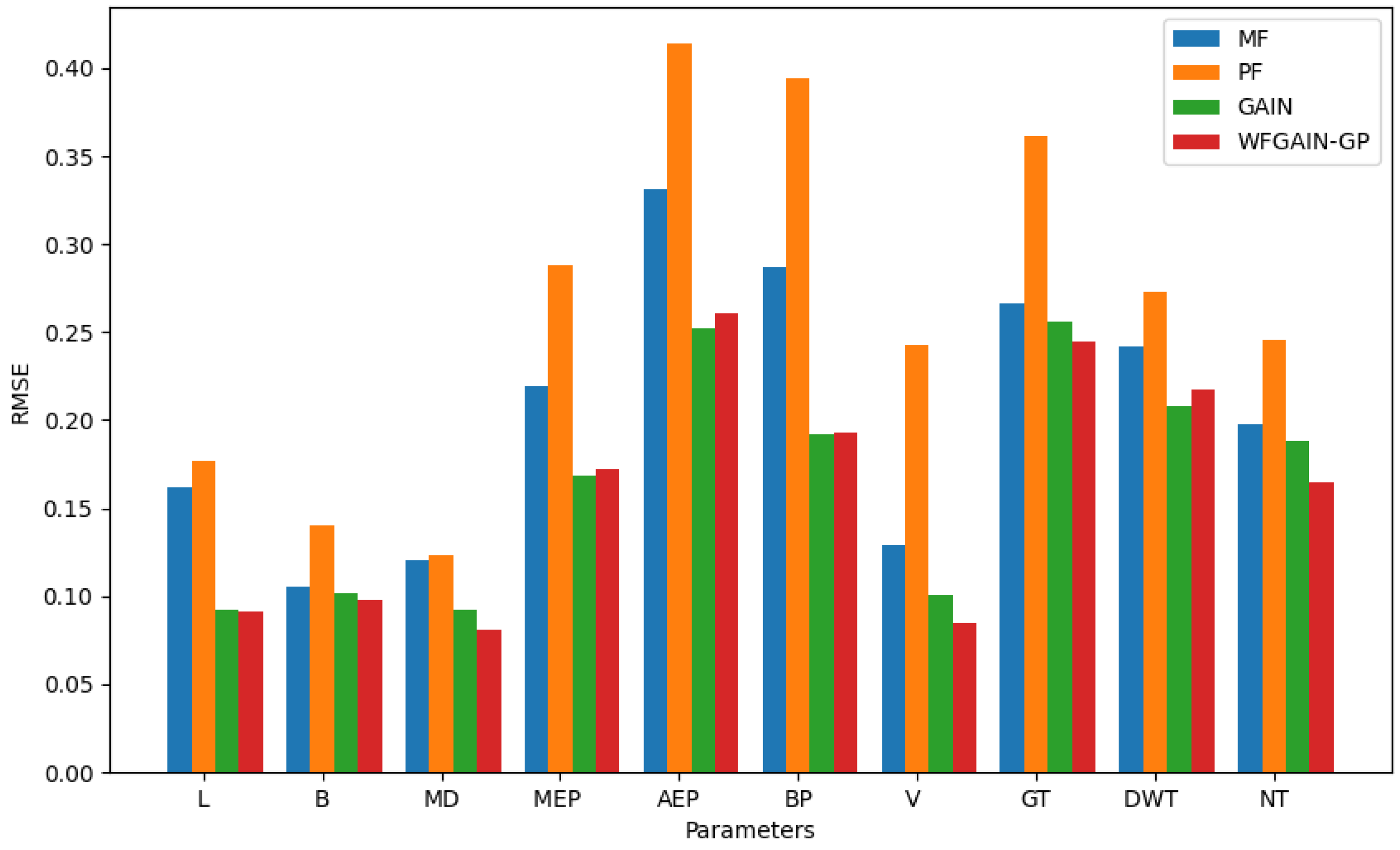
| MF | 0.162 | 0.105 | 0.120 | 0.219 | 0.331 | 0.287 | 0.129 | 0.266 | 0.242 | 0.198 |
| PF | 0.177 | 0.140 | 0.123 | 0.288 | 0.414 | 0.394 | 0.153 | 0.361 | 0.273 | 0.246 |
| GAIN | 0.092 | 0.102 | 0.092 | 0.168 | 0.252 | 0.192 | 0.101 | 0.256 | 0.208 | 0.188 |
| WFGAIN-GP | 0.091 | 0.098 | 0.081 | 0.172 | 0.261 | 0.193 | 0.085 | 0.245 | 0.217 | 0.165 |
| Ship Principal Parameters | Algorithm | The Number of Feature Dimensions | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| V | MF | 0.245 | 0.206 | 0.185 | 0.168 | 0.167 | 0.148 | 0.132 | 0.129 |
| GAIN | 0.137 | 0.116 | 0.112 | 0.109 | 0.105 | 0.102 | 0.099 | 0.101 | |
| WFGAIN-GP | 0.138 | 0.116 | 0.109 | 0.108 | 0.093 | 0.094 | 0.089 | 0.085 | |
| MEP | MF | 0.545 | 0.487 | 0.466 | 0.429 | 0.386 | 0.378 | 0.355 | 0.331 |
| GAIN | 0.282 | 0.279 | 0.271 | 0.261 | 0.259 | 0.254 | 0.255 | 0.252 | |
| WFGAIN-GP | 0.293 | 0.288 | 0.284 | 0.273 | 0.269 | 0.262 | 0.263 | 0.261 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, J.; Cai, Z.; Sun, W.; Jiao, Y. A Novel Method for Imputing Missing Values in Ship Static Data Based on Generative Adversarial Networks. J. Mar. Sci. Eng. 2023, 11, 806. https://doi.org/10.3390/jmse11040806
Gao J, Cai Z, Sun W, Jiao Y. A Novel Method for Imputing Missing Values in Ship Static Data Based on Generative Adversarial Networks. Journal of Marine Science and Engineering. 2023; 11(4):806. https://doi.org/10.3390/jmse11040806
Chicago/Turabian StyleGao, Junbo, Ze Cai, Wei Sun, and Yingqi Jiao. 2023. "A Novel Method for Imputing Missing Values in Ship Static Data Based on Generative Adversarial Networks" Journal of Marine Science and Engineering 11, no. 4: 806. https://doi.org/10.3390/jmse11040806
APA StyleGao, J., Cai, Z., Sun, W., & Jiao, Y. (2023). A Novel Method for Imputing Missing Values in Ship Static Data Based on Generative Adversarial Networks. Journal of Marine Science and Engineering, 11(4), 806. https://doi.org/10.3390/jmse11040806






