Hybrid Path Planning Using a Bionic-Inspired Optimization Algorithm for Autonomous Underwater Vehicles
Abstract
1. Introduction
- A HGWO algorithm is applied for optimizing total cost and generating a suboptimal path for single and multiple AUVs.
- The proposed HGWO is implemented underwater using the merits of GA followed by GWO for path planning of single and multiple AUVs in a static obstacle rich environment.
- The Kruskal–Wallis test is employed for a non-parametric statistical analysis and demonstrates the independence of the results given by the algorithms.
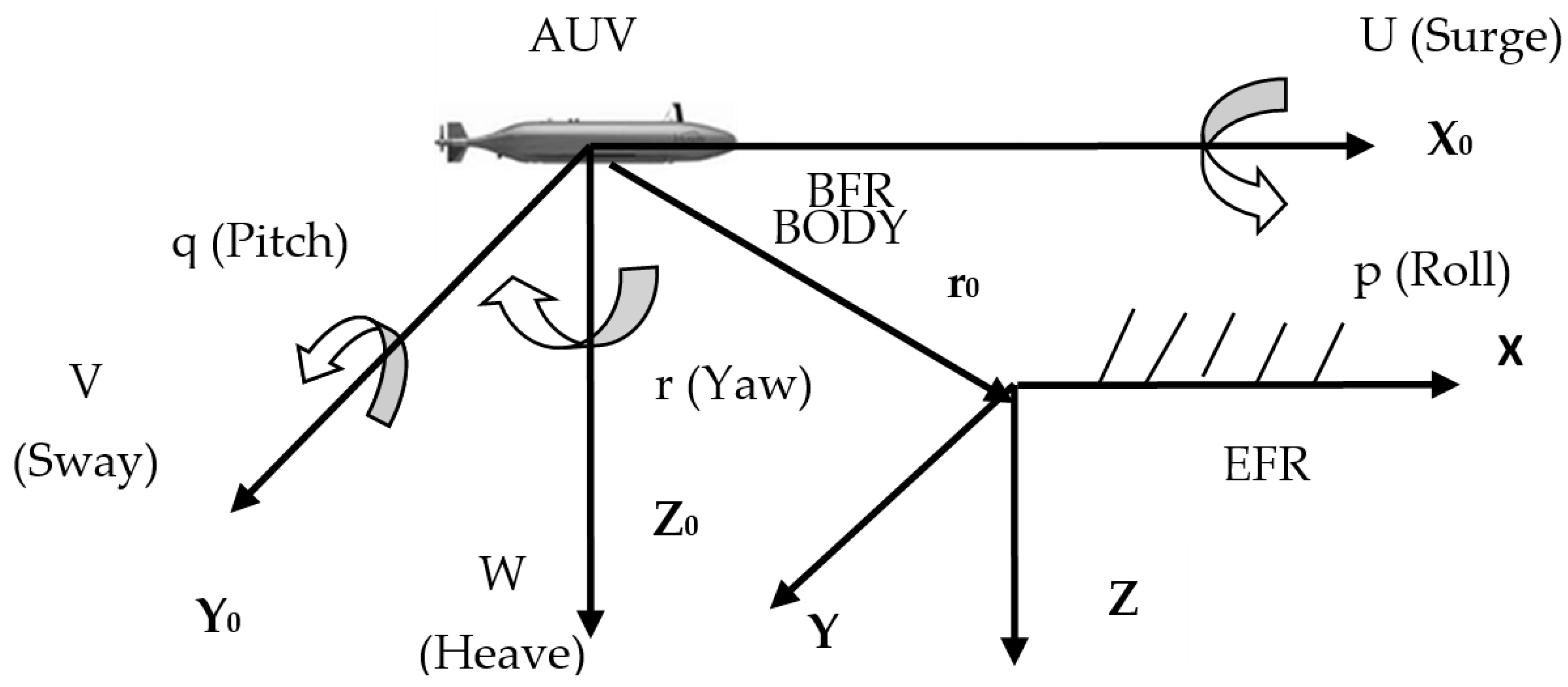
2. Problem Formulation
2.1. Path Distance
2.2. Collision Penalty
3. Proposed Algorithm for Path Planning of AUVs
3.1. Genetic Algorithm
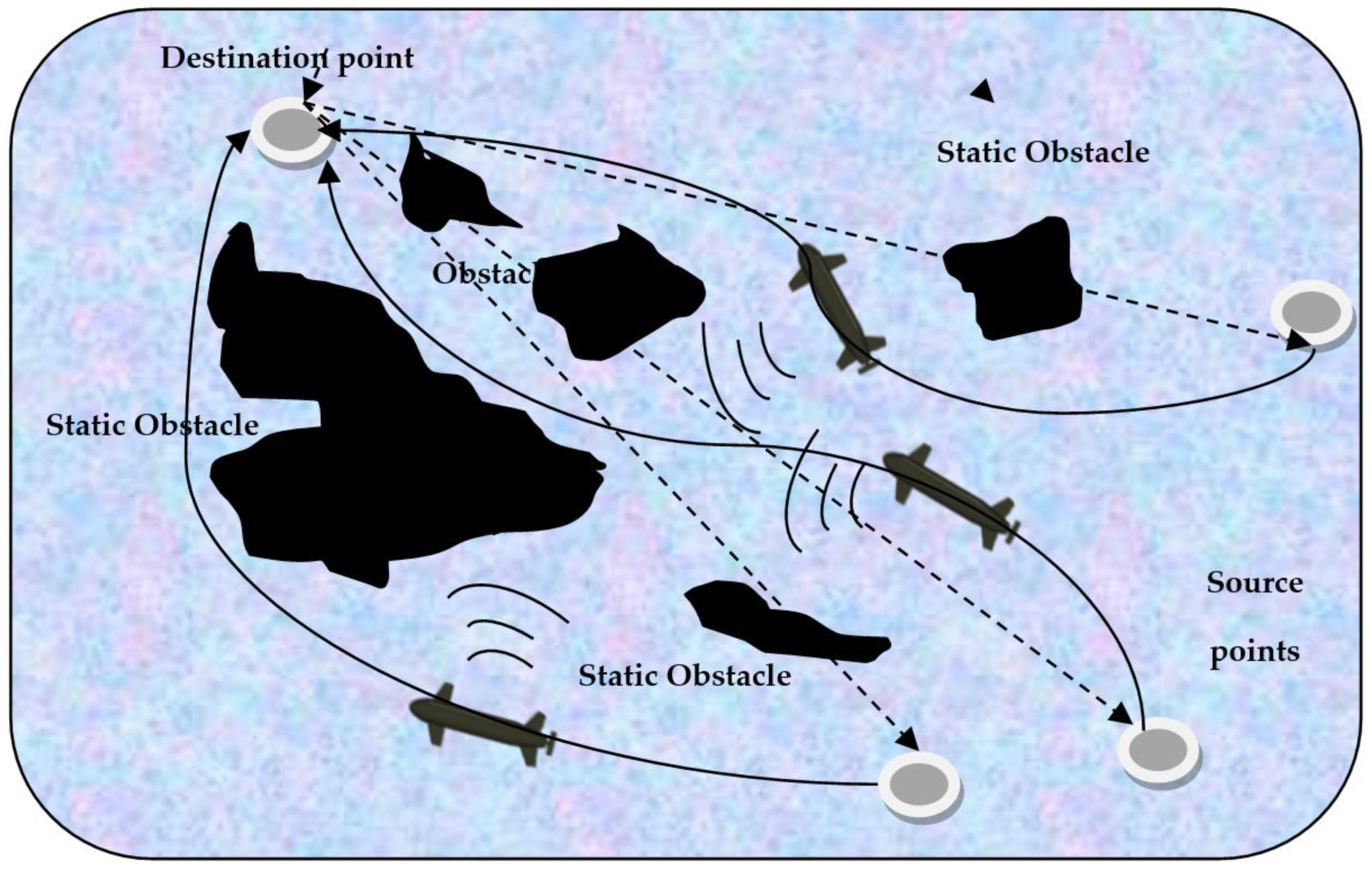
- The underwater environment is modeled as a 3D map consisting of intermediate, origin and destination nodes.
- The obstacle locations are properly defined.
- The total cost function of Equation (6) is optimized at each node until the destination is reached.
3.2. Grey Wolf Optimization
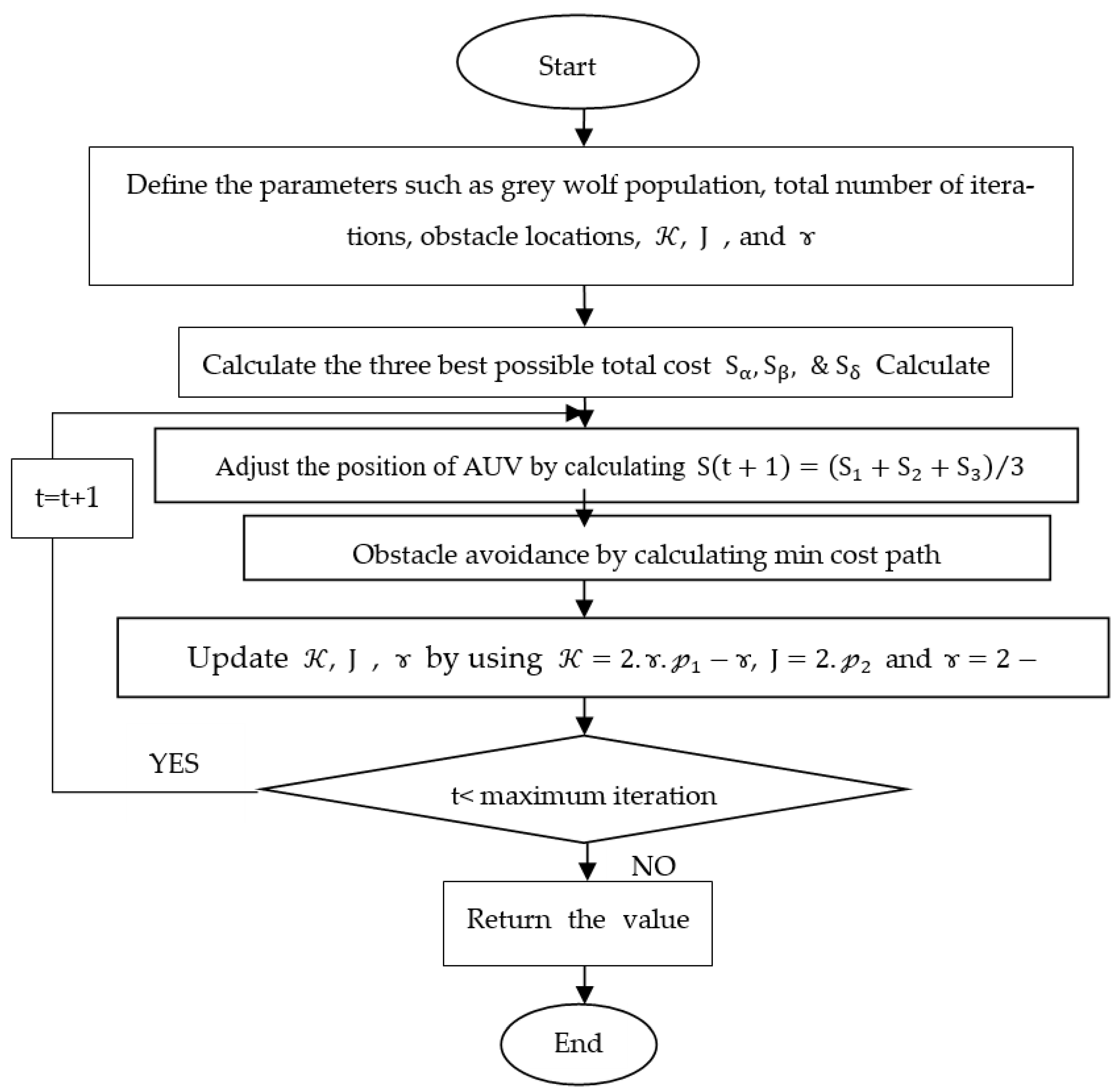
3.3. Proposed Hybrid GWO (HGWO) Algorithm
| Algorithm 1. Pseudocode for single AUV path planning |
| Initialize the total no. of nodes n, in the path as GW population Si, where (i = 1, 2,…, n). Destination = n + 1. Optimize the initial positions by optimizing the total cost (Equation (6)) using GA. Represent the first three best solutions as . Initialize , , and while (i < n + 1) For all Si do Update the position of the AUV using Equation (18), Update , , and using Equations (9), (10) and (11) respectively Update using Equations (12), (13) and (14) respectively End for End while Return End |
| Algorithm 2. Pseudocode for cooperative path planning [41] |
| Begin The 3D environment is modeled with origin, destination and fixed obstacle locations. Assume leader path knowledge and synchronization error is available to all the follower AUVs. For each Follower AUV While () Initialize the total no. of nodes n in the path as GW population Si, where (i = 1, 2, …, n). Destination = n + 1. Optimize the initial positions by optimizing the total cost (Equation (6)) using GA. Represent the first three best solutions as . Initialize , , and while (i < n + 1) For all Si do Update the position of the AUV using Equation (18) Update , , and using Equations (9), (10) and (11) respectively Update using Equations (12), (13) and (14) respectively End for End while Return End while End for End |
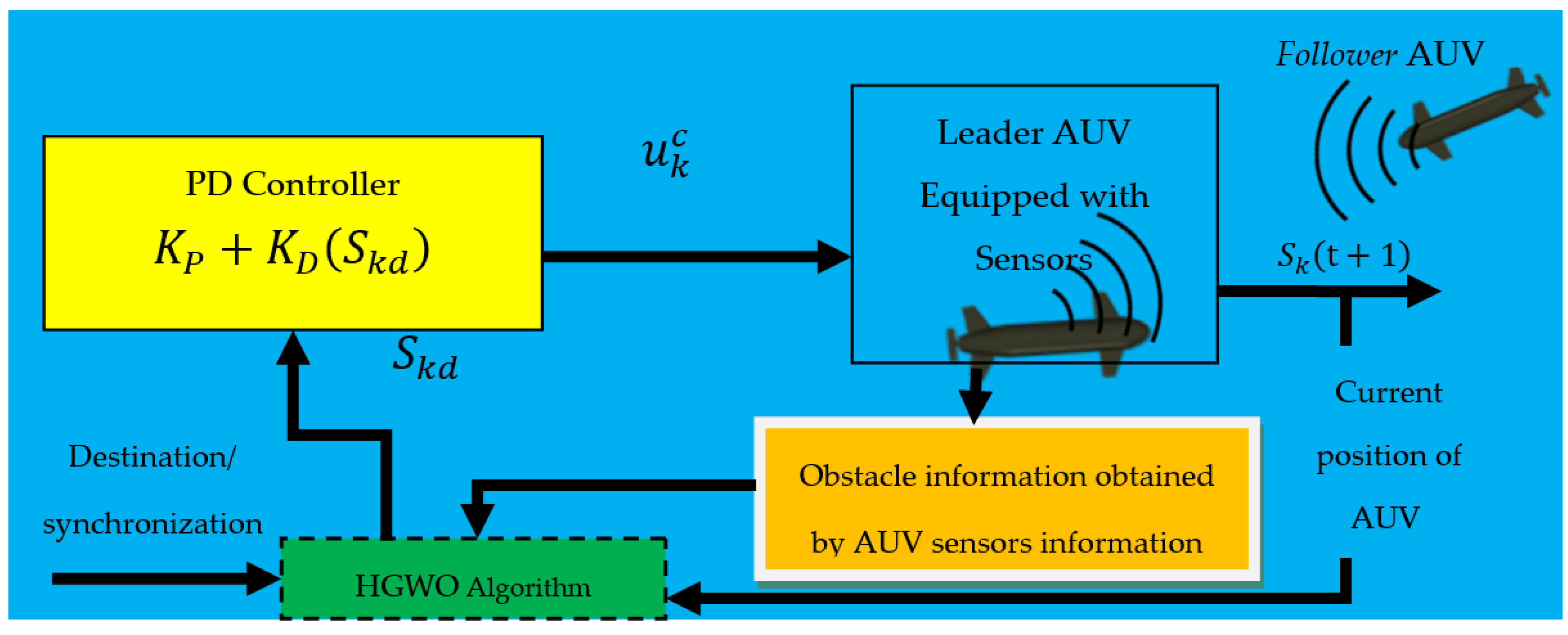
3.4. Proposed Path Planning Algorithm’s Communication Consesus
4. Simulation Setup and Result Analysis
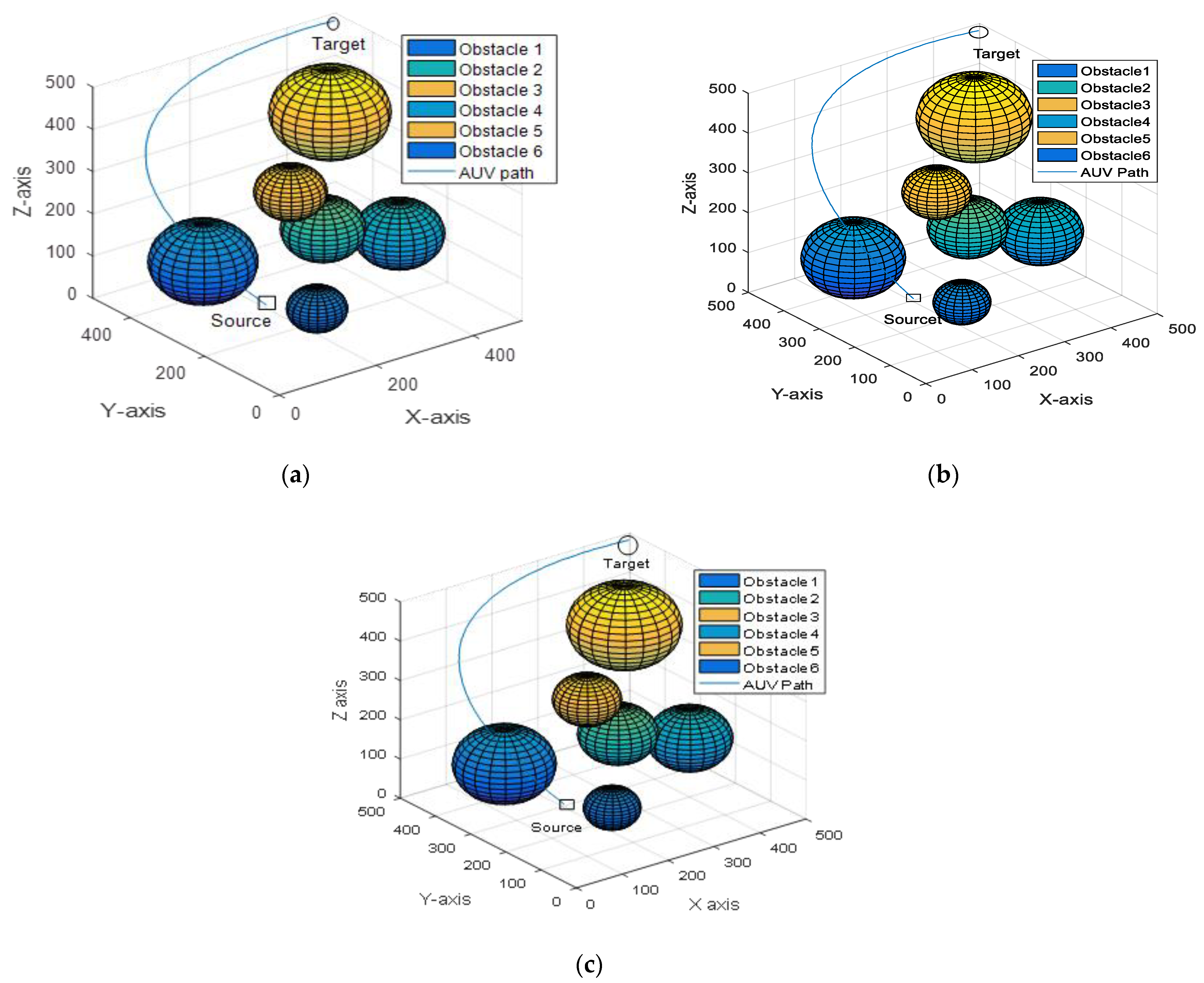
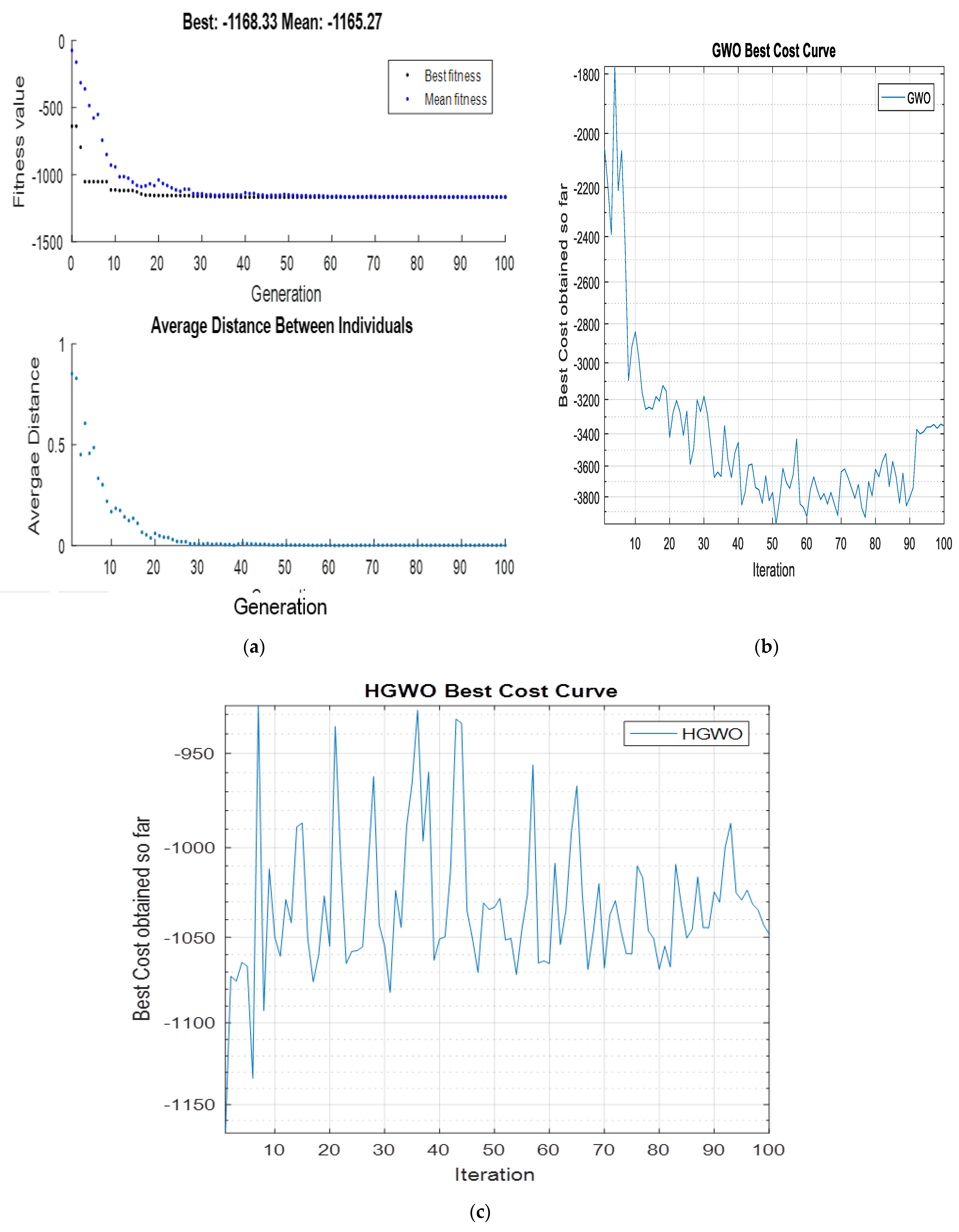
4.1. Result Analysis of a Single AUV
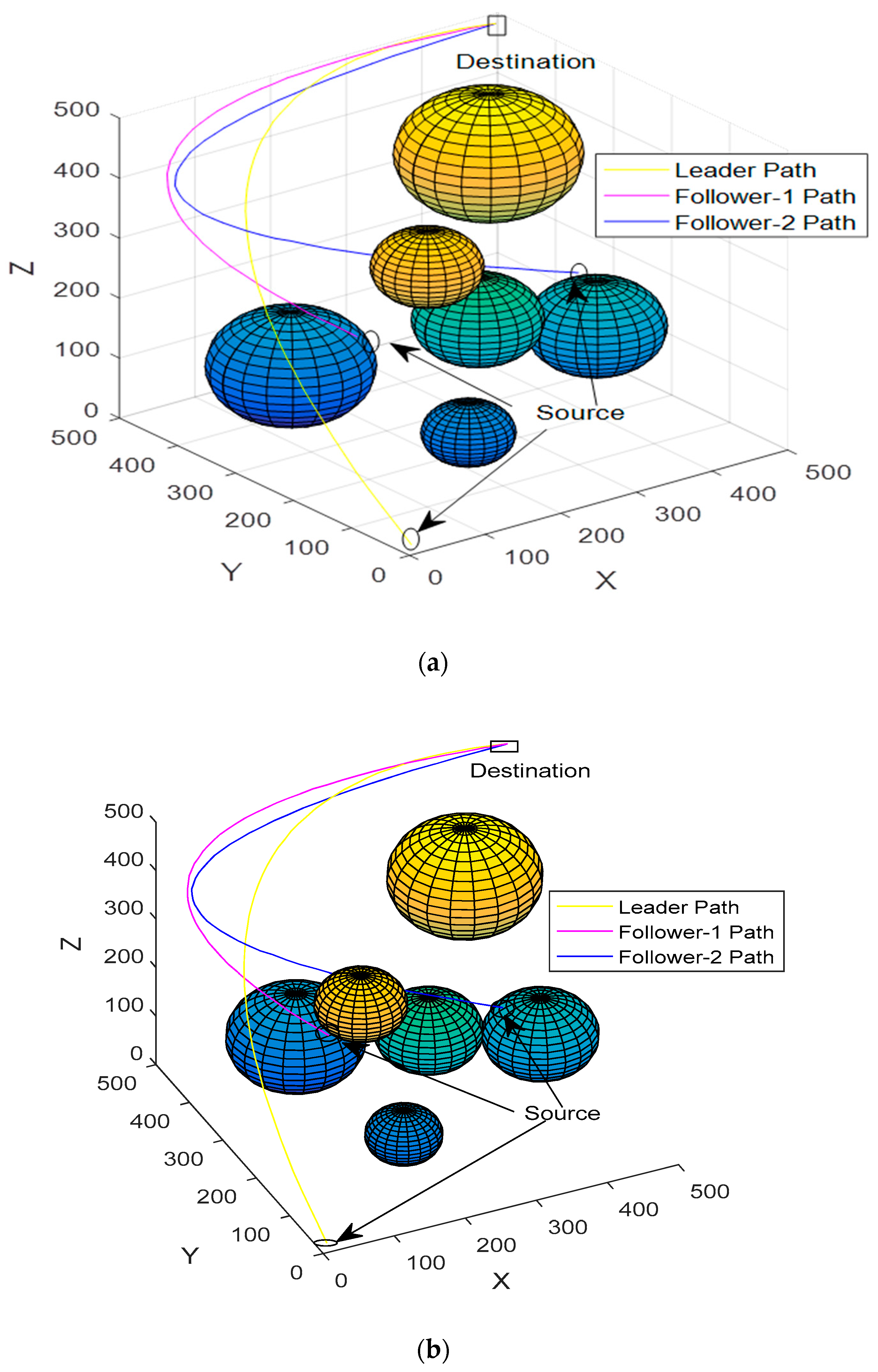
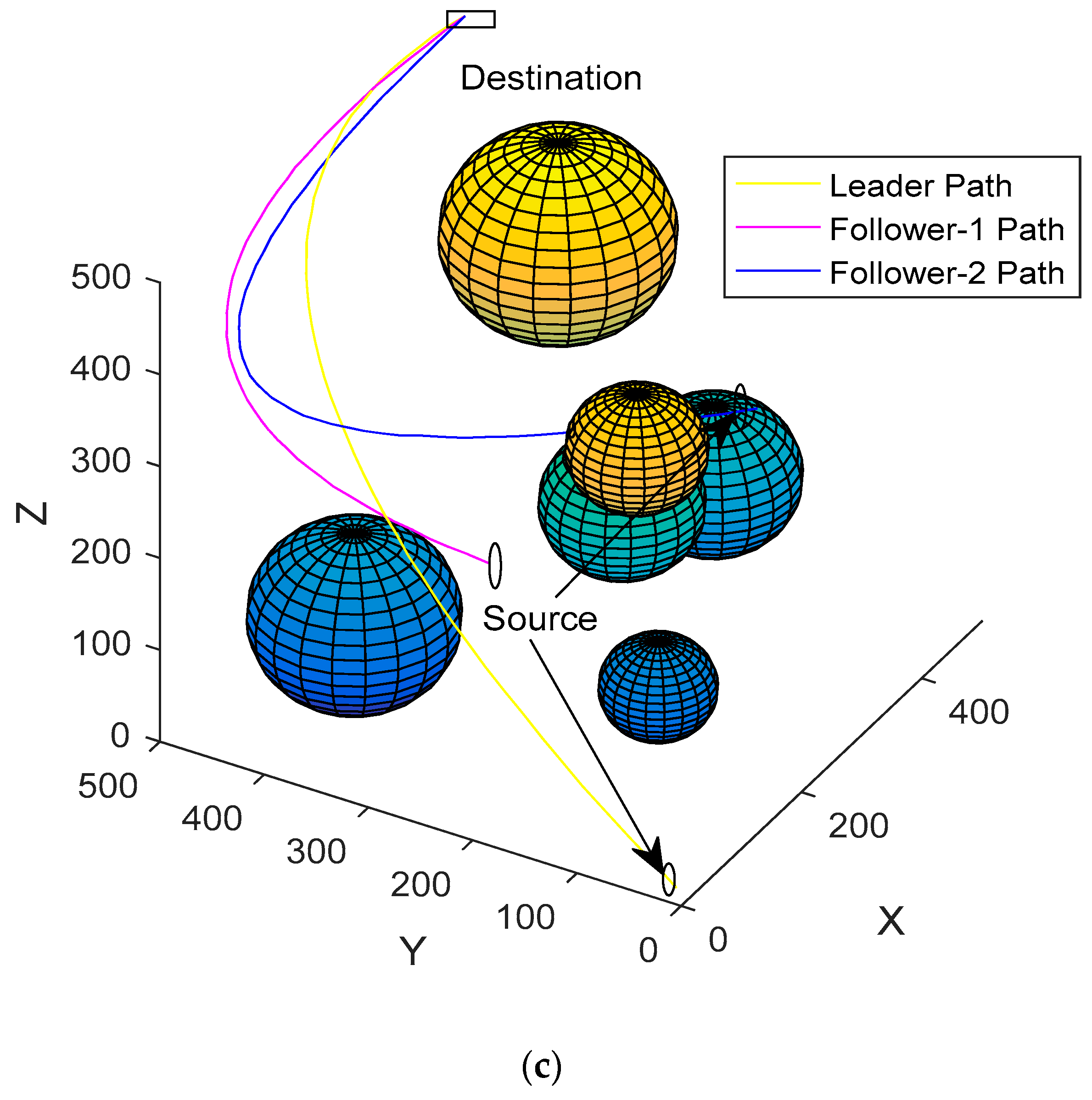
4.2. Result Analysis of Multiple AUVs
4.3. Non-Parametric Statistical Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Zhou, C.; Gu, S.; Wen, Y.; Du, Z.; Xiao, C.; Huang, L.; Zhu, M. The review unmanned surface vehicle path planning: Based on multi-modality constraint. Ocean Eng. 2020, 200, 107043. [Google Scholar] [CrossRef]
- Marini, S.; Gjeci, N.; Govindaraj, S.; But, A.; Sportich, B.; Ottaviani, E.; Márquez, F.P.G.; Bernalte Sanchez, P.J.; Pedersen, J.; Clausen, C.V.; et al. ENDURUNS: An Integrated and Flexible Approach for Seabed Survey through Autonomous Mobile Vehicles. J. Mar. Sci. Eng. 2020, 8, 633. [Google Scholar] [CrossRef]
- Mahmoud Zadeh, S.; Yazdani, A.M.; Sammut, K.; Powers, D.M.W. Online path planning for AUV rendezvous in dynamic cluttered undersea environment using evolutionary algorithms. Appl. Soft Comput. 2018, 70, 929–945. [Google Scholar] [CrossRef]
- Zamuda, A.; Hernández Sosa, J.D.; Adler, L. Constrained differential evolution optimization for underwater glider path planning in sub-mesoscale eddy sampling. Appl. Soft Comput. 2016, 42, 93–118. [Google Scholar] [CrossRef]
- Jin, X.; Er, M.J. Dynamic collision avoidance scheme for unmanned surface vehicles under complex shallow sea Environments. Ocean Eng. 2020, 218, 108102. [Google Scholar] [CrossRef]
- Morin, M.; Abi-Zeid, I.; Petillot, Y.; Quimper, C.-G. A hybrid algorithm for coverage path planning with imperfect sensors. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 5988–5993. [Google Scholar] [CrossRef]
- Panda, M.; Das, B.; Pati, B.B. A Hybrid Approach for Path Planning of Multiple AUVs. In Innovation in Electrical Power Engineering, Communication, and Computing Technology; Lecture Notes in Electrical Engineering; Sharma, R., Mishra, M., Nayak, J., Naik, B., Pelusi, D., Eds.; Springer: Singapore, 2020; pp. 327–338. [Google Scholar] [CrossRef]
- Tan, C.S.; Sutton, R.; Chudley, J. An Incremental Stochastic Motion Planning Technique for Autonomous Underwater Vehicles; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Khan, M.R.; Das, B.; Pati, B.B. Channel estimation strategies for underwater acoustic (UWA) communication: An overview. J. Frankl. Inst. 2020, 357, 7229–7265. [Google Scholar] [CrossRef]
- Kim, J. Control laws to avoid collision with three dimensional obstacles using sensors. Ocean Eng. 2019, 172, 342–349. [Google Scholar] [CrossRef]
- Sun, Y.; Ran, X.; Zhang, G.; Wang, X.; Xu, H. AUV path following controlled by modified Deep Deterministic Policy Gradient. Ocean Eng. 2020, 210, 107360. [Google Scholar] [CrossRef]
- Shi, L.; Hu, Y.; Su, S.; Guo, S.; Xing, H.; Hou, X.; Liu, Y.; Chen, Z.; Li, Z.; Xia, D. A Fuzzy PID Algorithm for a Novel Miniature Spherical Robots with Three-dimensional Underwater Motion Control. J. Bionic Eng. 2020, 17, 959–969. [Google Scholar] [CrossRef]
- Zhuang, Y.; Sharma, S.; Subudhi, B.; Huang, H.; Wan, J. Efficient collision-free path planning for autonomous underwater vehicles in dynamic environments with a hybrid optimization algorithm. Ocean Eng. 2016, 127, 190–199. [Google Scholar] [CrossRef]
- Guo, X.; Ji, M.; Zhao, Z.; Wen, D.; Zhang, W. Global path planning and multi-objective path control for unmanned surface vehicle based on modified particle swarm optimization (PSO) algorithm. Ocean Eng. 2020, 216, 107693. [Google Scholar] [CrossRef]
- Yao, P.; Zhao, S. Three-dimensional path planning for AUV based on interfered fluid dynamical system under ocean current. IEEE Access 2018, 6, 42904–42916. [Google Scholar] [CrossRef]
- Igor, B.; Maksim, K.; Nikolay, M. Task Allocation and Path Planning for Network of Autonomous Underwater Vehicles. IJCNC 2018, 10, 33–42. [Google Scholar] [CrossRef][Green Version]
- Yan, Z.; Li, J.; Wu, Y.; Zhang, G. A Real-Time Path Planning Algorithm for AUV in Unknown Underwater Environment Based on Combining PSO and Waypoint Guidance. Sensors 2019, 19, 20. [Google Scholar] [CrossRef]
- Khan, M.R.; Das, B. Multiuser Detection for MIMO-OFDM system in Underwater Communication Using a Hybrid Bionic Binary Spotted Hyena Optimizer. J. Bionic Eng. 2021, 18, 462–472. [Google Scholar] [CrossRef]
- Das, B.; Subudhi, B.; Pati, B.B. Co-operative control of a team of autonomous underwater vehicles in an obstacle-rich environment. J. Mar. Eng. Technol. (Taylor Fr.) 2016, 15, 139–151. [Google Scholar] [CrossRef]
- Li, Y.; Pan, D.; Ma, Z.; Zhao, Q. Aspect Ratio Effect of a Pair of Flapping Wings on the Propulsion of a Bionic Autonomous Underwater Glider. J. Bionic Eng. 2019, 16, 145–153. [Google Scholar] [CrossRef]
- Rezaei, H.; Bozorg-Haddad, O.; Chu, X. Grey Wolf Optimization (GWO) Algorithm. Adv. Optim. By Nat.-Inspired Algorithms 2018, 720, 81–91. [Google Scholar] [CrossRef]
- Panda, M.; Das, B.; Pati, B. Global Path Planning for Multiple AUVs Using GWO. Arch. Control Sci. 2020, 30, 77–100. [Google Scholar]
- Panda, M.; Das, B.; Pati, B.B. Grey wolf optimization for global path planning of autonomous underwater vehicle. In Proceedings of the Third International Conference on Advanced Informatics for Computing Research—ICAICR, Shimla, India, 15–16 June 2019. [Google Scholar] [CrossRef]
- Panda, M.; Das, B. Grey Wolf Optimizer and Its Applications: A Survey. In Proceedings of the Third International Conference on Microelectronics, Computing and Communication Systems; Nath, V., Mandal, J., Eds.; Lecture Notes in Electrical Engineering; Springer: Singapore, 2019; Volume 556. [Google Scholar] [CrossRef]
- Li, Q.; Liu, S.-Y.; Yang, X.-S. Influence of Initialization on the Performance of Metaheuristic Optimizers. Appl. Soft Comput. 2020, 91, 1–39. [Google Scholar] [CrossRef]
- Ramírez, I.S.; Bernalte Sánchez, P.J.; Papaelias, M.; Márquez, F.P.G. Autonomous Underwater Vehicles and Field of View in Underwater Operations. J. Mar. Sci. Eng. 2021, 9, 277. [Google Scholar] [CrossRef]
- Sans-Muntadas, A.; Kelasidi, E.; Pettersen, K.Y.; Brekke, E. Path planning and guidance for underactuated vehicles with limited field-of-view. Ocean Eng. 2019, 174, 84–95. [Google Scholar] [CrossRef]
- Fossen, T.I. Guidance and Control of Ocean Vehicles, 1st ed.; British Library: Trondheim, Norway, 1994; pp. 6–54. [Google Scholar]
- Moura, A.; Rijo, R.; Silva, P.; Crespo, S. A multi-objective genetic algorithm applied to autonomous underwater vehicles for sewage outfall plume dispersion observations. Appl. Soft Comput. 2010, 10, 1119–1126. [Google Scholar] [CrossRef]
- Ataei, M.; Yousefi-Koma, A. Three-dimensional optimal path planning for waypoint guidance of an autonomous underwater vehicle. Robot. Auton. Syst. 2015, 67, 23–32. [Google Scholar] [CrossRef]
- Ismail, A.T.; Sheta, A.; Al-Weshah, M. A mobile robot path planning using genetic algorithm in static environment. J. Comput. Sci. 2008, 4, 341–344. [Google Scholar]
- Khan, M.R.; Das, B.; Pati, B.B. A criterion based adaptive RSIC scheme in underwater communication. IEEE J. Syst. Eng. Electron. 2021, 32, 408–416. [Google Scholar]
- Das, B.; Subudhi, B.; Pati, B.B. Co-operative control coordination of a team of underwater vehicles with communication constraints. Trans. Inst. Meas. Control 2015, 38, 463–481. [Google Scholar] [CrossRef]
- Das, B.; Subudhi, B.; Pati, B.B. Adaptive sliding mode formation control of multiple underwater robots. Arch. Control Sci. 2014, 24, 515–543. [Google Scholar] [CrossRef]
- Saaj, C.M.; Lappas, V.; Richie, D.V.; Schaub, H. Satellite formation flying: Robust algorithms for propulsion, path planning and control. In Proceedings of the 2009 European Control Conference (ECC), Budapest, Hungary, 23–26 August 2009; pp. 2456–2463. [Google Scholar] [CrossRef]
- Sánchez, P.J.B.; Papaelias, M.; Márquez, F.P.G. Autonomous underwater vehicles: Instrumentation and measurements. IEEE Instrum. Meas. Mag. 2020, 23, 105–114. [Google Scholar] [CrossRef]
- García Márquez, F.P.; Papaelias, M.; Marini, S. Artificial Intelligence in Marine Science and Engineering. J. Mar. Sci. Eng. 2022, 10, 711. [Google Scholar] [CrossRef]
- Byun, S.; Papaelias, M.; Márquez, F.P.G.; Lee, D. Fault-Tree-Analysis-Based Health Monitoring for Autonomous Underwater Vehicle. J. Mar. Sci. Eng. 2022, 10, 1855. [Google Scholar] [CrossRef]
- Sánchez, P.J.B.; Asensio, M.T.; Papaelias, M.; Márquez, F.P.G. Life Cycle Assessment in Autonomous Marine Vehicles. In Proceedings of the Fifteenth International Conference on Management Science and Engineering Management—ICMSEM, Toledo, Spain, 2–3 August 2021; Lecture Notes on Data Engineering and Communications Technologies. Xu, J., García Márquez, F.P., Ali Hassan, M.H., Duca, G., Hajiyev, A., Altiparmak, F., Eds.; Springer: Cham, Switzerland, 2021; Volume 79. [Google Scholar] [CrossRef]
- Segovia Ramírez, I.; Bernalte Sánchez, P.J.; Papaelias, M.; García Márquez, F.P. Autonomous underwater vehicles inspection management: Optimization of field of view and measurement process. In Proceedings of the 13th International Conference on Industrial Engineering and Industrial Management, Gijón, Spain, 11–12 July 2019. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Panda, M.; Das, B. Multi-agent System of Autonomous Underwater Vehicles in Octagon Formation. In Intelligent Systems; Lecture Notes in Networks and Systems; Udgata, S.K., Sethi, S., Srirama, S.N., Eds.; Springer: Singapore, 2021; Volume 185. [Google Scholar] [CrossRef]
| Algorithm | Test Runs | Computational Delay (s) | Path Distance (m) | Total Cost (m) |
|---|---|---|---|---|
| GA | 1 | 27.97 | 962.34 | 488.69 |
| 2 | 28.28 | 982.59 | 540.17 | |
| 3 | 26.67 | 1010.30 | 517.13 | |
| 4 | 29.13 | 1079.42 | 479.93 | |
| 5 | 29.13 | 1089.75 | 483.49 | |
| Average | 28.24 | 1008.66 | 483.49 | |
| GWO | 1 | 24.34 | 984.47 | 280.90 |
| 2 | 23.19 | 997.78 | 279.43 | |
| 3 | 22.31 | 988.12 | 242.19 | |
| 4 | 23.75 | 993.53 | 269.11 | |
| 5 | 23.86 | 1065.87 | 175.32 | |
| Average | 23.49 | 1005.95 | 249.39 | |
| HGWO | 1 | 45.10 | 940.77 | 115.73 |
| 2 | 48.62 | 951.82 | 126.49 | |
| 3 | 58.61 | 972.60 | 116.39 | |
| 4 | 53.92 | 966.15 | 113.90 | |
| 5 | 47.51 | 955.84 | 125.65 | |
| Average | 50.75 | 957.43 | 119.63 |
| Algorithm | AUV | Computational Delay (s) | Path Distance (m) | Total Cost (m) |
|---|---|---|---|---|
| GA | Leader | 55.10 | 1120.04 | −45.93 |
| Follower1 | 58.62 | 1116.79 | −46.06 | |
| Follower2 | 58.61 | 1136.23 | −62.25 | |
| GWO | Leader | 28.97 | 1062.03 | −33.45 |
| Follower1 | 26.28 | 1069.25 | −31.3 | |
| Follower2 | 28.67 | 1080.45 | −35.67 | |
| HGWO | Leader | 23.3 | 1033.17 | −19.47 |
| Follower1 | 23.341 | 1063.59 | −22.91 | |
| Follower2 | 23.13 | 1063.03 | −19.31 |
| Algorithms | Rank | ||||
|---|---|---|---|---|---|
| GA | GWO | HGWO | GA | GWO | HGWO |
| −19.3 | 1 | ||||
| −19.47 | 2 | ||||
| −22.91 | 3 | ||||
| −31.3 | 4 | ||||
| −33.45 | 5 | ||||
| −35.67 | 6 | ||||
| −45.93 | 7 | ||||
| −46.06 | 8 | ||||
| −62.25 | 9 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sahoo, S.P.; Das, B.; Pati, B.B.; Garcia Marquez, F.P.; Segovia Ramirez, I. Hybrid Path Planning Using a Bionic-Inspired Optimization Algorithm for Autonomous Underwater Vehicles. J. Mar. Sci. Eng. 2023, 11, 761. https://doi.org/10.3390/jmse11040761
Sahoo SP, Das B, Pati BB, Garcia Marquez FP, Segovia Ramirez I. Hybrid Path Planning Using a Bionic-Inspired Optimization Algorithm for Autonomous Underwater Vehicles. Journal of Marine Science and Engineering. 2023; 11(4):761. https://doi.org/10.3390/jmse11040761
Chicago/Turabian StyleSahoo, Sarada Prasanna, Bikramaditya Das, Bibhuti Bhusan Pati, Fausto Pedro Garcia Marquez, and Isaac Segovia Ramirez. 2023. "Hybrid Path Planning Using a Bionic-Inspired Optimization Algorithm for Autonomous Underwater Vehicles" Journal of Marine Science and Engineering 11, no. 4: 761. https://doi.org/10.3390/jmse11040761
APA StyleSahoo, S. P., Das, B., Pati, B. B., Garcia Marquez, F. P., & Segovia Ramirez, I. (2023). Hybrid Path Planning Using a Bionic-Inspired Optimization Algorithm for Autonomous Underwater Vehicles. Journal of Marine Science and Engineering, 11(4), 761. https://doi.org/10.3390/jmse11040761









