Hybrid Path Planning Using a Bionic-Inspired Optimization Algorithm for Autonomous Underwater Vehicles

Abstract

This research presents a hybrid approach for path planning of autonomous underwater vehicles (AUVs). During path planning, static obstacles affect the desired path and path distance which result in collision penalties. In this study, the merits of grey wolf optimization (GWO) and genetic algorithm (GA) of bionic-inspired algorithms are integrated to implement a hybrid grey wolf optimization (HGWO) algorithm which allows AUVs to reach their destination safely in an obstacle rich environment. The proposed hybrid path planner is employed for path planning of a single AUV based on collision avoidance. It uses the GA as an initialization generator to overcome the random initialization problem of GWO. In this research, the total cost is considered to be a function of path distance and collision penalties. Further, the application of the proposed hybrid path planner is extended for cooperative path planning of AUVs while avoiding collision using communication consensus. Simulation results are obtained for both a single AUV and multiple AUV path planning in a 3D obstacle rich environment using a proportional-derivative controller. The Kruskal–Wallis test is employed for a non-parametric statistical analysis, where the independence of the results given by the algorithms is demonstrated.

1. Introduction

A hybrid approach integrates the merits of individual local and global path planning algorithms while improving the limitations and performance of local and global path planning [1,2]. The path planning (PP) problem of autonomous underwater vehicles (AUVs) can be divided into three subtasks: modeling the environment, path planning, and path traversal with collision avoidance [3,4]. A PP controller (PPC) decides the time and energy used by the optimal route from the start point to the destination point of operation while avoiding collision [5]. Morin et al. [6] proposed a dynamic programming (DP) sweeper algorithm, with minimal traveling and number of turns while achieving the required coverage, using an off-line hybrid algorithm based on dynamic programming.

Recently, hybrid path planning algorithms that combine two individual algorithms to enhance the performance of one of the algorithms have been gaining interest [7]. Researchers in [8,9,10] proposed a hybrid algorithm to improvise the rapidly exploring algorithm to solve a real-time path planning problem with short computational delay in underwater environment. Sun et al. studied AUV path following control using a modified deep deterministic policy gradient [11] algorithm, and Shi et al. employed a fuzzy PID algorithm [12].

A robust online path planner was employed by Zhuang et al. [13] to provide collision-free path planning and replanning with less computational cost. They used PSO as an initialization generator to enhance the searching ability of the Legendre pseudospectral method. Guo et al. studied global path planning and multi-objective path control for an unmanned surface vehicle based on modified PSO [14]. Yao et al. [15] used fluid dynamics for 3D real-time path planning to generate a flexible, smooth and energy optimal path considering both static and dynamic obstacles and the effects of ocean current. Igor et al. [16] proposed a hybrid evolutionary approach that employed an advanced algorithm to enhance the various task allocation search. It was aimed at multi-objective path following in a dynamic underwater environment with communication constraints. Yan et al. [17] combined PSO and waypoint guidance for real-time path optimization that generated a smooth, safe, time optimal shortest path. This research used multi-beam forward looking sonar for obstacle detection and PSO for waypoint optimization. Khan et al. studied various underwater communication strategies for cooperative communication system [18]. Das et al. [19] studied co-operative control of a team of autonomous underwater vehicles in an obstacle-rich environment. An approach to calculate the aspect ratio for Flapping Wings on the Propulsion of a Bionic Autonomous Underwater Glider is discussed based on bionic behaviour [20].

Motivated by the above studies, in this paper, a hybrid grey wolf optimization (HGWO) algorithm is proposed for path following of AUVs by combining the GA and grey wolf optimization (GWO) algorithm. Swarm intelligence (SI) methods, for example, GWO, are preferred for optimization as they are capable of dealing with incomplete information and computational difficulties inspired by a bionic algorithm [21]. GWO with good exploration capability has been demonstrated to be effective in escaping local optimal and, earlier, has been applied to address the AUV path following problem [22,23]. Though GWO, it has been verified that to produce a shorter path with minimum total cost the precision of the obtained solution is affected by its random initialization feature. The GA has been demonstrated to be robust to effect initialization and has been proven to provide consistent performance for optimizing total cost [24,25]. Thus, in this research, the proposed HGWO algorithm uses GA as an initialization generator to compensate for the effect of random initialization with increased population of the GWO algorithm.

The main novelties presented in this paper are summarized as follows:

• A HGWO algorithm is applied for optimizing total cost and generating a suboptimal path for single and multiple AUVs.
• The proposed HGWO is implemented underwater using the merits of GA followed by GWO for path planning of single and multiple AUVs in a static obstacle rich environment.
• The Kruskal–Wallis test is employed for a non-parametric statistical analysis and demonstrates the independence of the results given by the algorithms.

The remainder of the paper is structured as follows: Section 2 presents the problem formulation; Section 3 describes the development of the HGWO algorithm for path following of an AUV; the simulation results and analysis are described in Section 4; finally, the main conclusions are presented in Section 5.

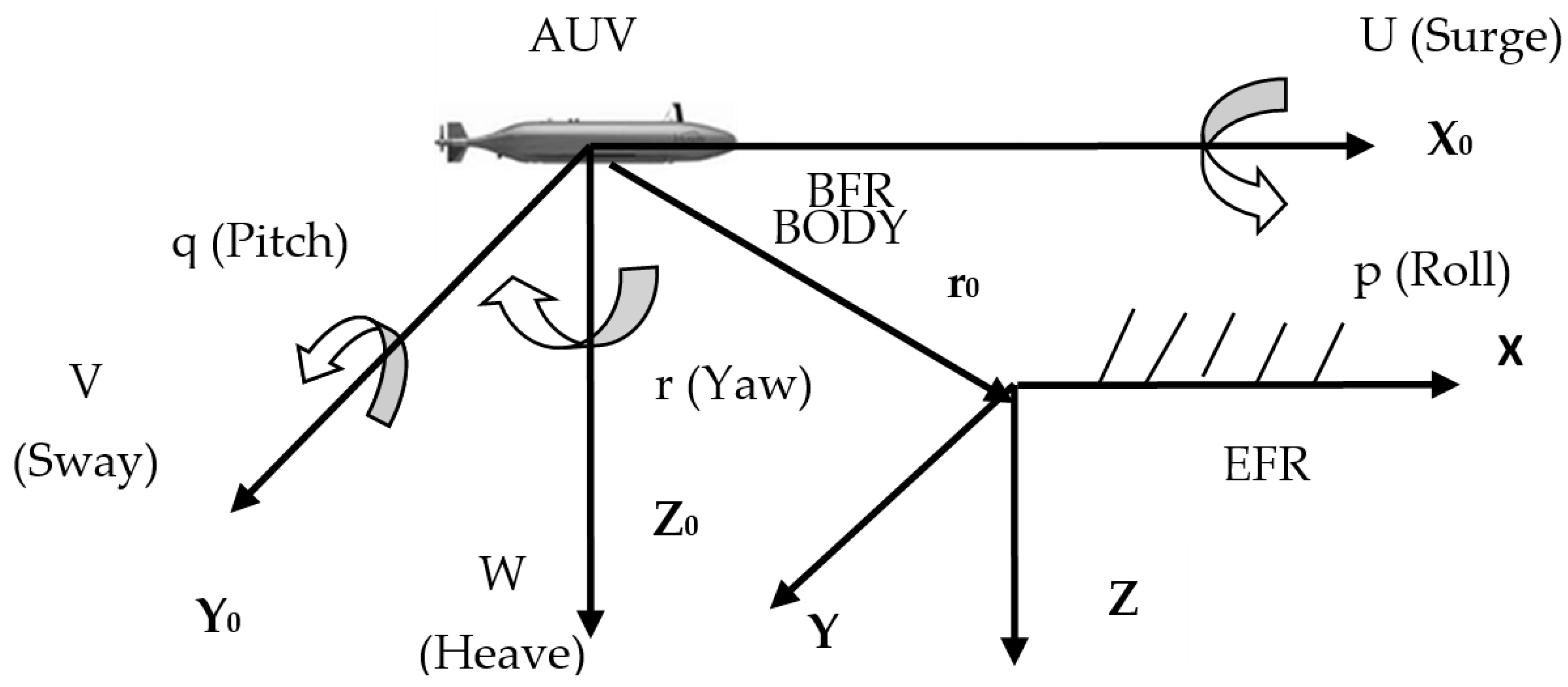
2. Problem Formulation

An AUV needs six degrees of freedom and two reference frames for complete description of its motion as shown in Figure 1 [26,27,28,29,30,31,32]. AUV system kinematics can be approximated as a second order liner system following Equation (1):

The nonlinear AUV model in inertial frame can be expressed as [33]:

$$M_{\eta }\left({\eta }_i\right){\ddot{\eta }}_i+C_{\eta }\left({\eta }_i,{\dot{\eta }}_i\right){\dot{\eta }}_i+D_{\eta }\left({\eta }_i,{\dot{\eta }}_i\right){\dot{\eta }}_i+g\left({\eta }_i\right)={\overline{\tau }}_i$$

(1)

${\dot{\eta }}_i=R\left({\psi }_i\right)v_i$ where ${\eta }_i={[x_i,y_i,z_i,{\varphi }_i,{\theta }_i,{\psi }_i]}^T$ is the position matrix, $v_i$ is the velocity matrix, ${\overline{\tau }}_i$ is the matrix of force and moments and $v_i\in R, {\eta }_i\in R,{\overline{\tau }}_i\in R$. For further details of the system dynamics, see [34]. Hybrid path planning of a group of AUVs is an optimization problem that needs to find a collision free path with the shortest distance between the origin and the destination point in a static obstacle environment, as shown in Figure 2 [35,36,37,38,39,40].

The problem formulation deals with modeling of the total cost function. In this research, total cost is considered to be a function of the path distance and collision penalties to avoid collisions with obstacles.

2.1. Path Distance

The path distance is the total distance travelled by an AUV to reach the destination. A shorter path distance requires less time and energy It is calculated by using Equation (2):

$$\mathrm{pathdistance}={{\displaystyle \sum }}_{m=0}^{M}d\left(p_m,p_{m+1}\right)$$

(2)

where $m=0,1\dots M$ is the number of nodes and $p$ is the path distance.

The Euclidian distance $d\left(p_m,p_{m+1}\right)$ between the m^th and (m + 1)^th points is given by Equation (3):

$$d\left(p_m,p_{m+1}\right)=\sqrt{{\left(x_{m+1}-x_m\right)}^2+{\left(y_{m+1}-y_m\right)}^2+{\left(z_{m+1}-z_m\right)}^2}$$

(3)

2.2. Collision Penalty

The total collision penalty depends on the distance between path points and the closest obstacle center. The collision penalty of a node on a planned route is given by Equation (4):

$$\mathrm{Collision} \mathrm{penlty} ={{\displaystyle \sum }}_{m=0}^M{P}_{km}\left(1+k\times m\right)$$

(4)

where $P_{km}$ is the extra cost incurred by selecting the $m^{\mathrm{th}}$ node on the $k^{\mathrm{th}}$ route and defined as Equation (5):

$$P_{km}=\left\{\begin{array}{c}{Ʀ}_{\min }-d_{\min }, \mathrm{for} d_{\min }>{Ʀ}_{\min }\\ e^{\sigma \left({Ʀ}_{\min }-d_{\min }\right)} \mathrm{for} d_{\min }\le {Ʀ}_{\min }\end{array}\right.$$

(5)

where $d_{\min }$ is the separation between the $m^{\mathrm{th}}$ node and the nearby obstacle center. ${Ʀ}_{\min }$ is the nearby obstacle radius. A collision means the total cost increases exponentially. The total cost function is defined by Equation (6):

$$\mathrm{total} \mathrm{cost} =\lambda \times \mathrm{pathdistance} +\left(1-\lambda \right)\times \left(\mathrm{collision} \mathrm{penalty}\right)$$

(6)

where $\lambda$ is the weighted coefficient that satisfies $\lambda$ ϵ [0,1]. On the one hand, when $\lambda$→1 suggests lower chances of collision and a shorter distance needed to be covered. On the other hand, $\lambda$→0 indicates greater collision probability and a longer distance to be covered in order to avoid the obstacle.

Let, the starting position of leader AUV in a cooperative motion be given by $\left(x_0, y_0, z_0\right)$ and the destination is at $\left(x_{I+1,}{y}_{I+1, }{z}_{I+1}\right)$, where I represents the total number of internal points. An internal point ${\mathrm{P}}_{\mathrm{i} }$ is written as $\left(x_{i,}{y}_{i,}{z}_i\right)$. The path is the combination of small segments between the source $\left(\mathrm{O}\right)$ and the destination $\left(\mathrm{D}\right),$ given by $\mathrm{OD}=\left(x_0, y_0, z_0\dots \dots \dots x_{i,}{y}_{i,}{z}_i\dots \dots \dots x_{I+1,}{y}_{I+1, }{z}_{I+1}\right)$. The path cost is evaluated based on three parameters that are the length of the path to be covered, the penalty for collision and the cost of diving. Here, it is assumed that there is no sudden direction change since the obstacle dimensions and positions are fixed, thus, the planar trajectory is smooth. The objective is to minimize the path cost, hence, minimizing all the factors contributing to path cost. Again, communication consensus is used to transfer the information regarding position so that all the AUVs cooperatively determine their paths to reach their destination by avoiding the static obstacles.

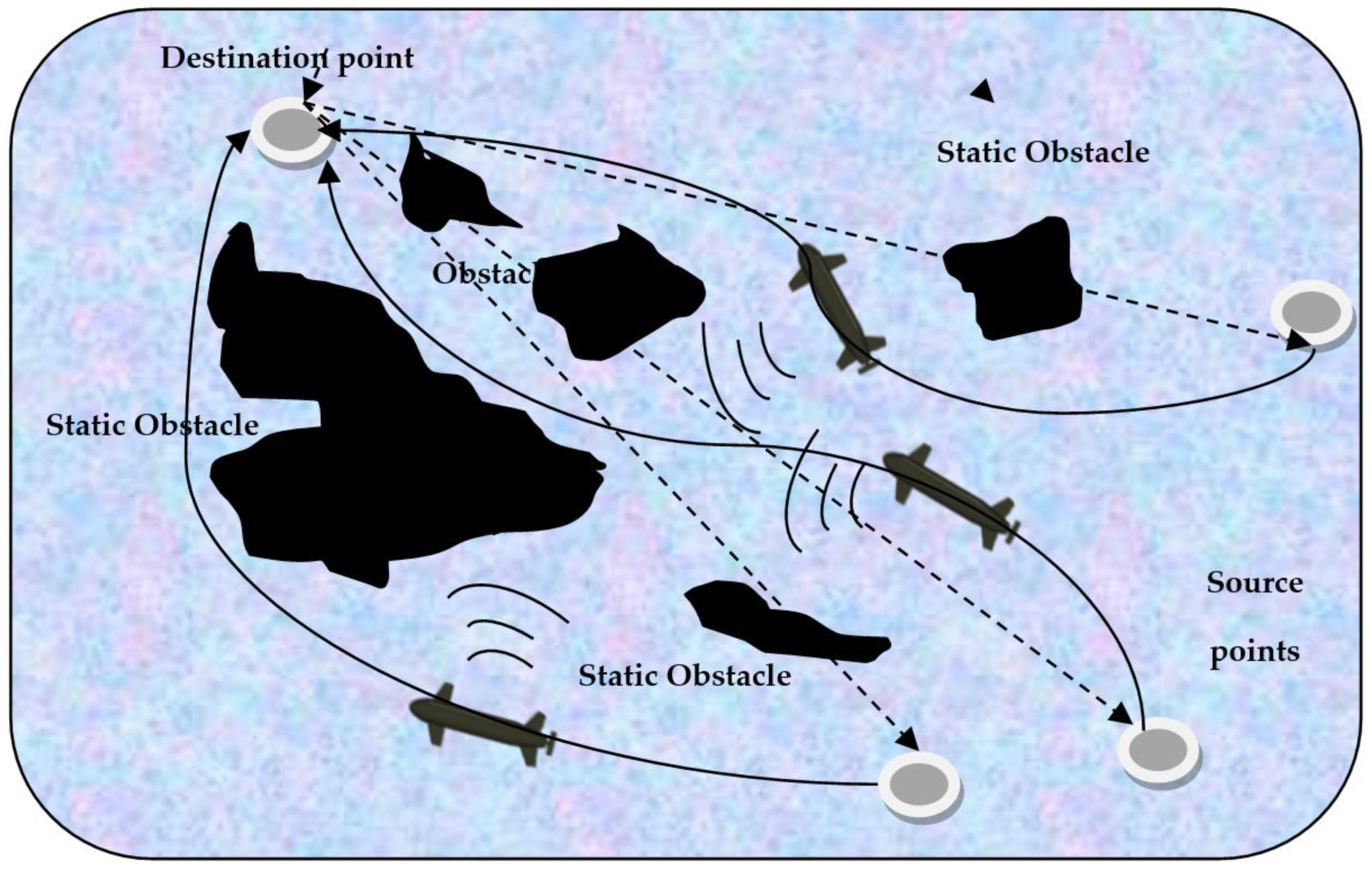
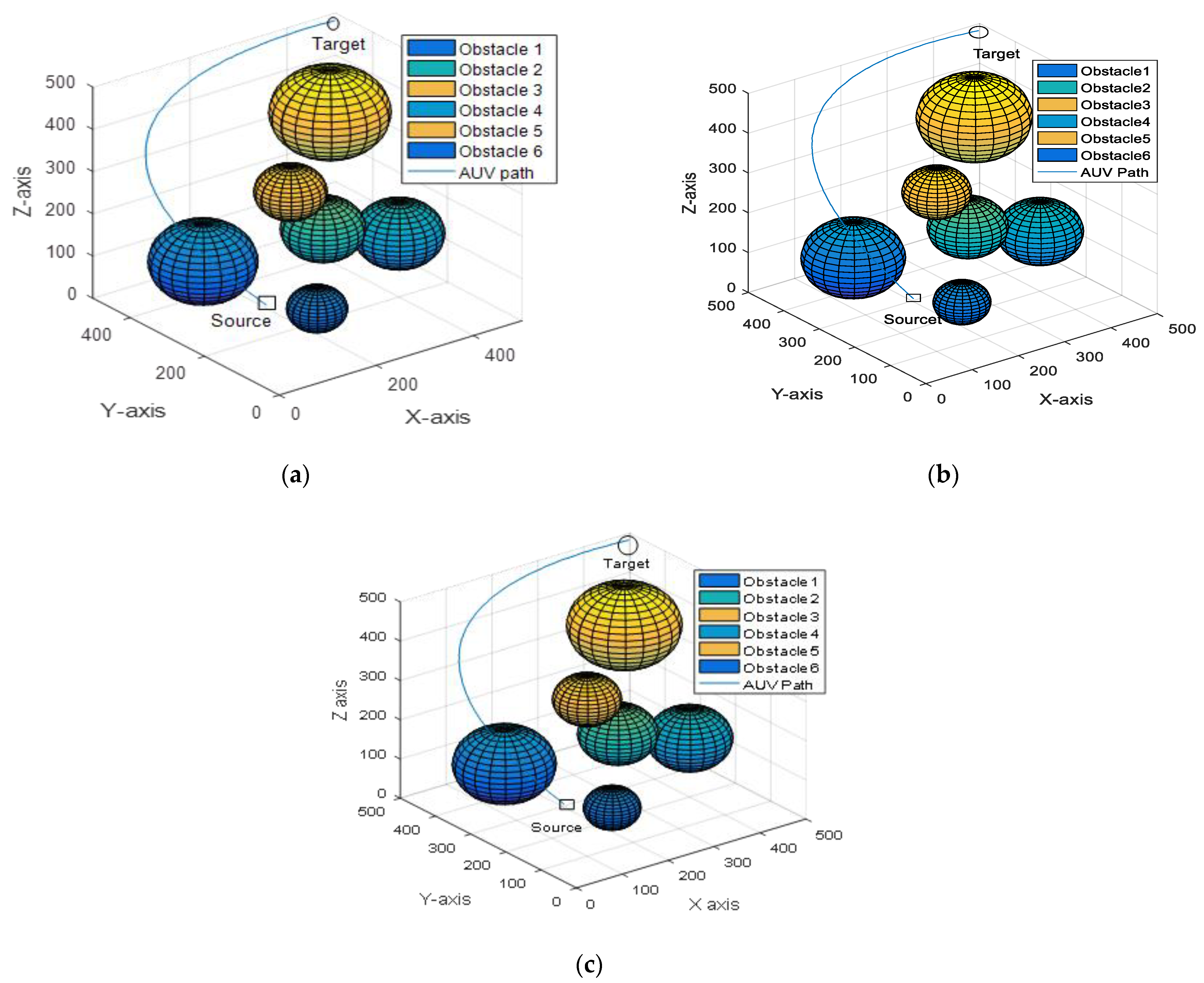
3. Proposed Algorithm for Path Planning of AUVs

This research applies the GA, the GWO algorithm and the proposed hybrid algorithm for solving the path planning problem of AUVs. In this section, each of the algorithms is introduced and the steps involved in applying these algorithms to the path planning problem are discussed in detail.

3.1. Genetic Algorithm

The GA is based on the natural gene selection process to find fit test solutions. It is a random process, but the randomness can be controlled. These can efficiently search a large solution space and does not require additional information regarding the problem. The above aspect makes the GA a more reliable algorithm to find solutions to problems with discontinuity, no derivatives and nonlinearity. The steps to solve the AUV path planning problem by using the GA are presented as follows:

• The underwater environment is modeled as a 3D map consisting of intermediate, origin and destination nodes.
• The obstacle locations are properly defined.
• The total cost function of Equation (6) is optimized at each node until the destination is reached.

3.2. Grey Wolf Optimization

GWO is a mathematical framework, modeled by Mirzali et al. [41], that inherits the social hierarchy and the pack hunting procedure of grey wolves. When GWO is used for path planning of an AUV, it provides three paths with minimum total cost that represent the alpha $(W_{\alpha })$, beta $(W_{\beta })$ and delta $( W_{\partial })$ wolves, respectively. The other paths represent the omega $\left(W_{\Omega }\right)$ wolves. The $W_{\alpha }$ wolf identifies the best resultant path towards the target. In the path planning problem, the resultant path is continuously updated to generate the optimized path. The path update process at the beginning of the operation is represented by Equations (7)–(18):

$$S\left(t+1\right)=S_p\left(t\right)-\mathcal{K}·L$$

(7)

where S is the position of the AUV, $S_p$ is the destination and t is the current iteration number. The distance is calculated as a vector L by using Equation (8):

$$L=\left|J·S_p\left(t\right)-S\left(t\right)\right|$$

(8)

$\mathcal{K}$ and J are the vectors of coefficients given by Equations (9) and (10) as follows:

$$\mathcal{K}=2·ɤ·{𝒫}_1-ɤ$$

(9)

$$J=2·{𝒫}_2$$

(10)

where $ɤ$ linearly varies from 2 to 0 with an increasing number of iterations, defined by Equation (11):

$$ɤ=2-t\left(2/N_{iter}\right)$$

(11)

$N_{iter}$ gives the total iterations required to obtain the optimized path. ${𝒫}_1$ and ${𝒫}_2$ can take any value between 0 and 1 randomly. The $W_{\alpha }$, $W_{\beta }$ and $W_{\partial }$ paths are used to generation the optimized path. For the $p^{\mathrm{th}}$ iteration, the three best paths are defined by using Equations (12)–(14), respectively:

$$S_1=\left|S_{\alpha }-{\mathcal{K}}_1·L_{\alpha }\right|$$

(12)

$$S_2=\left|S_{\beta }-{\mathcal{K}}_2·L_{\beta }\right|$$

(13)

$$S_3=\left|S_{\partial }-{\mathcal{K}}_3·L_{\partial }\right|$$

(14)

${\mathcal{K}}_1$, ${\mathcal{K}}_2$ and ${\mathcal{K}}_3$ are the coefficients and $L_{\alpha }$, $L_{\beta }$ and $L_{\partial }$ are the distance vectors for the $W_{\alpha }$, $W_{\beta }$ and $W_{\partial }$ paths. $L_{\alpha }$, $L_{\beta }$ and $L_{\partial }$ are calculated by using Equations (15)–(17):

$$L_{\alpha }=\left|J_1·S_{\alpha }-S\right|$$

(15)

$$L_{\beta }=\left|J_2·S_{\beta }-S\right|$$

(16)

$$L_{\delta }=\left|J_3·S_{\delta }-S\right|$$

(17)

The updated position of the AUV can be obtained by using Equation (18):

$$S\left(t+1\right)=\left(S_1+S_2+S_3\right)/3$$

(18)

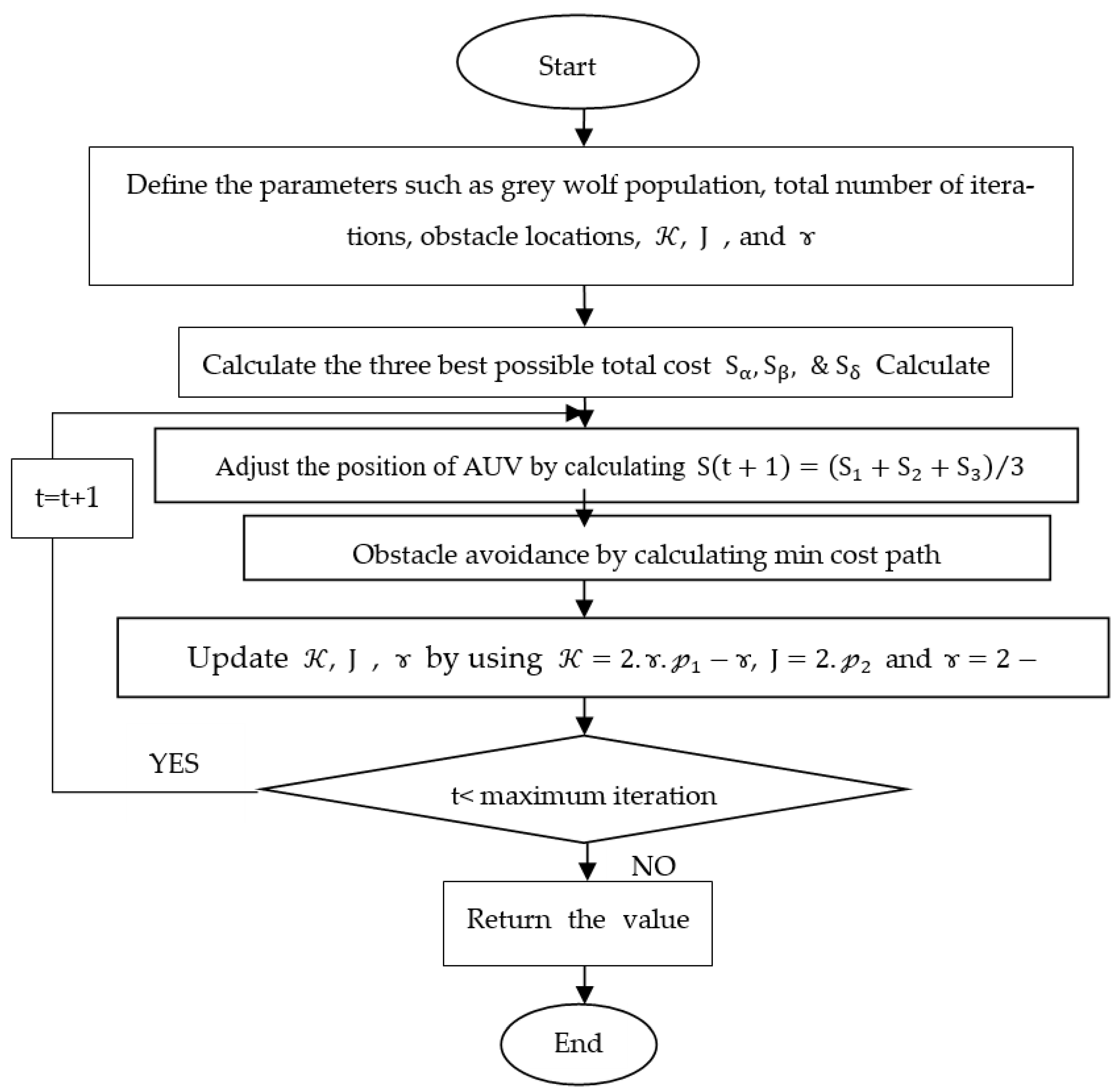
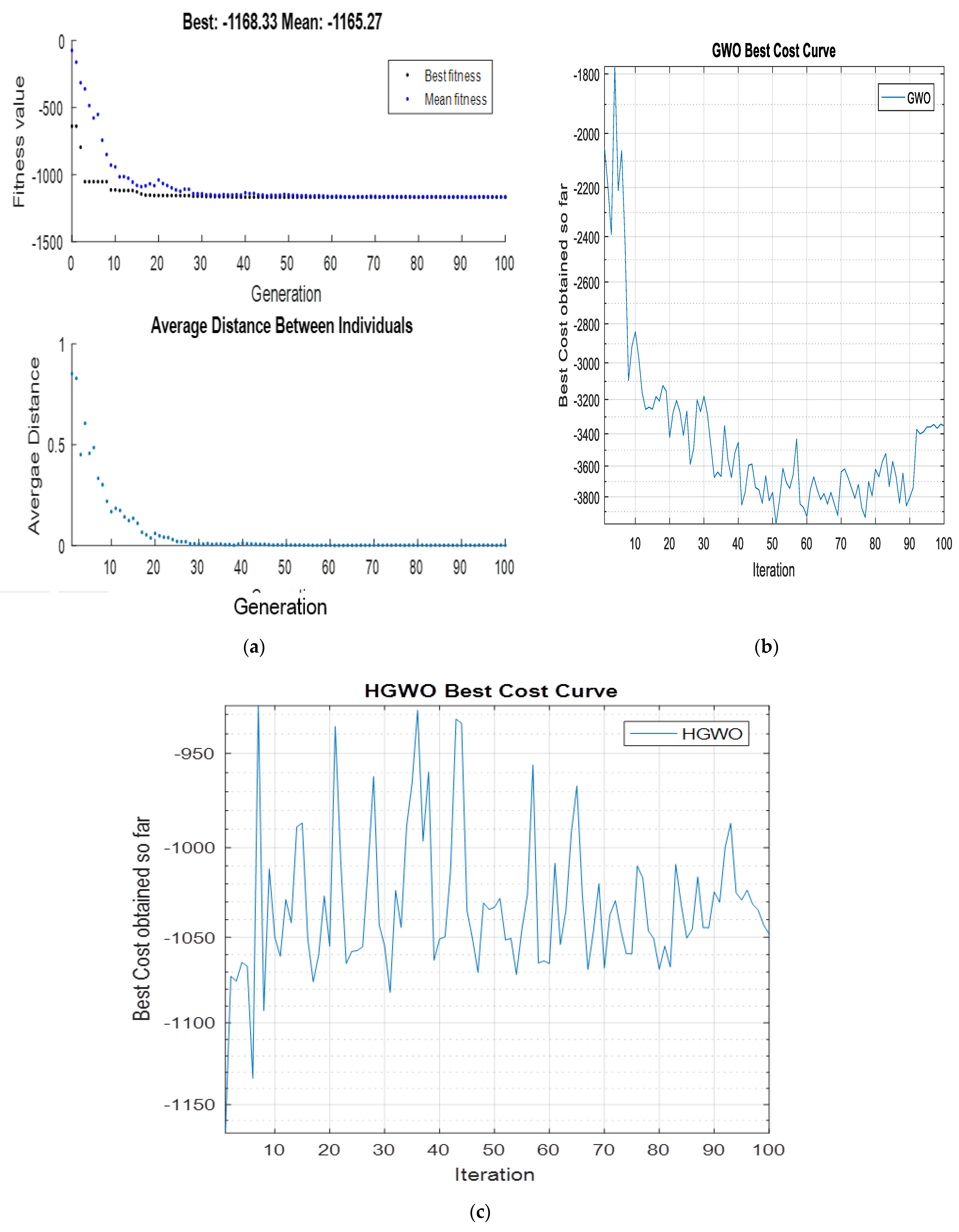
3.3. Proposed Hybrid GWO (HGWO) Algorithm

The GWO algorithm with good exploration capability is effective in escaping local optimal. Earlier research works have proven that the GWO algorithm produced optimized paths as compared to the GA and the ACO algorithm in terms of total cost. A step-by-step process to explain the application of the GWO algorithm for path planning of an AUV is presented in the planning flow diagram shown in Figure 3.

On the one hand, the precision of a solution obtained using the GWO algorithm suffers with an increase in the population size due to its random initialization feature. On the other side, the GA is a robust optimization method for solving a multi-objective problem, since it is independent of the initialization method. Thus, we propose a hybrid grey wolf optimization (HGWO) algorithm that explores the robustness of the GA to the initialization process, as shown in Figure 3. In the proposed HGWO algorithm, the GA through an extensive local search provides the best possible initial estimates to the GWO algorithm to start the global search. After receiving the initial estimates, the GWO algorithm is used to compute a safe path by optimizing the path cost function. The proposed algorithm for path planning of a single AUV as a step-by step procedure is described in the pseudocode as given as Algorithm 1. The proposed HGWO algorithm is also applied in the case of multiple AUVs, as demonstrated in Algorithm 2.

Algorithm 1. Pseudocode for single AUV path planning

Initialize the total no. of nodes n, in the path as GW population Si, where (i = 1, 2,…, n).  Destination = n + 1. Optimize the initial positions by optimizing the total cost (Equation (6)) using GA.  Represent the first three best solutions as $S_{\alpha }, S_{\beta },\& S_{\delta }$. Initialize $\mathcal{K}$, $J$, and $ɤ$  while (i < n + 1)  For all Si do  Update the position of the AUV using Equation (18),  Update $\mathcal{K}$, $J$, and $ɤ$ using Equations (9), (10) and (11) respectively  Update $S_1,S_2,\& S_3$ using Equations (12), (13) and (14) respectively  End for  End while  Return $S_1$  End

Algorithm 2. Pseudocode for cooperative path planning [41]

Begin The 3D environment is modeled with origin, destination and fixed obstacle locations. Assume leader path knowledge and synchronization error is available to all the follower AUVs. For each Follower AUV While ($\mathrm{synchronization} \mathrm{error} \ne 0$) Initialize the total no. of nodes n in the path as GW population Si, where (i = 1, 2, …, n). Destination = n + 1. Optimize the initial positions by optimizing the total cost (Equation (6)) using GA. Represent the first three best solutions as $S_{\alpha },S_{\beta }, \& S_{\delta }$. Initialize $\mathcal{K}$, $J$, and $ɤ$ while (i < n + 1) For all Si do Update the position of the AUV using Equation (18) Update $\mathcal{K}$, $J$, and $ɤ$ using Equations (9), (10) and (11) respectively Update $S_1, S_2,\& S_3$ using Equations (12), (13) and (14) respectively End for End while Return $S_1$ End while End for End

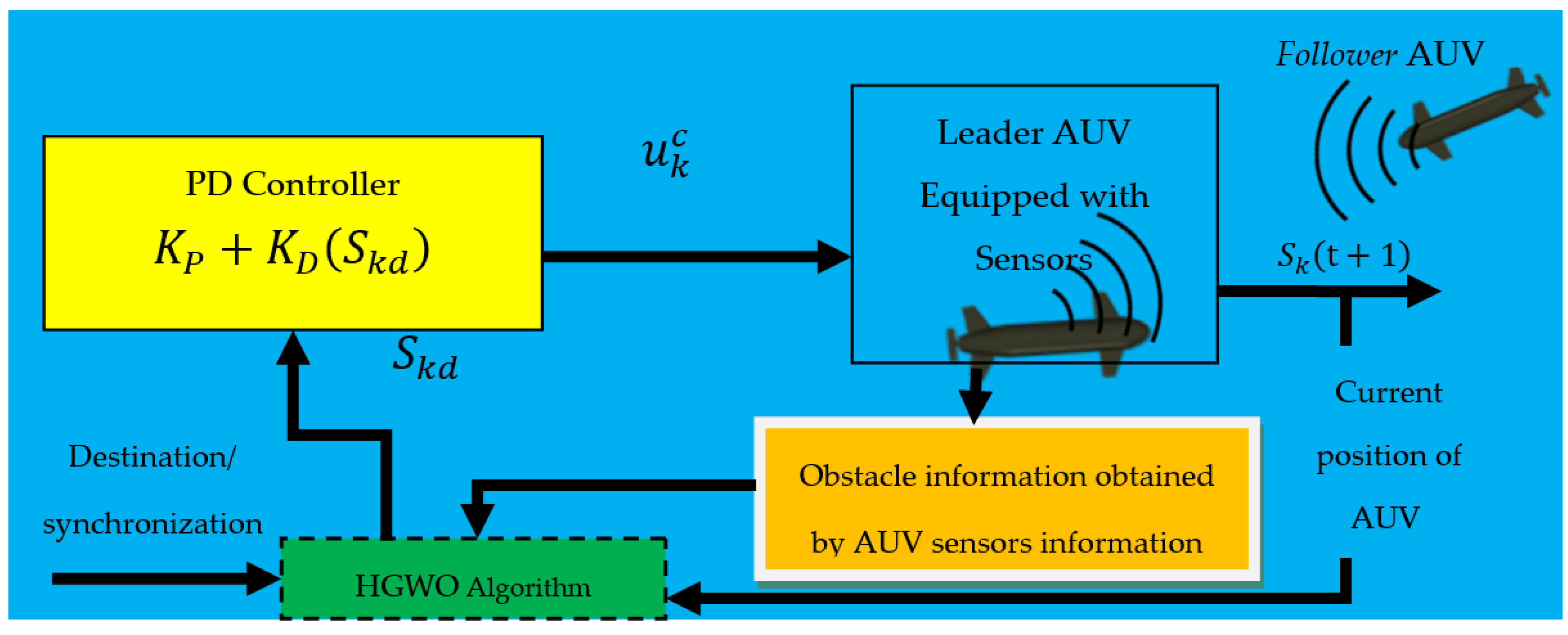
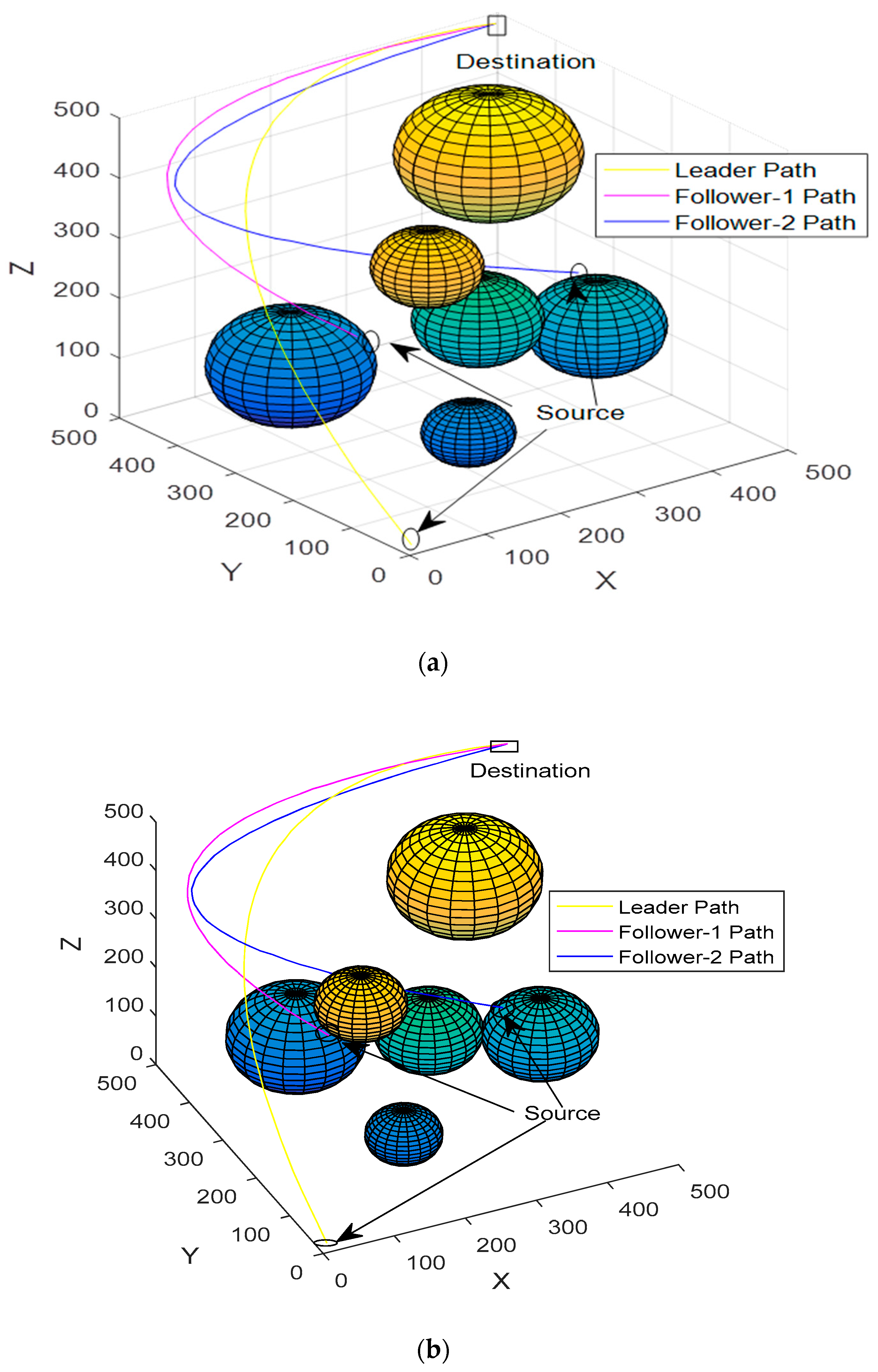
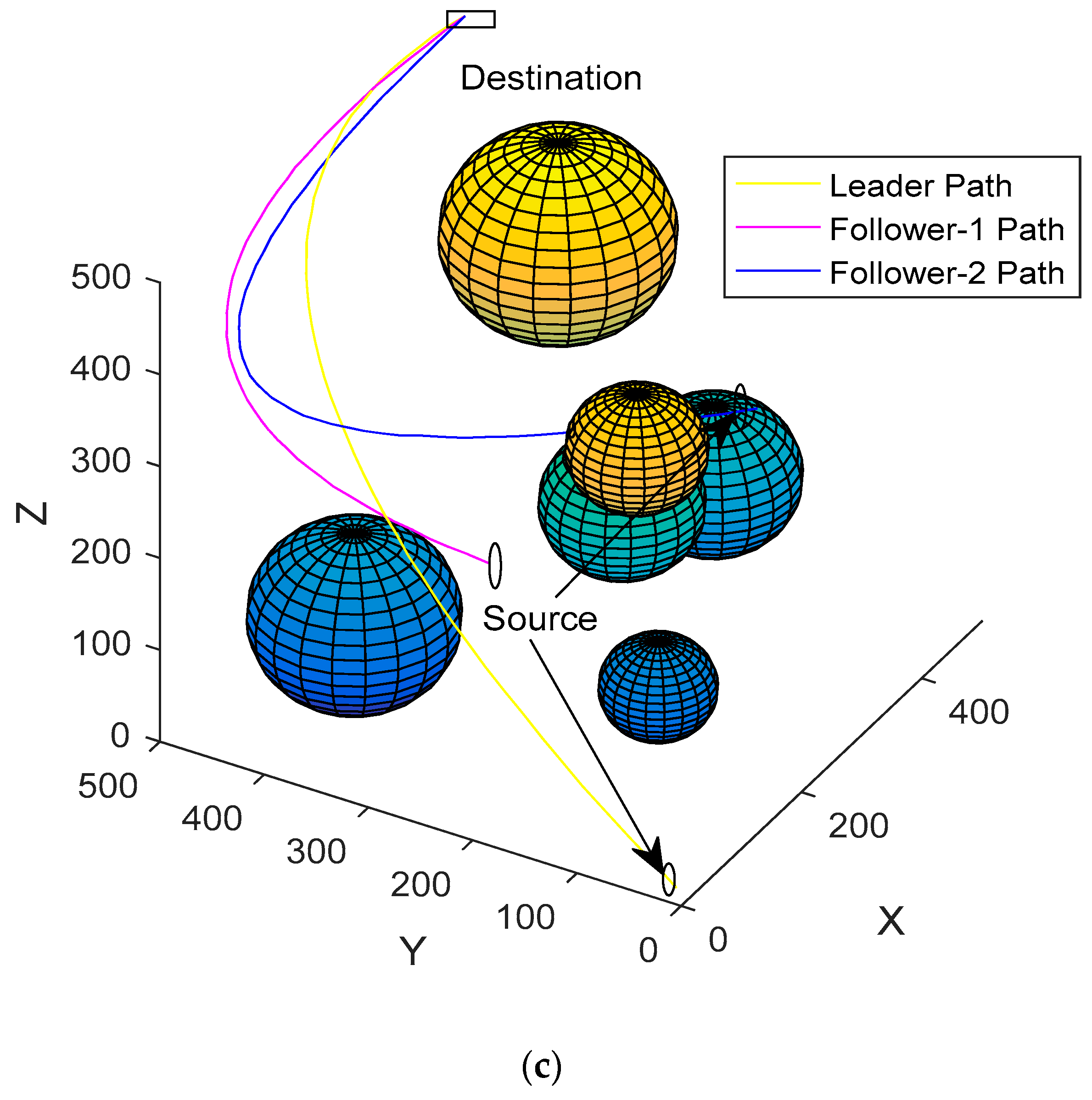
3.4. Proposed Path Planning Algorithm’s Communication Consesus

The proposed HGWO algorithm calculates the desired position (19) of the kth vehicle in a team of AUVs in path planning structure based on the synchronization error using communication consensus, as shown in Figure 4. The research work assumes a bidirectional flow of information among the AUVs, represented by an undirected graph. The difference between the desired position and the actual position of an AUV at any instant of time is the synchronization error. The follower AUVs try to follow the path of the leader AUV by exchanging the synchronization error information with their neighbors in the absence of velocity measurements. Assuming that, at any instant, an AUV is always connected to its neighbor AUV, then an incidence matrix (${\alpha }_{kl}$) can be defined by Equation (20):

$${\alpha }_{kl}=\left\{\begin{array}{c}+1 \mathrm{i}\mathrm{f} \mathrm{t}\mathrm{h}\mathrm{e} k^{\mathrm{th}} \mathrm{A}\mathrm{U}\mathrm{V} \mathrm{i}\mathrm{s} \mathrm{a}\mathrm{t} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{l}\mathrm{e}\mathrm{f}\mathrm{t} \mathrm{o}\mathrm{f} l^{\mathrm{th}}\mathrm{A}\mathrm{U}\mathrm{V}\\ -1 \mathrm{i}\mathrm{f} \mathrm{t}\mathrm{h}\mathrm{e} k^{\mathrm{th}}\mathrm{A}\mathrm{U}\mathrm{V} \mathrm{i}\mathrm{s} \mathrm{a}\mathrm{t} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{r}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t} \mathrm{o}\mathrm{f} l^{\mathrm{th}}\mathrm{A}\mathrm{U}\mathrm{V}\end{array}\right.$$

(19)

The associated adjacency matrix $\mathcal{A}$ is defined in graph theory as $\mathcal{A}=\left[E_{kl}\right]\in R^{N\times N}$. Two members, k and l, are neighbor AUVs if they can access the synchronization error $\left|{\theta }_k-{\theta }_l\right|$. It is assumed that all the follower AUVs are in full communication with the leader and follow the leader according to Equation (21):

$$\underset{t\to \infty }{\lim }\left|{\theta }_k-{\theta }_l\right|=0,\forall k\in \left(1,2,\dots N\right)$$

(20)

Therefore, the distributed consensus tracking theorem for $\dot{{\theta }_k}$ may be defined by Equation (22) according to

$$\dot{{\theta }_k}=-\beta {{\displaystyle \sum }}_{l\in {\overline{N}}_l\left(t\right)}{E}_{kl}\left({\theta }_k-{\theta }_l\right)-{\delta }_{c}sgn [{{\displaystyle \sum }}_{l\in {\overline{N}}_l\left(t\right)}{E}_{kl}\left({\theta }_k-{\theta }_l\right)]$$

(21)

where ${\overline{N}}_l\left(t\right)=\left\{1,2, \dots \right\}$ denotes the neighbor set of follower k in the team consisting of the N followers and the virtual leader, $\beta$ is a nonnegative constant and ${\delta }_c$ is a positive constant, $sgn\left[.\right]$ represents signum function, $E_{kl}$ is a positive constant, being $k,l=1,2\dots ·m$. For a switching network topology, it is assumed that $l\in \overline{N_k\left(t\right),} k=1,2\dots ·m,l=0,1,2\dots \dots ,m, if \left|{\theta }_k-{\theta }_l\right|<r$ at time t and $l\notin \overline{N_k\left(t\right),}$ where $𝕣$ denotes the communication sensing radius of the AUV. Since the undirected graph is connected, therefore, at least one value of $E_{k0}$ is nonzero. $E_{k0}$ is a positive constant if the virtual position of the leader is available to follower k.

4. Simulation Setup and Result Analysis

The simulation parameters for the AUV are taken from the experimental values shown in [42]. The PD controller parameters are: $K_P$ is unity for simulation purpose, and $K_D$ used for simulation is 17.1.

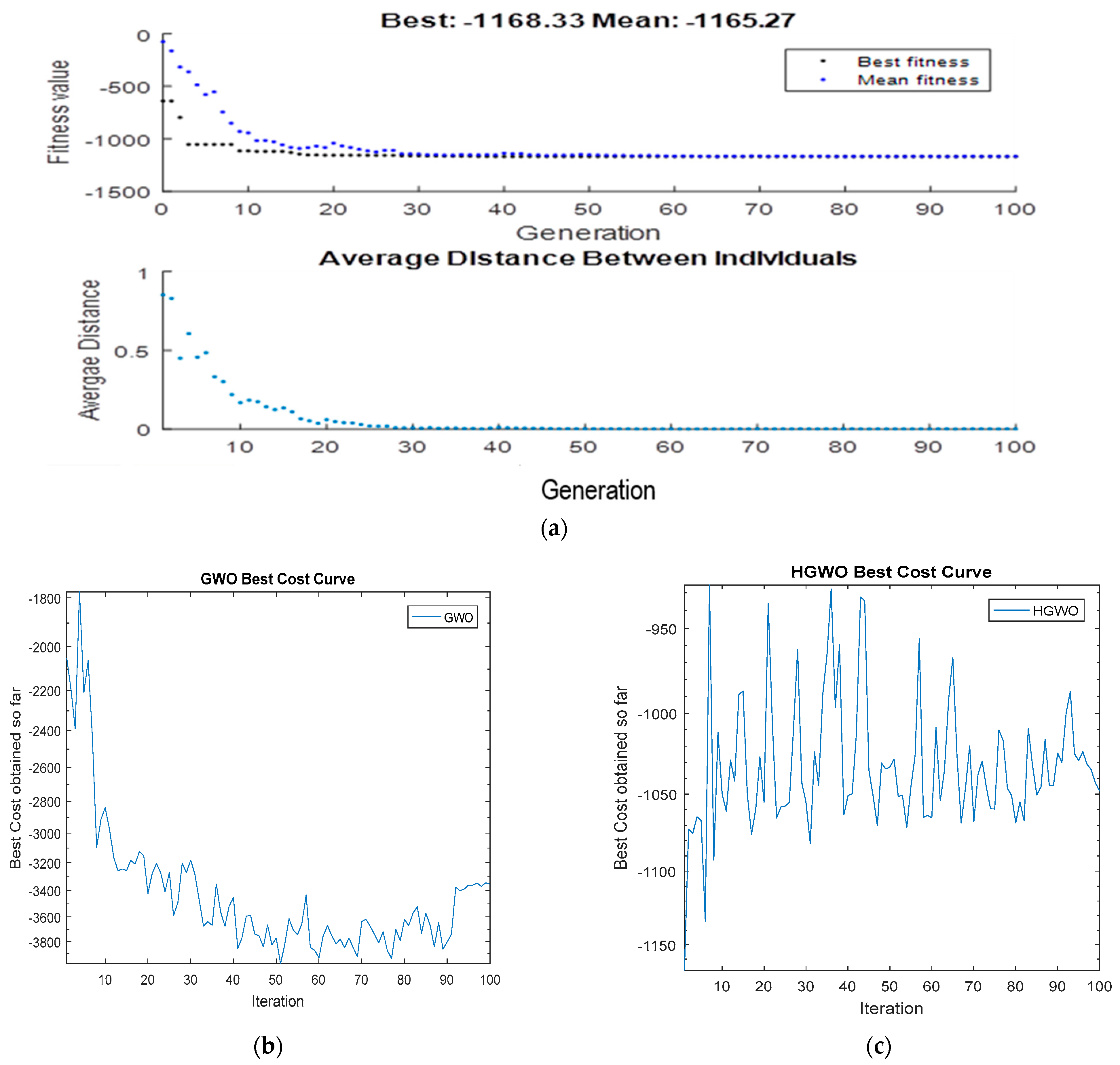
4.1. Result Analysis of a Single AUV

The environment was modeled as a 3D grid map of size (500 × 500 × 500). The origin and destination are at [50,100,150] and [490,490,490], respectively. In the results, the origin is represented by a rectangle and the destination by an ellipse

Figure 5 shows the complete optimized paths in a 3D obstacle rich environment using the GA, GWO and HGWO algorithms. The optimized path for the GA, as shown in Figure 5a, appears to be equal to that of the GWO algorithm in Figure 5b, but the former covers a longer distance of 1008.66 m than the latter, which covers a path distance of 1005.95 m in close observation. The optimized path obtained by using the HGWO algorithm, shown in Figure 5c, appears to cover the shortest distance of 957.43 m between the origin and the destination, as shown in

Table 1. Analysis of the GA, GWO and HGWO performances for path planning of a single AUV.

Algorithm	Test Runs	Computational Delay (s)	Path Distance (m)	Total Cost (m)
GA	1	27.97	962.34	488.69
	2	28.28	982.59	540.17
	3	26.67	1010.30	517.13
	4	29.13	1079.42	479.93
	5	29.13	1089.75	483.49
	Average	28.24	1008.66	483.49
GWO	1	24.34	984.47	280.90
	2	23.19	997.78	279.43
	3	22.31	988.12	242.19
	4	23.75	993.53	269.11
	5	23.86	1065.87	175.32
	Average	23.49	1005.95	249.39
HGWO	1	45.10	940.77	115.73
	2	48.62	951.82	126.49
	3	58.61	972.60	116.39
	4	53.92	966.15	113.90
	5	47.51	955.84	125.65
	Average	50.75	957.43	119.63

.

Figure 6 presents the simulation results that depict optimized paths with minimum total path cost obtained by applying the GA, GWO and HGWO algorithms to the path planning problem of a single AUV. The path is the trajectory with minimum path cost from the defined origin to the destination. In each case, the optimized path is shown by a blue line that represents the path distance from the source to the destination point that an AUV has to cover while avoiding collision with static obstacles. The obstacles are represented by circles of different color in two-dimensional (2D) view, and by spheres of different color in three-dimensional (3D) view.

The path is not a straight line but a curve, since the AUV has to avoid collision with obstacles in its path. The optimized cost curves obtained based on the GWO and HGWO algorithms are shown in Figure 6b,c, respectively. In both cases, the optimized cost seems to decrease with an increase in number of iterations, but the HGWO algorithm provides minimum totoal cost compared to the GWO algorithm for an equal number of iterations.

Table 1 shows the simulation results obtained by employing the GA, GWO and HGWO algorithms for planning the optimized path for a single AUV. The average values of computational delay, path distance and path cost over five runs of the algorithms are calculated to facilitate the analysis. It is observed from the analysis of the results that the average path distance and path cost given by the GA are 1008.66 m and 483.49 m, respectively. The average path distance is 1005.95 m and the path cost is 249.39 m for the GWO algorithm. Thus, the GWO algorithm provides a shorter path distance and path cost as compared to GA. The HGWO algorithm uses the GA to improve the performance of GWO algorithm, and it gives an average path distance of 957.43 m and path cost of 119.63 m. The HGWO algorithm performs better as compared to the other two algorithms based on the path cost.

4.2. Result Analysis of Multiple AUVs

Figure 7a–c show the 3D paths of the leader AUV and the follower AUVs based on the GA, GWO and HGWO algoriths, respectively. Figure 8 presents the optimized paths of the AUVs obtained from the multiple AUV path planning problem.

The obstacle rich environment was modeled as a 3D map of size (500 × 500 × 500) with predefined obstacle information. The obstacles are represented by spheres of different colors in the XYZ plane. The destination is at [490,490,490]. The origin coordinates for the leader AUV, Follower 1 and Follower 2 are at [10,10,10], [130,260,200], and [300,110,320], respectively. The path shown is the trajectory with minimum path cost from the origin to the destination obtained by employing the GA, GWO and HGWO algorithms. The optimized paths for the leader, Follower 1 and Follower 2 AUVs are shown by a yellow line, pink line and blue line, respectively. For each case, the optimized path represents the path distance from the start to the destination point that an AUV has to cover while avoiding collision with static obstacles. The curve paths justify the collision avoidance with static obstacles.

The best fitness function and average distance over the generations of the GA are presented in Figure 8a. Figure 8b,c show the best cost curves obtained based on the GWO and HGWO algorithms, respectively. The proposed HGWO algorithm provides the minimum totoal cost as compared to the GWO algorithm over 100 iterations. The performance analysis based on computational delay, path distance and path cost employing the GA, GWO and HGWO algorithms for cooperative path planning are shown in

Table 2. Analysis of the GA, GWO and HGWO performances for path planning of multiple AUVs.

Algorithm	AUV	Computational Delay (s)	Path Distance (m)	Total Cost (m)
GA	Leader	55.10	1120.04	−45.93
	Follower1	58.62	1116.79	−46.06
	Follower2	58.61	1136.23	−62.25
GWO	Leader	28.97	1062.03	−33.45
	Follower1	26.28	1069.25	−31.3
	Follower2	28.67	1080.45	−35.67
HGWO	Leader	23.3	1033.17	−19.47
	Follower1	23.341	1063.59	−22.91
	Follower2	23.13	1063.03	−19.31

.

For the leader AUV, the path distances covered are 1120.04 m, 1062.03 m and 1033.17 m and path costs are −45.95 m, −33.45 m, and −19.47 m by employing the GA, GWO and HGWO algorithms, respectively. The larger the negative number, the greater the chances of collision, and the greater the distance that has to be covered. Similar analyses for Follower 1 and Follower 2 AUVs shows that application of the HGWO algorithm results in less path distance and minimum total path cost. However, the HGWO algorithm is more complex as it combines the GA and GWO algorithms, and hence, requires more computational delay compared to the other two algorithms.

4.3. Non-Parametric Statistical Analysis

In this paper, the Kruskal–Wallis test is employed for the non-parametric statistical analysis. This test is useful for dealing with more than two independent test groups. It compares median among k populations. In this paper, we employed three algorithms (GA, GWO and HGWO), and three AUVs (one leader and two followers) are tested to find the algorithm that optimizes the path cost, see Table 2. The sample sizes for algorithms 1, 2 and 3 are as follows:

Treatment 1, n1 = 3;

Treatment 2, n2 = 3;

Treatment 3, n3 = 3;

n = n1 + n2 + n3 = 3 + 3 + 3 = 9.

The hypotheses, considering 5% level of significance, are:

$H_0:\hspace{0.33em}\mathrm{Three} \mathrm{algorithms} \mathrm{path} \cos \mathrm{ts} \mathrm{are} \mathrm{the} \mathrm{same}$.

$H_1:\hspace{0.33em}\mathrm{HGWO} \mathrm{algorithm} \mathrm{path} \cos \mathrm{t} \mathrm{is} \mathrm{minimum}$.

The sum of ranks will be n(n + 1)/2, and the sum of ranks 45 (n(n + 1)/2 = (9 × 10)/2 = 45).

Therefore, we studied three population medians to test the samples.

Table 3. Non-parametric statistical analysis of the GA, GWO and HGWO performances for path planning of multiple AUVs.

Algorithms			Rank
GA	GWO	HGWO	GA	GWO	HGWO
		−19.3			1
		−19.47			2
		−22.91			3
	−31.3			4
	−33.45			5
	−35.67			6
−45.93			7
−46.06			8
−62.25			9

shows the sample information in a test statistic based on ranks. The test statistic is denoted by H, and given by Equation (22):

$$H=\left(\frac{12}{n\left(n+1\right)}{{\displaystyle \sum }}_{j=1}^k\frac{R_j^2}{n_j}\right)- 3\left(n+1\right)$$

(22)

where k = number of comparison groups = no of algorithms = 3; n = total sample size = number of AUVs = 3; n_j = sample size in j^th group; and R_j = sum of the ranks in the j^th group.

In this case study, it is obtained: k = 3, n = 9, n1 = n2 = n3 = 3, R1 = 6, R2 = 15, R3 = 24

Thus, $H=\frac{12}{90}\left(\left(12+75+192\right)\right)-30=7.2$.

Then, the critical value of H using the table of critical values is obtained, which is 5.656. The test criterion is given by:

${\mathrm{Reject} H}_0: H \ge \mathrm{critical} \mathrm{value}$, ${\mathrm{Accept} H}_0: H \le \mathrm{critical} \mathrm{value}$.

The result for H is 7.2 and the critical value is 5.656. Therefore, the null hypothesis is rejected, i.e., there is no significant evidence to state that the three algorithms’ path costs are the same. The total path cost using the HGWO algorithm is also obtained, where the total path cost of the leader, Follower 1 and Follower 2 AUVs are less than that of the using the algorithms GA and GWO therefore, H₁ is accepted.

5. Conclusions

In this research work, the proposed HGWO algorith uses the GA followed by the GWO algorithm for path planning of AUVs. The main objective is to determine the minimum total cost which is a function of the distance covered and collision penalties in the presence of static obstacles. The HGWO algorthm using PD control is proposed to plan a minimum total cost for a single AUV and for multiple AUVs avoiding obstacles. The advantage of using the proposed HGWO algorithm is to overcome the random initialization of the GWO algorithm. The simulation results obtained with the conventional algorithms were compared to the performance of the proposed algorithm based on computational delay, path distance and total cost. The HGWO algoritm provides better path distance as well as total cost compared to both the GA and the GWO algorithm. The Kruskal–Wall test was employed for a non-parametric statistical analysis, where the independence of the results given by the algorithms was demonstrated. The test confirms that the HGWO algorithm can be considered to be a better optimization algorithm to produce a static collision-free path with optimized total cost for oceanographic surveys.