A Novel Finite Difference Scheme for Normal Mode Models in Underwater Acoustics
Abstract
1. Introduction
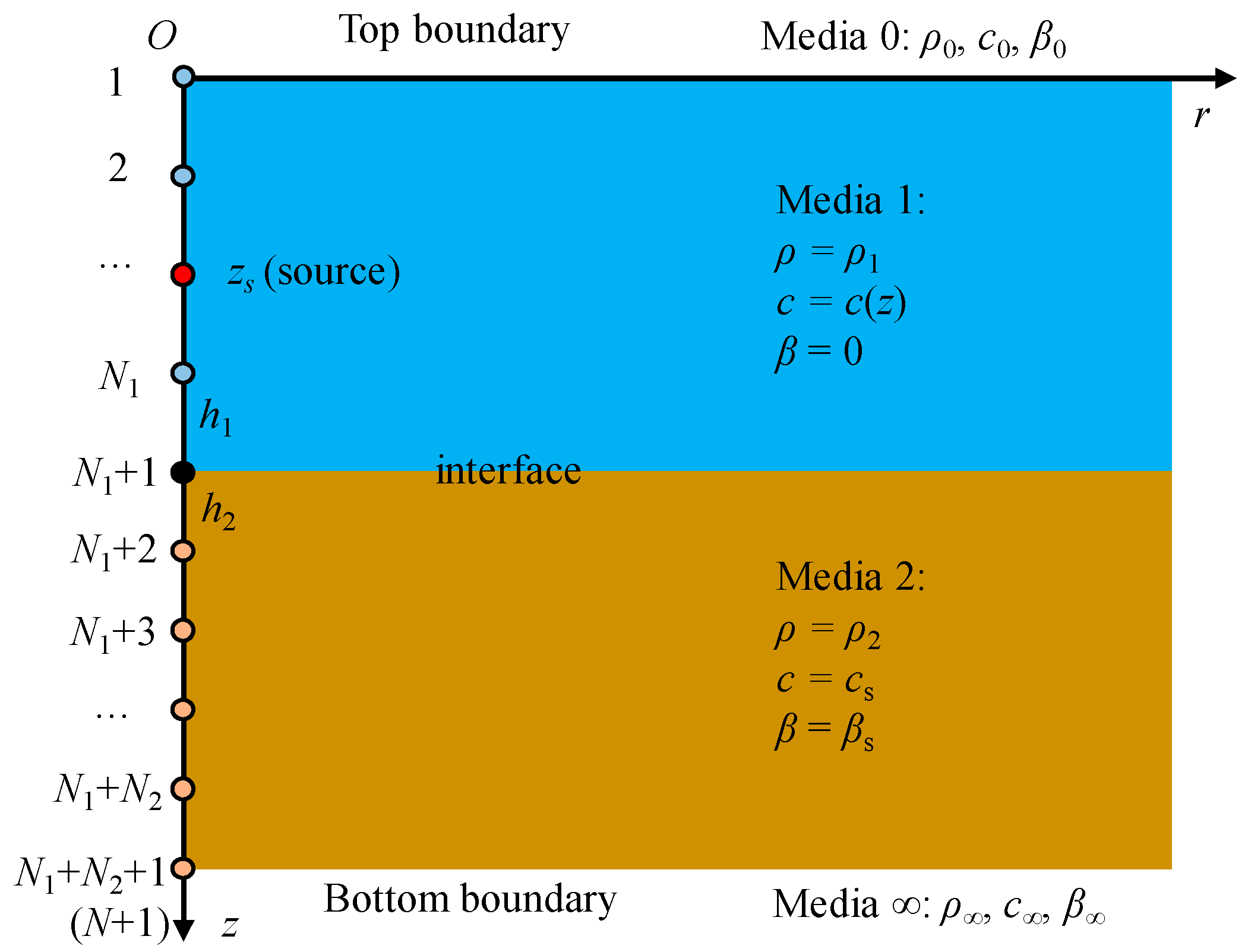
2. Mathematical Models
2.1. The SFD
2.1.1. Interface Scheme
2.1.2. Boundary Schemes
2.1.3. Interior Point Scheme
2.1.4. Linear System
2.2. The NFD
2.2.1. Interface Scheme
2.2.2. Boundary Schemes
2.2.3. Interior Point Scheme
2.2.4. Linear System
3. Test Cases
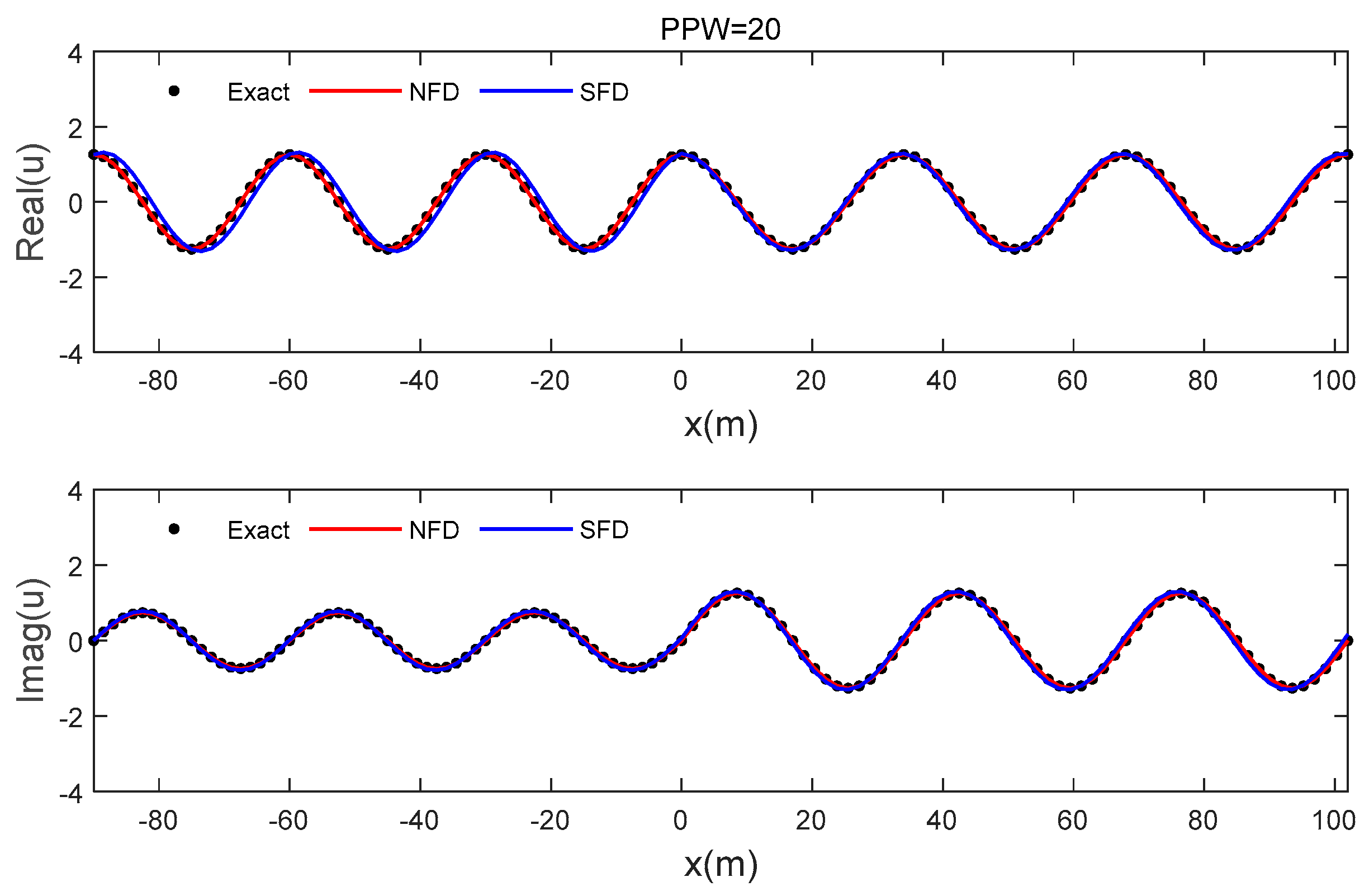
3.1. Plane-Wave Reflection
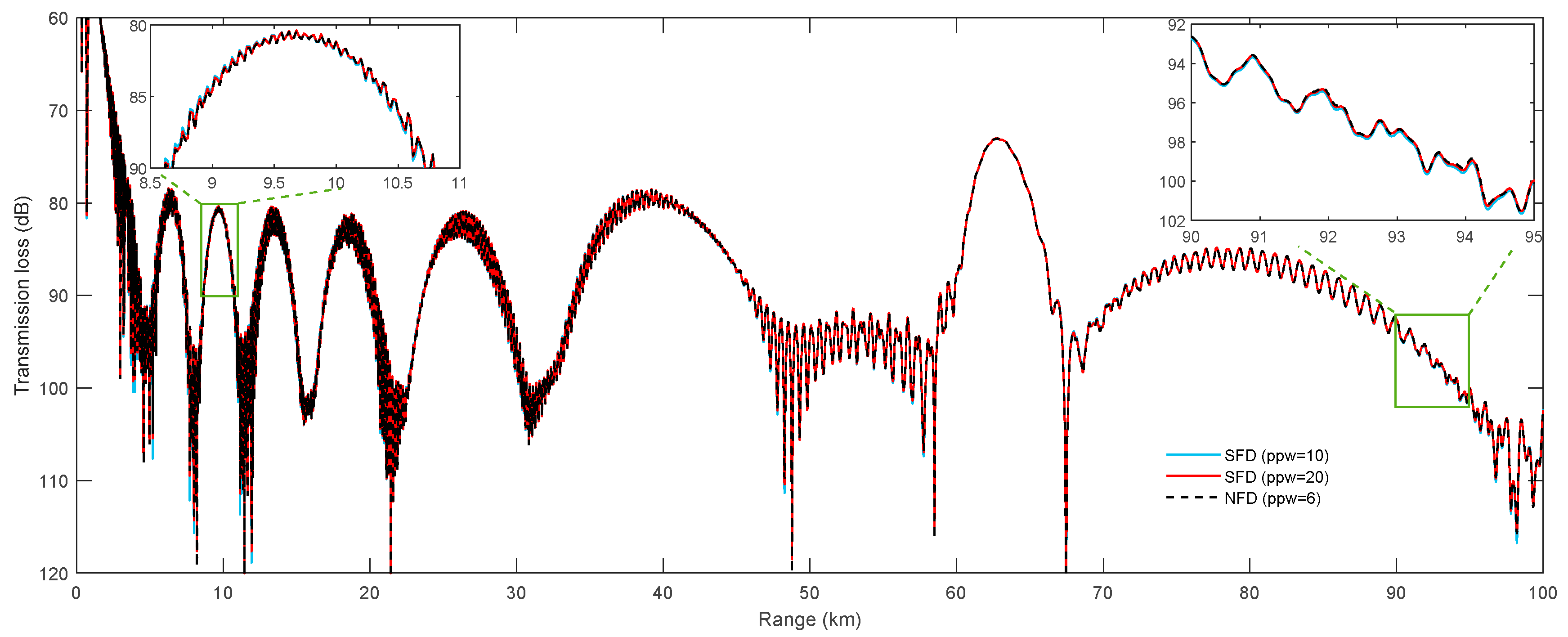
3.2. Pekeris Waveguide
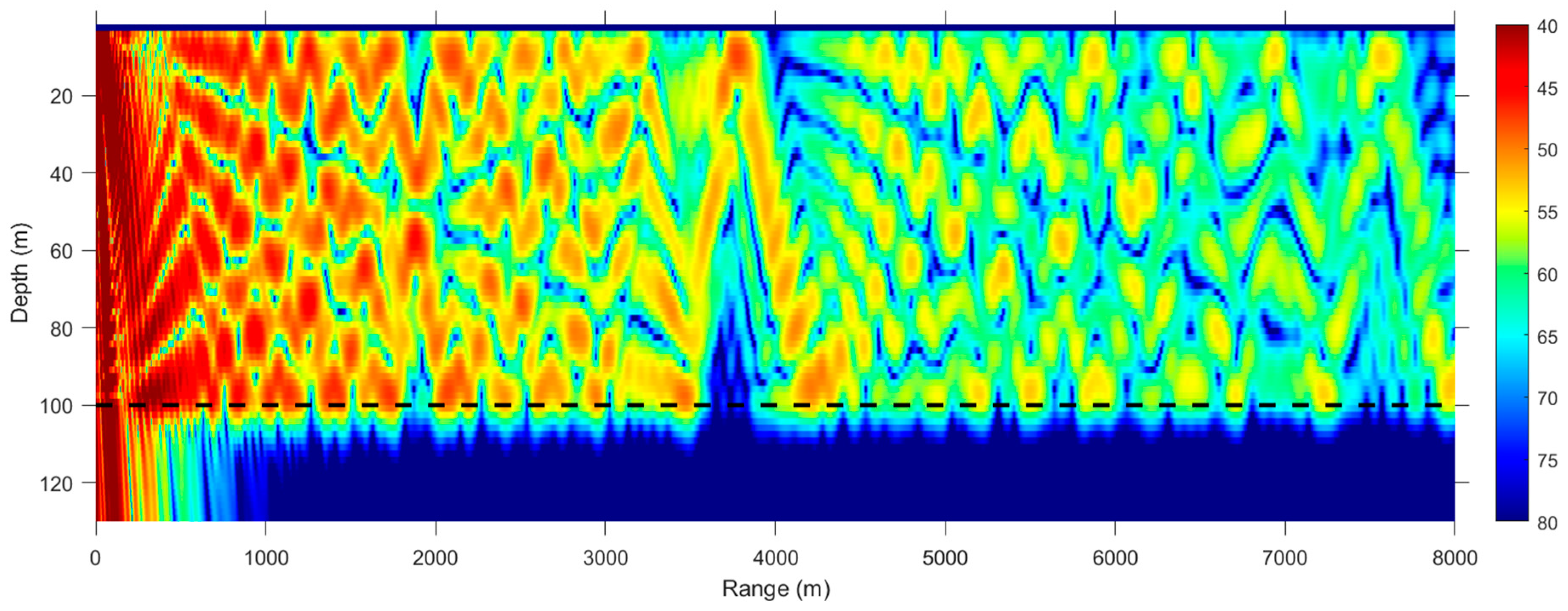
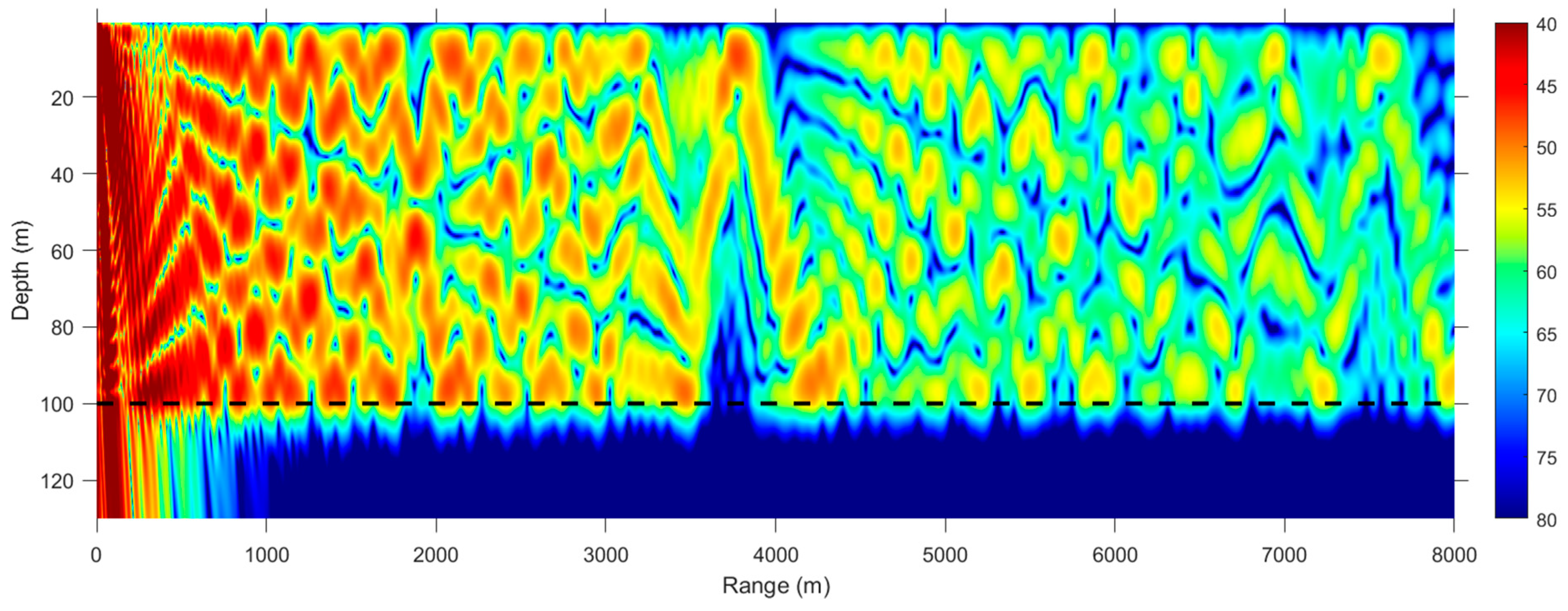
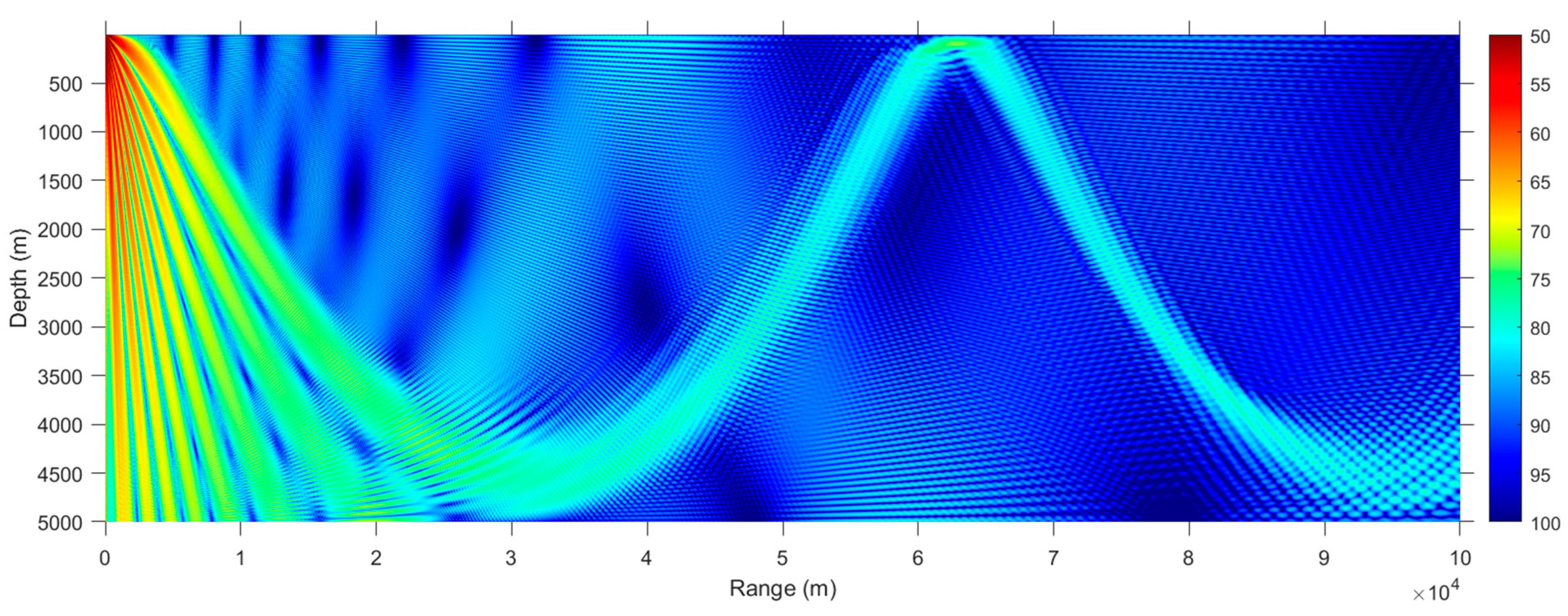
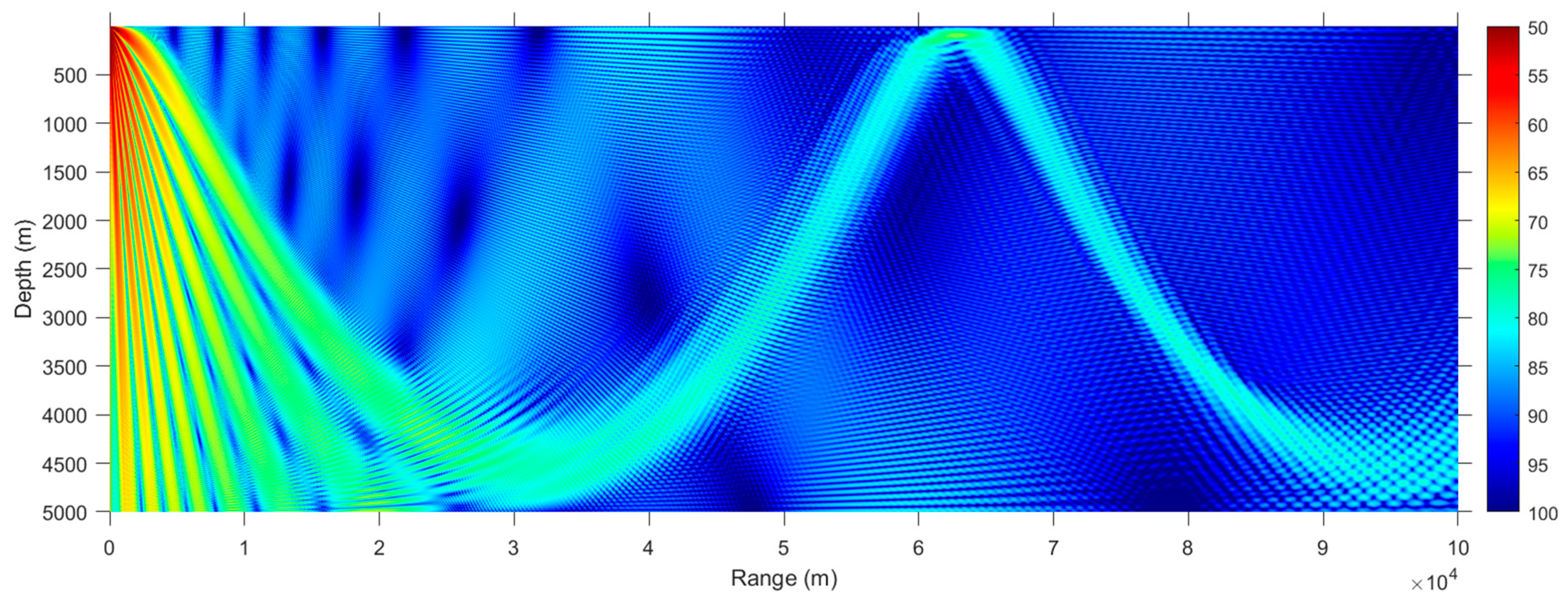
3.3. Munk Waveguide
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jensen, F.B.; Kuperman, W.A.; Porter, M.B.; Schmidt, H. Computational Ocean Acoustics, 2nd ed.; Springer: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Pekeris, C.L. Theory of propagation of explosive sound in shallow water. In Geological Society of America Memoirs; Geological Society of America: Boulder, CO, USA, 1948; Volume 27, pp. 1–116. [Google Scholar] [CrossRef]
- Porter, M.B. The KRAKEN Normal Mode Program; Naval Research Lab Washington DC: Washington, DC, USA, 1992. [Google Scholar]
- Etter, P.C. Underwater Acoustic Modeling and Simulation; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar] [CrossRef]
- Collis, J.M.; Frank, S.D.; Metzler, A.M.; Preston, K.S. Elastic parabolic equation and normal mode solutions for seismo-acoustic propagation in underwater environments with ice covers. J. Acoust. Soc. Am. 2016, 139, 2672–2682. [Google Scholar] [CrossRef] [PubMed]
- DeCourcy, B.J.; Duda, T.F. A coupled mode model for omnidirectional three-dimensional underwater sound propagation. J. Acoust. Soc. Am. 2020, 148, 51–62. [Google Scholar] [CrossRef] [PubMed]
- Westwood, E.K.; Tindle, C.T.; Chapman, N.R. A normal mode model for acousto-elastic ocean environments. J. Acoust. Soc. Am. 1996, 100, 3631–3645. [Google Scholar] [CrossRef]
- Levinson, S.J.; Westwood, E.K.; Koch, R.A.; Mitchell, S.K.; Sheppard, C.V. An efficient and robust method for underwater acoustic normal-mode computations. J. Acoust. Soc. Am. 1995, 97, 1576–1585. [Google Scholar] [CrossRef]
- Ding, R.; Liu, S. Underwater sound propagation for virtual environments. Vis. Comput. 2021, 37, 2797–2807. [Google Scholar] [CrossRef]
- Jihui, W.; Zhenshan, W.; Bing, J. Numerical simulation of underwater acoustical field with directional sources based on the normal modes model. In MATEC Web Conf., Proceedings of the 2017 International Conference on Electronic Information Technology and Computer Engineering (EITCE 2017), Zhuhai, China, 23–24 September 2017; EDP Sciences: Les Ulis, France, 2017; Volume 128. [Google Scholar] [CrossRef]
- Olson, A.H.; Orcutt, J.A.; Frazier, G.A. The discrete wavenumber/finite element method for synthetic seismograms. Geophys. J. Int. 1984, 77, 421–460. [Google Scholar] [CrossRef]
- Tu, H.; Wang, Y.; Lan, Q.; Liu, W.; Xiao, W.; Ma, S. A Chebyshev-Tau spectral method for normal modes of underwater sound propagation with a layered marine environment. J. Sound Vib. 2021, 492, 115784. [Google Scholar] [CrossRef]
- Tu, H.; Wang, Y.; Yang, C.; Wang, X.; Ma, S.; Xiao, W.; Liu, W. A novel algorithm to solve for an underwater line source sound field based on coupled modes and a spectral method. J. Comput. Phys. 2022, 468, 111478. [Google Scholar] [CrossRef]
- Acoustic Toolbox. Available online: oalib.hlsresearch.com/AcousticsToolbox/ (accessed on 3 February 2023).
- Sahu, K.S.; Jena, M.K. Combining the shooting method with an operational matrix method to solve two point boundary value problems. Int. J. Appl. Comput. Math. 2021, 7, 29. [Google Scholar] [CrossRef]
- Dubeau, F. A remark on Richardson’s extrapolation process and numerical differentiation formulae. J. Comput. Phys. X 2019, 2, 100017. [Google Scholar] [CrossRef]
- Porter, M.; Reiss, E.L. A numerical method for ocean-acoustic normal modes. J. Acoust. Soc. Am. 1984, 76, 244–252. [Google Scholar] [CrossRef]
- Ipsen, I.C.F. Computing an eigenvector with inverse iteration. SIAM Rev. 1997, 39, 254–291. [Google Scholar] [CrossRef]
- Chu, W.; Zhao, Y.; Yuan, H. A Modified inverse iteration method for computing the symmetric tridiagonal eigenvectors. Mathematics 2022, 10, 3636. [Google Scholar] [CrossRef]
- Koessler, M.W.; Duncan, A.J.; Gavrilov, A.N. Low-frequency acoustic propagation modelling for australian range-independent environments. Acoust. Aust. 2017, 45, 331–341. [Google Scholar] [CrossRef]
- Kun, W.; Yau Shu, W. Pollution-free finite difference schemes for non-homogeneous Helmholtz equation. Int. J. Numer. Anal. Model. 2014, 11, 787–815. [Google Scholar]
- Liu, W.; Zhang, L.; Wang, Y.; Cheng, X.; Xiao, W. A vector wavenumber integration model of underwater acoustic propagation based on the matched interface and boundary method. J. Mar. Sci. Eng. 2021, 9, 1134. [Google Scholar] [CrossRef]
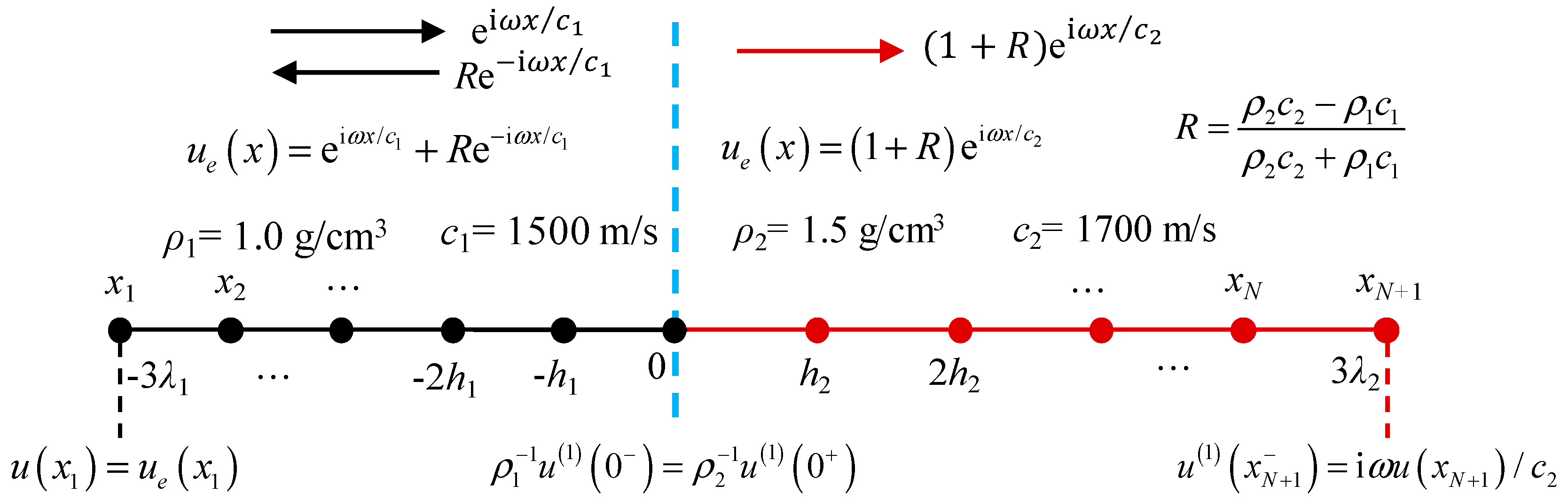
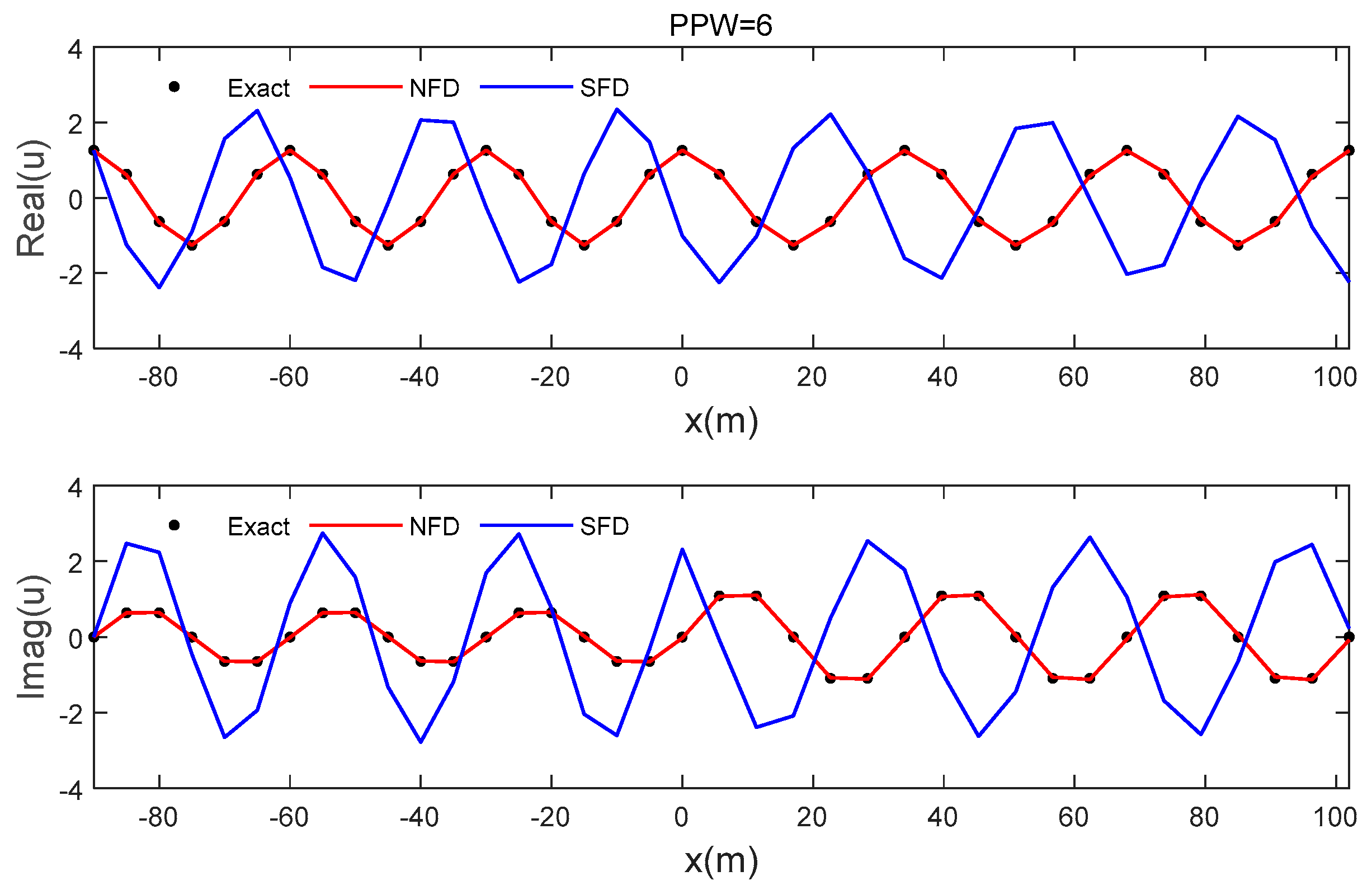
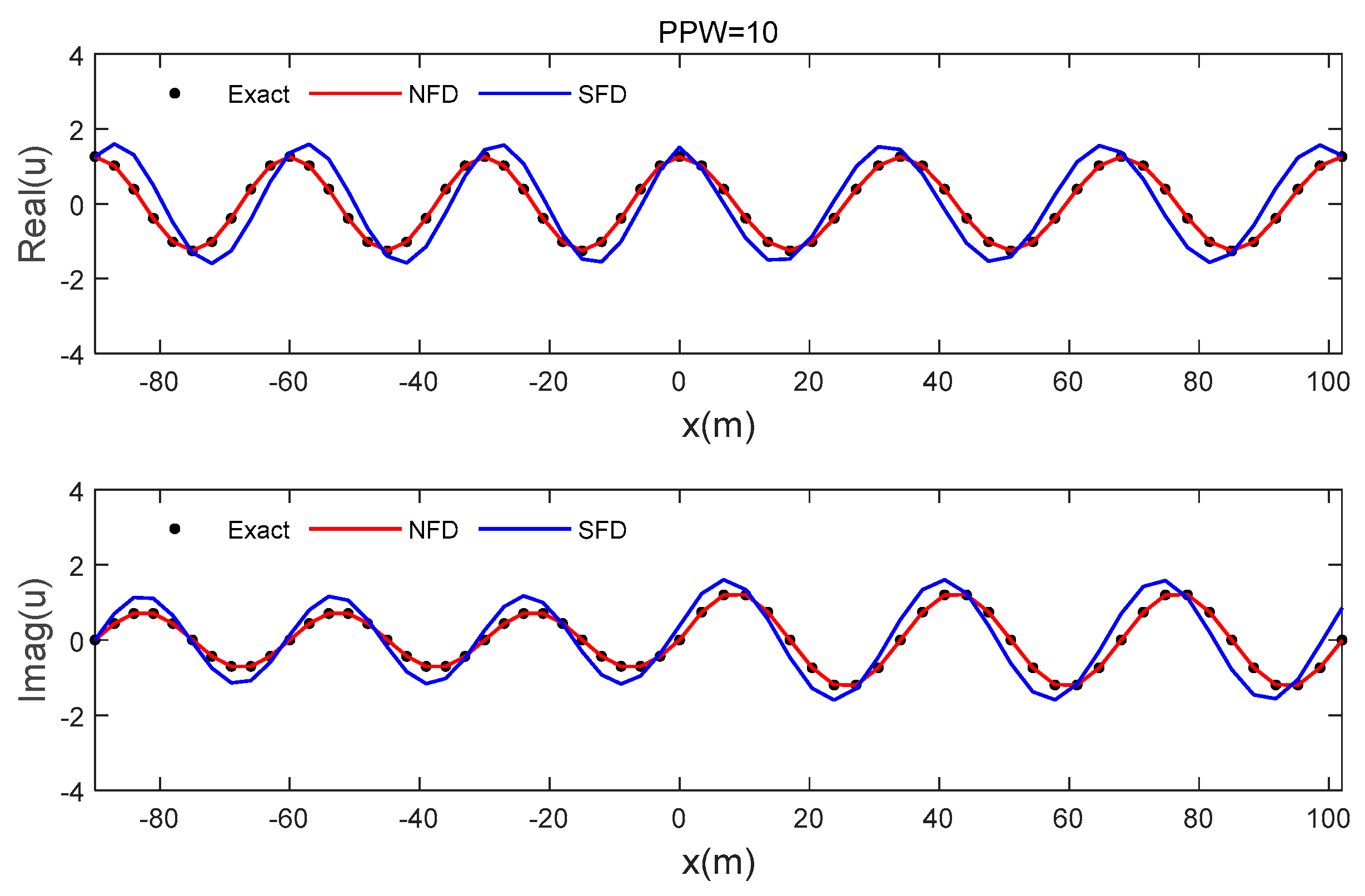

| n | NFD (PPW = 6) | SFD (PPW = 10) | SFD (PPW = 20) | |||
|---|---|---|---|---|---|---|
| / | / | |||||
| 01 | 6.27607882022858 × 10−1–1.43856482281990 × 10−6i | 4.61 × 10−5 | 6.27607882022858 × 10−1–1.43856482281990 × 10−6i | 1.00 × 100 | 6.27607882022858 × 10−1–1.43856402701203 × 10−6i | 1.00 × 100 |
| 02 | 6.25467598438263 × 10−1–5.58376723347465 × 10−6i | 2.23 × 10−5 | 6.25467598438263 × 10−1–5.58376723347465 × 10−6i | 1.00 × 100 | 6.25467598438263 × 10−1–5.58376768822200 × 10−6i | 1.00 × 100 |
| 03 | 6.21873557567596 × 10−1–1.20058493848774 × 10−5i | 1.87 × 10−5 | 6.21873557567596 × 10−1–1.20058493848774 × 10−5i | 1.00 × 100 | 6.21873557567596 × 10−1–1.20058493848774 × 10−5i | 1.00 × 100 |
| 04 | 6.16787314414978 × 10−1–2.02101928152842 × 10−5i | 4.34 × 10−6 | 6.16787314414978 × 10−1–2.02101928152842 × 10−5i | 1.00 × 100 | 6.16787314414978 × 10−1–2.02101928152842 × 10−5i | 1.00 × 100 |
| 05 | 6.10157787799835 × 10−1–2.98445593216456 × 10−5i | 7.65 × 10−6 | 6.10157787799835 × 10−1–2.98445593216456 × 10−5i | 1.00 × 100 | 6.10157787799835 × 10−1–2.98445593216456 × 10−5i | 1.00 × 100 |
| 06 | 6.01922035217285 × 10−1–4.08637897635344 × 10−5i | 5.79 × 10−6 | 6.01922035217285 × 10−1–4.08637897635344 × 10−5i | 1.00 × 100 | 6.01922035217285 × 10−1–4.08637897635344 × 10−5i | 1.00 × 100 |
| 07 | 5.92005014419556 × 10−1–5.36890329385642 × 10−5i | 1.96 × 10−6 | 5.92005014419556 × 10−1–5.36890329385642 × 10−5i | 1.00 × 100 | 5.92005014419556 × 10−1–5.36890329385642 × 10−5i | 1.00 × 100 |
| 08 | 5.80318808555603 × 10−1–6.95202397764660 × 10−5i | 2.49 × 10−5 | 5.80318808555603 × 10−1–6.95202397764660 × 10−5i | 1.00 × 100 | 5.80318808555603 × 10−1–6.95202397764660 × 10−5i | 1.00 × 100 |
| 09 | 5.66763103008270 × 10−1–9.13004550966434 × 10−5i | 6.94 × 10−6 | 5.66763103008270 × 10−1–9.13004550966434 × 10−5i | 1.00 × 100 | 5.66763103008270 × 10−1–9.13004550966434 × 10−5i | 1.00 × 100 |
| 10 | 5.51232635974884 × 10−1–1.27768376842141 × 10−4i | 4.11 × 10−5 | 5.51232635974884 × 10−1–1.27768376842141 × 10−4i | 1.00 × 100 | 5.51232635974884 × 10−1–1.27768376842141 × 10−4i | 1.00 × 100 |
| 11 | 5.33674001693726 × 10−1–2.26555464905687 × 10−4i | 1.35 × 10−4 | 5.33674001693726 × 10−1–2.26555464905687 × 10−4i | 1.00 × 100 | 5.33674001693726 × 10−1–2.26555450353771 × 10−4i | 1.00 × 100 |
| 12 | 4.63520050048828 × 10−1–3.02227609790862 × 10−3i | 4.06 × 10−6 | 3.81191879510880 × 10−1–5.55971916764975 × 10−3i | 5.13 × 105 | 4.63520050048828 × 10−1–3.02227609790862 × 10−3i | 1.00 × 100 |
| 13 | 4.32712376117706 × 10−1–3.96012421697378 × 10−3i | 5.82 × 10−6 | 3.36082935333252 × 10−1–7.09269661456347 × 10−3i | 3.33 × 105 | 4.32712376117706 × 10−1–3.96012421697378 × 10−3i | 1.00 × 100 |
| 14 | 3.97054076194763 × 10−1–5.04005001857877 × 10−3i | 2.10 × 10−6 | 2.80377447605133 × 10−1–9.42375324666500 × 10−3i | 8.70 × 105 | 3.97054076194763 × 10−1–5.04005001857877 × 10−3i | 1.00 × 100 |
| 15 | 3.55095088481903 × 10−1–6.39960262924433 × 10−3i | 4.50 × 10−6 | 2.05873236060143 × 10−1–1.39953233301640 × 10−2i | 3.89 × 105 | 3.55095088481903 × 10−1–6.39960449188948 × 10−3i | 1.01 × 100 |
| 16 | 3.04253190755844 × 10−1–8.32277443259955 × 10−3i | 2.88 × 10−6 | - | - | 3.04253190755844 × 10−1–8.32277256995440 × 10−3i | 1.01 × 100 |
| 17 | 2.38977894186974 × 10−1–1.16468686610460 × 10−2i | 7.58 × 10−7 | - | - | 2.38977909088135 × 10−1–1.16468686610460 × 10−2i | 2.28 × 100 |
| 18 | 1.41187623143196 × 10−1–2.14445460587740 × 10−2i | 6.40 × 10−8 | - | - | 1.41187608242035 × 10−1–2.14445423334837 × 10−2i | 2.21 × 101 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Xu, G.; Cheng, X.; Wang, Y. A Novel Finite Difference Scheme for Normal Mode Models in Underwater Acoustics. J. Mar. Sci. Eng. 2023, 11, 553. https://doi.org/10.3390/jmse11030553
Liu W, Xu G, Cheng X, Wang Y. A Novel Finite Difference Scheme for Normal Mode Models in Underwater Acoustics. Journal of Marine Science and Engineering. 2023; 11(3):553. https://doi.org/10.3390/jmse11030553
Chicago/Turabian StyleLiu, Wei, Guojun Xu, Xinghua Cheng, and Yongxian Wang. 2023. "A Novel Finite Difference Scheme for Normal Mode Models in Underwater Acoustics" Journal of Marine Science and Engineering 11, no. 3: 553. https://doi.org/10.3390/jmse11030553
APA StyleLiu, W., Xu, G., Cheng, X., & Wang, Y. (2023). A Novel Finite Difference Scheme for Normal Mode Models in Underwater Acoustics. Journal of Marine Science and Engineering, 11(3), 553. https://doi.org/10.3390/jmse11030553





