Developing Functional Recharge Systems to Control Saltwater Intrusion via Integrating Physical, Numerical, and Decision-Making Models for Coastal Aquifer Sustainability
Abstract
:1. Introduction
1.1. Traditional Saltwater Intrusion Countermeasures
1.2. Artificial Groundwater Recharge
1.3. Integrating Physical and Numerical Models
1.4. Analytical Hierarchy Process (AHP)
2. Materials and Methodologies
2.1. Experimental Setup
2.1.1. Drainage and Seepage Tank (DS Tank)
2.1.2. Configuration and Experimental Set
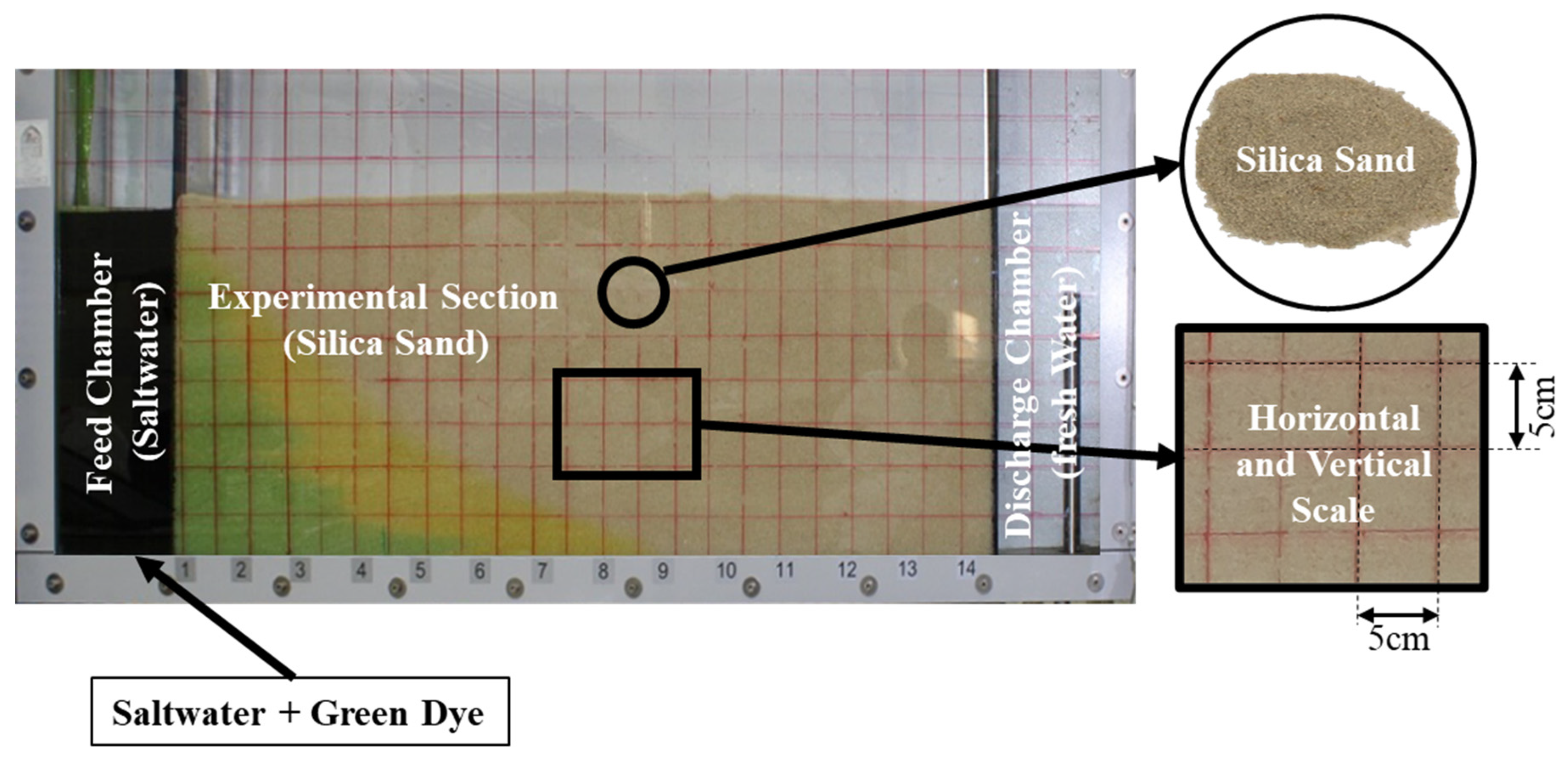
2.1.3. Experimental Procedures
- Freshwater saturation of the media sand: At the start of the experiment, the outflow pipes1 and 2 for both the feed and discharge chambers are set to be at the same level as the media sand surface (40 cm from the DS Tank bed). Following that, freshwater is discharged at a constant rate into both chambers until the media sand in the experimental section is saturated. The hydraulic heads along the experimental section are monitored by the 14 glass tube manometers until the water level reaches the sand surface in all the manometers to verify the saturation condition.
- Feeding the experiment with colored saltwater: In the feed chamber, an aluminum sheet pile is used to block water seepage through the experimental section. Following that, the feed chamber’s outflow pipe1 is moved to the DS Tank bed level to empty it of freshwater. The outflow pipe is then returned to its previous level (media sand surface level), and the storage tank is subsequently emptied and filled with the green-dyed saltwater. When the pump is turned on and the pump valve is opened, saltwater begins to fill the feed chamber all the way to the top of the outflow pipe1. Following that, the pump valve is manually adjusted to maintain the saltwater level at the surface of the media sand.
- Adjusting the water levels in the feed and discharge chambers: The first step in this process is to remove the aluminum sheet pile from the feed chamber. Furthermore, to achieve a suitable flow through the media sand, the difference in water levels between the feed and discharge chambers is tested several times and finally adjusted to 10 cm, resulting in a hydraulic gradient of 0.085. To accomplish this, the outflow pipe2 for the discharge chamber is adjusted to be 10 cm below the media sand surface.
- Monitoring of saltwater intrusion: In the experimental section, saltwater begins to infiltrate through the media sand and can be observed through the transparent front side of the DS Tank. The temporal saltwater intrusion could be measured using the horizontal and vertical scales drawn on the transparent front side. The saltwater intrusion is measured at 30 min intervals. Photos for each time interval are taken with a high-resolution digital camera and used to validate the observed saltwater lines with AutoCAD software (Version S.51.0.0 AutoCAD 2022). During the experiment, the freshwater level inside the discharge chamber rises until it reaches its maximum level by adjusting the outflow pipe2 level above the media sand surface level until it reaches a steady state.
2.2. Evaluation Ratios
- (1)
- Three variables, namely evaluation ratios, will be used to analyze the output results.
- (2)
- One parameter that operates as experimental run constraints is referred to as a conditional parameter.
- (3)
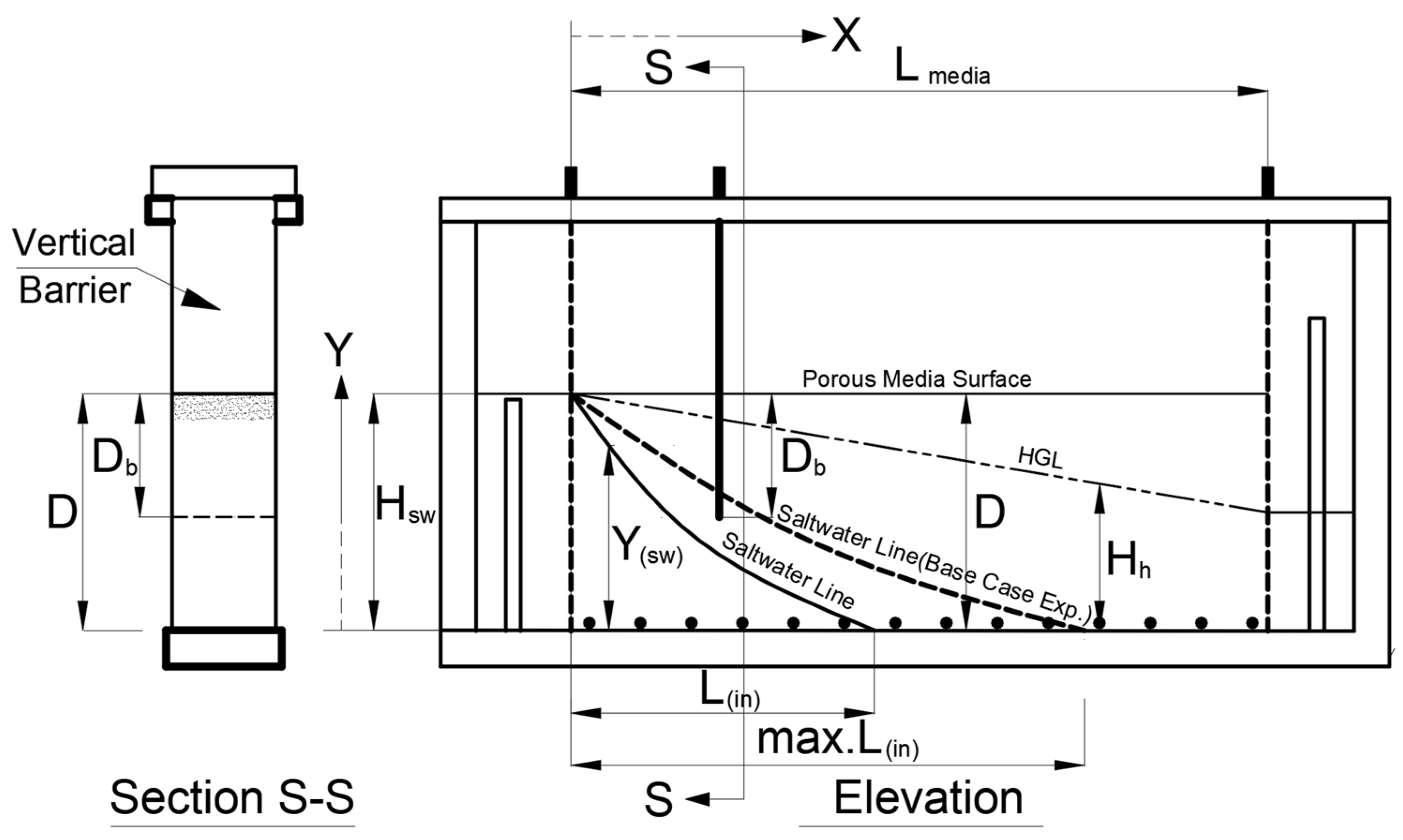
- Two geometric parameters are used to assign the hydraulic gradient and saltwater profile.
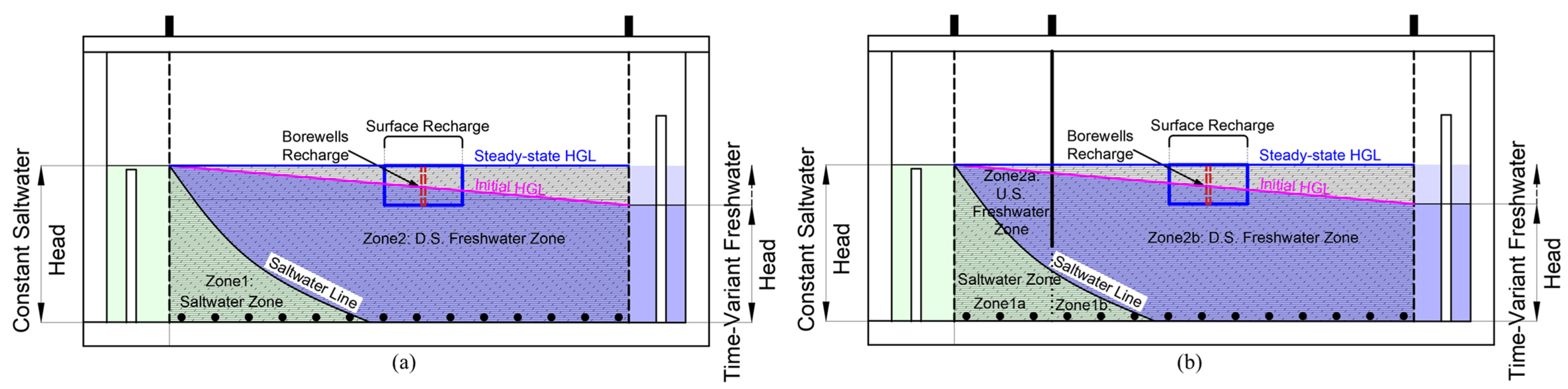
2.3. Conceptual Model
- A constant-head saltwater boundary.
- A time-variant head freshwater boundary that advances from the initial head to equilibrium with the saltwater boundary in the steady-state condition.
- A vertical barrier of variable depths at a certain location.
- A source of surface and subsurface artificial recharge.
2.4. Numerical Model Development
2.4.1. Calibration and Verification Processes
- Confirming the time when a steady-state condition occurs based on the results of experiment 1.
- Fitting the observed saltwater line in experiments 1 and 2 for the transient and steady-state conditions.
2.4.2. Classification Ratios
2.5. Decision-Making Model (AHP Technique)
3. Results and Discussion
3.1. Senstivity Analysis, Calibration and Verification of the Numerical Model
3.2. Behavior Evaluation of Saltwater Intrusion, Flow, and Hydraulic Heads for Categories (a), (b), and (c) Model Cases
3.2.1. Saltwater Intrusion and Flow Behaviors in Category (a) Model Cases
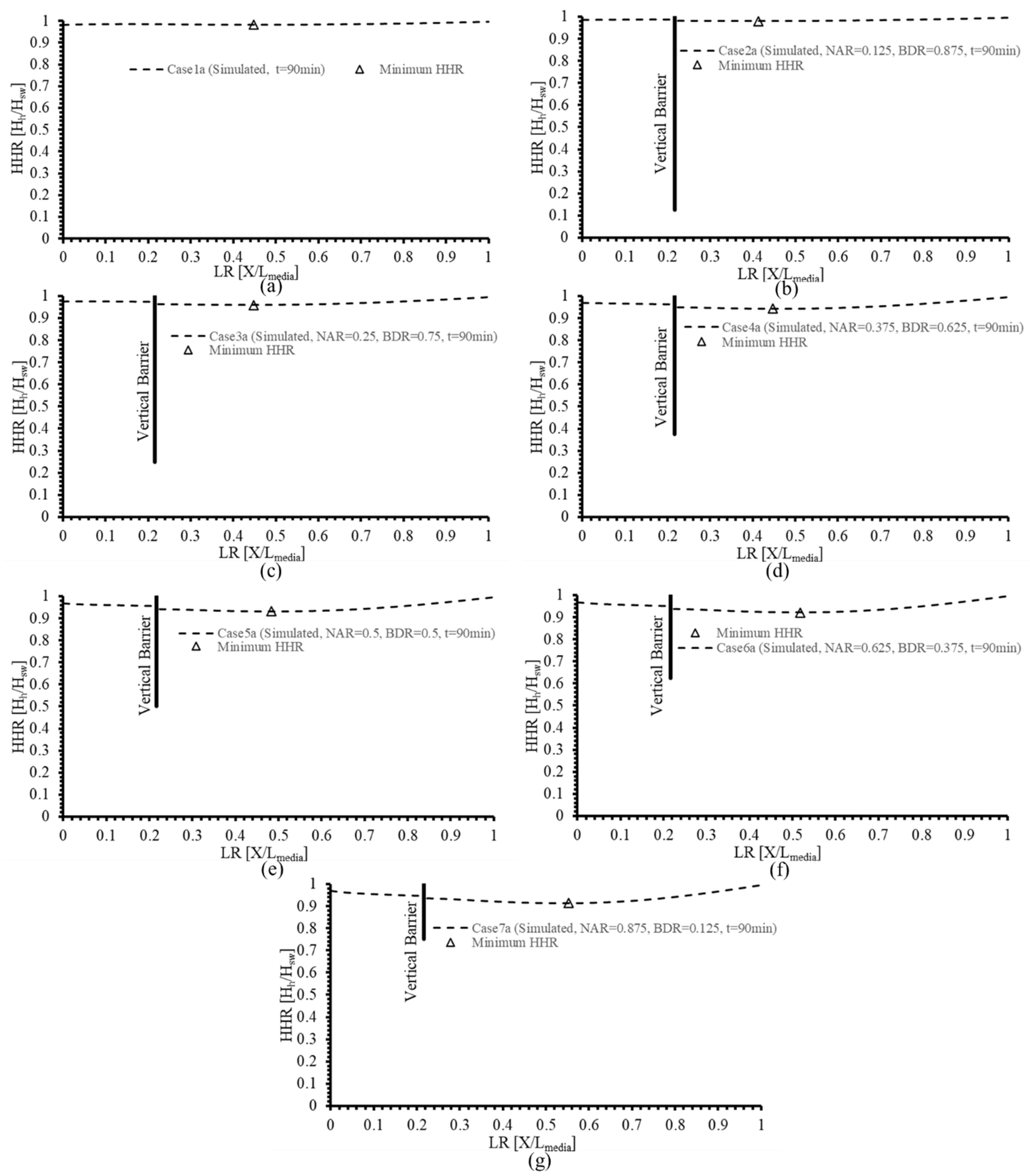
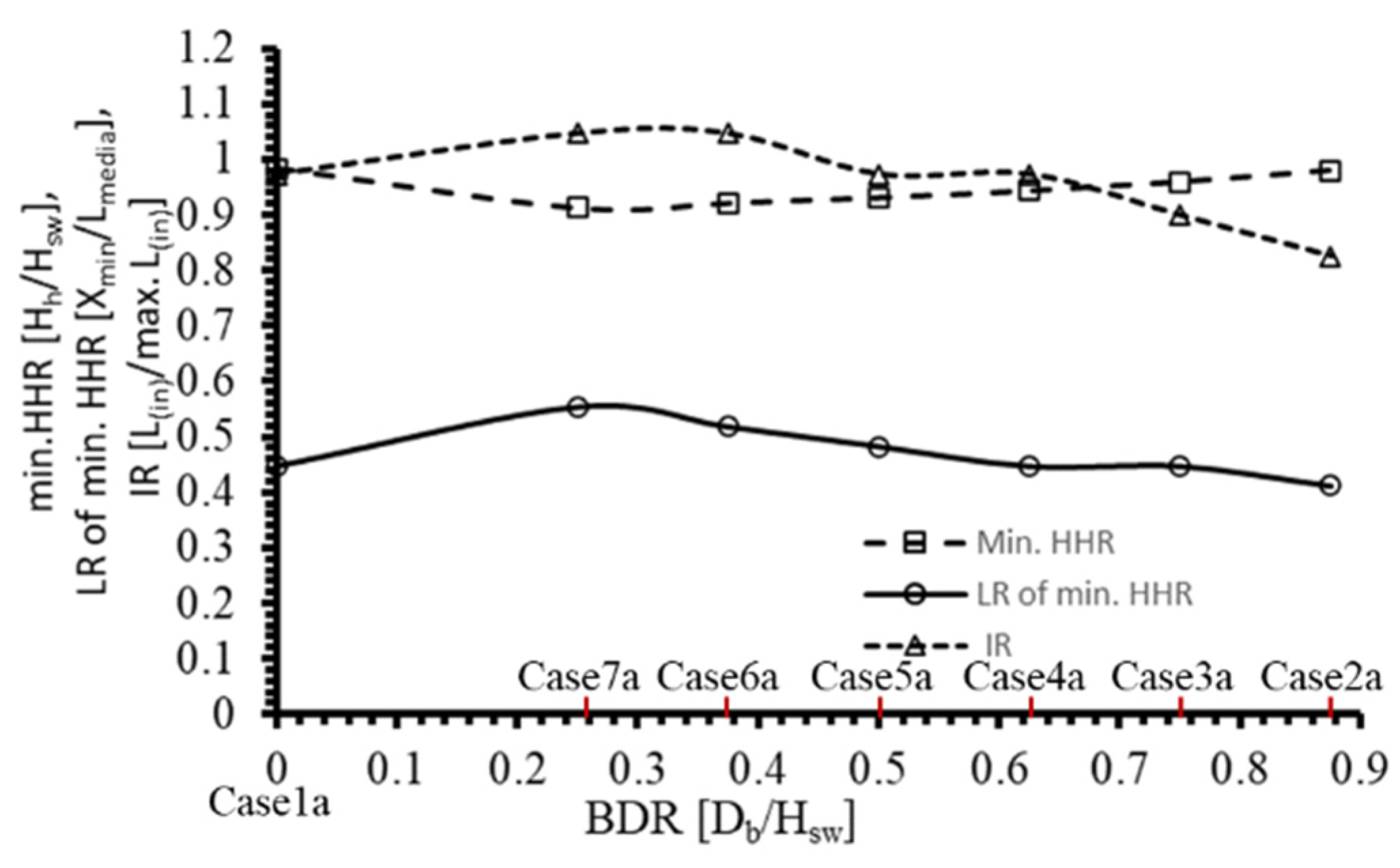
3.2.2. Hydraulic Head Variations in Category (a) Model Cases
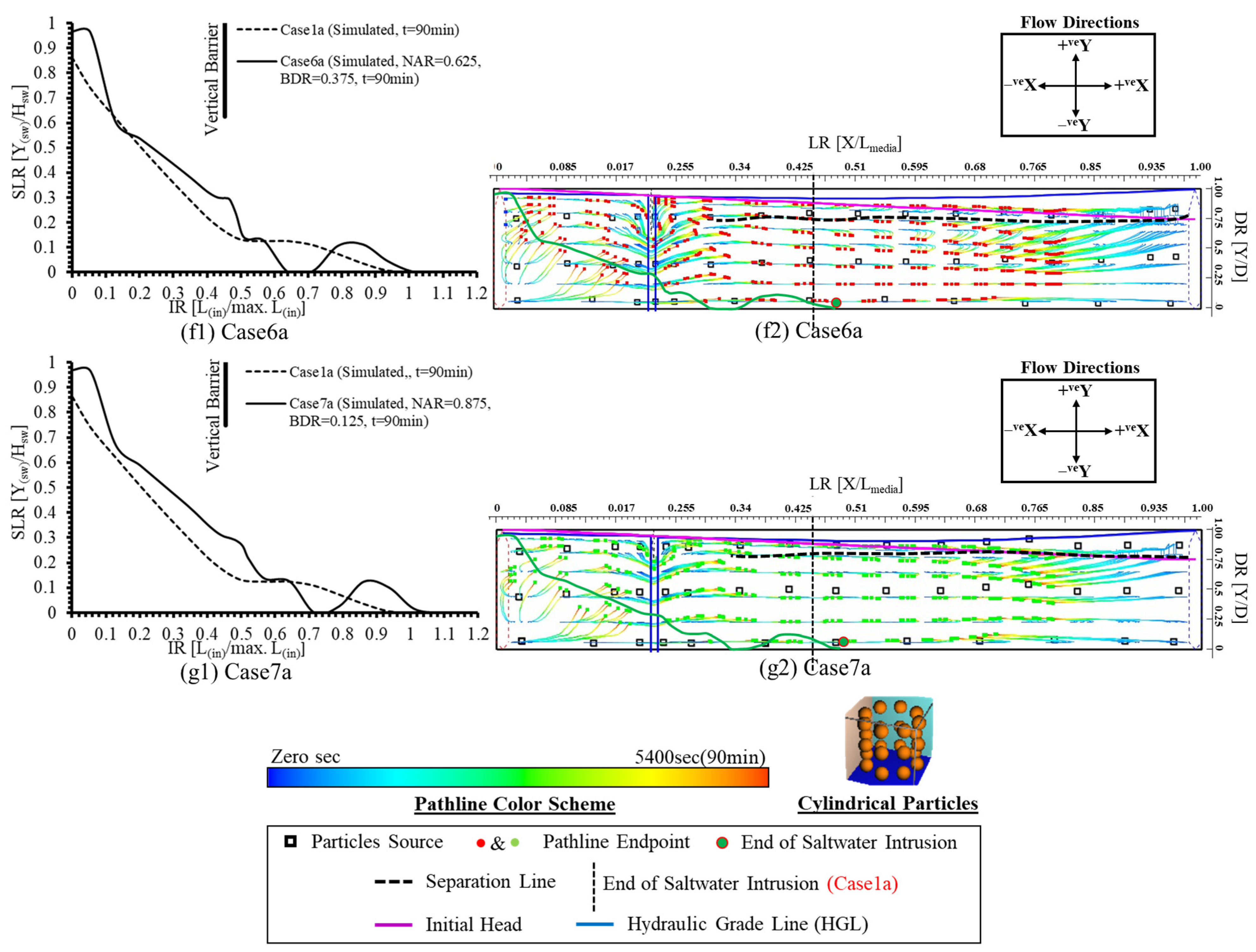
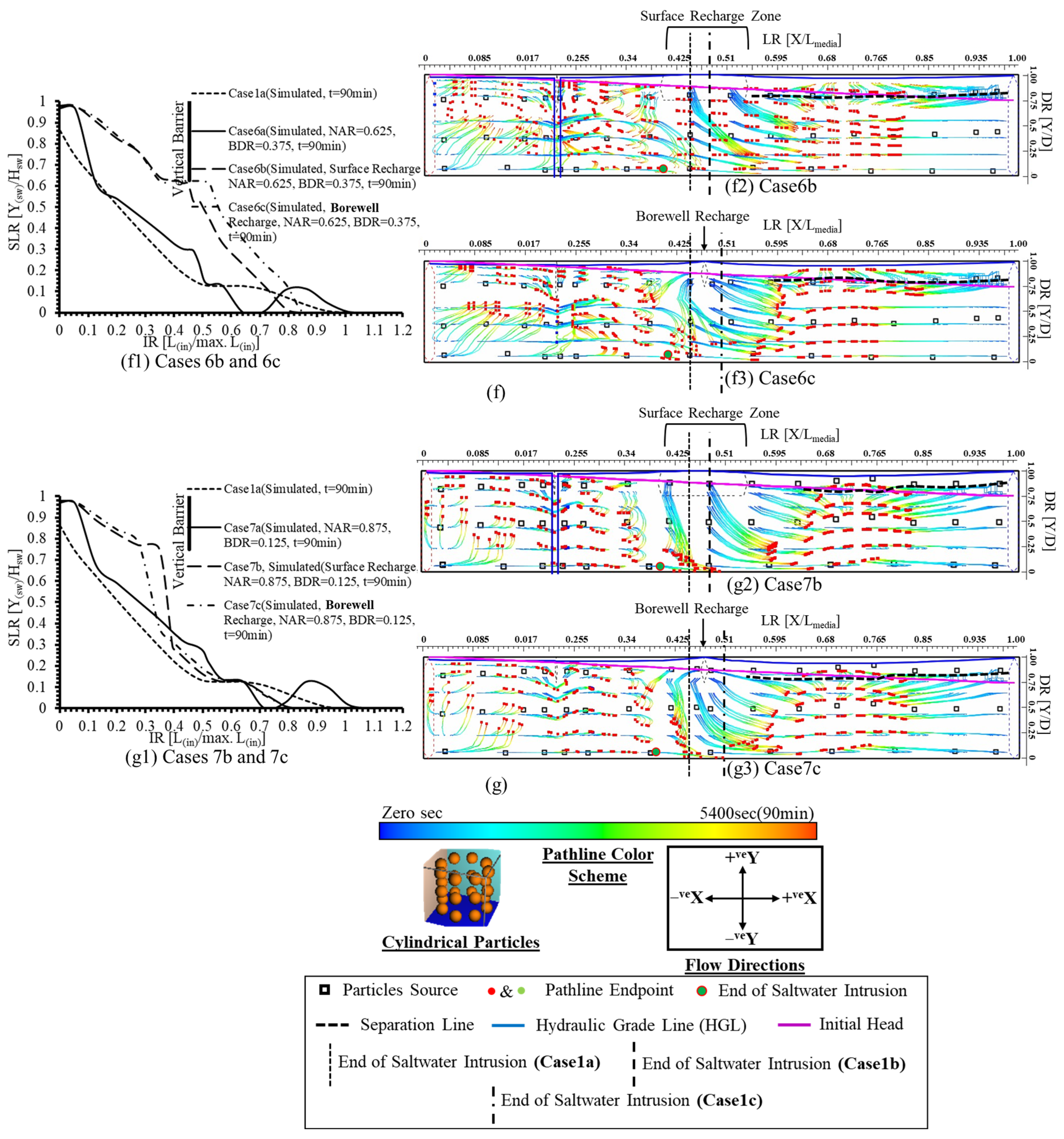
3.2.3. Saltwater Intrusion and Flow Behaviors in Categories (b) and (c) Model Cases
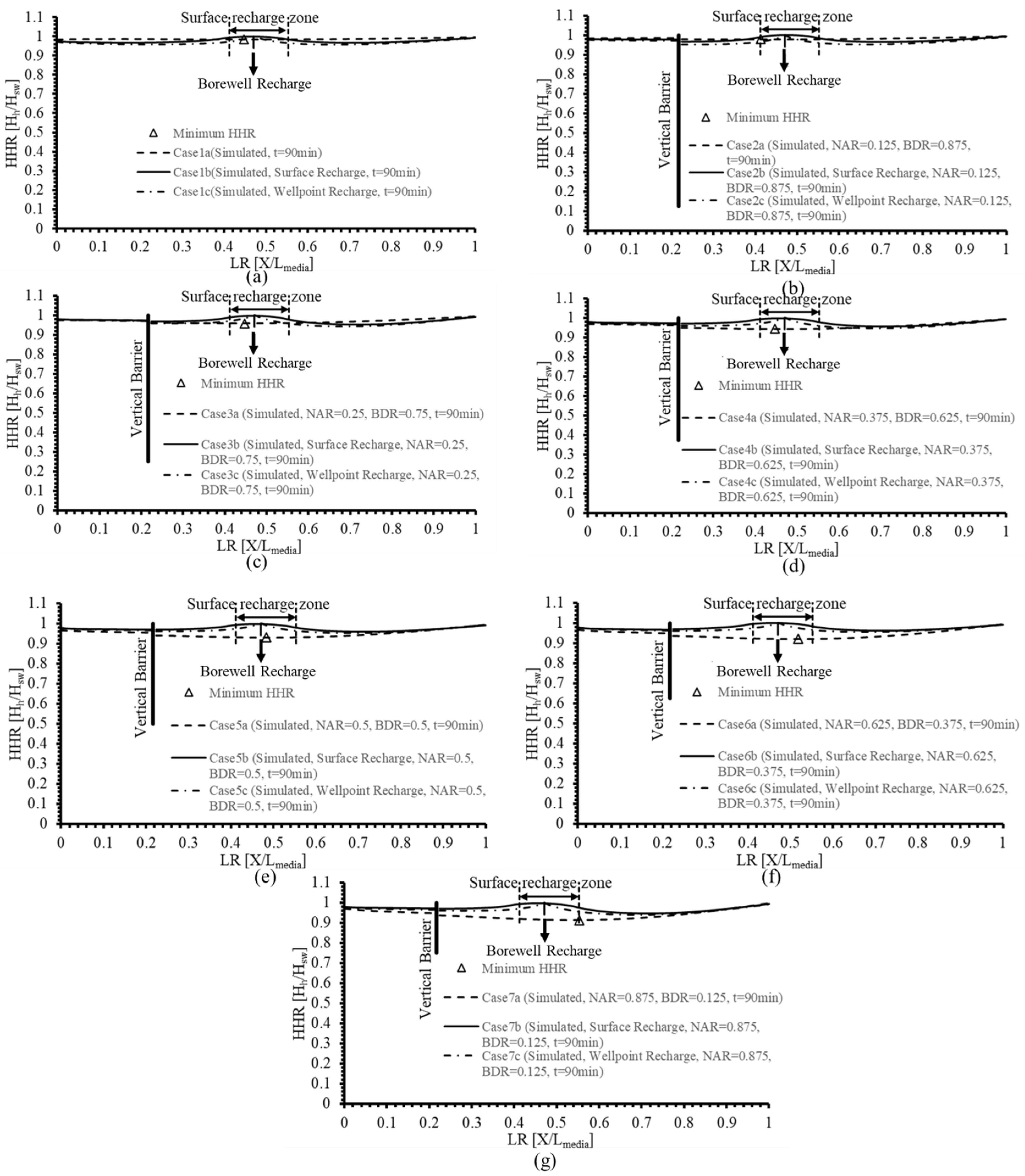
3.2.4. Hydraulic Head Variations in Categories (b) and (c) Model Cases
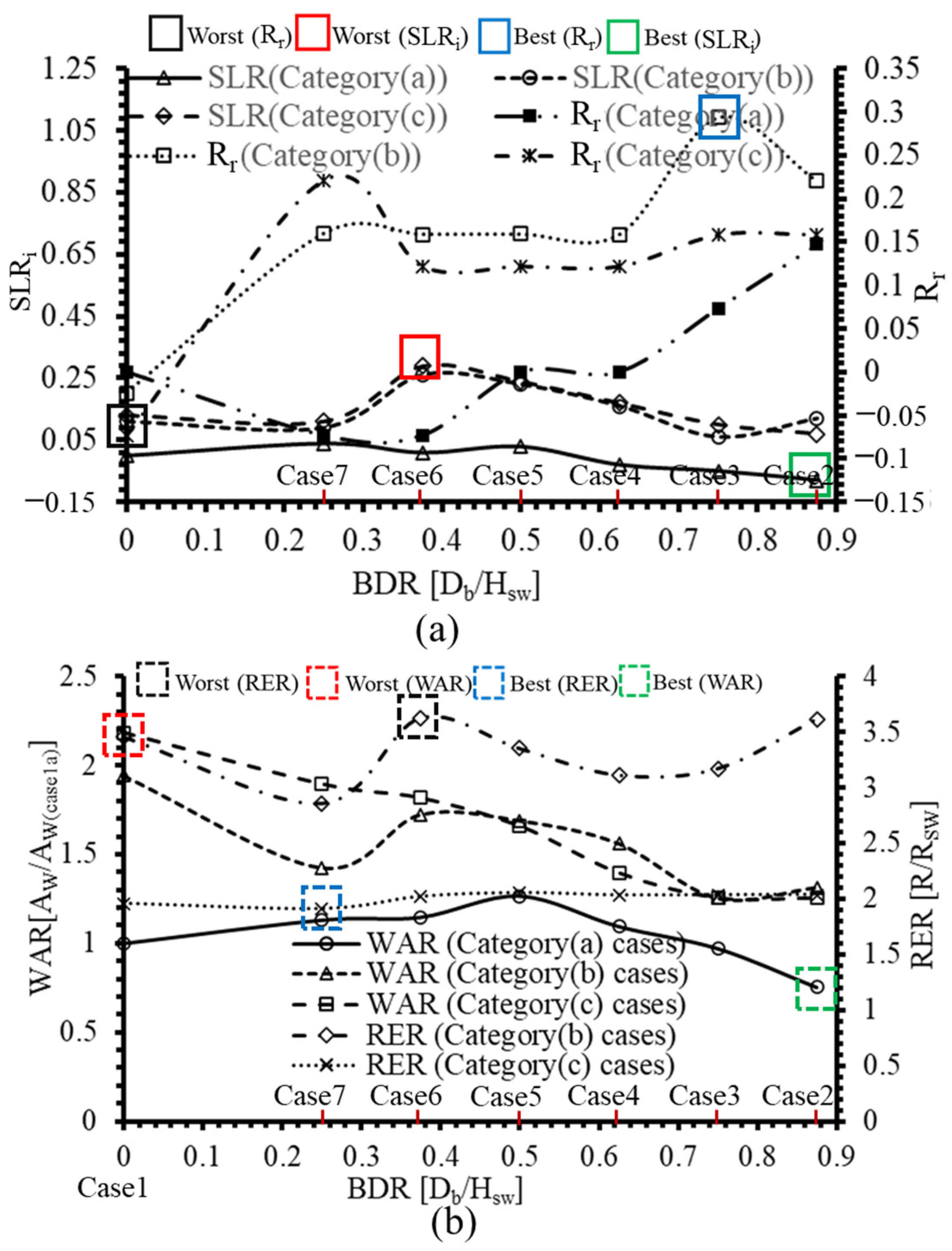
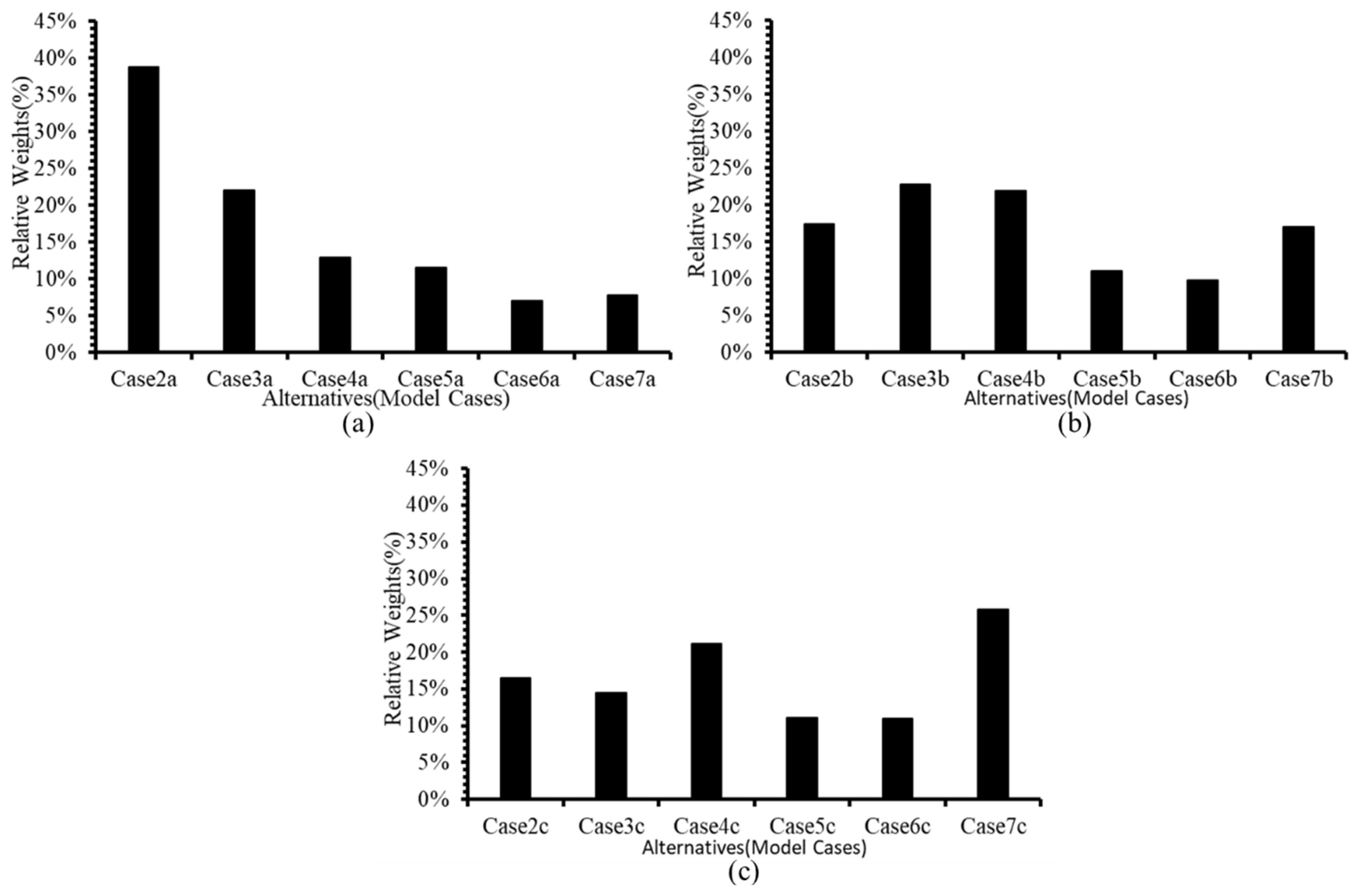
3.3. Classification of Model Cases
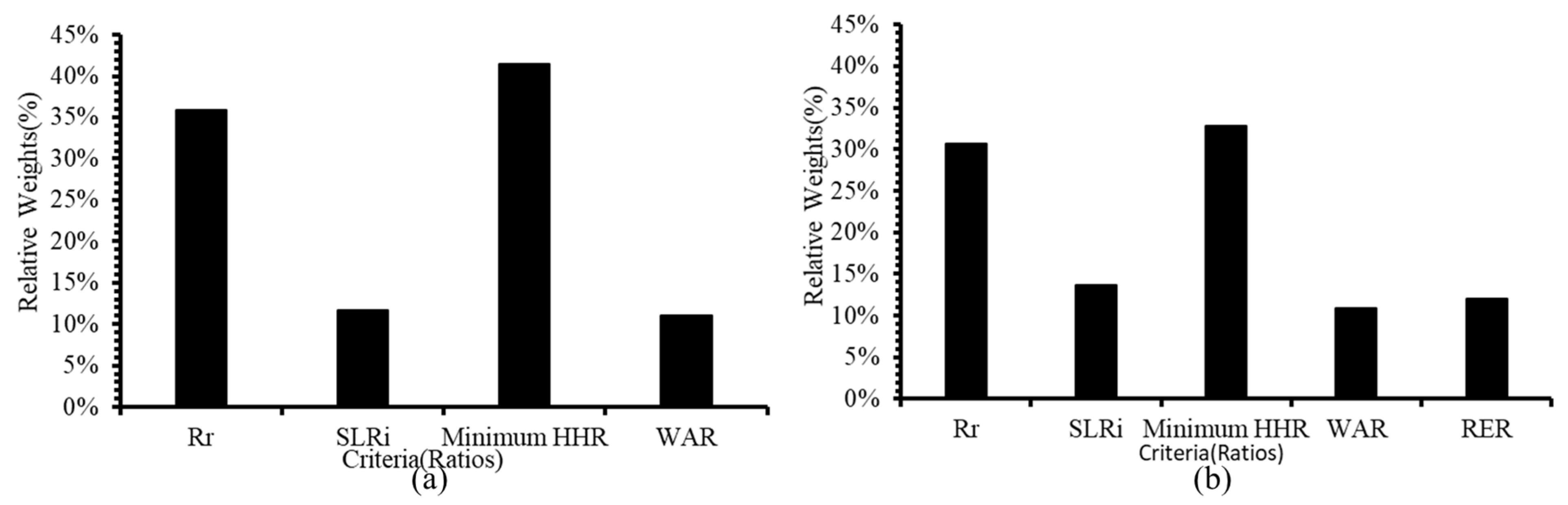
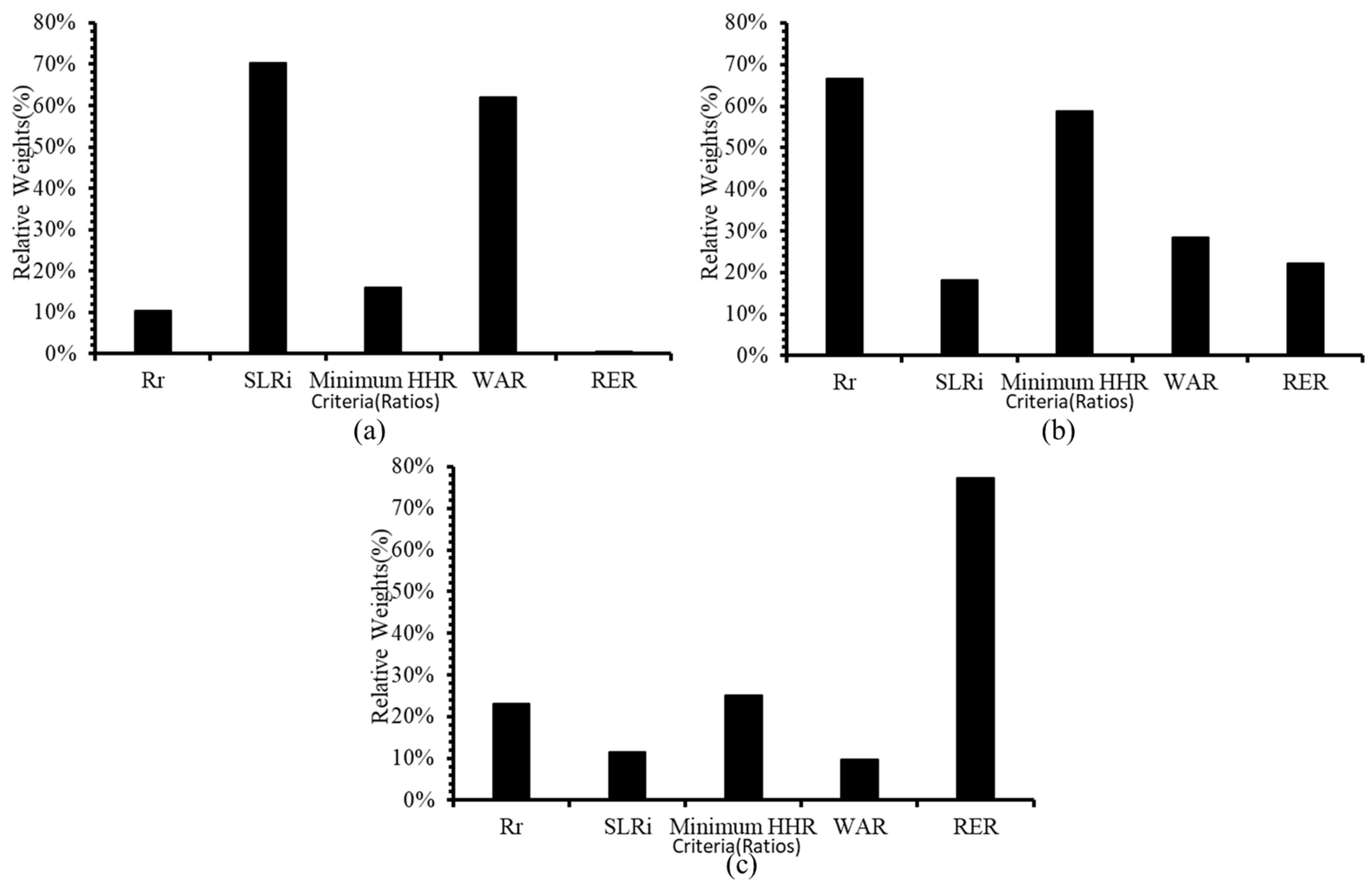
3.4. Selecting the Most Effective Model Case (AHP Application Results)
3.4.1. Level (1) Results
3.4.2. Level (2) Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abd-Elaty, I.; Abd-Elhamid, H.F.; Negm, A.M. Investigation of Saltwater Intrusion in Coastal Aquifers. In Groundwater in the Nile Delta; Negm, A.M., Ed.; Springer International Publishing: Cham, Switzerland, 2019; pp. 329–353. [Google Scholar] [CrossRef]
- Sutar, A.; Rotte, V. Prevention of Saltwater Intrusion: A Laboratory-Scale Study on Electrokinetic Remediation; Springer: Singapore, 2022; pp. 389–400. [Google Scholar]
- Qi, S.-Z.; Qiu, Q.-L. Environmental hazard from saltwater intrusion in the Laizhou Gulf, Shandong Province of China. Nat. Hazards 2011, 56, 563–566. [Google Scholar] [CrossRef]
- Shi, L.; Jiao, J.J. Seawater intrusion and coastal aquifer management in China: A review. Environ. Earth Sci. 2014, 72, 2811–2819. [Google Scholar] [CrossRef]
- Anders, R.; Mendez, G.O.; Futa, K.; Danskin, W.R. A Geochemical Approach to Determine Sources and Movement of Saline Groundwater in a Coastal Aquifer. Groundwater 2014, 52, 756–768. [Google Scholar] [CrossRef] [PubMed]
- Cary, L.; Petelet-Giraud, E.; Bertrand, G.; Kloppmann, W.; Aquilina, L.; Martins, V.; Hirata, R.; Montenegro, S.; Pauwels, H.; Chatton, E.; et al. Origins and processes of groundwater salinization in the urban coastal aquifers of Recife (Pernambuco, Brazil): A multi-isotope approach. Sci. Total. Environ. 2015, 530–531, 411–429. Available online: https://www.sciencedirect.com/science/article/pii/S0048969715300723 (accessed on 1 September 2023). [CrossRef] [PubMed]
- Gopinath, S.; Srinivasamoorthy, K. Application of Geophysical and Hydrogeochemical Tracers to Investigate Salinisation Sources in Nagapatinam and Karaikal Coastal Aquifers, South India. Aquat. Procedia 2015, 4, 65–71. [Google Scholar] [CrossRef]
- Abd-Elhamid, H.F. Investigation and control of seawater intrusion in the Eastern Nile Delta aquifer considering climate change. Water Supply 2016, 17, 311–323. [Google Scholar] [CrossRef]
- Eissa, M.A.; de Dreuzy, J.-R.; Parker, B. Integrative management of saltwater intrusion in poorly-constrained semi-arid coastal aquifer at Ras El-Hekma, Northwestern Coast, Egypt. Groundw. Sustain. Dev. 2018, 6, 57–70. Available online: https://www.sciencedirect.com/science/article/pii/S2352801X16300704 (accessed on 1 October 2023). [CrossRef]
- Abd-Elhamid, H.F.; Abd-Elaty, I.; Negm, A.M. Control of Saltwater Intrusion in Coastal Aquifers. In Groundwater in the Nile Delta; Negm, A.M., Ed.; Springer International Publishing: Cham, Switzerland, 2019; pp. 355–384. [Google Scholar] [CrossRef]
- Pramada, S.K.; Minnu, K.P.; Roshni, T. Insight into sea water intrusion due to pumping: A case study of Ernakulam coast, India. ISH J. Hydraul. Eng. 2021, 27, 442–451. [Google Scholar] [CrossRef]
- Abd-Elhamid, H.F.; Javadi, A.A. A Cost-Effective Method to Control Seawater Intrusion in Coastal Aquifers. Water Resour. Manag. 2011, 25, 2755–2780. [Google Scholar] [CrossRef]
- Kallioras, A.; Pliakas, F.-K.; Schüth, C.; Rausch, R. Methods to Countermeasure the Intrusion of Seawater into Coastal Aquifer Systems. In Wastewater Reuse and Management; Springer: Dordrecht, The Netherlands, 2013; pp. 470–490. [Google Scholar]
- Cai, J.; Taute, T.; Schneider, M. Recommendations of Controlling Saltwater Intrusion in an Inland Aquifer for Drinking-Water Supply at a Certain Waterworks Site in Berlin (Germany). Water Resour. Manag. 2015, 29, 2221–2232. [Google Scholar] [CrossRef]
- Huang, P.-S.; Chiu, Y.-C. A Simulation-Optimization Model for Seawater Intrusion Management at Pingtung Coastal Area, Taiwan. Water 2018, 10, 251. [Google Scholar] [CrossRef]
- Hussain, M.S.; Abd-Elhamid, H.F.; Javadi, A.A.; Sherif, M.M. Management of Seawater Intrusion in Coastal Aquifers: A Review. Water 2019, 11, 2467. [Google Scholar] [CrossRef]
- Raja Shekar, P.; Mathew, A. Assessing groundwater potential zones and artificial recharge sites in the monsoon-fed Murredu river basin, India: An integrated approach using GIS, AHP, and Fuzzy-AHP. Groundw. Sustain. Dev. 2023, 23, 100994. Available online: https://www.sciencedirect.com/science/article/pii/S2352801X23000942 (accessed on 1 October 2023). [CrossRef]
- Shafa, N.S.; Babazadeh, H.; Aghayari, F.; Saremi, A. Optimal utilization of groundwater resources and artificial recharge system of Shahriar plain aquifer, Iran. Phys. Chem. Earth Parts A/B/C 2023, 129, 103358. Available online: https://www.sciencedirect.com/science/article/pii/S1474706523000025 (accessed on 1 October 2023). [CrossRef]
- Wadi, D.; Wu, W.; Malik, I.; Fuad, A.; Thaw, M.M. Assessment and feasibility of the potential artificial groundwater recharge in semi-arid crystalline rocks context, Biteira district, Sudan. Sci. Afr. 2022, 17, e01298. Available online: https://www.sciencedirect.com/science/article/pii/S2468227622002058 (accessed on 1 September 2023). [CrossRef]
- Ríos, I.H.; Cruz-Pérez, N.; Chirivella-Guerra, J.I.; García-Gil, A.; Rodríguez-Alcántara, J.S.; Rodríguez-Martín, J.; Marazuela, M.; Santamarta, J.C. Proposed recharge of island aquifer by deep wells with regenerated water in Gran Canaria (Spain). Groundw. Sustain. Dev. 2023, 22, 100959. Available online: https://www.sciencedirect.com/science/article/pii/S2352801X23000590 (accessed on 1 October 2023). [CrossRef]
- Hasan, M.B.; Driessen, P.P.J.; Majumder, S.; Zoomers, A.; van Laerhoven, F. Factors Affecting Consumption of Water from a Newly Introduced Safe Drinking Water System: The Case of Managed Aquifer Recharge (MAR) Systems in Bangladesh. Water 2019, 11, 2459. [Google Scholar] [CrossRef]
- Maliva, R.G. Surface-Spreading AAR Systems (Non-basin). In Anthropogenic Aquifer Recharge: WSP Methods in Water Resources Evaluation Series No 5; Springer International Publishing: Cham, Switzerland, 2020; pp. 517–565. [Google Scholar] [CrossRef]
- Maliva, R.G. Surface Spreading System—Infiltration Basins. In Anthropogenic Aquifer Recharge: WSP Methods in Water Resources Evaluation Series No 5; Springer International Publishing: Cham, Switzerland, 2020; pp. 469–515. [Google Scholar] [CrossRef]
- Environmental and Water Resources Institute (U.S.). Standard Guidelines for Artificial Recharge of Ground Water; American Society of Civil Engineers: Reston, VA, USA, 2001; Available online: https://ascelibrary.org/doi/book/10.1061/9780784405482 (accessed on 26 October 2023).
- Maliva, R.G. ASR and Aquifer Recharge Using Wells. In Anthropogenic Aquifer Recharge: WSP Methods in Water Resources Evaluation Series No 5; Springer International Publishing: Cham, Switzerland, 2020; pp. 381–436. [Google Scholar] [CrossRef]
- Robinson, G.; Ahmed, A.A.; Hamill, G. Experimental saltwater intrusion in coastal aquifers using automated image analysis: Applications to homogeneous aquifers. J. Hydrol. 2016, 538, 304–313. Available online: https://www.sciencedirect.com/science/article/pii/S0022169416301986 (accessed on 1 August 2023). [CrossRef]
- Panthi, J.; Pradhanang, S.M.; Nolte, A.; Boving, T.B. Saltwater intrusion into coastal aquifers in the contiguous United States—A systematic review of investigation approaches and monitoring networks. Sci. Total. Environ. 2022, 836, 155641. Available online: https://www.sciencedirect.com/science/article/pii/S0048969722027371 (accessed on 1 September 2023). [CrossRef] [PubMed]
- Mantoglou, A. Pumping management of coastal aquifers using analytical models of saltwater intrusion. Water Resour. Res. 2003, 39, 1335. Available online: https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2002WR001891 (accessed on 1 April 2023). [CrossRef]
- Zhou, X.; Chen, M.; Liang, C. Optimal schemes of groundwater exploitation for prevention of seawater intrusion in the Leizhou Peninsula in southern China. Environ. Geol. 2003, 43, 978–985. [Google Scholar] [CrossRef]
- Abarca, E.; Vázquez-Suñé, E.; Carrera, J.; Capino, B.; Gámez, D.; Batlle, F. Optimal design of measures to correct seawater intrusion. Water Resour. Res. 2006, 42, W09415. Available online: https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2005WR004524 (accessed on 1 September 2023). [CrossRef]
- Sutherland, J.; Barfuss, S.L. Composite modelling: Combining physical and numerical models. In Proceedings of the 34th World Congress of the International Association for Hydro-Environment Engineering and Research (IAHR), Brisbane, Australia, 26 June–1 July 2011; pp. 4505–4512. [Google Scholar]
- Singh, A. Managing the environmental problem of seawater intrusion in coastal aquifers through simulation–optimization modeling. Ecol. Indic. 2015, 48, 498–504. Available online: https://www.sciencedirect.com/science/article/pii/S1470160X14004191 (accessed on 1 October 2023). [CrossRef]
- Guo, Q.; Huang, J.; Zhou, Z.; Wang, J. Experiment and Numerical Simulation of Seawater Intrusion under the Influences of Tidal Fluctuation and Groundwater Exploitation in Coastal Multilayered Aquifers. Geofluids 2019, 2019, 2316271. [Google Scholar] [CrossRef]
- Armanuos, A.M.; Ibrahim, M.G.; Mahmod, W.E.; Takemura, J.; Yoshimura, C. Analysing the Combined Effect of Barrier Wall and Freshwater Injection Countermeasures on Controlling Saltwater Intrusion in Unconfined Coastal Aquifer Systems. Water Resour. Manag. 2019, 33, 1265–1280. [Google Scholar] [CrossRef]
- Vaidya, O.S.; Kumar, S. Analytic hierarchy process: An overview of applications. Eur. J. Oper. Res. 2006, 169, 1–29. [Google Scholar] [CrossRef]
- Alwetaishi, M.; Gadi, M.; Issa, U. Reliance of building energy in various climatic regions using multi criteria. Int. J. Sustain. Built Environ. 2017, 6, 555–564. [Google Scholar] [CrossRef]
- Arunbose, S.; Srinivas, Y.; Rajkumar, S.; Nair, N.C.; Kaliraj, S. Remote sensing, GIS and AHP techniques based investigation of groundwater potential zones in the Karumeniyar river basin, Tamil Nadu, southern India. Groundw. Sustain. Dev. 2021, 14, 100586. [Google Scholar] [CrossRef]
- Osiakwan, G.M.; Gibrilla, A.; Kabo-Bah, A.T.; Appiah-Adjei, E.K.; Anornu, G. Delineation of groundwater potential zones in the Central Region of Ghana using GIS and fuzzy analytic hierarchy process. Model. Earth Syst. Environ. 2022, 8, 5305–5326. [Google Scholar] [CrossRef]
- Ahmadi, H.; Kaya, O.A.; Babadagi, E.; Savas, T.; Pekkan, E. GIS-Based Groundwater Potentiality Mapping Using AHP and FR Models in Central Antalya, Turkey. Environ. Sci. Proc. 2021, 5, 11. [Google Scholar]
- Castillo, J.L.U.; Cruz, D.A.M.; Leal, J.A.R.; Vargas, J.T.; Tapia, S.A.R.; Celestino, A.E.M. Delineation of Groundwater Potential Zones (GWPZs) in a Semi-Arid Basin through Remote Sensing, GIS, and AHP Approaches. Water 2022, 14, 2138. [Google Scholar] [CrossRef]
- Achu, A.L.; Thomas, J.; Reghunath, R. Multi-criteria decision analysis for delineation of groundwater potential zones in a tropical river basin using remote sensing, GIS and analytical hierarchy process (AHP). Groundw. Sustain. Dev. 2020, 10, 100365. [Google Scholar] [CrossRef]
- Kumar, P.J.S.; Elango, L.; Schneider, M. GIS and AHP Based Groundwater Potential Zones Delineation in Chennai River Basin (CRB), India. Sustainability 2022, 14, 1830. [Google Scholar] [CrossRef]
- Nithya, C.N.; Srinivas, Y.; Magesh, N.; Kaliraj, S. Assessment of groundwater potential zones in Chittar basin, Southern India using GIS based AHP technique. Remote. Sens. Appl. Soc. Environ. 2019, 15, 100248. [Google Scholar] [CrossRef]
- Zghibi, A.; Mirchi, A.; Msaddek, M.H.; Merzougui, A.; Zouhri, L.; Taupin, J.-D.; Chekirbane, A.; Chenini, I.; Tarhouni, J. Using Analytical Hierarchy Process and Multi-Influencing Factors to Map Groundwater Recharge Zones in a Semi-Arid Mediterranean Coastal Aquifer. Water 2020, 12, 2525. [Google Scholar] [CrossRef]
- Phin, T.T.; Hoa, D.T.B.; Trong, T.D.; Hai, D.T.; Que, P.T.N. Mapping vulnerability water supply in Rach Gia city due to saline intrusion on using analytical hierarchy process. Sustain. Water Resour. Manag. 2022, 8, 137. [Google Scholar] [CrossRef]
- Mallick, J.; Khan, R.A.; Ahmed, M.; Alqadhi, S.D.; Alsubih, M.; Falqi, I.; Hasan, M.A. Modeling Groundwater Potential Zone in a Semi-Arid Region of Aseer Using Fuzzy-AHP and Geoinformation Techniques. Water 2019, 11, 2656. [Google Scholar] [CrossRef]
- Shao, Z.; Huq, E.; Cai, B.; Altan, O.; Li, Y. Integrated remote sensing and GIS approach using Fuzzy-AHP to delineate and identify groundwater potential zones in semi-arid Shanxi Province, China. Environ. Model. Softw. 2020, 134, 104868. [Google Scholar] [CrossRef]
- Gangadharan, R.; Nila Rekha, P.; Vinoth, S. Assessment of groundwater vulnerability mapping using AHP method in coastal watershed of shrimp farming area. Arab. J. Geosci. 2016, 9, 107. [Google Scholar] [CrossRef]
- Güllü, Ö.; Kavurmacı, M. Investigation of temporal variation of groundwater salinity potential using AHP-based index. Environ. Monit. Assess. 2023, 195, 365. [Google Scholar] [CrossRef]
- Yang, H.; Jia, C.; Li, X.; Yang, F.; Wang, C.; Yang, X. Evaluation of seawater intrusion and water quality prediction in Dagu River of North China based on fuzzy analytic hierarchy process exponential smoothing method. Environ. Sci. Pollut. Res. 2022, 29, 66160–66176. [Google Scholar] [CrossRef] [PubMed]
- Pham, Q.N.; Ta, T.T.; Le Tran, T.; Pham, T.T.; Nguyen, T.C. Assessment of Saltwater Intrusion Vulnerability in the Coastal Aquifers in Ninh Thuan, Vietnam BT—Global Changes and Sustainable Development in Asian Emerging Market Economies. In Proceedings of EDESUS 2019; Nguyen, A.T., Hens, L., Eds.; Springer International Publishing: Cham, Switzerland, 2022; Volume 2, pp. 703–712. [Google Scholar]
- Yokochi, R.; Zappala, J.C.; Purtschert, R.; Mueller, P. Origin of water masses in Floridan Aquifer System revealed by 81Kr. Earth Planet. Sci. Lett. 2021, 569, 117060. Available online: https://www.sciencedirect.com/science/article/pii/S0012821X21003150 (accessed on 1 October 2023). [CrossRef]
- Halley, R.B.; Vacher, H.L.; Shinn, E.A. Geology and hydrogeology of the Florida Keys. In Geology and Hydrogeology of Carbonate Islands; Elsevier: Amsterdam, The Netherlands, 1997; pp. 217–248. Available online: https://pubs.usgs.gov/publication/70128983 (accessed on 26 October 2023).
- Faye, S.; Faye, S.C.; Ndoye, S.; Faye, A. Hydrogeochemistry of the Saloum (Senegal) superficial coastal aquifer. Environ. Geol. 2003, 44, 127–136. [Google Scholar] [CrossRef]
- Willis, S.S.; Johannesson, K.H. Controls on the geochemistry of rare earth elements in sediments and groundwaters of the Aquia aquifer, Maryland, USA. Chem. Geol. 2011, 285, 32–49. Available online: https://www.sciencedirect.com/science/article/pii/S0009254111000970 (accessed on 26 October 2023). [CrossRef]
- Iashvili, T. HYDrogeological Conditions in Urban Areas in the Georgian Black Sea Coastal Zone Bt—Urban Groundwater Management and Sustainability; Tellam, J.H., Rivett, M.O., Israfilov, R.G., Herringshaw, L.G., Eds.; Springer: Dordrecht, The Netherlands, 2006; pp. 441–446. [Google Scholar]
- G.U.N.T. G.U.N.T [Internet]. Equipment for Engineering Education. Available online: https://www.gunt.de/en/products/hydraulics-for-civil-engineering/hydraulic-engineering/seepage-flow/visualisation-of-seepage-flows/070.16900/hm169/glct-1:pa-148:ca-181:pr-768 (accessed on 14 September 2023).
- Harbaugh, A.W. MODFLOW-2005: The U.S. Geological Survey Modular Ground-Water Model—The Ground-Water Flow Process [Internet]. Techniques and Methods. 2005. Available online: https://pubs.usgs.gov/publication/tm6A16 (accessed on 1 April 2023).
- Bakker, M.; Schaars, F.; Hughes, J.D.; Christian DLangevin, A.; Dausman, A.M. Documentation of the Seawater Intrusion (SWI2) Package for MODFLOW: U.S. Geological Survey Techniques and Methods [Internet]. Book 6, Chap. A46, 47p. 2013. Available online: http://pubs.usgs.gov/tm/6a46/ (accessed on 1 April 2023).
- Pollock, D.W. User Guide for MODPATH Version 7—A Particle-Tracking Model for MODFLOW [Internet]. Open-File Report. Reston, VA. 2016. Available online: https://pubs.usgs.gov/publication/ofr20161086 (accessed on 1 April 2023).
- Domenico, P.A.; Schwartz, F.W.; Schwartz, F.A. Physical and Chemical Hydrogeology; Wiley: Hoboken, NJ, USA, 1998; (Physical and Chemical Hydrogeology); Available online: https://books.google.com.sa/books?id=1f9OAAAAMAAJ (accessed on 26 October 2023).
- Rotz, R. Hydrogeologic Properties of Earth Materials and Principles of Groundwater Flow. Groundwater 2021, 59, 320–321. [Google Scholar] [CrossRef]
- Saaty, T.L. Axiomatic Foundation of the Analytic Hierarchy Process. Manag. Sci. 1986, 32, 841–855. [Google Scholar] [CrossRef]
- Presley, A. ERP investment analysis using the strategic alignment model. Manag. Res. News 2006, 29, 273–284. [Google Scholar] [CrossRef]
- Singh, R.K.; Murty, H.; Gupta, S.; Dikshit, A. Development of composite sustainability performance index for steel industry. Ecol. Indic. 2007, 7, 565–588. [Google Scholar] [CrossRef]
- Albayrak, E.; Erensal, Y.C. Using analytic hierarchy process (AHP) to improve human performance: An application of multiple criteria decision making problem. J. Intell. Manuf. 2004, 15, 491–503. [Google Scholar] [CrossRef]
- Issa, U.H.; Mosaad, S.A.; Hassan, M.S. Evaluation and selection of construction projects based on risk analysis. Structures 2020, 27, 361–370. Available online: https://www.sciencedirect.com/science/article/pii/S2352012420302617 (accessed on 1 April 2023). [CrossRef]
- Abdelwahab, S.F.; Issa, U.H.; Ashour, H.M. A Novel Vaccine Selection Decision-Making Model (VSDMM) for COVID-19. Vaccines 2021, 9, 718. [Google Scholar] [CrossRef] [PubMed]
- Issa, U.H.; Miky, Y.H.; Abdel-Malak, F.F. A decision support model for civil engineering projects based on multi-criteria and various data. J. Civ. Eng. Manag. 2019, 25, 100–113. Available online: https://journals.vilniustech.lt/index.php/JCEM/article/view/7551 (accessed on 1 April 2023). [CrossRef]

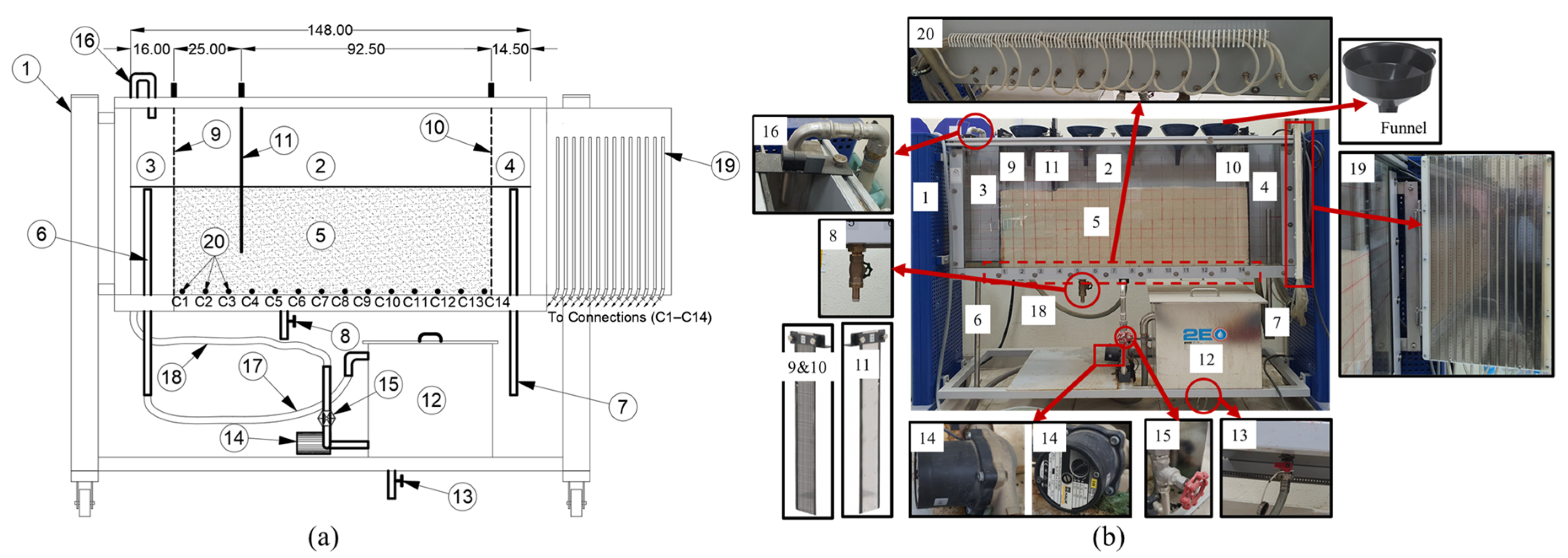








| No. | Component Name | Description | No. | Component Name | Description |
|---|---|---|---|---|---|
| 1 | Steel frame | The DS Tank’s frame | 11 | Vertical aluminum sheet pile | Vertical barrier to control saltwater intrusion |
| 2 | Experimental section | Tank with porous media for monitoring saltwater intrusion | 12 | Storage tank | The primary source of seawater |
| 3 | Feed Chamber | Source of saltwater | 13 | Draining pipe2 | Before the next experiment, drain the saltwater from the storage tank. |
| 4 | Discharge Chamber | Source of freshwater | 14 | Pump | Pumping saltwater to the feed chamber |
| 5 | Porous media | Silica sand (0.71–1.18 mm) | 15 | Pump valve | Pump flow rate adjustment |
| 6 | Outflow pipe1 | Changing the saltwater level in the feed chamber | 16 | Saltwater inflow pipe | Connecting with a pump to allow saltwater to flow from the pump to the feed chamber |
| 7 | Outflow pipe2 | Changing the level of freshwater in the discharge chamber | 17 | Hose1 | Connecting the outflow pipe1 to the storage tank |
| 8 | Draining pipe1 | Before beginning a new experiment, drain the water from the experimental section. | 18 | Hose2 | Linking the saltwater inflow pipe to the pump |
| 9 | Vertical screen1 | Separating the feed chamber from the experimental section | 19 | 14 glass manometer tubes | Hydraulic head monitoring along the experimental section |
| 10 | Vertical screen2 | Separating the discharge chamber from the experimental section | 20 | Measuring connections | Linked to the 14 glass manometer tubes |
| No. | Quantity | Type | Definition | ||
|---|---|---|---|---|---|
| Constant | Parameter | Variable | |||
| 1 | Hsw | √ | Hydraulic head of the saltwater boundary | ||
| 2 | D | √ | Sand media depth | ||
| 3 | Lmedia | √ | Sand media length (experimental section length) | ||
| 4 | max.L(in) | √ | Maximum length of saltwater intrusion (attained for experiment 1 (base case)) | ||
| 5 | Db | √ | Vertical barrier depth | ||
| 6 | X | √ | Horizontal distance from the saltwater boundary measured for any embedded point in the media sand | ||
| 7 | Y | √ | Vertical distance measured from the experimental section bed for any embedded point in the media sand | ||
| 8 | Y(sw) | √ | Observed saltwater intrusion depth at any X distance at a specific time (t). | ||
| 9 | Hh | √ | Observed hydraulic head at any X distance at a specific time (t). | ||
| 10 | L(in) | √ | The observed length of saltwater intrusion at a specific time (t) | ||
| Quantities | Definition (Abbreviation) | Physical Meaning | |
|---|---|---|---|
| Evaluation Ratios | L(in)/max.L(in) | Intrusion Ratio (IR) | Variation in intrusion length over time (t) with reference to the maximum intrusion length (base case) |
| Y(sw)/Hsw | Salt Line Ratio (SLR) | A function demonstrates the variation in intrusion depth as a function of distance X and time (t) due to saltwater boundary head. In the comparative analysis of the results, the average SLR value (SLRavg) will be used. | |
| Hh/Hsw | Hydraulic Head Ratio (HHR) | A function demonstrates the variation in the hydraulic head due to the influence of the saltwater boundary head at a particular distance X and time (t). In the comparative analysis of the results, the minimum value of HHR and its location will be taken into account. | |
| Conditional Parameter | Db/Hsw | Barrier Depth Ratio (BDR) | The ratio of barrier depth to saltwater boundary head depth. This ratio operates as an experimental run constraint. |
| Geometric Parameters | X/Lmedia | Length Ratio (LR) | The horizontal distance X for a certain location in the experimental section to the length of the sand media. |
| Y/D | Depth Ratio (DR) | The vertical distance Y for a certain location in the experimental section to the total media sand depth. |
| Category (a): Using Vertical Barrier | |
| Model Cases | Description |
| Case1a | Base Case (Verification of experiment 1) |
| Case2a | BDR = 0.875 |
| Case3a | BDR = 0.75 (Verification of experiment 2) |
| Case4a | BDR = 0.625 |
| Case5a | BDR = 0.50 |
| Case6a | BDR = 0.375 |
| Case7a | BDR = 0.125 |
| Category (b): using vertical barrier and surface recharge | |
| Model Cases | Conditional Parameters |
| Case1b | Case1a + Surface Recharge |
| Case2b | Case2a + Surface Recharge |
| Case3b | Case3a + Surface Recharge |
| Case4b | Case4a + Surface Recharge |
| Case5b | Case5a + Surface Recharge |
| Case6b | Case6a + Surface Recharge |
| Case7b | Case7a + Surface Recharge |
| Category (c): using vertical barrier and subsurface recharge | |
| Model Cases | Conditional Parameters |
| Case1c | Case1a + borewells Recharge |
| Case2c | Case2a + borewells Recharge |
| Case3c | Case3a + borewells Recharge |
| Case4c | Case4a + borewells Recharge |
| Case5c | Case5a + borewells Recharge |
| Case6c | Case6a + borewells Recharge |
| Case7c | Case7a + borewells Recharge |
| Hydrogeological Properties | kx (cm/s) | ky (cm/s) | kz (cm/s) | Sy | Ss | ŋ |
|---|---|---|---|---|---|---|
| Values | 0.0069 | 0.0069 | 0.03 | 0.04 | 0.0619 | 0.0428 |
| Cases | Conditional Parameters | Evaluation Ratios | Geometrical Parameters | ||
|---|---|---|---|---|---|
| BDR | IR | SLRavg | LRIntrusion | DRseparation | |
| Case1a | --- | 0.97 | 0.28 | 0.45 | 0.37–0.45 |
| Case2a | 0.875 | 0.83 | 0.20 | 0.39 | 0.40–0.50 |
| Case3a | 0.75 | 0.90 | 0.23 | 0.42 | 0.50–0.68 |
| Case4a | 0.625 | 0.97 | 0.25 | 0.45 | 0.60–0.70 |
| Case5a | 0.50 | 0.97 | 0.31 | 0.45 | 0.69–0.75 |
| Case6a | 0.375 | 1.05 | 0.29 | 0.48 | 0.71–0.78 |
| Case7a | 0.125 | 1.05 | 0.32 | 0.48 | 0.76–0.85 |
| Category | Cases | Conditional Parameters | Evaluation Ratios | Geometrical Parameters | ||
|---|---|---|---|---|---|---|
| BDR | IR | SLRavg | LRIntrusion | DRseparation | ||
| Category (a) | Case1a | --- | 0.97 | 0.28 | 0.45 | 0.37–0.45 |
| Case2a | 0.875 | 0.83 | 0.20 | 0.39 | 0.40–0.50 | |
| Case3a | 0.75 | 0.90 | 0.23 | 0.42 | 0.50–0.68 | |
| Case4a | 0.625 | 0.97 | 0.25 | 0.45 | 0.60–0.70 | |
| Case5a | 0.50 | 0.97 | 0.31 | 0.45 | 0.69–0.75 | |
| Case6a | 0.375 | 1.05 | 0.29 | 0.48 | 0.71–0.78 | |
| Case7a | 0.125 | 1.05 | 0.32 | 0.48 | 0.76–0.85 | |
| Category (b) | Case1b | --- | 1.0 | 0.39 | 0.47 | 0.80–0.85 |
| Case2b | 0.875 | 0.75 | 0.40 | 0.35 | 0.80–0.85 | |
| Case3b | 0.75 | 0.68 | 0.34 | 0.32 | 0.80–0.90 | |
| Case4b | 0.625 | 0.81 | 0.44 | 0.38 | 0.80–0.90 | |
| Case5b | 0.50 | 0.81 | 0.51 | 0.38 | 0.75–0.80 | |
| Case6b | 0.375 | 0.81 | 0.54 | 0.38 | 0.75–0.80 | |
| Case7b | 0.125 | 0.81 | 0.37 | 0.38 | 0.80–0.90 | |
| Category (c) | Case1c | --- | 1.05 | 0.41 | 0.49 | 0.80–0.85 |
| Case2c | 0.875 | 0.82 | 0.35 | 0.38 | 0.80–0.85 | |
| Case3c | 0.75 | 0.82 | 0.38 | 0.38 | 0.80–0.90 | |
| Case4c | 0.625 | 0.85 | 0.45 | 0.40 | 0.80–0.90 | |
| Case5c | 0.50 | 0.85 | 0.52 | 0.40 | 0.75–0.80 | |
| Case6c | 0.375 | 0.85 | 0.57 | 0.40 | 0.75–0.80 | |
| Case7c | 0.125 | 0.75 | 0.39 | 0.40 | 0.80–0.90 | |
| Classification Ratio | Best | Worst |
|---|---|---|
| SLRi | Case2a (−0.08) | Case6c (0.29) |
| Rr | Case3b (0.29) | Case1c (−0.07) |
| WAR | Case2a (0.76) | Case1c (2.18) |
| RER | Case7c (1.91) | Case6b (3.62) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miky, Y.; Issa, U.H.; Mahmod, W.E. Developing Functional Recharge Systems to Control Saltwater Intrusion via Integrating Physical, Numerical, and Decision-Making Models for Coastal Aquifer Sustainability. J. Mar. Sci. Eng. 2023, 11, 2136. https://doi.org/10.3390/jmse11112136
Miky Y, Issa UH, Mahmod WE. Developing Functional Recharge Systems to Control Saltwater Intrusion via Integrating Physical, Numerical, and Decision-Making Models for Coastal Aquifer Sustainability. Journal of Marine Science and Engineering. 2023; 11(11):2136. https://doi.org/10.3390/jmse11112136
Chicago/Turabian StyleMiky, Yehia, Usama Hamed Issa, and Wael Elham Mahmod. 2023. "Developing Functional Recharge Systems to Control Saltwater Intrusion via Integrating Physical, Numerical, and Decision-Making Models for Coastal Aquifer Sustainability" Journal of Marine Science and Engineering 11, no. 11: 2136. https://doi.org/10.3390/jmse11112136
APA StyleMiky, Y., Issa, U. H., & Mahmod, W. E. (2023). Developing Functional Recharge Systems to Control Saltwater Intrusion via Integrating Physical, Numerical, and Decision-Making Models for Coastal Aquifer Sustainability. Journal of Marine Science and Engineering, 11(11), 2136. https://doi.org/10.3390/jmse11112136








