Design and Optimization of a New Type of Magnetic Suspension Vibration Absorber for Marine Engineering

Abstract

The magnetic suspension damper, which is based on magnetic suspension technology, is receiving more and more attention from academics as active–passive hybrid damping technology develops. A new symmetric magnetic suspension structure is constructed in this study, and the accuracy of the simulation findings is confirmed by contrasting the output from finite element simulation with the theoretical formulations. On the basis of this, how the structure, size, and material of the electromagnet and armature affect the magnetic flux density, electromagnetic force, and suspension force is investigated. The structure optimization of the electromagnet and armature was performed in accordance with the simulation results, and a new symmetric magnetic suspension structure was produced. The results of the simulation demonstrate that DT4(electrical pure iron) is the ideal material for armatures and electromagnets. The reinforcing ring construction can be built up by the armature to increase suspension force. The suspension force output by the armature will be greatly increased when the size and placement of the reinforcing ring structure are right. The system stiffness adjustment range will expand at this point, enhancing the magnetic suspension damper’s functionality. This study offers novel perspectives for designing structures that reduce vibration and noise in various projects and serves as a guide to constructing magnetic suspension dampers.

1. Introductions

The magnetic suspension technology, which forms the basis of the passive hybrid vibration isolation technology, is drawing increasing attention from academics as the active–passive hybrid vibration isolation technology increasingly emerges as the hotspot of vibration and noise reduction. The first magnetically levitated platform, whose mobility is fueled by magnetism and motors, was created in 1998 by Kim et al. [1]. Due to its benefits of reduced friction, no contact, and adjustable stiffness [2,3,4], the magnetic suspension structure has a greater and wider range of uses as technology advances [5,6,7], for example, axial magnetic bearings [8,9] and magnetic suspension platform [10] designed using magnetic suspension structure.

In order to meet the vibration damping needs under various operating situations, magnetic suspension dampers feature both a damping structure and a magnetic suspension structure that may be changed in stiffness by modifying the control current [11]. In the realm of ship and marine engineering, the use of magnetic-related technologies for vibration dampening is now growing steadily. In the area of vibration damping, magnetic suspension technology has currently produced some results [12].

In a magnetic suspension damper, there is a damping structure as well as a magnetic suspension structure. The damping structure can promote energy dissipation [13,14], and the magnetic suspension structure is equivalent to a spring. The control current can be adjusted to modify the stiffness of the magnetic suspension structure to suit the needs of vibration damping under various operating situations. Among them, the magnetic suspension structure is similar to the magnetic suspension bearing structure, and the suspension force output by the former is mostly axial force [15,16,17,18]. There has never been a stop to research into how to make magnetic suspension structures work better. Jianfeng Lu et al. built a new braking-force-based magnetic suspension platform (DMSP) after using the finite element method to investigate the magnetic flux density distribution and the suspension force with the displacement relationship [19]. In order to obtain a larger suspension force, Xu et al. proposed a novel braking-force-based magnetic suspension system (DMSS), and the simulation results show that DMSS can generate a larger suspension force than the normal suspension system [20]. A new magnetic suspension technique utilizing permanent magnets was proposed by Higuchi T et al. in various overseas research studies. In the intended system, the attraction is altered by adjusting the magnetic circuit’s reluctance, which has the advantages of not requiring electromagnets, saving energy, and preventing the production of heat [21]. Cao, SN, and coworkers proposed a new magnetic suspension platform with three types of magnetic suspension bearings for ultra-precision, large stroke, and high start–stop acceleration. This platform uses a new kind of Halbach magnetic array, which can significantly increase the magnetic flux density in the air gap [18].

Additionally, a novel 2-DOF (two degrees-of-freedom) Lorentz force actuator was developed by designing the poses of windings and permanent magnets (PMs) in order to realize the integration of vertical and horizontal driving forces by Yang, F et al. [22]. By carefully planning the positions of the windings and permanent magnets (PM), the Lorentz force actuator is able to produce a wider range of motion and force coefficients than other similar setups. Han, WT, et al. proposed a new hybrid suspension solenoid, and the outcomes of the finite element method (FEM) study revealed that the proposed hybrid suspension solenoid has improved performance compared to the conventional structure, particularly low control current and low suspension power loss [23]. A unique permanent magnet was used as a magnetic suspension device in Sun et al.’s suggested zero-suspension force performance enhancement method, which reduced the zero-suspension force by nearly 80% [24]. To lessen the amplitude of a primary resonance produced in a high T-c superconducting (HTSC) magnetic suspension system, Taguchi, D. et al. used an auto-parametric vibration absorber [25].

Symmetrical magnetic suspension structure has been created in various studies due to its simplicity and dependability [26]. Regarding the shape of the armature, Bhat N and Kim invented a triangular-shaped magnetically levitated platform with triangles used in the actuator [27]. Currently, a pancake-like structure is employed more frequently with the armature of the magnetic suspension damper [28]. In light of the fact that the armature structure significantly affects the distribution of the magnetic flux density, this work designs and optimizes the armature structure and conducts a thorough investigation into the electromagnetic properties of the new symmetric magnetic suspension structure.

2. Materials and Methods

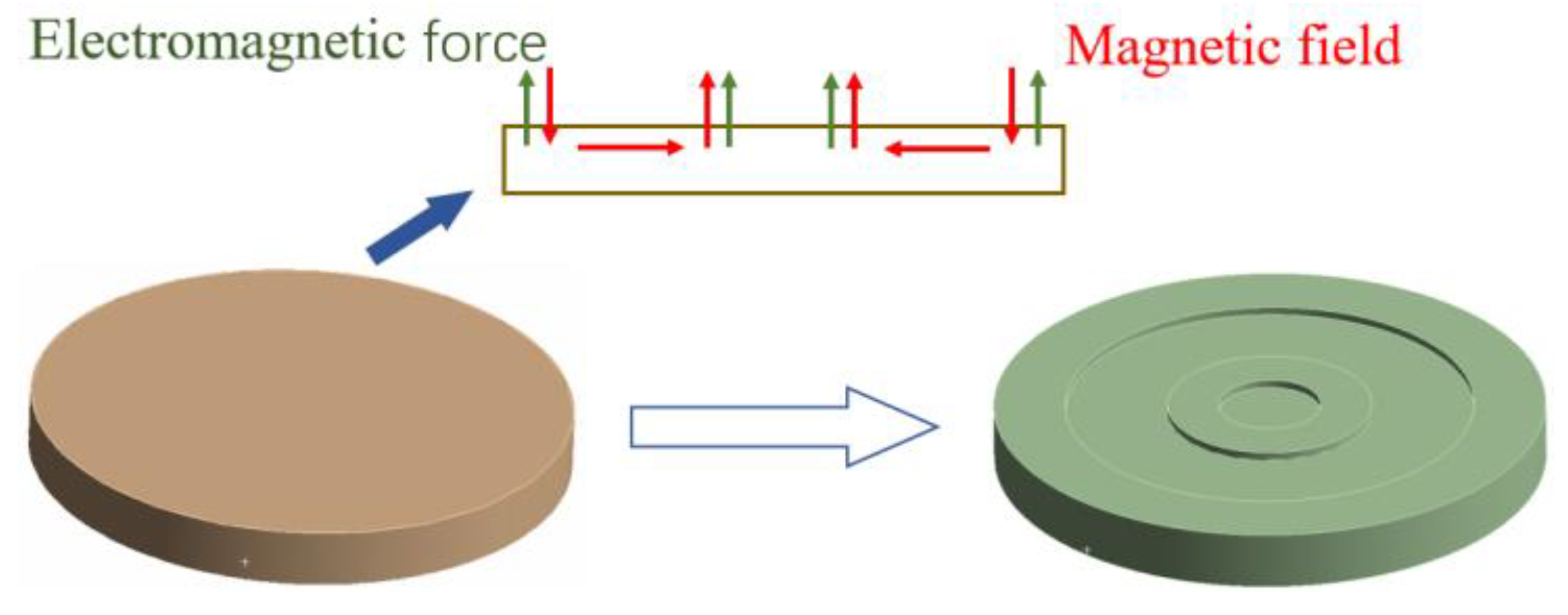
2.1. Topology and Working Principle

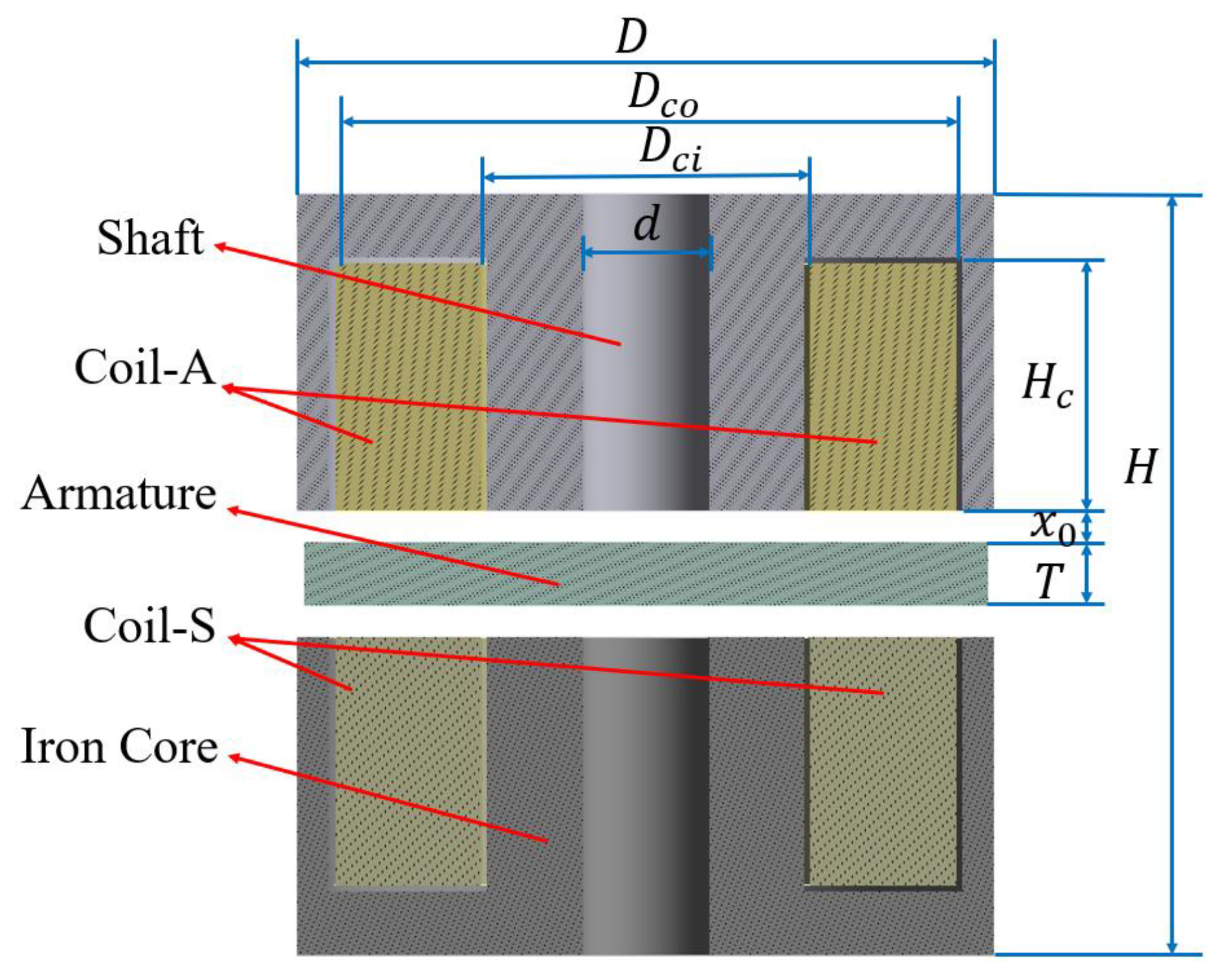
2.1.1. Magnetic Suspension Structure

The magnetic suspension damper contains a magnetic suspension structure and a damping structure. Four magnetic suspension structures are created in this work, as illustrated in Figure 1. Coil-A (the upper end coil) and Coil-S (the symmetric end coil) have 600 turns and $D=110 \mathrm{m}\mathrm{m}$, $D_{co}=98 \mathrm{m}\mathrm{m}$, $D_{ci}=52 \mathrm{m}\mathrm{m}$, $d=20 \mathrm{m}\mathrm{m}$, $H=130 \mathrm{m}\mathrm{m}$, $T=10 \mathrm{m}\mathrm{m}$, $x_0=5 \mathrm{m}\mathrm{m}$, and $H_c=39 \mathrm{m}\mathrm{m}$. When the magnetic suspension structure is in operation, control current is injected into the coil, which then transforms the electrical energy into magnetic energy. This creates a magnetic field surrounding the coil, which magnetizes the core and armature. The magnetic lines of force generated by the coil form a closed loop through the poles, armature, and air gap of the electromagnet, and there will be tension along the direction of the magnetic lines of force and pressure perpendicular to the direction of magnetic susceptibility, resulting in electromagnetic suction due to the contraction of the magnetic lines of force. When the magnetic suspension structure is working, the armature will be subjected to the combined action of gravity and suspension force. The suspension force output from the magnetic suspension structure is the difference between the electromagnetic suction force applied to the armature.

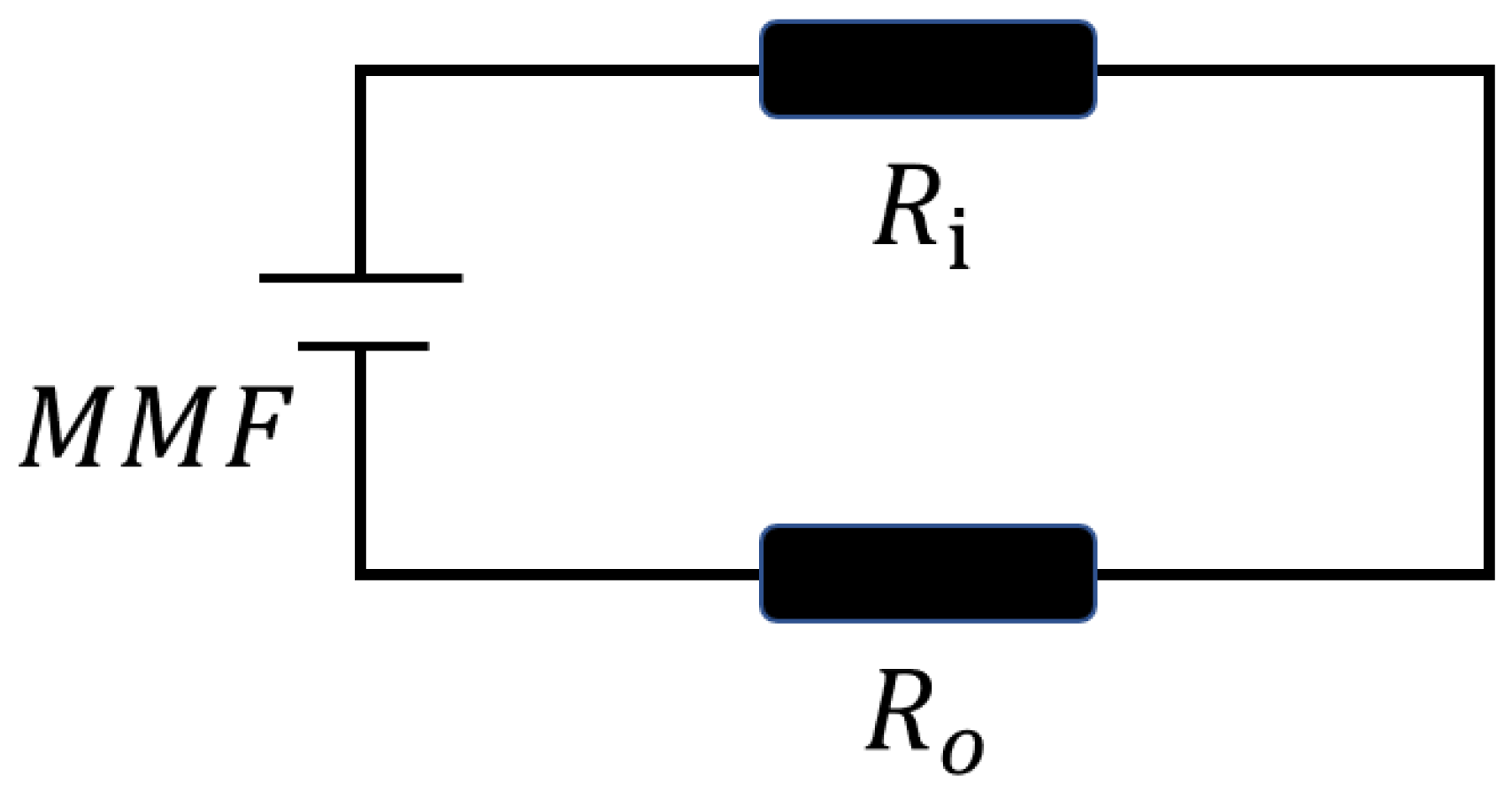
2.1.2. Mathematical Method

The magnetic suspension damper contains a damping structure and a magnetic suspension structure with the following dynamic equations:

$$m\ddot{x}+c\dot{x}+kx=c{\dot{x}}_0+k{x}_0+F_v-F_e$$

(1)

where $x$ is the displacement of armature, $c$ is the damping, $F_e$ is the suspension force of the magnetic suspension structure, $F_v$ is the amplitude of the excitation force, $k$ is the initial value of the system stiffness, and $m$ is the structural mass.

Transmissibility and system compliance are two evaluation criteria for vibration damping performance that typically go against one another.

Transmissibility is the ratio of the mass acceleration response to the acceleration input, and the transfer function can be obtained after Laplace transformation using the following equation:

$$\frac{d^{2}X}{d^2{X}_0}=\frac{cd+k}{m{d}^2+cd+k}.$$

(2)

${\mathsf{\Delta }}_T$ is the variation of transmissibility, which can be expressed as

$${\mathsf{\Delta }}_T=\frac{cd+k_d}{m{d}^2+cd+k_d}-\frac{cd+k}{m{d}^2+cd+k}$$

(3)

where $k$ is the initial value of the system stiffness. $k_d$ is the system stiffness.

$${\mathsf{\Delta }}_T=\frac{\left(k_d-k\right)m{d}^2}{\left(m{d}^2+cd+k\right)\left(m{d}^2+{cd+k}_d\right)}$$

(4)

The compliance of the structure can be expressed as the ratio of the mass block displacement to the external excitation force by the equation $\frac{X}{F_v}$, and after Laplace transformation the transfer function can be obtained using the following equation:

$$\frac{X}{F_v}=\frac{1}{m{d}^2+cd+k}.$$

(5)

The amount of change in structural compliance ${\mathsf{\Delta }}_c$ can be expressed as

$${\mathsf{\Delta }}_c=\frac{1}{m{d}^2+cd+k_d}-\frac{1}{m{d}^2+cd+k}$$

(6)

where $k$ is the initial value of the system stiffness. $k_d$ is the system stiffness.

$${\mathsf{\Delta }}_c=\frac{\left(k-k_d\right)}{\left(m{d}^2+cd+k\right)\left(m{d}^2+cd+k_d\right)}$$

(7)

It can be seen from the equation that the criteria for rating vibration reduction are conflicting. Taking the system stiffness as an example, when the system stiffness decreases, the vibration transmissibility decreases and the system compliance increases. At this time, the structure has a better vibration reduction effect but the resistance to external interference will be reduced. When the system stiffness increases, the vibration transmissibility decreases and the system flexibility increases. At this time, the structure’s ability to resist external interference is improved but the vibration reduction effect is reduced. Utilizing the magnetic suspension damper’s adjustable stiffness, the system stiffness is correctly adjusted by controlling the current to balance the compliance and transmissibility, in order to meet the requirements of compliance and transmission rate under various vibration damping working conditions.

Maxwell’s derivation formula is frequently employed in the examination of issues like the calculation of electromagnet suction because of its exceptionally clear structure. When the air gap is small, the magnetic flux density inside the air gap can be considered to be uniform (regardless of the edge flux). Typically, these computations use the magnetic circuit approach to derive the unilateral electromagnetic force. As shown in Figure 2, the magnetic circuit approach is based on the idea of an electric circuit and uses ‘outer pole–air gap–armature–inner pole’ to create a full magnetic circuit.

$MMF$ is the magnetomotive force, the formula is as follows:

$$MMF=N{I}_c$$

(8)

where N is the coil turn and $I_c$ is the control current.

The formulae for $R_i$ and $R_o$, which represents the magnetoresistance at the air gap between the armature’s inner and outer circular poles, respectively, are as follows:

$$R_i=\frac{g}{{\mu }_r{\mu }_0{A}_i},R_o=\frac{g}{{\mu }_r{\mu }_0{A}_o}$$

(9)

where $A_i \mathrm{a}\mathrm{n}\mathrm{d} A_o$ are the area of the magnetic pole, ${\mu }_r$ is the relative permeability, ${\mu }_0$ is the permeability of vacuum, and $g$ is the air gap.

A closed magnetic circuit made up of conductors has a constant magnetic flux because magnetic flux has continuity. According to Ohm’s law for magnetic circuits, if the magnetic flux in the circuit is $\mathrm{\varnothing }$, then

$$F=R_i\varnothing +R_o\varnothing .$$

(10)

The following exists assuming a uniform magnetic circuit:

$$\varnothing =B_i{A}_i=B_o{A}_o$$

(11)

where $B_i$ is the magnetic flux density in the air gap at the inner magnetic pole of the electromagnet. $B_o$ is the magnetic flux density in the air gap at the outer magnetic pole of the electromagnet. The magnetic field energy in the electromagnet and armature is much less than that in the air gap because the magnetic permeability of ferromagnetic materials is significantly greater than that of non-ferromagnetic materials. If the former is ignored, the magnetic field energy stored in the air gap is:

$$W_e=\frac{B_i^2{A}_{i}g}{2{\mu }_0}+\frac{B_o^2{A}_{o}g}{2{\mu }_0}.$$

(12)

The suspension force in the vertical direction provided by a single suspension unit can be obtained using the energy virtual displacement method:

$$F_e=\frac{B_i^2{A}_i}{2{\mu }_0}+\frac{B_o^2{A}_o}{2{\mu }_0}.$$

(13)

Combining the aforementioned equation yields the electromagnetic force formula:

$$F_e=\frac{{\mu }_0{\mu }_r^2{N}^2{A}_i{A}_o{I}^2}{2\left(A_i+A_o\right)g^2}.$$

(14)

2.2. Simulation Study of Magnetic Suspension Structure

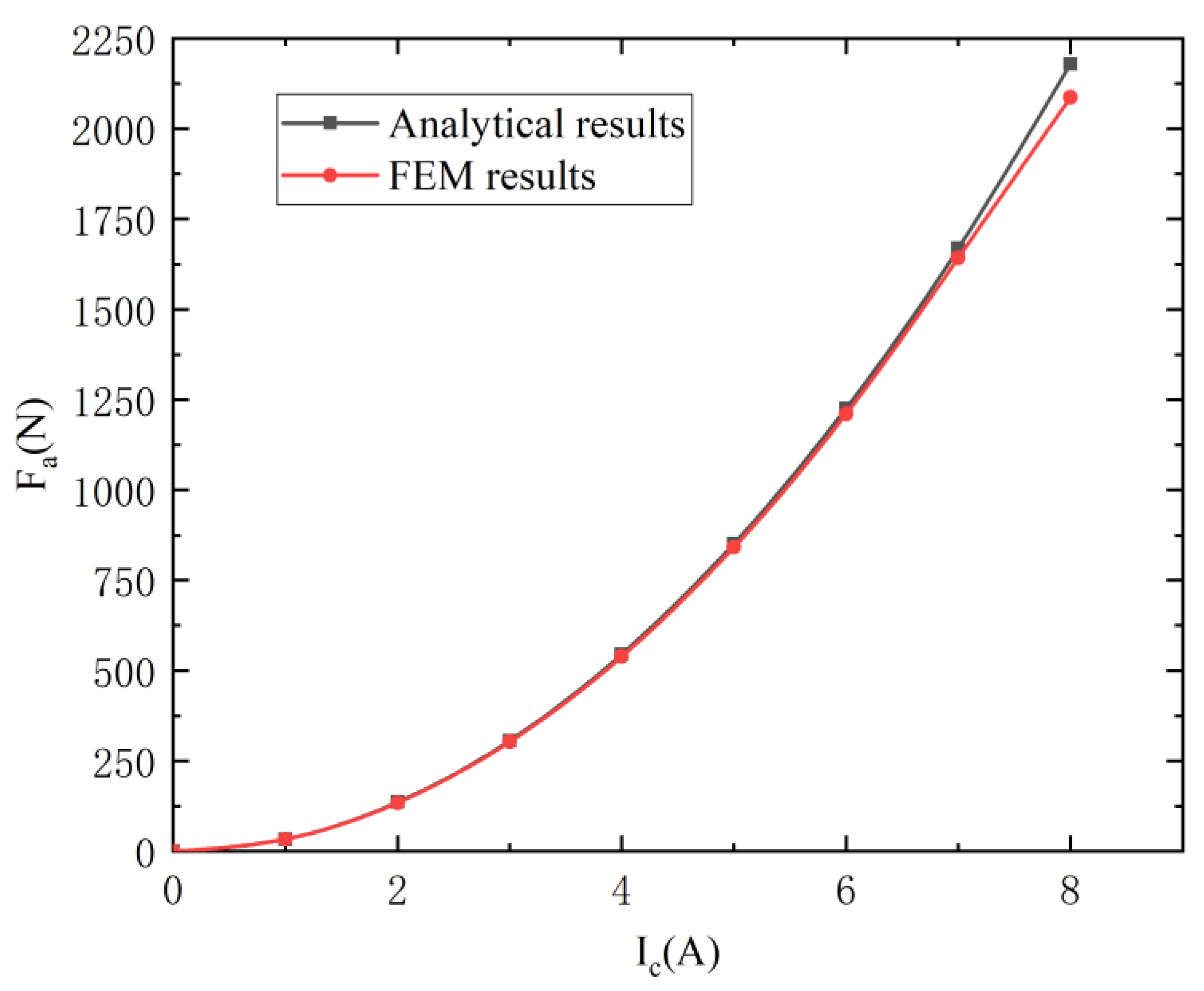
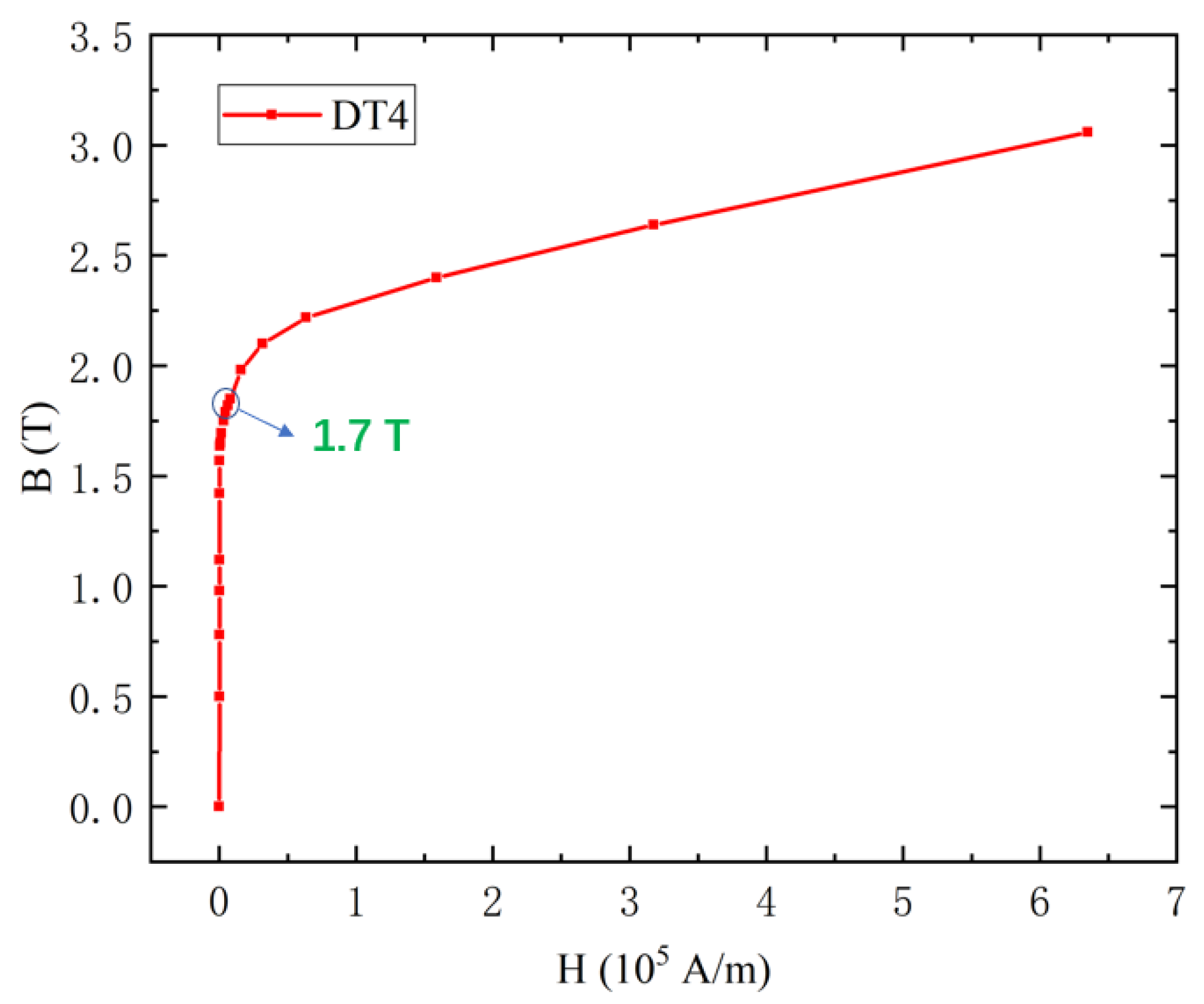
2.2.1. Numerical Verification

The finite element calculation results of the unilateral structure of symmetric magnetic suspension are compared with the analytical values of the equivalent magnetic circuit method in order to confirm the reliability of the simulation results.

The upper and lower coils of the magnetic suspension damper are loaded with control currents $I_s$ and $I_x$, respectively, and N is the coil turn in the proposed magnetic suspension damper structure. The air gaps at the upper and lower ends of the damper between the electromagnet and the armature are, respectively, $g_s=(x_0+x)$ and $g_x=(x_0-x)$, where $x$ is the displacement of the armature and $x_0$ is the air gap in the initial state between the armature and the lower end of the electromagnet.

The magnitude of the electromagnetic force $F_a$ on the armature by the electromagnet at the upper end is

$$F_a=\frac{{\mu }_0{\mu }_r^2{N}^2{A}_i{A}_o{I}_s^2}{2\left(A_i+A_o\right)x_s^2}=\frac{{\mu }_0{\mu }_r^2{N}^2{A}_i{A}_o{I}_s^2}{2\left(A_i+A_o\right){\left(x+x_0\right)}^2}.$$

(15)

The magnitude of the electromagnetic force $F_b$ on the armature by the lower solenoid is

$$F_b=\frac{{\mu }_0{\mu }_r^2{N}^2{A}_i{A}_o{I}_x^2}{2\left(A_i+A_o\right)x_s^2}=\frac{{\mu }_0{\mu }_r^2{N}^2{A}_i{A}_o{I}_x^2}{2\left(A_i+A_o\right){\left(x_0-x\right)}^2}.$$

(16)

Consequently, the magnetic suspension damper’s generated suspension force $F_e$ is as follows:

$$F_e=F_a-F_b=\frac{{\mu }_0{\mu }_r^2{N}^2{A}_i{A}_o}{2\left(A_i+A_o\right)}\left(\frac{I_s^2}{{\left(x_0+x\right)}^2}-\frac{I_x^2}{{\left(x_0-x\right)}^2}\right).$$

(17)

Ansys is used for finite element calculation, and the model involved in the calculation is shown in Figure 3.

The finite element model contains 147,035 elements. The air domain is set around the model, and the magnetic flux parallel is set on the boundary surface, so that the magnetic potential on the boundary surface is zero, ensuring that the whole model has no magnetic flux leakage.

In this paper, the current excitation is used, and the control current range in the unilateral structure coil is 1–8 A.

The simulation results of the symmetric maglev unilateral structure in Figure 3 are compared with the analytical solution derived from Equation (15) in order to confirm the reliability of the simulation findings, as shown in Figure 4.

The analytical results of the electromagnetic force are roughly the same as the simulated results, as shown in Figure 4, with the exception that the simulation results are slightly distorted and the analytical results are slightly higher than the finite element results, which is due to factors like magnetism leakage and iron loss. This difference will become more and more obvious with the increase in the air gap and current. The magnetic flux produced by the current is typically dispersed across the environment. However, since the electromagnet is made of ferromagnetic material, this drives the flux to be mostly concentrated in the circuit formed by the electromagnet and the air gap, which is called the effective flux. However, there is a small amount of magnetic flux that passes directly through the space around the coil and other magnetic conductors to form a magnetic circuit, which is called leakage flux. The theoretical calculation ignores the magnetic leakage phenomenon at the end of the core, whereas the finite element simulation accounts for the magnetic leakage of the structure. Therefore, the results obtained using the finite element method are reliable, and the finite element model can be used for the design and improvement of the magnetic suspension damping structure.

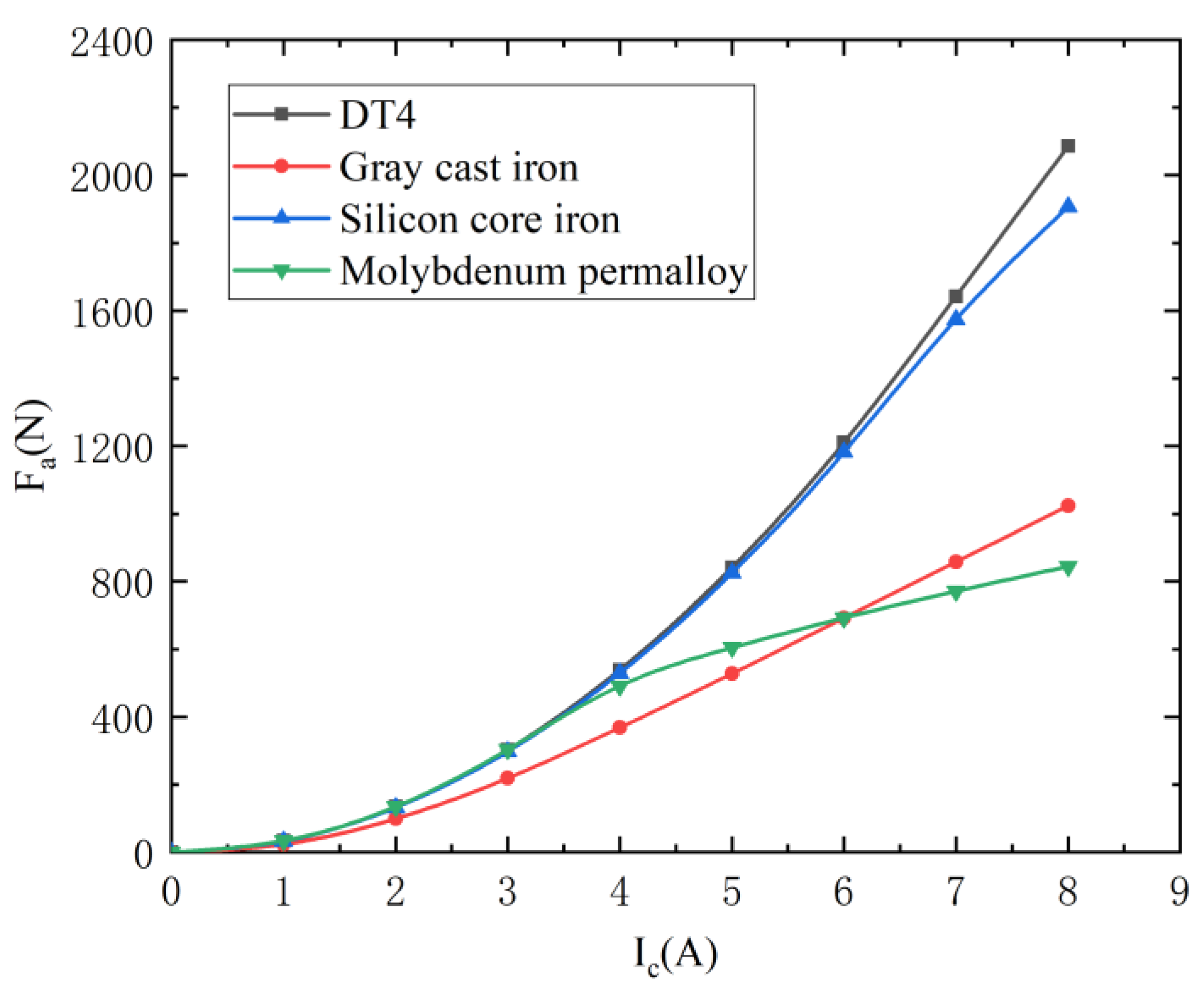
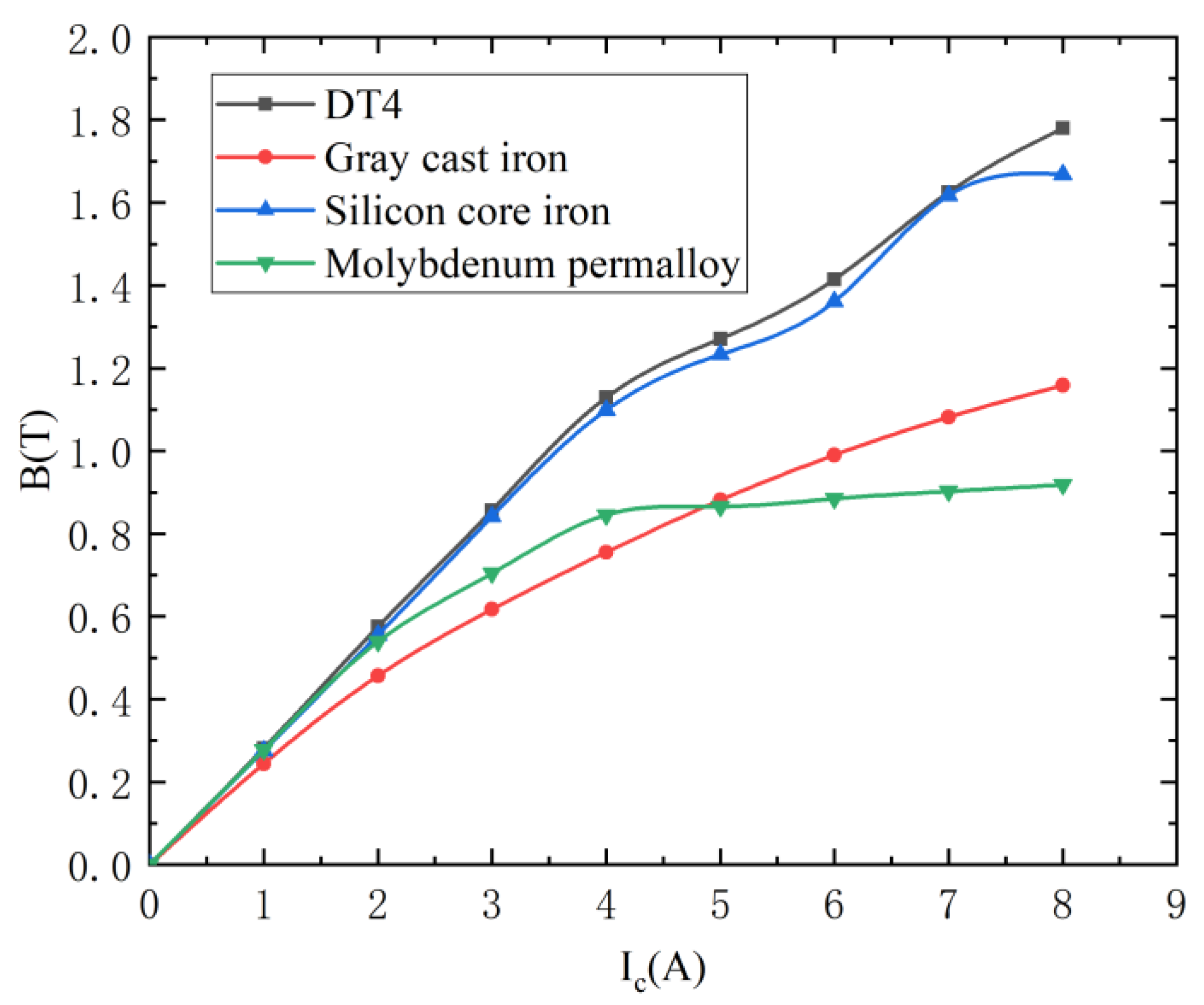
2.2.2. Material Research

According to how magnetically charged they become when subjected to an external magnetic field, materials can be roughly categorized as antimagnetic, paramagnetic, or ferromagnetic. According to their properties, ferromagnetic materials can be classified as moment magnetic materials, hard magnetic materials, and soft magnetic materials. The best materials for creating electromagnets and armatures among them are soft magnetic materials because of their high conductivity, low coercivity, ease of magnetization and demagnetization, narrow hysteresis line, and modest magnetic loss. DT4 (electrical pure iron), gray cast iron, silicon core iron, molybdenum permalloy, and other materials are examples of soft magnetic materials that are frequently utilized.

In order to investigate the influence of the material on the magnetic flux density and suspension force, the above four materials were selected for simulation; the symmetric unilateral structure shown in Figure 3 was still selected to complete the simulation, and the results are shown in Figure 5 and Figure 6.

The outcomes demonstrate the superiority of DT4 over the other three materials. Figure 5 and Figure 6 show that the output electromagnetic force of this material is greater than that of the other three materials when the control current is the same. In the meantime, when DT4 is employed, the saturation magnetic flux density is high and the positive connection between the magnetic flux density and the control current is stronger. Additionally, due to its excellent cold and hot processing characteristics and low cost, DT4 is a great material for DC magnetic fields. DT4 will be utilized in the next experiments.

2.2.3. Research on Control Current

Normally, the greater the control current produced, the stronger the suspension force; however, in practice, the suspension force cannot be increased indefinitely due to the material’s magnetic saturation, which means that even if the control current is increased after the material reaches magnetic saturation, the electromagnetic force produced will not increase further. In reality, when the control current keeps rising after the material’s magnetic flux density reaches a particular value, the rate of growth of the magnetic flux density becomes very slow. To ascertain the maximum control current or the maximum magnetic flux density that the structure can endure when design optimization of the structure is carried out, the following numerical simulation analysis of the symmetric maglev unilateral structure in Figure 3 is carried out.

The B–H curve of pure iron is plotted as shown in Figure 7 based on the pertinent data.

Both H and B are the quantities describing the magnetic field. H represents the external magnetic field strength and B represents the magnetic flux density of the material after magnetization. The B–H curve describes the relationship between the external magnetic field intensity and the magnetic flux density of the magnetized material during the magnetization of the magnetic material in the magnetic field. It is most effective to keep the magnetic induction below 1.7 T, because, as can be seen from the B–H curve of pure iron in Figure 7, when this value is reached, the growth rate of pure iron tends to flatten out.

By simulating the symmetric magnetic suspension unilateral structure of Figure 3, as shown in Figure 8.

According to the simulation results shown in Figure 8, the magnetic field is strongest around the inner and outer magnetic pole, and as the control current is increased, the electromagnet’s magnetic flux density increases. The electromagnet’s magnetic flux density reaches 1.6249 T when the control current is 7 A. The ideal range for controlling the current in the following experiments is 1 A–7 A since the magnetic induction of the electromagnet slows down when the magnetic induction surpasses 1.7 T.

3. Magnetic Suspension Structure Design and Optimization

3.1. Armature Optimization

The outcomes of the finite element simulation are displayed in Figure 9. It is discovered that the armature’s magnetic flux density, electromagnetic force distribution, and magnetic flux density all exhibit some regularity, with the annular region centered on the armature’s center exhibiting the highest magnetic flux density. The electromagnetic force acting on the armature is clearly felt not only in the circular region directly in the middle of the armature but also at its edge. On this basis, the armature structure is optimized.

According to the magnetic flux density and the force distribution characteristics, the armature is structurally optimized as shown in Figure 10.

On the basis of the original structure, inner and outer reinforcement rings are added to each of the two symmetrical surfaces of the armature, as shown in Figure 11.

In Figure 11, $R_{ii}$ is the inner diameter of the inner reinforcing ring, $L_I=R_{io}-R_{ii}$ is the inner reinforcing ring width, and $L_O=R_{oo}-R_{oi}$ is the outer reinforcing ring width. In order to clarify the effects of $R_{ii}$, $L_I$, and $L_O$ on the magnetic flux density and electromagnetic force, the control variable method was applied to simulate several sets of structural parameters.

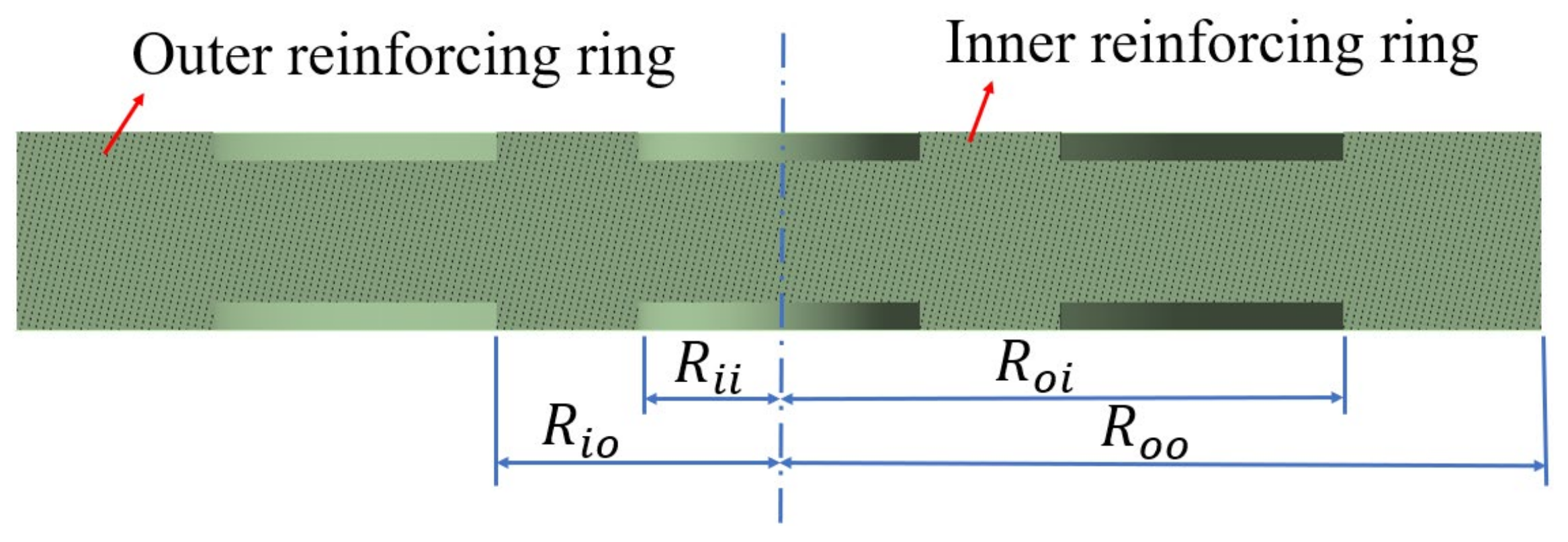
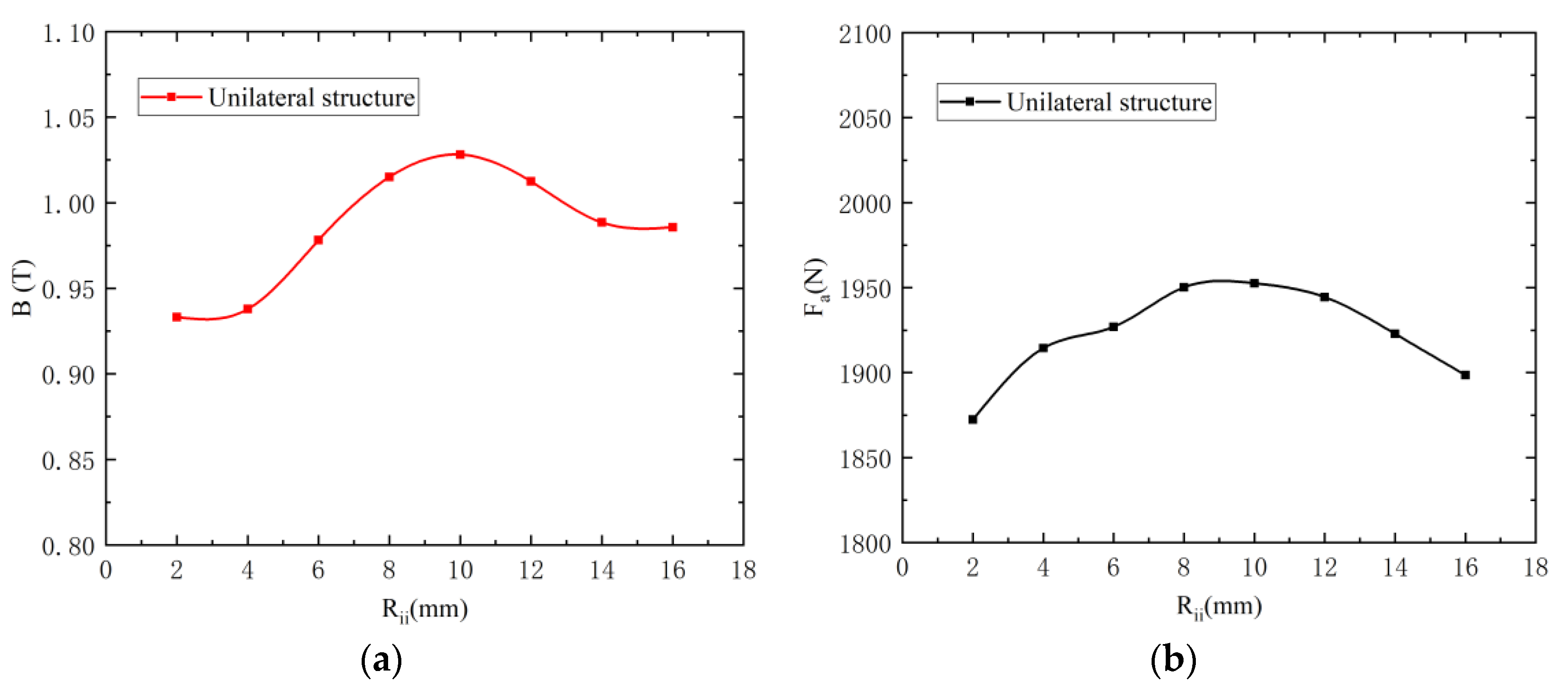
3.2. Inner Diameter of Inner Reinforcing Ring

The value of $R_{ii}$ is taken in the range of 2 mm to 16 mm, $L_I=20 \mathrm{m}\mathrm{m}$, and $L_O=10 \mathrm{m}\mathrm{m}$; the structure is simulated and the results are shown in Figure 12.

According to the simulation results, with the increase in $R_{ii}$, the magnetic flux density increases and then decreases, and reaches a great value when $R_{ii}$ is 10 mm, at which time the magnetic flux density is 1.0282 T; the electromagnetic force increases with the increase in $R_{ii}$, and shows the same trend of increasing and then decreasing, and reaches a maximum value when $R_{ii}$ is 10 mm, at which time the electromagnetic force is 1952.6 N. According to the simulation results, the optimal value of $R_{ii}$ is 10 mm. The optimum value of $R_{ii}$ is 10 mm.

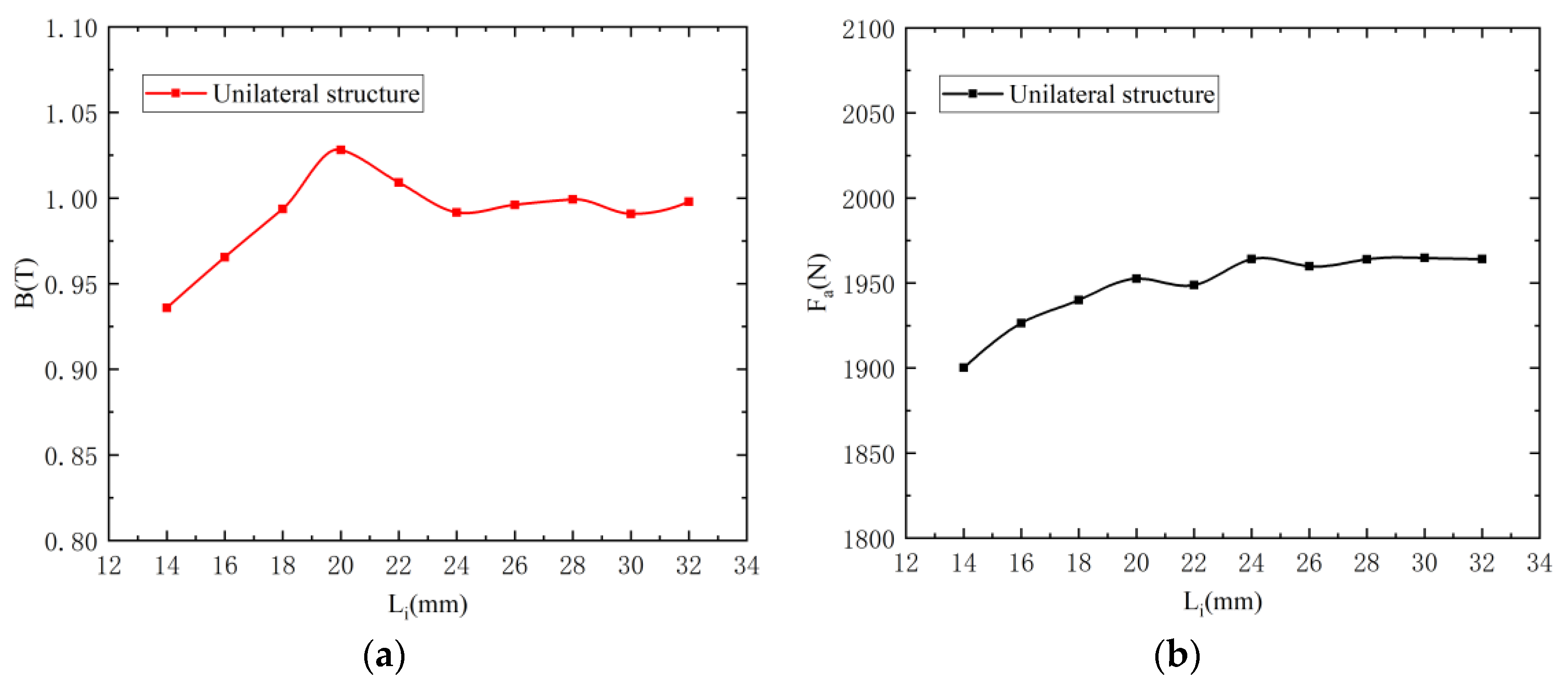
3.3. Width of Inner Reinforcing Ring

The value of $L_I$ is taken in the range of 14 mm to 32 mm, $L_O=10 \mathrm{m}\mathrm{m}$, and $R_{ii}=10 \mathrm{m}\mathrm{m}$; the structure is simulated and the results are shown in Figure 13.

According to the simulation results, with the increase in $L_I$, the magnetic induction shows a fluctuation trend. When $L_I$ is 24 mm, the magnetic induction is 0.99164 T. The electromagnetic force rises with the increase in $L_I$. When $L_I$ is 24 mm, the electromagnetic force exhibits an extreme value; at this time, the electromagnetic force is 1963.1 N. According to the simulation results, the optimal value of $L_I$ is 24 mm.

3.4. Width of Outer Reinforcing Ring

The value of $L_O$ is taken in the range of 6 mm to 14 mm, $L_I=24 \mathrm{m}\mathrm{m}$, and $R_{ii}=10 \mathrm{m}\mathrm{m}$; the structure is simulated and the results are shown in Figure 14.

According to the simulation results, with the increase in $L_O$, the change in magnetic flux density is very small and there is no obvious trend. The electromagnetic force shows a certain upward trend with the increase in $L_O$ and reaches the maximum value when the $L_O$ is 12 mm; at this time, the electromagnetic force is 1976 N. According to the simulation results, the optimal value of $L_O$ is 12 mm.

Both the electromagnetic force and the magnetic flux density varied for various parameters, with the electromagnetic force varying more wildly. The following are the causes of this outcome: (I) The angle of the magnetic line of force between the electromagnet and the armature is constantly changing, which may lead to a large fluctuation in the electromagnetic; (II) The change in the effective contact area will also have an impact on the electromagnetic force; (III) The increased thickness of the reinforcing ring is 0.5 mm, which has an impact on the air gap which in turn affects the magnitude of the electromagnetic force. From the simulation results, the armature parameters are taken as follows: $R_{ii}=10 \mathrm{m}\mathrm{m}, L_I=24 \mathrm{m}\mathrm{m}, L_O=10 \mathrm{m}\mathrm{m}$.

4. Results and Discussion

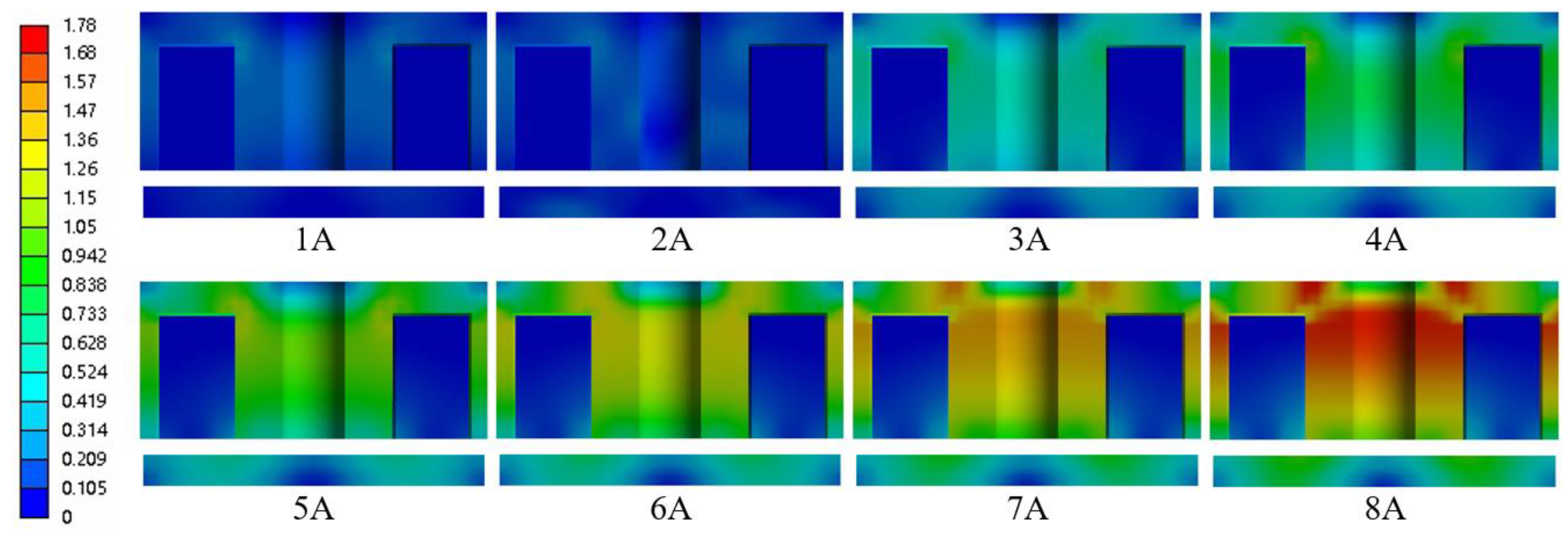
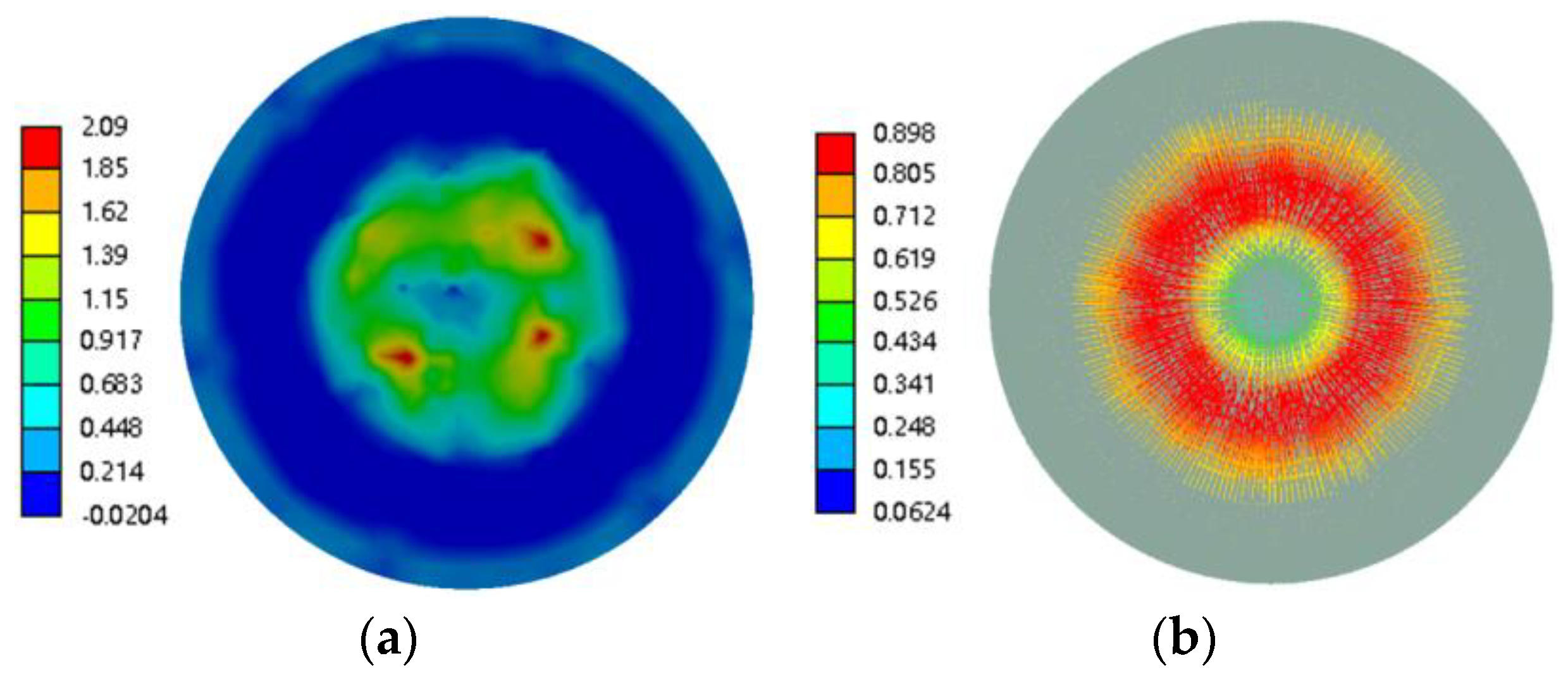
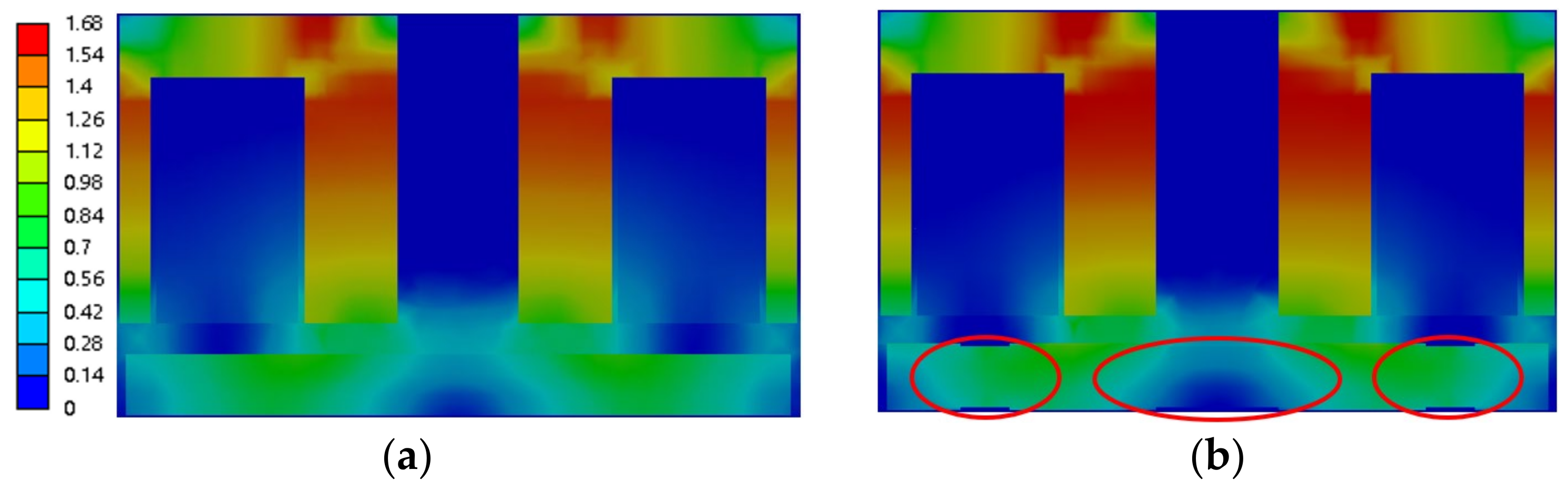
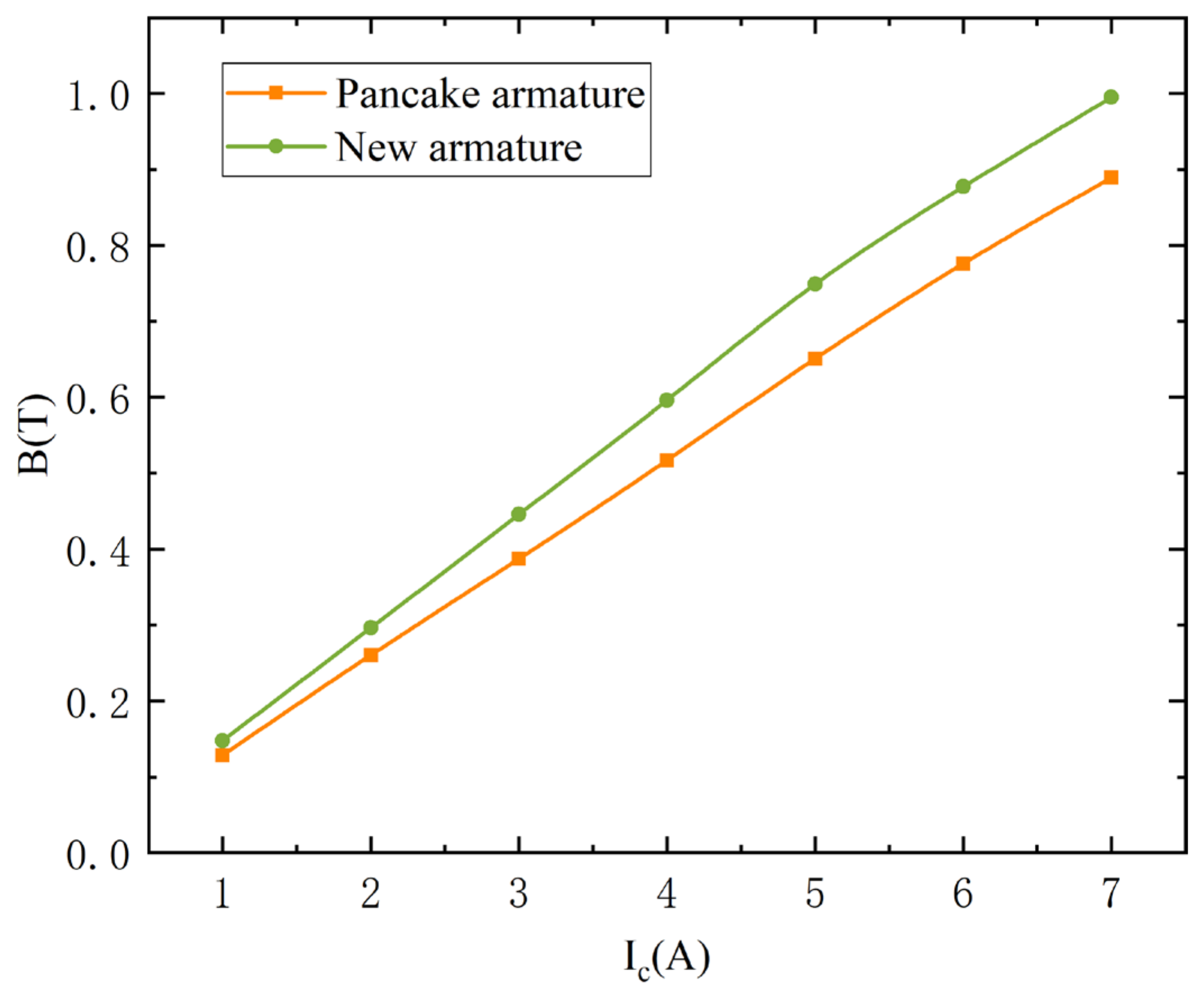
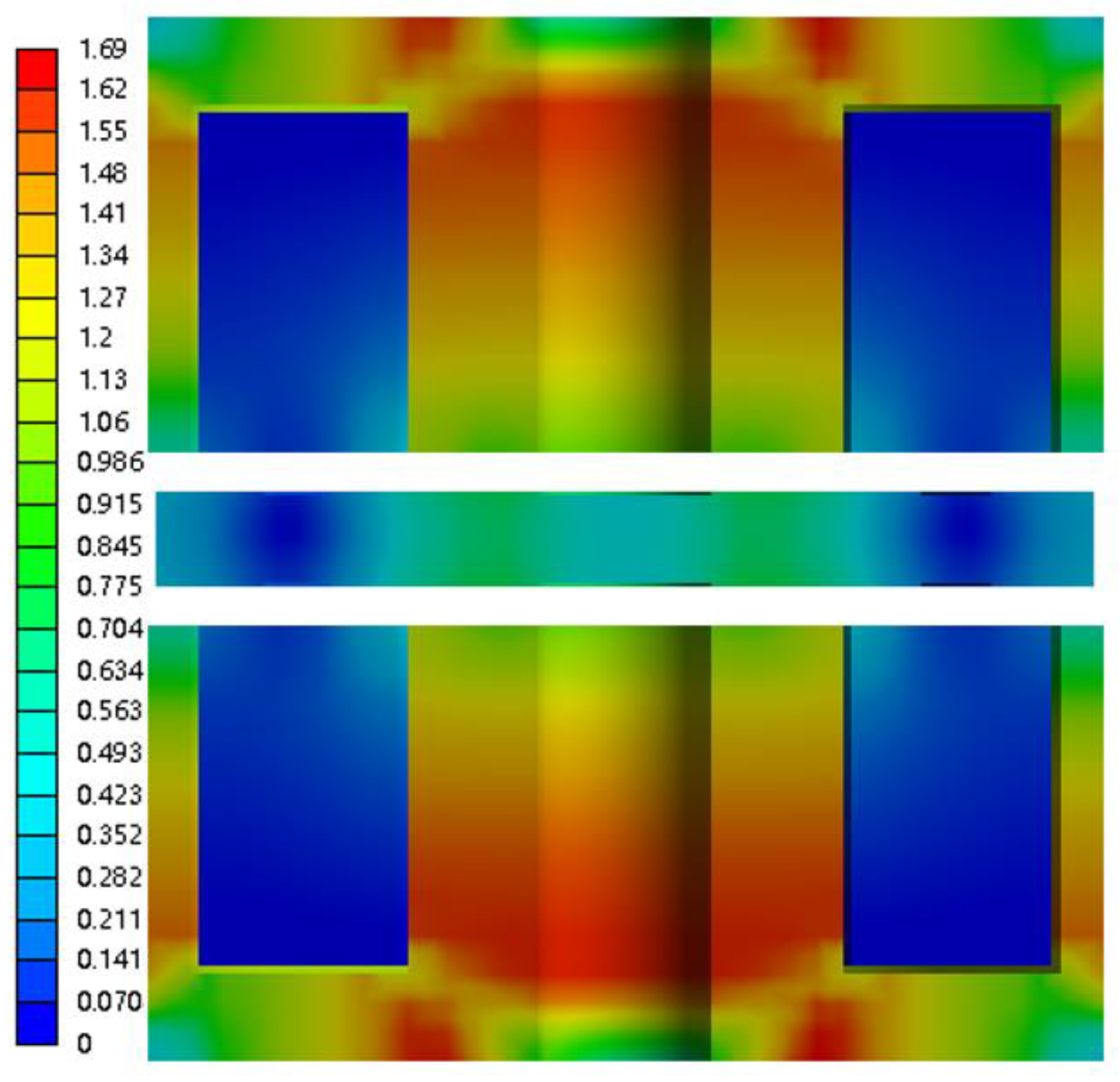
4.1. New Armature Structure Magnetic Flux Density

Based on the aforementioned simulation results, a new symmetric magnetic suspension structure is created. To demonstrate this structure’s superiority over the original magnetic suspension structure, simulations of both the new and original structures are run.

The magnetic flux density distribution of the two magnetic suspension structures is shown in Figure 15 (contains air area).

Although there is a difference in the value of the magnetic flux density between the two magnetic suspension structures, as can be seen from the distribution of the magnetic flux density of the two structures, the distribution of the magnetic flux density is not significantly different from the overall view.

The magnetic flux density of the armature of the two magnetic suspension structures at different control currents is shown in Figure 16.

The magnetic flux densities of the two types of armatures rise when the control current increases, as shown in Figure 16. The new type of armature has a higher magnetic flux density than the old type at each control current, and the maximum difference in magnetic flux density is 0.10573 T when the control current $I_c=7 \mathrm{A}$.

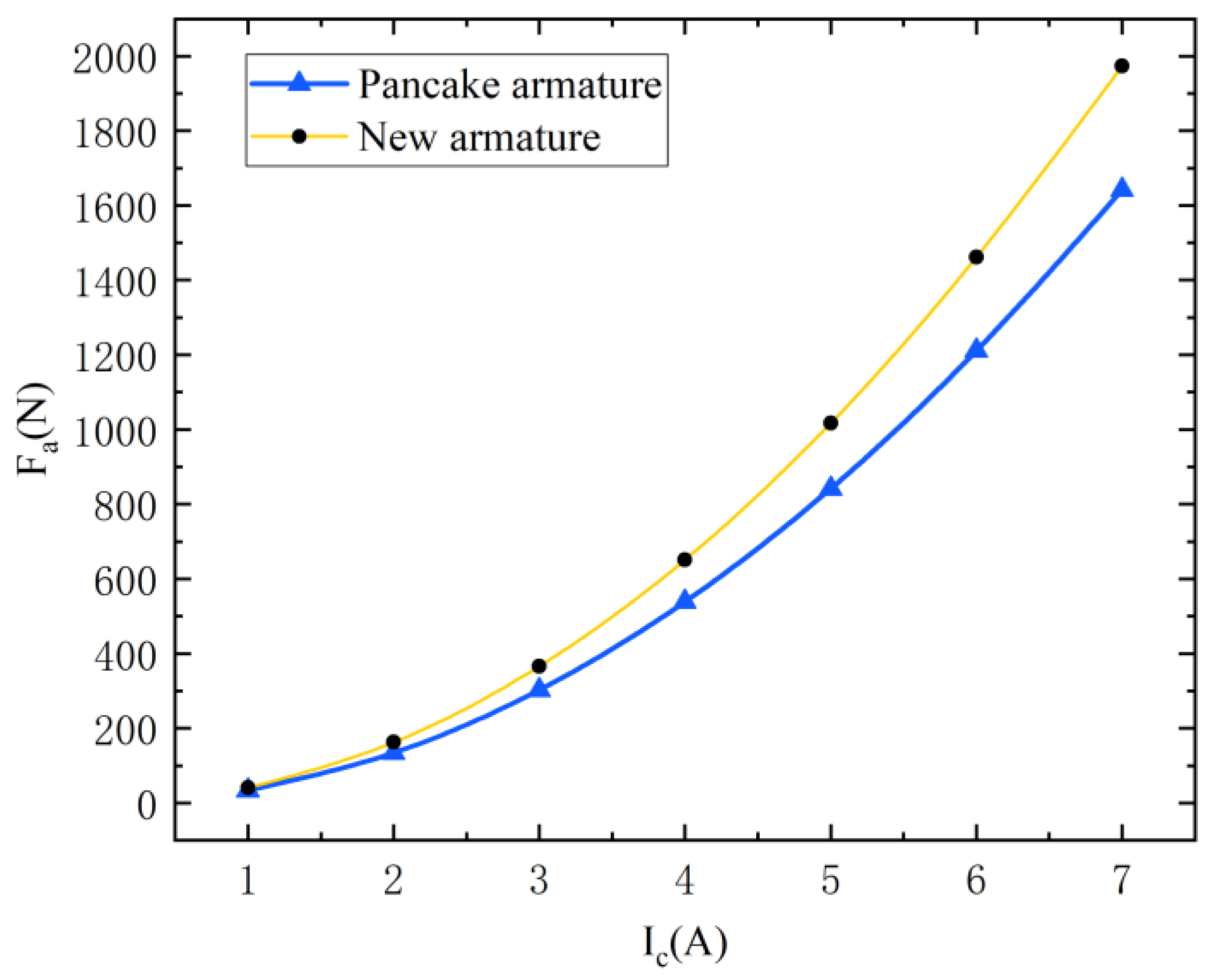
4.2. New Armature Structure Electromagnetic Force

The electromagnetic force of the two magnetic suspension structures is simulated and the effect of armature on the electromagnetic force is shown in Figure 17.

The electromagnetic force and the control current of the two different types of magnetic suspension structures are positively correlated, according to the simulation results. The electromagnetic force applied to the new armature at each control current is larger than that of the pancake armature. As the control current is increased, the difference between the two increases until it reaches a maximum of 331.6 N (by 20.19%).

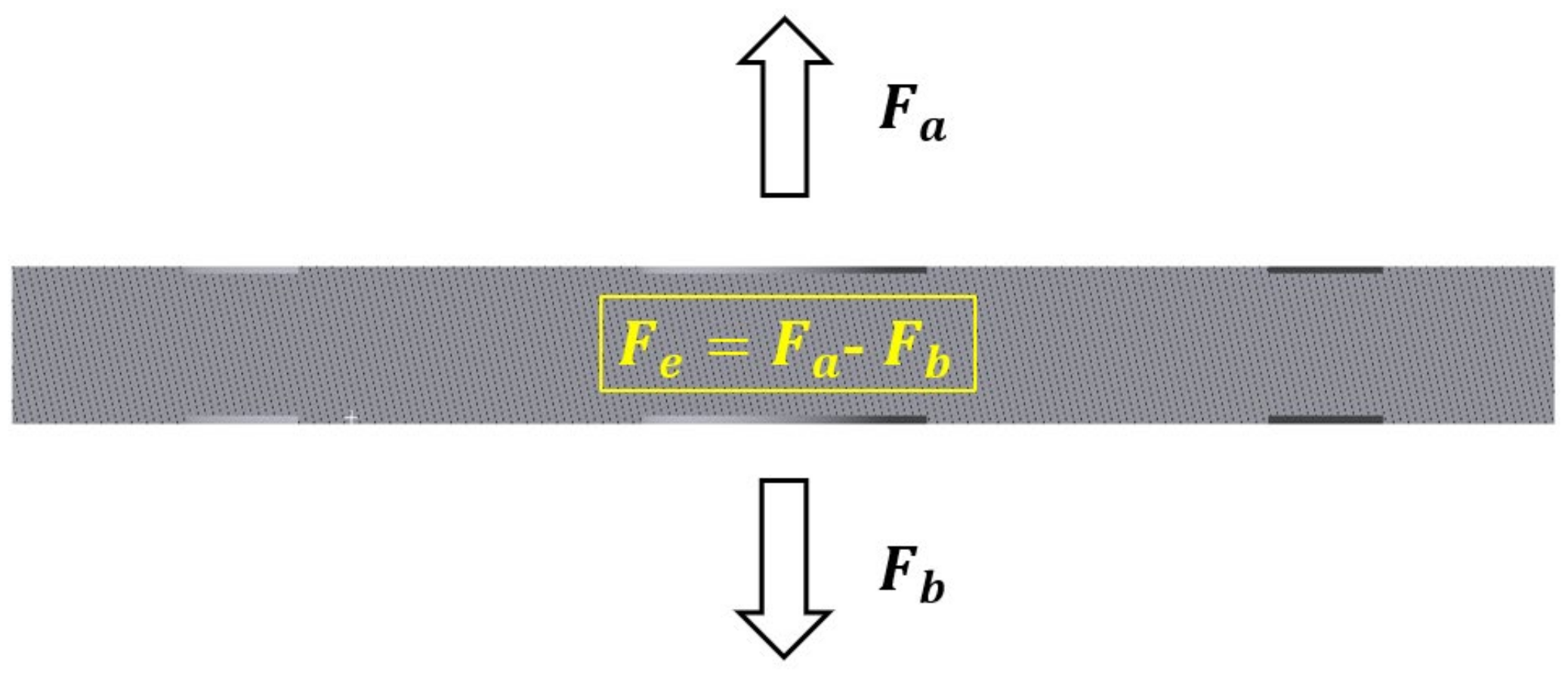
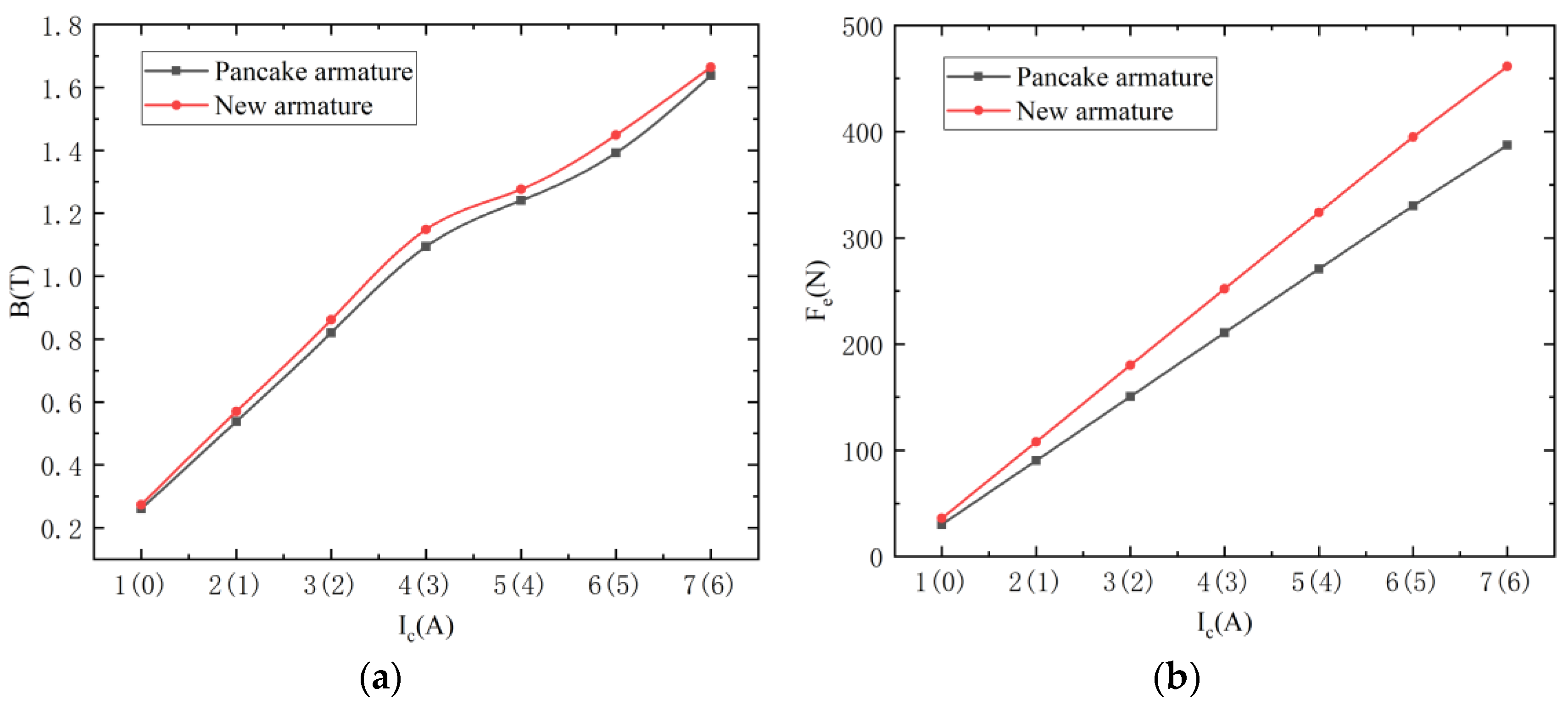
4.3. Performance Improvement

In the novel symmetric magnetic suspension structure, as shown in Figure 18, the two symmetric electromagnets produce an electromagnetic force on the armature in opposite directions, and the magnetic suspension structure’s output force equals the difference of the electromagnetic force.

Where $F_a$ denotes the electromagnetic force produced by the electromagnet at its upper end, $F_b$ denotes the electromagnetic force produced at its symmetric end, and $F_e$ denotes the suspension force produced by the magnetic suspension structure, the expression for which is

$$F_e=F_a-F_b$$

(18)

A magnetic suspension structure typically achieves its suspension force output by introducing various control currents into the coil. Here, the structure’s suspension force is tested using control currents of 1–7 A for Coil-A (the upper end coil) and 0–6 A for Coil-S (the symmetric end coil). The output suspension force of the two symmetric magnetic suspension structures as well as the overall magnetic flux densities are simulated, and the results are displayed in Figure 19.

The simulation results demonstrate that the magnetic flux densities of the two magnetic suspension structures change similarly in response to the control current, with the novel magnetic suspension structure having a clearly larger magnetic flux density under different control currents. The suspension force of the new magnetic suspension structure is greatly improved under each control current, and the improvement grows as the control current is increased. The largest difference in the suspension force output of the two magnetic suspension structures is 74.12 N (19.14% augmentation) when the control current is 7 A (6 A).

4.4. Electromagnetic Characteristics

A new symmetric magnetic suspension structure is developed from the studies mentioned above, and finite element simulation is used to ascertain its properties. The magnetic flux density distribution that follows from energizing the coils at both ends with a current of 7 A is depicted in Figure 20.

The magnetic field of the magnetic suspension structure appears to be at its maximum value in the inner pole column when both Coil-A and Coil-S are energized with the same direction 7 A control current, as shown in Figure 20. The maximum value of 1.6908 T is within the acceptable range and satisfies the design requirements.

The suspension force output is illustrated in Figure 21 for Coil-A with a control current of 1–7 A and Coil-S with a control current of 0–6 A.

As shown in Figure 21, as the control current is increased, the new symmetric magnetic suspension structure’s output suspension force and magnetic flux density rise. The suspension force output is 461.4 N and the highest magnetic flux density is 1.6642 T at a control current of 7 A (6 A).

5. Conclusions

In this study, the theoretical calculation and finite element simulation are compared and confirmed in order to assess the dependability of the research program. In light of this, the detailed analysis using the finite element method is performed on the designed magnetic suspension structure. The relationship between electromagnetic force, suspension force, magnetic flux density and material, structure, and control current is then examined, and the following conclusions are made:

(1)

DT4 demonstrated outstanding electromagnetic performance when used as the armature and electromagnet material, compared to gray cast iron, silicon core iron, and molybdenum permalloy, respectively. The armature is subjected to the most electromagnetic force (68.2 N–871.7 N more than the other three materials) when the electromagnet and armature material are DT4 under the same control current;

(2)

The electromagnetic performance of the new unilateral magnetically suspension structure is best when the inner reinforcing ring has an inner diameter of 10 mm, the inner reinforcing ring is 24 mm wide, and the outer reinforcing ring is 12 mm wide. At this point, the electromagnetic force output is also increased by 20.19% (by 331.6 N);

(3)

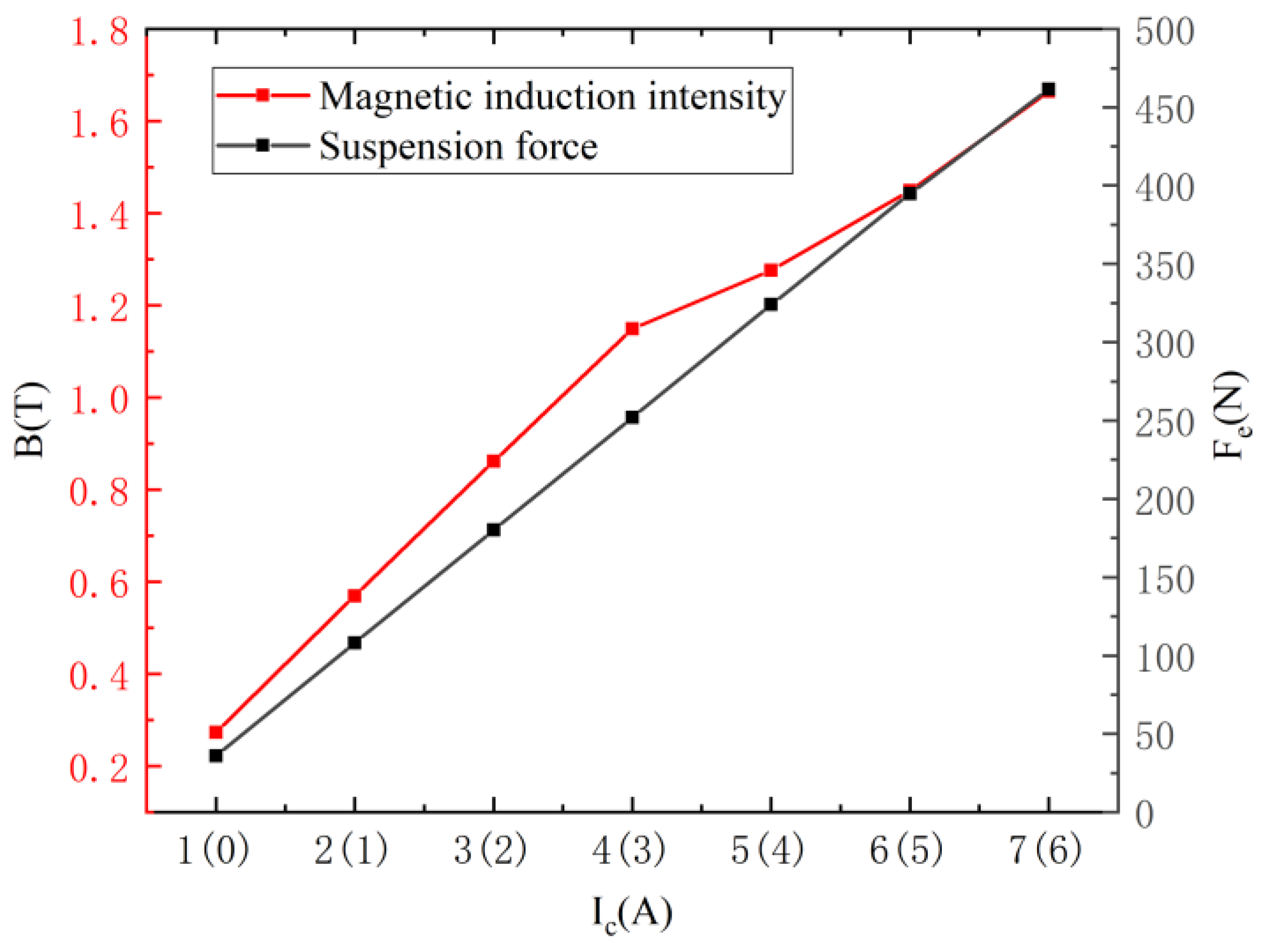
Suspension force and magnetic flux densities are more positively correlated with the control current in the new symmetric magnetic suspension structure at control currents of 7 A (6 A), where the maximum output suspension force is 461.4 N and the maximum magnetic flux density is 1.6642 T. This represents a 19.14% (by 74.12 N) increase in suspension force over the original version of the magnetic suspension structure;

(4)

The response interval of the suspension force is significantly stretched by the novel symmetric magnetic suspension structure, and the corresponding interval of system stiffness is also greatly increased. The magnetic suspension damper’s ability to adapt to more complex vibration-damping situations can be achieved by altering the control current, which also improves the magnetic suspension damper’s vibration-damping performance. This study can serve as a guide for improving and modernizing the magnetic suspension damper, and it also offers suggestions for reducing vibration and noise in engineering.