A Case Study Assessing the Liquefaction Hazards of Silt Sediments Based on the Horizontal-to-Vertical Spectral Ratio Method
Abstract
1. Introduction
2. Methodology
3. Application in the Yellow River Delta
3.1. Geologic Setting
3.2. Instruments and Field Investigation
3.3. Data Processing
3.4. Identify Fundamental Frequency
4. Discussion
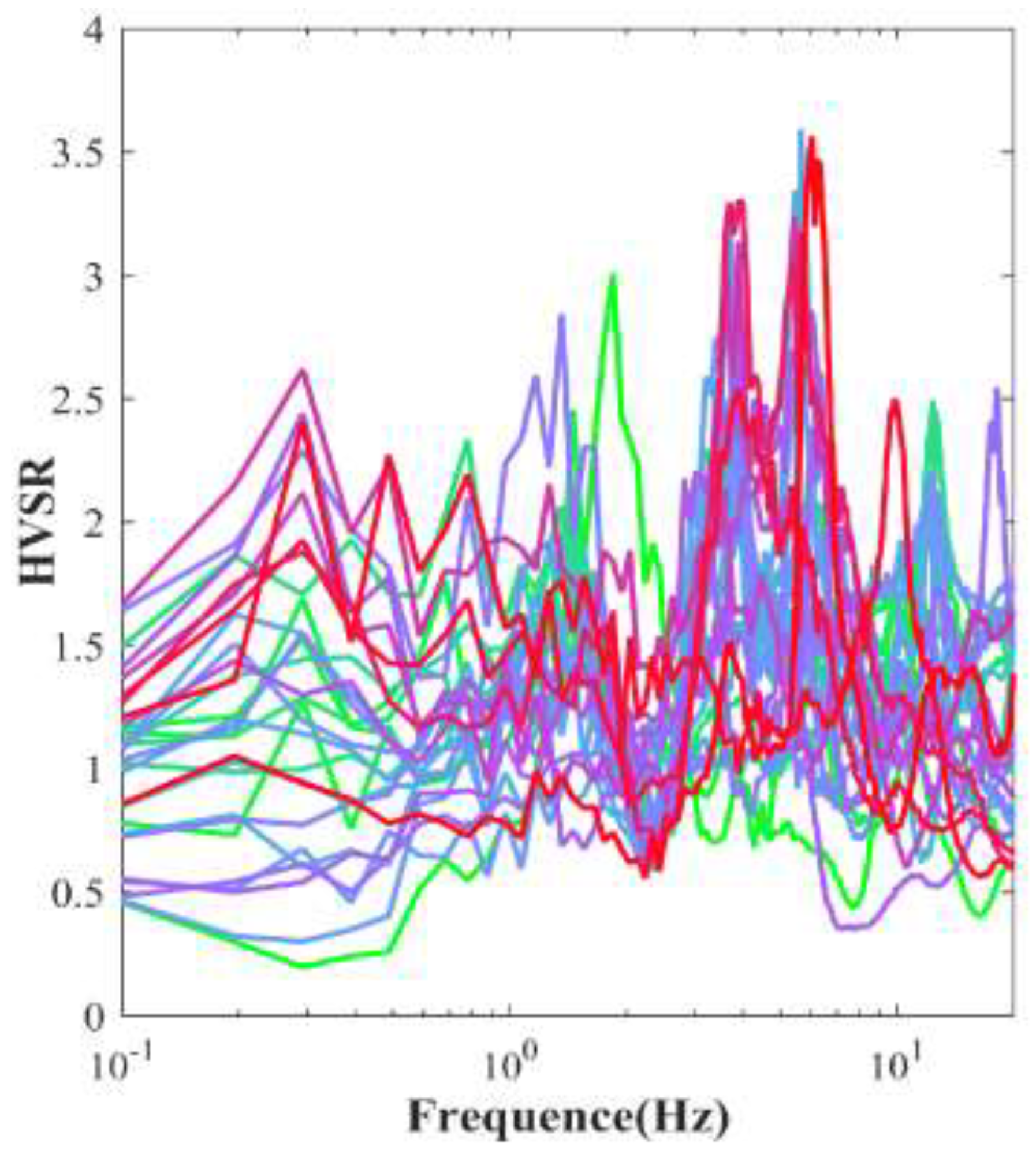
4.1. Fundamental Frequency
4.2. Amplification
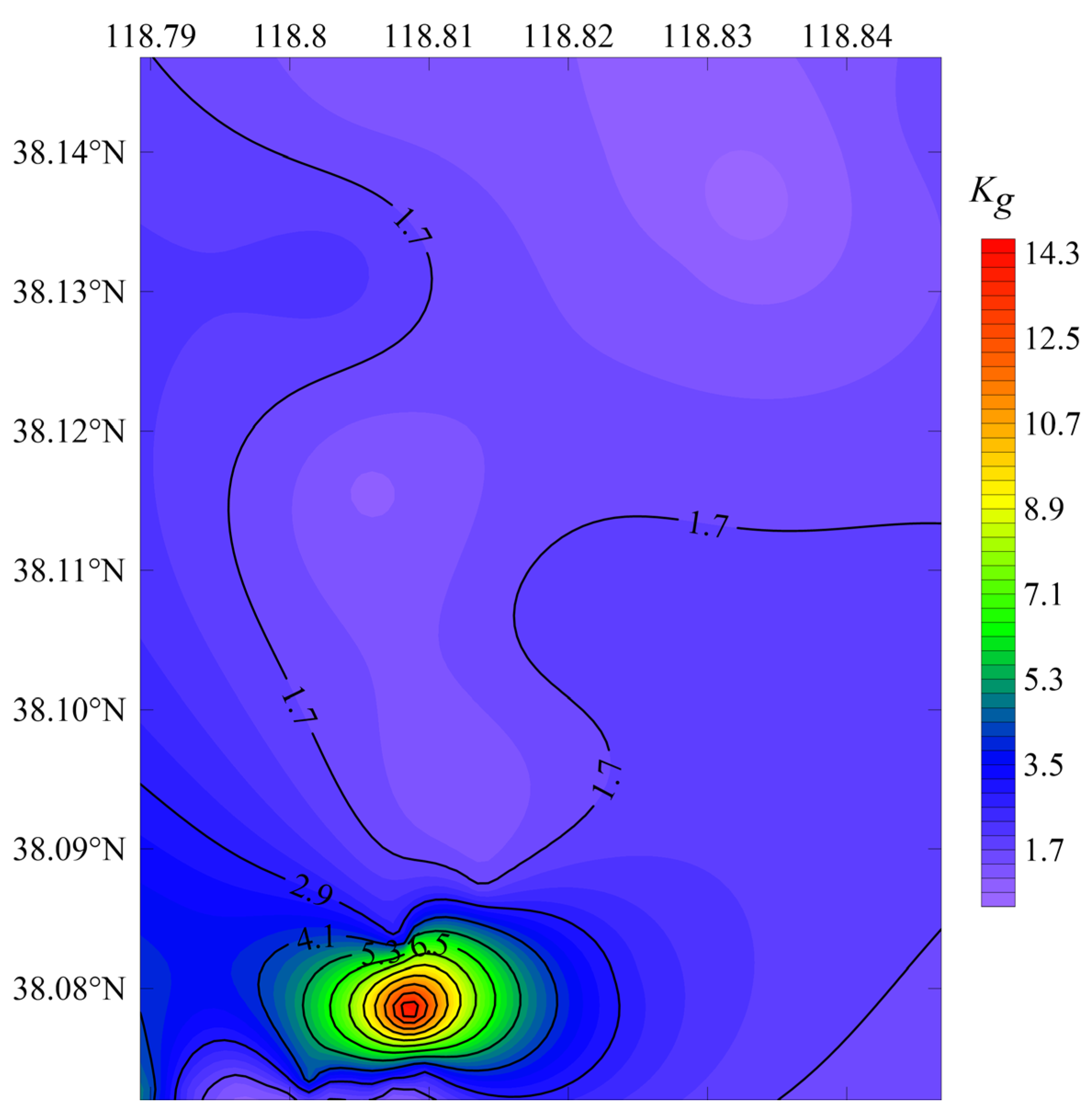
4.3. Vulnerability Index
5. Conclusions
- This study presents a new method to identify the fundamental frequency from ambient noise recording in the Yellow River Delta. The results show that the soils in the areas with different geological conditions have a stable range of the fundamental frequency respectively, and the results are consistent with the inverse relationship between the fundamental frequency and the thickness of the sediment layer. Thus, the new method is potentially applicable and reliable for identifying the fundamental frequency;
- The vulnerability indexes of the Yellow River Delta range from 0.6 to 15.3 and are dependent on the variability of the local geological conditions. In the southwestern part of the study area, the maximum value of Kg occurs on the beach in front of the corner of the two embankments, where the liquefaction hazard is greatest; therefore, the construction and maintenance of buildings should be carefully considered here. However, we suggest that combining the HVSR method with geotechnical investigation methods, such as field tests or indoor geotechnical tests, can further investigate the extent of liquefiable layers, which is essential for a more reliable assessment of the liquefaction potential of silty soils;
- The results show that the HVSR method, when based on single station noise recordings, is suitable for rapidly assessing liquefaction potential. Compared with other field or laboratory tests, the HVSR method is a convenient, practical, faster, and nondestructive tool for assessing the liquefaction potential of silty sedimentary, such as the Mississippi River Delta. This will help to carry out liquefaction hazard assessment of silty soil in a new perspective, which can provide services for urban disaster prevention and mitigation and can also provide a reference basis for establishing regional seismic codes with good practical application value.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Seed, H.B.; Idriss, I.M. Analysis of Soil Liquefaction: Niigata Earthquake. J. Soil Mech. Found. Div. 1967, 93, 83–108. [Google Scholar] [CrossRef]
- Holzer, T.L.; Bennett, M.J.; Ponti, D.J.; Tinsley, J.C., III. Liquefaction and Soil Failure During 1994 Northridge Earthquake. J. Geotech. Geoenviron. Eng. 1999, 125, 438–452. [Google Scholar] [CrossRef]
- Yuan, H.; Hui Yang, S.; Andrus, R.D.; Hsein Juang, C. Liquefaction-Induced Ground Failure: A Study of the Chi-Chi Earthquake Cases. Eng. Geol. 2004, 71, 141–155. [Google Scholar] [CrossRef]
- Chen, L.; Yuan, X.; Sun, R. Review of Liquefaction Phenomena and Geotechnical Damage in the 2011 New Zealand Mw6.3 Earthquake. World Earthq. Eng. 2013, 29, 1–9. (In Chinese) [Google Scholar] [CrossRef]
- Youd, T.L.; Idriss, I.M. Liquefaction Resistance of Soils: Summary Report from the 1996 NCEER and 1998 NCEER/NSF Workshops on Evaluation of Liquefaction Resistance of Soils. J. Geotech. Geoenviron. Eng. 2001, 127, 297–313. [Google Scholar] [CrossRef]
- Kumar, S.S.; Krishna, A.M.; Dey, A. Assessment of Dynamic Response of Cohesionless Soil Using Strain-Controlled and Stress-Controlled Cyclic Triaxial Tests. Geotech. Geol. Eng. 2020, 38, 1431–1450. [Google Scholar] [CrossRef]
- Seed, H.B.; Idriss, I.M.; Arango, I. Evaluation of Liquefaction Potential Using Field Performance Data. J. Geotech. Eng. 1983, 109, 458–482. [Google Scholar] [CrossRef]
- Boumpoulis, V.; Depountis, N.; Pelekis, P.; Sabatakakis, N. SPT and CPT Application for Liquefaction Evaluation in Greece. Arab. J. Geosci. 2021, 14, 1631. [Google Scholar] [CrossRef]
- Geyin, M.; Maurer, B.W. Evaluation of a Cone Penetration Test Thin-Layer Correction Procedure in the Context of Global Liquefaction Model Performance. Eng. Geol. 2021, 291, 106221. [Google Scholar] [CrossRef]
- Qin, L.; Ben-Zion, Y.; Bonilla, L.F.; Steidl, J.H. Imaging and Monitoring Temporal Changes of Shallow Seismic Velocities at the Garner Valley Near Anza, California, Following the M7.2 2010 El Mayor-Cucapah Earthquake. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018070. [Google Scholar] [CrossRef]
- Lin, A.; Wotherspoon, L.; Bradley, B.; Motha, J. Evaluation and Modification of Geospatial Liquefaction Models Using Land Damage Observational Data from the 2010–2011 Canterbury Earthquake Sequence. Eng. Geol. 2021, 287, 106099. [Google Scholar] [CrossRef]
- Amini, F.; Qi, G.Z. Liquefaction Testing of Stratified Silty Sands. J. Geotech. Geoenviron. Eng. 2000, 126, 208–217. [Google Scholar] [CrossRef]
- Hatzor, Y.H.; Gvirtzman, H.; Wainshtein, I.; Orian, I. Induced Liquefaction Experiment in Relatively Dense, Clay-Rich Sand Deposits. J. Geophys. Res. Solid Earth 2009, 114, B02311. [Google Scholar] [CrossRef]
- Dobry, R.; Abdoun, T. Recent Findings on Liquefaction Triggering in Clean and Silty Sands during Earthquakes. J. Geotech. Geoenviron. Eng. 2017, 143, 04017077. [Google Scholar] [CrossRef]
- Ye, B.; Hu, H.; Bao, X.; Lu, P. Reliquefaction Behavior of Sand and Its Mesoscopic Mechanism. Soil Dyn. Earthq. Eng. 2018, 114, 12–21. [Google Scholar] [CrossRef]
- Nakamura, Y. A method for Dynamic Characteristics Estimation of Subsurface Using Microtremor on the Ground Surface. Railw. Tech. Res. Inst. Q. Rep. 1989, 30, 25–33. [Google Scholar]
- Lunedei, E.; Albarello, D. Theoretical HVSR Curves from Full Wavefield Modelling of Ambient Vibrations in a Weakly Dissipative Layered Earth. Geophys. J. Int. 2010, 181, 1093–1108. [Google Scholar] [CrossRef]
- Sánchez-Sesma, F.J.; Rodríguez, M.; Iturrarán-Viveros, U.; Luzón, F.; Campillo, M.; Margerin, L.; García-Jerez, A.; Suarez, M.; Santoyo, M.A.; Rodríguez-Castellanos, A. A Theory for Microtremor H/V Spectral Ratio: Application for a Layered Medium. Geophys. J. Int. 2011, 186, 221–225. [Google Scholar] [CrossRef]
- Bonnefoy-Claudet, S.; Cotton, F.; Bard, P.Y. The Nature of Noise Wavefield and Its Applications for Site Effects Studies: A Literature Review. Earth-Sci. Rev. 2006, 79, 205–227. [Google Scholar] [CrossRef]
- Maghami, S.; Sohrabi-Bidar, A.; Bignardi, S.; Zarean, A.; Kamalian, M. Extracting the shear wave velocity structure of deep alluviums of “Qom” Basin (Iran) employing HVSR inversion of microtremor recordings. J. Appl. Geophys. 2021, 185, 104246. [Google Scholar] [CrossRef]
- Panou, A.A.; Theodulidis, N.; Hatzidimitriou, P.; Stylianidis, K.; Papazachos, C.B. Ambient Noise Horizontal-to-Vertical Spectral Ratio in Site Effects Estimation and Correlation with Seismic Damage Distribution in Urban Environment: The Case of the City of Thessaloniki (Northern Greece). Soil Dyn. Earthq. Eng. 2005, 25, 261–274. [Google Scholar] [CrossRef]
- Leyton, F.; Ruiz, S.; Sepúlveda, S.A.; Contreras, J.P.; Rebolledo, S.; Astroza, M. Microtremors’ HVSR and Its Correlation with Surface Geology and Damage Observed after the 2010 Maule Earthquake (Mw 8.8) at Talca and Curicó, Central Chile. Eng. Geol. 2013, 161, 26–33. [Google Scholar] [CrossRef]
- Ullah, I.; Prado, R.L. Soft Sediment Thickness and Shear-Wave Velocity Estimation from the H/V Technique up to the Bedrock at Meteorite Impact Crater Site, Sao Paulo City, Brazil. Soil Dyn. Earthq. Eng. 2017, 94, 215–222. [Google Scholar] [CrossRef]
- Moon, S.W.; Subramaniam, P.; Zhang, Y.; Vinoth, G.; Ku, T. Bedrock Depth Evaluation Using Microtremor Measurement: Empirical Guidelines at Weathered Granite Formation in Singapore. J. Appl. Geophys. 2019, 171, 103866. [Google Scholar] [CrossRef]
- Nakamura, Y. Basic Structure of QTS (HVSR) and Examples of Applications. In Proceedings of the Increasing Seismic Safety by Combining Engineering Technologies and Seismological Data, Dubrovnik, Croatia, 19–21 September 2007; pp. 33–51. [Google Scholar]
- Nakamura, Y. What Is the Nakamura Method? Seismol. Res. Lett. 2019, 90, 1437–1443. [Google Scholar] [CrossRef]
- Nakamura, Y. On the H/V Spectrum. In Proceedings of the 14th Word Conference on the Earthquake Engineering, Beijing, China, 12–17 October 2008; pp. 12–17. [Google Scholar]
- Nakamura, Y. Clear Identification of Fundamental Idea of Nakamura’s Technique and Its Applications. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000; pp. 1–8. [Google Scholar]
- Nakamura, Y. Seismic Vulnerability Indices for Ground and Structures Using Microtremor. In Proceedings of the World Congress on Railway Research, Florence, Italy, 16–19 November 1997; pp. 1–7. [Google Scholar]
- Zhao, G.; Ye, Q.; Ye, S.; Ding, X.; Yuan, H.; Wang, J. Holocene Stratigraphy and Paleoenvironmental Evolution of the Northern Yellow River Delta. Mar. Geol. Quat. Geol. 2014, 34, 25–32. (In Chinese) [Google Scholar]
- Wang, K.; Li, N.; Wang, W. Characteristics of Coastline Change and Multiyear Evolution of the Yellow River Delta. J. Appl. Oceanogr. 2018, 37, 330–338. (In Chinese) [Google Scholar]
- Chatelain, J.L.; Guillier, B.; Cara, F.; Duval, A.M.; Atakan, K.; Bard, P.Y.; The WP02 SESAME Team. Evaluation of the influence of experimental conditions on H/V results from ambient noise recordings. Bull. Earthq. Eng. 2008, 6, 33–74. [Google Scholar] [CrossRef]
- Guillier, B.; Atakan, K.; Chatelain, J.L.; Havskov, J.; Ohrnberger, M.; Cara, F.; Duval, A.M.; Zacharopoulos, S.; Teves-Costa, P.; The SESAME Team. Influence of Instruments on the H/V Spectral Ratios of Ambient Vibrations. Bull. Earthq. Eng. 2008, 6, 3–31. [Google Scholar] [CrossRef]
- Bignardi, S.; Yezzi, A.J.; Fiussello, S.; Comelli, A. OpenHVSR—Processing Toolkit: Enhanced HVSR Processing of Distributed Microtremor Measurements and Spatial Variation of Their Informative Content. Comput. Geosci. 2018, 120, 10–20. [Google Scholar] [CrossRef]
- Konno, K.; Ohmachi, T. Ground-Motion Characteristics Estimated from Spectral Ratio between Horizontal and Vertical Components of Microtremor. Bull. Seismol. Soc. Am. 1998, 88, 228–241. [Google Scholar] [CrossRef]
- Field, E.; Jacob, K. The Theoretical Response of Sedimentary Layers to Ambient Seismic Noise. Geophys. Res. Lett. 1993, 20, 2925–2928. [Google Scholar] [CrossRef]
- Bard, P.Y.; Acerra, C.; Aguacil, G.; Anastasiadis, A.; Atakan, K.; Azzara, R.; Basili, R.; Bertrand, E.; Bettig, B.; Blarel, F.; et al. Guidelines for the Implementation of the H/V Spectral Ratio Technique on Ambient Vibrations Measurements, Processing and Interpretation. Bull. Earthq. Eng. 2008, 6, 1–2. [Google Scholar] [CrossRef]
- Parolai, S.; Bormann, P.; Milkereit, C. New Relationships between Vs, Thickness of Sediments, and Resonance Frequency Calculated by the H/V Ratio of Seismic Noise for the Cologne Area (Germany). Bull. Seismol. Soc. Am. 2002, 92, 2521–2527. [Google Scholar] [CrossRef]
- Gosar, A.; Rošer, J.; Šket Motnikar, B.; Zupančič, P. Microtremor Study of Site Effects and Soil-Structure Resonance in the City of Ljubljana (Central Slovenia). Bull. Earthq. Eng. 2010, 8, 571–592. [Google Scholar] [CrossRef]
- Guéguen, P.; Chatelain, J.L.; Guillier, B.; Yepes, H.; Egred, J. Site Effect and Damage Distribution in Pujili (Ecuador) after the 28 March 1996 Earthquake. Soil Dyn. Earthq. Eng. 1998, 17, 329–334. [Google Scholar] [CrossRef]
- D’Amico, V.; Picozzi, M.; Baliva, F.; Albarello, D. Ambient Noise Measurements for Preliminary Site-Effects Characterization in the Urban Area of Florence, Italy. Bull. Seismol. Soc. Am. 2008, 98, 1373–1388. [Google Scholar] [CrossRef]
- Matsushima, S.; Hirokawa, T.; De Martin, F.; Kawase, H.; Sánchez-Sesma, F.J. The Effect of Lateral Heterogeneity on Horizontal-to-Vertical Spectral Ratio of Microtremors Inferred from Observation and Synthetics. Bull. Seismol. Soc. Am. 2014, 104, 381–393. [Google Scholar] [CrossRef]
- Khan, M.Y.; Turab, S.A.; Riaz, M.S.; Atekwana, E.A.; Muhammad, S.; Butt, N.A.; Abbas, S.M.; Zafar, W.A.; Ohenhen, L.O. Investigation of Coseismic Liquefaction-Induced Ground Deformation Associated with the 2019 Mw 5.8 Mirpur, Pakistan, Earthquake Using near-Surface Electrical Resistivity Tomography and Geological Data. Near Surf. Geophys. 2021, 19, 169–182. [Google Scholar] [CrossRef]
- Beroya, M.A.A.; Aydin, A.; Tiglao, R.; Lasala, M. Use of Microtremor in Liquefaction Hazard Mapping. Eng. Geol. 2009, 107, 140–153. [Google Scholar] [CrossRef]
- Akkaya, İ. Availability of Seismic Vulnerability Index (Kg) in the Assessment of Building Damage in Van, Eastern Turkey. Earthq. Eng. Eng. Vib. 2020, 19, 189–204. [Google Scholar] [CrossRef]



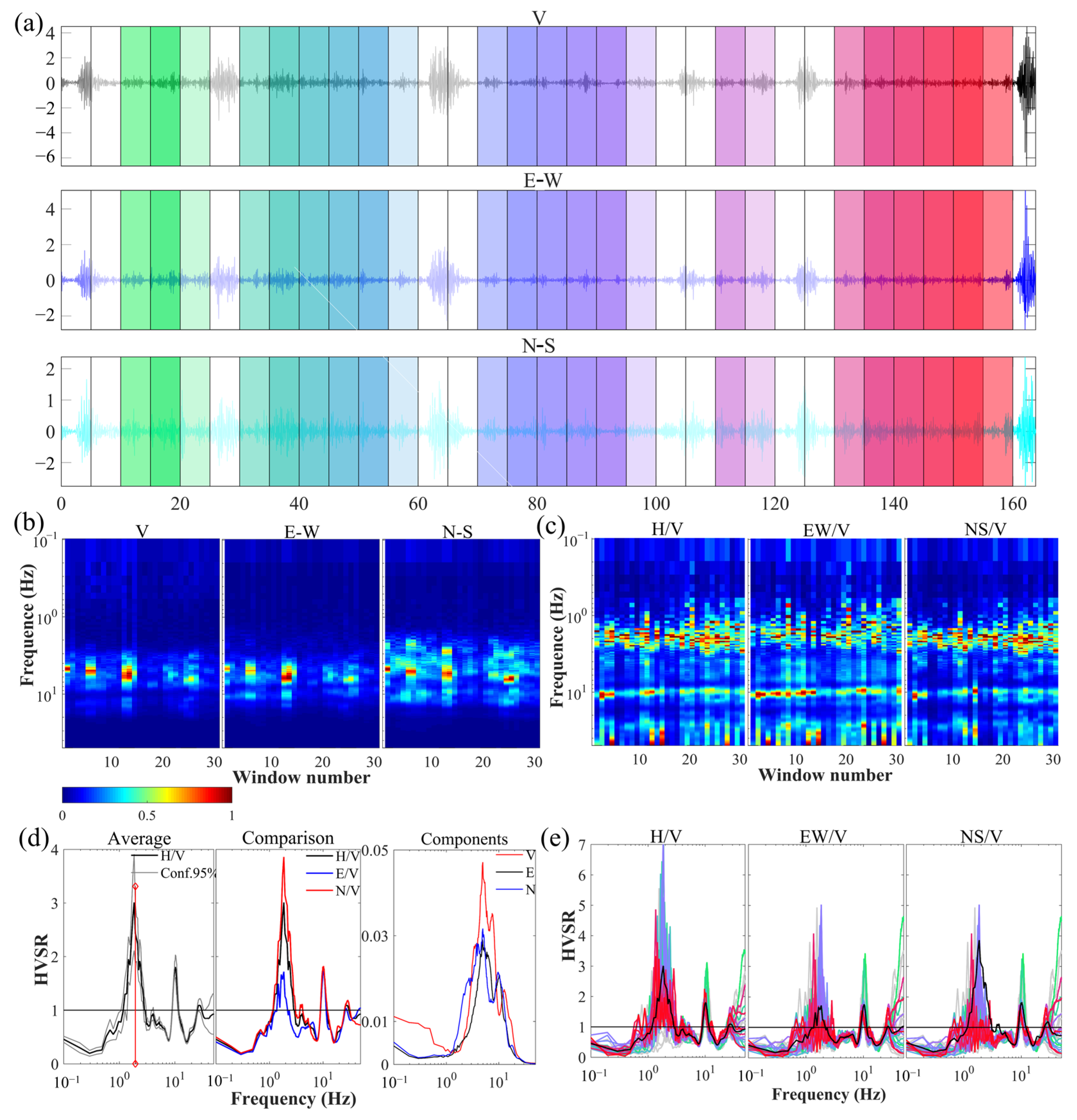
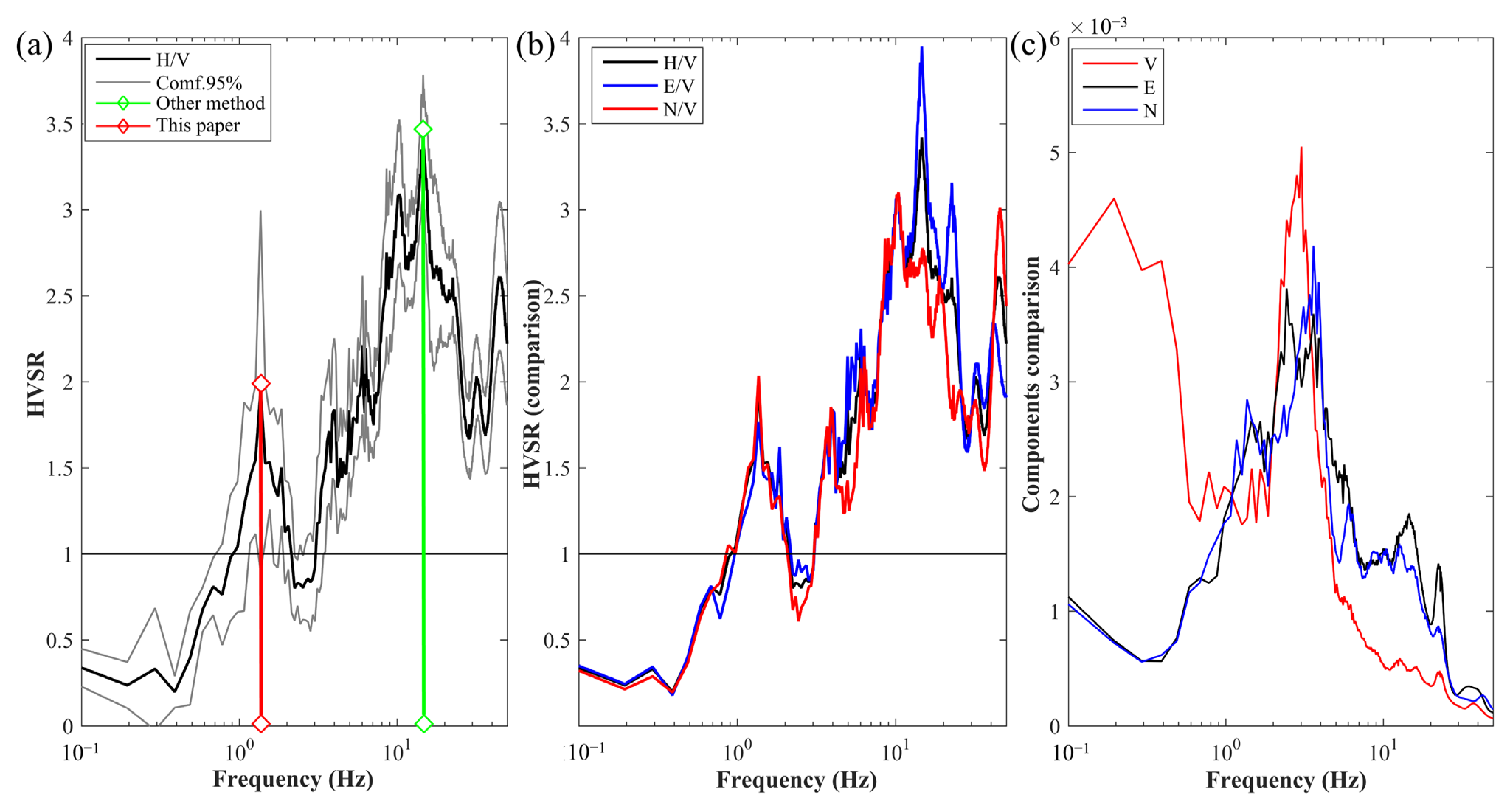

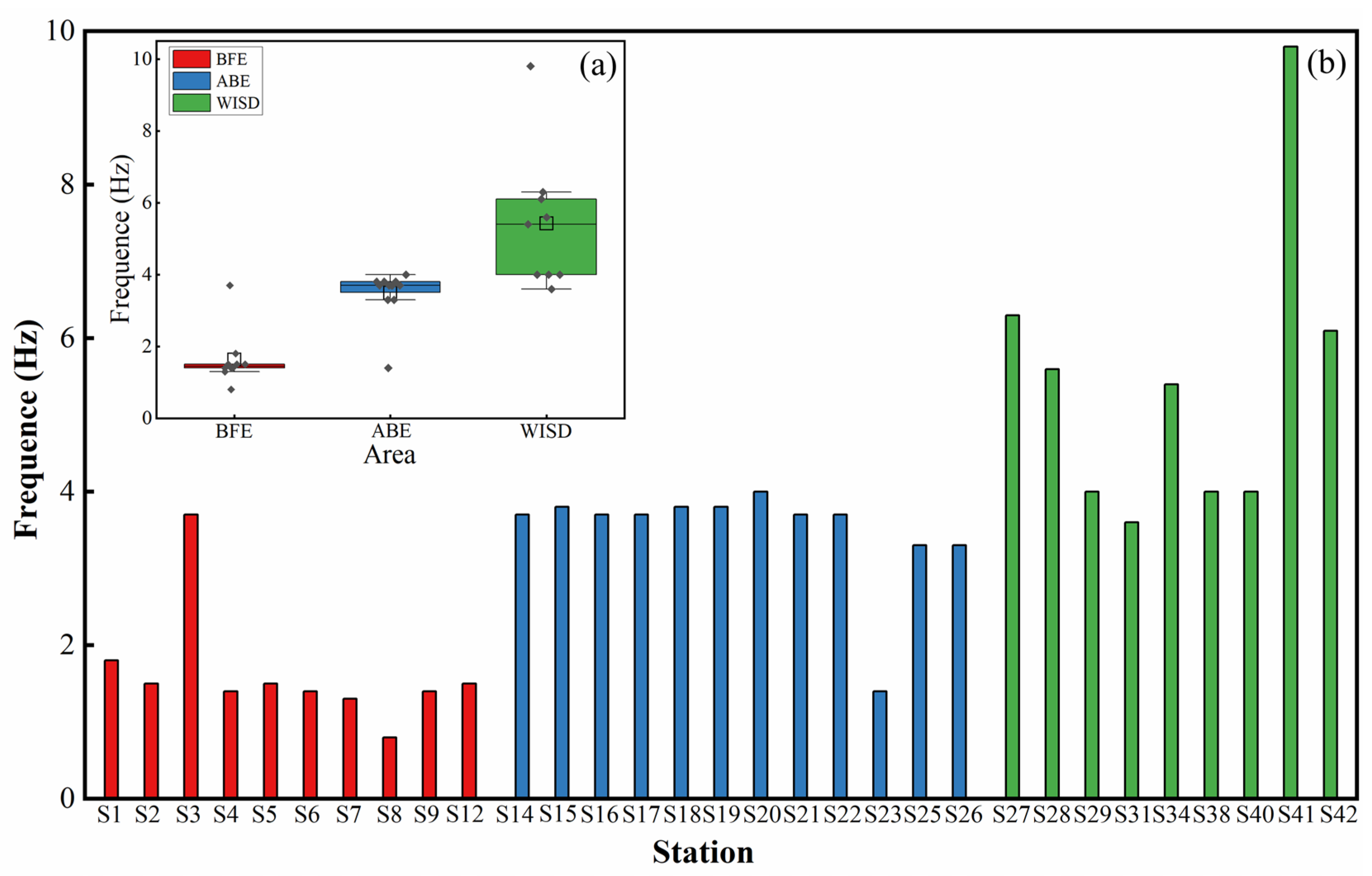
| ID | Longitude | Latitude | Altitude | f0 (Hz) | A | Kg | Number of Stationary Window |
|---|---|---|---|---|---|---|---|
| S1 | 4,226,376 | 920,357 | 0.2 | 1.8 | 3.0 | 5.0 | 23 |
| S2 | 4,226,434 | 920,654 | −0.1 | 1.5 | 1.8 | 2.2 | 19 |
| S3 | 4,226,474 | 920,970 | 0.0 | 3.7 | 2.1 | 1.2 | 20 |
| S4 | 4,216,312 | 394,829 | 0.0 | 1.4 | 2.5 | 4.5 | 21 |
| S5 | 4,226,555 | 921,692 | 0.0 | 1.5 | 2.1 | 2.9 | 22 |
| S6 | 4,226,608 | 922,055 | 0.3 | 1.4 | 2.1 | 3.2 | 25 |
| S7 | 4,216,401 | 395,467 | 0.0 | 1.3 | 2.0 | 3.1 | 32 |
| S8 | 4,227,136 | 922,019 | 0.6 | 0.8 | 3.5 | 15.3 | 28 |
| S9 | 4,227,697 | 921,944 | 0.3 | 1.4 | 1.9 | 2.6 | 23 |
| S10 | 4,229,229 | 921,736 | 0.0 | N/A | N/A | N/A | 19 |
| S11 | 4,231,335 | 921,477 | 0.3 | N/A | N/A | N/A | 8 |
| S12 | 4,232,986 | 921,262 | 0.4 | 1.5 | 1.8 | 2.2 | 22 |
| S13 | 4,226,335 | 920,364 | 1.2 | N/A | N/A | N/A | 20 |
| S14 | 4,226,417 | 920,992 | 1.1 | 3.7 | 2.0 | 1.1 | 28 |
| S15 | 4,226,485 | 921,521 | 1.3 | 3.8 | 2.8 | 2.1 | 26 |
| S16 | 4,226,524 | 921,809 | 1.1 | 3.7 | 3.2 | 2.8 | 26 |
| S17 | 4,226,518 | 922,066 | 1.0 | 3.7 | 2.5 | 1.7 | 24 |
| S18 | 4,216,175 | 394,172 | 1.3 | 3.8 | 2.5 | 1.6 | 22 |
| S19 | 4,216,212 | 394,689 | 1.2 | 3.8 | 2.3 | 1.4 | 28 |
| S20 | 4,216,244 | 395,354 | 1.1 | 4.0 | 2.5 | 1.6 | 22 |
| S21 | 4,216,373 | 395,557 | 1.2 | 3.7 | 3.0 | 2.4 | 23 |
| S22 | 4,226,579 | 922,147 | 0.8 | 3.7 | 3.0 | 2.4 | 29 |
| S23 | 4,227,677 | 922,001 | 0.9 | 1.4 | 3.0 | 6.4 | 23 |
| S24 | 4,232,495 | 921,369 | 0.9 | N/A | N/A | N/A | 10 |
| S25 | 4,234,639 | 921,337 | 0.6 | 3.3 | 1.9 | 1.1 | 27 |
| S26 | 4,234,362 | 922,710 | 1.5 | 3.3 | 1.9 | 1.1 | 20 |
| S27 | 4,231,288 | 921,546 | 1.6 | 6.3 | 2.5 | 1.0 | 20 |
| S28 | 4,234,481 | 924,999 | 1.9 | 5.6 | 3.0 | 1.6 | 26 |
| S29 | 4,233,906 | 922,691 | 1.9 | 4.0 | 2.2 | 1.2 | 28 |
| S30 | 4,233,200 | 924,451 | 0.0 | N/A | N/A | N/A | 24 |
| S31 | 4,233,063 | 923,358 | 0.9 | 3.6 | 2.1 | 1.2 | 27 |
| S32 | 4,232,411 | 922,703 | 1.8 | N/A | N/A | N/A | 27 |
| S33 | 4,231,969 | 924,106 | 1.7 | N/A | N/A | N/A | 31 |
| S34 | 4,230,155 | 925,059 | 0.8 | 5.4 | 3.2 | 1.9 | 23 |
| S35 | 4,228,883 | 925,090 | 1.0 | N/A | N/A | N/A | 7 |
| S36 | 4,228,696 | 923,460 | 1.6 | N/A | N/A | N/A | 9 |
| S37 | 4,228,105 | 924,045 | 2.1 | N/A | N/A | N/A | 11 |
| S38 | 4,227,490 | 923,386 | 1.9 | 4.0 | 3.3 | 2.7 | 28 |
| S39 | 4,227,375 | 924,408 | 1.6 | N/A | N/A | N/A | 29 |
| S40 | 4,228,228 | 922,430 | 1.0 | 4.0 | 2.5 | 1.6 | 30 |
| S41 | 4,233,658 | 923,826 | 0.3 | 9.8 | 2.4 | 0.6 | 26 |
| S42 | 4,219,971 | 396,474 | 1.3 | 6.1 | 3.5 | 2.0 | 29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, Q.; Li, Y.; Wang, W.; Chen, Y.; Wang, S. A Case Study Assessing the Liquefaction Hazards of Silt Sediments Based on the Horizontal-to-Vertical Spectral Ratio Method. J. Mar. Sci. Eng. 2023, 11, 104. https://doi.org/10.3390/jmse11010104
Meng Q, Li Y, Wang W, Chen Y, Wang S. A Case Study Assessing the Liquefaction Hazards of Silt Sediments Based on the Horizontal-to-Vertical Spectral Ratio Method. Journal of Marine Science and Engineering. 2023; 11(1):104. https://doi.org/10.3390/jmse11010104
Chicago/Turabian StyleMeng, Qingsheng, Yang Li, Wenjing Wang, Yuhong Chen, and Shilin Wang. 2023. "A Case Study Assessing the Liquefaction Hazards of Silt Sediments Based on the Horizontal-to-Vertical Spectral Ratio Method" Journal of Marine Science and Engineering 11, no. 1: 104. https://doi.org/10.3390/jmse11010104
APA StyleMeng, Q., Li, Y., Wang, W., Chen, Y., & Wang, S. (2023). A Case Study Assessing the Liquefaction Hazards of Silt Sediments Based on the Horizontal-to-Vertical Spectral Ratio Method. Journal of Marine Science and Engineering, 11(1), 104. https://doi.org/10.3390/jmse11010104





