Abstract
Laboratory experiments were performed in the wave flume of the Laboratorio di Idraulica e Costruzioni Marittime of the Università Politecnica delle Marche (Ancona, Italy) to study the hydrodynamic performance of coastal protection structures made of a new type of geotextile sand containers (GSCs). Such structures are used as softer and flexible alternatives to traditional hard coastal defenses made of concrete or rubble mound material. The GSC structures can also be used as temporary coastal protections during the winter period. The physical model reproduced two main configurations: in the former one, the GSCs were used as coastal revetments with three different slopes. In the latter one, the GSCs were applied to make detached submerged breakwaters with different submergences and berm widths. The geometric scale of the models was 1:10, and the weight of each GSC in the prototype was 5 t. The geotextile material of the containers and the wave characteristics were reproduced by using the Reynolds and the Froude similarity criteria, respectively. Reflection coefficients and hydraulic stability behaviors for the revetments, as well as transmission coefficients and piling-up amount for breakwaters, were obtained.
1. Introduction
Softer and flexible structures made of geotextile sand containers (GSCs) can be used instead of hard structures made of rubble-mound or concrete elements as coastal defense structures. However, the use of geotextile sand containers as shoreline protection systems has grown moderately due to the lack of understanding of coastal processes and, hence, due to the problems of stability and durability of the structures under the wave action [1]. A major attention on the container design and on the geotextile durability leads GSCs to be an important alternative in the protection of coastal areas. GSCs have a low environmental impact because they are filled with material available in situ, thus minimizing costs and pollution associated with rock transport from the borrow pit.
A new generation of containers is composed by a specific non-woven geotextile made of synthetic polypropylene fibers. Such a material is very different with respect to that used in the past, both in terms of resistance and of surface roughness: the previous short duration of the GSC-structures was due to the damage of the containers themselves. In the last few years, thanks to the introduction of innovative materials and to new technologies, past difficulties have been overcome. Moreover, the geotextile has a roughness useful to the development of habitats for marine animal and plants species, and it resists mechanical damages or vandalisms. The construction of these structures requires very short times and therefore does not require the use of wide coastal areas during the work. Each single container can reach a weight of about 5 t, corresponding to a natural stone of high weight category.
The aim of the study is to evaluate the efficiency of the new generation of GSC structures for coastal protection. In order to characterize the hydrodynamic behavior of adherent revetment structures and submerged breakwaters made of GSCs, two laboratory campaigns were performed for the evaluation of the reflection coefficient (depending on the slope of the structure and on the steepness of the incident waves), the transmission coefficient (as a function of the submergence of the structure) and the water level elevation behind the structures. All tests were also aimed at evaluating the stability of the containers under different wave attack conditions. The analyses of stability of GSCs were concentrated on the revetment configuration.
The paper is organized as follows. In Section 2, the theory of the main phenomena involved in the present study, as the wave reflection and transmission, the piling-up and the structural stability are described. In Section 3, an overview of the features and the application of GSCs is reported. In Section 4, the experimental setup and the two model configurations are described. In Section 5, the results are shown in comparison with the theory findings and a discussion is reported. Finally, in Section 6, the main achievements of the work are discussed.
2. Theory
2.1. Wave Reflection of Emerged Structures
Physical model studies have been performed at various laboratories around the world, including measurements of wave reflection of a lot of coastal structures with a wide range of monochromatic and spectral wave conditions.
Seelig [2] investigated the rubble-mound breakwaters behavior under monochromatic and irregular waves. Additional breakwater reflection data are available in [3,4]. Allsop and Channell [5] tested in the “non-breaking” and “transitional” regions and two values of structural permeability were used. Postma [6] included numerous tests in the “breaking” region for a variety of structural permeabilities, as developed by [7,8], employing wave spectra in smooth and rough permeable plane slopes. Zanuttigh and Van der Meer [9] analyzed wave reflection for various types of structures; a database was prepared based on existing databases for wave transmission and overtopping.
When a wave encounters a coastal structure or a beach, a part of the wave energy is dissipated. The remaining energy is reflected seaward, except in the cases of permeable or overtopped structures. In the former case, a fraction of the wave energy is dissipated during the flow through the permeable structure; in the latter case, the overtopping allows transmission of a part of the energy to the leeward side. Wave reflection may have undesirable effects, because the reflected waves are superimposed on the incident waves to increase the magnitude of water particle velocities and water level fluctuations seaward of the structure. In the case of shoreline adherent structures, reflected waves propagate toward the surrounding coasts, altering the shoreline equilibrium conditions.
Due to the adverse effects of wave reflection, coastal engineers need design criteria that enable to build coastal structures with acceptable reflection performances.
One should be aware that two different definitions, or ways of calculations, for the reflection coefficient are possible:
- -
- for a regular (monochromatic) wave, the definition is , where is the reflection coefficient, is the reflected wave height and is the incident wave height;
- -
- for random (irregular) waves, in wave flume tests, this definition could not be applied, and the reflection coefficient is calculated as , where is the reflected wave energy, and is the incident wave energy.
The partition of wave energy is given by
where is the reflection coefficient, is the ratio between the wave energy lost through dissipation and the total incident wave energy and is the transmission coefficient, including the transmission through a permeable structure and by overtopping for a low-crested structure.
For smooth impermeable slopes, Battjes [10] recommends the equation:
where is the surf similarity parameter (also known as Iribarren index), α is the seaside slope of the structure and L0 is the wavelength evaluated in deep water.
A revised version of [10]’s formula led to:
Seelig and Ahrens [4] presented a formula of the form:
which has been fitted, among other cases, for smooth impermeable slopes () and rough permeable rock slopes ().
Zanuttigh and Van der Meer [9] refitted the coefficients and for armour units, rock permeable and impermeable slopes. They obtained different values of a and b: for rock permeable and armor units, ; for rock impermeable slopes, and for smooth structures, .
Zanuttigh and Van der Meer [9] found that such a formula was still inadequate for a proper fitting of all data; thus, they presented a new formula of the type:
where the calibrated values of the coefficients and are: for rock permeable, ; for armor units, ; for rock impermeable, and for smooth structures, .
The surf similarity parameter is not able to describe the combined slope and the wave steepness influence in a sufficient way. Postma [6] presented a formula for the estimation of the reflection coefficient for a prototype rock-sloped structure by taking into account both the parameters but separately, as reported in the following expression:
where is the wave steepness, and is the core permeability described by [11].
2.2. Wave Transmission and Induced Piling-Up for Submerged Barriers
The hydro-morphodynamics that evolve around traditional rubble-mound breakwaters are quite complex and interact with the swash zone dynamics [12]. In particular, erosion of the submerged beach can be induced by wave-forced circulation, while the morphodynamics of the emerged part of the beach mainly depend on the swash motions and, for beaches with coarser sediments, also on their permeability (e.g., see [13,14]). The high-energy generated swash motions force rapid morphological changes associated with the generation of an emerged berm.
During sea storms, low-crested breakwaters induce superelevations of the mean water level within the protected zone, i.e., water “piling-up” (or wave set-up). For emerged structures, the piling-up is due to the shoreward flowing water overpassing or filtering through the structure. Such a process forces the water to filter seaward through the structure and, mostly, to flow out to sea through the narrow gaps between two contiguous barriers, promoting intense rip currents. In the case of submerged breakwaters, the mechanism is almost the same, with a further seaward flow over the breakwater [15].
Several studies ([16] among the others) have tried to describe the entire flow pattern for both submerged and emerged low-crested structures. Further, many experimental tests have been carried out in wave flumes to estimate the water piling-up (see, for example, [17]), while an analytical evaluation can be achieved by means of the momentum equation for the hydrodynamic equilibrium around the submerged breakwater [18]. The water piling-up consists of two contributions, obtained by enforcing mass and momentum balance, depending on: position of the breaking point, breaking depth, breakwater freeboard, incident significant wave height, transmission coefficient, breakwater geometry, flow rate and friction factor.
Calabrese et al. [19] proposed a method (CVB) to calculate the setup on the lee side of a submerged barrier combining the approaches of [20] and of [21]. The model is obtained applying the momentum equation, projected in the horizontal direction, to the volume of fluid surrounding the structure. Based on random wave forcing, their experimental results have shown that the calculated setup is smaller than the observed one. To correct this behavior, Calabrese et al. [19,22] proposed, following the interpretation of [20], to add some extra “overtopping water mass to flow offshore restoring the continuity”. However, computation of such an extra water mass has been made by associating it with an extra shear stress exerted on the berm of submerged breakwaters by offshore flowing currents and explicitly calculated by means of a “Gauckler–Strickler” formula, finding a good agreement between the experimental and the analytical results. The above-mentioned system of estimation was applied and verified by Soldini et al. [23].
Ruol et al. [17] carried out a series of experimental tests on low-crested breakwater to evaluate, among other aspects, the influence of fluxes overflowing and filtrating through the barrier on the measured setup. The emerging (low-crested) rubble mound breakwater placed in the wave flume induces a 2D flow (in the vertical plane). Quasi-3D flow conditions were simulated, similarly to what was done by [21], by pumping away the water piled up inshore of the structure. A comparison of the measured data with the formulae of [21,24] showed that, while the former model overestimates the setup of about 30%, the latter gives a major underestimation of the measured data. The overestimation of [24]’s relationship has been attributed to Diskin’s use of regular waves only, while no explanation has been proposed by [17] for the measured data underpredictions given by [21]’s formula.
Many studies were dedicated to characterizing the efficiency of emerged/submerged breakwaters (e.g., [16,25]). Some of them focus on hydrodynamics, sediment transport and water quality (e.g., see [26]). Some mainly deal with wave characteristics, i.e., transmission and reflection (e.g., [7,8,9,27,28]), i.e., water levels and piling-up (e.g., [19,22,29]), run-up, set-up, overtopping (e.g., [30]) and their effect on the shoreline (e.g., [31,32]).
2.3. The GSC Structural Stability
The stability of structures built with geotextile bags filled with sand has been the subject of some studies, especially by the Technical University of Braunschweig in Germany. Through extensive experimental tests, carried out by [33], formulae have been derived for the evaluation of the parameters that influence the structure stability from a static point of view [34,35] and of the importance of the engineering properties of GSCs on their hydraulic stability and damaging [36,37].
In general, gravity structures subject to wave actions are designed so that the stabilizing actions generated by the weight force counteract the destabilizing ones due to the drag, lift and inertia forces, which are proportional to the velocity (drag and lift) and acceleration (inertia) of the water flow generated around the structure.
The aforementioned studies have shown that, for the maritime structures made of geotextile bags, the single container subjected to the most critical stresses, in terms of stability, is the one located immediately below the level of the free water surface or at the top of the structure, which, unlike the others, cannot count on the stabilizing support due to the gravity of the above elements. The two main types of displacement of GSCs induced by waves are sliding and overturning. Failure is defined as any large displacement of container that compromises the overall stability of GSC structure. The available stability formulae are generally simple, such as Hudson’s formula [38] for nondeformable armor units, and they do not take into account the effect of deformation of GSCs [34]. Explicit stability formulae are derived for the two modes of failure: the [34]’s formula, considering the deformability of the elements, provides the critical bag length lc and weight W required to avoid sliding and overturning. In order to design stable bags, the shape changeability of elements during wave attack must also be considered. In [34]’s formulae, deformation coefficients are introduced to consider the changes of the areas affected by the strengths. These coefficients depend on the magnitude of the deformation, the degree of filling of the bag, the inclination of the exposed face of the structure, the wave conditions, the stiffness of the geotextile and the properties of the filling material. In particular, it is assumed that the bag is 80% filled, the deformation angle is 45° and the effective length not affected by deformation is 0.8lc. The equilibrium relationships are obtained by considering the dimensional ratios of the geotextile bags as follows: the length of the container equal to lc, the height of the container equal to lc/5 and the width of the container equal to lc/2. The weight of the container is , where g is the gravitational acceleration and ρs the density of the sand.
By considering the deformations of the container on the mobilizing and resisting forces, the stability equations change. Recio and Oumeraci [34] reported that, due to the uplift deformations, the exposed surface area and, thus, the drag force are increased up to 40%, while the resisting force is reduced up to −30%.
The stability against the sliding, including the effect of the deformations, yields to:
where u is the velocity calculated at the depth of Hi/6 from the free surface; μ is the coefficient of friction between the non-woven geotextile material bags (estimated as 0.48) and is the density of the sand relative to the water, with ρ and ρs the densities of water and sand, respectively; CD, CL and CM are the drag, lift and inertia coefficients respectively; KSCD, KSCL and KSCM are the relative deformation factors and KSR the resistance deformation factor (see [34]).
The analysis of the overturning stability, including the effect of the deformations, leads to:
where KOCD, KOCL, KOR and KOCM are the deformation factors (see [34]).
Therefore, the required weight of the container should satisfy the following condition:
where lc is given by Equations (7) and (8).
The effect of deformation affects the required length of the container by a factor up to two times and, hence, the required container weight by a factor up to eight times.
The above-reported stability formulae require the knowledge of the force coefficients CD, CL and CM. The drag and lift coefficients mainly depend on the Reynolds number. The laboratory conditions should agree with the range of applicability in which the force and deformations coefficients are obtained.
The stability formulae, deformation factors and force coefficients reported in Ref. [34] are obtained for (i) a non-woven geotextile, (ii) a sand fill ratio of GSC of 80%, (iii) specific geometry—the container length is twice as large as its width and five times as large as its height, (iv) GSC structure with a slope 1:1, (v) shallow water conditions h/L < 0.10 and (vi) Reynolds number Re = 104–106. The present experimental study satisfied almost all such conditions.
The deformation factors depend on the slope angle; hence, Recio and Oumeraci (2009a) derived their corrections for the other GSC structure slope angle, while no information is available regarding the relation between the sand fill ratio and the deformations factor. However, it can be assumed that lower fill ratio needs larger deformation factors to account for the larger deformations. Dassanayake and Oumeraci [37] reported that the stability increases with the sand fill ratio; however, an overfilled sand container (e.g., 120%) can produce excessive elongations that should be avoided. They found that the sand fill ratio between 90% and 100% is the optimal one.
A GSC with a very low sand fill ratio will be much more unstable with respect to a GSC with an optimal filling ratio (balance between flexibility and small movement of sand). It is also important to notice that, since fines are smaller than the geotextile opening, most of the fines within the container will “escape” from the container during wave action, reducing the fill ratio of the container and thus reducing the overall stability of the GSC-structure [35].
3. GSC Features and Application
A new generation of sand containers (as those produced by Tessilbrenta srl and named “Stopwave”) is made by a specific non-woven fabric, needle-punched woven, made of synthetic polypropylene fibers that give a very high toughness, strength, durability and chemical stability to the material. They are characterized by a very large resistance to punching, abrasion and weathering, such as UV rays, and they are suitable to adequately contain the fine sediment.
The dimensions of each single container can reach a length of 2.5 m and a weight of about 5 t, corresponding to a natural stone of high weight category (3–7 t). Such dimensions are strongly larger than those used in geobags. Moreover, with respect to old applications, when nylon containers were used, Stopwave withstands much better acts of vandalism or accidents.
A lot of coastal structures, such as revetments, artificial littoral dunes, little jetties, detached submerged or emerged barriers and submerged retaining sills at the nourishment toe, called a perched or hanging or suspended beach, can be made by using these new generation of sand--filled containers (Figure 1). They could be used also for other hydraulic structures, such as river or lagoon bank defenses, protection of underwater pipelines, protection of offshore cylinder, etc.

Figure 1.
Application of “Stopwave” as coastal revetments: Grottammare, Italy (left panel) and Senigallia, Italy (right panel).
Such geotextile containers can substitute the natural rock elements, still very often used in Italy and all over the world, reducing the environmental impact due to the lack of borrow pits from which find natural rocks and the pollution problems due to their transport from the pit to the coastal site. Moreover, the non-woven fabric of the GSC has a roughness suitable for the development of habitats for marine animal and plant species. Indeed, Jackson et al. [39] found that these materials provide a good substratum for a wide range of benthic species. Polypropylene represented a good substratum that was also superior to other plastics [40]. However, the non-woven fabric could affect organism settlement and the biodiversity of the resident community in coastal ecosystems by disturbing biofouling settlement and growth (High-Density Polyethylene fabrics) or favoring species that become dominant (Polypropylene fabrics). Therefore, the impact on ecosystem biodiversity requires attention [41].
The use of such sand containers for coastal defense structures could be important in beach areas when rock finding is difficult and/or too expensive. Moreover, they can be simply used also to make temporary structures to protect beach facilities or to create artificial dunes or revetments during the winter (Figure 1 and left panel of Figure 2), with very simple, fast and not expensive assembly and removal activities, which does not compromise the enjoyment of beach activities. Moreover, it can be used as scour protection around the subsea pipelines (right panel of Figure 2) and offshore piles (e.g., [42]).

Figure 2.
Application of “Stopwave” as temporary groin in Senigallia, Italy (left panel) or as pipeline protection (right panel).
To better design coastal revetments and detached structures composed by this new type of geotextile sand containers, it is necessary to characterize the hydrodynamic performance of each kind of structure.
4. Experimental Setup
In the wave channel of the Laboratorio di Idraulica e Costruzioni Marittime of the Dipartimento di Ingegneria Civile, Edile e Architteura of the Università Politecnica delle Marche (Ancona, Italy), experimental tests were carried out to study the effectiveness of some coastal structures made of a new generation of geotextile sand containers (GSCs) in order to evaluate their application and efficiency for the protection of the shoreline.
The analyzed bags, specifically produced for coastal protection purposes, correspond to prototype sizes of 2.50 × 1.80 × 0.55 m3, identified by the nominal weight of 5 t (once filled with sand), and the weight (or mass per unit area) of the fabric is 1500 g/m2.
The wave flume is 50 m long, 1 m wide and 1.3 m deep (Figure 3), and it is equipped with a piston-type wavemaker for the generation of regular and random waves.
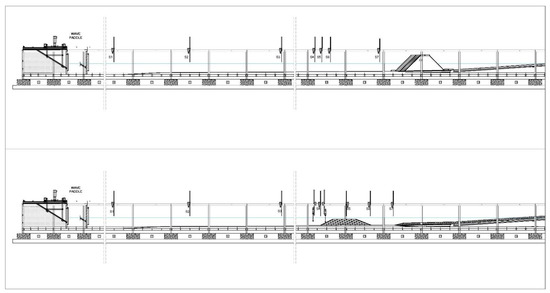
Figure 3.
Sketch of the physical models in the wave flume of Dipartimento di Ingegneria Civile, Edile e Architteura, Università Politecnica delle Marche, Ancona (Italy): adherent revetment (upper panel) and submerged breakwater (lower panel).
The wave characteristics were chosen by applying the Froude similarity criterion. Two different types of geotextile sand containers (GSCs) structures were studied: (i) adherent revetment structure (Figure 3—upper panel); (ii) submerged breakwater (Figure 3—lower panel).
Both structures have been reproduced using a reduced geometrical scale of 1:10.
The wave motion was measured by means of eight wave gauges. Two three-dimensional Acoustic Doppler Velocimeters (ADV) were employed to define the velocity fields over the adherent revetment GSC structures.
Exsiccated sand was used as filling material of the container, having a median grain size of D50 = 0.6 mm, with no fine materials below 0.3 mm, and a density of ρs = 1800 kg/m3. All the physical model here presented used 4.1 kg of sand to fill approximately 80% of the volume of each container in order to ensure that the geometric dimensions of model containers (25 × 20 × 5.5 cm3) suitable to adequately reproduce the dimensions of the prototype bag and were able to resist to two possible modes of failure (sliding and overturning) during most of the wave attacks. As reported in [37], small-scale models present some limitations on the simulation of all the engineering properties of GSC material. The material of the geotextile container was reproduced at a reduced scale, considering the ability of the model to simulate the water permeability of the prototype by using the Reynolds similitude criterion. Particular care was taken in the choice of the bag fabric for the physical model on a reduced scale, respecting the filtering capacities. In Table 1, the main properties of GSC used in the model compared to the prototype reported. The main characteristic to be reproduced for the physical modeling of the geocontainer material is the capacity of the bag (of the model) to simulate the water permeability, i.e., the so-called filtering water flow (of the prototype), due to the wave impact. Therefore, among the different hydrodynamic similarity criteria that can be adopted, the Reynolds’ one was chosen, which is governed by the general relationship between velocity, time and geometric length of the prototype and of the model, respectively, and from which the filtration rate of the fabric for the physical model can be derived. With the adopted geometric scale ratio of 1:10, the reduction of the scale for the reproduction of the filtering flow, according to the above-mentioned Reynolds similitude criterion, becomes equal to 10:1. Therefore, since the filtering capacity of the prototype fabric, with a grammage of 1500 g/m2, is approximately 17 l/(m2·s), a geotextile material with a permeability of the order of 170 l/(m2·s) was sought for the reduced scale model. The correct fabric size for this exact feature was, however, too thin and not able to adequately retain the used filling sand. The filling material was not scaled in the model to avoid that the fine parts will be removed from the container during the wave action, due to the retaining problems for thinner geotextiles and, also, to maintain similar chemical characteristics of the filling material in the prototype (no flocculation conditions, etc.). Therefore, the geotextile fabric with a weight of 100 g/m2 and a permeability of 120 l/(m2·s) were adopted, which was the most suitable compromise to satisfy both the required filtering capacity and the retaining of the filling material.

Table 1.
Properties of nonwoven geotextile material in the model and in the prototype.
Some other important properties of GSC are the stiffness, the strength and the elasticity, which influence the container resistance and deformations. The elasticity of the container used in the model, expressed by the elongation, is smaller (45%) with respect to that of the prototype (60%), while the average tensile strength is 6.7 kN/m in the model with respect to 85 kN/m and 130 kN/m of the prototype, respectively, along the longitudinal and the transversal directions, respectively. The reduced force per unit length (tensile strength) should be smaller; hence, the container in the model could be affected by smaller deformations with respect to the prototype.
4.1. Test Configurations for the Adherent Revetment Structure
The revetment structures were studied by analyzing three different GSC configurations characterized by different structure slopes: 1:1, 1:1.5 and 1:2.
Regular waves of various steepness have been reproduced in the channel by using Froude criterion as the hydrodynamic similitude. The waves were generated at constant water depths at wave paddle of 0.58 m and 0.79 m, which correspond to water depths h at the toe of the structures of 0.40 m and 0.61 m.
In Table 2, the characteristics of the regular waves (wave height H and wave period T) were reported.

Table 2.
Regular wave characteristics for adherent revetment structure.
The configurations of the revetment model (Figure 4) consisted in two overlapped sloped layers of horizontally arranged containers stacked on top of each other, in adherence to the inclined face of the support structure. The support structure was made by homogeneous stones. In order to make the structure more stable, an additional line of geobags was placed at the toe of the structure, and other geobags were placed at the dike top to prevent instability due to wave overtopping (see from Figure 4, Figure 5 and Figure 6). The physical models are also shown in Figure 5 and Figure 6.
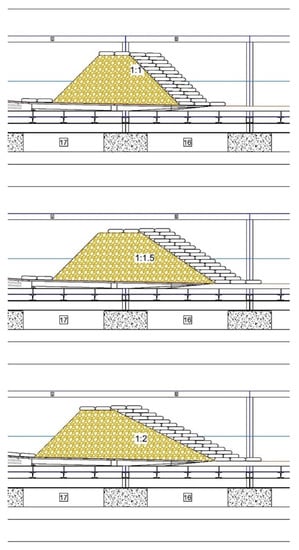
Figure 4.
Coastal adherent revetments of the geotextile sand container. Longitudinal views of GSCs with seaside slopes of 1:1 (upper panel), 1:1.5 (middle panel) and 1:2 (lower panel).

Figure 5.
GSC revetment structure with a slope of 1:1 (lateral and front views).

Figure 6.
GSC revetment structure with a slope of 1:2.
Comparison tests were also carried out (for the analysis of the wave reflection) with the configuration of the adherent structure with a slope equal to 1:1 but consisting of stones, thus representing the behavior of a rubble-mound breakwater with a water depth of 0.40 m at the toe of the structure.
4.2. Test Configurations for Submerged Breakwaters
For the submerged breakwaters, two configurations were tested, which differ in their submergence and in their top berm width (see Figure 7 and Figure 8). One barrier configuration consisted of seven overlapping layers of bags (for a submergence Rc = −0.032 m and a top berm width of 1.25 m), while the second configuration consisted of six overlapping layers of containers (for a submergence Rc = −0.087m and a top berm width of 1.0 m). Both breakwaters had the seaside slope of 1:2 and the landside slope of 1:2.5, and they were tested with a water depth h of 0.42 m, so representing typical beach defense structures placed at a depth of 4.2 m. The vertical z-axis points upward, and the origin is placed at the still water level; hence, the seabed is placed at z = −h. The regular arrangement of the geobags is difficult to obtain in real conditions; however, the general behavior of a GSC breakwater with the same geometrical characteristics can be analyzed.
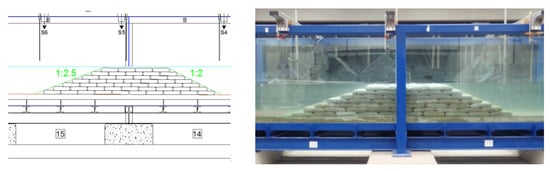
Figure 7.
Sketch and physical model of the submerged barrier with 7 layers of GSCs and a submergence Rc = −0.032 m.
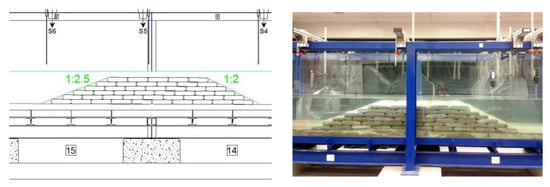
Figure 8.
Sketch and physical model of the submerged barrier with 6 layers of GSCs and a submergence Rc = −0.087 m.
The tested wave conditions include both regular and random waves, as reported in Table 3. Regular waves consist of the different combinations of wave height H = 5, 10, 15 and 20 cm and wave period T = 2.0, 2.5 and 3.0 s. Two random waves were studied by using JONSWAP-type spectra with a peak factor γ = 3.3, significant wave heights Hs = 0.18 m and 0.20 m and peak periods Tp = 3.0 s and 2.7 s, respectively. Both the two configurations with different submergences and berm widths were attacked by all the aforementioned waves.

Table 3.
Regular and random wave characteristics for submerged breakwaters.
5. Experimental Results
5.1. Wave Reflection
The reflection coefficient Kr is expressed as the ratio between the height of the reflected wave Hr and the height of the incident wave Hi (Kr = Hr/Hi). The reflection coefficient value has been evaluated by the Least Squares Method applied to measurements from three probes [43,44]. This is a technique of separation of wave heights (incident and reflected) operating in the frequency domain that considers the simultaneous measurements of the water surface displacement at three suitable positions in which three probes are located. The analysis was performed by also considering higher harmonics.
In general, the parameters influencing the Kr coefficient are the wave period T, the water depth h, the wave steepness Hi/L, the permeability P of the structure and the slope α of the structure.
The analysis of the results shows that the reflection coefficient Kr decreases as the wave steepness increases, finding a greater dependence on the wave period than on the wave height. A more detailed analysis of the results reveals that the use of the slope of 1:2 reduces significantly the value of Kr compared to the slope of 1:1, even though, in the case of a GSC structure with a slope angle of 1:2, some problems of stability emerged. In this case, due to the smaller overlapped areas among neighboring containers, the container results were more exposed with respect to the structure with a slope of 1:1, in which the container structure was more compact, with a larger overlapping area between elements of different layers.
The values of the reflection coefficient Kr of the GSC structure are about 50% higher than those typically obtained for rubble-mound structures with the same slope. A comparative analysis between the performance of the GSC structure with a permeable structure made by homogeneous stones, which reproduce a natural rubble-mound breakwater, was performed. The comparison was made for the case of a structure with seaside slope of 1:1 and a water depth at the toe of the structure h = 0.4 m.
As expected, a traditional permeable structure made of stones induces a larger wave dissipation with respect to the GSC structure, due to its larger permeability. Recio and Oumeraci [45] studied the permeability effects of sand container barriers, providing different permeability values for different compositions and dispositions of sand containers. By using [45]’s results, it can be assumed that our structures have a permeability of about 1.1 × 10−1 m/s. Therefore, the GSC structure can be assumed as a permeable structure due to the flow through the gaps between the overlapped layers of the sand containers; however, it presents a permeability smaller than that of a traditional natural rubble-mound breakwater.
Apart from the breaking process, the geotextile sand container structure dissipates wave energy by means of two different mechanisms: (1) by the drag force dissipation generated in the irregular macro-steps between the different stacked GSCs and (2) by the dissipation generated for the flow through the gaps between the sand container layers. In Figure 9, the experimental data about the wave reflection of the GSC structure and stones structures are reported for the case of a structure slope of 1:1 and a water depth of 0.4 m. Such experimental data were compared to the literature formula by [4] provided for both impermeable and permeable structures. It can be easily observed that the rubble-mound breakwater induces a smaller wave reflection. The experimental data about the stone structures agree very well with [4]’s formula for permeable structures. The data of GSCs are closer to [4]’s formula for impermeable structures; however, most of the test cases are smaller than those of the impermeable structure.
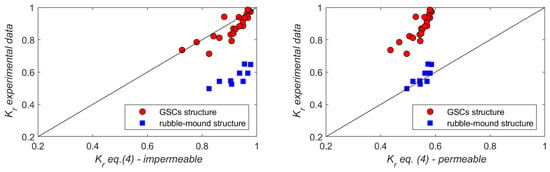
Figure 9.
Comparison of the experimental reflection coefficient of the GSC structure (circle red data) and rubble mound structure (blues square data) with Equation (4), proposed by Seeling and Arhens (1981) for impermeable (left panel) and permeable (right panel) structures.
The general behavior of GSCs is discussed below by analyzing all the data of the experimental campaign for the three different slope configurations and different water depths. Sollit and deBok [3] found that, for both regular and random waves, the reflection increases with the decreasing water depth. On the contrary, we found that such a dependence is quite negligible, and a small decrease of the wave reflection with the water depth was observed. We believe that the influence of the water depth was very moderate on the wave reflection with respect to the other parameters, such as the slope of the structure and the wavelength.
Figure 10 reports the dependence of the reflection coefficient Kr with the surf similarity parameter, as frequently done in the literature. In Figure 10, our experimental data are also compared with different wave reflection formula from the literature. The wave reflection observed in our experiments is quite smaller than those proposed by the literature’s formula for impermeable structures. In particular, it is found that, for smaller structure slope and wavelength (smaller ), the experimental data better agree with the formula of [4] used for permeable structures, while larger reflection coefficient values were found with the increase of . Such a result can be warranted, because wave energy dissipation occurs not only by means of the flow through a permeable structure but also by the drag force generated over the steps between different GSC layers. The surface drag force increases with the square of local velocities, which increase with an increased wave steepness and reduced period (smaller ). Such conditions induce larger drag forces, larger energy dissipation and therefore a reduction of available energy that generates a reflected wave. On the contrary, for larger values of the behavior of the GSC structure becomes more similar to that of impermeable structures. Indeed, we believe that, for larger values of (smaller structure slope and wave steepness or larger wave period), the GSC structure is not still able to behave like a traditional permeable structure: the data moves away from permeable line of [4]’s formula due to the decreasing of the velocities and the flow through the gaps between the overlapped layers being more difficult. Even if the two dissipation mechanisms become less significant, the macro-roughness between the steps of the stacked containers is still able to induce dissipation, which, on the contrary, is absent in an impermeable smooth slope, as well as the flow through the gaps of the layers; therefore, these are the reasons, because most of the reflection coefficient data are smaller than those predicted by the [4]’s formula for impermeable slopes.
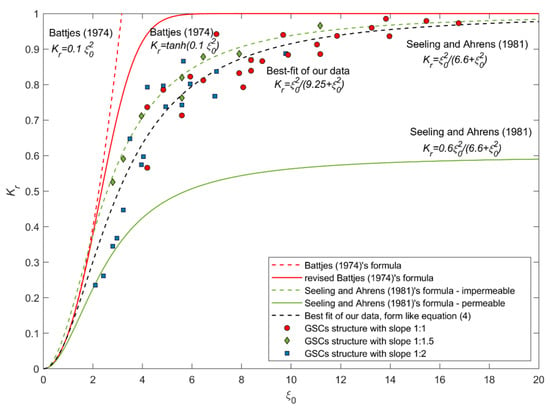
Figure 10.
Comparison of our experimental data and reflection coefficient Kr formula given in the literature [4,10].
The Iribarren Index seems to be a good parameter for the study of the wave reflection induced by a structure and, also, for GSC structures. Therefore, a best-fit formula of our experimental data, with a form like Equation (4), is proposed, leading to:
In the best-fit formula of our experimental data, the values of a and b are, respectively, equal to 1 and 9.25 (note that b is larger than in an impermeable structure, in which it corresponds to 6.6).
5.2. Wave Transmission of Submerged Barriers
The main parameter that defines the dissipative effectiveness of the incident wave energy of a submerged barrier is the transmission coefficient Kt expressed as the ratio between the height of the transmitted wave behind the breakwater and that of the incident wave (Kt = Ht/Hi). Different wave characteristics were tested in the present study to evaluate the performance of the GSC structure.
The behavior of the wave height resulted in the propagation/overflowing/overtopping of regular and random waves above the submerged structures in the two configurations of submerged GSC barriers (Rc = −0.087 m and Rc = −0.032 m) is shown in Figure 11 and Figure 12.
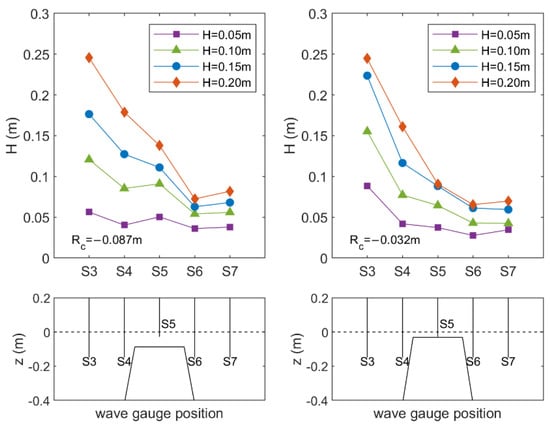
Figure 11.
Wave height evolution before, over and behind a submerged breakwater with Rc = −0.087 m (left panel) and Rc = −0.032 m (right panel) for regular waves with different wave heights H = 0.05 m–0.20 m and a wave period T = 2.0 s.
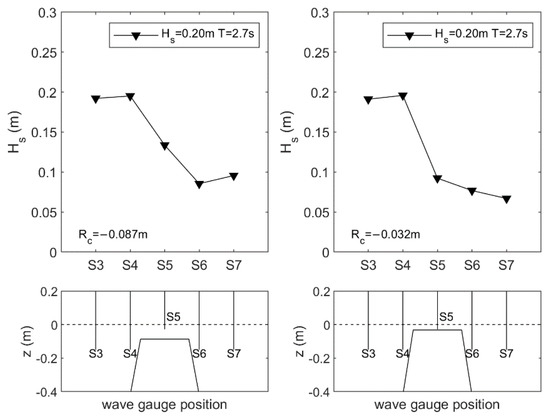
Figure 12.
Wave height evolution before, over and behind a submerged breakwater with Rc = −0.087 m (left panel) and Rc = −0.032 m (right panel) for random waves with a significant wave height Hs = 0.20 m the peak period Tp = 2.7s.
Figure 11 shows an example of the evolution of regular waves with the same wave period (T = 2.0 s) and different wave heights H in the range 0.05 m–0.20 m. By inspecting such a figure, it is clear the effect of the barrier in the reduction of the wave height and, also, the significant role of the submergence on the dissipation (see the right panel of Figure 11).
A higher structure (smaller absolute value of the submergence Rc) induces a larger and faster energy dissipation due to wave breaking. The wave height and period influence the position of the breaking point, moving it from the berm of the structure to the front slope face of the barrier.
A higher structure also enhances the effect of wave reflection. The same waves at the same water depths show larger values of H in correspondence with S3.
In the left panel of Figure 11 an increase of the wave height from S4 to S5 is observed for the smaller waves (H = 0.05 m and H = 0.10 m), because lower waves steepen when traveling over the slope.
The increase in the wave height between S6 and S7 could be due to the generation of super-harmonics when waves propagate over a submerged structure. Such super-harmonics are composed by bound waves moving with the same velocity of the primary component and free waves, which propagate with their own celerity. Their interaction produces a spatial oscillation of the total wave height behind the breakwater [46]. This effect increases with the nonlinearity parameter (ε = a/Rc, where a = H/2). Therefore, for the same submergence of the structure, it increases with the wave height, as shown in the left panel of Figure 11.
In the right panel of Figure 11, even if the submergence decreases, this effect is less evident because the energy dissipation due to wave breaking is larger and the intensity of the nonlinear wave interactions decreases [47].
In Figure 12, an example of the evolution over the submerged barrier of the random wave characterized by a significant wave height Hs = 0.20 m and a peak period Tp = 2.7 s is reported. Additionally, for random waves, the effect of the GSC barrier on the reduction of the incident wave height is significant.
The general performance of the submerged GSC breakwater in terms of transmitted energy is summarized in Figure 13, where all the transmission coefficient values are reported as a function of the ratio between the submergence Rc and the incident wave height H (or Hs), as usually done in the literature. The experimental results show a very good agreement with the trend of [8] obtained for low-crested rubble-mound breakwaters.
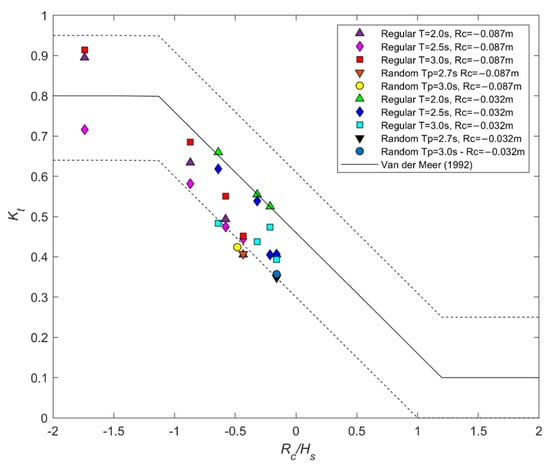
Figure 13.
Wave transmission coefficients vs. nondimensional submergence for both regular and random waves. Trend line [8]. Regular waves with periods: T = 2.0 s (upward triangle), T = 2.5 s (diamond) and T = 3.0 s (square). Random waves with peak periods Tp = 2.7 s (downward triangle) and Tp = 3.0 s (circle). Submergence Rc = −0.087 m (hot colors) and Rc = −0.032 m (cold colors).
For the same ratio of Rc/Hs, the role of the wave period is not clear, the role of the wave height and, mainly, of the submergence being more important. Most of the data are within the trend line of [8] and the lower limit of its confidence band. The results for the random waves are around the lower limit of the confidence band. Globally, GSC structures show lower transmission coefficients than rubble-mound barriers with the same submergence. Such results can be explained by the occurrence of both dissipation mechanisms: the wave breaking on the top berm or at the slope face and the impact of drag forces on the steps of the sloped shape of GSC structures. Moreover, even if the permeability of the submerged container structure is lower than a traditional breakwater, it dissipates also for the internal flow through the gaps between the layers.
Such results are encouraging about the application of GSCs as submerged barriers for coastal protection. The application in a practical case needs to be associated with a structural stability analysis, as reported in Section 5.4.
5.3. Piling-Up for Submerged GSC Breakwater
The variation of the mean water level (with respect to the still water level) induced by the overflowing of regular and random waves above the submerged structures of the tested configurations is analyzed in this section. The presence of submerged barriers raises the mean sea level on the beach side of the structure, inducing the return currents through the gaps between two contiguous barriers, typical of beaches protected by systems of detached submerged breakwater arrays.
The elevation of the mean water level in the protected area, the so-called piling-up, is shown in Figure 14 and Figure 15 for regular and random waves, respectively. As expected, a smaller submergence induces a larger elevation of the mean water level behind the structures. Moreover, a larger mean water level in the protected area is found when the incident wave height increases.
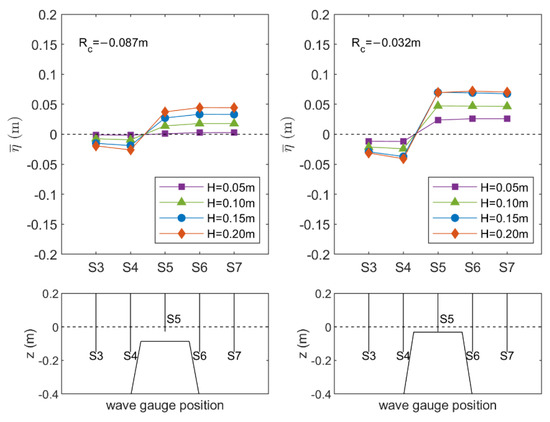
Figure 14.
Piling-up behind the submerged breakwater with Rc = −0.087 m (left panel) and Rc = −0.032 m (right panel) for regular waves with different wave heights H = 0.05 m–0.020 m and a wave period T = 2.0 s.
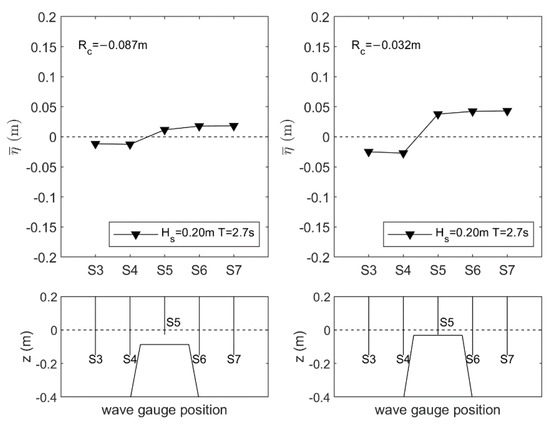
Figure 15.
Piling-up behind the submerged breakwater with Rc = −0.087 m (left panel) and Rc = −0.032 m (right panel) for random waves, with a significant wave height Hs = 0.20 m the peak period Tp = 2.7s.
The experimental data were compared with the piling-up behind submerged barriers formula proposed by [19,22], the so-called CVB method and by [24], which is based on tests over small permeability structures. The experimental data about the piling-up reported in Figure 16 show larger values of piling-up with respect to those computed by both the formula. The discrepancy is smaller when [24] is used, maybe because the GSC structures have a smaller permeability with respect to the classical permeable rubble-mound breakwater. Therefore, the GSC structure behaves more like a quasi-impermeable breakwater in terms of piling-up.
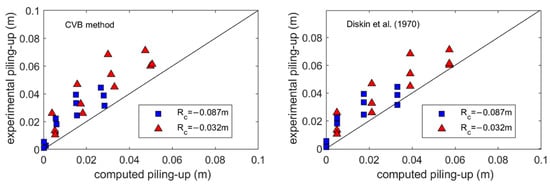
Figure 16.
Comparison of experimental data with the literature formula: CVB method [19,22] in the left panel; [24] in the right panel.
Moreover, we believe that the underestimation of the piling-up obtained by comparing our experimental data with the literature findings is also due to the absence of water recirculation in our laboratory tests and, thus, the experimental results were obtained under more severe conditions, which justify larger values of the measured piling-up.
5.4. Structural Stability Analysis of Geotextile Container Structures
The analysis of the structural stability of geotextile sand containers is reported. The stability of the sand containers, which are located shortly below the still water level and at the crest, are the most critical [33]. The crest elements’ stability usually depends on the relative freeboard, whereas the stability of the slope elements is mainly governed by the wave height, the wave period and the slope of the structure. The latter has a major influence, since it directly affects the degree of overlapping of the slope elements. Subsequently, the length of the sand containers should be large enough to ensure a proper overlapping. The development of technology allows making bigger geocontainers with respect to the past and, hence, to overcome some of the stability problems of GSC structures.
The behavior of the tested GSC structure is quite good with respect to global stability. The experimental results are in agreement with the results obtained by [33,34], both with regard to the displacement limits of the individual containers and to the global stability of the entire structure. In Figure 17, the experimental data are compared with the findings of [33], where ξ is the Iribarren Index, and Ns is the stability number expressed as:
in which D is the thickness of the armor layer that, for GSC, can be assumed as D = lc sinα (lc is the length of the container).
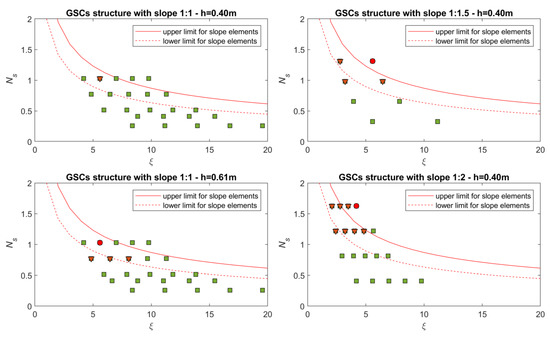
Figure 17.
Stability number ns vs. Iribarren’s parameter. Experimental data and line trends of [33]. Stable elements in green squares, sliding elements in orange triangles and global instability of the structure in red circle.
In Figure 17, the experimental data were reported by evaluating the stability number by means of Equation (11), where lc = 0.25 m, α is the front slope, which changes with the configurations (1:1, 1:1.5 and 1:2), and = 0.76, the dotted line indicates the beginning of the movement of the single element and the red line marks the beginning of the global instability of the whole structure (according to the studies of [33]. The red circles symbols refer to the global instability of the GSC structure, and the data in orange triangles refer to containers that move or slide, while the green squares symbols correspond to the elements that are almost stable. During each test, the containers, being deformable elements, are subjected to uplift force when wave uprush occurs, in which it is responsible for the reduced contact areas between overlapped elements. By inspecting Figure 17 a better agreement between experimental data and [33]’s results is observed for the GSC structure with slope 1:1.5 and 1:2, for which the initial movement of the elements, and the global instability corresponds, respectively, to the lower and the upper limits.
The GSC structure with a slope of 1:1 is more stable with respect to a gentler slope in terms of the failure of individual elements. Such a result is mainly due to a larger overlapped area between elements, which plays a fundamental role on their stability. In most of the test cases for slope 1:1, the containers were deformed during the test without moving from their initial positions at the end of the test. In gentler slopes, a single element failure is more typical because of structure failure, while, in steeper slopes, structures are more subject to failing in overall instability. In the present study, the only test case in which a global instability was found for a structure with a slope of 1:1 is due to the sliding of the entire structure on the preferential sliding surface between the geocontainers and the support structure (see Figure 18); however, it does not correspond to the strongest hydrodynamic conditions. It is important to pay attention to this sliding surface when a revetment with containers is applied, especially when steep slopes are used.

Figure 18.
Configuration with slope 1:1. Instability of the structure in the stability test with H = 0.20 m, T = 2.0 s and h = 0.61 m.
In Figure 19 and Figure 20, some local failure mechanisms, such as the sliding or movement of some elements or removal of a container, are shown.

Figure 19.
Configuration with slope 1:1.5. Uplift and movement of some elements in the stability test with H = 0.20 m, T = 1.5 s and h = 0.40 m.

Figure 20.
Configuration with slope 1:2. Sliding of some elements in the stability test with H = 0.20 m, T = 2.0 s and h = 0.40 m (left panel) and removal of elements in the stability test with H = 0.20 m, T = 3.0 s and h = 0.40 m (right panel).
The small-scale laboratory test presents some limitations in the simultaneous reproduction of all the geobag characteristics (elasticity, stiffness, permeability, etc.) due to the problems about the scale effects of different parameters; however, the general almost good correspondence of the experimental results with those of [33] allows the use of the predicted stability number of Equation (11), also conservative. Our results confirm the validity of the analytical formula proposed by [34] for the static design of GSC structures, as reported from Equations (7)–(9).
6. Conclusions
A lot of parameters have an influence on the reflection coefficient Kr, such as the wave period T, the twave steepness Hi/L, the water depth h, the permeability and the slope angle α. The last one is the most obvious, and certainly, it has a very strong influence. The experimental tests of [45] showed that the flow through the GSC structure is solely governed by the gaps between neighboring containers and that the flow through the sand filling in the containers can be neglected; therefore, our tested sand container structure can be assumed as a permeable structure. For what concerns the other parameters, it was found that Kr increases with the increasing period and decreasing steepness. When the period becomes very long, the wave will be almost totally reflected from the breakwater when it is impermeable and largely transmitted through the breakwater when it is porous, thus giving little reflection. The response of the wave reflection to the period and steepness is consistent with energy dissipation considerations along a classical breakwater surface.
By analyzing the reflection obtained by our experiments, it was found that, for surf similarity parameters lower than 3, Kr becomes comparable to that predicted by using the [4] formula for permeable structures. Such a result can be warranted, because the wave energy dissipation occurs not only by means of the flow through a permeable structure, but also by the drag force generated over the steps between different GSC layers. The surface drag is a nonconservative force that increases with the square of local velocities. Wave particles’ velocities increase with increased wave steepness and a reducing period. These changes induce larger drag forces, larger energy dissipation and, therefore, a reduction of available energy that generates a reflected wave. Conversely, a reduction in wave steepness or increase in period causes a reduction in local velocities and energy dissipation, thereby increasing reflection. Indeed, for longer waves, the reflection increases, and the GSC structure behaves more similar to an impermeable structure. Even if the experimental results data reside closer to [4] formula for impermeable structures, a residual capacity of dissipation induced by both the mechanisms still remains, indeed most of the experimental data have a smaller value of Kr with respect to a smooth impermeable slope. With the Iribarren number a good parameter for the study of the reflection, a best-fit formula for the evaluation of the reflection coefficient Kr for the GSC structure is proposed in the present study.
The general performance of the submerged GSC breakwater in terms of transmitted energy is good. The experimental results show a very good agreement with the trend of [8] obtained for low-crested rubble-mound breakwaters. In particular, GSC structures show lower transmission coefficients than rubble-mound barriers with the same submergence. Such results can be explained by the occurrence of both dissipation mechanisms: the wave breaking on the top berm or at the slope face and the impact of the drag force on the steps of the sloped shapes of GSC structures. The observed piling-up is affected by the severe conditions of the experimental test (absence of the water recirculation). As a consequence, the experimental data are larger than those computed by applying [19,22,24] formula. In addition, this discrepancy can be explained by the difference in breakwater permeability: the GSC structure behaves more similar to an impermeable one, especially when it is exposed to stronger waves, which can generate piling-up.
The small-scale laboratory test presents some limitations in the simultaneous reproduction of all the geobag engineering characteristics (elasticity, stiffness, permeability, etc.) due to the problems about the scale effects of different parameters. However, the present stability analysis reinforces the findings of [33,34], confirming both the limits of displacement of the single container and those regarding the stability of the entire structure. Therefore, the design of the GSC can be made by using Equations (7)–(9) to find the length of the geotextile sand container lc and the required weight W. The length lc should be large enough to ensure a proper overlapping, such an aspect being the most critical for the stability of GSC structures. When a steeper slope is used, the overall stability is the critical aspect, while, when a gentler slope is used, the single element is the cause of the failure due to the shorter overlapped length. The development of technology allows to make bigger geocontainers with respect to the past, overcoming some of the stability problems of GSC structures. Moreover, the technology allows to make a geocontainer in non-woven fabric with very high mechanical characteristics of toughness, strength and durability and large resistance to punching, abrasion and weathering; hence, nowadays, they are less vulnerable to vandalism or accidental acts.
Therefore, the use of GSCs as a softer and flexible defense structure can be considered in the design of alternatives to traditional hard coastal protection structures made of concrete or rubble mound material. The present study verifies the good performance of GSC structures in terms of transmitted/reflected energy and of structural stability. Such a good performance also enforces the choice of GSC structures as temporary coastal protections during the winter period, and from the authors’ experiences, these defenses were found to be efficient.
Author Contributions
Conceptualization, S.C., C.L. and A.M.; methodology, S.C., C.L.; formal analysis, S.C., C.L. and A.M.; investigation, S.C., C.L.; data curation, S.C. and F.M.; writing—original draft preparation, S.C.; writing—review and editing, S.C., F.M. and S.R.; supervision, S.C., C.L. and A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no public funding.
Acknowledgments
Thanks to the company Tessilbrenta srl from Pove del Grappa (Vicenza, Italy), for the supply of suitable geotextile materials for the tested bags (GSCs) for carrying out the experimental tests and for partially financing the laboratory activities.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses or interpretation of the data; in the writing of the manuscript or in the decision to publish the results.
References
- Hornsey, W.P.; Carley, J.T.; Coghlan, R.J.; Cox, R.J. Geotextile sand container shoreline protection systems: Design and application. Geotextile Geomembr. 2011, 29, 425–439. [Google Scholar] [CrossRef]
- Seelig, W.N. Two-Dimensional Tests of Wave Transmission and Reflection Characteristics of Laboratory Breakwaters; Technical Report 80-1; U.S. Army Corps of Engineers, Coastal Engineering Research Center: Washington, DC, USA, 1980. [Google Scholar]
- Sollitt, C.K.; DeBok, D.H. Large Scale Model Tests of Placed Stone Breakwaters. In Proceedings of the 15th International Conference on Coastal Engineering, Honolulu, HI, USA, 11–17 July 1976; Volume 3, pp. 2572–2588. [Google Scholar]
- Seelig, W.N.; Ahrens, J.P. Estimation of Wave Reflection and Energy Dissipation Coefficients for Beaches, Revetments, and Breakwaters. Technical Paper NO. 81-1; U.S. Army Corps of Engineers, Coastal Engineering Research Center: Washindton, DC, USA, 1981. [Google Scholar]
- Allsop, N.W.H.; Channell, A.R. Wave Reflections in Harbours; Report OD 102; Hydraulic Research Wallingford: Wallingford, UK, 1989. [Google Scholar]
- Postma, G.M. Wave Reflection from Rock Slopes Under Random Wave Attack. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 1989. [Google Scholar]
- Van der Meer, J.W. Data on Wave Transmission due to Overtopping; Delft Hydraulics: Marknesse, The Netherlands, Lab. Report H986; 1990. [Google Scholar]
- Van der Meer, J.W. Conceptual design of rubble mound breakwaters. In Proceedings of the Short Course on Design and Reliability of Coastal Structures attached to the 23rd International Conference on Coastal Engineering, Venice, Italy, 1–3 October 1992; pp. 447–510. [Google Scholar]
- Zanuttigh, B.; Van der Meer, J.W. Wave reflection for coastal structures. In Proceedings of the 30th International Conference on Coastal Engineering, Diego, CA, USA, 3–8 September 2006; Volume 5, pp. 4337–4349. [Google Scholar]
- Battjes, J.A. Surf similarity. In Proceedings of the 14th International Conference on Coastal Engineering, Copenhagen, Denmark, 24–28 June 1974; Volume 1, pp. 154–172. [Google Scholar]
- Van der Meer, J.W.; Pilarczyc, K.V. Stability of Breakwater Armour Layers—Deterministic and Probabilistic Design; Delft Hydraulic Communication No. 378; Rijkswaterstaat: Utrecht, The Netherlands, 1987. [Google Scholar]
- Lorenzoni, C.; Postacchini, M.; Brocchini, M.; Mancinelli, A. Experimental study of the short-term efficiency of different breakwater configurations on beach protection. J. Ocean. Eng. Mar. Energy 2016, 2, 195–210. [Google Scholar] [CrossRef]
- Steenhauer, K.; Pokrajac, D.; O’Donoghue, T. Numerical model of swash motion and air entrapment within coarse-grained beaches. Coast. Eng. 2012, 64, 113–126. [Google Scholar] [CrossRef]
- Kikkert, G.A.; Pokrajac, D.; O’Donoghue, T.; Steenhauer, K. Experimental study of bore-driven swash hydrodynamics on permeable rough slopes. Coast. Eng. 2013, 79, 42–56. [Google Scholar] [CrossRef]
- Lorenzoni, C.; Postacchini, M.; Mancinelli, A.; Brocchini, M. The morphological response of beaches protected by different breakwater configurations. In Proceedings of the 33rd International Conference of Coastal Engineering, Santander, Spain, 15 December 2012; Volume 1. Number 33, sediment.52. [Google Scholar] [CrossRef]
- Burcharth, H.F.; Hawkins, S.J.; Zanuttigh, B.; Lamberti, A. Environmental Design Guidelines for Low Crested Coastal Structures; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Ruol, P.; Faedo, A.; Paris, A. Prove sperimentali sul comportamento di una scogliera a cresta bassa e sul fenomeno del piling-up a tergo di essa. Studi Costieri 2003, 7, 41–59. (In Italian) [Google Scholar]
- Calabrese, M.; Vicinanza, D.; Buccino, M. 2D wave setup behind submerged breakwaters. Ocean. Eng. 2008, 35, 1015–1028. [Google Scholar]
- Calabrese, M.; Vicinanza, D.; Buccino, M. 2D wave set up behind low crested and submerged breakwaters. In Proceedings of the 13th International Society of Offshore and Polar Engineers (ISOPE), Honolulu, HI, USA, 25–30 May 2003; Volume 3, pp. 831–836. [Google Scholar]
- Dalrymple, R.; Dean, R. Discussion of Piling-up behind low and submerged permeable breakwaters by Diskin et al. J. Waterw. Harb. Coast. Eng. Div. 1971, 97, 423–427. [Google Scholar] [CrossRef]
- Loveless, J.; Debski, D.; MacLeod, A. Sea level set-up behind detached breakwaters. In Proceedings of the 26th International Conference on Coastal Engineering, Copenhagen, Denmark, 22–26 June 1998; ASCE: Reston, VA, USA, 1998; Volume 2, pp. 1665–1678. [Google Scholar]
- Calabrese, M.; Vicinanza, D.; Buccino, M. Verification and re-calibration of an engineering method for predicting 2D wave set up behind submerged breakwaters. In Proceedings of the Second International Coastal Symposium (ICS) 2005, Icelandic Maritime Administration, Höfn, Iceland, 5–8 June 2005; Volume B8-4, p. 14. [Google Scholar]
- Soldini, L.; Lorenzoni, C.; Brocchini, M.; Mancinelli, A.; Cappietti, L. Modeling of the wave setup inshore of an array of submerged breakwaters. J. Waterw. Port Coast. Ocean. Eng. 2009, 135, 38–51. [Google Scholar] [CrossRef]
- Diskin, M.; Vajda, M.; Amir, I. Piling-up behind low and submerged permeable breakwaters. J. Waterw. Harb. Coast. Eng. Div. 1970, 96, 359–372. [Google Scholar] [CrossRef]
- Pilarczyk, K.W. Design of low-crested (submerged) structures—An overview. In Proceedings of the 6th International Conference on Coastal and Port Engineering in Developing Countries, Colombo, Sri Lanka, 15–19 September 2003; pp. 1–16. [Google Scholar]
- Lorenzoni, C.; Piattella, A.; Soldini, L.; Mancinelli, A.; Brocchini, M. An experimental investigation of the hydrodynamic circulation in the presence of submerged breakwaters. In Proceedings of the 5th International Symposium on Ocean Measurements and Analysis, Madrid, Spain, 3–7 July 2005. Paper 125. [Google Scholar]
- Van der Meer, J.W.; Briganti, R.; Zanuttigh, B.; Wang, B. Wave transmission and reflection at low-crested structures: Design formulae, oblique wave attack and spectral change. Coast. Eng. 2005, 52, 915–929. [Google Scholar] [CrossRef]
- Postacchini, M.; Brocchini, M.; Corvaro, S.; Lorenzoni, C.; Mancinelli, A. Comparative analysis of sea wave dissipation induced by three flow mechanisms. J. Hydraul. Res. 2011, 49, 554–561. [Google Scholar] [CrossRef]
- Lorenzoni, C.; Soldini, L.; Brocchini, M.; Mancinelli, A.; Postacchini, M.; Seta, E.; Corvaro, S. Working of defense coastal structures dissipating by macroroughness. J. Waterw. Port Coast. Ocean. Eng. 2010, 136, 79–90. [Google Scholar] [CrossRef]
- Losada, I.J.; Lara, J.L.; Guanche, R.; Gonzalez-Ondina, J.M. Numerical analysis of wave overtopping of rubble mound breakwaters. Coast. Eng. 2008, 55, 47–62. [Google Scholar] [CrossRef]
- Marini, F.; Mancinelli, A.; Corvaro, S.; Rocchi, S.; Lorenzoni, C. Coastal submerged structures adaptation to sea level rise over different beach profiles. Ital. J. Eng. Geol. Environ. 2020, 20, 87–98. [Google Scholar]
- Marini, F.; Corvaro, S.; Rocchi, S.; Lorenzoni, C.; Mancinelli, A. Semi-Analytical Model for the Evaluation of Shoreline Recession Due to Waves and Sea Level Rise. Water 2022, 14, 1305. [Google Scholar] [CrossRef]
- Oumeraci, H.; Hinz, M.; Bleck, M.; Kortenhaus, A. Sand-filled Geotextile Containers for Shore Protection. In Proceedings of the Coastal Structures 2003, Portland, OR, USA, 26–30 August 2003. [Google Scholar]
- Recio, J.M.; Oumeraci, H. Process based stability formulae for coastal structures made of geotextile sand containers. Coast. Eng. 2009, 56, 632–658. [Google Scholar] [CrossRef]
- Recio, J.M.; Oumeraci, H. Processes affecting the hydraulic stability of coastal revetments made of geotextile sand containers. Coast. Eng. 2009, 56, 260–284. [Google Scholar] [CrossRef]
- Dassanayake, D.T.; Oumeraci, H. Hydraulic stability of coastal structures made of geotextile sand containers (GSCs): Effect of engineering properties of GSCs. In Proceedings of the 33th International Conference on Coastal Engineering, Santander, Spain, 1–6 July 2012; Volume 1. structures 55. [Google Scholar]
- Dassanayake, D.T.; Oumeraci, H. Engineering Properties of geotextile sand containers and their effect on hydraulic stability and damage. Development of low-crested/submerged structures. Int. J. Ocean. Clim. Syst. 2012, 3, 135–150. [Google Scholar] [CrossRef]
- Hudson, R. Laboratory investigation of rubble-mound breakwaters. J. Waterw. Harb. Div. 1956, 93–118. [Google Scholar]
- Jackson, L.A.; Reichelt, R.E.; Restall, S.; Corbett, B.; Tomlinson, R.; McGrath, J. Marine ecosystem enhancement on a geotextile coastal protection reef-Narrowneck reef case study. In Proceedings of the 29th International Conference on Coastal Engineering, Lisbon, Potugal, 19–24 September 2004; pp. 3940–3952. [Google Scholar]
- Taylor, J.T.; Southgate, P.C.; Rose, R.A. Assessment of artificial substrates for collection of hatchery-reared silver-lip pearl oyster (Pinctada maxima, Jameson) spat. Aquaculture 1998, 162, 219–230. [Google Scholar] [CrossRef]
- Varrello, R.; Wetzel, M.A.; Cima, F. Two facets of geotextiles in coastal ecosystems: Anti- or profouling effects? Mar. Environ. Res. 2021, 170, 105414. [Google Scholar] [CrossRef] [PubMed]
- Corvaro, S.; Marini, F.; Mancinelli, A.; Lorenzoni, C. Scour protection around a single slender pile exposed to waves. In Proceedings of the 36th International Conference of Coastal Engineering, Baltimore, MD, USA, 30 July–3 August 2018. [Google Scholar]
- Mansard, E.P.D.; Funke, E.R. The measurement of incident and reflected spectra using a least squares method. In Proceedings of the 17th International Conference on Coastal Engineering, Sydney, Australia, 23–28 March 1980; Volume 1, pp. 154–172. [Google Scholar]
- Isaacson, M. Measurement of Regular Wave Reflection. J. Waterw. Port Coast. Ocean. Eng. 1991, 117, 553–569. [Google Scholar] [CrossRef]
- Recio, J.; Oumeraci, H. Hydraulic permeability of structures made of geotextile sand containers: Laboratory tests and conceptual model. Geotextile Geomembr. 2008, 27, 473–487. [Google Scholar] [CrossRef]
- Goda, Y.; Morinobu, K. Breaking wave heights on horizontal bed affected by approach slope. Coast. Eng. J. 1998, 40, 307–326. [Google Scholar] [CrossRef]
- Eldeberky, Y. Nonlinear Transformation of Wave Spectra in the Nearshore Zone; Communications on hydraulic and geotechnical engineering, Delft University of Technology: Delft, The Netherlands, 1996; Report No. 96-4. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).