Simulated Short- and Long-Term Deformation in Coastal Karst Caves
Abstract
1. Introduction
2. Contents and Methods
2.1. Numerical Modeling of Short-Term and Long-Term Deformation Surrounding Caves
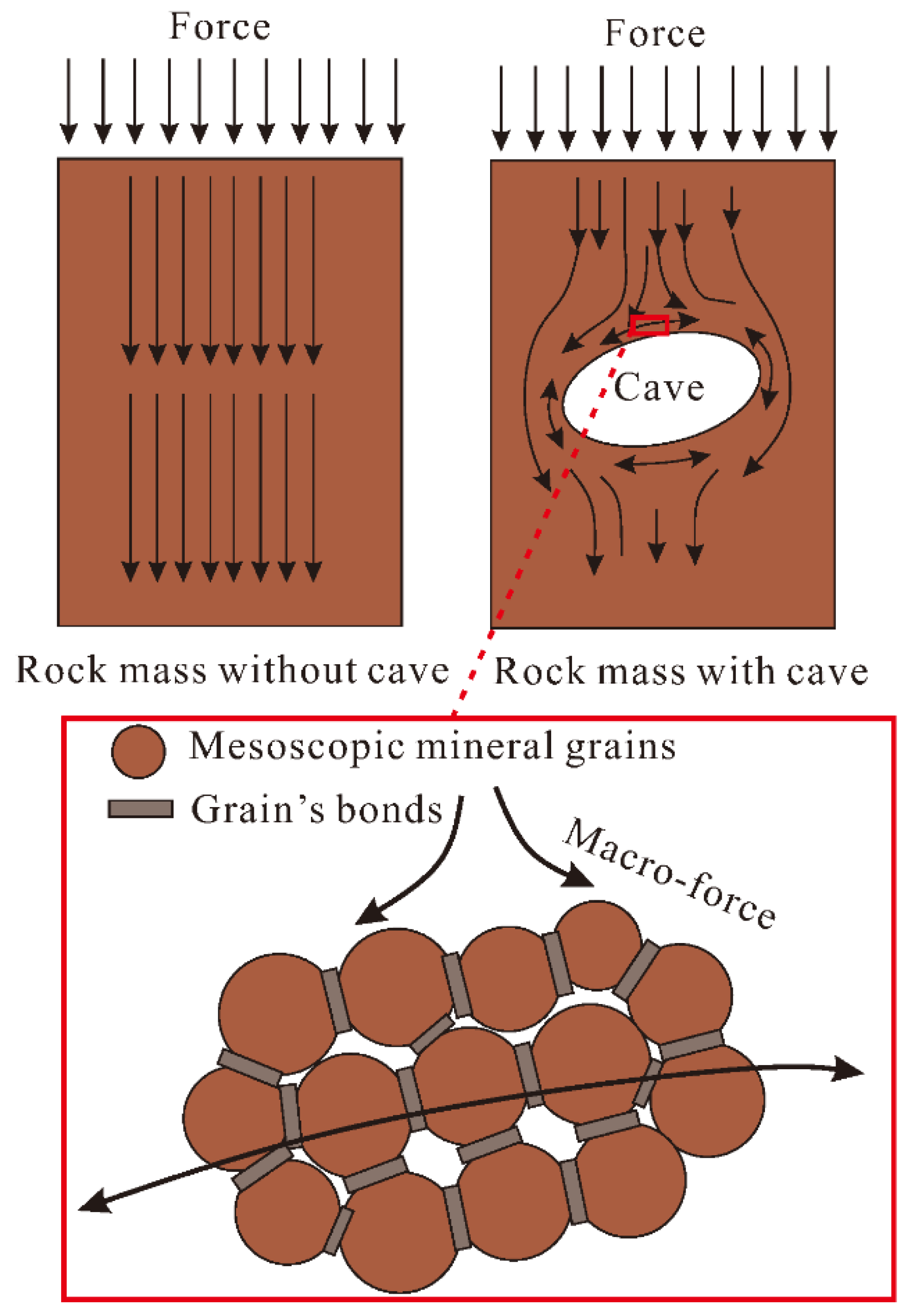
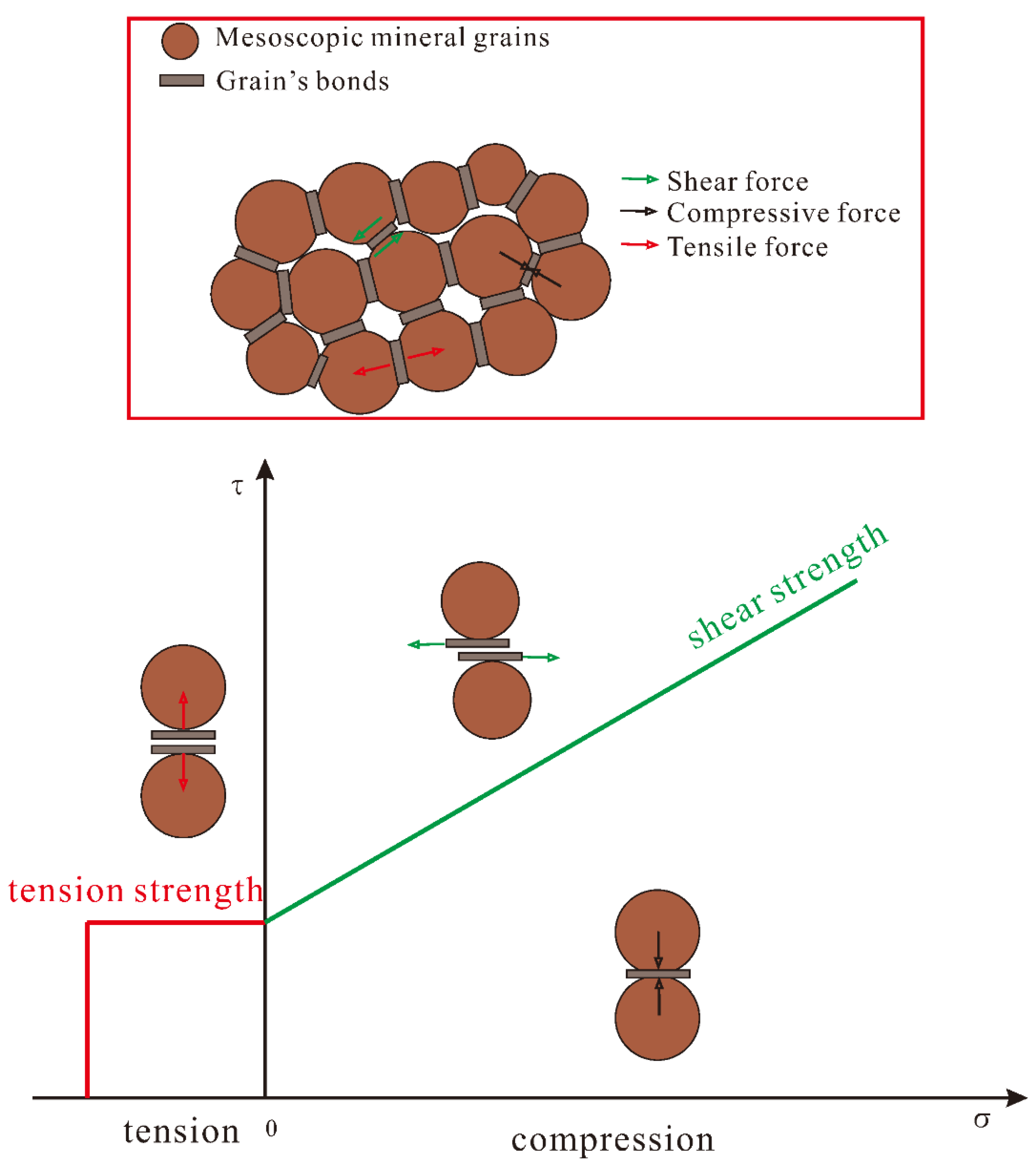
2.2. The Mesoscopic Controlling Mechanism of Self-Balance Pressure Arches of Caves
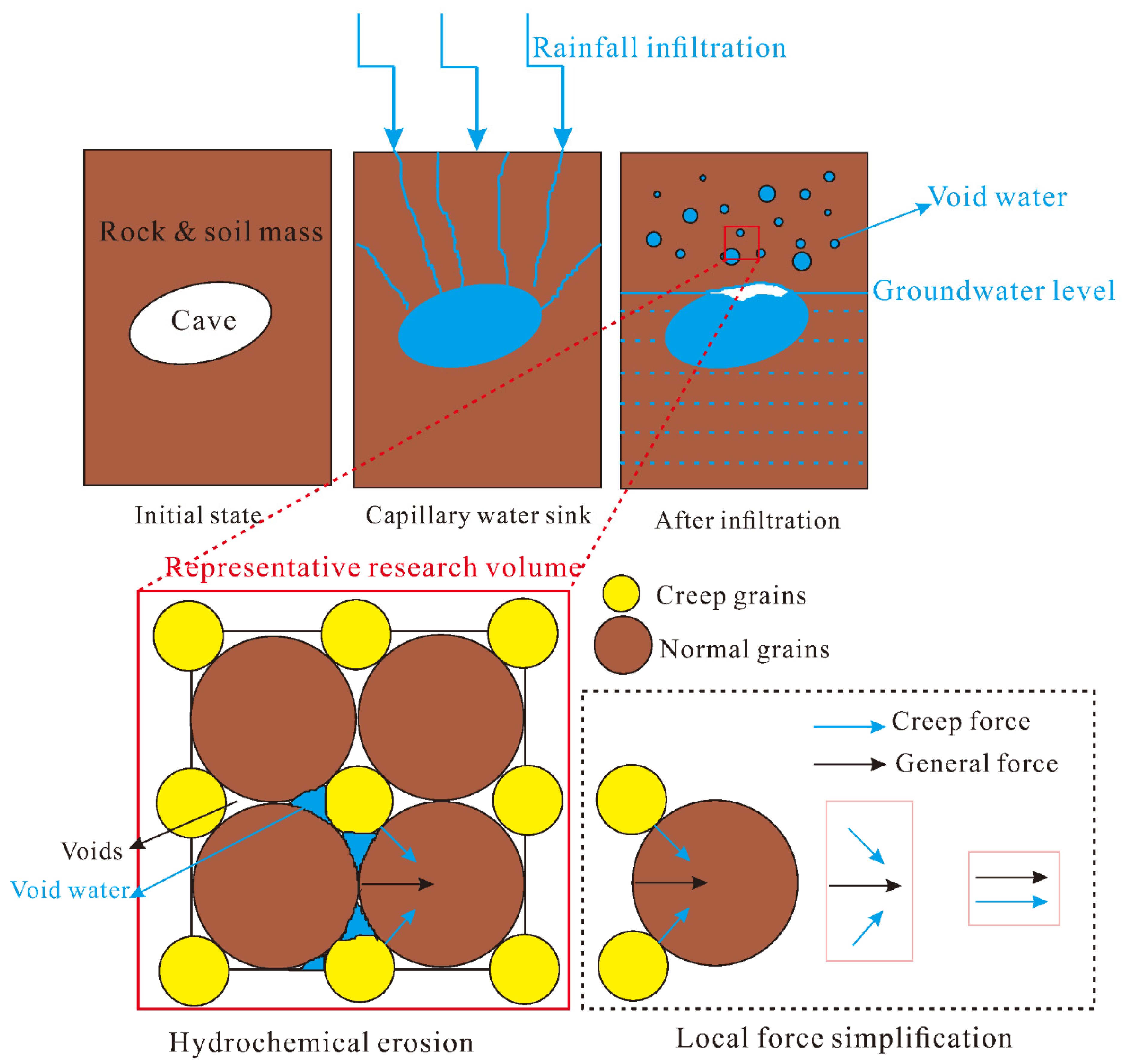
2.3. Time-Dependent Deformation under Pressure Arches
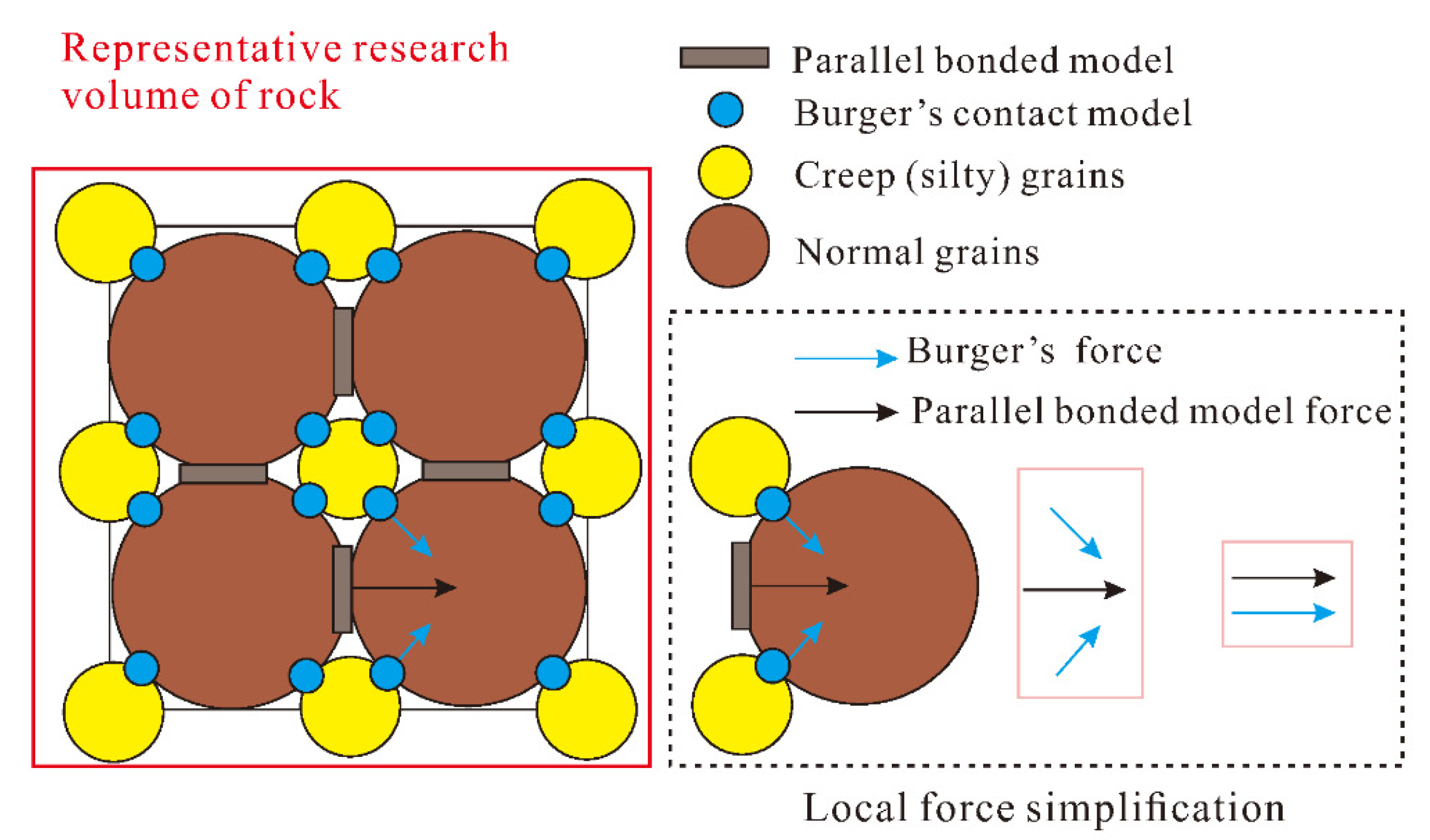
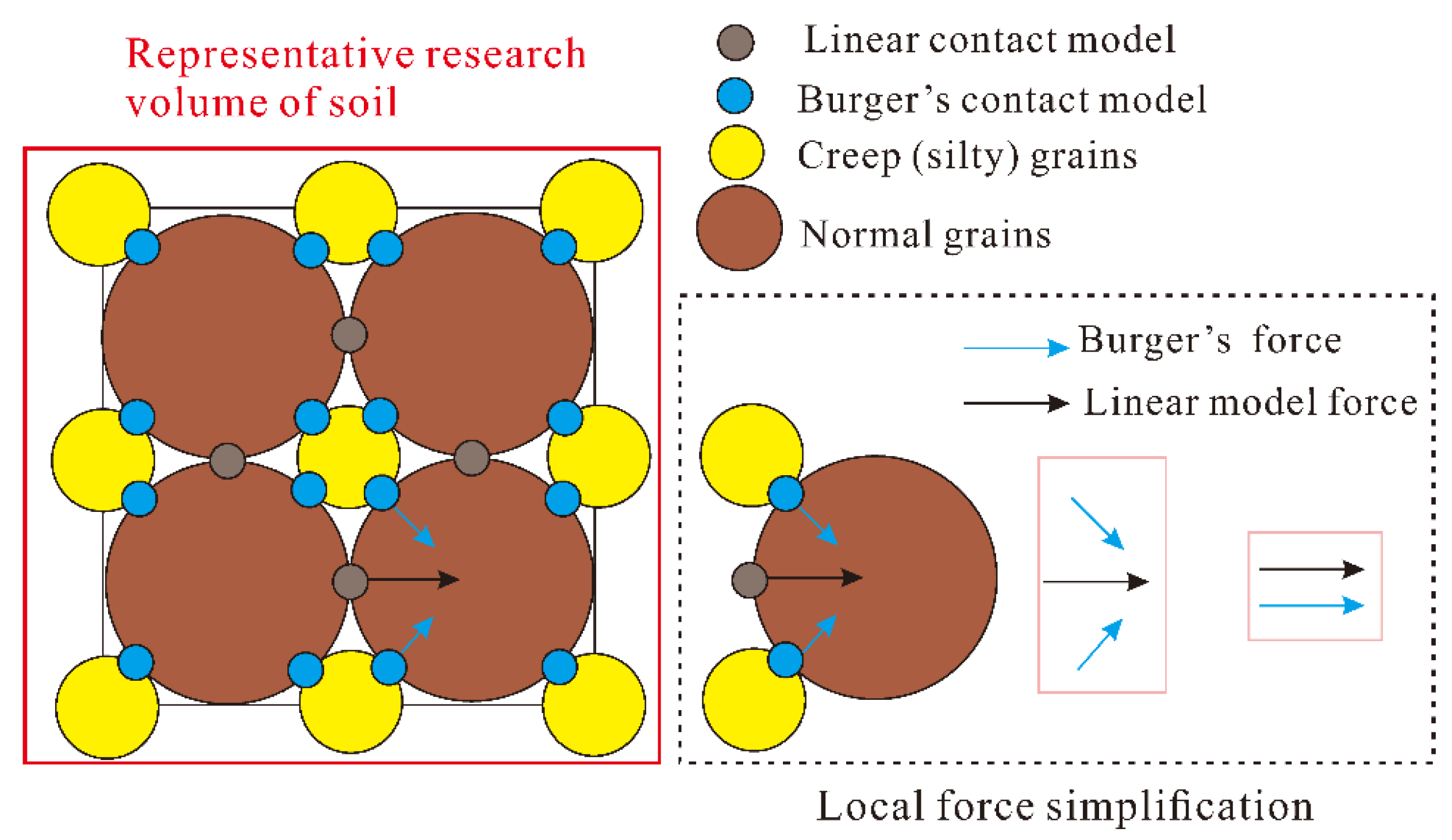
2.4. The Discrete Element Analysis Method for Rheological Mechanisms under the Pressure Arches
3. Results and Discussion
3.1. Case Study
3.1.1. Overview of the Selected Case Study
3.1.2. Excavation Deformation Monitoring Data
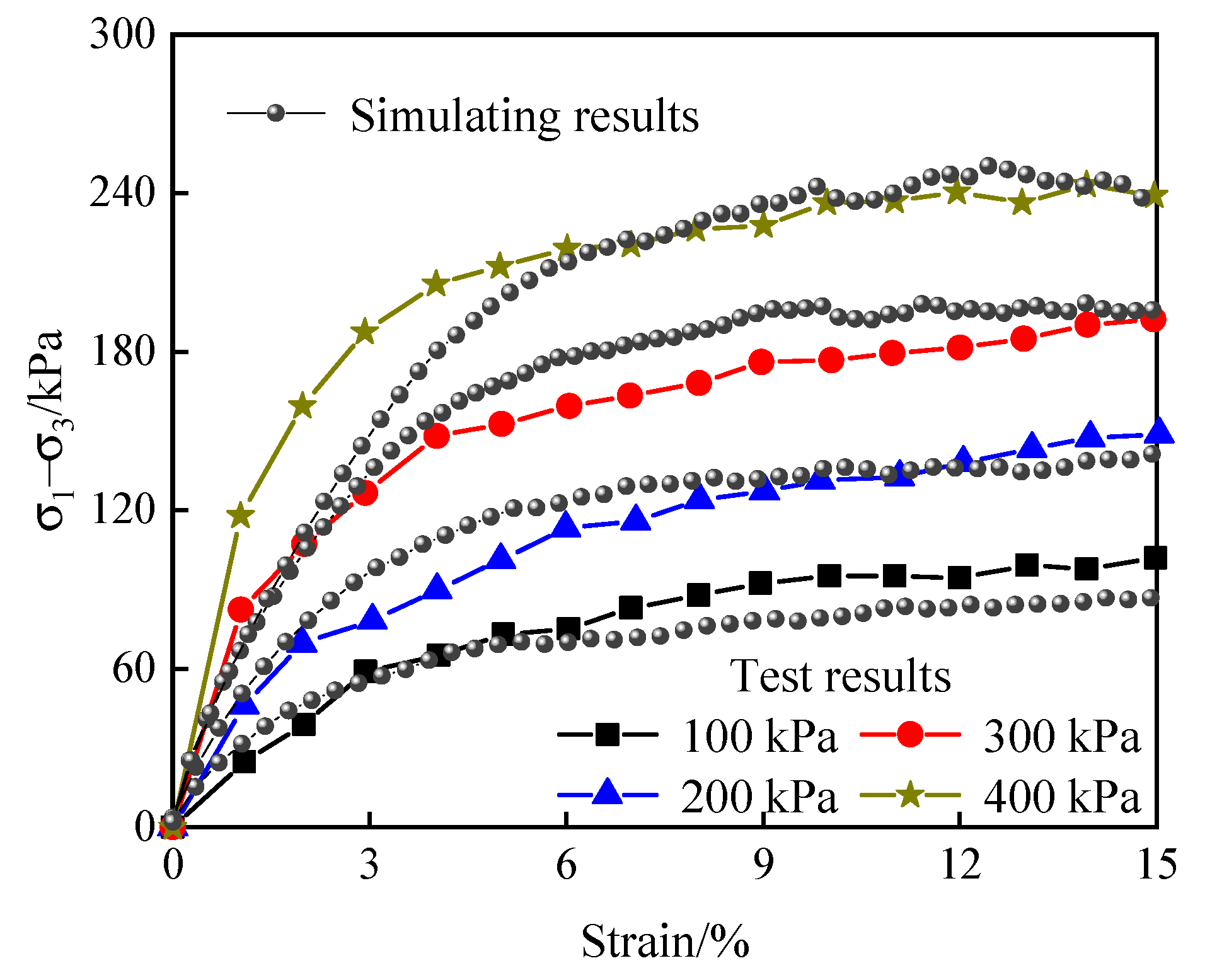
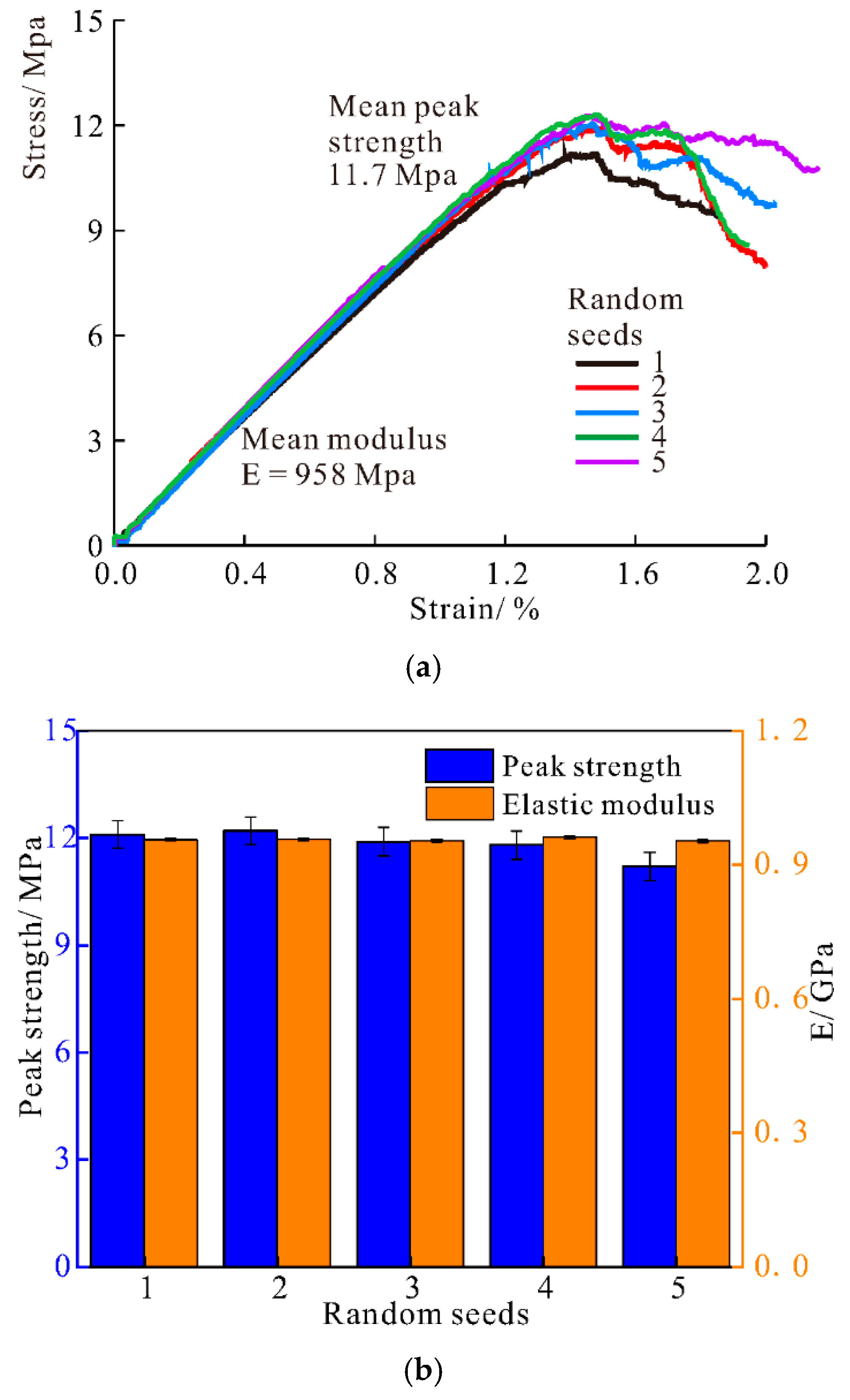
3.1.3. Rock and Soil Parameters and the DEM Model
- (1)
- Select models’ modulus, friction angle, tensile and cohesion strength according to the experience.
- (2)
- Alter the modulus based on stress–strain curves or rock strength.
- (3)
- Alter the tensile and cohesion strength according to rock strength.
- (4)
- Change the friction angle according to soils’ ultimate stress in the stress–strain curves.
- (5)
- Repeat (2)~(4) to obtain a reasonable result.
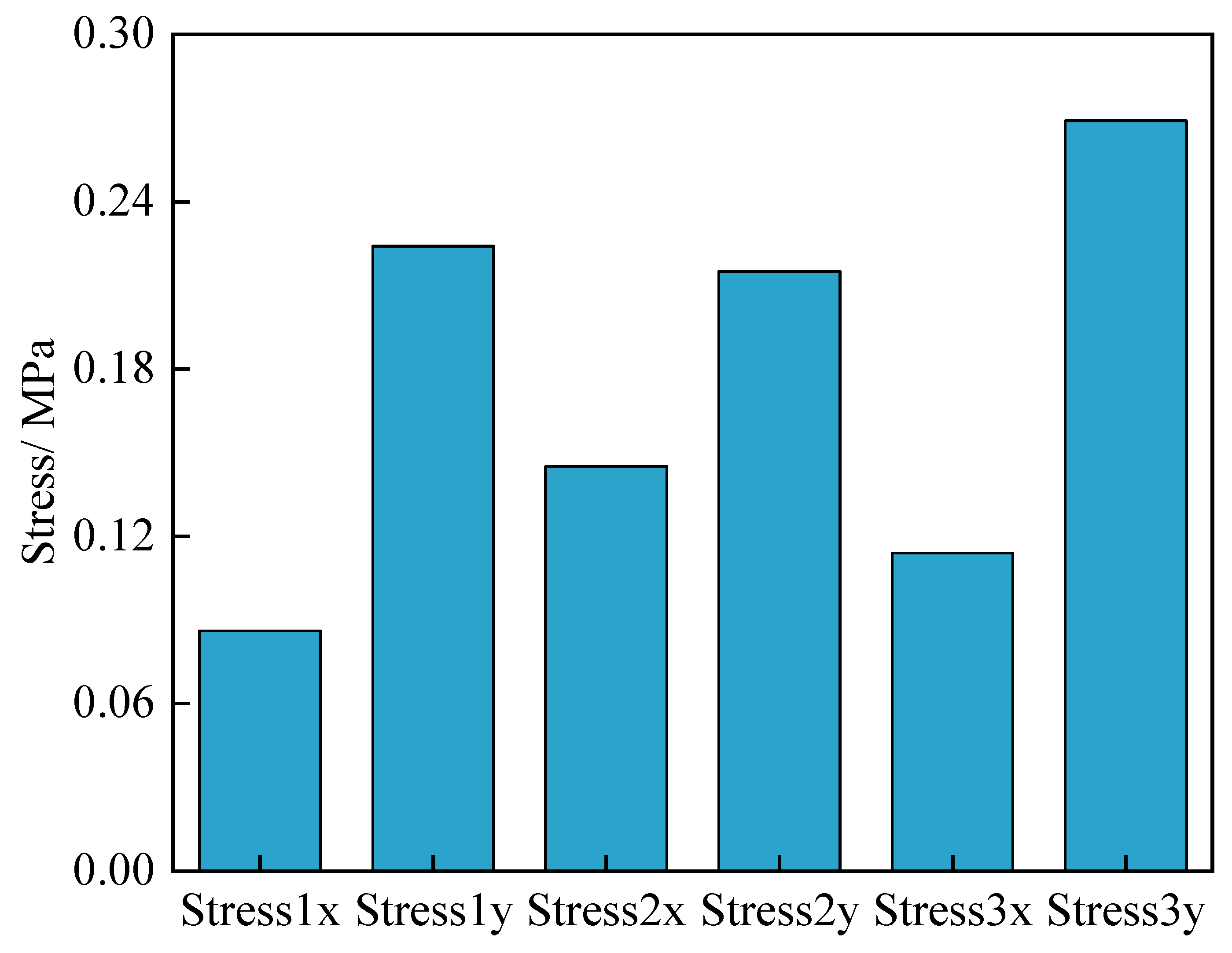
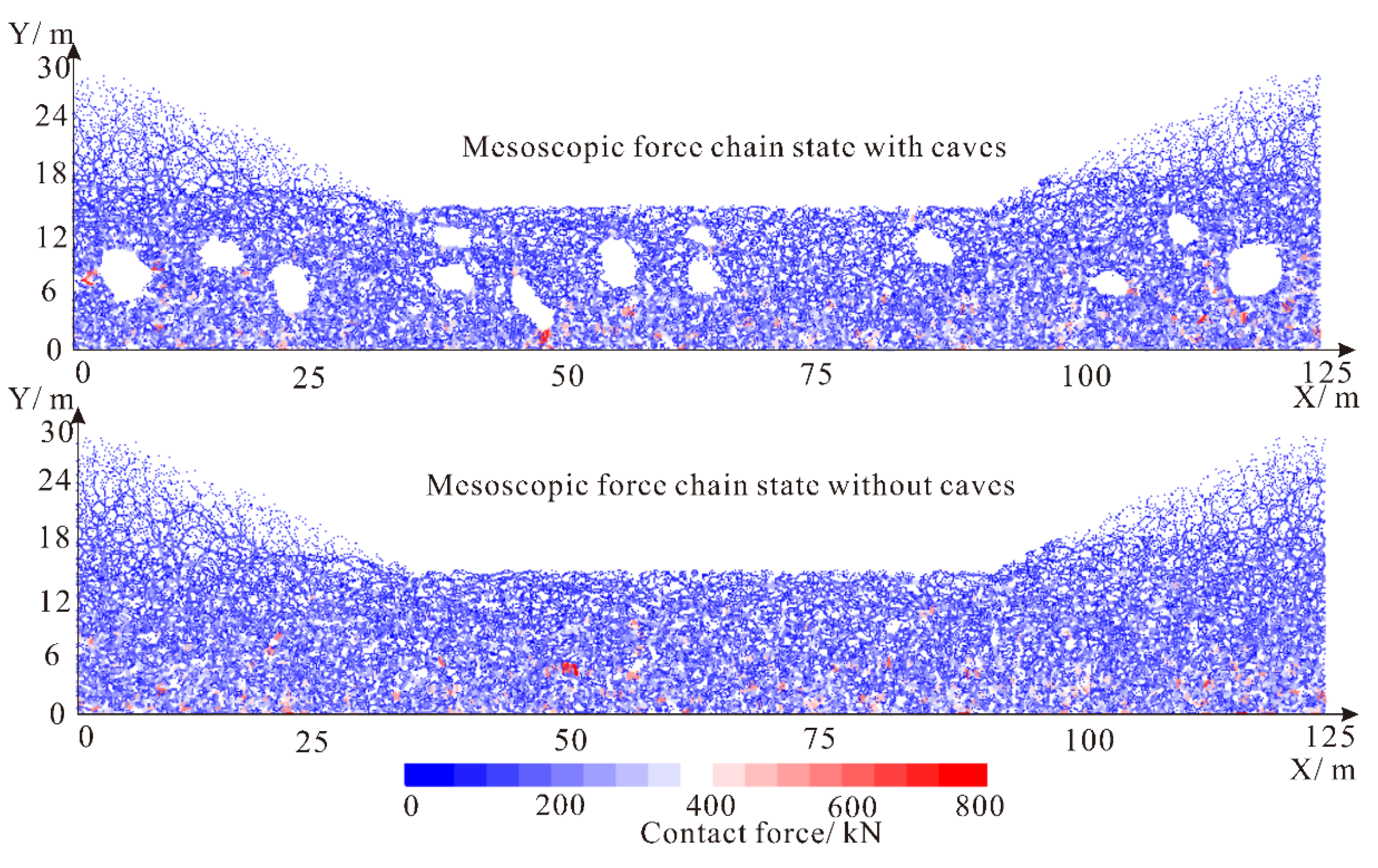
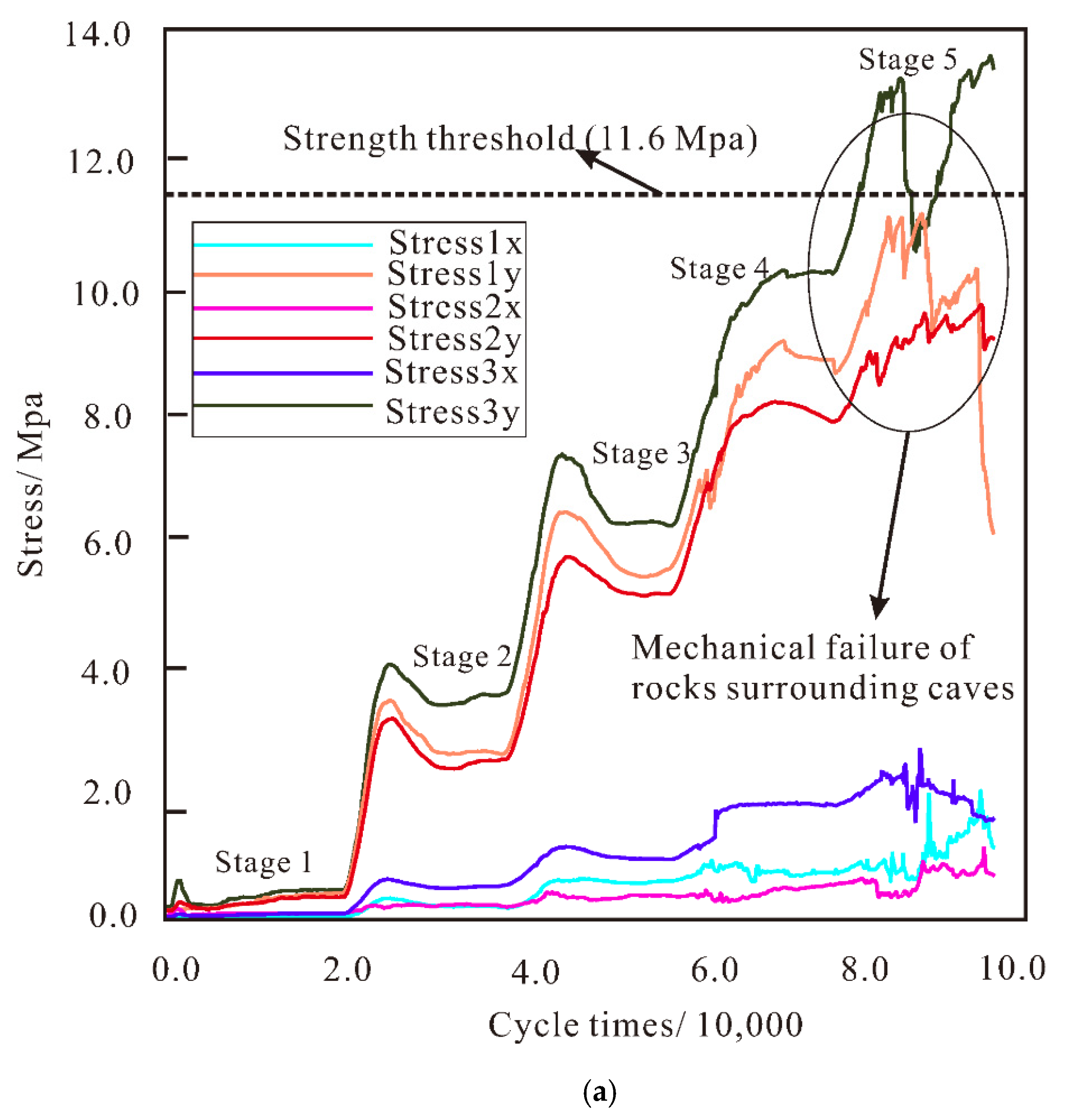
3.2. The Mesoscopic Mechanical Characteristics under the Self-Balanced Pressure Arch
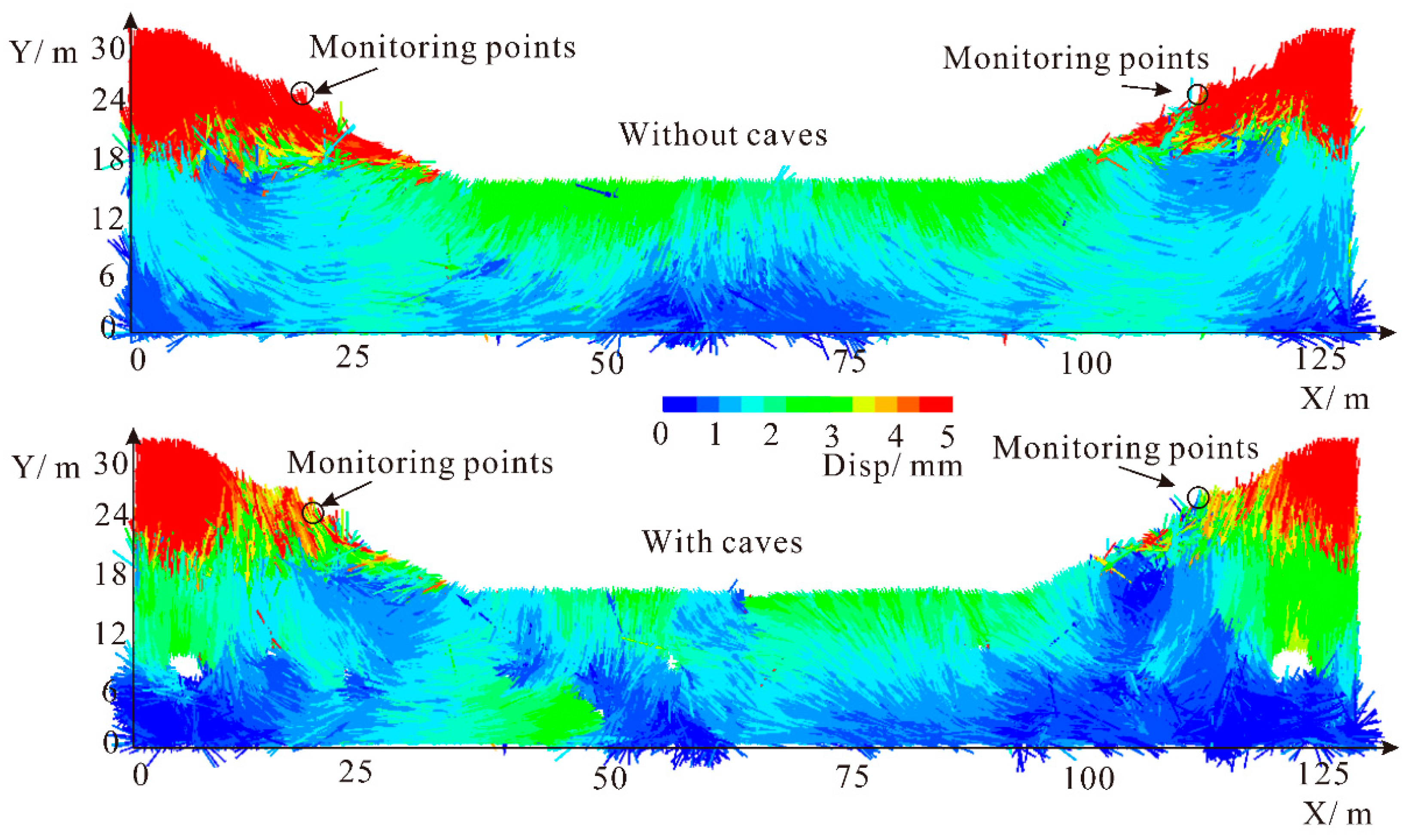
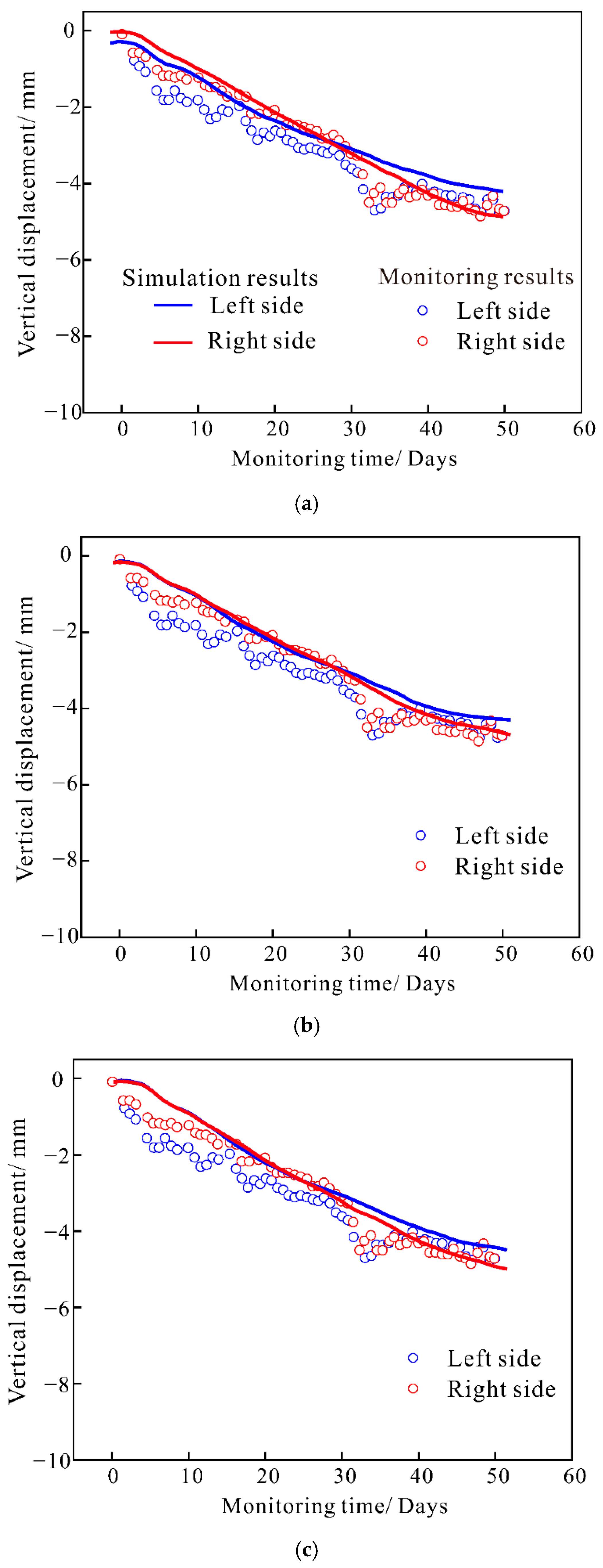
3.3. The Displacement Results Considering Rheological Deforming
3.4. Discussion for Short-Term Stability under Different Overlying Loadings
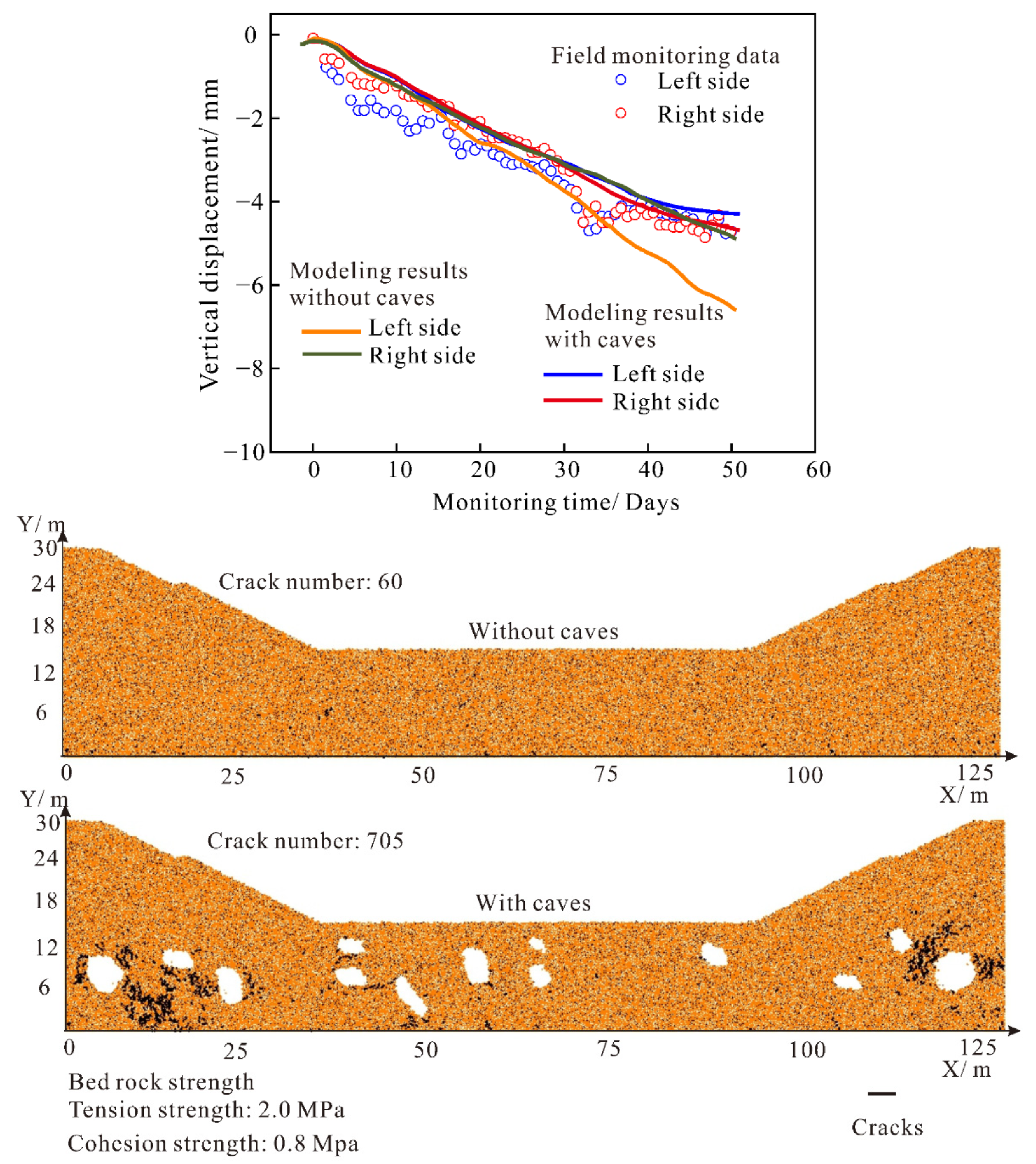
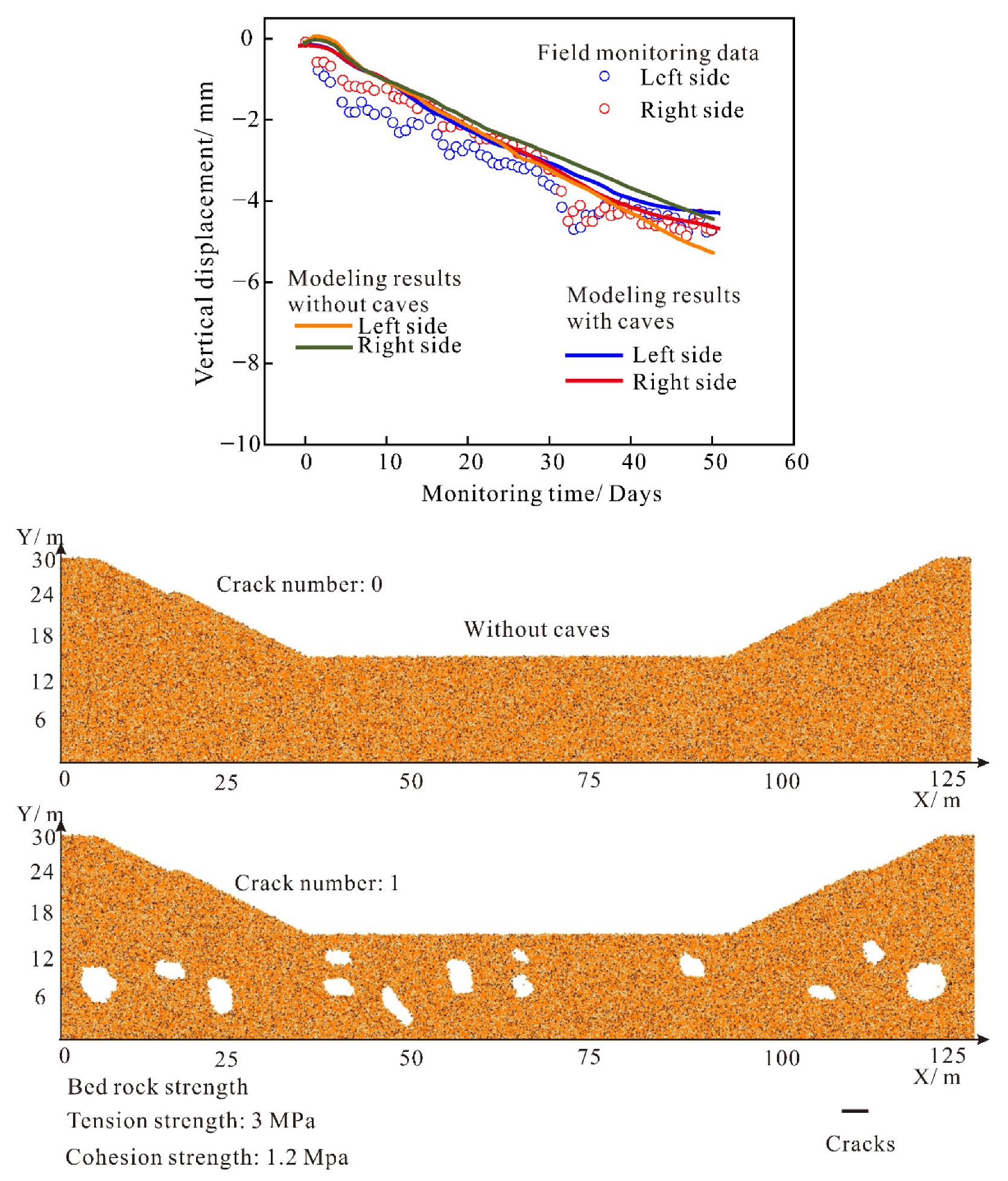
3.5. Discussion for Caves’ Influence on Deformation under Different Rock Strengths
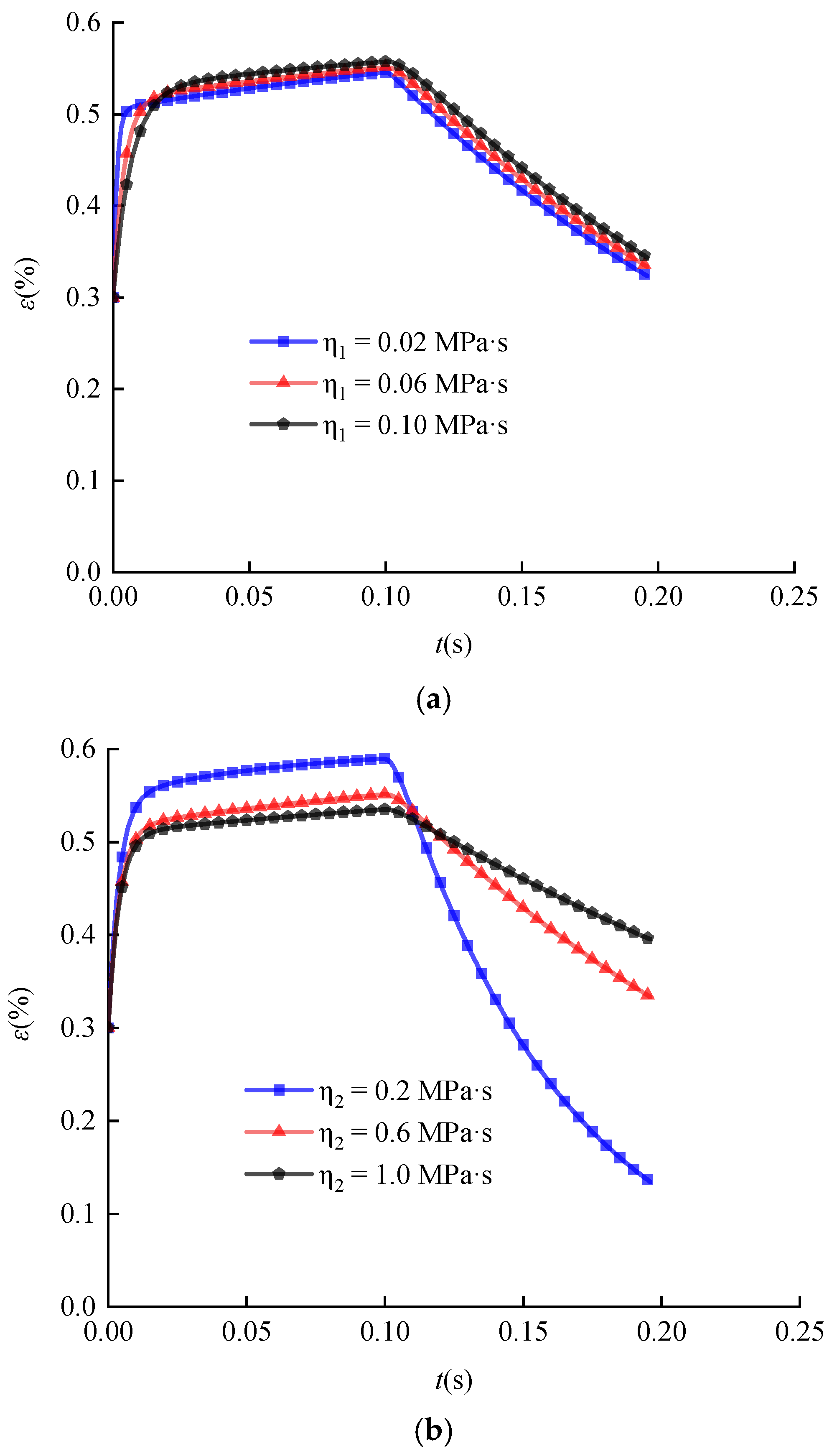
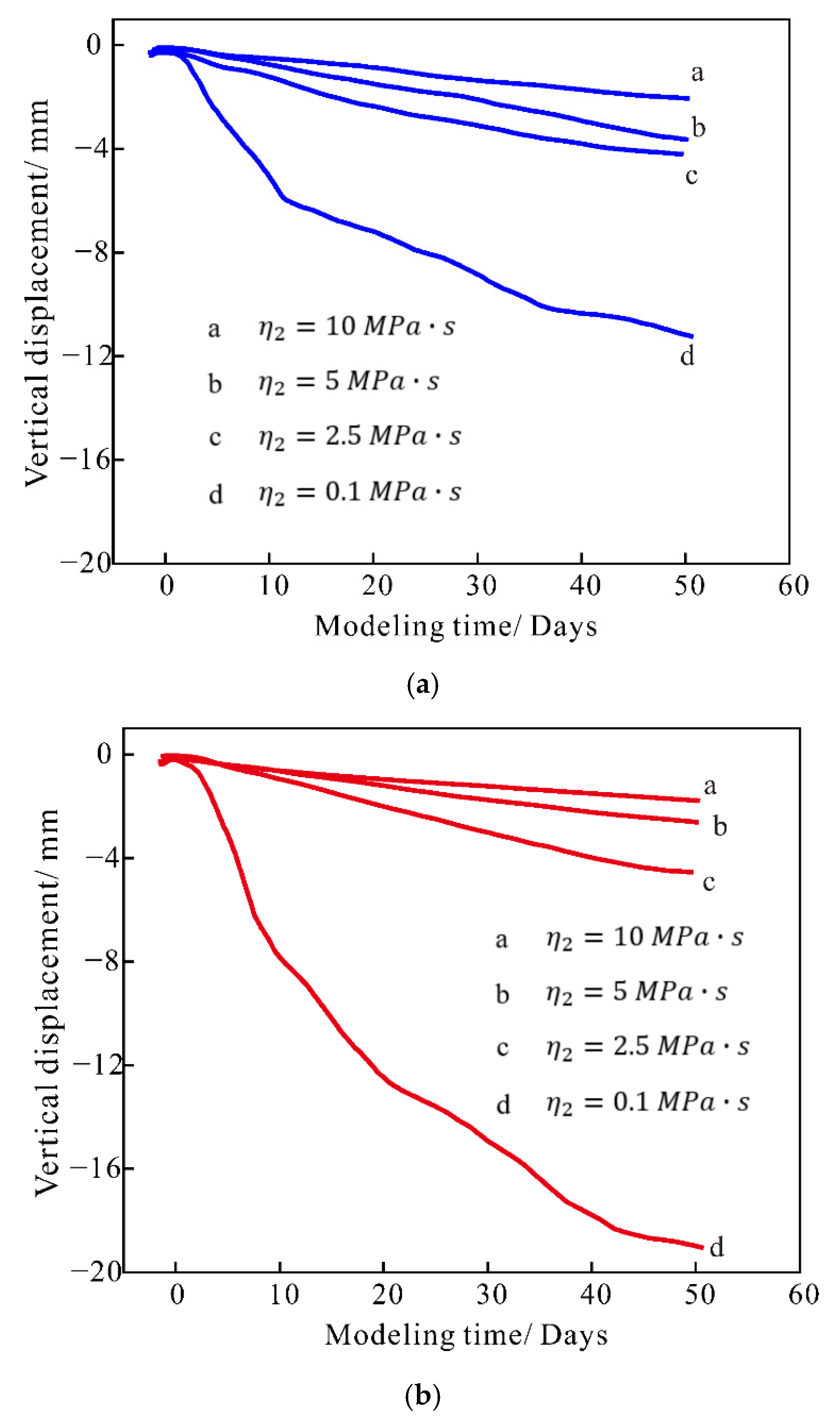
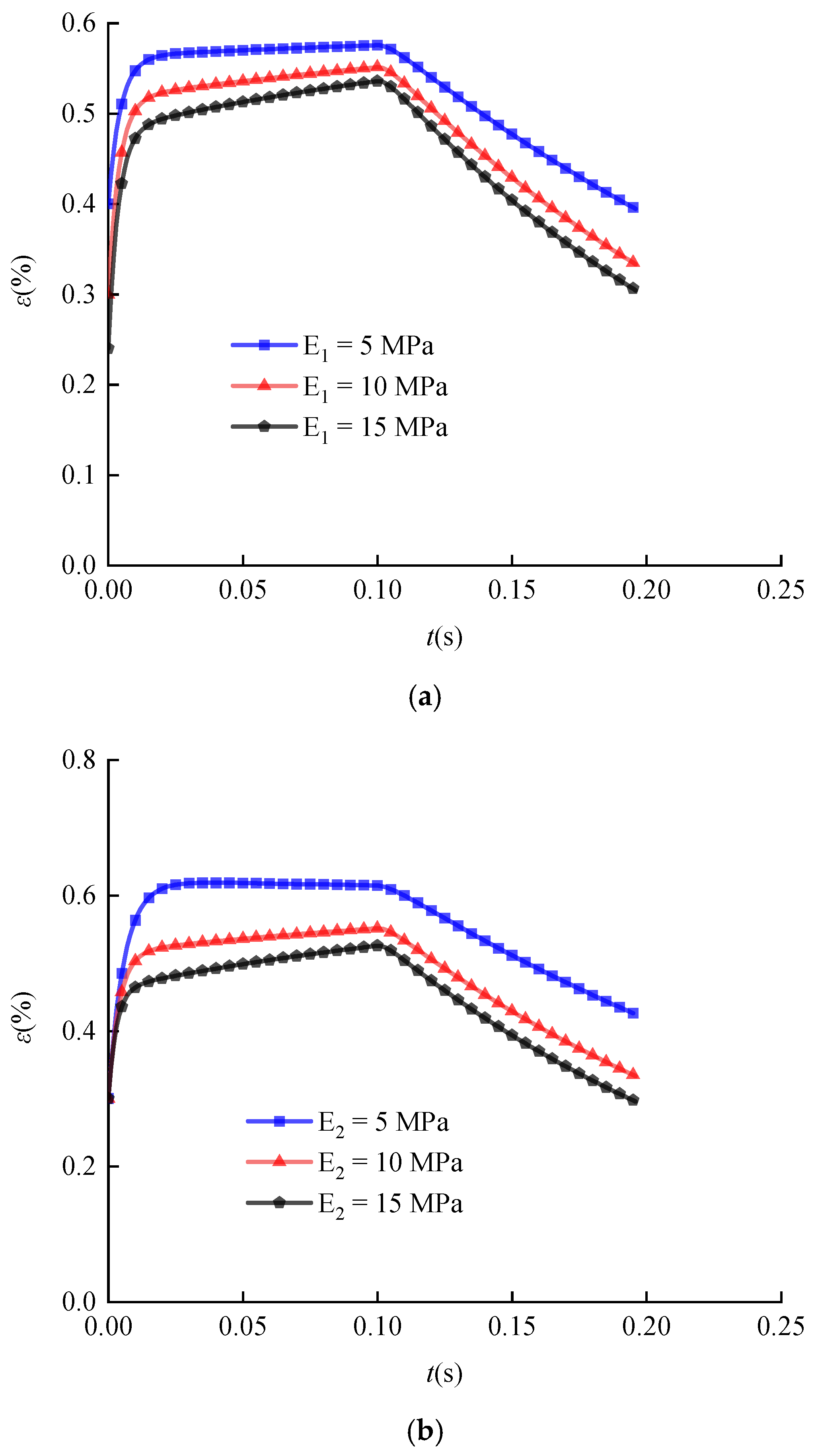
3.6. Discussion for the Long-term Deformation under Different Viscosity Coefficients and Elasticity Modulus
4. Conclusions
- This paper presented a DEM-based method to evaluate the short-term and long-term stability of coastal karst caves. The long-term settlements of sinkholes are mainly dependent on viscosity, and the short-term collapsing only appears in weak bedrocks, which causes a much larger final deformation.
- The local stress concentration surrounding caves brings potential risk to the local zones. If the bedrock has a relatively high strength, the presence of caves has little influence on the final modeling. In this study, when the value of rock strength reduced by 90%, the short-term and long-term behaviors of sinkholes were affected extensively.
- The modeling proposed in this paper can predict long-term deformation after foundation pit excavation, and the prediction error is less than 10%. The modeling process can be calibrated from geological borehole data and applied to other geotechnical engineering practices in coastal karst areas.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Al-Halbouni, D.; Holohan, E.P.; Taheri, A.; Schoepfer, M.P.J.; Emam, S.; Dahm, T. Geomechanical modelling of sinkhole development using distinct elements: Model verification for a single void space and application to the Dead Sea area. Solid Earth 2018, 9, 1341–1373. [Google Scholar] [CrossRef]
- Gutierrez, F.; Parise, M.; De Waele, J.; Jourde, H. A review on natural and human-induced geohazards and impacts in karst. Earth-Sci. Rev. 2014, 138, 61–88. [Google Scholar] [CrossRef]
- Liu, Z.; Liang, J.; Zhu, S.; Tan, J. Stability analysis of soil cave foundation in karst area. Hydrogeol. Eng. Geol. 2003, 30, 24–28. [Google Scholar]
- Huang, F.; Zhang, M.; Jiang, Z. Collapse mode of rock mass induced by a concealed karst cave above a deep cavity. J. Cent. South Univ. 2019, 26, 1747–1754. [Google Scholar] [CrossRef]
- Jiang, C.; Liu, L.; Wu, J.-P. A new method determining safe thickness of karst cave roof under pile tip. J. Cent. South Univ. 2014, 21, 1190–1196. [Google Scholar] [CrossRef]
- Liu, Z.; Liang, J.; Zhu, S.; Zhang, G. Stability analysis of rock foundation with cave in karst area. Chin. J. Geotech. Eng. 2003, 25, 629–633. [Google Scholar]
- Wadas, S.H.; Polom, U.; Krawczyk, C.M. High-resolution shear-wave seismic reflection as a tool to image near-surface subrosion structures—A case study in Bad Frankenhausen, Germany. Solid Earth 2016, 7, 1491–1508. [Google Scholar] [CrossRef]
- Arkin, Y.; Gilat, A. Dead Sea sinkholes—An ever-developing hazard. Environ. Geol. 2000, 39, 711–722. [Google Scholar] [CrossRef]
- Polom, U.; Alrshdan, H.; Al-Halbouni, D.; Holohan, E.P.; Dahm, T.; Sawarieh, A.; Atallah, M.Y.; Krawczyk, C.M. Shear wave reflection seismic yields subsurface dissolution and subrosion patterns: Application to the Ghor Al-Haditha sinkhole site, Dead Sea, Jordan. Solid Earth 2018, 9, 1079–1098. [Google Scholar] [CrossRef]
- Taqieddin, S.A.; Abderahman, N.S.; Atallah, M. Sinkhole hazards along the eastern Dead Sea shoreline area, Jordan: A geological and geotechnical consideration. Environ. Geol. 2000, 39, 1237–1253. [Google Scholar] [CrossRef]
- Yechieli, Y.; Abelson, M.; Bein, A.; Crouvi, O.; Shtivelman, V. Sinkhole “swarms” along the Dead Sea coast: Reflection of disturbance of lake and adjacent groundwater systems. Geol. Soc. Am. Bull. 2006, 118, 1075–1087. [Google Scholar] [CrossRef]
- Zheng, Y.; Qiu, C. On the Limitations of Protodyakonov’s Pressure Arch Theory. Mod. Tunn. Technol. 2016, 53, 1–8. [Google Scholar]
- Wang, Y.; Jing, H.; Zhang, Q.; Luo, N.; Yin, X. Prediction of Collapse Scope of Deep-Buried Tunnels Using Pressure Arch Theory. Math. Probl. Eng. 2016, 2016, 2628174. [Google Scholar] [CrossRef]
- Chen, C.-N.; Huang, W.-Y.; Tseng, C.-T. Stress redistribution and ground arch development during tunneling. Tunn. Undergr. Space Technol. 2011, 26, 228–235. [Google Scholar] [CrossRef]
- Li, L.C.; Tang, C.A.; Zhao, X.D.; Cai, M. Block caving-induced strata movement and associated surface subsidence: A numerical study based on a demonstration model. Bull. Eng. Geol. Environ. 2014, 73, 1165–1182. [Google Scholar] [CrossRef]
- Wang, S.R.; Wu, X.G.; Zhao, Y.H.; Hagan, P.; Cao, C. Evolution Characteristics of Composite Pressure-Arch in Thin Bedrock of Overlying Strata During Shallow Coal Mining. Int. J. Appl. Mech. 2019, 11, 1950030. [Google Scholar] [CrossRef]
- Zhou, P.; Jiang, Y.; Zhou, F.; Li, J.; Lin, M.; Lin, J.; Wang, Z. Study on pressure arch effect of xigeda strata tunnel based on experiment and discrete element simulation. Bull. Eng. Geol. Environ. 2022, 81, 199. [Google Scholar] [CrossRef]
- Al-Halbouni, D.; Holohan, E.P.; Taheri, A.; Watson, R.A.; Polom, U.; Schopfer, M.P.J.; Emam, S.; Dahm, T. Distinct element geomechanical modelling of the formation of sinkhole clusters within large-scale karstic depressions. Solid Earth 2019, 10, 1219–1241. [Google Scholar] [CrossRef]
- Carranza-Torres, C.; Reich, T. Analytical and numerical study of the stability of shallow underground circular openings in cohesive ground. Eng. Geol. 2017, 226, 70–92. [Google Scholar] [CrossRef]
- Carranza-Torres, C.; Fosnacht, D.; Hudak, G. Geomechanical analysis of the stability conditions of shallow cavities for Compressed Air Energy Storage (CAES) applications. Geomech. Geophys. Geo-Energy Geo-Resour. 2017, 3, 131–174. [Google Scholar] [CrossRef]
- Ding, J.; Wan, X.; Hong, Z.; Wang, J.; Mou, C. Excess Pore Water Pressure Induced by Installation of Precast Piles in Soft Clay. Int. J. Geomech. 2021, 21, 05021002. [Google Scholar] [CrossRef]
- Liu, Z.; He, X.; Fan, J.; Zhou, C. Study on the Softening Mechanism and Control of Red-Bed Soft Rock under Seawater Conditions. J. Mar. Sci. Eng. 2019, 7, 235. [Google Scholar] [CrossRef]
- Guo, L.; Jin, H.X.; Wang, J.; Shi, L. Undrained monotonic shear behavior of marine soft clay after long-term cyclic loading. Mar. Georesour. Geotechnol. 2020, 38, 854–866. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, C.; Li, B.; Zhang, L.; Liang, Y. Effects of grain dissolution-diffusion sliding and hydro-mechanical interaction on the creep deformation of soft rocks. Acta Geotech. 2020, 15, 1219–1229. [Google Scholar] [CrossRef]
- Zhang, R. Catastrophe analysis of deep tunnel above water-filled caves. J. Cent. South Univ. 2019, 26, 1820–1829. [Google Scholar] [CrossRef]
- Ren, F.; Zhang, D.; Cao, J.; Yu, M.; Li, S. Study on the Rock Mass Caving and Surface Subsidence Mechanism Based on an In Situ Geological Investigation and Numerical Analysis. Math. Probl. Eng. 2018, 2018, 6054145. [Google Scholar] [CrossRef]
- Guo, L.; Wang, S.; Sun, L.; Kang, Z.; Zhao, C. Numerical Simulation and Experimental Studies of Karst Caves Collapse Mechanism in Fractured-Vuggy Reservoirs. Geofluids 2020, 2020, 8817104. [Google Scholar] [CrossRef]
- Zhang, J.; Fang, C.; Zhu, J. Finite element phase analysis of karst-roof stability under pile foundation. J. Eng. Geol. 2014, 22, 78–85. [Google Scholar]
- Hu, Q.-g.; Zhang, K.-n.; Yang, J.-s. Finite element analysis of ultimate bearing capacity of strip footing above Karst cave. J. Cent. South Univ. (Sci. Technol.) 2005, 36, 694–697. [Google Scholar]
- Yang, J.; Zhang, J.; Zhang, Q.; Zhang, J. Finite element analysis of ultimate bearing capacity of circular footing above karst cave. Chin. J. Rock Mech. Eng. 2005, 24, 296–301. [Google Scholar]
- Slee, A.; McIntosh, P.D.; Woodward, C.; Wang, N.; Gadd, P. A rapid sediment pulse induced by glacial melting during the MIS 8/7e transition buried well-developed karst in the Railton Valley, Tasmania, Australia. Boreas 2022, 51, 185–200. [Google Scholar] [CrossRef]
- Hart, E.A. Dating and interpretation of recent clastic sediments in an urban cave. J. Cave Karst Stud. 2021, 83, 20–28. [Google Scholar] [CrossRef]
- Wang, J.; Zou, B.; Liu, Y.; Tang, Y.; Zhang, X.; Yang, P. Erosion-creep-collapse mechanism of underground soil loss for the karst rocky desertification in Chenqi village, Puding county, Guizhou, China. Environ. Earth Sci. 2014, 72, 2751–2764. [Google Scholar] [CrossRef]
- Yang, P.; Tang, Y.-Q.; Zhou, N.-Q.; Wang, J.-X.; She, T.-Y.; Zhang, X.-H. Characteristics of red clay creep in karst caves and loss leakage of soil in the karst rocky desertification area of Puding County, Guizhou, China. Environ. Earth Sci. 2011, 63, 543–549. [Google Scholar] [CrossRef]
- Salmi, E.F.; Nazem, M.; Giacomini, A. A Numerical Investigation of Sinkhole Subsidence Development over Shallow Excavations in Tectonised Weak Rocks: The Dolaei Tunnel’s Excavation Case. Geotech. Geol. Eng. 2017, 35, 1685–1716. [Google Scholar] [CrossRef]
- Fazio, N.L.; Perrotti, M.; Lollino, P.; Parise, M.; Vattano, M.; Madonia, G.; Di Maggio, C. A three-dimensional back-analysis of the collapse of an underground cavity in soft rocks. Eng. Geol. 2017, 228, 301–311. [Google Scholar] [CrossRef]
- Ezersky, M.G.; Legchenko, A.; Eppelbaum, L.; Al-Zoubi, A. Overview of the geophysical studies in the Dead Sea coastal area related to evaporite karst and recent sinkhole development. Int. J. Speleol. 2017, 46, 277–302. [Google Scholar] [CrossRef]
- Al-Halbouni, D.; Holohan, E.P.; Saberi, L.; Alrshdan, H.; Sawarieh, A.; Closson, D.; Walter, T.R.; Dahm, T. Sinkholes, subsidence and subrosion on the eastern shore of the Dead Sea as revealed by a close-range photogrammetric survey. Geomorphology 2017, 285, 305–324. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Xia, C.; Liu, Z.; Zhou, C. Burger’s Bonded Model for Distinct Element Simulation of the Multi-Factor Full Creep Process of Soft Rock. J. Mar. Sci. Eng. 2021, 9, 945. [Google Scholar] [CrossRef]
- Li, B.; Wong, R.C.K. Quantifying structural states of soft mudrocks. J. Geophys. Res. -Solid Earth 2016, 121, 3324–3347. [Google Scholar] [CrossRef]
- Pinyol, N.M.; Vaunat, J.; Alonso, E.E. A constitutive model for soft clayey rocks that includes weathering effects. Geotechnique 2007, 57, 137–151. [Google Scholar] [CrossRef]
- Maheshwari, P. Analysis of deformation of linear viscoelastic two layered laminated rocks. Int. J. Rock Mech. Min. Sci. 2021, 141, 104681. [Google Scholar] [CrossRef]
- Fahimifar, A.; Tehrani, F.M.; Hedayat, A.; Vakilzadeh, A. Analytical solution for the excavation of circular tunnels in a visco-elastic Burger’s material under hydrostatic stress field. Tunn. Undergr. Space Technol. 2010, 25, 297–304. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Lo Presti, D.C.F.; Pallara, O.; Cavallaro, A.; Jamiolkowski, M. Influence of reconsolidation techniques and strain rate on the stiffness of undisturbed clays from triaxial tests. Geotech. Test. J. 1999, 22, 211–225. [Google Scholar]
- Cheng, Y.; Wong, L.N.Y. A study on mechanical properties and fracturing behavior of Carrara marble with the flat-jointed model. Int. J. Numer. Anal. Methods Geomech. 2020, 44, 803–822. [Google Scholar] [CrossRef]
- Li, B.; Guo, L.; Zhang, F.-S. Macro-micro investigation of granular materials in torsional shear test. J. Cent. South Univ. 2014, 21, 2950–2961. [Google Scholar] [CrossRef]
- Lin, C.; Xia, C.; Liu, Z.; Zhou, C. A Comprehensive Correlation Study of Structured Soils in Coastal Area of South China about Structural Characteristics. J. Mar. Sci. Eng. 2022, 10, 508. [Google Scholar] [CrossRef]
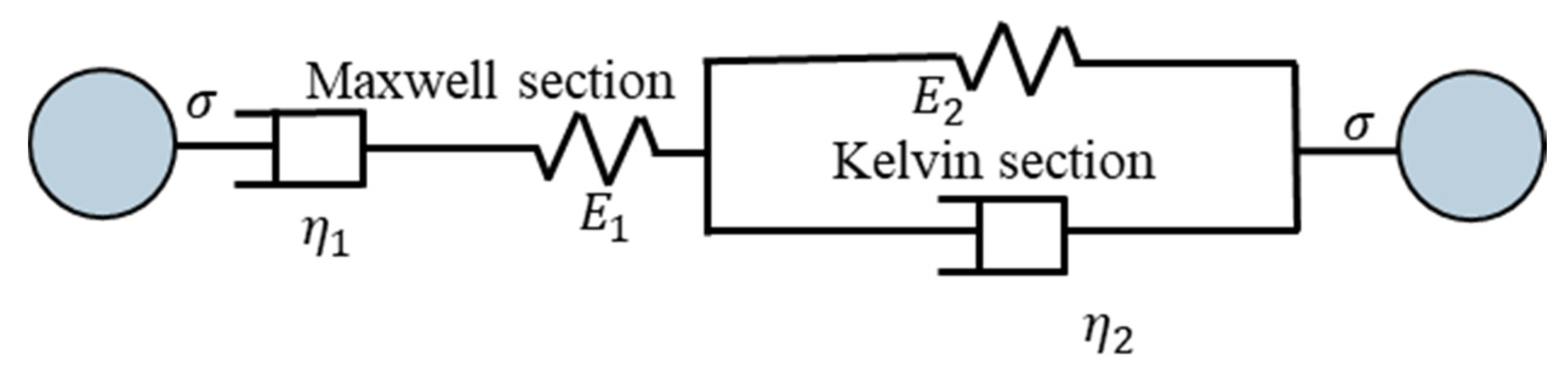








| Type of Model | Governing Equation | Creep Equation |
|---|---|---|
| Maxwell model | ||
| Kelvin model | ||
| Burger’s model |
| Soil Types | Unit Weight (kN/m3) | Modulus (MPa) | Friction Angle (°) | Cohesion (kPa) |
|---|---|---|---|---|
| Filled soil | 18.5 | 4.00 | 12.0 | 4.0 |
| Medium coarse sand | 20 | 4.00 | 12.0 | 4.0 |
| Clay | 20 | 7.00 | 18.0 | 20.0 |
| Rock Types | Uniaxial Strength (MPa) | Saturated Strength (MPa) | Modulus (MPa) | Unit Weight (kN/m3) |
|---|---|---|---|---|
| Limestone | 25 | 12 | 956 | 26 |
| Parameters Used in DEM Elastic Analysis | Value |
|---|---|
| PBM tensile strength (MPa) | 30 |
| PBM cohesion strength (MPa) | 11 |
| PBM modulus (GPa) | 0.6 |
| PBM friction angle (°) | 20 |
| Linear elastic modulus of “filled soil” and “coarse sand” (MPa) | 2 |
| Friction angle of “filled soil” and “coarse sand” (°) | 20 |
| Linear elastic modulus of “silty clay” (MPa) | 2.5 |
| Friction angle of “silty clay” (°) | 30 |
| Ratio of normal to shear stiffness | 1.2 |
| Particle friction coefficient | 0.57 |
| Density of particles (kg/m3) | 1850~2500 |
| Mean particle radius (mm) | 0.42 |
| Damping coefficient | 0.5 |
| Parameters used in DEM time-dependent analysis | |
| Kelvin viscosity coefficient (106) | 1 |
| Maxwell viscosity coefficient (106) | 2.5 |
| Kelvin modulus of rock (GPa) | 0.6 |
| Kelvin modulus of “filled soil” and “coarse sand” (MPa) | 2 |
| Kelvin modulus of “filled soil” and “coarse sand” (MPa) | 2 |
| Maxwell modulus of rock (GPa) | 0.6 |
| Maxwell modulus of “silty clay” (MPa) | 2 |
| Maxwell modulus of “silty clay” (MPa) | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.; Xia, C.; Zhang, H.; Liu, Z.; Zhou, C. Simulated Short- and Long-Term Deformation in Coastal Karst Caves. J. Mar. Sci. Eng. 2022, 10, 1315. https://doi.org/10.3390/jmse10091315
Lin C, Xia C, Zhang H, Liu Z, Zhou C. Simulated Short- and Long-Term Deformation in Coastal Karst Caves. Journal of Marine Science and Engineering. 2022; 10(9):1315. https://doi.org/10.3390/jmse10091315
Chicago/Turabian StyleLin, Chunxiu, Chang Xia, Hong Zhang, Zhen Liu, and Cuiying Zhou. 2022. "Simulated Short- and Long-Term Deformation in Coastal Karst Caves" Journal of Marine Science and Engineering 10, no. 9: 1315. https://doi.org/10.3390/jmse10091315
APA StyleLin, C., Xia, C., Zhang, H., Liu, Z., & Zhou, C. (2022). Simulated Short- and Long-Term Deformation in Coastal Karst Caves. Journal of Marine Science and Engineering, 10(9), 1315. https://doi.org/10.3390/jmse10091315







