Solitary Wave Interaction with a Floating Pontoon Based on Boussinesq Model and CFD-Based Simulations
Abstract
:1. Introduction
2. Mathematical Model Based on Boussinesq Equations
2.1. Governing Equations of the Interior Region and Matching Conditions
2.2. Velocity Potential in Interior Region
2.3. Solitary Waveform in Outer Region
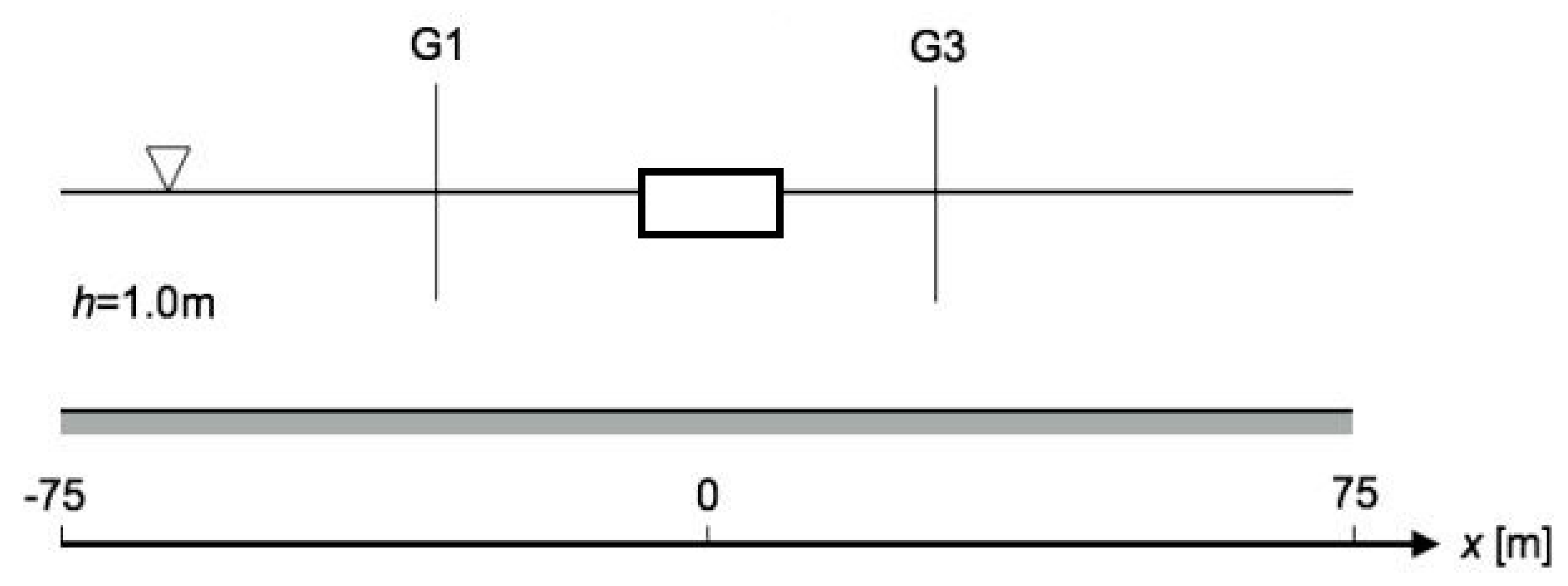
3. Description of Numerical Models
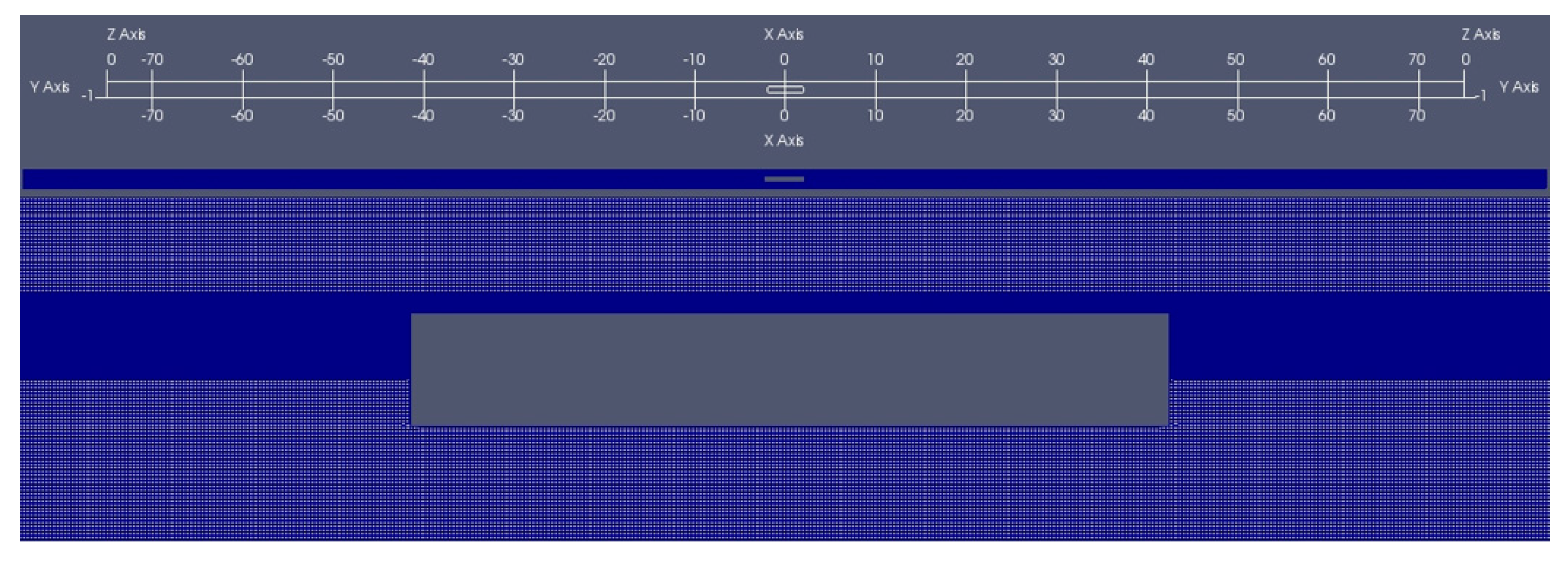
3.1. Brief Description of the CFD Model
CFD Setup
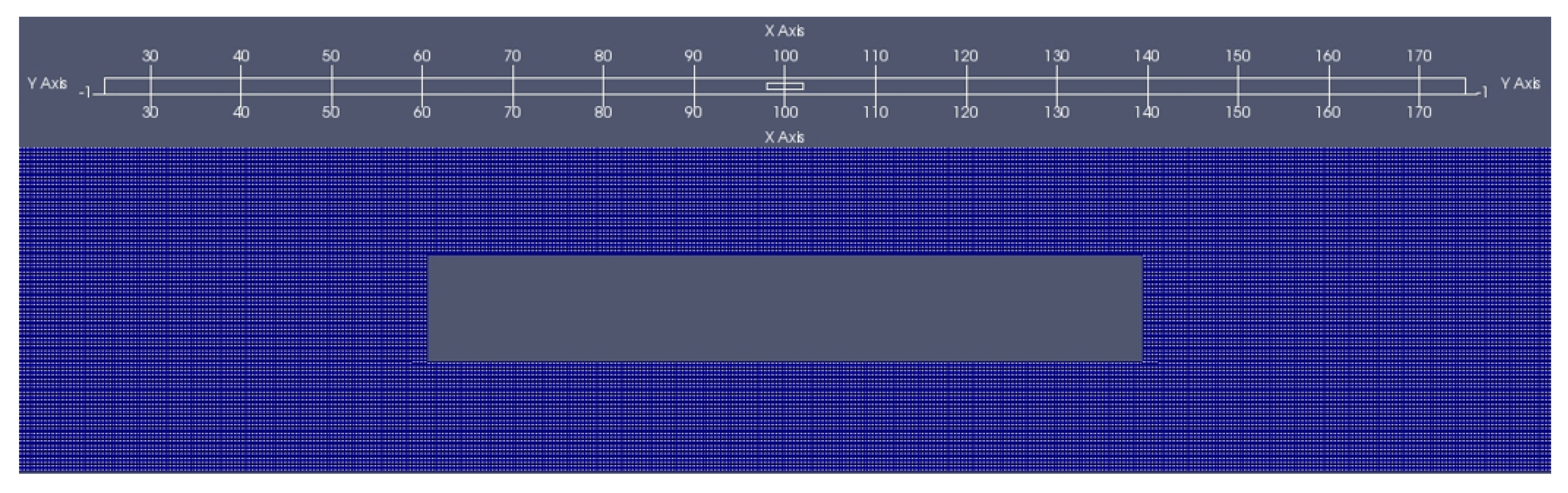
3.2. OceanWave3D Model Description
OceanWave3D Setup
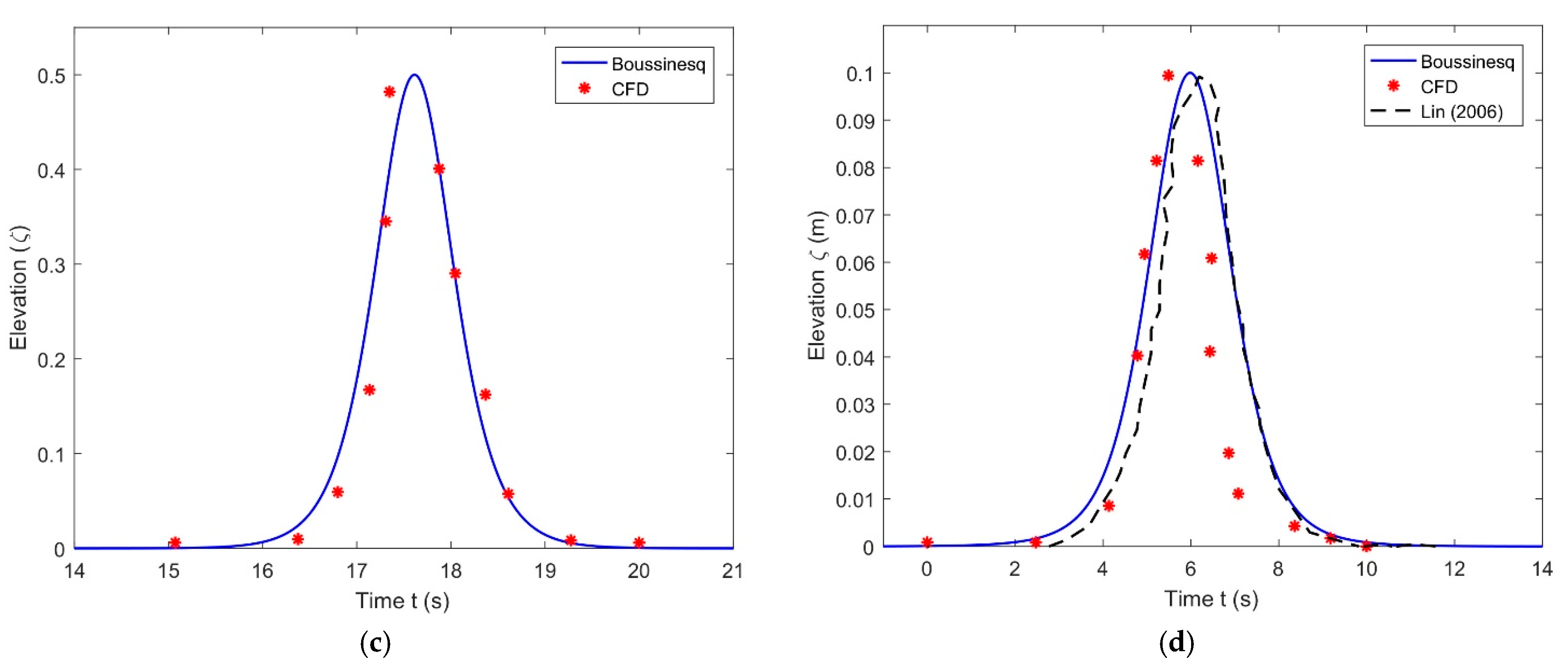
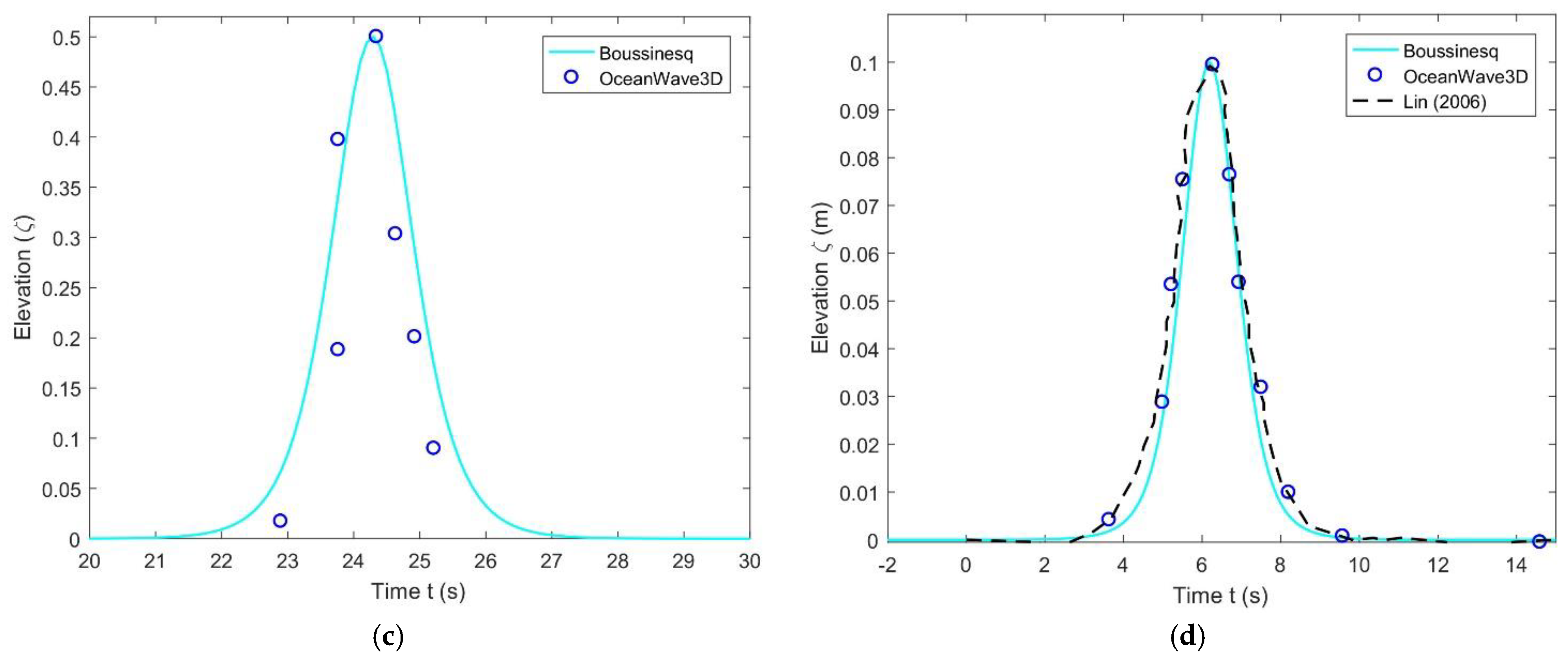
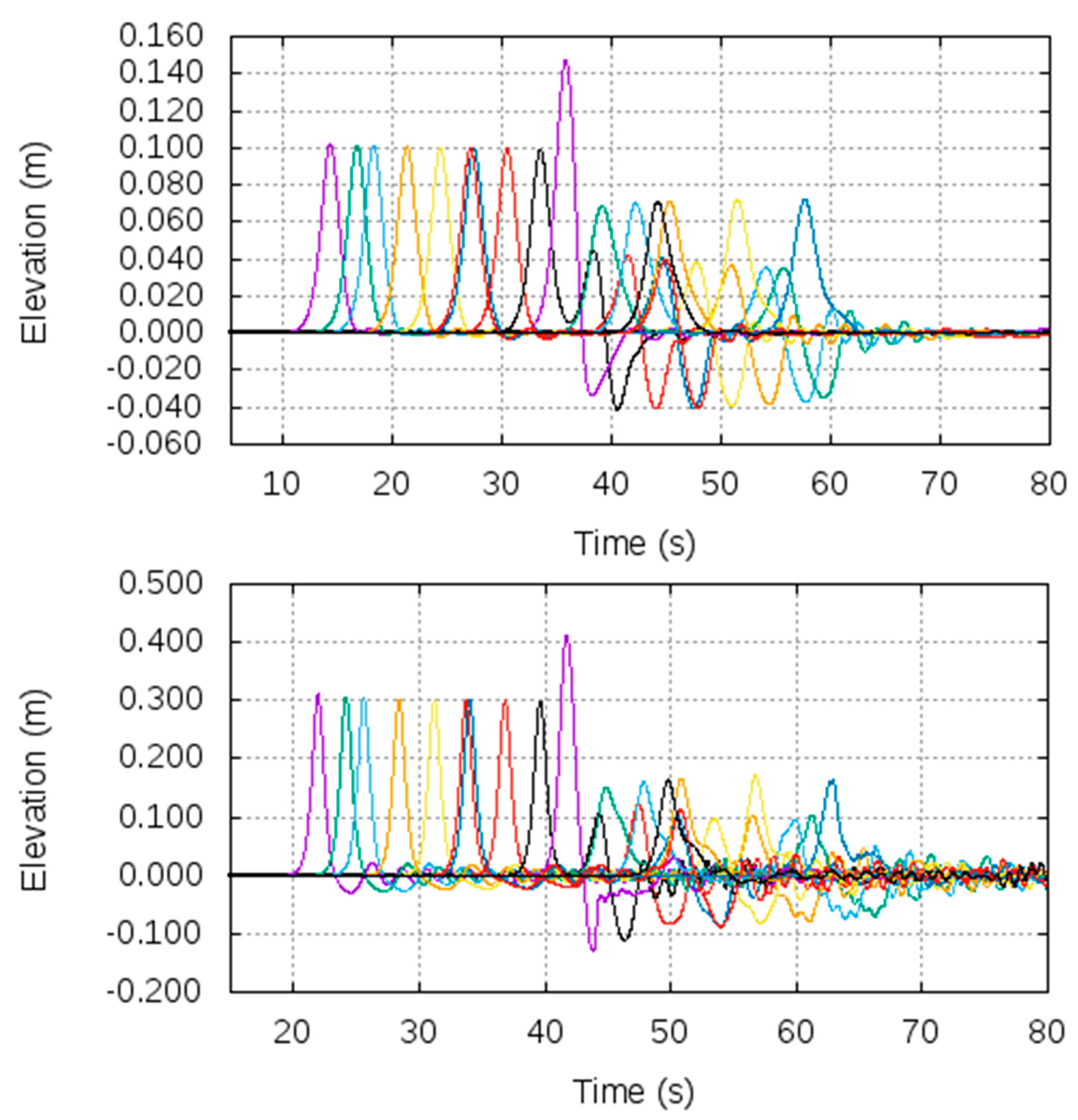
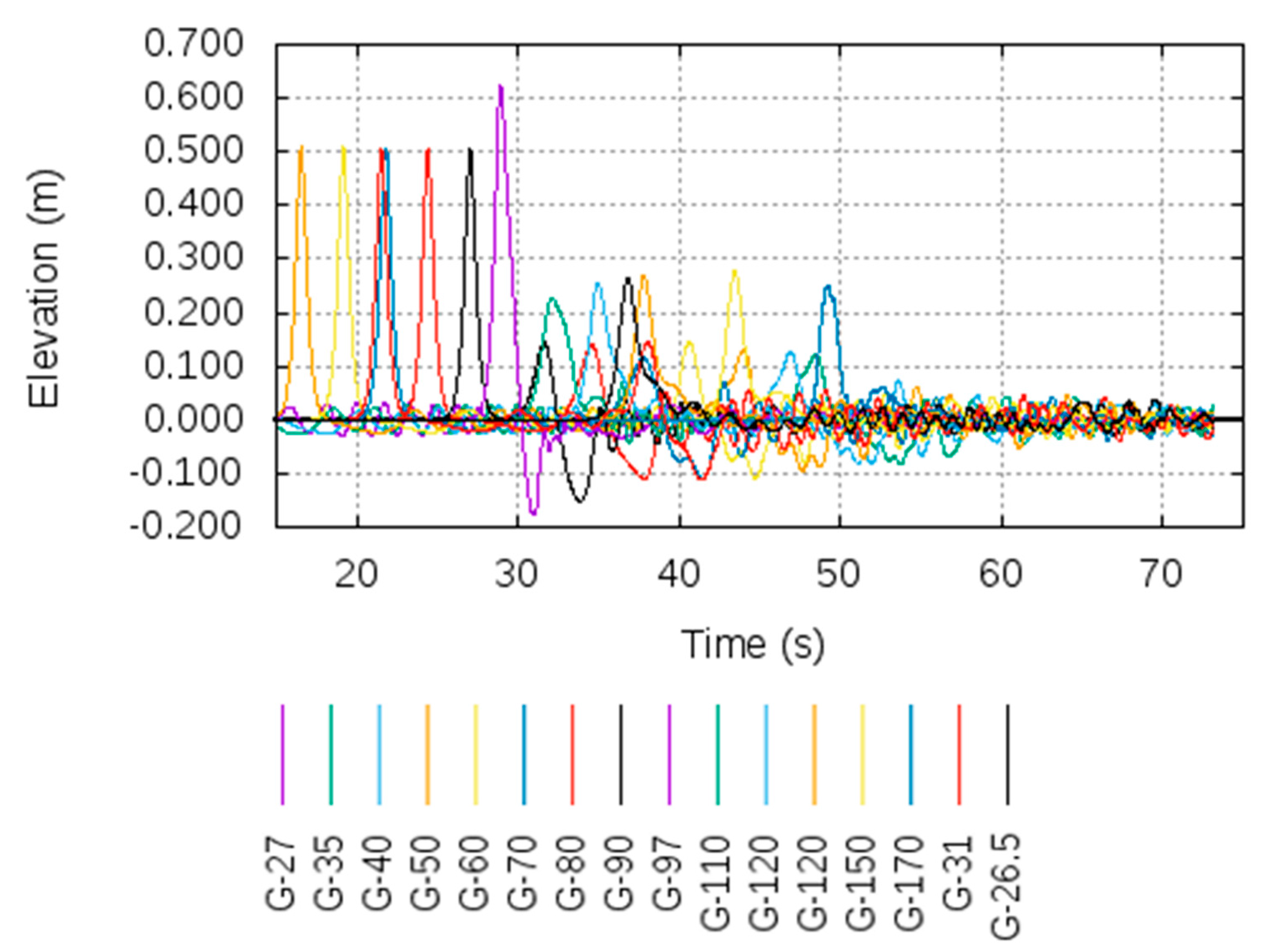
4. Comparison of Wave Elevation from Different Models
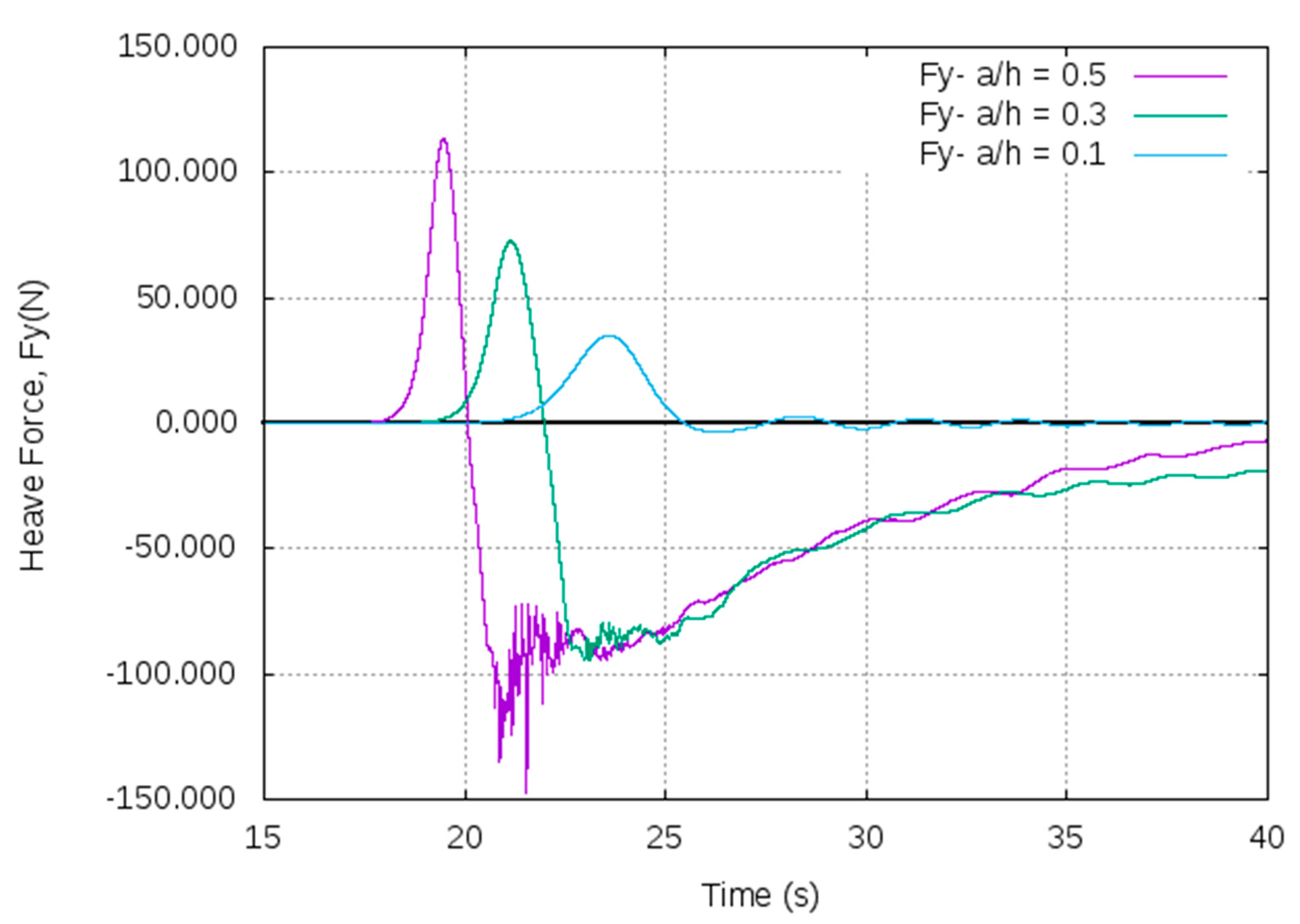
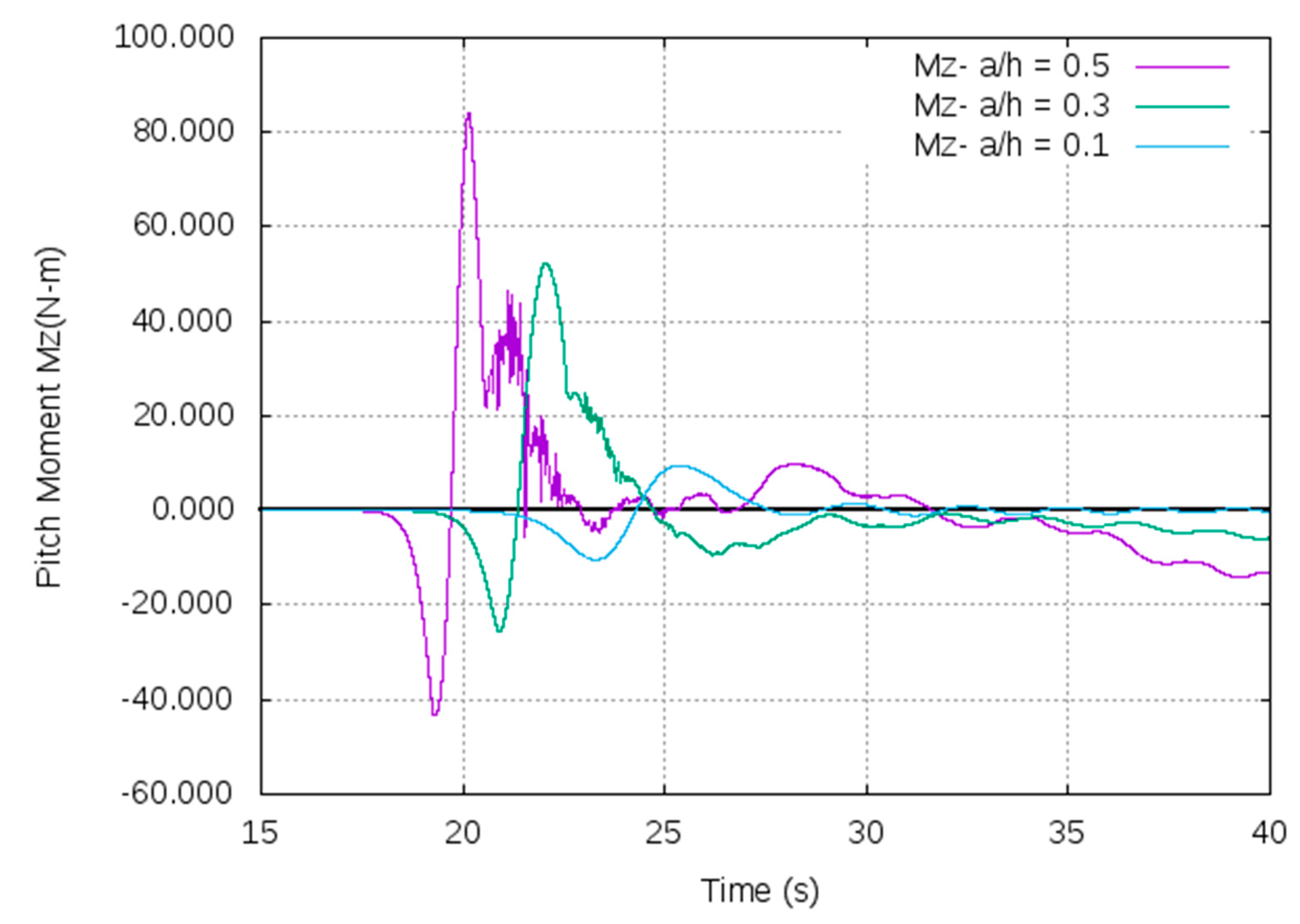
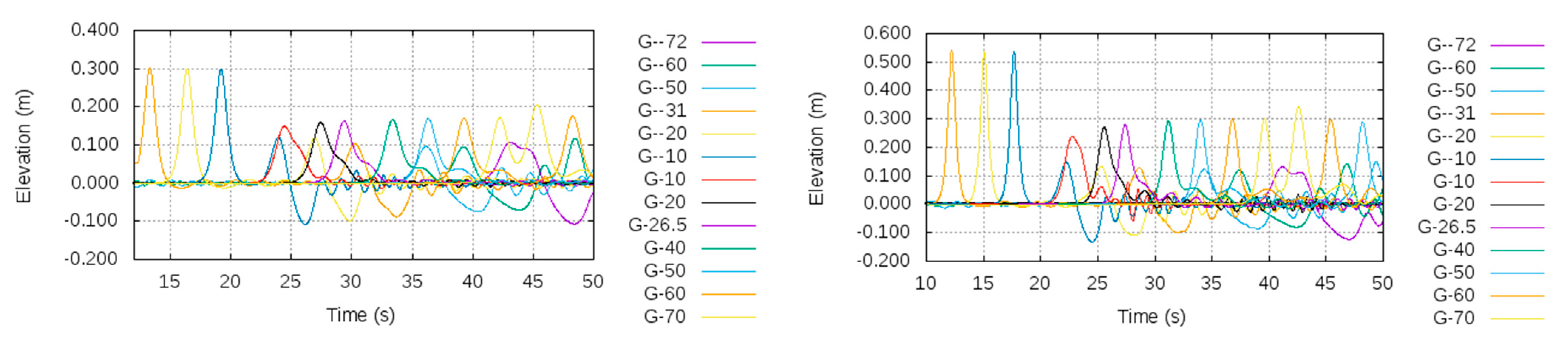
5. Analysis of Results from CFD, OceanWave3D, and Analytical Model Simulations
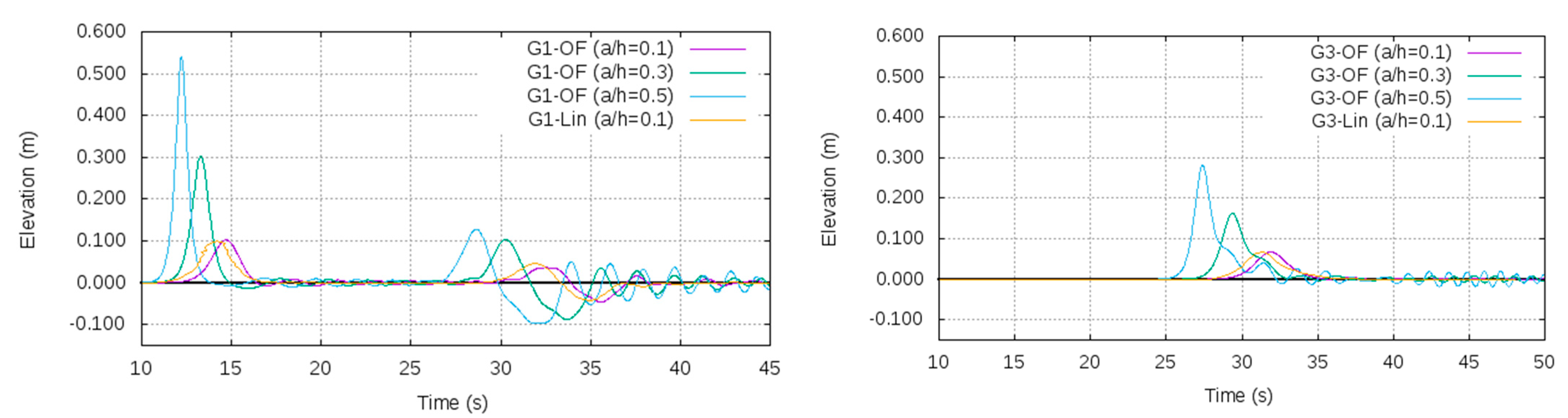
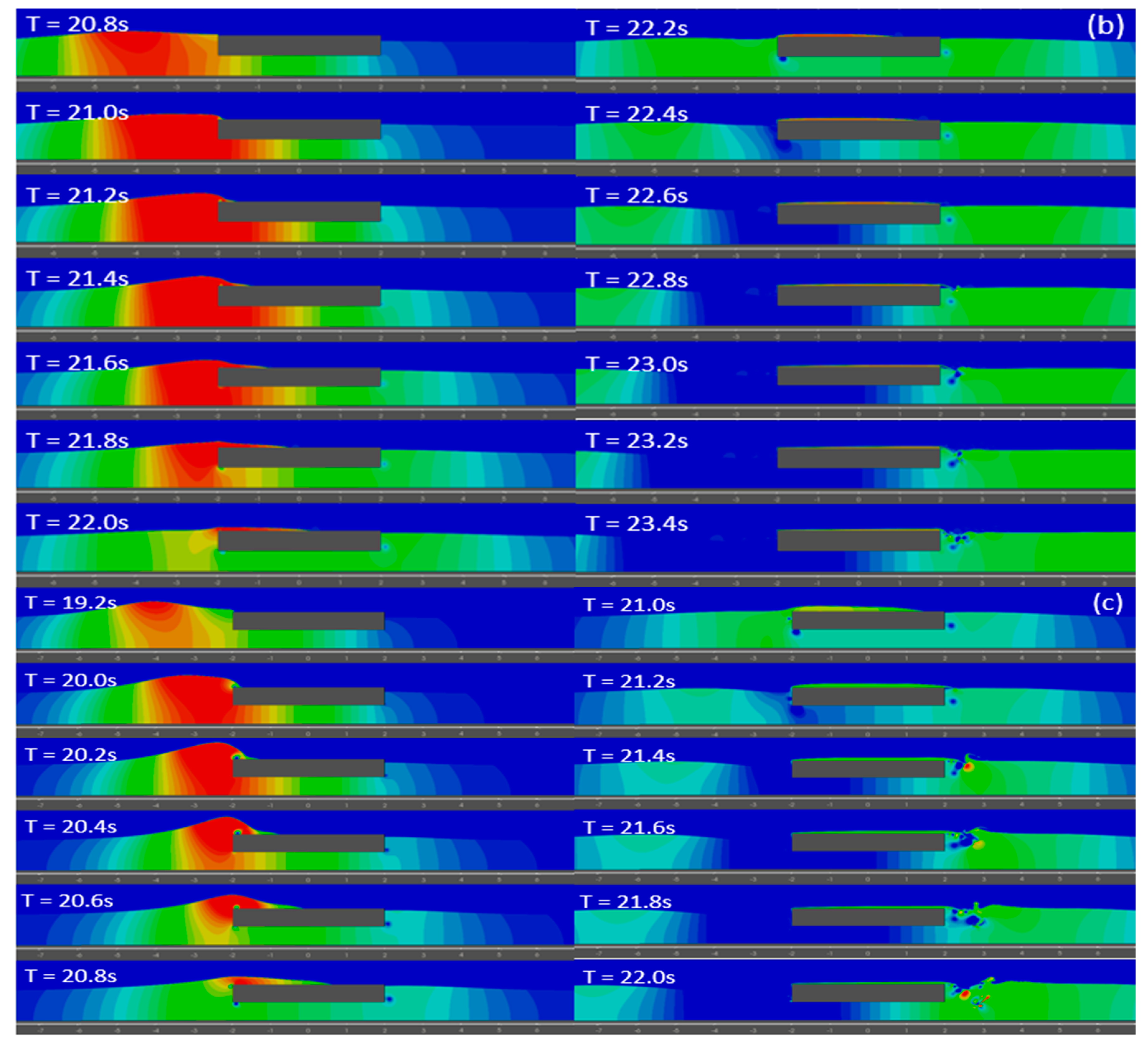
5.1. Solitary Waveform Generated Using the Chappelear Model (Waves2Foam)
5.2. Solitons Generated Using the OceanWave3D Model
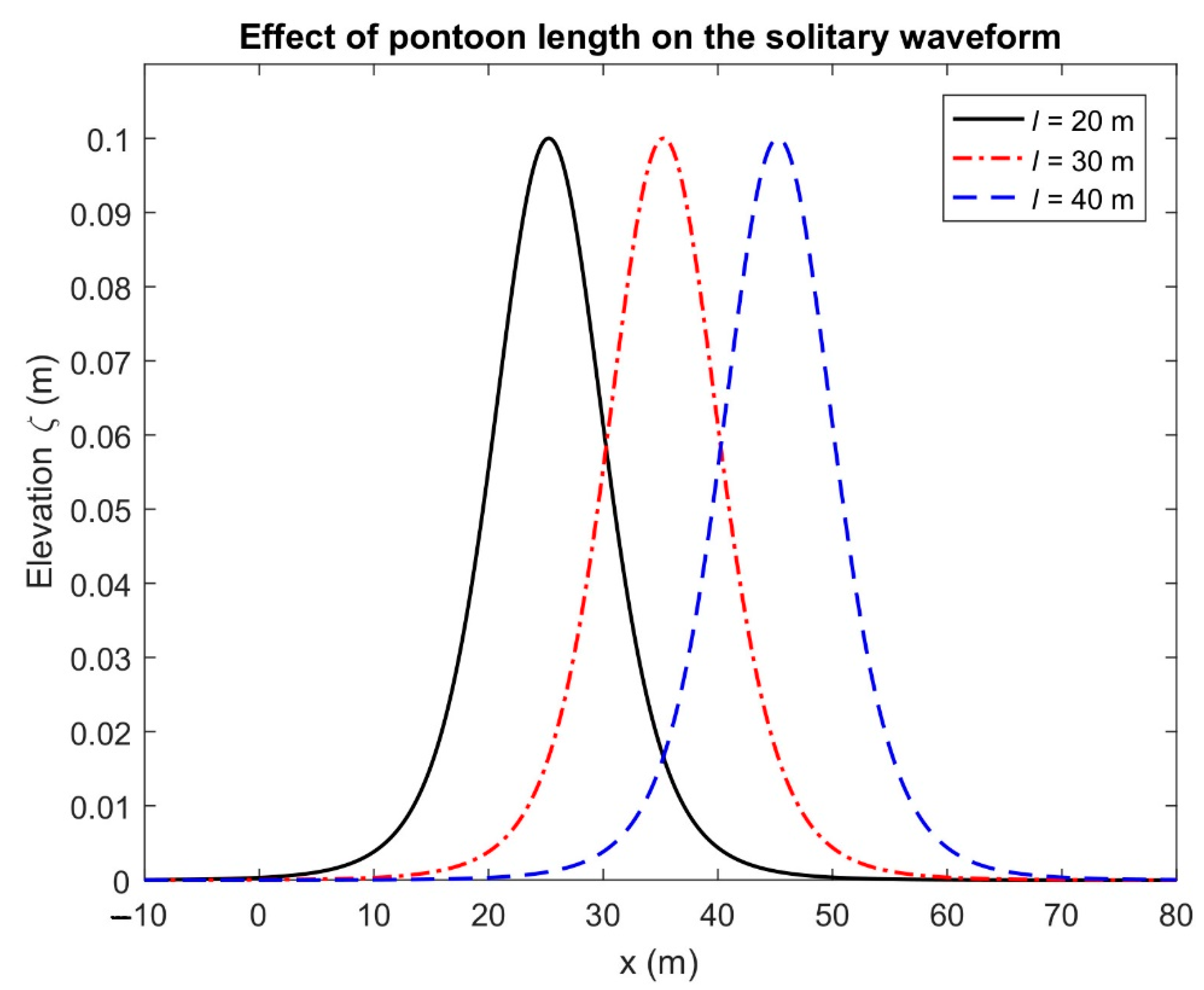
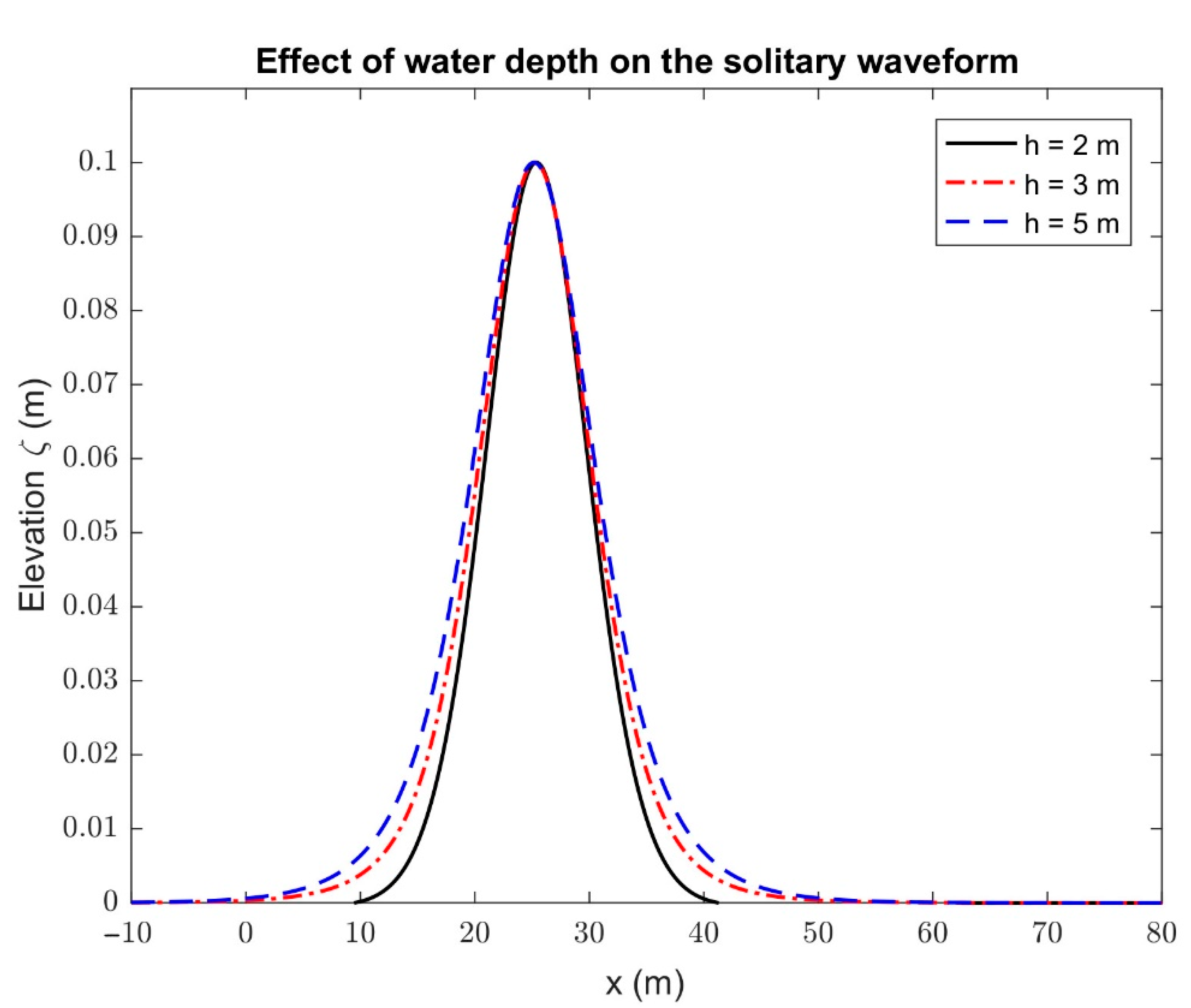
5.3. Behavior of Solitary Waves Based on Analytical Solution
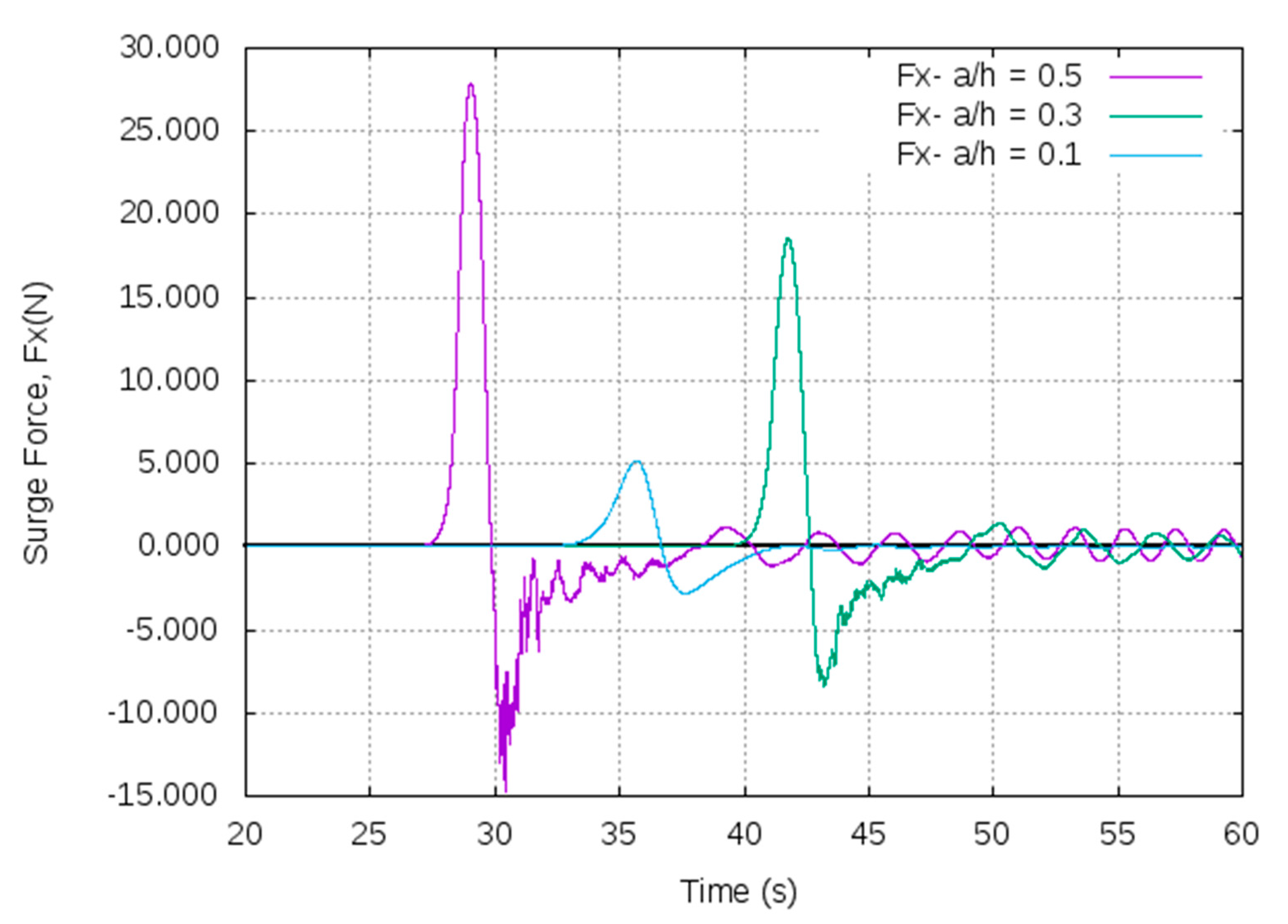
5.4. Wave Energy Analysis
6. Conclusions
- The compared results of the analytical model showed that the solitary waveform in the outer region is very close to CFD, OceanWave3D, and previous numerical results from the literature.
- From both the CFD and OceanWave3D, the analysis of wave forces indicated that with the increase in the amplitude of solitons, the surge and heave force gradually increase. The quantitative information is important to ensure station keeping of such structures. Further, the heave force encountered by the pontoon is substantially larger than the encountered surge force, which confirms the higher potential for application of the OWC type devices. The pressure distribution around the pontoon indicates that vortices are observed at the sharp ends of the pontoon, which might induce vibration and erosion of structure.
- The higher the initial soliton amplitude, the higher the loss of energy during interaction with the pontoon, and the higher the dissipation of energy into the dispersive tail.
- The Ursell number has a significant effect on the solitary wave profiles than those of water depth and pontoon length.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mohapatra, S.C.; Guedes Soares, C. Comparing solutions of the coupled Boussinesq equations in shallow water. In Maritime Technology and Engineering; Guedes Soares, C., Santos, T.A., Eds.; Taylor & Francis Group: London, UK, 2015; pp. 947–954. ISBN 978-1-138-02727-5. [Google Scholar]
- Mohapatra, S.C.; Fonseca, R.B.; Guedes Soares, C. A comparison between analytical and numerical simulations of solutions of the coupled Boussinesq equations. In Maritime Technology and Engineering; Guedes Soares, C., Santos, T.A., Eds.; Taylor & Francis Group: London, UK, 2016; pp. 1175–1180. ISBN 978-1-138-03000-8. [Google Scholar]
- Mohapatra, S.C.; Fonseca, R.B.; Guedes Soares, C. Comparison of analytical and numerical simulations of long nonlinear internal waves in shallow water. J. Coast. Res. 2018, 34, 928–938. [Google Scholar] [CrossRef]
- Hallak, T.S.; Islam, H.; Mohapatra, S.C.; Guedes Soares, C. Comparing numerical and analytical solutions of solitary water waves over finite and variable depth. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Cancún, Mexico, 5–6 April 2021; ASME: New York, NY, USA, 2021. Paper No: OMAE2021-62642, V006T06A062. [Google Scholar]
- Chang, C.H. Interaction of a Solitary Wave with Vertical Fully/Partially Submerged Circular Cylinders with/without a Hollow Zone. J. Mar. Sci. Eng. 2020, 8, 1022. [Google Scholar] [CrossRef]
- Wang, Q.; Fang, Y.; Liu, H. An experimental study of run-up and loads on a vertical truncated cylinder in a solitary wave. Ocean Eng. 2021, 219, 108346. [Google Scholar] [CrossRef]
- Mohapatra, S.C.; Islam, H.; Guedes Soares, C. Boussinesq Model and CFD Simulations of Non-Linear Wave Diffraction by a Floating Vertical Cylinder. J. Mar. Sci. Eng. 2020, 8, 575. [Google Scholar] [CrossRef]
- Mohapatra, S.C.; Islam, H.; Guedes Soares, C. Wave diffraction by a floating fixed truncated vertical cylinder based on Boussinesq equations. In Advances in Renewable Energies Offshore; Guedes Soares, C., Ed.; Taylor & Francis Group: London, UK, 2019; pp. 281–289. ISBN 978-1-138-58535-5. [Google Scholar]
- Lu, X.; Wang, K.H. Modeling a solitary wave interaction with a fixed floating body using an integrated analytical–numerical approach. Ocean Eng. 2015, 109, 691–704. [Google Scholar] [CrossRef]
- Sun, J.I.; Wang, C.Z.; Wu, G.X.; Khoo, B.C. Fully nonlinear simulations of interactions between solitary waves and structures based on the finite element method. Ocean Eng. 2015, 108, 202–215. [Google Scholar] [CrossRef]
- Xiang, T.; Istrati, D.; Yim, S.C.; Buckle, I.G.; Lomonaco, P. Tsunami Loads on a Representative Coastal Bridge Deck: Experimental Study and Validation of Design Equations. J. Waterw. Port Coast. Ocean Eng. 2020, 146, 04020022. [Google Scholar] [CrossRef]
- Hasanpour, A.; Istrati, D. Extreme Storm Wave Impact on Elevated Coastal Buildings. In Proceedings of the 3rd International Conference on Natural Hazards & Infrastructure (ICONHIC2022), Athens, Greece, 5–7 July 2022. [Google Scholar]
- Zhu, H.; Wang, L.L.; Avital, E.J.; Tang, H.W.; Williams, J.J.R. Numerical Simulation of Shoaling Broad-Crested Internal Solitary Waves. J. Hydraul. Eng. 2017, 143, 04017006. [Google Scholar] [CrossRef]
- Seiffert, B.; Hayatdavoodi, M.; Ertekin, R.C. Experiments and computations of solitary-wave forces on a coastal-bridge deck. Part I: Flat plate. Coast. Eng. 2014, 88, 194–209. [Google Scholar] [CrossRef]
- Hayatdavoodi, M.; Seiffert, B.; Ertekin, R.C. Experiments and computations of solitary-wave forces on a coastal-bridge deck. Part II: Deck with girders. Coast. Eng. 2014, 88, 210–228. [Google Scholar] [CrossRef]
- Cuomo, G.; Shimosako, K.I.; Takahashi, S. Wave-in-deck loads on coastal bridges and the role of air. Coast. Eng. 2009, 56, 793–809. [Google Scholar] [CrossRef]
- Istrati, D.; Buckle, I.G.; Lomonaco, P.; Yim, S.; Itani, A. Tsunami induced forces in bridges: Large-scale experiment and the role of air-entrapment. Coast. Eng. Proc. 2017, 35, 1–14. [Google Scholar] [CrossRef]
- Martinelli, L.; Lamberti, A.; Gaeta, M.G.; Tirindelli, M.; Alderson, J.; Schimmels, S. Wave loads on exposed jetties: Description of large scale experiments and preliminary results. Coast. Eng. Proc. 2011, 32, 1–13. [Google Scholar] [CrossRef]
- Wu, N.-J.; Tsay, T.-K.; Chen, Y.-Y. Generation of stable solitary waves by a piston-type wave maker. Wave Motion 2014, 51, 240–255. [Google Scholar] [CrossRef]
- Goring, D.G. Tsunamis—The Propagation of Long Waves onto a Shelf. In W. M. Keck Laboratory of Hydraulics and Water Resources; California Institute of Technology: Pasadena, CA, USA, 1978. [Google Scholar]
- Wu, N.J.; Hsiao, S.C.; Chen, H.H.; Yang, R.Y. The study on solitary waves generated by a piston-type wave maker. Ocean Eng. 2016, 117, 114–129. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, Z.; Liu, Y. Numerical study of solitary wave interaction with a vegetated platform. Ocean Eng. 2019, 192, 106561. [Google Scholar] [CrossRef]
- Martins, K.; Bonneton, P.; Michallet, H. Dispersive characteristics of nonlinear waves propagating and breaking over a mildly sloping laboratory beach. Coast. Eng. 2021, 167, 103917. [Google Scholar] [CrossRef]
- Gadelho, J.F.M.; Mohapatra, S.C.; Guedes Soares, C. CFD analysis of a fixed floating box-type structure under regular waves. In Development in Maritime Transportation and Harvesting of Sea Resources; Guedes Soares, C., Teixeira, Â.P., Eds.; Taylor & Francis Group: London, UK, 2017; pp. 513–520. [Google Scholar]
- Jasak, H. OpenFOAM: Open source CFD in research and industry. Int. J. Nav. Archit. Ocean Eng. 2009, 1, 89–94. [Google Scholar]
- Jacobsen, N.G.; Fuhrman, D.R.; Fredsoe, J. A wave generation toolbox for the open-source CFD library: OpenFOAM. Int. J. Numer. Methods Fluids 2011, 70, 1073–1088. [Google Scholar] [CrossRef]
- Chappelear, J.E. Shallow-water waves. J. Geophys. Res. 1962, 67, 4693–4704. [Google Scholar] [CrossRef]
- Islam, H.; Mohapatra, S.C.; Gadelho, J.; Guedes Soares, C. OpenFOAM analysis of the wave radiation by a box-type floating structure. Ocean Eng. 2019, 193, 106532. [Google Scholar] [CrossRef]
- Engsig-Karup, A.P.; Bingham, H.B.; Lindberg, O. An efficient flexible-order model for 3D nonlinear water waves. J. Comput. Phys. 2009, 228, 2100–2118. [Google Scholar] [CrossRef]
- Dutykh, D.; Clamond, D. Efficient computation of steady solitary gravity waves. Wave Motion 2014, 51, 86–99. [Google Scholar] [CrossRef]
- Lin, P. A multiple-layer σ-coordinate model for simulation of wave–structure interaction. Comput. Fluids 2006, 35, 147–167. [Google Scholar] [CrossRef]
- Rijnsdorp, D.P.; Zijlema, M. Simulating waves and their interactions with a restrained ship using a non-hydrostatic wave-flow model. Coast. Eng. 2016, 114, 119–136. [Google Scholar] [CrossRef]
- Sarfaraz, M.; Pak, A. SPH numerical simulation of tsunami wave forces impinged on bridge superstructures. Coast. Eng. 2017, 121, 145–157. [Google Scholar] [CrossRef]
- Istrati, D.; Buckle, I.; Lomonaco, P.; Yim, S. Deciphering the tsunami wave impact and associated connection forces in open-girder coastal bridges. J. Mar. Sci. Eng. 2018, 6, 148. [Google Scholar] [CrossRef] [Green Version]







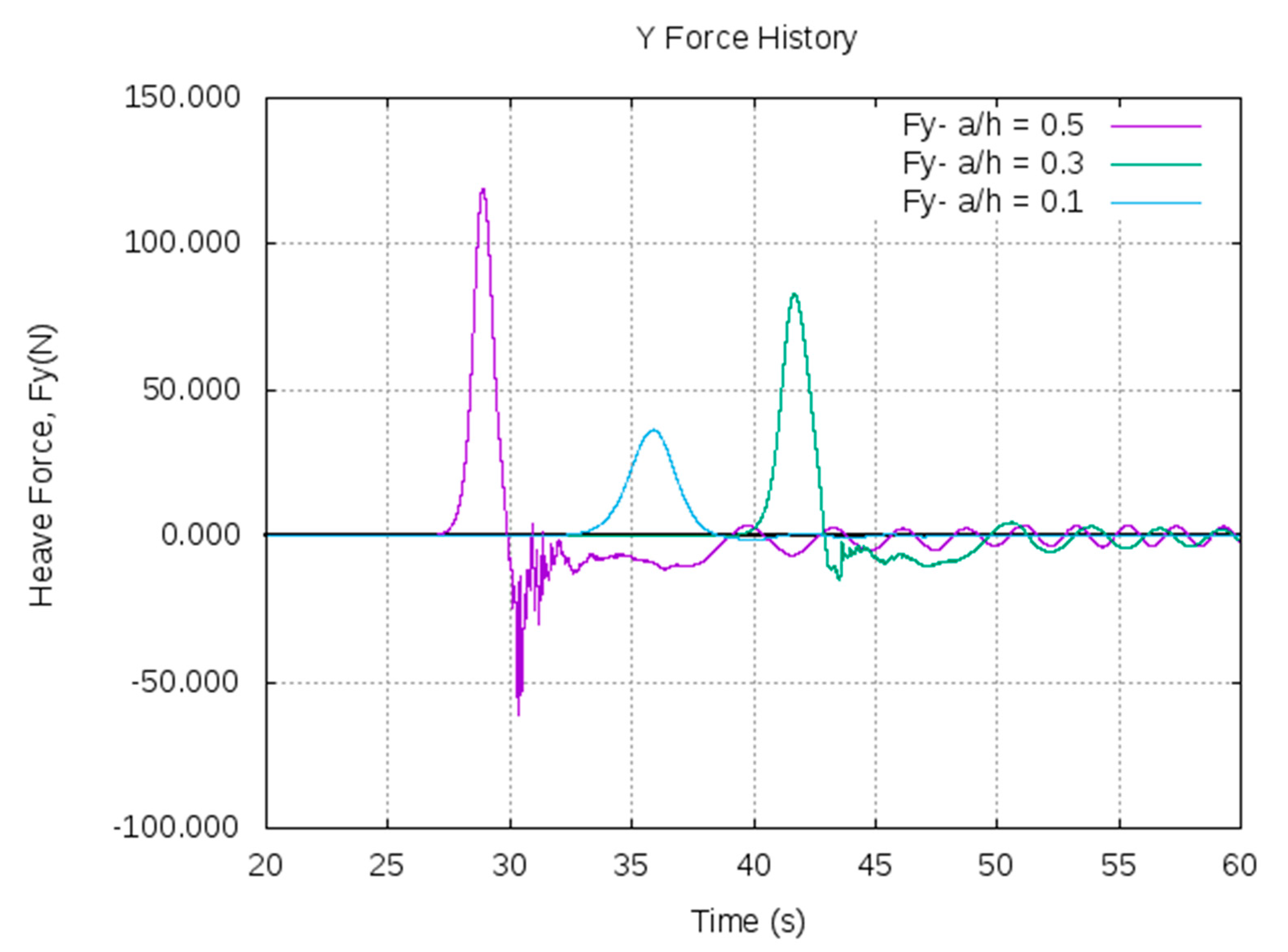
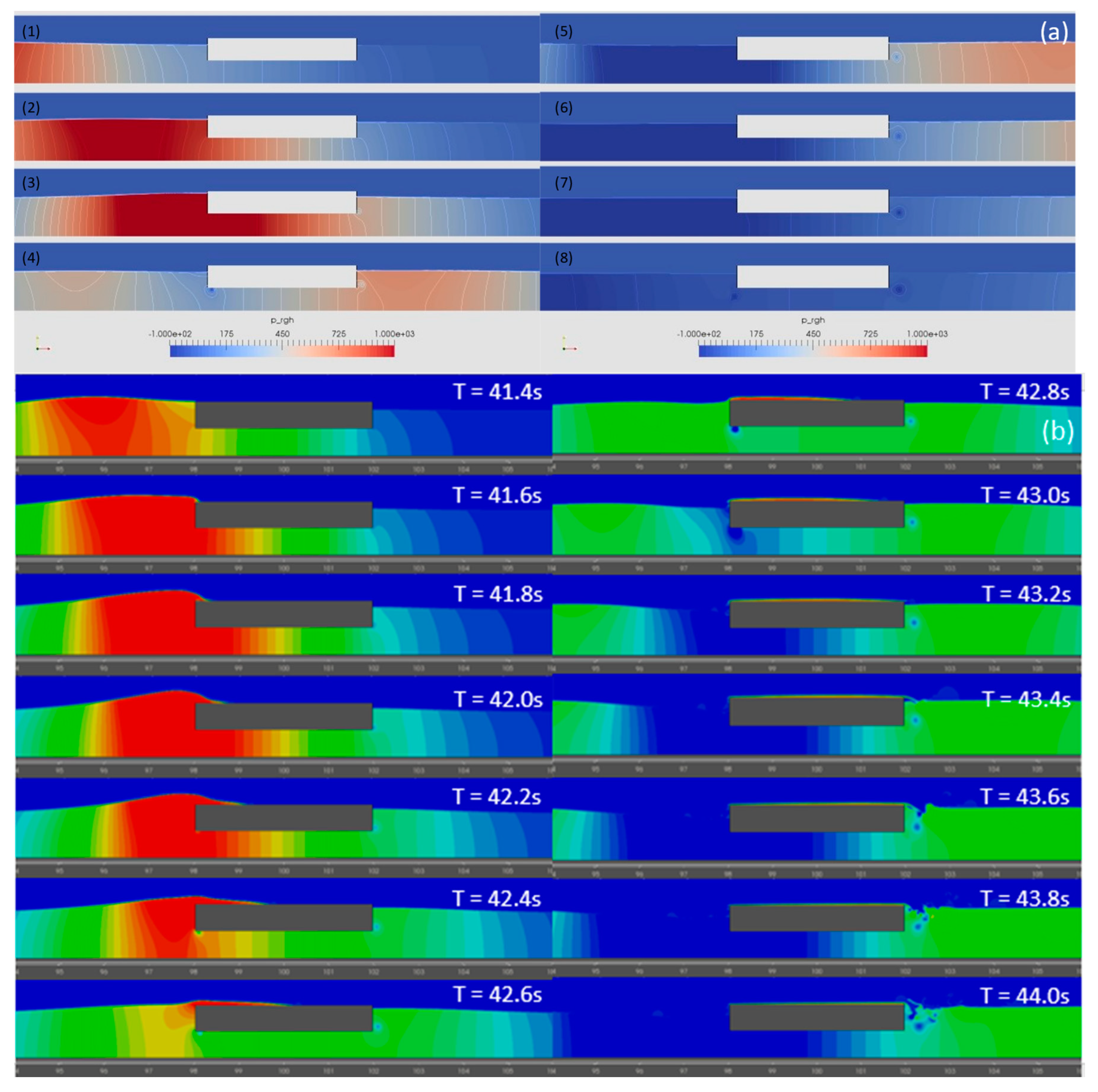
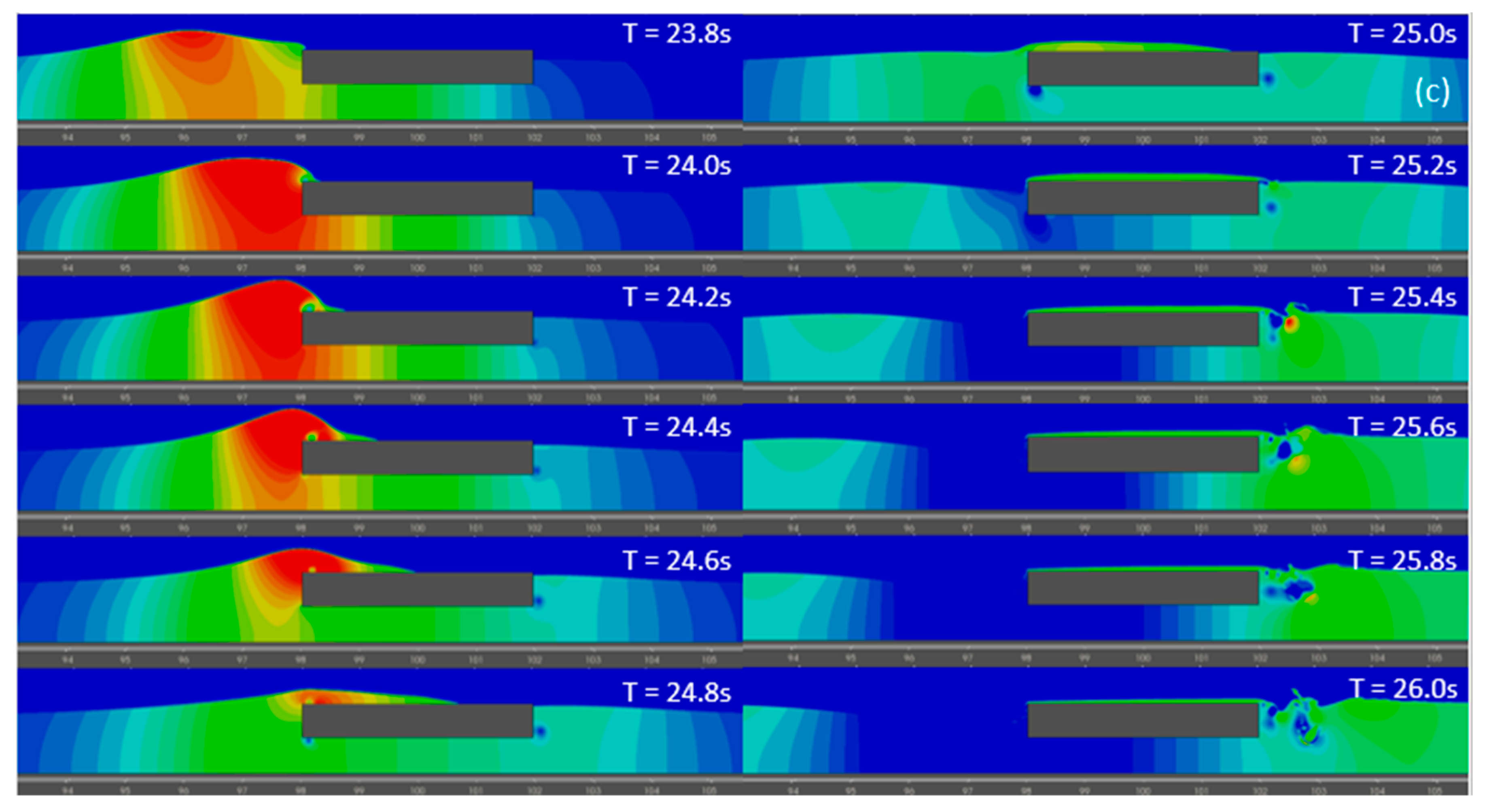
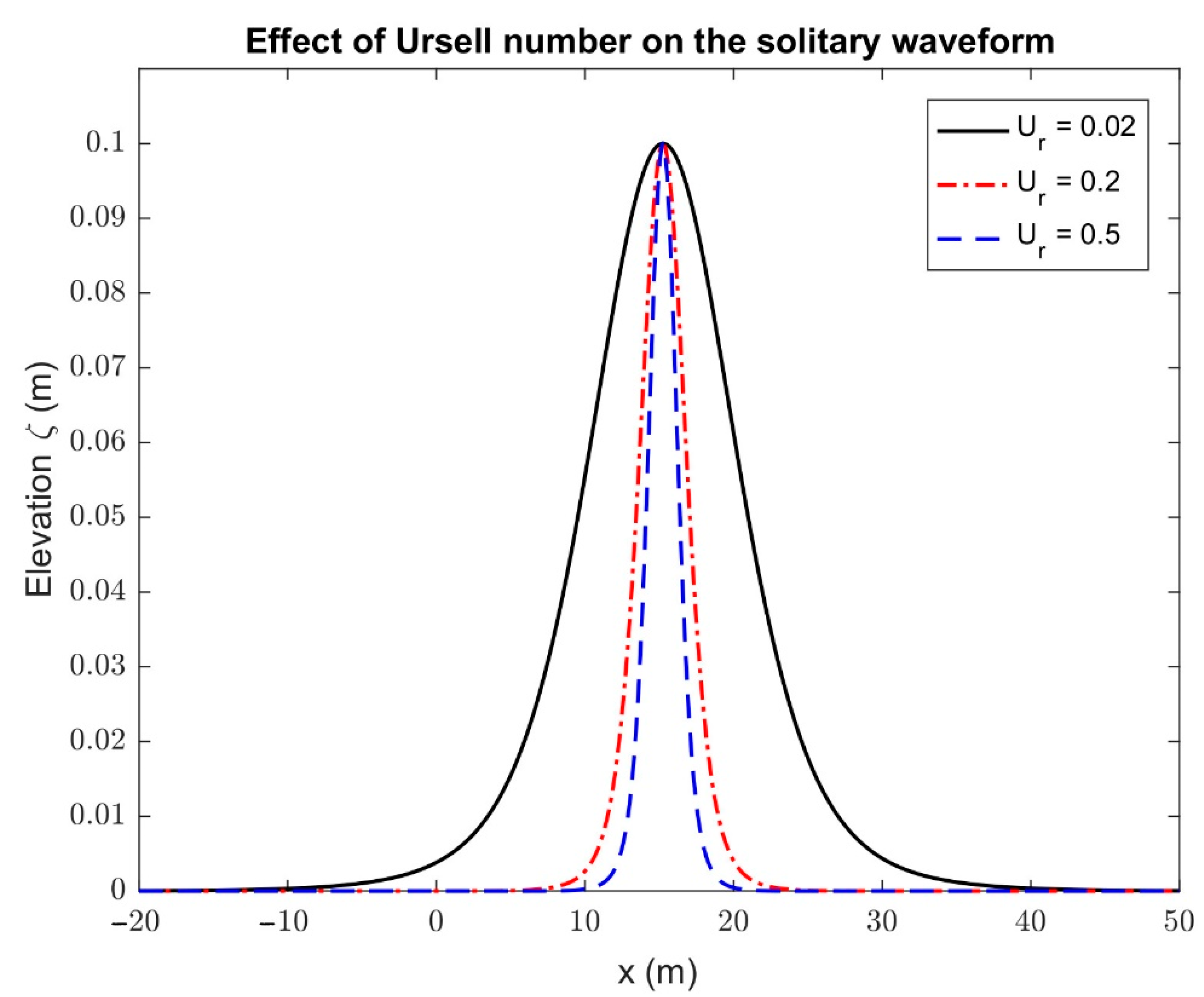
| Amplitude (a/h) | Input Energy (J) | Transmitted Energy (J) | Loss of Energy after Interaction | Loss of Amplitude after Interaction |
|---|---|---|---|---|
| 0.1 | 5.10 × 10−2 | 2.76 × 10−2 | 46% | 33% |
| 0.3 | 2.82 × 10−1 | 1.23 × 10−1 | 57% | 41% |
| 0.5 | 6.87 × 10−1 | 2.71 × 10−1 | 60% | 45% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohapatra, S.C.; Islam, H.; Hallak, T.S.; Soares, C.G. Solitary Wave Interaction with a Floating Pontoon Based on Boussinesq Model and CFD-Based Simulations. J. Mar. Sci. Eng. 2022, 10, 1251. https://doi.org/10.3390/jmse10091251
Mohapatra SC, Islam H, Hallak TS, Soares CG. Solitary Wave Interaction with a Floating Pontoon Based on Boussinesq Model and CFD-Based Simulations. Journal of Marine Science and Engineering. 2022; 10(9):1251. https://doi.org/10.3390/jmse10091251
Chicago/Turabian StyleMohapatra, Sarat Chandra, Hafizul Islam, Thiago S. Hallak, and C. Guedes Soares. 2022. "Solitary Wave Interaction with a Floating Pontoon Based on Boussinesq Model and CFD-Based Simulations" Journal of Marine Science and Engineering 10, no. 9: 1251. https://doi.org/10.3390/jmse10091251
APA StyleMohapatra, S. C., Islam, H., Hallak, T. S., & Soares, C. G. (2022). Solitary Wave Interaction with a Floating Pontoon Based on Boussinesq Model and CFD-Based Simulations. Journal of Marine Science and Engineering, 10(9), 1251. https://doi.org/10.3390/jmse10091251









