Shipping Decarbonization: An Overview of the Different Stern Hydrodynamic Energy Saving Devices
Abstract
1. Introduction
2. Background
2.1. Target Ships
2.2. Propulsive Coefficients
2.3. How to Find the Correct ESD?
3. Typical ESD Features
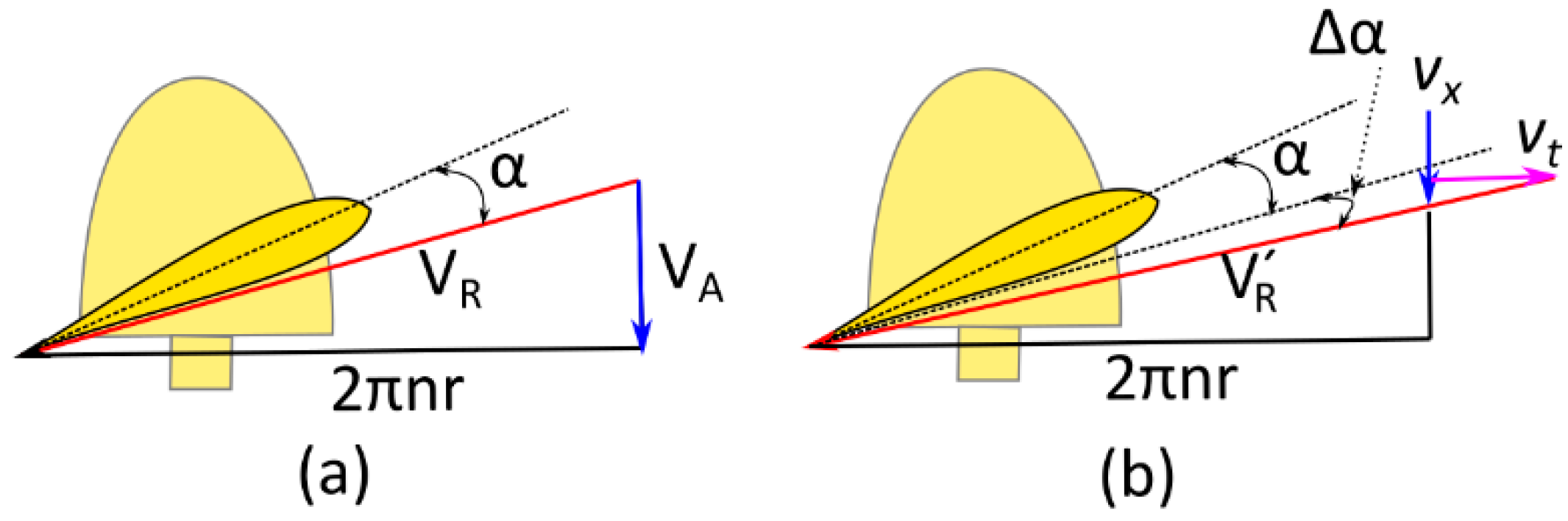
3.1. Pre-Swirl Stator (PSS)
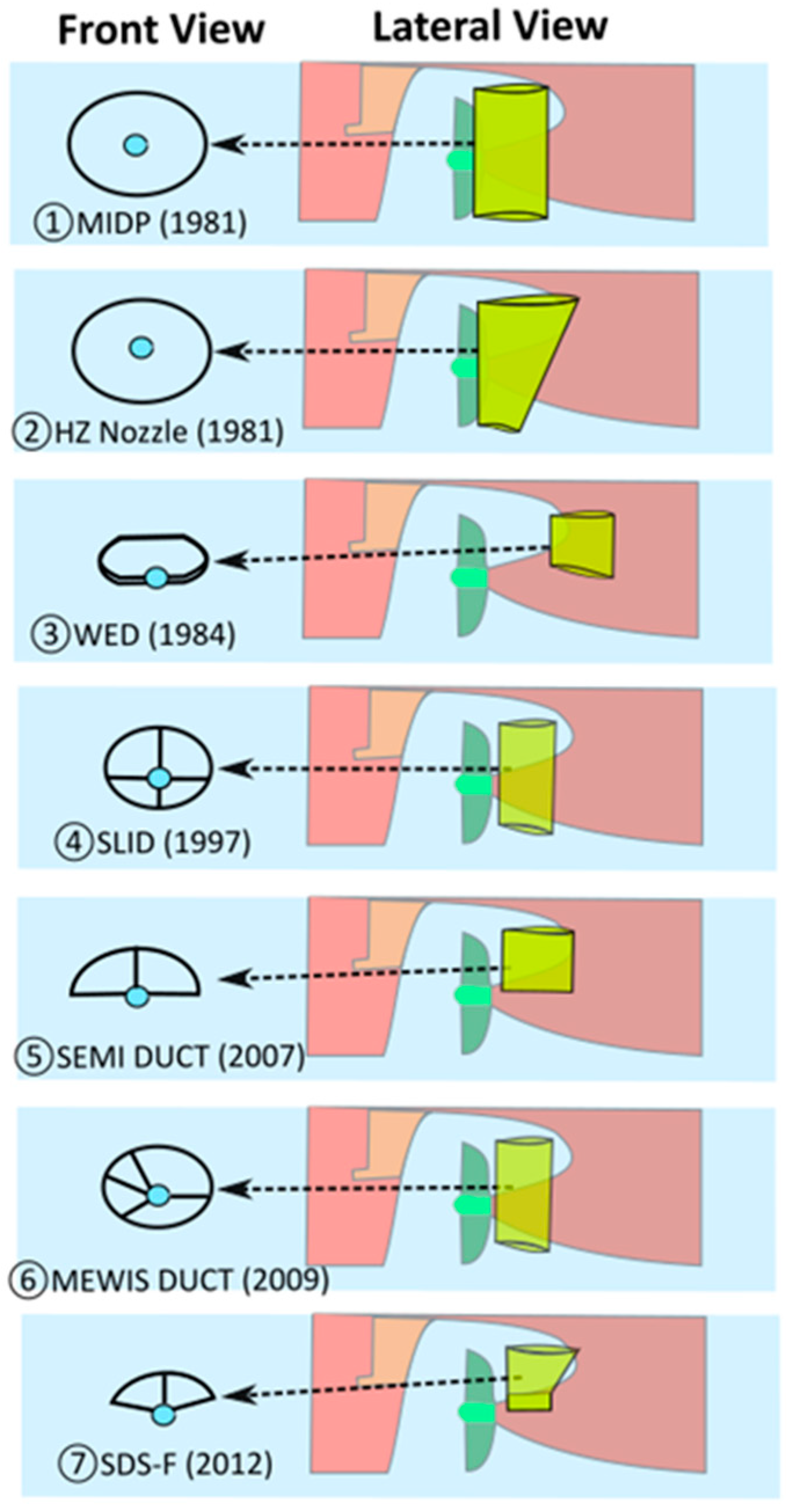
3.2. Pre-Swirl Duct (PSD)
- The first pre-duct principle, published by Van Lammeren in 1949 [20], promoted a duct ahead of the propeller, whose axis is above the shaft so that it guarantees a more equalized propeller inflow;
- Enhancing the propeller efficiency.
- Improving the propeller-hull interaction, to require less thrust.
3.3. Post-Swirl
- Propeller Boss Cap Fins (PBCF). The PBCF (Figure 4), originally developed by Mitsui OSK, consists of small fins attached to the boss cap fixed to the propeller. It recovers energy from the propeller hub vortex. The number of fins is the same as that of the propeller blades [34]. A study by Katayama et al. [35] included a list of typical profiles of general propeller caps and a specific propeller cap (contraction type) with fins (namely called ECO-Cap). The authors found an increase in the total efficiency due to the ECO-Cap was predicted by CFD and confirmed by the model test. The ECO-Cap prevents, as expected, the generation of the hub vortex. It is expected that this phenomenon makes the hub vortex weak, providing an overall improvement of about 1.28%. The PBCF performances are usually evaluated at the model scale.
- Grim Vane Wheel. The Grime Vane Wheel is a freely rotating device located behind the propeller, and it is composed of a turbine section inside the propeller slipstream and a propeller section (vane tips) outside the propeller slipstream. It is even called “Grimsches Leitrad” and was first developed by Otto Grim. Its main function is to extract energy from the propeller slipstream in the turbine portion and convert this energy into additional thrust in the propeller portion. The vane wheel became unpopular after several reports of mechanical failures, most notably for the cruise ship Queen Elizabeth 2 in 1986. A joint project between Hyundai Heavy Industries (HHI) and Det Norske Veritas (DNV) restored its reputation by developing a modern vane wheel supported on the rudder [34,37].
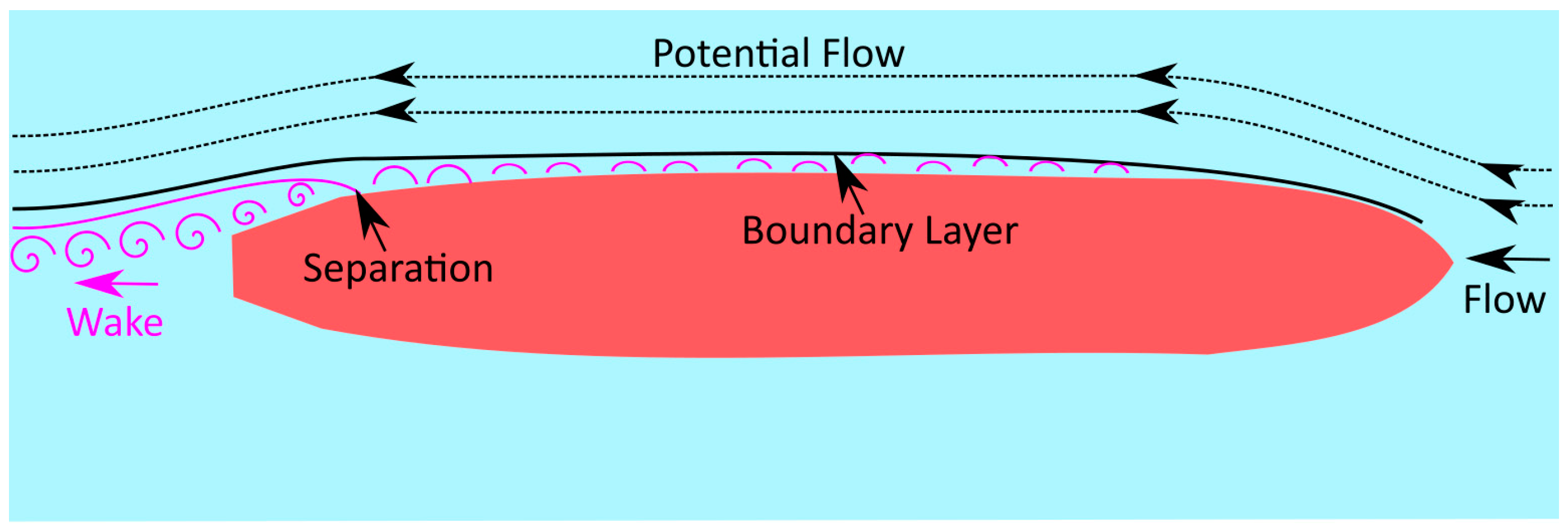
4. ESD Performance Assessment: Scale Effects
- hull boundary layer, the thickness of which is greater in model scale than in ship scale. The duct is partly inside the boundary layer of the bottom;
- separation of the aft flow that occurs on the model scale may not occur at full scale. Therefore, depending on the scale, parts of the duct may or may not be within the separation area;
- friction coefficient (), whose dependence on the Re () is about two times larger in model scale) causes differences in the resistance between model and true size. Its effect on the propeller load can be eliminated during model tests (e.g., by means of a pulling force), but the effect on the viscous wake in the propeller position remains. If the ESD acts by changing the viscous trail, its effect should be greater in the model than in the full scale. Much less is the space between the hull and the ESD, and much more significant is the increase of local resistance [16].
5. CFD Simulations for ESD Devices
5.1. Propeller Modelization
5.2. Turbulence Models
6. ESD Optimization Methods
- Select retrofit using data indicated by the owner/supplier;
- Optimize by applying CFD and check viability;
- Model test to validate;
- Trial to confirm.
7. Conclusions
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
References
- Tien, A. Reducing Greenhouse Gas Emissions from Ships through analysis of marginal abatement cost (MAC) curves. Glob. J. Eng. Sci. Res. 2018, 17. Available online: https://globaljournals.org/GJSFR_Volume17/3-Reducing-Greenhouse-Gas-Emissions.pdf (accessed on 31 March 2022).
- European Union Law. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX:52021PC0558 (accessed on 21 November 2021).
- International Chamber of Shipping, «EUROPEAN UNION MRV REGULATION» August 2020. Available online: https://www.ics-shipping.org/wp-content/uploads/2020/08/ics-guidance-on-eu-mrv.pdf (accessed on 13 March 2022).
- Mallouppas, G.; Yfantis, E. Decarbonization in Shipping Industry: A Review of Research, Technology Development, and Innovation Proposals. J. Mar. Sci. Eng. 2021, 9, 415. [Google Scholar] [CrossRef]
- Hasselaar, T.W.; Xing-Kaeding, Y. Evaluation of an energy-saving device via validation speed/power trials and full-scale CFD investigation. Int. Shipbuild. Prog. 2017, 63, 169–195. [Google Scholar] [CrossRef]
- RESOLUTION MEPC.333(76), ANNEX 7; Guidelines on the Method of Calculation of the Attained Energy Efficiency Existing Ship Index (EEXI). IMO: London, UK, 2021.
- BIMCO. 2020. Available online: https://bi-cd02.bimco.org/news/environment-protection/20200219-eexi-proposal-to-imo (accessed on 21 December 2021).
- Rutherford, D.; Mao, X.; Comer, B. Potential CO2 Reductions under the Energy Efficiency Existing Ship Index; International Council on Clean Transportation (ICCT): Washington, DC, USA, 2020. [Google Scholar]
- Olsen, A.S. Energy coefficients for a propeller series. Ocean Eng. 2004, 31, 401–416. [Google Scholar] [CrossRef]
- Terwisga, T. On the working principles of Energy Saving Devices. In Proceedings of the Third International Symposium on Marine Propulsors (SMP’13), Launceston, Australia, 5–8 May 2013. [Google Scholar]
- Bulten, N.W.H.; Stoltenkamp, P.W.; van Hooijdonk, J.J.A. Efficient propeller designs based on full-scale CFD simulations. In Proceedings of the International Conference on High Performance Marine Vehicles, Athens, Greece, 3–5 December 2014. [Google Scholar]
- Mewis, F. A novel power-saving device for full form vessels. In Proceedings of the International Symposium on Marine Propulsion, Trondheim, Norway, 22–24 June 2009. [Google Scholar]
- de Jong, J.H.; Zondervan, G.J.D. A Framework for Energy Saving Device (ESD) Decision Making; MARIN: Wageningen, The Netherlands, 2011. [Google Scholar]
- Schuiling, B.; van Terwisga, T. Hydrodynamic working principles of Energy Saving Devices in ship propulsion systems. Int. Shipbuild. Prog. 2016, 63, 255–290. [Google Scholar] [CrossRef]
- Carlton, J.S. Marine Propellers and Propulsion, 4th ed.; Butterworth-Heinemann: Oxford, UK, 2019. [Google Scholar]
- Prins, H.J.; Flikkema, M.B.; Schuiling, B.; Kaeding, Y.X.; Voermans, A.A.M.; Müller, M.; Coache, S.; Hasselaar, T.W.F.; Paboeuf, S. Green retrofitting through optimisation of hull-propulsion interaction—GRIP. In Proceedings of the 6th Transport Research Arena (TRA), Warsaw, Poland, 18–21 April 2016. [Google Scholar]
- Flikkema, M.; Goorden, B.; Cervicato, C.; Verhulst, M.; Schuiling, B.; Janse, G.; Voermans, A.; de Bot, B.; Terwisga, T.; Portolano, A.; et al. Design and demonstration of an Energy Saving Device for a ship with controllable pitch propeller. In Proceedings of the 8th Transport Research Arena (TRA), Helsinki, Finland, 27–30 April 2020. [Google Scholar]
- Dang, J.; Chen, H.; Guoxiang, D.; van der Ploeg, A.; Hallmann, R.; Mauro, F. An exploratory study on the working principles of Energy Saving Devices (ESDs). In Proceedings of the Symposium on Green Ship Technology (Greenship’11), Wuxi, China, 10–11 October 2011. [Google Scholar]
- Nadery, A.; Ghassemi, H.; Chybowski, L. The effect of the PSS configuration on the hydrodynamic performance of the KP505 propeller behind the KCS. Ocean Eng. 2021, 234, 109310. [Google Scholar] [CrossRef]
- The Maritime Executive. Available online: https://www.maritime-executive.com/corporate/New-EnergySaving-Device-The-Becker-Twisted-Fin (accessed on 16 July 2020).
- Force Technology. Available online: https://forcetechnology.com/en/cases/how-a-fin-and-a-duct-save-fuel (accessed on 19 July 2020).
- Mewis, F.; Peters, H.E. Power savings through a novel fin system. In Proceedings of the 15th SMSSH Conference, Varna, Bulgaria, 6–11 October 1986. [Google Scholar]
- Lee, J.T.; Kim, M.C.; Suh, J.C.; Kim, S.H.; Choi, J.K. Development of a Pre Swirl Stator Propeller System for Improvement of Propulsion Efficiency: A Symmetric Stator Propulsion System; Society of Naval Architects of Korea (SNAK): Busan, Korea, 1992. [Google Scholar]
- Nowruzi, H.; Najafi, A. An experimental and CFD study on the effects of different pre-swirl ducts on propulsion performance of series 60 ship. Ocean Eng. 2019, 173, 491–509. [Google Scholar] [CrossRef]
- Maasch, M.; Mizzi, K.; Atlar, M.; Fitzsimmons, P.; Turan, O. A generic wake analysis tool and its application to the Japan Bulk Carrier test case. Ocean Eng. 2019, 171, 575–589. [Google Scholar] [CrossRef]
- Furcas, F.; Vernengo, G.; Villa, D.; Gaggero, S. Desing of Wake Equalizing Ducts using RANSE-based SBDO. Appl. Ocean Res. 2020, 97, 102087. [Google Scholar] [CrossRef]
- Bekhit, A.S. Numerical simulation of the ship self-propulsion prediction using body force method and fully discretized propeller model. IOP Conf. Ser. Mater. Sci. Eng. 2018, 400, 042004. [Google Scholar] [CrossRef]
- Windén, B.; Huang, Z.; Kawamura, T. Comparative self-propulsion simulations of the JBC bulk carrier. In Proceedings of the Japan Society of Naval Architects and Marine Engineers (JASNAOE) Spring Meeting, Kobe, Japan, 25 May 2015. [Google Scholar]
- Andersson, J.; Hyensjö, M.; Eslamdoost, A.; Bensow, R. CFD simulations of the Japan Bulk Carrier Test case. In Proceedings of the Numerical Towing Tank Symposium, Cortona, Italy, 27–29 September 2015. [Google Scholar]
- Korkmaz, K.B. CFD Predictions of Resistance and Propulsion for the Japan Bulk Carrier (JBC) with and without an Energy Saving Device. Master’s Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2015. [Google Scholar]
- Bakica, A.; Vladimir, N.; Ančić, I. Improving ship energy efficiency performance by energy-saving devices. In Proceedings of the International Conference on Smart & Green Technology for the Future of Marine Industries (SMATECH 2019), Glasgow, UK, 11–12 July 2019. [Google Scholar]
- Jasak, H.; Vukcevic, V.; Gatin, I.; Lalovic, I. CFD validation and grid sensitivity studies of full-scale ship self-propulsion. Int. J. Nav. Archit. Ocean Eng. 2018, 11, 33–43. [Google Scholar] [CrossRef]
- Vukcevic, V.; Jasak, H.; Gatin, I.; Uroic, T. Ship scale self-propulsion CFD simulation results compared to sea trials measurements. In Proceedings of the International Conference on Computational Methods in Marine Engineering, Nantes, France, 15–17 May 2017. [Google Scholar]
- Hochkirk, K.; Bertram, V. Options for fuel-saving for ships. In Proceedings of the Mare Forum: Maritime Transportation of Energy, Houston, TX, USA, 19 February 2010. [Google Scholar]
- Katayama, K.; Yoshihisa, O.; Okazaki, A. Optimization of the propeller with ECO-cap by CFD. In Proceedings of the International Symposium on Marine Propulsors (SMP’15), Austin, TX, USA, 31 May–4 June 2015. [Google Scholar]
- Shiffbau-Versuchsanstalt Postdam (SVA). Available online: https://www.sva-potsdam.de/en/energy-saving-devices/ (accessed on 22 March 2022).
- Safety4Sea. Available online: https://safety4sea.com/hhi-and-dnv-gl-take-a-fresh-look-at-grims-vane-wheel/?__cf_chl_jschl_tk__ (accessed on 25 July 2020).
- Dang, J.; Chen, H.; Guoxiang, D. An exploratory study on the working principles of Energy Saving Devices (ESDs)—PIV, CFD investigations and ESD design guidelines. In Proceedings of the 31st International Conference on Ocean, Offshore and Arctic Engineering (OMAE12), Rio de Janeiro, Brazil, 10–15 July 2012. [Google Scholar]
- Guo, C.; Wu, T.; Zhang, Q.; Luo, W.; Su, Y. Numerical simulation and experimental studies on aft hull local parameterized non-GEOSIM deformation for correcting scale effects of nominal wakefield. Brodogradnja/Shipbuilding 2017, 68, 77–96. [Google Scholar]
- Bocchetti, D.; Lepore, A.; Palumbo, B.; Vitiello, L. A Statistical Approach to Ship Fuel Consumption Monitoring. J. Ship Res. 2015, 59, 162–171. [Google Scholar] [CrossRef]
- Bocchetti, D.; Lepore, A.; Palumbo, B.; Vitiello, L. A statistical control of the ship fuel consumption. In Proceedings of the Design & Operation of Passenger Ship, London, UK, 20–21 November 2013. [Google Scholar]
- Heinke, H.; Hellwig-Rieck, K. Investigation of scale effects on ships with a Wake Equalizing Duct or with Vortex Generator Fins. In Proceedings of the Second International Symposium on Marine Propulsors, Hamburg, Germany, 15–17 June 2011. [Google Scholar]
- Friesch, J.; Johannsen, C. Propulsion optimization tests at high Reynolds numbers. In Transactions; The Society of Naval Architects and Marine Engineers (SNAME): Jersey City, NJ, USA, 1994; Volume 102, pp. 1–21. [Google Scholar]
- Ok, J.P. Numerical Investigation of Scale Effects of Schneekluth’s Duct; TU Hamburg-Harburg: Hamburg, Germany, 2004. [Google Scholar]
- Final report of the specialist committee on scaling of wakefield. In Proceedings of the International Towing Tank Conference (ITTC), Rio de Janeiro, Brazil, 28 August–3 September 2011.
- Van, S.H.; Kim, M.C.; Lee, J.T. Some remarks on the powering performance prediction method for a ship equipped with a pre swirl stator propeller system. In Proceedings of the International Towing Tank Conference (ITTC), Daejeon, Korea, 19–25 September 1993. [Google Scholar]
- 7.5-02-03-01.4; Performance, Propulsion 1978 ITTC Performance Prediction Method. ITTC: Zürich, Switzerland, 2017.
- Choi, J.E.; Kim, J.H.; Choi, B.J.; Lee, S.B.; Chung, S.H.; Seo, H.W. Development of energy-saving devices for a hull slow speed ship through improving propulsion performance. In Proceedings of the 12th International Symposium on Practical Design of Ships and other Floating Structures, Changwon, Korea, 20–25 October 2013. [Google Scholar]
- Park, S.; Oh, G.; Rhee, S.H.; Koo, B.; Lee, H. Full-scale wake prediction of an Energy Saving Device by using Computational Fluid Dynamics. Ocean Eng. 2015, 101, 254–263. [Google Scholar] [CrossRef]
- ITTC. Final Report of the Specialist Committee on Unconventional Propulsors; ITTC: Seoul, Korea; Shangai, China, 1999. [Google Scholar]
- Kim, M.C.; Shin, Y.J.; Lee, W.J.; Lee, J.H. Study on extrapolation method for self-propulsion test with pre-swirl device. In Proceedings of the International Symposium on Marine Propulsion (SMP’17), Espoo, Finland, 12–15 June 2017. [Google Scholar]
- ITTC. Final Report and Recommendations to the 28th ITTC—The Specialist Committee on Energy Saving Devices; ITTC: Wuxi, China, 2017. [Google Scholar]
- Xu, L.; Wan, D. Numerical Investigation of Scale Effect for Propeller Boss Cap Fins. In Proceedings of the Twenty-Eighth International Ocean and Polar Engineering Conference (ISOPE), Sapporo, Japan, 10–15 June 2018. [Google Scholar]
- Larsson, L.; Stern, F.; Bertram, V. Benchmarking of Computational Fluid Dynamics. J. Ship Res. 2003, 47, 63–81. [Google Scholar] [CrossRef]
- MARIN. Available online: https://www.marin.nl/jips/refit2save (accessed on 21 June 2020).
- Shin, H.J.; Lee, J.S.; Han, M.R.; Hur, E.B.; Shin, S.C. Numerical and experimental investigation of conventional and unconventional pre-swirl duct for VLCC. Int. J. Nav. Archit. Ocean Eng. 2013, 5, 414–430. [Google Scholar] [CrossRef][Green Version]
- Queutey, P.; Gulmineau, E. A comparison between full RANSE and coupled RANSE-BEM approaches in ship propulsion performance prediction. In Proceedings of the 32nd International Conference on Ocean, Offshore and Arctic Engineering (OMAE), Nantes, France, 9–14 June 2013. [Google Scholar]
- Go, J.S.; Yoon, H.S.; Jung, J.H. Effects of a duct before a propeller on propulsion performance. Ocean Eng. 2017, 136, 54–66. [Google Scholar] [CrossRef]
- Baek, D.G.; Jung, J.H.; Yoon, H.S. Effects on the advance ratio on the evolution of propeller wake. In Proceedings of the International Conference on Environment, Energy, Ecosystems and Development (EEEAD’13), Energy, Venice, Italy, 28–30 September 2013. [Google Scholar]
- Guiard, T.; Leonard, S.; Mewis, F. The Becker Mewis duct challenges in full-scale design and new development for fast ships. In Proceedings of the Third International Symposium on Marine Propulsors (smp’13), Launceston, Australia, 5–8 May 2013. [Google Scholar]
- Ichinose, Y.; Tahara, Y. A wakefield design system utilizing a database analysis to enhance the performance of energy-saving devices and propellers. J. Mar. Sci. Technol. 2018, 24, 1119–1133. [Google Scholar] [CrossRef]
- Tahara, Y.; Ichinose, Y.; Kaneko, A.; Kasahara, Y. Variable decomposition approach applied to multi-objective optimization for minimum powering of commercial ships. J. Mar. Sci. Technol. 2018, 24, 260–283. [Google Scholar] [CrossRef]
- van der Ploeg, A.; Raven, H.C. CFD based optimization for minimal power and wakefield quality. In Proceedings of the International Symposium on practical design of ships and other floating structures, Rio de Janeiro, Brazil, 19–24 September 2010. [Google Scholar]
- Chen, P.F.; Huang, C.H. An inverse hull design problem in optimizing the desidered wake of a ship. J. Ship Res. 2002, 46, 138–147. [Google Scholar] [CrossRef]
- Stuck, A.; Kroger, J.; Rung, T. Adjoint based hull design for wake optimization. Ship Technol. Res. 2011, 58, 34–44. [Google Scholar] [CrossRef]


| Axial losses Rotational losses Viscous losses Non-uniformity (e.g., blades, etc.) | Wake adaption (represents the swirl kinetic energy added to the wake behind the propeller.) | Propeller-hull interactions |
| Type | Name of Device | Energy-Saving Mechanism | Energy-Saving Rate% Model Test/Sea Trials |
|---|---|---|---|
| Pre-swirl stator | Reaction fins | PRI | 4–6/3–9 |
| Pre-swirl duct | Becker Mewis duct® | IPI, AFS | 6–11/8 |
| Fan-shaped Mewis duct® | IPI, AFS | 6–11/9 | |
| Becker twisted fins® | IPI, AFS | 6–11/10 | |
| Schneekluth duct/WED | IPI, AFS | 4–11/11 | |
| WED with Grothues spoilers | IPI, AFS | 6–11/12 | |
| Unconventional half-circular duct | IPI, AFS | 6–11/13 | |
| IPI, AFS | 6–11/14 | ||
| Post-swirl | Propeller boss cap fins | DEP | 2–5/2–5 |
| Hub vortex vane | DEP | 2–5/2–5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spinelli, F.; Mancini, S.; Vitiello, L.; Bilandi, R.N.; De Carlini, M. Shipping Decarbonization: An Overview of the Different Stern Hydrodynamic Energy Saving Devices. J. Mar. Sci. Eng. 2022, 10, 574. https://doi.org/10.3390/jmse10050574
Spinelli F, Mancini S, Vitiello L, Bilandi RN, De Carlini M. Shipping Decarbonization: An Overview of the Different Stern Hydrodynamic Energy Saving Devices. Journal of Marine Science and Engineering. 2022; 10(5):574. https://doi.org/10.3390/jmse10050574
Chicago/Turabian StyleSpinelli, Flaminia, Simone Mancini, Luigi Vitiello, Rasul Niazmand Bilandi, and Maria De Carlini. 2022. "Shipping Decarbonization: An Overview of the Different Stern Hydrodynamic Energy Saving Devices" Journal of Marine Science and Engineering 10, no. 5: 574. https://doi.org/10.3390/jmse10050574
APA StyleSpinelli, F., Mancini, S., Vitiello, L., Bilandi, R. N., & De Carlini, M. (2022). Shipping Decarbonization: An Overview of the Different Stern Hydrodynamic Energy Saving Devices. Journal of Marine Science and Engineering, 10(5), 574. https://doi.org/10.3390/jmse10050574








