Ship Bow Wings with Application to Trim and Resistance Control in Calm Water and in Waves
Abstract
:1. Introduction
2. Numerical Methodology
Solver Desription
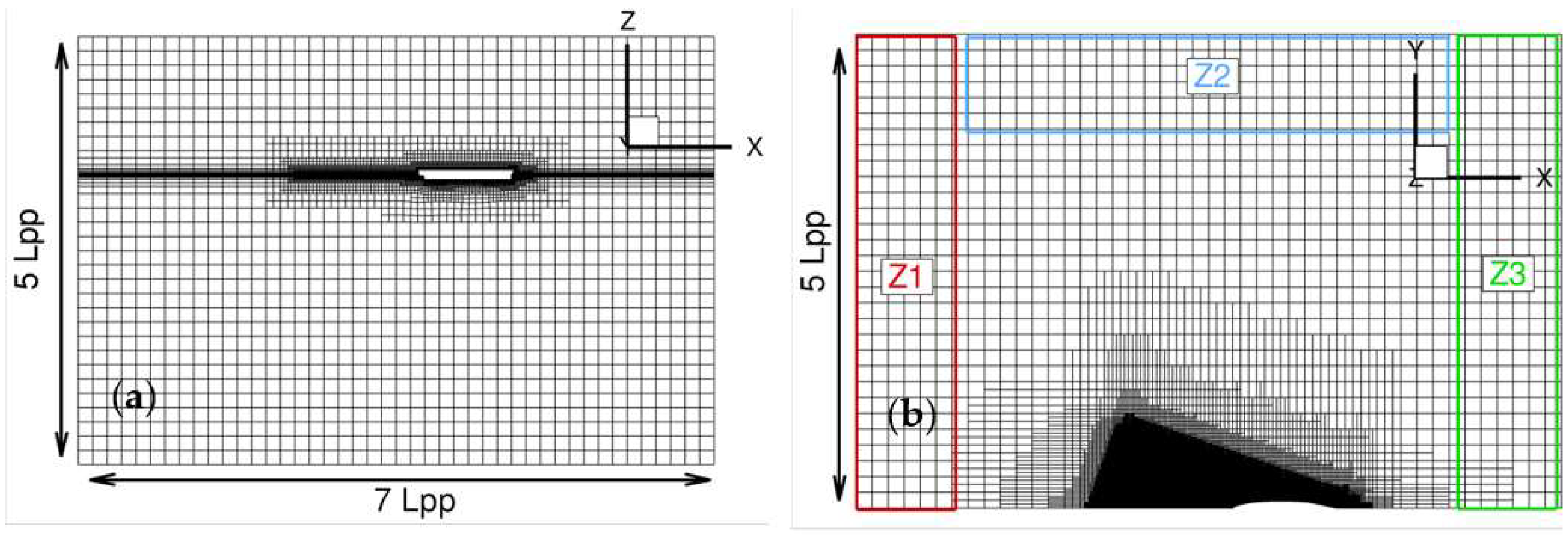
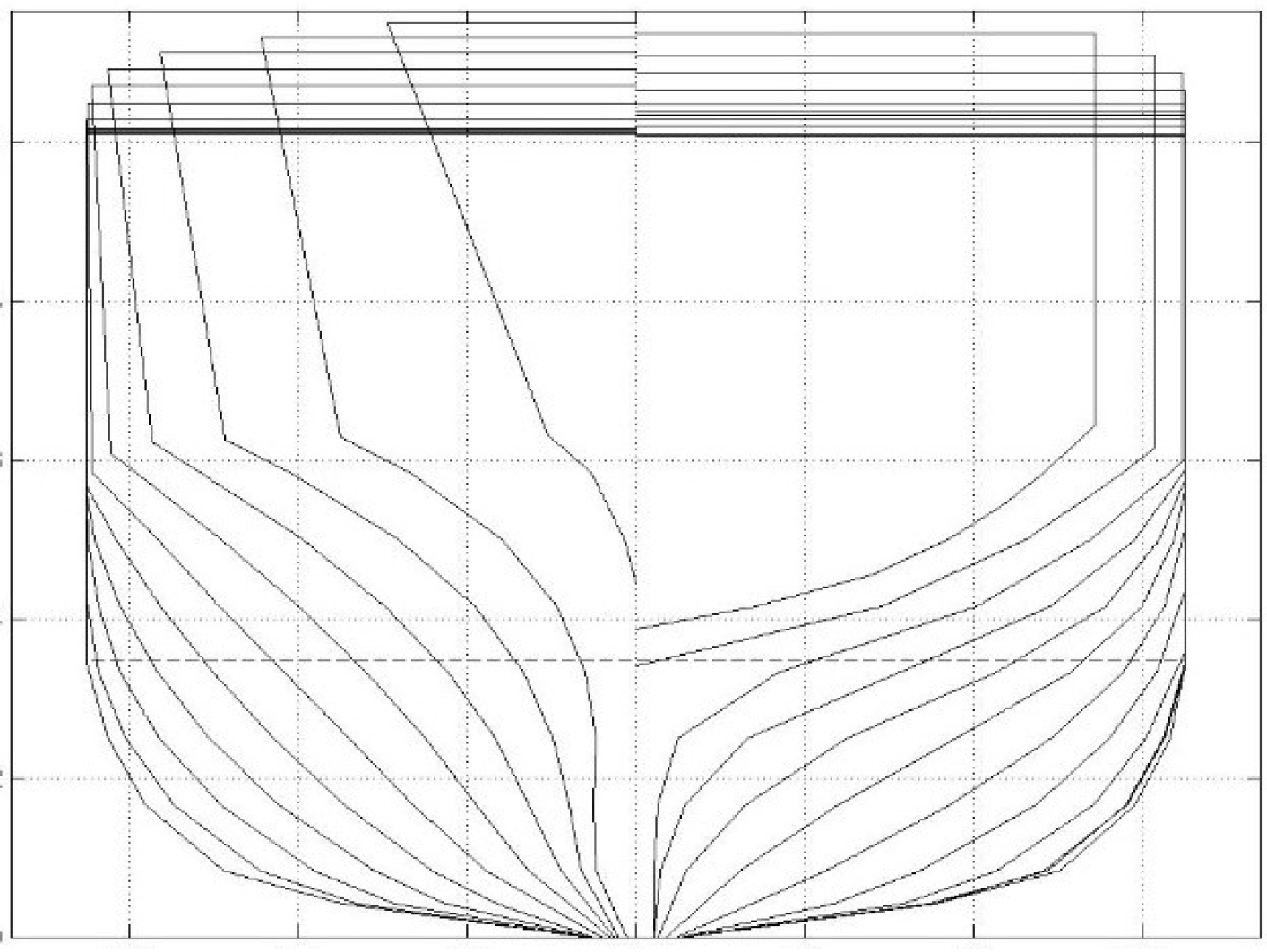
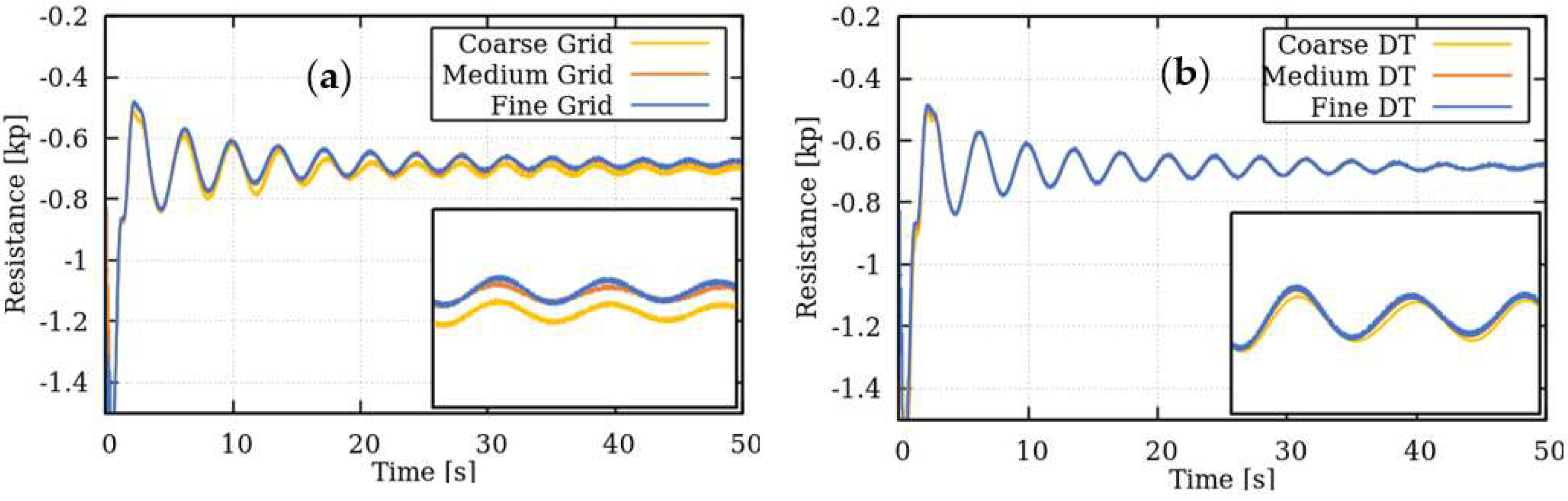
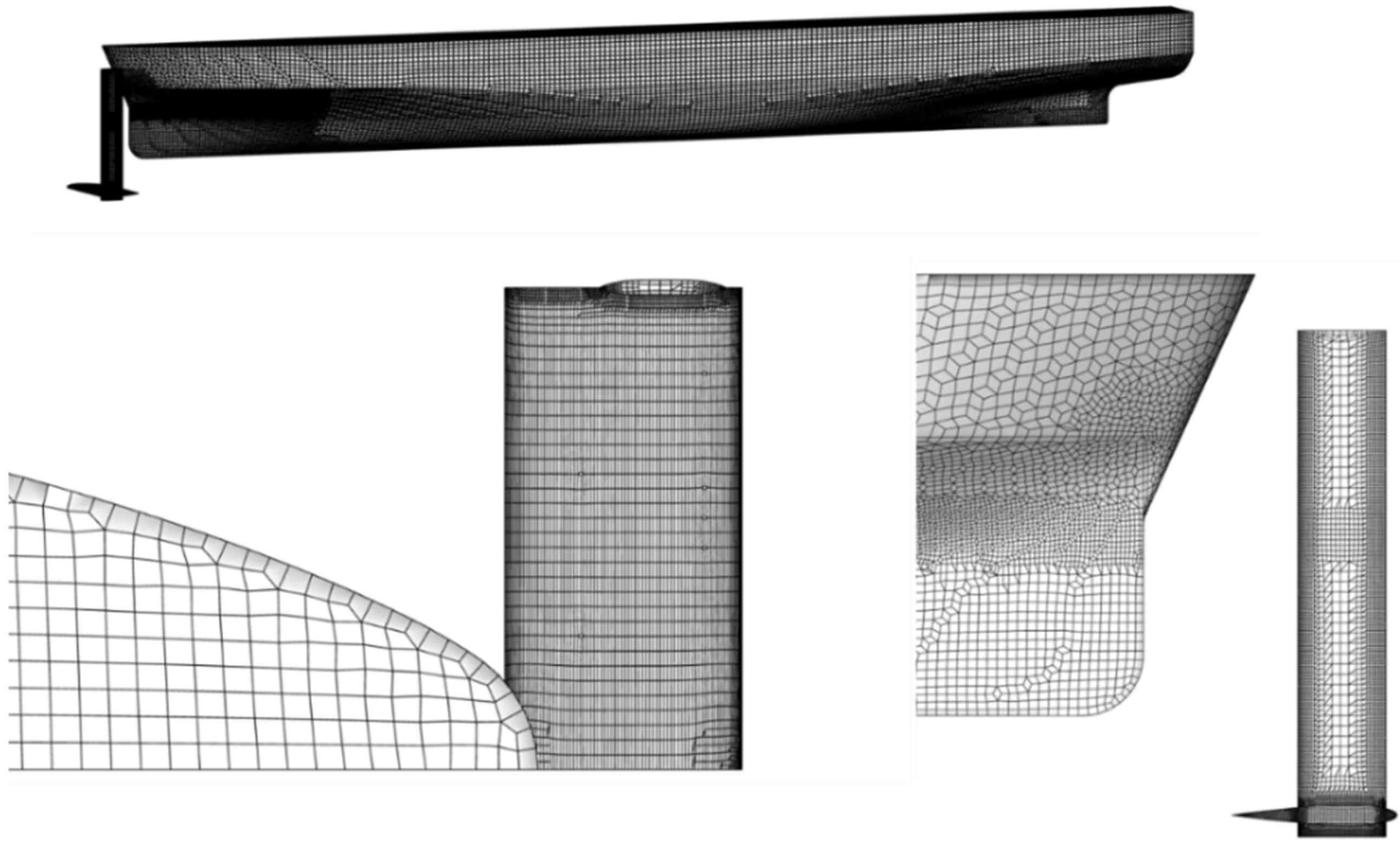
3. Numerical Setup
- (i)
- the extrapolated value
- (ii)
- the approximate relative error
- (iii)
- the extrapolated relative error
- (iv)
- the fine GCI
4. Results and Discussion
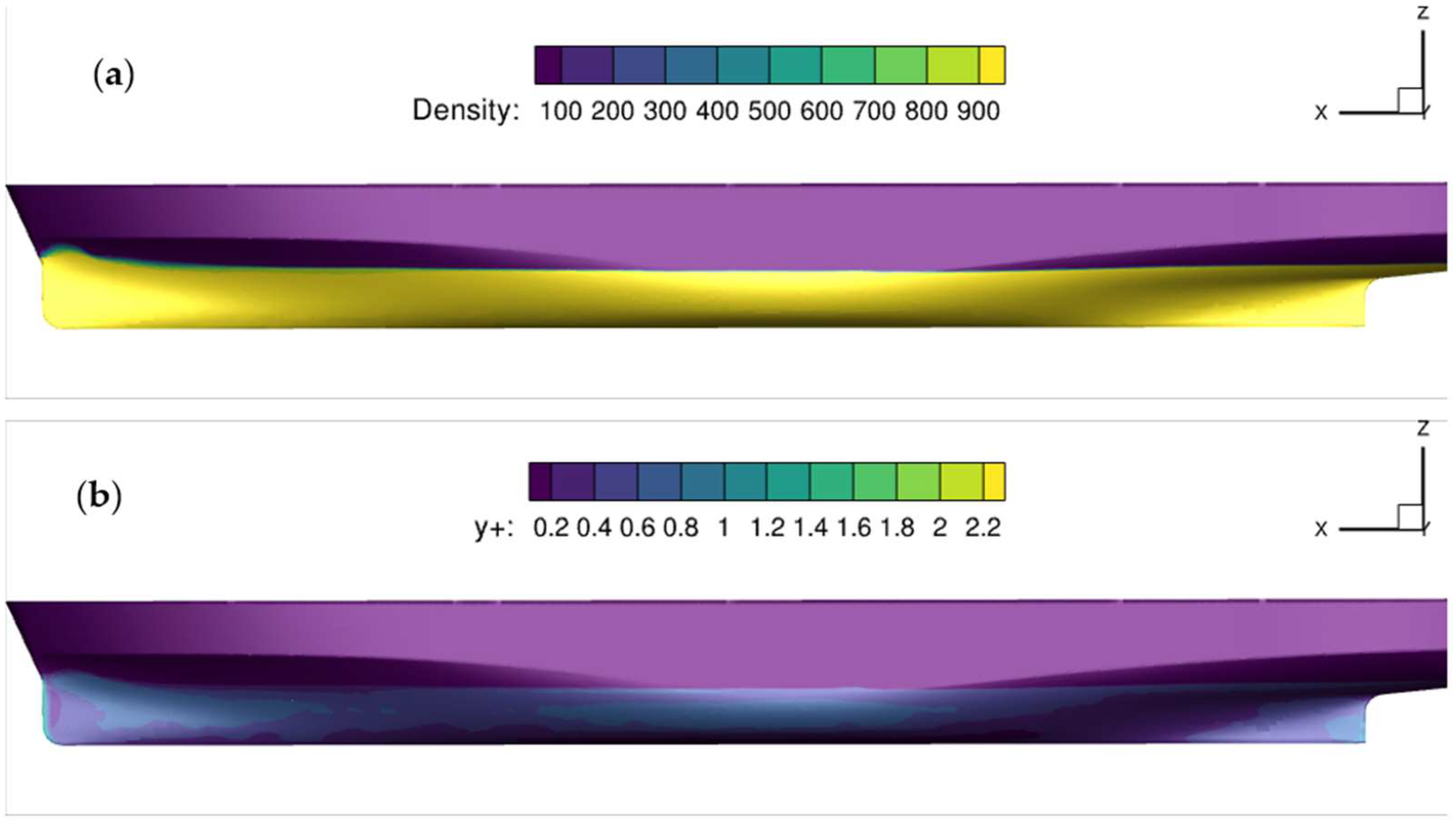
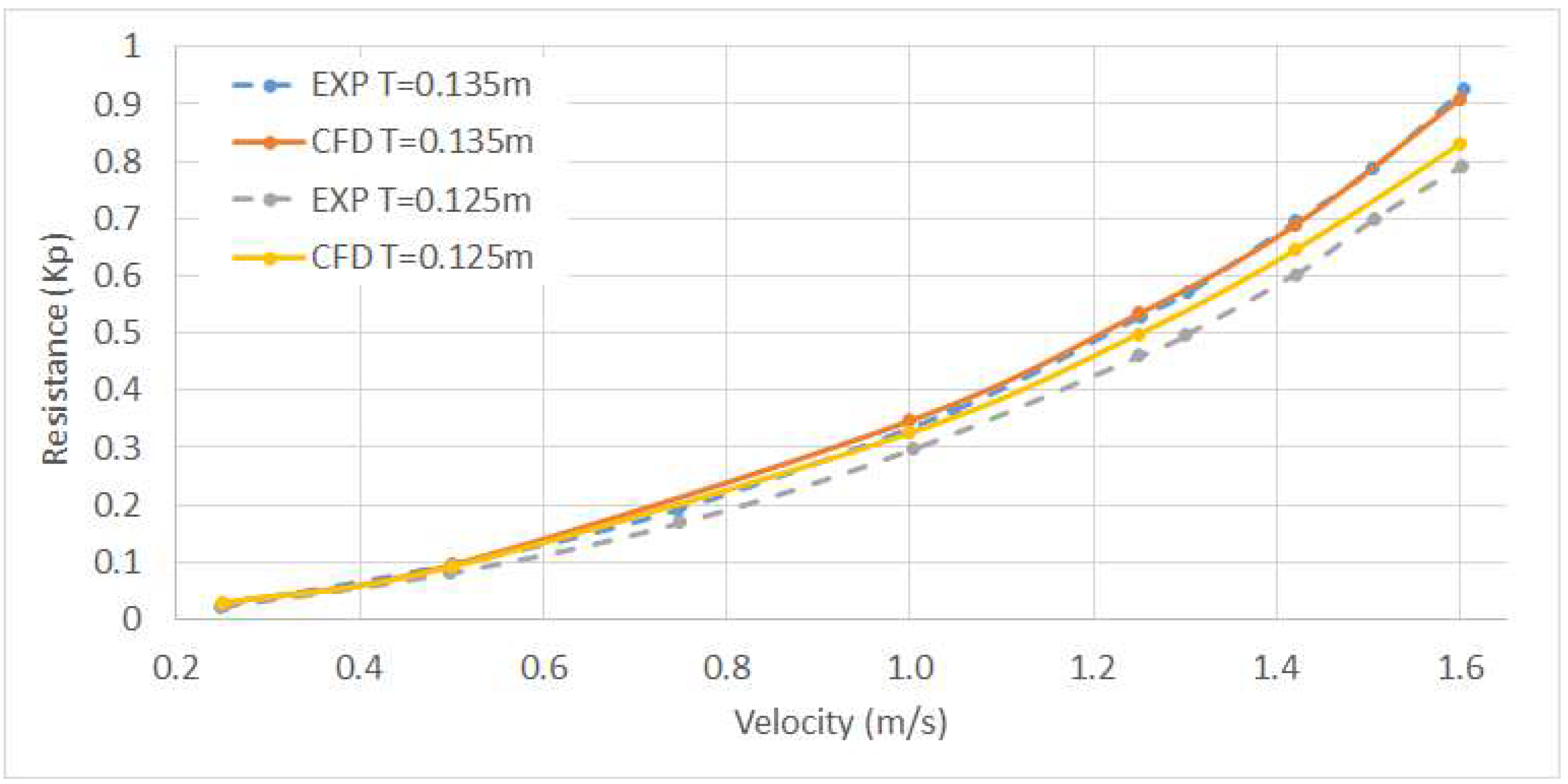
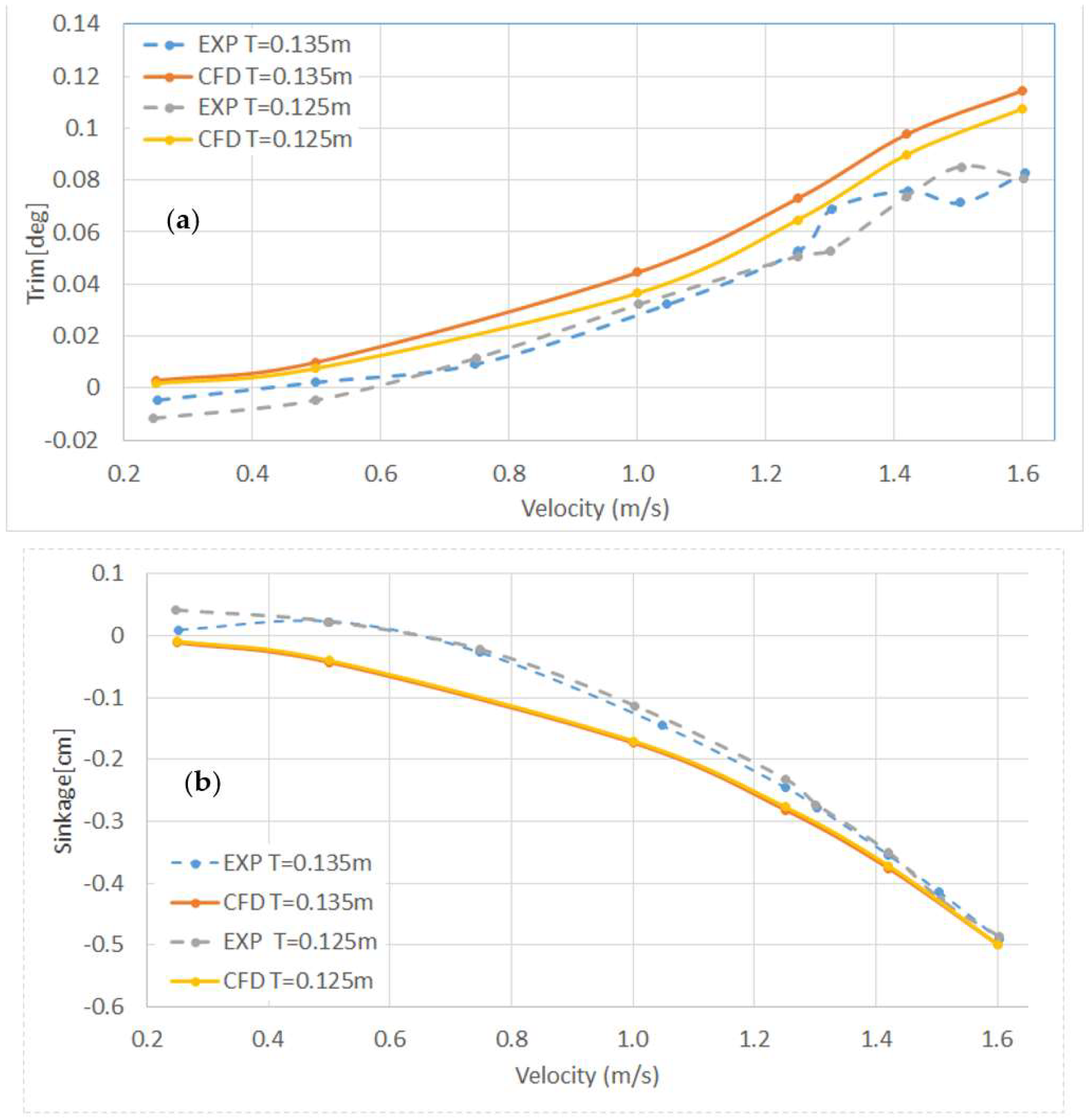
4.1. Dynamic Trim and Sinkage of the Bare Hull
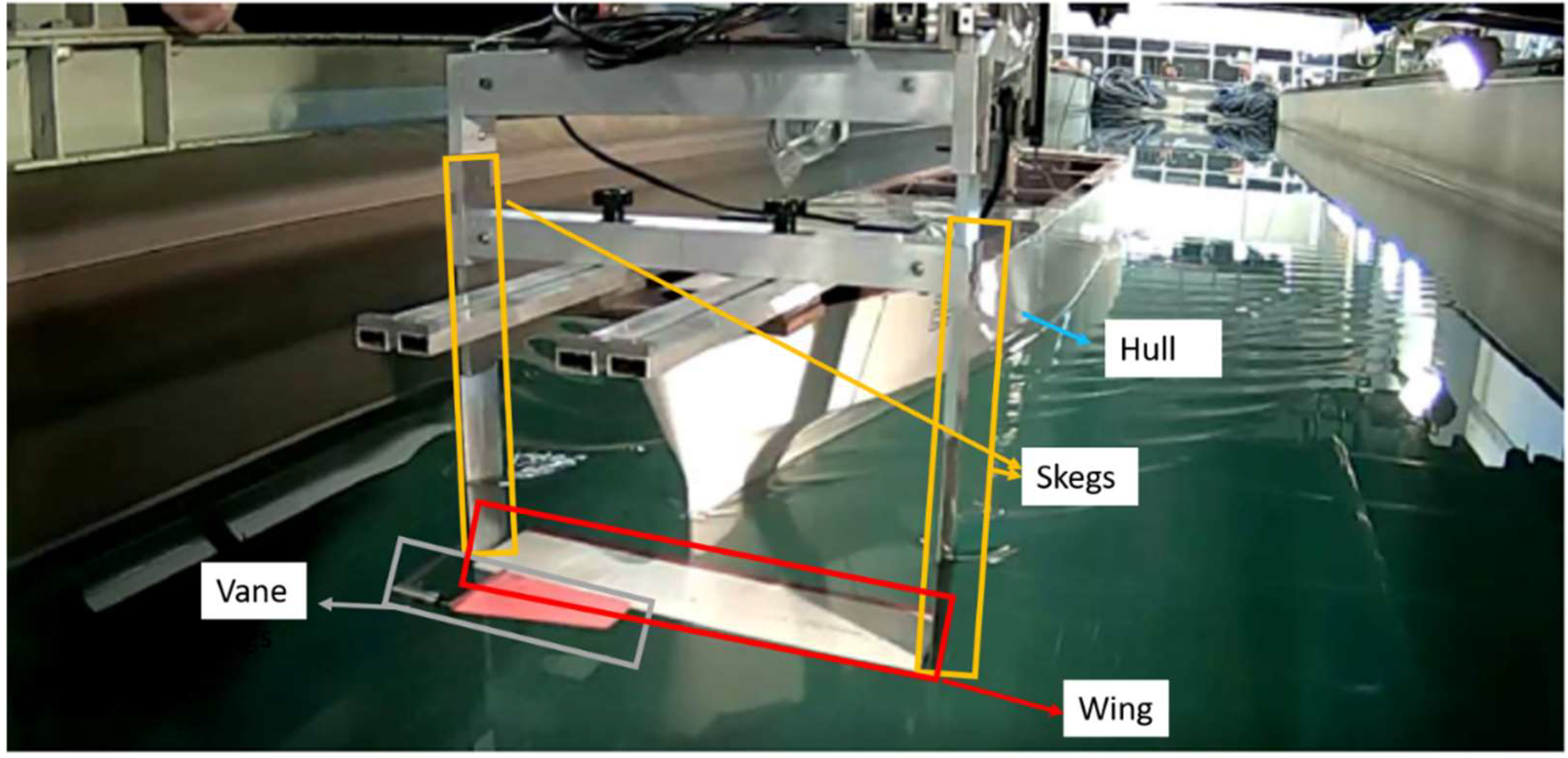
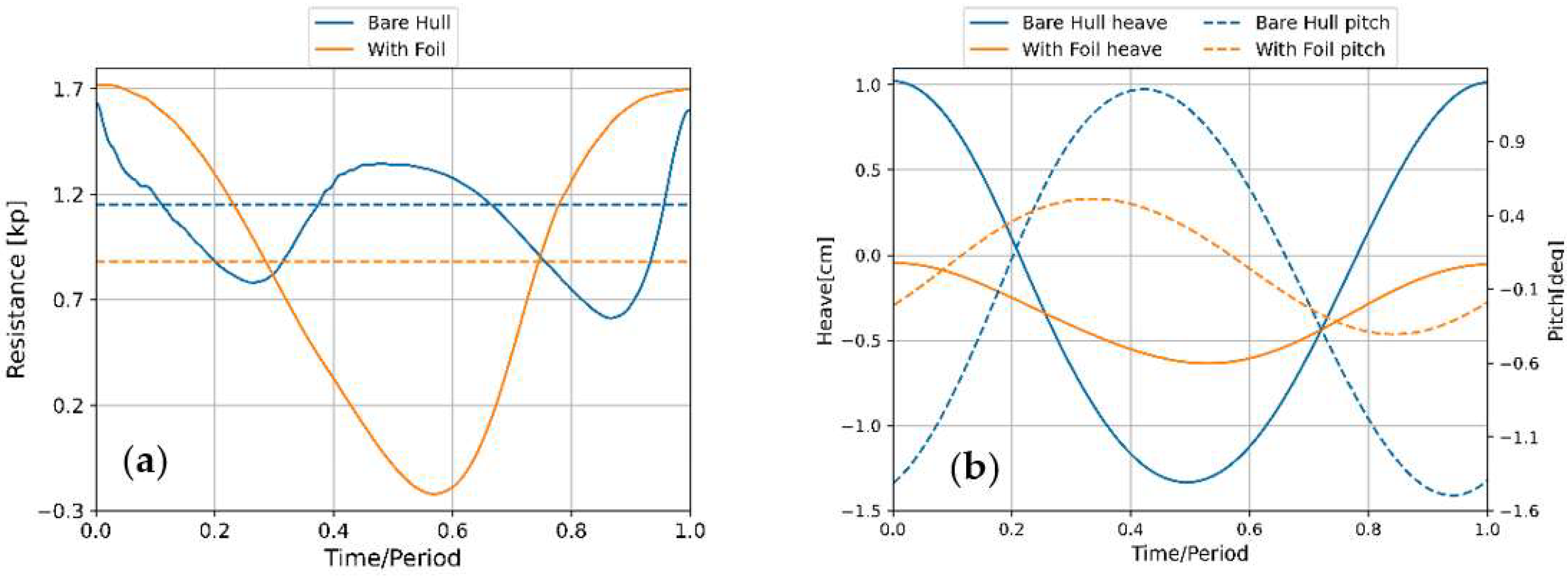
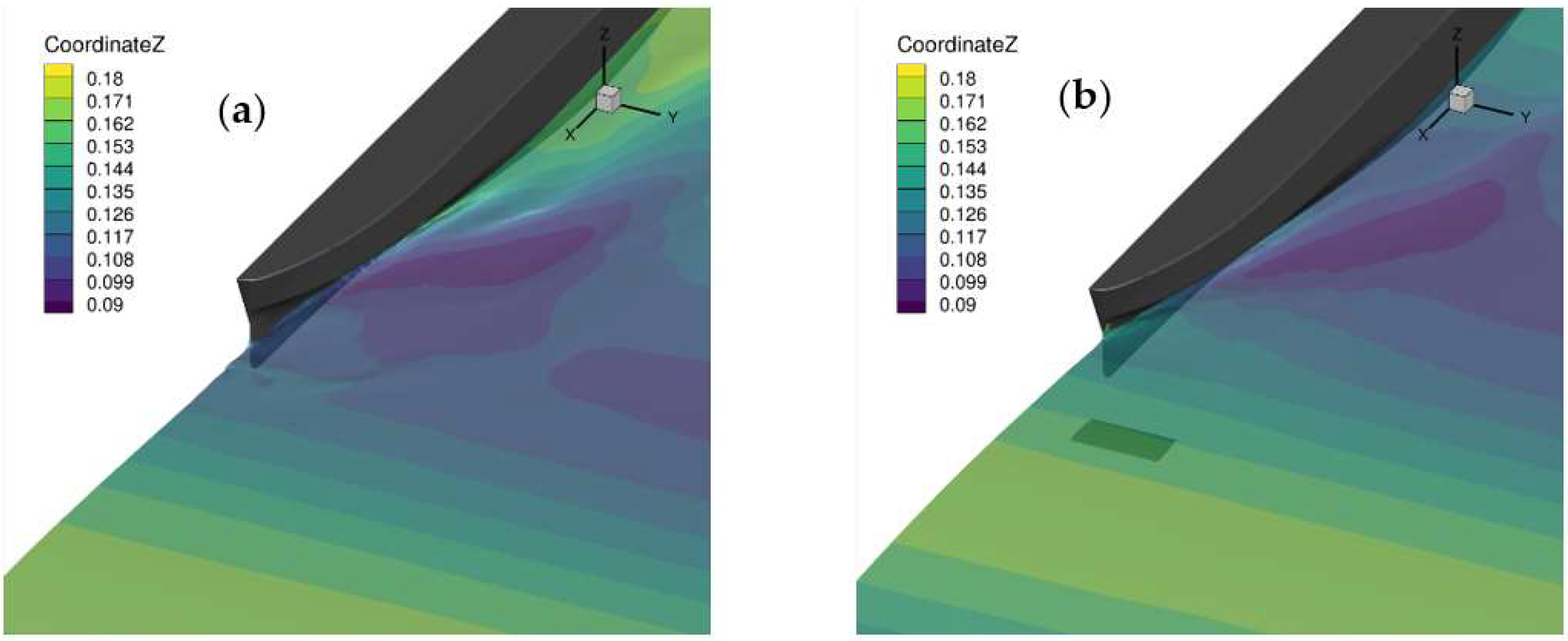
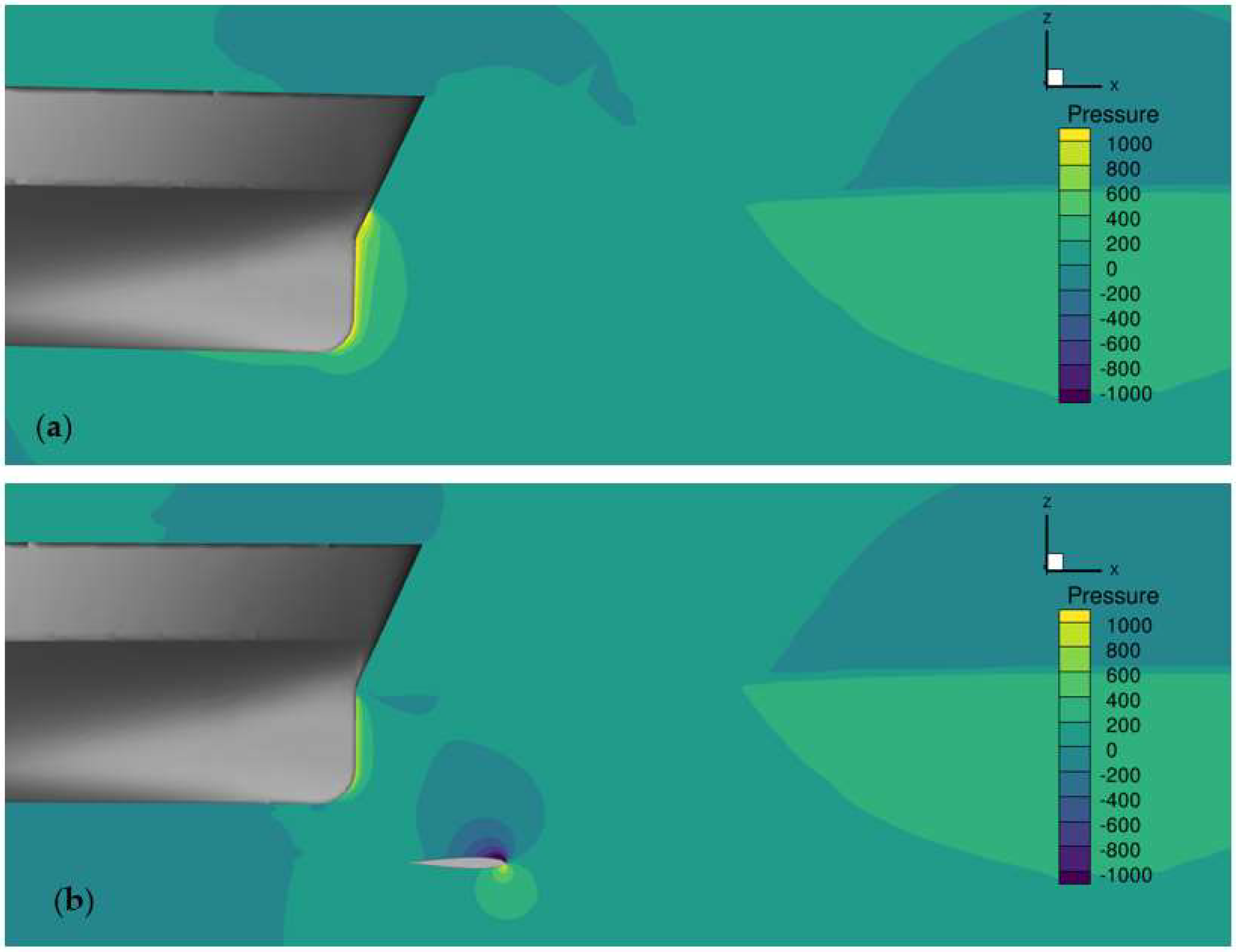
4.2. Effect of a Wing Arranged in Front of the Bow in Calm Water Conditions
4.3. Effect of the Foil Inclination in Calm Water Conditions
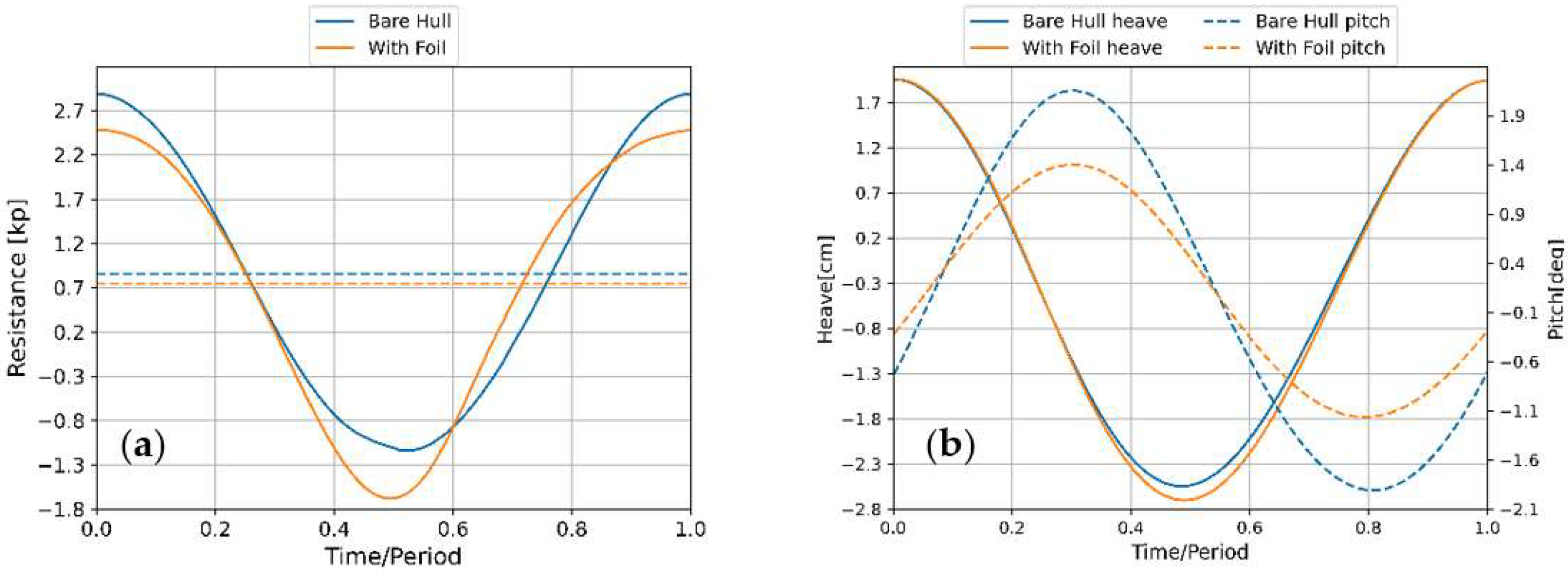
4.4. Effect of the Wing in the Presence of Regular Waves
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Ship Froude Number | |
| V | Ship Advance Speed |
| Ship Nominal Advance Speed (1.42 m/s) | |
| T | Ship Draft |
| Ls | Ship Length |
| s, c | Wing Span and chord length |
| Lw | Wave Length |
| f | Wave Frequency |
| k | Wave Number |
| A | Wave Amplitude |
| Mean Resistance | |
| ξ3, ξ5 | Heave, Pitch |
| Amplitude of Parameter φ | |
| Mean Value of Parameter φ |
References
- Triantafyllou, M.S.; Triantafyllou, G.S.; Yue, D.K.P. Hydrodynamics of Fishlike Swimming. Annu. Rev. Fluid Mech. 2000, 32, 33–53. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, X.; Tian, X.; Li, X.; Lu, W. A review on fluid dynamics of flapping foils. Ocean Eng. 2020, 195, 106712. [Google Scholar] [CrossRef]
- Bøckmann, E.; Steen, S. Model test and simulation of a ship with wavefoils. Appl. Ocean Res. 2016, 57, 8–18. [Google Scholar] [CrossRef]
- Bøckmann, E.; Steen, S. Experiments with actively pitch-controlled and spring-loaded oscillating foils. Appl. Ocean Res. 2014, 48, 227–235. [Google Scholar] [CrossRef]
- Filippas, E.S.; Papadakis, G.P.; Belibassakis, K.A. Free-surface effects on the performance of flapping-foil thruster for augmenting ship propulsion in waves. J. Mar. Sci. Eng. 2020, 8, 357. [Google Scholar] [CrossRef]
- Belibassakis, K.A.; Politis, G.K. Hydrodynamic performance of flapping wings for augmenting ship propulsion in waves. Ocean Eng. 2013, 72, 227–240. [Google Scholar] [CrossRef]
- Belibassakis, K.; Filippas, E.; Papadakis, G. Numerical and Experimental Investigation of the Performance of Dynamic Wing for Augmenting Ship Propulsion in Head and Quartering Seas. J. Mar. Sci. Eng. 2021, 10, 24. [Google Scholar] [CrossRef]
- Papadakis, G. Development of a Hybrid Compressible Vortex Particle Method and Application to External Problems including Helicopter Flows. Ph.D. Thesis, National Technical University of Athens, Athens, Greece, 2014. [Google Scholar]
- Ntouras, D.; Papadakis, G. A Coupled Artificial Compressibility Method for Free Surface Flows. J. Mar. Sci. Eng. 2020, 8, 590. [Google Scholar] [CrossRef]
- Mavrakos, A.S.; Konispoliatis, D.N.; Ntouras, D.G.; Papadakis, G.P.; Mavrakos, S.A. Hydrodynamics of Moonpool-type Floaters: A theoretical and a CFD formulation. Energy 2021, 15, 570. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Kunz, R.F.; Boger, D.A.; Stinebring, D.R.; Chyczewski, T.S.; Lindau, J.W.; Gibeling, H.J.; Venkateswaran, S.; Govindan, T.R. A preconditioned Navier-Stokes method for two-phase flows with application to cavitation prediction. Comput. Fluids 2000, 29, 849–875. [Google Scholar] [CrossRef]
- Venkateswaran, S.; Lindau, J.; Kunz, R.; Merkle, C. Preconditioning algorithms for the computation of multi-phase mixture flows. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001. [Google Scholar] [CrossRef] [Green Version]
- Ntouras, D.; Manolas, D.; Papadakis, G.; Riziotis, V. Exploiting the limit of BEM solvers in moonpool type floaters. J. Phys. Conf. Ser. 2020, 1618, 052059. [Google Scholar] [CrossRef]
- Perić, R.; Vukčević, V.; Abdel-Maksoud, M.; Jasak, H. Optimizing wave-generation and wave-damping in 3D-flow simulations with implicit relaxation-zones. Coast. Eng. 2021, 171, 104035. [Google Scholar] [CrossRef]
- Biedron, R.; Vatsa, V.; Atkins, H. Simulation of Unsteady Flows Using an Unstructured Navier-Stokes Solver on Moving and Stationary Grids. In Proceedings of the 23rd AIAA Applied Aerodynamics Conference, Toronto, ON, Canada, 6–9 June 2005; pp. 1–17. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Tai, J.; Ahmed, F. Simulation of micro flows with moving boundaries using high-order upwind FV method on unstructured grids. Comput. Mech. 2001, 28, 66–75. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar] [CrossRef] [Green Version]
- Nichols, D.S. Development of a Free Surface Method Utilizing an Incompressible Multi-Phase Algorithm to Study the Flow about Surface Ships and Underwater Vehicles. Ph.D. Thesis, Mississippi State University, Starkville, MS, USA, 2002. [Google Scholar]
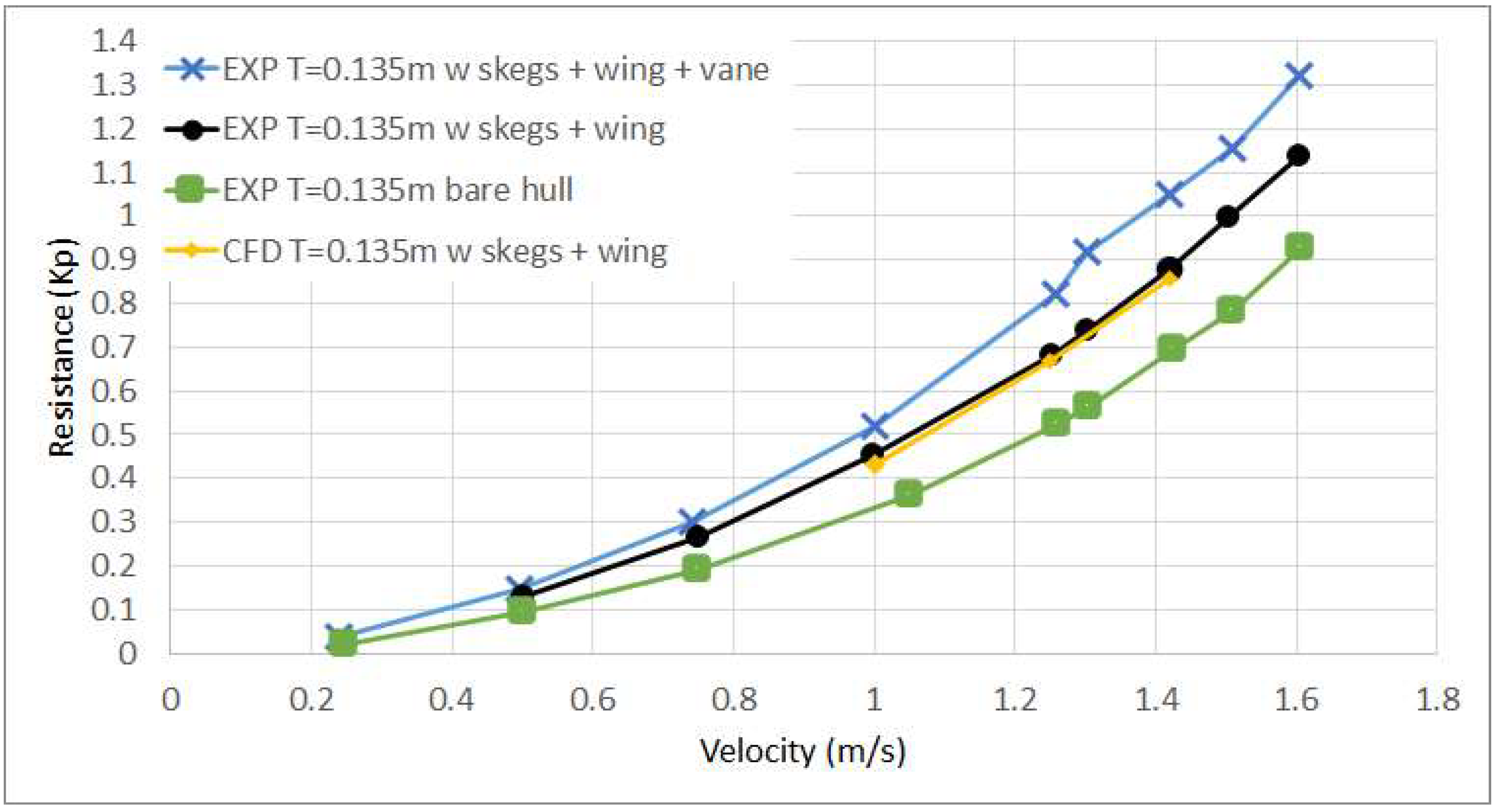
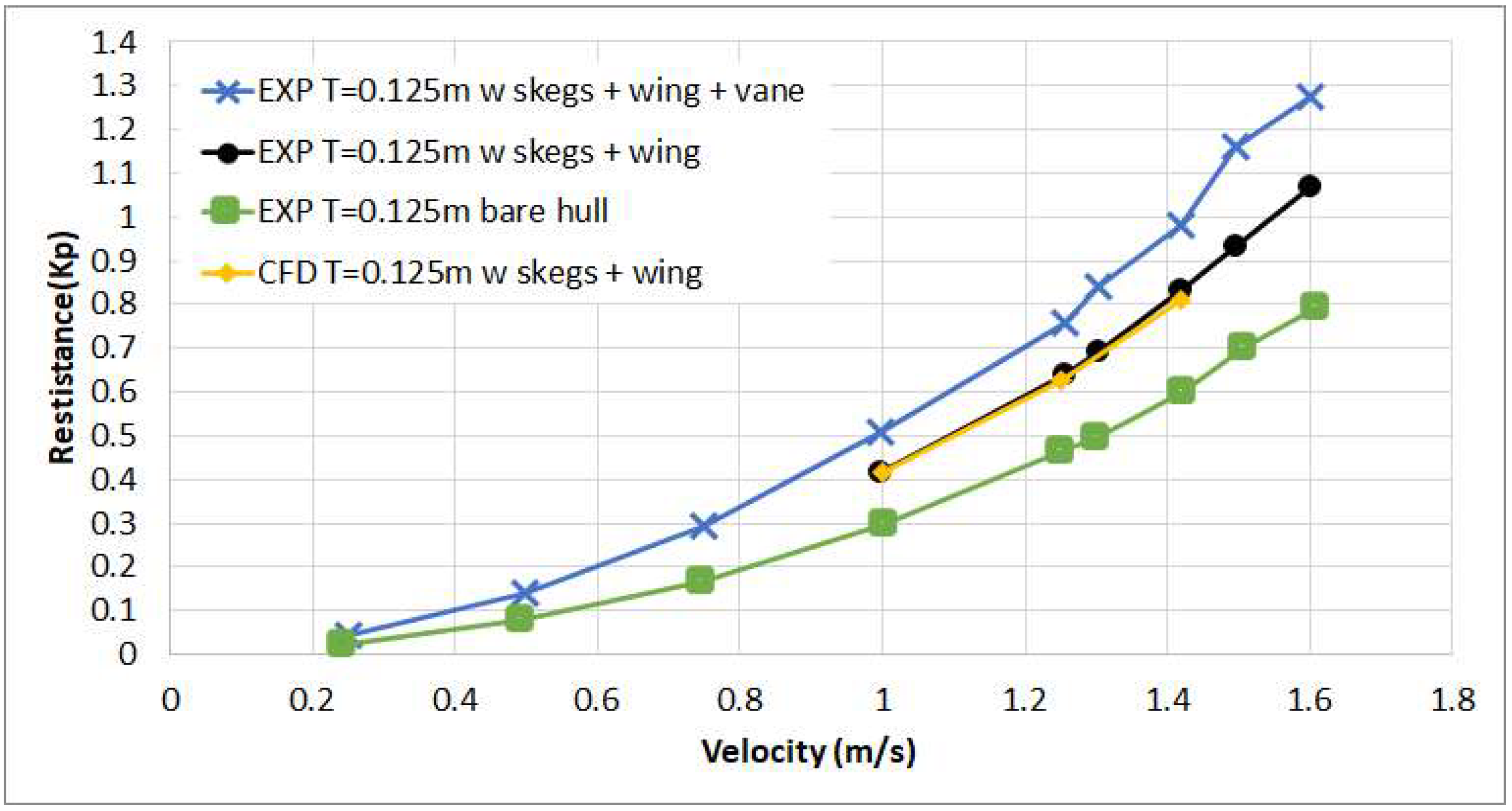

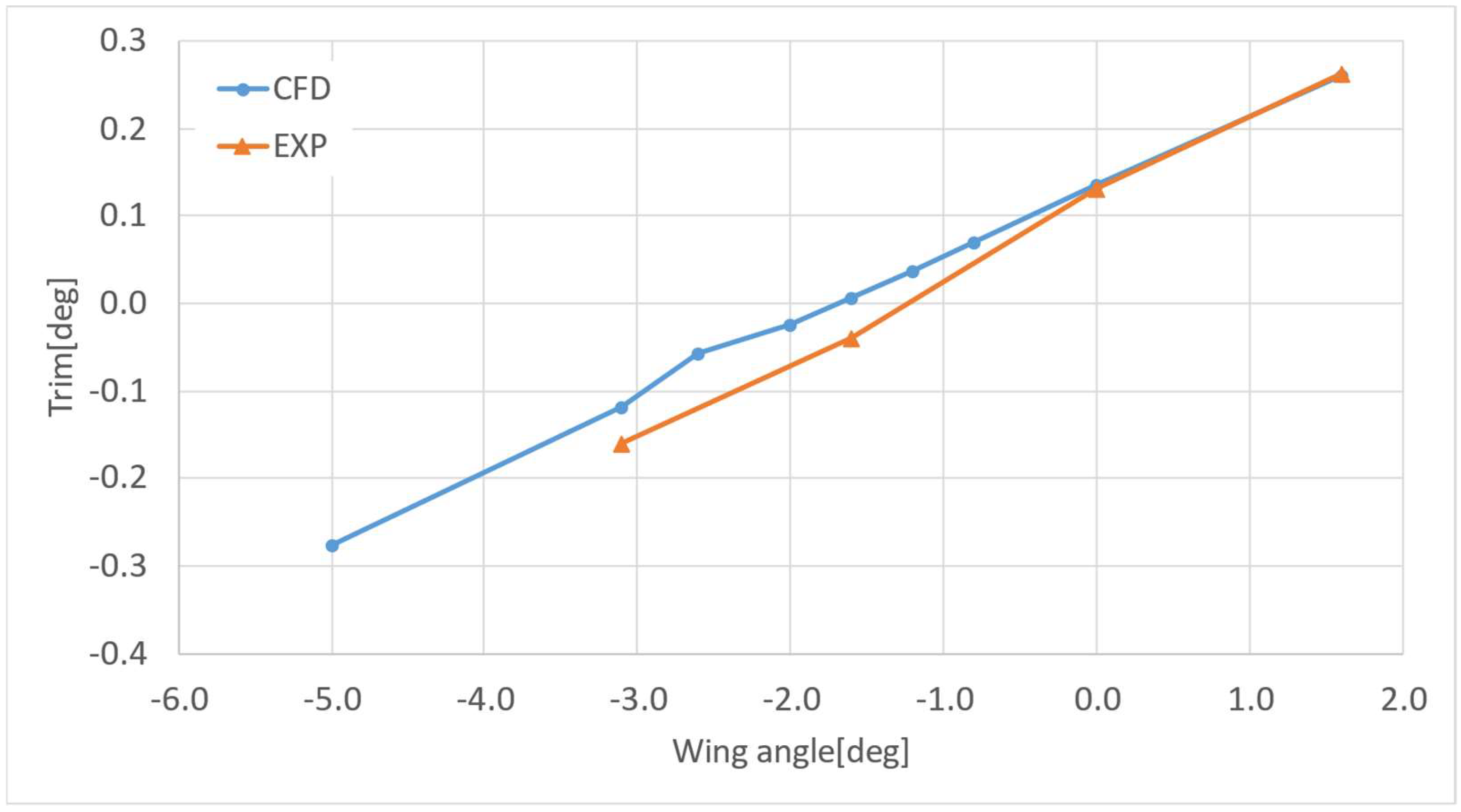
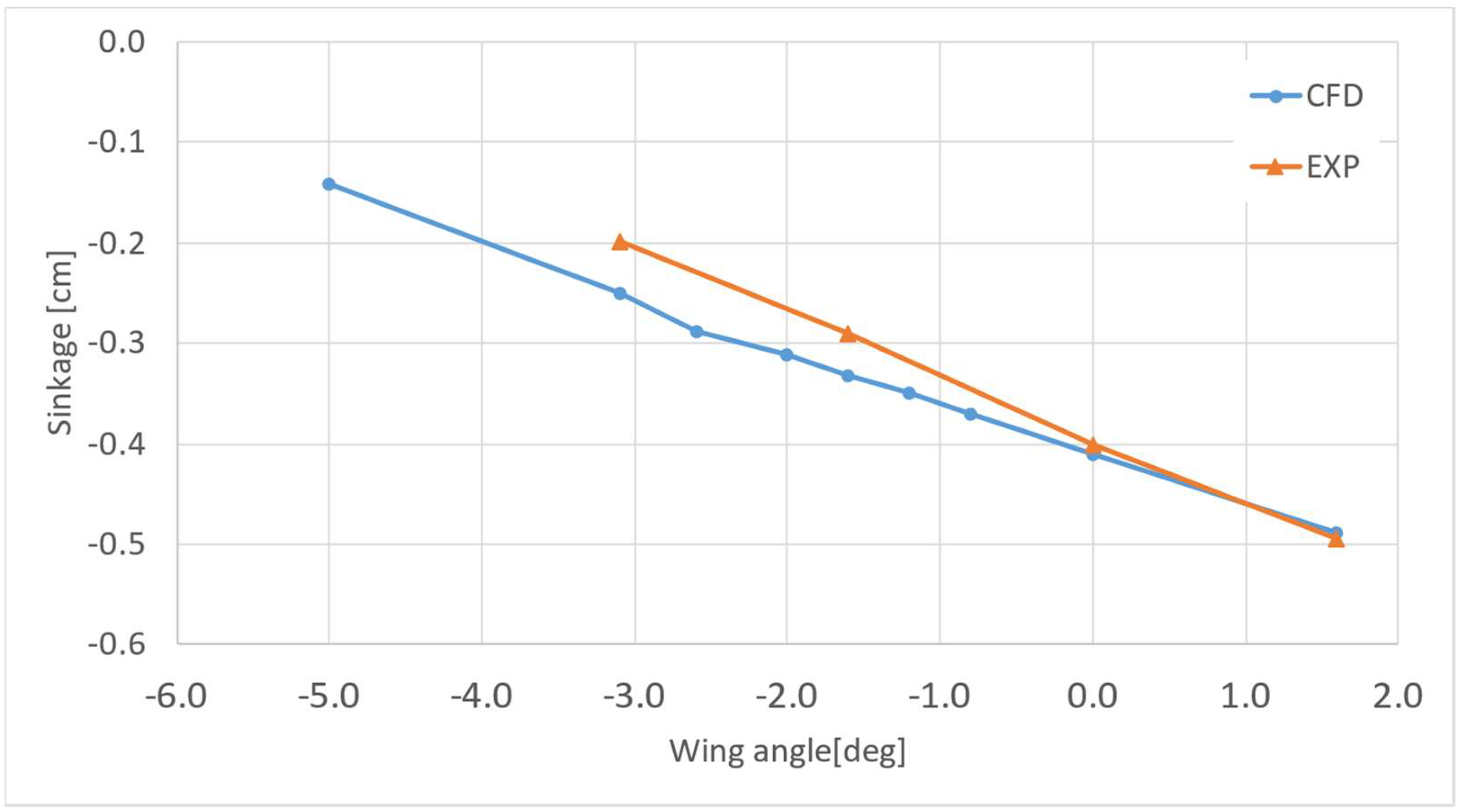


| Grid-Time-Step | Resistance (kp) | Trim (deg) | Sinkage (cm) |
|---|---|---|---|
| G3-Tref/2500 | 0.704 | 0.0977 | −0.386 |
| G2-Tref/2500 | 0.687 | 0.0954 | −0.388 |
| G1-Tref/2500 | 0.682 | 0.0922 | −0.392 |
| G2-Tref/500 | 0.686 | 0.0959 | −0.387 |
| G2-Tref/250 | 0.686 | 0.0958 | −0.387 |
| h1 | h2 | h3 | r21 | r32 | p | ||||
|---|---|---|---|---|---|---|---|---|---|
| 0.0455 | 0.0616 | 0.0860 | 1.35 | 1.40 | 1.53 | 0.674 | 0.73% | 1.26% | 1.56% |
| Froude No. | Total [kp] | Hull [kp] | Skegs [kp] | Wing [kp] |
|---|---|---|---|---|
| 0.25 | 0.829 | 0.66 | 0.077 | 0.092 |
| 0.22 | 0.653 | 0.52 | 0.061 | 0.072 |
| 0.176 | 0.431 | 0.34 | 0.043 | 0.048 |
| Froude No. | Total [kp] | Hull [kp] | Skegs [kp] | Wing [kp] |
|---|---|---|---|---|
| 0.25 | 0.788 | 0.62 | 0.073 | 0.095 |
| 0.22 | 0.614 | 0.48 | 0.059 | 0.075 |
| 0.176 | 0.413 | 0.32 | 0.042 | 0.051 |
| Angle of Attack [deg] | Resistance [kp] | Trim [deg] | Sinkage [cm] |
|---|---|---|---|
| −3.1 | 1.031 | −0.159 | −0.198 |
| −1.6 | 1.007 | −0.039 | −0.291 |
| 1.6 | 1.028 | 0.264 | −0.494 |
| 0 | 1.042 | 0.132 | −0.401 |
| dt [s] | ||||||
|---|---|---|---|---|---|---|
| 0.003 | 1.93 | 2.27 | 1.18 | 1.93 | 2.27 | 1.18 |
| 0.002 | 1.79 | 2.19 | 1.10 | 1.79 | 2.19 | 1.10 |
| 0.001 | 1.75 | 2.14 | 1.08 | 1.75 | 2.14 | 1.08 |
| Wavelength to Ship Length Lw/Ls | Resistance [kp] Bare Hull | Resistance [kp] with Foil | Gain (%) |
|---|---|---|---|
| 0.87 | 1.153 | 0.883 | +23.5 |
| 1.09 | 1.165 | 0.801 | +31.2 |
| 1.16 | 1.177 | 0.774 | +34.2 |
| 1.62 | 0.854 | 0.747 | +12.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ntouras, D.; Papadakis, G.; Belibassakis, K. Ship Bow Wings with Application to Trim and Resistance Control in Calm Water and in Waves. J. Mar. Sci. Eng. 2022, 10, 492. https://doi.org/10.3390/jmse10040492
Ntouras D, Papadakis G, Belibassakis K. Ship Bow Wings with Application to Trim and Resistance Control in Calm Water and in Waves. Journal of Marine Science and Engineering. 2022; 10(4):492. https://doi.org/10.3390/jmse10040492
Chicago/Turabian StyleNtouras, Dimitris, George Papadakis, and Kostas Belibassakis. 2022. "Ship Bow Wings with Application to Trim and Resistance Control in Calm Water and in Waves" Journal of Marine Science and Engineering 10, no. 4: 492. https://doi.org/10.3390/jmse10040492
APA StyleNtouras, D., Papadakis, G., & Belibassakis, K. (2022). Ship Bow Wings with Application to Trim and Resistance Control in Calm Water and in Waves. Journal of Marine Science and Engineering, 10(4), 492. https://doi.org/10.3390/jmse10040492








