Wave Forces on a Partially Reflecting Wall by Oblique Bragg Scattering with Porous Breakwaters over Uneven Bottoms
Abstract
:1. Introduction
2. Materials and Methods
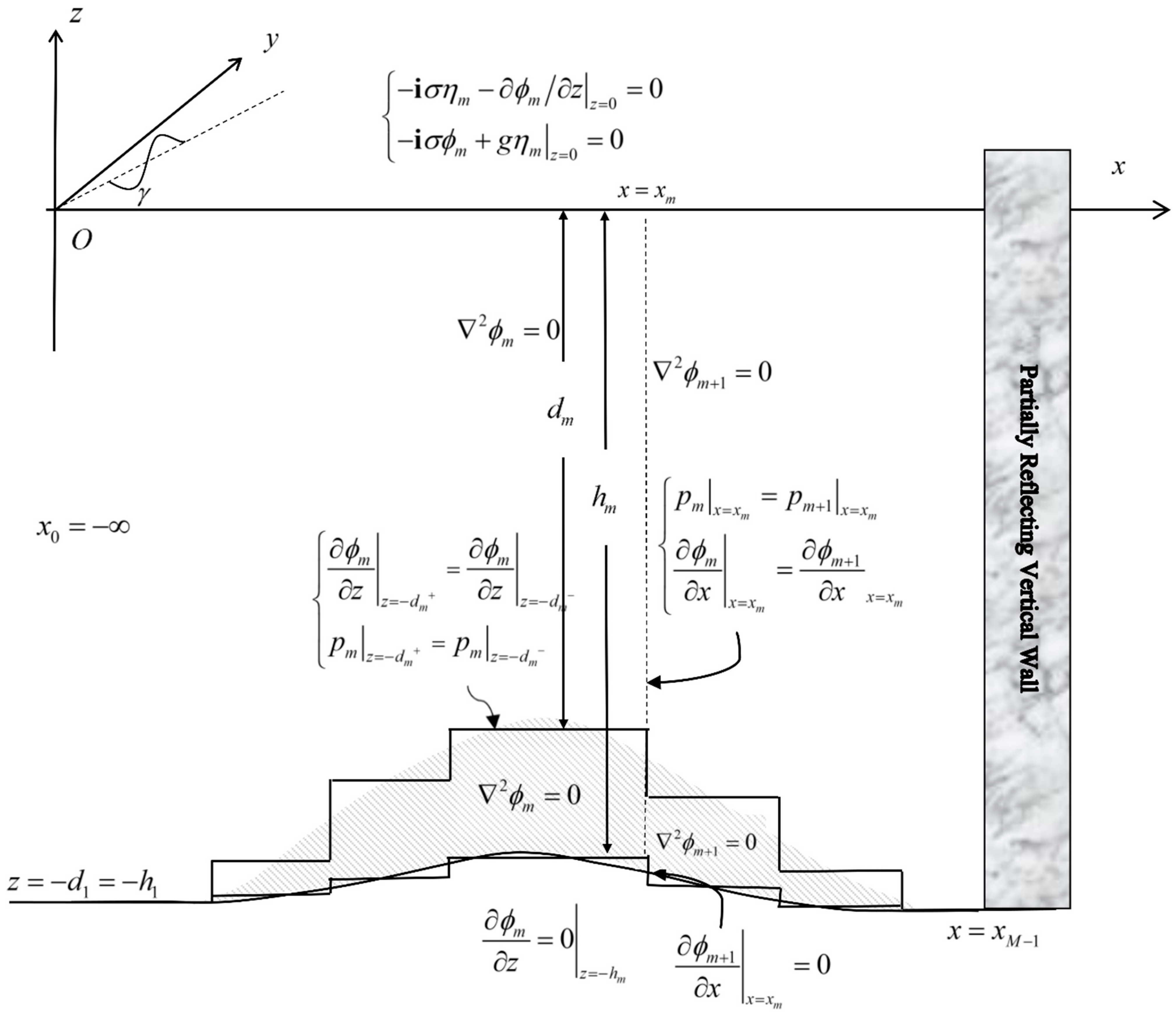
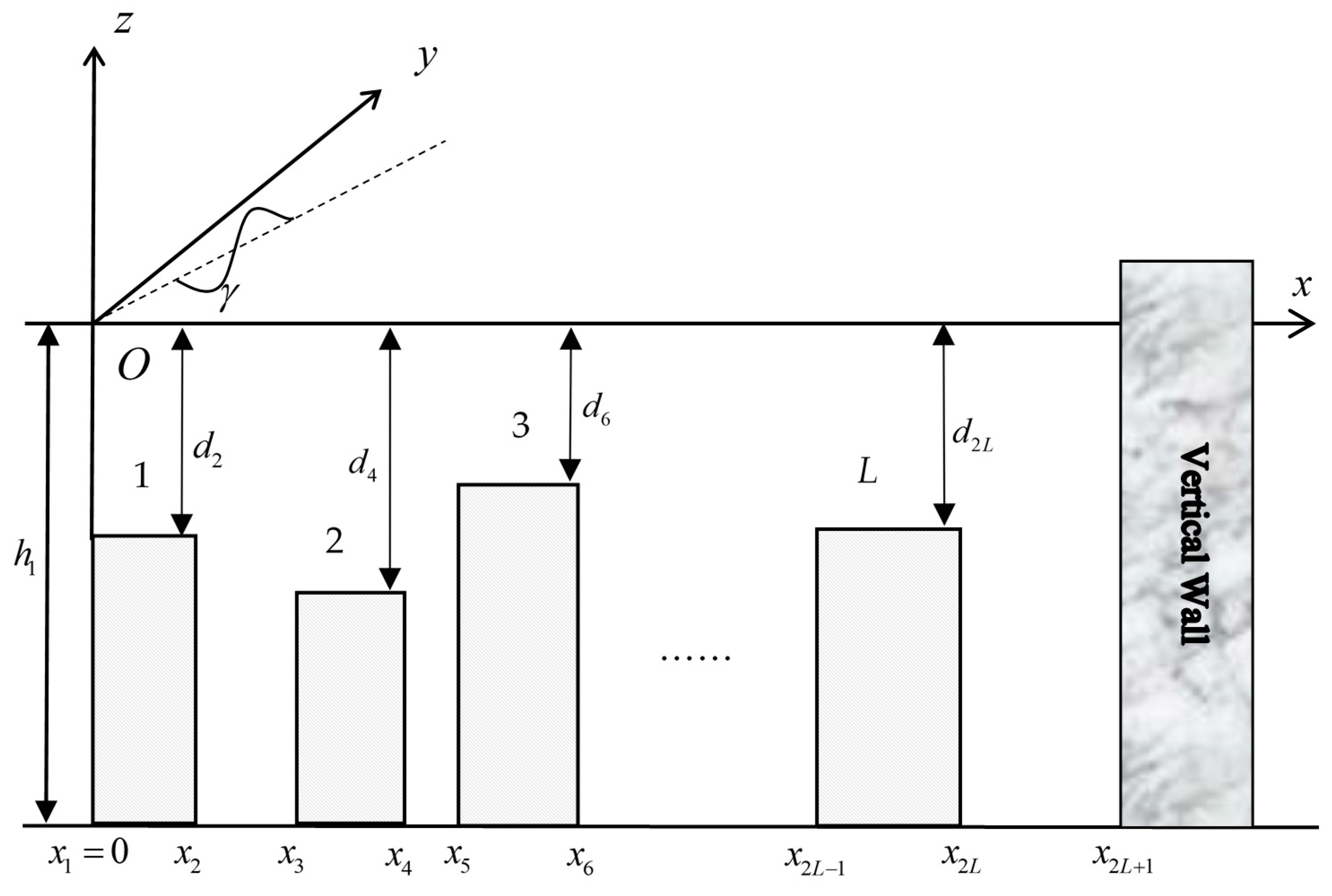
2.1. Problem Definition
2.2. Dispersion Relations and Eigenfunctions
2.3. Subaerial Porous Breakwaters
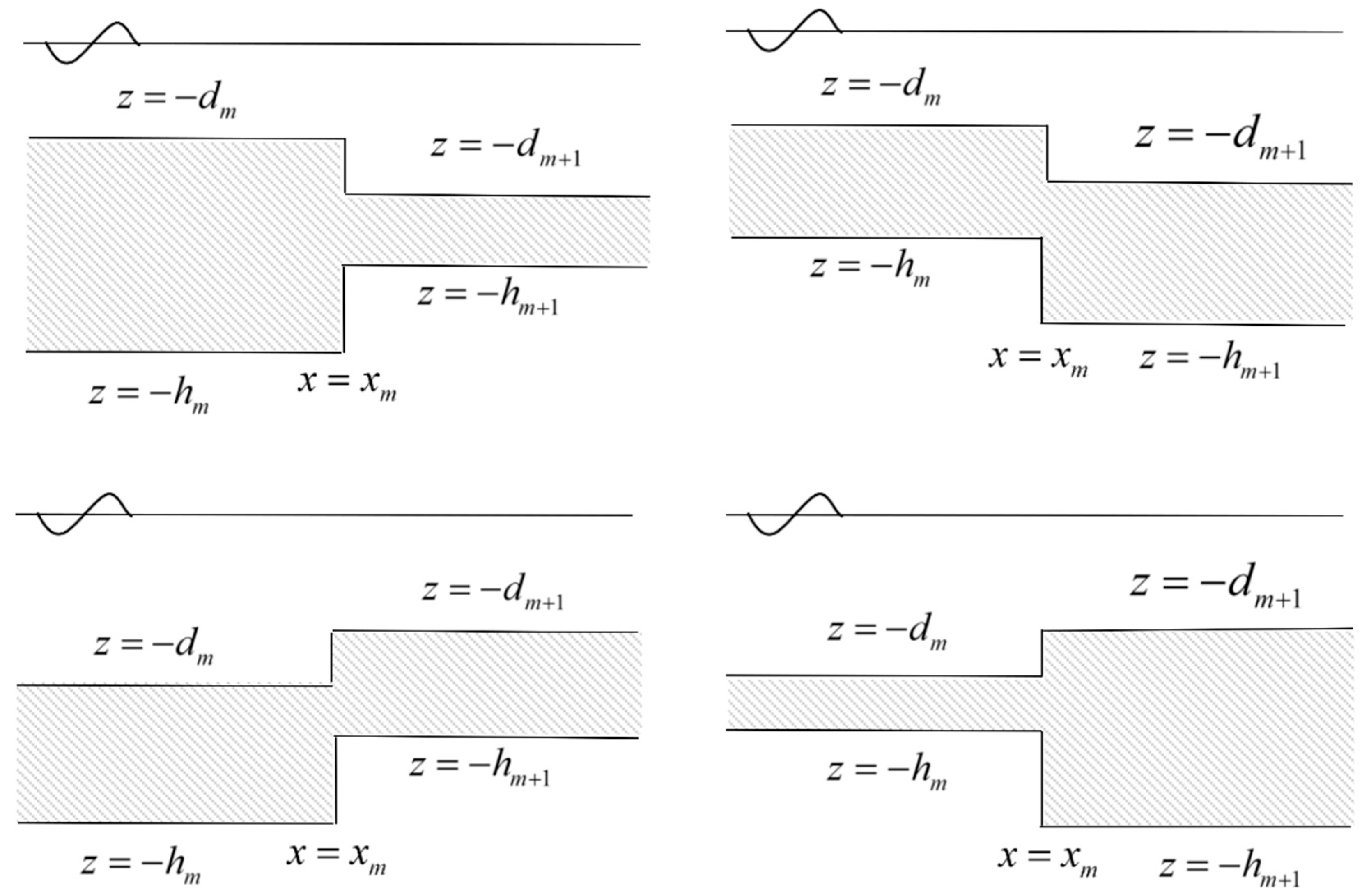
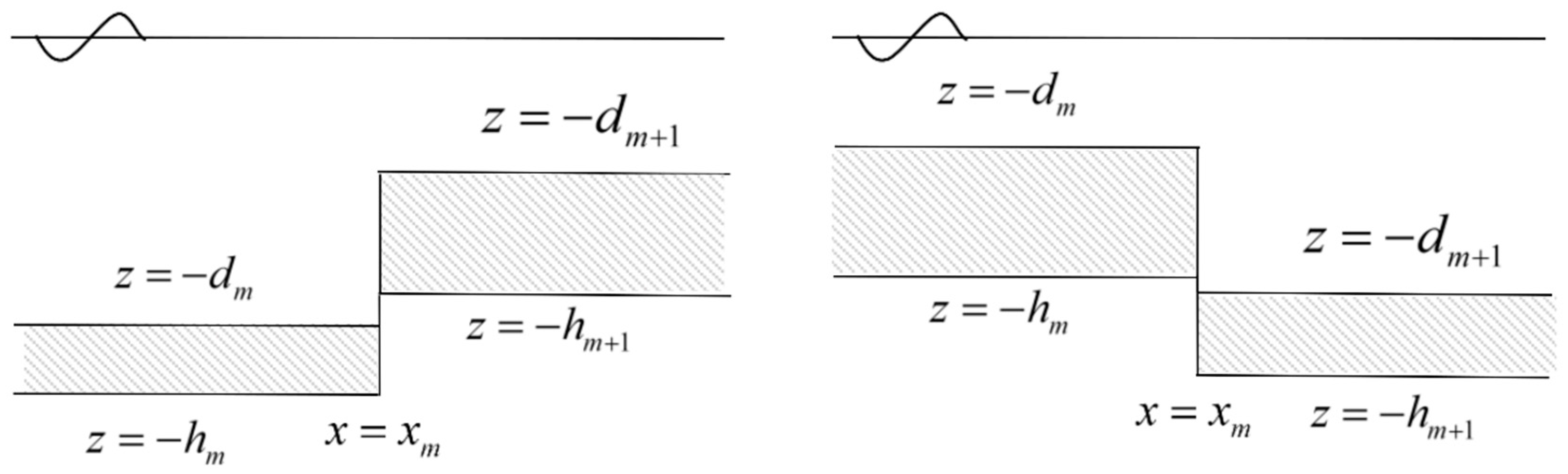
2.4. Eigenfunction Matching Method
2.5. Wave Force on the Partially Reflecting Wall
3. Results
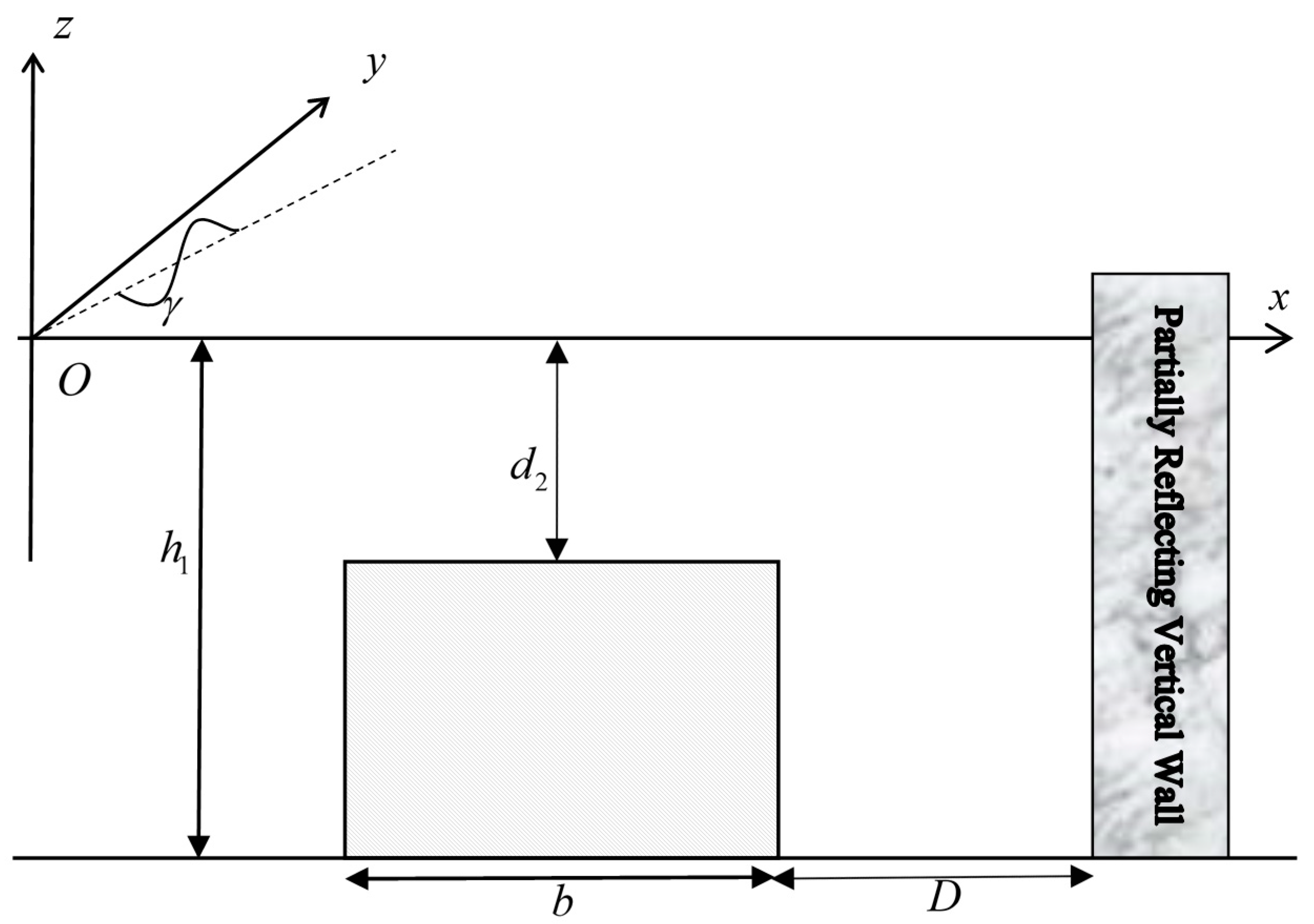
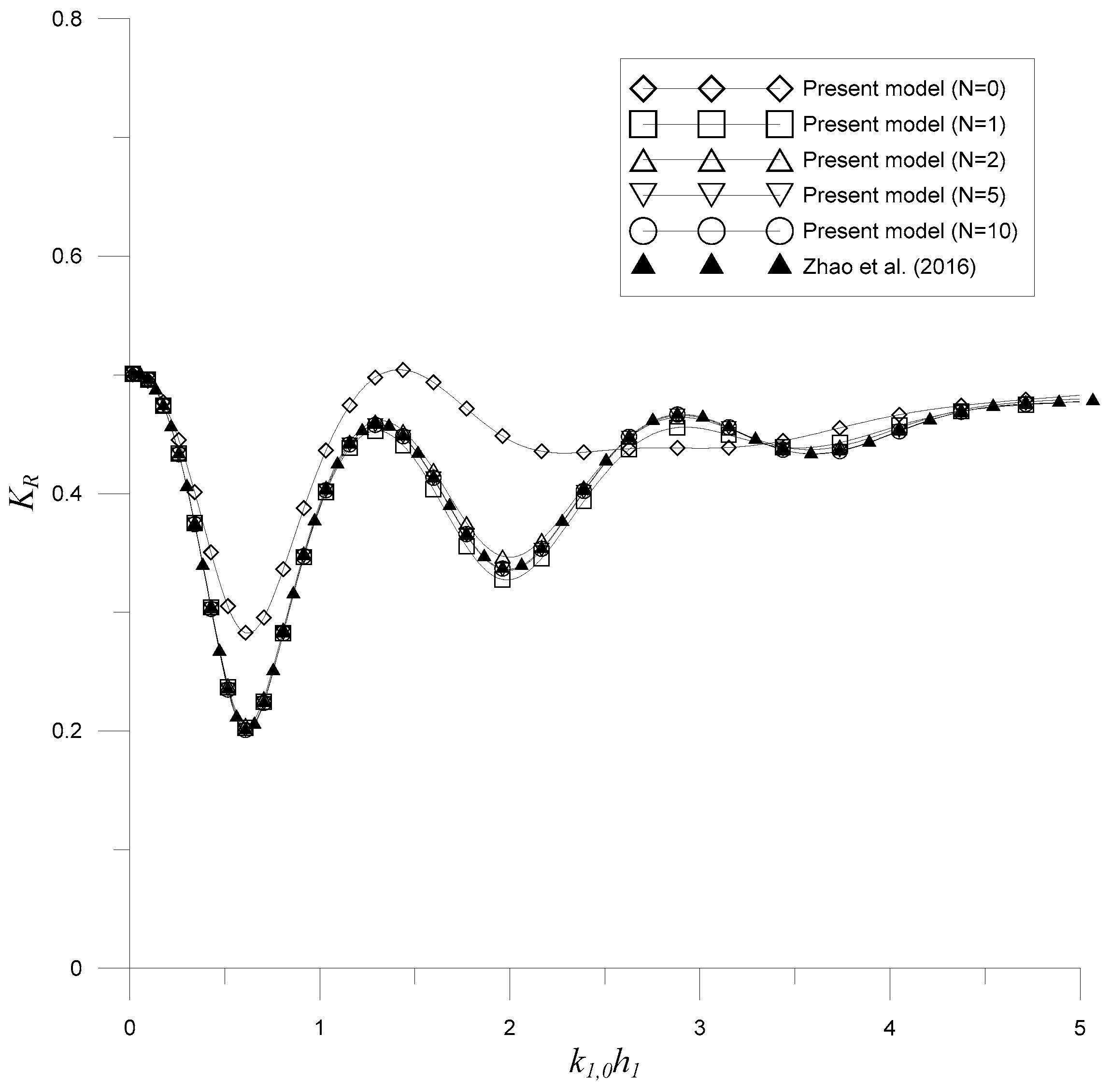
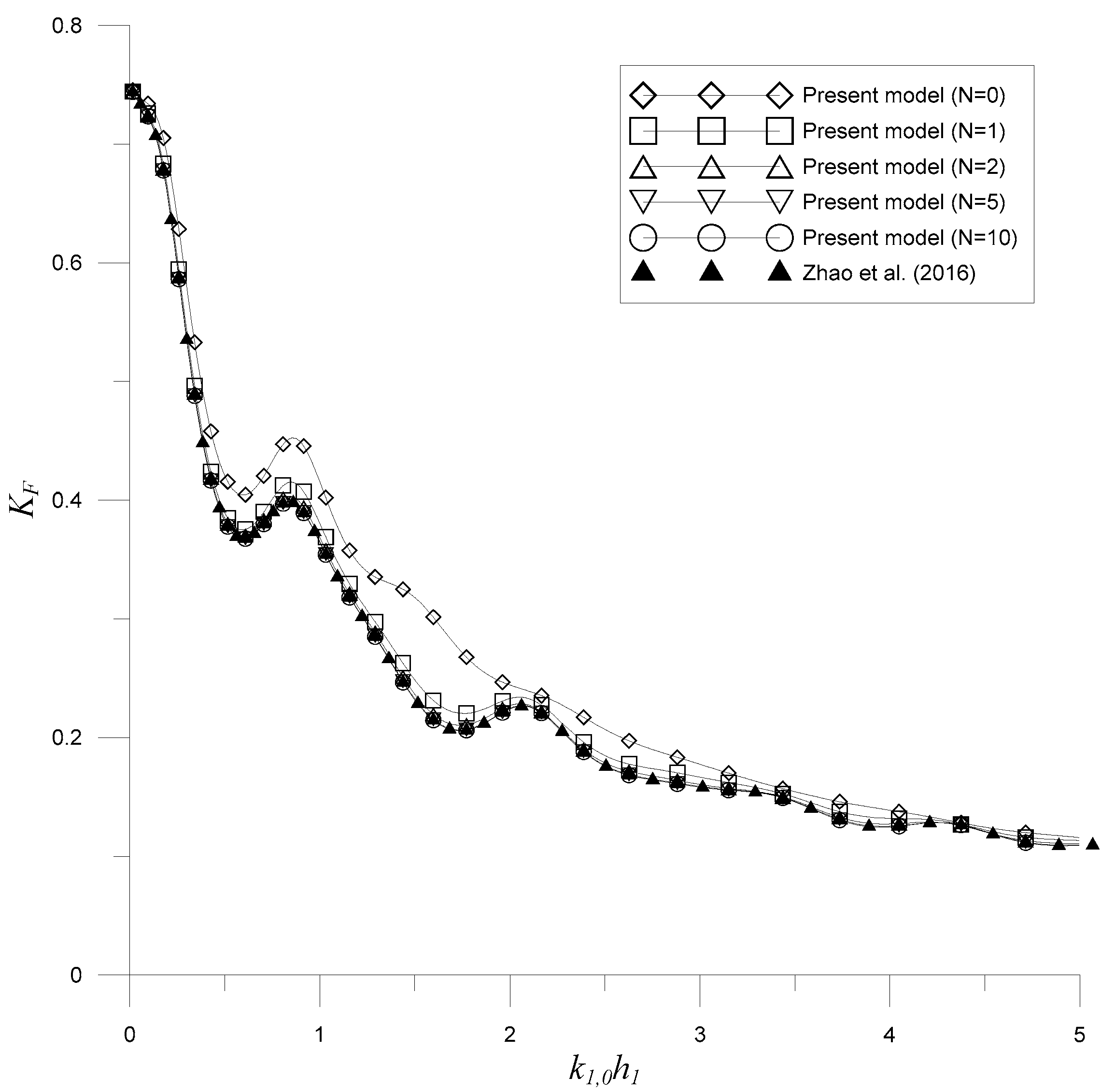
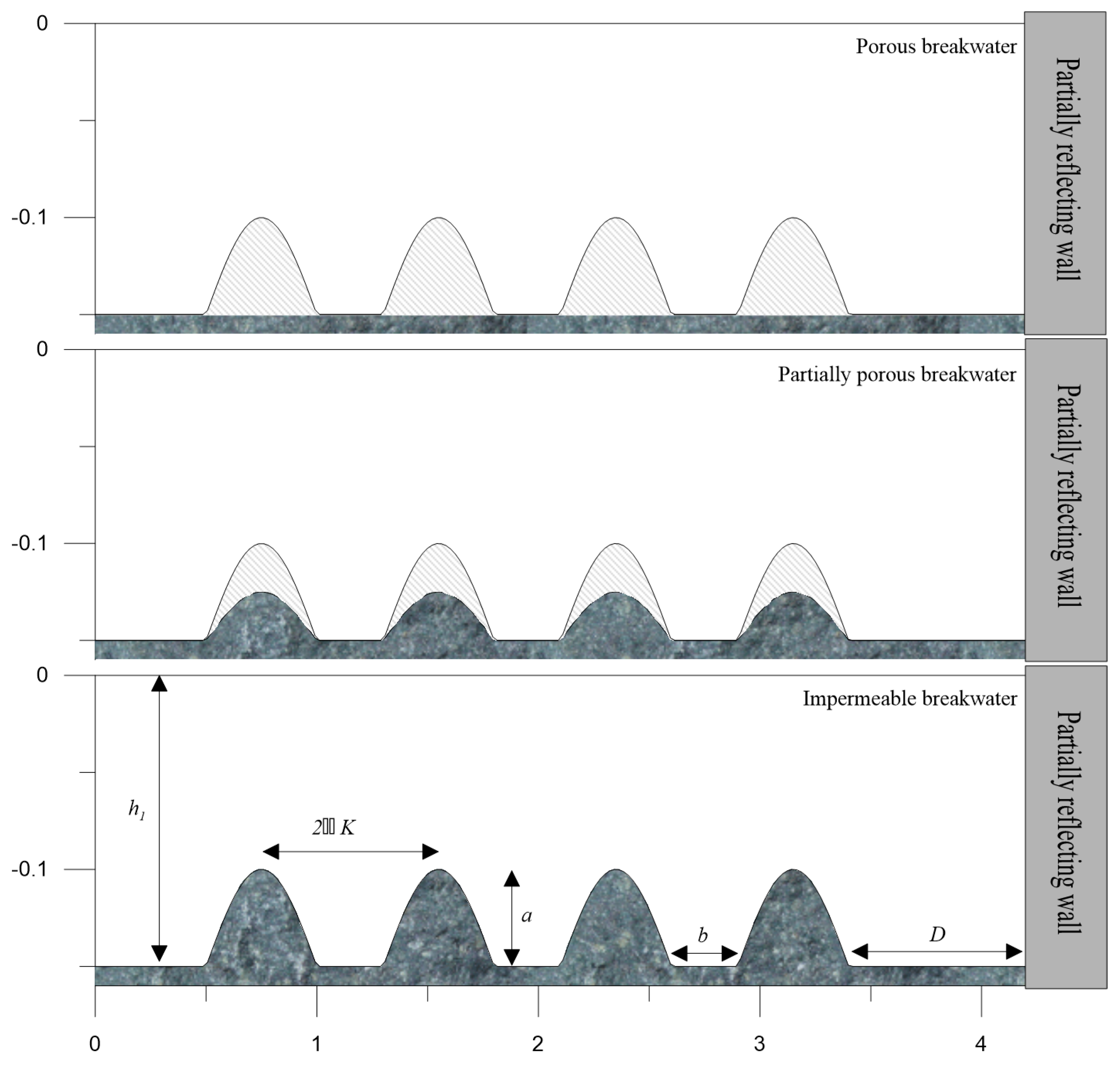
3.1. A Rectangular Porous Structure near a Partially Reflecting Vertical Wall
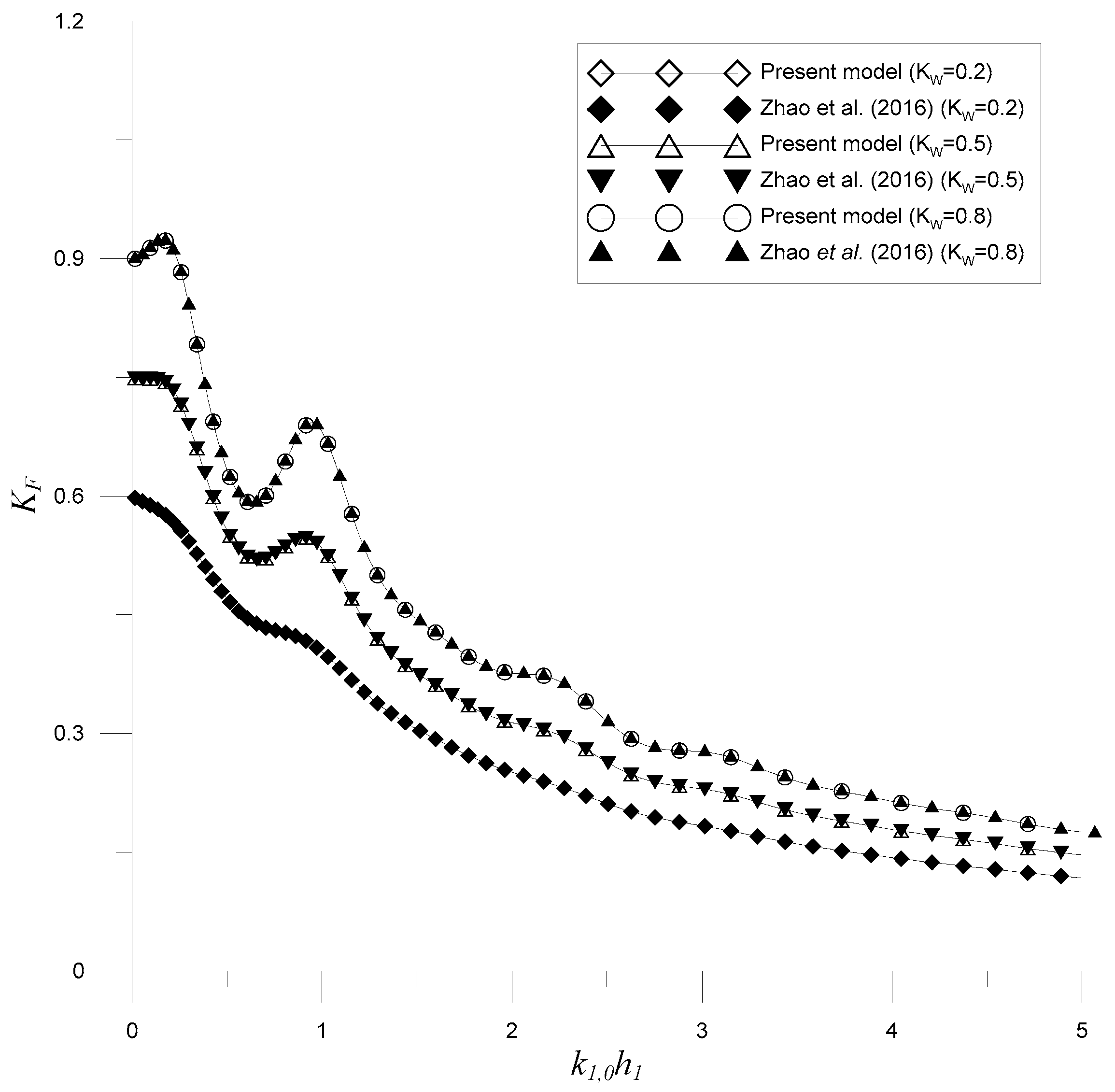
3.2. Wave Force on the Vertical Wall
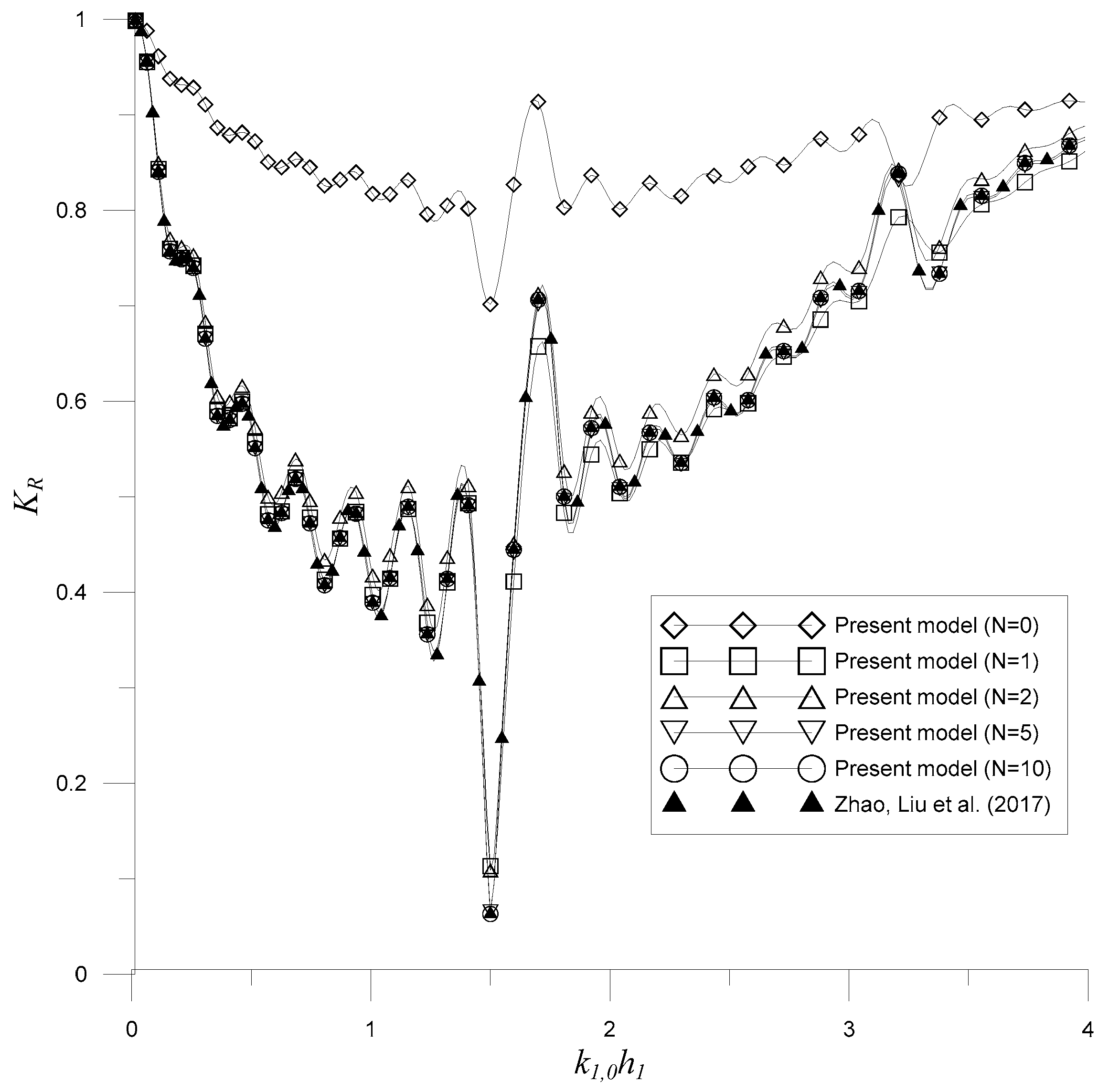
3.3. Multiple Porous Structures near a Totally Reflecting Vertical Wall
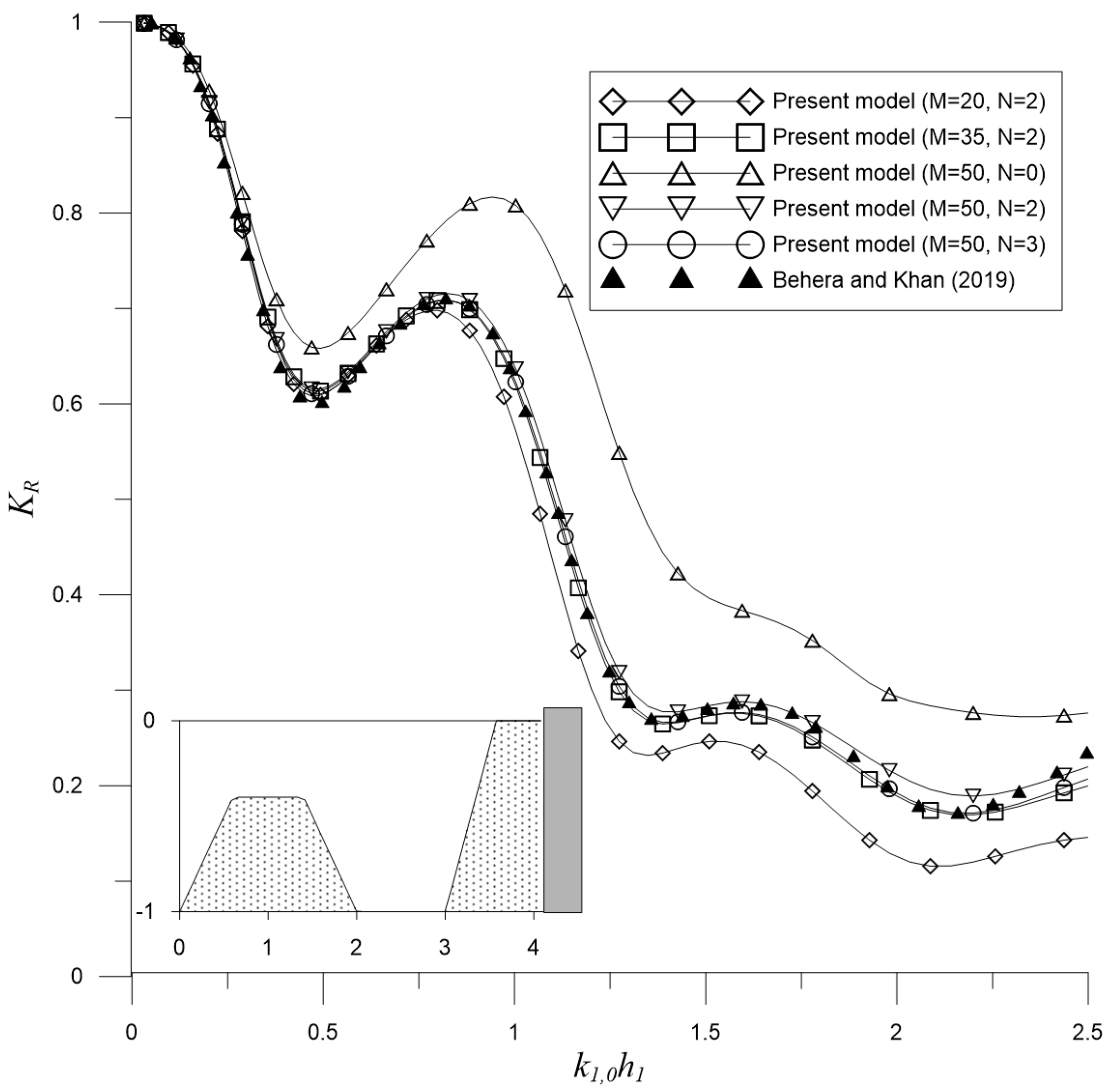
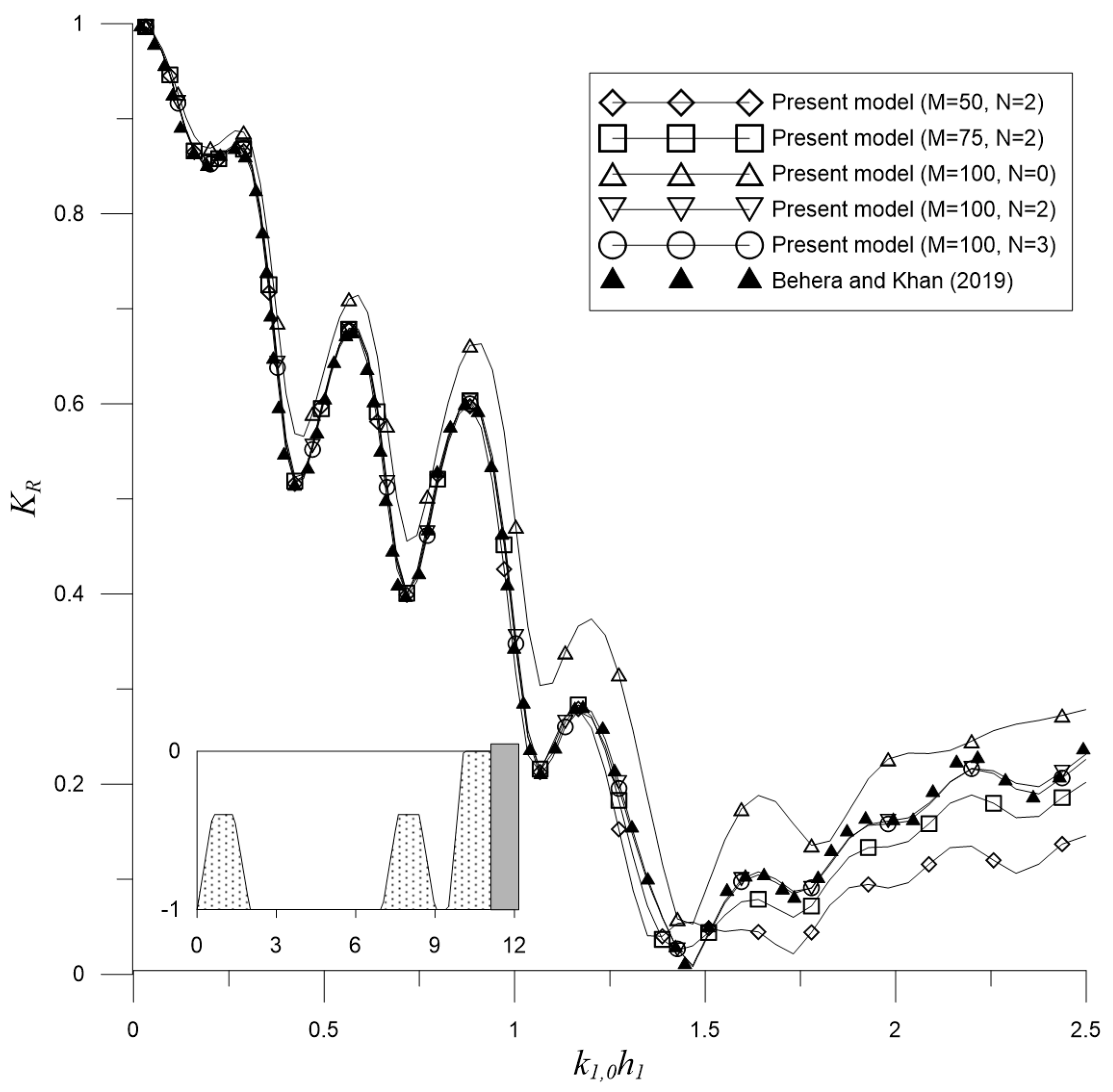
3.4. Trapezoidal Porous Breakwaters near a Porous Seawall
4. Discussion
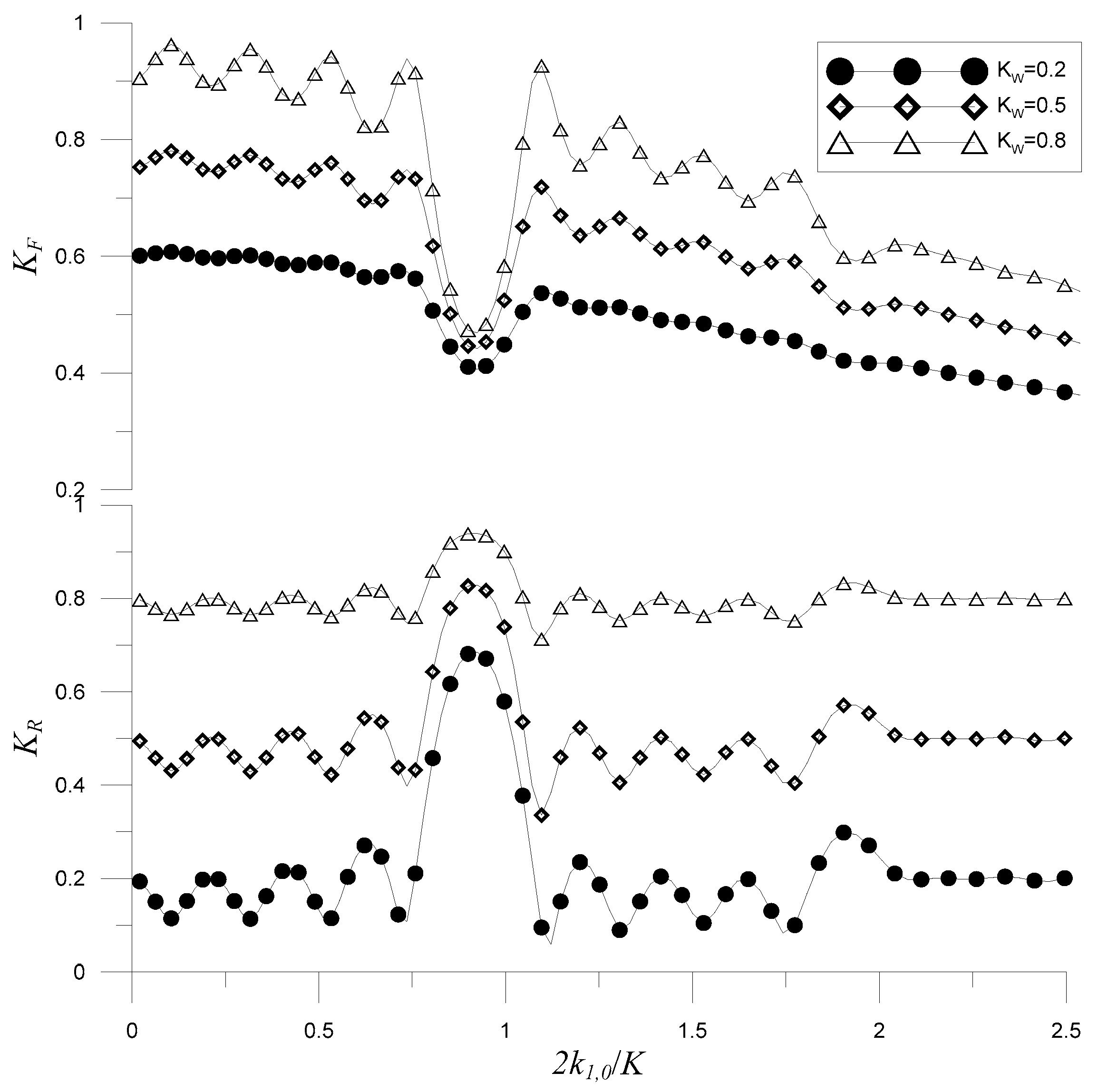
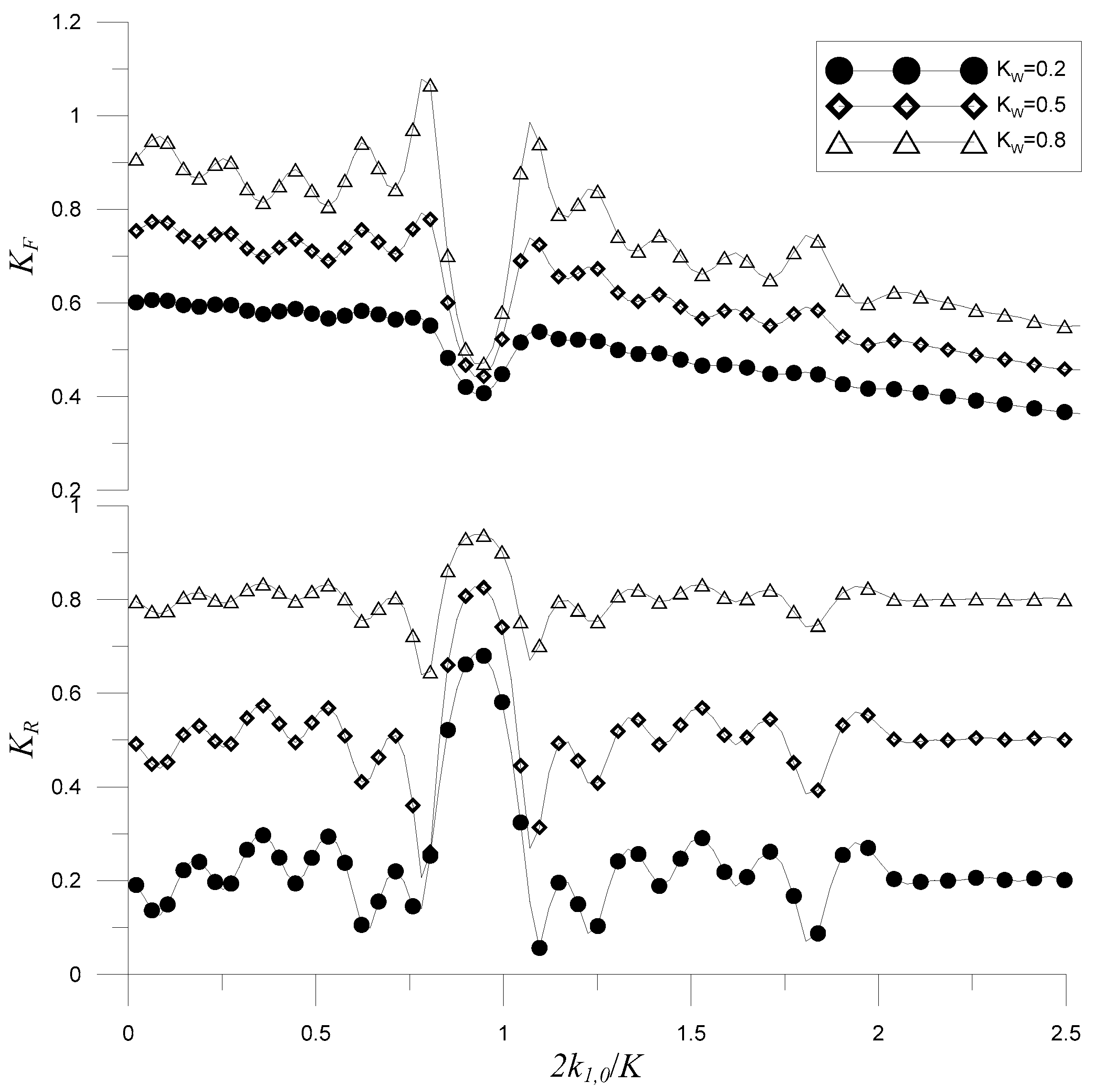
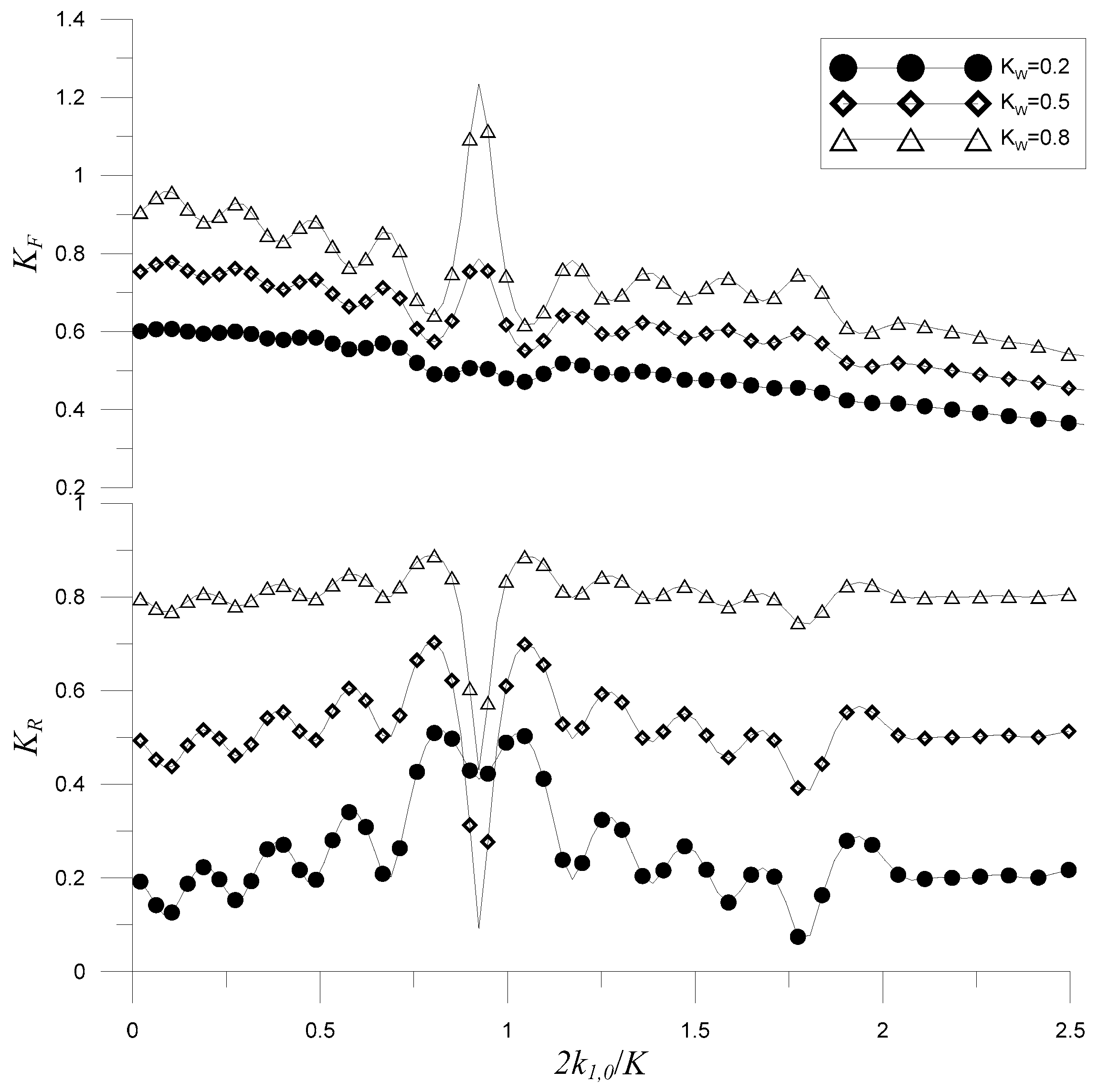
4.1. Constructive Bragg Scattering by the Partially Reflecting Wall
4.2. Destructive Bragg Scattering by the Partially Reflecting Wall
4.3. Oblique Incidence
4.4. Periodic Porous Breakwaters
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| coefficient of vertical eigenfunction | |
| coefficient of vertical eigenfunction | |
| coefficient of vertical eigenfunction | |
| coefficient of vertical eigenfunction | |
| incidence angle | |
| porosity of porous media | |
| wavelength of incident wave | |
| angular frequency of incident wave | |
| density of water | |
| velocity potential on the shelf | |
| surface elevation on the shelf | |
| parameter for porous layer | |
| phase angle | |
| vertical eigenfunction | |
| the first horizontal eigenfunction | |
| the second horizontal eigenfunction | |
| vertical eigenfunction for the larger total depth | |
| vertical eigenfunction for the smaller total depth | |
| three-dimensional gradient operator | |
| three-dimensional Laplace operator | |
| operator for porous pressure | |
| amplitude of incident wave | |
| amplitude of the half-cosine shaped breakwater in Section 4 | |
| width of the rectangular porous breakwater in Section 3.1 and Section 3.2 or separation distance between half-cosine breakwaters in Section 4 | |
| water depth on the shelf | |
| friction coefficient of porous media | |
| acceleration of gravity | |
| total depth on the shelf | |
| unit of complex numbers | |
| transverse wavenumber | |
| lateral wavenumber of the evanescent mode on the shelf | |
| absolute wavenumber of the evanescent mode on the shelf | |
| lateral wavenumber of the propagating mode on the shelf | |
| absolute wavenumber of the propagating mode on the shelf | |
| index of modes | |
| index for shelves and steps | |
| pressure on the shelf | |
| index for constructive Bragg scattering | |
| index for destructive Bragg scattering | |
| time | |
| inertial coefficient of porous media | |
| fluid velocity or discharge velocity on the shelf | |
| coordinate of the step | |
| reference location of the | |
| three-dimensional Cartesian coordinates | |
| EMM unknown coefficients | |
| EMM unknown coefficients | |
| Separation distance between the last porous breakwater and the vertical wall in Section 3.1, Section 3.2 and Section 4. | |
| or | variable for depth eigenfunction |
| partially reflecting factor of the vertical wall | |
| reflection coefficient | |
| dimensionless horizontal wave force on the vertical wall | |
| number of shelves plus one | |
| number of evanescent modes | |
| wave period of incident wave | |
| wavelength of the periodic bottom in Section 4 |
References
- Sollitt, C.K.; Cross, R.H. Wave transmission through permeable breakwaters. Coast. Eng. 1972, 1973, 1827–1846. [Google Scholar]
- Dalrymple, R.A.; Losada, M.A.; Martin, P.A. Reflection and transmission from porous structures under oblique wave attack. J. Fluid Mech. 1991, 224, 625–644. [Google Scholar] [CrossRef]
- Losada, I.J.; Dalrymple, R.A.; Losada, M.A. Water waves on crown breakwaters. J. Waterw. Port Coast. Ocean Eng. 1993, 119, 367–380. [Google Scholar] [CrossRef]
- Rojanakamthorn, S.; Isobe, M.; Watanabe, A. A mathematical model of wave transformation over a submerged breakwater. Coast. Eng. Jpn. 1989, 32, 209–234. [Google Scholar] [CrossRef]
- Rojanakamthorn, S.; Isobe, M.; Watanabe, A. Modeling of wave transformation on submerged breakwater. Coast. Eng. 1990, 1, 1060–1073. [Google Scholar]
- Twu, S.-W.; Liu, C.-C.; Hsu, W.-H. Wave Damping Characteristics of Deeply Submerged Breakwaters. J. Waterw. Port Coast. Ocean Eng. 2001, 127, 97–105. [Google Scholar] [CrossRef]
- Twu, S.-W.; Liu, C.-C. Interaction of non-breaking regular waves with a periodic array of artificial porous bars. Coast. Eng. 2004, 51, 223–236. [Google Scholar] [CrossRef]
- Venkateswarlu, V.; Karmakar, D. Wave scattering by vertical porous block placed over flat and elevated seabed. Mar. Syst. Ocean Technol. 2019, 14, 85–109. [Google Scholar] [CrossRef]
- Silva, R.; Salles, P.; Palacio, A. Linear waves propagating over a rapidly varying finite porous bed. Coast. Eng. 2002, 44, 239–260. [Google Scholar] [CrossRef]
- Ni, Y.-L.; Teng, B. Bragg resonant reflection of water waves by a Bragg breakwater with porous rectangular bars on a sloping permeable seabed. Ocean Eng. 2021, 235, 109333. [Google Scholar] [CrossRef]
- Silva, R.; Salles, P.; Govaere, G. Extended solution for waves travelling over a rapidly changing porous bottom. Ocean Eng. 2003, 30, 437–452. [Google Scholar] [CrossRef]
- Wang, J.; He, G.; You, R.; Liu, P. Numerical study on interaction of a solitary wave with the submerged obstacle. Ocean Eng. 2018, 158, 1–14. [Google Scholar] [CrossRef]
- Luo, M.; Khayyer, A.; Lin, P. Particle methods in ocean and coastal engineering. Appl. Ocean Res. 2021, 114, 102734. [Google Scholar] [CrossRef]
- Jacobsen, N.G.; van Gent, M.R.A.; Capel, A.; Borsboom, M. Numerical prediction of integrated wave loads on crest walls on top of rubble mound structures. Coast. Eng. 2018, 142, 110–124. [Google Scholar] [CrossRef]
- Dattatri, J.; Raman, H.; Shankar, N.J. Performance characteristics of submerged breakwaters. Coast. Eng. 1978, 1978, 2153–2171. [Google Scholar]
- Dick, T.M.; Brebner, A. Solid and permeable submerged breakwaters. Coast. Eng. 1968, 1969, 1141–1158. [Google Scholar] [CrossRef] [Green Version]
- Goda, Y. Random Seas and Design of Maritime Structures; World Scientific: Singapore, 2010. [Google Scholar]
- Xiang, T.; Istrati, D. Assessment of Extreme Wave Impact on Coastal Decks with Different Geometries via the Arbitrary Lagrangian-Eulerian Method. J. Mar. Sci. Eng. 2021, 9, 1342. [Google Scholar] [CrossRef]
- Isaacson, M.; Qu, S. Waves in a harbour with partially reflecting boundaries. Coast. Eng. 1990, 14, 193–214. [Google Scholar] [CrossRef]
- Elchahal, G.; Younes, R.; Lafon, P. The effects of reflection coefficient of the harbour sidewall on the performance of floating breakwaters. Ocean Eng. 2008, 35, 1102–1112. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Y.; Li, H. Wave interaction with a partially reflecting vertical wall protected by a submerged porous bar. J. Ocean Univ. China 2016, 15, 619–626. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, H.-J.; Liu, Y. Oblique wave scattering by a submerged porous breakwater with a partially reflecting sidewall. J. Mar. Sci. Technol. 2017, 25, 3. [Google Scholar]
- Behera, H.; Khan, M.B. Numerical modeling for wave attenuation in double trapezoidal porous structures. Ocean Eng. 2019, 184, 91–106. [Google Scholar] [CrossRef]
- Khan, M.B.M.; Gayathri, R.; Behera, H. Wave attenuation properties of rubble mound breakwater in tandem with a floating dock against oblique regular waves. Waves Random Complex Media 2021, 1–19. [Google Scholar] [CrossRef]
- Khan, M.B.M.; Behera, H. Analysis of wave action through multiple submerged porous structures. J. Offshore Mech. Arct. Eng. 2019, 142, 011101. [Google Scholar] [CrossRef]
- Khan, M.; Behera, H.; Sahoo, T.; Neelamani, S. Boundary element method for wave trapping by a multi-layered trapezoidal breakwater near a sloping rigid wall. Meccanica 2021, 56, 317–334. [Google Scholar] [CrossRef]
- Pakozdi, C.; Kendon, T.E.; Stansberg, C.-T. Breaking Wave Impact on a Platform Column: An Introductory CFD Study. In Proceedings of the ASME 30th International Conference on Ocean, Offshore and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011; pp. 645–654. [Google Scholar]
- Xiang, T.; Istrati, D.; Yim, S.C.; Buckle, I.G.; Lomonaco, P. Tsunami Loads on a Representative Coastal Bridge Deck: Experimental Study and Validation of Design Equations. J. Waterw. Port Coast. Ocean Eng. 2020, 146, 04020022. [Google Scholar] [CrossRef]
- Pan, K.; Ijzermans, R.H.A.; Jones, B.D.; Thyagarajan, A.; van Beest, B.W.H.; Williams, J.R. Application of the SPH method to solitary wave impact on an offshore platform. Comput. Part. Mech. 2016, 3, 155–166. [Google Scholar] [CrossRef] [Green Version]
- Hasanpour, A.; Istrati, D.; Buckle, I. Coupled SPH–FEM Modeling of Tsunami-Borne Large Debris Flow and Impact on Coastal Structures. J. Mar. Sci. Eng. 2021, 9, 1068. [Google Scholar] [CrossRef]
- Canelas, R.; Ferreira, R.; Crespo, A.; Domínguez, J. A generalized SPH-DEM discretization for the modelling of complex multiphasic free surface flows. In Proceedings of the 8th International SPHERIC Workshop, Trondheim, Norway, 4–6 June 2013; pp. 74–79. [Google Scholar]
- Berkhoff, J.C.W. Computation of combined refraction-diffraction. In Proceedings of the 13th International Conference on Coastal Engineering, Vancouver, BC, Canada, 10–14 July 1972; pp. 471–490. [Google Scholar]
- Takano, K. Effets d’un obstacle parallelepipedique sur la propagation de la houle. Houille Blanche 1960, 15, 247–267. [Google Scholar] [CrossRef] [Green Version]
- Miles, J.W. Oblique surface-wave diffraction by a cylindrical obstacle. Dyn. Atmos. Ocean 1981, 6, 121–123. [Google Scholar] [CrossRef]
- Martha, S.C.; Bora, S.N.; Chakrabarti, A. Oblique water-wave scattering by small undulation on a porous sea-bed. Appl. Ocean Res. 2007, 29, 86–90. [Google Scholar] [CrossRef] [Green Version]
- Massel, S.R. Extended refraction-diffraction equation for surface waves. Coast. Eng. 1993, 19, 97–126. [Google Scholar] [CrossRef]
- Liu, H.-W.; Zeng, H.-D.; Huang, H.-D. Bragg resonant reflection of surface waves from deep water to shallow water by a finite array of trapezoidal bars. Appl. Ocean Res. 2020, 94, 101976. [Google Scholar] [CrossRef]
- Belibassakis, K.; Touboul, J.; Laffitte, E.; Rey, V. A mild-slope system for bragg scattering of water waves by sinusoidal bathymetry in the presence of vertically sheared currents. J. Mar. Sci. Eng. 2019, 7, 9. [Google Scholar] [CrossRef] [Green Version]
- Belibassakis, K.; Touboul, J. A nonlinear coupled-mode model for waves propagating in vertically sheared currents in variable bathymetry—collinear waves and currents. Fluids 2019, 4, 61. [Google Scholar] [CrossRef] [Green Version]
- Belibassakis, K.; Athanassoulis, G. A coupled-mode model for the hydroelastic analysis of large floating bodies over variable bathymetry regions. J. Fluid Mech. 2005, 531, 221–249. [Google Scholar] [CrossRef]
- Porter, D. The mild-slope equations: A unified theory. J. Fluid Mech. 2020, 887, A29. [Google Scholar] [CrossRef]
- Mei, C.C.; Black, J.L. Scattering of surface waves by rectangular obstacles in waters of finite depth. J. Fluid Mech. 1969, 38, 499–511. [Google Scholar] [CrossRef]
- Kirby, J.T.; Dalrymple, R.A.; Seo, S.N. Propagation of obliquely incident water waves over a trench. Part 2. Currents flowing along the trench. J. Fluid Mech. 1987, 176, 95–116. [Google Scholar] [CrossRef]
- Losada, I.J.; Losada, M.A.; Losada, R. Wave spectrum scattering by vertical thin barriers. Appl. Ocean Res. 1994, 16, 123–128. [Google Scholar] [CrossRef]
- O’Hare, T.J.; Davies, A.G. A comparison of two models for surface-wave propagation over rapidly varying topography. Appl. Ocean Res. 1993, 15, 1–11. [Google Scholar] [CrossRef]
- Devillard, P.; Dunlop, F.; Souillard, B. Localization of gravity waves on a channel with a random bottom. J. Fluid Mech. 1988, 186, 521–538. [Google Scholar] [CrossRef]
- Tsai, C.C.; Lin, Y.-T.; Hsu, T.-W. On the weak viscous effect of the reflection and transmission over an arbitrary topography. Phys. Fluids 2013, 25, 043103–043121. [Google Scholar] [CrossRef]
- Tsai, C.-C.; Tai, W.; Hsu, T.-W.; Hsiao, S.-C. Step approximation of water wave scattering caused by tension-leg structures over uneven bottoms. Ocean Eng. 2018, 166, 208–225. [Google Scholar] [CrossRef]
- Tseng, I.-F.; You, C.-S.; Tsai, C.-C. Bragg reflections of oblique water waves by periodic surface-piercing and submerged breakwaters. J. Mar. Sci. Eng. 2020, 8, 522. [Google Scholar] [CrossRef]
- Tran, C.-T.; Chang, J.-Y.; Tsai, C.-C. Step approximation for water wave scattering by multiple thin barriers over undulated bottoms. J. Mar. Sci. Eng. 2021, 9, 629. [Google Scholar] [CrossRef]
- Liu, X.; Wang, X.; Xu, S. A DMM-EMM-RSM hybrid technique on two-dimensional frequency-domain hydroelasticity of floating structures over variable bathymetry. Ocean Eng. 2020, 201, 107135. [Google Scholar] [CrossRef]
- Kaur, A.; Martha, S. Reduction of wave impact on seashore as well as seawall by floating structure and bottom topography. J. Hydrodyn. 2020, 32, 1191–1206. [Google Scholar] [CrossRef]
- Tsai, C.-C.; Chou, W.-R. Comparison between consistent coupled-mode system and eigenfunction matching method for solving water wave scattering. J. Mar. Sci. Technol.-Taiw. 2015, 23, 870–881. [Google Scholar] [CrossRef]
- Li, X.S. An overview of SuperLU: Algorithms, implementation, and user interface. ACM Trans. Math. Softw. 2005, 31, 302–325. [Google Scholar] [CrossRef]
- Koley, S.; Behera, H.; Sahoo, T. Oblique wave trapping by porous structures near a wall. J. Eng. Mech. 2015, 141, 04014122. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Y.; Li, H.; Chang, A. Oblique wave motion over multiple submerged porous bars near a vertical wall. J. Ocean Univ. China 2017, 16, 568–574. [Google Scholar] [CrossRef]
- Mei, C.C.; Stiassnie, M.A.; Yue, D.K.-P. Theory and Applications of Ocean Surface Waves: Part 1: Linear Aspects; World Scientific: Singapore, 2005. [Google Scholar]
- Losada, I.J.; Silva, R.; Losada, M.A. 3-D non-breaking regular wave interaction with submerged breakwaters. Coast. Eng. 1996, 28, 229–248. [Google Scholar] [CrossRef]
- Meade, R.; Winn, J.N.; Joannopoulos, J. Photonic Crystals: Molding the Flow of Light; Princeton University Press: Princeton, NJ, USA, 2008; p. 305. [Google Scholar]
- Van der Meer, J.W.; Briganti, R.; Zanuttigh, B.; Wang, B. Wave transmission and reflection at low-crested structures: Design formulae, oblique wave attack and spectral change. Coast. Eng. 2005, 52, 915–929. [Google Scholar] [CrossRef]
- Rudmana, M.; Cleary, P.W. Oblique impact of rogue waves on a floating platform. In Proceedings of the Nineteenth International Offshore and Polar Engineering Conference, Osaka, Japan, 21–26 July 2009. [Google Scholar]
- Istrati, D.; Buckle, I.G. Tsunami Loads on Straight and Skewed Bridges–Part 1: Experimental Investigation and Design Recommendations; Technical Report No. FHWA-OR-RD-21-12; Oregon Department of Transportation Research Section: Washington, DC, USA, 2021.
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C++: The Art of Scientific Computing; Cambridge University Press: New York, NY, USA, 2002; p. 1002. [Google Scholar]
- Silva, R. Transformación del Oleaje Debido a Obras de Defensa del Litoral. Ph.D. Thesis, University of Cantabria Santander, Cantabria, Spain, 1995. [Google Scholar]
- Kirby, J.T.; Anton, J.P. Bragg Reflection of Waves by Artificial Bars. Coast. Eng. 1990, 1991, 757–768. [Google Scholar]
- Tsai, C.-C.; Lin, Y.-T.; Chang, J.-Y.; Hsu, T.-W. A coupled-mode study on weakly viscous Bragg scattering of surface gravity waves. Ocean Eng. 2016, 122, 136–144. [Google Scholar] [CrossRef]
- Mei, C.C. Resonant reflection of surface water waves by periodic sandbars. J. Fluid Mech. 1985, 152, 315–335. [Google Scholar] [CrossRef]
- Dalrymple, R.A.; Kirby, J.T. Water waves over ripples. J. Waterw. Port Coast. Ocean Eng. 1986, 112, 309–319. [Google Scholar] [CrossRef] [Green Version]
- Isobe, M. A Parabolic Equation Model for Transformation of Irregular Waves Due to Refraction, Diffraction and Breaking. Coast. Eng. Jpn. 1987, 30, 33–47. [Google Scholar] [CrossRef]
- Tsai, C.-P.; Chen, H.-B.; Hsu, J.R.C. Calculations of wave transformation across the surf zone. Ocean. Eng. 2001, 28, 941–955. [Google Scholar] [CrossRef]
- Hsu, T.-W.; Chang, J.-Y.; Lan, Y.-J.; Lai, J.-W.; Ou, S.-H. A parabolic equation for wave propagation over porous structures. Coast. Eng. 2008, 55, 1148–1158. [Google Scholar] [CrossRef] [Green Version]
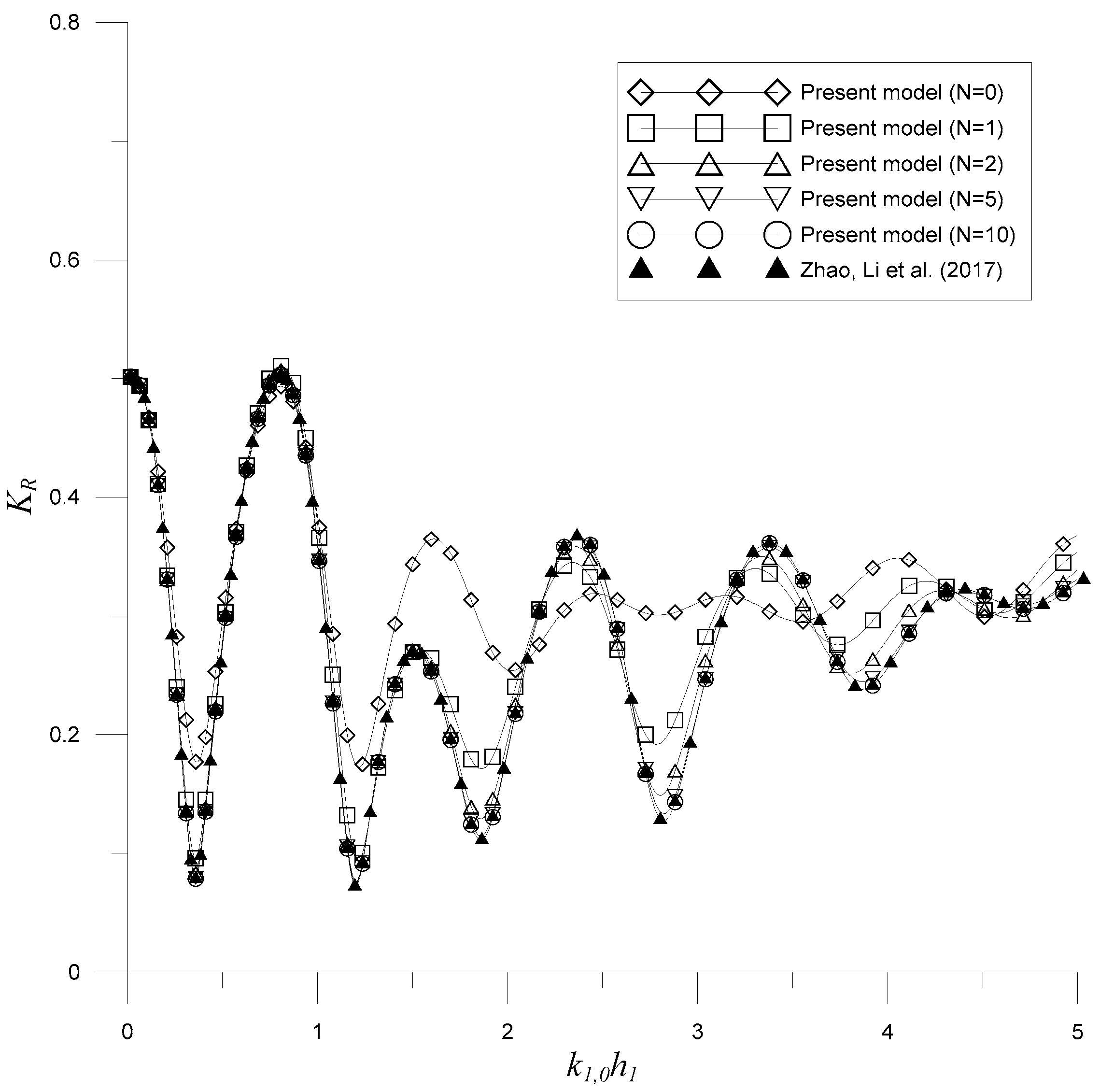


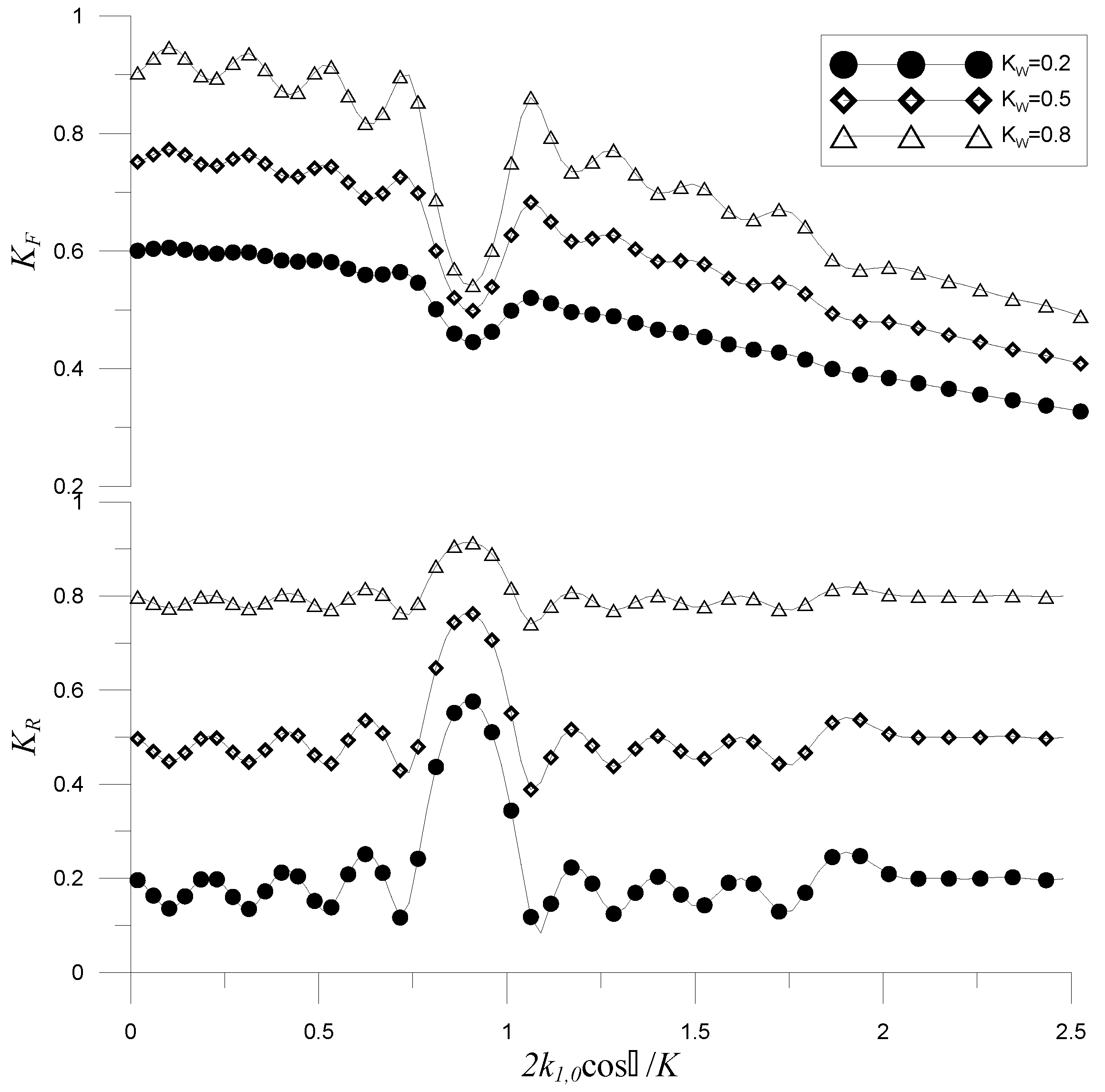
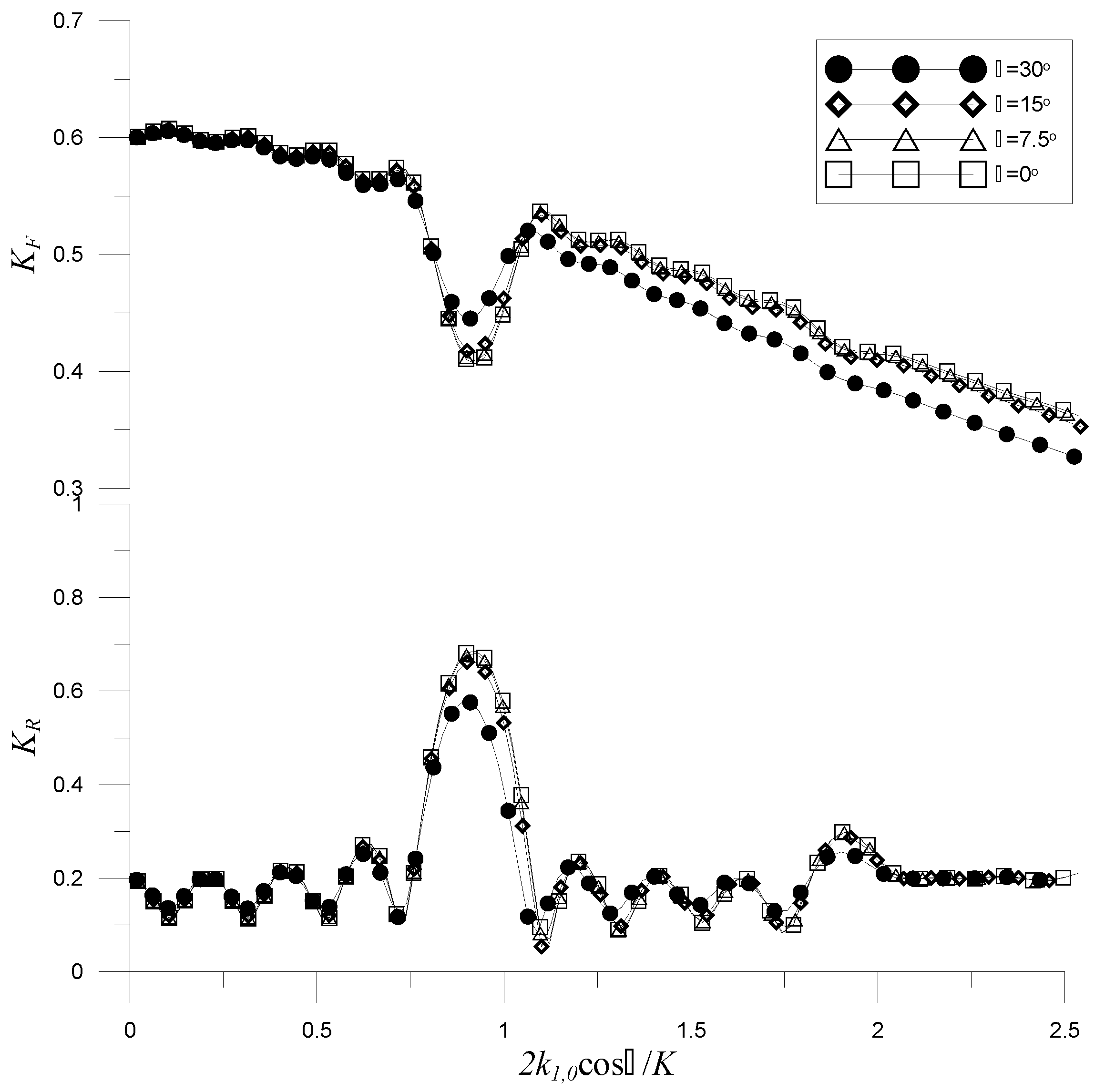

| 0 | 0.4167 | 0.4419 | 0.4387 |
| 1 | 0.3960 | 0.4070 | 0.4499 |
| 2 | 0.3962 | 0.4110 | 0.4555 |
| 3 | 0.3954 | 0.4085 | 0.4550 |
| 5 | 0.3953 | 0.4087 | 0.4560 |
| 10 | 0.3952 | 0.4088 | 0.4566 |
| 15 | 0.3952 | 0.4087 | 0.4566 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, J.-Y.; Tsai, C.-C. Wave Forces on a Partially Reflecting Wall by Oblique Bragg Scattering with Porous Breakwaters over Uneven Bottoms. J. Mar. Sci. Eng. 2022, 10, 409. https://doi.org/10.3390/jmse10030409
Chang J-Y, Tsai C-C. Wave Forces on a Partially Reflecting Wall by Oblique Bragg Scattering with Porous Breakwaters over Uneven Bottoms. Journal of Marine Science and Engineering. 2022; 10(3):409. https://doi.org/10.3390/jmse10030409
Chicago/Turabian StyleChang, Jen-Yi, and Chia-Cheng Tsai. 2022. "Wave Forces on a Partially Reflecting Wall by Oblique Bragg Scattering with Porous Breakwaters over Uneven Bottoms" Journal of Marine Science and Engineering 10, no. 3: 409. https://doi.org/10.3390/jmse10030409
APA StyleChang, J.-Y., & Tsai, C.-C. (2022). Wave Forces on a Partially Reflecting Wall by Oblique Bragg Scattering with Porous Breakwaters over Uneven Bottoms. Journal of Marine Science and Engineering, 10(3), 409. https://doi.org/10.3390/jmse10030409







