Nonlinear Predictive Framework of the Undrained Clay Slope Effect on the Initial Stiffness of p-y Curves of Laterally Loaded Piles by FEM
Abstract
1. Introduction
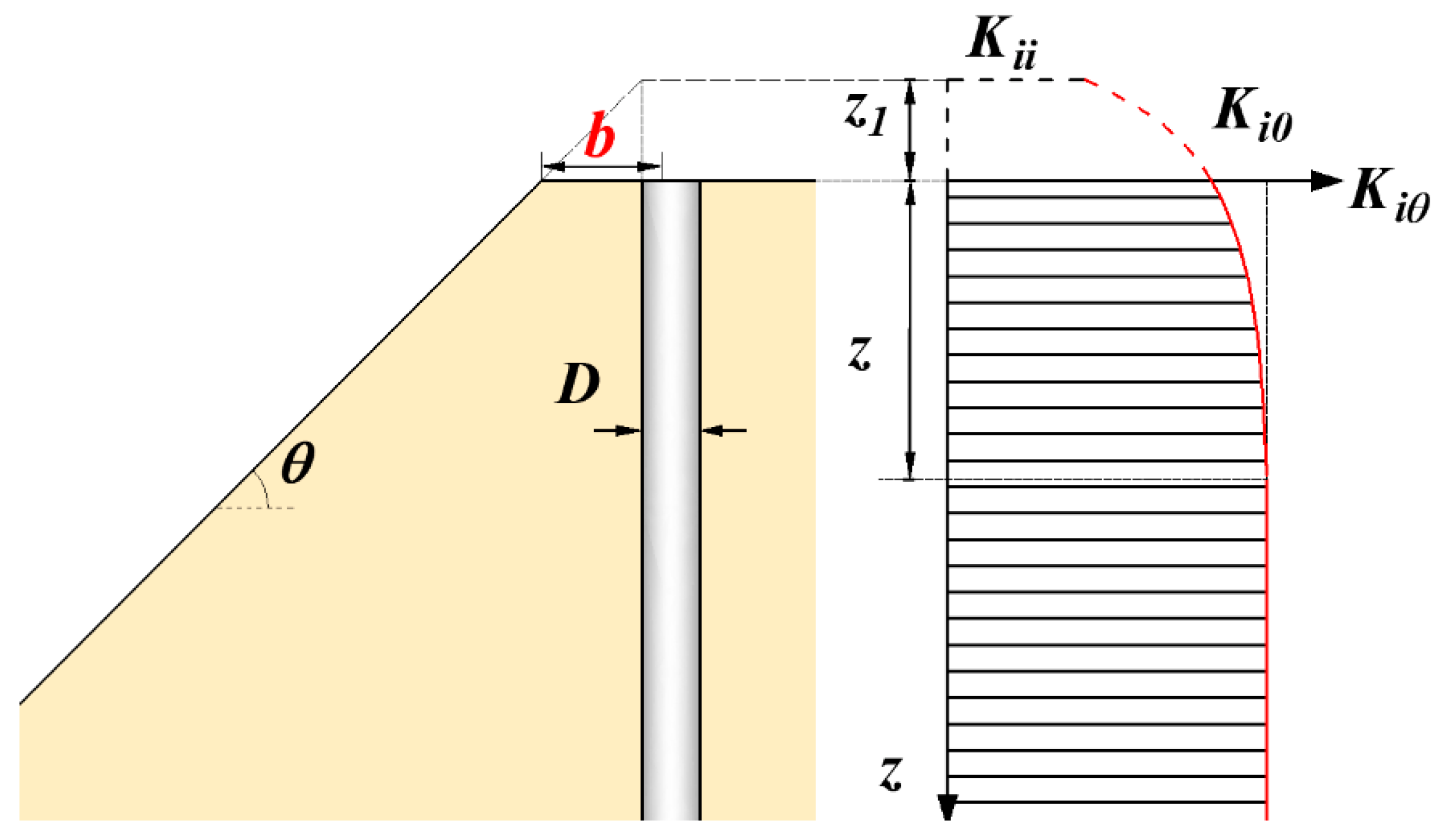
2. Basic Assumptions
- (1)
- The slope is stable and flat without a sliding surface, and the pile head is free.
- (2)
- The pile bends because of the pile head lateral load. Based on the discussions on p-y curves by Reese et al. [21] and Terzaghi [32], the soil resistance is assumed to be nonlinear with pile displacement. The popular hyperbolic p-y curve method is adopted to reflect the nonlinear response of laterally loaded piles as the following:where is the ultimate lateral load per unit length, and is the initial stiffness.
- (3)
- (4)
- Based on the study of Georgiadis and Georgiadis [18], a reduction factor () is adopted to reflect the undrained clay slope effect on the initial stiffness:where is the initial stiffness in the slope condition, and is the initial stiffness in the level ground condition. For the convenience of readers, this paper provides the description of some used symbols, as shown in Table 2.
- (5)
- Poulos’ relative stiffness () method is used to judge whether a pile is flexible or rigid, as follows [33]:where is the bending stiffness, is the soil Young’s modulus, and is the pile length. When , the pile is not rigid or flexible, which is named elastic pile.
3. Finite-Element Analysis
4. Theoretical Analysis for FEA Results
4.1. The “No Slope Geometry Effect” Case
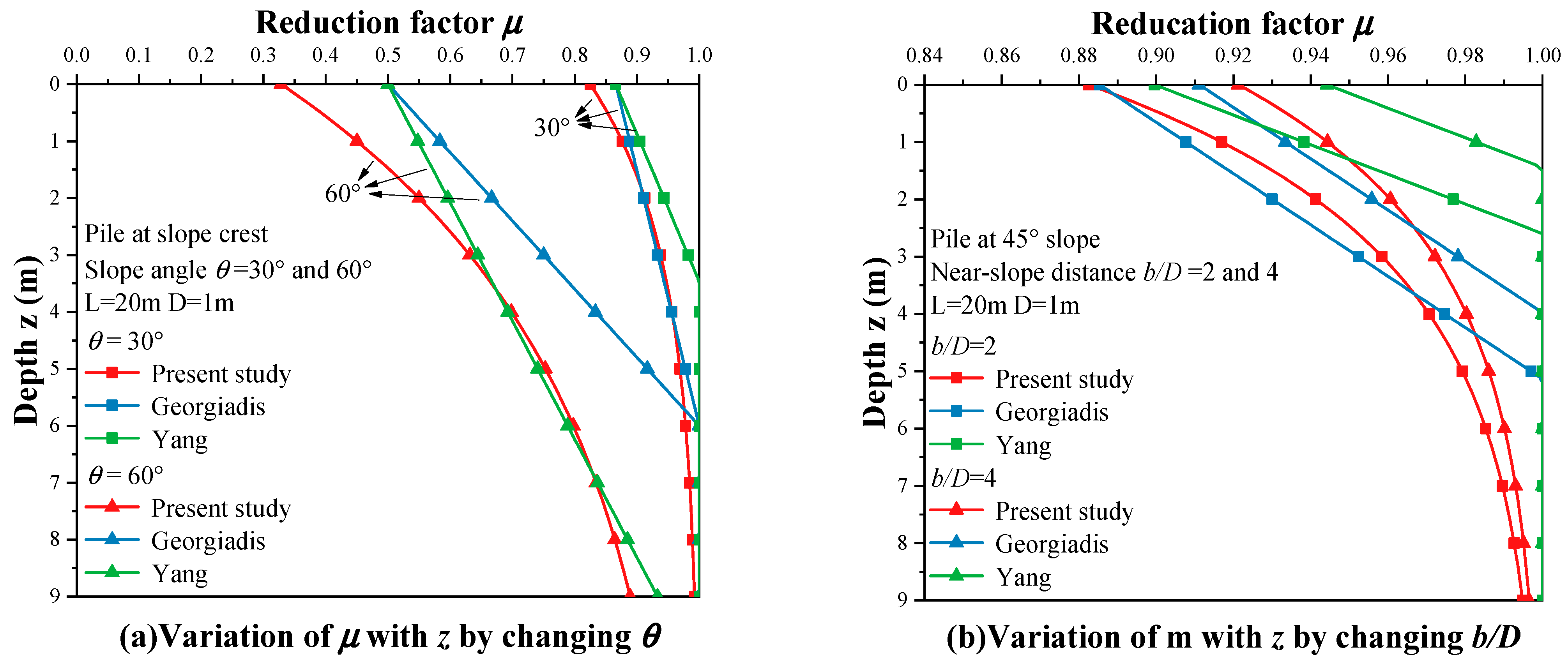
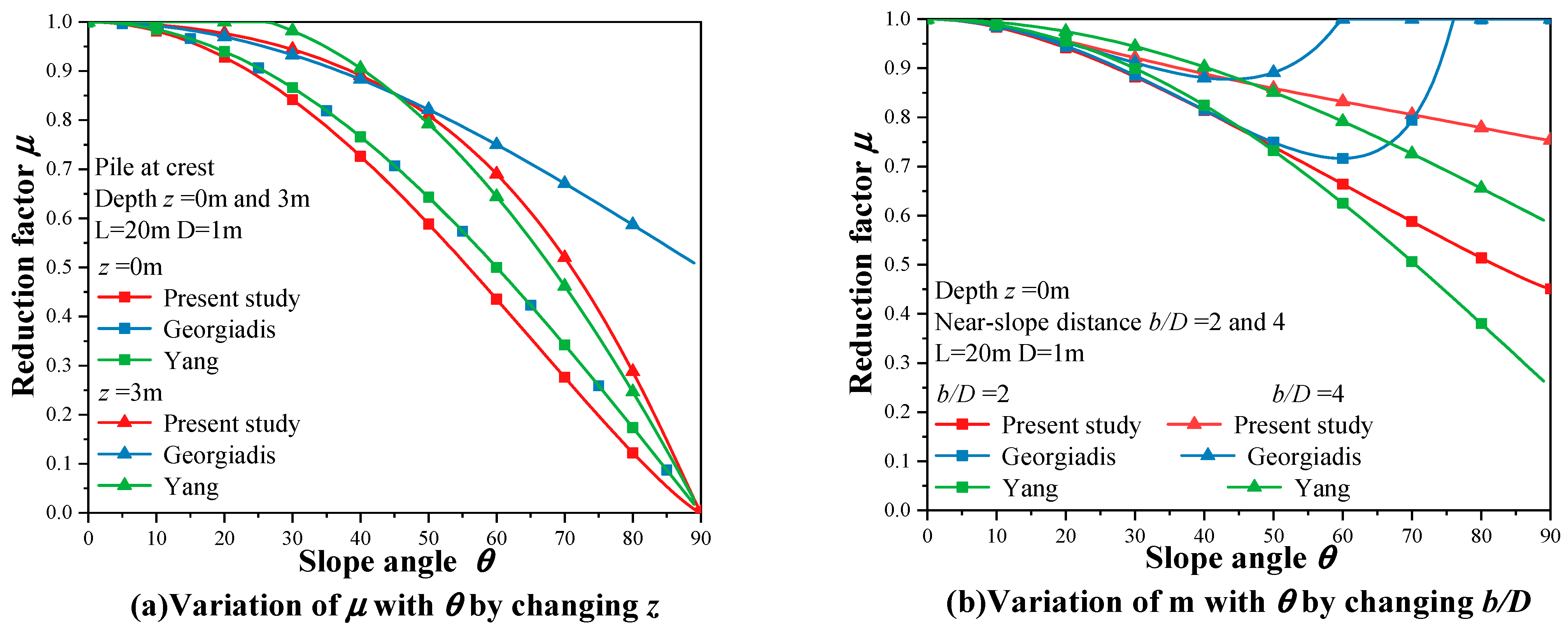
4.1.1. Case 1: Variation of Slope Angle ()
4.1.2. Case 2: Variation of Dimensionless Near-Slope Distance ()
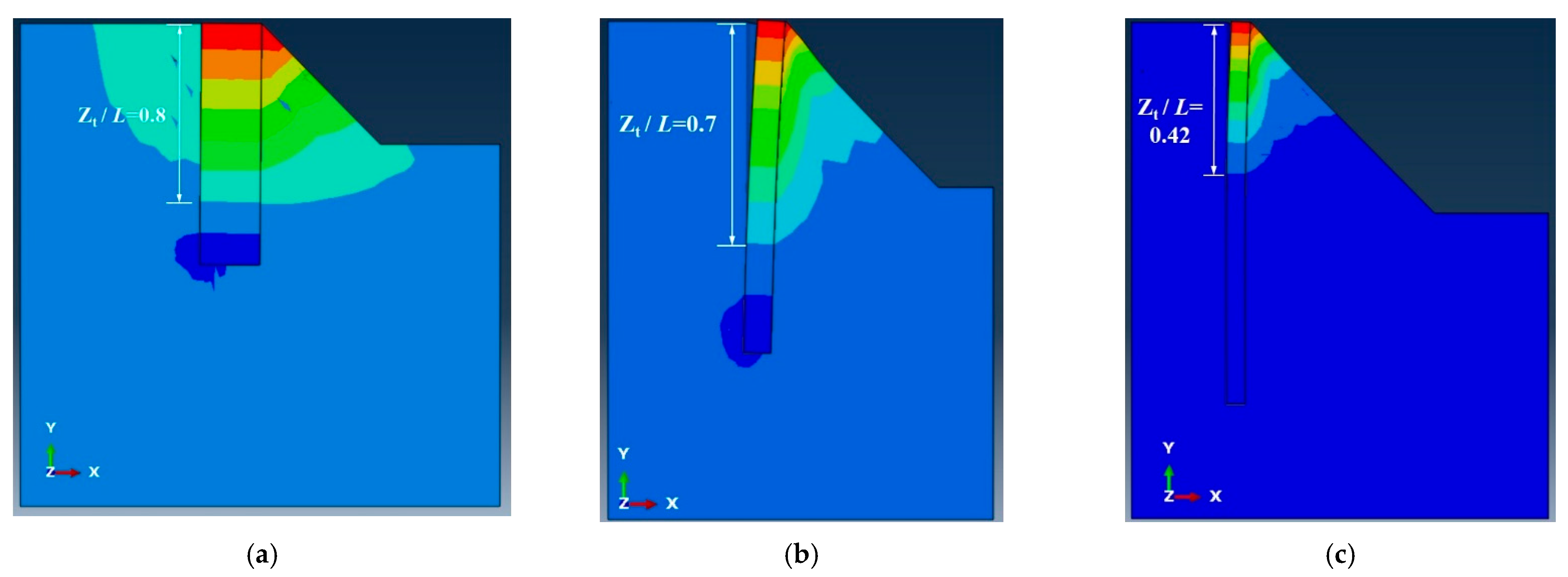
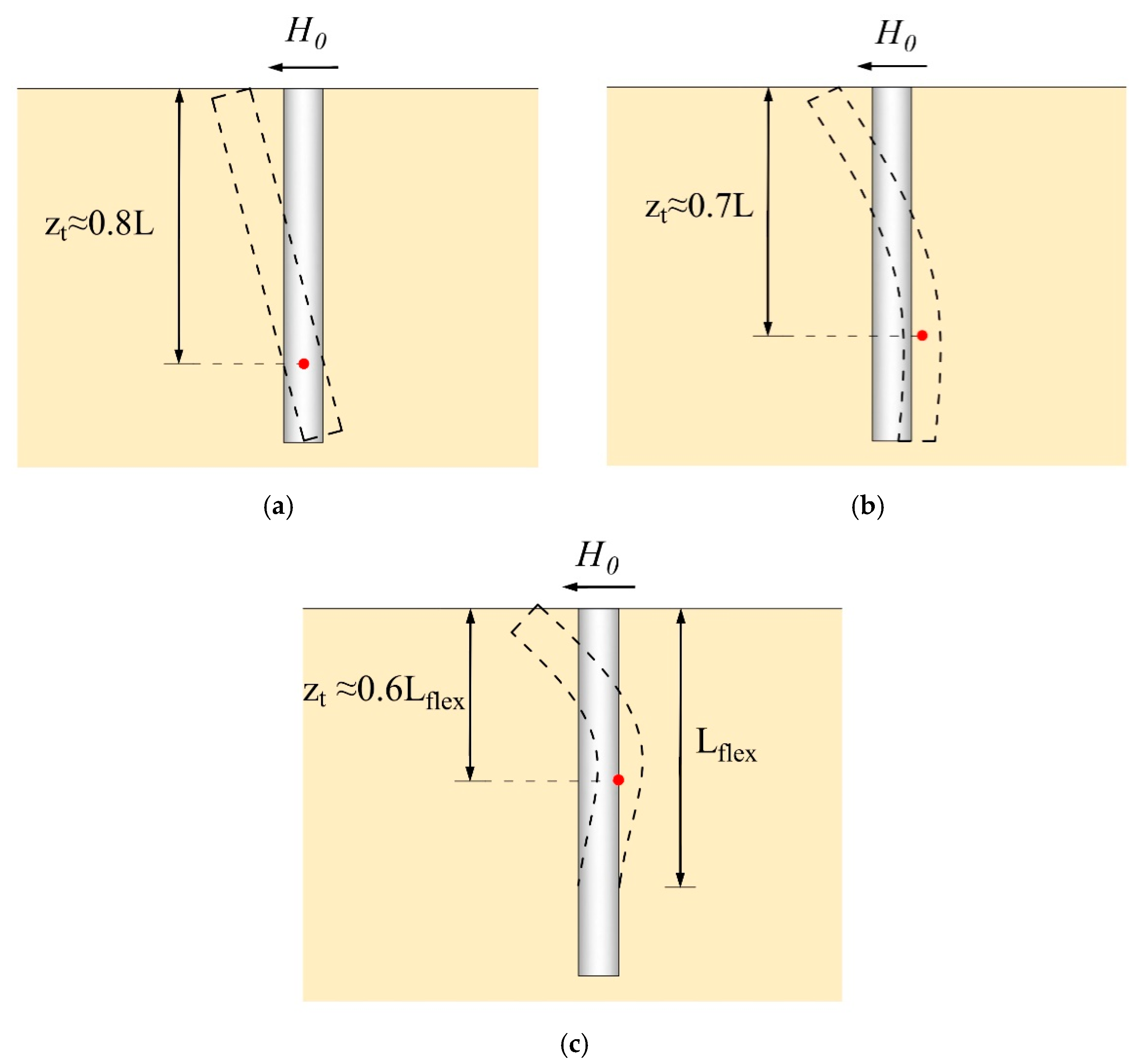
4.1.3. Case 3: Variation of Dimensionless Pile Head-Crest Distance ()
4.2. The “Existence of the Slope Geometry Effect” Case
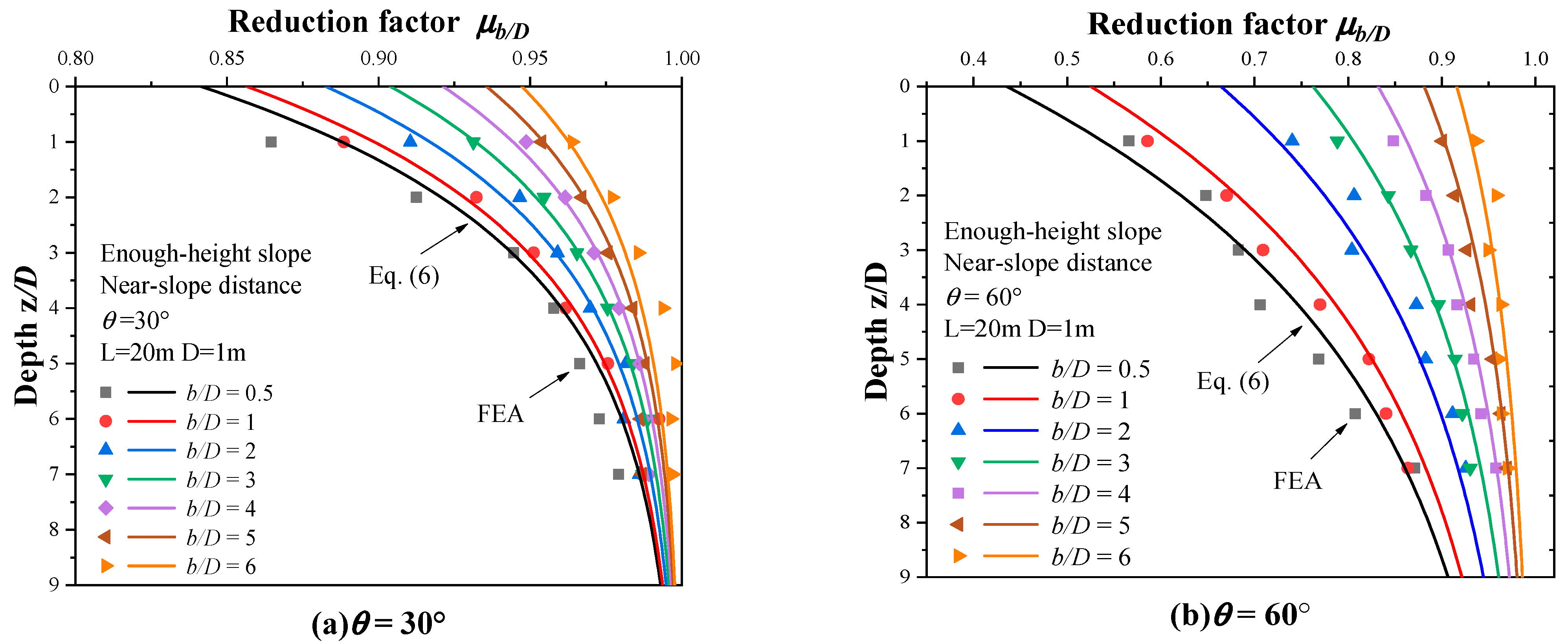
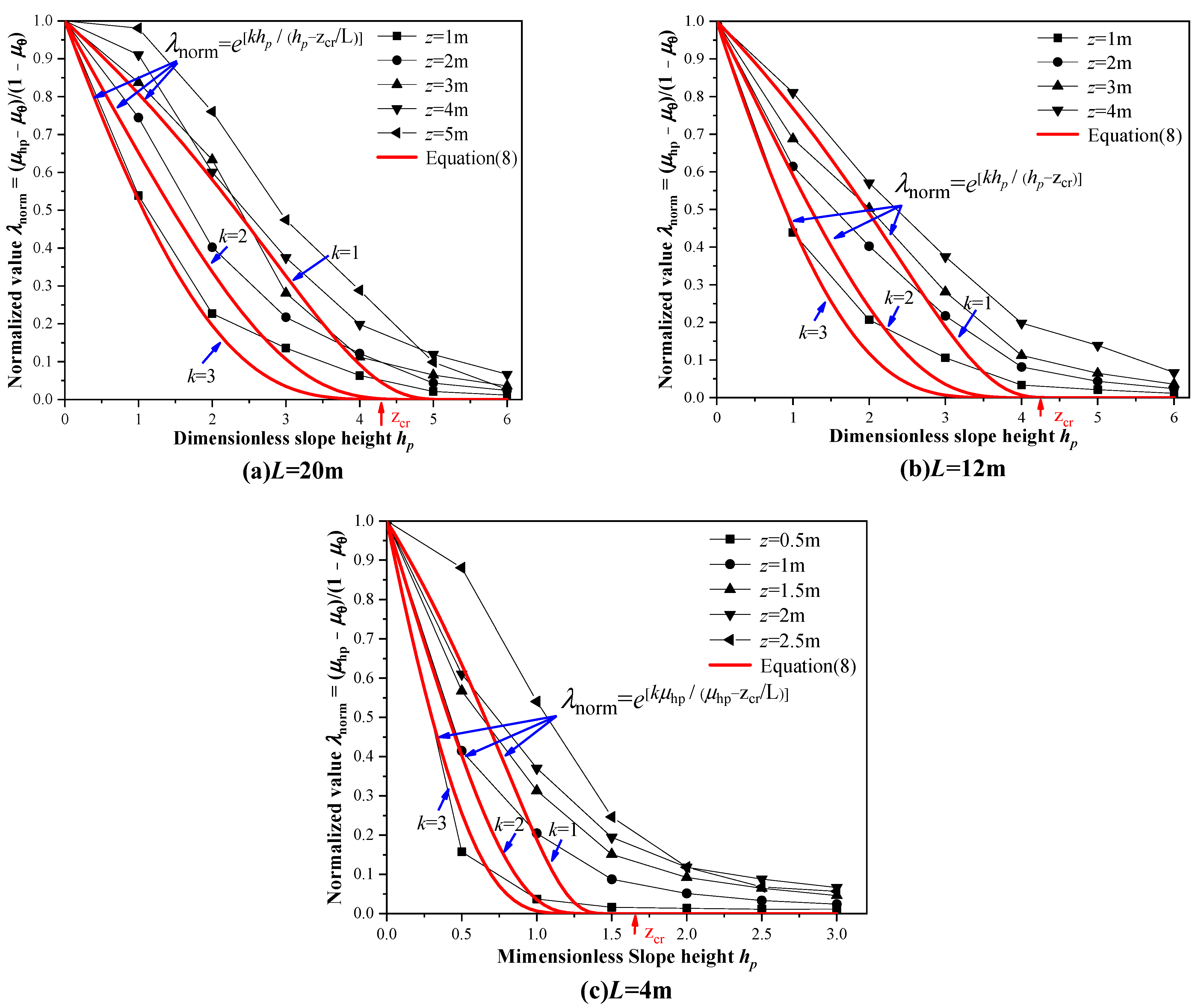
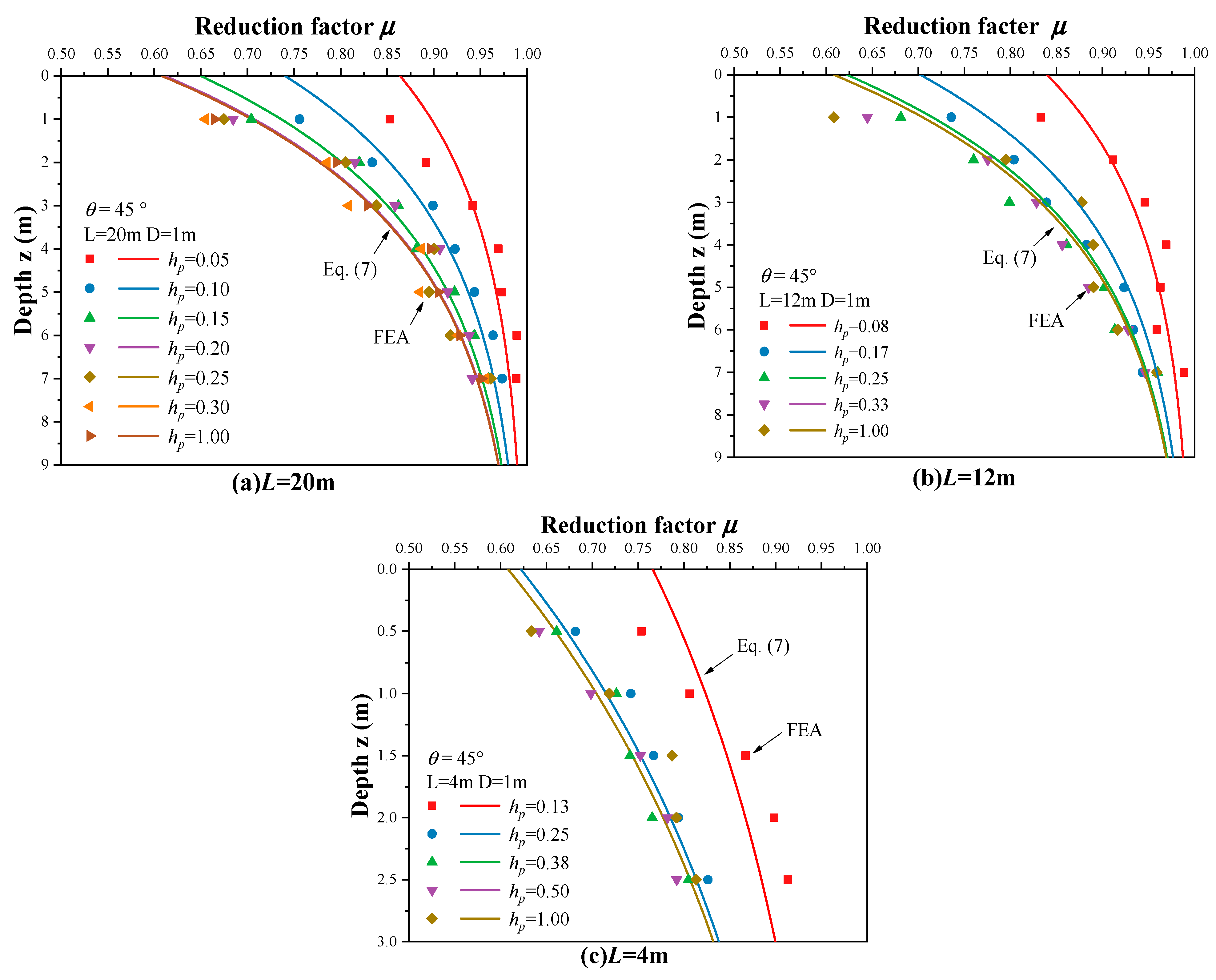
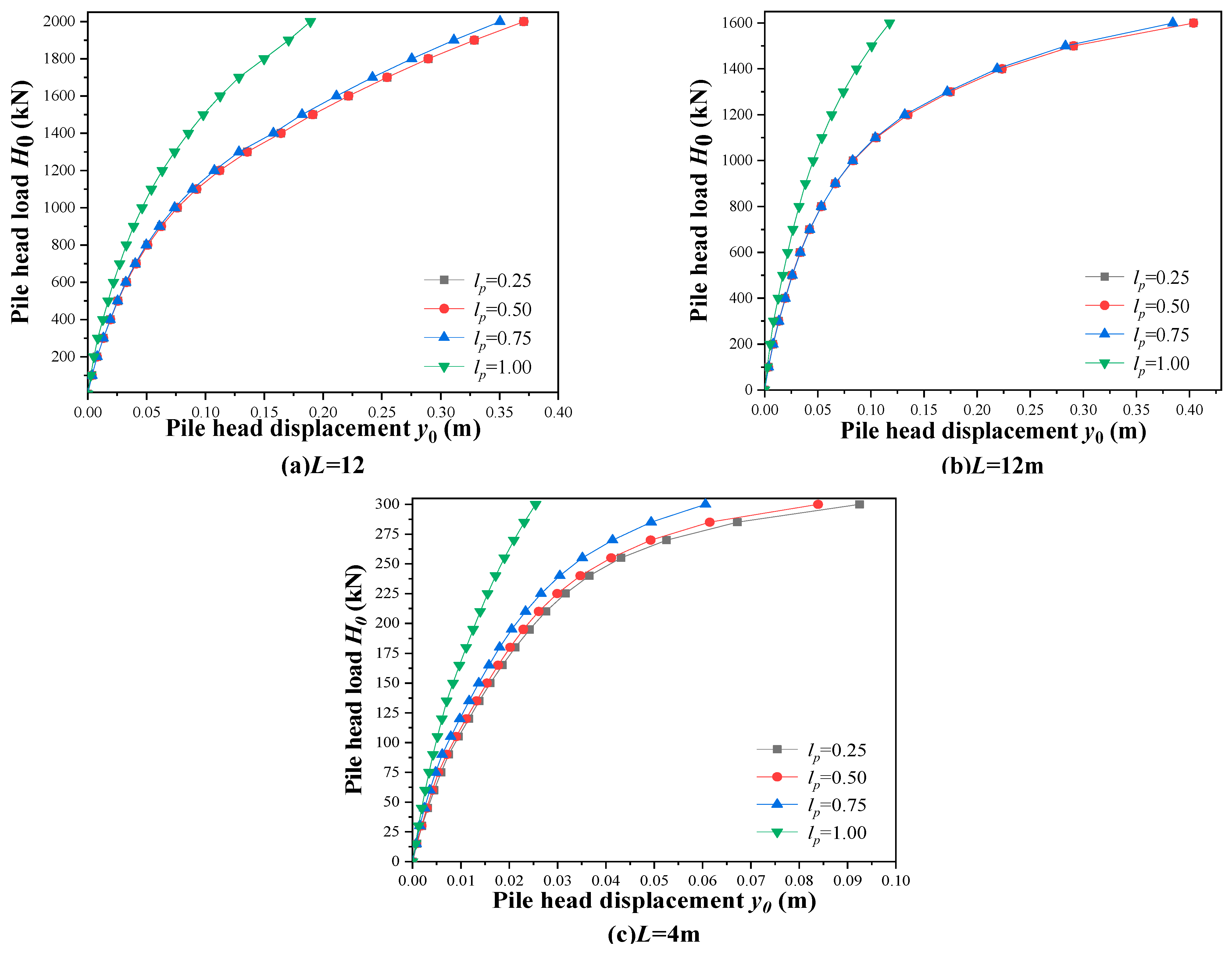
4.2.1. Case 4: Variation of Dimensionless Slope Height ()
Calculation Method of
Calculation Method of
4.2.2. Case 5: Variation of Pile Location on Slope ()
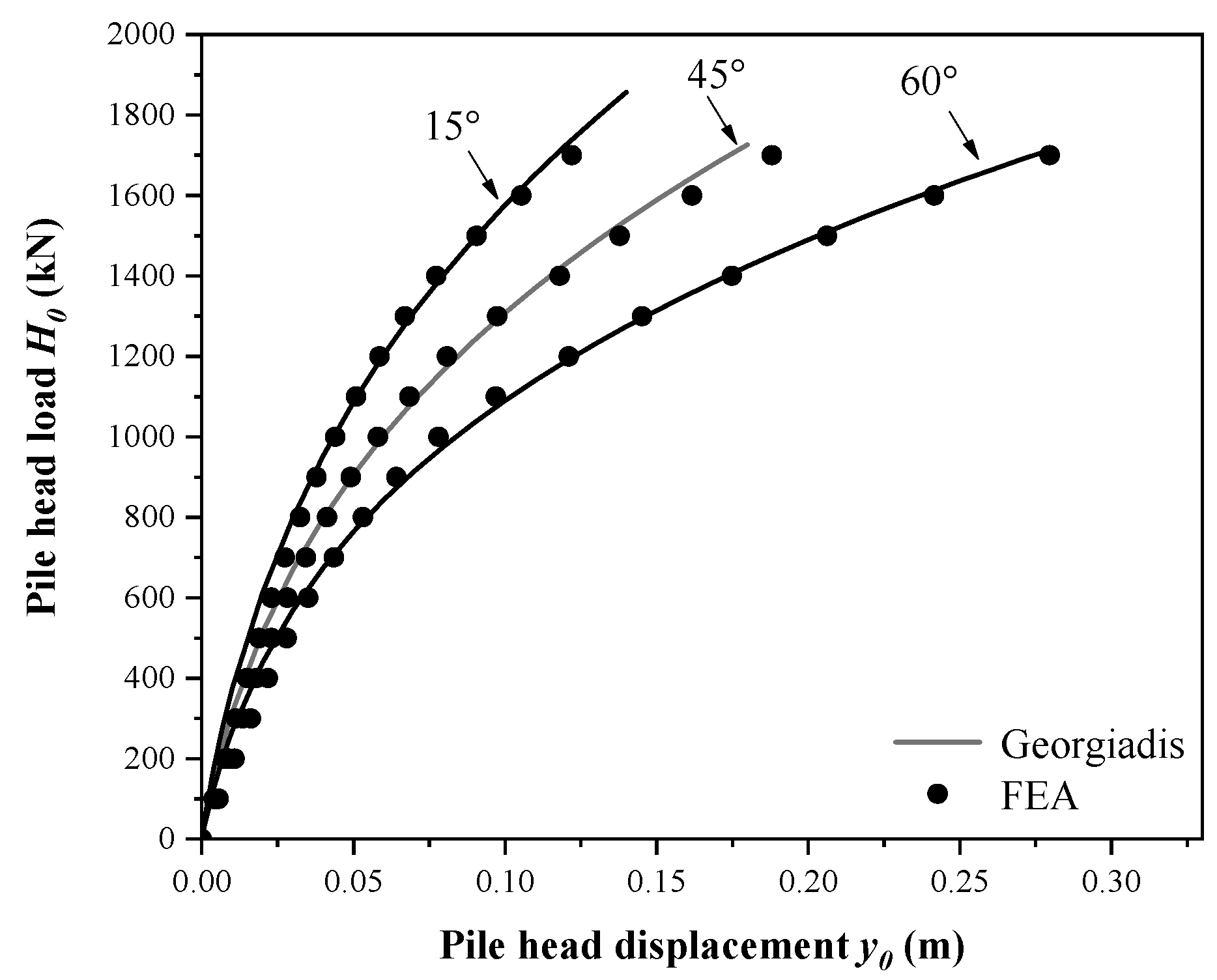
5. Comparison and Validation
5.1. Comparison with Other Methods
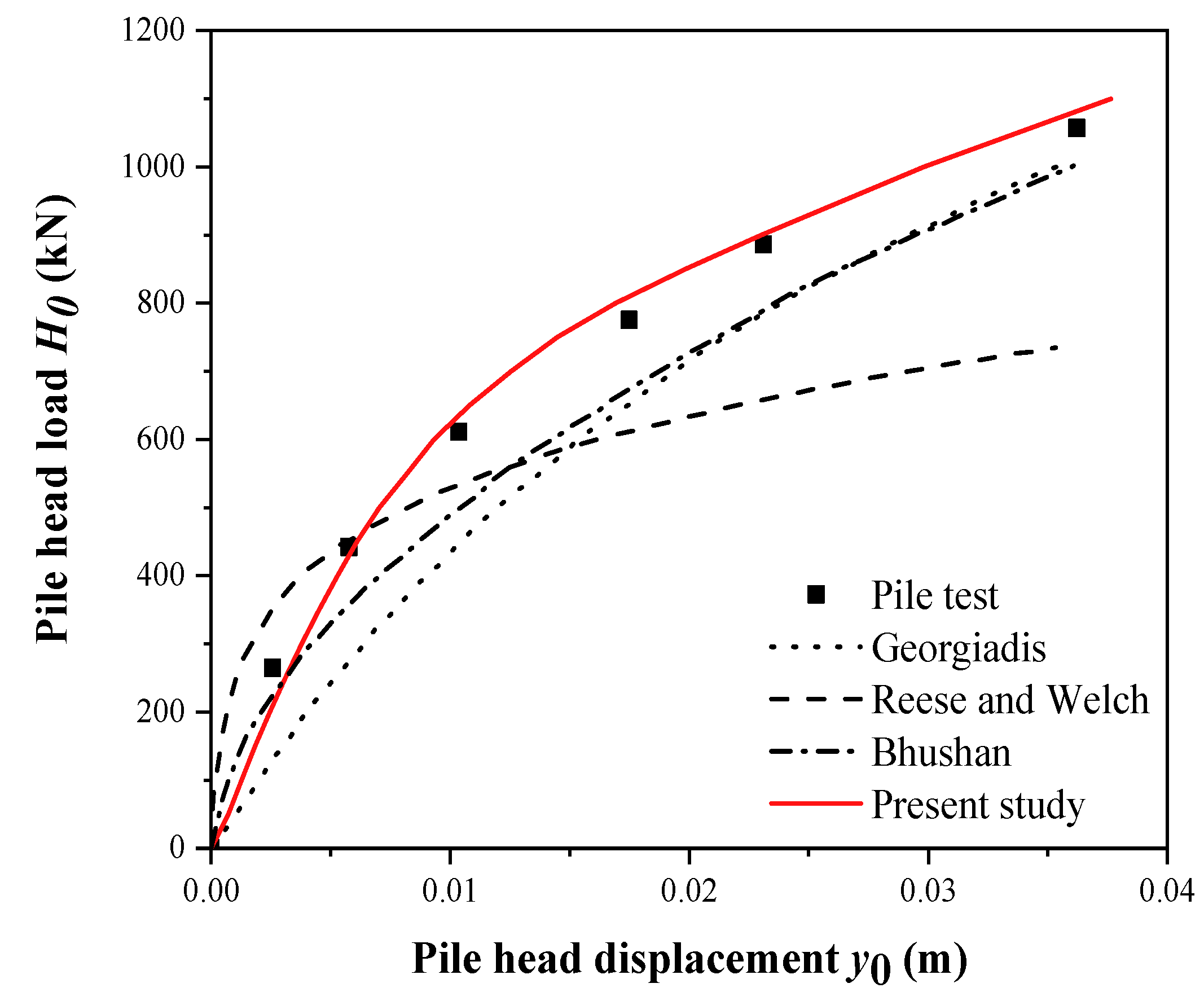
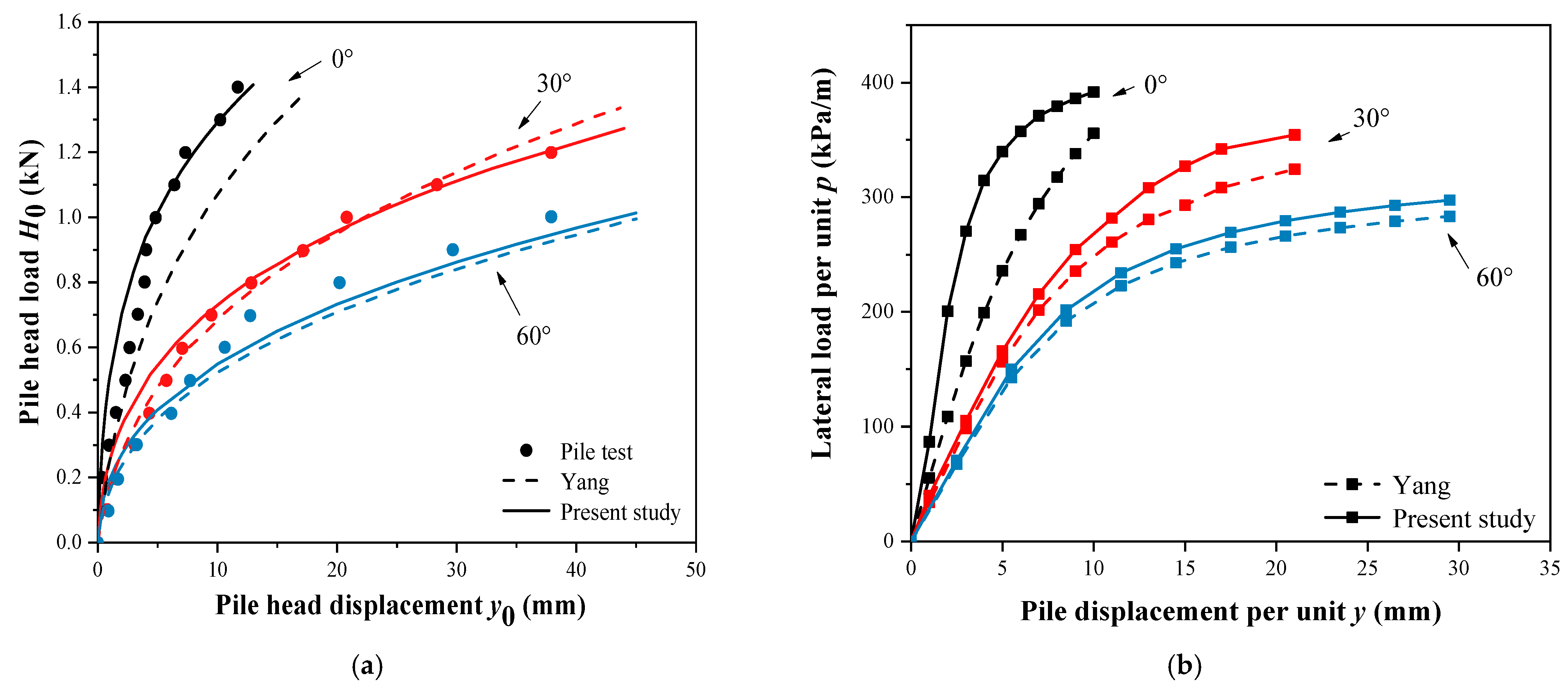
5.2. Application to Test Cases
5.2.1. Case 1: Bhushan’s Pile Test
5.2.2. Case 2: Yang’s Pile Test
6. Conclusions
- (1)
- The pile–soil response in undrained clay conditions was nearly independent of the dimensionless pile head-crest distance () for the “no slope geometry effect” case, which can be explained by the theory of Coulomb earth pressure.
- (2)
- The depth of the first turning point of the pile under undrained loading was explored as for the flexible pile, for the elastic pile, and for the flexible pile. The soil–pile response for the case of was found to be the same as the case of (“no slope geometry effect” case).
- (3)
- Compared with the available initial stiffness () calculation methods, the results are more reasonable for large slope angle cases, and can predict some ideal cases, such as the case of by using the method of the present study.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Theoretical Method of Georgiadis and Georgiadis [18] and Yang et al. [16]
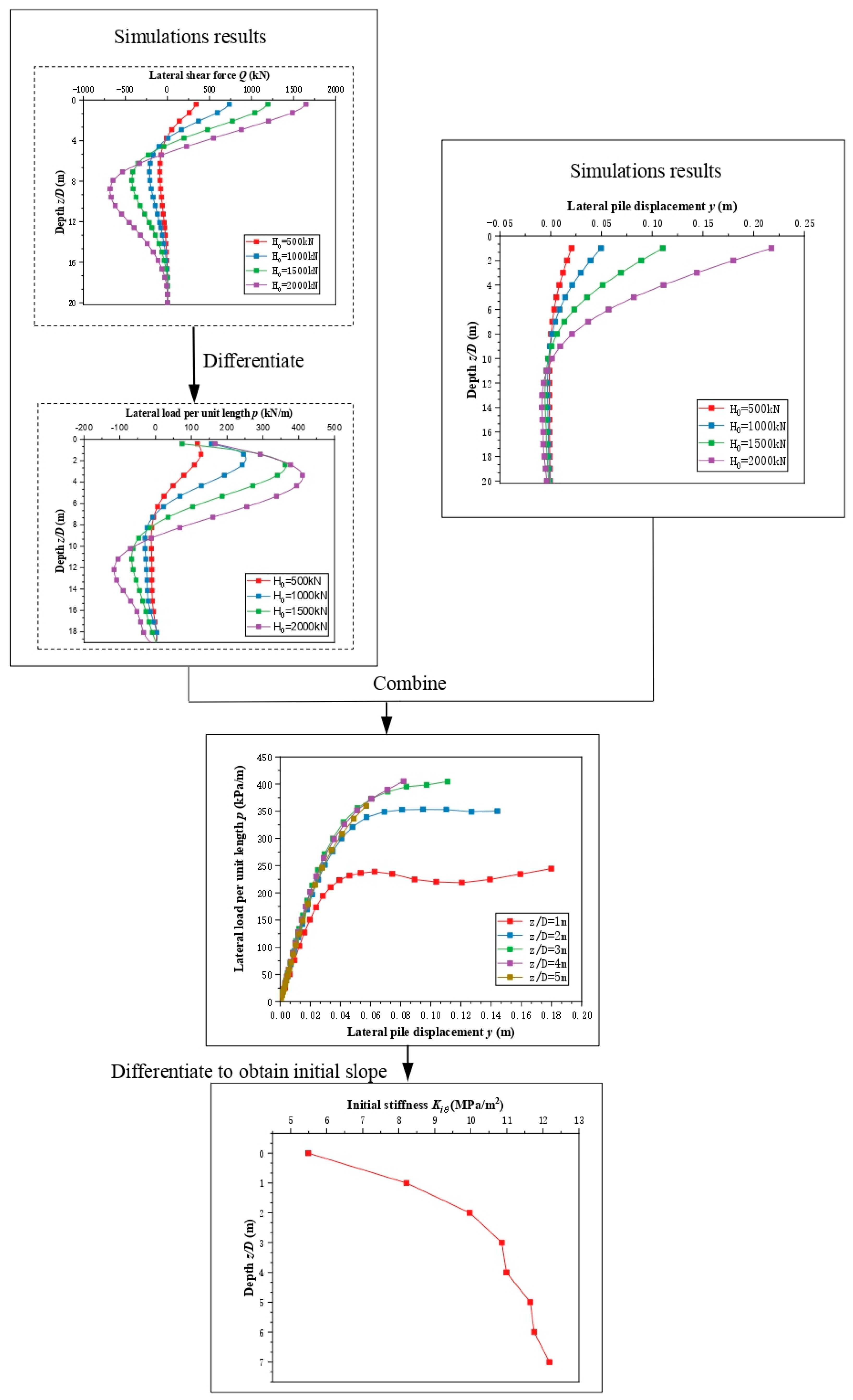
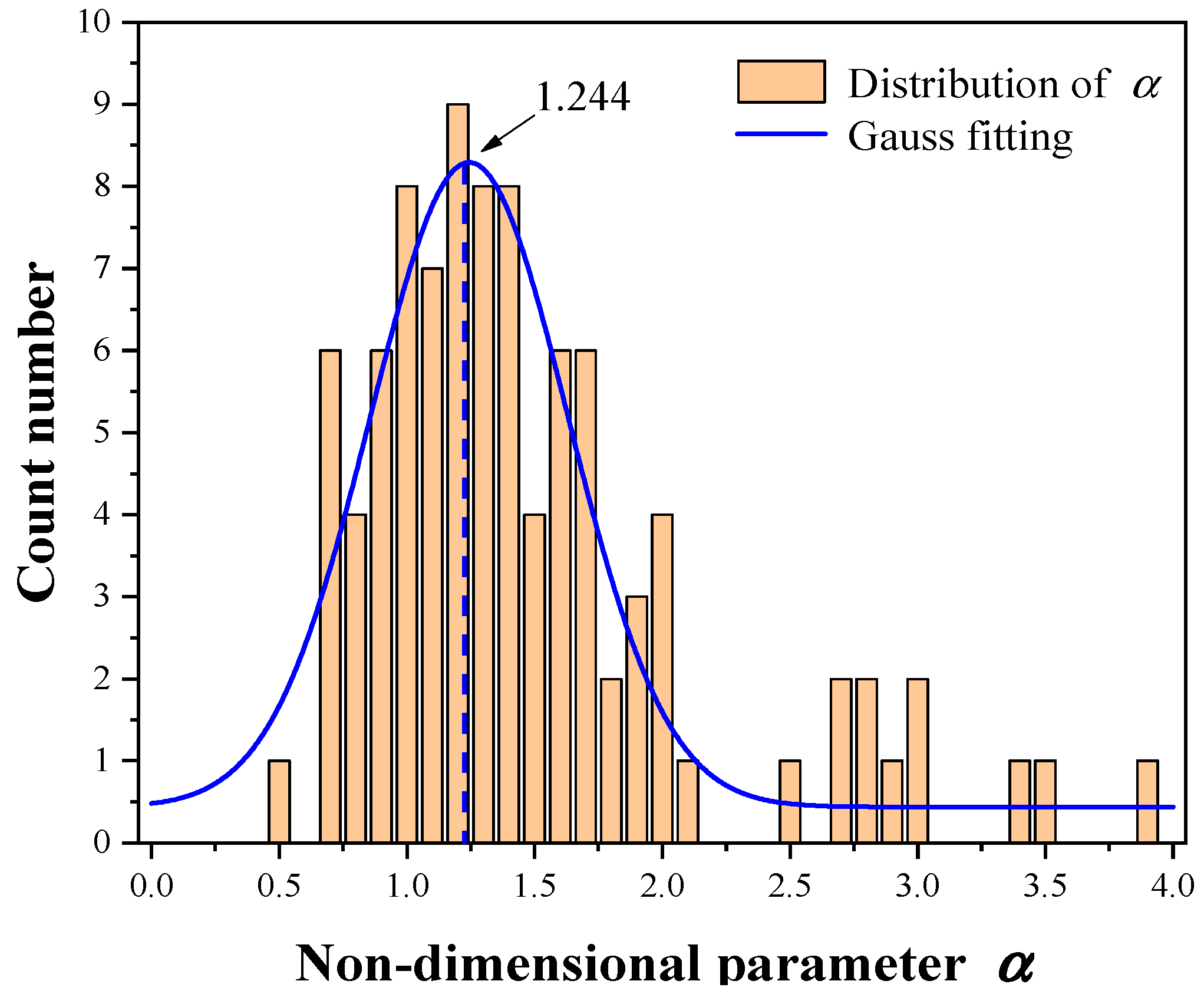
Appendix B. The Process of Deriving the from Simulation Results
References
- Wang, S.; Wang, P.; Zhai, H.; Zhang, Q.; Chen, L.; Duan, L.; Liu, Y.; Jeng, D. Experimental study for wave-induced pore-water pressures in a porous seabed around a mono-pile. J. Mar. Sci. Eng. 2019, 7, 237–255. [Google Scholar]
- Wan, Z.; Dai, G.; Gong, W. Field study on post-grouting effects of cast-in-place bored piles in extra-thick fine sand layers. Acta Geotech. 2019, 14, 1357–1377. [Google Scholar]
- Liu, X.; Lu, Y.; Yu, H.; Ma, L.; Ma, L.; Li, X.; Li, W.; Zhang, H.; Bian, C. In-situ observation of storm-induced wave-supported fluid mud occurrence in the subaqueous Yellow River delta. J. Geophys. Res. Ocean. 2022, 127, e2021JC018190. [Google Scholar] [CrossRef]
- Liu, X.; Yang, Q.; Wang, Y.; Jeng, D.; Sturm, H. New advances in marine engineering geology. J. Mar. Sci. Eng. 2021, 9, 66. [Google Scholar]
- Rajashree, S.; Sitharam, T. Nonlinear finite-element modeling of batter piles under lateral load. J. Geotech. Geoenviron. Eng. 2001, 127, 604–612. [Google Scholar]
- Kim, B.; Kim, N.; Jin, L.; Kim, Y. Experimental load–transfer curves of laterally loaded piles in Nak-Dong river sand. J. Geotech. Geoenviron. Eng. 2004, 130, 416–425. [Google Scholar]
- Sawant, V.; Shukla, S. Effect of edge distance from the slope crest on the response of a laterally loaded pile in sloping ground. Geotech. Geol. Eng. 2014, 32, 197–204. [Google Scholar] [CrossRef]
- Yin, P.; He, W.; Yang, Z. A Simplified Nonlinear Method for a Laterally Loaded Pile in Sloping Ground. Adv. Civ. Eng. 2018, 2018, 5438618. [Google Scholar] [CrossRef]
- Jiang, C.; Zhang, Z.; He, J. Nonlinear analysis of combined loaded rigid piles in cohesionless soil slope. Comput. Geotech. 2020, 117, 117. [Google Scholar] [CrossRef]
- Matlock, H. Correlation for design of laterally loaded piles in soft clay. In Proceedings of the 2nd Offshore Technology Conference, Houston, TX, USA, 22–24 April 1970; pp. 577–594. [Google Scholar]
- O’Neill, M.W.; Gazioglu, S.M. An Evaluation of P-y Relationships in Clays; University of Houston, Department of Civil Engineering: Houston, TX, USA, 1984. [Google Scholar]
- Sharafi, H.; Maleki, Y.; Karimpour-Fard, M. Three-dimensional finite difference modeling of static soil-pile interactions to calculate p-y curves in pile-supported slopes. Arab. J. Geosci. 2015, 9, 5. [Google Scholar] [CrossRef]
- Yin, J.; Li, S.; Sun, L.; Li, T. Pile installation assessment of offshore wind jacket foundation in completely weathered rock: A case study of the South China Sea. J. Mar. Sci. Eng. 2022, 10, 900. [Google Scholar] [CrossRef]
- Sun, W. A p-y model for predicting the lateral nonlinear interaction between pile and soil-rock mixture material based on discrete element modeling. Simul. Model. Pract. Theory 2020, 100, 102060. [Google Scholar] [CrossRef]
- Rathod, D.; Muthukkumaran, K.; Thallak, S. Experimental investigation on behavior of a laterally loaded single pile located on sloping ground. Int. J. Geomech. 2019, 19, 04019021. [Google Scholar] [CrossRef]
- Yang, M.; Deng, B.; Zhao, M. Experimental and theoretical studies of laterally loaded single piles in slopes. J. Zhejiang Univ. Sci. A 2019, 20, 838–851. [Google Scholar] [CrossRef]
- Nimityongskul, N.; Kawamata, Y.; Rayamajhi, D.; Scott, A. Full-scale tests on effects of slope on lateral capacity of piles installed in cohesive soils. J. Geotech. Geoenviron. Eng. 2018, 144, 04017103. [Google Scholar] [CrossRef]
- Georgiadis, K.; Georgiadis, M. Development of p-y curves for undrained response of piles near slopes. Comput. Geotech. 2012, 40, 53–61. [Google Scholar] [CrossRef]
- Peng, W.; Zhao, M.; Yao, X.; Yang, C.; Zhao, H. Analysis of laterally loaded piles in sloping ground using a modified strain wedge model. Comput. Geotech. 2018, 107, 163–175. [Google Scholar] [CrossRef]
- Liu, J.; Guo, Z.; Han, B. Load transfer of offshore open-ended piles considering the effect of soil plugging. J. Mar. Sci. Eng. 2019, 7, 313. [Google Scholar] [CrossRef]
- Reese, L.; Cox, W.; Koop, F. Analysis of laterally loaded piles in sand. In Offshore Technology in Civil Engineering: Hall of Fame Papers from the Early Years; American Society of Civil Engineers: Reston, VA, USA, 1974; pp. 95–105. [Google Scholar]
- Georgiadis, K.; Georgiadis, M. Undrained lateral pile response in sloping ground. J. Geotech. Geoenviron. Eng. 2010, 136, 1489–1500. [Google Scholar] [CrossRef]
- Brown, D.; Shie, C. Some numerical experiments with a three dimensional finite element model of a laterally loaded pile. Comput. Geotech. 1991, 12, 149–162. [Google Scholar] [CrossRef]
- Murff, J.; Hamilton, J. P-ultimate for undrained analysis of laterally loaded piles. J. Geotech. Eng. 1993, 119, 91–107. [Google Scholar] [CrossRef]
- Pedram, B. Effects of pile shape in improving the performance of monopiles embedded in onshore clays. Can. Geotech. J. 2015, 52, 1144–1158. [Google Scholar] [CrossRef]
- Vesic, A. Bending of beams resting on isotropic elastic solid. J. Eng. Mech. Div. 1961, 87, 35–54. [Google Scholar] [CrossRef]
- Carter, D.P. A Non-Linear Soil Model for Predicting Lateral Pile Response. Ph.D. Thesis, Department of Civil and Environmental Engineering, University of Auckland, Auckland, New Zealand, 1984. [Google Scholar]
- Kim, Y.; Jeong, S.; Lee, S. Wedge failure analysis of soil resistance on laterally loaded piles in clay. J. Geotech. Geoenviron. Eng. 2011, 137, 678–694. [Google Scholar] [CrossRef]
- Jeong, S.; Kim, Y.; Kim, J. Influence on lateral rigidity of offshore piles using proposed p–y curves. Ocean Eng. 2011, 38, 397–408. [Google Scholar] [CrossRef]
- Yang, Y.; Shen, M.; Juang, C. Assessing initial stiffness models for laterally loaded piles in undrained clay: Robust design perspective. J. Geotech. Geoenviron. Eng. 2019, 145, 04019073. [Google Scholar]
- Yang, M.; Zhu, L.; Luo, H.; Feng, C. Experiment and numerical simulation of p-y curve method for laterally loaded single pile in sloping ground. Jounral Highw. Transp. Res. Dev. 2017, 24, 83–90. [Google Scholar]
- Terzaghi, K. Evaluation of coefficient of subgrade reaction. Geotechnique 1955, 5, 297–326. [Google Scholar] [CrossRef]
- Poulos, H. Single pile response to cyclic lateral load. J. Geotech. Geoenviron. Eng. 1982, 108, 355–375. [Google Scholar] [CrossRef]
- Zhou, J.; Gong, X.; Wang, K.; Zhang, R.; Yan, J. A simplified nonlinear calculation method to describe the settlement of pre-bored grouting planted nodular piles. J. Zhejiang Univ. Sci. A 2007, 18, 895–909. [Google Scholar] [CrossRef]
- Wang, A.; Zhang, D.; Deng, Y. Lateral response of single piles in cement-improved soil: Numerical and theoretical investigation. Comput. Geotech. 2018, 102, 164–178. [Google Scholar] [CrossRef]
- Sun, Y.; Xu, C.; Du, X.; Naggar, M.; Jia, J. Nonlinear lateral response of offshore large-diameter monopile in sand. Ocean. Eng. 2020, 216, 108013. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, C.; Huang, M.; Yuan, H. Lateral loading of a pile using strain wedge model and its application under scouring. Mar. Georesour. Geotechnol. 2018, 36, 340–350. [Google Scholar] [CrossRef]
- Chen, L.; Jiang, C.; Pang, L.; Liu, P. Lateral soil resistance of rigid pile in cohesionless soil on slope. Comput. Geotech. 2021, 135, 104163. [Google Scholar] [CrossRef]
- Sivapriya, S.; Gandhi, S. Soil–Structure Interaction of Pile in a Sloping Ground Under Different Loading Conditions. Geotech. Geol. Eng. 2019, 38, 1185–1194. [Google Scholar] [CrossRef]
- Reese, L.; Wlech, R. Lateral loading of deep foundations in stiff clay. J. Geotech. Eng. Div. 1975, 101, 633–649. [Google Scholar] [CrossRef]
- Reese, L.; Isenhower, W.; Wang, S. Analysis of Design of Shallow and Deep Foundations; John Wiley and Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Bhushan, K.; Haley, S.; Fong, P. Lateral load tests on drilled piers in stiff clays. J. Geotech. Eng. Div. 1979, 105, 969–985. [Google Scholar] [CrossRef]



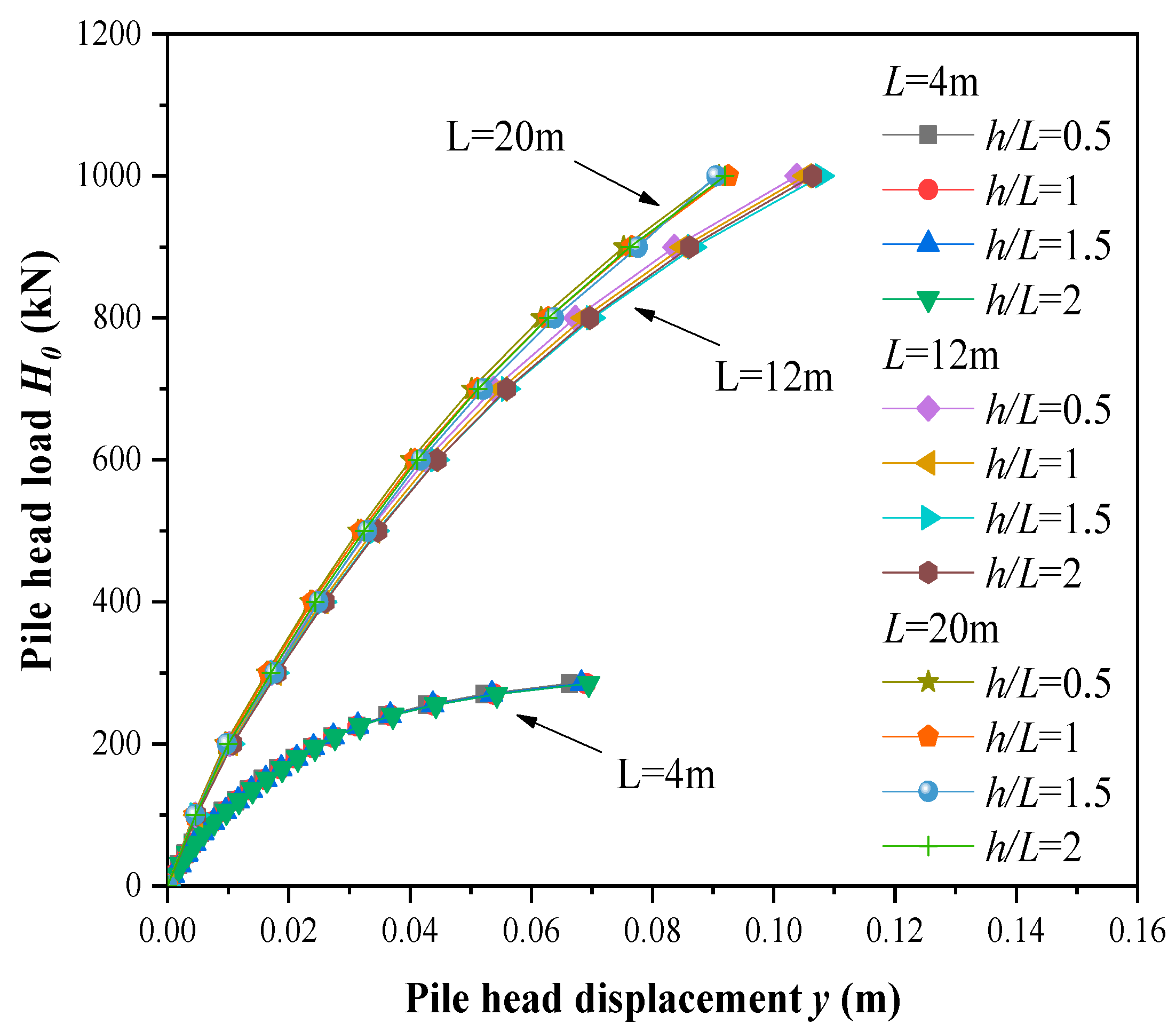
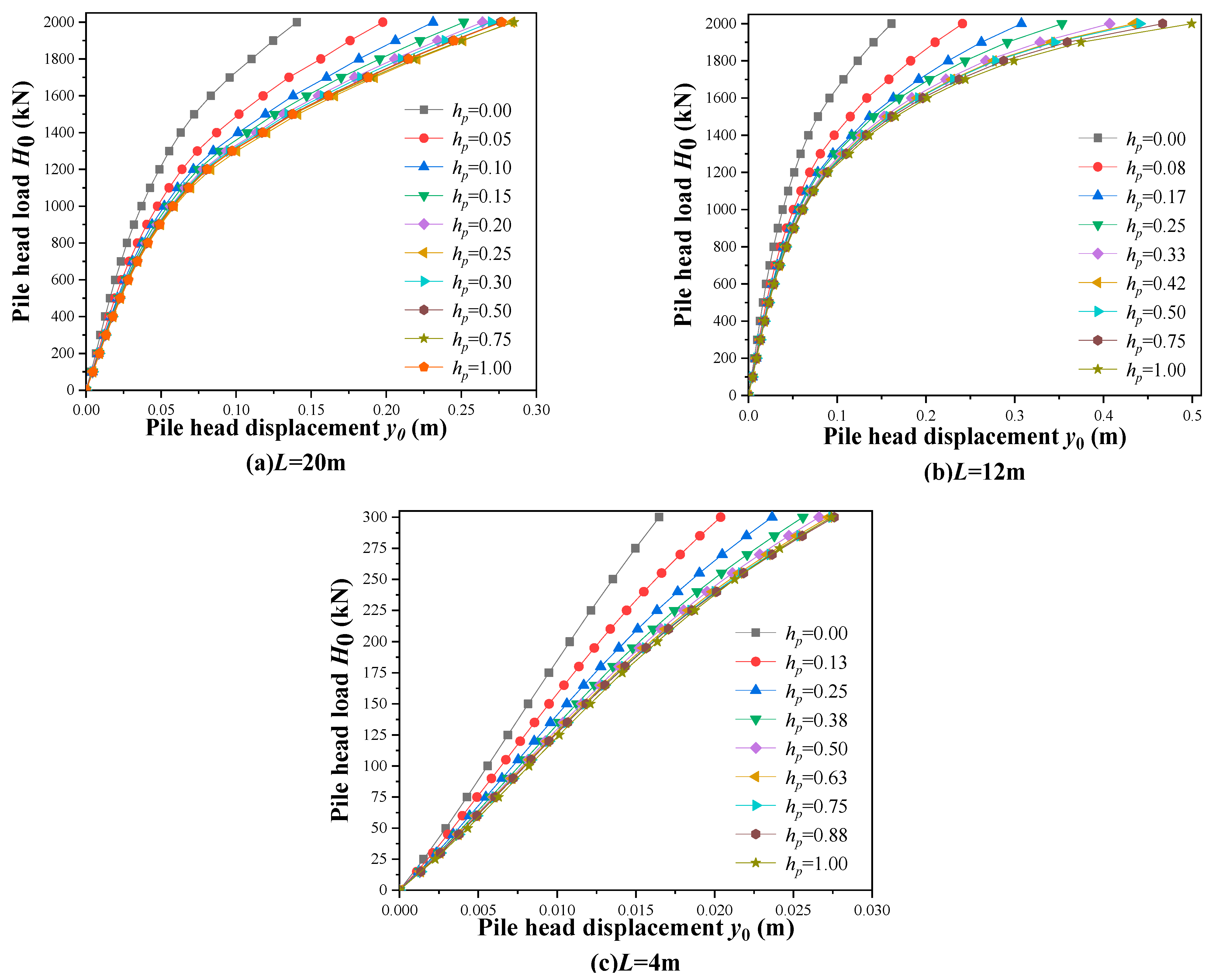
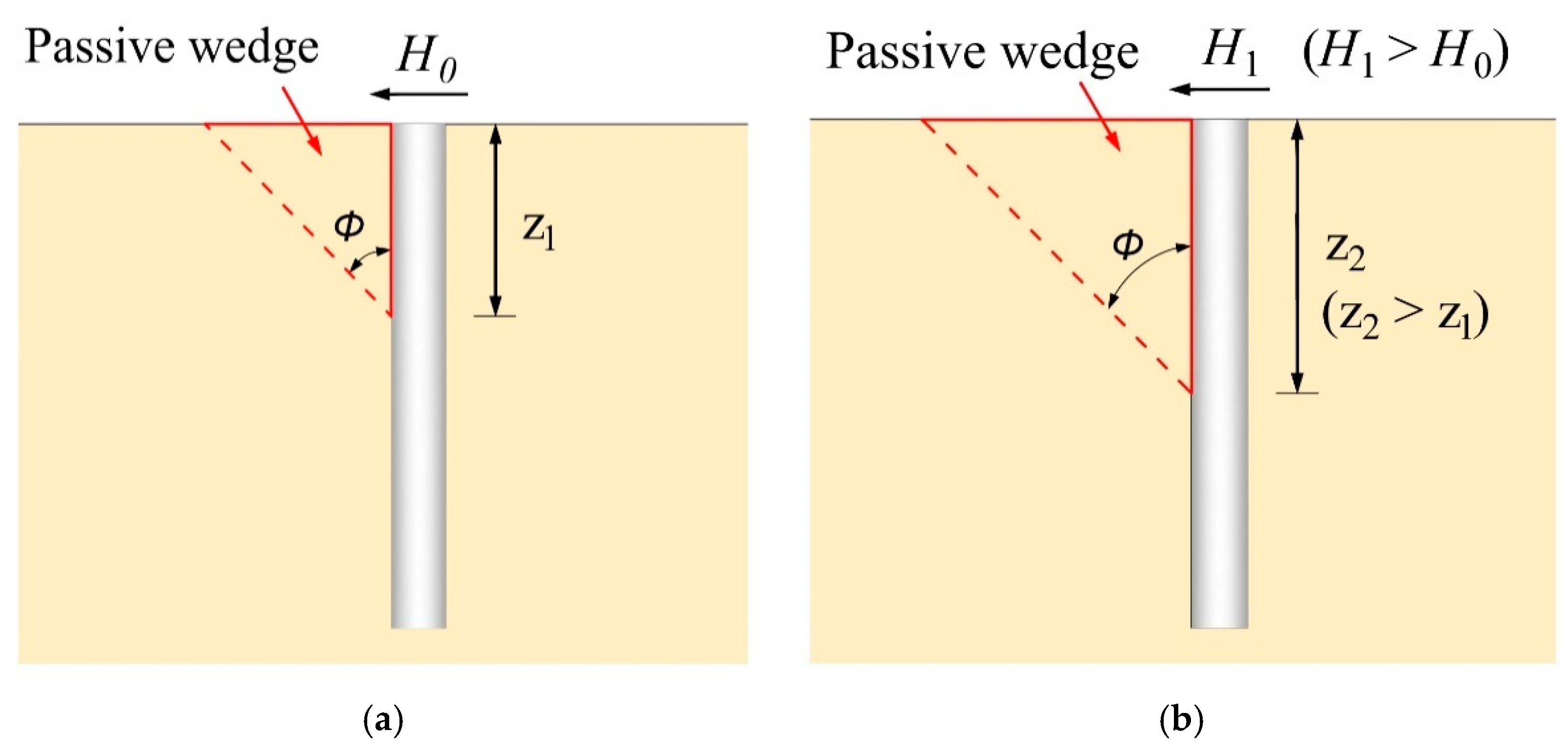

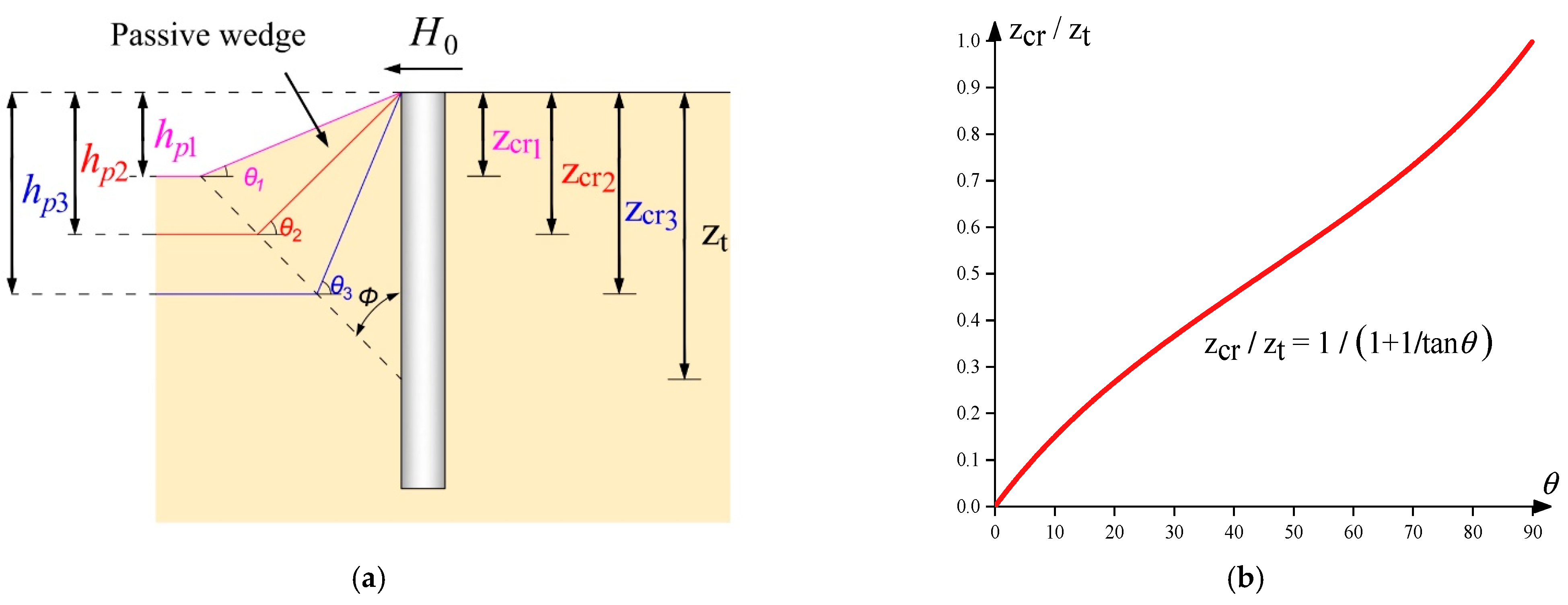

| Pile-Slope Geometry Relationships | Variables | ||
| (a) Slope Angle | (b) Dimensionless Near-Slope Distance | (c) Dimensionless Pile Head-Crest Distance | |
| No slope geometry effect | 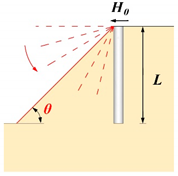 | 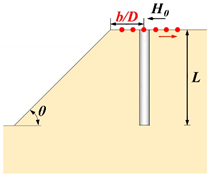 | 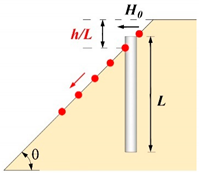 |
| Pile-Slope Geometry Relationships | Variables | ||
| (d) Dimensionless Slope Height | (e) Pile Location in the Slope | ||
| Existence of the slope geometry effect |  | 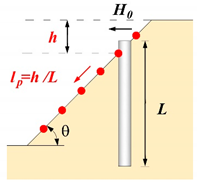 | |
| Symbols | Description |
|---|---|
| Initial stiffness | |
| Initial stiffness in the level ground condition | |
| Initial stiffness in the slope condition | |
| Initial stiffness at the ground surface | |
| Reduction factor | |
| Reduction factor in the “no slope geometry effect” case with varying () | |
| Reduction factor in the “no slope geometry effect” case with varying | |
| Reduction factor in the “no slope geometry effect” case with varying | |
| Reduction factor in the “existence of the slope geometry effect” case with varying | |
| Reduction factor in the “existence of the slope geometry effect” case with varying |
| Properties | Value |
|---|---|
| Soil | |
| Young’s module (MPa) | 14 |
| Undrained shear strength (kPa) | 70 |
| Bulk unit weight (kN/m3) | 18 |
| Poisson’s ratio | 0.49 |
| Adhesion factor | 0.5 |
| Pile | |
| Young’s module (MPa) | 2.9 × 104 |
| Bulk unit weight (kN/m3) | 25 |
| Poisson’s ratio | 0.1 |
| Pile length (m) | 4, 12, 20 |
| Pile diameter (m) | 1 |
| Variables | Conditions | Values |
|---|---|---|
| “no slope geometry effect” case | ||
| Slope angle | ; pile at crest | 0, 15, 30, 45, 60, 75, 90 |
| Dimensionless near-slope distance | 1, 2, 3, 4, 5, 6 | |
| Dimensionless pile head-crest distance | ; pile in slope | 0.5, 1, 1.5, 2 |
| “existence of the slope geometry effect” case | ||
| Dimensionless slope height | ; pile in slope | = 0.5, 1, 1.5, 2 |
| Pile location in slope | ; pile in slope | = 0.25, 0.5, 0.75, 1 |
| Pile Test | Geometrical Characteristics | Soil Properties | |||||
|---|---|---|---|---|---|---|---|
| (m) | (m) | (m) | |||||
| Bhushan | 5.185 | 1.22 | 2.25 × 106 | 0.23 | 20 | 220 | 24,440 |
| Yang | 1 | 0.025 | 0.1 | 0.15 | 0, 30, 60 | 53.2 | 30,120 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pang, L.; Jiang, C.; Chen, L. Nonlinear Predictive Framework of the Undrained Clay Slope Effect on the Initial Stiffness of p-y Curves of Laterally Loaded Piles by FEM. J. Mar. Sci. Eng. 2022, 10, 1684. https://doi.org/10.3390/jmse10111684
Pang L, Jiang C, Chen L. Nonlinear Predictive Framework of the Undrained Clay Slope Effect on the Initial Stiffness of p-y Curves of Laterally Loaded Piles by FEM. Journal of Marine Science and Engineering. 2022; 10(11):1684. https://doi.org/10.3390/jmse10111684
Chicago/Turabian StylePang, Li, Chong Jiang, and Lujie Chen. 2022. "Nonlinear Predictive Framework of the Undrained Clay Slope Effect on the Initial Stiffness of p-y Curves of Laterally Loaded Piles by FEM" Journal of Marine Science and Engineering 10, no. 11: 1684. https://doi.org/10.3390/jmse10111684
APA StylePang, L., Jiang, C., & Chen, L. (2022). Nonlinear Predictive Framework of the Undrained Clay Slope Effect on the Initial Stiffness of p-y Curves of Laterally Loaded Piles by FEM. Journal of Marine Science and Engineering, 10(11), 1684. https://doi.org/10.3390/jmse10111684