Probability Prediction Approach of Fatigue Failure for the Subsea Wellhead Using Bayesian Regularization Artificial Neural Network
Abstract
1. Introduction
2. Background
2.1. BRANN
2.2. Parametric and Non-Parametric Estimation
2.2.1. Weibull Distribution
2.2.2. Lognormal Distribution
2.2.3. Kernel Density Estimation
2.3. Logistic Regression
3. Methodology of Establishing the Probability Density Function of Fatigue Damage of SW
4. Case Study
4.1. Fatigue Damage Analysis of SW
4.1.1. Basic Data
4.1.2. Fatigue Damage Calculation Based on Semi-Decoupled Model
4.2. BRANN Fatigue Damage Model
4.3. Probability Density Function of Fatigue Damage
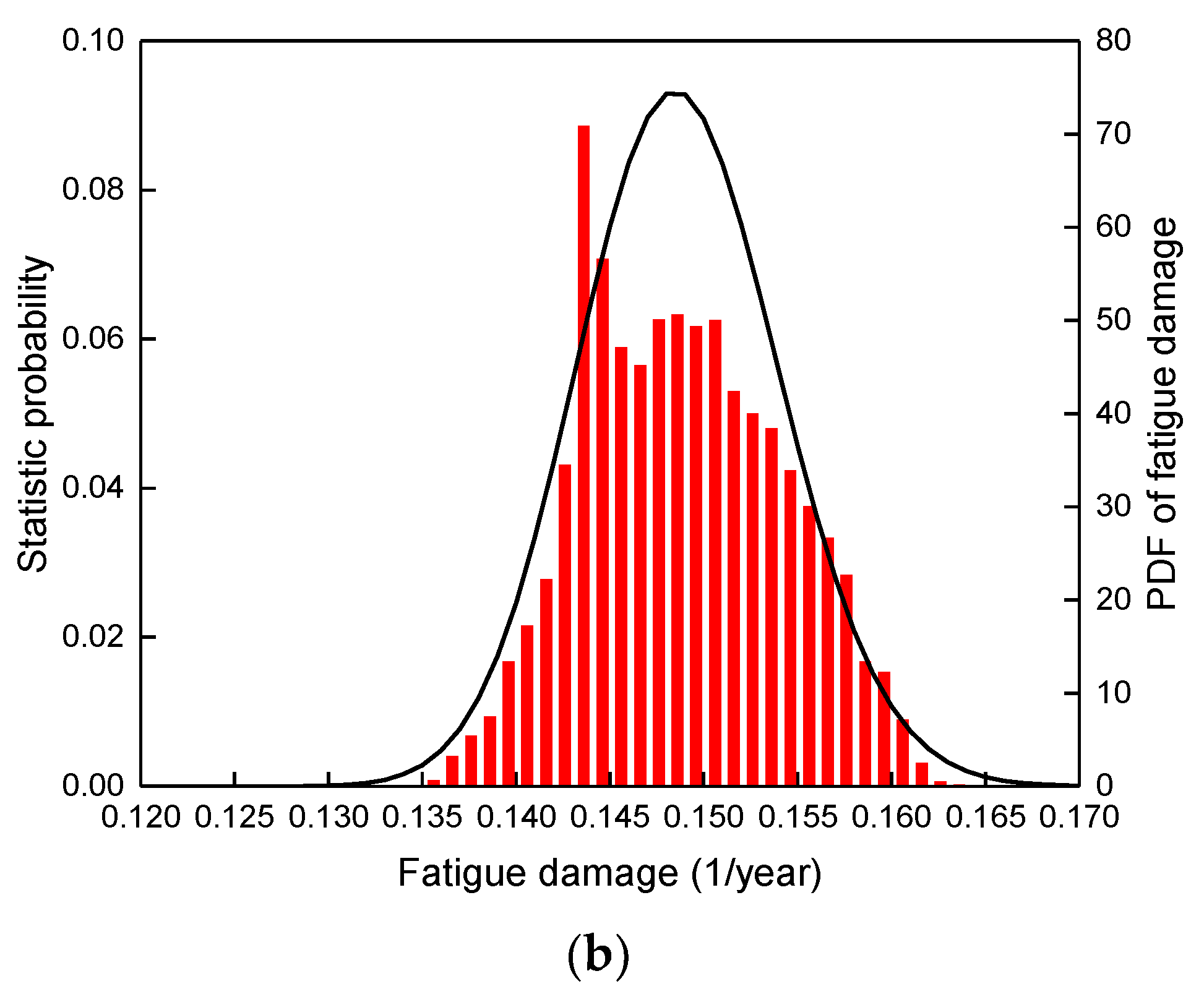
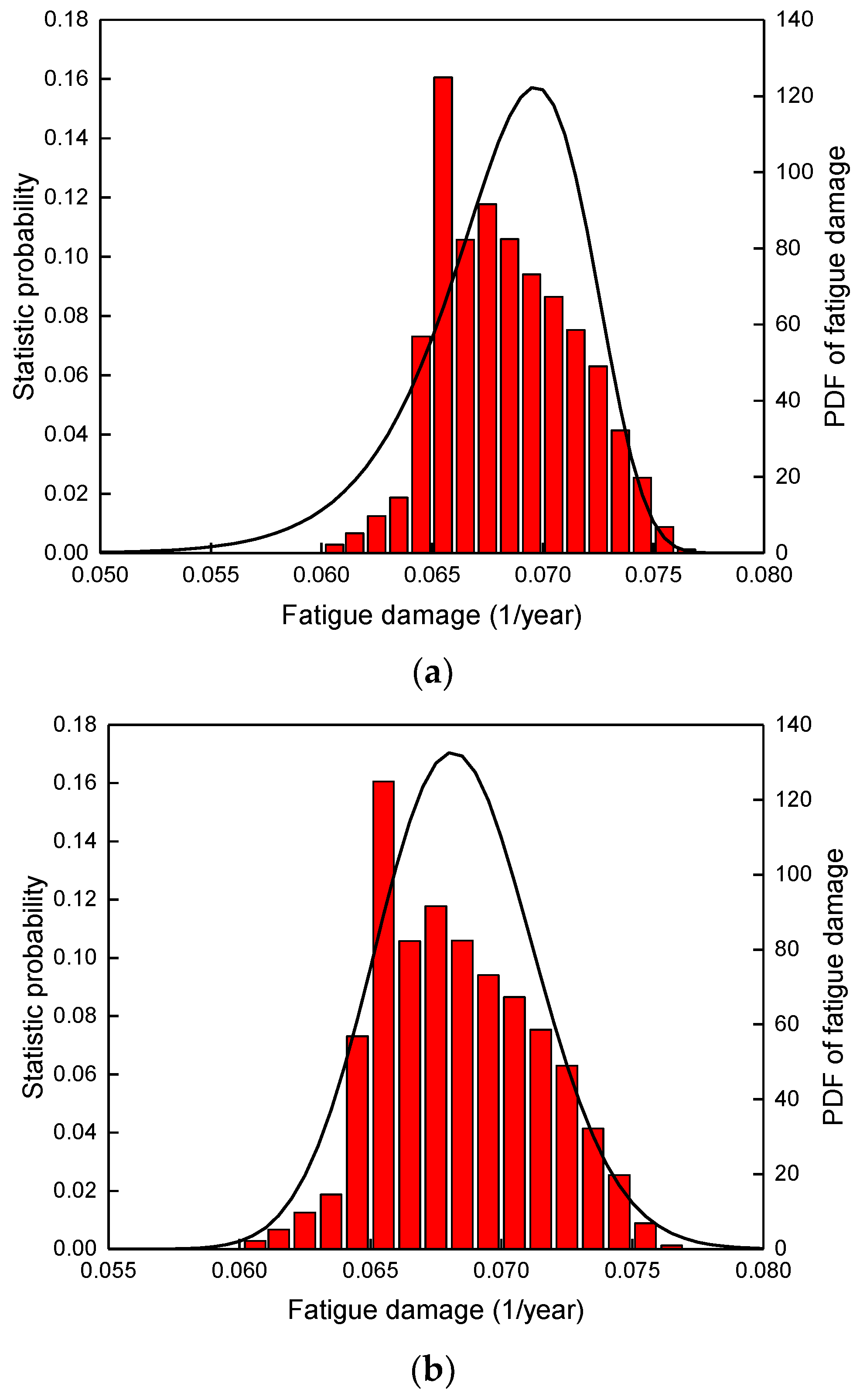
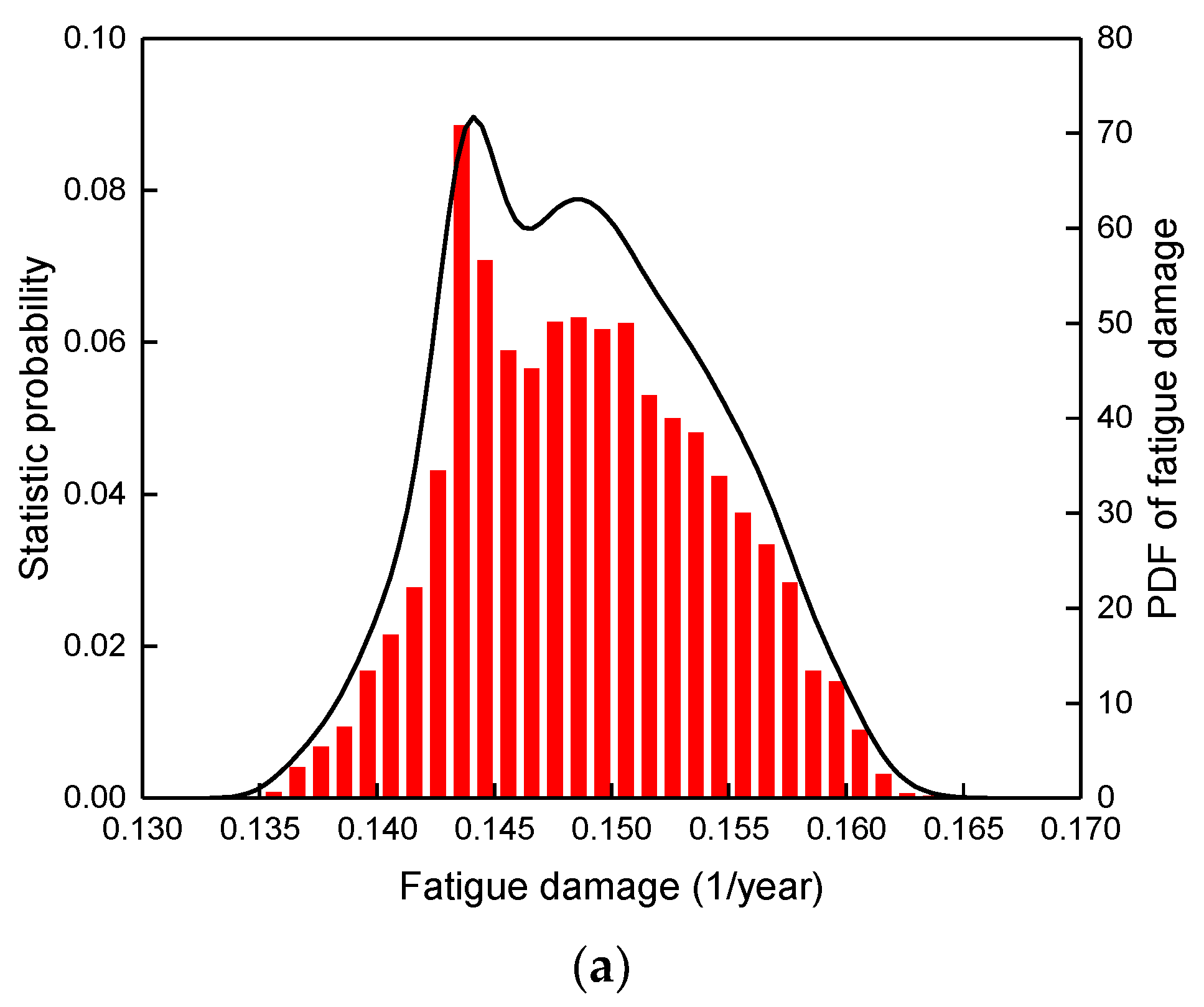
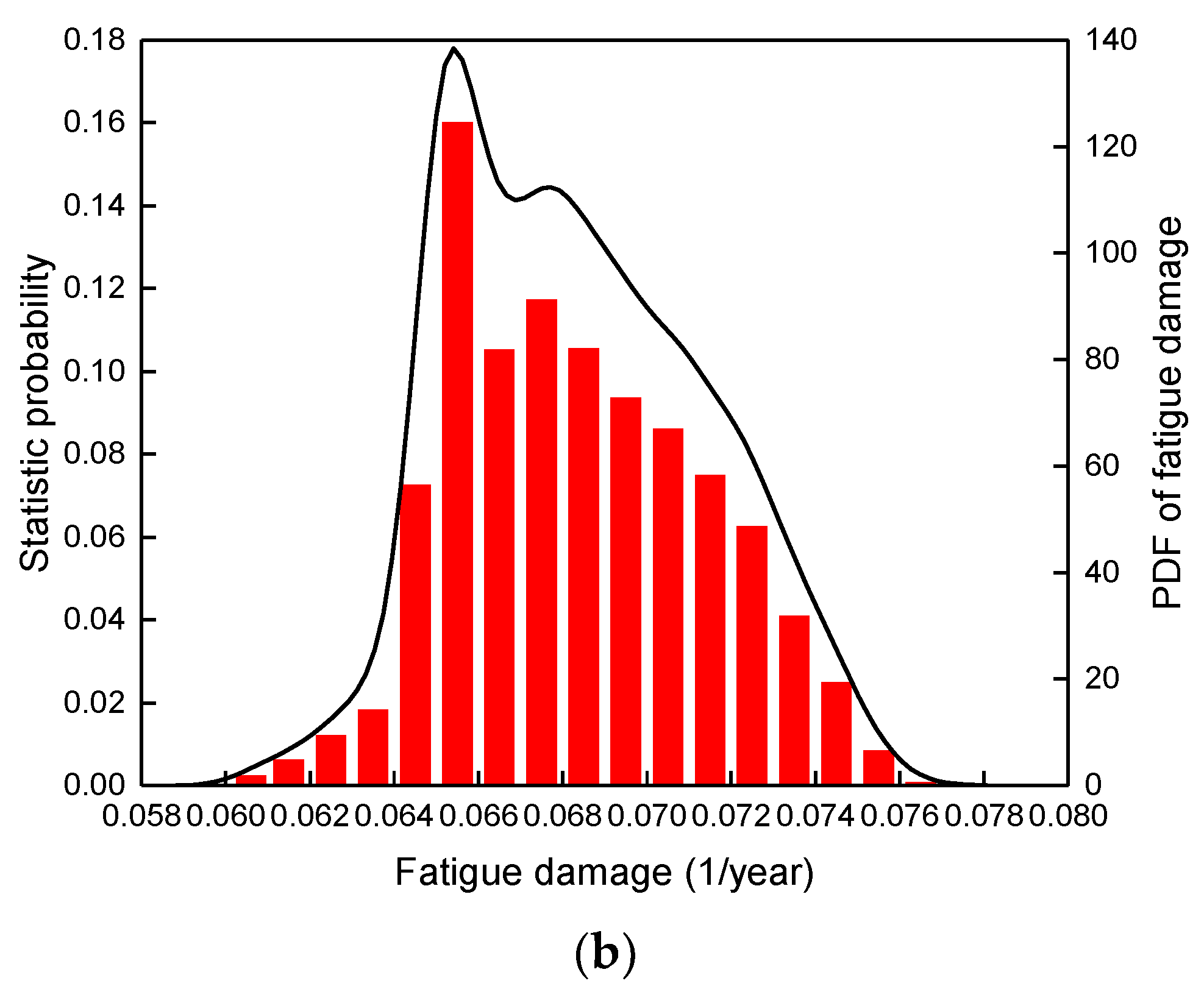
4.3.1. PDF of Fatigue Damage Determined by Parametric Estimation
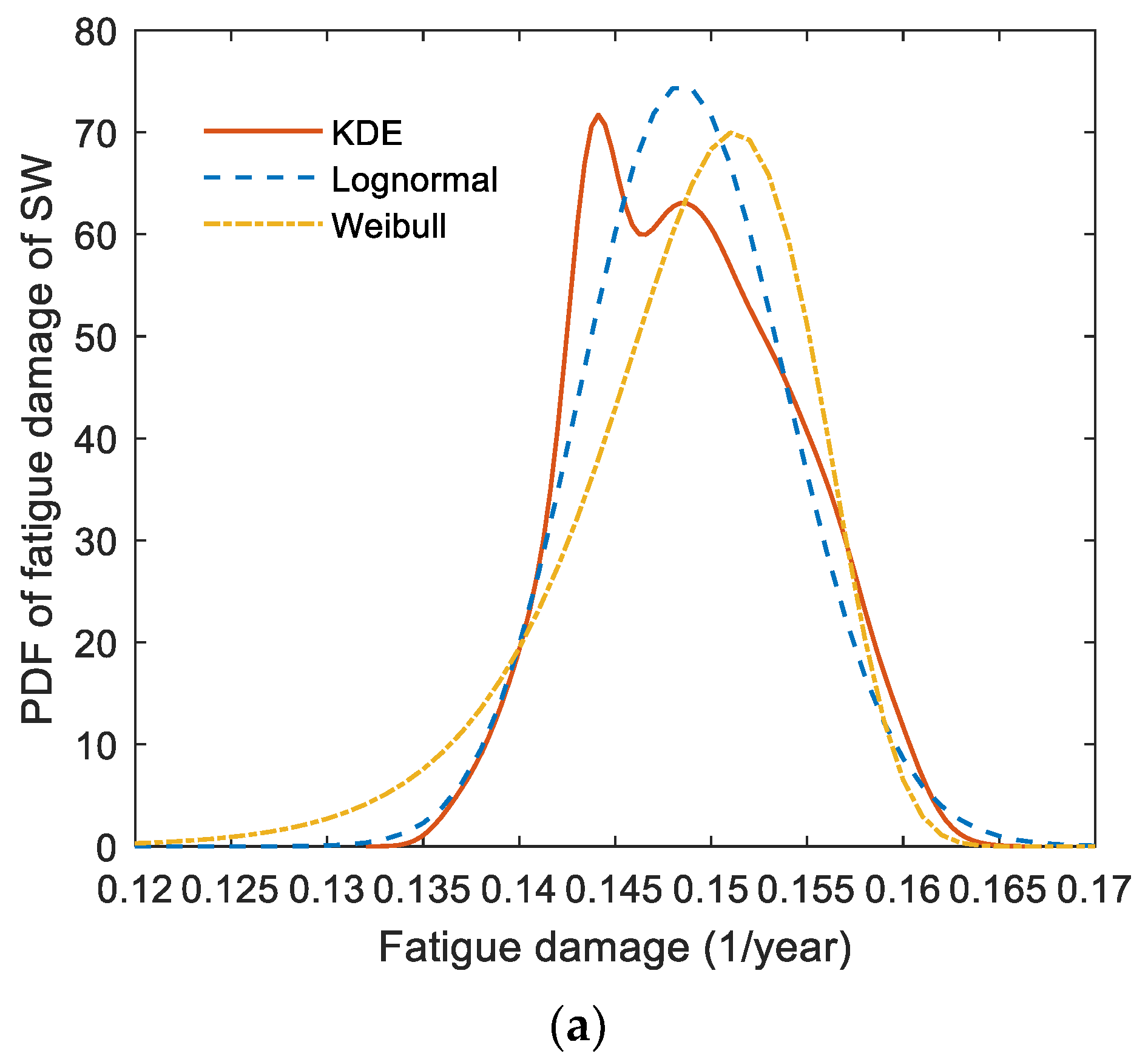
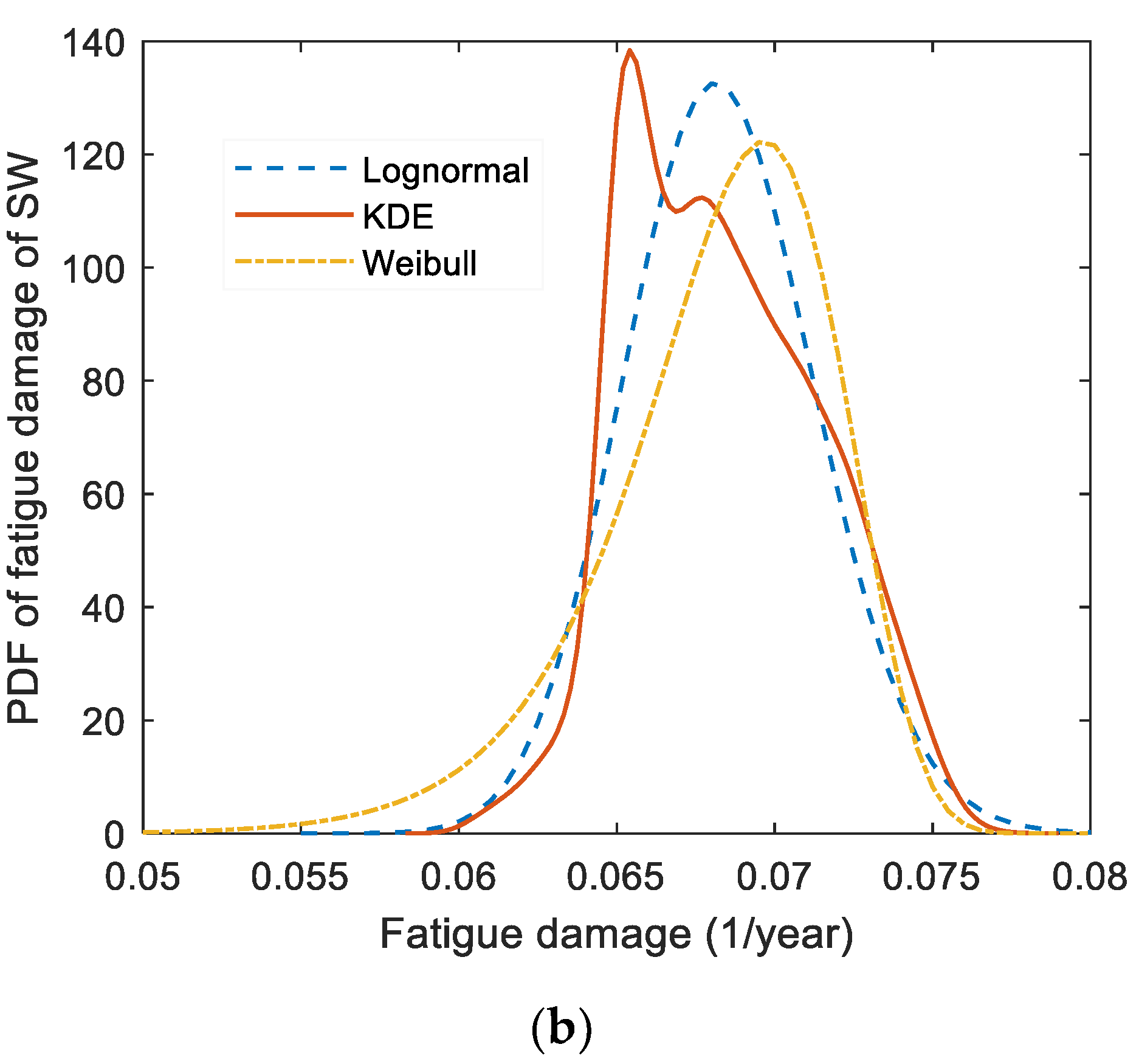
4.3.2. PDF of Fatigue Damage Determined by Non-Parametric Estimation
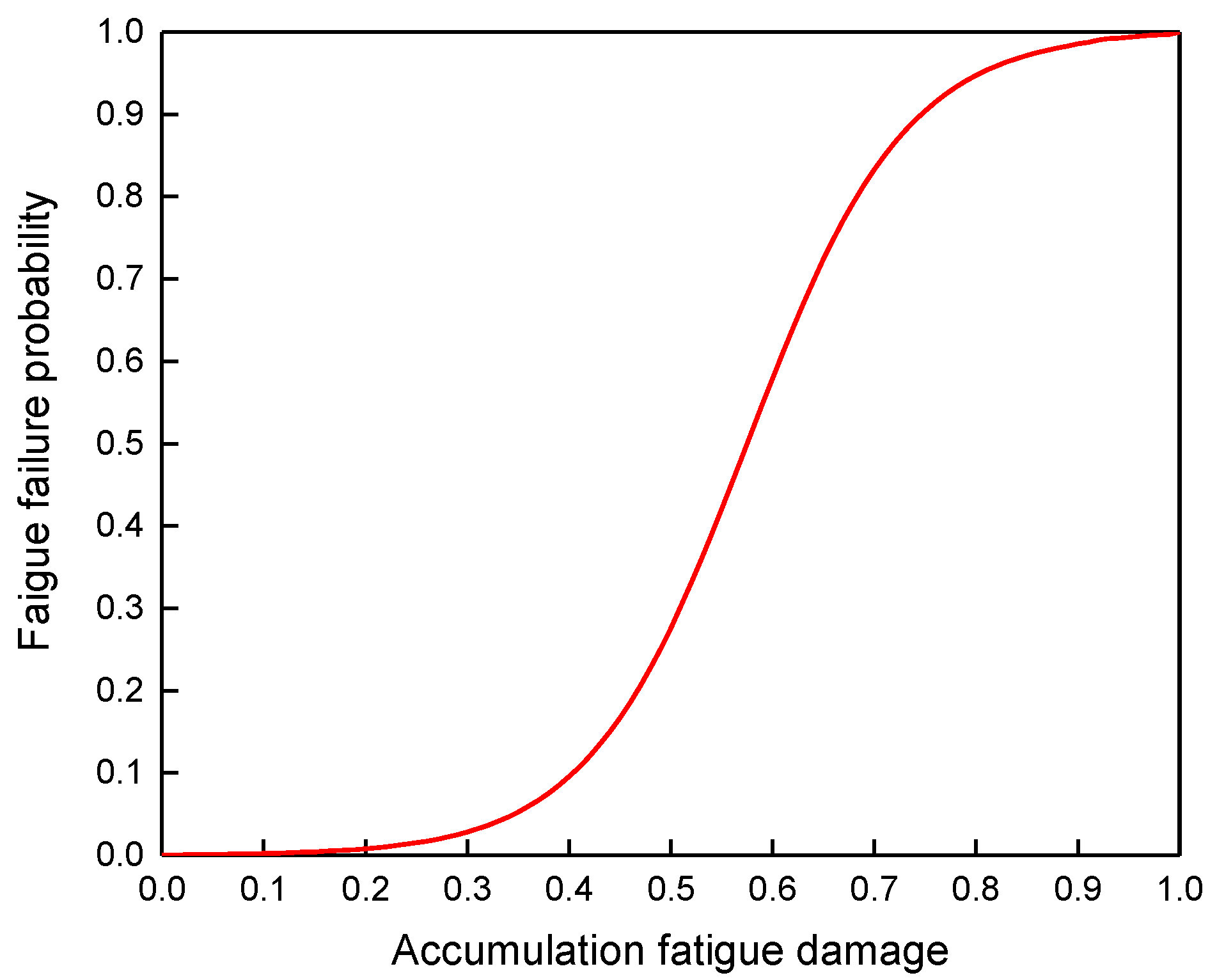
4.4. Fatigue Failure Probability of SW
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, G.; Li, J.; Chang, Y.; Wang, K.; Xiu, Z.; Liu, H.; Xu, L.; Sheng, L. Influencing factors for fatigue damage of underwater wellhead system of deepwater oil and gas. Acta Pet. Sincia 2019, 40, 141–151. [Google Scholar]
- Rørgård, O.; Sønåsen, K.O.; Ellefsen, Ø. Introducing reactive flex-joint: 10–15 times prolonged wellhead life. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 1–4 May 2017. [Google Scholar]
- Milberger, L.J.; Yu, A.; Hosie, S.; Hines, F. Structural requirements for the effective transfer of environmental loadings in a subsea wellhead system. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 1991. [Google Scholar]
- Chang, Y.; Wu, X.; Zhang, C.; Chen, G.; Liu, X.; Li, J.; Cai, B.; Xu, L. Dynamic Bayesian Networks based approach for risk analysis of subsea wellhead fatigue failure during service life. Reliab. Eng. Syst. Eng. 2019, 188, 454–462. [Google Scholar] [CrossRef]
- Greene, J.F.; Williams, D. The influence of drilling rig and riser system selection on wellhead fatigue loading (OMAE2012-83754). In Proceedings of the 31st International Conference on Ocean, Offshore and Arctic Engineering ASME OMAE, Rio de Janeiro, Brazil, 1–6 July 2012. [Google Scholar]
- Grytøyr, G.; Reinås, L.; Eilertsen, L.E.; Russo, M. Full scale measurement of cyclic bending moments on subsea wellheads on the Norwegian Continental Shelf. In Proceedings of the Society of Petroleum Engineers, Stavanger, Norway, 11–13 April 2016. [Google Scholar]
- Sunday, K.; Ward, P.; Griffin, C.; Lorenson, P. Detailed approach for the assessment of accumulated wellhead fatigue. In Proceedings of the Society of Petroleum Engineers, Aberdeen, Scotland, 8–11 September 2015. [Google Scholar]
- Ruschel, A.; Dantas, C.M.S.; Sousa, F.J.M.; Simão, M.L.; Sagrilo, L.V.S.; Percy, J.G.; Oliveira, F.L. Wellhead fatigue analysis considering the effect of wind-sea and swell waves by using Univariate Dimension Reduction Method. J. Pet. Sci. Eng. 2021, 206, 108989. [Google Scholar] [CrossRef]
- Chang, Y.; Li, J.; Wang, J.; Nie, Z.; Cao, B.; Liu, X.; Chen, G.; Xue, A. Comparative investigation of dynamic analysis models for subsea wellhead in deepwater. In Proceedings of the International Ocean and Polar Engineering Conference, Honolulu, HI, USA, 16–21 June 2019. [Google Scholar]
- Li, J.; Chang, Y.; Xiu, Z.; Liu, H.; Xue, A.; Chen, G.; Xu, L.; Sheng, L. A local stress-strain approach for fatigue damage prediction of subsea wellhead system based on semi-decoupled model. Appl. Ocean. Res. 2020, 102, 102306. [Google Scholar] [CrossRef]
- Neill, M.S.; Agarwal, P.; Bhalla, K.; Ge, M.; Leonard, J. Wellhead fatigue monitoring during subsea well plug and abandonment activities. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 1–4 May 2017. [Google Scholar]
- Hørte, T.; Reinås, L.; Mathisen, J. Wellhead fatigue analysis method: Benefits of a structural reliability analysis approach (OMAE2012-83141). In Proceedings of the 31st International Conference on Ocean, Offshore and Arctic Engineering ASME OMAE, Rio de Janeiro, Brazil, 1–6 July 2012. [Google Scholar]
- Jaculli, M.A.; Mendes, J.R.P.; Colombo, D. Evaluation of excessive wellhead motions: Reliability assessment and wellhead integrity index (Part II). J. Pet. Sci. Eng. 2022, 208, 109570. [Google Scholar] [CrossRef]
- Zhou, Y.; Xu, B.; Pang, R.; Zou, D.; Kong, X. Stochastic seismic response and stability reliability analysis of a vertical retaining wall in front of the pumping station of a nuclear power plant using the probability density evolution method. Nucl. Eng. Des. 2018, 334, 110–120. [Google Scholar] [CrossRef]
- Kwon, K.; Frangopol, D.M. Bridge fatigue reliability assessment using probability density functions of equivalent stress range based on field monitoring data. Int. J. Fatigue 2010, 32, 1221–1232. [Google Scholar] [CrossRef]
- Chen, T. Structural Integrity Assessment and Risk Management for Ageing Offshore Platforms; China University of Petroleum (East China): Qingdao, China, 2011. [Google Scholar]
- Miao, H.; Liu, W.; Li, J. Seismic reliability analysis of water distribution networks on the basis of the probability density evolution method. Struct. Saf. 2020, 86, 101960. [Google Scholar] [CrossRef]
- Liu, W.; Song, Z.; Wan, Z.; Li, J. Lifecycle operational reliability assessment of water distribution networks based on the probability density evolution method. Probabilistic Eng. Mech. 2020, 59, 103037. [Google Scholar] [CrossRef]
- Xian, J.; Sua, C.; Guo, H. Seismic reliability analysis of energy-dissipation structures by combining probability density evolution method and explicit time-domain method. Struct. Saf. 2021, 88, 102010. [Google Scholar] [CrossRef]
- Feng, D.; Xie, S.; Xu, J.; Qian, K. Robustness quantification of reinforced concrete structures subjected to progressive collapse via the probability density evolution method. Eng. Struct. 2020, 202, 109877. [Google Scholar] [CrossRef]
- Gao, K.; Liu, G. Novel nonlinear time-varying fatigue reliability analysis based on the probability density evolution method. Int. J. Fatigue 2021, 149, 106257. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Reed, R.D.; Marks, R.J. Neural Smithing; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Lim, H.; Sohn, H.; Kim, Y. Data-driven fatigue crack quantification and prognosis using nonlinear ultrasonic modulation. Mech. Syst. Signal Process. 2018, 109, 185–195. [Google Scholar] [CrossRef]
- Shi, J.; Zhu, Y.; Kong, D.; Khan, F.; Li, J. Stochastic analysis of explosion risk for ultra-deep-water semi-submersible offshore platforms. Ocean. Eng. 2019, 172, 844–856. [Google Scholar] [CrossRef]
- Kaur, H.; Salaria, D.S. Bayesian regularization based neural network tool for software effort estimation. Glob. J. Comput. Sci. Technol. 2013, 13, 154–160. [Google Scholar]
- Gianola, D.; Okut, H.; Weigel, K.A.; Rosa, G.J. Predicting complex quantitative traits with Bayesian neural networks: A case study with Jersey cows and wheat. BMC Genet. 2011, 12, 87–93. [Google Scholar] [CrossRef]
- Shi, J.; Khan, F.; Zhu, Y.; Li, J.; Chen, G. Robust data-driven model to study dispersion of vapor cloud in offshore facility. Ocean. Eng. 2018, 161, 98–110. [Google Scholar] [CrossRef]
- Li, X.; Jia, R.; Zhang, R.; Yang, S.; Chen, G. A KPCA-BRANN based on data-driven approach to model corrosion degradation of subsea oil pipelines. Reliab. Eng. Syst. Saf. 2022, 219, 108231. [Google Scholar] [CrossRef]
- Kayri, M. Predictive abilities of Bayesian Regularization and Levenberg–Marquardt Algorithms in Artificial Neural Networks: A comparative empirical study on social data. Math. Comput. Appl. 2016, 21, 20. [Google Scholar] [CrossRef]
- Shi, J.; Xie, W.; Huang, X.; Xiao, F.; Usmani, A.S.; Khan, F.; Yin, X.; Chen, G. Real-time natural gas release forecasting by using physics-guided deep learning probability model. J. Clean. Prod. 2022, 368, 133201. [Google Scholar] [CrossRef]
- Shaneh, A.; Butler, G. Bayesian learning for feed-forward neural network with application to proteomic data: The glycosylation sites detection of the epidermal growth factor-like proteins associated with cancer as a case study. Lect. Notes Comput. Sci. 2006, 4013, 121–132. [Google Scholar]
- Dong, W.; Moan, T.; Gao, Z. Long-term fatigue analysis of multi-planar tubular joints for jacket-type offshore wind turbine in time domain. Eng. Struct. 2011, 33, 2002–2014. [Google Scholar] [CrossRef]
- Castellares, F.; Lemonte, A.J. A new generalized Weibull distribution generated by gamma random variables. J. Egypt. Math. Soc. 2014, 23, 382–390. [Google Scholar] [CrossRef]
- Li, H.; Du, J.; Wang, S.; Sun, M.; Chang, A. Investigation on the probabilistic distribution of mooring line tension for fatigue damage assessment. Ocean. Eng. 2016, 124, 204–214. [Google Scholar] [CrossRef]
- Li, L.; Papaioannou, I.; Straub, D. Global reliability sensitivity estimation based on failure samples. Struct. Saf. 2019, 81, 101871. [Google Scholar] [CrossRef]
- Van, E.N.; Van, P. Bayesian logistic regression analysis. In Proceedings of the International Workshop on Bayesian Inference and Maximum Entropy Methods in Science and Engineering, Garching, Germany, 15–20 July 2012. [Google Scholar]
- Hosmer, D.; Lemeshow, S.; Sturdivant, R. Applied Logistic Regression, 3rd ed.; Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Liu, X.; Chen, G.; Chang, Y.; Ju, S.; Xu, L. Time domain random wave-loading fatigue analysis on deepwater drilling risers. J. China Univ. Pet. 2012, 36, 146–151. [Google Scholar]
- Zhang, S.; Liu, X.; Chang, Y.; Chen, G. Wave-loading fatigue analysis on deep-water drilling platform/riser system. J. Ship Mech. 2019, 23, 843–850. [Google Scholar]
- Det Norkse Veritas. DNV-RP-C203: Fatigue Design of Offshore Steel Structures; Det Norske Veritas: Oslo, Norway, 2010. [Google Scholar]
- Det Norske Veritas. DNV RP 0142: Wellhead Fatigue Analysis; Det Norske Veritas: Oslo, Norway, 2015. [Google Scholar]
- Zhang, N.; Chang, Y.; Shi, J.; Chen, G.; Zhang, S.; Cai, B. Fragility assessment approach of deepwater drilling risers subject to harsh environments using Bayesian regularization artificial neural network. Ocean. Eng. 2021, 225, 108793. [Google Scholar] [CrossRef]
- Buchmiller, D.; Hørte, T.; Grytøyr, G. Establishing an industry best practice on subsea wellhead fatigue. In Proceedings of the Society of Petroleum Engineers, San Diego, CA, USA, 6–8 March 2012. [Google Scholar]
- Jaiswal, V.; Feng, L.; Saraswat, R.; Healy, B.; Hørte, T.; Sharma, P. Fatigue analysis of non-rigid locked wellhead. In Proceedings of the International Ocean and Polar Engineering Conference, Rhodes, Greece, 26 June–2 July 2016. [Google Scholar]
- International Organization for Standardization. ISO/TR 13624-2: Deepwater Drilling Riser Methodologies, Operation, and Integrity Technical Report; International Organization for Standardization: Geneva, Switzerland, 2009. [Google Scholar]
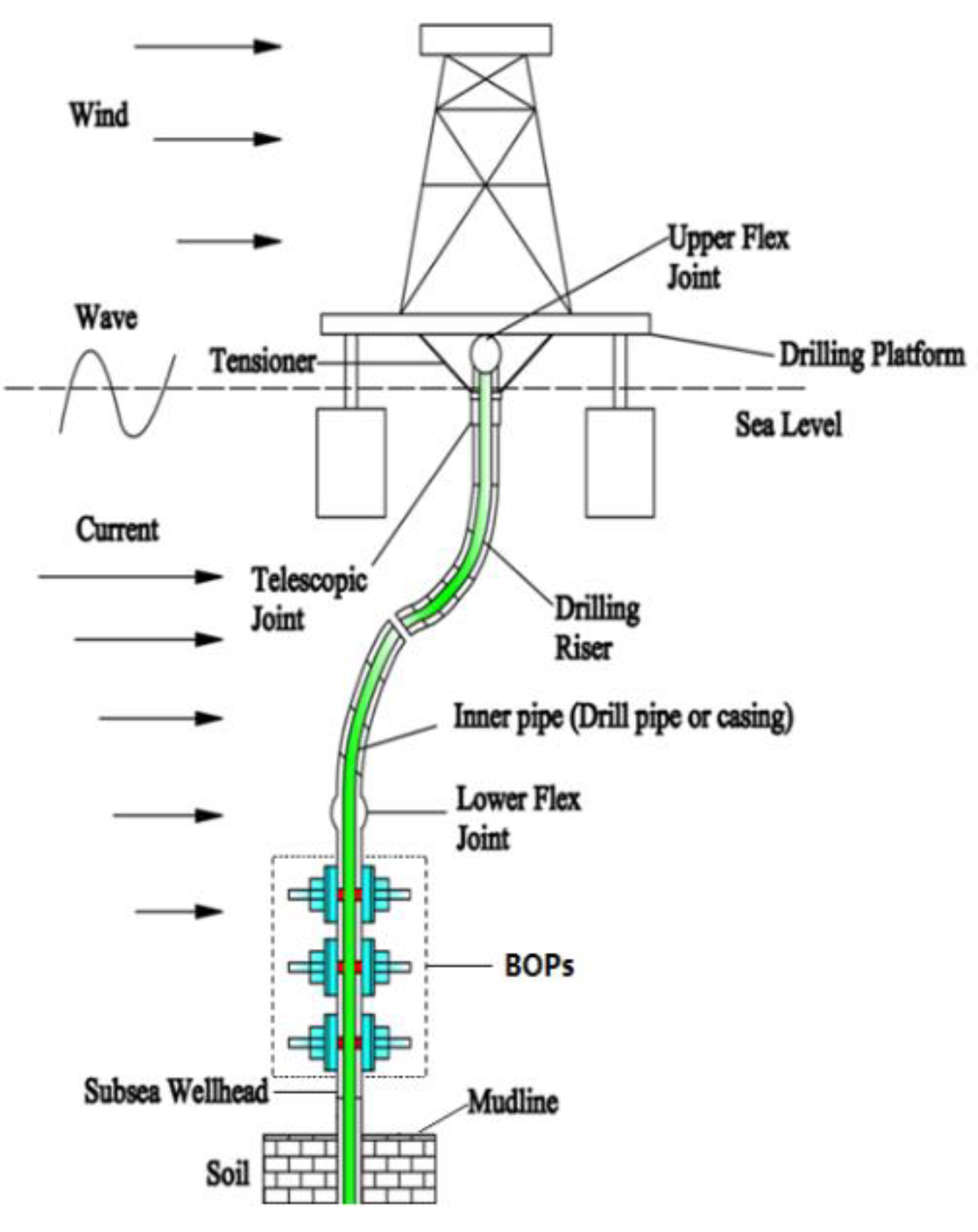
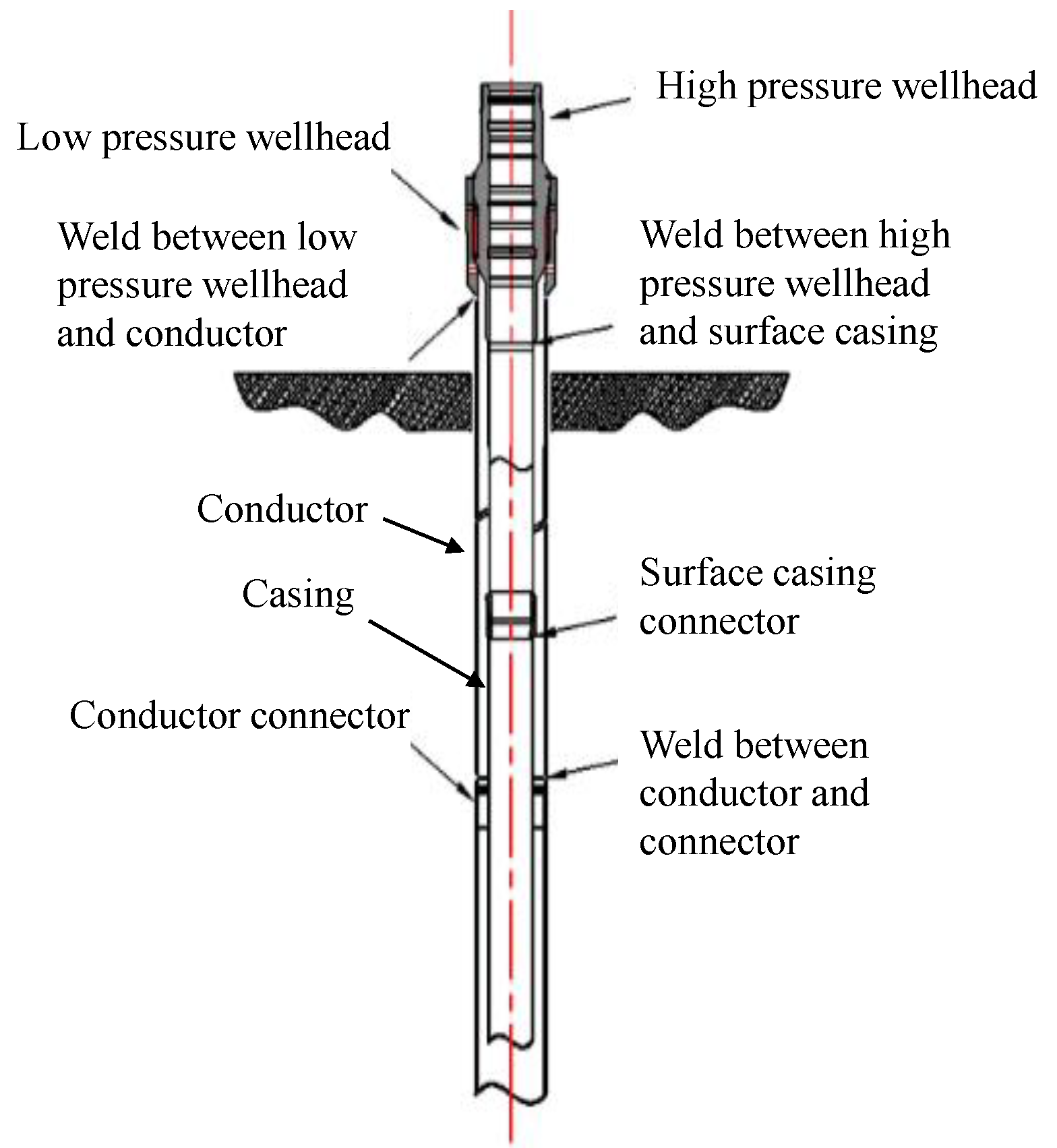
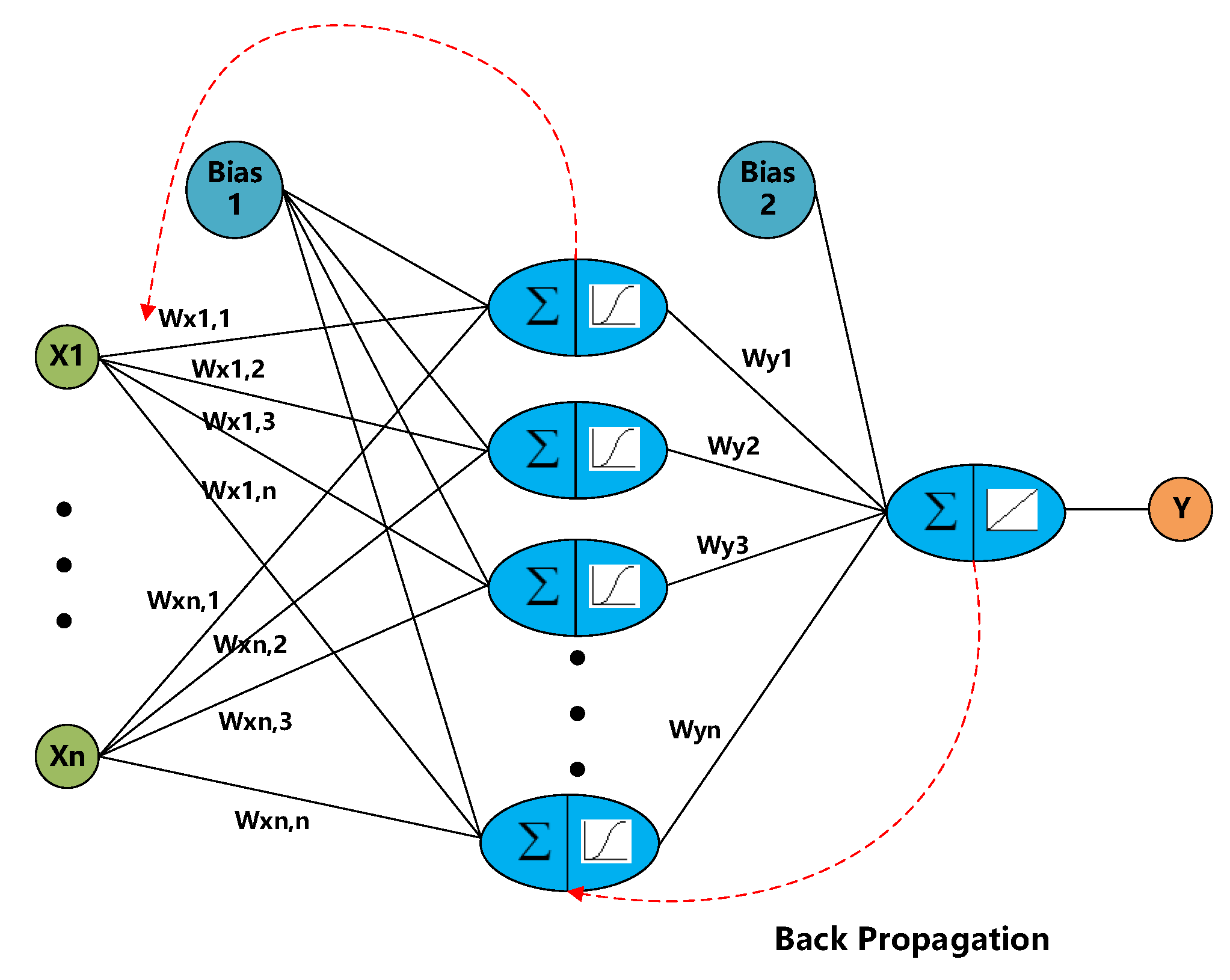
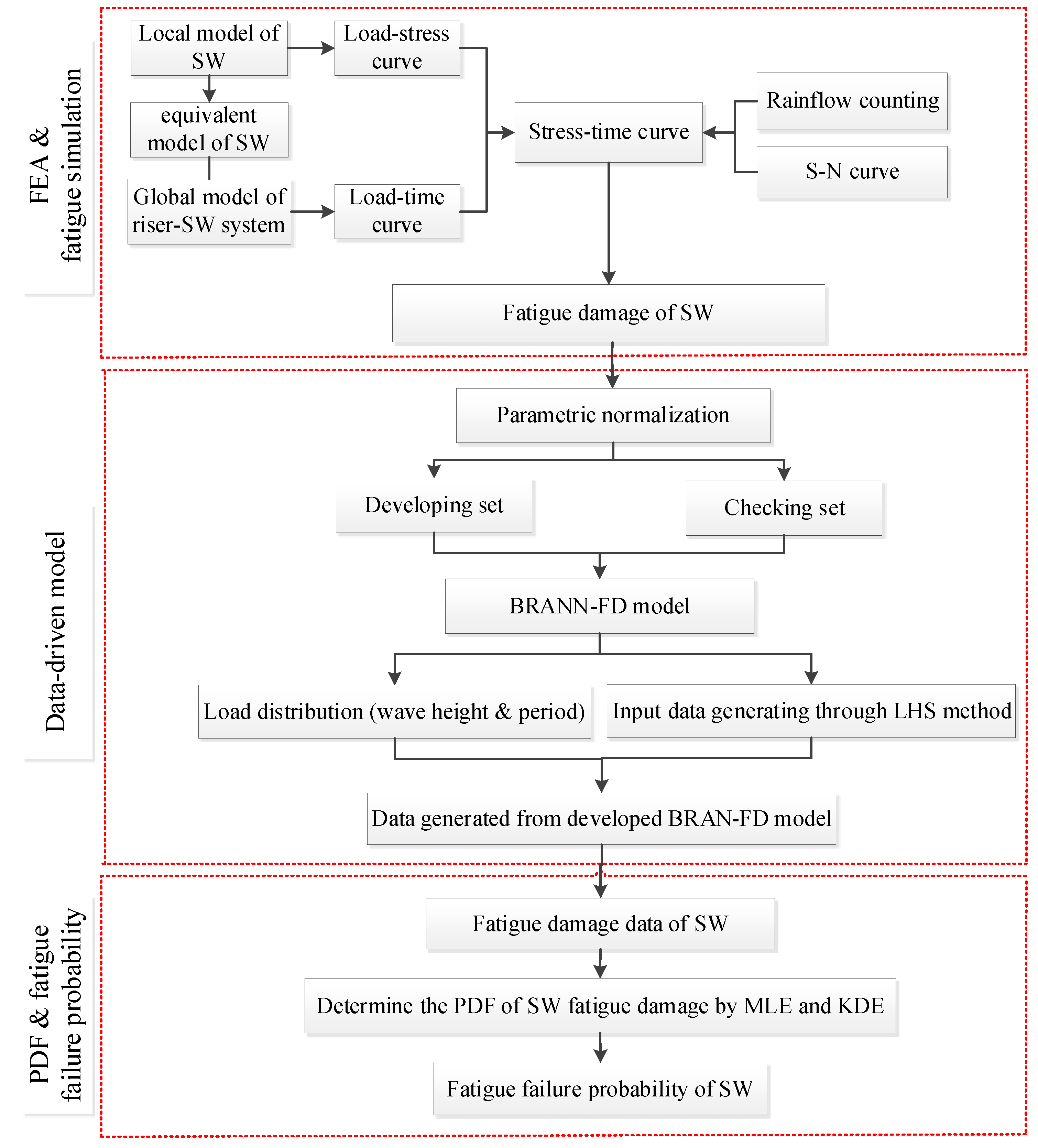

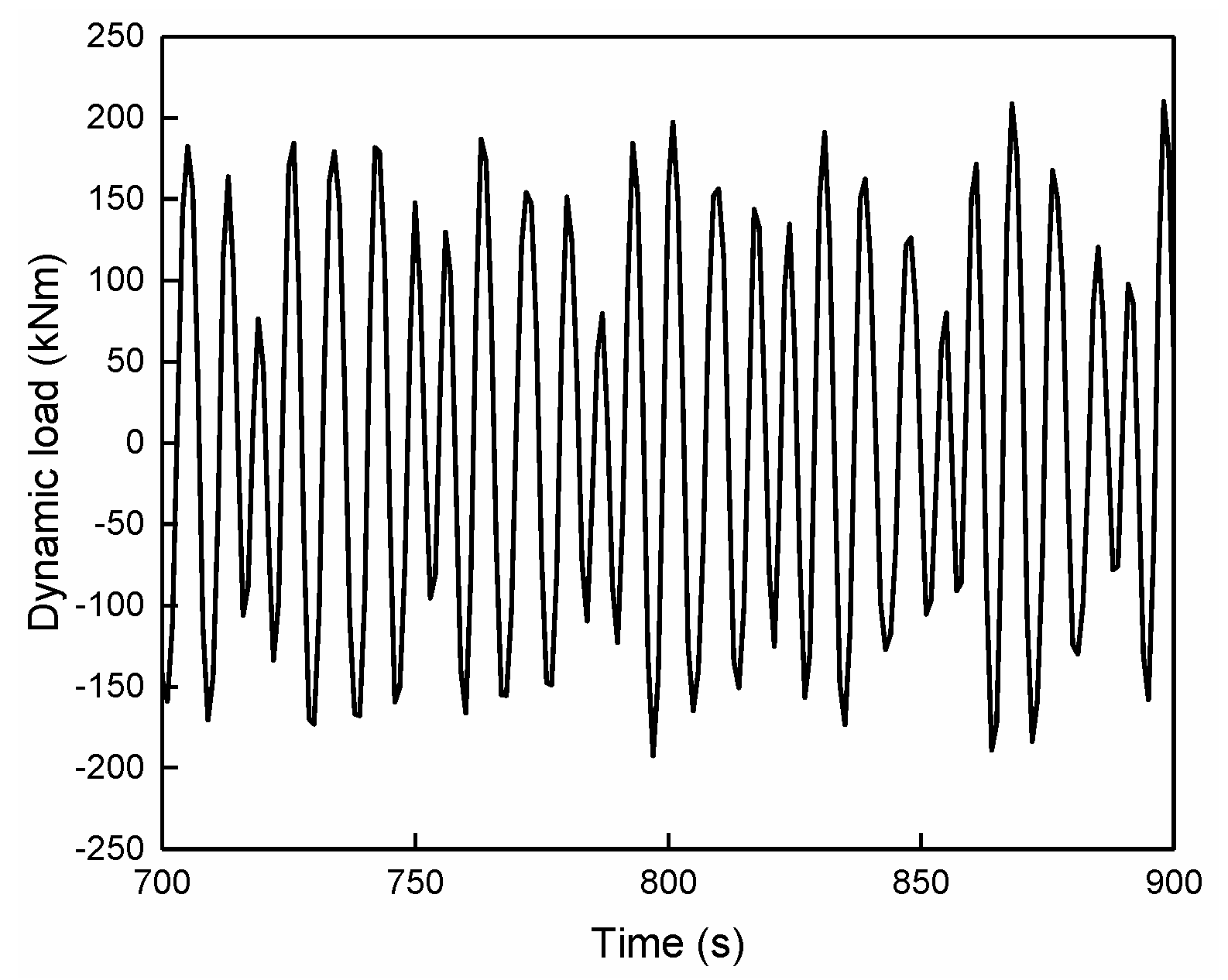
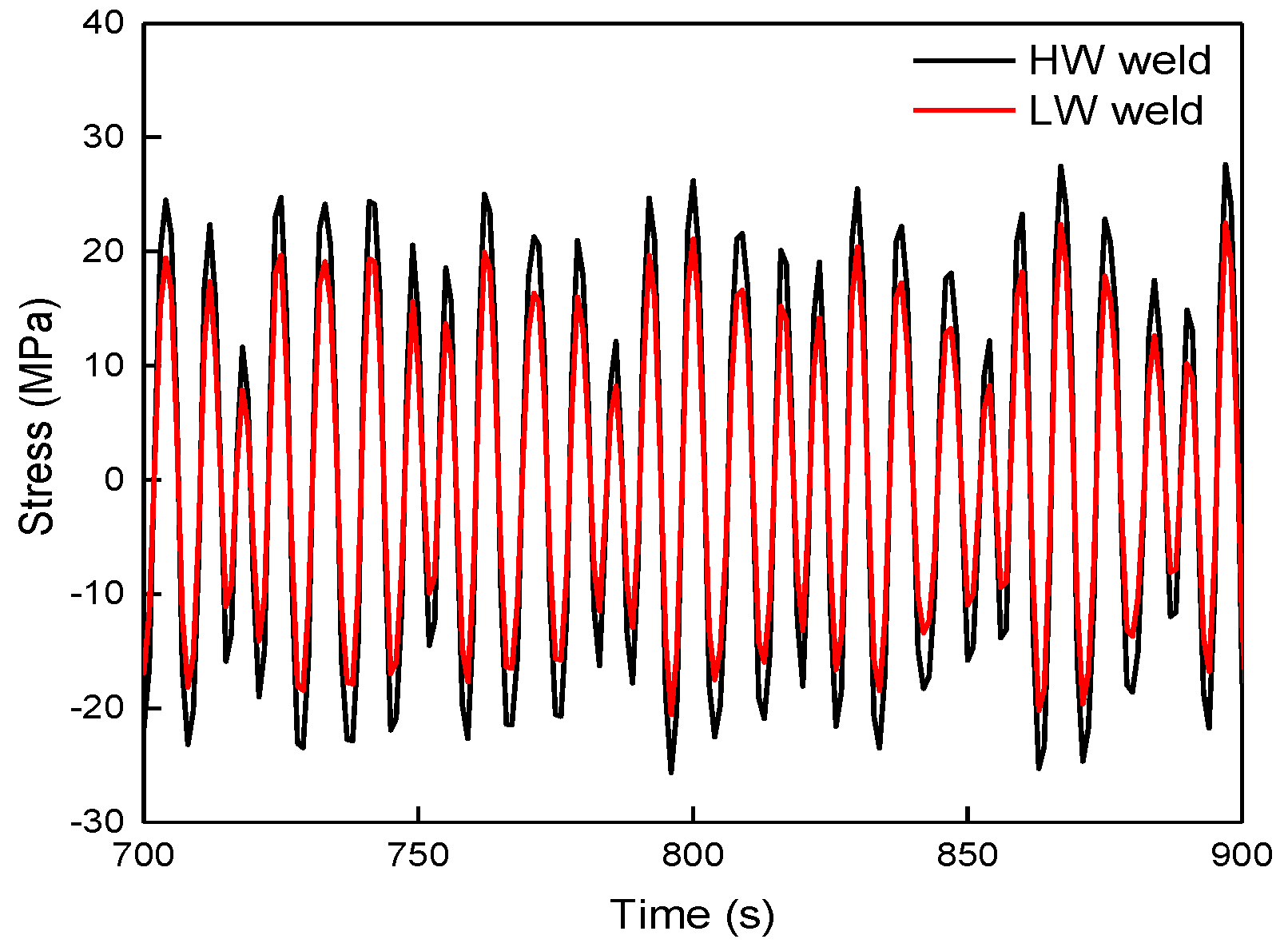
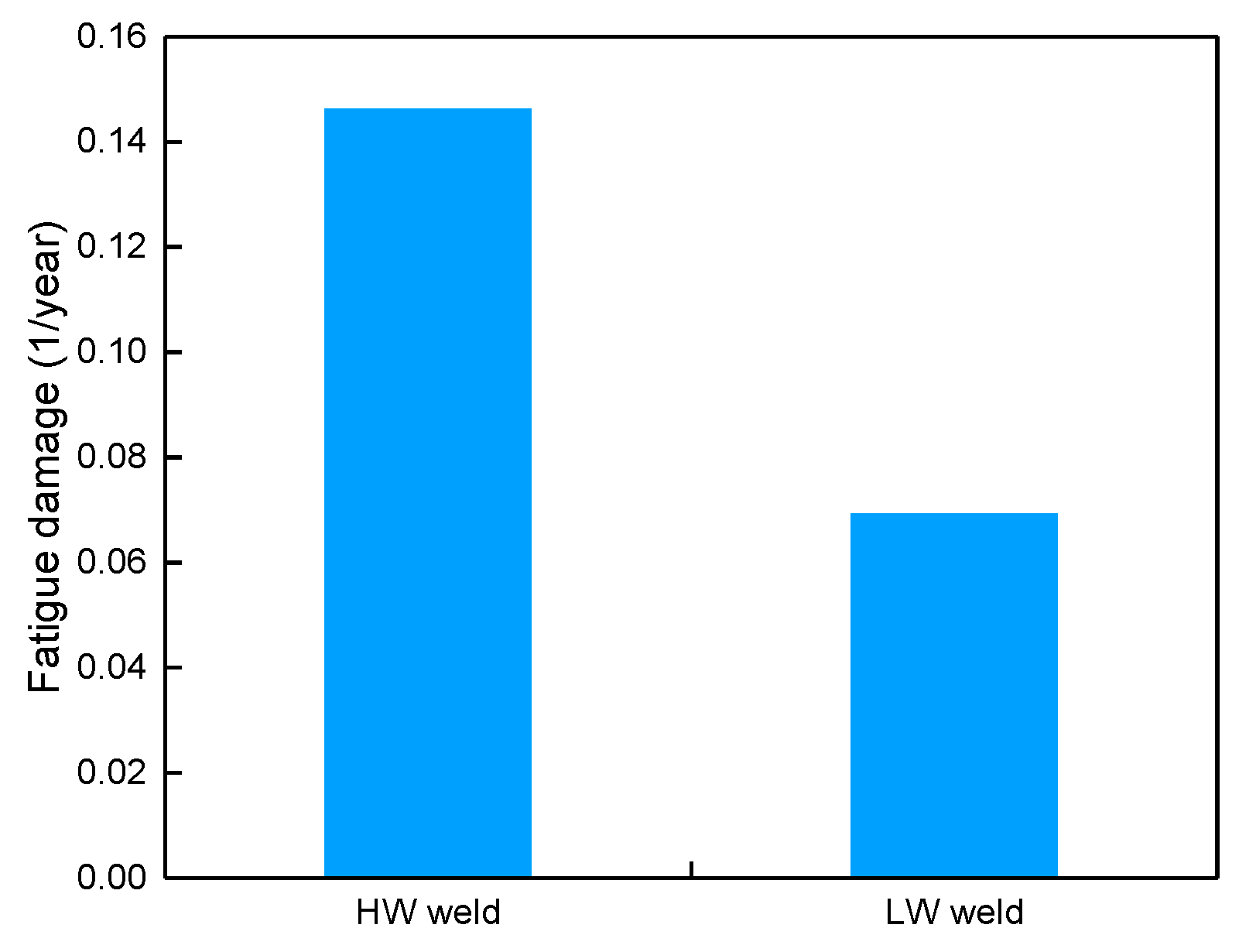

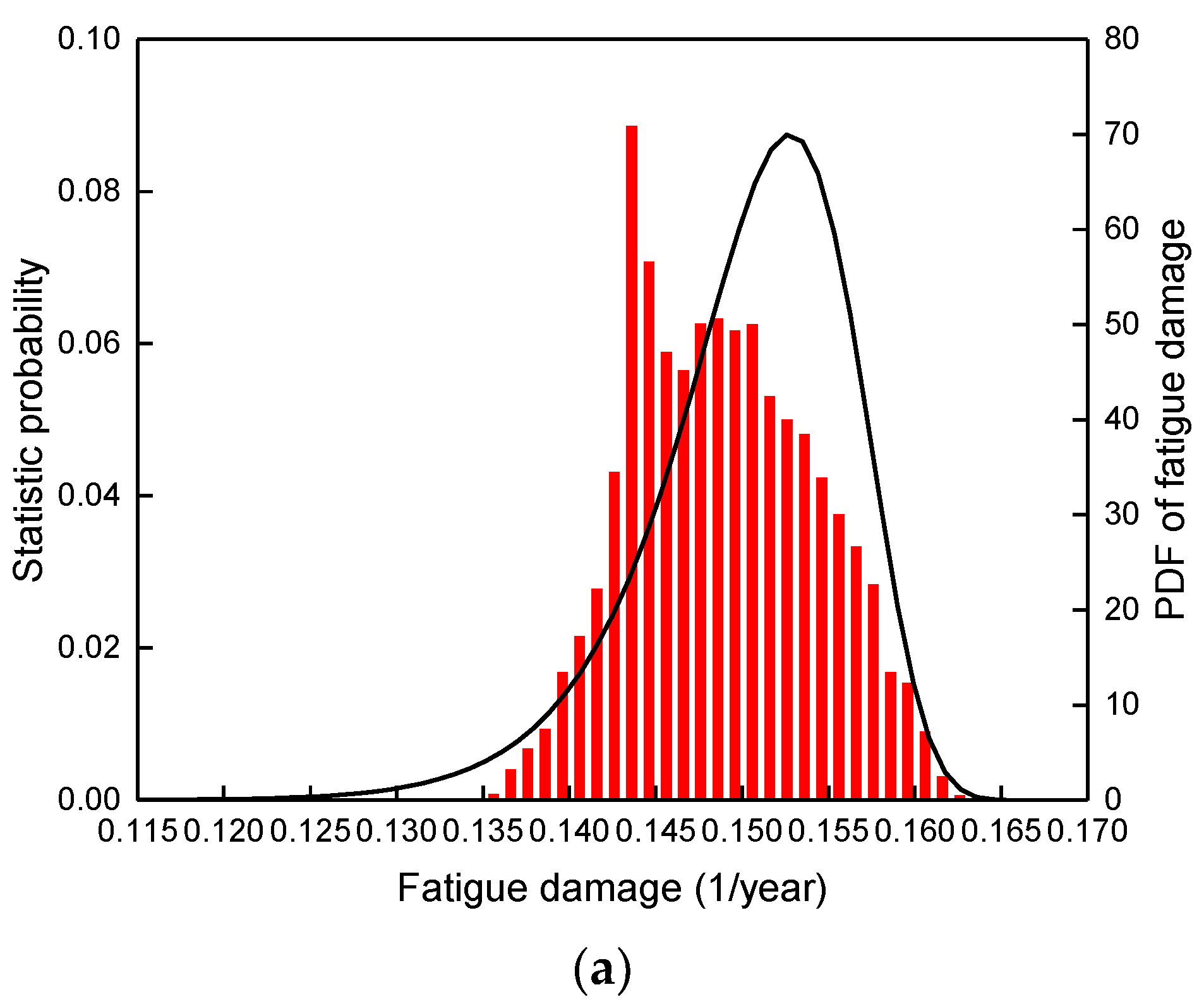
| Parameters | Type/m | Max O.D/m | Min I.D/m | Height/m | Weight/kg | Bending Capacity/Nm |
|---|---|---|---|---|---|---|
| HW | 0.476 | 0.851 | 0.446 | 1.476 | 2653.56 | 7.797 × 106 |
| LW | 0.762 | 0.946 | 0.685 | 0.762 | 850.5 | 4.204 × 106 |
| Name | Number/Piece | Name | Number/Piece |
|---|---|---|---|
| Upper flex joint | 1 | Slip joint | 1 |
| Telescopic joint | 1 | Lower flex joint | 1 |
| Pup joint | 1 | BOPs | 1 |
| Buoyancy riser joints | 26 | SW | 1 |
| Hs/m | Tp/s | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3.5 | 4.5 | 5.5 | 6.5 | 7.5 | 8.5 | 9.5 | 10.5 | 11.5 | 12.5 | 13.5 | 14.5 | 15.5 | 16.5 | |
| 0.25 | 0.01 | 0.04 | 0.09 | 0.06 | 0.07 | 0.07 | 0.13 | 0.03 | ||||||
| 0.75 | 0.11 | 1.1 | 3.4 | 3.7 | 2.9 | 1.8 | 1.1 | 1.2 | 0.44 | 0.23 | 0.13 | 0.09 | 0.07 | 0.08 |
| 1.25 | 0.01 | 0.39 | 3.6 | 6.7 | 5.5 | 5 | 2.2 | 0.91 | 0.42 | 0.35 | 0.24 | 0.23 | 0.35 | 0.11 |
| 1.75 | 0.01 | 0.62 | 5 | 6.6 | 3 | 1.6 | 0.61 | 0.24 | 0.21 | 0.21 | 0.16 | 0.26 | 0.13 | |
| 2.25 | 0.01 | 0.01 | 1.3 | 5.7 | 4 | 1 | 0.6 | 0.24 | 0.16 | 0.16 | 0.16 | 0.21 | 0.14 | |
| 2.75 | 0.14 | 2.2 | 5 | 1.1 | 0.3 | 0.12 | 0.1 | 0.09 | 0.12 | 0.11 | 0.09 | |||
| 3.25 | 0.01 | 0.26 | 3.1 | 1.9 | 0.25 | 0.11 | 0.05 | 0.07 | 0.06 | 0.1 | 0.08 | |||
| 3.75 | 0.04 | 0.92 | 2 | 0.44 | 0.07 | 0.03 | 0.02 | 0.04 | 0.05 | 0.07 | ||||
| 4.25 | 0.01 | 0.15 | 1.2 | 0.72 | 0.06 | 0.02 | 0.01 | 0.03 | 0.04 | 0.04 | ||||
| 4.75 | 0.04 | 0.46 | 0.7 | 0.07 | 0.01 | 0.01 | 0.01 | 0.02 | 0.02 | |||||
| 5.25 | 0.01 | 0.11 | 0.47 | 0.08 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | |||||
| 5.75 | 0.01 | 0.04 | 0.15 | 0.12 | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 | |||||
| 6.25 | 0.02 | 0.03 | 0.09 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | ||||||
| 6.75 | 0.01 | 0.02 | 0.03 | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 | ||||||
| 7.25 | 0.01 | 0.02 | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | ||||||
| 7.75 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | |||||||||
| Hst/m | H/m | EI/Nm2 | Spring Stiffness/N/m |
|---|---|---|---|
| 0.5 | 10.6 | 7.6 × 108 | 1.36 × 107 |
| Random Variables | Distribution | Parameters | |
|---|---|---|---|
| Significant wave height | Weibull | = 1.837 | = 2.225 |
| Wave period | Lognormal | = | = |
| Working Condition | Drilling | Well Completion | Workover |
|---|---|---|---|
| Parameters | −1.906 | −1.514 | −1.565 |
| Parameters | 0.036 | 0.036 | 0.036 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Chang, Y.; Shi, J.; Liu, X.; Chen, G.; Zhang, N.; Guan, Q.; Dai, Y. Probability Prediction Approach of Fatigue Failure for the Subsea Wellhead Using Bayesian Regularization Artificial Neural Network. J. Mar. Sci. Eng. 2022, 10, 1627. https://doi.org/10.3390/jmse10111627
Li J, Chang Y, Shi J, Liu X, Chen G, Zhang N, Guan Q, Dai Y. Probability Prediction Approach of Fatigue Failure for the Subsea Wellhead Using Bayesian Regularization Artificial Neural Network. Journal of Marine Science and Engineering. 2022; 10(11):1627. https://doi.org/10.3390/jmse10111627
Chicago/Turabian StyleLi, Jiayi, Yuanjiang Chang, Jihao Shi, Xiuquan Liu, Guoming Chen, Nan Zhang, Qingtao Guan, and Yongguo Dai. 2022. "Probability Prediction Approach of Fatigue Failure for the Subsea Wellhead Using Bayesian Regularization Artificial Neural Network" Journal of Marine Science and Engineering 10, no. 11: 1627. https://doi.org/10.3390/jmse10111627
APA StyleLi, J., Chang, Y., Shi, J., Liu, X., Chen, G., Zhang, N., Guan, Q., & Dai, Y. (2022). Probability Prediction Approach of Fatigue Failure for the Subsea Wellhead Using Bayesian Regularization Artificial Neural Network. Journal of Marine Science and Engineering, 10(11), 1627. https://doi.org/10.3390/jmse10111627






